Replacement of Cobalt in Lithium-Rich Layered Oxides by n-Doping: A DFT Study
Abstract
:Featured Application
Abstract
1. Introduction
2. Methods
3. Results
3.1. Crystal Structures of Cobalt Doped LRLO
| Supercells | ||||
|---|---|---|---|---|
| LNMC12 | LNMC08 | LNMC04 | LNM | |
| a (Å) | 2.893 | 2.902 (2.874) | 2.907 | 2.907 (2.893) |
| c (Å) | 14.430 | 14.477 (14.28) | 14.500 | 14.498 (14.292) |
| V (Å3/f.u.) | 34.87 | 35.21 (34.24) | 35.38 | 35.36 (34.72) |
| α = β (°) | 90 | 90 | 90 | 90 |
| γ (°) | 120 | 120 | 120 | 120 |
| a/c | 0.200 | 0.200 | 0.200 | 0.200 |
3.2. Electronic Structure of the LRLOs
- Co sites: 0.00 μB, for LNMC12, LNMC08, and LNMC04;
- Ni sites of 1.649 μB, 1.609 μB, 1.521 μB, 1.489 μB for LNMC12, LNMC08, LNMC04, and LNM respectively;
- Mn sites of 3.199 μB, 3.216 μB, 3.236 μB, 3.239 μB for LNMC12, LNMC08, LNMC04, and LNM respectively.
3.3. Phase Stability of LRLO
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Whittingham, M.S. Introduction: Batteries. Chem. Rev. 2014, 114, 11413. [Google Scholar] [CrossRef] [PubMed]
- Burke, M.J.; Stephens, J. Political power and renewable energy futures: A critical review. Energy Res. Soc. Sci. 2018, 35, 78–93. [Google Scholar] [CrossRef]
- Budde-Meiwes, H.; Drillkens, J.; Lunz, B.; Muennix, J.; Rothgang, S.; Kowal, J.; Sauer, D.U. A review of current automotive battery technology and future prospects. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2013, 227, 761–776. [Google Scholar] [CrossRef]
- Hossain, E.; Faruque, H.; Sunny, S.H.; Mohammad, N.; Nawar, N. A Comprehensive Review on Energy Storage Systems: Types, Comparison, Current Scenario, Applications, Barriers, and Potential Solutions, Policies, and Future Prospects. Energies 2020, 13, 3651. [Google Scholar] [CrossRef]
- Yang, J.; Kim, H.; Ceder, G. Insights into Layered Oxide Cathodes for Rechargeable Batteries. Molecules 2021, 26, 3173. [Google Scholar] [CrossRef] [PubMed]
- Hao, G.; Lai, Q.; Zhang, H. Nanostructured Mn-based oxides as high-performance cathodes for next generation Li-ion batteries. J. Energy Chem. 2020, 59, 547–571. [Google Scholar] [CrossRef]
- Li, Y.; Li, Z.; Chen, C.; Yang, K.; Cao, B.; Xu, S.; Yang, N.; Zhao, W.; Chen, H.; Zhang, M.; et al. Recent progress in Li and Mn rich layered oxide cathodes for Li-ion batteries. J. Energy Chem. 2021, 61, 368–385. [Google Scholar] [CrossRef]
- Xiao, B.; Omenya, F.; Reed, D.; Li, X. A glance of the layered transition metal oxide cathodes in sodium and lithium-ion batteries: Difference and similarities. Nanotechnology 2021, 32, 422501. [Google Scholar] [CrossRef]
- Kasnatscheew, J.; Evertz, M.; Kloepsch, R.; Streipert, B.; Wagner, R.; Laskovic, I.C.; Winter, M. Learning from Electrochemical Data: Simple Evaluation and Classification of LiMO2 -type-based Positive Electrodes for Li-Ion Batteries. Energy Technol. 2017, 5, 1670–1679. [Google Scholar] [CrossRef]
- Foix, D.; Sathiya, M.; McCalla, E.; Tarascon, J.-M.; Gonbeau, D. X-ray Photoemission Spectroscopy Study of Cationic and Anionic Redox Processes in High-Capacity Li-Ion Battery Layered-Oxide Electrodes. J. Phys. Chem. C 2016, 120, 862–874. [Google Scholar] [CrossRef] [Green Version]
- Saubanère, M.; McCalla, E.; Tarascon, J.-M.; Doublet, M.-L. The intriguing question of anionic redox in high-energy density cathodes for Li-ion batteries. Energy Environ. Sci. 2016, 9, 984–991. [Google Scholar] [CrossRef]
- Grimaud, A.; Hong, W.T.; Shao-Horn, Y.; Tarascon, J.-M. Anionic redox processes for electrochemical devices. Nat. Mater. 2016, 15, 121–126. [Google Scholar] [CrossRef] [PubMed]
- Delmas, C.; Fouassier, C.; Hagenmuller, P. Structural classification and properties of the layered oxides. Phys. B+C 1980, 99, 81–85. [Google Scholar] [CrossRef]
- Yu, H.; Kim, H.; Wang, Y.; He, P.; Asakura, D.; Nakamura, Y.; Zhou, H. High-energy ‘composite’ layered manganese-rich cathode materials via controlling Li2MnO3 phase activation for lithium-ion batteries. Phys. Chem. Chem. Phys. 2012, 14, 6584–6595. [Google Scholar] [CrossRef] [PubMed]
- Yu, Z.; Shang, S.-L.; Gordin, M.L.; Mousharraf, A.; Liu, Z.-K.; Wang, D. Ti-substituted Li[Li0.26Mn0.6−xTixNi0.07Co0.07]O2 layered cathode material with improved structural stability and suppressed voltage fading. J. Mater. Chem. A 2015, 3, 17376–17384. [Google Scholar] [CrossRef]
- Bareño, J.; Balasubramanian, M.; Kang, S.H.; Wen, J.G.; Lei, C.H.; Pol, S.V.; Petrov, I.; Abraham, D.P. Long-Range and Local Structure in the Layered Oxide Li1.2Co0.4Mn0.4O2. Chem. Mater. 2011, 23, 2039–2050. [Google Scholar] [CrossRef]
- Yu, H.; Zhou, H. High-Energy Cathode Materials (Li2MnO3–LiMO2) for Lithium-Ion Batteries. J. Phys. Chem. Lett. 2013, 4, 1268–1280. [Google Scholar] [CrossRef]
- Rozier, P.; Tarascon, J.M. Review—Li-Rich Layered Oxide Cathodes for Next-Generation Li-Ion Batteries: Chances and Challenges. J. Electrochem. Soc. 2015, 162, A2490–A2499. [Google Scholar] [CrossRef]
- Thackeray, M.M.; Johnson, C.S.; Vaughey, J.T.; Li, N.; Hackney, S.A. Advances in manganese-oxide ‘composite’ electrodes for lithium-ion batteries. J. Mater. Chem. 2005, 15, 2257–2267. [Google Scholar] [CrossRef]
- Ren, Q.; Xie, H.; Wang, M.; Ding, X.; Cui, J.; Luo, D.; Liu, C.; Lin, Z. Deciphering the effects of hexagonal and monoclinic structure distribution on the properties of Li-rich layered oxides. Chem. Commun. 2021, 57, 3512–3515. [Google Scholar] [CrossRef]
- Jarvis, K.A.; Deng, Z.; Allard, L.F.; Manthiram, A.; Ferreira, P.J. Atomic Structure of a Lithium-Rich Layered Oxide Material for Lithium-Ion Batteries: Evidence of a Solid Solution. Chem. Mater. 2011, 23, 3614–3621. [Google Scholar] [CrossRef]
- Gu, M.; Genc, A.; Belharouak, I.; Wang, D.; Amine, K.; Thevuthasan, S.; Baer, D.R.; Zhang, J.-G.; Browning, N.D.; Liu, J.; et al. Nanoscale Phase Separation, Cation Ordering, and Surface Chemistry in Pristine Li1.2Ni0.2Mn0.6O2 for Li-Ion Batteries. Chem. Mater. 2013, 25, 2319–2326. [Google Scholar] [CrossRef]
- Kim, I.; Do, J.; Kim, H.; Jung, Y. Charge-transfer descriptor for the cycle performance of β-Li2MO3 cathodes: Role of oxygen dimers. J. Mater. Chem. A 2020, 8, 2663–2671. [Google Scholar] [CrossRef]
- Muhammad, S.; Kim, H.; Kim, Y.; Kim, D.; Song, J.H.; Yoon, J.; Park, J.-H.; Ahn, S.-J.; Kang, S.-H.; Thackeray, M.M.; et al. Evidence of reversible oxygen participation in anomalously high capacity Li- and Mn-rich cathodes for Li-ion batteries. Nano Energy 2016, 21, 172–184. [Google Scholar] [CrossRef] [Green Version]
- Strehle, B.; Kleiner, K.; Jung, R.; Chesneau, F.; Mendez, M.; Gasteiger, H.; Piana, M. The Role of Oxygen Release from Li- and Mn-Rich Layered Oxides during the First Cycles Investigated by On-Line Electrochemical Mass Spectrometry. J. Electrochem. Soc. 2017, 164, A400–A406. [Google Scholar] [CrossRef]
- Mohanty, D.; Kalnaus, S.; Meisner, R.A.; Rhodes, K.J.; Li, J.; Payzant, E.; Wood, D.; Daniel, C. Structural transformation of a lithium-rich Li1.2Co0.1Mn0.55Ni0.15O2 cathode during high voltage cycling resolved by in situ X-ray diffraction. J. Power Sources 2013, 229, 239–248. [Google Scholar] [CrossRef]
- Gu, M.; Belharouak, I.; Zheng, J.; Wu, H.; Xiao, J.; Genc, A.; Amine, K.; Thevuthasan, S.; Baer, D.R.; Zhang, J.-G.; et al. Formation of the Spinel Phase in the Layered Composite Cathode Used in Li-Ion Batteries. ACS Nano 2013, 7, 760–767. [Google Scholar] [CrossRef]
- Sathiya, M.; Abakumov, A.M.; Foix, D.; Rousse, G.; Ramesha, K.; Saubanere, M.; Doublet, M.-L.; Vezin, H.; Laisa, C.P.; Prakash, A.S.; et al. Origin of voltage decay in high-capacity layered oxide electrodes. Nat. Mater. 2014, 14, 230–238. [Google Scholar] [CrossRef]
- Croy, J.R.; Gallagher, K.G.; Balasubramanian, M.; Long, B.R.; Thackeray, M.M. Quantifying Hysteresis and Voltage Fade in xLi2MnO3●(1-x)LiMn0.5Ni0.5O2Electrodes as a Function of Li2MnO3Content. J. Electrochem. Soc. 2013, 161, A318–A325. [Google Scholar] [CrossRef]
- Nayak, P.K.; Grinblat, J.; Levi, M.; Levi, E.; Kim, S.; Choi, J.W.; Aurbach, D. Al Doping for Mitigating the Capacity Fading and Voltage Decay of Layered Li and Mn-Rich Cathodes for Li-Ion Batteries. Adv. Energy Mater. 2016, 6, 1502398. [Google Scholar] [CrossRef]
- Dahiya, P.P.; Ghanty, C.; Sahoo, K.; Basu, S.; Majumder, S.B. Suppression of Voltage Decay and Improvement in Electrochemical Performance by Zirconium Doping in Li-Rich Cathode Materials for Li-Ion Batteries. J. Electrochem. Soc. 2018, 165, A3114–A3124. [Google Scholar] [CrossRef]
- Kam, K.C.; Mehta, A.; Heron, J.T.; Doeff, M.M. Electrochemical and Physical Properties of Ti-Substituted Layered Nickel Manganese Cobalt Oxide (NMC) Cathode Materials. J. Electrochem. Soc. 2012, 159, A1383–A1392. [Google Scholar] [CrossRef]
- Liu, Y.; Ning, D.; Zheng, L.; Zhang, Q.; Gu, L.; Gao, R.; Zhang, J.; Franz, A.; Schumacher, G.; Liu, X. Improving the electrochemical performances of Li-rich Li1.20Ni0.13Co0.13Mn0.54O2 through a cooperative doping of Na+ and PO43− with Na3PO4. J. Power Sources 2018, 375, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Commission Staff Working Document. Report on Raw Materials for Battery Applications; JRC118410; Publications Office of the European Union: Luxembourg, 2020. [Google Scholar] [CrossRef]
- Committee of the Regions and the European Investment Bank. On the Implementation of the Strategic Action Plan on Batteries: Building a Strategic Battery Value Chain in Europe; European Union, Report number COM(2019) 176; Publications Office of the European Union: Luxembourg; Available online: https://ec.europa.eu/transparency/documents-register/detail?ref=COM(2019)176&lang=en (accessed on 1 November 2021).
- Wang, Z.; Lin, X.; Zhang, J.; Wang, D.; Ding, C.; Zhu, Y.; Gao, P.; Huang, X.; Wen, G. Spherical layered Li-rich cathode material: Unraveling the role of oxygen vacancies on improving lithium ion conductivity. J. Power Sources 2020, 462, 228171. [Google Scholar] [CrossRef]
- Lo, W.-T.; Yu, C.; Leggesse, E.G.; Nachimuthu, S.; Jiang, J.-C. Understanding the Role of Dopant Metal Atoms on the Structural and Electronic Properties of Lithium-Rich Li1.2Ni0.2Mn0.6O2 Cathode Material for Lithium-Ion Batteries. J. Phys. Chem. Lett. 2019, 10, 4842–4850. [Google Scholar] [CrossRef]
- Wimmer, E.; Christensen, M.; Eyert, V.; Wolf, W.; Reith, D.; Rozanska, X.; Freeman, C.; Saxe, P. Computational Materials Engineering: Recent Applications of VASP in the MedeA® Software Environment. J. Korean Ceram. Soc. 2016, 53, 263–272. [Google Scholar] [CrossRef] [Green Version]
- Hafner, J.; Kresse, G. The Vienna AB-Initio Simulation Program VASP: An Efficient and Versatile Tool for Studying the Structural, Dynamic, and Electronic Properties of Materials. In Properties of Complex Inorganic Solids; Springer: Boston, MA, USA, 1997; pp. 69–82. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [Green Version]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef] [Green Version]
- Pavone, M.; Ritzmann, A.; Carter, E.A. Quantum-mechanics-based design principles for solid oxide fuel cell cathode materials. Energy Environ. Sci. 2011, 4, 4933–4937. [Google Scholar] [CrossRef]
- Dudarev, S.L.; Botton, G.A.; Savrasov, S.Y.; Humphreys, C.J.; Sutton, A.P. Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA+U study. Phys. Rev. B 1998, 57, 1505–1509. [Google Scholar] [CrossRef]
- Muñoz-García, A.B.; Sannino, F.; Vitiello, G.; Pirozzi, D.; Minieri, L.; Aronne, A.; Pernice, P.; Pavone, M.; D’Errico, G. Origin and Electronic Features of Reactive Oxygen Species at Hybrid Zirconia-Acetylacetonate Interfaces. ACS Appl. Mater. Interfaces 2015, 7, 21662–21667. [Google Scholar] [CrossRef] [PubMed]
- Muñoz-García, A.B.; Tuccillo, M.; Pavone, M. Computational design of cobalt-free mixed proton–electron conductors for solid oxide electrochemical cells. J. Mater. Chem. A 2017, 5, 11825–11833. [Google Scholar] [CrossRef]
- Tuccillo, M.; Palumbo, O.; Pavone, M.; Muñoz-García, A.B.; Paolone, A.; Brutti, S. Analysis of the Phase Stability of LiMO2 Layered Oxides (M = Co, Mn, Ni). Crystals 2020, 10, 526. [Google Scholar] [CrossRef]
- Bader, R.F.W. Atoms in Molecules: A Quantum Theory; Oxford University Press: Oxford, UK, 1990; 438p. [Google Scholar]
- Sanville, E.; Kenny, S.D.; Smith, R.; Henkelman, G. Improved grid-based algorithm for Bader charge allocation. J. Comput. Chem. 2007, 28, 899–908. [Google Scholar] [CrossRef] [PubMed]
- Tang, W.; Sanville, E.; Henkelman, G. A grid-based Bader analysis algorithm without lattice bias. J. Phys. Condens. Matter 2009, 21, 084204. [Google Scholar] [CrossRef] [PubMed]
- Zunger, A.; Wei, S.-H.; Ferreira, L.G.; Bernard, J.E. Special quasirandom structures. Phys. Rev. Lett. 1990, 65, 353. [Google Scholar] [CrossRef] [Green Version]
- Massaro, A.; Muñoz-García, A.B.; Prosini, P.P.; Gerbaldi, C.; Pavone, M. Unveiling Oxygen Redox Activity in P2-Type NaxNi0.25Mn0.68O2 High-Energy Cathode for Na-Ion Batteries. ACS Energy Lett. 2021, 6, 2470–2480. [Google Scholar] [CrossRef]
- Mayer, J.E.; Montroll, E. Molecular Distribution. J. Chem. Phys. 1941, 9, 2–16. [Google Scholar] [CrossRef]
- Van de Walle, A.; Asta, M.; Ceder, G. The alloy theoretic automated toolkit: A user guide. Calphad 2002, 26, 539–553. [Google Scholar] [CrossRef] [Green Version]
- Nayak, P.K.; Grinblat, J.; Levi, M.; Aurbach, D. Electrochemical and structural characterization of carbon coated Li1.2Mn0.56Ni0.16Co0.08O2 and Li1.2Mn0.6Ni0.2O2 as cathode materials for Li-ion batteries. Electrochim. Acta 2014, 137, 546–556. [Google Scholar] [CrossRef]
- Wu, F.; Kim, G.; Kuenzel, M.; Zhang, H.; Asenbauer, J.; Geiger, D.; Kaiser, U.; Passerini, S. Elucidating the Effect of Iron Doping on the Electrochemical Performance of Cobalt-Free Lithium-Rich Layered Cathode Materials. Adv. Energy Mater. 2019, 9, 1902445. [Google Scholar] [CrossRef]
- Simonelli, L.; Sorrentino, A.; Marini, C.; Ramanan, N.; Heinis, D.; Olszewski, W.; Mullaliu, A.; Birrozzi, A.; Laszczynski, N.; Giorgetti, M.; et al. Role of Manganese in Lithium- and Manganese-Rich Layered Oxides Cathodes. J. Phys. Chem. Lett. 2019, 10, 3359–3368. [Google Scholar] [CrossRef] [PubMed]
- Jin, Y.; Xu, Y.; Sun, X.; Xiong, L.; Mao, S. Electrochemically active MnO2 coated Li1.2Ni0.18Co0.04Mn0.58O2 cathode with highly improved initial coulombic efficiency. Appl. Surf. Sci. 2016, 384, 125–134. [Google Scholar] [CrossRef]
- Wu, F.; Kim, G.; Diemant, T.; Kuenzel, M.; Schür, A.R.; Gao, X.; Qin, B.; Alwast, D.; Jusys, Z.; Behm, R.J.; et al. Reducing Capacity and Voltage Decay of Co-Free Li 1.2 Ni 0.2 Mn 0.6 O2 as Positive Electrode Material for Lithium Batteries Employing an Ionic Liquid-Based Electrolyte. Adv. Energy Mater. 2020, 10, 2001830. [Google Scholar] [CrossRef]
- Shannon, R.D.; Prewitt, C.T. Effective ionic radii in oxides and fluorides. Acta Cryst. 1969, 25, 925–946. [Google Scholar] [CrossRef]
- Kugel, K.; I Khomskiĭ, D. The Jahn-Teller effect and magnetism: Transition metal compounds. Sov. Phys. Uspekhi 1982, 25, 231. [Google Scholar] [CrossRef]
- Voronina, N.; Sun, Y.-K.; Myung, S.-T. Co-Free Layered Cathode Materials for High Energy Density Lithium-Ion Batteries. ACS Energy Lett. 2020, 5, 1814–1824. [Google Scholar] [CrossRef]
- Nakamura, T.; Gao, H.; Ohta, K.; Kimura, Y.; Tamenori, Y.; Nitta, K.; Ina, T.; Oishi, M.; Amezawa, K. Defect chemical studies on oxygen release from the Li-rich cathode material Li1.2Mn0.6Ni0.2O2−δ. J. Mater. Chem. A 2019, 7, 5009–5019. [Google Scholar] [CrossRef]
- Longuet-Higgins, H.C.; Opik, U.; Pryce, M.H.L.; Sack, R.A. Studies of the Jahn-Teller effect. II. The dynamical problem. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1958, 244, 1–16. [Google Scholar] [CrossRef]
- Tan, S.; Zhang, Z.; Li, Y.; Li, Y.; Zheng, J.; Zhou, Z.; Yang, Y. Tris (hexafluoro-iso-propyl) phosphate as an SEI-Forming Additive on Improving the Electrochemical Performance of the Li[Li0.2Mn0.56Ni0.16Co0.08]O2Cathode Material. J. Electrochem. Soc. 2012, 160, A285. [Google Scholar] [CrossRef]
- Sun, Y.-K. Structural degradation mechanism of oxysulfide spinel LiAl 0.24Mn1.76O3.98S0.02 cathode materials on high temperature cycling. Electrochem. Commun. 2001, 3, 199–202. [Google Scholar] [CrossRef]
- Mohanty, D.; Huq, A.; Payzant, E.A.; Sefat, A.S.; Li, J.; Abraham, D.P.; Wood, D.; Daniel, C. Neutron Diffraction and Magnetic Susceptibility Studies on a High-Voltage Li1.2Mn0.55Ni0.15Co0.10O2 Lithium Ion Battery Cathode: Insight into the Crystal Structure. Chem. Mater. 2013, 25, 4064–4070. [Google Scholar] [CrossRef]
- Celeste, A.; Tuccillo, M.; Santoni, A.; Reale, P.; Brutti, S.; Silvestri, L. Exploring a Co-Free, Li-Rich Layered Oxide with Low Content of Nickel as a Positive Electrode for Li-Ion Battery. ACS Appl. Energy Mater. 2021, 4, 11290–11297. [Google Scholar] [CrossRef]

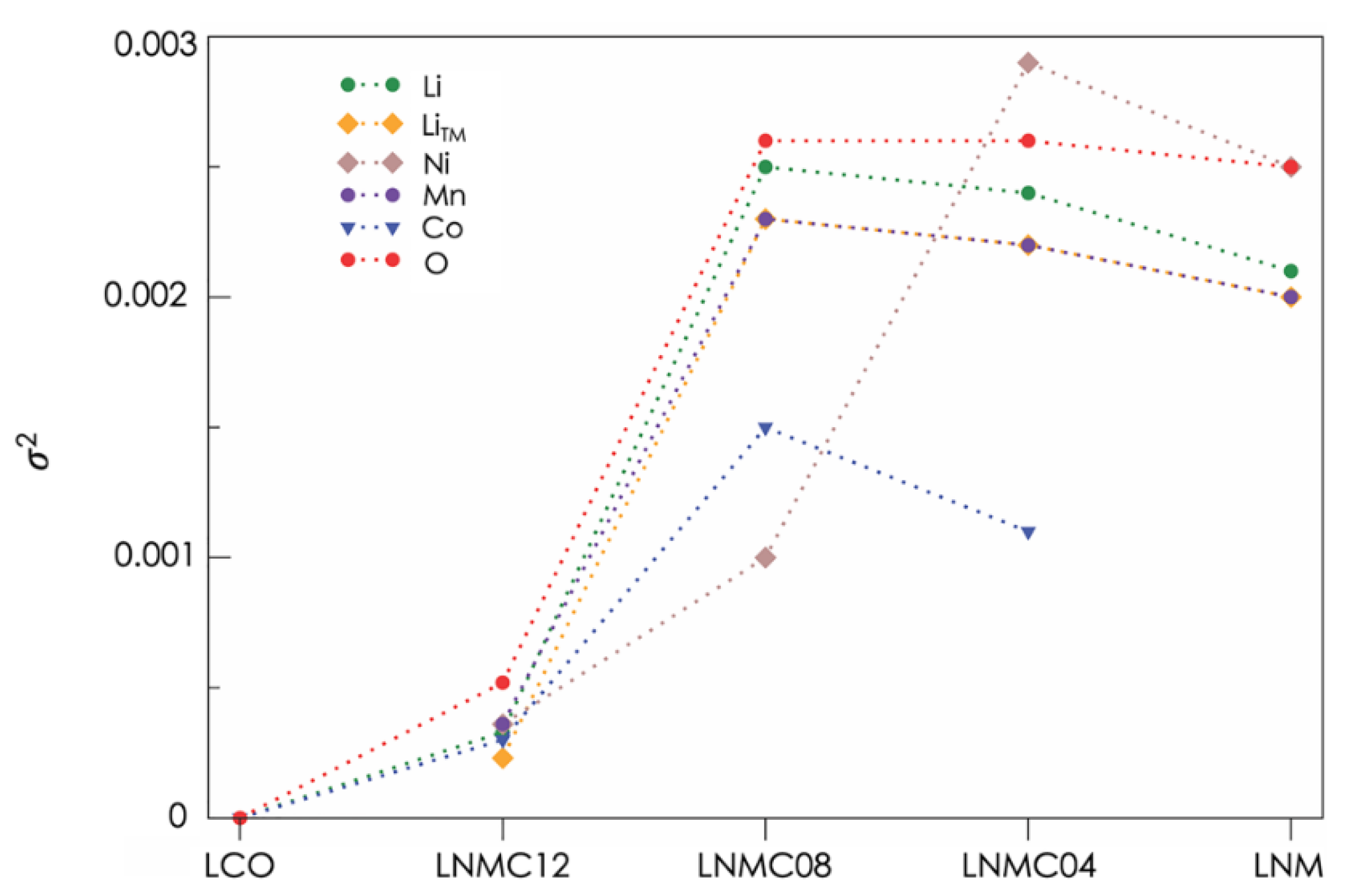
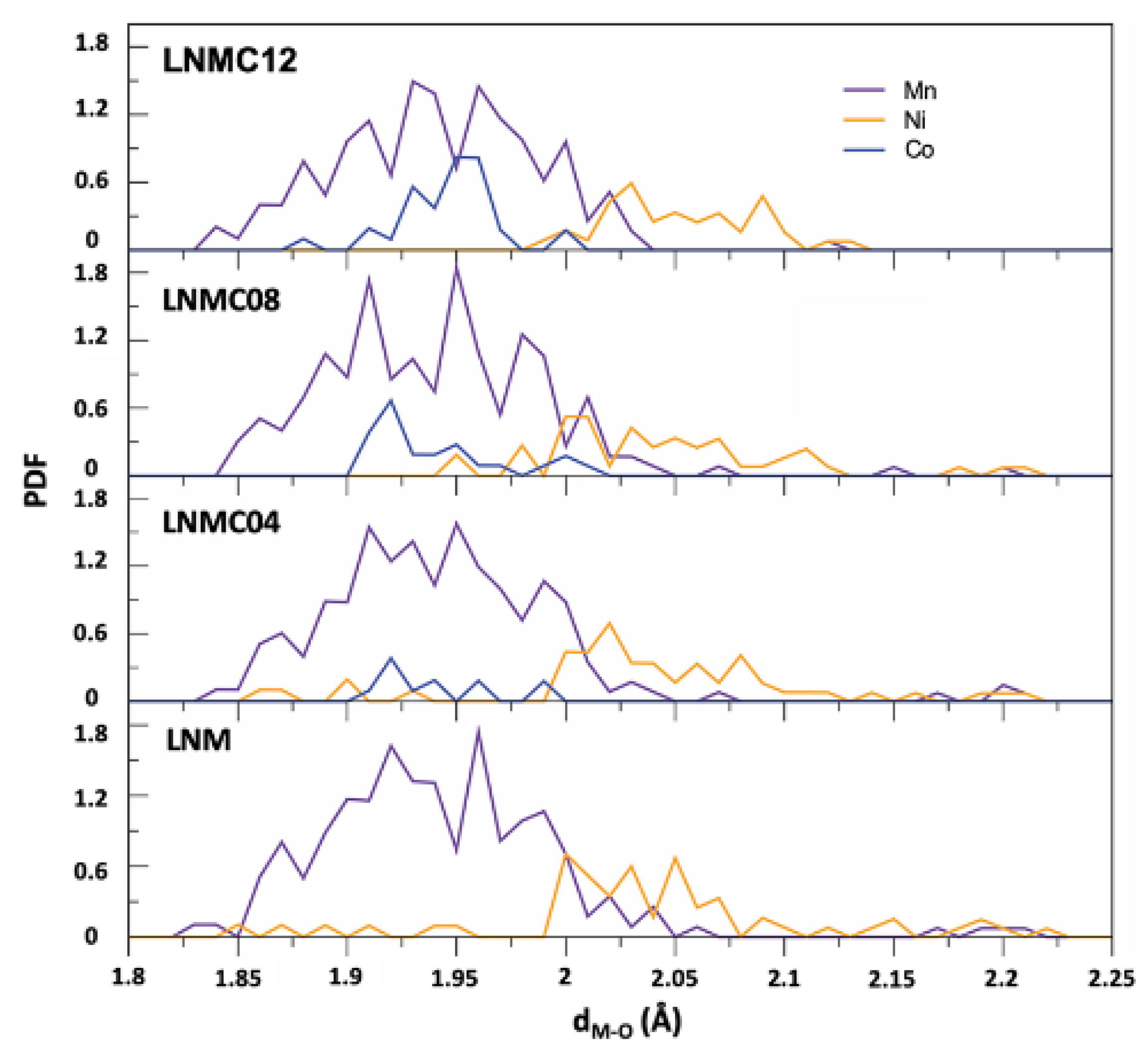
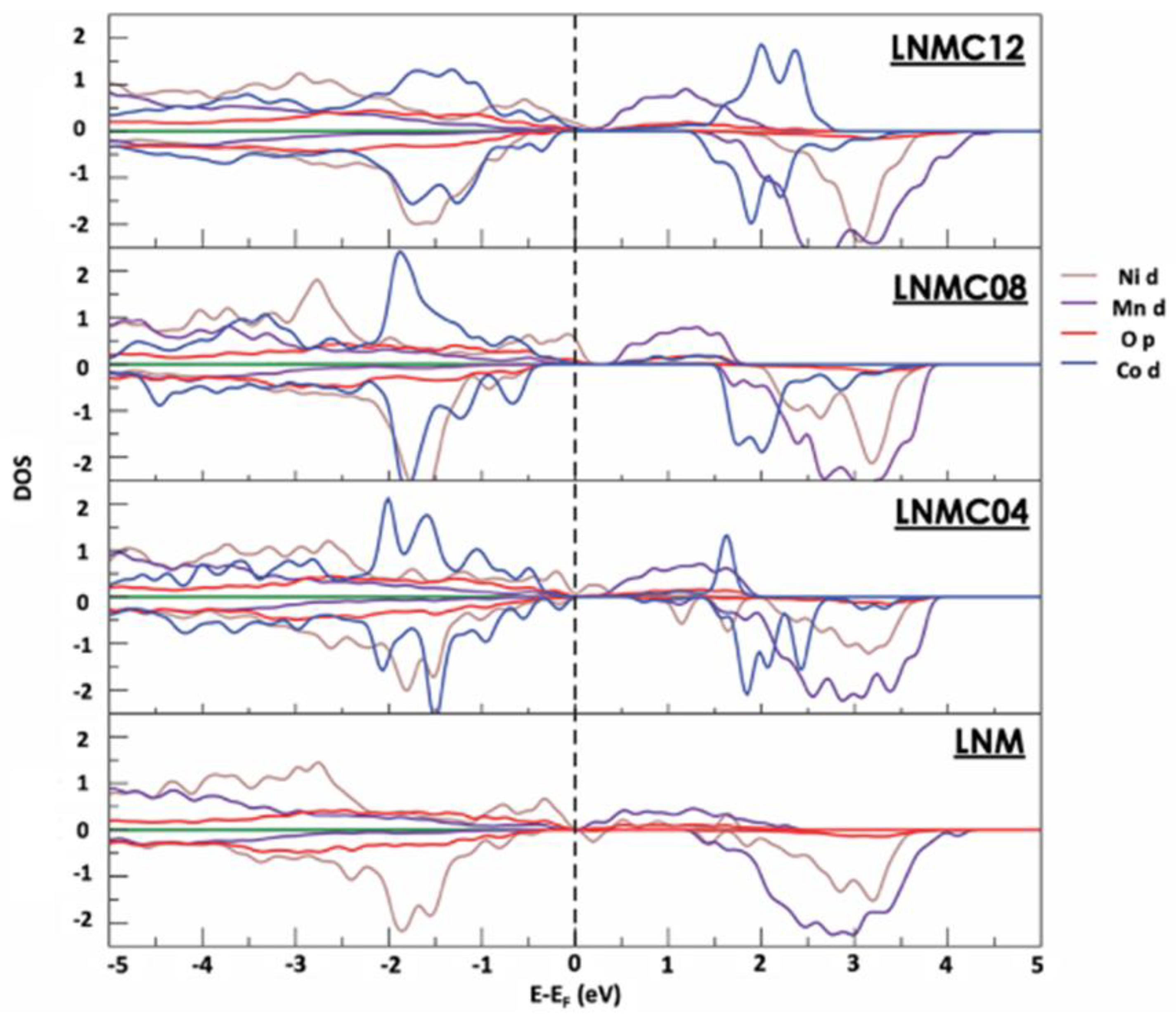
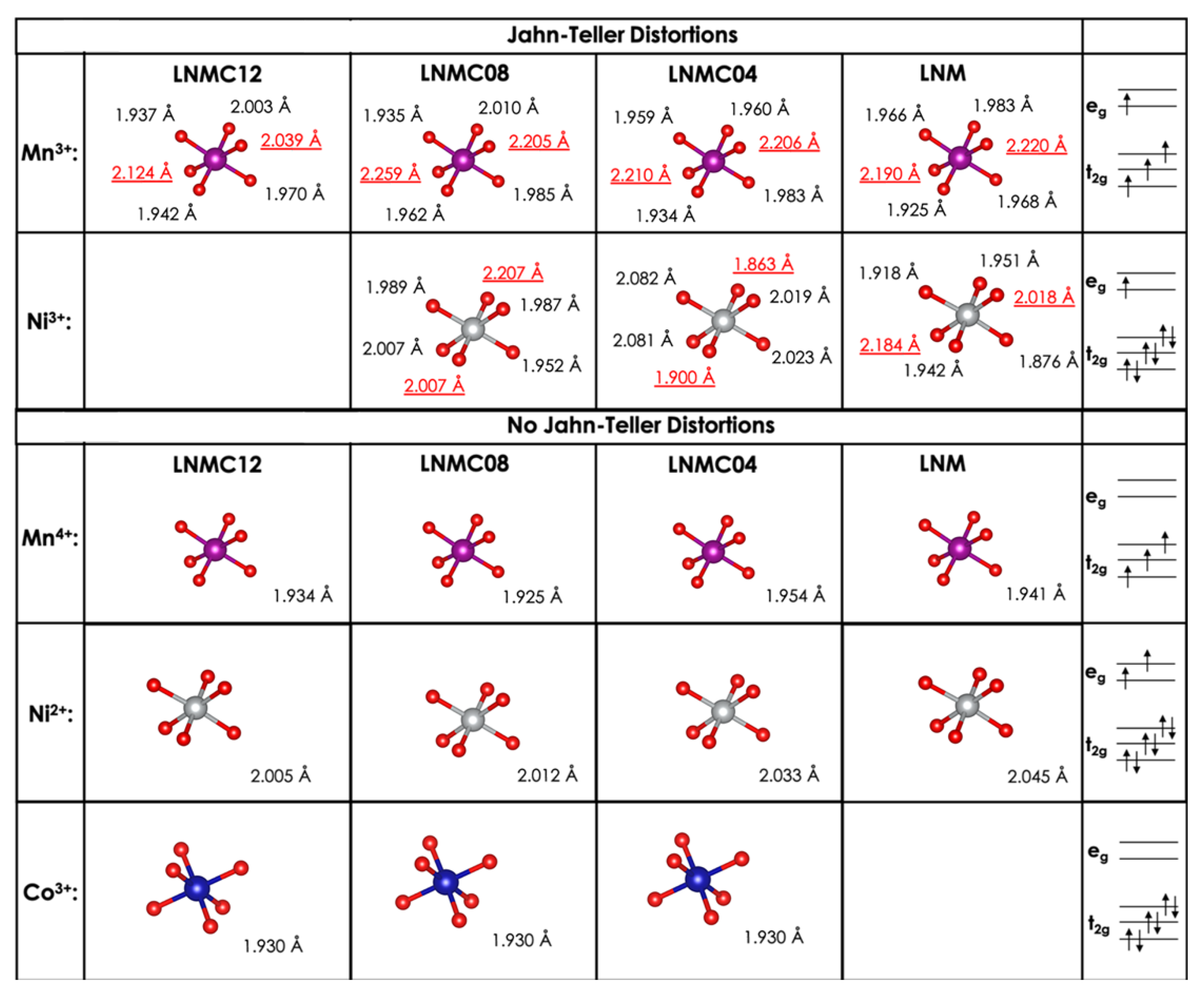

| Phases | ||||
|---|---|---|---|---|
| LNMC12 | LNMC08 | LNMC04 | LNM | |
| ΔformH°0K/eV at−1 | −0.040 | −0.044 | −0.054 | −0.079 |
| ΔformS°0K /eV at−1 K−1 | 1.02·10−4 | 9.9·10−5 | 9.3·10−5 | 8.2·10−5 |
| ΔformG°298K/eV at−1 | −0.070 | −0.073 | −0.082 | −0.103 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tuccillo, M.; Mei, L.; Palumbo, O.; Muñoz-García, A.B.; Pavone, M.; Paolone, A.; Brutti, S. Replacement of Cobalt in Lithium-Rich Layered Oxides by n-Doping: A DFT Study. Appl. Sci. 2021, 11, 10545. https://doi.org/10.3390/app112210545
Tuccillo M, Mei L, Palumbo O, Muñoz-García AB, Pavone M, Paolone A, Brutti S. Replacement of Cobalt in Lithium-Rich Layered Oxides by n-Doping: A DFT Study. Applied Sciences. 2021; 11(22):10545. https://doi.org/10.3390/app112210545
Chicago/Turabian StyleTuccillo, Mariarosaria, Lorenzo Mei, Oriele Palumbo, Ana Belén Muñoz-García, Michele Pavone, Annalisa Paolone, and Sergio Brutti. 2021. "Replacement of Cobalt in Lithium-Rich Layered Oxides by n-Doping: A DFT Study" Applied Sciences 11, no. 22: 10545. https://doi.org/10.3390/app112210545
APA StyleTuccillo, M., Mei, L., Palumbo, O., Muñoz-García, A. B., Pavone, M., Paolone, A., & Brutti, S. (2021). Replacement of Cobalt in Lithium-Rich Layered Oxides by n-Doping: A DFT Study. Applied Sciences, 11(22), 10545. https://doi.org/10.3390/app112210545










