Abstract
Cloud computing systems are rapidly evolving toward multicloud architectures supported on heterogeneous hardware. Cloud service providers are widely offering different types of storage infrastructures and multi-NUMA architecture servers. Existing cloud resource allocation solutions do not comprehensively consider this heterogeneous infrastructure. In this study, we present a novel approach comprised of a hierarchical framework based on genetic programming to solve problems related to data placement and virtual machine allocation for analytics applications running on heterogeneous hardware with a variety of storage types and nonuniform memory access. Our approach optimizes data placement using the Hadoop File System on heterogeneous storage devices on multicloud systems. It guarantees the efficient allocation of virtual machines on physical machines with multiple NUMA (nonuniform memory access) domains by minimizing contention between workloads. We prove that our solutions for data placement and virtual machine allocation outperform other state-of-the-art approaches.
1. Introduction
We live in an ever-growing digital world with an increasing reliance on data. Enormous volumes of data are now being generated, and it is expected that the amount of global data accumulated will exponentially increase to 175 Zettabytes (ZB) by 2025 [1]. Due to the potential benefits of big data to business, companies and information technology leaders now need to obtain value from all kinds of data [2]. The use of cloud computing (CC) systems is a suitable choice for dealing with massive data by providing sufficient analytic capabilities and processing power necessary to extract the value from these data, which must be stored, processed, and analyzed efficiently [3].
Multicloud architectures have emerged as solutions to improve scalability and availability, and to reduce vendor lock-in risks. These systems are also increasingly incorporating different types of storage and multi-NUMA servers. Recently, few efforts have tackled the problems of data placement separately on heterogeneous storage infrastructure [4] and virtual machine allocation on servers with multiple NUMA domains [5], and intelligent cloud resource allocation [6,7]. However, these approaches exclude some cloud storage types and shared memory patterns of applications, which are meaningful considerations for efficient resource allocation. There is a need for comprehensive approaches to take advantage of this increasingly available infrastructure.
Apache Hadoop is an overall cloud framework for running analytics applications on commodity clusters [8], and the Hadoop Distributed File System (HDFS) allows for the storage and processing of a significant amount of data. This file system can also work with heterogeneous storage systems and can take advantage of their benefits, although data placement algorithms are usually unaware of this. Additionally, most cloud environments offer NUMA physical machines, which can be exploited to improve the performance of an application. Resource allocation algorithms can take advantage of the NUMA infrastructure by mapping computation close to memory while avoiding overheads related to shared memory and data movement. In this work, we propose a hierarchical framework comprised of a set of genetic programming algorithms to solve data placement problems on heterogeneous storage and virtual machine allocation on multi-NUMA servers present in current cloud systems.
In Section 2, we provide key background information on cloud infrastructure for data storage and processing and a brief introduction to virtual machine allocation on NUMA nodes. The contributions of this study are then described in detail (Section 3 and Section 4), as follows:
- A resource allocation hierarchical framework (Section 3) based on: (i) an improved version of our data placement algorithm previously presented in [9], which can now handle multicloud storage, and (ii) an algorithm for efficient virtual machine allocation that can handle NUMA domains and the shared memory patterns of applications.
- A formulation of the problem of virtual machine placement on NUMA nodes as a genetic programming problem, and an implementation of an algorithm based on this formulation that optimizes virtual machine allocation, with the aim of improving the performance of applications running on virtual machines allocated to NUMA nodes (Section 3.1).
- A comparison of our genetic programming algorithms against alternative resource allocation algorithms by applying them to a big data cluster and NUMA nodes, and running a set of benchmarks that represent scientific applications (Section 4).
2. Background
In this section, we describe the cloud infrastructure for data storage and processing considered for our approach. We also describe several optimization methods that have been used to solve the problem of resource allocation in CC environments.
2.1. Cloud Infrastructure for Data Storage and Processing
The use of a distributed infrastructure in the cloud to support ample data storage and processing is widespread. One of the most commonly used file systems is HDFS. Similarly, most cloud providers provide NUMA nodes that can be used to optimize the allocation of virtual machines. Our approach takes advantage of this computational infrastructure and is described below.
2.1.1. Hadoop Framework
Apache Hadoop is a framework written in Java that can be used for the distributed processing of large datasets across clusters of computers using simple programming models [8]. Hadoop distributes data via nodes and parallelizes analysis tasks so that each node in the cluster processes part of the data, which speeds up the process. Hadoop allows working with the analysis of structured, semistructured, and unstructured datasets.
Hadoop Distributed File System
HDFS allows for the storage of very large files and runs on clusters of commodity hardware [10]. Although Hadoop provides its own file system, its use is not mandatory, and the option to use other file systems is offered. However, HDFS has features that make it unique and particularly appropriate for the storage of data for analysis. The number of data replicas used for storage and the size of the data block can be set. The use of replicas ensures high availability in the cluster, protects data against losses, and improves data locality by reducing data movement between nodes. The default block size in HDFS is 128 MB, which is large in comparison with the block sizes used by other systems [10]. Since HDFS is optimized for large archives, a large block size improves the performance of data transfers.
Hadoop Heterogeneous Storage
Hadoop Heterogeneous Storage has been integrated since version 2.3, and allows for the use of four different storage types: RAM_DISK, SSD, HDD, and ARCHIVE (an external storage resource). These storage types are controlled or used via storage policies that define where each file or folder is to be stored.
Hadoop offers six storage policies: Lazy_Persist, ALL_SSD, One_SSD, Hot (default), Warm, and Cold [11]. Each of these policies uses a specified type of storage or a mix of types. Although several of these policies use only one type of storage, none exclusively use RAM_DISK; we therefore created a new policy called ALL_RAM, which allows us to store files only in RAM_DISK [9].
2.2. Virtual Machine Allocation on NUMA Nodes
The number of cores per chip is constantly increasing, meaning that the memory bandwidth is becoming a performance bottleneck in centralized memory architectures such as uniform memory access (UMA). The processing speeds of CPUs are becoming faster than those of memory, and memory access, especially when it is remote, is typically inefficient. NUMA architecture helps to solve this problem, as it allows each processor to access the memory used by other processors [12]. On-chip interconnections allow processors to access each other’s memory using their memory controller, which reduces memory contention and increases the memory bandwidth per core [12]. The efficient allocation of NUMA domains and shared memory can impact the performance of virtual machines, and these should therefore be considered when designing an efficient virtual machine allocation scheme.
2.3. Optimization Methods for Cloud Resource Allocation
In the following sections, we describe the optimization schemes used by several algorithms used to solve the problem of resource allocation in CC environments.
2.3.1. Simplex
In this method, the problem usually has some constraints that can be represented by a region called the feasible region. The point that can take on an objective function’s maximum or minimum value is generally located in this region.
The simplex method is based on the following assumption: if an objective function Z does not have a maximum/minimum value at a vertex A, there is then an edge from A to another vertex that improves the value of the objective function.
This algorithm applies an iterative process that improves on the solution to the objective function in each iteration. The process finishes when this value stops changing, i.e., when the optimal solution has been found [13].
The process can start at any point, and the value of this point in terms of the objective function is evaluated. At each iteration, the algorithm will find another point that improves on the previous solution. A central feature of this method is that these points form the vertices of the region determined by the problem constraints. A search is performed by moving along the edges of this area, moving from the current vertex to an adjacent one that gives a better value of the objective function. Whenever there is a feasible region, it will be possible to find a solution, as the numbers of vertices and edges are finite [13].
This method only works when the constraints on the problem are inequalities of type “≤” (less than or equal to). The independent coefficients of the constraints must also be greater than or equal to zero. This method is used to solve linear problems, meaning that the constraints must be standardized so that they comply with these requirements before the simplex algorithm is applied. If restrictions of type “≥” (greater than or equal to) or “=” (equality) arise after this process, or if these cannot be changed, other methods must be applied to find a solution [13].
Although linear problems can be solved using the simplex algorithm with a graphical method, this approach is limited by the number of decision variables in the formulated problem, since it is not possible to show more than three dimensions graphically. In this method, each vertices is evaluated using the objective function to select the best solution.
2.3.2. Generalized Reduced Gradient
In the same way as simplex, the generalized reduced gradient (GRG) is a numerical method that can solve a linear problem, although there are several differences between the two methods. The first is that GRG can solve nonlinear problems. It is also an indirect method, as it uses derivatives to find the direction of the possible solution [14].
Numerical methods are typically iterative processes that involve the following operations:
- 1.
- Selection of a direction;
- 2.
- Movement in the selected direction;
- 3.
- Analysis of the convergence criteria.
If the convergence criteria are not met after Step 3, the algorithm returns to Step 1. Numerical methods can be classified into two types:
- Direct, in which the objective function determines Step 1;
- Indirect, in which the derivative of the objective function determines Step 1.
Step 1—Selection of a Direction
GRG is an indirect numerical method that uses the derivative of the objective function to select the direction of the search. This search aims to find the optimal value of the solution [14].
The gradient of the function indicates the maximum growth in the value of the solution. The maximum value is therefore the goal, and the direction of the gradient () should be selected. If the best value is a minimum, the correct direction will be opposite to the direction of the gradient () [15].
Step 2—Movement in the Selected Direction
After the direction of movement has been selected, the step length (also known as the sensibility factor) must be chosen. This factor may be constant or variable.
In this step, the algorithm looks for the next vertex that will give a better value for the objective function, i.e., we start from and go to .
If we are searching for a minimum, will be obtained as follows:
whereas if we are searching for a maximum, it will be obtained as follows:
Step 3—Analysis of the convergence criteria
This method needs to define a threshold value to determine if we have found a critical point or a solution.
When the value of has been obtained, it will be evaluated using the objective function .
We then need to evaluate the next operation, and if the result is less than the threshold value, we have obtained a critical point or a solution.
Other convergence criteria are met when the value of the gradient is very small; if is less than the threshold, we have obtained a critical point [15].
In the case where none of the convergence criteria are fulfilled, we return to Step 1 and look for another possible critical point.
2.3.3. Genetic Algorithm
One of the most popular evolutionary algorithms is the GA. This type of algorithm represents the solution to the problem in the form of a bit string. GAs are well known due to their effectiveness and simplicity of implementation. Another reason for the popularity of GAs is the existence of numerous theoretical studies of the underlying mechanisms used to apply them to a problem [16].
Genetic algorithms begin generating problem solutions as a population of individuals. This population then undergoes an evolutionary loop. Each iteration includes the following processes: (i) selection, in which its composition is modified by eliminating specific individuals and reinforcing others; (ii) reproduction, in which new individuals are introduced; and (iii) evaluation, in which evolution data such as the fitness value are updated [16].
3. Allocating Resources in Heterogeneous Cloud Infrastructures
This section describes the problems of data placement in heterogeneous storage systems and the allocation of virtual machines on NUMA nodes and our approach, comprised of a hierarchical framework, to solving them using genetic programming. Figure 1 shows the workflow of a user who requests VMs in order to run an application. In this workflow, two main processes (shown in grey squares) are impacted by our genetic algorithms. Both VM allocation and data placement are crucial in terms of maximizing the performance of the application. In Tier-1 of the framework, our proposed VM allocation scheme is aware of memory sharing patterns on NUMA nodes, and leverages a data placement mechanism, in Tier-2, to take advantage of the available different types of storage.
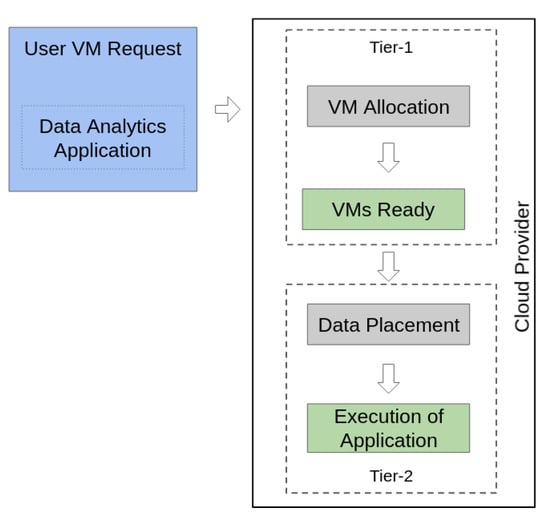
Figure 1.
Workflow for virtual machines resource allocation and data placement.
3.1. Tier 1: Node Allocation in the Cloud Using Genetic Programming
In CC environments, sharing computational resources such as memory and processors creates performance impacts when workloads are run simultaneously. The proper allocation of resources can mitigate these impacts [17].
In this section, we describe our approach to mapping workloads to nodes in CC systems. Specifically, we map virtual machines to physical nodes using a novel approach based on genetic programming. To map virtual processors to physical processors efficiently and to minimize the power consumption through server consolidation, our algorithm considers how memory is shared between virtual machines when allocating physical machines with multiple NUMA domains.
3.1.1. Allocating Nodes to Virtual Machines
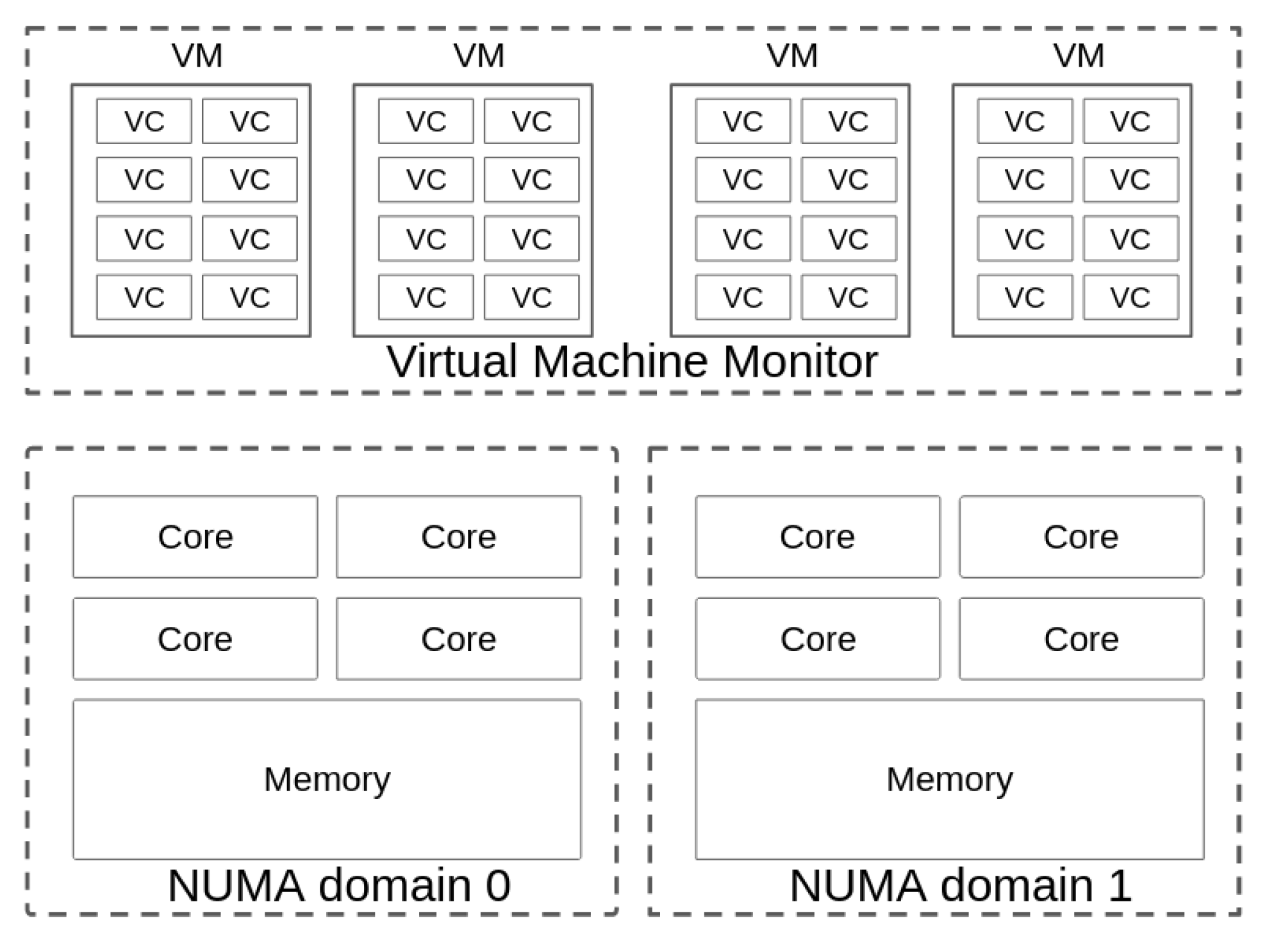
The CPU allocation problem in a multiprocessor system has a highly complex computational solution. This is an NP-hard problem [18], and several approximate solutions have been proposed based on heuristics [19,20]. This section focuses on mapping the cores of a set of virtual machines to the cores of NUMA nodes in a CC system. Figure 2 shows an example of a possible mapping scenario. In this case, four virtual machines, each with eight virtual cores, are mapped to a node with eight cores distributed in two NUMA domains. For efficient mapping, the degree to which virtual cores share memory should be considered in order to reduce the contention between them. Likewise, an ideal algorithm would consolidate the virtual cores in the least number of cores in the physical node to apply low energy consumption mechanisms to the idle physical cores.
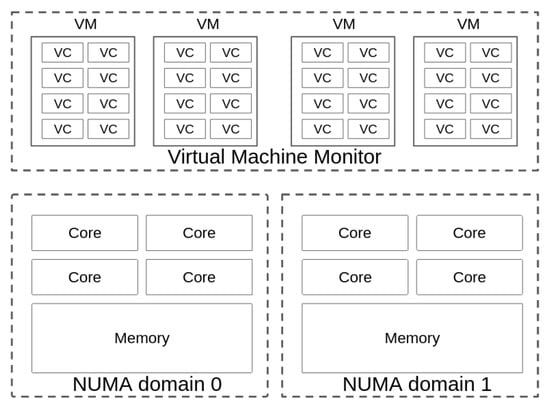
Figure 2.
Mapping 32 virtual cores to eight physical cores on two NUMA domains.
Additionally, this system should take advantage of the NUMA domains present in physical machines by mapping virtual cores with a high degree of shared memory to the same NUMA domain to reduce communication costs. Likewise, virtual cores that do not share memory to a high degree should be mapped to different NUMA domains, with the aim of reducing interference problems. Simultaneously, the algorithm should seek to maximize the use of physical cores and reduce power consumption by consolidating virtual cores into the fewest possible number of physical cores.
3.1.2. Problem Formulation
To solve the problem described above, we propose an evolutionary algorithm inspired by genetic programming. Our objective function measures the utilization of each of the cores in a physical node. Since the problem of mapping workloads to cores in multiprocessor systems is complex, this is a suitable problem to be addressed by a genetic algorithm. In addition, in order to optimize the mapping to maximize utilization and facilitate consolidation, several constraints and penalties must be considered to ensure that the benefits of the NUMA architecture are exploited. In the following, we describe the objective function and the variables used, and the restrictions on our model.
Variables
Table 1 summarizes the variables used in our formulation.

Table 1.
Problem model variables.
Constraints
A virtual core must be mapped only to one single physical core:
The maximum utilization of a physical core is 1:
Objective Function
We consider two objective functions: one that seeks to maximize the utilization without considering penalties for mappings that do not take advantage of the NUMA architecture in an efficient way, and another that takes into account these penalties. We describe both of these functions below.
Objective function without a penalty for NUMA mapping:
where .
Objective function using penalties for inefficient NUMA mapping:
where if a penalization is considered, and otherwise. The value chosen for depends on how critical the penalty is. We consider two penalty levels: (i) a penalty for each pair of virtual cores with a high degree of shared memory mapped to different NUMA domains, and (ii) a penalty for each pair of virtual cores with a low degree of shared memory mapped to the same NUMA domain.
3.1.3. The Genetic Programming Algorithm
Our algorithm initially generates a random set of mappings from virtual to physical cores (represented as individuals in the population) and evolves towards the optimal mapping solution. The algorithm carries out iterations (or generations) and evaluates the optimality of the mappings generated in this way by selecting the individuals with the best characteristics in each iteration. At the end of the iterations, the result will be the best mapping solution. This algorithm is designed to respond quickly (usually within a few seconds) and can be used in production environments for the allocation of computing resources in real time.
Chromosome
In our approach, a chromosome consists of a matrix in which the rows are virtual cores, and the columns are physical cores. A value of one in a matrix cell indicates that a virtual core is mapped to a physical core, while a zero means that the virtual core is not mapped to the physical core. A valid chromosome must meet the following minimum conditions: (i) each virtual core must be mapped only to one physical core, and (ii) the utilization of a physical core must be less than or equal to one (100%). Furthermore, on a chromosome with efficient mapping, virtual cores with a high degree of shared memory are mapped to the same NUMA domain, while virtual cores that share less memory are mapped to different NUMA domains.
Population Initialization
The initial population supplied to the genetic algorithm consists of a set of valid chromosomes (usually 100 or more). Mapping matrices are generated randomly but without violating the restrictions on mapping and maximum utilization.
Evaluation, Chromosome Repair, and Population Planning
For each of the chromosomes generated by the algorithm, their fitness is calculated by applying the objective function described above. Our algorithm ensures a valid mapping: all virtual cores must be mapped, and each must be mapped to only one physical core. However, distributing the mapping of virtual cores to physical cores while guaranteeing less than 100% utilization for each physical core is complex. This is an NP-hard problem that is generally solved using heuristics. To ensure that our algorithm is efficient, we do not attempt to repair a chromosome that violates the criteria for use. Instead, these chromosomes are penalized. Finally, the population is ordered, using the obtained value for the fitness as a criterion.
Penalties
Chromosomes that do not meet the restriction of maximum use of physical cores are penalized. A penalty is applied to each core that does not meet the restriction. In order to achieve a mapping that allows for the optimal use of the NUMA domains, we apply a penalty to each pair of virtual cores with a high degree of shared memory that are mapped to different NUMA domains, and also to each pair of virtual cores with a low degree of shared memory that are mapped to the same NUMA domain.
Elitism
When the elitism technique is used in genetic programming, a small fraction of the individuals with the best fitness are transferred without modification to the next generation. Our genetic mapping algorithm uses elitism and selects two individuals by each generation, which are then included in the next generation.
Selection
In this step, the chromosomes with the best fitness are chosen, and these will be recombined and passed to the next generation. The tournament selection and roulette selection algorithms are implemented in this solution. The tournament selection algorithm randomly selects individuals from the population which then “compete” to enter the crossover phase. In each tournament, the individual with the best fitness will “win” while in the roulette selection algorithm, individuals with a fitness value higher than a randomly chosen threshold are selected, in a similar way to a ball falling into a slot in a roulette wheel [21].
Crossover
In this step, the chromosomes are recombined. The algorithm uses a two-point crossover [22], an approach in which two points representing positions on a chromosome are randomly selected, and the parts of the chromosome between these two points are exchanged between the recombined individuals. In this case, the mapping of a virtual core to a physical core in the target region is exchanged.
Mutation
In this step, the values of the mapping matrix cells are randomly modified based on a predefined mutation probability.
3.2. Tier 2: Data Placement in Heterogeneous Storage
Intelligent algorithms are widely used for resource allocation in CC [23]. In general, evolutionary algorithms are used, such as the particle swarm method and artificial neural networks. This section focuses on improving data placement for heterogeneous storage in order to obtain better performance.
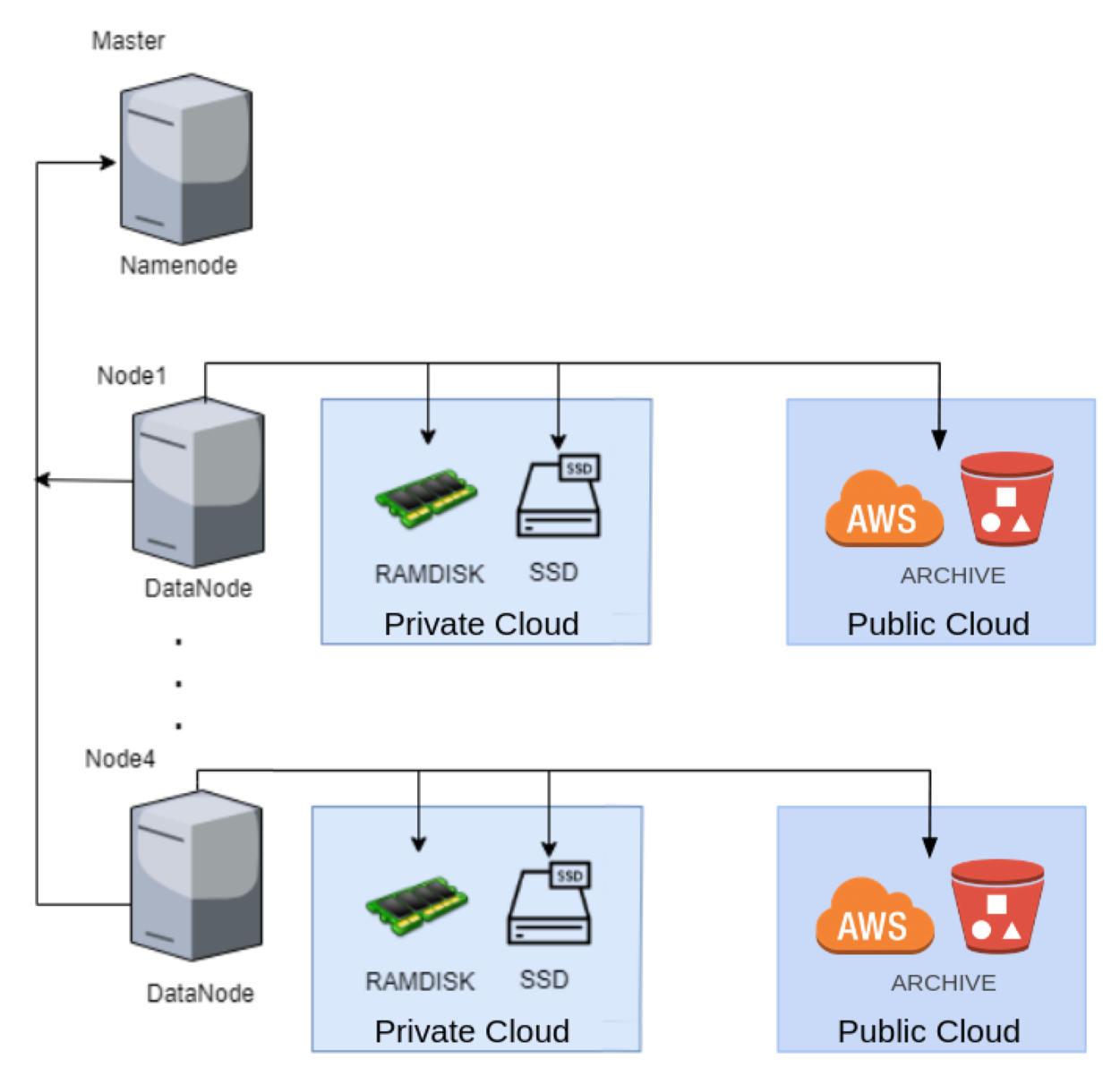
In the following, we formulate the problem to be solved by our data placement algorithm, which represents an improved version of our solution presented in [9]. In the present work, we have integrated an additional type of storage (ARCHIVE) that can be handled by our algorithm. This type of storage is provided as part of a multicloud arrangement. Figure 3 illustrates the architecture and the types of storage considered in this problem.
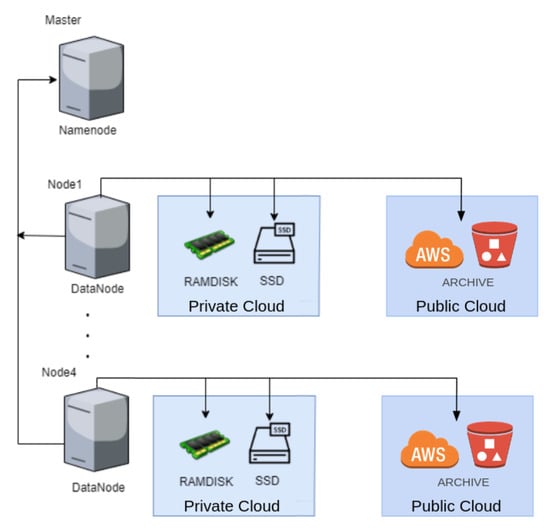
Figure 3.
Hadoop cluster architecture and public cloud.
One of the most widely used file systems in CC is HDFS. This file system supports heterogeneous types of storage, and to improve the performance of the applications running on it, we can optimize the way in which it uses these different types of storage. For this problem, we need to store N datasets in M different types of storage. We can formulate this problem as an integer linear programming (ILP) problem using the objective function given below:
And the following constraints:
In this problem, we have one variable that relates to the files, i.e., the dataset size (DSS), and several that are related to the types of storage, i.e., the capacity (C) and the data write rate (B). The solution we are looking for is the best data placement (X) for each dataset (DS). In this case, we propose the use of a genetic algorithm (GA) to solve the described ILP, in order to optimize the use of the heterogeneous storage using the ARCHIVE storage type. Algorithm 1 shows the GA that is used to find the best data placement on heterogeneous types of storage. For a more detailed explanation of the GA used for data placement, the reader is referred to our previous paper, in which this was developed [9]. In this work, we use the GA to integrate ARCHIVE into a public cloud, and a third party cluster is responsible for allocating the data.
| Algorithm 1 Genetic algorithm for heterogeneous storage. |
|
Generate random population solutions (Chromosomes) while do evaluate each chromosome in the fitness function add penalty factor to the fitness function value if condition for crossover is satisfied then select parents with the best fitness value choose crossover parameters perform crossover end if if condition for mutation is satisfied then choose mutation point perform mutation end if end while |
4. Results and Discussion
In this section, we validate our genetic programming algorithms by applying them to the problem of resource allocation on a CC infrastructure and comparing their performance with other approaches.
4.1. Validating the VM Mapping Genetic Programming Algorithm
To validate our genetic programming algorithm for VM mapping, we performed a set of experiments in which we used the algorithm to generate the optimal mappings of virtual machines to NUMA nodes. We then used our algorithm to allocate Xen virtual machines [24] running typical scientific benchmarks to time-shared NUMA nodes, and compared the performance of our method against other approaches.
4.1.1. NUMA Placement Generation
To evaluate the capacity of our genetic programming algorithm to generate optimal NUMA placements, we used it to allocate different sets of virtual machines to NUMA nodes. We considered scenarios in which we used various combinations of input parameters: the number of virtual cores, the number of physical cores, the number of NUMA domains, and the percentage of maximum CPU utilization. The output was the progress of the best fitness and the average fitness across generations. We used a crossover rate of 0.1 for these tests, a mutation rate of 0.001, a random initial population of 100 chromosomes, 50 generations, and a tournament selection method. Virtual cores on the same virtual machine were assigned a high level of memory shared communication, and virtual cores of different virtual machines were assigned a low level.
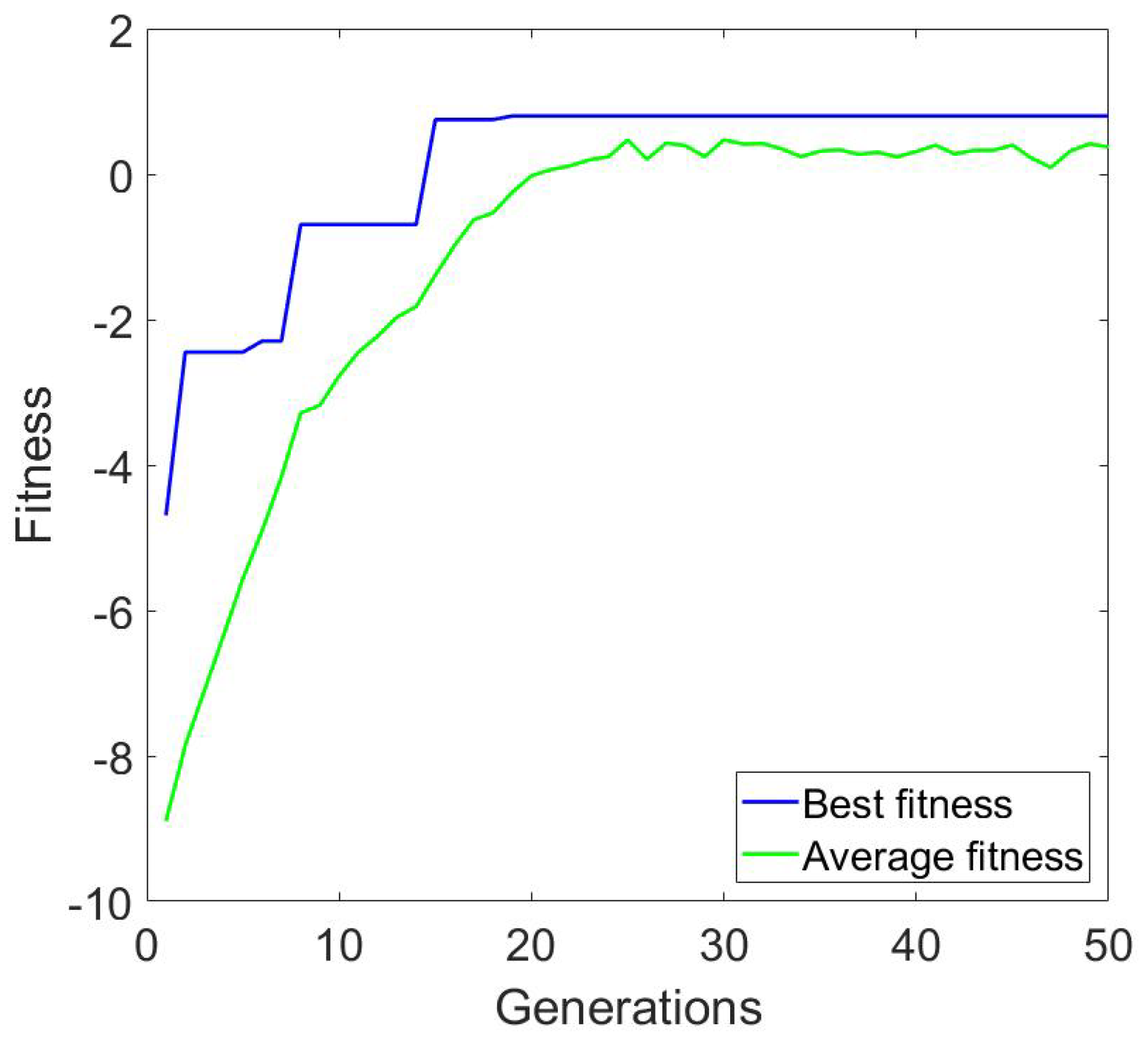
In the first experiment, we created three configurations, using the objective function without penalties for suboptimal NUMA mappings. For this experiment, we used a CPU utilization of 90%. The algorithm performance was optimal, and the evolution towards the best results happened very fast, as shown in Table 2. Although we ran 50 generations for each experiment, we achieved the best results from the 20th generation. This means that the algorithm is very practical for real world use, since 20 generations can be run very quickly, and our algorithm can therefore be used in real CC environments. Figure 4 shows the average and best fitness values for , , , .

Table 2.
Experiment 1. GP algorithm using objective function without penalties for suboptimal NUMA mappings.
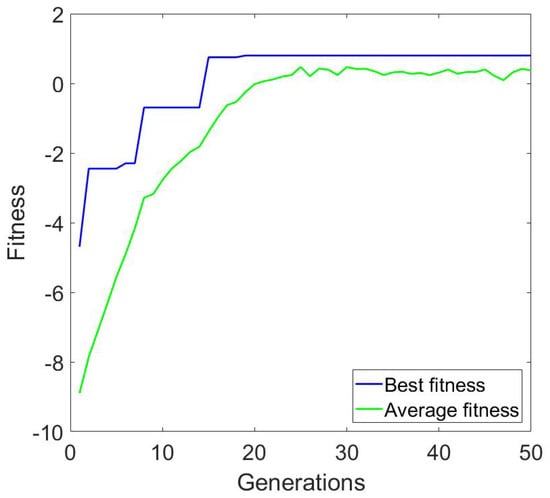
Figure 4.
Average and best fitness for experiment with input , , , . No penalization used for suboptimal NUMA allocations.
In the second experiment, we used the objective function with a penalty for suboptimal NUMA assignments while keeping the CPU utilization at 90%. In the same way as in the first experiment, significant improvements in fitness were evident across the generations. Figure 5 shows the average and best fitness values for , , , . Although the performance of the algorithm is affected by the penalty operations, as shown in Table 3, it is still efficient.
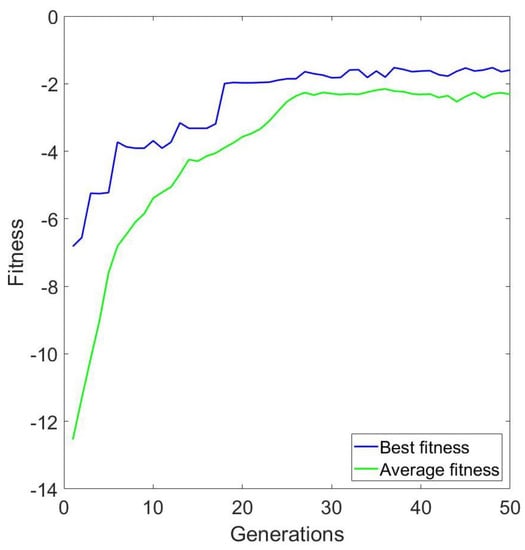
Figure 5.
Average and best fitness using penalization for suboptimal NUMA placements and , , , as input.

Table 3.
Experiment 2. GP algorithm using objective function with penalties for suboptimal NUMA mappings.
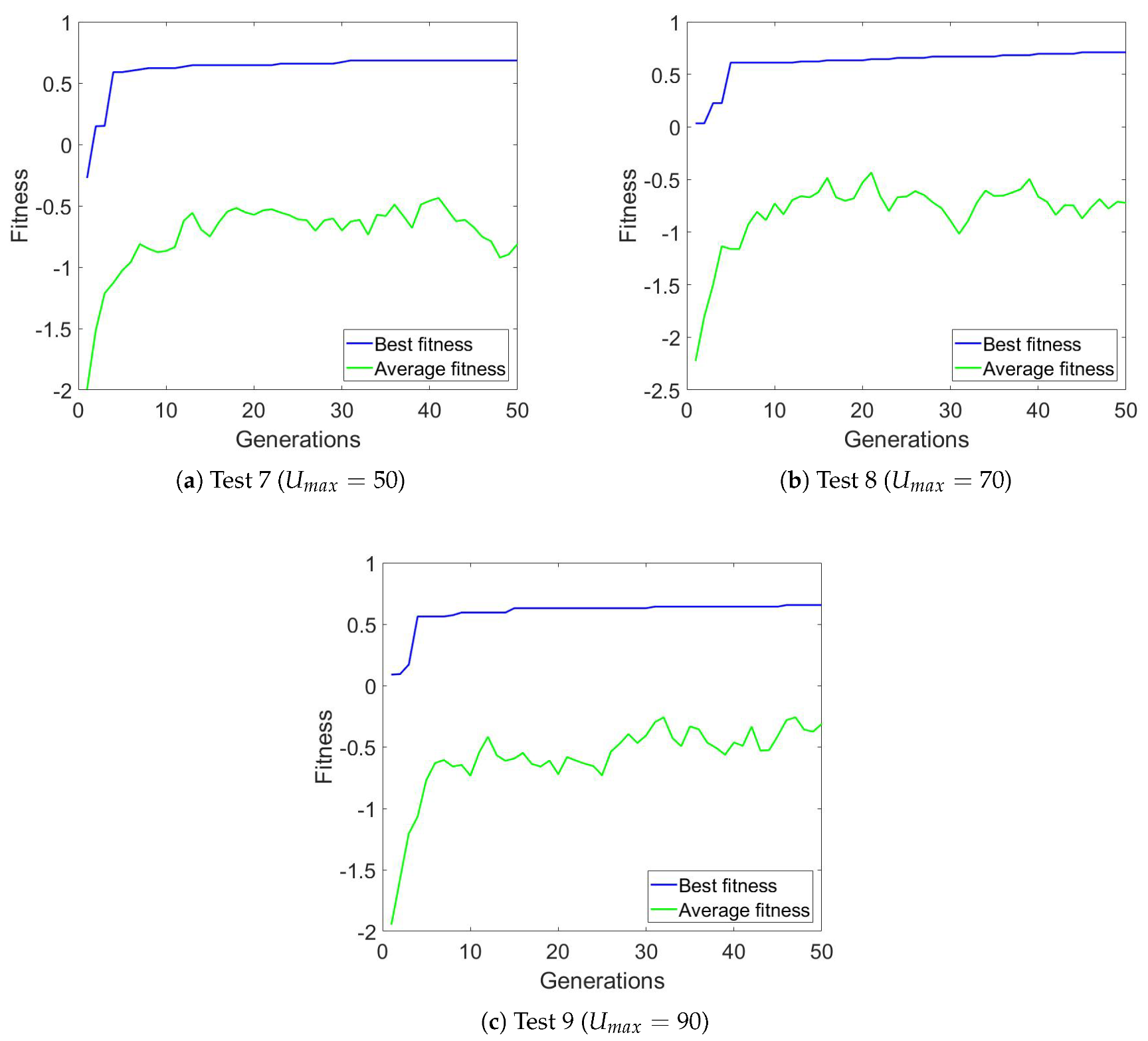
In the third experiment, we used different values for the CPU utilization, ranging from 50% to 90%. The results were comparable to those obtained in the second experiment (see Table 4). For these experiments, we used the version of the algorithm with penalties and the following parameters for all the tests , , , . Figure 6 shows the average and best fitness values.

Table 4.
Experiment 3. GP algorithm using objective function without penalties for suboptimal NUMA mappings.
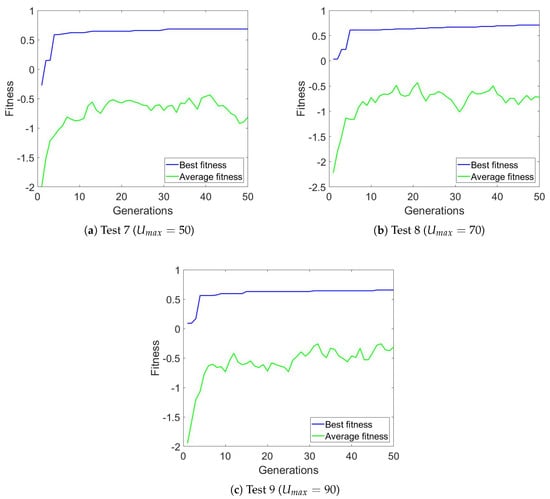
Figure 6.
Average and best fitness for Experiment 3 configurations.
4.1.2. NUMA Placement Performance
To validate the performance of our algorithm in terms of the allocations made, we used Xen virtual machines running typical scientific benchmarks mapped to time-shared NUMA nodes. This experiment was conducted on CloudLab [25], using University of Wisconsin Madison nodes. For this study, we used the c220g2 nodes, each of which had two Intel E5-2660 v3 10-core CPUs at 2.60 GHz (Haswell EP) with two NUMA nodes, 160 GB ECC memory (10x 16 GB DDR4 2133 MHz dual-rank RDIMMs), one Intel DC S3500 480 GB 6G SATA SSDs, two 1.2 TB 10 K RPM 6G SAS SFF HDDs, and dual-port Intel X520 10 GB NIC (PCIe v3.0, eight lanes). Frequency scaling was disabled for all nodes. The operating system was CentOs 7 and Linux kernel 3.10.0-1127.19.1.el7.x86_64.
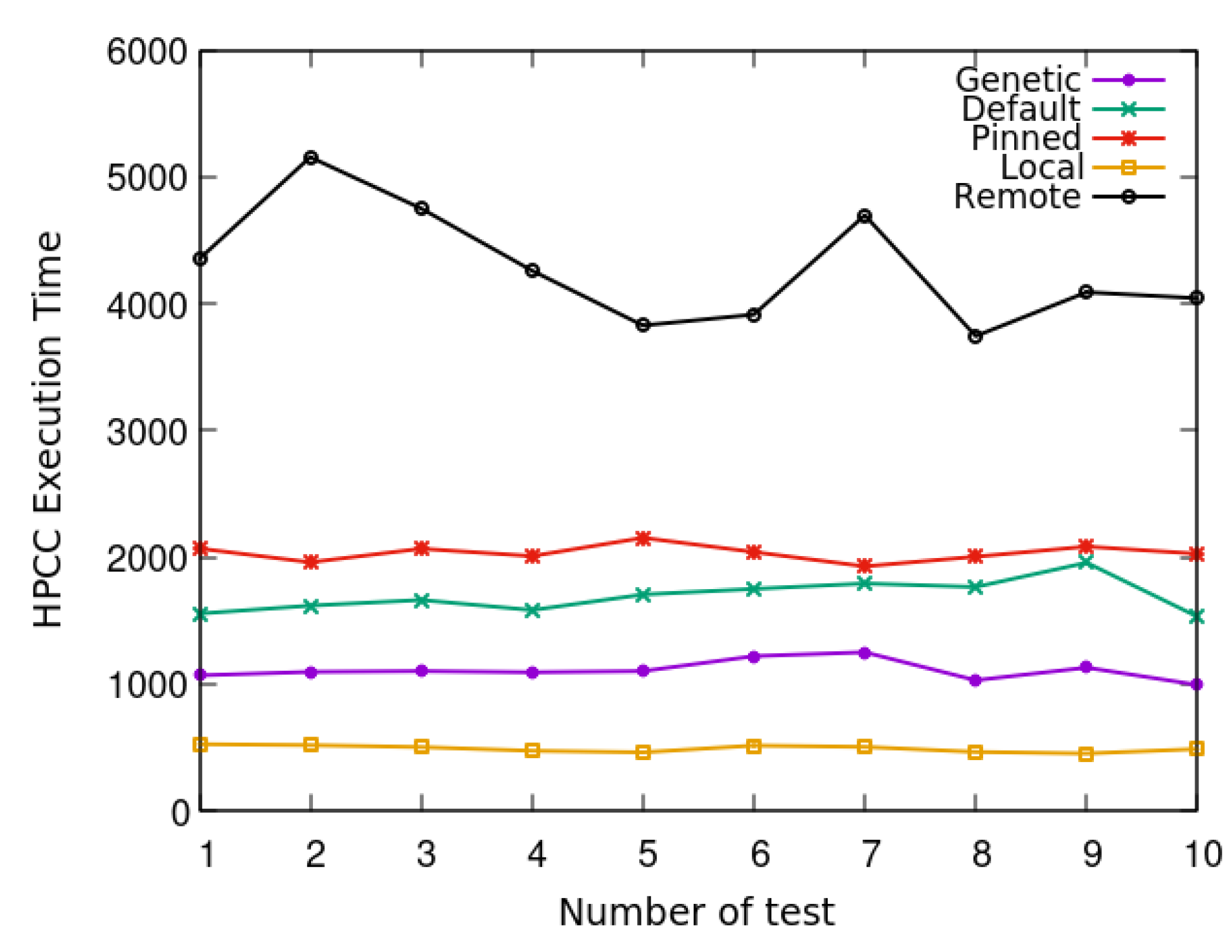
The benchmark suite used to test the resulting allocation of the virtual machines was HPC Challenge (HPCC) [26], a suite of benchmarks with different memory access patterns designed to run on petascale computing systems. We ran this suite concurrently on four virtual machines with four virtual cores and 1 GB of RAM mapped to a NUMA node. We compared the performance obtained with our genetic algorithm to the default settings and other types of mapping (see Figure 7). Our genetic algorithm was compared against the following configurations:
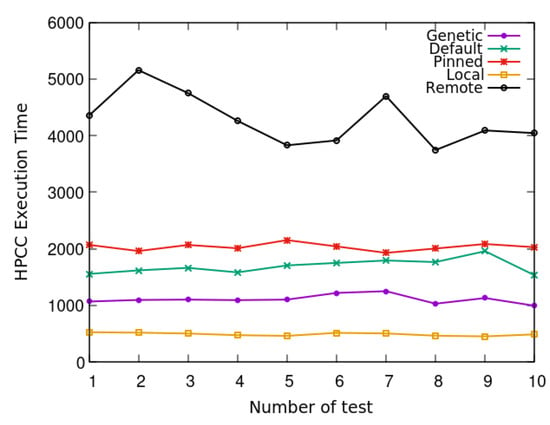
Figure 7.
Mapping 16 virtual cores to 40 physical cores.
- Default: This is the default mapping of the virtual cores to the physical Xen cores. The default allocation has been modified since Xen 4.2, and now uses a heuristic method to find the VM allocation [27].
- Pinned: After creating a default virtual machine, we can pin each virtual core to each physical core. In this case, each virtual core of a virtual machine is pinned to a different physical core in the same NUMA domain.
- All memory local: After creating a virtual machine, each virtual core is pinned to different physical cores in the same NUMA node. Regarding performance, this is the best case.
- All memory remote: The virtual machine is created and pinned to one node, and is then moved to another node, meaning that all memory accesses are remote.
The results in Figure 7 show the execution times for a test of the HPCC suite which was run concurrently on four virtual machines and repeated 10 times. The time at which the last VM was finished is reported for each run. As expected, the All Memory Remote allocation scheme had the slowest execution time, while the All Memory Local allocation had the fastest. When the memory is remote from all of the processors, the time taken to process data will be longer; conversely, if the memory is located close to the processors, a shorter time will be required. This is the default allocation since Xen 4.2 works as a bin packing algorithm, where a heuristic tries to achieve the best allocation for the virtual machines [28]. Pinning a virtual machine after it has been created means that some of its memory becomes remote. Finally, due to the use of penalties in our genetic algorithm, the allocation scheme reduces remote memory accesses by allocating each virtual machine core to the same NUMA node. Therefore, our genetic programming solution performs better than the alternative algorithms, apart from the ideal All Memory Local algorithm.
4.2. Allocating Storage in a Hadoop Cluster
We used instances of Amazon S3 as ARCHIVE storage. For each node, we used an S3 bucket configured with S3fs-fuse, which allows a bucket to be mounted in Linux via FUSE (Filesystem in Userspace). In this way, a virtual file system can work transparently by making a remote system operate in the same way as a local directory.
4.2.1. Experimental Setup
We used the Chameleon Cloud testbed [29] to build a cluster of five nodes, one of which was the master node, and the other four were the workers, on which the datasets are stored. For more information about the cluster parameters, please see Table 5.

Table 5.
Experimental setup.
4.2.2. Placing Datasets into an HDFS Cluster Using ARCHIVE
We compared the performance of the data placement solution obtained by our GA with the performance of other algorithms such as simplex and GRG. To test these solutions, we developed a synthetic benchmark that created a different number of datasets and wrote them into the HDFS cluster.
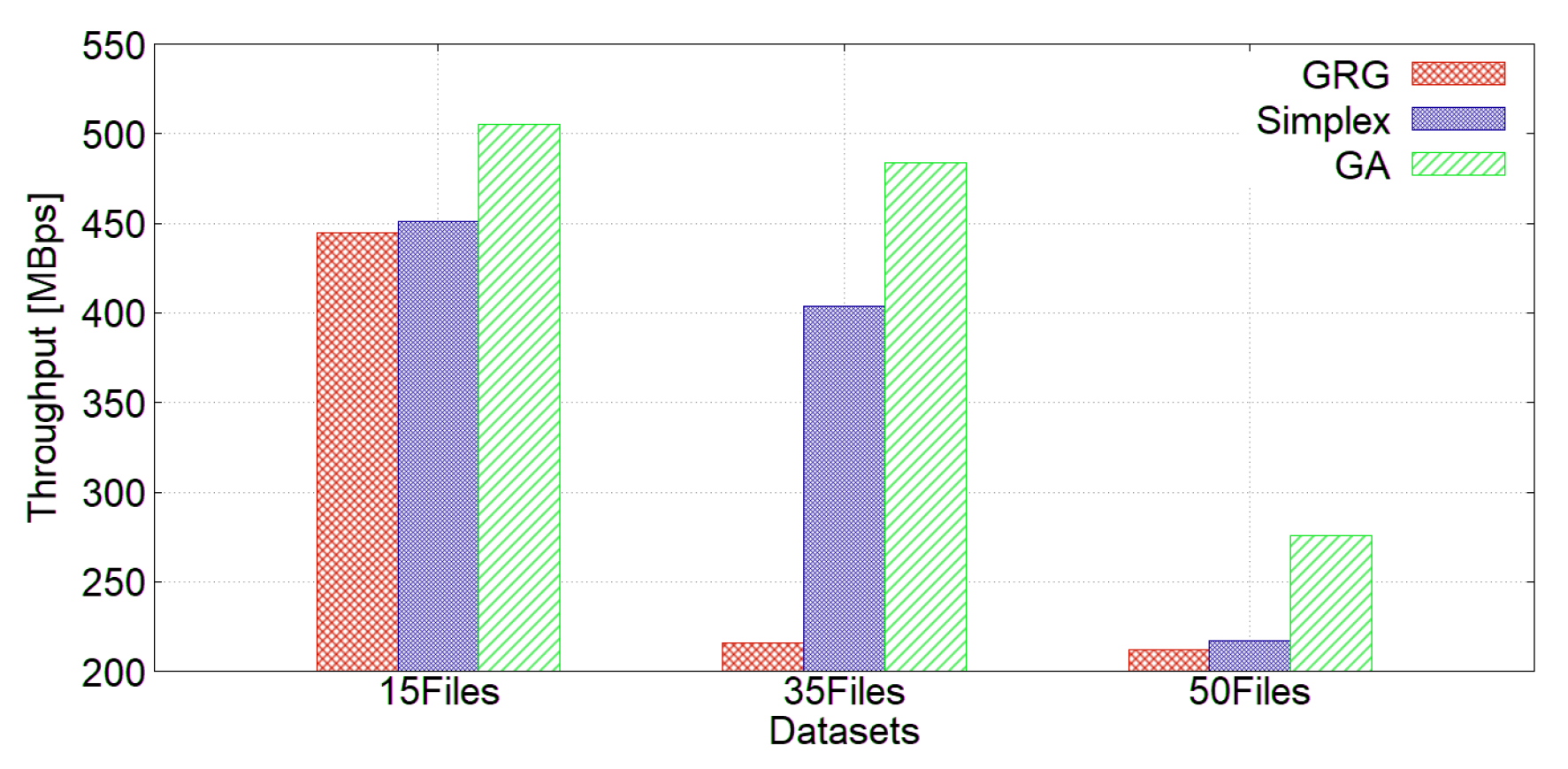
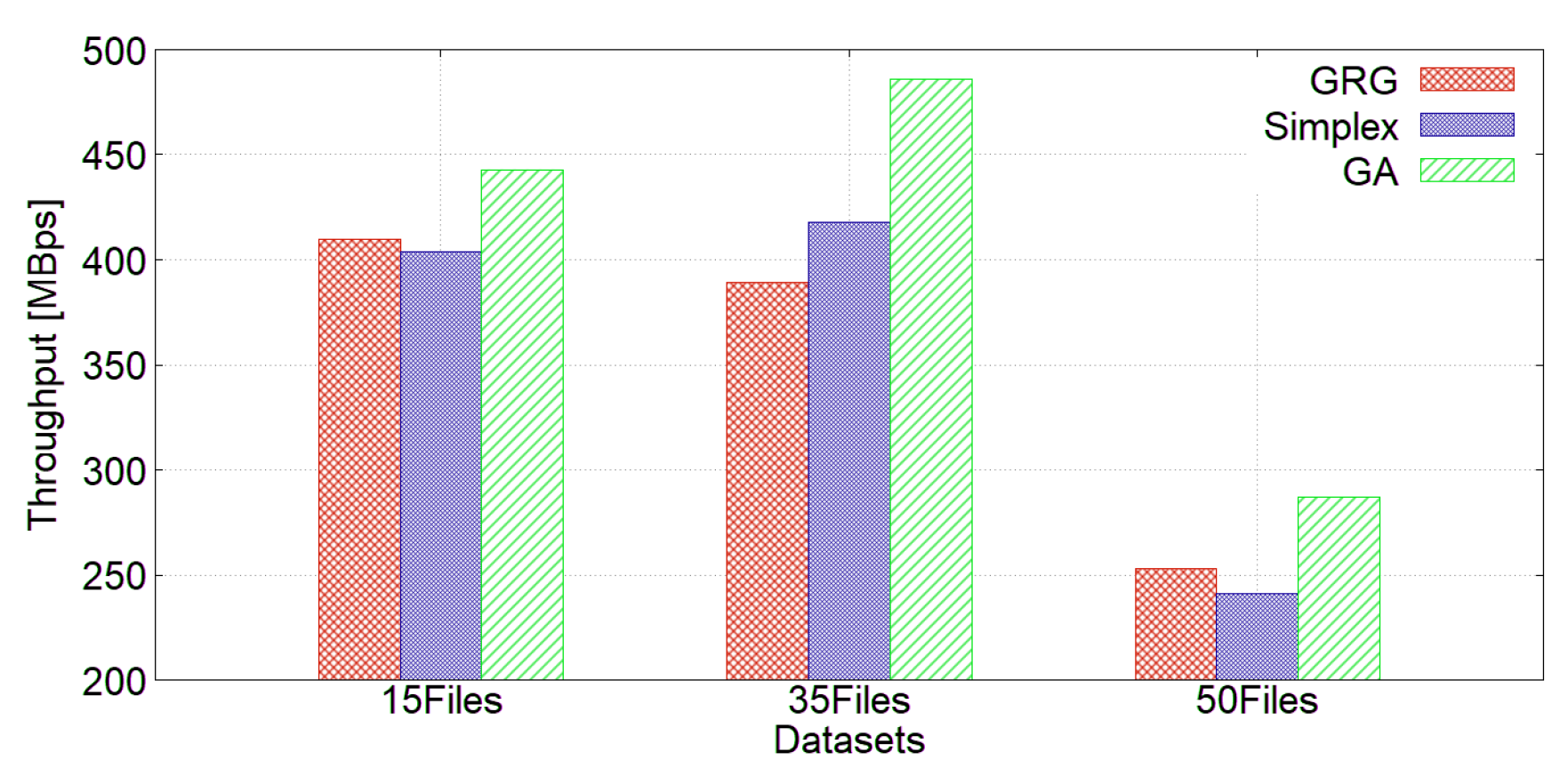
We performed an experiment using a replication factor of three and the following storage types: RAM_DISK with the ALL_RAM policy, SSD with the ALL_SSD policy, and ARCHIVE with the COLD policy. Figure 8 shows the write throughput, and Figure 9 shows the read throughput. Our GA achieved the best writing and reading performance. It should be borne in mind that the bandwidth of the file corresponds to the speed of the internet connection, since the stored files are being uploaded to a public cloud.
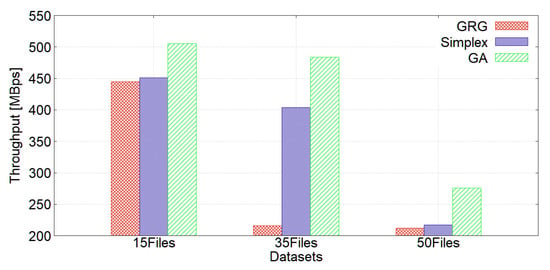
Figure 8.
Write throughput using replication factor 3.
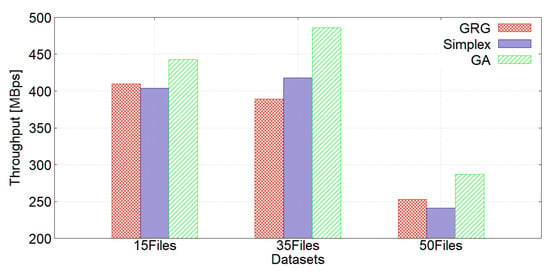
Figure 9.
Read throughput using replication factor 3.
5. Related Work
In [5], Sheng et al. model the virtual machine allocation on multi-NUMA servers using the Markov Decision Process (MDP) mathematical framework and propose a reinforcement learning algorithm to solve the problem. This approach, however, has scalability limitations, since the state space and action space increase exponentially, making the Markov decision process difficult. Their approach is based mainly on maximizing the number of created virtual machines during scheduling. In contrast, our work aims to efficiently allocate virtual machines on multi-NUMA servers taking into consideration the memory share patterns of the workloads running on the allocated VMs. In addition to the VM allocation problem, our work presents a solution for data placement in cloud environments.
Qian et al. in [30] present a framework for virtual machine consolidation on NUMA systems that optimizes the performance of cloud workloads. This framework includes management for load-aware global resources, and manages the resources of the virtual machines according to demand. This scheme has an overhead due to the CPU runtime of close to 9% higher than the Linux resource management tool, due to the other tasks that are carried out. This optimization approach is based on the number of memory accesses and I/O transfers, and does not consider memory sharing.
vProbe, proposed by Wu et al. in [31], is a virtual CPU scheduler that is aware of NUMA domains and can improve memory-intensive performance applications by reassigning VCPUs to NUMA nodes based on their memory access patterns.
The authors of [32], describe some of the disadvantages of applying quadratic programming to the problem of mapping virtual machines to NUMA domains. They show that for a problem formulated as a nonconvex quadratic, the solutions are suboptimal, and that reducing the complexity by dividing the mapping problem into subproblems can improve the algorithm. However, the scalability of their solution is limited compared to the genetic algorithm proposed in the present work.
Rao et al. in [33] propose a NUMA-aware approach for virtual machine scheduling that uses penalties to access memory subsystems. This solution can be applied to scenarios in which a few virtual machines are mapped to a limited number of nodes. However, an analysis of the different mapping options can become unmanageable for more complex systems, which require intelligent analysis methods such as the one described in this paper.
Ali et al. in [34] present a Discrete Nondominated Sorting Genetic Algorithm II (DNSGA-II) as an optimization model to allocate tasks to fog and cloud nodes. They formulated the problem as multiobjective to minimize nodes’ total makespans and cost. This model considers different factors like the total number of task instructions, required memory, bandwidth, and computing rate, as well as the cost of those computing resources. Their genetic algorithm uses randomly selected parents for the crossover, while we use the elitism method to select them. Contrary to our work, they run their experiments on a simulation environment and not on real cloud infrastructure.
The authors in [35] propose a Cooperative Coevolution Genetic programming approach to allocate containers to virtual machines, and then virtual machines to physical nodes. In their approach, they consider virtual machine overheads, virtual machine types, and affinity constraints. Containers are allocated into virtual machines according to their CPU occupation, memory occupation, and operating system. A limitation in their model is that neither virtual machines nor physical nodes are time-shared. Conversely, our approach allocates virtual machines in a time-shared environment, trying to minimize interference based on workload memory patterns.
Belgacem et al. propose in [36] a metaheuristic for resource allocation that reduces the execution time of different tasks. This heuristic is based on the Symbiotic Search Algorithm. Authors neither consider virtual machine allocation nor data placement techniques; they allocate tasks according to the millions of instructions per second (MIOPS) supported by every virtual machine and the task execution time. Their experiments were simulated using CloudSim with different tasks requirements and virtual machine characteristics.
Wang et al. formulated in [37] a mixed-integer linear programming problem and used some heuristics algorithms to solve it. Their model goal is virtual machine placement and workload assignment, trying to minimize the use of infrastructure in edge and cloud computing, according to applications’ latencies. Similarly, we formulated resource allocation problems as an ILP, but we propose genetic programming solutions focusing on heterogeneous hardware infrastructure in multicloud environments.
The authors in [6] analyze a task scheduling problem in edge computing formulated as a Markov Decision Process. They propose a deep reinforcement learning approach to solve this problem, seeking to optimize the mapping of tasks to virtual machines, considering heterogeneity in terms of the VMs computing capacity. In contrast, our work focuses on allocation of data and virtual machines to heterogeneous physical infrastructure, where heterogeneity is considered in terms of servers with nonuniform memory access and different storage types. Additionally, their results are based on simulations, while we focus on validation on real hardware.
Gao et al. present in [7] a hierarchical multi-agent optimization algorithm to maximize resource utilization and reduce the cost of the bandwidth. They present some simulated experiments where their algorithms have better performance than greedy and Viterbi heuristics. Their work is neither focused on storage nor virtual machine allocation on multi-NUMA servers.
Liu et al. [38] present an approach to virtual machine resource allocation which focuses on minimizing latency degradation while optimizing power consumption. To that end, they propose a hierarchical solution comprised of a global tier based on deep reinforcement learning (DRL) to solve the problem of virtual machine allocation to servers, and a local tier that leverages a long short-term memory (LSTM) network for workload prediction and a model-free reinforcement learning for power management. On the contrary, the optimization goals of our hierarchical solution are different: we propose a solution that includes two tiers based on genetic algorithms to tackle the allocation of resources on heterogeneous hardware comprised of multi-NUMA servers and different types of storage. The first tier solves the problem of VM allocation on servers with multi-NUMA architecture, trying to achieve server consolidation and considering the way in which memory is shared between virtual machines when allocating physical machines with multiple NUMA domains. A second layer performs data placement considering the different types of storage present in heterogeneous storage infrastructure.
In [4], Jeong et al. propose a data classification method to use hybrid SSDs. They use dynamic data separation for the allocation of the data in different blocks or regions to support a merge-tree based key-value store system. Their method consists in moving data from single-level cell NAND (SLC) to multilevel cell (MLC) NAND and vice versa. Hot data is moved to SLC and cold data is moved to MLC. Authors use storage simulators for experiments and show that their approach reduces I/O latency and improves device durability. Our solution takes into consideration multiple types of storage, in addition to SSDs, for data placements.
In [39], Yang et al. propose a cloud service platform based on software-defined storage (SDS) that integrates heterogeneous storage technologies such as Hadoop, Ceph, and GlusterFS to offer users a virtual storage pool. They also put forward a policy for the allocation of storage resources. SDS can operate with several storage file systems, and these authors used file systems rather than heterogeneous storage devices, and therefore did not take advantage of their benefits. All of the file systems integrated into their system were mounted over HDD without using any other as SSD.
In [40], the authors propose a strategy for optimizing the use of HDFS that includes hierarchical storage, which makes use of the hotness or coldness of the data. The data are classified as hot or cold based on the access frequency. This strategy involves moving data from one type of storage to another after the data are already in HDFS. In contrast, our algorithm allows us to store the dataset directly in a particular type of storage, thus optimizing the write and read times.
The authors in [41] use a genetic algorithm to find the optimal configuration parameters for a MapReduce application in a Hadoop cluster. They also propose a model of job execution times that uses random forest regression and a packing algorithm. The proposed model defines the input for the genetic algorithm, which is in charge of selecting the best configuration of Hadoop parameters, in order to get the best execution time of MapReduce jobs. Our approach attempts to maximize an application’s performance in a Hadoop environment by taking advantage of each storage device’s characteristics in a hierarchical storage infrastructure.
Qian et al. in [42] propose a randomized algorithm that selects a heterogeneous storage device (SSD or HDD) to execute each task, based on certain probabilities. This algorithm solves a workload scheduling problem that is formulated to avoid the redundant fetching of tremendous amounts of data from different types of storage. This work mainly focuses on optimizing the average data fetching, whereas our algorithm optimizes the data placement process in order to fetch and write data under the best conditions.
In [43], Guerrero et al. describe a multiobjective optimization algorithm based on genetic programming that solves the problem of VM allocation and replicas for Hadoop. The objectives of this scheme are to minimize power consumption, the waste of physical resource, and the unavailability of files. VM allocation is carried out based on the distribution of the chunk replicas to data nodes. To optimize storage, they consider the replica factor for Hadoop. Their methods of VM allocation and data placement are different from ours, as they neither consider the mapping of virtual cores nor take advantage of the heterogeneous storage capabilities of Hadoop.
6. Conclusions and Future Work
Cloud computing still poses challenges in terms of efficient resource allocation that must be considered in order to offer better systems for users. This study proposes a novel approach comprised of a hierarchical framework to virtual machine allocation on NUMA nodes and efficient data placement in the current cloud infrastructure, using multicloud storage.
Using two types of optimization (data placement and node placement), we have formulated problems with constraints that are related to the resources we are optimizing. However, genetic algorithms cannot usually integrate constraints when used alone. An optimal approach for work with genetic algorithms while applying constraints is to include a penalty system to guarantee that each selected chromosome fulfils the constraints. Our genetic programming approach, therefore, includes the use of penalty mechanisms.
One possible direction for future work would be to design a performance model to inform resource allocation optimization algorithms. Statistical models can supply essential data to improve the performance of these algorithms. Genetic algorithms consider different inputs, and these models can provide some relevant information about the resources to be optimized, with the aim of obtaining better solutions from algorithms.
Author Contributions
Conceptualization, J.M. and O.H.M.; methodology, O.H.M.; software, J.M., J.D.G. and O.H.M.; validation, J.M., J.D.G. and O.H.M.; formal analysis, J.M., J.D.G. and O.H.M.; investigation, J.M., J.D.G. and O.H.M.; resources, J.M., J.D.G. and O.H.M.; data curation, J.M. and O.H.M.; writing—original draft preparation, J.M., J.D.G. and O.H.M.; writing—review and editing, J.M. and O.H.M.; visualization, J.M. and O.H.M.; supervision, O.H.M.; project administration, O.H.M.; funding acquisition, J.M. and O.H.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
Results presented in this paper were obtained using the Chameleon and CloudLab testbed supported by the US National Science Foundation.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rydning, D.R.J.G.J. The Digitization of the World from Edge to Core; International Data Corporation: Framingham, MA, USA, 2018; p. 16. [Google Scholar]
- Li, H.; Li, H.; Wen, Z.; Mo, J.; Wu, J. Distributed heterogeneous storage based on data value. In Proceedings of the 2017 IEEE 2nd Information Technology, Networking, Electronic and Automation Control Conference (ITNEC), Chengdu, China, 15–17 December 2017; pp. 264–271. [Google Scholar] [CrossRef]
- Bezerra, A.; Hernandez, P.; Espinosa, A.; Moure, J.C. Job scheduling in Hadoop with Shared Input Policy and RAMDISK. In Proceedings of the 2014 IEEE International Conference on Cluster Computing, CLUSTER 2014, Madrid, Spain, 22–26 September 2014; pp. 355–363. [Google Scholar] [CrossRef]
- Jeong, J.; Kwak, J.; Lee, D.; Choi, S.; Lee, J.; Choi, J.; Song, Y.H. Level Aware Data Placement Technique for Hybrid NAND Flash Storage of Log-Structured Merge-Tree Based Key-Value Store System. IEEE Access 2020, 8, 188256–188268. [Google Scholar] [CrossRef]
- Sheng, J.; Hu, Y.; Zhou, W.; Zhu, L.; Jin, B.; Wang, J.; Wang, X. Learning to schedule multi-NUMA virtual machines via reinforcement learning. Pattern Recognit. 2022, 121, 108254. [Google Scholar] [CrossRef]
- Sheng, S.; Chen, P.; Chen, Z.; Wu, L.; Yao, Y. Deep Reinforcement Learning-Based Task Scheduling in IoT Edge Computing. Sensors 2021, 21, 1666. [Google Scholar] [CrossRef] [PubMed]
- Gao, X.; Liu, R.; Kaushik, A. Hierarchical multi-agent optimization for resource allocation in cloud computing. IEEE Trans. Parallel Distrib. Syst. 2020, 32, 692–707. [Google Scholar] [CrossRef]
- Apache Software Foundation. Hadoop; Apache Software Foundation: Snow Hill, MD, USA, 2009. [Google Scholar]
- Marquez, J.; Gonzalez, J.; Mondragon, O.H. Heterogeneity-aware data placement in Hybrid Clouds. In Proceedings of the 2019 International Conference on Cloud Computing (CLOUD 2019), San Diego, CA, USA, 25–30 June 2019. [Google Scholar]
- White, T. Hadoop: The Definitive Guide; Oreilly and Associate Series; O’Reilly: Sebastopol, CA, USA, 2012. [Google Scholar]
- Hadoop. Archival Storage, SSD & Memory; Apache Software Foundation: Snow Hill, MD, USA, 2009. [Google Scholar]
- Blagodurov, S.; Fedorova, A.; Zhuravlev, S.; Kamali, A. A case for NUMA-aware contention management on multicore systems. In Proceedings of the 2010 19th International Conference on Parallel Architectures and Compilation Techniques (PACT), Vienna, Austria, 11–15 September 2010; pp. 557–558. [Google Scholar]
- Nelder, J.A.; Mead, R. A simplex method for function minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Lasdon, L.S.; Fox, R.L.; Ratner, M.W. Nonlinear optimization using the generalized reduced gradient method. Rev. Française D’automatique Inform. Rech. Opérationnelle Rech. Opérationnelle 1974, 8, 73–103. [Google Scholar] [CrossRef] [Green Version]
- Gabriele, G.; Ragsdell, K. The generalized reduced gradient method: A reliable tool for optimal design. J. Eng. Ind. 1977, 99, 394–400. [Google Scholar] [CrossRef]
- Mitchell, M. An Introduction to Genetic Algorithms; MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Mondragon, O.H.; Bridges, P.G.; Levy, S.; Ferreira, K.B.; Widener, P. Understanding performance interference in next-generation HPC systems. In Proceedings of the SC’16: Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis, Salt Lake City, UT, USA, 13–18 November 2016; pp. 384–395. [Google Scholar]
- Chen, X.; Li, W.; Lu, S.; Zhou, Z.; Fu, X. Efficient resource allocation for on-demand mobile-edge cloud computing. IEEE Trans. Veh. Technol. 2018, 67, 8769–8780. [Google Scholar] [CrossRef] [Green Version]
- Shabeera, T.; Kumar, S.M.; Salam, S.M.; Krishnan, K.M. Optimizing VM allocation and data placement for data-intensive applications in cloud using ACO metaheuristic algorithm. Eng. Sci. Technol. Int. J. 2017, 20, 616–628. [Google Scholar] [CrossRef] [Green Version]
- Farzai, S.; Shirvani, M.H.; Rabbani, M. Multi-objective communication-aware optimization for virtual machine placement in cloud datacenters. Sustain. Comput. Inform. Syst. 2020, 28, 100374. [Google Scholar] [CrossRef]
- Razali, N.M.; Geraghty, J. Genetic algorithm performance with different selection strategies in solving TSP. In Proceedings of the World Congress on Engineering, Hong Kong, China, 6–8 July 2011; Volume 2, pp. 1–6. [Google Scholar]
- Gwiazda, T.D. Genetic Algorithms Reference Vol. I. Crossover for Single-Objective Numerical Optimization Problems [Online]. TOMASZGWIAZDA E-BOOKS. 2006. Available online: http://www.tomaszgwiazda.com/Genetic_algorithms_reference_first_40_pages.pdf (accessed on 26 June 2021).
- Guzek, M.; Bouvry, P.; Talbi, E.G. A survey of evolutionary computation for resource management of processing in cloud computing. IEEE Comput. Intell. Mag. 2015, 10, 53–67. [Google Scholar] [CrossRef]
- Barham, P.; Dragovic, B.; Fraser, K.; Hand, S.; Harris, T.; Ho, A.; Neugebauer, R.; Pratt, I.; Warfield, A. Xen and the art of virtualization. ACM SIGOPS Oper. Syst. Rev. 2003, 37, 164–177. [Google Scholar] [CrossRef]
- Duplyakin, D.; Ricci, R.; Maricq, A.; Wong, G.; Duerig, J.; Eide, E.; Stoller, L.; Hibler, M.; Johnson, D.; Webb, K.; et al. The Design and Operation of CloudLab. In Proceedings of the USENIX Annual Technical Conference (ATC), Renton, WA, USA, 10–12 July 2019; pp. 1–14. [Google Scholar]
- Luszczek, P.; Dongarra, J.J.; Koester, D.; Rabenseifner, R.; Lucas, B.; Kepner, J.; McCalpin, J.; Bailey, D.; Takahashi, D. Introduction to the HPC Challenge Benchmark Suite; Technical Report; Ernest Orlando Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 2005. [Google Scholar]
- Project, X. Xen 4.2 Automatic NUMA Placement; Xen Project: San Francisco, CA, USA, 2015. [Google Scholar]
- Voron, G.; Thomas, G.; Quéma, V.; Sens, P. An interface to implement NUMA policies in the Xen hypervisor. In Proceedings of the Twelfth European Conference on Computer Systems, Belgrade, Serbia, 23–26 April 2017; pp. 453–467. [Google Scholar]
- Keahey, K.; Anderson, J.; Zhen, Z.; Riteau, P.; Ruth, P.; Stanzione, D.; Cevik, M.; Colleran, J.; Gunawi, H.S.; Hammock, C.; et al. Lessons Learned from the Chameleon Testbed. In Proceedings of the 2020 USENIX Annual Technical Conference (USENIX ATC ’20), Online, 15–17 July 2020. [Google Scholar]
- Qian, J.; Li, J.; Ma, R.; Guan, H. Optimizing Virtual Resource Management for Consolidated NUMA Systems. In Proceedings of the 2018 IEEE 36th International Conference on Computer Design (ICCD), Orlando, FL, USA, 7–10 October 2018; pp. 573–576. [Google Scholar]
- Wu, S.; Sun, H.; Zhou, L.; Gan, Q.; Jin, H. vprobe: Scheduling virtual machines on numa systems. In Proceedings of the 2016 IEEE International Conference on Cluster Computing (CLUSTER), Taipei, Taiwan, 12–16 September 2016; pp. 70–79. [Google Scholar]
- Mondragon, O.H.; Bridges, P.G.; Jones, T. Quantifying scheduling challenges for exascale system software. In Proceedings of the 5th International Workshop on Runtime and Operating Systems for Supercomputers, Portland, OR, USA, 16 June 2015; pp. 1–8. [Google Scholar]
- Rao, J.; Wang, K.; Zhou, X.; Xu, C.Z. Optimizing virtual machine scheduling in NUMA multicore systems. In Proceedings of the 2013 IEEE 19th International Symposium on High Performance Computer Architecture (HPCA), Shenzhen, China, 23–27 February 2013; pp. 306–317. [Google Scholar]
- Ali, I.M.; Sallam, K.M.; Moustafa, N.; Chakraborty, R.; Ryan, M.J.; Choo, K.K.R. An automated task scheduling model using non-dominated sorting genetic algorithm ii for fog-cloud systems. IEEE Trans. Cloud Comput. 2020. [Google Scholar] [CrossRef]
- Tan, B.; Ma, H.; Mei, Y.; Zhang, M. A Cooperative Coevolution Genetic Programming Hyper-Heuristic Approach for On-line Resource Allocation in Container-based Clouds. IEEE Trans. Cloud Comput. 2020. [Google Scholar] [CrossRef]
- Belgacem, A.; Beghdad-Bey, K.; Nacer, H. Dynamic resource allocation method based on Symbiotic Organism Search algorithm in cloud computing. IEEE Trans. Cloud Comput. 2020. [Google Scholar] [CrossRef]
- Wang, W.; Tornatore, M.; Zhao, Y.; Chen, H.; Li, Y.; Gupta, A.; Zhang, J.; Mukherjee, B. Infrastructure-efficient Virtual-Machine Placement and Workload Assignment in Cooperative Edge-Cloud Computing over Backhaul Networks. IEEE Trans. Cloud Comput. 2021. [Google Scholar] [CrossRef]
- Liu, N.; Li, Z.; Xu, J.; Xu, Z.; Lin, S.; Qiu, Q.; Tang, J.; Wang, Y. A hierarchical framework of cloud resource allocation and power management using deep reinforcement learning. In Proceedings of the 2017 IEEE 37th International Conference on Distributed Computing Systems (ICDCS), Atlanta, GA, USA, 5–8 June 2017; pp. 372–382. [Google Scholar]
- Yang, C.T.; Chen, S.T.; Cheng, W.H.; Chan, Y.W.; Kristiani, E. A heterogeneous cloud storage platform with uniform data distribution by software-defined storage technologies. IEEE Access 2019, 7, 147672–147682. [Google Scholar] [CrossRef]
- Guan, Y.; Ma, Z.; Li, L. HDFS Optimization Strategy Based On Hierarchical Storage of Hot and Cold Data. Procedia CIRP 2019, 83, 415–418. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, J.; Shi, Y. Resource and Job Execution Context-Aware Hadoop Configuration Tuning. In Proceedings of the 2020 IEEE 13th International Conference on Cloud Computing (CLOUD), Beijing, China, 19–23 October 2020; pp. 116–123. [Google Scholar]
- Qian, Z.; Gao, Y.; Ji, M.; Peng, H.; Chen, P.; Jin, Y.; Lu, S. Workload-Aware Scheduling for Data Analytics upon Heterogeneous Storage. In Proceedings of the 2019 IEEE Intl Conf on Parallel & Distributed Processing with Applications, Big Data & Cloud Computing, Sustainable Computing & Communications, Social Computing & Networking (ISPA/BDCloud/SocialCom/SustainCom), Xiamen, China, 16–18 December 2019; pp. 580–587. [Google Scholar]
- Guerrero, C.; Lera, I.; Bermejo, B.; Juiz, C. Multi-objective optimization for virtual machine allocation and replica placement in virtualized hadoop. IEEE Trans. Parallel Distrib. Syst. 2018, 29, 2568–2581. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).