Determination of Prestress in Circular Inhomogeneous Solid and Annular Plates in the Framework of the Timoshenko Hypotheses

Abstract

Determination of prestress fields in structures is of the utmost importance, since they have a significant impact on operational characteristics, and their level and distribution must be strictly controlled. In this paper, we present modeling of bending vibrations of solid and annular round inhomogeneous prestressed plates within the framework of the Timoshenko hypotheses. New inverse problems of prestress identification in plates are studied on the basis of the acoustic response subjected to some probing load. To solve direct problems on calculating oscillations and amplitude-frequency characteristics, a computational Galerkin-method-based scheme has been developed. In order to treat the inverse problems, we use a special projection approach based on the constructed weak problems statements, which makes it possible to determine the desired characteristics in the given classes of functions. The developed techniques for solving direct problems are implemented in the form of software packages realized via Maple. For both solid and annular plates, we estimate the sensitivity of the amplitude-frequency characteristics the values of which are used as the additional data in the inverse problems to a change in the prestress level; we conclude that the most favorable frequency range should be selected in the resonance vicinity. We have conducted a series of computational tests on reconstructing the plate’s prestresses of various levels and distribution patterns (decreasing, increasing, sign-changing laws). The results of computational tests revealed that the technique developed allows for the determination of the prestresses with a low error for two cases: when the cause of prestress formation and its type are known and when arbitrary prestress changing laws are considered.

1. Introduction and Purpose of the Study

A strategic direction of modern mathematical modeling is the development and improvement of models of inhomogeneous materials, including functionally graded material (FGM), taking into account the presence of characteristic prestress (PS) fields in them. Such materials are widely used in the modern high-tech industry, in particular, in instrument making, aviation and space industries, and the production of components for nuclear reactors. A distinctive feature of these materials is that their mechanical properties and PS are functions of spatial coordinates and can vary significantly over the volume of the body. The reasons for the gradient of the characteristics of such materials can be inhomogeneities in the structure of the chemical composition, microstructure, or atomic order arising from the peculiarities of their manufacture. The nature of the occurrence of PS [1,2] in them is most often technological temperature treatments followed by cooling, used in the production of FGM. Operational problems arising from the use of FGM can affect the strength characteristics, in particular, fragility and susceptibility to extreme operating conditions, caused by the possible development of defects and residual stress concentrators [3]. Another problem is the need to verify that the values of mechanical properties correspond to those specified at the design stage. In this regard, the inverse problems [4] of identifying the characteristics of such materials, both mechanical properties and PS, are of particular importance, both for checking these materials at the manufacturing stage and for current operational monitoring. For identification, it is necessary to develop new diagnostic non-destructive techniques that meet the requirements for speed, accuracy, and ease of practical implementation. These requirements are met by the acoustic sensing method, which has proven itself in other identification problems. This method makes it possible to determine the necessary parameters by analyzing the acoustic response when measuring dynamic characteristics.

One of the strategic directions of FGM application is the production of plated structures used in the production of both military and civilian technical systems, such as cutting systems, membrane sensors, shielding elements, ceilings, partitions, dampers, etc. To take into account the various factors required within a particular formulation of the problem, many classical and non-classical models have been developed that describe the dynamic behavior of plates [5], based on various hypotheses, in particular, based on the theories of Timoshenko, Reissner, Mindlin, and others [6,7,8,9], making it possible to simulate the dynamic behavior of the plates. One should especially note the works of the outstanding Russian mechanic Tovstik, in particular [6,7], in which a detailed comparative analysis of models of plates within the framework of the Timoshenko-Reissner and Kirchhoff hypotheses is presented, as well as a comparison of these models with the equations of the three-dimensional theory of elasticity. It is shown that the Kirchhoff theory for plates is the first asymptotic approximation for an isotropic material; the Timoshenko-Reissner theory, taking into account the shear, in the case of thick plates, significantly refines the Kirchhoff theory.

The inverse problems of determining the characteristics of homogeneous and piecewise homogeneous plates are currently well studied; however, a fairly large number of modern papers are devoted to them. In [10] (by Lopes H. and others), a method for identifying the material constants of a multilayer composite plate is presented based on solving an optimization problem with an objective function connecting the experimental and calculated natural frequencies. In [11] (by Ablitzer F. and others), a method for determining the bending stiffness of an orthotropic plate is proposed based on the method for determining the distribution of external forces acting on a structure. To solve the inverse ill-posed problem, a regularization method is constructed that allows overcoming the high sensitivity to noise in the input data. The study in the field of modeling plates with PS in the case of Kirchhoff’s hypotheses was carried out by Uglich P.S. in [12], in which a scheme for their identification for a homogeneous plate was constructed in the case of an inverse problem of the first type (when the deflection function at all points of the plate is considered known).

As for the modeling of inhomogeneous plates, in particular, functional-gradient (FG) plates, their study is also presented in modern papers, for example, [13,14,15,16]. The papers [13,14] are quite extensive studies of methods for measuring the properties of FGM based on the study of free vibrations and dynamic stability of FG plates. Various types of mixtures of initial materials, from which FG plates are made, and the influence of their distribution over the volume of the body on the dynamic characteristics are considered. In [15,16], the modeling of FG vibrations in finite element packages, in particular, ANSYS, is presented. The study of the influence of the laws of change in the properties of plates on their dynamic characteristics, i.e., deflection and amplitude-frequency characteristics is carried out.

A large number of modern publications are devoted to the measurement of prestresses. Many of them are devoted to the determination of PS arising in the process of welding operations during plate processing. In the paper [17], F. Uzun and A. Korsunsky present the modeling of the three-dimensional distribution of residual stresses in welds in high-temperature nickel-based alloys used in the development of robust and reliable aeroengine components. Artificial intelligence (AI) and fuzzy techniques, showing a good match with experiments, were used to build a three-dimensional eigenstrain-creep model. In the article [18], the PS field in the weld of an annular structure simulated by a cylindrical hoop is studied. The blind hole method was used to test the residual stress distribution of the hoop structure, and the test results were compared with the finite element simulation results to verify the reliability of the simulation calculation method and the reliability of the calculation results. This made it possible to give recommendations on the optimal mode of welding of circular structures. In [19], the residual stresses arising in two samples of composite three-layer plates during the manufacture of the gas tungsten arc welding method were investigated. The values of tensile PS were measured at the boundaries of the joining of materials. Article [20] is devoted to the measurement of longitudinal and transverse PS arising from friction stir welding at different temperatures. It was shown that with a slight deepening into the weld, the longitudinal stresses are tensile in nature, and the transverse stresses are compressive, while welding with a lower temperature caused a higher level of PS. Article [21] contains an experimental study on the application of a new method of formation of residual stresses—laser shock peening. The influence of the thickness of the processed plates on the formed PS field is investigated. It is shown that in thicker plates, a significantly higher level of PS is achieved.

Other practical methods for measuring PN are also worth mentioning. In [22], the authors proposed an ultrasonic experimental technique for measuring the PS distribution. The studies were carried out for samples of rails, the delay in the passage of longitudinal waves caused by the presence of tensile stresses was investigated, which made it possible to evaluate their level during non-destructive diagnostics. The article [23] is devoted to the experimental study of thin-walled aircraft frames obtained from plates by milling, in which, due to low stiffness, residual stresses have a significant effect on deformation. Based on experimental data, the residual stress prediction model for milling 7075 aluminum alloy plates is proposed based on a back-propagation neural network and genetic algorithm. The model was tested on real data and showed good forecasting accuracy.

It should be noted that a number of inverse problems of the identification of properties and PS for objects made from FGM were considered earlier [24,25,26,27] based on the acoustic approach. In particular, the paper [24] is devoted to the modeling of FGM plates without PS within the framework of Kirchhoff hypotheses; it presents a solution to the inverse problem of identifying the function of the cylindrical stiffness of a circular plate made from FGM using an iterative approach. In [25], the results for a circular plate are developed for the case of the Timoshenko hypotheses. In [27], rectangular plates with PS were considered in the framework of the Timoshenko hypotheses in a Cartesian coordinate system. The inverse problems of identification of the two-dimensional PS field were studied using several techniques based on the acoustic approach.

At the moment, in modern studies, the problem of constructing general complex models of prestressed round plates, which takes into account shear deformation and allows for setting the change in mechanical properties and prestresses as arbitrary functions, which can be both continuous (for FGM) or have a finite number of discontinuities (for layered composites), is practically not presented. Additionally, effective and fast methods for determining the mechanical properties of such plates are currently poorly developed. This manuscript is devoted to the creation of a theoretical basis for solving these new important problems. In this paper, models of steady-state vibrations of circular solid and annular prestressed plates in the framework of the Timoshenko theory for the general case of inhomogeneity of all the problem parameters, including material characteristics and the distribution of PS, are presented. On the basis of the general form of the linearized equations of vibrations of a body with PS [2], the statements of problems on bending vibrations of the considered plates, caused by the probing load, are obtained. New inverse problems of determining the PS in plates are formulated on the basis of additional information on the values of the amplitude-frequency characteristic (AFC) at some points of the plates (acoustic response). To solve inverse problems, a special technique has been developed based on the projection approach proposed earlier [28]. The results of the corresponding computational tests on the solution of direct and inverse problems are discussed.

2. Statement of the Problems

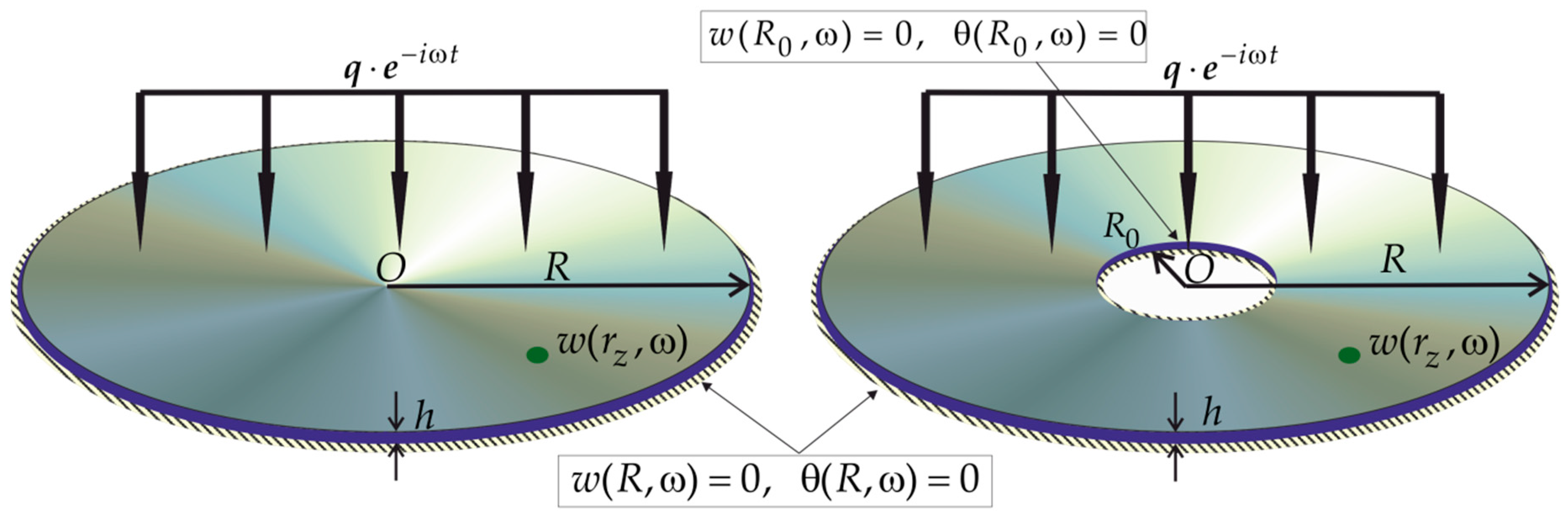
Let us consider in a cylindrical coordinate system ($r,\mathsf{\phi },z$) the axisymmetric bending vibrations of a prestressed circular inhomogeneous plate having a radius $R$ and a thickness $h$ within the framework of the Timoshenko hypotheses. We consider cases of both solid and annular plates with an inner radius $R_0$ (Figure 1). Due to the symmetry of the plate along the angular coordinate, the components of the displacement vector within the framework of the Timoshenko hypotheses [5] take the form:

$$u_r=z\mathsf{\theta },\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{u}_{\mathsf{\phi }}=0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{u}_z=w,$$

(1)

where $w$ is the plate deflection function, and $\mathsf{\theta }$ is the angle of rotation of the normal along the axis of the radial coordinate.

For modeling preliminary stresses, let us write down the general form of the Piola asymmetric stress tensor [2]:

$$\underset{\_}{\underset{\_}{T}}={\underset{\_}{\underset{\_}{\mathsf{\sigma }}}}^0\cdot \nabla \underset{\_}{u}+\underset{\_}{\underset{\_}{\mathsf{\sigma }}},$$

(2)

where $\underset{\_}{u}$ is displacement vector, $\underset{\_}{\underset{\_}{\mathsf{\sigma }}}$ is symmetric Kirchhoff stress tensor, and ${\underset{\_}{\underset{\_}{\mathsf{\sigma }}}}^0$ is prestress tensor. This model makes it possible to describe inhomogeneous fields of PS of various natures, in particular, arising during unloading after the formation of localized plastic zones.

Further constructions are common for solid and annular plates. Here, the most common case of a plane PS state [29] in plates will be considered, in which ${\mathsf{\sigma }}_{rr}^0(r)\ne 0\hspace{0.17em}$ and ${\mathsf{\sigma }}_{\mathsf{\phi }\mathsf{\phi }}^0(r)\ne 0$ are different from zero. In this case, the PS tensor will have the following non-zero components:

$$\begin{array}{l}{T}_{rr}={\mathsf{\sigma }}_{rr}+z{\mathsf{\theta }}_{,r}{\mathsf{\sigma }}_{rr}^0=\frac{Ez}{1-{\mathsf{\nu }}^2}\left({\mathsf{\theta }}_{,r}+\frac{\mathsf{\nu }\mathsf{\theta }}{r}\right)+z{\mathsf{\theta }}_{,r}{\mathsf{\sigma }}_{rr}^0,\\ T_{\mathsf{\phi }\mathsf{\phi }}={\mathsf{\sigma }}_{\mathsf{\phi }\mathsf{\phi }}+\frac{z\mathsf{\theta }}{r}{\mathsf{\sigma }}_{\mathsf{\phi }\mathsf{\phi }}^0=\frac{Ez}{1-{\mathsf{\nu }}^2}\left(\mathsf{\nu }{\mathsf{\theta }}_{,r}+\frac{\mathsf{\theta }}{r}\right)+\frac{z\mathsf{\theta }}{r}{\mathsf{\sigma }}_{\mathsf{\phi }\mathsf{\phi }}^0,\\ T_{rz}={\mathsf{\sigma }}_{rz}+w_{,r}{\mathsf{\sigma }}_{rr}^0=\frac{E}{2\left(1+\mathsf{\nu }\right)}\left(\mathsf{\theta }+w_{,r}\right)+w_{,r}{\mathsf{\sigma }}_{rr}^0,\\ T_{zr}={\mathsf{\sigma }}_{rz}=\frac{E}{2\left(1+\mathsf{\nu }\right)}\left(\mathsf{\theta }+w_{,r}\right).\end{array}$$

(3)

Let us write out the relations for the bending moments and shearing forces of the Timoshenko plate:

$$\begin{array}{l}{M}_r={\displaystyle \underset{-h/2}{\overset{h/2}{\int }}z{T}_{rr}dz=}D\left({\mathsf{\theta }}_{,r}+\frac{\mathsf{\nu }\mathsf{\theta }}{r}\right)+\frac{h^3}{12}{\mathsf{\theta }}_{,r}{\mathsf{\sigma }}_{rr}^0,\\ M_{\mathsf{\phi }}={\displaystyle \underset{-h/2}{\overset{h/2}{\int }}z{T}_{\mathsf{\phi }\mathsf{\phi }}dz=}D\left(\mathsf{\nu }{\mathsf{\theta }}_{,r}+\frac{\mathsf{\theta }}{r}\right)+\frac{h^3}{12}\frac{\mathsf{\theta }}{r}{\mathsf{\sigma }}_{\mathsf{\phi }\mathsf{\phi }}^0,\\ M_{r\mathsf{\phi }}=0,\\ Q_r={\displaystyle \underset{-h/2}{\overset{h/2}{\int }}{T}_{rz}dz=}\frac{Eh}{2\left(1+\mathsf{\nu }\right)}\left(\mathsf{\theta }+w_{,r}\right)+h{w}_{,r}{\mathsf{\sigma }}_{rr}^0,\hspace{0.17em}\hspace{0.17em}\\ Q_{\mathsf{\phi }}=0.\end{array}$$

(4)

Here, $D(r)=\frac{E(r)h^3}{12(1-{\mathsf{\nu }}^2)}\hspace{0.17em}$ is a function of the cylindrical rigidity.

The equations of steady-state axisymmetric bending vibrations of a plate caused by a normal load $\mathrm{q}(r)$ in a cylindrical coordinate system within the framework of the Timoshenko model [25,30] take the form:

$$\begin{array}{l}{Q}_r-\frac{1}{r}\left(\frac{\partial (r{M}_r)}{\partial r}-M_{\mathsf{\phi }}\right)=\frac{\mathsf{\rho }{h}^3}{12}{\omega }^2\mathsf{\theta },\\ \frac{1}{r}\frac{\partial (r{Q}_r)}{\partial r}=\mathsf{\rho }h{\omega }^{2}w-\mathrm{q}.\end{array}$$

(5)

Here, $\mathsf{\rho }(r)$ is a density, and $\omega$ is a vibration frequency.

Substituting (4) into (5) and carrying out transformations, one can write down the problem as regards the dimensionless functions of the deflection and the angle of rotation of the normal in the form:

$$\begin{array}{l}\mathsf{\gamma }\mathsf{\xi }\left[D\frac{(1-\mathsf{\nu })}{2}\left(\mathsf{\theta }+w^{\prime }\right)+s_{rr}^0{w}^{\prime }\right]-{\left(\mathsf{\xi }\left[D\left({\mathsf{\theta }}^{\prime }+\frac{\mathsf{\nu }\mathsf{\theta }}{\mathsf{\xi }}\right)+s_{rr}^0{\mathsf{\theta }}^{\prime }\right]\right)}^{\prime }+D\left(\mathsf{\nu }{\mathsf{\theta }}^{\prime }+\frac{\mathsf{\theta }}{\mathsf{\xi }}\right)+s_{\mathsf{\phi }\mathsf{\phi }}^0\frac{\mathsf{\theta }}{\mathsf{\xi }}-{\mathsf{\kappa }}^2\mathsf{\rho }\mathsf{\xi }\mathsf{\theta }=0,\\ {\left(\mathsf{\xi }\left[D\frac{(1-\mathsf{\nu })}{2}\left(\mathsf{\theta }+w^{\prime }\right)+s_{rr}^0{w}^{\prime }\right]\right)}^{\prime }-{\mathsf{\kappa }}^2\mathsf{\rho }\mathsf{\xi }w+\mathrm{q}\mathsf{\xi }=0.\end{array}$$

(6)

The following dimensionless parameters and variables are introduced in (6): $r=R\mathsf{\xi }$, $w=R\tilde{w},$ $D=D_0\tilde{D},$ $R_0=R{\mathsf{\xi }}_0$, $D_0=D(R)$, ${\mathsf{\sigma }}_{rr}^0=\frac{12D_0}{h^3}{s}_{rr}^0$ ${\mathsf{\sigma }}_{\mathsf{\phi }\mathsf{\phi }}^0=\frac{12D_0}{h^3}{s}_{\mathsf{\phi }\mathsf{\phi }}^0$, $\mathsf{\rho }={\mathsf{\rho }}_0(R)\tilde{\mathsf{\rho }}$, ${\mathsf{\kappa }}^2=\frac{h^3{\mathsf{\rho }}_0}{12D_0}{R}^2{\omega }^2$, $\mathrm{q}=\frac{12D_0}{h^{2}R}\tilde{\mathrm{q}}(\mathsf{\xi })$, $\mathsf{\gamma }=12\frac{R^2}{h^2}$. The tilde signs “~” in (6) are omitted, and the derivative with respect to the dimensionless coordinate $\mathsf{\xi }$ is indicated by the prime «′».

It can be assumed that the plates are rigidly clamped along the contour, which is expressed by the following boundary conditions:

$$w(1,\mathsf{\kappa })=0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathsf{\theta }(1,\mathsf{\kappa })=0.$$

(7)

For a solid plate, add conditions to zero (due to the symmetry of the plate):

$$w^{\prime }(0,\mathsf{\kappa })=0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathsf{\theta }(0,\mathsf{\kappa })=0.$$

(8)

For an annular plate, the condition of rigid restraint is also considered on the inner radius:

$$w({\mathsf{\xi }}_0,\mathsf{\kappa })=0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathsf{\theta }({\mathsf{\xi }}_0,\mathsf{\kappa })=0.$$

(9)

The Poisson ratio $\mathsf{\nu }$ can be assumed to be constant, which is the most common situation in practice.

The inverse problems for both plates consist of determining a set of dimensionless functions of prestress $s_{rr}^0(\mathsf{\xi })$, $s_{\mathsf{\phi }\mathsf{\phi }}^0(\mathsf{\xi })$, as well as the corresponding functions of the deflection $w(\mathsf{\xi })$ and the angle of rotation of the normal $\mathsf{\theta }(\mathsf{\xi })$ using additional information about the amplitude frequency characteristic (AFC) measured at the point $\mathsf{\xi }={\mathsf{\xi }}_z$ in a certain frequency range:

$$w({\mathsf{\xi }}_z,\mathsf{\kappa })=f(\mathsf{\kappa }),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathsf{\kappa }\in [{\mathsf{\kappa }}_1,{\mathsf{\kappa }}_2].$$

(10)

Additionally, let us take into account that the functions of PS must satisfy the Cauchy equilibrium equation [29], which in the considered axisymmetric case, is written in the form ${{\mathsf{\sigma }}_{rr}^0}^{\prime }+\frac{{\mathsf{\sigma }}_{rr}^0-{\mathsf{\sigma }}_{\mathsf{\phi }\mathsf{\phi }}^0}{\mathsf{\xi }}=0$, from which ${\mathsf{\sigma }}_{\mathsf{\phi }\mathsf{\phi }}^0=\mathsf{\xi }{{\mathsf{\sigma }}_{rr}^0}^{\prime }+{\mathsf{\sigma }}_{rr}^0$. Then, the function $s_{\mathsf{\phi }\mathsf{\phi }}^0(\mathsf{\xi })$ can be excluded from the oscillation equations by expressing it in terms of $s_{rr}^0(\mathsf{\xi })$, and we can write (6) in the form:

$$\begin{array}{l}\mathsf{\gamma }\mathsf{\xi }\left[D\frac{(1-\mathsf{\nu })}{2}\left(\mathsf{\theta }+w^{\prime }\right)+s_{rr}^0{w}^{\prime }\right]-{\left(\mathsf{\xi }\left[D\left({\mathsf{\theta }}^{\prime }+\frac{\mathsf{\nu }\mathsf{\theta }}{\mathsf{\xi }}\right)+s_{rr}^0{\mathsf{\theta }}^{\prime }\right]\right)}^{\prime }+D\left(\mathsf{\nu }{\mathsf{\theta }}^{\prime }+\frac{\mathsf{\theta }}{\mathsf{\xi }}\right)+\frac{\left(\mathsf{\xi }{s_{rr}^0}^{\prime }+s_{rr}^0\right)\mathsf{\theta }}{\mathsf{\xi }}-{\mathsf{\kappa }}^2\mathsf{\rho }\mathsf{\xi }\mathsf{\theta }=0,\\ {\left(\mathsf{\xi }\left[D\frac{(1-\mathsf{\nu })}{2}\left(\mathsf{\theta }+w^{\prime }\right)+s_{rr}^0{w}^{\prime }\right]\right)}^{\prime }-{\mathsf{\kappa }}^2\mathsf{\rho }\mathsf{\xi }w+\mathrm{q}\mathsf{\xi }=0.\end{array}$$

(11)

Thus, in inverse problems, it is also sufficient to define only a function $s_{rr}^0(\mathsf{\xi })$.

Note that the formulated problem of finding the PS field is a coefficient inverse problem [4], the solution of which is a nonlinear ill-posed problem [31] and requires the use of special methods.

Additionally, to construct a scheme for solving inverse problems, it is necessary to develop a method for solving direct problems for calculating bending vibrations of plates with PS, the realization of which is possible using the numerical methods only, due to the nonlinearity of Equations (11). On the basis of the constructed method, it is possible to analyze the effect of PS on AFCs of plates, as well as on the deflection function.

3. Solving the Direct Problems of Vibration Analysis of Plates: Analysis of Amplitude-Frequency Characteristics

A technique based on the Galerkin method [32,33] was developed for solving the direct problems of calculating the vibrations of plates. The functions of the deflection and the angle of rotation of the normal were represented in the form of expansions in the following sets of orthogonal functions, satisfying the boundary conditions, in the following form:

$$w(\mathsf{\xi },\mathsf{\kappa })={\displaystyle \sum _{m=1}^N{a}_m^{}(\mathsf{\kappa }){\mathsf{\phi }}_{1m}^{}(\mathsf{\xi })},\hspace{0.17em}\hspace{0.17em}\mathsf{\theta }(\mathsf{\xi },\mathsf{\kappa })={\displaystyle \sum _{m=1}^N{b}_m^{}(\mathsf{\kappa }){\mathsf{\phi }}_{2m}^{}(\mathsf{\xi })}.$$

(12)

The basic functions for a solid plate are selected in the form:

$${\mathsf{\phi }}_{1m}^{}(\mathsf{\xi })={(1-{\mathsf{\xi }}^2)}^2{\mathsf{\xi }}^{2(m-1)},\hspace{0.17em}\hspace{0.17em}{\mathsf{\phi }}_{2m}^{}(\mathsf{\xi })=\sin (m\mathsf{\pi }\mathsf{\xi }).$$

(13)

The basic functions for an annular plate are selected in the form:

$${\mathsf{\phi }}_{1m}^{}(\mathsf{\xi })={(1-{\mathsf{\xi }}^2)}^2{(\mathsf{\xi }-{\mathsf{\xi }}_0)}^2{\mathsf{\xi }}^{2(m-1)},\hspace{0.17em}\hspace{0.17em}{\mathsf{\phi }}_{2m}^{}(\mathsf{\xi })=\sin \left(m\mathsf{\pi }\frac{\mathsf{\xi }-{\mathsf{\xi }}_0}{1-{\mathsf{\xi }}_0}\right).$$

(14)

The numerical Galerkin method for solving direct problems of calculating oscillations and amplitude-frequency characteristics was implemented in the Maple package. To achieve an accuracy of 10, it is enough to use 6–7 basis functions. The numerical scheme for solving direct problems was tested on model examples, including homogeneous plates without PS, for which the solution can be written in an analytical form, and showed sufficiently high accuracy.

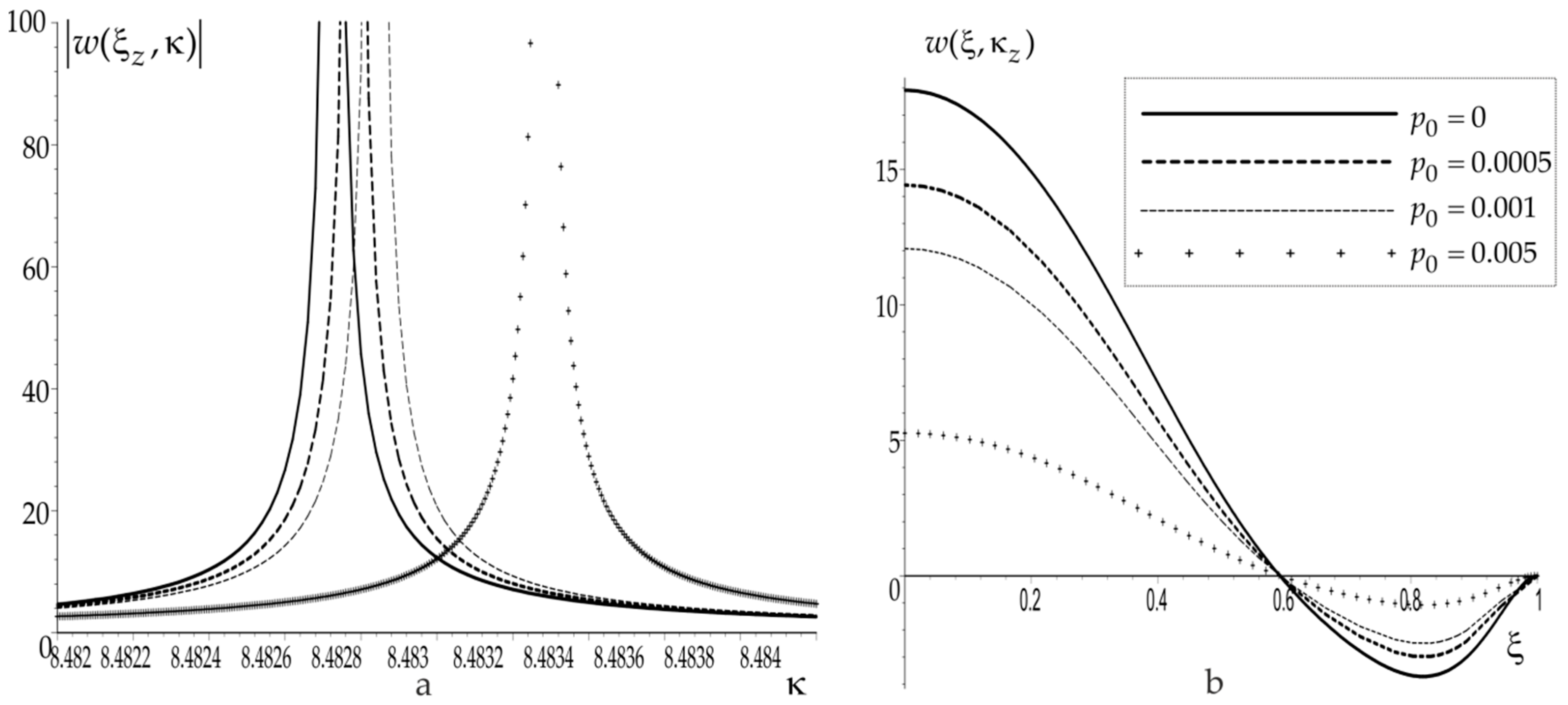
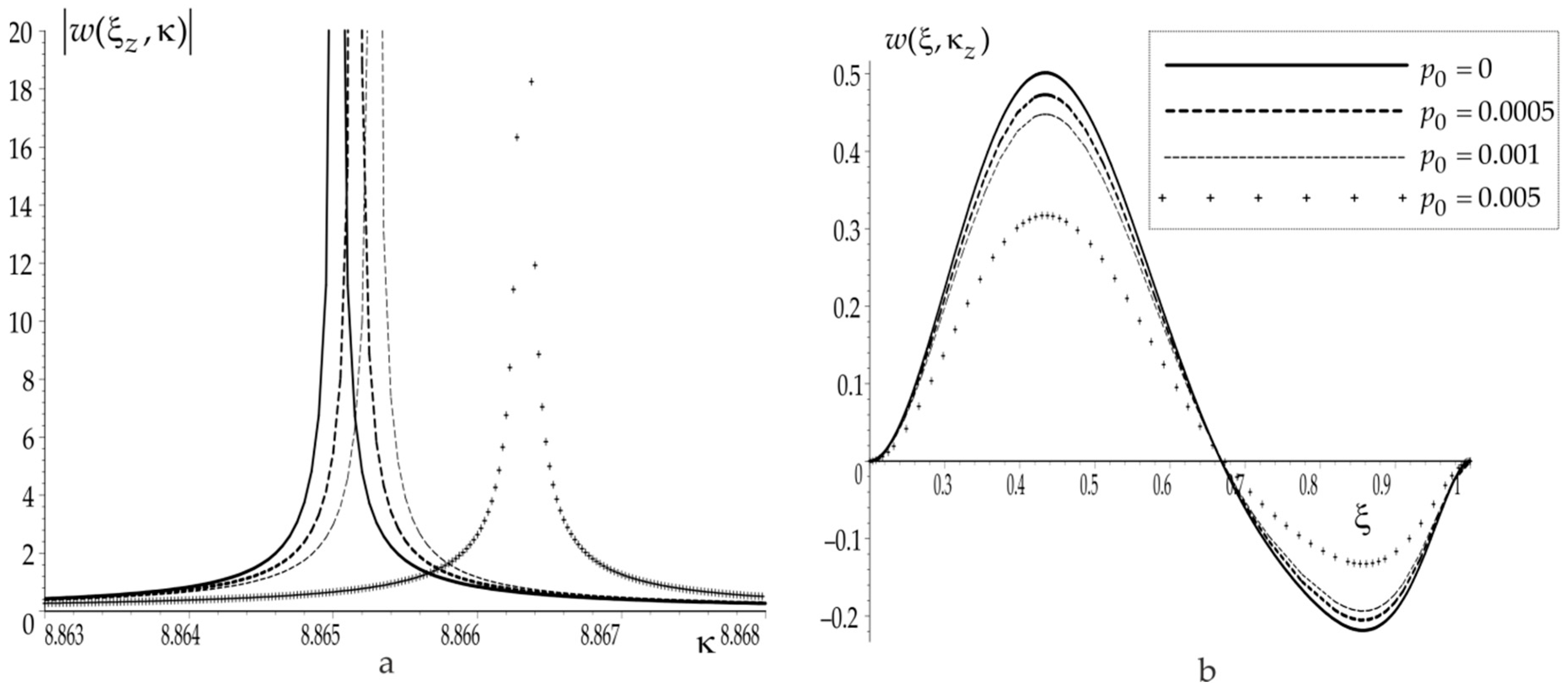
For each studied problem, a set of computational tests was carried out to calculate the frequency response and deflection functions in the neighborhood of the first dimensionless resonant frequency for different levels of PS. As an example, in the problem for a solid plate, a uniform PS field, corresponding to the solution of the problem of planar vibrations of a plate [29], was considered, and for an annular plate of inner radius ${\mathsf{\xi }}_0=0.2$, the solution of the corresponding Lamé problem for a ring [34] loaded with latent internal pressure, the form of which is given below (19). The dimensionless level of PS in both cases was determined as a level of the dimensionless initial loading $p_0$ and varied in the range of $p_0={10}^{-4},\dots ,{10}^{-3}$ corresponding to the most common cases in practice. The results of tests on calculating the AFC at the probing point ${\mathsf{\xi }}_z$ and deflection functions at the probing frequency ${\mathsf{\kappa }}_z$ for a solid plate are shown, respectively, in Figure 2a,b and for an annular plate in Figure 3a,b. In the figures, the problem solutions at $p_0=0$ (no PS) are marked by a solid line, and the values of the dimensionless PS level $p_0=5\cdot {10}^{-4},{10}^{-3},5\cdot {10}^{-3}$ are marked by dotted lines.

It can be seen from the graphs that there are differences in the AFC, but they become significant near the resonance only. Accordingly, near resonance, the amplitude of vibrations depends most of all on the PS level. It should be noted that a similar situation arose in the study of other problems of modeling PS [2,26,27]. Based on the analysis performed, it should be concluded that for the identification of PS, it is necessary to select frequency ranges in the neighborhood of resonances for both of the studied inverse problems. It should also be noted that in both cases, with an increase in the PS level, the resonant frequencies shift to the right, and the vibration amplitude decreases (the effective stiffness of the plates increases).

4. Scheme for Solving Inverse Problems of PS Identification

To solve inverse problems, we use a special projection method based on the representation of all unknown functions in the form of expansions in systems of linearly independent functions. To use it, let us formulate a weak statement of problem (11) taking into account boundary conditions (7) and (8) or (9). We scalarly multiply the first equation by the function of the possible field of the angle of rotation ${\mathsf{\theta }}_1(\mathsf{\xi },\mathsf{\kappa })$ of the normal and scalarly multiply the second equation by the function of the possible deflection field $w_1(\mathsf{\xi },\mathsf{\kappa })$. Using the formula for integration by parts, boundary conditions and carrying out transformations, a weak statement of the problem was obtained in the form:

$$\begin{array}{l}{\displaystyle \underset{0}{\overset{1}{\int }}(\mathsf{\gamma }\mathsf{\xi }{\mathsf{\theta }}_1\left(D\frac{(1-\mathsf{\nu })}{2}+s_{rr}^0\right)w^{\prime }+\left(\left(\mathsf{\gamma }\mathsf{\xi }D\frac{(1-\mathsf{\nu })}{2}+\frac{D+\mathsf{\xi }{{\mathsf{\sigma }}_{rr}^0}^{\prime }+{\mathsf{\sigma }}_{rr}^0}{\mathsf{\xi }}-{\mathsf{\kappa }}^2\mathsf{\rho }\mathsf{\xi }\right){\mathsf{\theta }}_1-D\mathsf{\nu }{{\mathsf{\theta }}_1}^{\prime }\right)\mathsf{\theta }-}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}-\left(\mathsf{\xi }\left(D+s_{rr}^0\right){{\mathsf{\theta }}_1}^{\prime }-D\mathsf{\nu }{\mathsf{\theta }}_1\right){\mathsf{\theta }}^{\prime })\mathsf{\xi }d\mathsf{\xi }=0,\\ {\displaystyle \underset{0}{\overset{1}{\int }}\left(\mathsf{\xi }\left(D\frac{(1-\mathsf{\nu })}{2}+s_{rr}^0\right){w_1}^{\prime }{w}^{\prime }+D\frac{(1-\mathsf{\nu })}{2}\mathsf{\xi }{w_1}^{\prime }\mathsf{\theta }-{\mathsf{\kappa }}^2\mathsf{\rho }\mathsf{\xi }{w}_{1}w\right)}\mathsf{\xi }d\mathsf{\xi }=-{\displaystyle \underset{0}{\overset{1}{\int }}\mathrm{q}{\mathsf{\xi }}^2{w}_{1}d\mathsf{\xi }}.\end{array}$$

(15)

A detailed description of the used projection technique is presented in [29]. Let us give its basic scheme for the problems under consideration. The required function $s_{rr}^0(\mathsf{\xi })$ can be represented in the form of an expansion in terms of a system of orthogonal functions ${\mathsf{\psi }}_j^{}(\mathsf{\xi })$:

$$s_{rr}^0(\mathsf{\xi })={\displaystyle \sum _{j=1}^M{C}_j^{}{\mathsf{\psi }}_j^{}(\mathsf{\xi })}.$$

(16)

Using the linearity of Equation (15) with respect to the functions $w$, $\mathsf{\theta }$, ${\mathsf{\theta }}_1$, and $w_1$, substituting expansions (12) and (16) into relation (15), and sequentially choosing the basic functions $w_1={\mathsf{\phi }}_n,\hspace{0.17em}{\mathsf{\theta }}_1={\mathsf{\gamma }}_n,\hspace{0.17em}\hspace{0.17em}n=1\dots N$ as possible functions, a system of $2N$ linear equations with respect to the coefficient functions $a_i(\mathsf{\kappa })$ and $b_i(\mathsf{\kappa })$ can be obtained from Equation (15). Having determined the coefficients $a_i(\mathsf{\kappa })$, $b_i(\mathsf{\kappa })$ in the form of expressions with respect to $C_j^{}$ and $\mathsf{\kappa }$, they are substituted into the expansion (12). Thus, it is possible to obtain an expression for the deflection function $w(\mathsf{\xi },\mathsf{\kappa },C_j)$, which must satisfy the additional condition (10) of inverse problems. Choosing frequencies ${\mathsf{\kappa }}_m(m=1\dots M)$, we obtain a system of $M$ nonlinear equations of order $2M$ with respect to a set of $M$ coefficients $C_j^{},j=1\dots M$ in a form (17), from the solution of which we can determine the expansion coefficients (16) of the desired function $s_{rr}^0(\mathsf{\xi })$.

$$w({\mathsf{\xi }}_z,{\mathsf{\kappa }}_m,C_j)=f({\mathsf{\kappa }}_m),\hspace{0.17em}\hspace{0.17em}j=1\dots M,\hspace{0.17em}\hspace{0.17em}m=1\dots M.$$

(17)

The developed projection approach was implemented in the Maple package. Its realization combined the solution of direct problems using the Galerkin method, as well as numerical integration and solution of systems of linear and nonlinear equations using built-in solvers. For the functions of the deflection and the angle of rotation of the normal, 6–7 basis functions were used, and the number and type of basis functions for determining the prestress were selected for each test separately and are given in their descriptions.

5. Computational Tests for Identification of PS

On the basis of the projection scheme proposed in Section 4, a number of computational tests were carried out to identify the distribution function $s_{rr}^0(\mathsf{\xi })$ of the flat PS for both plates. In the first two tests, the stresses arising during the initial radial loading of the plate by a normal load $p_0$ applied on the outer radius in the case of a solid plate and on the inner radius in the case of an annular plate were considered as the PS field. In this case, under elastic deformation for the initial problems, it is possible to write out exact solutions in stresses. For a solid plate, the distribution of radial stresses is constant [29]:

$$s_{rr}^0(\mathsf{\xi })=p_0.$$

(18)

For an annular plate, it can be defined as a solution to the corresponding Lamé problem for a disk [34]:

$$s_{rr}^0(\mathsf{\xi })=\frac{p_0}{{\mathsf{\xi }}_0^{-2}-1}\left(1-\frac{1}{{\mathsf{\xi }}^2}\right).$$

(19)

In this case, for both formulations of inverse problems, the form of the function $s_{rr}^0(\mathsf{\xi })$ is known, and it is necessary to find only the parameter of the initial load, which determines the level of PS. For this, the developed scheme can also be applied, while in expansion (16), it is necessary to use only one basis function of the form (18) or (19), respectively. Then, we can determine the desired parameter $p_0$ from the solution of Equation (17) for one selected probe frequency.

Test 1. The level of the uniform field of the PS was determined in the case of a solid plate for different values. The probing frequency was chosen near the first resonance $\mathsf{\kappa }=8.45$. In addition, tests were carried out with an additive noise (according to normal distribution law) of the input data by 0.5%, which by a significant margin exceeds the error of modern measuring instruments used in the implementation of the acoustic method. The obtained identification results are shown in

Table 1. Identification of the prestress level for a solid plate and test with noise.

No	$\mathbf{Exact} {\mathit{p}}_0$	Recovery (error, %)	Noise 0.5%, (error, %)
1	0.01	0.00999 (0.10%)	0.00986 (1.40%)
2	0.005	0.00497 (0.60%)	0.00487 (2.60%)
3	0.001	0.00098 (2.00%)	0.00096 (4.00%)
4	0.0005	0.00048 (4.00%)	0.00045 (10.0%)

; the identification error is indicated in parentheses.

The above results show that the developed technique is applicable, among other things, to noisy input data.

Test 2. Determination of the initial loading parameter, which caused a PS of the form (19) in an annular plate, was carried out for its various values. The results of the test are presented in

Table 2. Identification of the prestress level for an annular plate.

No	$\mathbf{Exact} {\mathit{p}}_0$	Recovery (error, %)
1	0.01	0.01003 (0.30%)
2	0.005	0.00497 (0.60%)
3	0.001	0.00101 (1.00%)
4	0.0005	0.00049 (2.00%)

.

Note that with a decrease in the value of the PS level, its influence on the frequency response decreases, and therefore, the accuracy of its determination deteriorates, which is also evidenced by the results given in Section 3.

In the following tests, situations are considered when the origin of PS is generally unknown; they could arise both in the case of elastic or inhomogeneous plastic deformation and could be influenced by temperature or other influences. In such cases, an economical and easy-to-implement approach is needed to assess the level and nature of the PS distribution in the plate. Similar advantages are possessed by the projection technique proposed in this work, which makes it possible to determine the approximation of the sought functions in the class of given ones, for example, linear or quadratic.

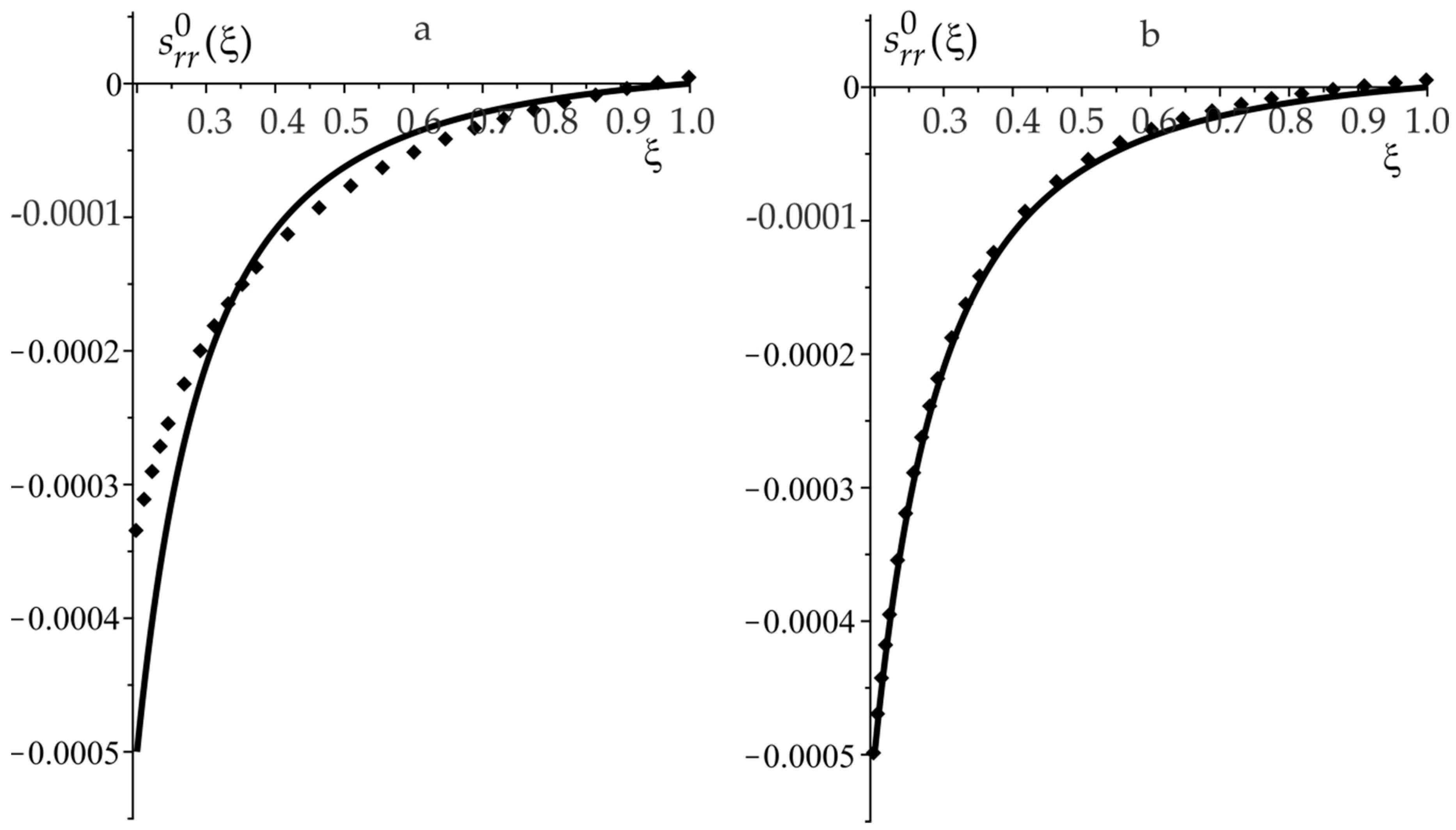
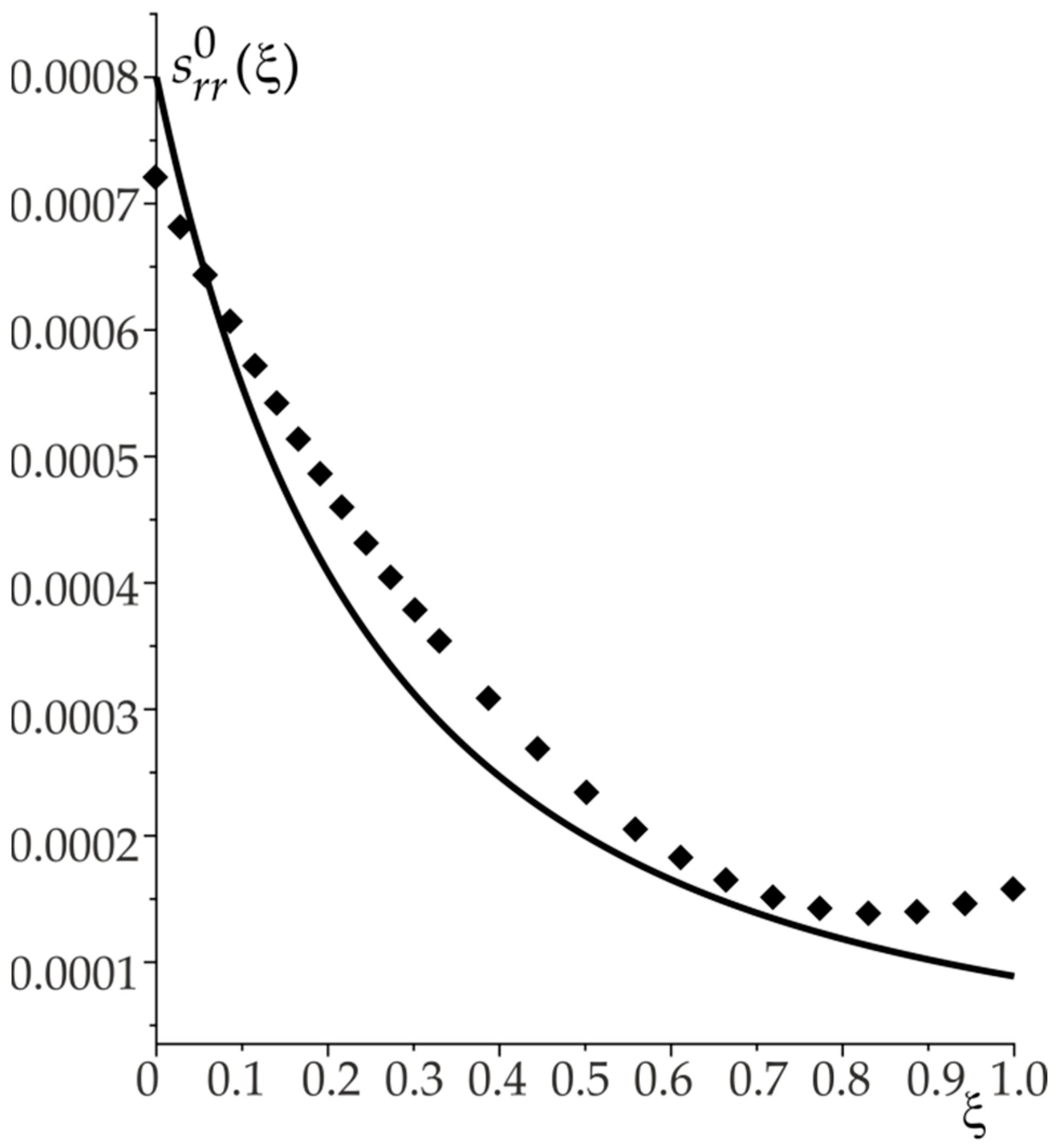
Test 3. Reconstruction of the PS distribution function $s_{rr}^0(\mathsf{\xi })=\frac{5\cdot {10}^{-3}}{{\mathsf{\xi }}_0^{-2}-1}\left(1-\frac{1}{{\mathsf{\xi }}^2}\right)$ corresponding to the case of elastic deformation in the presence of the initial internal pressure (19) in the annular plate of the inner radius ${\mathsf{\xi }}_0^{}=0.2$. The frequency range $\left[8.1,\hspace{0.17em}\hspace{0.17em}8.5\right]$ is selected for identification. The renewal was carried out in the class of quadratic functions ($M=3$,${\mathsf{\psi }}_j^{}(\mathsf{\xi })={\mathsf{\xi }}^{j-1}$). In this case, the relative error of reconstruction does not exceed 5% throughout the entire section, except for the vicinity of the inner radius (rigid restraint), where it reaches 20%. Figure 4a shows the results of the reconstruction; the solid line denotes the exact function, and the dots denote the reconstructed function.

Note that the developed approach can be applied in two stages: at the first stage, the PS is renewed as an arbitrary function; then, if the form of the renewed function is similar to the solution in the case of elastic or plastic deformations [26,35], it is possible to carry out repeated renewal in order to determine the parameters of the solution, the form of which is known (as in tests 1 and 2), and significantly improve the identification accuracy. The result can be evaluated by the coincidence of the AFC. This was carried out in this test; the relative error did not exceed 1%. The result of the reconstruction is shown in Figure 4b.

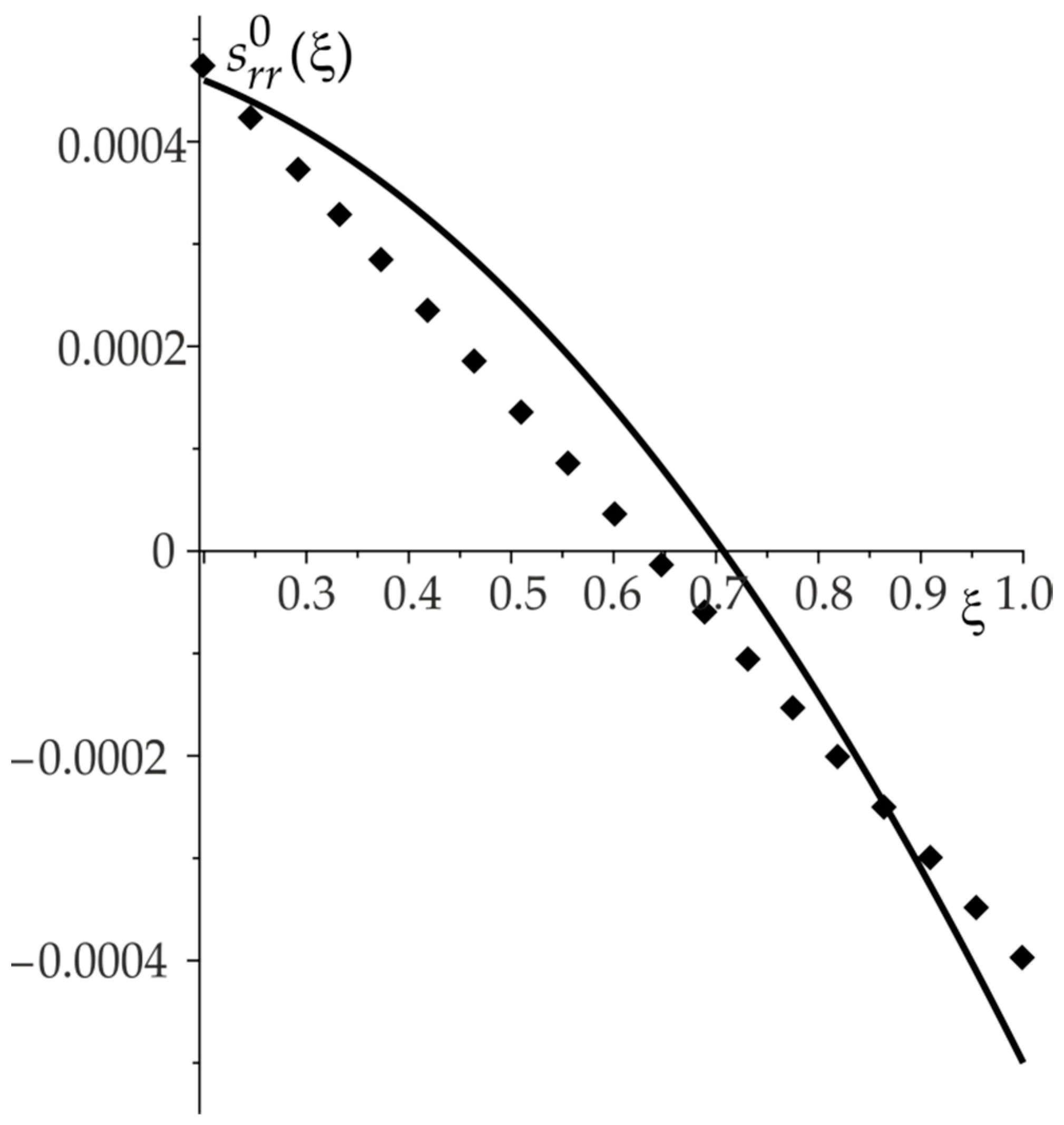
Test 4. Model example. Reconstruction of the function $s_{rr}^0(\mathsf{\xi })=0.2\cdot {10}^{-3}{(\mathsf{\xi }+0.5)}^{-2},$ similar to a distribution function of the PS, corresponding to the case of elastic deformation of an annular plate under radial loading. The case of a solid plate was considered, which can be obtained from a prestressed annular plate using an insert. The frequency range $\left[7.8,\hspace{0.17em}\hspace{0.17em}8.1\right]$ is selected for identification. The identification was carried out in the class of quadratic functions ($M=3$, ${\mathsf{\psi }}_j^{}(\mathsf{\xi })={\mathsf{\xi }}^{j-1}$). The relative error of reconstruction does not exceed 9%. Figure 5 shows the results of the reconstruction; the solid line denotes the exact function, the dots denote the reconstructed function.

Test 5. Model example. Reconstruction of the function $s_{rr}^0(\mathsf{\xi })={10}^{-3}\cdot \left(0.5-{\mathsf{\xi }}^2\right)$ describing the PS field, which is compressive for a part of an annular plate of radius ${\mathsf{\xi }}_0^{}=0.2$, and stretching for another part, that is, it changes sign. The frequency range $\left[8.2,\hspace{0.17em}\hspace{0.17em}8.5\right]$ is selected for identification. The identification was carried out in the class of linear functions ($M=2$,${\mathsf{\psi }}_j^{}(\mathsf{\xi })={\mathsf{\xi }}^{j-1}$). The relative error of reconstruction does not exceed 8%. Figure 6 shows the results of the reconstruction; the solid line denotes the exact function, and the dots denote the reconstructed function.

Note that in practice, the problems of identification of a level and character of monotonicity of the laws of PS variation in plates, which are most often monotonic functions arising as a result of elastic or plastic deformation of the plates, are of the greatest importance. In view of this, renewal in the class of linear functions, which is the most efficient in terms of speed in action, can be considered the most promising.

6. Conclusions

The main goal of this study was to create a theoretical basis for the determination of preliminary stresses in solid and annular circular plates using the non-destructive method of acoustic sounding. In this case, it was necessary to take into account the transverse shear deformations, for which the Timoshenko hypothesis was used, as well as the inhomogeneity of all characteristics of the plates along the radial coordinate and the effect of prestresses. As a result, using the previously obtained results, it was possible to construct the desired model, taking into account all the features, and, on its basis, to construct a method for determining the PS from the data of the frequency response. The technique was implemented in the form of a computing software package realized via Maple. On its basis, computational tests for identification of the function of changing the PS in the range of levels corresponding to their common practical values were carried out. Reconstruction was performed in the cases of known conditions of the initial action, which caused the PS, when it is necessary to estimate the level of the PS, and in the cases of arbitrary laws of change in the PS. Additionally, the computational scheme was tested on noisy input data (according to normal distribution law) and has shown its effectiveness in the case when the input data have an error that exceeds the accuracy of modern instruments used to measure frequency response. Additionally, note that the developed methodology allows for the determination of the desired functions, including in simple classes of functions, which is important in practical use and can significantly reduce the time spent on identification in comparison with the iterative methods. When analyzing the solution of inverse problems, practical recommendations were given on the use of the computational scheme and the choice of the frequency range of probing to achieve the best quality of reconstruction. They allow flexible adjustment of the method for each specific case.

The proposed technique can become a theoretical basis for the development of diagnostic equipment designed to determine the level and distribution of prestresses in circular and annular plates. At the same time, its advantage is that the samples under study are not damaged and retain their performance. For the practical implementation of the technique, it is necessary to provide a mechanism for fixing plates of various external and internal radius, as well as an oscillator, for example, on a piezoelectric basis. Then, using sensors installed in a certain area, an acoustic response should be taken in a selected frequency range, near resonance (based on recommendations). These data, together with the initial characteristics of the plate (radius, thickness, material parameters, coordinates of sensors, etc.), must be transferred to the processing system or unloaded as numerical data for the computing software package in the Maple package, where further processing of the input information takes place and a developed method for determining prestress is applied. The verification of the obtained results can be carried out based on the comparison of the acoustic response measured in the experiment and calculated in the computing software package for the found values of the PS.