Design, Modeling, and Analysis of Piezoelectric-Actuated Device for Blood Sampling
Abstract
:1. Introduction and Purpose of the Study
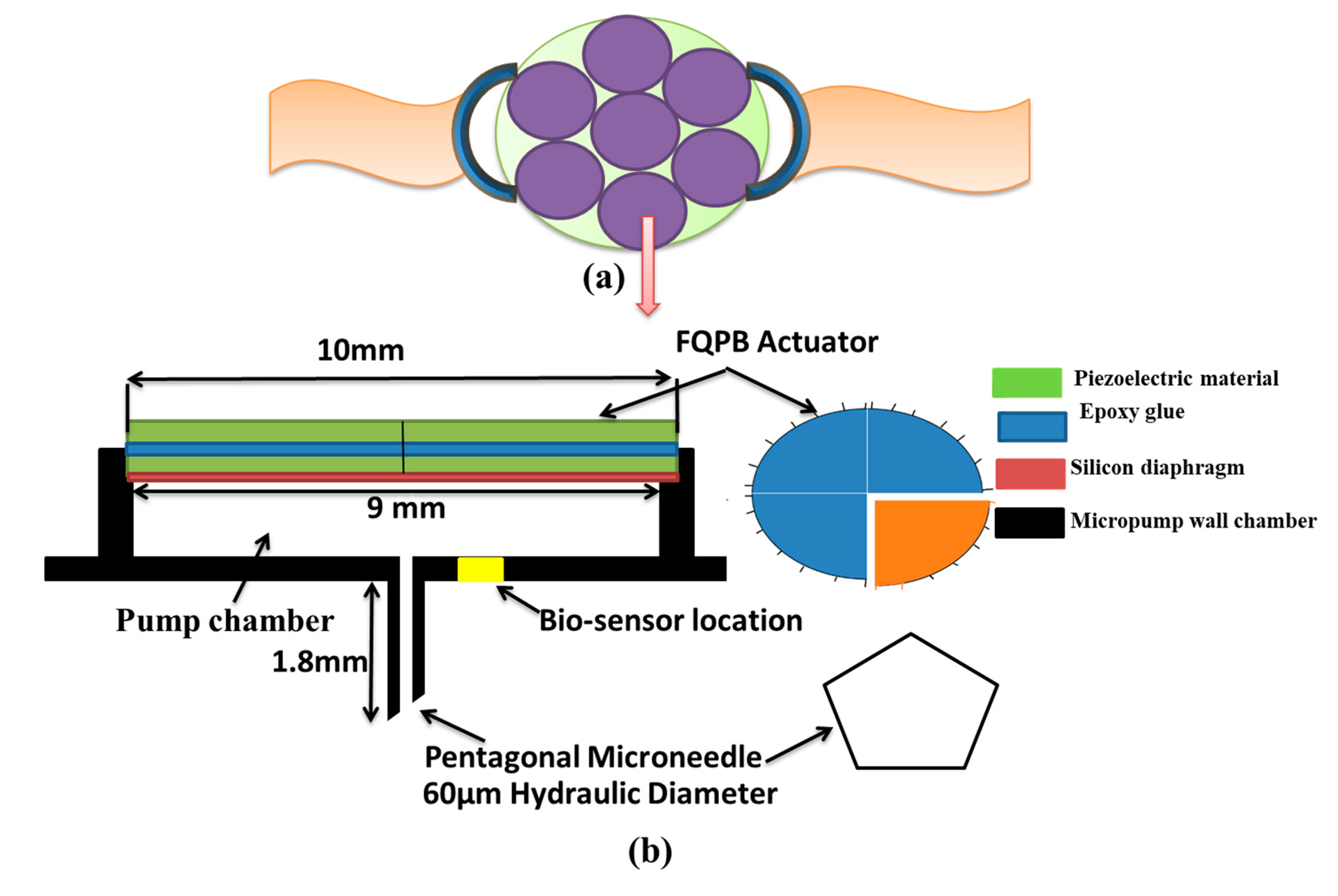
2. Physical Modeling of the Device
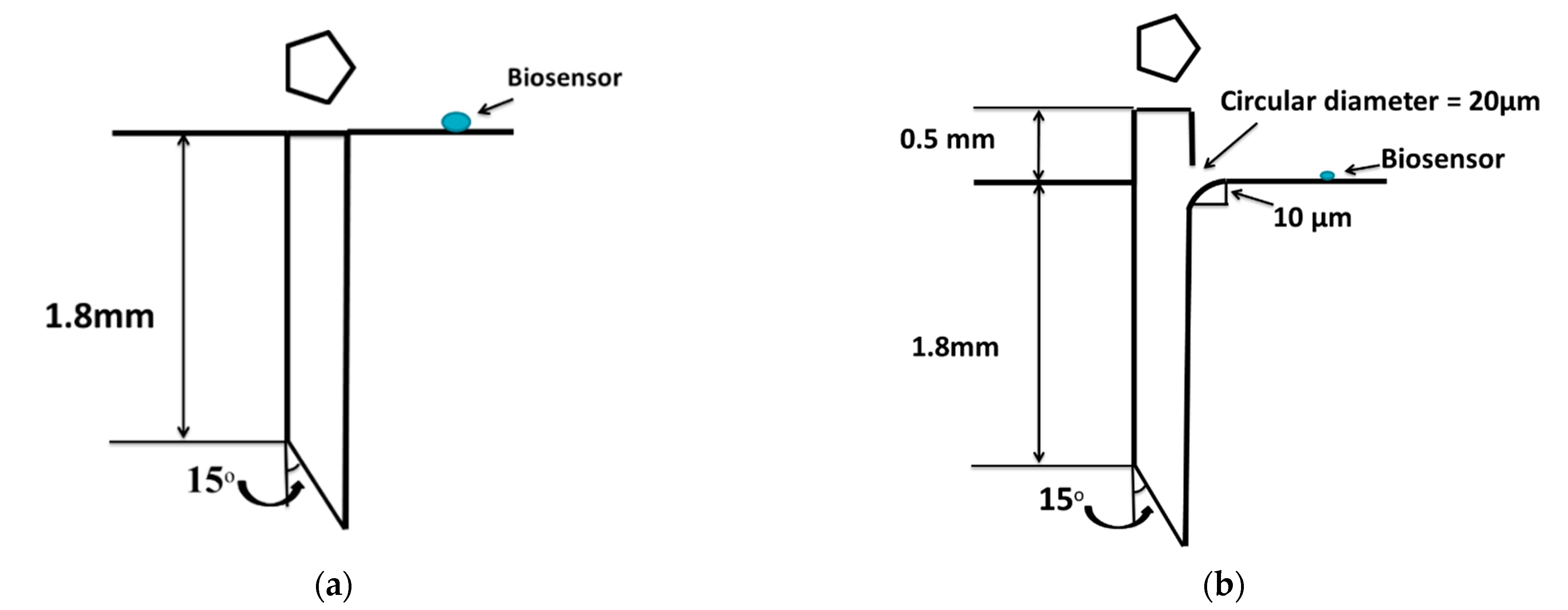
2.1. Microneedle
2.2. Biosensor
2.3. FQPB Actuator
2.4. Working Principle
3. Finite Element Modeling of the Micropump
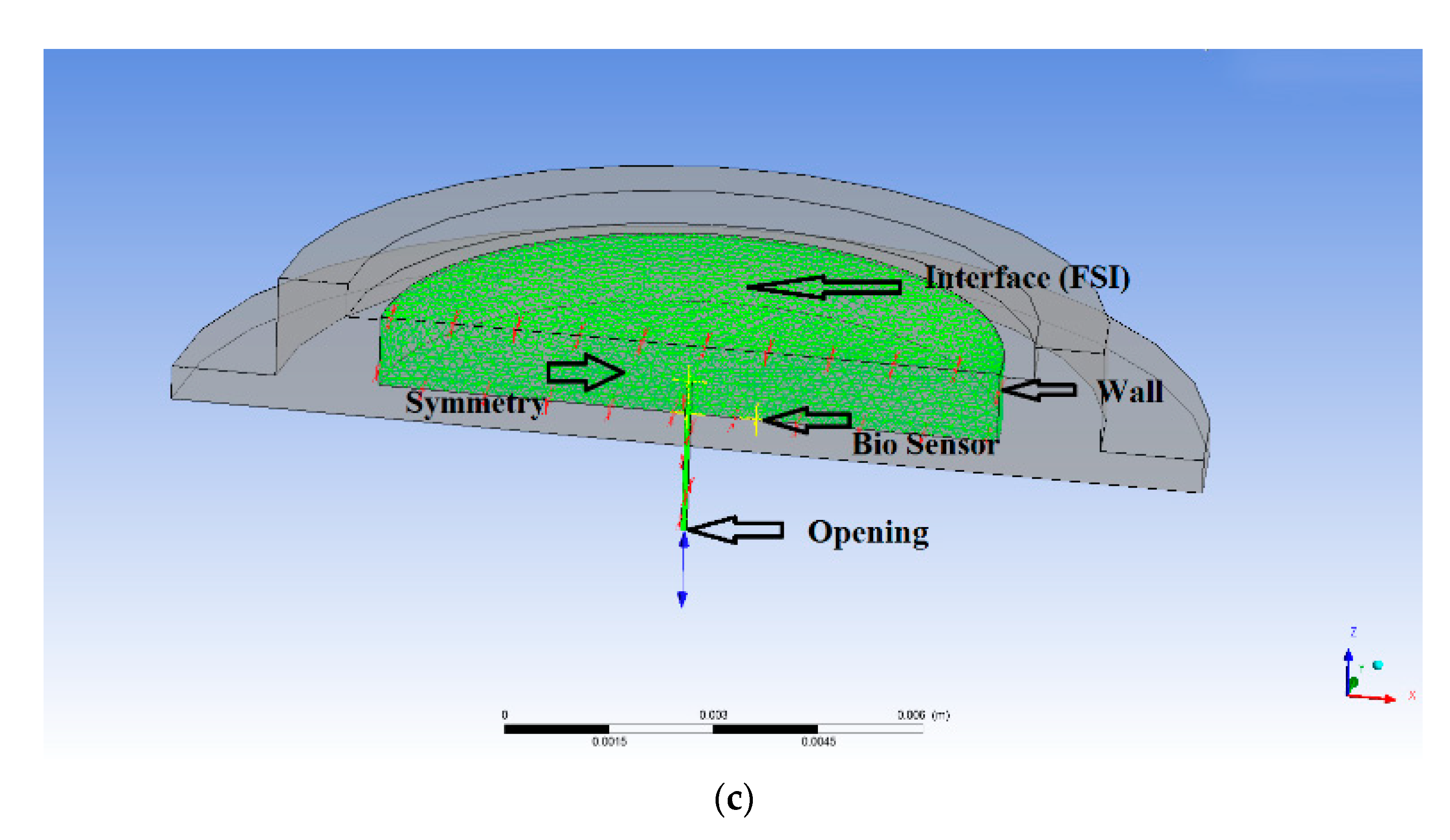
3.1. Fluid–Structure Interaction (FSI)
3.2. Boundary Conditions
3.2.1. Opening Condition
3.2.2. Wall Condition
3.2.3. Symmetry Condition
3.2.4. Interface Condition
3.3. Mesh Independence Test for FQPB and Micropump
4. Results of the Micropump Simulation
4.1. Static and Modal Analysis of the Actuator (FQPB)
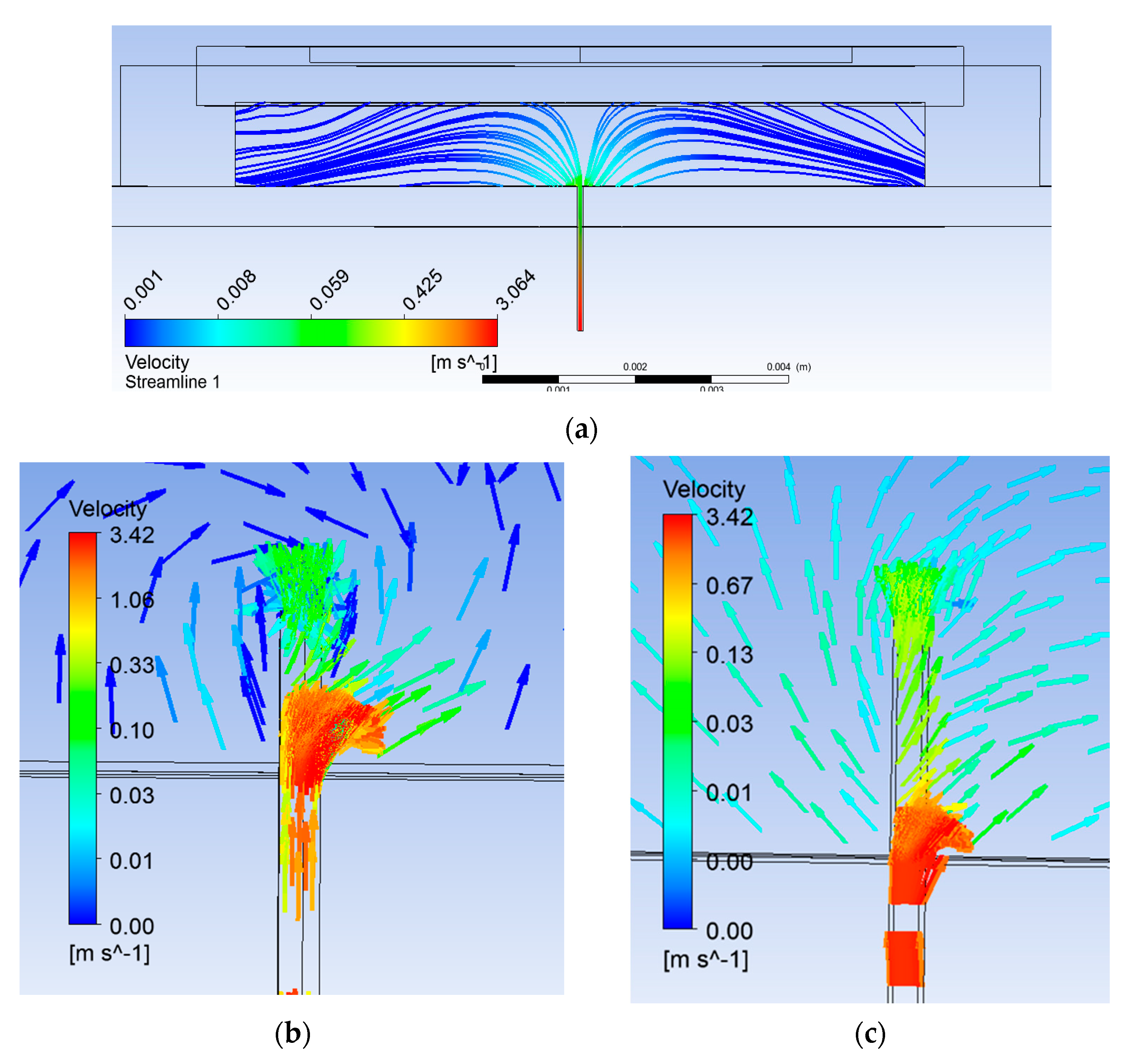
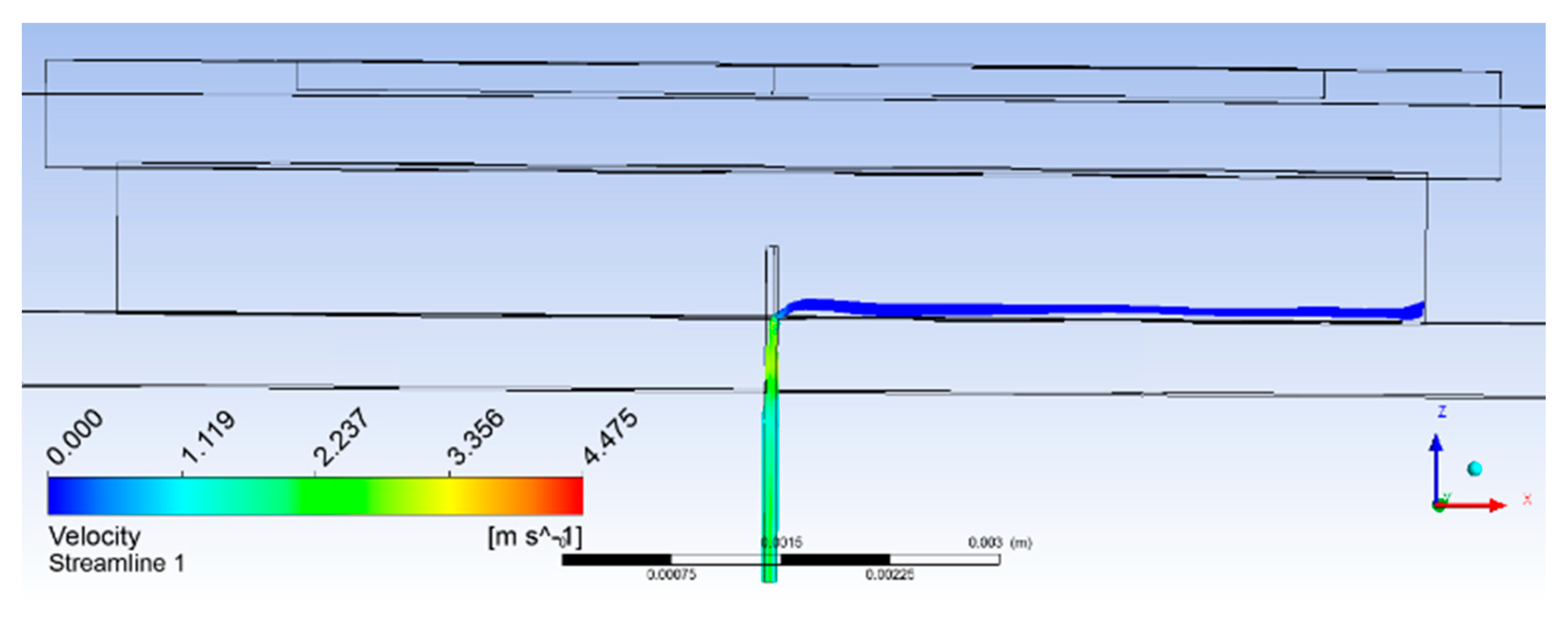
4.2. Flow Analysis with Flushed Microneedle
4.3. Flow Analysis with Modified Microneedle
- Extension of the microneedle into the pump chamber,
- Provision of the orifice (hole) towards biosensor location, and
- Filleting of microneedle tip.
4.4. Flow Analysis at Reduced Actuation Frequency
5. Conclusions
- The design may be implemented as a wearable device. Considering advancements in the manufacturing of microfluidic systems, manufacturability should not be a problem.
- The design may be modified to accommodate more sensors for testing other diseases.
- The FQPB-based micropump with extended microneedle length inside the pump chamber brings the benefit of flow channelization towards the biosensor location, resulting in a reduction in applied voltage (2.5 V) and reduced operating frequency (22 kHz).
- The simulation results showed that 1.256 µL of the sample was collected at the biosensor in 1 s, which is more than the required volume.
- The designed device will be easy to use and may allow multiple samplings with a single replacement.
- The blood was collected in a closed chamber, thereby giving higher accuracy in comparison to the finger-stick, as well as preventing environmental contamination.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Atlas, I.D.F.D. IDF Diabetes Atlas Ninth Edition, 9th ed.; International Diabetes Federation: Brussels, Belgium, 2019; ISBN 9782930229874. [Google Scholar]
- Li, H.; Liu, J.; Li, K.; Liu, Y. A review of recent studies on piezoelectric pumps and their applications. Mech. Syst. Signal Process. 2021, 151, 107393. [Google Scholar] [CrossRef]
- Asadi Dereshgi, H.; Dal, H.; Yildiz, M.Z. Piezoelectric micropumps: State of the art review. Microsyst. Technol. 2021, 1–29. [Google Scholar] [CrossRef]
- Laser, D.J.; Santiago, J.G. A review of micropumps. J. Micromech. Microeng. 2004, 14, R35–R64. [Google Scholar] [CrossRef]
- Ha, D.-H.; Phan, V.P.; Goo, N.S.; Han, C.H. Three-dimensional electro-fluid–structural interaction simulation for pumping performance evaluation of a valveless micropump. Smart Mater. Struct. 2009, 18, 104015. [Google Scholar] [CrossRef]
- Fan, B.; Song, G.; Hussain, F. Simulation of a piezoelectrically actuated valveless micropump. Smart Mater. Struct. 2005, 14, 400–405. [Google Scholar] [CrossRef]
- Kan, J.; Yang, Z.; Peng, T.; Cheng, G.; Wu, B. Design and test of a high-performance piezoelectric micropump for drug delivery. Sens. Actuators A Phys. 2005, 121, 156–161. [Google Scholar] [CrossRef]
- Gattiker, G.E.; Kaler, K.V.I.S.; Mintchev, M.P. Electronmc Mosquito: Designing a semi-invasive microsystem for blood sampling, analysis and drug delivery applications. Microsyst. Technol. 2005, 12, 44–51. [Google Scholar] [CrossRef]
- Tsuchiya, K.; Nakanishi, N.; Uetsuji, Y.; Nakamachi, E. Development of blood extraction system for health monitoring system. Biomed. Microdevices 2005, 7, 347–353. [Google Scholar] [CrossRef]
- Wang, B.; Chu, X.; Li, E.; Li, L. Simulations and analysis of a piezoelectric micropump. Ultrasonics 2006, 44, 643–646. [Google Scholar] [CrossRef]
- Haldkar, R.K.; Sheorey, T.; Gupta, V.K.; Ansari, M.Z. Four segment piezo based micropump. Proc. SPIE Smart Sens. Actuators MEMS VIII 2017, 10246, 102461B. [Google Scholar] [CrossRef]
- Yazdi, S.A.F.F.; Corigliano, A.; Ardito, R. 3-D design and simulation of a piezoelectric micropump. Micromachines 2019, 10, 259. [Google Scholar] [CrossRef] [Green Version]
- Cui, Q.; Liu, C.; Zha, X.F. Simulation and optimization of a piezoelectric micropump for medical applications. Int. J. Adv. Manuf. Technol. 2008, 36, 516–524. [Google Scholar] [CrossRef]
- Haldkar, R.K.; Sheorey, T.; Gupta, V.K. The Effect of Operating Frequency and Needle Diameter on Performance of Piezoelectric Micropump. In Advanced Materials; Parinov, I.A., Chang, S.-H., Gupta, V.K., Eds.; Springer International Publishing AG: Cham, Switzerland, 2018; Volume 207, pp. 567–578. [Google Scholar]
- Aboubakri, A.; Ahmadi, V.E. Modeling of a Passive-Valve Piezoelectric Micro-Pump: A Parametric Study. Micromachines 2020, 11, 752. [Google Scholar] [CrossRef]
- Bodén, R.; Hjort, K.; Schweitz, J.-Å.; Simu, U. A metallic micropump for high-pressure microfluidics. J. Micromech. Microeng. 2008, 18, 115009. [Google Scholar] [CrossRef]
- Sayar, E.; Farouk, B. Multifield analysis of a piezoelectric valveless micropump: Effects of actuation frequency and electric potential. Smart Mater. Struct. 2012, 21, 075002. [Google Scholar] [CrossRef]
- Haldkar, R.K.; Khalatkar, A.; Gupta, V.K.; Sheorey, T. New piezoelectric actuator design for enhance the micropump flow. Mater. Today Proc. 2021, 44, 776–781. [Google Scholar] [CrossRef]
- Ali, M.Y.; Kuang, C.; Khan, J.; Wang, G. A dynamic piezoelectric micropumping phenomenon. Microfluid. Nanofluid. 2010, 9, 385–396. [Google Scholar] [CrossRef]
- Jang, L.S.; Kan, W.H. Peristaltic piezoelectric micropump system for biomedical applications. Biomed. Microdevices 2007, 9, 619–626. [Google Scholar] [CrossRef] [PubMed]
- Amirouche, F.; Zhou, Y.; Johnson, T. Current micropump technologies and their biomedical applications. Microsyst. Technol. 2009, 15, 647–666. [Google Scholar] [CrossRef]
- Rao, K.S.; Sateesh, J.; Guha, K.; Baishnab, K.L.; Ashok, P.; Sravani, K.G. Design and analysis of MEMS based piezoelectric micro pump integrated with micro needle. Microsyst. Technol. 2018, 4, 3153–3159. [Google Scholar] [CrossRef]
- Kimoto, H.; Inoue, T.; Tsuchiya, K.; Kajiwara, K.; Kimura, M. Selection of the best shape for a micro painless needle. In Proceedings of the 2014 International Symposium on Micro-NanoMechatronics and Human Science (MHS), Nagoya, Japan, 10–12 November 2014; pp. 1–5. [Google Scholar] [CrossRef]
- Haldkar, R.K.; Gupta, V.K.; Sheorey, T. Modeling and flow analysis of piezoelectric based micropump with various shapes of microneedle. J. Mech. Sci. Technol. 2017, 31, 2933–2941. [Google Scholar] [CrossRef]
- Jhunjhunwala, P.; Padole, P.M.; Thombre, S.B. CFD Analysis of Pulsatile Flow and Non-Newtonian Behavior of Blood in Arteries CFD Analysis of Pulsatile Flow and Non-Newtonian Behavior of Blood in Arteries. MCB 2015, 12, 37–47. [Google Scholar]
- Li, C.G.; Lee, C.Y.; Lee, K.; Jung, H. An optimized hollow microneedle for minimally invasive blood extraction. Biomed. Microdevices 2013, 15, 17–25. [Google Scholar] [CrossRef]
- Ahmad, R.; Tripathy, N.; Hahn, Y.B.; Umar, A.; Ibrahim, A.A.; Kim, S.H. A robust enzymeless glucose sensor based on CuO nanoseed modified electrodes. Dalton Trans. 2015, 44, 12488–12492. [Google Scholar] [CrossRef]
- Sandhyarani, N. Surface modification methods for electrochemical biosensors. Electrochem. Biosens. 2019, 45–75. [Google Scholar] [CrossRef]
- Stemme, E.; Larsson, S.-G. The Piezoelectric Capillary Injector—A New Hydrodynamic Method for Dot Pattern Generation. IEEE Trans. Electron Devices 1973, 20, 14–19. [Google Scholar] [CrossRef]
- Choi, A.; Vatanabe, S.L.; de Lima, C.R.; Silva, E.C.N. Computational and experimental characterization of a low-cost piezoelectric valveless diaphragm pump. J. Intell. Mater. Syst. Struct. 2011, 23, 53–63. [Google Scholar] [CrossRef]
- Lerch, R. Simulation of Piezoelectric Devices by Two- and Three-Dimensional Finite Elements. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1990, 37, 233–247. [Google Scholar] [CrossRef]
- Cho, Y.I.; Kensey, K.R. Effects of the non-Newtonian viscosity of blood on flows in a diseased arterial vessel. Part 1: Steady flows. Biorheology 1991, 28, 241–262. [Google Scholar] [CrossRef] [PubMed]
- Jhunjhunwala, P.; Padole, P.M.; Thombre, S.B. Non-Newtonian Blood Flow in Left Coronary Arteries with Varying Stenosis: A Comparative Study. Mol. Cell. Biomech. 2016, 13, 1–21. [Google Scholar] [CrossRef]
- Pfützner, A.; Schipper, C.; Ramljak, S.; Flacke, F.; Sieber, J.; Forst, T.; Musholt, P.B. Evaluation of the effects of insufficient blood volume samples on the performance of blood glucose self-test meters. J. Diabetes Sci. Technol. 2013, 7, 1522–1529. [Google Scholar] [CrossRef] [PubMed] [Green Version]

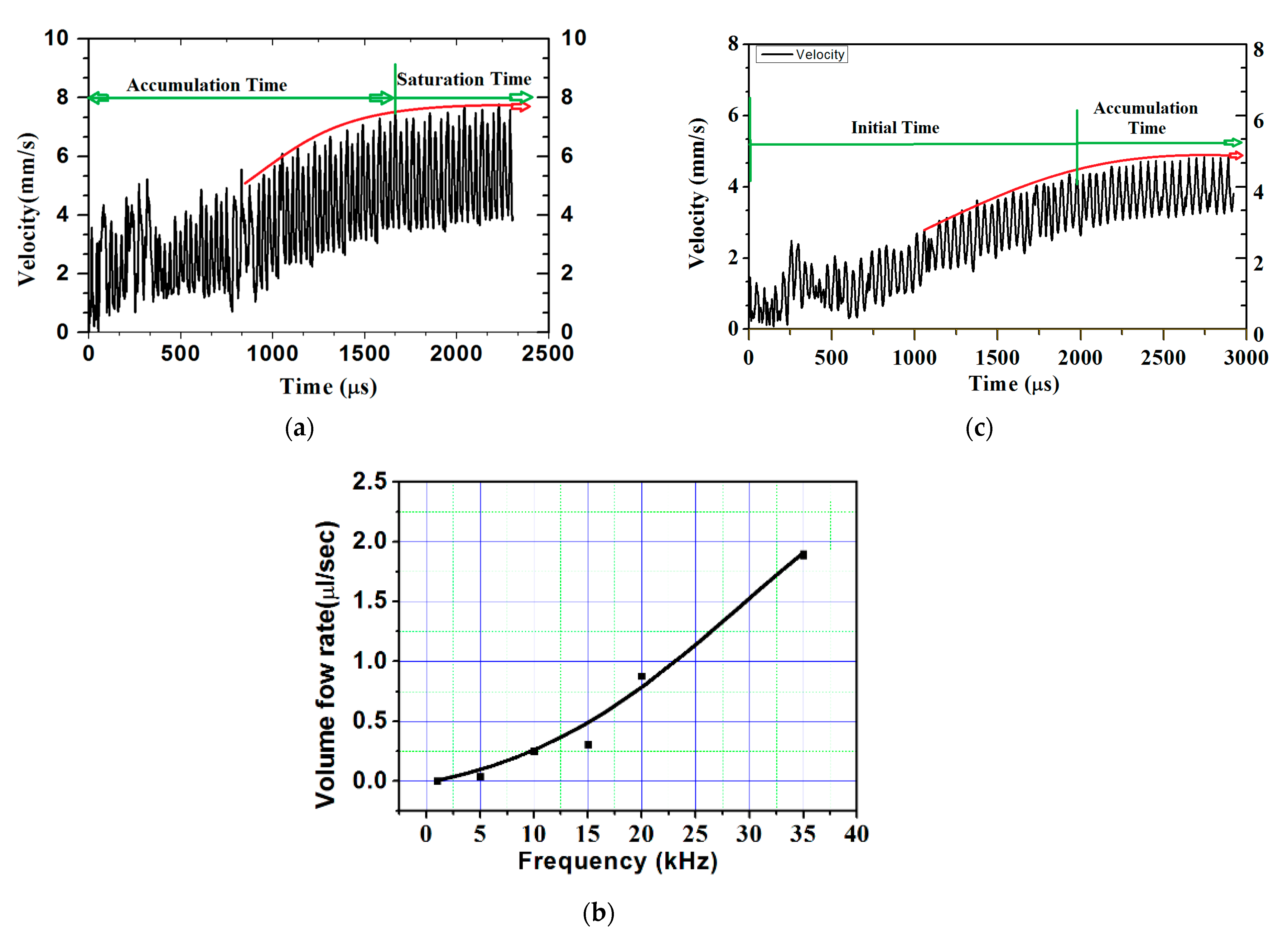
| Materials | Properties | Value | |
|---|---|---|---|
| Piezoelectric | Piezoelectric charge constant (C/N) | d31 = d32 | ‒320 × 10−12 |
| d33 | 650 × 10−12 | ||
| Relative dielectric constant | ε | 3600 | |
| Density (kg/m3) | ρ | 7800 | |
| Epoxy Glue | Module of elasticity (GPa) | 2.478 | |
| Density (kg/m3) | 1400 | ||
| Stainless steel | Module of elasticity (GPa) | 200 | |
| Density (kg/m3) | 7700 | ||
| Silicon | Module of elasticity (GPa) | 168.3 | |
| Density (kg/m3) | 2329 | ||
| Microneedle Type | Velocity at Biosensor Location (mm/s) | Volume Flow Rate at Biosensor Location (µL/sec) | Max Pressure (MPa) |
|---|---|---|---|
| Flush type | 3 | 0.471 | 8 |
| 0.25 mm extended | 4.5 | 1.413 | 4 |
| 0.50 mm extended | 5.6 | 1.758 | 3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haldkar, R.K.; Gupta, V.K.; Sheorey, T.; Parinov, I.A. Design, Modeling, and Analysis of Piezoelectric-Actuated Device for Blood Sampling. Appl. Sci. 2021, 11, 8449. https://doi.org/10.3390/app11188449
Haldkar RK, Gupta VK, Sheorey T, Parinov IA. Design, Modeling, and Analysis of Piezoelectric-Actuated Device for Blood Sampling. Applied Sciences. 2021; 11(18):8449. https://doi.org/10.3390/app11188449
Chicago/Turabian StyleHaldkar, Rakesh Kumar, Vijay Kumar Gupta, Tanuja Sheorey, and Ivan A. Parinov. 2021. "Design, Modeling, and Analysis of Piezoelectric-Actuated Device for Blood Sampling" Applied Sciences 11, no. 18: 8449. https://doi.org/10.3390/app11188449
APA StyleHaldkar, R. K., Gupta, V. K., Sheorey, T., & Parinov, I. A. (2021). Design, Modeling, and Analysis of Piezoelectric-Actuated Device for Blood Sampling. Applied Sciences, 11(18), 8449. https://doi.org/10.3390/app11188449








