Three-Dimensional Buckling Analysis of Functionally Graded Saturated Porous Rectangular Plates under Combined Loading Conditions
Abstract
1. Introduction
2. Theoretical Definition of the Problem
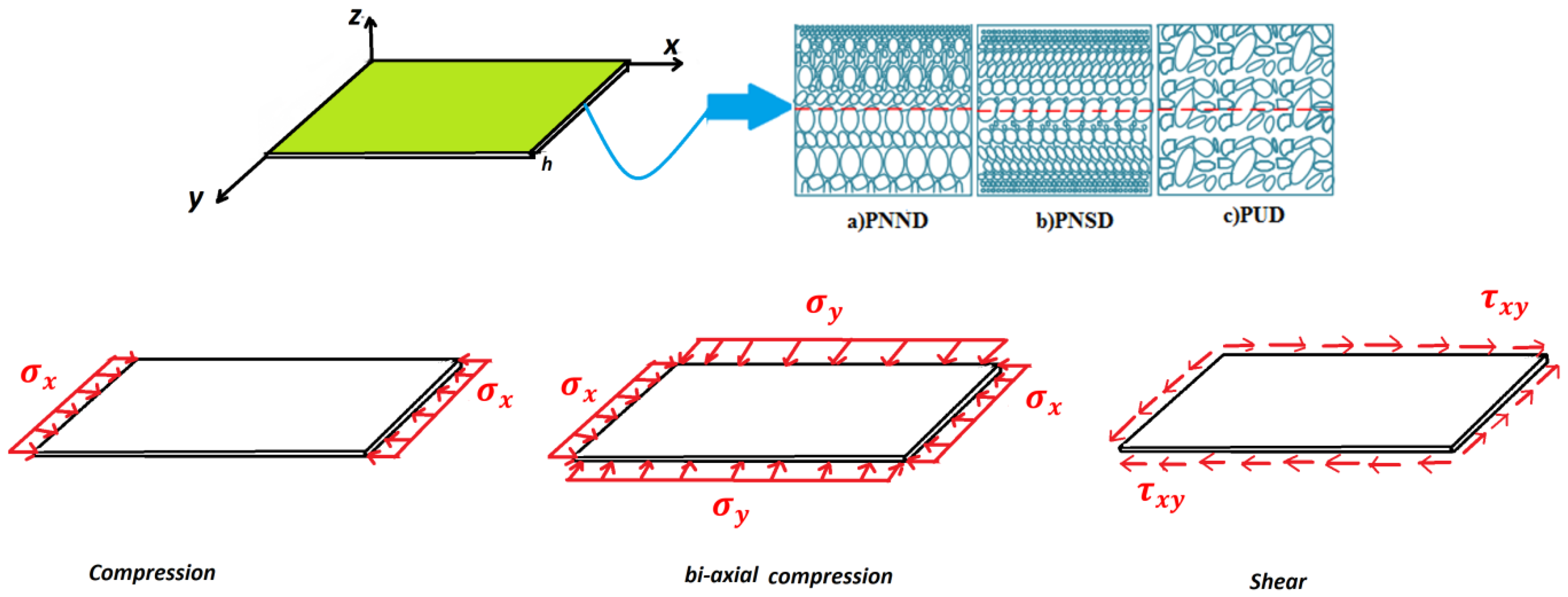
2.1. Poroelastic Modeling of Plates
2.2. Governing Equations
3. Mixed FE-GDQ Numerical Formulation
- (i)
- Simply supported BCs at all edges (SSSS):
- (ii)
- Clamped BCs at edges parallel to the y-axis (i.e., at ) and free BCs at edges parallel to the x-axis (i.e., at ) (CFCF):
- (iii)
- Clamped BCs at edges parallel to the x-axis (i.e., at ) and free BCs at edges parallel to the y-axis (i.e., at ) (FCFC):
4. Numerical Investigation
5. Conclusions
- The porosity coefficient more significantly affects the buckling load than the Skempton coefficient. In detail, an increased porosity coefficient and a decreased Skempton coefficient yield an overall decrease of the buckling load.
- Among different boundary and loading conditions, the maximum and minimum values of the buckling load are reached for a FCFC plate under a shear loading and a SSSS plate under a biaxial loading condition, respectively.
- The influence of the porosity coefficient on the buckling load for a uniform distribution is larger than other types of non-uniform porosity distributions.
- The effect of the Skempton coefficient on the buckling load, for a uniform distribution, is larger than other types of porosity distributions.
- By increasing the ratio, the buckling load generally decreases, except for a FCFC plate under a shear load and a SSSS plate under a normal uniaxial load, because of the variability in stiffness of the overall structure.
- The proposed method is verified to be a reliable tool for the computational study of saturated porous materials and structures, even from a design standpoint.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Fluid compressibility in pores | |
| Solid compressibility in pores | |
| Shear modulus | |
| Porosity coefficient | e0 |
| Biot’s effective stress coefficient | |
| Skempton coefficient | |
| Variation of fluid volume content | |
| Volumetric strain | |
| Poisson’s ratio | |
| Undrained Poisson’s ratio | u |
| Lamè constant | |
| Pore fluid pressure | P |
| Bulk modules | K |
| Undrained bulk modules | Ku |
| Biot’s modulus | |
| Total strain potential energy | |
| Potential energy related to geometry | |
| Elasticity modulus | E |
| Stress tensor | |
| Strain tensor | |
| Elasticity matrix | |
| Displacement components along x, y and z directions | u, v, w |
| Global Lagrange interpolation functions | |
| Weighted coefficients at the grid nodes of the solution domain | , |
| Buckling load | λ |
| Stability matrix due to the in-plane stresses | |
| Stiffness matrix |
References
- Biot, M.A. Theory of buckling of a porous slab and its thermoelastic analogy. J. Appl. Mech. ASME 1964, 31, 94–198. [Google Scholar] [CrossRef]
- Magnucki, K.; Stasiewicz, P. Elastic buckling of a porous beam. J. Theor. Appl. Mech. 2004, 42, 859–868. [Google Scholar]
- Magnucka-Blandzi, E. Axi-symmetrical deflection and buckling of circular porous-cellular plate. Thin-Walled Struct. 2008, 46, 333–337. [Google Scholar] [CrossRef]
- Magnucki, K.; Malinowski, M.; Kasprzak, J. Bending and buckling of a rectangular porous plate. Steel Compos. Struct. 2006, 6, 319–333. [Google Scholar] [CrossRef]
- Chen, D.; Yang, J.; Kitipornchai, S. Elastic buckling and static bending of shear deformable functionally graded porous beam. Compos. Struct. 2015, 133, 54–61. [Google Scholar] [CrossRef]
- Jasion, P.; Magnucka-Blandzi, E.; Szyc, W.; Magnucki, K. Global and local buckling of sandwich circular and beam-rectangular plates with metal foam core. Thin-Walled Struct. 2012, 61, 154–161. [Google Scholar] [CrossRef]
- Gao, K.; Huang, Q.; Kitipornchai, S.; Yang, J. Nonlinear dynamic buckling of functionally graded porous beams. Mech. Adv. Mater. Struct. 2019, 28, 418–429. [Google Scholar] [CrossRef]
- Tang, H.; Li, L.; Hu, Y. Buckling analysis of two-directionally porous beam. Aerosp. Sci. Techn. 2018, 78, 471–479. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Jafari, A. Buckling behavior of smart MEE-FG porous plate with various boundary conditions based on refined theory. Adv. Mater. Res. 2016, 5, 279–298. [Google Scholar] [CrossRef][Green Version]
- Kumar, R.; Lal, A.; Singh, B.N.; Singh, J. Meshfree approach on buckling and free vibration analysis of porous FGM plate with proposed IHHSDT resting on the foundation. Curved Layer. Struct. 2019, 6, 192–211. [Google Scholar] [CrossRef]
- Cong, P.H.; Chien, T.M.; Khoa, N.D.; Duc, N.D. Nonlinear thermomechanical buckling and post-buckling response of porous FGM plates using Reddy’s HSDT. Aerosp. Sci. Technol. 2018, 77, 419–428. [Google Scholar] [CrossRef]
- Bourada, M.; Bouadi, A.; Bousahla, A.A.; Senouci, A.; Bourada, F.; Tounsi, A.; Mahmoud, S.R. Buckling behavior of rectangular plates under uniaxial and biaxial compression. Struct. Eng. Mech. 2019, 70, 113–123. [Google Scholar]
- Thang, P.T.; Nguyen-Thoi, T.; Lee, D.; Kang, J.; Lee, J. Elastic buckling and free vibration analyses of porous-cellular plates with uniform and non-uniform porosity distributions. Aerosp. Sci. Techn. 2018, 79, 278–287. [Google Scholar] [CrossRef]
- Chen, D.; Yang, J.; Kitipornchai, S. Buckling and bending analyses of a novel functionally graded porous plate using Chebyshev-Ritz method. Arch. Civ. Mech. Eng. 2019, 19, 157–170. [Google Scholar] [CrossRef]
- Yang, J.; Chen, D.; Kitipornchai, S. Buckling and free vibration analyses of functionally graded graphene reinforced porous nanocomposite plates based on Chebyshev-Ritz method. Compos. Struct. 2018, 193, 281–294. [Google Scholar] [CrossRef]
- Tu, T.M.; Hoa, L.K.; Hung, D.X.; Hai, L.T. Nonlinear buckling and post-buckling analysis of imperfect porous plates under mechanical loads. J. Sandw. Struct. Mater. 2018, 22, 1910–1930. [Google Scholar] [CrossRef]
- Sekkal, M.; Fahsi, B.; Tounsi, A.; Mahmoud, S.R. A new quasi-3D HSDT for buckling and vibration of FG plate. Struct. Eng. Mech. 2017, 64, 737–749. [Google Scholar]
- Shahsavari, D.; Karami, B.; Fahham, H.R.; Li, L. On the shear buckling of porous nanoplates using a new size-dependent quasi-3D shear deformation theory. Acta Mech. 2018, 229, 4549–4573. [Google Scholar] [CrossRef]
- Safaei, B.; Moradi-Dastjerdi, R.; Behdinan, K.; Chu, F. Critical buckling temperature and force in porous sandwich plates with CNT-reinforced nanocomposite layers. Aerosp. Sci. Techn. 2019, 91, 175–185. [Google Scholar] [CrossRef]
- Li, Q.; Wu, D.; Chen, X.; Liu, L.; Yu, Y.; Gao, W. Nonlinear vibration and dynamic buckling analyses of sandwich functionally graded porous plate with graphene platelet reinforcement resting on Winkler–Pasternak elastic foundation. Int. J. Mech. Sci. 2018, 148, 596–610. [Google Scholar] [CrossRef]
- Shahgholian, D.; Safarpour, M.; Rahimi, A.R.; Aligeigloo, A. Buckling analyses of functionally graded graphene-reinforced porous cylindrical shell using the Rayleigh–Ritz method. Acta Mech. 2020, 231, 1887–1902. [Google Scholar] [CrossRef]
- Zhao, S.; Yang, Z.; Kitipornchai, S.; Yang, J. Dynamic instability of functionally graded porous arches reinforced by graphene platelets. Thin-Walled Struct. 2020, 147, 106491. [Google Scholar] [CrossRef]
- Jabbari, M.; Rezaei, M.; Mojahedin, A.; Eslami, M. Mechanical buckling of FG saturated porous rectangular plate under temperature field. Iranian J. Mech. Eng. Tran. ISME 2016, 17, 61–78. [Google Scholar]
- Jabbari, M.; Rezaei, M.; Mojahedin, A. Mechanical buckling of FG saturated porous rectangular plate with piezoelectric actuators. Iranian J. Mech. Eng. Tran. ISME 2016, 17, 46–66. [Google Scholar]
- Mojahedin, A.; Jabbari, M.; Salavati, M. Axisymmetric buckling of saturated circular porous-cellular plate based on first-order shear deformation theory. Int. J. Hydromech. 2019, 2, 144–158. [Google Scholar] [CrossRef]
- Jabbari, M.; Mojahedin, A.; Khorshidvand, A.R.; Eslami, M.R. Buckling analysis of functionally graded thin circular plate made of saturated porous materials. ASCE J. Eng. Mech. 2014, 34, 287–295. [Google Scholar] [CrossRef]
- Jabbari, M.; Hashemitaheri, M.; Mojahedin, A.; Eslami, M.R. Thermal buckling analysis of functionally graded thin circular plate made of saturated porous materials. J. Therm. Stresses 2014, 37, 202–220. [Google Scholar] [CrossRef]
- Jabbari, M.; Mojahedin, A.; Haghi, M. Buckling analysis of thin circular FG plates made of saturated porous-soft ferromagnetic materials in transverse magnetic field. Thin-Walled Struct. 2014, 85, 50–56. [Google Scholar] [CrossRef]
- Khorshidvand, A.R.; Joubaneh, E.F.; Jabbari, M.; Eslami, M.R. Buckling analysis of a porous circular plate with piezoelectric sensor–actuator layers under uniform radial compression. Acta Mech. 2014, 225, 179–193. [Google Scholar] [CrossRef]
- Feyzi, M.R.; Khorshidvand, A.R. Axisymmetric post-buckling behavior of saturated porous circular plates. Thin-Walled Struct. 2017, 1, 149–158. [Google Scholar] [CrossRef]
- Rezaei, A.S.; Saidi, A.R. Buckling response of moderately thick fluid-infiltrated porous annular sector plates. Acta Mech. 2017, 228, 3929–3945. [Google Scholar] [CrossRef]
- Anyfantis, K.N. Evaluating the influence of geometric distortions to the buckling capacity of stiffened panels. Thin-Walled Struct. 2014, 140, 450–465. [Google Scholar] [CrossRef]
- Shahani, A.R.; Kiarasi, F. Numerical and experimental investigation on post-buckling behavior of stiffened cylindrical shells with cutout subject to uniform axial compression. J. Appl. Comput. Mech. 2021, in press. [Google Scholar] [CrossRef]
- Zhang, Y.; Huang, Y.; Meng, F. Ultimate strength of hull structural stiffened plate with pitting corrosion damage under unaxial compression. Mar. Struct. 2017, 56, 117–136. [Google Scholar] [CrossRef]
- Kiarasi, F.; Babaei, M.; Dimitri, R.; Tornabene, F. Hygrothermal modeling of the buckling behavior of sandwich plates with nanocomposite face sheets resting on a Pasternak foundation. Contin. Mech. Thermodyn. 2021, 33, 911–932. [Google Scholar] [CrossRef]
- Babaei, M.; Hajmohammad, M.H.; Asemi, K. Natural frequency and dynamic analyses of functionally graded saturated porous annular sector plate and cylindrical panel based on 3D elasticity. Aerosp. Sci. Technol. 2020, 96, 105524. [Google Scholar] [CrossRef]
- Babaei, M.; Asemi, K.; Safarpour, P. Natural frequency and dynamic analyses of functionally graded saturated porous beam resting on viscoelastic foundation based on higher order beam theory. J. Solid Mech. 2019, 11, 615–634. [Google Scholar]
- Babaei, M.; Asemi, K.; Safarpour, P. Buckling and static analyses of functionally graded saturated porous thick beam resting on elastic foundation based on higher order beam theory. Iranian J. Mech. Eng. Tran. ISME 2019, 20, 94–112. [Google Scholar]
- Babaei, M.; Asemi, K. Stress analysis of functionally graded saturated porous rotating thick truncated cone. Mech. Based Des. Struct. Mach. 2020, 1–28. [Google Scholar] [CrossRef]
- Babaei, M.; Asemi, K.; Kiarasi, F. Static response and free-vibration analysis of a functionally graded annular elliptical sector plate made of saturated porous material based on 3D finite element method. Mech. Based Des. Struct. Mach. 2020, 1–25. [Google Scholar] [CrossRef]
- Detournay, E.; Cheng, A.H.D. Fundamentals of poroelasticity. In Analysis and Design Methods; Pergamon: Oxford, UK, 1993; pp. 113–171. [Google Scholar]
- Babaei, M.; Asemi, K.; Kiarasi, F. Dynamic analysis of functionally graded rotating thick truncated cone made of saturated porous materials. Thin-Walled Struct. 2021, 164, 107852. [Google Scholar] [CrossRef]
- Arshid, E.; Khorshidvand, A.R. Free vibration analysis of saturated porous FG circular plates integrated with piezoelectric actuators via differential quadrature method. Thin-Walled Struct. 2018, 125, 220–233. [Google Scholar] [CrossRef]
| FE-GDQ | FE | Difference (%) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| BC | ||||||||||
| Shear load | CFCF | 0.314 | 0.529 | 0.624 | 0.317 | 0.574 | 0.678 | 0.94 | 7.83 | 7.96 |
| Shear load | FCFC | 1.405 | 1.406 | 2.168 | 1.430 | 1.430 | 2.117 | 1.74 | 1.67 | 2.35 |
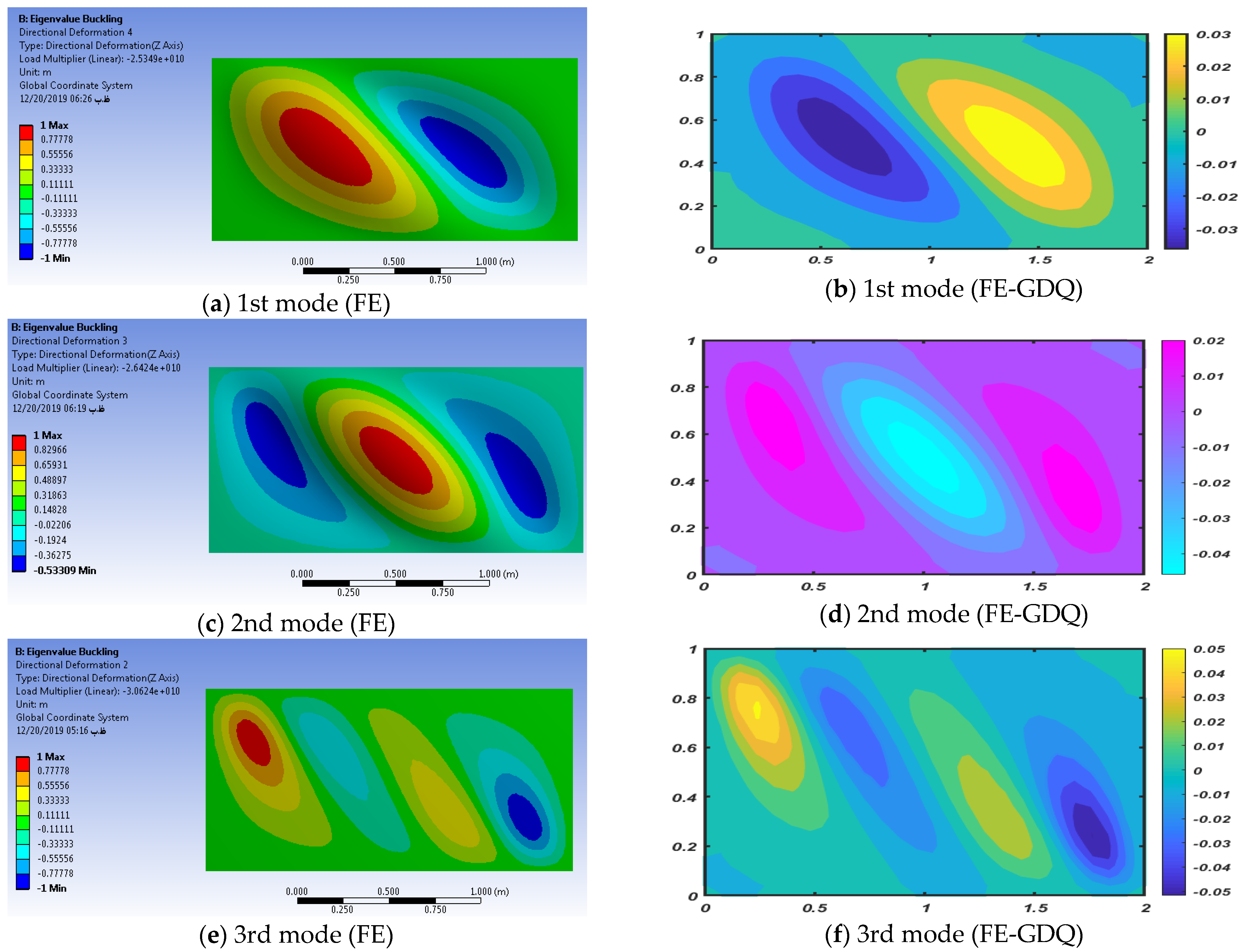
| Shear load | SSSS | 2.534 | 2.642 | 3.062 | 2.575 | 2.691 | 3.0628 | 1.59 | 1.82 | 0 |
| Axial load (x-direction) | SSSS | 1.197 | 1.231 | 2.381 | 1.206 | 1.240 | 2.401 | 0.74 | 0.72 | 6.7 |
| Biaxial load | SSSS | 0.259 | 0.489 | 0.790 | 0.264 | 0.494 | 0.794 | 1.89 | 1.01 | 0.506 |
| Aspect Ratio | Buckling Load (10 GPa) | PNND | PNSD | PUD | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| a/b = 1 | 2.666 | 1.935 | 1.226 | 2.674 | 1.961 | 1.263 | 2.269 | 1.212 | 0.275 | |
| 2.666 | 1.936 | 1.226 | 2.674 | 1.961 | 1.263 | 2.269 | 1.212 | 0.275 | ||
| 2.958 | 2.255 | 1.442 | 2.998 | 2.265 | 1.390 | 2.595 | 1.482 | 0.354 | ||
| 2.984 | 2.261 | 1.447 | 3.016 | 2.266 | 1.390 | 2.607 | 1.483 | 0.354 | ||
| a/b = 2 | 2.281 | 1.863 | 1.162 | 2.392 | 2.005 | 1.269 | 2.083 | 1.281 | 0.2952 | |
| 2.339 | 1.865 | 1.162 | 2.438 | 2.029 | 1.271 | 2.105 | 1.282 | 0.2954 | ||
| 2.558 | 1.968 | 1.237 | 2.627 | 2.068 | 1.379 | 2.248 | 1.334 | 0.3464 | ||
| 2.719 | 2.044 | 1.307 | 2.761 | 2.094 | 1.388 | 2.350 | 1.356 | 0.3467 | ||
| Aspect Ratio | Buckling Load (10 GPa) | PNND | PNSD | PUD | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| a/b = 1 | 1.143 | 0.897 | 0.536 | 1.199 | 0.978 | 0.692 | 1.020 | 0.636 | 0.177 | |
| 1.150 | 0.900 | 0.543 | 1.208 | 0.983 | 0.693 | 1.020 | 0.645 | 0.182 | ||
| 1.653 | 1.267 | 0.773 | 1.705 | 1.337 | 0.845 | 1.455 | 0.865 | 0.219 | ||
| 1.664 | 1.275 | 0.778 | 1.717 | 1.343 | 0.849 | 1.464 | 0.868 | 0.219 | ||
| a/b = 2 | 1.216 | 0.954 | 0.576 | 1.276 | 1.039 | 0.737 | 1.082 | 0.680 | 0.191 | |
| 1.217 | 0.955 | 0.576 | 1.277 | 1.040 | 0.738 | 1.083 | 0.680 | 0.191 | ||
| 1.768 | 1.360 | 0.834 | 1.824 | 1.401 | 0.912 | 1.558 | 0.931 | 0.238 | ||
| 1.768 | 1.360 | 0.834 | 1.824 | 1.402 | 0.912 | 1.558 | 0.931 | 0.238 | ||
| Aspect Ratio | Buckling Load (10 GPa) | PNND | PNSD | PUD | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| a/b = 1 | 1.143 | 0.897 | 0.536 | 1.199 | 1.006 | 0.692 | 1.020 | 0.636 | 0.177 | |
| 1.150 | 0.900 | 0.543 | 1.208 | 1.007 | 0.693 | 1.020 | 0.645 | 0.182 | ||
| 1.653 | 1.267 | 0.773 | 1.705 | 1.434 | 0.845 | 1.455 | 0.865 | 0.219 | ||
| 1.664 | 1.275 | 0.778 | 1.717 | 1.350 | 0.849 | 1.464 | 0.868 | 0.219 | ||
| a/b = 2 | 0.310 | 0.255 | 0.153 | 0.330 | 0.292 | 0.241 | 0.287 | 0.186 | 0.055 | |
| 0.497 | 0.393 | 0.229 | 0.538 | 0.470 | 0.375 | 0.449 | 0.281 | 0.078 | ||
| 0.598 | 0.466 | 0.281 | 0.610 | 0.520 | 0.405 | 0.528 | 0.325 | 0.096 | ||
| 0.805 | 0.622 | 0.374 | 0.817 | 0.682 | 0.504 | 0.708 | 0.430 | 0.116 | ||
| Aspect Ratio | Buckling Load (10 GPa) | PNND | PNSD | PUD | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| a/b = 1 | 0.392 | 0.303 | 0.166 | 0.406 | 0.362 | 0.309 | 0.346 | 0.216 | 0.069 | |
| 0.929 | 0.723 | 0.408 | 0.949 | 0.830 | 0.658 | 0.827 | 0.523 | 0.151 | ||
| 0.929 | 0.723 | 0.408 | 0.949 | 0.830 | 0.658 | 0.827 | 0.523 | 0.151 | ||
| 0.141 | 0.108 | 0.604 | 0.144 | 0.127 | 0.926 | 1.245 | 0.763 | 0.210 | ||
| a/b = 2 | 0.233 | 0.186 | 0.106 | 0.240 | 0.221 | 0.193 | 0.209 | 0.138 | 0.0420 | |
| 0.434 | 0.336 | 0.188 | 0.405 | 0.400 | 0.329 | 0.384 | 0.239 | 0.0680 | ||
| 0.698 | 0.564 | 0.333 | 0.703 | 0.634 | 0.519 | 0.634 | 0.426 | 0.120 | ||
| 0.778 | 0.603 | 0.341 | 0.804 | 0.702 | 0.570 | 0.688 | 0.427 | 0.131 | ||
| Aspect Ratio | Buckling Load (10 GPa) | PNND | PNSD | PUD | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| a/b = 1 | 0.781 | 0.603 | 0.330 | 0.808 | 0.721 | 0.614 | 0.690 | 0.430 | 0.122 | |
| 0.981 | 0.774 | 0.446 | 0.983 | 0.875 | 0.703 | 0.879 | 0.568 | 0.168 | ||
| 1.554 | 1.225 | 0.724 | 1.526 | 1.320 | 0.981 | 1.394 | 0.895 | 0.261 | ||
| 2.147 | 1.688 | 1.017 | 2.081 | 1.856 | 1.218 | 1.925 | 1.225 | 0.350 | ||
| a/b = 2 | 1.053 | 0.816 | 0.462 | 1.073 | 0.943 | 0.771 | 0.930 | 0.574 | 0.159 | |
| 1.101 | 0.860 | 0.495 | 1.117 | 0.982 | 0.795 | 0.977 | 0.613 | 0.173 | ||
| 2.097 | 1.553 | 0.880 | 2.082 | 1.725 | 1.314 | 1.801 | 1.020 | 0.260 | ||
| 2.331 | 1.771 | 1.042 | 2.293 | 1.907 | 1.405 | 2.035 | 1.204 | 0.319 | ||
| Aspect Ratio | Buckling Load (10 GPa) | PNND | PNSD | PUD | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| β = 0.0 | β = 0.6 | β = 0.9 | β = 0.0 | β = 0.6 | β = 0.9 | β = 0.0 | β = 0.6 | β = 0.9 | ||
| a/b = 1 | 1.839 | 1.935 | 1.941 | 1.954 | 1.961 | 1.982 | 1.196 | 1.212 | 1.303 | |
| 1.913 | 1.944 | 1.951 | 1.957 | 1.961 | 1.986 | 1.196 | 1.212 | 1.303 | ||
| 2.216 | 2.255 | 2.264 | 2.236 | 2.265 | 2.274 | 1.478 | 1.480 | 1.486 | ||
| 2.240 | 2.261 | 2.273 | 2.250 | 2.266 | 2.275 | 1.478 | 1.483 | 1.486 | ||
| a/b = 2 | 1.689 | 1.863 | 1.963 | 1.942 | 2.005 | 2.012 | 1.190 | 1.281 | 1.326 | |
| 1.738 | 1.865 | 1.964 | 1.953 | 2.029 | 2.043 | 1.203 | 1.283 | 1.326 | ||
| 1.913 | 1.968 | 2.018 | 2.050 | 2.068 | 2.094 | 1.284 | 1.334 | 1.341 | ||
| 2.038 | 2.044 | 2.048 | 2.130 | 2.139 | 2.147 | 1.343 | 1.356 | 1.386 | ||
| Aspect Ratio | Buckling Load (10 GPa) | PNND | PNSD | PUD | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| β = 0.0 | β = 0.6 | β = 0.9 | β = 0.0 | β = 0.6 | β = 0.9 | β = 0.0 | β = 0.6 | β = 0.9 | ||
| a/b = 1 | 0.848 | 0.897 | 0.955 | 0.969 | 0.978 | 0.989 | 0.583 | 0.636 | 0.709 | |
| 0.853 | 0.900 | 0.967 | 0.978 | 0.983 | 0.993 | 0.583 | 0.645 | 0.728 | ||
| 1.231 | 1.267 | 1.299 | 1.329 | 1.337 | 1.346 | 0.831 | 0.865 | 0.878 | ||
| 1.240 | 1.275 | 1.306 | 1.338 | 1.343 | 1.371 | 0.836 | 0.868 | 0.879 | ||
| a/b = 2 | 0.903 | 0.954 | 1.021 | 1.031 | 1.039 | 1.042 | 0.618 | 0.680 | 0.765 | |
| 0.904 | 0.955 | 1.026 | 1.032 | 1.040 | 1.068 | 0.619 | 0.680 | 0.765 | ||
| 1.318 | 1.360 | 1.399 | 1.423 | 1.401 | 1.414 | 0.890 | 0.931 | 0.955 | ||
| 1.318 | 1.360 | 1.399 | 1.423 | 1.402 | 1.416 | 0.890 | 0.931 | 0.955 | ||
| Aspect Ratio | Buckling Load (10 GPa) | PNND | PNSD | PUD | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| β = 0.0 | β = 0.6 | β = 0.9 | β = 0.0 | β = 0.6 | β = 0.9 | β = 0.0 | β = 0.6 | β = 0.9 | ||
| a/b = 1 | 0.848 | 0.897 | 0.955 | 0.969 | 0.978 | 0.989 | 0.583 | 0.636 | 0.709 | |
| 0.853 | 0.900 | 0.967 | 0.978 | 0.983 | 0.993 | 0.583 | 0.645 | 0.728 | ||
| 1.231 | 1.267 | 1.299 | 1.329 | 1.337 | 1.346 | 0.831 | 0.865 | 0.878 | ||
| 1.240 | 1.275 | 1.306 | 1.338 | 1.343 | 1.371 | 0.836 | 0.868 | 0.879 | ||
| a/b = 2 | 0.237 | 0.255 | 0.280 | 0.284 | 0.292 | 0.296 | 0.164 | 0.186 | 0.222 | |
| 0.367 | 0.393 | 0.425 | 0.494 | 0.470 | 0.482 | 0.254 | 0.281 | 0.314 | ||
| 0.458 | 0.466 | 0.500 | 0.520 | 0.524 | 0.529 | 0.302 | 0.325 | 0.387 | ||
| 0.600 | 0.622 | 0.615 | 0.682 | 0.689 | 0.798 | 0.404 | 0.430 | 0.465 | ||
| Aspect Ratio | Buckling Load (10 GPa) | PNND | PNSD | PUD | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| β = 0.0 | β = 0.6 | β = 0.9 | β = 0.0 | β = 0.6 | β = 0.9 | β = 0.0 | β = 0.6 | β = 0.9 | ||
| a/b = 1 | 0.288 | 0.303 | 0.325 | 0.361 | 0.362 | 0.389 | 0.198 | 0.216 | 0.246 | |
| 0.683 | 0.723 | 0.781 | 0.825 | 0.830 | 0.846 | 0.472 | 0.523 | 0.603 | ||
| 0.683 | 0.723 | 0.781 | 0.825 | 0.830 | 0.846 | 0.472 | 0.523 | 0.603 | ||
| 0.103 | 0.108 | 0.146 | 0.123 | 0.127 | 0.131 | 0.711 | 0.763 | 0.843 | ||
| a/b = 2 | 0.171 | 0.186 | 0.207 | 0.213 | 0.221 | 0.229 | 0.119 | 0.138 | 0.168 | |
| 0.319 | 0.369 | 0.362 | 0.397 | 0.400 | 0.405 | 0.219 | 0.239 | 0.273 | ||
| 0.513 | 0.564 | 0.635 | 0.616 | 0.634 | 0.638 | 0.362 | 0.426 | 0.480 | ||
| 0.573 | 0.603 | 0.644 | 0.697 | 0.702 | 0.713 | 0.393 | 0.427 | 0.526 | ||
| Aspect Ratio | Buckling Load (10 GPa) | PNND | PNSD | PUD | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| β = 0.0 | β = 0.6 | β = 0.9 | β = 0.0 | β = 0.6 | β = 0.9 | β = 0.0 | β = 0.6 | β = 0.9 | ||
| a/b = 1 | 0.572 | 0.603 | 0.648 | 0.719 | 0.721 | 0.737 | 0.394 | 0.430 | 0.491 | |
| 0.722 | 0.774 | 0.848 | 0.867 | 0.875 | 0.884 | 0.502 | 0.568 | 0.672 | ||
| 1.147 | 1.225 | 1.331 | 1.318 | 1.320 | 1.384 | 0.796 | 0.895 | 1.046 | ||
| 1.589 | 1.688 | 1.817 | 1.756 | 1.856 | 1.878 | 1.100 | 1.225 | 1.403 | ||
| a/b = 2 | 0.777 | 0.816 | 0.868 | 0.938 | 0.943 | 0.941 | 0.531 | 0.574 | 0.636 | |
| 0.813 | 0.860 | 0.923 | 0.977 | 0.982 | 0.993 | 0.558 | 0.613 | 0.693 | ||
| 1.560 | 1.553 | 1.550 | 1.720 | 1.725 | 1.749 | 1.009 | 1.020 | 1.042 | ||
| 1.735 | 1.771 | 1.817 | 1.901 | 1.907 | 1.923 | 1.163 | 1.204 | 1.276 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kiarasi, F.; Babaei, M.; Asemi, K.; Dimitri, R.; Tornabene, F. Three-Dimensional Buckling Analysis of Functionally Graded Saturated Porous Rectangular Plates under Combined Loading Conditions. Appl. Sci. 2021, 11, 10434. https://doi.org/10.3390/app112110434
Kiarasi F, Babaei M, Asemi K, Dimitri R, Tornabene F. Three-Dimensional Buckling Analysis of Functionally Graded Saturated Porous Rectangular Plates under Combined Loading Conditions. Applied Sciences. 2021; 11(21):10434. https://doi.org/10.3390/app112110434
Chicago/Turabian StyleKiarasi, Faraz, Masoud Babaei, Kamran Asemi, Rossana Dimitri, and Francesco Tornabene. 2021. "Three-Dimensional Buckling Analysis of Functionally Graded Saturated Porous Rectangular Plates under Combined Loading Conditions" Applied Sciences 11, no. 21: 10434. https://doi.org/10.3390/app112110434
APA StyleKiarasi, F., Babaei, M., Asemi, K., Dimitri, R., & Tornabene, F. (2021). Three-Dimensional Buckling Analysis of Functionally Graded Saturated Porous Rectangular Plates under Combined Loading Conditions. Applied Sciences, 11(21), 10434. https://doi.org/10.3390/app112110434










