An Analytical Model for Transient Heat Transfer with a Time-Dependent Boundary in Solar- and Waste-Heat-Assisted Geothermal Borehole Systems: From Single to Multiple Boreholes †
Abstract
:1. Introduction
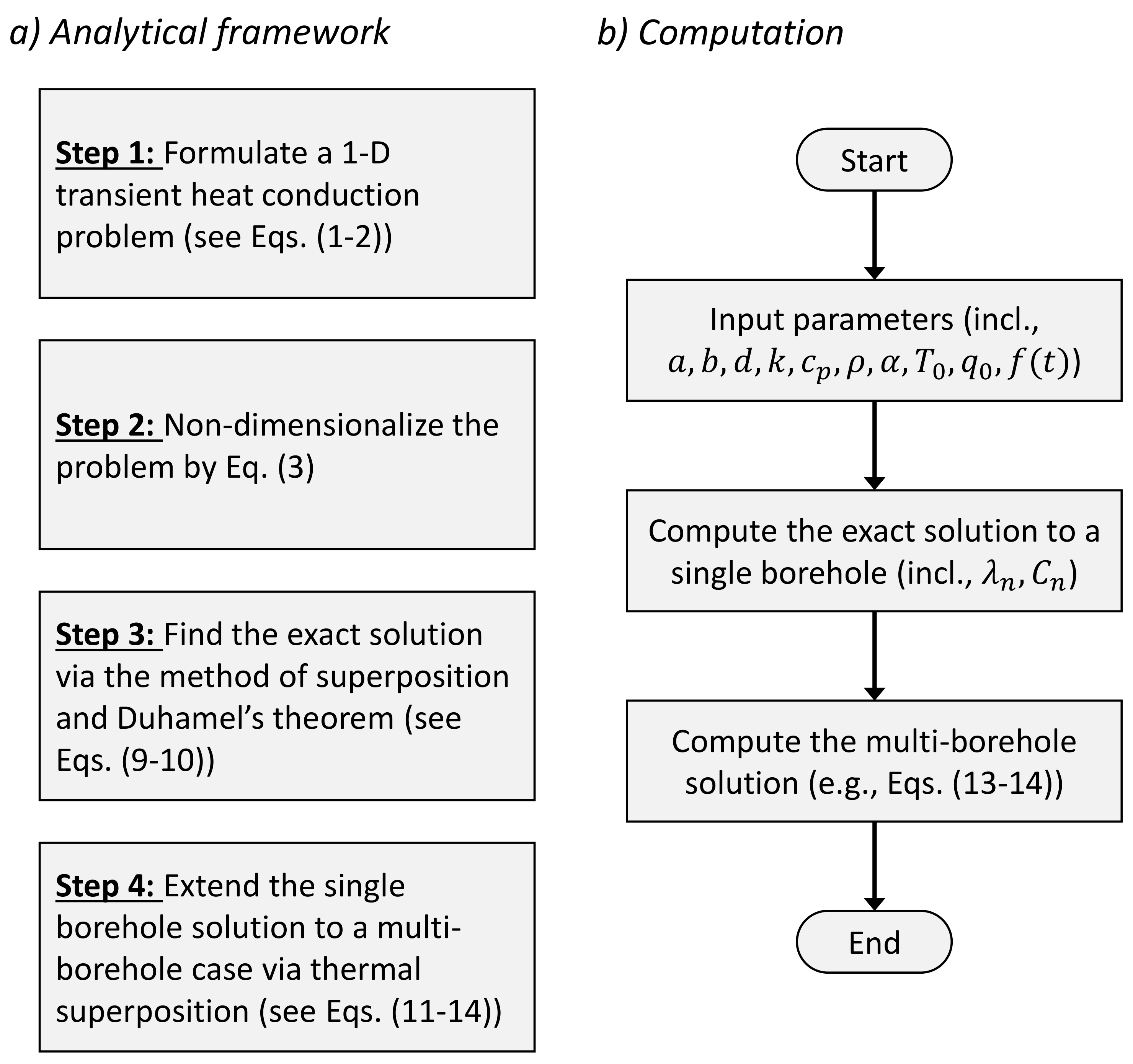
2. Analytical Methods
- (1)
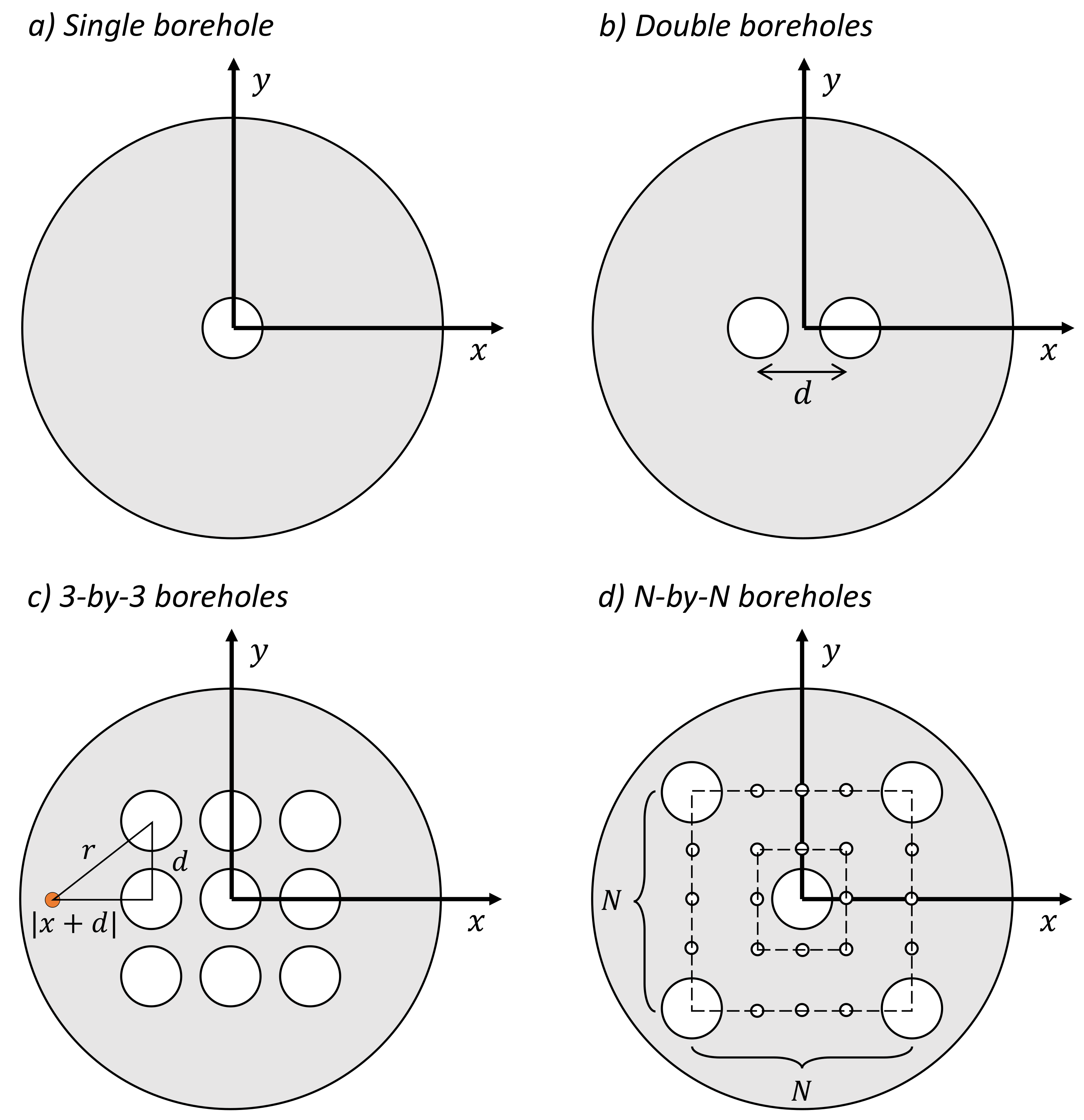
- The distance between neighboring boreholes, d [m], are equal in each scenario.
- (2)
- The boreholes are symmetrically located at the center of the domain (i.e., coaxial heat exchangers).
- (3)
- The effect of the axial direction in the geothermal system is ignored, which reduces the model to a two-dimensional system in the x- and y-coordinates.
- (4)
- The conductor pipe in the casing usually has a high thermal conductivity, thus making its thermal resistance negligible.
- (5)
- The cement/grout filled in the casing assumes to have the same order of magnitude as the ground in terms of thermophysical properties, so there is no need to consider the cement separately from the ground.
- (6)
- Thermophysical properties of the grout are assumed to be constant, since the temperature variation gives minimal influences on the properties.
2.1. Problem Formulation
2.2. Dimensionless Analysis
2.3. Use of Duhamel’s Theorem
2.4. Use of Symmetry: From Single to Multiple Boreholes
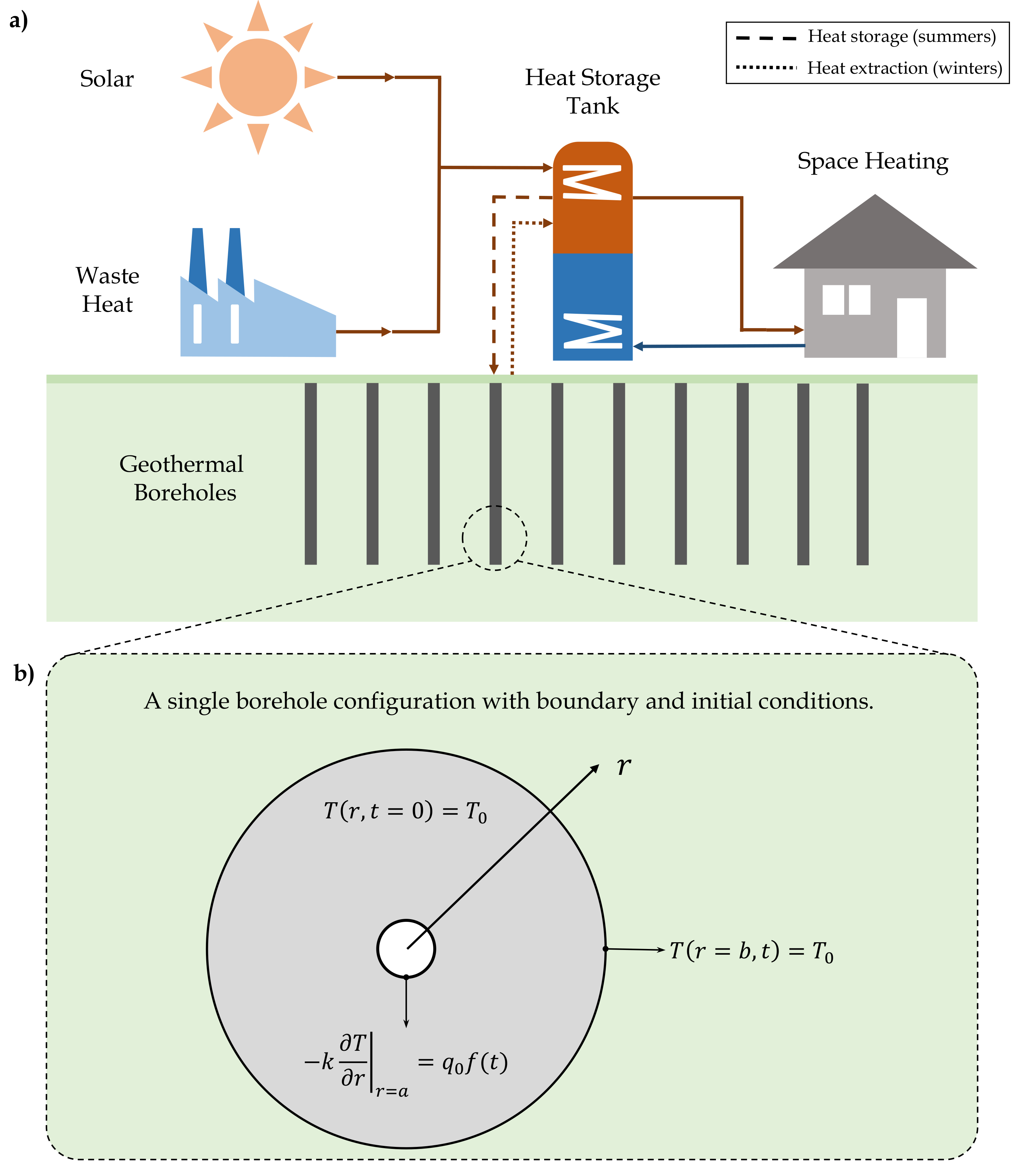
3. Model Development
3.1. S-GBS Models
- (i)
- Prescribe geometry, thermophysical properties, and time-dependent heat flux boundary of S-GBS;
- (ii)
- For a single borehole case, compute the exact solution, as expressed in Equation (10), to a 1-D radial transient cylindrical heat conduction problem subjected to a time-dependent heat flux boundary; and
- (iii)
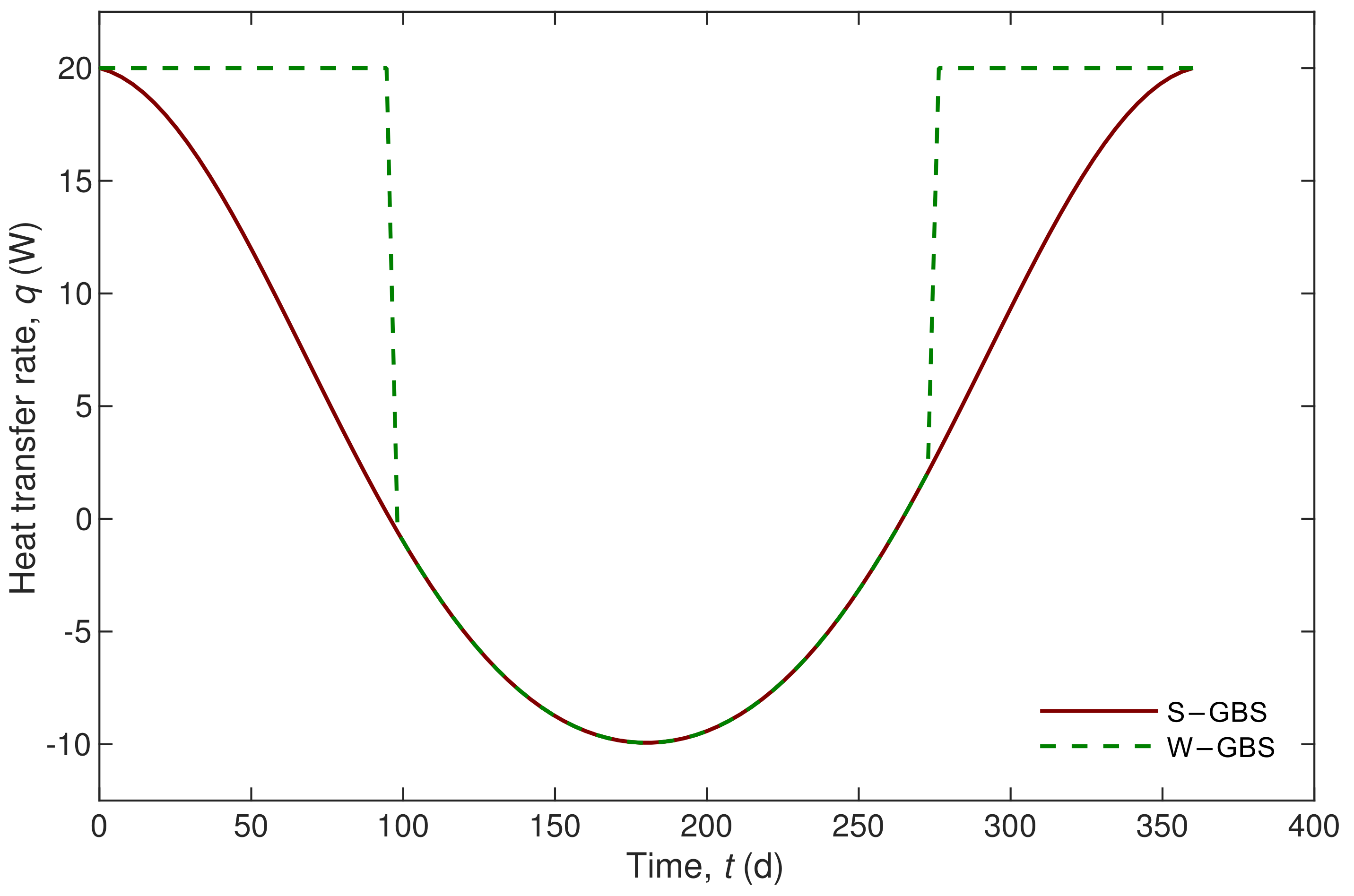
3.2. W-GBS Models
3.3. Numerical Models
4. Results and Discussion
4.1. Model Verification
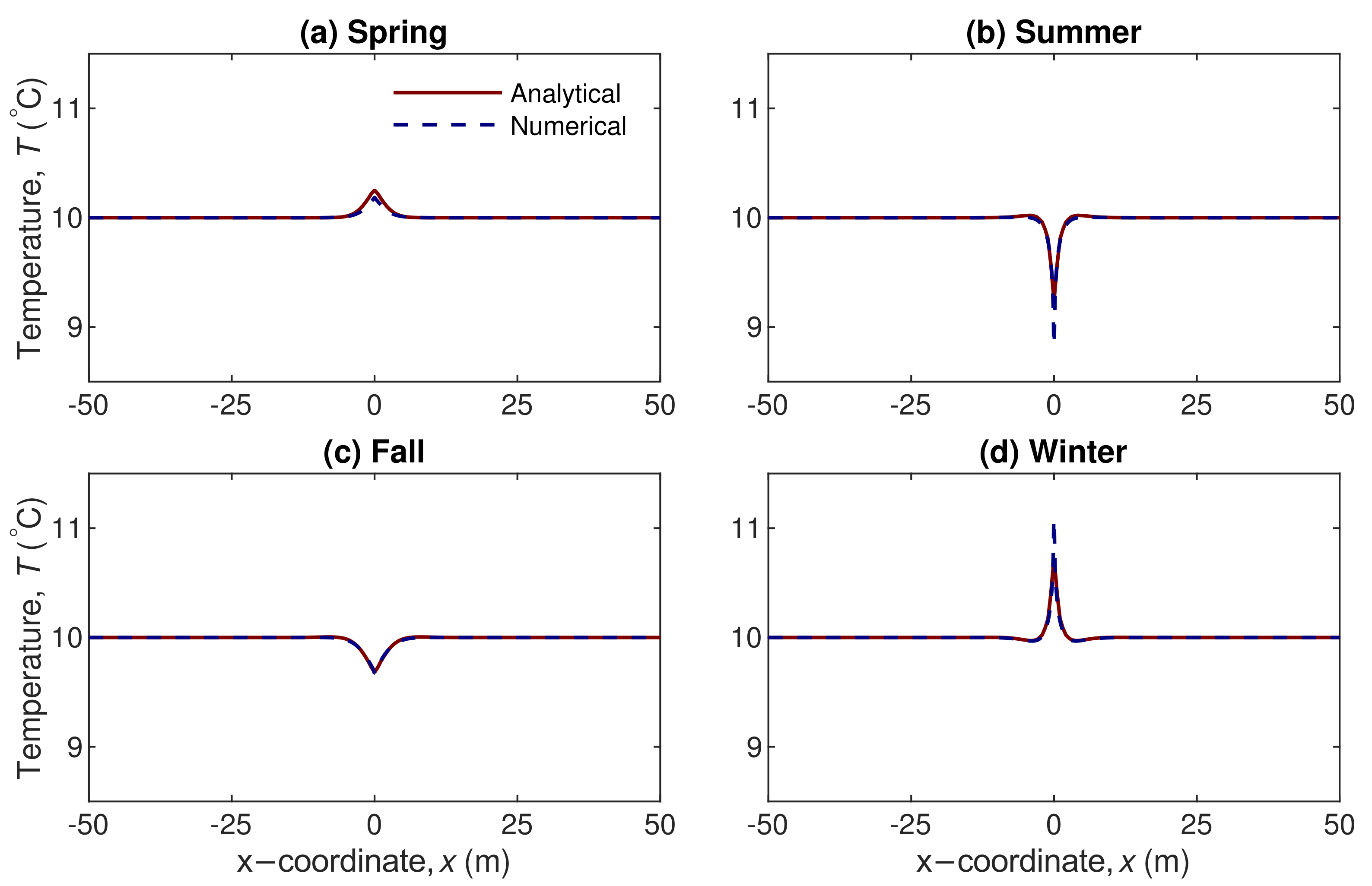
4.1.1. Single Borehole
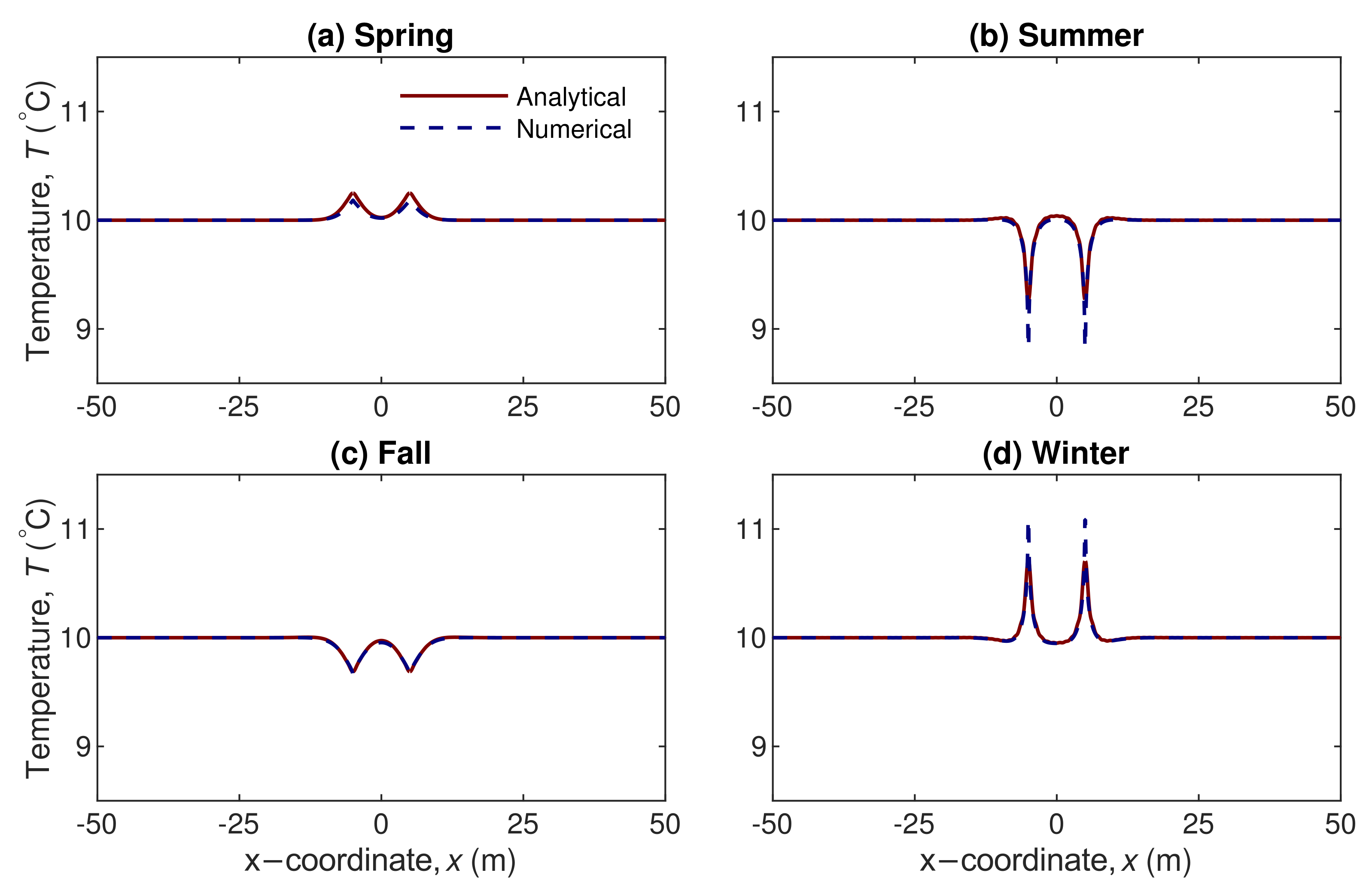
4.1.2. Double and 3-by-3 Boreholes
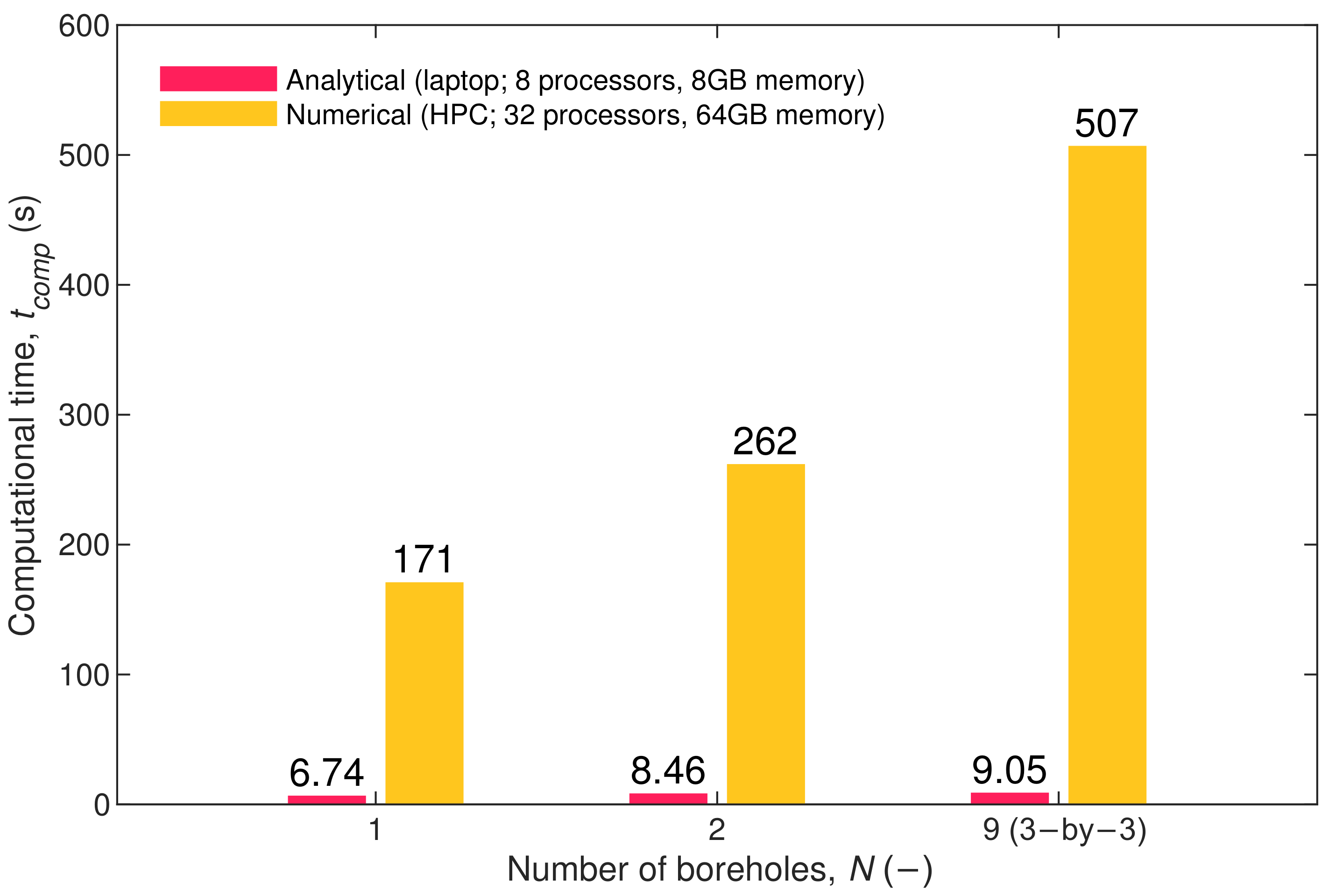
4.1.3. Computational Efficiency
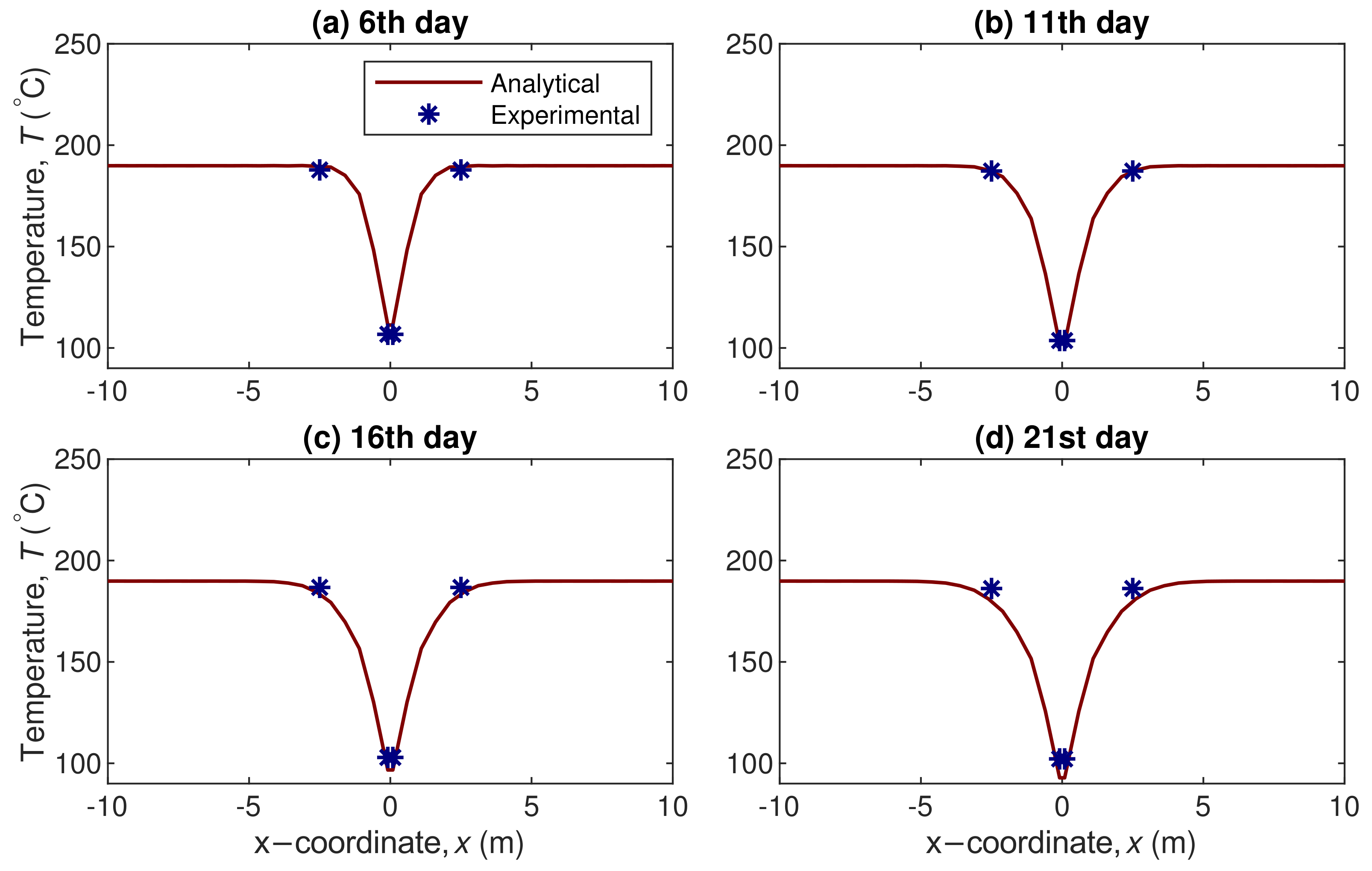
4.2. Model Validation
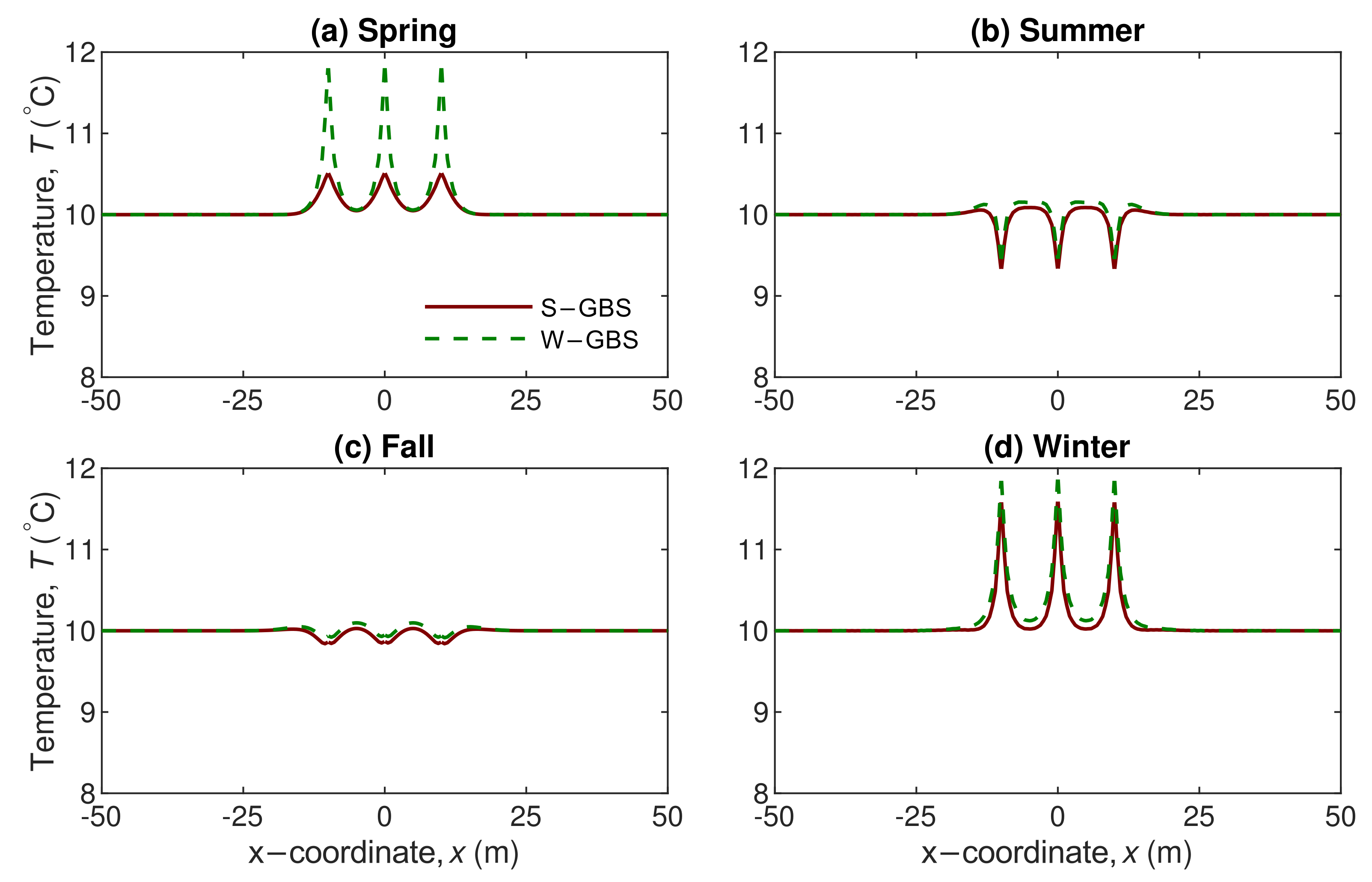
4.3. Comparison between S-GBS and W-GBS
5. Conclusions
- (i)
- The closed-form analytical solution developed here is verified with a 2-D FEM numerical model (having a mean absolute deviation of below 0.7% in all borehole scenarios) as well as validated against a field-scale experiment in the literature (having an absolute error of below 6.3%) to ensure its accuracy and reliability.
- (ii)
- The analytical solution is much more computationally efficient to be computed than numerical models, requiring 4∼8 times less computational power and 24∼55 times less computational time.
- (ii)
- The analytical framework is capable of evaluating the ground temperature in GBS with any time-varying boundary, regardless the number of boreholes. Case studies for S-GBS and W-GBS are also conducted.
- (iv)
- It was recommended that future studies could consider: the optimal design of borehole spacing and the number of boreholes used; and the economic assessment of such system from the energy demand/supply.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BHE | Borehole heat exchanger |
| CFD | Computational fluid dynamics |
| FEM | Finite-element method |
| HPC | High performance computing |
| MAD | Mean absolute deviation |
| ODE | Ordinary differential equation |
| GSHP | Ground-source heat pump |
| PDE | Partial differential equation |
| S-GBS | Solar-assisted geothermal borehole system |
| W-GBS | Waste-heat-assisted geothermal borehole system |
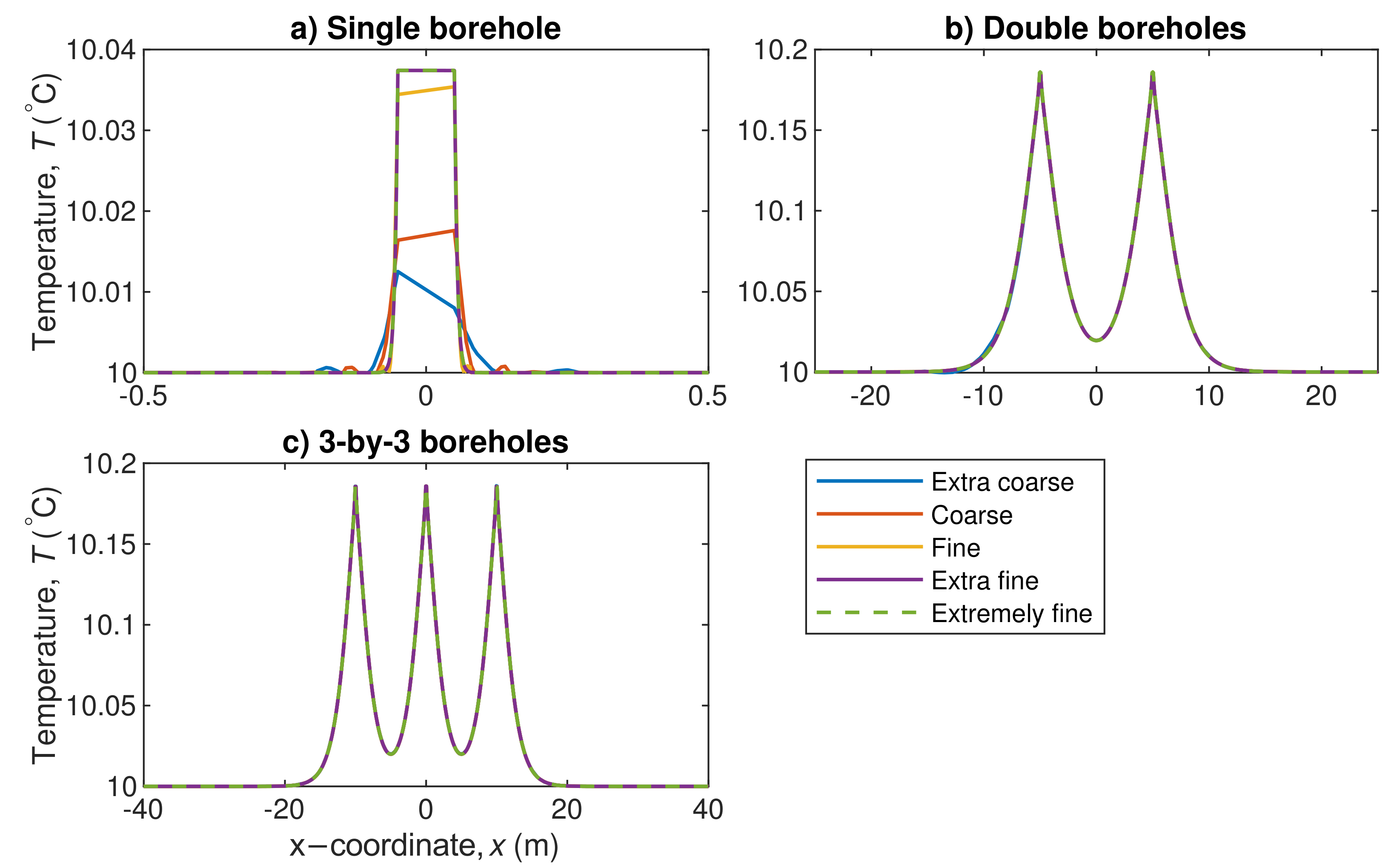
Appendix A. Mesh Type and Mesh Independency Study in the Numerical Models
| Single Borehole | Double Boreholes | 3-by-3 Boreholes | |
|---|---|---|---|
| Extra coarse | 220 | 372 | 1580 |
| Coarse | 692 | 1056 | 4293 |
| Fine | 2012 | 3162 | 10,832 |
| Extra fine | 9516 | 12,290 | 31,578 |
| Extremely fine | 33,834 | 41,244 | 93,672 |

References
- Templeton, J.D.; Ghoreishi-Madiseh, S.A.; Hassani, F.; Al-Khawaja, M.J. Abandoned petroleum wells as sustainable sources of geothermal energy. Energy 2014, 70, 366–373. [Google Scholar] [CrossRef]
- Moya, D.; Aldás, C.; Kaparaju, P. Geothermal energy: Power plant technology and direct heat applications. Renew. Sustain. Energy Rev. 2018, 94, 889–901. [Google Scholar] [CrossRef]
- Lund, J.W.; Toth, A.N. Direct utilization of geothermal energy 2020 worldwide review. Geothermics 2020, 90, 101915. [Google Scholar] [CrossRef]
- Lund, J.W.; Boyd, T.L. Direct utilization of geothermal energy 2015 worldwide review. Geothermics 2016, 60, 66–93. [Google Scholar] [CrossRef]
- Dehghani-Sanij, A.; Jatin, N. New trends in enhanced, hybrid and integrated geothermal Systems. Appl. Sci. 2021, 11, 3765. [Google Scholar] [CrossRef]
- Ghoreishi-Madiseh, S.A.; Hassani, F.; Abbasy, F. Numerical and experimental study of geothermal heat extraction from backfilled mine stopes. Appl. Therm. Eng. 2015, 90, 1119–1130. [Google Scholar] [CrossRef]
- Templeton, J.D.; Ghoreishi-Madiseh, S.A.; Hassani, F.P.; Sasmito, A.P.; Kurnia, J.C. Numerical and experimental study of transient conjugate heat transfer in helical closed-loop geothermal heat exchangers for application of thermal energy storage in backfilled mine stopes. Int. J. Energy Res. 2020, 44, 9609–9616. [Google Scholar] [CrossRef]
- Fong, M.; Alzoubi, M.A.; Kurnia, J.C.; Sasmito, A.P. On the performance of ground coupled seasonal thermal energy storage for heating and cooling: A Canadian context. Appl. Energy 2019, 250, 593–604. [Google Scholar] [CrossRef]
- Amiri, L.; Madadian, E.; Hassani, F.P. Energo-and exergo-technical assessment of ground-source heat pump systems for geothermal energy production from underground mines. Environ. Technol. 2019, 40, 3534–3546. [Google Scholar] [CrossRef]
- Cui, Y.; Zhu, J.; Twaha, S.; Chu, J.; Bai, H.; Huang, K.; Chen, X.; Zoras, S.; Soleimani, Z. Techno-economic assessment of the horizontal geothermal heat pump systems: A comprehensive review. Energy Convers. Manag. 2019, 191, 208–236. [Google Scholar] [CrossRef]
- Kurnia, J.C.; Shatri, M.S.; Putra, Z.A.; Zaini, J.; Caesarendra, W.; Sasmito, A.P. Geothermal energy extraction using abandoned oil and gas wells: Techno-economic and policy review. Int. J. Energy Res. 2021, 1–33. [Google Scholar] [CrossRef]
- Kurnia, J.C.; Putra, Z.A.; Muraza, O.; Ghoreishi-Madiseh, S.A.; Sasmito, A.P. Numerical evaluation, process design and techno-economic analysis of geothermal energy extraction from abandoned oil wells in Malaysia. Renew. Energy 2021, 175, 868–879. [Google Scholar] [CrossRef]
- Lamarche, L.; Kajl, S.; Beauchamp, B. A review of methods to evaluate borehole thermal resistances in geothermal heat-pump systems. Geothermics 2010, 39, 187–200. [Google Scholar] [CrossRef]
- Yang, H.; Cui, P.; Fang, Z. Vertical-borehole ground-coupled heat pumps: A review of models and systems. Appl. Energy 2010, 87, 16–27. [Google Scholar] [CrossRef]
- Wang, G.; Song, X.; Shi, Y.; Yulong, F.; Yang, R.; Li, J. Comparison of production characteristics of various coaxial closed-loop geothermal systems. Energy Convers. Manag. 2020, 225, 113437. [Google Scholar]
- Song, X.; Wang, G.; Shi, Y.; Li, R.; Xu, Z.; Zheng, R.; Wang, Y.; Li, J. Numerical analysis of heat extraction performance of a deep coaxial borehole heat exchanger geothermal system. Energy 2018, 164, 1298–1310. [Google Scholar] [CrossRef]
- Zarrella, A.; Scarpa, M.; Carli, M.D. Short time-step performances of coaxial and double U-tube borehole heat exchangers: Modeling and measurements. HVAC R Res. 2011, 17, 959–976. [Google Scholar]
- Acuña, J.; Palm, B. Distributed thermal response tests on pipe-in-pipe borehole heat exchangers. Appl. Energy 2013, 109, 312–320. [Google Scholar]
- Bouhacina, B.; Saim, R.; Oztop, H.F. Numerical investigation of a novel tube design for the geothermal borehole heat exchanger. Appl. Therm. Eng. 2015, 79, 153–162. [Google Scholar] [CrossRef]
- Gustafsson, A.M.; Westerlund, L.; Hellström, G. CFD-modelling of natural convection in a groundwater-filled borehole heat exchanger. Appl. Therm. Eng. 2010, 30, 683–691. [Google Scholar] [CrossRef] [Green Version]
- Iry, S.; Rafee, R. Transient numerical simulation of the coaxial borehole heat exchanger with the different diameters ratio. Geothermics 2019, 77, 158–165. [Google Scholar] [CrossRef]
- Khalajzadeh, V.; Heidarinejad, G.; Srebric, J. Parameters optimization of a vertical ground heat exchanger based on response surface methodology. Energy Build. 2011, 43, 1288–1294. [Google Scholar] [CrossRef]
- Al-Khoury, R.; Bonnier, P.G.; Brinkgreve, R.B.J. Efficient finite element formulation for geothermal heating systems. Part I: Steady state. Int. J. Num. Methods Eng. 2005, 63, 988–1013. [Google Scholar] [CrossRef]
- Al-Khoury, R.; Bonnier, P.G. Efficient finite element formulation for geothermal heating systems. Part II: Transient. Int. J. Num. Methods Eng. 2006, 67, 725–745. [Google Scholar] [CrossRef]
- Yu, X.; Li, H.; Yao, S.; Nielsen, V.; Heller, A. Development of an efficient numerical model and analysis of heat transfer performance for borehole heat exchanger. Renew. Energy 2020, 152, 189–197. [Google Scholar] [CrossRef]
- Ozudogru, T.Y.; Olgun, C.G.; Senol, A. 3D numerical modeling of vertical geothermal heat exchangers. Geothermics 2014, 51, 312–324. [Google Scholar] [CrossRef]
- Eskilson, P. Thermal Analysis of Heat Extraction Boreholes. Ph.D. Thesis, University of Lund, Lund, Sweden, 1987. [Google Scholar]
- Yavuzturk, C.; Spitler, J.D. A short time step response factor model for vertical ground loop heat exchangers. ASHRAE Trans. 1999, 105, 475–485. [Google Scholar]
- Cimmino, M.; Bernier, M.; Adams, F. A contribution towards the determination of g-functions using the finite line source. Appl. Therm. Eng. 2013, 51, 401–412. [Google Scholar] [CrossRef]
- Cimmino, M.; Bernier, M. A semi-analytical method to generate g-functions for geothermal bore fields. Int. J. Heat Mass Transf. 2014, 70, 641–650. [Google Scholar] [CrossRef]
- Johnsson, J.; Adl-Zarrabi, B. Modelling and evaluation of groundwater filled boreholes subjected to natural convection. Appl. Energy 2019, 253, 113555. [Google Scholar] [CrossRef]
- Cimmino, M.; Baliga, B.R.R. A hybrid numerical-semi-analytical method for computer simulations of groundwater flow and heat transfer in geothermal borehole fields. Int. J. Therm. Sci. 2019, 142, 366–378. [Google Scholar] [CrossRef]
- Pokhrel, S.; Amiri, L.; Zueter, A.; Poncet, S.; Hassani, F.P.; Sasmito, A.P.; Ghoreishi-Madiseh, S.A. Thermal performance evaluation of integrated solar-geothermal system; a semi-conjugate reduced order numerical model. Appl. Energy 2021, 303, 117676. [Google Scholar] [CrossRef]
- Philippe, M.; Bernier, M.; Marchio, D. Validity ranges of three analytical solutions to heat transfer in the vicinity of single boreholes. Geothermics 2009, 38, 407–413. [Google Scholar] [CrossRef]
- Lamarche, L.; Beauchamp, B. New solutions for the short-time analysis of geothermal vertical boreholes. Int. J. Heat Mass Transf. 2007, 50, 1408–1419. [Google Scholar] [CrossRef]
- Lamarche, L.; Beauchamp, B. A new contribution to the finite line-source model for geothermal boreholes. Energy Build. 2007, 39, 188–198. [Google Scholar] [CrossRef]
- Zeng, H.; Diao, N.; Fang, Z. Heat transfer analysis of boreholes in vertical ground heat exchangers. Int. J. Heat Mass Transf. 2003, 46, 4467–4481. [Google Scholar] [CrossRef]
- Lamarche, L. Mixed arrangement of multiple input-output borehole systems. Appl. Therm. Eng. 2017, 124, 466–476. [Google Scholar] [CrossRef]
- Ghoreishi-Madiseh, S.A.; Kuyuk, A.F.; de Brito, M.A.R. An analytical model for transient heat transfer in ground-coupled heat exchangers of closed-loop geothermal systems. Appl. Therm. Eng. 2019, 150, 696–705. [Google Scholar] [CrossRef]
- Pokhrel, S.; Sasmito, A.P.; Sainoki, A.; Tosha, T.; Tanaka, T.; Nagai, C.; Ghoreishi-Madiseh, S.A. Field-scale experimental and numerical analysis of a downhole coaxial heat exchanger for geothermal energy production. Renew. Energy 2022, 157, 227–246. [Google Scholar]
- Cimmino, M.; Eslami-Nejad, P. A simulation model for solar assisted shallow ground heat exchangers in series arrangement. Energy Build. 2017, 182, 521–535. [Google Scholar] [CrossRef]

| Parameter | Value | Unit |
|---|---|---|
| Inner radius, a | 0.05 | m |
| Outer radius, b | 50 | m |
| Distance between neighboring boreholes, d | 10 | m |
| Specific heat, | 1000 | J/(kg·K) |
| Thermal conductivity, k | 1.5 | W/(m·K) |
| Mass density, | 2500 | kg/m |
| Thermal diffusivity, | m /s | |
| Undisturbed temperature, | 283.15 | K |
| Parameter | Value | Unit |
|---|---|---|
| Inner radius, a | 0.0889 | m |
| Outer radius, b | 50 | m |
| Specific heat (ground), | 1100 | J/(kg·K) |
| Specific heat (water), | 4182 | J/(kg·K) |
| Thermal conductivity (ground), | 2 | W/(m·K) |
| Mass density (ground), | 2490 | kg/m |
| Thermal diffusivity (ground), | m /s | |
| Undisturbed temperature, | 463.01 | K |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hefni, M.A.; Xu, M.; Hassani, F.; Ghoreishi-Madiseh, S.A.; Ahmed, H.M.; Saleem, H.A.; Ahmed, H.A.M.; Hassan, G.S.A.; Ahmed, K.I.; Sasmito, A.P. An Analytical Model for Transient Heat Transfer with a Time-Dependent Boundary in Solar- and Waste-Heat-Assisted Geothermal Borehole Systems: From Single to Multiple Boreholes . Appl. Sci. 2021, 11, 10338. https://doi.org/10.3390/app112110338
Hefni MA, Xu M, Hassani F, Ghoreishi-Madiseh SA, Ahmed HM, Saleem HA, Ahmed HAM, Hassan GSA, Ahmed KI, Sasmito AP. An Analytical Model for Transient Heat Transfer with a Time-Dependent Boundary in Solar- and Waste-Heat-Assisted Geothermal Borehole Systems: From Single to Multiple Boreholes . Applied Sciences. 2021; 11(21):10338. https://doi.org/10.3390/app112110338
Chicago/Turabian StyleHefni, Mohammed A., Minghan Xu, Ferri Hassani, Seyed Ali Ghoreishi-Madiseh, Haitham M. Ahmed, Hussein A. Saleem, Hussin A. M. Ahmed, Gamal S. A. Hassan, Khaled I. Ahmed, and Agus P. Sasmito. 2021. "An Analytical Model for Transient Heat Transfer with a Time-Dependent Boundary in Solar- and Waste-Heat-Assisted Geothermal Borehole Systems: From Single to Multiple Boreholes " Applied Sciences 11, no. 21: 10338. https://doi.org/10.3390/app112110338
APA StyleHefni, M. A., Xu, M., Hassani, F., Ghoreishi-Madiseh, S. A., Ahmed, H. M., Saleem, H. A., Ahmed, H. A. M., Hassan, G. S. A., Ahmed, K. I., & Sasmito, A. P. (2021). An Analytical Model for Transient Heat Transfer with a Time-Dependent Boundary in Solar- and Waste-Heat-Assisted Geothermal Borehole Systems: From Single to Multiple Boreholes . Applied Sciences, 11(21), 10338. https://doi.org/10.3390/app112110338












