Synergistic Bond Properties of Different Deformed Steel Fibers Embedded in Mortars Wet-Sieved from Self-Compacting SFRC
Abstract
:1. Introduction
2. Materials and Methods
2.1. Steel Fibers
2.2. Preparation of Mortar
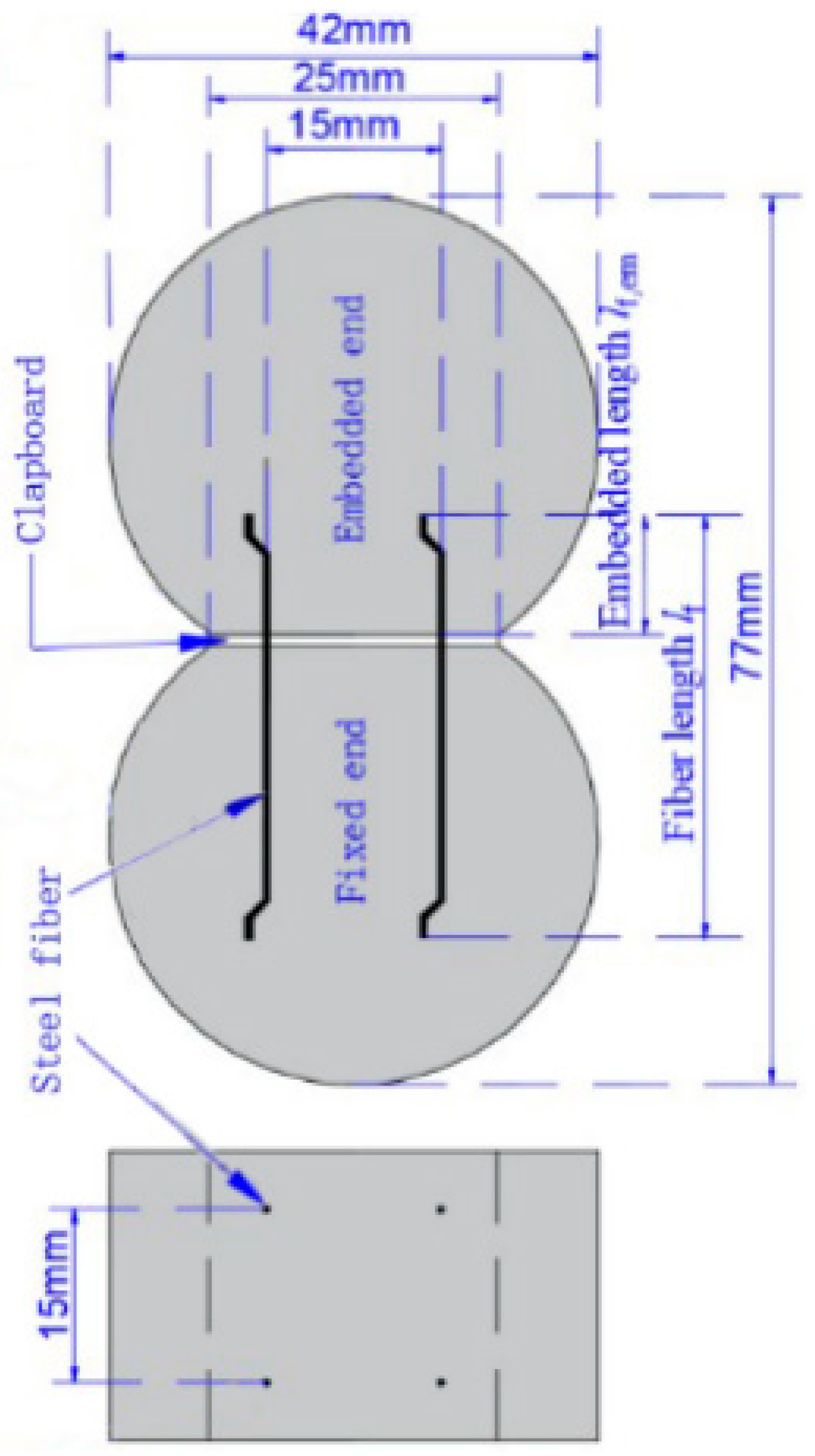
2.3. Experimental Design for Pull-Out Test
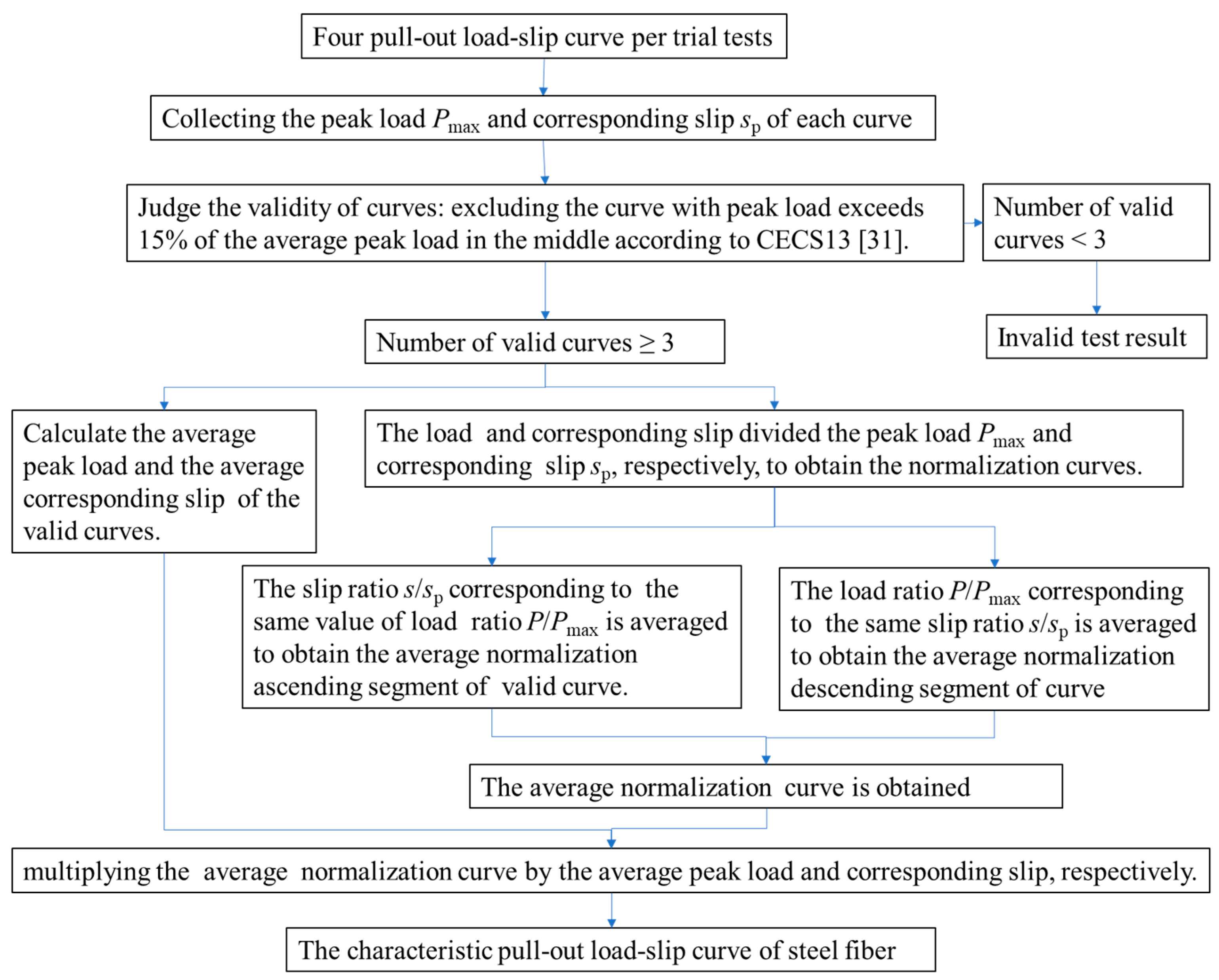
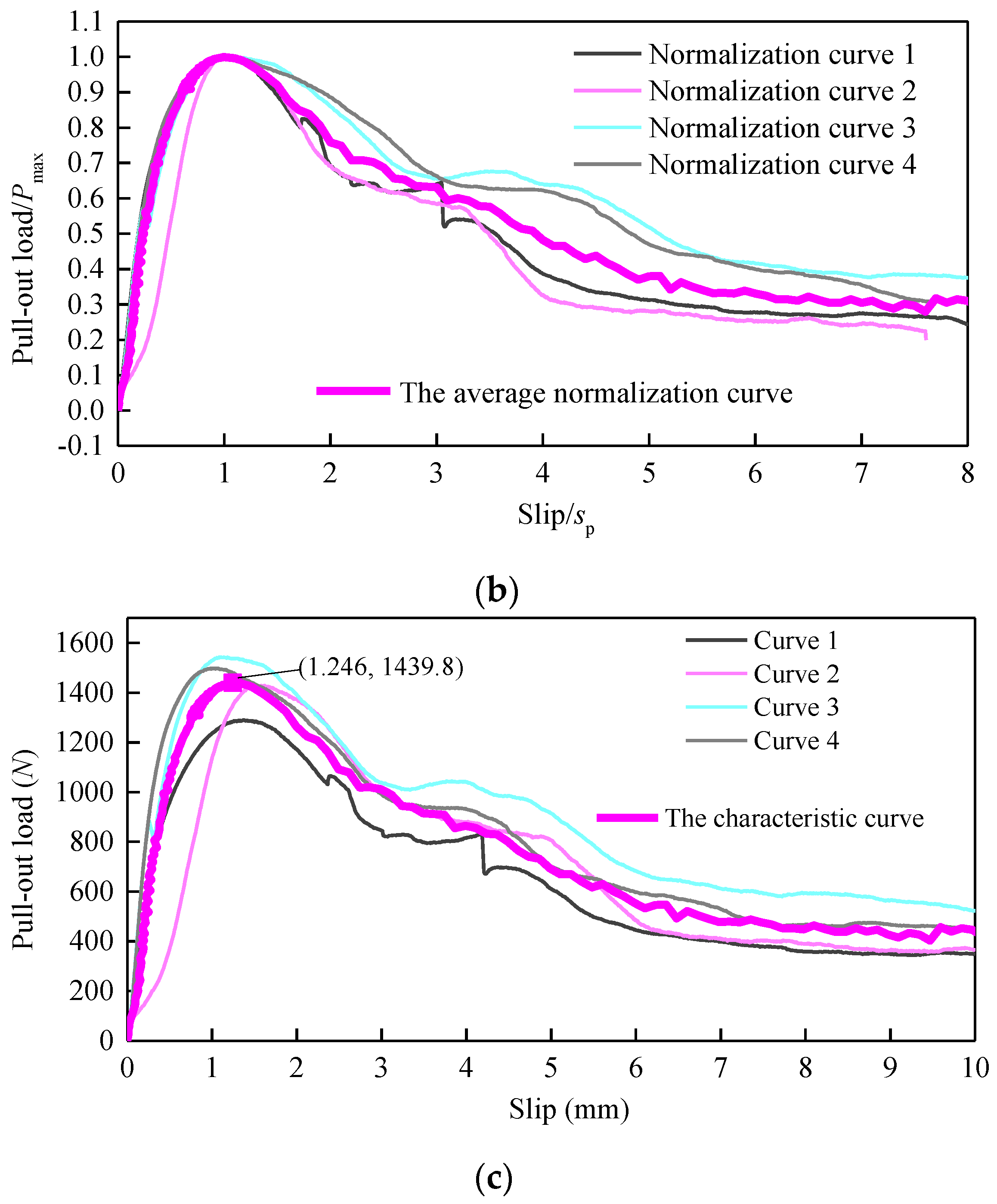
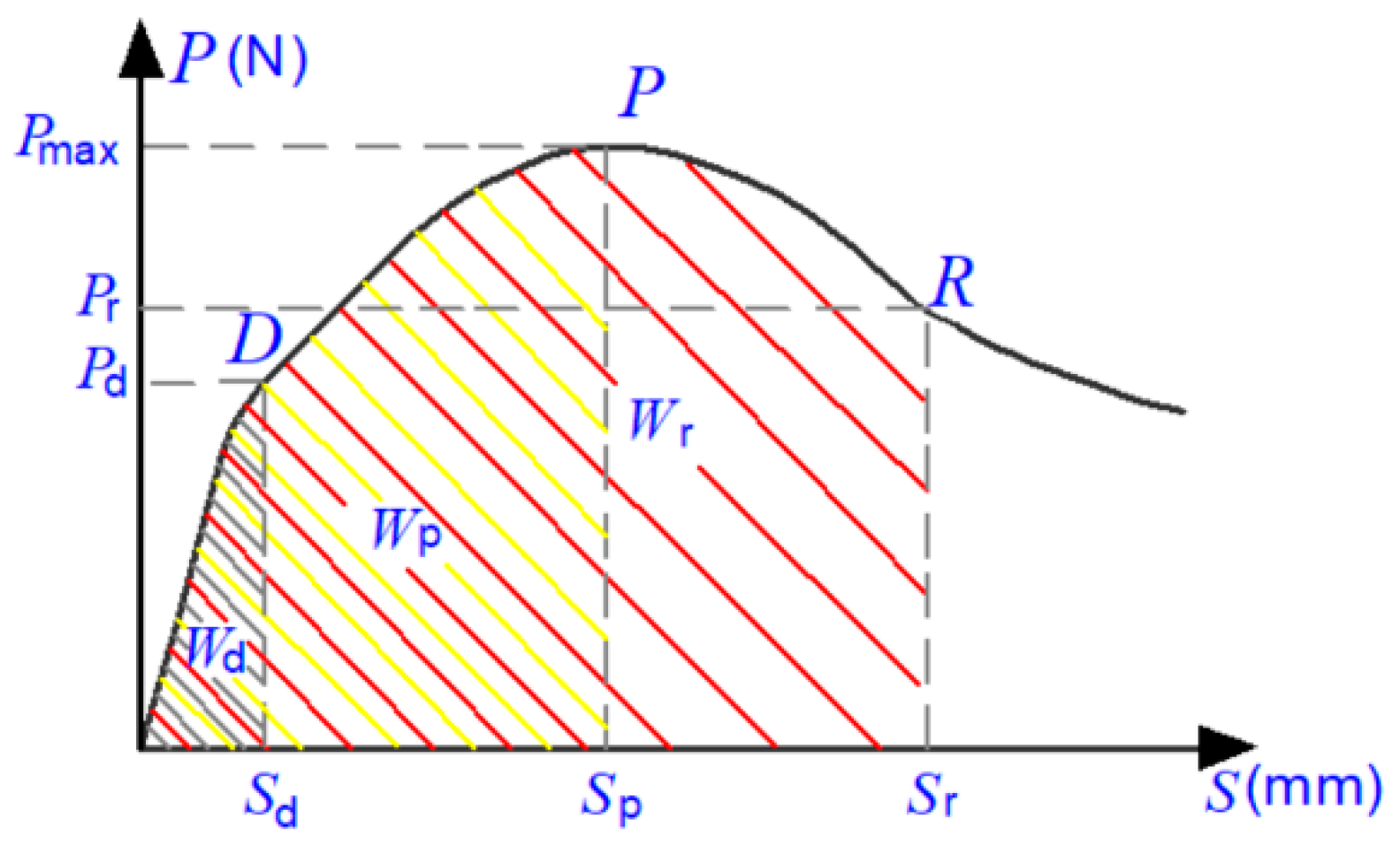
2.4. Test Data Processing Method for Pull-Out Test
3. Multi-Index Synthetical Evaluation Method of Bond Properties
3.1. Evaluation for Bond Property of Single Steel Fiber
3.2. Evaluation for Synergistic Bond Property of Unit Weight Steel Fibers
4. Test Results and Analyses
4.1. Failure Modes
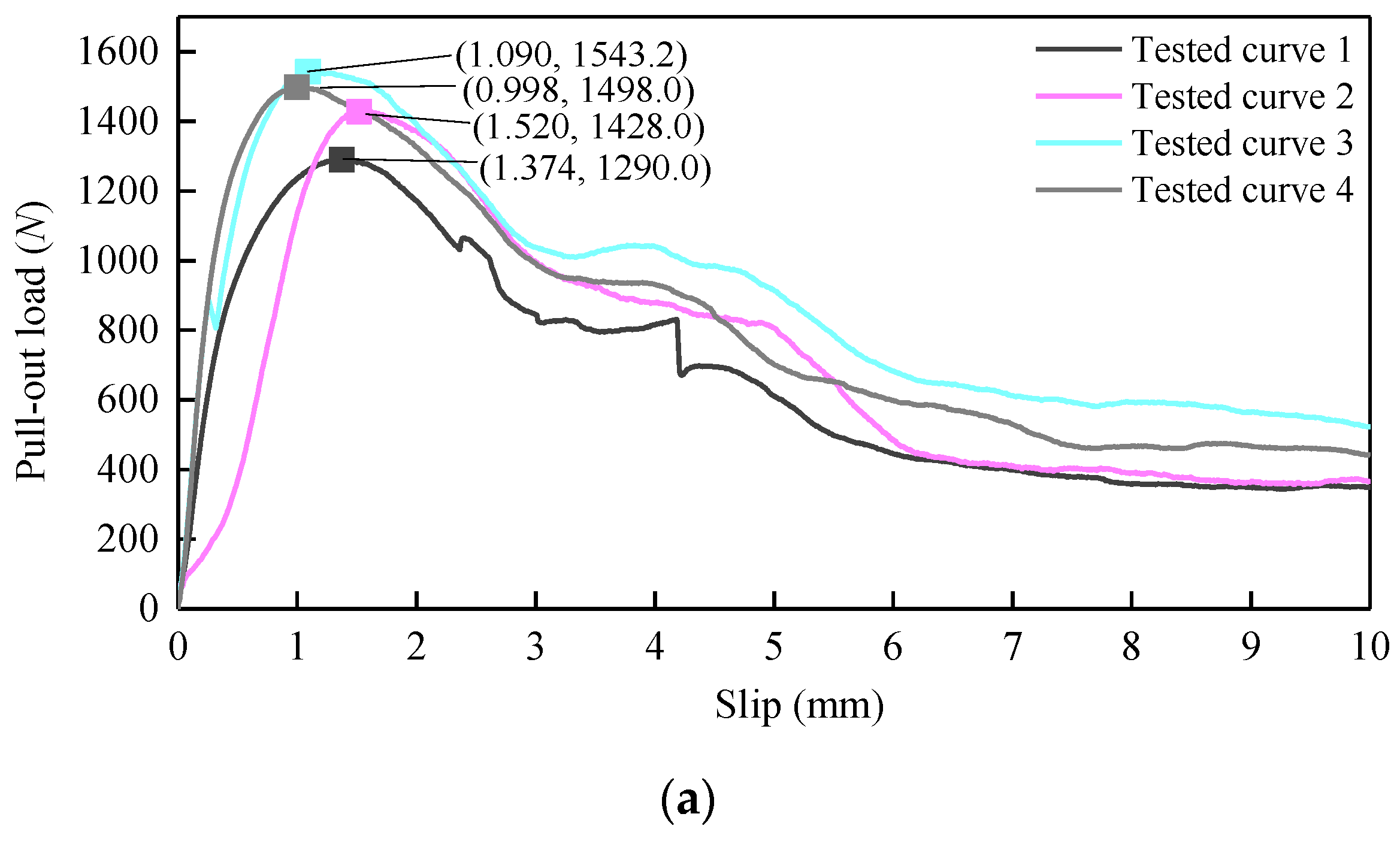
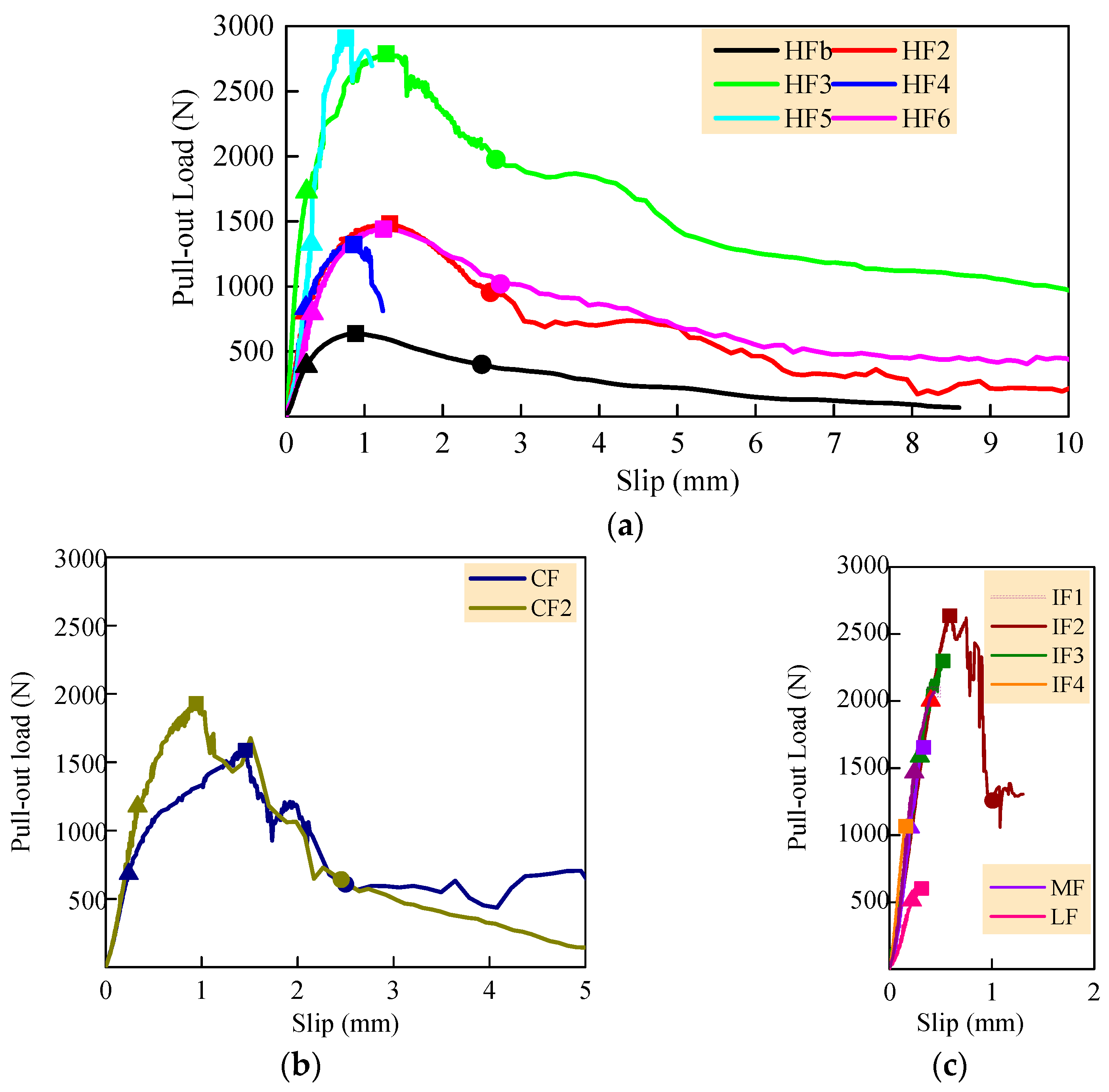
4.2. Pull-Out Load-Slip Curves
4.3. Bond Properties of Single Steel Fiber
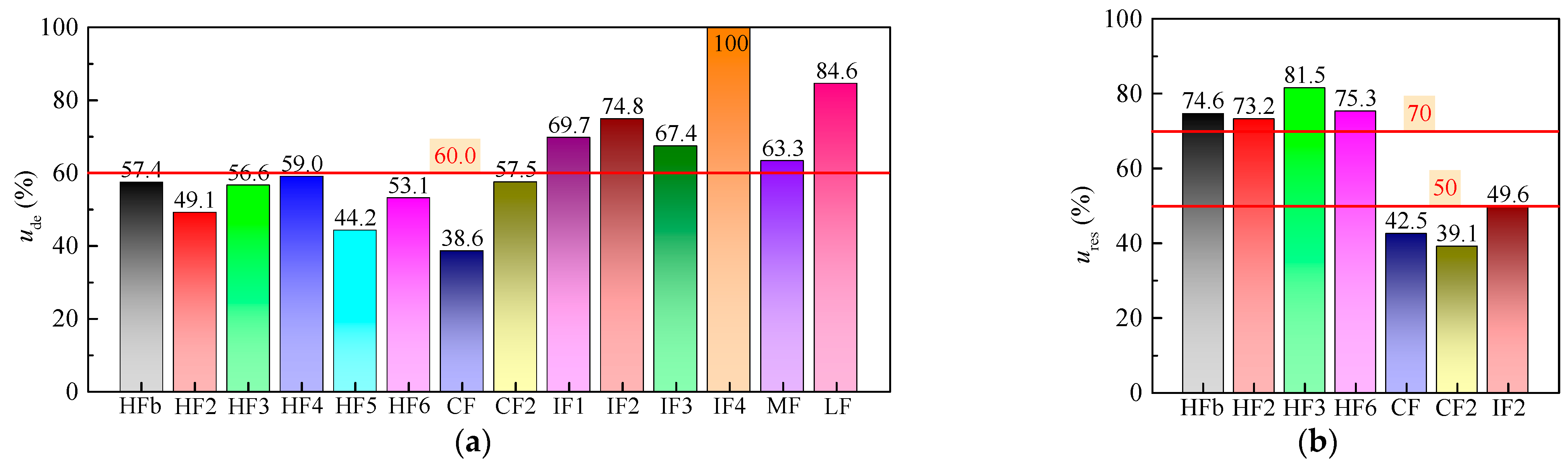
4.3.1. Bond Strength
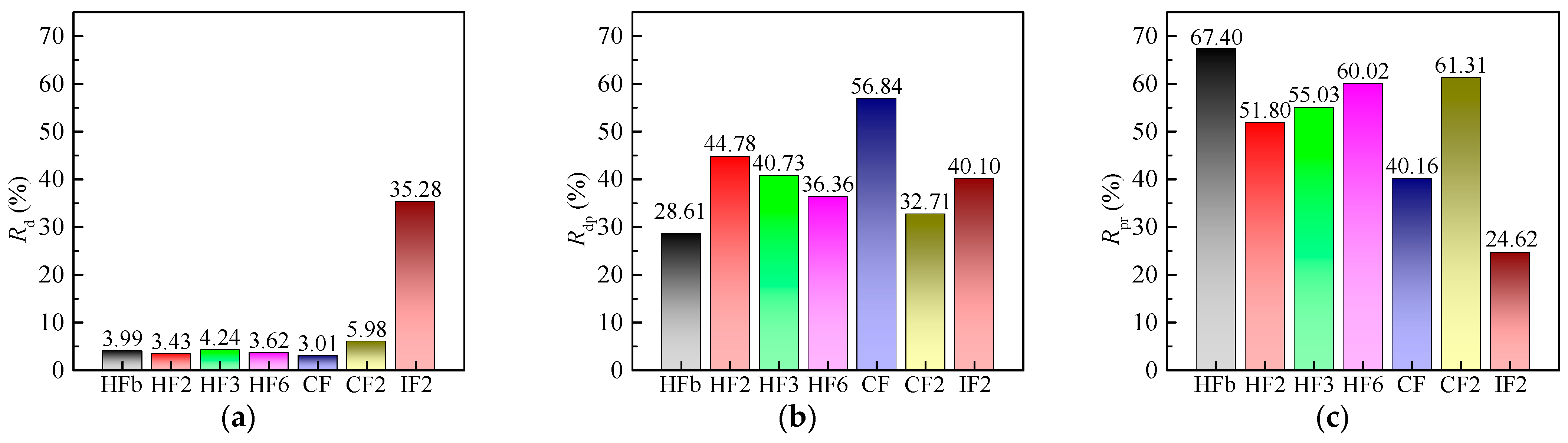
4.3.2. Energy Ratios
4.4. Synergistic Bond Properties of Per Unit Weight Steel Fiber
4.4.1. Bond Loads of Hooked-End Steel Fiber
4.4.2. Bond Loads on Per Embedded Length of Other Types of Steel Fiber
4.4.3. Pull-Out Works of Per Unit Weight Steel Fibers
5. Conclusions
- Based on the multi-index synthetical evaluation of pull-out behaviors of hooked-end steel fiber embedded in mortars, the indices for evaluating the synergistic bond properties of different deformed steel fibers are proposed by using the concept of per unit weight of steel fibers. The bond strength indices of the loads of per unit weight steel fibers and the load on per embedded length of per unit weight steel fibers, the expended energy indices of the work of per unit weight steel fibers and the toughness indices of energy ratios are proposed to comprehensively express the bond properties, considering the geometry and numbers of different deformed steel fibers.
- Hooked-end steel fibers with a tensile strength higher than 1150 MPa are strength and toughness enhanced type fibers with different degrees of enhancement. HFb, HF2, and HF3 with tensile strengths between 1150–1500 MPa have excellent strengthening, energy dissipation effect, and toughening capacity in the normal serviceability and ultimate bearing capacity of concrete. Their strength use efficiency usf was close to the limit of 71.4% for high-strength steel bar. However, HF5 with a tensile strength of 1150 MPa could develop a higher strength use efficiency usf that reached about 100%, which led the broken steel fiber due to the strong anchorage of a 4-D type hooked-end. HF6 with a tensile strength of 2200 MPa had a large affluence with a smaller strength use efficiency usf of 37.1%. Although they all match the self-compacting SFRC with cubic compressive strength of 60 MPa, it is better to produce steel fiber with appropriate geometry and tensile strength for the economical application with the premise of reliability. Hooked-end steel fiber HF4 with a tensile strength of 600 MPa was broken during the pull-out process, which can be used mainly for the improvement of the strength of concrete.
- Crimped steel fiber CF2 with a tensile strength of 2000 MPa had excellent bond strength and toughness, which provides the strengthening and energy dissipation effect and the toughening capacity in the cracking resistance, normal serviceability, and ultimate bearing capacity of concrete, due to matching with the self-compacting SFRC with a cubic compressive strength of 60 MPa. The rectangular sectional crimped steel fiber CF with a tensile strength of 800 MPa had a poor bond behavior in this test.
- The indentation, milled, and large-end steel fibers are strength enhanced type fibers with a certain energy dissipation ability and toughening capacity, before the bond strength reached the maximum. The bond relies mainly on the geometry of steel fiber with different tensile strength.
- To realize the expected properties of concrete reinforced by steel fibers, the bond property of steel fiber in mortar can be used for the fiber selection. Not all kinds of steel fiber can simultaneously improve the strength and toughness of concrete. Even if the same kind of steel fiber is used, the reinforcing effect may be different in quantity. Therefore, the in-depth study of bond properties in relation to the mechanical properties of SFRC is necessary to increase the reinforcing and economic efficiency of steel fibers.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| lf | the length of steel fiber, |
| df | The equivalent diameter of steel fiber. |
| lf/df | The aspect ratio of steel fiber. |
| Nsf | The number of steel fiber per kilogram. |
| fsf | The tensile strength of steel fiber. |
| fcu | The cube compressive strength of self-compacting SFRC. |
| fst | The splitting tensile strength of self-compacting SFRC. |
| fcm | The compressive strength of wet-sieved mortar. |
| ffm | The flexural strength of wet-sieved mortar. |
| lf.em | The embedded length of steel fiber in mortar. |
| lf.f | The anchored length of steel fiber in mortar. |
| P | The pull-out load of steel fiber. |
| Pmax | The peak value of pull-out load of steel fiber. |
| Pd | The debonding pull-out load of steel fiber. |
| Pr | The residual pull-out load of steel fiber. |
| s | The bond slip of steel fiber under the P. |
| sp | The peak bond slip of steel fiber under the Pmax. |
| sd | The bond slip corresponded to the Pd. |
| sr | The bond slip corresponded to Pr. |
| τmax | The bond strength of steel fiber. |
| usf | The strength use efficiency of steel fiber. |
| τd | The debonding strength of steel fiber. |
| ude | The strength ratio corresponded to the τd. |
| τres | The residual bond strength of steel fiber. |
| ures | The strength ratio corresponded to the τres. |
| Wd | The debonding work of single steel fiber. |
| Ws | The slipping work of single steel fiber. |
| Wp | The work corresponded to the peak load. |
| Wr | The pull-out work of single steel fiber. |
| Rd | The debonding energy ratio. |
| Rdp | The slipping energy ratio. |
| Rpr | The pull-out energy ratio. |
| Ld | The debonding load of per unit weight hooked-end steel fibers. |
| Lm | The bonding load of per unit weight hooked-end steel fibers. |
| Lr | The residual bond load of per unit weight hooked-end steel fibers. |
| Ldl | The debonding load on per embedded length of per unit weight steel fibers except for hooked-end ones. |
| Lml | The bonding load on per embedded length of per unit weight steel fibers except for hooked-end ones. |
| Lrl | The residual bond load on per embedded length of per unit weight steel fibers except for hooked-end ones. |
| UWd | The debonding work of per unit weight steel fibers. |
| UWp | The slipping work of per unit weight steel fibers. |
| UWr | The pull-out work of per unit weight steel fibers. |
References
- Ministry of Housing and Urban-Rural Development of the People’s Republic of China. Steel Fiber Reinforced Concrete, JG/T 472-2015; China Architecture & Building Press: Beijing, China, 2015. [Google Scholar]
- Zhao, M.L.; Li, J.; Law, D. Effects of flowability on SFRC fibre distribution and properties. Magaz. Concr. Res. 2017, 69, 1043–1054. [Google Scholar] [CrossRef]
- Ding, X.X.; Li, C.Y.; Han, B.; Lu, Y.Z.; Zhao, S.B. Effects of different deformed steel-fibers on preparation and fundamental properties of self-compacting SFRC. Constr. Build. Mater. 2018, 168, 471–481. [Google Scholar] [CrossRef]
- Zhao, M.L.; Zhao, M.S.; Chen, M.H.; Li, J.; David, L. An experimental study on strength and toughness of steel fiber reinforced expanded-shale lightweight concrete. Constr. Build. Mater. 2018, 183, 493–501. [Google Scholar] [CrossRef]
- Ding, X.X.; Li, C.Y.; Zhao, M.L.; Li, J.; Geng, H.B.; Lian, L. Tensile strength of self-compacting steel fiber reinforced concrete evaluated by different test methods. Crystals 2021, 11, 251. [Google Scholar] [CrossRef]
- Li, C.Y.; Shang, P.R.; Li, F.L.; Feng, M.; Zhao, S.B. Shrinkage and mechanical properties of self-compacting SFRC with calcium sulfoaluminate expansive agent. Materials 2020, 13, 588. [Google Scholar] [CrossRef] [Green Version]
- Ding, X.X.; Li, C.Y.; Li, Y.Z.; Song, C.; Zhao, S.B. Experimental and numerical study on stress-strain behavior of self-compacting SFRC under uniaxial compression. Constr. Build. Mater. 2018, 185, 30–38. [Google Scholar] [CrossRef]
- Jerath, S.; Shibani, M.M. Dynamic modulus for reinforced concrete beams. J. Struct. Eng. 1984, 110, 1405–1410. [Google Scholar] [CrossRef]
- Bonopera, M.; Chang, K.C.; Chen, C.C.; Sung, Y.C.; Tullini, N. Prestress force effect on fundamental frequency and deflection shape of PCI beams. Struct. Eng. Mech. 2018, 67, 255–265. [Google Scholar]
- Zhao, M.S.; Zhang, X.Y.; Song, W.H.; Li, C.Y.; Zhao, S.B. Development of steel fiber reinforced expanded- shale lightweight concrete with high freeze-thaw resistance. Adv. Mater. Sci. Eng. 2018, 2018, 9573849. [Google Scholar] [CrossRef] [Green Version]
- Cunha, V.M.C.F.; Barros, J.A.O.; Sena-Cruz, J.M. Pullout behavior of steel fibers in self-compacting concrete. J. Mater. Civil. Eng. 2010, 22, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Abdallah, S.; Fan, M.; Cashell, K.A. Bond-slip behaviour of steel fibres in concrete after exposure to elevated temperatures. Constr. Build. Maters. 2017, 140, 542–551. [Google Scholar] [CrossRef]
- Soetens, T.; Gysel, A.V.; Matthys, S.; Taerwe, L. A semi-analytical model to predict the pull-out behaviour of inclined hooked-end steel fibres. Constr. Build. Mater. 2013, 43, 253–265. [Google Scholar] [CrossRef]
- Isla, F.; Ruano, G.; Luccioni, B. Analysis of steel fibers pull-out. Experimental study. Constr. Build. Mater. 2015, 100, 183–193. [Google Scholar] [CrossRef]
- Oliveira, F.L.D. Design-Oriented Constitutive Model for Steel Fiber Reinforced Concrete. Ph.D. Thesis, Universitat Politècnica De Catalunya, Barcelona, Spain, 2010. [Google Scholar]
- Zhao, S.B.; Du, H.; Qian, X.J.; Li, C.Y. Study on direct mix design method for steel fiber reinforced high-strength concrete. China Civ. Eng. J. 2008, 41, 1–6. [Google Scholar]
- Zhao, S.B.; Li, C.Y.; Du, H.; Qian, X.J. Study of steel fiber reinforced high-strength concrete containing large coarse aggregate. J. Build. Mater. 2010, 13, 155–160. [Google Scholar]
- Ding, X.X.; Zhao, M.L.; Li, J.; Shang, P.R.; Li, C.Y. Mix proportion design of self-compacting SFRC with manufactured sand based on the steel fiber-aggregates skeleton packing test. Materials 2020, 13, 2833. [Google Scholar] [CrossRef]
- Caggiano, A.; Xargay, H.; Folino, P.; Martinelli, E. Experimental and numerical characterization of the bond behavior of steel fibers recovered from waste tires embedded in cementitious matrices. Cement. Concrete. Comp. 2015, 62, 146–155. [Google Scholar] [CrossRef]
- Xu, J.E.; Sun, J.Y.; Luo, G.D. Experimental study on the bond load between steel fiber and concrete based on orthogonal design method. In Proceedings of the Fourth National Conference on Fiber Cement and Fiber Concrete (I), Jiujiang, China, 20–23 July 1992. [Google Scholar]
- Yang, M. Strengthening and Toughening Mechanism of Steel Fiber Reinforced High-Strength Concrete and Design Method Based on Toughness. Ph.D. Thesis, Dalian University of Technology, Dalian, China, 2006. [Google Scholar]
- Sun, W.; Gao, J.M.; Qin, H.G. Studies on bond strength of interface between fiber and matrix in steel fiber reinforced concrete. J. Chin. Ceram. Soc. 1985, 3, 292–300. [Google Scholar]
- Banholzer, B.; Brameshuber, W.; Jung, W. Analytical evaluation of pull-out tests-the inverse problem. Cement. Concrete. Comp. 2006, 28, 564–571. [Google Scholar] [CrossRef]
- Meschke, R.B.G.; Song, F.B.; Zhan, Y.J. Experimental, analytical and numerical analysis of the pullout behaviour of steel fibres considering different fibre types, inclinations and concrete strengths. Struct. Concr. 2014, 15, 126–135. [Google Scholar]
- Esmaeili, J.; Andalibi, K.; Gencel, O.; Maleki, F.K.; Malekid, V.A. Pull-out and bond-slip performance of steel fibers with various ends shapes embedded in polymer-modified concrete. Constr. Build. Mater. 2021, 271, 121531. [Google Scholar] [CrossRef]
- Kim, D.J.; El-Tawil, S.; Naaman, A.E. Effect of matrix strength on pullout behavior of high strength deformed steel fibers. In Symposium—Four Decades of Progress in Prestressed Concrete, Fiber Reinforced Concrete, and Thin Laminate Composites; Montesinos, G.J., Balaguru, P., Eds.; ACI Special Publications: Farmington Hills, MI, USA, 2010; pp. 135–150. [Google Scholar]
- Lu, J.; Lin, L. Upgrading effect of new end-hooked steel fiber on properties of concrete. New Build. Mater. 2014, 2, 19–22. [Google Scholar]
- Abdallah, S.; Rees, D.W.A. Comparisons between pull-out behaviour of various hooked-end fibres in normal–high strength concretes. Int. J. Concr. Struct. Mater. 2019, 13, 27. [Google Scholar] [CrossRef]
- Zhao, L.J.; Li, N. Drawing test of profiled steel fiber in cement mortar matrix. Opencast Min. Technol. 2015, 9, 99–101. [Google Scholar]
- Feng, H.; Sheikh, M.N.; Hadi, M.N.S.; Feng, L.; Gao, D.Y.; Zhao, J. Pullout behaviour of different types of steel fibres embedded in magnesium phosphate cementitious matrix. Int. J. Concr. Struct. Mater. 2019, 13, 33. [Google Scholar] [CrossRef]
- Lee, J.H.; Kighuta, K. Twin-twist effect of fibers on the pullout resistance in cementitious materials. Constr. Build. Mater. 2017, 146, 555–562. [Google Scholar] [CrossRef]
- Ding, X.X.; Zhao, M.L.; Li, C.Y.; Li, J.; Zhao, X.S. A multi-index synthetical evaluation of pull-out behaviors of hooked-end steel fiber embedded in mortars. Constr. Build. Mater. 2021, 276, 122219. [Google Scholar] [CrossRef]
- China Association for Engineering Construction Standardization. Standard Test Methods for Fiber Reinforced Concrete, CECS13: 2009; China Planning Press: Beijing, China, 2009. [Google Scholar]
- Zhao, M.L.; Ding, X.X.; Li, J.; Law, D. Numerical analysis of mix proportion of self-compacting concrete compared to ordinary concrete. Key Eng. Mater. 2018, 789, 69–75. [Google Scholar] [CrossRef]
- Ding, X.X.; Zhao, M.L.; Zhou, S.Y.; Fu, Y.; Li, C.Y. Statistical analysis and preliminary study on the mix proportion design of self-compacting steel fiber reinforced concrete. Materials 2019, 12, 637. [Google Scholar] [CrossRef] [Green Version]
- Ministry of Housing and Urban-Rural Development of the People’s Republic of China. Standard for Test Methods of Concrete Physical and Mechanical Properties, GB/T 50081-2019; China Building Industry Press: Beijing, China, 2019. [Google Scholar]
- The State Bureau of Quality and Tehnical Supervision. Method of Testing Cements-Determination of Strength, GB/T 17671-1999; Standards Press of China: Beijing, China, 1999. [Google Scholar]
- Ministry of Housing and Urban-Rural Development of the People’s Republic of China. Design Code for Concrete Structures, GB/T 50010-2010; China Building Industry Press: Beijing, China, 2015. [Google Scholar]
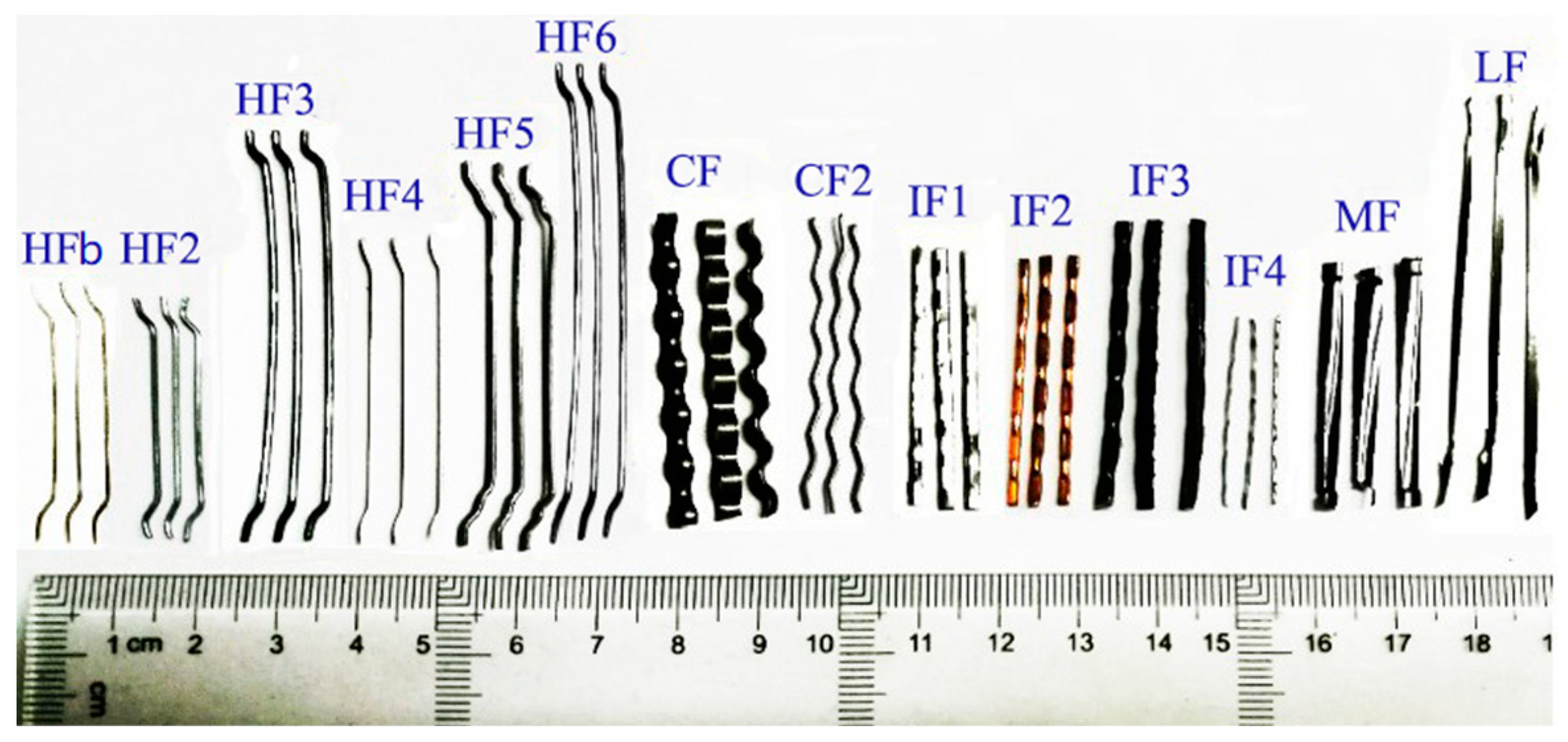






| No. | Type | Cross-Section | lf (mm) | lf/df | Nsf | fsf (MPa) | ||
|---|---|---|---|---|---|---|---|---|
| Shape | Perimeter (mm) | df (mm) | ||||||
| HFb | Hooked-end | Circular | 1.57 | 0.50 | 29.8 | 60.0 | 21,637 | 1150 |
| HF2 | Hooked-end | Circular | 2.20 | 0.70 | 31 | 44.3 | 10,680 | 1150 |
| HF3 | Hooked-end | Circular | 2.51 | 0.80 | 50.6 | 63.3 | 5006 | 1500 |
| HF4 | Hooked-end | Circular | 3.00 | 0.84 | 38 | 45.2 | 5980 | 600 |
| HF5 | Hooked-end | Circular | 2.83 | 0.90 | 51 | 56.7 | 3990 | 1150 |
| HF6 | Hooked-end | Circular | 2.36 | 0.75 | 60 | 80.0 | 4800 | 2200 |
| CF | Crimped | Rectangular | 5.33 | 1.17 | 38.8 | 33.2 | 3347 | 800 |
| CF2 | Crimped | Circular | 2.20 | 0.70 | 37.5 | 53.6 | 8830 | 2000 |
| IF1 | Indentation | Rectangular | 5.00 | 1.13 | 32.3 | 28.5 | 4599 | 550 |
| IF2 | Indentation | Irregular | 4.18 | 1.12 | 32 | 28.6 | 3550 | 1500 |
| IF3 | Indentation | Irregular | 6.20 | 0.82 | 36.5 | 44.5 | 1660 | 1700 |
| IF4 | Indentation | Irregular | 1.80 | 0.50 | 24 | 48.0 | 26,540 | 1400 |
| MF | Milled | Irregular | 2.51 | 0.80 | 31 | 38.8 | 8180 | 850 |
| LF | Large-end | Rectangular | 3.46 | 0.77 | 52.2 | 67.4 | 5027 | 350 |
| w/b | Sand Ratio (%) | Mix Proportion of Self-Compacting SFRC (kg/m3) | ||||||
| Water | Cement | Fly-Ash | Crushed Stone | Manufactured Sand | Water Reducer | Steel Fiber (HFb) | ||
| 0.31 | 56 | 219 | 494 | 212 | 527 | 783 | 5.65 | 94.2 |
| Properties of self-compacting SFRC | Properties of wet-sieved mortar | |||||||
| Slump flow (mm) | Flow time T500 (s) | fcu (MPa) | fst (MPa) | Micro-slump flow (mm) | fcm (MPa) | ffm (MPa) | ||
| 610 | 4.5 | 60.4 | 4.60 | 245 | 79.6 | 11.5 | ||
| Fiber Type | Embedded Length lf.em (mm) | Anchored Length lf.f (mm) | Fiber Type | Embedded Length lf.em (mm) | Anchored Length lf.f (mm) |
|---|---|---|---|---|---|
| HFb | 11 | 17.8 | HF2 | 12 | 18 |
| HF3 | 12 | 37.6 | HF4 | 10 | 27 |
| HF5 | 15 | 35.0 | HF6 | 26 | 33 |
| CF | 12 | 25.8 | CF2 | 11 | 25.5 |
| IF1 | 11 | 20.3 | IF2 | 12 | 19 |
| IF3 | 10 | 25.5 | IF4 | 8 | 15.0 |
| MF | 10 | 20 | LF | 20 | 31.2 |
| Fiber Type | Failure Mode | Fiber Type | Failure Mode | Fiber Type | Failure Mode |
|---|---|---|---|---|---|
| HFb, HF2, HF3 | Fiber pull-out | HF4, HF5 | Fiber breakage | HF6 | Fiber pull-out |
| CF, CF2 | Mortar cracking | IF1 | Fiber breakage | IF2, IF3 | Mortar cracking |
| IF4 | Fiber breakage | MF | Fiber breakage | LF | Fiber breakage |
| NO. | Key Point P | Key Point D | Key Point R | |||
|---|---|---|---|---|---|---|
| Pmax (N) | sp (mm) | Pd (N) | sd (mm) | Pr (N) | sr (mm) | |
| HFb | 637.2 | 0.888 | 388.6 | 0.258 | 399.7 | 2.50 |
| HF2 | 1481.6 | 1.332 | 800.0 | 0.256 | 953.6 | 2.61 |
| HF3 | 2788.4 | 1.276 | 1728.8 | 0.26 | 1974.6 | 2.68 |
| HF4 | 1320.4 | 0.864 | 831.9 | 0.252 | -- | -- |
| HF5 | 2908.8 | 0.76 | 1326.1 | 0.322 | -- | -- |
| HF6 | 1439.8 | 1.246 | 792 | 0.335 | 1018.5 | 2.74 |
| CF | 1587.2 | 1.457 | 682.5 | 0.241 | 607.5 | 2.5 |
| CF2 | 1929.6 | 0.944 | 1177.1 | 0.333 | 641.5 | 2.46 |
| IF1 | 2064.4 | 0.439 | 1465.7 | 0.243 | -- | -- |
| IF2 | 2636.0 | 0.59 | 2003.4 | 0.404 | 1258.2 | 1.01 |
| IF3 | 2297.4 | 0.52 | 1585.2 | 0.297 | -- | -- |
| IF4 | 1066.8 | 0.156 | 1066.8 | 0.156 | -- | -- |
| MF | 1652.4 | 0.334 | 1057.5 | 0.22 | -- | -- |
| LF | 601.3 | 0.314 | 511.1 | 0.22 | -- | -- |
| No. | HFb | HF2 | HF3 | HF4 | HF5 | HF6 |
|---|---|---|---|---|---|---|
| Ld (×103 kN/kg) | 2.102 | 2.136 | 2.164 | 1.244 | 1.323 | 0.950 |
| Lm (×103 kN/kg) | 3.447 | 3.956 | 3.490 | 1.974 | 2.902 | 1.728 |
| Lr (×103 kN/kg) | 2.162 | 2.546 | 2.471 | - | - | 1.222 |
| No. | CF | CF2 | IF1 | IF2 | IF3 | IF4 | MF | LF |
|---|---|---|---|---|---|---|---|---|
| Ldl (×103 kN/(mm·kg)) | 0.049 | 0.244 | 0.157 | 0.153 | 0.068 | 0.902 | 0.221 | 0.032 |
| Lml (×103 kN/(mm·kg)) | 0.126 | 0.424 | 0.225 | 0.205 | 0.101 | 0.902 | 0.350 | 0.038 |
| Lrl (×103 kN/(mm·kg)) | 0.054 | 0.166 | - | 0.102 | - | - | - | - |
| No. | HFb | HF2 | HF3 | HF4 | HF5 | HF6 | CF |
| UWde (×106 N·mm/kg) | 0.268 | 0.282 | 0.321 | 0.139 | 0.173 | 0.137 | 0.067 |
| UWmax (×106 N·mm/kg) | 2.193 | 3.971 | 3.412 | 1.203 | 1.238 | 1.514 | 1.338 |
| UWres (×106 N·mm/kg) | 6.727 | 8.238 | 7.588 | - | - | 3.788 | 2.236 |
| No. | IF1 | IF2 | IF3 | IF4 | MF | LF | CF2 |
| UWde (×106 N·mm/kg) | 0.184 | 0.343 | 0.095 | 0.553 | 0.219 | 0.063 | 0.399 |
| UWmax (×106 N·mm/kg) | 0.599 | 0.733 | 0.283 | 0.553 | 0.555 | 0.131 | 2.582 |
| UWres (×106 N·mm/kg) | - | 0.972 | - | - | - | - | 6.673 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, X.; Geng, H.; Zhao, M.; Chen, Z.; Li, J. Synergistic Bond Properties of Different Deformed Steel Fibers Embedded in Mortars Wet-Sieved from Self-Compacting SFRC. Appl. Sci. 2021, 11, 10144. https://doi.org/10.3390/app112110144
Ding X, Geng H, Zhao M, Chen Z, Li J. Synergistic Bond Properties of Different Deformed Steel Fibers Embedded in Mortars Wet-Sieved from Self-Compacting SFRC. Applied Sciences. 2021; 11(21):10144. https://doi.org/10.3390/app112110144
Chicago/Turabian StyleDing, Xinxin, Haibin Geng, Minglei Zhao, Zhen Chen, and Jie Li. 2021. "Synergistic Bond Properties of Different Deformed Steel Fibers Embedded in Mortars Wet-Sieved from Self-Compacting SFRC" Applied Sciences 11, no. 21: 10144. https://doi.org/10.3390/app112110144
APA StyleDing, X., Geng, H., Zhao, M., Chen, Z., & Li, J. (2021). Synergistic Bond Properties of Different Deformed Steel Fibers Embedded in Mortars Wet-Sieved from Self-Compacting SFRC. Applied Sciences, 11(21), 10144. https://doi.org/10.3390/app112110144







