Abstract
Nonlinear active control is very important in many practical applications. Many well-known nonlinear active noise control algorithms may suffer from high computational complexity and low convergence speed, especially in the nonlinear secondary path case. Thus, it is still an actively researched topic for reducing complexity and improving the convergence rate. This paper presents a low-complexity Volterra filtered-error least mean square algorithm when taking a decomposable Volterra model into account for active control of nonlinear noise processes, which is referred as DVMFELMS. The computational complexity analysis shows that the proposed DVMFELMS algorithm can significantly reduce the nonlinear active noise control system’s complexity. The simulation results further show that the proposed algorithm can achieve promising performance compared with the Volterra-based FELMS algorithm and other state-of-the-art nonlinear filters, while the decomposable error of the Volterra kernel may be introduced inevitably. Moreover, the proposed DVMFELMS algorithm shows a better convergence rate in the broadband primary noise case due to fewer parameters used in each sub-filter.
1. Introduction
Active noise control has developed rapidly in the last few decades [1,2], and it has been successfully applied in many fields, such as heating, ventilating and air-conditioning systems [3], motor systems [4], and active headrests [5,6]. An active noise control system can generate a sound wave with the same amplitude but inverse phase at the canceling point by utilizing the secondary loudspeaker. Compared with passive methods, active noise control has shown its potential in canceling low-frequency environmental noises. A huge amount of research has been conducted in this field that focuses on the performance limitation of the active noise control system [7,8], algorithms [9], and stability [10].
The most commonly used algorithm for a single-channel feedforward active noise control system is the filtered-reference least mean square (FXLMS) algorithm modeled by the finite impulse response (FIR) filter due to its stability and low computational complexity. Although the FXLMS algorithm has already been successfully applied in active noise control systems, its performance may degrade in controlling nonlinear noise processes [11]. It is well-known that nonlinear phenomena may occur in many circumstances. First, when the primary noise has a high sound pressure level, the primary path may suffer nonlinear processes. Second, when the secondary actuator works at a high sound pressure level or the size of the secondary loudspeaker is small but works at low frequencies, nonlinear distortion may occur at the secondary actuator [12]. Third, the primary noise may come from a dynamic system, such as a chaotic noise process. The transfer function of the secondary path may have a non-minimum phase, so that the causality constraint will be violated [11]. In all of these situations, the traditional linear structure cannot model the nonlinear part of the system accurately enough. To overcome these challenges, many researchers have proposed numerous ways when taking the nonlinearity of the system into account, which can be roughly divided into two categories [13,14]. The former one uses artificial neural networks to model the nonlinearity of the system [15,16]. However, most artificial neural network-based algorithms are too computationally consuming for real applications of active noise control systems, which is out of the scope of this paper. The latter one employs the modeling capability of adaptive nonlinear filters including adaptive Volterra filters [11,17], the functional link network (FLNN) [18] and its generalized form (GFLNN) [19], the exponential functional link network (EFLNN) [20], the even mirror Fourier nonlinear (EMFN) filter [21], the Legendre neural network (LeNN) [22], Chebyshev filters (CF) [23,24], and so on. Furthermore, due to the different properties of different algorithms, convex combinations of the above-mentioned nonlinear filters have also been studied to achieve better performance [25,26].
For active noise control systems, the influence of the secondary path must be considered for most algorithms. The NANC algorithm with a linear secondary path (LSP) and with a nonlinear secondary path (NSP) was unified in [27] by introducing a virtual secondary path into NANC with the NSP case. For most nonlinear filters, NANC with NSP case is more computationally consuming compared to NANC with the LSP case. The NANC problem with a nonlinear secondary path (NSP), however, is more important in real applications [12]. When the memory length becomes large, the algorithms mentioned above often require high computational complexity that cannot be neglected. There are two ways to reduce the computational complexity of the NANC algorithm. One way is to use the recursive structure, which can be seen as an expansion of the infinite impulse response (IIR) filter. This kind of NANC algorithm includes the bilinear filter algorithm [28,29], recursive second-order Volterra filter [30], recursive even mirror Fourier nonlinear filter [31,32], adaptive function expansion bilinear filter [33,34], and so on. However, it is worth noting that the stability of all recursive algorithms mentioned above should be carefully considered, and more efforts must be made to make the recursive algorithm stable [35]. The other way is to use the simplified structure firstly introduced in [36], which uses a diagonal channel structure of nonlinear filters and channel reduced strategy that only uses a few channels near the main one. Note that the choice of the number of the reduced channels may significantly influence the steady-state performance.
This paper focuses on a group of adaptive Volterra filter-based algorithms, which are widely used in practice and perform well in a low-order nonlinear case. The major challenge of these traditional Volterra filter-based algorithms is that the computational complexity increases rapidly with the increase of the length of the memory and the order of the Volterra kernel. Recently, the Kronecker product decomposition has been introduced to linear system identification [37] and acoustic echo cancellation [38]. When using the Kronecker product decomposition, the computational complexity can be reduced dramatically in theory. In addition, it is demonstrated that the decomposable Volterra model outperforms the simplified structure in [36]. Motivated by these latest works, this paper proposes an adaptive Volterra-filtered error least mean square algorithm (DVMFELMS) that takes a decomposable Volterra model and filtered-error structure into account for the nonlinear active control problem. By comparing the computational complexity and the convergence performance of the proposed algorithm with the linear FELMS algorithm, VFELMS algorithm [11], FEGFLNN algorithm [19], and FEEMFNL algorithm [39], this paper shows that the proposed algorithm not only reduces the computational complexity, but also improves the convergence behavior slightly in the broadband noise cases.
The remainder of this paper is organized as follows. Section 2 formulates the problem of nonlinear active noise control. Section 3 derives the proposed DVMFELMS algorithm, and Section 4 compares its computational complexity with some state-of-the-art nonlinear filter algorithms. Simulation and conclusions are presented in Section 5 and Section 6, respectively.
2. Problem Formulation
2.1. Linear Feedforward ANC System
Before describing the nonlinear active noise control problem, the standard linear feedforward active noise control structure is first depicted in Figure 1 [1]. is the reference signal at the time index n recorded by the reference microphone, and is the output of the secondary actuator, which can be expressed as
where is the coefficient of the active noise control filter, and * denotes the linear convolution. is the residual error sensed by the error microphone, which can be expressed as
where and are the secondary path transfer function and its estimation, respectively. is the primary path transfer function, and is the primary noise signal at the error microphone.
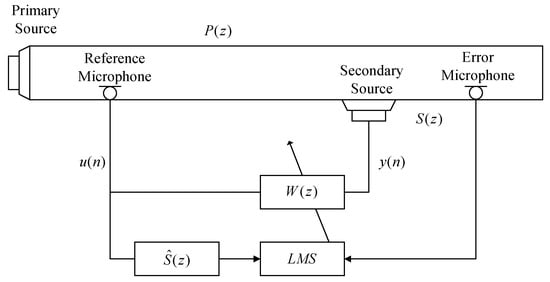
Figure 1.
Block diagram of linear feedforward ANC system.
In a standard linear feedforward active noise control structure, our goal is to find a suitable output signal to minimize the mean square of the error signal . All transfer functions and control filters are assumed to be linear, which may be violated in many circumstances, as mentioned above.
2.2. Nonlinear Feedforward ANC System
This paper expresses the nonlinear process using the well-known Volterra structure [11], where the Volterra series representation of can be given by
where
is the p-th-order Volterra kernel, and is the length of the memory. Equation (4) can be further expressed in the vector form as below:
where T denotes transportation operation, and is the p-th-order reference vector with the length , which is: -4.6cm0cm
and similarly, is the p-th-order Volterra kernel vector with length given by
This Volterra expression can be regarded as a Taylor expansion of the generally nonlinear function. Generally, only the first P order Volterra kernels are used to model the system’s nonlinearity, although the truncated error may be introduced inevitably.
3. Proposed Algorithm
After considering a decomposable Volterra model, a low-complexity adaptive Volterra algorithm based on a filtered-error structure is proposed in this section for both nonlinear active noise control (NANC) with a linear secondary path (LSP) and that with a nonlinear secondary path (NSP). By using the Kronecker product decomposition, the system’s computational complexity can be reduced dramatically, which is promising for active noise control systems.
3.1. DVMFXLMS
To derive the DVMFELMS algorithm, the adaptive Volterra algorithm based on a filtered-reference structure (DVMFXLMS) is first derived in this part. To model the system’s nonlinearity, a P-order Volterra model with the length of the memory is utilized. By using the Kronecker product decomposition and the characteristic of the Kronecker product [38], Equation (5) can be rewritten as
where ⊗ denotes the Kronecker product, and is the primary noise vector given by
where is the nearest Kronecker product decomposition of , which can be expressed as
where is the -norm of a vector, and is the q-th filter of the p-th-order of the decomposed Volterra structure with memory length , which is defined as
Minimizing the mean square error can be given by
According to the steepest descent algorithm, the proposed FXLMS can update the sub-filter as follows:
where is the single sample estimation of the gradient of J, and is the step size. Defining , can be rewritten as
We further assume that only changes slowly, and we can derive the gradient in Equation (13) by substituting Equations (12) and (14) into Equation (15):
defining the virtual secondary path filter with memory length :
and, for notation convenience, defining an auxiliary sub-vector:
where . Substituting Equations (15)–(17) into Equation (13), we can derive the updating equation of for all p and q as
It is worth noting that for NANC with the LSP case, the virtual secondary path filter can be modeled offline using a linear FIR filter. For NANC with the NSP case, the virtual secondary path filter will change with the iteration, even though the nonlinear secondary path is time-invariant. Thus, the nonlinear secondary path must be modeled firstly based on one of the nonlinear filters mentioned above, such as the Volterra filter. Then, the derivation in Equation (16) is calculated using the modeled nonlinear filter. A sparse modeling method of the nonlinear secondary path using a second-order Volterra filter can be used here to reduce the computational complexity [39].
To improve the stability of the proposed algorithm, a normalized method is considered, and a regularization parameter is also introduced, which is similar to [38]. The updating equation of each sub-filter is finally given by
where
3.2. DVMFELMS
It should be noted that the auxiliary vector defined in Equation (17) did not hold the time-shifting property due to the presence of defined in Equation (17) did not hold the time-shifting property due to the presence of ; thus, each element of must be filtered by the virtual secondary path filter even in the LSP case, which is a computationally consuming process. It was found that the filtered-error structure-based ANC system can offer comparable performance with less computational and structural complexity compared to a filtered-reference structure-based ANC [40]. Zhou and Debrunner introduced the filtered-error structure to nonlinear active noise to reduce the computational complexity in the NSP case [27]. The filtered-error structure’s main advantage is that only the error signal needs to be filtered by the virtual secondary path filter, which benefits the proposed nonlinear active noise control algorithm based on the decomposable Volterra structure.
The diagram of the proposed DVMFELMS algorithm is depicted in Figure 2. To derive the DVMFELMS algorithm, the final updating equation of the DVMFXLMS algorithm is first recalled in the following:
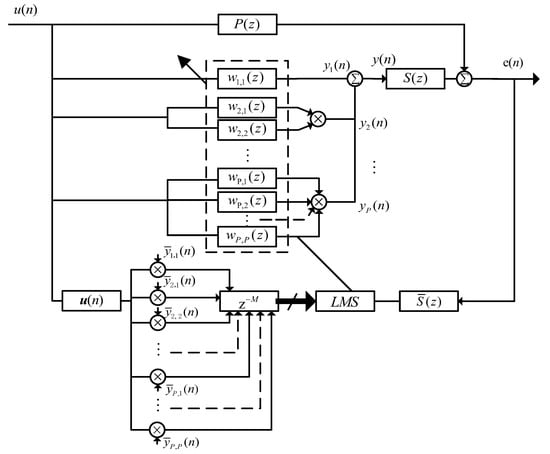
Figure 2.
Block diagram of the proposed DVMFELMS algorithm.
By substituting the time variable, only the error signal is filtered by the adjoint virtual secondary path filter , which is defined in the following instead of the whole new auxiliary sub-vector .
It should be noted that in the LSP case, the adjoint virtual secondary path filter is just the flip of the linear FIR filter in Equation (16), while for the NSP case, due to the time-variant property of the virtual secondary path filter, the last M values of the virtual secondary path filter must be stored to reconstruct the adjoint virtual secondary path filter. The final update equation of the proposed DVMFELMS algorithm is given by
where is the filtered-error signal calculated by filtering the error signal by the adjoint virtual secondary path filter defined in Equation (24). From Equation (25), one can see that the auxiliary vector is just delayed by the M time scale without being filtered by the virtual secondary path filter, while only the error signal needs to be filtered by the adjoint virtual secondary path filter. Thus, the computational complexity of the proposed algorithm can be further reduced, especially when the memory of the secondary path becomes large. The detailed implementation of the proposed DVMFELMS algorithm is summarized in Algorithm 1.
| Algorithm 1 Pseudo code of the proposed DVMFELMS algorithm. |
| Input:L, M, P, ,reference signals , desired signals , secondary path , adjoint virtual secondary path |
| Initialization: |
|
| Iteration: |
|
| Output: error signals , output signals , and filter coefficients |
4. Computational Complexity
The proposed algorithm’s computational complexity is analyzed and compared with state-of-the-art nonlinear filters in NANC, including the Volterra filter [11], GFLNN [19], and second-order EMFNL (2OEMFNL) [39]. The computational complexity based on the filtered-reference and the filtered-error structure is considered. The computational load per iteration can be calculated according to L, M, and P. Note that only the multiplications required for all algorithms are considered in this section.
The number of multiplications of the proposed DVMFXLMS algorithm is first calculated in the following. The number of multiplications for generating the pth-order output is . The number of multiplications for the pth-order filtered-reference signal vector is , and for the updating weights, the number of multiplications is . In all, the total number of multiplications of the proposed DVMFXLMS algorithm is
The computational complexity required for VFXLMS, FXGFLNN, 2OFXEMFNL, and the proposed DVMFXLMS algorithm for NANC with NSP is summarized in Table 1. It can be seen that the VFXLMS algorithm has the highest computational complexity. The 2OFXEMFNL algorithm and the FXGFLNN algorithm can achieve comparable performance with less computational complexity in higher-order nonlinearity. The proposed DVMFXLMS algorithm has the lowest computational complexity due to the Kronecker product decomposition and a similar property against the VFXLMS algorithm; however, due to the decomposition error of Equation (10), its performance may have some degradations in some real applications, which will be analyzed in next section. From Table 1, it should be noted that the number of multiplications of the DVMFXLMS algorithm for generating the filtered signal are computationally consuming. The computational complexity required for the DVMFELMS algorithm is then calculated. From Equation (25), the difference between the filtered-reference and filtered-error structure is the generation of the filtered signal. In the DVMFELMS algorithm, only the error vector needed to be filtered by the adjoint virtual secondary path filter; thus, only M multiplications are needed for all the sub-filter updates. While the generation of all p-th order auxiliary vector needs multiplications, the total complexity of the DVMFELMS algorithm is calculated as

Table 1.
Computational complexity of different algorithms for NANC with the NSP using filtered-reference structure.
The computational complexity required for the VFELMS algorithm, the FEGFLNN algorithm, the 2OFEEMFNL algorithm, and the proposed DVMFELMS algorithm for NANC with an NSP case is summarized in Table 2. In order to make the computational complexity required for all algorithms visible, the number of multiplications required for all algorithms versus memory length is shown in Figure 3, while the length of the secondary path M is 10 for all the cases. It is worth noting that only the NANC with the NSP case is considered in this section because the NANC with the LSP can be seen as a special case for NANC with NSP. In addition, for structures that have a time-shifting property, such as the Volterra filter, GFLNN, and EMFNL, the computational complexity required for all algorithms in NANC with the LSP case based on the filtered-reference structure is almost the same as in NANC with the NSP case based on the filtered-error structure, while for the proposed algorithm, the computational complexity required for all algorithms in NANC with the LSP case based on the filtered-reference structure is the same as in NANC with the NSP case regardless of the computational complexity of the generation of the virtual secondary path filter. Figure 3 shows that the filtered-error structure can reduce the computational complexity in the NANC with the NSP case for all algorithms. With the growth of memory length, the computational complexity of the VFELMS algorithm can be intolerable for ANC systems. The computational complexity of the GFLNN and EMFNL structure is smaller than the VFELMS algorithm, while it is still large for a real-time system. However, by utilizing a decomposable Volterra structure and filtered-error structure, the proposed DVMFELMS algorithm can significantly reduce the computational complexity of the algorithm, which is promising in NANC systems, especially for the NSP case.

Table 2.
Computational complexity of different algorithms for NANC with the NSP using filtered-error structure.
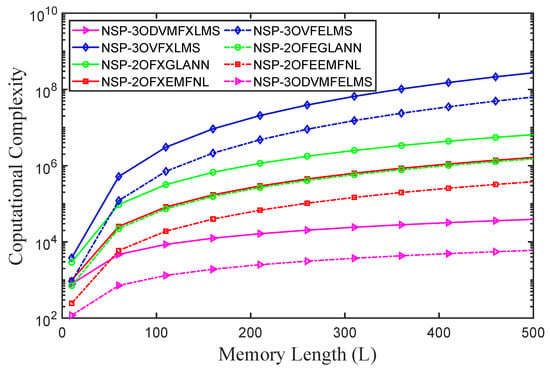
Figure 3.
Number of multiplications versus memory length.
5. Performance Evaluation
This section evaluates the proposed DVMFELMS algorithm’s performance and compares it with the FELMS algorithm, the VFELMS algorithm, the FEGFLNN algorithm, and the FEEMFNL algorithm. We evaluate the algorithms in three different nonlinear situations; the primary path has a nonlinear process in the first case, the primary and secondary paths have nonlinearity in the second case, and there is a real measured path with an intensely saturated signal in the last case. The normalized mean square error (NMSE) [11] is used to evaluate the performance of the algorithm, which is defined as
where is the mean square energy of the primary noise. All results presented in this section are based on an ensemble average of 100 independent runs for each algorithm. The primary path is set to be in the middle of the iteration to study all algorithms’ stability and tracking capability. Furthermore, the step-sizes are all selected to achieve the maximum convergence rate with the minimum achievable NMSE.
5.1. Simulation with Nonlinear Primary Path
In the first experiment, the situation where the primary path has a nonlinear process is studied. The primary noise recorded by the error microphone is generated by passing the reference signal through a third-order Volterra model with cross terms, which is given by
where the transfer function of the secondary path is . The reference noise signal is considered to be two cases; a sinusoidal wave of 500 Hz with a sampling rate of 8000 Hz is utilized in the first case, and a band-limited white Gaussian noise in the second case. The sinusoidal reference signal is given by
where is a white Gaussian noise with zero mean and unit variance, and the signal-to-noise ratio (SNR) is set to be 30 dB. The memory length for all algorithms is chosen to be 10. The order of the Volterra kernel is chosen to be 3, and the order of the functional link neural network and even mirror Fourier nonlinear filter is chosen to be 2. The step size for the FELMS algorithm is chosen to be , step sizes for the third-order Volterra filter are set to , step sizes for the 2OFEGFLNN algorithm and 2OFEEMFNL algorithm are set to , and step sizes for the 3ODVMFELMS algorithm are set to .
Figure 4 shows the NMSE achieved by all five algorithms versus the number of iterations in the sinusoidal noise case. It can be seen from Figure 4 that the reduction of primary noise achieved by the FELMS algorithm, the 3OVFELMS algorithm, the 2OFEGFLNN algorithm, the 2OFEEMFNL algorithm, and the 3ODVMFELMS algorithm is about 22.5 dB, 25.3 dB, 25.9 dB, 26.2 dB, and 26.3 dB, respectively. All nonlinear algorithms achieve better performance against the FELMS algorithm. The proposed DVMFELMS algorithm performs slightly better in the steady-state performance and the convergence rate in this case. It should be noted that the proposed DVMFELMS algorithm can even outperform the VFELMS algorithm in NMSE, which might be explained by the Volterra model used in the VFELMS algorithm being over-fitting for this simulation case.
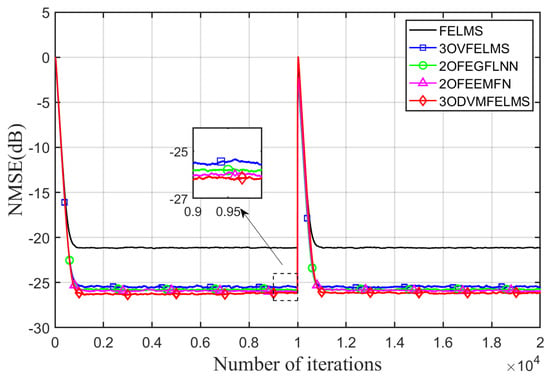
Figure 4.
Performance comparison using the nonlinear primary path with sinusoidal reference signal.
For results of the broadband noise, the frequency range of the band-limited noise is chosen to be from 50 Hz to 1000 Hz, among which the ANC system usually works well. The signal is normalized to unity, and a white Gaussian noise with zero mean and unit variance with an SNR of 30 dB is also added. All the transfer functions and nonlinearities used are exactly the same as in the first case. The step size for the FELMS algorithm is chosen to be , step sizes for the third-order Volterra filter are set to , step sizes for the 2OFEGFLNN algorithm and 2OEMFNL algorithm are set to , and step sizes for the 3ODVMFELMS algorithm are set to . Figure 5 shows that the reduction of primary noise achieved by the FELMS algorithm, the 3OVFELMS algorithm, the FEGFLNN algorithm, the 2OEMFNL algorithm, and the 3ODVMFELMS algorithm in the broadband noise case is about 19.8 dB, 23.8 dB, 23.2 dB, 23 dB, and 23.6 dB, respectively. It is worth noting that in the broadband case, the VFELMS algorithm outperforms the 2OFEGFLNN algorithm and the 2OEMFNL algorithm in NMSE, which coincides with the results in [19]. Nevertheless, the 2OEMFNL algorithm has a fast convergence rate due to its inherent property, as shown in [27]. The proposed DVMFELMS algorithm can achieve comparable steady-state performance against the VFELMS algorithm, while with a slightly faster convergence rate. This may be explained by the fewer parameters used in the DVMFELMS algorithm.
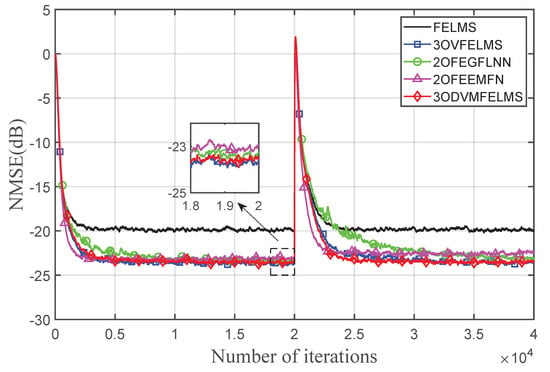
Figure 5.
Performance comparison using the nonlinear primary path with band-limited white Gaussian reference signal.
5.2. Simulation with Nonlinear Primary Path and Nonlinear Secondary Path
To further demonstrate the effectiveness of the proposed DVMFELMS algorithms in the NANC/NSP case, both primary and secondary paths are considered to have nonlinearity in this experiment. The primary noise recorded by the error microphone is generated by passing the reference signal through a second-order Volterra model given by
while the secondary path is considered to be an NLN model used in [27], which is expressed as
Figure 6 depicts the NMSE obtained by all five active noise control algorithms versus the number of iterations by using the same sinusoidal signal as the reference signal in Equation (30). The memory length for all algorithms is chosen to be 10, and the order of the Volterra kernel is chosen to be 2. The step size for the FELMS algorithm is chosen to be , step sizes for the second-order Volterra filter are set to , step sizes for the FEGFLNN algorithm are chosen to be , step sizes for the 2OEMFNL algorithm are set to , and step sizes for the 2ODVMFELMS algorithm are set to . Figure 6 shows that the reductions of primary noise achieved by the FELMS algorithm, the 2OVFELMS algorithm, the 2OFEGFLNN algorithm, the 2OFEEMFNL algorithm, and the proposed 2ODVMFELMS algorithm are about 20.8 dB, 29.7 dB, 29.3 dB, 29.1 dB, and 29.7 dB, respectively. It should be noted that the FEEMFNL algorithm shows bad convergence speed in the NSP case. The proposed DVMFELMS algorithm can still achieve comparable performance with the lowest computational complexity in the NSP case. However, the convergence rate of the proposed 2ODVMFELMS algorithm is worse in these cases because of the sinusoidal signal and NSP used.
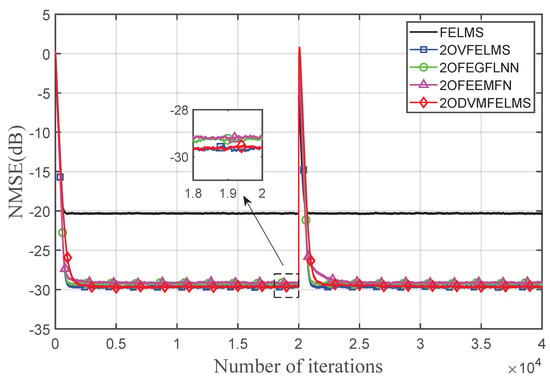
Figure 6.
Performance comparison using the nonlinear primary path and secondary path with sinusoidal reference signal.
For broadband results, the band-limited white Gaussian noise used here is exactly the same as in experiment 2. The SNR is also set to be 30 dB. All the transfer functions are exactly the same as in the first case. Figure 7 shows the NMSE achieved by all five algorithms versus the number of iterations. The step size for the FELMS algorithm is chosen to be , step sizes for the second-order Volterra filter are set to , step sizes for the 2OFEGFLNN algorithm are chosen to be , step sizes for the 2OEMFNL algorithm are set to , and step sizes for the 2ODVMFELMS algorithm are set to . One can see from Figure 7 that the reductions of primary noise achieved by the FELMS algorithm, the 2OVFELMS algorithm, the 2OFEGFLNN algorithm, the 2OEMFNL algorithm, and the 2ODVMFELMS algorithm are about 17.3 dB, 24.1 dB, 23.7 dB, 23.5 dB, and 23.8 dB, respectively. It can be seen that the FEFLNN algorithm and the FEEMFNL algorithm show worse performance in steady-state NMSE and convergence speed than the Volterra filter-based algorithm in the broadband reference signal and NSP case. The proposed DVMFELMS algorithm has performance comparable with the VFELMS algorithm, with a dramatic reduction of computational complexity.
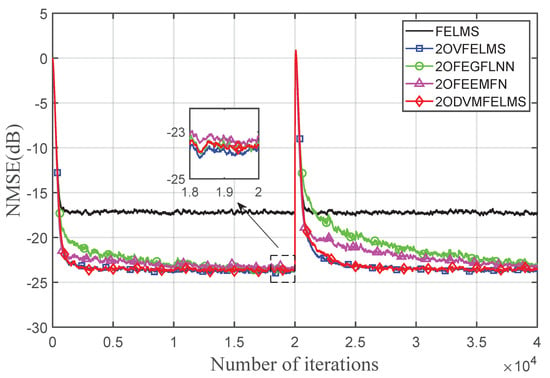
Figure 7.
Performance comparison using the nonlinear primary path and secondary path with band-limited white Gaussian reference signal.
5.3. Simulation with Measured Primary Path and Secondary Path
In this experiment, a real measured primary and secondary path is used to justify the proposed DVMFELMS algorithm’s effectiveness in a real application. The amplitude and phase response of both primary and secondary paths is shown in Figure 8. The reference signal is chosen to be three sinusoidal waves at normalized frequencies of 0.01, 0.02, and 0.08, which is normalized to unity power [29]. A white Gaussian noise with zero mean and unit variance with a signal-to-noise ratio of 30 dB is also added. Furthermore, the reference signal is assumed to have strong saturation generated by clipping the reference at 50% of the maximum signal value. The memory length of the primary and secondary path is chosen to be 80. Figure 9 shows the NMSE achieved by all five algorithms versus the number of iterations. The step size for the FELMS algorithm is chosen to be , step sizes for the second-order Volterra filter are set to , step sizes for the 2OFEGFLNN algorithm are chosen to be , step sizes for the 2OFEEMFNL algorithm are set to , and step sizes for the 2ODVMFELMS algorithm are set to . Figure 9 shows that the reduction of primary noise achieved by the FELMS algorithm, the 2OVFELMS algorithm, the FEGFLNN algorithm, the 2OEMFNL algorithm, and the 2ODVMFELMS algorithm in the real measured primary and secondary path cases is about 27.5 dB, 29.7 dB, 29.6 dB, 29.9 dB, and 29.6 dB, respectively. From Figure 9, it can be seen that the 2OEMFNL algorithm outperforms all algorithms in NMSE, while having the lowest convergence speed. The proposed DVMFELMS algorithm can achieve almost the same NMSE compared with the VFELMS algorithm in this case. The number of multiplications in this experiment for all four nonlinear algorithms are 278960, 39210, 10289, and 958, respectively, which shows the potential in the real application of the proposed DVMFELMS algorithm.
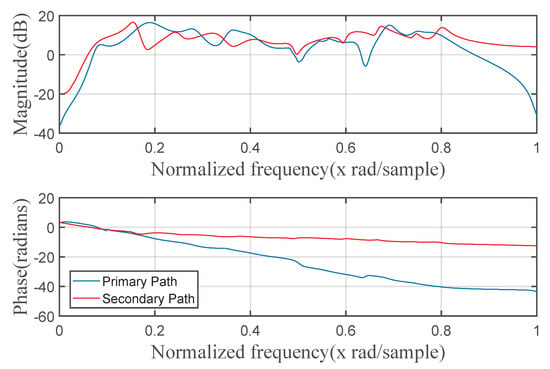
Figure 8.
Amplitude and phase response of measured primary and secondary path.
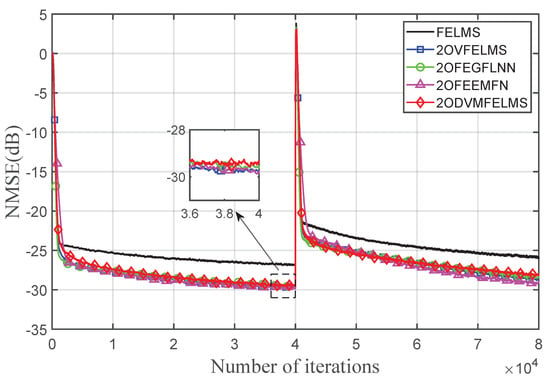
Figure 9.
Performance comparison using measured primary and secondary path with saturated reference signal.
6. Conclusions
This paper proposes a very low-complexity adaptive Volterra filter-error least mean square algorithm for the active control of nonlinear noise processes after considering a decomposable Volterra model and filtered-error structure. The computational complexity analysis shows that the proposed DVMFELMS algorithm can significantly reduce the complexity, especially for the NANC system with the NSP case. The simulation result shows that the proposed algorithm can achieve comparable performance with the VFELMS algorithm and other state-of-the-art nonlinear filters in simulation conditions, while the decomposable error of the Volterra kernel may inevitably be introduced. In addition, the proposed DVMFELMS algorithm shows potential in a better convergence property due to the fewer parameters used in each sub-filter. Further work should concentrate on studying the step control to improve the stability of the DVMFELMS algorithm for practical applications.
Author Contributions
All authors have contributed to the work presented in this article. J.Z. derived the algorithm and conducted the analysis and simulation; C.Z. proposed the scheme, directed the work, analyzed the obtained results, and revised the manuscript. F.Z. conducted the simulation and interpreted the obtained results; X.L. analyzed the the obtained results and revised the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest. We declare that we do not have any commercial or associative interest that represents a conflict of interest in connection with the work submitted.
Abbreviations
The following abbreviations are used in this manuscript:
| FXLMS | Filtered-Reference Least Mean Square |
| FELMS | Filtered-Error Least Mean Square |
| FIR | Finite Impulse Response |
| IIR | Infinite Impulse Response |
| NANC | Nonlinear Active Noise Control |
| LSP | Linear Secondary Path |
| NSP | Nonlinear Secondary Path |
| FLNN | Functional Link Neural Network |
| GFLNN | Generalized Functional Link Neural Network |
| EFLNN | Exponential Functional Link Neural Network |
| EMFN | Even Mirror Fourier Nonlinear |
| LeNN | Legendre Neural Network |
| VFXLMS | Volterra Filtered-Reference Least Mean Square |
| VFELMS | Volterra Filtered-Error Least Mean Square |
| DVMFXLMS | Volterra Filtered-Reference Least Mean Square Based on Decomposable Volterra Model |
| DVMFELMS | Volterra Filtered-Error Least Mean Square Based on Decomposable Volterra Model |
| FXGFLNN | Filtered-Reference Functional Link Neural Network |
| FEGFLNN | Filtered-Error Functional Link Neural Network |
| FXEMFNL | Filtered-Reference Even Mirror Fourier Nonlinear Filter with a Linear Part |
| FEEMFNL | Filtered-Error Even Mirror Fourier Nonlinear Filter with a Linear Part |
| NMSE | Normalized Mean Square Error |
| SNR | Signal-to-Noise Ratio |
References
- Elliott, S.J. Signal Processing for Active Control; Academic: New York, NY, USA, 2001. [Google Scholar]
- Hansen, C.; Snyder, S.; Qiu, X.; Brooks, L.; Moreau, D. Active Control of Noise and Vibration; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Kuo, S.M.; Morgan, D.R. Active noise control: A tutorial review. Proc. IEEE 1999, 87, 943–973. [Google Scholar] [CrossRef] [Green Version]
- Cheer, J.; Elliott, S.J. Multichannel control systems for the attenuation of interior road noise in vehicles. Mech. Syst. Signal Process. 2015, 60–61, 753–769. [Google Scholar] [CrossRef] [Green Version]
- Kajikawa, Y.; Gan, W.S.; Kuo, S.M. Recent advances on active noise control: Open issues and innovative applications. APSIPA Trans. Signal Inf. Process. 2012, e3, 753–769. [Google Scholar] [CrossRef] [Green Version]
- Han, R.; Wu, M.; Gong, C.; Jia, S.; Han, T.; Sun, H.; Yang, J. Combination of robust algorithm and head-tracking for a feedforward active headrest. Appl. Sci. 2019, 9, 1760. [Google Scholar] [CrossRef] [Green Version]
- Rafaely, B. Zones of quiet in a broadband diffuse sound field. J. Acoust. Soc. Am. 2001, 110, 296–302. [Google Scholar] [CrossRef] [Green Version]
- Elliott, S.J.; Cheer, J. Modeling local active sound control with remote sensors in spatially random pressure fields. J. Acoust. Soc. Am. 2015, 137, 1936–1946. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rafaely, B.; Elliott, S.J. A computationally efficient frequency-domain LMS algorithm with constraints on the adaptive filter. IEEE Trans. Signal Process. 2000, 48, 1649–1655. [Google Scholar] [CrossRef]
- Zhang, G.; Tao, J.; Qiu, X.; Burnett, I. Decentralized two-channel active noise control for single frequency by shaping matrix eigenvalues. IEEE/ACM Trans. Audio Speech Lang. Process. 2019, 27, 44–52. [Google Scholar] [CrossRef]
- Tan, L.; Jiang, J. Adaptive volterra filters for active control of nonlinear noise processes. IEEE Trans. Signal Process. 2001, 49, 1667–1676. [Google Scholar] [CrossRef]
- Zhu, L.; Yang, T.; Pan, J. Design of nonlinear active noise control earmuffs for excessively high noise level. J. Acoust. Soc. Am. 2019, 146, 1547–1555. [Google Scholar] [CrossRef] [PubMed]
- George, N.V.; Panda, G. Advances in active noise control: A survey, with emphasis on recent nonlinear techniques. Signal Process. 2013, 93, 363–377. [Google Scholar] [CrossRef]
- Lu, L.; Yin, K.L.; de Lamare, R.C.; Zheng, Z.; Yu, Y.; Yang, X.; Chen, B. A survey on active noise control in the past decade–part II: Nonlinear systems. Signal Process. 2020, 181, 10729. [Google Scholar]
- Snyder, S.D.; Tanaka, N. Active control of vibration using a neural network. IEEE Trans. Neural Netw. 1995, 6, 819–828. [Google Scholar] [CrossRef]
- Zhou, Y.L.; Zhang, Q.Z.; Li, X.D.; Gan, W.S. Analysis and DSP implementation of an ANC system using a filtered-error neural network. J. Sound Vib. 2005, 285, 1–25. [Google Scholar] [CrossRef]
- Sicuranza, G.L.; Carini, A. Filtered-x affine projection algorithm for multichannel active noise control using second-order volterra filters. IEEE Signal Process. Lett. 2004, 11, 853–857. [Google Scholar] [CrossRef]
- Das, D.P.; Panda, G. Active mitigation of nonlinear noise processes using a novel filtered-s LMS algorithm. IEEE/ACM Trans. Audio Speech Lang. Process. 2004, 12, 313–322. [Google Scholar] [CrossRef]
- Sicuranza, G.; Carini, A. A generalized FLANN filter for nonlinear active noise control. IEEE/ACM Trans. Audio Speech Lang. Process. 2011, 19, 2412–2417. [Google Scholar] [CrossRef]
- Patel, V.; Gandhi, V.; Heda, S.; George, N.V. Design of adaptive exponential functional link network-based nonlinear filters. IEEE Trans. Circuits Syst. I Reg. Pap. 2016, 63, 1434–1442. [Google Scholar] [CrossRef]
- Carini, A.; Sicuranza, G.L. Even mirror fourier nonlinear filters. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; pp. 5608–5612. [Google Scholar]
- Carini, A.; Cecchi, S.; Romoli, L.; Sicuranza, G.L. Legendre nonlinear filters. Signal Process. 2015, 109, 84–94. [Google Scholar] [CrossRef]
- Carini, A.; Sicuranza, G.L. A study about chebyshev nonlinear filters. Signal Process. 2016, 122, 24–32. [Google Scholar] [CrossRef]
- Chen, B.; Yu, S.; Yu, Y.; Guo, R. Nonlinear active noise control system based on correlated EMD and chebyshev filter. Mech. Syst. Signal Process. 2019, 130, 74–86. [Google Scholar] [CrossRef]
- George, N.V.; Gonzalez, A. Convex combination of nonlinear adaptive filters for active noise control. Appl. Acoust. 2014, 76, 157–161. [Google Scholar] [CrossRef]
- Zhao, H.; Zeng, X.; He, Z.; Yu, S.; Chen, B. Improved functional link artificial neural network via convex combination for nonlinear active noise control. Appl. Soft Comput. 2016, 42, 351–359. [Google Scholar] [CrossRef] [Green Version]
- Zhou, D.; Debrunner, V. Efficient adaptive nonlinear filters for nonlinear active noise control. IEEE Trans. Circuits Syst. I Reg. Pap. 2007, 54, 669–681. [Google Scholar] [CrossRef]
- Kuo, S.M.; Wu, H.T. Nonlinear adaptive bilinear filters for active noise control systems. IEEE Trans. Circuits Syst. I Reg. Pap. 2005, 52, 617–624. [Google Scholar] [CrossRef]
- Tan, L.; Dong, C.; Du, S. On implementation of adaptive bilinear filters for nonlinear active noise control. Appl. Acoust. 2016, 106, 122–128. [Google Scholar] [CrossRef]
- Zhao, H.; Zeng, X.; He, Z.; Li, T. Adaptive RSOV filter using the felms algorithm for nonlinear active noise control systems. Mech. Syst. Signal Process. 2013, 34, 378–392. [Google Scholar] [CrossRef]
- Carini, A.; Sicuranza, G.L. Recursive even mirror fourier nonlinear filters and simplified structures. IEEE Trans. Signal Process. 2014, 62, 6534–6544. [Google Scholar] [CrossRef]
- Guo, X.; Jiang, J.; Tan, L.; Du, S. Improved adaptive recursive even mirror fourier nonlinear filter for nonlinear active noise control. Appl. Acoust. 2018, 146, 310–319. [Google Scholar] [CrossRef]
- Le, D.C.; Zhang, J.; Pang, Y. A bilinear functional link artificial neural network filter for nonlinear active noise control and its stability condition. Appl. Acoust. 2018, 132, 19–25. [Google Scholar] [CrossRef]
- Guo, X.; Jiang, J.; Chen, J.; Du, S.; Tan, L. Bibo-stable implementation of adaptive function expansion bilinear filter for nonlinear active noise control. Appl. Acoust. 2020, 168, 107407. [Google Scholar] [CrossRef]
- Carini, A.; Sicuranza, G.L. Bibo-stable recursive functional link polynomial filters. IEEE Trans. Signal Process. 2017, 65, 1595–1606. [Google Scholar] [CrossRef]
- Fermo, A.; Carini, A.; Sicuranza, G.L. Low-complexity nonlinear adaptive filters for acoustic echo cancellation in GSM handset receivers. Eur. Trans. Telecommun. 2003, 14, 161–169. [Google Scholar] [CrossRef]
- Paleologu, C.; Benesty, J.; Ciochină, S. Linear system identification based on a kronecker product decomposition. IEEE/ACM Trans. Audio Speech Lang. Process. 2018, 26, 1793–1808. [Google Scholar] [CrossRef]
- Pinheiro, F.C.; Lopes, C.G. A low-complexity nonlinear least mean squares filter based on a decomposable volterra model. IEEE Trans. Signal Process. 2019, 67, 5463–5478. [Google Scholar] [CrossRef]
- Guo, X.; Li, Y.; Jiang, J.; Dong, C.; Du, S.; Tan, L. Sparse modeling of nonlinear secondary path for nonlinear active noise control. IEEE Trans. Instrum. Meas. 2018, 67, 482–496. [Google Scholar] [CrossRef]
- Miyagi, S.; Sakai, H. Performance comparison between the filtered-error LMS and the filtered-x LMS algorithms ANC. In Proceedings of the 2001 IEEE International Symposium on Circuits and Systems, Sydney, NSW, Australia, 6–9 May 2001; pp. 661–664. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).