Integration of Freeplay-Induced Limit Cycles Based On a State Space Iterating Scheme
Abstract
Featured Application
Abstract
1. Introduction
2. State Space Equations and the Hénon–RK45 Method
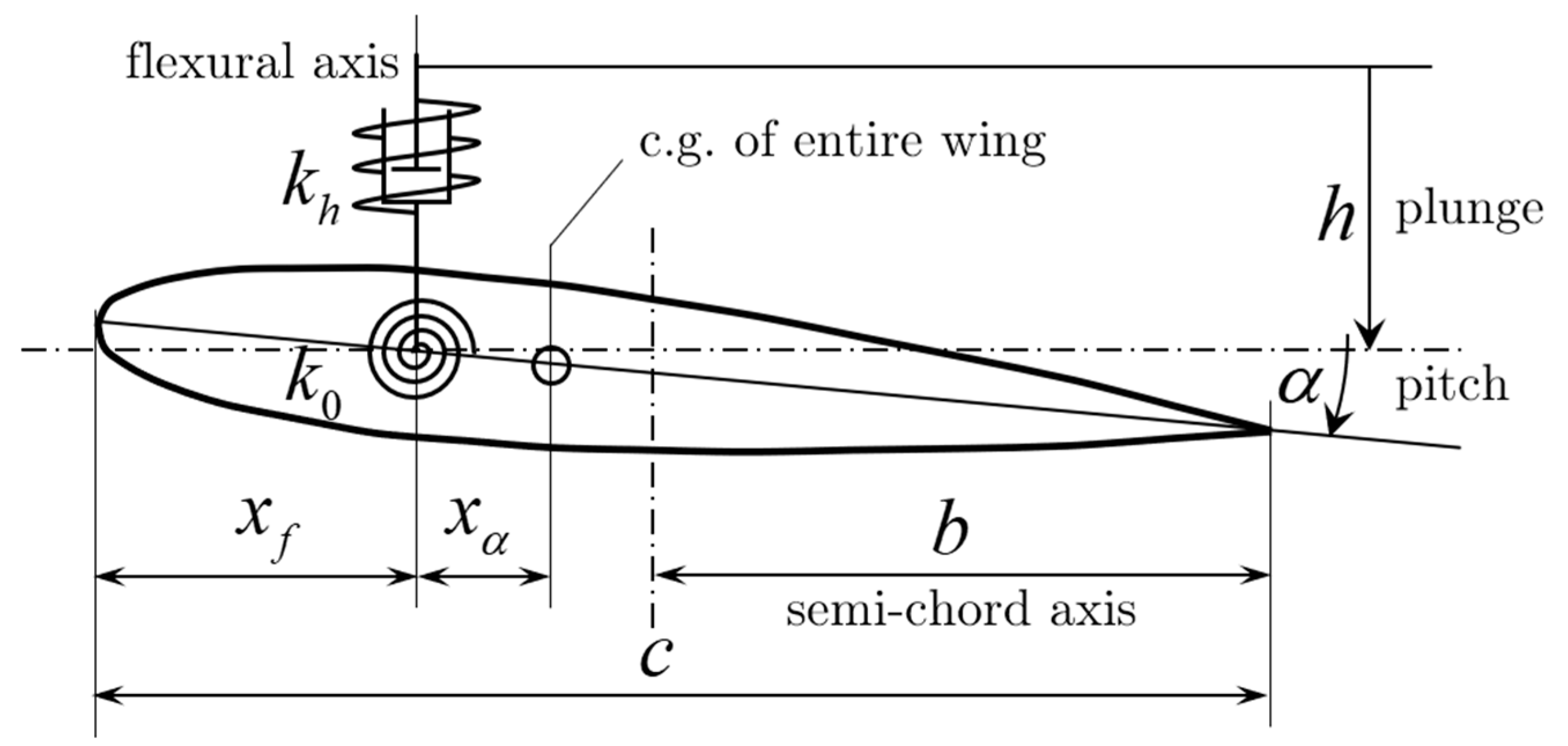
2.1. State Space Equations of an Aeroelastic System with Freeplay
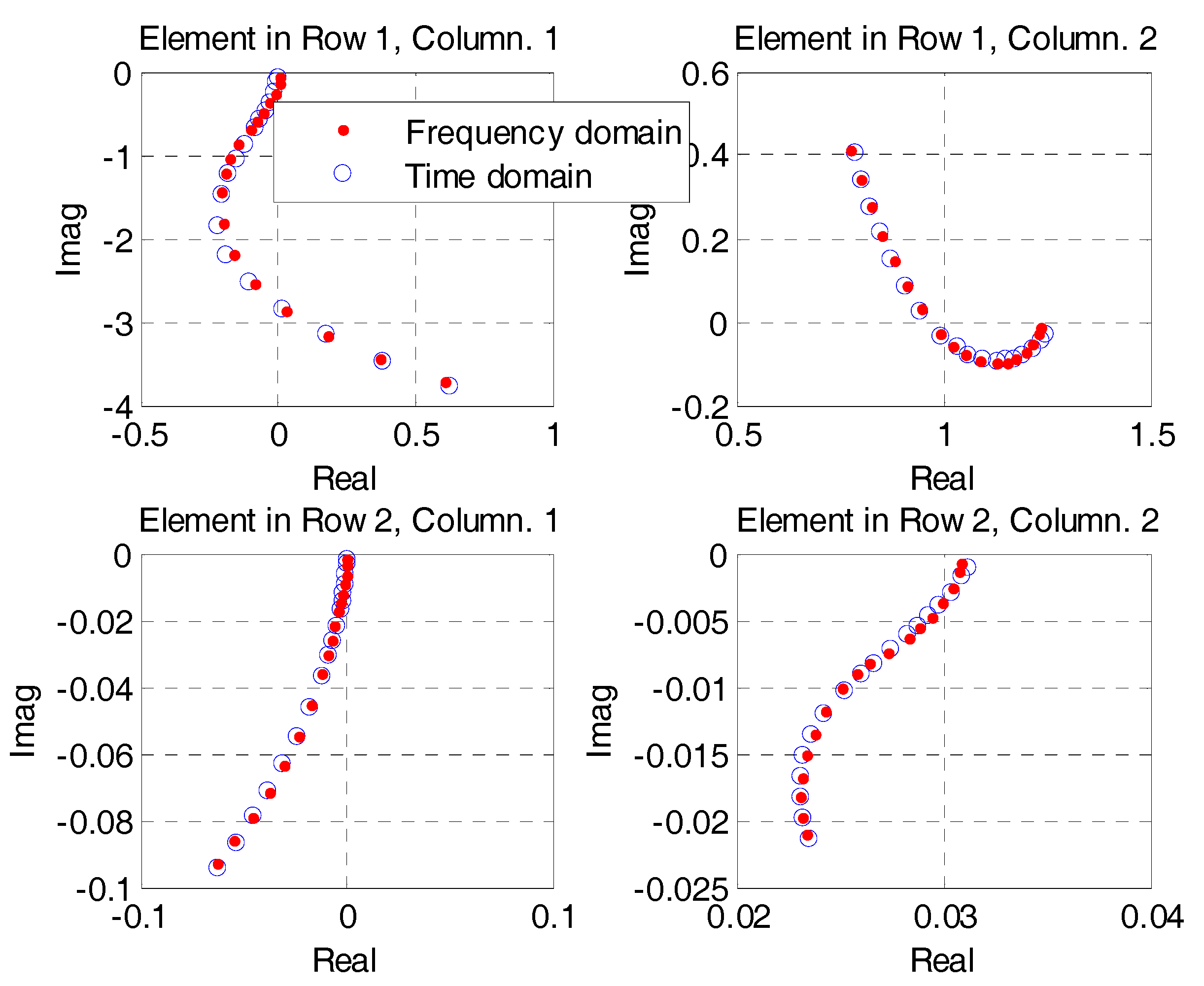
2.2. Time Integrations Based on the Runge–Kutta and Hénon Methods
3. State Space Iterating (SSI) Scheme
3.1. Preliminary Concepts
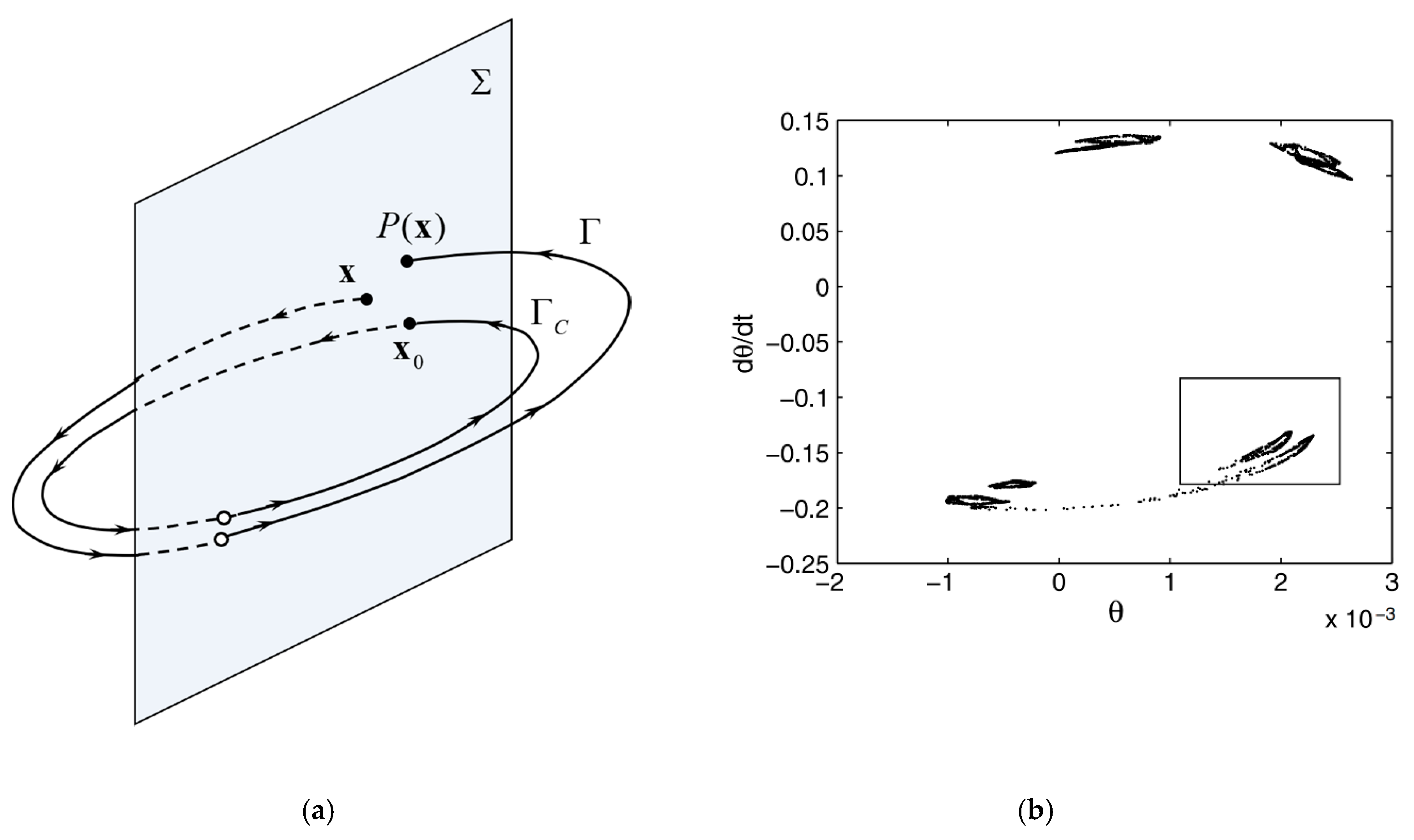
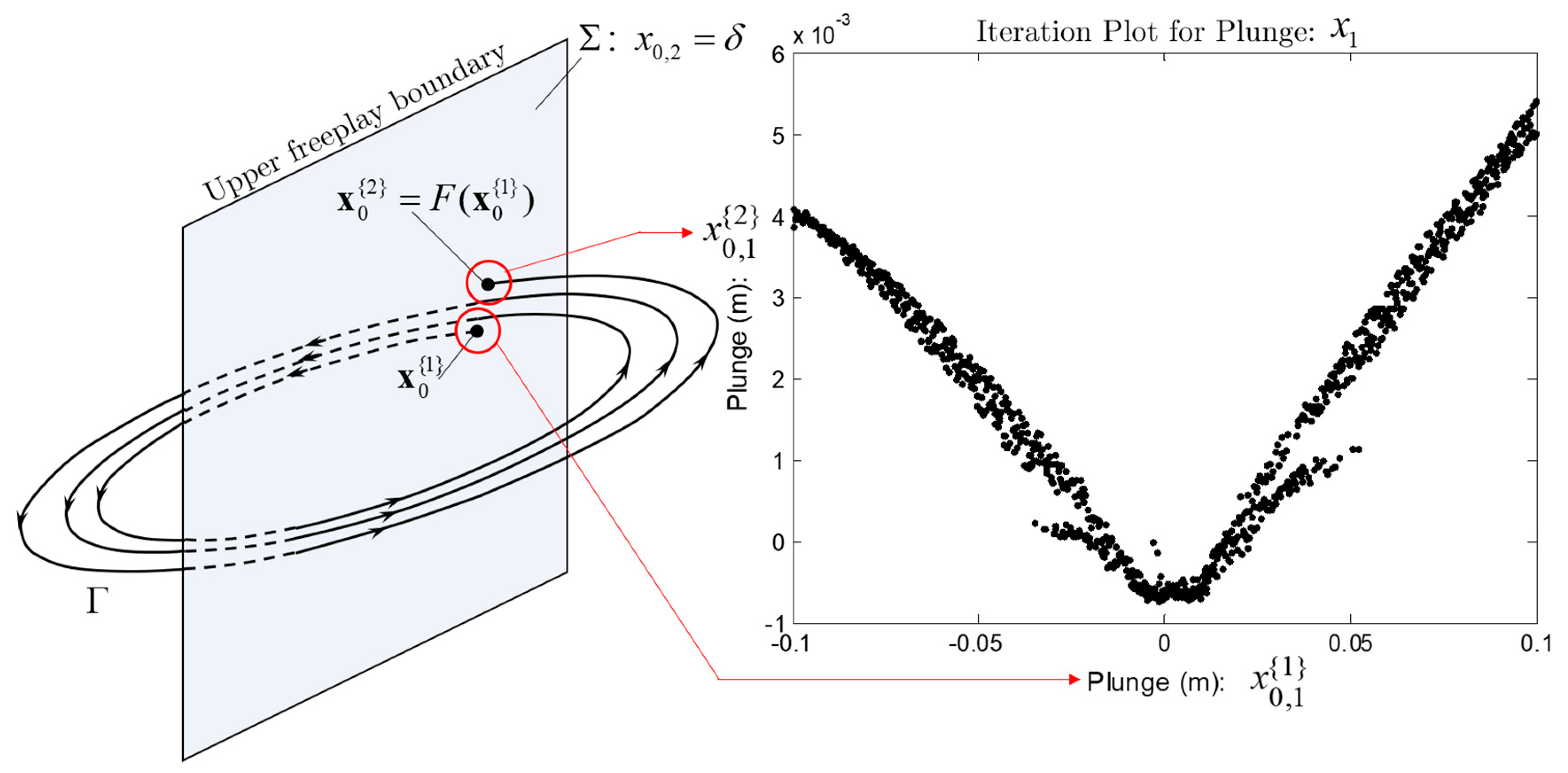
3.1.1. Poincaré Map and Lorenz Map
3.1.2. Attractor and Basin of Attraction
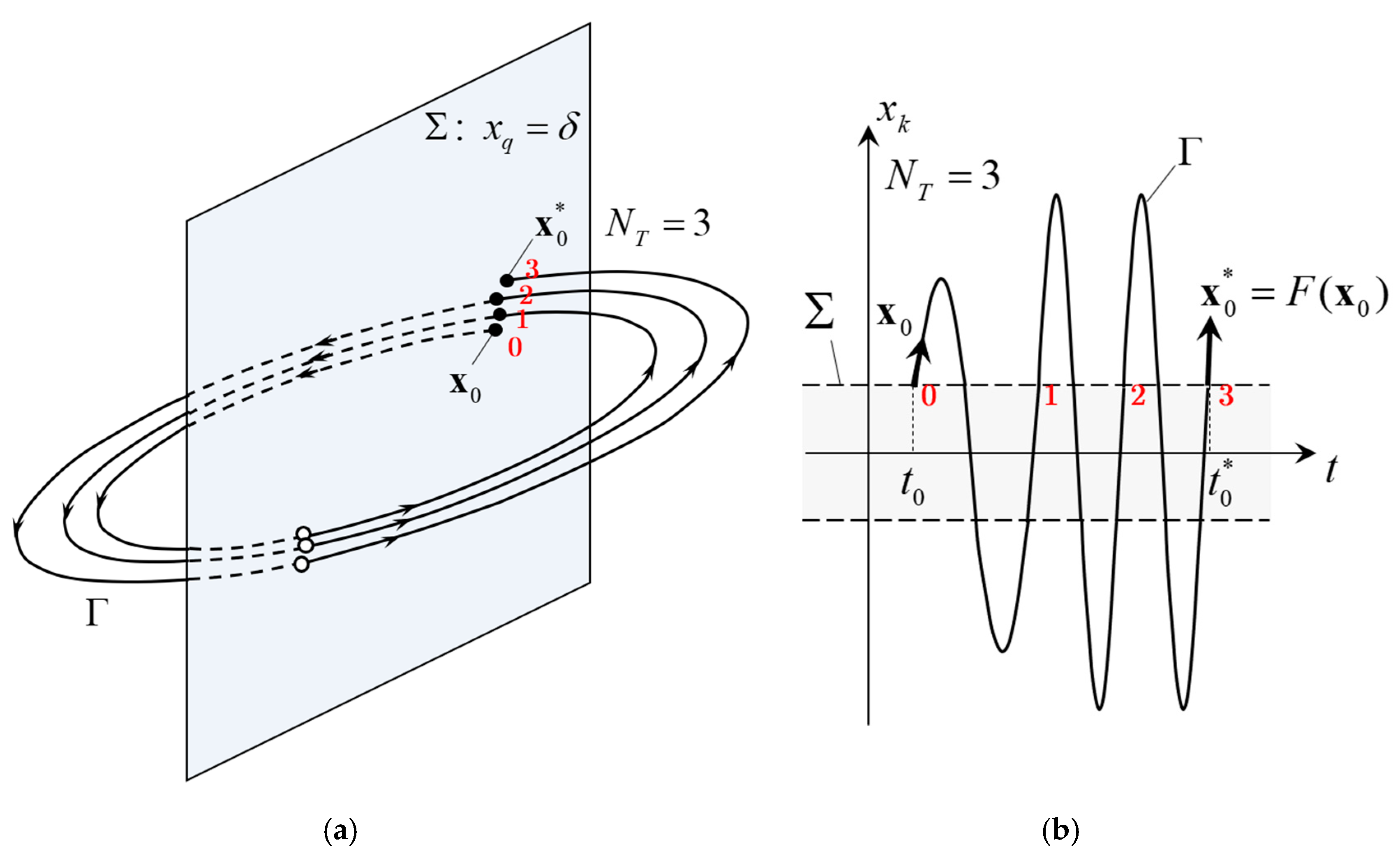
3.2. Basic Ideas of SSI
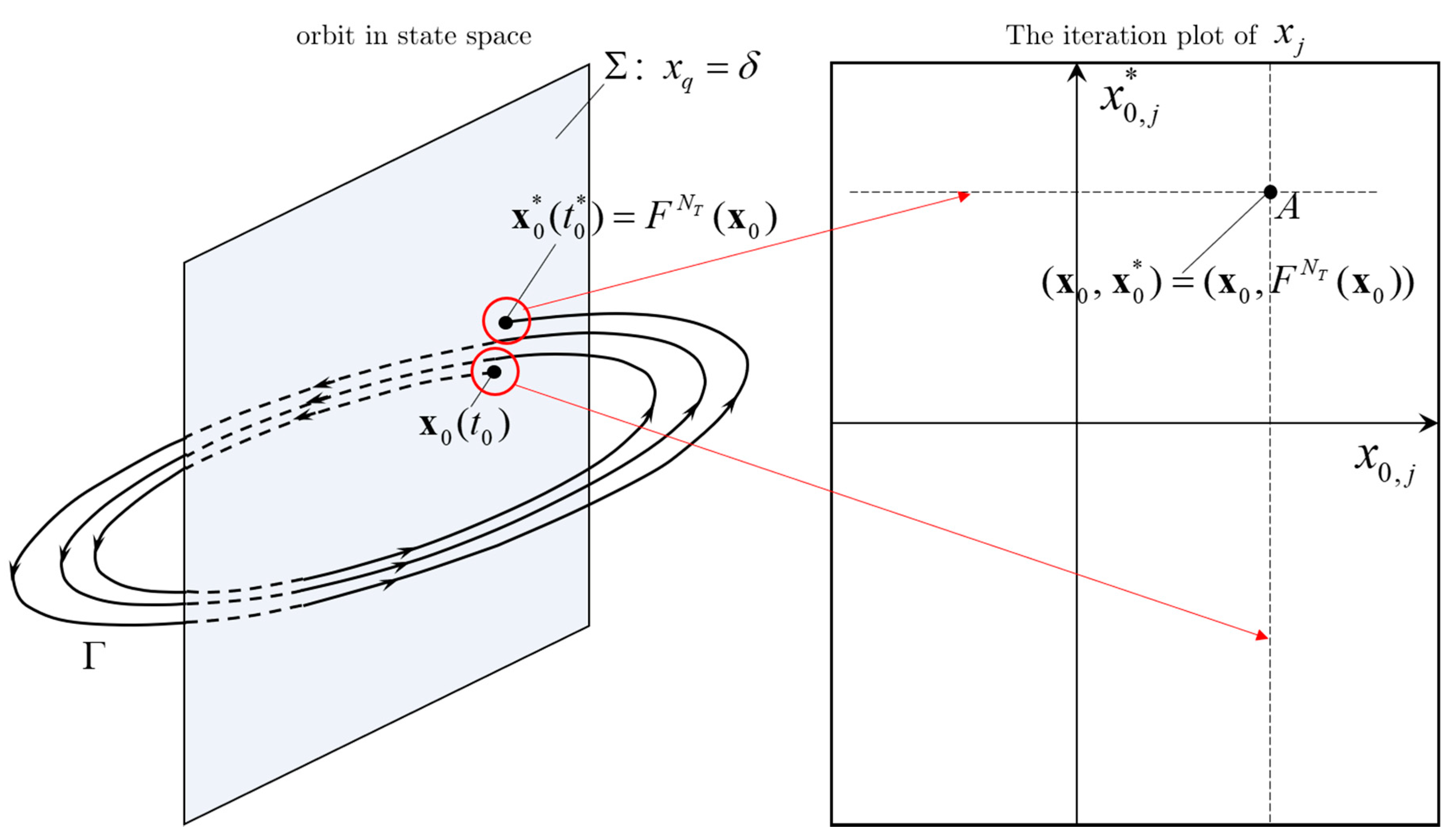
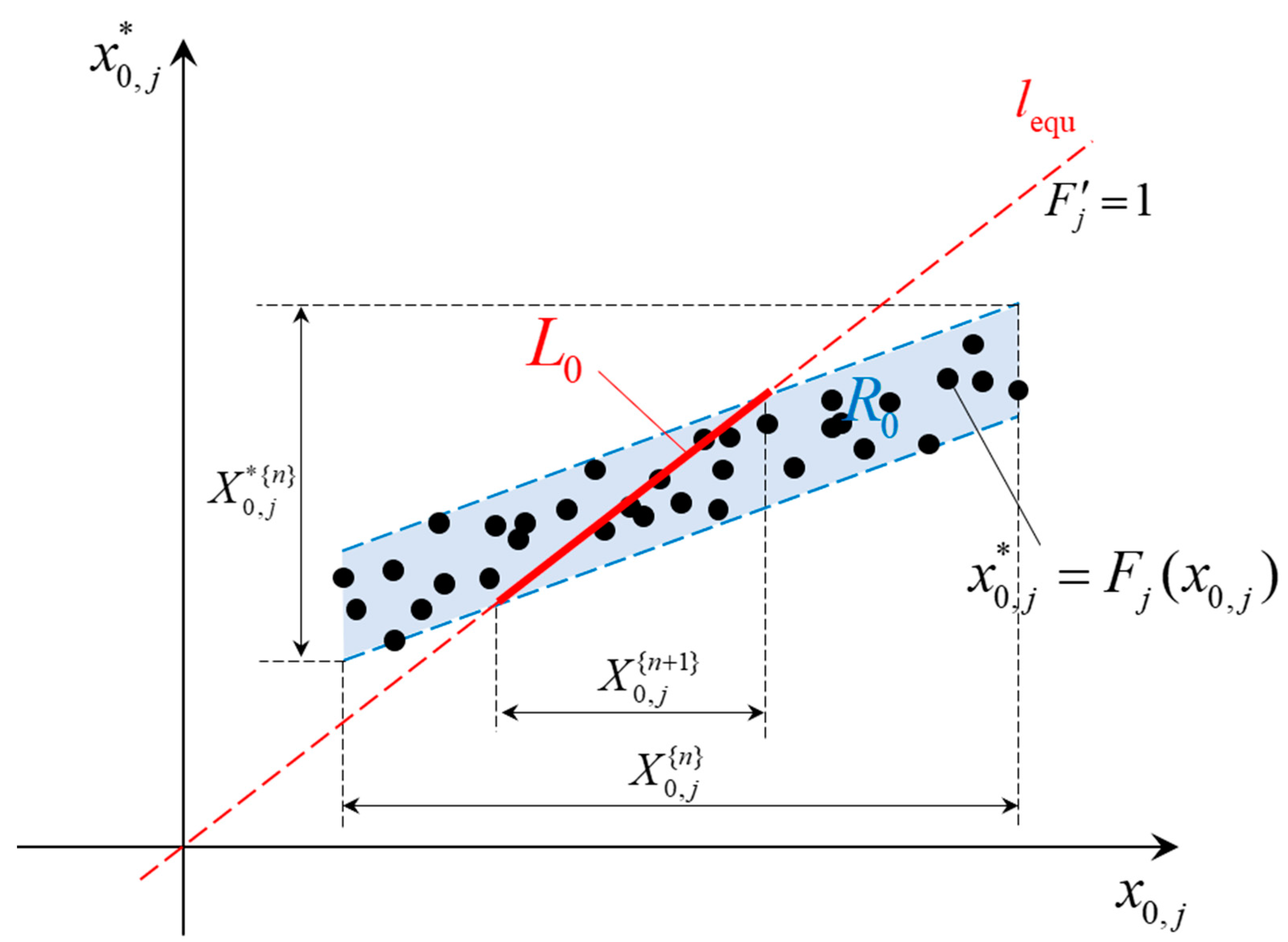
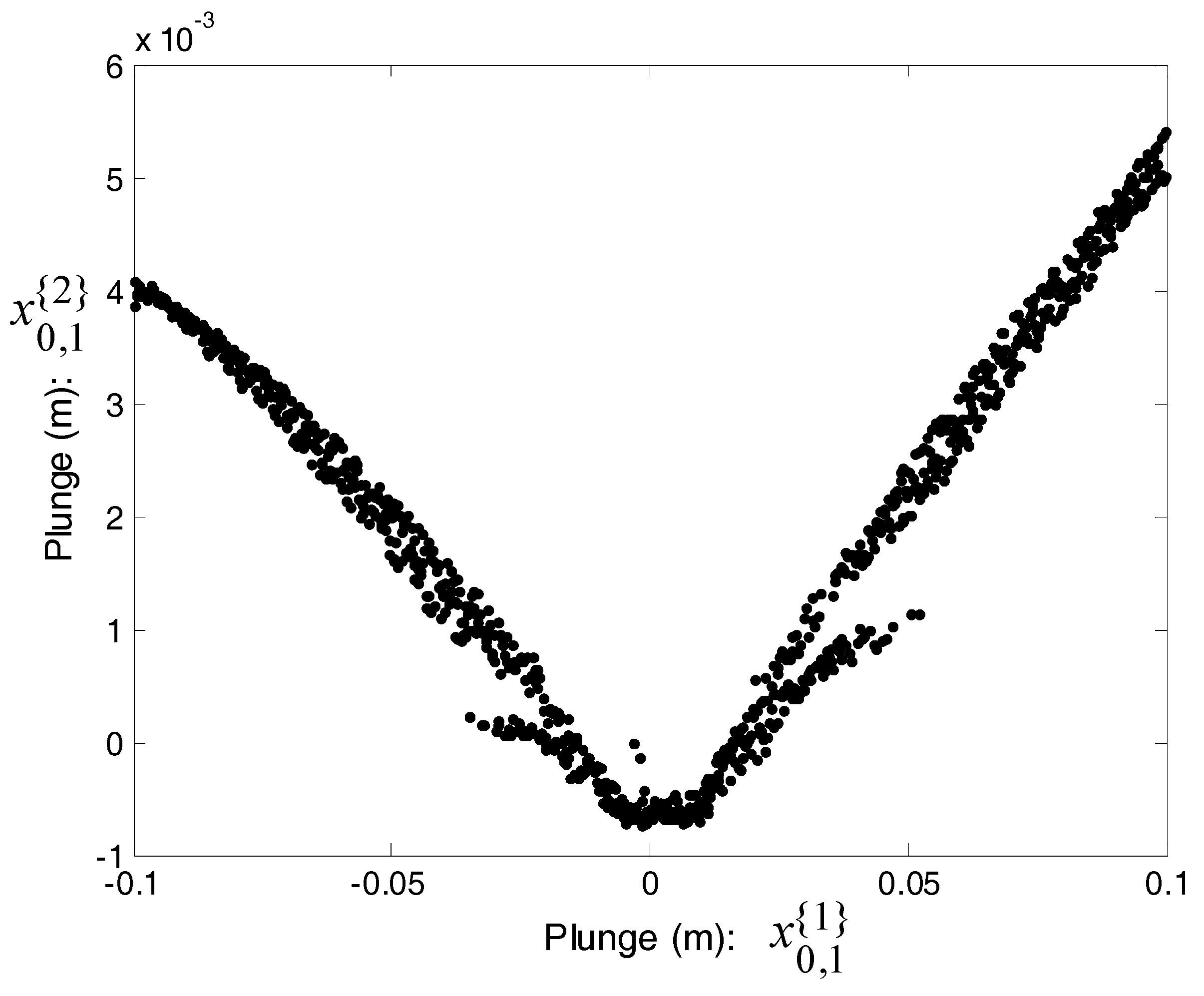
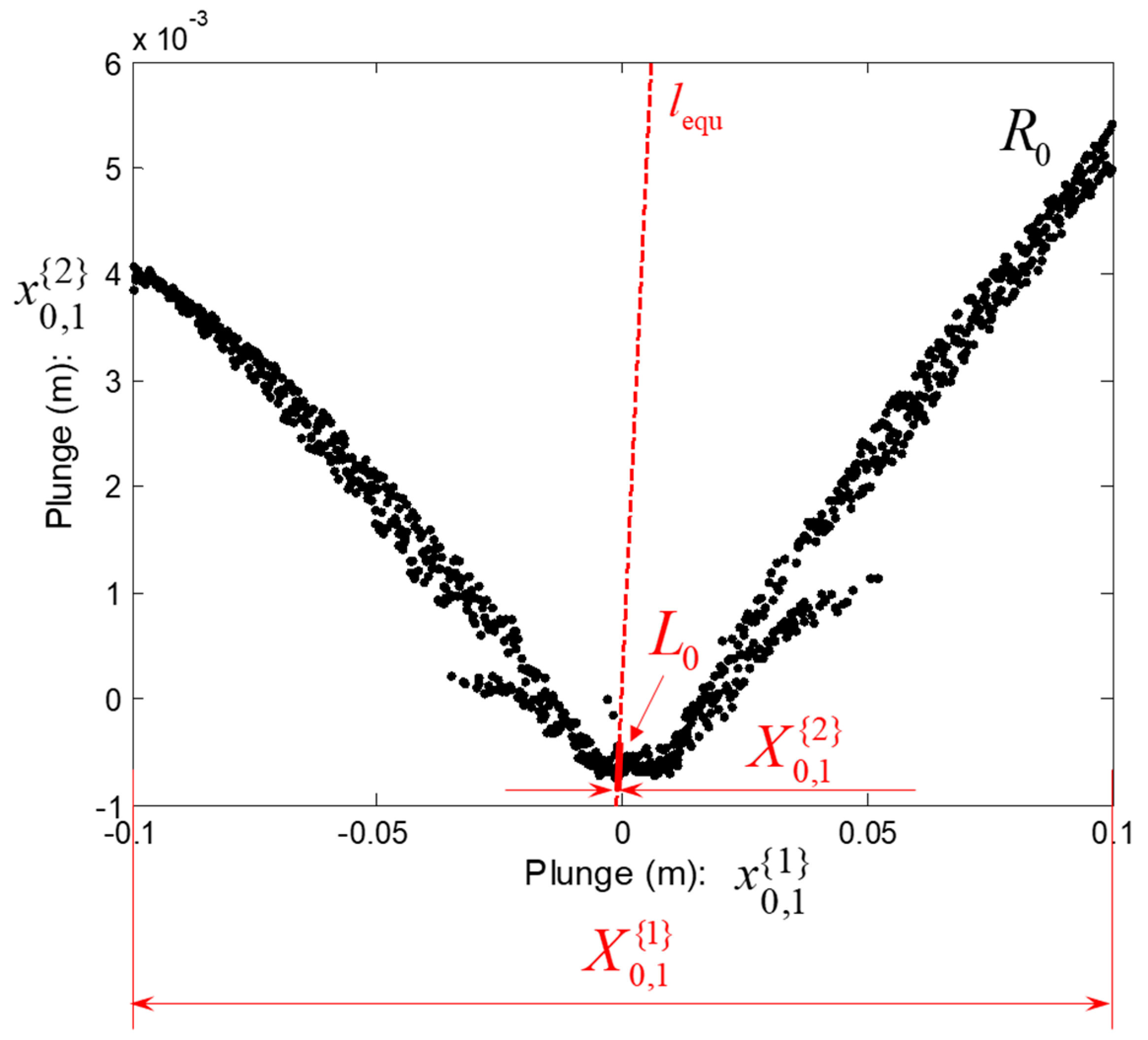
3.3. Modification of the Poincaré Map and Iteration Plots
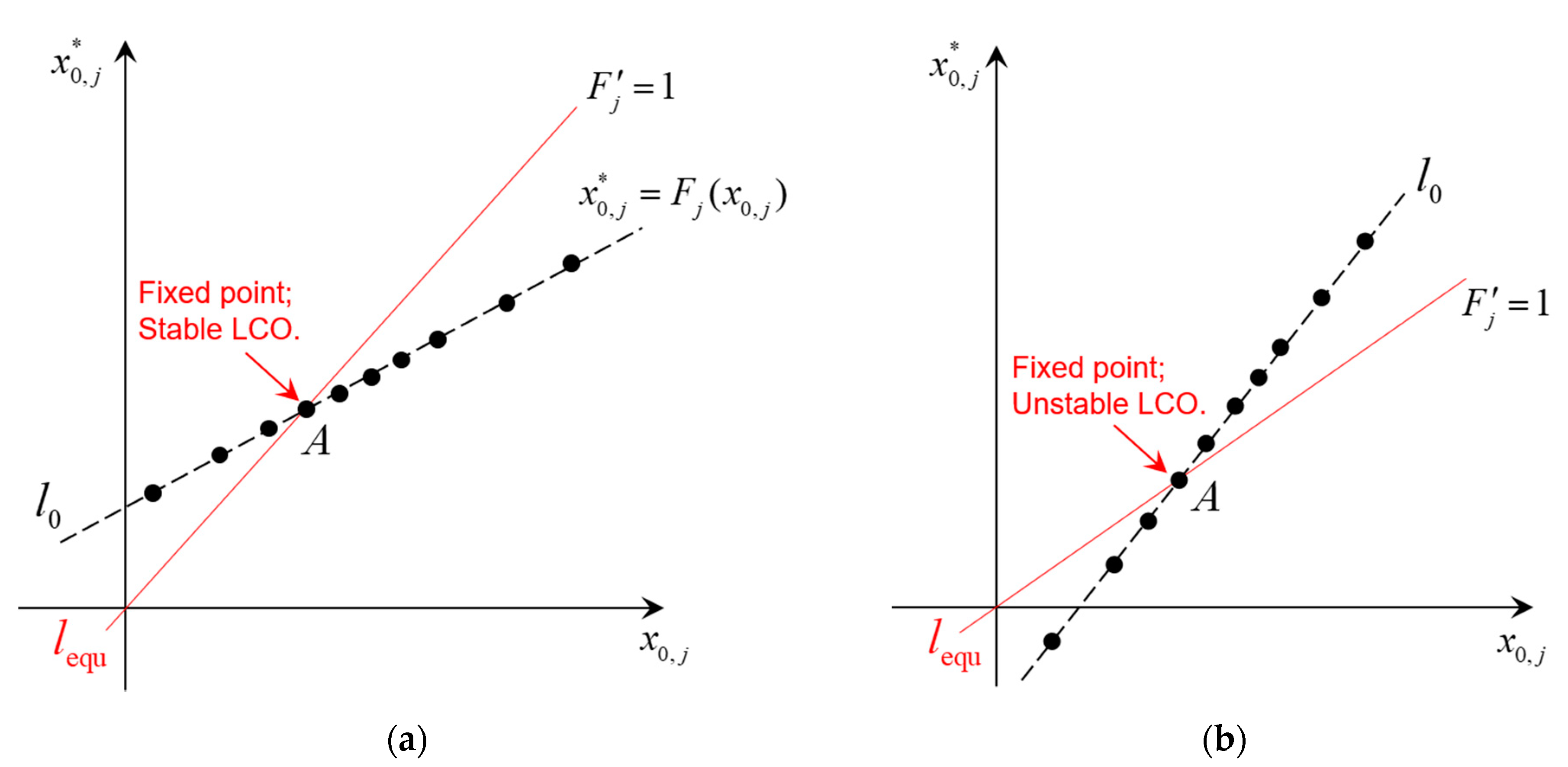
3.4. LCO Anlaysis Using the SSI Scheme
4. Numerical Model and Results of the Hénon–RK45 Method
5. LCO Results of Time Integrations with the Hénon–RK45 Method
6. LCO Analysis of Time Integrations with the SSI Scheme
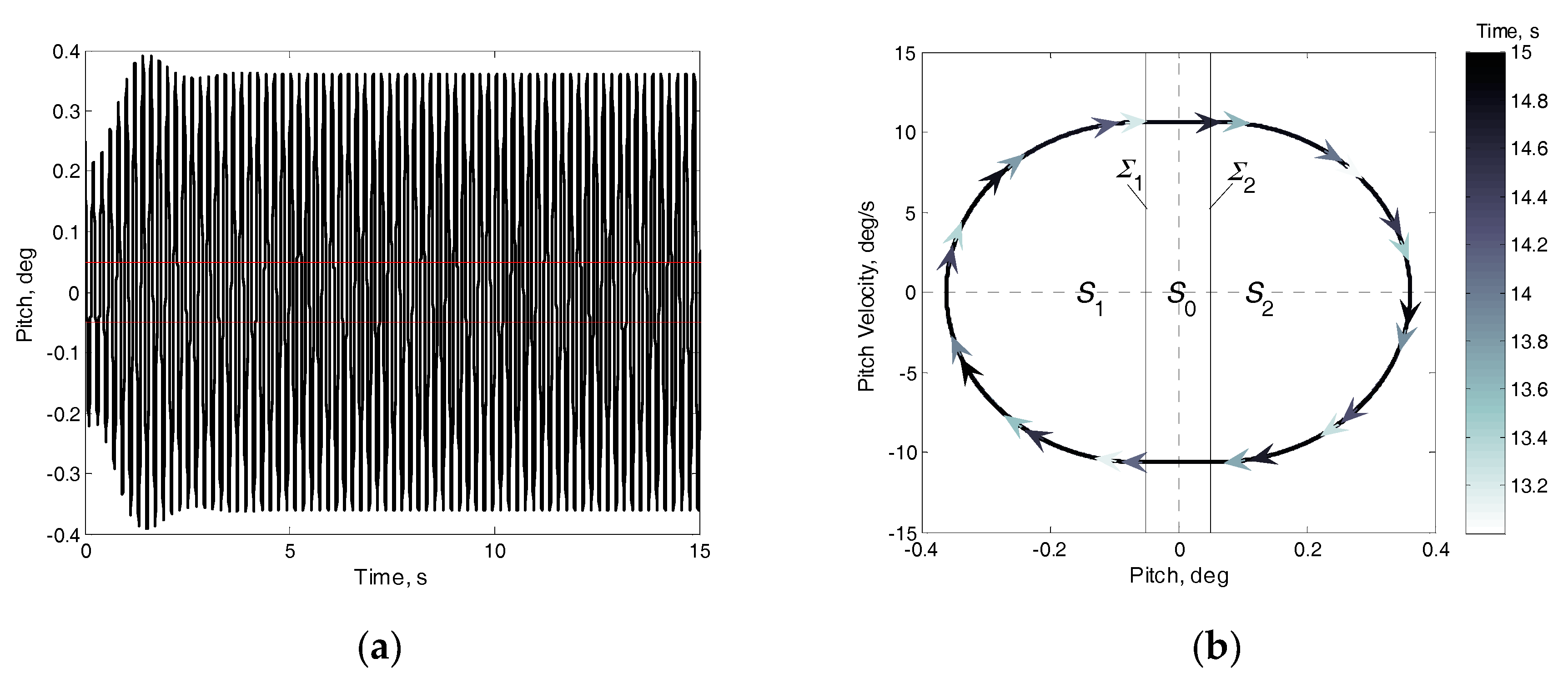
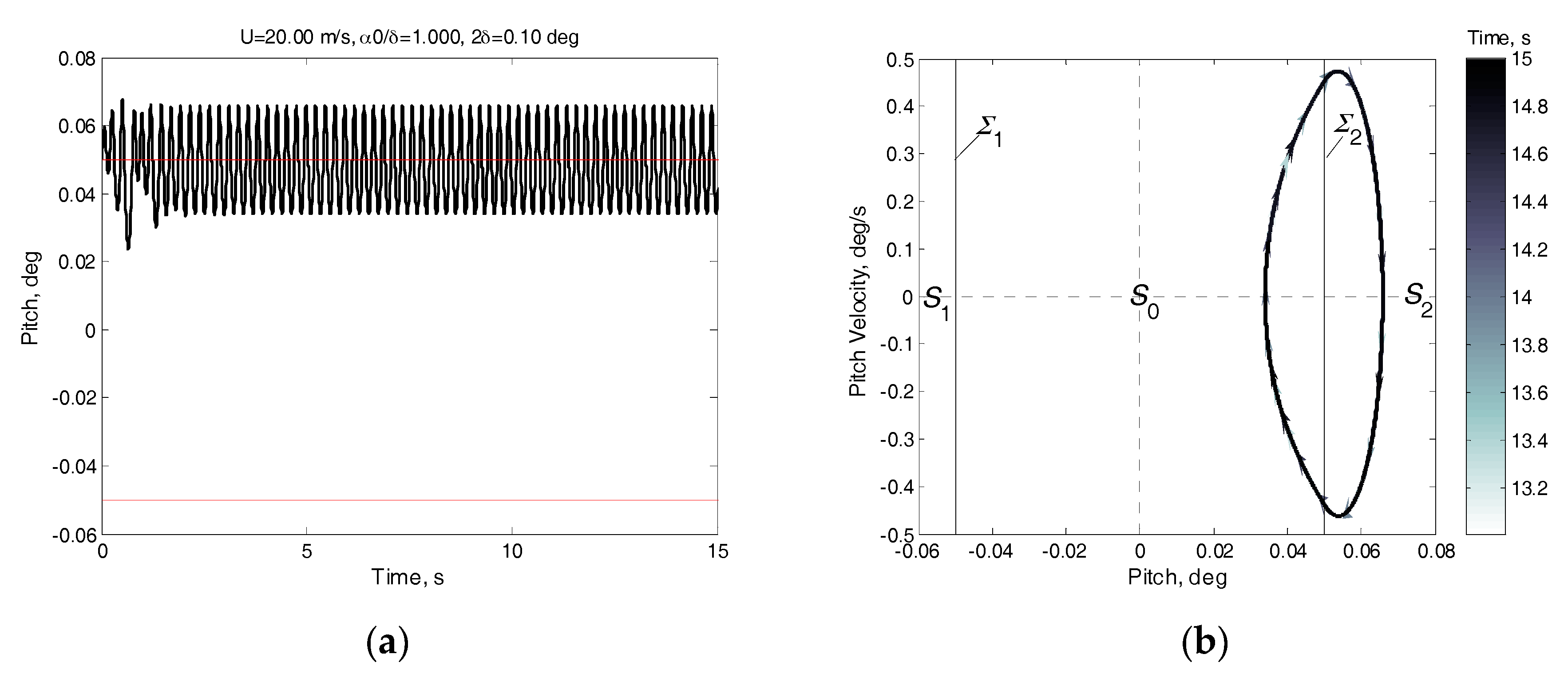
6.1. LCO Results under an Airspeed of 20 m/s
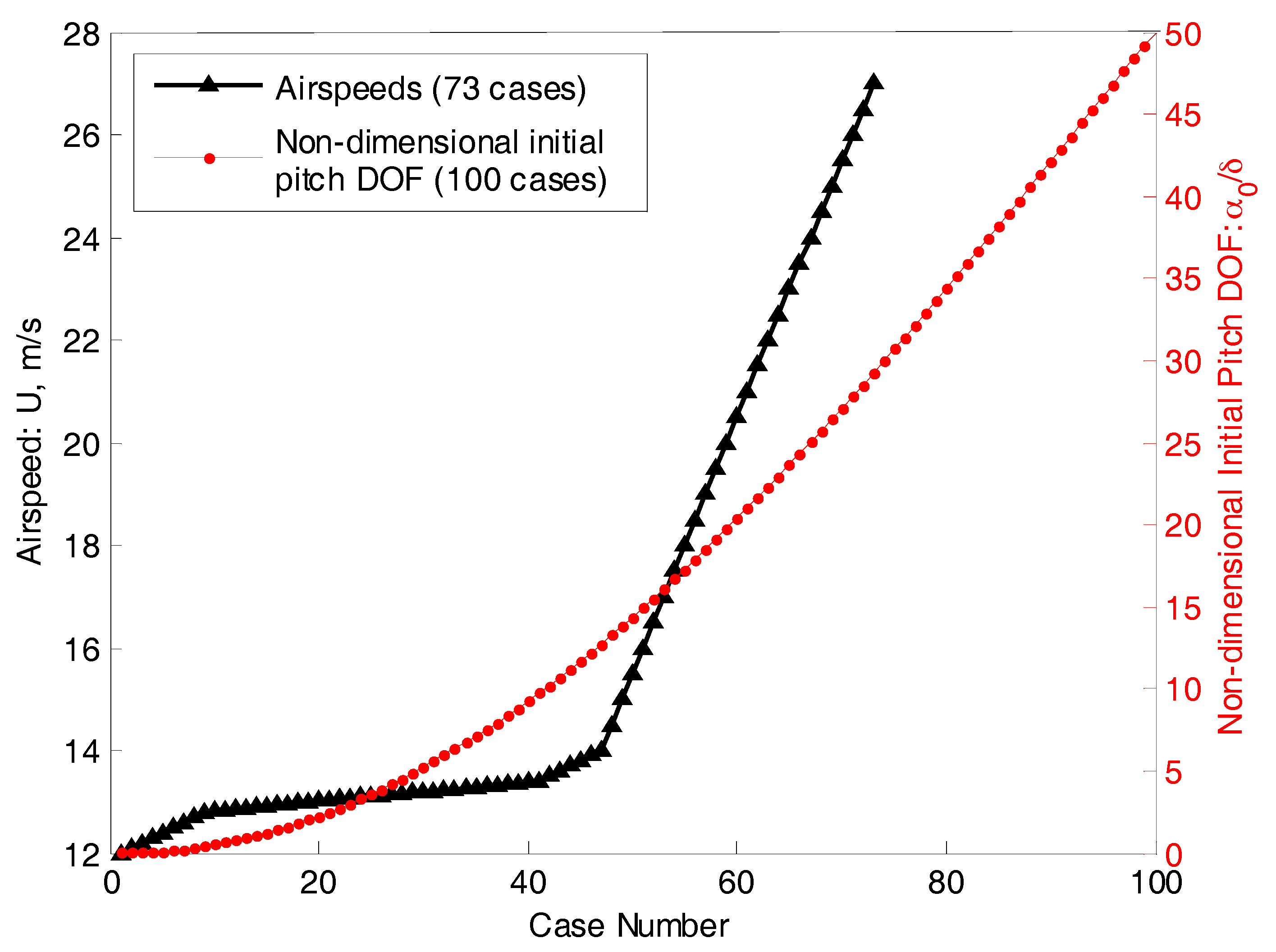
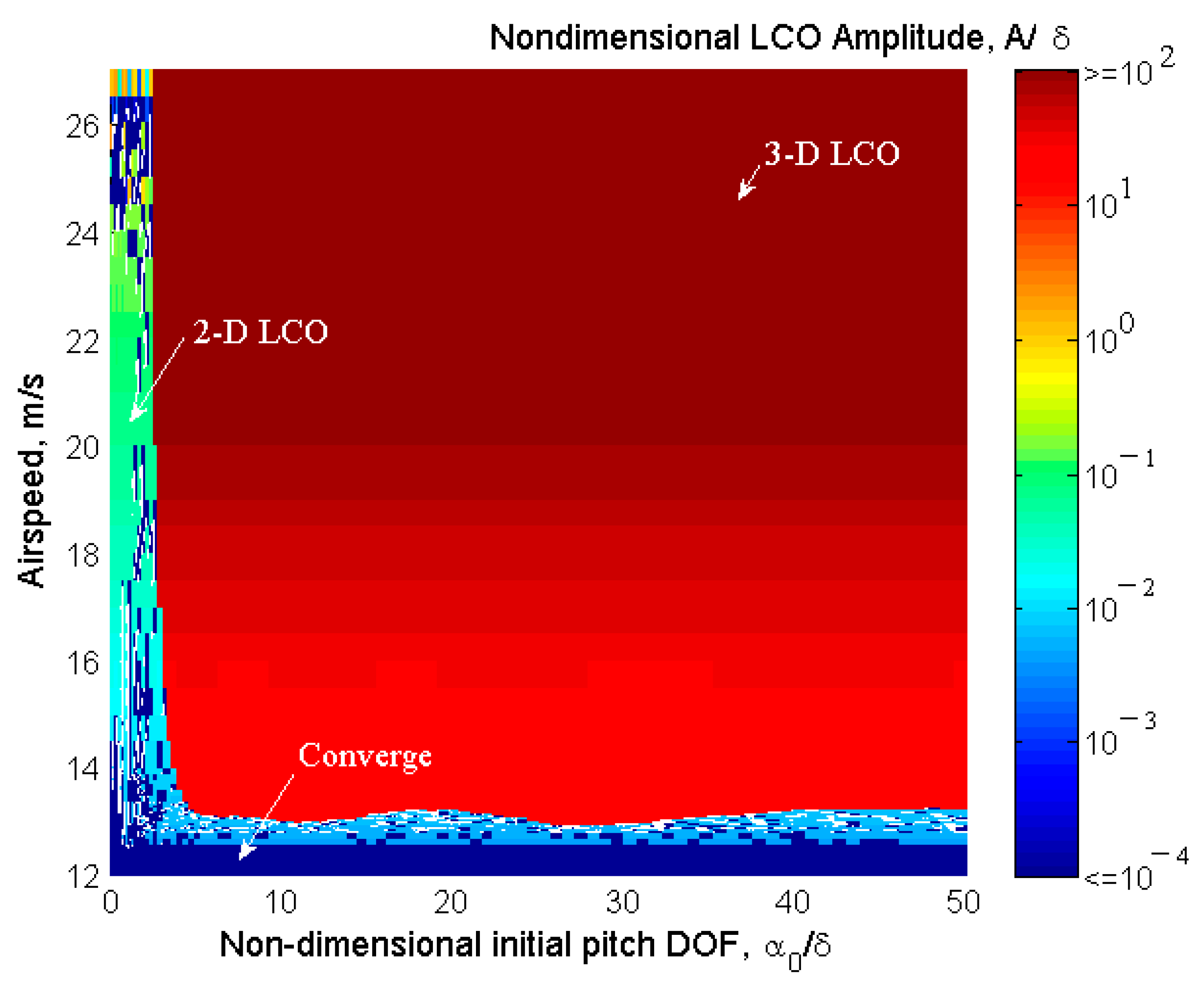
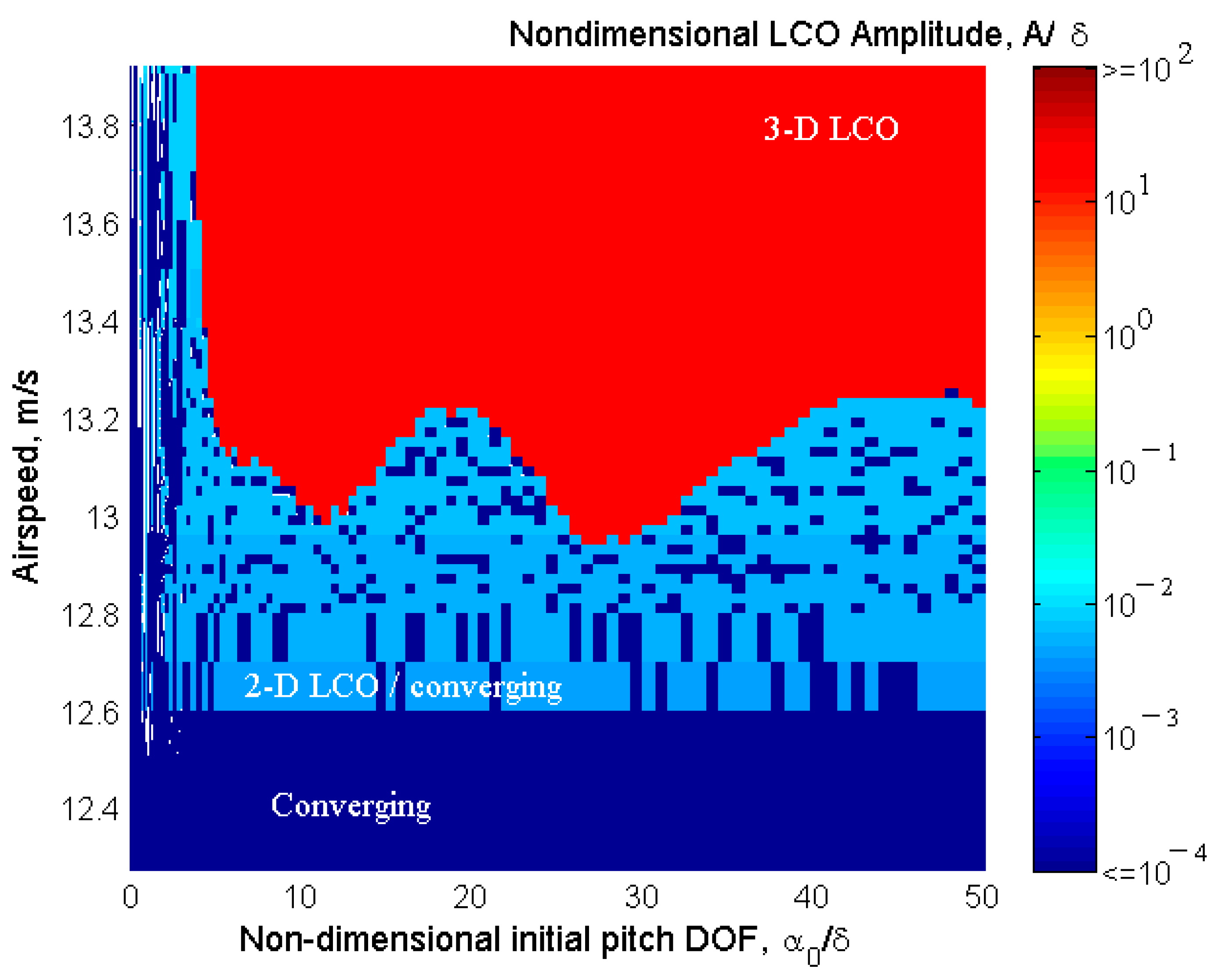
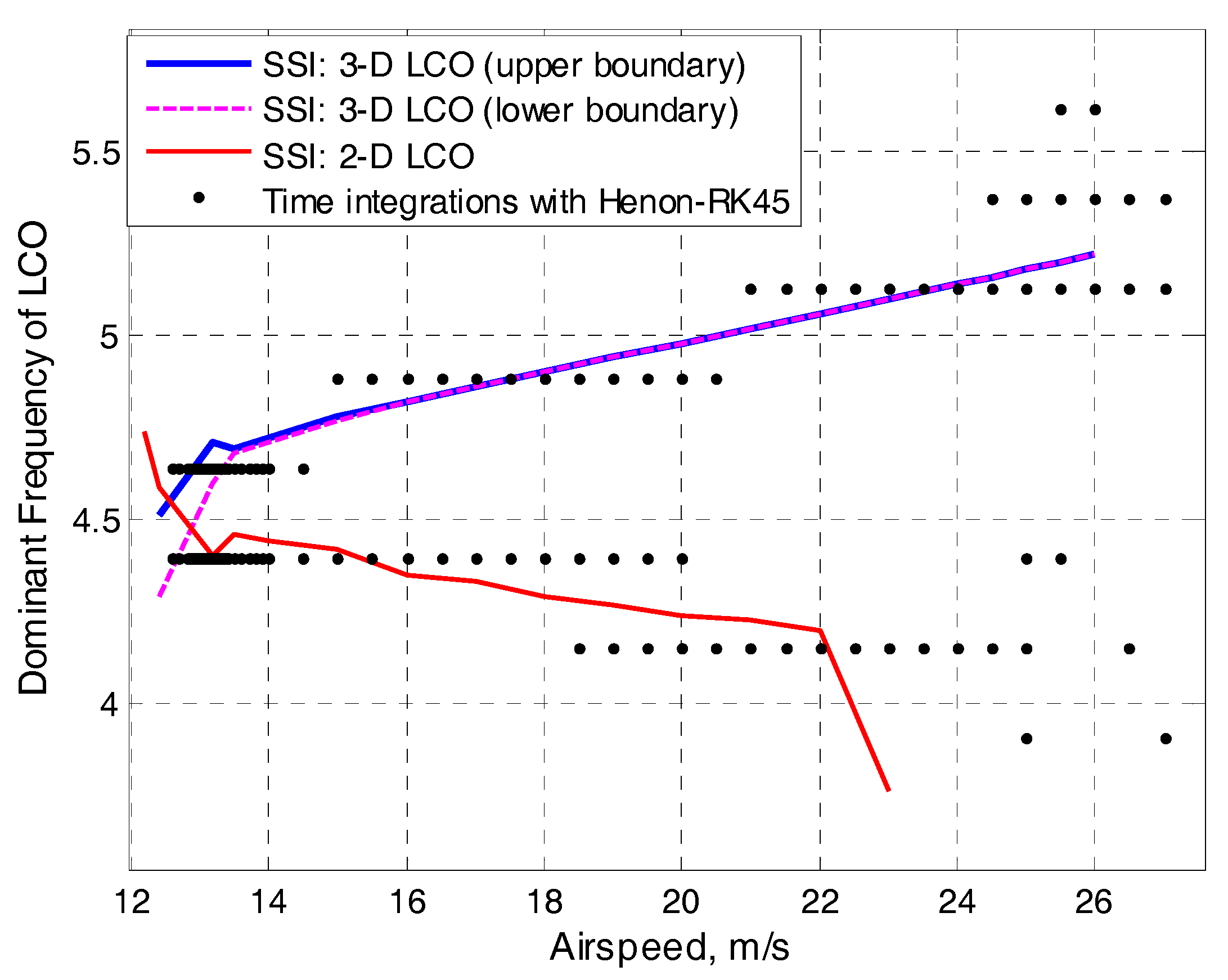
6.2. LCO Results Varying with the Airspeed and a Comparison to Hénon–RK45
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Parameters of the Wing Section Model
| Symbol | Explanation | Value | Unit |
|---|---|---|---|
| Chord length | 0.200 | m | |
| Half chord length | 0.100 | m | |
| Wing span | 0.400 | m | |
| Distance between flexural axis and central of gravity | 0.010 | m | |
| Distance between leading edge and flexural axis | 0.075 | m | |
| −0.250 | — | ||
| Gross weight of the wing section | 2.900 | kg | |
| Static moment: | −0.029 | kg∙m | |
| Inertia moment of the wing section | 0.024 | kg∙m2 | |
| Linear plunge stiffness | 2372.0 | kg∙m/s2 | |
| Linear pitch stiffness | 35.50 | kg∙m2/s2 | |
| Plunge damping | 3.32 | kg∙m/s | |
| Pitch damping | 0.04 | kg∙m2/s |
| 0.0081 | 1.2336 | −5.0805 | 1.4583 | −7.4112 | −0.1568 |
| 0.0002 | 0.0308 | −0.1270 | −0.0264 | 0.1289 | −0.0196 |
| 0.9756 | 0.9756 | −0.3265 | −0.2824 | −0.08 | 0 |
| 0.0244 | 0.0244 | −2.3639 | −0.5666 | 0 | −0.60 |
References
- Grigorios, D. Introduction to Nonlinear Aeroelasticitiy; John Wiley & Sons, Inc.: Chichester, West Sussex, UK, 2017. [Google Scholar]
- Abdelkefi, A.; Vasconcellos, R.; Marques Flavio, D. Modeling and identification of freeplay nonlinearity. J. Sound Vib. 2012, 331, 1898–1907. [Google Scholar] [CrossRef]
- Edouard, V.; Grigorios, D.; Gustavo, D.B.R. Two-domain and three-domain limit cycles in a typical aeroelastic system with freeplay in pitch. J. Fluids Struct. 2017, 89–107. [Google Scholar] [CrossRef]
- Tian, W.; Yang, Z.; Gu, Y. Dynamic analysis of an aeroelastic airfoil with freeplay nonlinearity by precise integration method based on Pade approximation. Nonlinear Dynam. 2017, 89, 2173–2194. [Google Scholar] [CrossRef]
- Zhong, W.X.; Williams, F.W. A precise time step integration method. Proc. Inst. Mech. Eng. 1994, 427–430. [Google Scholar] [CrossRef]
- Wang, M.F.; Au, F.T.K. On the precise integration methods based on Padé approximations. Comput. Struct. 2009, 380–390. [Google Scholar] [CrossRef]
- Hénon, M. On the numerical computation of Poincaré maps. Physica 1982, 5D, 412–414. [Google Scholar] [CrossRef]
- Padmanabhan Madhusudan, A.; Dowell, E.H.; Pasiliao Crystal, L. Computational study of aeroelastic limit cycles due to localized structural nonlinearities. J. Aircraft 2018, 1–11. [Google Scholar] [CrossRef]
- Tang, D.; Dowell, E.H. Flutter and limit-cycle oscillations for a wing-store model with freeplay. J. Aircraft. 2006, 43, 487–503. [Google Scholar] [CrossRef]
- Tang, D.M.; Dowell Earl, H. Flutter and stall response of a helicopter blade with structural nonlinearity. J. Aircraft 1992, 25–45. [Google Scholar] [CrossRef]
- Deman, T.; Earl, D.H. Computational/Experimental aeroelastic study for a horizontal-tail model with free play. AIAA J. 2013, 51, 341–352. [Google Scholar] [CrossRef]
- Padmanabhan Madhusudan, A.; Pasiliao, C.L.; Dowell, E.H. Simulation of aeroelastic limit-cycle oscillations of aircraft wings with stores. AIAA J. 2014, 52, 2291–2299. [Google Scholar] [CrossRef]
- Dimitriadis, G. Shooting-based complete bifurcation prediction for aeroelastic systems with freeplay. J. Aircraft 2011, 48, 1864–1878. [Google Scholar] [CrossRef]
- Dimitriadis, G. Complete Bifurcation Behaviour of Aeroelastic Systems with Freeplay. In Proceedings of the 52nd AIAA/ASCE/ASC Structures, Structural Dynamics, and Materials Conference, Denver, CO, USA, 4–7 April 2011. [Google Scholar] [CrossRef]
- Poincaré, H. Mémoire sur les courbes définies par une équation différentielle (I). J. Mathématiques Puresappliquées Série 1881, 7, 375–422. [Google Scholar]
- Lawrence, P. Differential Equations and Dynamical Systems, 2nd ed.; Springer: New York, NY, USA, 1990. [Google Scholar]
- Monfared, Z.; Afsharnezhad, Z.; Esfahani, J.A. Flutter, limit cycle oscillation, bifurcation and stability regions of an airfoil with discontinuous freeplay nonlinearity. Nonlinear Dynam. 2017, 1965–1986. [Google Scholar] [CrossRef]
- Price, S.J.; Lee, B.H.K.; Alighanbari, H. Postinstability behavior of a two-dimensional airfoil with a structural nonlinearity. J. Aircraft 1994, 31, 1401–1935. [Google Scholar] [CrossRef]
- Vasconcellos, R.; Abdelkefi, A.; Marques Flavio, D. Representation and analysis of control surface freeplay nonlinearity. J. Fluid. Struct. 2012, 31, 79–91. [Google Scholar] [CrossRef]
- Wei, H.; Yang, Z.; Gu, Y. The nonlinear aeroelastic characteristics of a folding wing with cubic stiffness. J. Sound Vib. 2017, 22–39. [Google Scholar] [CrossRef]
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar]
- Strogatz Steven, H. Nonlinear Dynamics and Chaos, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Tucker, W. The Lorenz attractor exists. Dyn. Syst. 1999, 328, 1197–1202. [Google Scholar] [CrossRef]
- Tucker, W. A rigorous ODE solver and Smale’s 14th problem. Found. Comput. Math. 2002, 53–117. [Google Scholar] [CrossRef]
- Ian, S. The Lorenz attractor exists. Nature 2000, 406, 948. [Google Scholar]
- Marcelo, V. Waht’s new on Lorenz strange attractors. Math. Intell. 2000, 22, 6–19. [Google Scholar]
- Theodorsen, T. General Theory of Aerodynamic Instability and the Mechanism of Flutter: Technical Report 496; NACA: Moffett Field, CA, USA, 1935. [Google Scholar]
- Roger Kenneth, L. Airplane Math Modeling and Active Aeroelastic Control Design. Struct. Asp. Act. Control. 1977, 228, 4. [Google Scholar]
- Karpel, M. Design for active flutter suppression and gust alleviation using state-space aeroelastic modeling. J. Aircraft 1982, 19, 221–227. [Google Scholar] [CrossRef]
- Tiffany, S.H.; Mordechay, K. Aeroservoelastic modeling and applications using minimum-state approximations of the unsteady aerodynamics. In NASA Technical Memorandum; Langley Research Center, NASA: Hampton, Virginia, 1989. [Google Scholar]
- Edwards, J.W.; Ashley, H.; Breakwell, J.V. Unsteady aerodynmic modeling for arbitrary motions. AIAA J. 1979, 365–374. [Google Scholar] [CrossRef]





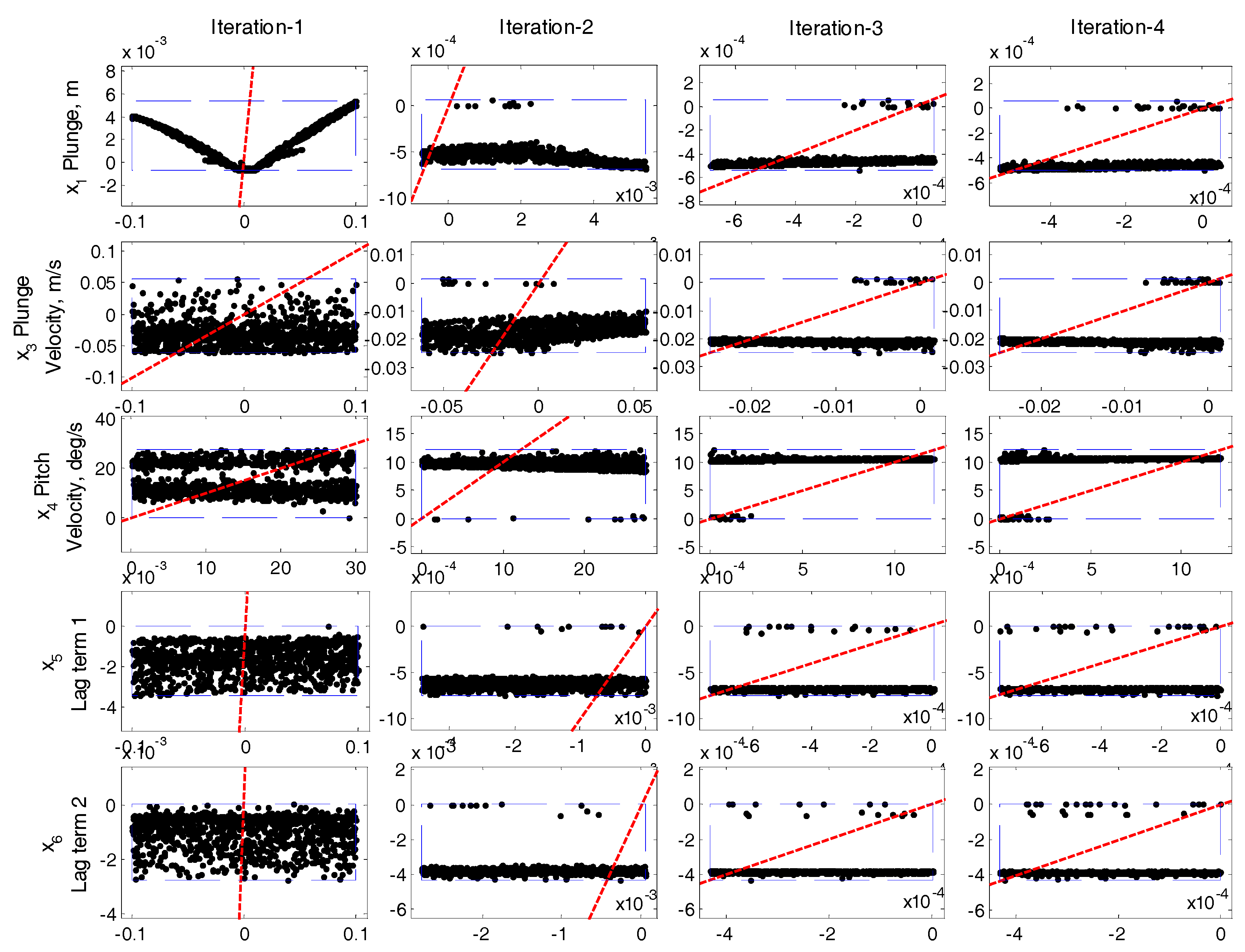



| Iteration- | , m | , m/s | , °/s | CPU time | |||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | min. | −0.1 | −0.1 | 0.00 | −0.1 | −0.1 | — | ||
| max. | +0.1 | +0.1 | 30.00 | +0.1 | +0.1 | ||||
| 2 | min. | 0.00 | 0.00 | 82.82 s | |||||
| max. | 29.98 | 0.00 | |||||||
| −96.92% | −41.23% | 0.06% | −8.12% | −98.29% | |||||
| 3 | min. | 0.02 | 0.00 | 78.54 s | |||||
| max. | 27.42 | ||||||||
| −87.93% | −77.46% | 8.61% | −55.81% | −77.97% | |||||
| 4 | min. | 0.00 | 0.00 | 78.66 s | |||||
| max. | 12.09 | 0.00 | |||||||
| −21.20% | 0.23% | 55.88% | 0.77% | −1.39% | |||||
| 5 | min. | 0.00 | 0.00 | 78.27 s | |||||
| max. | 12.14 | ||||||||
| −3.32% | 0.81% | −0.41% | −0.30% | 1.86% | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Wu, Z.; Yang, C. Integration of Freeplay-Induced Limit Cycles Based On a State Space Iterating Scheme. Appl. Sci. 2021, 11, 741. https://doi.org/10.3390/app11020741
Wang X, Wu Z, Yang C. Integration of Freeplay-Induced Limit Cycles Based On a State Space Iterating Scheme. Applied Sciences. 2021; 11(2):741. https://doi.org/10.3390/app11020741
Chicago/Turabian StyleWang, Xiangyu, Zhigang Wu, and Chao Yang. 2021. "Integration of Freeplay-Induced Limit Cycles Based On a State Space Iterating Scheme" Applied Sciences 11, no. 2: 741. https://doi.org/10.3390/app11020741
APA StyleWang, X., Wu, Z., & Yang, C. (2021). Integration of Freeplay-Induced Limit Cycles Based On a State Space Iterating Scheme. Applied Sciences, 11(2), 741. https://doi.org/10.3390/app11020741






