Reversible and Plausibly Deniable Covert Channels in One-Time Passwords Based on Hash Chains ^†

Abstract

Covert channels enable stealthy communications over innocent appearing carriers. They are increasingly applied in the network context. However, little work is available that exploits cryptographic primitives in the networking context to establish such covert communications. We present a covert channel between two devices where one device authenticates itself with Lamport’s one-time passwords based on a cryptographic hash function. Our channel enables plausible deniability jointly with reversibility and is applicable in different contexts, such as traditional TCP/IP networks, CPS/IoT communication, blockchain-driven systems and local inter-process communications that apply hash chains. We also present countermeasures to detect the presence of such a covert channel, which are non-trivial because hash values are random-looking binary strings, so that deviations are not likely to be detected. We report on experimental results with MD5 and SHA-3 hash functions for two covert channel variants running in a localhost setup. In particular, we evaluate the channels’ time performance, conduct statistical tests using the NIST suite and run a test for matching hash values between legitimate and covert environments to determine our channels’ stealthiness.

1. Introduction

A covert channel (CC) is an unforeseen communication channel in a system design. While the first covert channels for local computers were described in the 1970s (cf. [1]), the research of recent decades has discovered a plethora of new and sophisticated covert channels that aid the secret exchange of information between hosts, databases, network hosts and IoT devices. Due to their stealthy and policy-breaking nature, covert channels enable several actions related to cybercrime, such as the secret extraction of confidential information, barely detectable botnet command and control channels, and unobservable communication for cybercriminals. While legitimate use cases are imaginable as well, e.g., journalists using covert channels for secure exchange of dissident-related information, criminal use seems foremost, so that presentation of new covert channels also serves presentation of countermeasures.

We present the first CC that exploits cryptographic hash chains, which have become popular because some form (blockchain) is used in cryptocurrencies, although they had been used much earlier, e.g., by Lamport [2]. Hash chains are widely used, which renders them an attractive carrier for covert information that can be applied in various cybersecurity contexts, such as authentication systems, cryptocurrencies and blockchain-driven systems of all kinds. Thus, our proposed covert channels can be applied in several domains and contexts, which is an advantage in comparison to covert channels designed for legitimate communication systems (such as covert channels for specific smart building communication protocols).

Our covert channels can be considered an example of plausible deniability: Alice communicates with Bob over the covert channel. Both can state that every possible hash value is equally likely to occur. By modifying (alternating) bits of hash values, Alice and Bob can thus plausibly deny the existence of the covert channel. Moreover, we show that our channel allows Bob to restore the original message before forwarding it to the overt receiver, making our covert channel reversible. Alice and Bob, the covert sender and receiver, can be located directly with sender and receiver of the overt channel, but they can also be located on the communication path, realizing a man-in-the-middle (MitM) scenario.

Moreover, we present the CC in a parameterized manner so that our proposal really comprises a large number of possible CC instances that differ in steganographic bandwidth, robustness and stealthiness.

We sketch possible countermeasures against this CC, which are non-trivial because hash values are random-looking bit strings. To this end, we also perform experiments with MD5 and SHA-3 as cryptographic hash functions in Lamport’s application of hash chains as one-time passwords, and give experimental results on the performance and detectability of CC use.

2. Fundamentals and Related Work

We will first introduce related fundamental concepts, followed by coverage of more sophisticated related work.

2.1. Fundamentals

A hash function is a function $h:U\to R$ that maps a possibly infinite universe, e.g., $U={\{0,1\}}^{🟉}$, onto a finite set of hash values, e.g., $R={\{0,1\}}^m$ [3]. A cryptographic hash function should have pre-image resistance, i.e., from a hash value $y\in R$ it is not possible (with reasonable effort) to compute a string $x\in U$ such that $h\left(x\right)=y$, 2nd pre-image resistance, i.e., from a given x with $h\left(x\right)=y$ it is not possible to compute $x^{\prime }\in U,x^{\prime }\ne x$ such that $h\left(x^{\prime }\right)=y$, and collision resistance, i.e., it is not possible to compute two strings $x,x^{\prime }\in U,x^{\prime }\ne x$ such that $h\left(x\right)=h\left(x^{\prime }\right)$. Examples of cryptographic hash functions are MD5 (message digest 5) [4], now outdated, and SHA-3 (secure hash algorithm 3) [5], the current standard for cryptographic hashing, based on the KECCAK hash function [6]. As $R\subset U$, a hash function can be applied repeatedly, i.e., for a seed $x_0=s$, we can compute $x_{i+1}=h\left(x_i\right)$ for $i=0,1,2,\dots ,n-1$. This sequence is called a hash chain. While it is easy to compute a hash chain in a forward direction, it cannot be computed in a backward direction, starting from $x_n$, because of the pre-image resistance property.

A one-time password (OTP) is a password only used once to authenticate an entity. As such, it is secure as long as it is secret and cannot be guessed prior to its use. Lamport [2] presented a scheme to generate OTPs from a hash function with pre-image resistance. Entity A uses a random and secret seed s to compute a hash chain $x_0,\dots ,x_n$, and transfers $x_n$ to entity B via a secure channel. To authenticate, A sends $z=x_{n-1}$ over an insecure channel to B. B checks if $h\left(z\right)=x_n$. If yes, the authentication is approved, and B replaces $x_n$ by $z=x_{n-1}$. If not, authentication has failed. For the next authentication, A sends $z=x_{n-2}$, and so on. Each password is only used once, and by the pre-image resistance, the next password cannot be guessed from the previous password. In addition, B need not keep $x_n$ secret, as nothing can be inferred from this value. Haller’s S/Key [7] and the TESLA protocol [8] use similar ideas.

A covert channel, as one form of steganography, defines a parasitic communication channel nested inside a computing environment that allows at least two different legitimate processes (or nodes) to access a shared resource. The covert channel exploits the legitimate processes in a way that allows the signaling of hidden information via the shared resource. The sender and receiver of a covert channel are called covert sender (CS) and covert receiver (CR), respectively. CS and CR are not necessarily identical with the overt sender and overt receiver (OS and OR) as CS and CR might act in an indirect manner or as a man-in-the-middle. Covert channels inside computer networks follow a set of known hiding patterns [9] to transfer information, e.g., by placing secret data inside unused or reserved header bits of network packets, by modifying header fields with random values, or by modulating the timings between succeeding network packets.

Reversible steganography allows the reconstruction of the original carrier message to the state before the steganographic data was embedded. For instance, it would allow an original image to be completely restored after the extraction of hidden data embedded in a cover image [10]. In man-in-the-middle scenarios, reversibility enables covert receivers to forward non-modified, i.e., innocent, original data to the overt receiver. As shown by Mazurczyk et al., reversibility is feasible for network covert channels: full reversibility refers to covert channels where the original carrier data can be restored completely, while quasi-reversibility refers to those covert channels that allow only the partial reconstruction of the original data [11]. Different categories of reversible data hiding are feasible. In our case, intrinsic data-hiding is applied, in which the covert receiver is able to achieve full reversibility without guessing (implicit reversibility techniques) or embedding of additional information that describe the original message (explicit reversibility techniques) [11].

Plausible deniability for a synthetic record is achieved when there exists a set of real data records that could have generated the same synthetic data with (more or less) the same probability by which it was generated from its own seed [12]. Plausible deniability is usually achieved by replacing pseudo-random data with encrypted covert data that also appear pseudo-random. Sometimes, it is also achieved by nesting secret information inside multiple layers of hidden information, where the surrounding layer is revealed to an observer in order to show cooperation. For instance, a steganographic filesystem might contain multiple layers of steganographic filesystems nested inside each other. Only outer layers are revealed to a warden while inner layers remain hidden.

2.2. Related Work

Covert channels have been proposed for several domains. For instance, Carrara and Adams surveyed out-of-band covert channels over physical media, such as light, sound and air [13] while other authors analyzed details of such channels, e.g., Hanspach and Goetz [14], Cronin et al. [15] and Matyunin et al. [16]. Network covert channel techniques have been summarized by Mazurczyk et al. [17], Wendzel et al. [9] and Zander et al. [18]. Detailed studies of specific network covert channels and their countermeasures were performed by Cabuk et al. [19], Xing et al. [20], Saenger et al. [21], Zander et al. [22] and Zhang et al. [23], just to mention a few. Further, several local covert channels have been studied, e.g., on smartphones by Mazurczyk et al. [24] and Urbanski et al. [25], in the architecture of processors by Wang and Lee [26], as well as in real-time schedulers by Chen et al. [27]. Most recently, covert channels in the Internet of Things has gained increasing attention, cf. works by Mileva et al. [28], Wendzel et al. [29] and Hildebrandt et al. [30].

Calhoun et al. [31] described a covert channel in which OTPs are used as an element for generating random data for a covert channel that exploits rate switching in 802.11 b WiFi networks. In comparison, our approach allows an Internet-wide application that is not limited to wireless environments. Moreover, our approach represents an indirect covert channel based on hash chain exploitation. To the best of our knowledge, no other covert channel has been published that exploits cryptographic hash chains.

Plausible deniability for steganography has been proposed by several authors, especially for filesystems (e.g., [32]). In the context of video streams, PRNG-output was utilized [33]. Rutkowska published a covert channel that embeds DES-encrypted data into third-party TCP initial sequence numbers (ISN) [34]. However, Murdoch and Lewies have shown that the channel by Rutkowska is detectable, since the distribution of ISN values does not match the distribution of DES-encrypted covert data [35]. Abad [36] presents a covert channel in the check sum of IP packets, which, however, does not use a cryptographic hash function.

Several methods for reversibility analysis of network covert channels have been studied by Mazurczyk et al. [11], while earlier works studied reversibility in digital media steganography, e.g., Chang and Lin in [10,37].

The remainder of this paper is structured as follows. Our two covert channels based on hash chains are introduced in Section 3. We discuss countermeasures for our covert channels in Section 4 and evaluate the performance and stealthiness characteristics of our channels in Section 5. Section 6 concludes and provides an outlook on future work.

3. Covert Channels in Hash Chains

We present multiple variants of a covert channel that can be used in OTPs based on hash chains. We assume that each hash value is transmitted as part of network packets between A and B, so that a modification of the hash value by CS can be hidden by re-computing the packet’s check sum. The information flow would be $A\to CS\to CR\to B$. In such a case, our channel assumes a man-in-the-middle scenario. Alternatively, A and CS can be the same entity while B and CR can also be the same entity. However, our covert channel would also function if A and B are local processes inside an operating system, while CS and CR are part of an inter-process communication between A and B, or when A and B are CPS or IoT devices.

3.1. Channel Characteristics

Our channel has certain features that are traditionally used to categorize and describe covert channels:

(1)

Our channel variants allow plausible deniability as they replace selected bits of hash values in a pseudo-random manner so that the probability distribution of original and modified hash values are similar.

(2)

If CR is not just a passive observer but a hop on the path to B, CR is able to reconstruct the original hash value and can thus forward the illicit original message to B, rendering our approach reversible. This is feasible if, for example, B is a routing hop on a program in an IPC-chain between A and B. Due to the fact that we achieve full reversibility and do not exploit implicit or explicit reversibility methods, our technique is an intrinsic reversibility method.

(3)

Finally, our channel does not rely on indirect signaling methods, which makes it a direct covert channel. However, if CS applied a method to indirectly influence the transferred hash value, our channel would be a semi-passive one, while it would also be passive (indirect) if CR indirectly obtained the sent hash value (e.g., using a side channel) [38].

(4)

It does not matter for our covert channel whether the hash value is transmitted over a network or between local processes. The hash value can also be stored in a file at some point in time and then read later by another process, i.e., sender and receiver processes must not necessarily be active at the same time. However, in practice, most authentication scenarios would require A and B to be active simultaneously.

3.2. Covert Channel Variants

The secret message that CS wants to send is broken into t symbols from an alphabet $V=\{0,1,\dots ,v-1\}$, i.e., the message comprises at most $l=\lfloor t{log}_{2}v\rfloor$ bits.

To embed a symbol $s_j\in V$ into a password $x_i$ that is going to be transmitted, CS modifies the password by applying a transformation $T:R\times V\to R$, i.e., replaces $x_i$ by a different password $x_i^{\prime }=T(x_i,s_j)$. In the following, we will mostly use the notation $T_{s_j}\left(x_i\right)$ instead.

This password is intercepted by CR, who knows the previous password $x_{i+1}$. CR first tests if $h\left(x_i^{\prime }\right)=x_{i+1}$. In that case, no symbol has been embedded and $x_i=x_i^{\prime }$. Otherwise, for each possible symbol s, CR applies $T_s^{-1}$ to $x_i^{\prime }$ and checks if hashing produces $x_{i+1}$. CR stops with the first hit, extracts symbol $s_j$ of the secret message, and forwards the original password $x_i=T_{s_j}^{-1}\left(x_i^{\prime }\right)$ to B.

Embedding is repeated until the complete message is transmitted. This requires that the number of symbols in the message is $t<n$, as we do not embed a symbol in the first password $x_{n-1}$ to enable reversibility (see below).

The extracting procedure requires that T is injective in each argument, and that $T_s\left(x\right)\ne x$.

To implement T, we identify V with a subset of size v of $R={\{0,1\}}^m$, and define $T_{s_j}\left(x\right)=x\oplus s_j$, where ⊕ denotes the bitwise exclusive OR operation. Then T is self-inverse, i.e., $T_s^{-1}=T_s$. An upper bound for $v=\left|V\right|$ is $2^m-1=|R\backslash \{00\cdots 0\}|$, so that the message might comprise up to $l=\lfloor (n-1){log}_2(2^m-1)\rfloor$ bits, i.e., almost $n·m$ bits can be transmitted.

A first variant is found by defining set V of size $v=m$ comprising all m-bit strings with exactly one bit set to 1, i.e., embedding symbol $s_j$ means to flip bit j of the password to be transmitted. We illustrate this variant in Figure 1.

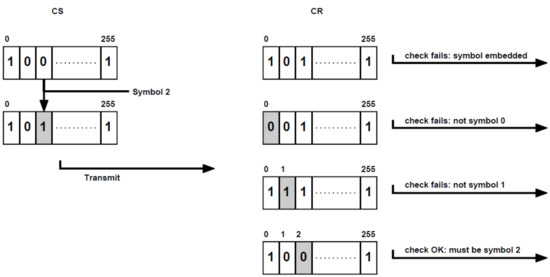
Figure 1. Example of variant 1. Covert sender (CS) embeds symbol 2 by flipping bit 2 of a password. Covert receiver (CR) first tries out which bit of the transmitted password must be flipped so that the check is successful, i.e., that its hash corresponds to the password stored at CR. Thus CR extracts symbol 2.

A much more restrictive variant could embed only one bit per password, e.g., by using $V=\{100·0,010·0\}$. Please note that when a symbol is embedded in each password (except $x_{n-1}$), then we might even use $V=\{000·0,100·0\}$, i.e., flipping bit 0 of the password only when a 1 is embedded, and leaving the password unmodified for embedding 0.

More liberal variants are also possible, e.g., defining V as the set of strings with one or two bits set to 1, resulting in $v=\left(\genfrac{}{}{0pt}{}{m}{1}\right)+\left(\genfrac{}{}{0pt}{}{m}{2}\right)=m(m+1)/2$, or taking all strings with at least $m/2$ bits set to 1, so that

$$v=\left|V\right|=\sum _{k=m/2}^m\left(\genfrac{}{}{0pt}{}{m}{k}\right)=2^{m-1},$$

by applying the binomial theorem with $a=b=1$ and taking the symmetry of binomials into account [39]. Those variants might be useful for cases where m is small, e.g., when hash chains of a small width are used in WSN networks [40].

In order to decouple the embedded symbols from the particular message, i.e., to get random-looking symbols, the message might be encrypted before embedding, using a stream cipher or a block cipher with a chaining method such as cipher block chaining (CBC), to avoid the case when two identical symbols result in two identical encrypted symbols [3]. While this may increase stealthiness during communication, the computational effort on the receiver side, which may also threaten stealthiness (see below), can alternatively be optimized by using an encoding based on the frequency of symbols: the symbol with the highest frequency gets a code symbol that is checked first by CR, and so on. When using the frequencies of letters a to z in English texts from [41] and applying such coding, we get 7.5 evaluations on average, compared to 13 if symbols are encrypted and considered equi-probable.

Furthermore, if $t<n-1$ symbols are embedded, we have the freedom to choose which of the $n-1$ passwords are used for embedding, resulting in $\left(\genfrac{}{}{0pt}{}{n-1}{t}\right)$ possibilities, and increasing stealthiness if not all passwords can be controlled by a warden.

Finally, the transformation function T might depend on i and/or on the index of the symbol to be embedded. For example, if we only embed one bit per password, we might modify bits $imodm$ or $(i+1)modm$ of $x_i$ to embed symbols 0 and 1, respectively, instead of always using the same bit positions.

3.3. Hiding Pattern-Based Categorization

All variants perform a manipulation of (pseudo-)random packet fields as described by the random value pattern [9]. The random value pattern covers all hiding techniques that replace a legitimate (pseudo-)random bit string with a covert bit string that also follows a random distribution. Random value techniques have been implemented by several authors, rendering our proposed covert channel variants applicable in realistic environments. Moreover, such random values can be found in many network protocols, such as the IPID field in IPv4 or the ISN field in TCP.

On the sender side, the variants have very low effort and are thus hardly detectable. During transmission, an isolated packet will look innocent, as the one-time passwords look like random bitstrings, so that a possible bit flip is not likely to leave any trace or signature. Hence, detection during transmission seems non-trivial.

4. Countermeasures

Before experimentally evaluating our proposed channel, we first consider a broader set of potential countermeasures.

Note that in all variants, CR needs no knowledge of $x_n$ stored by B. In the first transmitted password $x_{n-1}$, no symbol is transmitted. Then CR knows $x_{n-1}$ when intercepting and forwarding that password, and can refer to it later on, duplicating B’s work.

Variants that embed more symbols per password might be detectable more easily on the receiver side, as they encompass more evaluations of h. For example, the variant that embeds one of $v=m$ symbols by flipping one bit needs $m/2$ evaluations on average if symbols are equidistributed, which is the case if they are encrypted. This is a notable amount of computation if we consider that m might be 128 (MD5) or 512 (SHA-3). Yet those variants also have higher steganographic bandwidth.

Possible countermeasures on the receiver side, i.e., checking for unusual timing or energy due to repeated evaluation of the hash function, have been described in the previous section. However, they apply mostly if CR resides with the overt receiver (a similar scenario for energy-consumption-based covert channel detection has been proven to be feasible by Caviglione et al. [42]). If we have a man-in-the-middle scenario, only a jitter in transmission time from overt sender to overt receiver might be detectable.

Countermeasures during transmission are possible if a warden has knowledge of two successive packets with passwords $x_i^{\prime }$ and $x_{i-1}^{\prime }$, i.e., has some knowledge of the application logic behind the packets. In this case, the warden can check if $h\left(x_{i-1}^{\prime }\right)=x_i^{\prime }$. If either password has been modified by CS, this equality will most likely not hold because of the hash function’s collision resistance properties.

If the warden has only superficial knowledge of the application, i.e., knows only that the transmitted password must be a random bitstring, the warden can collect some passwords and submit them to a random number test suite such as Diehard [43] or NIST’s suite [44]. If embedding of symbols creates artefacts, then the randomness should decrease if a CC is active. However, the test suites require a notable amount of bits to run, which might not be available, or take very long to collect. Thus, this might be an ex post analysis. Furthermore, if the set of code words V is a randomly chosen subset of R, and/or the symbols to be embedded are chosen in a quasi-random manner, e.g., by using encryption first, then the bitwise exclusive OR of two random bit strings might not be distinguishable.

Another possible countermeasure would be that A and B modify the passwords themselves, in a way that is not foreseeable by CS or CR. When A is about to send $x_i$, it already has knowledge about the following password $x_{i-1}$. Let us assume that both A and B have knowledge of a hash function $g:{\{0,1\}}^m\to \{0,1\}$. If $g\left(x_{i-1}\right)=0$, then A sends $x_i$. If $g\left(x_{i-1}\right)=1$, then A sends $\overline{x_i}$, i.e., $x_i$ with all bits inverted. If g is a good hash function, then the second possibility will occur half of the time. If B receives a password $x_i^{\prime }$, then it checks if either $h\left(x_i^{\prime }\right)$ or $h\left(\overline{x_i^{\prime }}\right)$ equals $x_{i+1}$. In the latter case, B stores $\overline{x_i^{\prime }}$.

As only two instead of one password value will be accepted, this scheme is still secure. But life is now more complicated for CR. It must now compare the four possible combinations of inverted and non-inverted passwords, i.e., its effort is notably increased, and stealthiness thus reduced. More complicated schemes are possible. Even if they are not preventing this covert channel, they can restrict bandwidth and/or can reduce stealthiness by forcing CR to perform more computation.

5. Experiments

We have implemented one variant of our covert channel in a hypothetical system that uses one-time passwords based on hash chains with cryptographic hash functions MD5 ($m=128$) and SHA-3 ($m=256$). The implementation was done in C, and we used existing open-source implementations for the cryptographic hash functions. For MD5, we used Peter Deutsch’s 1999 free implementation that is based on the RFC 1321 specification [4] but does not use the reference implementation given there. For SHA-3 we used Andrey Jivsov’s 2015 code from brainhub.org. As the system is not doing any real application, we implemented client and server, i.e., overt sender and receiver, together with CS and CR in one thread on the same computer, so that they transfer passwords through memory instead of an insecure network. In addition, client and server do no work besides computation of passwords. Hence, this implementation can be considered an extreme test with respect to stealthiness. The covert sender and receiver are placed directly with the client (sender) and server (receiver).

The covert channel transfers a null-terminated character string. We use $v=64$ symbols with the following coding. Lower case letters are converted into upper case letters. ASCII characters 1 to 31 and from 95 onward are converted to blanks (ASCII character 32). ASCII characters 32 to 94, comprising upper case letters, digits and some punctuation marks, are converted to symbols 0 to 62, and ASCII character 0 (termination symbol) is converted to symbol 63. Please note that for the purpose of embedding into the binary hash value, we denote by symbol i a bit string of length m where only bit i is set to 1.

If encryption is used, then we employ a stream cipher that produces key stream symbols in the range 0 to 62, and encrypt by adding symbol and key symbol modulo 63, while termination symbol 63 remains unaltered. As the stream cipher, we employ the same cryptographic hash function as used in the OTP application. The seed is the cryptographic key, and we repeatedly hash. The bytes from the produced hash values are taken as modulo 63 and used as key stream symbols.

All experiments were performed on a Dell Latitude 5500 notebook with an Intel Core i5-8265U CPU at 1.6 GHz and 8 Gibibytes of main memory, running a Windows 10 operating system. We used gcc version 9.2.0 as the compiler, without activating optimizations.

5.1. Performance

To measure the performance impact of the covert channel, especially on the receiver, we use a hash chain of length $n=\mathrm{16,384}$ and a string of length $t=\mathrm{16,382}$ (plus termination symbol), i.e., we embed a symbol in each password except the first. As seed s, we use the string Wonderful seed for Hash Chain. As the secret message, we use a string solely comprising the repeated letter ‘?’ (symbol 31). As the cryptographic key, we use the same string as for the seed.

The secret message is chosen such that, no matter if we use encryption or not, the number of hash function evaluations by CR is 32 (on average if encryption is used, with standard deviation 18), as we use only 63 of the 64 possible symbols during the message, and can ignore the influence for recognizing the last symbol because of the message length.

The results can be seen in Table 1. If a CC is used, the runtime is notably higher than without, while the runtimes for CC with encryption only marginally deviate from runtimes for CC without encryption. The difference between runtimes with and without CC, divided by $32·n$, amounts to 0.63 $\mathsf{\mu }$s and 12.1 $\mathsf{\mu }$s per evaluation of MD5 and SHA-3, respectively, which, multiplied by n, amounts to about half the runtime without CC.

Table 1. Runtime results of performance test.

OTP Hash Function	Without CC	With CC	With CC and Encrypt.
MD5	0.019 s	0.350 s	0.349 s
SHA-3	0.386 s	6.737 s	6.803 s

5.2. Randomness

To test if the covert channel can be detected by using a random number test suite, the exchanged passwords (with or without CC) were collected into a file of 256 kibibytes (MD5) or 512 kibibytes (SHA-3), respectively. Then we submitted the files to the NIST [44] suite. The results from test 1 of the NIST suite (frequency of zeroes and ones should be close to 0.5 for each), given as p-values, can be seen in Table 2. As the p-values are close to 1, all sequences seem random.

Table 2. p-values from NIST frequency test.

OTP Hash Function	Without CC	With CC	With CC and Encrypt.
MD5	0.968052	0.973558	0.986777
SHA-3	0.864040	0.905754	0.864040

Yet already the results from test 2 (cumulative sums) differ for the sequences, cf. Table 3. Thus we conclude that at least the CC without encryption might be detectable. This hope is fostered because in total 15 tests are available in the NIST suite, so there are more chances to detect CCs than we have explored. However, there is also a downside. Some of the tests need much more data than we provided, and already these data might need a long time to be collected. If we imagine that each minute an authentication takes place, then 11.3 days are needed to collect the data. Indeed, this assumption is only valid if authentications take place during night and day without any interruption or reduction of frequency. If limited to eight-hour working days Monday to Friday, it would take almost 7 weeks instead. Thus we have a tradeoff between chance of detection and time to detection.

Table 3. p-values from NIST cumulative sums test, averaged between forward and reverse tests.

OTP Hash Function	Without CC	With CC	With CC and Encrypt.
MD5	0.8212000	0.7555420	0.8038680
SHA-3	0.6928455	0.6198775	0.6928455

5.3. Detectability

If a warden would be capable of observing the originally generated as well as the transmitted hash values, it could compare both values. We assume that such a scenario is rather unlikely but it is of theoretical interest in order to determine the detectability of our channels.

We used the same covert channel as before, but the message comprised $t=\mathrm{16,382}$ letters “A” plus the termination symbol.

As shown in Figure 2, the differences between the covert channel without encryption (denoted as simple) and the legitimate hash values are only visually recognizable if a suitable visualization method (in our case: differences modulo 8) is selected (in large hash values of e.g., 512 bit size, a (randomized) modification of the least significant bits would be invisible on charts that cover the whole range of hash values). The encrypted covert channel’s values (denoted as improved) match those of the legitimate traffic.

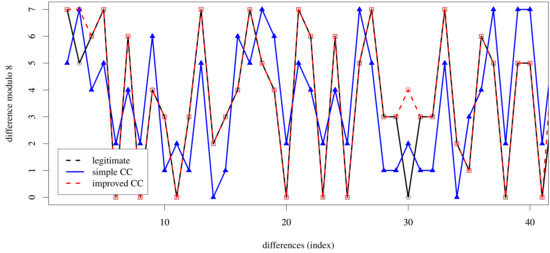
Figure 2. Differences between consecutive hash values for legitimate hash chains and covert channel with and without encryption, denoted as improved and simple, respectively.

However, both covert channels’ hash values are barely distinguishable from legitimate values if the original traffic is not available. Several hash values of both channels are either close to (and a few matching) the legitimate values (simple channel) or partially close and mostly matching (improved channel) while following a pseudo-random distribution typical for hash values. In our tests, approx. 6.7% of the modulo results of the improved channel did not match those of the legitimate traffic while all other values matched exactly.

6. Conclusions

Hash chains are an important element of today’s inter-networked computing systems and are found, for example, in cryptocurrencies and authentication systems. For this reason, the exploitation of hash chains for covert channels is an attractive goal for attackers in several domains. We have presented the first covert channel in hash chains that is plausibly deniable and reversible. We have detailed how to create variants that differ in steganographic bandwidth and stealthiness. We have also presented non-trivial countermeasures against such a covert channel. Our experiments have shown that our channel might be detectable under realistic conditions only if no encryption is applied and authentication data are collected over a longer time-span. Thus, there are limitations both to the use of the covert channel—short-term only—and to the detection or limitation capabilities. The exact time spans will depend on the particular variant of the covert channel deployed, which in turn hangs on the width of the hash function used.

The covert channel has been presented in the context of network communication, yet it is not restricted to that. Instead of using network packets, the covert channel could also use a local system to break a security policy if A authenticates against B over an IPC path to which both CS and CR have access.

Future work will comprise further experiments, e.g., on other implementation variants, including the validation of countermeasures that can either prevent/limit or detect (e.g., with sophisticated machine learning methods) the proposed covert channels, and exploration of further application areas.