Hybrid Encoding Scheme for AMBTC Compressed Images Using Ternary Representation Technique

Abstract

Absolute moment block truncated coding (AMBTC) is a lossy image compression technique aiming at low computational cost, and has been widely studied. Previous studies have investigated the performance improvement of AMBTC; however, they often over describe the details of image blocks during encoding, causing an increase in bitrate. In this paper, we propose an efficient method to improve the compression performance by classifying image blocks into flat, smooth, and complex blocks according to their complexity. Flat blocks are encoded by their block means, while smooth blocks are encoded by a pair of adjusted quantized values and an index pointing to one of the k representative bitmaps. Complex blocks are encoded by three quantized values and a ternary map obtained by a clustering algorithm. Ternary indicators are used to specify the encoding cases. In our method, the details of most blocks can be retained without significantly increasing the bitrate. Experimental results show that, compared with prior works, the proposed method achieves higher image quality at a better compression ratio for all of the test images.

1. Introduction

With the rapid development of imaging technology, digital images are perhaps the most widely used media of the Internet. Because digital images themselves contain significant amounts of spatial redundancy, an efficient lossy image compression technique is required for lower storage requirement and faster transmission. The Joint Photographic Experts Group (JPEG) [1,2], vector quantization (VQ) [3,4], and block truncation coding (BTC) [5,6] are well-known lossy compression methods and have been extensively investigated in the literature. Among these techniques, BTC requires significantly less computation cost than others while offering acceptable image quality. BTC has been widely investigated in the disciplines of remote sensing and portable devices, in which computational costs are limited. BTC was firstly proposed by Delp and Mitchell [7]. This method partitions image into blocks, and each block is represented by two quantized values and a bitmap. Inspired by [7], Lema and Mitchel [8] propose a variant method called absolute moment block truncation coding (AMBTC), which offers a simpler computation than that of BTC.

The applications of AMBTC are studied in video compression [9], image authentication [10,11,12], and image steganography [13,14]. Moreover, some recoverable authentication methods adopt AMBTC codes as the recovery information to recover the tampered regions. Because the recovery codes have to be embedded into the host image, a more efficient coding of AMBTC is always desirable because the burden of the embedment can be reduced and the quality of the recovered regions can be enhanced. To improve the compression efficiency of the AMBTC method, several approaches, including bitmap omission [15], block classification [16,17], and quantized value adjustment [18], are adopted to lower the bitrate while maintaining the image quality. For example, Hu [15] recognizes that if the difference between two quantized values is smaller than a predefined threshold, the bitmap plays an insignificant role in reconstructed image quality. Therefore, Hu employs the bitmap omission approach by neglecting the recording of a bitmap if a block is considered to be flat, and only uses block means to represent the flat block. Chen et al. [17] adopt quadtree partitioning and propose a variable-rate AMBTC compression method for color images. The basic idea of [17] is to partition the image into blocks with various sizes according to their complexities. The AMBTC and bitmap omission technique are then employed to encode the image blocks. In some applications, such as data hiding or image authentication, bitmaps have to be altered to carry some required information, causing a degradation in image quality. Hong [18] optimizes the quantized values so that the impact of bitmap alteration can be reduced. Mathews and Nair [19] propose an adaptive AMBTC method based on edge quantization by considering human visual characteristics. This method separates image blocks into edge and non-edge blocks, and quantized values are calculated based on the edge information. Because the edge characteristics are considered, their method provides better image quality than other AMBTC variants.

Xiang et al. [16] in 2019 proposed a dynamic multi-grouping scheme for AMBTC focusing on improving the reconstructed image quality and reducing the bitrate. Their method partitions an image into non-overlapping blocks. According to the block complexity, varied grouping techniques are designed. An indicator is employed to distinguish the grouping types. In addition, instead of recording the quantized values, the differences between them are recorded so as to reduce the bitrate. Xiang et al.’s method provides better compression performance than those of prior works.

In Xiang et al.’s method, the number of pixel groups of an image block directly affects the reconstructed image quality and bitrate. Their method divides pixels of complex blocks into three or four groups during encoding, which may improve the image quality insignificantly but requires more bits for encoding. In this paper, we propose a ternary representation technique, which uses two thresholds to classify image blocks into three types, namely flat, smooth, and complex. We use the bitmap omission technique [15] to code flat blocks. The adjusted quantized values and an index pointing to one of the representative bitmaps are used to encode the smooth blocks. The complex blocks are encoded using three quantized values and a ternary bitmap. Compared with the AMBTC and Xiang et al.’s work, the proposed method achieves a higher reconstructed image quality with a smaller bitrate.

The reminder of this paper is organized as follows: Section 2 introduces AMBTC and Xiang et al.’s methods. Section 3 introduces the algorithms of this paper in detail. Section 4 presents the experimental results of the proposed method, and concluding remarks are provided in the final section.

2. Related Works

In this section, we briefly introduce AMBTC and Xiang et al.’s methods, which are compared with the proposed method for evaluating the encoding performance.

2.1. The AMBTC Method

The AMBTC method [8] compresses image blocks into two quantized values and a bitmap. The detailed approaches are as follows. Let $I$ be the original image of size $w\times h$ and partition $I$ into non-overlapping blocks ${\left\{I_i\right\}}_{i=0}^{N-1}$ of size $n\times n$, where $N=(w/n)\times (h/n)$ is the total number of blocks. Let $I_{i,j}$ be the $j-\mathrm{th}$ pixel of $i-\mathrm{th}$ block. Therefore, $I_i={\left\{I_{i,j}\right\}}_{j=0}^{n\times n-1}$. For block $I_i$, the averaged value $m_i$ can be calculated by:

$$m_i=\frac{1}{n\times n}{\displaystyle \sum _{j=0}^{n\times n-1}{I}_{i,j}}.$$

(1)

The $j-\mathrm{th}$ bit of bitmap $B_i$, indicated by $B_{i,j}$, is used to indicate the relationship between $I_{i,j}$ and $m_i$. $B_{i,j}$ can be obtained by:

$$B_{i,j}=\{\begin{array}{cc}0,& I_{i,j}<m_i;\\ 1,& I_{i,j}\ge m_i.\end{array}$$

(2)

The lower quantized value $a_i$ and higher quantized value $b_i$ are obtained by averaging the pixels in $I_i$ with values smaller than and larger than or equal to $m_i$, respectively. This can be implemented by sequentially visiting pixels in $I_i$. The lower quantized value $a_i$ is obtained by calculating the averaged value of visited pixels with values smaller than $m_i$. Similarly, the higher quantized value $b_i$ is the averaged values of the other pixels. Therefore, the compressed code ${\Phi }_i$ of $I_i$ is $\{a_i,b_i,B_i\}$. Each block is processed using the same manner, and the AMBTC compressed codes ${\left\{{\Phi }_i\right\}}_{i=0}^{N-1}={\{a_i,b_i,B_i\}}_{i=0}^{N-1}$ of image $I$ are then obtained.

To decode ${\left\{{\Phi }_i\right\}}_{i=0}^{N-1}={\{a_i,b_i,B_i\}}_{i=0}^{N-1}$, blocks ${\left\{I_i^{\prime }\right\}}_{i=0}^{N-1}$ of size $n\times n$ are prepared, where $I_i^{\prime }={\left\{I_{i,j}^{\prime }\right\}}_{j=0}^{n\times n-1}$. The $j-\mathrm{th}$ pixel of $I_i^{\prime }$ can be decoded by:

$$I_{i,j}^{\prime }=\{\begin{array}{ll}{a}_i,& B_{i,j}=0;\\ b_i,& B_{i,j}=1.\end{array}$$

(3)

After all of the image blocks are reconstructed, the image $I^{\prime }$ can then be obtained.

2.2. Xiang et al.’s Method

AMBTC uses the same approach to compress all image blocks. However, the same approach may not suitable for flat and complex blocks. As a result, Xiang et al. proposed an improved scheme to efficiently encode blocks according to their complexity, and achieve a better image quality than that of AMBTC with a satisfactory bitrate.

Let ${\left\{{\Phi }_i\right\}}_{i=0}^{N-1}={\{a_i,b_i,B_i\}}_{i=0}^{N-1}$ be the AMBTC compressed code of the original image $I={\left\{I_i\right\}}_{i=0}^{N-1}$. To determine the complexity of block $I_i$, a threshold ${\tau }_0$ is set. If $b_i-a_i\le {\tau }_0$, the variations of pixel values in block $I_i$ are relatively small. Therefore, all the pixels in this block are categorized as one group. In this case, the block mean $m_i$ is calculated, and this block is encoded by ${(m_i)}_2$, which is the 8-bit binary representation of $m_i$.

If $b_i-a_i>{\tau }_0$, the variations of pixels in block $I_i$ are large and these pixels need to be regrouped to achieve a better reconstructed image quality. Let $G_i^0$ and $G_i^1$ be the group of pixels with $B_{i,j}=0$ and $B_{i,j}=1$, respectively. Apply the AMBTC method to $G_i^0$ and $G_i^1$ to obtain codes ${\Phi }_i^0=\{a_i^0,b_i^0,B_i^0\}$ and ${\Phi }_i^1=\{a_i^1,b_i^1,B_i^1\}$. According to a given threshold $d_{\min }$, this method uses the following rules to determine whether $G_i^0$ and $G_i^1$ should be regrouped:

Rule 1: If $b_i^0-a_i^0>{\tau }_0$ and the total number of pixels in $G_i^0$ is greater than $d_{\min }$.

Rule 2: If $b_i^1-a_i^1>{\tau }_0$ and the total number of pixels in $G_i^1$ is greater than $d_{\min }$.

If neither rule is met, block $I_i$ does not need to be further divided. Otherwise, block $I_i$ will be sub-divided into three or four groups using the following rules:

(1)

If only rules 1 or 2 are met, group $G_i^0$ or $G_i^1$ needs to be subdivided. The number of pixels needing to be subdivided is denoted by $P_i$, and $P_i-\mathrm{bit}$ bitmap $B_i^0$ or $B_i^1$ has to be used to record the bitmap of $G_i^0$ or $G_i^1$. In this case, block $I_i$ is eventually divided into three groups.

(2)

If both rules 1 and 2 are met, both $G_i^0$ and $G_i^1$ need to be subdivided, and block $I_i$ is eventually divided into four groups. Bitmap $B_i^0$ and $B_i^1$ have to be recorded to maintain the grouping information.

Xiang et al.’s method uses a 2-bit indicator $I_{ND}$ to record grouping information of $I_i$. When block $I_i$ is divided into one to four groups, the indicator $I_{ND}$ is set to be ${00}_2$, ${01}_2$, ${10}_2$, and ${11}_2$, respectively. Moreover, if $I_i$ needs to be divided into three groups, an extra indicator is required to show which group is subdivided. Specifically, if $G_i^0$ is sub-divided, then $J_i=0$. On the contrary, if $G_i^1$ is sub-divided, then $J_i=1$.

To record the quantized values, Xiang et al.’s method records the smallest quantized value of a block using 8 bits, and utilizes a difference encoding scheme (DES) to encode the difference $d_i$ between two quantized values. In DES, if $d_i<\gamma$, where $\gamma$ is a predefined threshold, $d_i$ is recorded using ${\log }_2(\gamma )$ bits. Otherwise, $d_i$ is recorded using $\lceil {\log }_2(\sigma )\rceil$ bits, where $\sigma$ is the maximum difference between quantized values in all blocks. An extra indicator $Y_i$ is used to distinguish these two methods. That is, if $d_i<\gamma$, $Y_i=0$ is set. Otherwise, $Y_i=1$. The number of bits $R_i$ used to record the difference can be expressed as:

$$R_i=\{\begin{array}{cc}{\log }_2(\gamma )+1,& d_i<\gamma ;\\ \lceil {\log }_2(\sigma )\rceil +1,& d_i\ge \gamma .\end{array}$$

(4)

We use the symbol ${(x-y)}_2$ to represent the R-bit encoded result of the difference between $x$ and $y$ using DES. For example, if $x=40$, $y=28$, and $\gamma =64$, then $d_i=12<\gamma$. Therefore, $R=7$ and the encoding result is ${(40-28)}_2=0_2\left|\right|{001100}_2$, where $\left|\right|$ is the concatenation operator.

The compressed code and the number of bits required to record blocks $I_i$ of different grouping cases are summarized in Table 1. Each block is compressed using the same procedures and the final compressed code stream $C{S}_f$ of image $I$ is obtained.

Table 1. Number of bits required to record a compressed block.

Number of Groups	$\mathbf{Compressed}\mathbf{Code}\mathbf{of}{\mathit{I}}_{\mathit{i}}$	Number of Bits
1	$\{{00}_2,{(m_i)}_2\}$	$2+8$
2	$\{{01}_2,(a_i{)}_2,{(b_i-a_i)}_2,B_i\}$	$2+8+R_i+n\times n$
3	$\{{10}_2,(a_i^0{)}_2,{(b_i^0-a_i^0)}_2,{(b_i-b_i^0)}_2,B_i,J_i,B_i^0\}$ or	$2+8+2R_i+n\times n+1+P_i$
	$\{{10}_2,(a_i{)}_2,{(a_i^1-a_i)}_2,{(b_i^1-a_i^1)}_2,B_i,J_i,B_i^1\}$
4	$\{{11}_2,{(a_i^0)}_2,{(b_i^0-a_i^0)}_2,{(a_i^1-b_i^0)}_2,{(b_i^1-a_i^1)}_2,B_i,B_i^0,B_i^1\}$	$2+8+3R_i+2\times n\times n$

To decode $C{S}_f$, the 2-bit indicator $I_{ND}$ is read. According to the read bits, four possible compressed codes shown in Table 1 with different lengths can be extracted. The image blocks can be reconstructed from the compressed codes, and the decompressed image can be obtained. The detailed decoding procedures can be referred to [16].

3. Proposed Method

The traditional AMBTC compression method uses the same number of bits to compress each block. However, coding in this way requires more bits than necessary for flat blocks and neglects too much image detail for complex blocks. Xiang et al.’s method improves AMBTC, resulting in better compression effects for both flat and complex blocks. However, in the processing of complex blocks, Xiang et al.’s method reconstructs the gray values of the image block by four quantized values. Although the quality of the reconstructed block is improved, it requires quantized values to be recorded and bitmaps with more bits. In addition, Xiang et al. adopt the traditional AMBTC method to compress the smooth blocks, which may increase the cost of recording bitmaps and quantized values.

In this paper, we propose a more effective solution by classifying image blocks into flat, smooth, and complex blocks based on thresholds ${\tau }_0$ and ${\tau }_1$ (${\tau }_0\le {\tau }_1$). Let ${\Phi }_i=\{a_i,b_i,B_i\}$ be the AMBTC codes of $I_i$. If $b_i-a_i\le {\tau }_0$, $I_i$ is classified as a flat block. Because pixel variations in a flat block are small, all pixels in a flat block can be simply reconstructed by their mean to a satisfactory visual quality. If ${\tau }_0<b_i-a_i<{\tau }_1$, $I_i$ is classified as a smooth block. For the smooth block, we use a clustering algorithm to obtain representative bitmaps, and the original bitmaps are replaced by the indices pointing to the obtained bitmap. The two quantized values are also adjusted to reduce the error caused by the bitmap replacement. If $b_i-a_i\ge {\tau }_1$, $I_i$ is classified as a complex block. We use three quantized values and a ternary map to represent the complex block to maintain better texture details. The encoding algorithms of these three types of blocks will be presented in the following sections.

3.1. Encoding of Flat Blocks

The pixel values of a flat block $I_i$ (i.e., $b_i-a_i\le {\tau }_0$) are relatively close, and thus the bitmap plays an insignificant role in reconstructing the image block. Therefore, we omit the recording of the quantization value in addition to the bitmap, and use an 8-bit mean value ${(m_i)}_2$ to represent the flat block, where:

$$m_i=\mathrm{round}\left(\frac{b_i+a_i}{2}\right)$$

(5)

and $\mathrm{round}(x)$ is the function rounding $x$ to the nearest integer.

3.2. Encoding of Smooth Blocks

If ${\tau }_0<b_i-a_i<{\tau }_1$, the fluctuation of pixel values of block $I_i$ is more than that of a flat block. Therefore, we refer to $I_i$ as a smooth block. To reduce the bitrate, a codebook consisting of the $k$ most representative bitmaps (codewords) is found, and the bitmap of the smooth block will be replaced by an index pointing to one of the codewords in the codebook. We use the k-means algorithm [20] to obtain the $k$ most representative bitmaps. Let ${\{a_s,b_s,B_s\}}_{s=0}^{N_s-1}$ be the set of AMBTC codes satisfying ${\tau }_0<b_i-a_i<{\tau }_1$ for $0\le i\le N-1$, where $N_s$ is the number of smooth blocks. Firstly, an initial codebook ${\left\{C_{\alpha }^0\right\}}_{\alpha =0}^{k-1}$ is constructed by randomly selecting $k$ bitmaps from ${\left\{B_s\right\}}_{s=0}^{N_s-1}$, where $k$ is much less than $N_s$. Secondly, the bitmaps ${\left\{B_s\right\}}_{s=0}^{N_s-1}$ are classified into $k$ clusters according to the similarities between ${\left\{B_s\right\}}_{s=0}^{N_s-1}$ and ${\left\{C_{\alpha }^0\right\}}_{\alpha =0}^{k-1}$. That is, if $B_s$ has more bits identical to $C_{\alpha }^0$ than other codewords, then $B_s$ is classified into group $\alpha$, where $0\le \alpha \le k-1$. Thirdly, ${\left\{B_s\right\}}_{s=0}^{N_s-1}$ of the same group are averaged and rounded to obtain the updated codebook ${\left\{C_{\alpha }^1\right\}}_{\alpha =0}^{k-1}$. Repeat the classification process $t$ times and the final representative bitmaps ${\left\{C_{\alpha }^t\right\}}_{\alpha =0}^{k-1}$ are obtained. Normally, setting $t=6$ can already obtain a satisfactory result. We denote the final representative bitmaps as ${\left\{C_{\alpha }^{}\right\}}_{\alpha =0}^{k-1}$. Once the classification process is completed, the classification results ${\left\{{\alpha }_s^{\ast }\right\}}_{s=0}^{N_s-1}$ of bitmaps ${\left\{B_s\right\}}_{s=0}^{N_s-1}$ are also obtained. Note that the codeword with index ${\alpha }_s^{\ast }$ has the nearest distance to $B_s$, that is:

$${\alpha }_s^{\ast }=\underset{\alpha }{\arg \min }{\left({\displaystyle \sum _{j=0}^{n\times n-1}{(B_{s,j}-C_{\alpha ,j})}^2}\right)}^{1/2}$$

(6)

where $B_{s,j}$ and $C_{\alpha ,j}$ represent the $j-\mathrm{th}$ element of $B_s$ and $C_{\alpha }$, respectively. Instead of recording ${\left\{B_s\right\}}_{s=0}^{N_s-1}$, the proposed method uses the binary representation of ${\left\{{\alpha }_s^{\ast }\right\}}_{s=0}^{N_s-1}$ as the required bitmap information. Therefore, the bits required to record the bitmap are reduced from $n\times n$ bits to ${\log }_2(k)$ bits. To successfully decode the bitmap, we must have cluster centers ${\left\{C_{\alpha }\right\}}_{\alpha =0}^{k-1}$ and cluster indices ${\left\{{\alpha }_s^{\ast }\right\}}_{s=0}^{N_s-1}$. Therefore, ${\left\{C_{\alpha }\right\}}_{\alpha =0}^{k-1}$ must be included as part of the compressed codes.

When decoding a smooth block, because we use cluster center $C_{{\alpha }_s^{\ast }}$ to replace the original bitmap $B_s$, the quality of the reconstructed image block will be reduced. To minimize the reduced quality, a quantized value adjustment (QA) technique [18] is employed. QA is a technique originally used in a data hiding technique to reduce the distortions of the reconstructed AMBTC block when the original bitmap is replaced by secret data. Because bits in the bitmap are altered, distortions of the reconstructed block are inevitable. QA subtly adjusts the quantized values by counting the bit difference between the original bitmap and secret data. In the proposed method, the original bitmap is replaced by a cluster center, which resembles the situations in which the bitmap is replaced by secret data. Therefore, the QA technique can be applied in the proposed method. To find the minimum distortion, the QA technique adjusts $a_s$ and $b_s$ to ${\widehat{a}}_s$ and ${\widehat{b}}_s$ by calculating:

$${\widehat{a}}_s=\frac{a_s{\rho }_{00}+b_s{\rho }_{10}}{{\rho }_{00}+{\rho }_{10}}$$

(7)

and:

$${\widehat{b}}_s=\frac{a_s{\rho }_{01}+b_s{\rho }_{11}}{{\rho }_{01}+{\rho }_{11}}$$

(8)

respectively, where ${\rho }_{pq}$ is the number of bits with $B_{s,j}=p$ and $C_{{\alpha }_s^{\ast },j}=q$, $(p,q)\in \{0,1\}$. For example, ${\rho }_{01}$ indicates the number of bits with $B_{s,j}=0$ and $C_{{\alpha }_s^{\ast },j}=1$. After adjustment of quantized values, the distortion due to the bitmap replacement will be smaller than that without adjustment.

3.3. Encoding of Complex Blocks

Blocks with $b_i-a_i\ge {\tau }_1$ are classified as complex blocks. Let ${\left\{I_c\right\}}_{c=0}^{N_c-1}$ be the set of $N_c$ complex blocks in $I$. For a given complex block $I_c={\left\{I_{c,j}\right\}}_{j=0}^{n\times n-1}$, the proposed method uses the k-means clustering algorithm to obtain three most representative quantized values $\{q_c^0,q_c^1,q_c^2\}$ and a ternary map $T_c={\left\{T_{c,j}\right\}}_{c=0}^{n\times n-1}$, where $T_{c,j}$ is a ternary digit ranging from 0 to 2 used to indicate which quantized value should be used to reconstruct the $j-\mathrm{th}$ pixel of $I_c$. Because the value of $T_{c,j}$ is equally distributed over 0 to 2, we can simply encode the ternary digits $0_3$, $1_3$, and $2_3$ by $0_2$, ${10}_2$, and ${11}_2$, respectively. We assume the encoded result of $T_c$ is ${T^{\prime }}_c$ of L-bit. Once the decoder has ${\left\{{T^{\prime }}_c\right\}}_{c=0}^{N_c-1}$ and ${\{q_c^0,q_c^1,q_c^2\}}_{c=0}^{N_c-1}$, blocks ${\left\{I_c\right\}}_{c=0}^{N_c-1}$ can be reconstructed.

When encoding a $4\times 4$ ternary map, the average number of bits required in the proposed method is:

$$\frac{1\times 16}{3}+\frac{2\times 2\times 16}{3}=26.67\mathrm{bits}.$$

Theoretically, recording 16 ternary digits requires $\lceil 16\times {\log }_{2}3\rceil =26$ bits, which is almost the same as in the proposed method. Therefore, the encoding of the ternary map used in the proposed method is effective.

3.4. Encoding Procedures

This section describes the procedures of the proposed method. To distinguish the encoding methods of three types of image blocks, an indicator is prepended to the code stream of each encoded block. The indicators $0_2$,${10}_2$, and ${11}_2$ are used to indicate a flat, smooth, and complex block is encoded, respectively. The detailed encoding procedures are shown as follows:

Input:

Original image $I$, block size $n\times n$, thresholds ${\tau }_0$ and ${\tau }_1$, parameter $\gamma$, and cluster size $k$.

Output:

Code stream $C{S}_f$.

Step 1:

Partition the original image $I$ into blocks ${\left\{I_i\right\}}_{i=0}^{N-1}$ of size $n\times n$. Encode ${\left\{I_i\right\}}_{i=0}^{N-1}$ using the AMBTC encoder and obtain codes ${\Phi }_i={\{a_i,b_i,B_i\}}_{i=0}^{N-1}$, as described in Section 2.1.

Step 2:

Scan codes ${\{a_i,b_i,B_i\}}_{i=0}^{N-1}$. Let ${\left\{B_s\right\}}_{s=0}^{N_s-1}$ be the bitmap of smooth blocks. Clustering ${\left\{B_s\right\}}_{s=0}^{N_s-1}$ into $k$ groups using the k-means clustering algorithm, we obtain $k$ cluster centers ${\left\{C_{\alpha }\right\}}_{\alpha =0}^{k-1}$ and $N_s$ cluster indices ${\left\{{\alpha }_s^{\ast }\right\}}_{s=0}^{N_s-1}$. Concatenate the binary representation of ${\left\{C_{\alpha }\right\}}_{\alpha =0}^{k-1}$ and obtain the concatenated code stream $C{S}_A$. The $N_s$ pairs of adjusted quantized values ${\{{\widehat{a}}_s,{\widehat{b}}_s\}}_{s=0}^{N_s-1}$ of smooth blocks are also obtained, as described in Section 3.2. Similarly, quantized values ${\{q_c^0,q_c^1,q_c^2\}}_{c=0}^{N_c-1}$ and ternary maps ${\left\{T_c\right\}}_{c=0}^{N_c-1}$ of complex blocks are also obtained, as described in Section 3.3.

Step 3:

Scan codes ${\{a_i,b_i,B_i\}}_{i=0}^{N-1}$ again and perform the encoding according to the cases listed below:

Case 1:

If $b_i-a_i\le {\tau }_0$, a flat block is visited and the code stream of block $I_i$ is $C{S}_i=0_2\left|\right|(m_i{)}_2$.

Case 2:

If ${\tau }_0<b_i-a_i<{\tau }_1$, a smooth block is visited. Extract ${\widehat{a}}_s$, ${\widehat{b}}_s$, and ${\alpha }_s^{\ast }$ from ${\{{\widehat{a}}_s,{\widehat{b}}_s,{\alpha }_s^{\ast }\}}_{s=0}^{N_s-1}$ obtained in Step 2, and block $I_i$ is encoded by $C{S}_i={10}_2\left|\right|({\widehat{a}}_s{)}_2\left|\right|{({\widehat{b}}_s-{\widehat{a}}_s)}_2\left|\right|{({\alpha }_s^{\ast })}_2$. Note that ${({\widehat{b}}_s-{\widehat{a}}_s)}_2$ is encoded using the DES, as described in Section 2.2.

Case 3:

If $b_i-a_i\ge {\tau }_1$, block $I_i$ is a complex one. Extract $q_c^0$, $q_c^1$, $q_c^2$, and $T_c$ from ${\{q_c^0,q_c^1,q_c^2,T_c\}}_{c=0}^{N_c-1}$ obtained in Step 2, and block $I_i$ is encoded by $C{S}_i={11}_2\left|\right|(q_c^0{)}_2\left|\right|{(q_c^1-q_c^0)}_2\left|\right|{(q_c^2-q_c^1)}_2\left|\right|{T^{\prime }}_c$. Note that ${(q_c^1-q_c^0)}_2$ and ${(q_c^2-q_c^1)}_2$ are encoded using the DES (see Section 2.2).

Step 4:

Repeat Step 3 until the code stream ${\left\{C{S}_i\right\}}_{i=0}^{N-1}$ of blocks ${\left\{I_i\right\}}_{i=0}^{N-1}$ are obtained. Concatenate ${\left\{C{S}_i\right\}}_{i=0}^{N-1}$, we have the concatenated code stream $C{S}_B$.

Step 5:

Concatenate $C{S}_A$ and $C{S}_B$; we obtain the final code stream $C{S}_f$ of image $I$, i.e., $C{S}_f=C{S}_A\left|\right|C{S}_B$.

The encoding of a given image block and the number of required bits for each block types are shown in Figure 1.

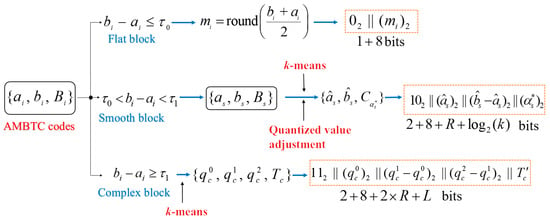
Figure 1. Illustration of image block encoding.

We take a simple example to illustrate the encoding of smooth and complex blocks. Let $I_0$ be a $4\times 4$ block to be encoded, as shown in Figure 2a. Suppose ${\tau }_0=4$, ${\tau }_1=16$, $\gamma =64$, $\sigma =128$, and $k=128$ are used in this example. The AMBTC compressed code of $I_0$ is $\{a_0,b_0,B_0\}=\{28,40,111011101100{1100}_2\}$, and $B_0$ is depicted in Figure 2b. Because ${\tau }_0<b_0-a_0<{\tau }_1$, $I_0$ is a smooth block. Assume ${\alpha }_0^{\ast }=43$ and $C_{43}=101001100101{0100}_2$ (see Figure 2c). By comparing $B_0$ and $C_{43}$, we have ${\rho }_{00}=5$, ${\rho }_{01}=1$, ${\rho }_{10}=4$, and ${\rho }_{11}=6$. Using Equations (7) and (8), we have ${\widehat{a}}_0=33$ and ${\widehat{b}}_0=38$. Because ${\widehat{b}}_0-{\widehat{a}}_0=5<\gamma$, we have $Y=0$. Because ${({\widehat{a}}_0)}_2={00100001}_2$, ${({\widehat{b}}_0-{\widehat{a}}_0)}_2=0\left|\right|{000101}_2$, and ${({\alpha }_0^{\ast })}_2={0101011}_2$, the code stream of $I_0$ should be $C{S}_0=10\left|\right|00100001\left|\right|0\left|\right|000101\left|\right|{0101011}_2$.

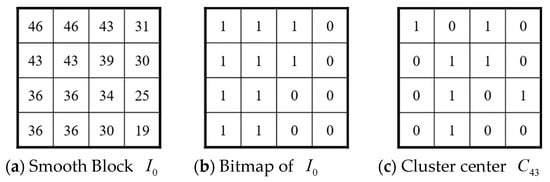
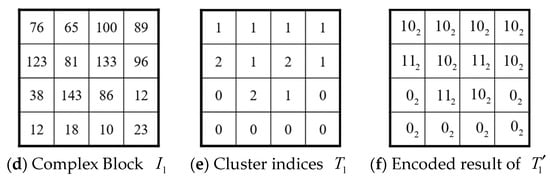
Figure 2. An example of image encoding.

Figure 2d shows another block $I_1$ to be encoded. For this block, quantized values $a_1=25$ and $b_1=103$ of the AMBTC code are calculated. Because $b_1-a_1\ge {\tau }_1$, $I_1$ is regarded as a complex block. Suppose after applying the k-means clustering algorithm to $I_1$, we obtain three quantized values $\{q_1^0,q_1^1,q_1^2\}=\{19,85,133\}$ and the ternary cluster indices of pixels $T_1=\{1111212102100000\}$, as shown in Figure 2e. The difference between the first two quantized values is $q_1^1-q_1^0=66>\gamma$. Therefore, indicator $Y_{1,0}=1$ should be placed in front of the ${\log }_2(\sigma )=7-\mathrm{bit}$ binary representation of 66 (i.e., $1\left|\right|{1000010}_2$). Similarly, because $q_1^2-q_1^1=48<\gamma$, indicator $Y_{1,1}=0$ should be placed in front of the ${\log }_2(\gamma )=6-\mathrm{bit}$ binary representation of 48 (i.e., ${0\left|\right|110000}_2$). Finally, the ternary cluster indices $T_1$ are encoded by $1010101011101110011100{0000}_2$, which is illustrated in Figure 2f. Therefore, according to Step 3 of Case 3 in Section 3.4, the code stream of block $I_1$ should be $C{S}_1=11\left|\right|00010011\left|\right|1\left|\right|1000010\left|\right|0\left|\right|110000\left|\right|1010101011101110{0111000000}_2$.

3.5. Decoding Procedures

In decoding, data bits are sequentially read and decoded, and image blocks are reconstructed by decoding the read data bits. The detailed steps of decoding are listed as follows:

Input:

Code stream $C{S}_f$, block size $n\times n$, parameter $\gamma$, $\sigma$, and cluster size $k$.

Output:

Decompressed image $I^{\prime }={\left\{I_i^{\prime }\right\}}_{i=0}^{N-1}$.

Step 1:

Extract $C{S}_A$ from $C{S}_f$ and reconstruct $k$ cluster centers ${\left\{C_{\alpha }\right\}}_{\alpha =0}^{k-1}$.

Step 2:

Extract one bit $b$ from $C{S}_f$. According to the extracted bit, one of the following decoding cases is then performed:

Case 1:

If $b=0_2$, the block to be reconstructed is a flat block. All the pixel values of block $I_i^{\prime }$ are the decimal value of the next 8 bits extracted from $C{S}_f$.

Case 2:

If $b=1_2$ and the next extracted bit is $0_2$, the block to be reconstructed is a smooth block. Extract the next 8 bits and convert them to a decimal value to obtain the quantized value ${\widehat{a}}_s$. Read the next bit from $C{S}_f$. If the read bit is $0_2$, ${\widehat{b}}_s$ is reconstructed by the decimal value of the next ${\log }_2(\gamma )$ bits plus ${\widehat{a}}_s$. Otherwise, ${\widehat{b}}_s$ is reconstructed by the decimal value of next $\lceil {\log }_2(\sigma )\rceil$ bits plus ${\widehat{a}}_s$. The clustering index ${\alpha }_s^{\ast }$ is the decimal value of next $k$ bits, and the bitmap $C_{{\alpha }_s^{\ast }}$ can be obtained from ${\left\{C_{\alpha }\right\}}_{\alpha =0}^{k-1}$. Using the AMBTC decoder to decode $\{{\widehat{a}}_s,{\widehat{b}}_s,C_{{\alpha }_s^{\ast }}\}$, the image block can be reconstructed.

Case 3:

If $b=1_2$ and the next extracted bits is $1_2$, the block to be reconstructed is a complex block. Extract the next 8 bits and convert them to a decimal value to obtain the quantized value $q_c^0$. Read the next bit from $C{S}_f$. If the read bit is $0_2$, $q_c^1$ is reconstructed by the $q_c^0$ plus the decimal value of the next ${\log }_2(\gamma )$ bits; otherwise, $q_c^1$ is reconstructed by the decimal value of the next $\lceil {\log }_2(\sigma )\rceil$ bits plus $q_c^0$. Using a similar manner, $q_c^2$ is reconstructed. To reconstruct the ternary map ${\left\{T_{c,j}\right\}}_{j=0}^{n\times n-1}$, we start from $j=0$ to $j=n\times n-1$ and repeat the following process: Read a bit $b_0$ from $C{S}_f$. If $b_0=0_2$, we have $T_{c,j}=0$. Otherwise, read the next bit $b_1$ from $C{S}_f$. If $b_0{b}_1={10}_2$, $T_{c,j}=1$. If $b_0{b}_1={11}_2$, $T_{i,j}=2$. Once we have $\{q_c^0,q_c^1,q_c^2\}$ and ${\left\{T_{c,j}\right\}}_{j=0}^{n\times n-1}$, the j-th pixel of the image block is reconstructed by $q_c^0$, $q_c^1$, or $q_c^2$ if $T_{c,j}=0$, 1, or 2, respectively.

Step 3:

Repeat Step 2 until all image blocks are reconstructed, and the final decompressed image $I^{\prime }$ is obtained.

We continue the example given in Section 3.4 to illustrate the decoding process. The detailed process and the decoded result are depicted in Figure 3. To decode the code stream $C{S}_0=10\left|\right|00100001\left|\right|0000101\left|\right|{0101011}_2$, because the first bit is $1_2$ and the second bit is $0_2$, the to-be-reconstructed block is a smooth block. Extract the next 8 bits from $C{S}_0$ and convert them into decimal representation; we obtain ${\widehat{a}}_0=33$. The next extracted bit is 0. Therefore, the difference $d_0=5$ is the decimal value of the next ${\log }_2(\gamma )$ bits, and we have ${\widehat{b}}_0={\widehat{a}}_0+5=38$. Finally, extract ${\log }_2(k)$ bits and convert them to a decimal value; we have ${\alpha }_s^{\ast }=43$ and the bitmap $C_{43}$ is obtained. The image block can then be constructed by decoding $\{{\widehat{a}}_0,{\widehat{b}}_0,C_{43}\}$ using the AMBTC decompression technique.

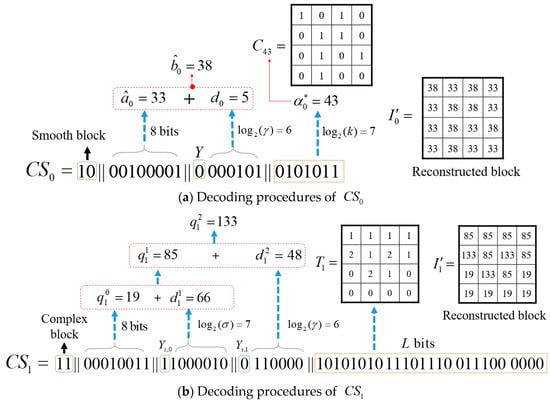
Figure 3. Illustration of the decoding procedures of image blocks.

To decode $C{S}_1=11\left|\right|00010011\left|\right|11000010\left|\right|0110000\left|\right|1010101011101110{0111000000}_2$, because the first two extracted bits are ${11}_2$, the block to be decompressed is a complex block. Extract 8 bits and $q_1^0=19$ is the decimal value of these 8 bits. The next bit is $1_2$; therefore, $d_1^1=66$ is the decimal value of the next $\lceil {\log }_2(\sigma )\rceil =7$ bits and $q_1^1=19+66=85$ can be obtained. Similarly, the next extracted bit is $0_2$; therefore, $d_1^2=48$ is obtained by converting the next ${\log }_2(\gamma )=6$ bits to their decimal value, and $q_1^2=85+48=133$ can be obtained. Finally, we have to reconstruct ${\left\{T_{1,j}\right\}}_{j=0}^{15}$ from the remaining bits. Because the next extracted bit is $1_2$, we extract one more bit, which is $0_2$. Therefore, $T_{1,0}=1$ is obtained. The remaining 15 ternary digits ${\left\{T_{1,j}\right\}}_{j=1}^{15}$ can be decoded in the similar manner. Once we have $\{q_1^0,q_1^1,q_1^2\}$ and ${\left\{T_{1,j}\right\}}_{j=0}^{15}$, block $I_1^{\prime }$ can be reconstructed. Figure 3b illustrates the decoding process of $C{S}_1$.

4. Experimental Results

In this section, we conduct several experiments to show the effectiveness and applicability of the proposed scheme. We take eight grayscale images of size $512\times 512$, namely, Lena, Jet, Baboon, Tiffany, Boat, Stream, Peppers and House, as the test images, as shown in Figure 4. These images can be obtained from the USC-SIPI image database [21]. We use the peak signal-to-noise ratio (PSNR) and bitrate to measure the performance. The PSNR is calculated by:

$$\mathrm{PSNR}=10{\log }_{10}\frac{{255}^2}{\frac{1}{n\times n\times N}{\displaystyle \sum {}_{i=0}^{n\times n\times N-1}{(x_i-{x^{\prime }}_i)}^2}},$$

(9)

where $x_i$ and ${x^{\prime }}_i$ represent the pixel values of the original and decompressed images, respectively. The bitrate metric is measured by the number of bits required to record each pixel (i.e., bit per pixel, bpp).

Figure 4. Eight test images.

In all of the experiments, we set ${\tau }_0=4$ because the flat blocks under this setting show no apparent block boundary artifacts.

4.1. The Performance of the Proposed Method

Because the number of cluster centers k and threshold greatly affect the coding efficiency in the application of the quantized value adjustment (QA) technique [18], we evaluate how the QA technique and these parameters influence the bitrate and image quality in this section.

4.1.1. Coding Efficiency Comparisons

In the coding of smooth blocks, the original bitmaps of smooth blocks are used to obtain the cluster centers, and the quantized values are adjusted using the QA technique to lower the distortions. Table 2 and Table 3 show how the QA technique improves the image quality when the block size is set to $4\times 4$ and $8\times 8$, respectively. In this experiment, ${\tau }_1=16$ and $\gamma =32$ are set. As seen from the tables, the QA technique effectively enhances the quality of reconstructed images for every $k$. For example, in Table 2 and $k=128$, the averaged quality of the reconstructed images with and without the QA technique is 34.63 and 34.52 dB, respectively. The averaged quality has improved by $34.63-34.52=0.11$ dB. Similarly, in Table 3 when $k=128$, the PSNR improvement is $31.86-31.76=0.10$ dB. Therefore, the QA technique indeed reduces the distortion caused by replacing the original bitmap with a cluster center.

Table 2. Peak signal-to-noise ratio (PSNR) and bitrate of compressed images with $4\times 4$ block size.

Images	$\mathit{k}=128$			$\mathit{k}=256$			$\mathit{k}=512$
	Bitrate	w/o QA	w/QA	Bitrate	w/o QA	w/QA	Bitrate	w/o QA	w/QA
Lena	1.60	35.83	35.96	1.63	35.95	36.05	1.68	36.07	36.15
Jet	1.52	35.85	35.91	1.55	35.92	35.97	1.58	35.99	36.03
Baboon	2.73	30.80	30.85	2.76	30.85	30.89	2.79	30.89	30.93
Tiffany	1.47	37.18	37.38	1.50	37.39	37.55	1.55	37.57	37.69
Boat	2.00	33.97	34.13	2.05	34.15	34.27	2.10	34.27	34.36
Stream	2.68	32.43	32.49	2.70	32.49	32.53	2.73	32.55	32.57
Peppers	1.68	35.34	35.57	1.73	35.52	35.71	1.78	35.71	35.85
House	1.95	34.73	34.78	1.97	34.79	34.82	2.01	34.85	34.88
Average	1.95	34.52	34.63	1.99	34.63	34.72	2.03	34.74	34.81

Table 3. PSNR and bitrate of compressed images with $8\times 8$ block size.

Images	$\mathit{k}=128$			$\mathit{k}=256$			$\mathit{k}=512$
	Bitrate	w/o QA	w/QA	Bitrate	w/o QA	w/QA	Bitrate	w/o QA	w/QA
Lena	0.97	32.96	33.07	1.01	33.03	33.12	1.08	33.13	33.21
Jet	1.00	32.77	32.82	1.04	32.83	32.86	1.11	32.90	32.92
Baboon	1.79	28.67	28.72	1.83	28.72	28.75	1.89	28.80	28.82
Tiffany	0.89	34.63	34.81	0.93	34.79	34.93	1.00	34.99	35.09
Boat	1.30	31.17	31.32	1.34	31.24	31.37	1.41	31.36	31.46
Stream	1.89	29.79	29.82	1.92	29.84	29.86	1.99	29.93	29.93
Peppers	1.01	32.59	32.74	1.05	32.66	32.80	1.12	32.79	32.90
House	1.36	31.52	31.57	1.39	31.57	31.61	1.46	31.65	31.67
Average	1.28	31.76	31.86	1.31	31.83	31.91	1.38	31.94	32.00

Table 2 and Table 3 also reveal that the increase in cluster size $k$ also enhances the image quality. For example, in Table 3 when $k=128$, the averaged PSNR of eight test images is 31.86 dB. When $k=256$ and 512, the PSNR increases $31.91-31.86=0.05$ dB and $32.00-31.86=0.14$ dB, respectively. The reason is that a larger cluster size provides a greater chance to reduce the difference between the cluster centers and original bitmaps.

To evaluate how threshold ${\tau }_1$ affects the performance of the QA, we plot the gain of PSNR when using the QA for various ${\tau }_1$ with $k=128$ and 512. The results are shown in Figure 5. Note that, in this experiment, a block size of $4\times 4$ is set.

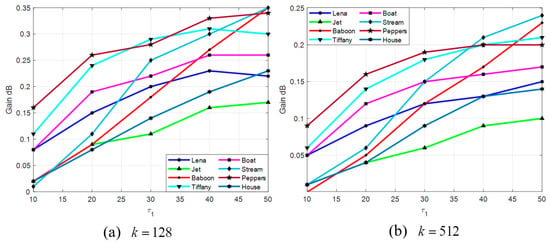
Figure 5. The gain of PSNR when the quantized value adjustment (QA) technique is applied.

Figure 5a,b shows that the gain in PSNR increases as ${\tau }_1$ increases, and this is mainly because the number of smooth blocks also increases as ${\tau }_1$ increases. Because more blocks are classified as smooth for larger ${\tau }_1$, more blocks will be processed using the QA technique. As a result, the gain in PSNR is higher when ${\tau }_1$ is larger. It also can be observed that for each test image, the gain in PSNR is larger when $k=128$ than that when $k=512$. The reason is that a smaller $k$ implies larger differences between the original bitmaps and cluster centers. Because the QA technique is capable of reducing the distortion caused by the differences, a larger PSNR improvement can be achieved for smaller $k$.

It is interesting to note that the gain in PSNR of the Stream and Baboon images increases more than that of other test images when varying ${\tau }_1=10$ to ${\tau }_1=50$ for both $k=128$ and $k=512$. Because these two images are more complex than the others, their bitmaps of smooth blocks are expected to be more different from the selected cluster centers used to replace the bitmaps. As previously mentioned, the QA technique is effective in reducing the distortion caused by the differences, and the bitmaps of Stream and Baboon images are more different from the cluster centers than the other images. Therefore, the improvement in PSNR after applying the QA technique is more significant than for the others.

4.1.2. Performance Comparison of Various ${\tau }_1$

The parameter ${\tau }_1$ controls the number of smooth and complex blocks. The number of complex blocks decreases as ${\tau }_1$ increases. To see the distribution of flat, smooth, and complex blocks of a test image, we take the Lena image as an example to illustrate their distribution by varying ${\tau }_1$. Figure 6a–d shows the distributions of blocks when ${\tau }_1=8$, 16, 32, and 64 are set. The block sizes in these figures are $8\times 8$ and ${\tau }_0=4$. In this figure, the blue squares, red dots, and black cross marks represent flat, smooth, and complex blocks, respectively.

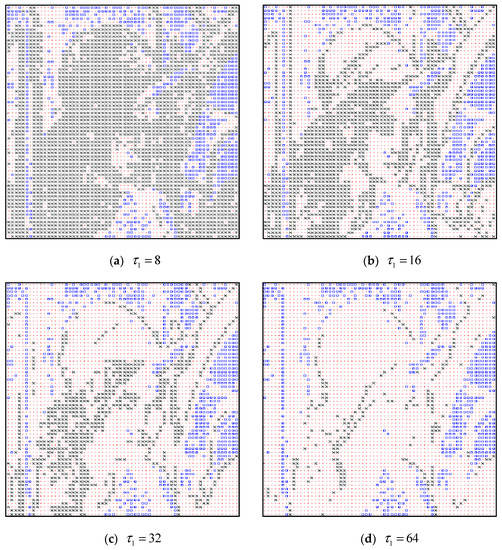
Figure 6. Distribution of flat, smooth and complex blocks.

Because the same ${\tau }_0$ is applied, it can be seen that the number of blue squares (flat blocks) is the same in Figure 6a–d. However, as ${\tau }_1$ increases, the red dots increase and black cross marks decrease. The reason is that an increase in ${\tau }_1$ leads more blocks to be categorized as smooth. It can also be inferred that a better image quality can be achieved at a smaller ${\tau }_1$ but the bitrate will be higher because more blocks are deemed to be complex. Note that in the proposed method, more bits are required to represent a complex block than a smooth block.

Table 4 and Table 5 show the PSNR and bitrate for all of the test images under various ${\tau }_1$ with block size $4\times 4$ and $8\times 8$, respectively. In this experiment, ${\tau }_0=4$, $\gamma =64$, and $k=256$ are set. We also list the PSNR and bitrate of the standard AMBTC method as a comparison. Note that the bitrates of the AMBTC with block size $4\times 4$ and $8\times 8$ are 2.0 and 1.25 bpp, respectively.

Table 4. PSNR and bitrate of the proposed method for various ${\tau }_1$ (block size $4\times 4$).

Images	AMBTC bpp = 2.0	PSNR (dB)			Bitrate (bpp)
		${\mathit{\tau }}_1=16$	${\mathit{\tau }}_1=32$	${\mathit{\tau }}_1=64$	${\mathit{\tau }}_1=16$	${\mathit{\tau }}_1=32$	${\mathit{\tau }}_1=64$
Lena	33.24	36.05	34.62	32.85	1.68	1.46	1.33
Jet	31.97	35.98	34.79	32.50	1.56	1.39	1.24
Baboon	26.98	30.89	29.55	25.74	2.75	2.34	1.75
Tiffany	35.77	37.55	35.72	34.26	1.54	1.34	1.25
Boat	31.16	34.27	32.87	30.81	2.09	1.77	1.57
Stream	28.59	32.53	30.20	27.27	2.73	2.11	1.66
Peppers	33.42	35.71	34.49	32.80	1.77	1.59	1.49
House	30.89	34.82	32.00	30.42	2.00	1.65	1.38
Average	31.50	34.73	33.03	30.83	2.02	1.71	1.46

Table 5. PSNR and bitrate of the proposed method for various ${\tau }_1$ (block size $8\times 8$).

Images	AMBTC bpp = 1.25	PSNR (dB)			Bitrate (bpp)
		${\mathit{\tau }}_1=16$	${\mathit{\tau }}_1=32$	${\mathit{\tau }}_1=64$	${\mathit{\tau }}_1=16$	${\mathit{\tau }}_1=32$	${\mathit{\tau }}_1=64$
Lena	29.93	33.12	31.80	29.24	1.02	0.76	0.51
Jet	28.84	32.86	31.72	29.40	1.04	0.82	0.62
Baboon	25.18	28.75	27.66	23.06	1.81	1.43	0.71
Tiffany	32.55	34.93	32.76	30.74	0.94	0.62	0.47
Boat	28.07	31.37	29.78	27.44	1.35	0.90	0.61
Stream	26.10	29.85	27.99	24.18	1.92	1.34	0.63
Peppers	29.66	32.80	31.49	29.43	1.06	0.78	0.58
House	27.68	31.60	30.20	26.92	1.39	1.02	0.62
Average	28.50	31.91	30.43	27.55	1.32	0.96	0.59

As seen in Table 4 and Table 5, the PSNR of block size $8\times 8$ is lower than that of block size $4\times 4$. For example, when ${\tau }_1=16$, the PSNR of the Lena image of block sizes $4\times 4$ and $8\times 8$ are 34.73 and 31.91 dB, respectively. However, the former requires $1.68-1.02=0.66$ more bits per pixel than the latter. In addition, the experiments also reveal the fact that a large ${\tau }_1$ effectively reduces the bitrate at the expense of image quality. On the contrary, a small ${\tau }_1$ provides better image quality, but requires more bitrate. This result is expected because a small ${\tau }_1$ increases the number of complex blocks and, therefore, the bitrate, however, the image quality also increases.

Figure 7 shows the bitrate–PSNR curves of each of the eight test images by varying the threshold ${\tau }_1$ from 8 to 64. The figure shows that for all of the test images, the PSNR increases as the bitrate increases. Moreover, the figure also reveals that smooth images, such as Tiffany or Jet, have a better compression efficiency than those of complex images, such as Stream or Baboon. The reason is that a smooth block not only requires less bits to record its compressed code but also provides better reconstructed quality. Because the smooth images naturally possess more smooth blocks than complex blocks, their bitrate–PSNR curves are higher than those of complex ones.

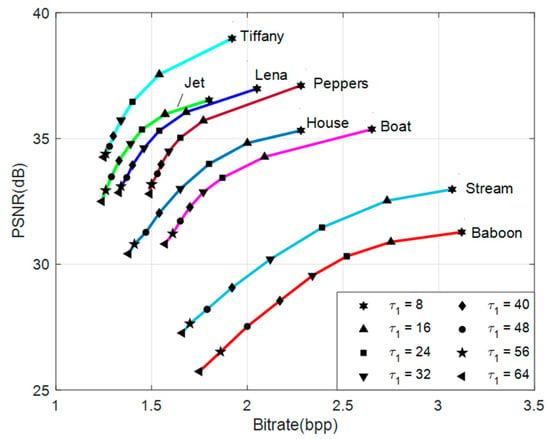
Figure 7. Bitrate–PSNR curves of each of the eight test images.

It also can be seen from Figure 7 that the PSNR and bitrate vary as the threshold ${\tau }_1$ changes. A larger ${\tau }_1$ gives a lower bitrate with lower PSNR. In contrast, a smaller ${\tau }_1$ offers a higher image quality, but the bitrate is also higher. Therefore, the selection of threshold ${\tau }_1$ depends on real applications. For example, if an application requires higher image quantity, a smaller ${\tau }_1$ is required.

It is worth noting that, for most of the test images, the proposed method provides better performance than AMBTC, particularly for smooth images. For example, Lena, Jet, Tiffany, Boat, and Peppers are considered to be smooth. For these smooth images, regardless of the value of ${\tau }_1$, the PSNR is always higher and the bitrate is always lower than those of the AMBTC method. In contrast, for the complex images such as Baboon or Stream, few blocks are classified as flat, which require only 8 bits to record them. Therefore, the reduction in bitrate is limited. Nevertheless, the proposed method either provides a better image quality or lower bitrate than those of AMBTC.

4.2. Comparisons with Xiang et al.’s Work

Xiang et al.’s method [16] also improves the AMBTC method by dynamically splitting images into multiple groups and achieves a good performance. In this section, we compare the proposed method with that of Xiang et al. in terms of PSNR and bitrate. To make a fair comparison, threshold ${\tau }_0=4$ and $\gamma =64$ are set in both methods. The proposed method uses ${\tau }_1$ to control the number of smooth and complex blocks, whereas Xiang et al.’s method uses $d_{\min }$ to control the number of pixel groups. We select ${\tau }_1=8$, 16, and 24 in the proposed method and compare the results with those of Xiang et al. by setting $d_{\min }=6$, 7, and 8 for block size $4\times 4$. The results are shown in Table 6. Table 7 shows the same experimental results, except block size is $8\times 8$ and $d_{\min }=28$, 32, and 36. The settings of $d_{\min }$ in Xiang et al.’s method ensure that best performance can be achieved.

Table 6. Comparisons of PSNR and bitrate with block size $4\times 4$.

Images	Metrics	Proposed ${\mathit{\tau }}_1=8$	[16] ${\mathit{d}}_{\min }=6$	Proposed ${\mathit{\tau }}_1=16$	[16] ${\mathit{d}}_{\min }=7$	Proposed ${\mathit{\tau }}_1=24$	[16] ${\mathit{d}}_{\min }=8$
Lena	PSNR	36.98	36.31	36.05	35.12	35.31	33.91
	Bitrate	2.05	2.35	1.68	2.20	1.54	1.95
Jet	PSNR	36.53	34.96	35.97	33.74	35.36	32.69
	Bitrate	1.80	1.98	1.57	1.87	1.45	1.71
Baboon	PSNR	31.28	31.40	30.89	29.59	30.32	28.11
	Bitrate	3.12	3.57	2.75	3.24	2.52	2.75
Tiffany	PSNR	38.98	38.42	37.55	37.29	36.46	36.41
	Bitrate	1.92	2.12	1.54	1.99	1.40	1.81
Boat	PSNR	35.37	34.81	34.27	33.43	33.44	32.11
	Bitrate	2.65	3.02	2.09	2.79	1.87	2.43
Stream	PSNR	32.98	32.69	32.53	31.14	31.46	29.69
	Bitrate	3.07	3.45	2.73	3.18	2.39	2.75
Peppers	PSNR	37.11	36.38	35.71	35.23	35.03	34.16
	Bitrate	2.28	2.64	1.77	2.45	1.65	2.20
House	PSNR	35.32	35.06	34.82	33.52	33.99	31.86
	Bitrate	2.28	2.52	2.00	2.35	1.80	2.05

Table 7. Comparisons of PSNR and bitrate with $8\times 8$ block size.

Images	Metrics	Proposed ${\mathit{\tau }}_1=14$	[16] ${\mathit{d}}_{\min }=28$	Proposed ${\mathit{\tau }}_1=22$	[16] ${\mathit{d}}_{\min }=32$	Proposed ${\mathit{\tau }}_1=30$	[16] ${\mathit{d}}_{\min }=36$
Lena	PSNR	33.32	31.88	32.66	30.85	32.00	30.27
	Bitrate	1.09	1.64	0.90	1.45	0.79	1.27
Jet	PSNR	32.99	30.37	32.44	29.66	31.87	29.23
	Bitrate	1.09	1.36	0.94	1.24	0.84	1.13
Baboon	PSNR	28.84	28.14	28.43	26.44	27.84	25.50
	Bitrate	1.88	2.23	1.65	1.88	1.47	1.50
Tiffany	PSNR	35.36	34.44	33.97	33.48	32.95	32.89
	Bitrate	1.04	1.51	0.77	1.33	0.64	1.16
Boat	PSNR	31.62	30.12	30.68	29.11	29.95	28.54
	Bitrate	1.46	1.99	1.11	1.75	0.93	1.50
Stream	PSNR	29.94	28.62	29.39	27.30	28.31	26.54
	Bitrate	1.99	2.20	1.71	1.90	1.41	1.58
Peppers	PSNR	33.01	31.35	32.27	30.52	31.68	30.03
	Bitrate	1.14	1.86	0.91	1.62	0.81	1.40
House	PSNR	31.71	30.20	31.22	28.79	30.45	28.09
	Bitrate	1.45	1.70	1.24	1.47	1.06	1.26

Table 6 shows that in Xiang et al.’s method, as $d_{\min }$ increases, the image quality and bitrate decrease. The reason is that a large $d_{\min }$ prevents more blocks from being split, leading to a decrease in bitrate and PSNR. Note that for most of the test images, the proposed method performs better than that of Xiang et al. We take the Lena image as an example: when ${\tau }_1=16$ and $d_{\min }=7$ are set, the PSNR of the proposed and Xiang et al.’s methods are 36.05 dB with 1.68 bpp and 35.12 dB with 2.20 bpp, respectively. The PSNR of the proposed method is $36.05-35.12=0.93$ dB higher and the bitrate is $2.20-1.68=0.52$ bpp lower than that of Xiang et al.’s method. Comparisons with other images and another set of parameters also reveal similar results, with the exception of the Baboon image. When ${\tau }_1=8$ and $d_{\min }=6$ are set, the PSNR of Xiang et al.’s method is $31.40-31.28=0.12$ dB higher than the proposed method. The reason is that under these settings, more blocks are divided into four groups and thus a better image quality is achieved. However, their method requires $3.57-3.12=0.45$ bpp more than the proposed method.

In the performance comparisons with block size $8\times 8$, the proposed method shows better results for all test images. For example, as shown in Table 7 when ${\tau }_1=14$ and $d_{\min }=28$, the PSNR of the Baboon image of the proposed method is 28.84 dB at 1.88 bpp. The PSNR is $28.84-28.14=0.70$ dB higher and the bitrate is $2.23-1.88=0.35$ bpp lower than those of Xiang et al.’s method.

Figure 8a–f shows the visual quality comparisons of the AMBTC, Xiang et al.’s, and the proposed methods. As seen from Figure 8a when the block size is $4\times 4$ and the AMBTC method is applied, apparent distortions can be seen in the image edges, and noticeable boundary artifacts are observed (see Figure 8a). Note that the PSNR of the AMBTC is 33.27 dB with 2.0 bpp. Xiang et al. improve the AMBTC method by adding more details to complex blocks. As a result, the PSNR (36.31 dB) is significantly higher and blocks at the edges look more natural than those of AMBTC (Figure 8c, $d_{\min }=6$). However, their method requires $2.35-2=0.35$ bpp more to achieve this effect. In contrast, the visual quality of the proposed method (Figure 8e, ${\tau }_1=8$) is comparable with that of Xiang et al.’s method, but the bitrate is $2.35-2.05=0.30$ bpp lower with a slightly higher PSNR.

Figure 8. Visual quality comparisons of the proposed method and that of Xiang et al.

When the block size is $8\times 8$, the distortion of AMBTC is more apparent (Figure 8b) than that of $4\times 4$, but the bitrate reduces from 2.0 to 1.25 bpp. The visual quality of Xiang et al.’s method (Figure 8d, $d_{\min }=28$) is significantly better than that of AMBTC, and has no noticeable block boundary artifacts. However, their method requires $1.64-1.25=0.39$ bpp more to improve the image quality. In addition, some edges in Lena’s face, eyes, and shoulder exhibit apparent distortions because the pixel splitting operation may not be triggered due to the setting of $d_{\min }$. In contrast, the edges of the proposed method exhibit no apparent distortion (see Figure 8f, ${\tau }_1=14$). Moreover, the bitrate required in the proposed method is even lower than that of AMBTC by $1.25-1.09=0.16$ bpp.

5. Conclusions

In this paper, we propose a hybrid encoding scheme for AMBTC compressed images using a ternary representation technique. Considering that the number of quantized values greatly affects the quality of the reconstructed image, the proposed method classifies image blocks into flat, smooth, and complex. These three types of blocks are encoded by using one, two, or three quantized values. Flat blocks require no bitmap, whereas smooth and complex blocks require binary and ternary maps, respectively, to record the quantized values to be used to reconstruct the corresponding pixels. A sophisticated design indicator is prepended before the code stream of a block to signify the block type. The proposed method achieves a better image quality than that of prior works with a smaller bitrate. The effectiveness of the proposed method is observed from the experimental results. Note that although the k-means algorithm used in the proposed method may require slightly higher computational cost than that of the discrete cosine transform (DCT) based methods, it is only applied to smooth blocks in the encoding stage to obtain the representative bitmaps rather than the whole image. Furthermore, the k-means algorithm does not need to be applied again during decoding. Therefore, the overall computational cost of the proposed method is smaller than that of DCT-based compression methods.