Novel Multiple-Image Encryption Scheme Based on Coherent Beam Combining and Equal Modulus Decomposition
Abstract
:1. Introduction
2. Methods
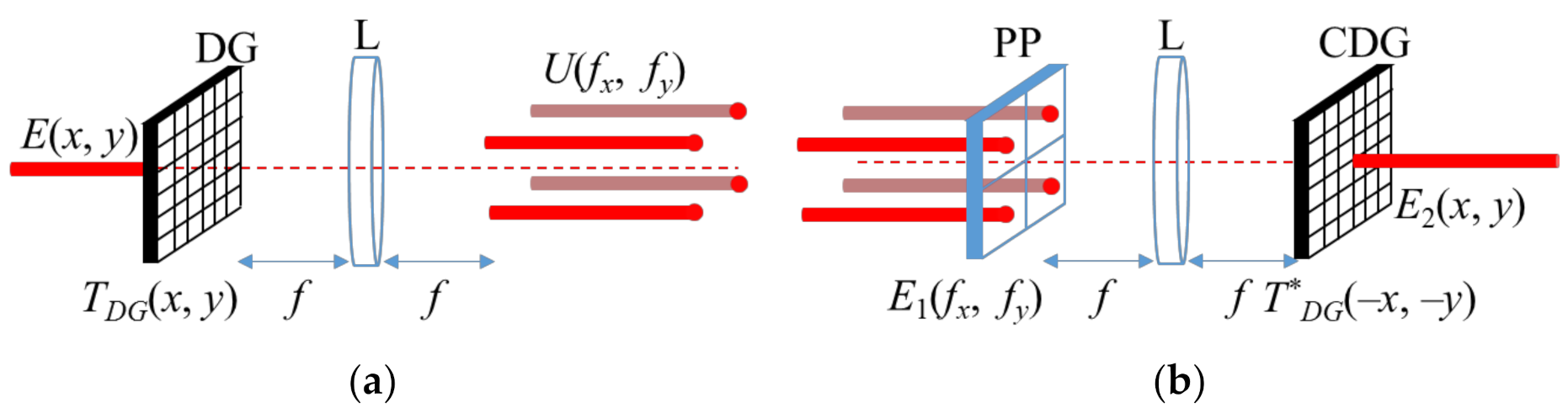
2.1. Coherent Beam Combining
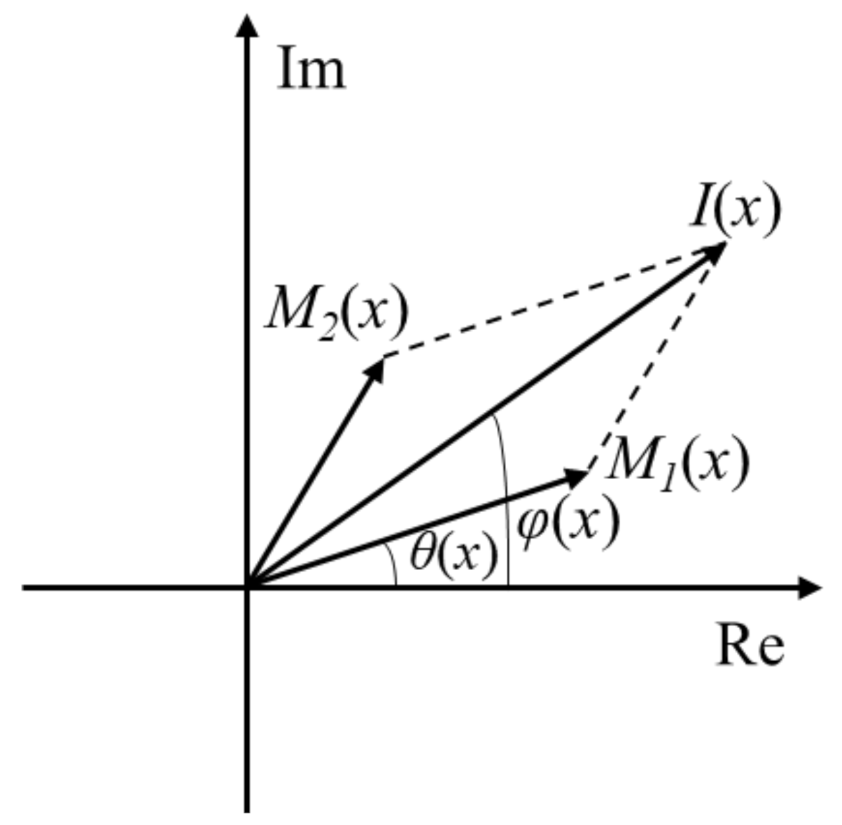
2.2. Cryptosystem
3. Simulation
4. Discussion
4.1. Error Analysis
4.2. Occlusion Attack Analysis
4.3. Noise Attack Analysis
4.4. Key Space and Exhaustive Search Attack Analysis
4.5. Known Plaintext Attack Analysis
4.6. Noise Cross-Talk Analysis
4.7. Main Advantages
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Matoba, O.; Nomura, T.; Perez-Cabre, E.; Millan, M.; Javidi, B. Optical techniques for information security. Proc. IEEE. 2009, 97, 1128–1148. [Google Scholar] [CrossRef]
- Manzo, M. KGEARSRG: Kernel Graph Embedding on Attributed Relational SIFT-Based Regions Graph. Mach. Learn. Knowl. Extr. 2019, 1, 962–973. [Google Scholar] [CrossRef] [Green Version]
- Flores-Vergara, A.; Inzunza-González, E.; García-Guerrero, E.E.; López-Bonilla, O.R.; Rodríguez-Orozco, E.; Hernández-Ontiveros, J.M.; Cárdenas-Valdez, J.R.; Tlelo-Cuautle, E. Implementing a Chaotic Cryptosystem by Performing Parallel Computing on Embedded Systems with Multiprocessors. Entropy 2019, 21, 268. [Google Scholar] [CrossRef] [Green Version]
- Ghadirli, H.; Nodehi, A.; Enayatifar, R. An overview of encryption algorithms in color images. Signal. Process. 2019, 164, 163–185. [Google Scholar] [CrossRef]
- Kaur, M.; Kumar, V. A comprehensive review on image encryption techniques. Arch. Comput. Method. E. 2020, 27, 15–43. [Google Scholar] [CrossRef]
- Chen, W.; Javidi, B.; Chen, X. Advances in optical security systems. Adv. Opt. Photonics. 2014, 6, 120–155. [Google Scholar] [CrossRef]
- Refregier, P.; Javidi, B. Optical image encryption based on input plane and Fourier plane random encoding. Opt. Lett. 1995, 20, 767–769. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Peng, B.; Gan, W.; Liu, Y. Plaintext attack on joint transform correlation encryption system by convolutional neural network. Opt. Exp. 2020, 28, 28154–28163. [Google Scholar] [CrossRef]
- Chang, X.; Yan, A.; Zhang, H. Ciphertext-only attack on optical scanning cryptography. Opt. Laser. Eng. 2020, 126, 105901. [Google Scholar] [CrossRef]
- Wang, X.; Su, Y. Color image encryption based on chaotic compressed sensing and two-dimensional fractional Fourier transform. Sci. Rep. 2020, 10, 18556. [Google Scholar] [CrossRef]
- Yan, A.; Dong, J.; Li, Y. A novel nonlinear double image encryption based on affine transform and gyrator transform. J. Opt. 2018, 20, 115702. [Google Scholar] [CrossRef]
- Yan, A.; Wei, Y.; Zhang, J. Security enhancement of optical encryption based on biometric array keys. Opt. Commun. 2018, 419, 134–140. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, Z.; Kang, Y.; Ye, H.; Xiong, R.; Yuan, X.; Wang, Z.; Wang, K.; Zhang, D. Research on double-layers optical information encryption based on ghost imaging. Opt. Commun. 2020, 455, 124585. [Google Scholar]
- Qin, W.; Peng, X. Asymmetric cryptosystem based on phase-truncated Fourier transforms. Opt. Lett. 2010, 35, 118–120. [Google Scholar] [CrossRef]
- Zhong, Z.; Qin, H.; Liu, L.; Zhang, Y.; Shan, M. Silhouette-free image encryption using interference in the multiple-parameter fractional Fourier transform domain. Opt. Exp. 2017, 25, 6974–6982. [Google Scholar] [CrossRef]
- Chen, L.; Chang, G.; He, B.; Mao, H.; Zhao, D. Optical image conversion and encryption by diffraction, phase retrieval algorithm and incoherent superposition. Opt. Laser. Eng. 2017, 88, 221–232. [Google Scholar] [CrossRef]
- Shi, Y.; Liu, Y.; Sheng, W.; Zhu, D.; Wang, J.; Wu, T. Multiple-image double-encryption via 2D rotations of a random phase mask with spatially incoherent illumination. Opt. Exp. 2019, 27, 26050–26059. [Google Scholar] [CrossRef]
- Li, W.; Chang, X.; Yan, A.; Zhang, H. Asymmetric multiple image elliptic curve cryptography. Opt. Laser. Eng. 2021, 136, 106319. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, B. Optical image encryption based on interference. Opt. Lett. 2008, 33, 2443–2445. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.; Song, J.; Moon, I.; Lee, Y. Interference-based multiple-image encryption using binary phase masks. Opt. Laser. Eng. 2018, 107, 281–287. [Google Scholar] [CrossRef]
- Cai, J.; Shen, X.; Lei, M.; Lin, C.; Dou, S. Asymmetric optical cryptosystem based on coherent superposition and equal modulus decomposition. Opt. Lett. 2015, 40, 475–478. [Google Scholar] [CrossRef]
- Chen, L.; Gao, X.; Chen, X.; He, B.; Liu, J.; Li, D. A new optical image cryptosystem based on two-beam coherent superposition and unequal modulus decomposition. Opt. Laser Technol. 2016, 78, 167–174. [Google Scholar] [CrossRef]
- Sui, L.; Du, C.; Zhang, X.; Tian, A.; Anand, A. Double-image encryption based on interference and logistic map under the framework of double random phase encoding. Opt. Laser. Eng. 2019, 122, 113–122. [Google Scholar]
- Luan, G.; Chen, Z.; Huang, C. Silhouette-free multiple image encryption using coherent superposition and Fresnel transform. Optik 2020, 224, 165498. [Google Scholar] [CrossRef]
- Abuturab, M.R. A superposition based multiple-image encryption using Fresnel-Domain high dimension chaotic phase encoding. Opt. Lasers Eng. 2020, 129, 106038. [Google Scholar] [CrossRef]
- Zhou, C.; Liu, L. Numerical study of Dammann array illuminators. Appl. Opt. 1995, 34, 5961–5969. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Lu, Y. Coherent beam combination using non-separable phase-controlled Dammann grating. Opt. Commun. 2018, 407, 321–326. [Google Scholar] [CrossRef]
- Murillo-Escobar, M.; Meranza-Castillon, M.; Lopez-Gutierrez, R.; Cruz-Hernandez, C. Suggested Integral Analysis for Chaos-Based Image Cryptosystems. Entropy 2019, 21, 815. [Google Scholar] [CrossRef] [Green Version]
- Alvarez, G. Some basic cryptographic requirements for chaos-based cryptosystems. Int. J. Bifurcation. Chaos. 2006, 16, 2129–2151. [Google Scholar] [CrossRef] [Green Version]
- Flores-Vergara, A.; García-Guerrero, E.; Inzunza-González, E.; López-Bonilla, O.; Rodríguez-Orozco, E.; Cardenas-Valdez, J.; Tlelo-Cuautle, E. Implementing a chaotic cryptosystem in a 64-bit embedded system by using multiple-precision arithmetic. Nonlinear. Dyn. 2019, 96, 497–516. [Google Scholar] [CrossRef]
- De la Fraga, L.G.; Mancillas-Lopez, C.; Tlelo-Cuautle, E. Designing an authenticated Hash function with a 2D chaotic map. Nonlinear. Dyn. 2021, 104, 4569–4580. [Google Scholar] [CrossRef]
- González-Zapata, A.M.; Tlelo-Cuautle, E.; Cruz-Vega, I.; Leon-Salas, W.D. Synchronization of chaotic artificial neurons and its application to secure image transmission under MQTT for IoT protocol. Nonlinear. Dyn. 2021, 104, 4581–4600. [Google Scholar] [CrossRef]
- Liang, H.; Zhang, G.; Hou, W.; Huang, P.; Liu, B.; Li, S. A Novel Asymmetric Hyperchaotic Image Encryption Scheme Based on Elliptic Curve Cryptography. Appl. Sci. 2021, 11, 5691. [Google Scholar] [CrossRef]










Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, W.; Yan, A.; Zhang, H. Novel Multiple-Image Encryption Scheme Based on Coherent Beam Combining and Equal Modulus Decomposition. Appl. Sci. 2021, 11, 9310. https://doi.org/10.3390/app11199310
Li W, Yan A, Zhang H. Novel Multiple-Image Encryption Scheme Based on Coherent Beam Combining and Equal Modulus Decomposition. Applied Sciences. 2021; 11(19):9310. https://doi.org/10.3390/app11199310
Chicago/Turabian StyleLi, Wei, Aimin Yan, and Hongbo Zhang. 2021. "Novel Multiple-Image Encryption Scheme Based on Coherent Beam Combining and Equal Modulus Decomposition" Applied Sciences 11, no. 19: 9310. https://doi.org/10.3390/app11199310
APA StyleLi, W., Yan, A., & Zhang, H. (2021). Novel Multiple-Image Encryption Scheme Based on Coherent Beam Combining and Equal Modulus Decomposition. Applied Sciences, 11(19), 9310. https://doi.org/10.3390/app11199310





