Design Options to Improve the Dynamic Behavior and the Control of Small H-Darrieus VAWTs
Abstract
1. Introduction
2. Background
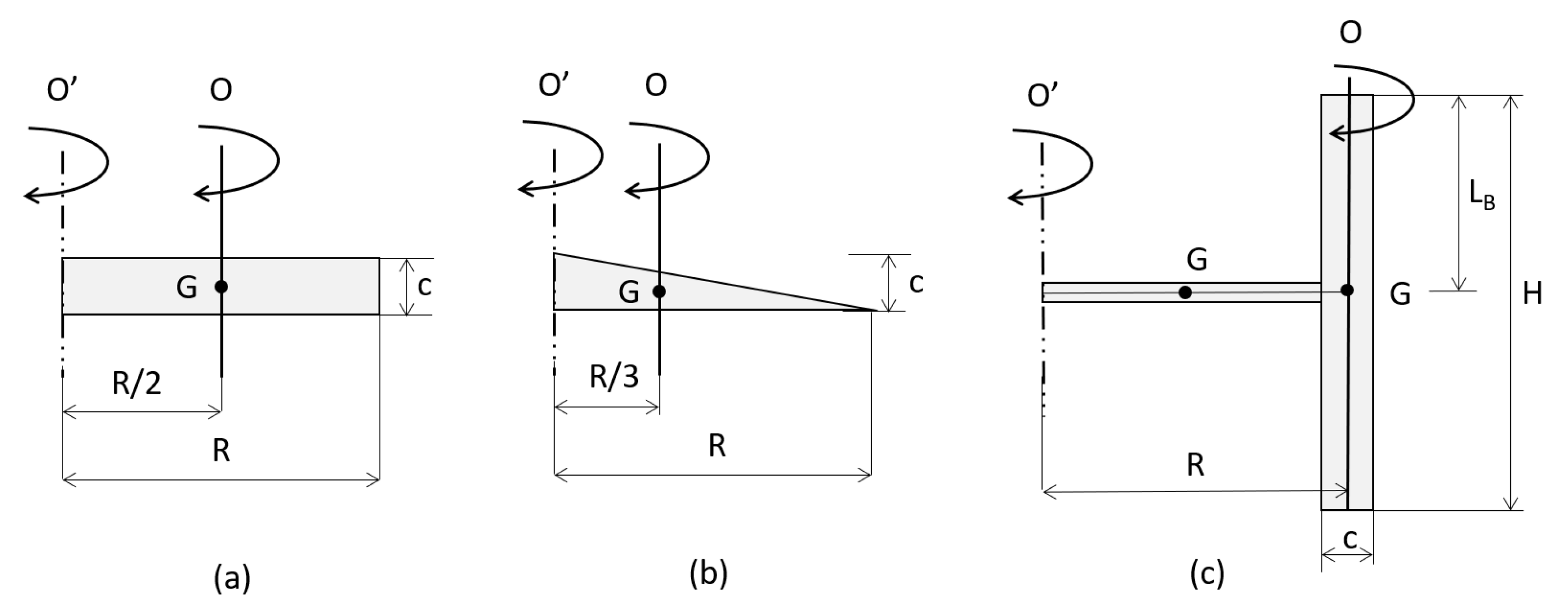
2.1. Inertial Properties of the Rotors
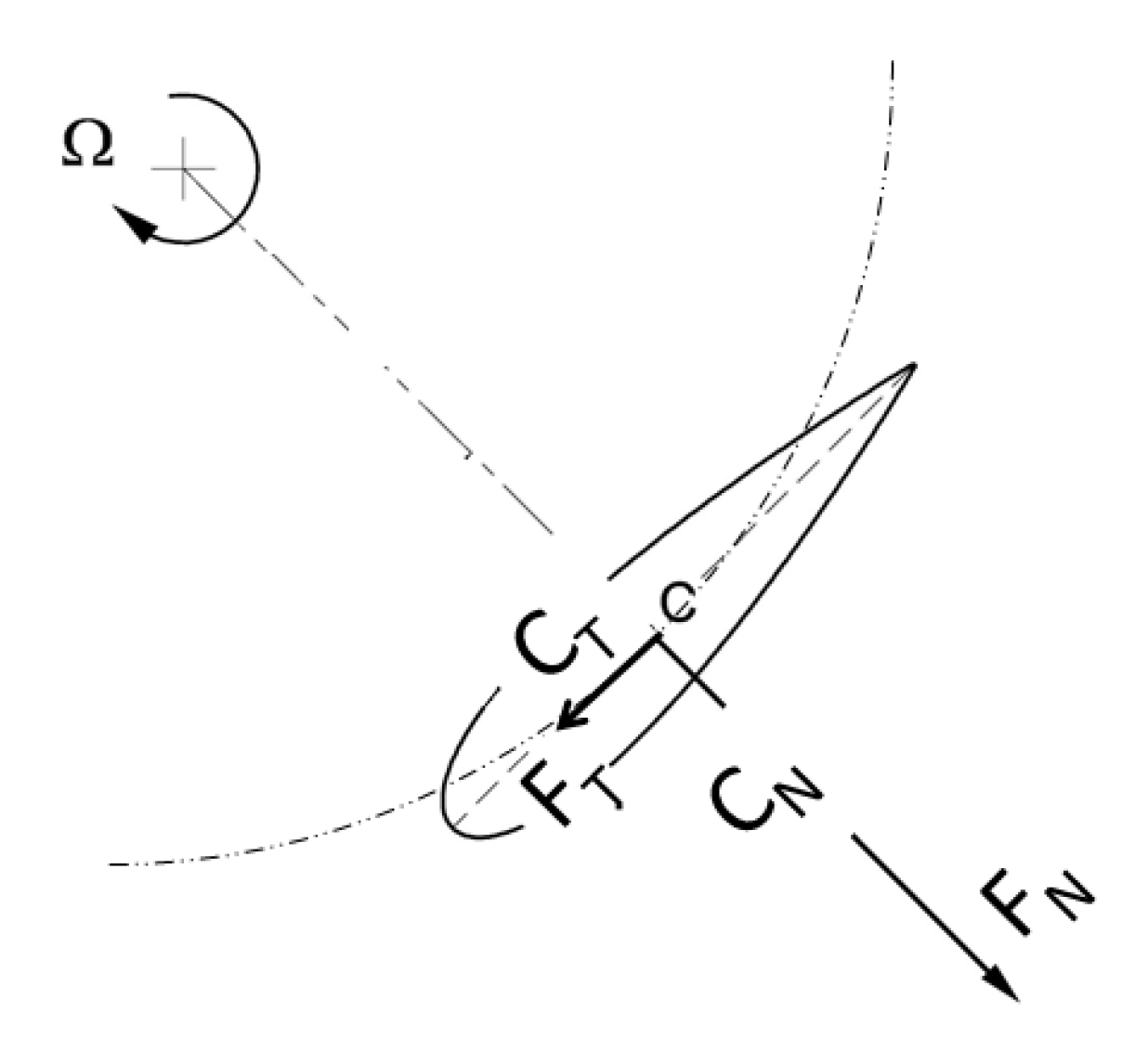
2.2. Response to Aerodynamic Unsteadiness
2.3. Gusts Tracking
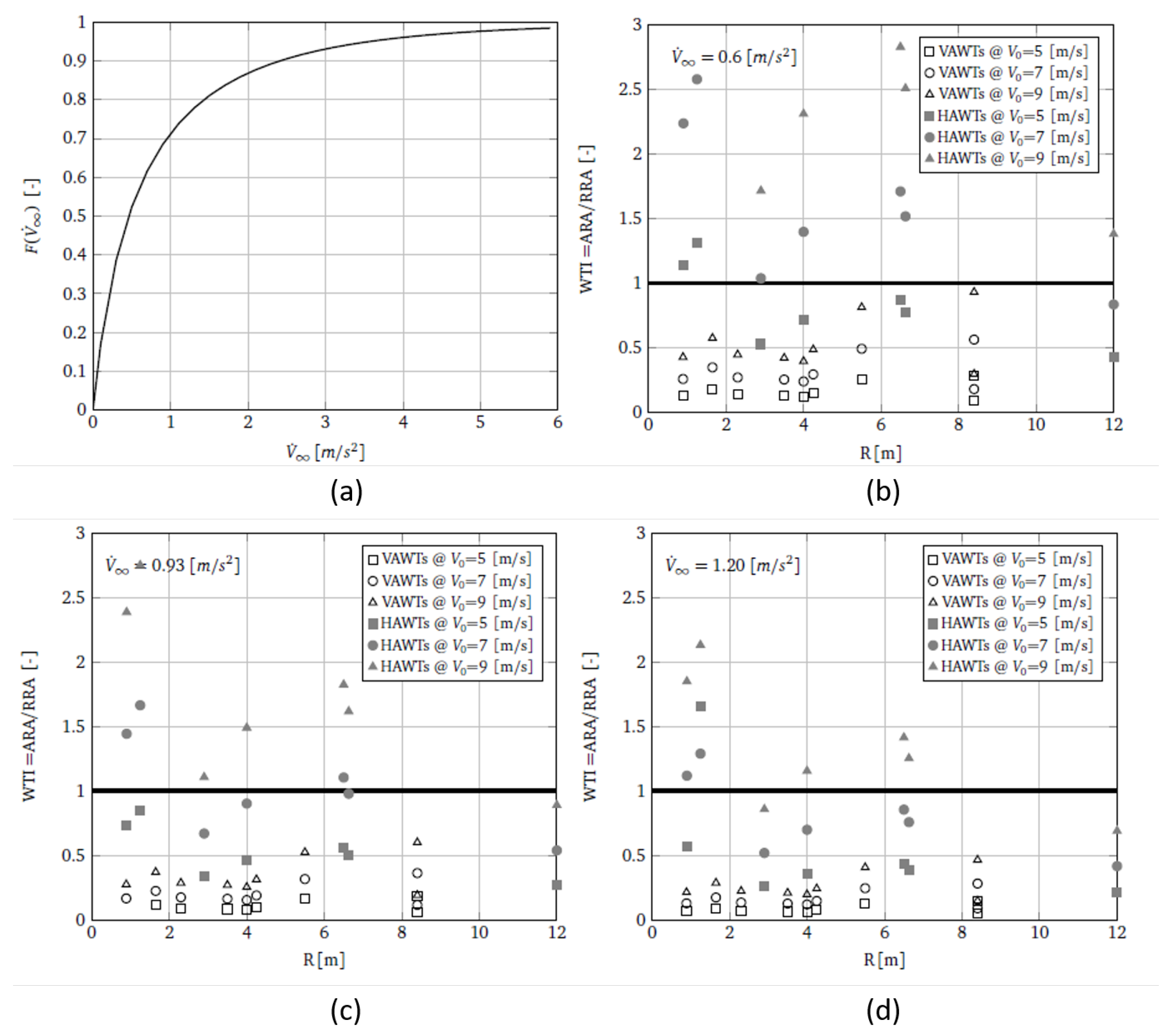
2.4. Acceleration/Deceleration Capability
3. Wind Tracking Index Maximization Procedure
4. Discussion
4.1. Variation of the E (Environment) Index
4.2. Variation of the G (Geometry) Index
4.3. Variation of the F (Functional) Index
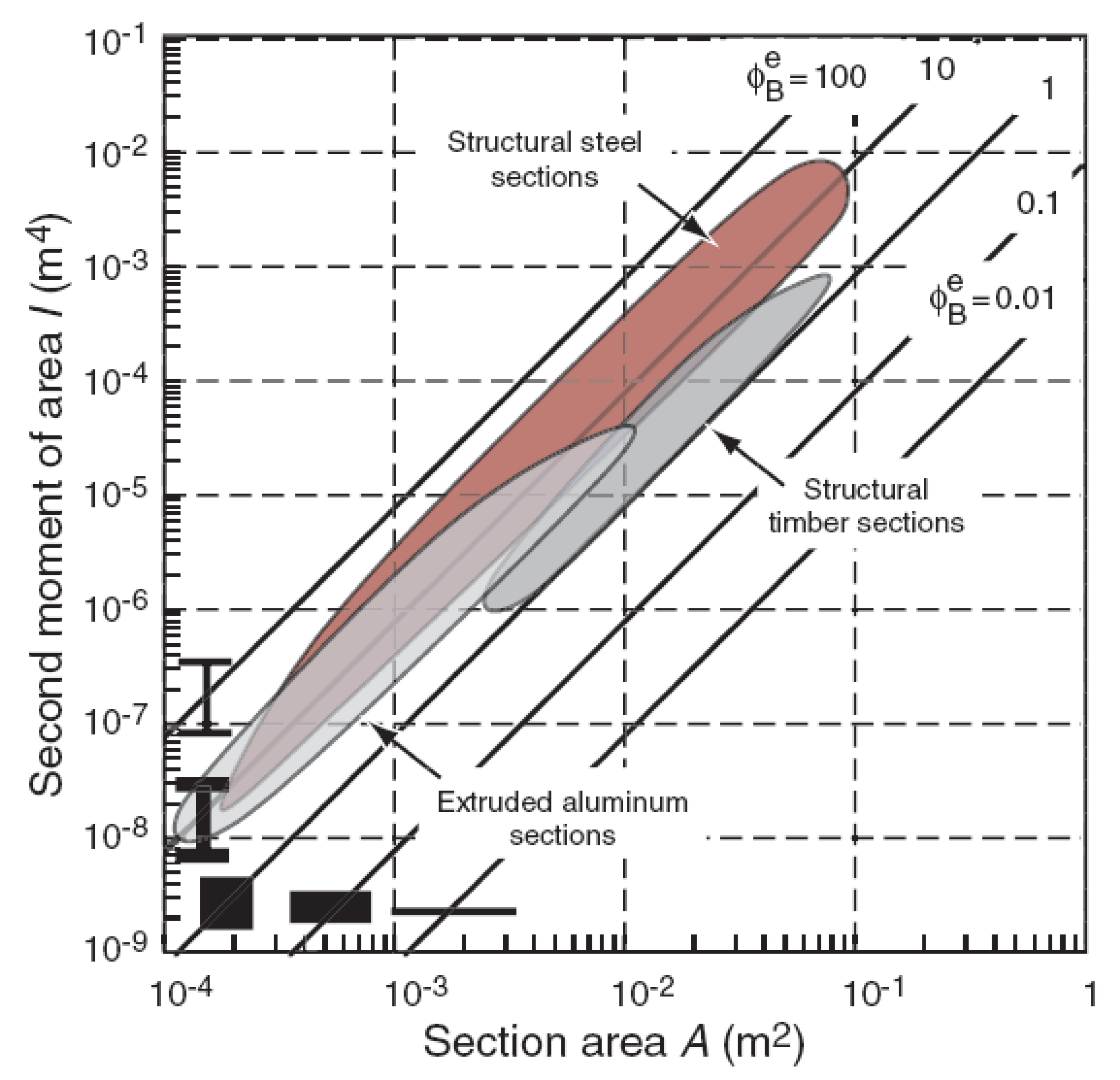
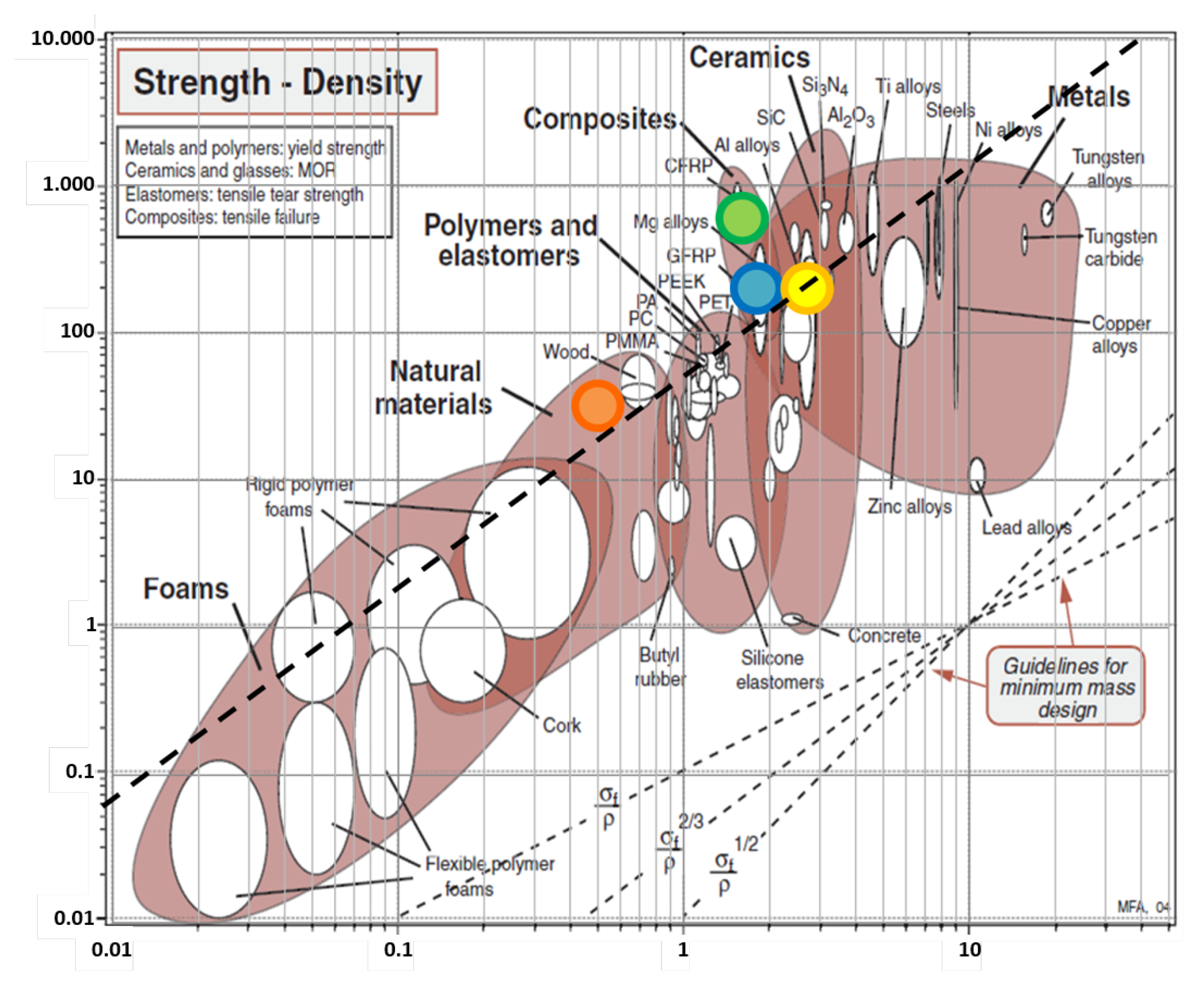
4.4. Variation of the M (Material) Index
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| A | blade section area [m] |
| A | rotor swept area [m] |
| AEP | Annual Energy Production |
| AR | rotor aspect ratio H/D |
| ARA | available rotor acceleration [m/s] |
| b | blade section dimension [m] |
| c | blade chord length [m] |
| blade normal force coefficient [-] | |
| power coefficient [-] | |
| blade tangent force coefficient [-] | |
| D | rotor diameter [m] |
| E | environmental index or parameter |
| F | functional index or parameter |
| blade aerodynamic bending force [N] | |
| G | geometrical index or parameter |
| H | rotor height [m] |
| HAWT | Horizontal Axis Wind Turbine |
| H-VAWT | Straight-blades Vertical Axis Wind Turbine |
| I’ | single blade inertia respect to the axis of rotation [kgm] |
| blade length [m] | |
| number of blades [-] | |
| M | material index or parameter |
| blade mass [kg] | |
| blade bending moment [Nm] | |
| normal force coefficient magnification factor [-] | |
| numerical constants [-] | |
| aerodynamic torque [Nm] | |
| electric generator torque [Nm] | |
| R | radius [m] |
| RRA | required rotor acceleration [m/s] |
| P | performance |
| t | time [s] |
| initial wind speed [m/s] | |
| free stream wind speed [m/s] | |
| free stream wind acceleration [m/s] | |
| VAWT | Vertical Axis Wind Turbine |
| W | blade section modulus [] |
| WTI | wind tracking index [-] |
| constant | |
| constant | |
| section strength efficiency | |
| tip speed ratio [-] | |
| optimum tip speed ratio [-] | |
| angular rotor speed [rad/s] | |
| angular rotor acceleration [rad/s] | |
| air density [kg/m] | |
| blade density [kg/m] | |
| rotor solidity [-] | |
| allowable mechanical stress [Pa] | |
| material safety factor [-] |
Appendix A. Collection of Data of Commercial and Prototype H-VAWTs
| Parameter | Unit | [27] | [47] | [48] | [48] | [48] | [48] | [48] | [48] | [49] | [50] | [51] | [6] | [52] | [53] | [54] | [16] | [55] |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Diameter D | m | 0.6 | 1.78 | 3.30 | 4.60 | 7.00 | 8.00 | 8.50 | 11.00 | 2.00 | 17.70 | 1.03 | 25 | 2.50 | 1.03 | 8.00 | 26 | 6 |
| Radius R | m | 0.3 | 0.89 | 1.65 | 2.30 | 3.50 | 4.00 | 4.25 | 5.50 | 1 | 8.85 | 0.515 | 12.5 | 1.25 | 0.515 | 4 | 13 | 3 |
| Blade length | m | 0.47 | 2.49 | 2.20 | 2.50 | 5.70 | 4.30 | 5.80 | 12.00 | 3.46 | 12.8 | 1.456 | 18 | 3 | 1 | 4.8 | 24 | 5 |
| Rotor height H | m | 0.47 | 3.74 | 2.20 | 2.50 | 5.70 | 4.30 | 5.8 | 12 | 3 | 12.8 | 1.456 | 18 | 3 | 1 | 2.4 | 24 | 5 |
| Swept area | m | 0.28 | 4.44 | 7.26 | 11.50 | 39.90 | 34.40 | 49.3 | 132.00 | 6 | 227 | 1.50 | 450 | 7.5 | 1.03 | 19.2 | 624 | 30 |
| Rated power | kW | - | 0.7 | 3.00 | 6.00 | 10.00 | 20.00 | 20.00 | 30 | - | 45 | 0.20 | 130 | - | - | 10 | 200 | 12 |
| Rated wind speed | m/s | 9.75 | 11.40 | 14.00 | 14.00 | 14.00 | 14.00 | 12.36 | 11.2 | 13 | 9 | 10 | 11 | 8 | 12 | 12 | 12 | 12 |
| Rated rot. speed | rpm | 620.5 | 320 | 144.00 | 100.00 | 87.85 | 60.00 | 50.00 | 47.64 | 372 | 33.5 | 200 | 27 | 183 | - | 86 | 33 | 127 |
| Rotor inertia | kg m | 0.1 | 18 | 404 | 1600 | 5630 | 12,000 | 15,800 | 23,000 | - | - | 1.5 | - | - | - | - | - | - |
| Blades number | - | 4 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 2 | 3 | 3 | 3 | 3 | 3 |
| Cp max | - | - | 0.32 | 0.32 | 0.31 | 0.338 | 0.338 | 0.34 | - | 0.385 | 0.3 | - | 0.3 | - | 0.475 | - | - | 0.40 |
| Solidity | - | 0.5 | 0.25 | 0.745 | 0.457 | 0.300 | 0.263 | 0.247 | 0.273 | 0.173 | 0.117 | 0.25 | 0.100 | 0.480 | - | 0.300 | 0.096 | 0.374 |
| Rated | - | 2 | 2.62 | 1.78 | 1.72 | 2.30 | 1.80 | 1.80 | 2.45 | 3.00 | 3.45 | 2.8 | 3.21 | 1.6 | 2.33 | 3.01 | 3.74 | 3 |
| Chord c | m | 0.075 | 0.15 | 0.82 | 0.70 | 0.70 | 0.70 | 0.70 | 1.00 | 0.1 | 0.69 | 0.085 | 1.25 | 0.40 | 0.09 | 0.40 | 0.83 | 0.25 |
| I/R | kg | - | - | 49 | 101 | 153 | 250 | 292 | 253 | - | - | 8 | - | - | - | - | - | - |
References
- Darrieus, G.J.M. Turbine Having Its Rotating Shaft Transverse to the Flow of Current. U.S. Patent US1835018, 8 December 1931. [Google Scholar]
- Blackwell, B.F.; Sullivan, W.N.; Reuter, R.C.; Banas, J.F. Engineering development status of the Darrieus wind turbine. J. Energy 1977, 1, 50–64. [Google Scholar] [CrossRef]
- Sutherland, H.J.; Berg, D.E.; Ashwill, T.D. A Retrospective of VAWT Technology SANDIA Report; SAND2012-0304, Unlimited Release; U.S. Department of Energy Office of Scientific and Technical Information Albuquerque: New Mexico, CA, USA, 2012. [Google Scholar]
- Templin, R.; Rangi, R. Vertical-axis wind turbine development in Canada. IEEE Proc. A Phys. Sci. Meas. Instrum. Manag. Educ. Rev. 1983, 130, 555–661. [Google Scholar] [CrossRef]
- FloWind Corporation. Final Project Report: High Energy Rotor Development, Test and Evaluation; SAND96-2205; FloWind Corporation: San Rafael, CA, USA, 1996. [Google Scholar]
- Musgrove, P.J. Wind energy conversion: Recent progress and future prospects. Sol. Wind Technol. 1987, 4, 37–49. [Google Scholar] [CrossRef]
- Mertens, S. Wind Energy in the Built Environment: Concentrator Effects of Buildings; Multi-Science: Essex, UK, 2006; 169p. [Google Scholar]
- Micallef, D.; Bussel, G.V. A Review of Urban Wind Energy Research: Aerodynamics and Other Challenges. Energies 2018, 11, 2204. [Google Scholar] [CrossRef]
- Battisti, L.; Dell’Anna, S.; Castelli, M.R.; Brighenti, A. Effectiveness of Wind Turbines in Urban Environment. In Colloquium on Research and Innovation on Wind Energy on Exploitation in Urban Environment Colloquium; Springer: Berlin/Heidelberg, Germany, 2018; Volume 8. [Google Scholar]
- Hand, B.; Cashman, A. A review on the historical development of the lift-type vertical axis wind turbine: From onshore to offshore floating application. Sustain. Energy Technol. Assess. 2020, 38, 100646. [Google Scholar] [CrossRef]
- Battisti, L.; Benini, E.; Brighenti, A.; Raciti Castelli, M.; Dell’Anna, S.; Dossena, V.; Persico, G.; Schmidt Paulsen, U.; Pedersen, T. Wind tunnel testing of the DeepWind demonstrator in design and tilted operating conditions. Energy 2016, 111, 484–497. [Google Scholar] [CrossRef]
- Vita, L.; Paulsen, U.S.; Madsen, H.A.; Nielsen, P.H.; Berthelsen, P.A.; Cartsensen, S. Design and aero-elastic simulation of a 5 MW floating vertical axis wind turbine. In Proceedings of the ASME 2012 31st International Conference on Ocean, Offshore and Arctic Engineering (OMAE2012), ASME, Rio de Janeiro, Brazil, 1–6 July 2012; pp. 1–10. [Google Scholar]
- Carstensen, S. Future Deep Sea Wind Turbine Technologies; Technical Report on the Physical Model Experiments [Techn. rep.]; FP7-ENERGY-Specific Programme “Cooperation”: Energy, ENERGY.2010.10.2-1—Future Emerging Technologies for Energy Applications (FET); Available online: https://cordis.europa.eu/project/id/256769/reporting (accessed on 29 August 2021).
- INFLOW, Industrialization Setup of a Floating Offshore Wind Turbine. Available online: https://www.inflow-fp7.eu/ (accessed on 25 January 2015).
- Tjiu, W.; Marnoto, T.; Mat, S.; Ruslan, M.H.; Sopian, K. Darrieus vertical axis wind turbine for power generation II: Challenges in HAWT and the opportunity of multi-megawatt Darrieus VAWT development. Renew. Energy 2015, 75, 560–571. [Google Scholar] [CrossRef]
- Ottermo, F.; Bernhoff, H. An upper size of vertical axis wind turbines. Wind Energy 2014, 17, 1623–1629. [Google Scholar] [CrossRef]
- Kjellin, J.; Eriksson, S.; Bernhoff, H. Electric control substituting pitch control for large wind turbines. J. Wind Energy 2013, 2013, 1–4. [Google Scholar] [CrossRef]
- Tang, C.; Pathmanathan, M.; Soong, W.; Ertugrul, N. Effects of inertia on dynamic performance of wind turbines. In Proceedings of the Power Engineering Conference (AUPEC’08), Sydney, Australia, 14–17 December 2008; pp. P087.1–P087.6. [Google Scholar]
- Islam, M.; Fartaj, A.; Carriveau, R. Analysis of the Design Parameters related to a Fixed-pitch Straight-Bladed Vertical Axis Wind Turbine. Wing Eng. 2008, 32, 491–507. [Google Scholar] [CrossRef]
- Brusca, S.; Lanzafame, R.; Messina, M. Design of a vertical-axis wind turbine: How the aspect ratio affects the turbine’s performance. Int. J. Energy Environ. Eng. 2014, 5, 129. [Google Scholar] [CrossRef]
- Raciti Castelli, M.; Benini, E. Effect of blade number on a straight-bladed Vertical-Axis Darreius wind turbine. World Acad. Sci. Eng. Technol. 2012, 61, 305e11. [Google Scholar]
- Tangler, J.L. The Evolution of Rotor and Blade Design; National Renewable Energy Laboratory: Golden, CO, USA, 2000. [Google Scholar]
- Li, S.; Li, Y. Numerical study on the performance effect of solidity on the straight-bladed vertical axis wind turbine. In Proceedings of the Power and Energy Engineering Conference (APPEEC), 2010 Asia-Pacific, Chengdu China, 28–31 March 2010; IEEE: Manhattan, NY, USA, 2010; pp. 1–4. [Google Scholar]
- Li, Q.; Maeda, T.; Kamada, Y.; Murata, J.; Furukawa, K.; Yamamoto, M. Effect of number of blades on aerodynamic forces on a straight-bladed Vertical Axis Wind Turbine. Energy 2015, 90, 784–795. [Google Scholar] [CrossRef]
- Subramanian, A.; Yogesh, S.A.; Sivan, H.; Giri, A.; Vasudevan, M.; Mugundhan, V.; Velamat, R.K. Effect of airfoil and solidity on performance of small scale vertical axis wind turbine using three dimensional CFD model. Energy 2017, 133, 179–190. [Google Scholar] [CrossRef]
- Carrigan, T.J.; Dennis, B.H.; Han, Z.X.; Wang, B.P. Aerodynamic Shape Optimization of a Vertical-Axis Wind Turbine Using Differential Evolution. Int. Sch. Res. Netw. ISRN Renew. Energy 2012, 2012, 528418. [Google Scholar] [CrossRef]
- Hara, Y.; Hara, K.; Hayashi, T. Moment of Inertia Dependence of Vertical Axis Wind Turbines in Pulsating Winds. Int. J. Rotating Mach. 2012, 2012, 910940. [Google Scholar] [CrossRef][Green Version]
- Nguyen, L.; Metzger, M. Enhanced energy capture by a vertical axis wind turbine during gusty winds in an urban/suburban environment. J. Renew. Sustain. Energy 2015, 7, 053118. [Google Scholar] [CrossRef]
- Nguyen, L.; Metzger, M. Optimization of a vertical axis wind turbine for application in an urban/suburban area. J. Renew. Sustain. Energy 2017, 9, 043302. [Google Scholar] [CrossRef]
- Battisti, L.; Benini, E.; Brighenti, A.; Persico, G.; Paradiso, B. A review based on evaluation experiences with ten-years activity in VAWT experimental wind tunnel testing. Green Energy Technol. 2018, 1, 139–154. [Google Scholar]
- Ashby, M.F. Materials Selection in Mechanical Design, 3rd ed.; Elsevier Butterworth-Heinemann: Oxford, UK, 2005. [Google Scholar]
- Rodriguez, G.A.G.; Rodriguez, A.G.; Payan, M.B. Estimating Wind Turbines Mechanical Constants. In Proceedings of the International Conference Renewable Energies and Power Quality (ICREPQ’07), Sevilla, Spain, 28–30 March 2007; Volume 1, pp. 697–704. [Google Scholar]
- Burton, T.; Sharpe, D.; Jenkins, N.; Bossanyi, E. Wind Energy Handbook; John Wiley and Sons, Ltd.: Hoboken, NJ, USA, 2001. [Google Scholar]
- Paraschivoiu, I. Wind Turbine Design: With Emphasis on Darrieus Concept; Presses inter Polytechnique: Montréal, QC, Canada, 2002. [Google Scholar]
- Homicz, G.F. VAWT stochastic loads produced by atmospheric turbulence. J. Sol. Energy Eng. 1989, 111, 358–367. [Google Scholar] [CrossRef]
- Kooiman, S.; Tullis, S. Response of a vertical axis wind turbine to time varying wind conditions found within the urban environment. Wind. Eng. 2010, 34, 389401. [Google Scholar] [CrossRef]
- Dutton, A.; Halliday, J.; Blanch, M. The Feasibility of Building-mounted/integrated Wind Turbines (BUWTs): Achieving Their Potential for Carbon Emission Reductions; Tech. Rep., Energy Research Unit Final Report of Carbon Trust Contract 2002-07-028-1-6; Energy Research Unit CCLRC: London, UK, 2005. [Google Scholar]
- Cook, N. Designers Guide to Wind Loading of Building Structures; Part 1, Building Research Establishment Report; 1986. Available online: https://www.osti.gov/biblio/5854920 (accessed on 29 August 2021).
- Battisti, L.; Benini, E.; Brighenti, A.; Dell’Anna, S.; Castelli, M.R. Small wind turbine effectiveness in the urban environment. Renew. Energy 2018, 129, 102–113. [Google Scholar] [CrossRef]
- Campo Eolico Sperimentale di Trento (Experimental Wind Turbine Test Field of Trento), 2006–2018. DICAM (University of Trento, Italy). Available online: http://www.eolicotrento.ing.unitn.it (accessed on 29 August 2021).
- Ionescu, R.D.; Ragazzi, M.; Battisti, L.; Rada, E.C.; Ionescu, G. Potential of electricity generation from renewable energy sources in standard domestic houses. Wit Trans. Ecol. Environ. 2013, 176, 245–253. [Google Scholar]
- Balduzzi, F.; Bianchini, A.; Carnevale, E.A.; Ferrari, L.; Magnani, S. Feasibility analysis of a Darrieus vertical-axis wind turbine installation in the rooftop of a building. Appl. Energy 2012, 97, 921–929. [Google Scholar] [CrossRef]
- Menet, J.L.; Valdes, L.C.; Menart, B. A comparative calculation of the wind turbines capacities on the basis of the Lσ criterion. Renew. Energy 2001, 22, 491–506. [Google Scholar] [CrossRef]
- Milborrow, D.J. Performance, blade loads and size limits for horizontal axis wind turbines. In Proceedings of the 4th BWEA Wind Energy Conversion (Cranfield: BHRA), Cranfield, UK, 24–26 March 1982. [Google Scholar]
- Siddiqui, M.S.; Durrani, N.; Akhtar, I. Quantification of the effects of geometric approximations on the performance of a vertical axis wind turbine. Renew. Energy 2015, 74, 661–670. [Google Scholar] [CrossRef]
- IEC 61400-2:2013. Wind Turbines—Part 2: Small Wind Turbines; IEC: Geneva, Switzerland, 2013. [Google Scholar]
- Wind Tunnel Test on Gorlov-Type H-VAWT, DICAM Internal Report. Not published. 2005.
- Personal Communication from International Manufacturer (name without disclosure permission), 2015.
- Van Bussel, G.J.W.; Mertens, S.; Polinder, H.; Sidler, H.F.A. The development of Turby, a small VAWT for the built environment. In Proceedings of the Global Wind Energy Conference 2004 Session Advanced Small Turbine Technology, Chicago, IL, USA, 30 March 2004. [Google Scholar]
- Anderson, J.W.; Brulle, R.V.; Birchfield, E.B.; Duwe, W.D. McDonnell 40-kW Giromill Wind System: Phase I—Design and Analysis; Technical report; Rockwell International Corp.: Golden, CO, USA; Rocky Flats Plant; McDonnell Aircraft Co.: St. Louis, MO, USA, 1979; Volume II. [Google Scholar]
- Wang, Y.; Shen, S.; Li, G.; Huang, D.; Zheng, Z. Investigation on aerodynamic performance of vertical axis wind turbine with different series airfoil shapes. Renew. Energy 2018, 126, 801–818. [Google Scholar] [CrossRef]
- Bravo, R.; Tullis, S.; Ziada, S. Performance testing of a small vertical-axis wind turbine. In Proceedings of the 43rd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 10–13 January 2005. [Google Scholar]
- Castelli, M.R.; Ardizzon, G.; Battisti, L.; Benini, E.; Pavesi, G. Modeling strategy and numerical validation for a darrieus vertical axis micro-wind turbine. In ASME 2010 International Mechanical Engineering Congress and Exposition; Citeseer: Princeton, NJ, USA, 2010; pp. 409–418. [Google Scholar]
- Naseema, A.; Uddina, E.; Alia, Z.; Aslama, J.; Shaha, S.R.; Sajida, M.; Zaidia, A.A.; Javedb, A.; Younisc, M.Y. Effect of vortices on power output of vertical axis wind turbine (VAWT). Sustain. Energy Technol. Assess. 2020, 37, 100586. [Google Scholar] [CrossRef]
- Solum, A.; Deglaire, P.; Eriksson, S.; Stålberg, M.; Leijon, M.; Bernhoff, H. Design of a 12 kW Vertical Axis Wind Turbine Equipped with a Direct Driven PM Synchronous Generator. In Proceedings of the EWEC 2006-European wind energy conference & exhibition, Athens, Greece, 27 February–2 March 2006. [Google Scholar]





| E | G | F | M | |
|---|---|---|---|---|
| ↓ | ↓ | ↓ | ↓ | |
| E → | - | o | o | o |
| G → | o | - | x | o |
| F → | o | x | - | o |
| M → | o | o | o | - |
| Material | Index M | ||
|---|---|---|---|
| [MPa] | [Mg/m] | [Pa/g/m] | |
| GFRP | 200 | 1.8 | 19.0 |
| CFRP | 600 | 1.6 | 44.5 |
| Aluminum alloy | 200 | 2.7 | 12.7 |
| Microlaminar wood | 32 | 0.5 | 20.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Battisti, L. Design Options to Improve the Dynamic Behavior and the Control of Small H-Darrieus VAWTs. Appl. Sci. 2021, 11, 9222. https://doi.org/10.3390/app11199222
Battisti L. Design Options to Improve the Dynamic Behavior and the Control of Small H-Darrieus VAWTs. Applied Sciences. 2021; 11(19):9222. https://doi.org/10.3390/app11199222
Chicago/Turabian StyleBattisti, Lorenzo. 2021. "Design Options to Improve the Dynamic Behavior and the Control of Small H-Darrieus VAWTs" Applied Sciences 11, no. 19: 9222. https://doi.org/10.3390/app11199222
APA StyleBattisti, L. (2021). Design Options to Improve the Dynamic Behavior and the Control of Small H-Darrieus VAWTs. Applied Sciences, 11(19), 9222. https://doi.org/10.3390/app11199222





