On the Properties of a Class of Impulsive Competition Beverton–Holt Equations

Abstract

This paper is devoted to a type of combined impulsive discrete Beverton–Holt equations in ecology when eventual discontinuities at sampling time instants are considered. Such discontinuities could be interpreted as impulses in the corresponding continuous-time logistic equations. The set of equations involve competition-type coupled dynamics among a finite set of species. It is assumed that, in general, the intrinsic growth rates and the carrying capacities are eventually distinct for the various species. The impulsive parts of the equations are parameterized by harvesting quotas and independent consumptions which are also eventually distinct for the various species and which control the populations’ evolution. The performed study includes the existence of extinction and non-extinction equilibrium points, the conditions of non-negativity and boundedness of the solutions for given finite non-negative initial conditions and the conditions of asymptotic stability without or with extinction of the solutions.

1. Introduction

The single-species non-autonomous discrete Beverton–Holt equation has been widely proposed for the study of the dynamics of populations in ecology and, in particular, for the characterization of the population growth dynamics. Its typical usefulness is related to the evolution of some species which reproduce by eggs. See, for instance, [1,2,3,4] and some of the references therein. Some usefulness of the models has been pointed out related to the fishery industry relying on the exploitation of species such as, for instance, coho salmon, plaice, haddock and others [1]. The model has also been reported to be useful for describing the evolution of the acorn wood pecker. Therefore, a certain effort has been devoted to researching the mathematical properties of such an equation as, for instance, the equilibrium points and their stability properties, as well as proving some classical conjectures on Beverton–Holt equations concerning the positivity of the solutions and the existence of stable oscillations [5,6,7,8,9,10,11,12,13,14]. The discretization could potentially be extended to time intervals, including two samples of, in general, distinct sampling periods, to separate the evolution of egg/larvae from that of reproductive adults in some species. In particular, two different sampling periods can be involved when the stages of egg/larvae evolution and those of adult evolution have different relevant average time intervals. For theoretical multirate sampling techniques of analysis involving two or more combined sampling periods, see, for instance, [15] and some of the references therein; see also [16,17,18,19,20,21,22]. An important effort has been devoted to rigorously prove the so-called Cushing–Henson Conjectures [8]. The standard single-species non-autonomous Beverton–Holt Equation is

$$x\left(k+1\right)=\frac{\mu \left(k\right)K\left(k\right)x\left(k\right)}{K\left(k\right)+\left(\mu \left(k\right)-1\right)x\left(k\right)},k\in {\mathit{N}}_0:=\mathit{N}\cup \left\{0\right\}$$

where $\mathit{N}$ is the set of natural numbers, for some given $x\left(0\right)=x_0\ge 0$, where $\left\{\mu \left(k\right)\right\}{}_{k=0}^{\infty }$ and ${\left\{K\left(k\right)\right\}}_{k=0}^{\infty }$ are, respectively, the intrinsic growth rate sequences of the species and the sequences of the carrying capacity of the habitat. The subscript $k$ refers to each sampling instant in the evolution of the equation. In the above equation, biologists refer to the population $x_k$ as the spawning stock at the continuous time $k{T}_s$, with $T_s$ being the sampling period in-between consecutive samples [4]. An interpretation of the Beverton–Holt equation is that it is the discrete version of the logistic equation running at a sampling period $T_s$ which is the time interval in-between two consecutive sampling instants $t_k=k{T}_s$ and $t_{k+1}=\left(k+1\right)T_s$; $\forall k\in {\mathit{N}}_0$. It is well-known that the Beverton–Holt equation, sometimes referred to as the Pielou logistic difference equation, is equivalent to the discrete Verhulst logistic equation $x\left(k\right)=r\left(k\right)x\left(k\right)/\left(x\left(k\right)+\nu \left(k\right)\right)$; $\forall k\in {\mathit{N}}_0$, under a given initial condition $x\left(0\right)=x_0$ [13]. The time-invariant version of the Verhulst equation is the discretization of the logistic continuous-time time-invariant equation $\dot{x}\left(t\right)=rx\left(t\right)\left(1-x\left(t\right)/K\right)$; $\forall t\in {\mathit{R}}_{0+}={\mathit{R}}_{+}\cup \left\{0\right\}$, $x\left(0\right)=x_0$ with $x\left(t\right)$ being the size of the resource population [13]. On the other hand, Stevic [12] has proved the conjectures of Beverton–Holt analytically [8], for periodically varying carrying capacities, which have been then rigorously confirmed. The first one of such conjectures claims the existence of a periodic steady-state regime in the event that the carrying capacity varies in a periodic fashion. Such a periodic steady-state is a global attractor of all the positive solutions. The second conjecture establishes that the average value of the periodically varying values of the solution is smaller than the average value of the carrying capacity over one such sampling interval. In addition, the Beverton–Holt equation has been extended by including discontinuities at the sampling time instants. Such discontinuities might be interpreted as a presence of spawning stock impulses in the corresponding continuous-time equation. The discontinuities are parameterized by two more sequences of parameters, the so-called harvesting (typically, fishing or hunting) quota sequence ${\left\{\left(1-b\left(k\right)\right)\right\}}_{k=1}^{\infty }$ and the so-called independent consumption sequence ${\left\{d\left(k\right)\right\}}_{k=1}^{\infty }$, which can include migrations “into” and “from” the studied region, namely, of positive and negative values, respectively. It could also include, in the first case, re-population by adults which is not properly reflected in the non-impulsive version of the equation since it is not related to the evolution from the larva stage to the adult one. In this way, an artificial repopulation may be interpreted in this context as a migration into the region considered for the population study. On the other hand, the loss of population by dead are included in the basic Beverton–Holt equation by appropriate settings of the environment carrying capacity and intrinsic growth rate. It can be pointed out that the regulation of the fishing quota is a very relevant problem since the fishing resources are becoming increasingly scarce. As a result, the impulsive extended Beverton–Holt model is parameterized by four parameters, or sequences, namely, the environment carrying capacity, the intrinsic growth rate, the harvesting quota and the independent consumption. It has to be clarified that, since input impulses in continuous-time dynamic systems translate into bounded discontinuities in the state (see, for instance, [23,24,25]), it is usual to refer to their counterpart discretized versions (with bounded steps at sampling time instants) as impulsive discrete systems. See, for instance, [13,26,27]. The Beverton–Holt equation has also been studied from a control point of view. For instance, the carrying capacity is designed in [28,29] as a control variable, within certain limiting bounds, to achieve a prefixed suitable solution. That strategy is feasible in certain closed or semi-closed habitats, such as, for instance, in fisheries or certain agricultural exploitations. There are also some more recent studies available where two-stage extended Beverton–Holt equations have been described in the sense that the solution depends on its values on two consecutive previous samples. The relevant functions of two arguments (that is, the two preceding values of the sampled solution) that define the evolution dynamics are assumed, by different researchers, to be non-decreasing in both or one of those arguments [30,31]. The study of periodic solutions has been also studied in the non-impulsive and in the impulsive Beverton–Holt equation since some of its parameterizing parameters, such as, for instance, the carrying capacity or the harvesting quota, are often subject to cyclic variations. See, for instance, [26,32,33] and some of the references therein. The dynamics associated with strong and weak Allee effects are studied in [34]; these lead, respectively, to extinction, for population stocks under a critical density, and to recovery, after small density levels are reached without the presence of a critical value. The results are applied to the study of the coexistence of two competing species subject to Allee effects and contest competition. It can be pointed out that a Beverton–Holt equation type is proposed and studied in [35] for a set with, in general, more than two competing species. It is found that the species with the best fitness outcompete the remaining ones. For the study of the involvement of two sampling periods for two stages of evolution of mosquito, see, for instance [35] and some of the references therein.

In this paper, a group of impulsive discrete Beverton–Holt equations reflecting competition among a finite number of species within the same habitat is considered with eventual discontinuities of the solution at the sampling instants due to harvesting or independent consumption influences. The above-mentioned set of equations involve competition-type coupled dynamics among the involved species. It is assumed that, in general, the intrinsic growth rates might be eventually distinct for the various species and, since they can have, in general, different fitness to the habitat, the various carrying capacities might be also distinct, in general. The impulsive effects at sampling instants in the equations are parameterized by the various harvesting quotas and the independent consumptions that can be also distinct for the various competing species. The performed study includes the existence of extinction and non-extinction equilibrium points, provided that the sequences of parameters converge to appropriate values, the conditions of non-negativity and boundedness of the solutions, for any given sets of finite non-negative initial conditions, and the description of sufficiency-type conditions, for asymptotic stability to any equilibrium point and, in particular, for either non-extinction or extinction situations. The case of intrinsic growth rates being less than unity and implying asymptotic extinction under supplementary conditions involving the independent consumption to the harvesting quota is also discussed through the second Lyapunov stability method.

The paper is organized as follows: Section 2 defines the whole impulsive competition Beverton–Holt model, the equilibrium points and the positivity and boundedness properties of the solution. The role of the intrinsic growth rate, carrying capacity, independent consumption and harvesting quota (the two last ones being closely related to the “impulsive” characteristic of the model at sampling instants) are explained and their relevance to the properties of the model are emphasized in the various given results. The concepts of best fitness, or dominance, of some species on the remaining ones, as well as the species consensus, are given and some related results are addressed. Section 3 is concerned with the Lyapunov stability properties of the equation, with special emphasis given to the case when its parameterization is time-varying. Some specific extinction conditions are investigated in Section 4, while some numerical investigation is discussed in Section 5. Finally, our conclusions end the paper.

2. The Competition Equation and Its Main Properties

2.1. The Single-Species Impulsive Beverton–Holt Equation

The subsequent impulsive discrete Beverton–Holt equation for a single species, [26,27,33] extends the standard one, which has been described in the introduction:

$$x^{-}\left(k+1\right)=\frac{\mu \left(k\right)K\left(k\right)x\left(k\right)}{K\left(k\right)+\left(\mu \left(k\right)-1\right)x\left(k\right)},$$

$$x\left(k+1\right)=x^{+}\left(k+1\right)=b\left(k+1\right)x^{-}\left(k+1\right)-d\left(k+1\right);\forall k\in {\mathit{N}}_0$$

(1)

with given finite initial conditions $x\left(0\right)\ge 0$, where $\mu \left(k\right)\in {\mathit{R}}_{0+}:={\mathit{R}}_{+}\cup \left\{0\right\}$ is the so-called intrinsic growth rate of the population, determined by life cycle and demographic properties (such as, for instance, species growth rate, survivorship rate, etc.) and $K\left(k\right)\in {\mathit{R}}_{+}$ is the so-called carrying capacity, a characteristic of the habitat dependent on resource availability, temperature, humidity, etc. Typically, the constraints $\mu \left(k\right)>1$ and $K\left(k\right)\in {\mathit{R}}_{+}$ for all $k\in {\mathit{N}}_0$ are assumed for the Beverton–Holt equation, since if, otherwise, the carrying capacity is zero, then the habitat is incompatible with the species evolution within it; if $\mu \left(k\right)\equiv 1$, then the species stock remains constant through time; if $0<\mu \left(k\right)<1$, then $x^{-}\left(k+1\right)/x\left(k\right)=\mu \left(k\right)/\left[1-\left(1-\mu \left(k\right)\right)x\left(k\right)/K\left(k\right)\right]$, so that two special atypical situations can happen, namely, if $1>\mu \left(k\right)>1-\left(1-\mu \left(k\right)\right)x\left(k\right)/K\left(k\right)$ for the initial samples and there is a sufficiently small population stock, which keeps the right-hand-side positivity, then the species stock grows over time, but it can tend to negative values, making the model to be not well-posed for a sufficiently extended time. If, on the contrary, $\mu \left(k\right)<1-\left(1-\mu \left(k\right)\right)x\left(k\right)/K\left(k\right)$ for all samples, then the population asymptotically extinguishes.

On the other hand, the impulsive parameters, which can modify the stocks of population, to the right of the sampling instants related to their left-values are the harvesting quota $\left(1-b\left(k\right)\right)\in {\mathit{R}}_{+}$; $\forall k\in {\mathit{N}}_0$, which depends on the authorities policy depending on the spawning stock and foreseen recruitments and the independent consumption $d\left(k\right)\left(\le b\left(k\right)x\left(k\right)\right)\in \mathit{R}$; $\forall k\in {\mathit{N}}_0$ that implies recruitment variations depending on unforeseen disturbances, artificial re-population actions and local migrations “towards” or “from” the studied habitat. For easy presentation of some of the technical results, the complementary harvesting quota $b\left(k\right)\in {\mathit{R}}_{0+}$; $\forall k\in {\mathit{N}}_0$ is used. Some particular results in this paper are given for the case of intrinsic growth rates under unity and for negative harvesting quotas, or, equivalently, for complementary harvesting quotas exceeding unity. The physical interpretation of this situation is that a re-population with a number of adults exceeding to population stock is performed with a ratio larger than unity.

Remark 1.

Note that the public regulations on fishing or hunting taking into account the stocks of population imply that $b\left(k\right)\le 1$; $\forall k\in {\mathit{N}}_0$. However, if a repopulation with adults is intended, which is sometimes the case, then it can be decided to increase the above coefficient exceeding unity in the case that the population stock is low. Therefore, we admit, at the level of a general formulation, that the complementary harvesting quota is non-negative and bounded. It turns out that the independent consumption is positive, if there is a net flux of individuals from the studied habitat to outside of it, so that the population stock decreases, and it is negative, if there is a net flux entering the habitat, so that the population stock increases. Finally, it is zero if there is no interchange of population of the habitat with the environment. The independent consumption can also take into account repopulation actions that are not linked to a proportion on the existing population stock.

Note that, if $x\left(0\right)=0$, or if $K\left(0\right)=0$ and ${\left\{d\left(k\right)\right\}}_{k=0}^{\infty }\equiv 0$, then ${\left\{x\left(k\right)\right\}}_{k=0}^{\infty }\equiv 0$. It can be argued that, although it is a common hypothesis to assume that $\left\{K\left(k\right)\right\}\subset {\mathit{R}}_{+}$ and $\left\{\mu \left(k\right)-1\right\}\subset {\mathit{R}}_{+}$, it is possible, under certain extra constraints on the state of sufficient smallness, related to information about the equation parameters, that $\mu \left(k\right)$ could take values under unity. To clarify this concern, let us assume Equation (1) without impulsive effects, that is, ${\left\{b\left(k\right)\right\}}_{k=0}^{\infty }\equiv 1$ and ${\left\{d\left(k\right)\right\}}_{k=0}^{\infty }\equiv 0$, so that $x\left(k\right)=x^{-}\left(k\right)$; $\forall k\in {\mathit{N}}_0$. Thus, for any given $k\in {\mathit{N}}_0$, if $\mu \left(k\right)\in \left[0,1\right]$, then $x\left(k+1\right)\ge 0$ if $0\le x\left(k\right)\le \frac{K\left(k\right)}{1-\mu \left(k\right)}$, and $x\left(k+1\right)$ is, furthermore, finite if $x\left(k\right)<\frac{K\left(k\right)}{1-\mu \left(k\right)}$. Furthermore, if $\mu \left(k\right)=0$, then ${\left\{x\left(j\right)\right\}}_k^{\infty }\equiv 0$, so that extinction happens in finite time. If ${\left\{\mu \left(j\right)\right\}}_k^{\infty }\equiv 1$, then ${\left\{x\left(j\right)\right\}}_k^{\infty }\equiv x\left(k\right)$, so that the population remains constant and fixed to its value at the $k-th$ sample.

Now, let us assume that $\mu \left(k\right)\in \left(0,1\right)$ and $0<x\left(k\right)<\frac{K\left(k\right)}{1-\mu \left(k\right)}$, implying that $x\left(k+1\right)>0$ and finite. Let us also assume that $\mu \left(k+1\right)\in \left(0,1\right)$. Then, $0<x\left(k+1\right)<\frac{K\left(k+1\right)}{1-\mu \left(k+1\right)}$ for $x\left(k+2\right)>0$ and finite. One obtains

$$x\left(k+1\right)=\frac{\mu \left(k\right)K\left(k\right)x\left(k\right)}{K\left(k\right)-\left(1-\mu \left(k\right)\right)x\left(k\right)}<\frac{K\left(k+1\right)}{1-\mu \left(k+1\right)}$$

which implies that

$$\left[\mu \left(k\right)K\left(k\right)\left(1-\mu \left(k+1\right)\right)+K\left(k+1\right)\left(1-\mu \left(k\right)\right)\right]x\left(k\right)<K\left(k\right)K\left(k+1\right)$$

so that the former non-negativity constraint $x\left(k\right)<\frac{K\left(k\right)}{1-\mu \left(k\right)}$ is amended by the stronger one

$$x\left(k\right)<\frac{K\left(k\right)K\left(k+1\right)}{\mu \left(k\right)K\left(k\right)\left(1-\mu \left(k+1\right)\right)+K\left(k+1\right)\left(1-\mu \left(k\right)\right)}<\frac{K\left(k\right)}{1-\mu \left(k\right)}$$

And, proceeding recursively in the same way, it follows that $x\left(k\right)$ has a strictly decreasing infinite sequence of bounded non-negative upper-bounds. However, note that, if $\mu \left(k+1\right)=1$, then the upper-bound remains unaltered. Thus, we have the following results.

Lemma 1.

Let us assume that ${\left\{d\left(k\right)\right\}}_{k=0}^{\infty }\equiv 0$ and ${\left\{b\left(k\right)\right\}}_{k=0}^{\infty }\equiv 1$ (namely, there is no impulsive effect). Let us also assume that, for some finite $k\in {\mathit{N}}_0$, ${\left\{\mu \left(j\right)\right\}}_{k_0}^{\infty }\subset \left(0,1\right)$, ${\left\{x\left(j\right)\right\}}_{k_0}^{\infty }\subset {\mathit{R}}_{0+}$ is bounded and either ${\left\{K\left(k\right)\right\}}_{k=k_0}^{\infty }$ is non-decreasing or ${\left\{K\left(k\right)\right\}}_{j=k_0}^{\infty }\subset \left(0,2\right)$. Then, $\exists k_1\ge 1$ such that $x\left(k\right)=0$ for $k\ge k_0+k_1$ (that is, there is extinction in finite time).

Proof. 

Note that, since ${\left\{\mu \left(j\right)\right\}}_{k_0}^{\infty }\subset \left(0,1\right)$, ${\left\{x\left(k\right)\right\}}_{k=0}^{\infty }\subset \left[0,\infty \right)$ is strictly decreasing if and only if

$$x\left(k+1\right)-x\left(k\right)=\left(\frac{\mu \left(k\right)K\left(k\right)}{K\left(k\right)-\left(1-\mu \left(k\right)\right)x\left(k\right)}-1\right)x\left(k\right)<0;\forall k\left(\ge k_0\right)\in {\mathit{N}}_0$$

If $x\left(k\right)=0$ for some finite $k$, then the result is already proved. Thus, let us assume that $x\left(k\right)>0$; $\forall k\left(\ge k_0\right)\in {\mathit{N}}_0$. Note that $x\left(k\right)>0$, if and only if $x\left(k\right)<\min \left(K\left(k\right),\frac{K\left(k\right)}{1-\mu \left(k\right)}\right)=K\left(k\right)$, since $\frac{\mu \left(k\right)K\left(k\right)}{K\left(k\right)-\left(1-\mu \left(k\right)\right)x\left(k\right)}<1$, that is, since $\left(1-\mu \left(k\right)\right)x\left(k\right)<\left(1-\mu \left(k\right)\right)K\left(k\right)$, leading to $x\left(k\right)<K\left(k\right)$; $\forall k\left(\ge k_0\right)\in {\mathit{N}}_0$, in order for it to be jointly strictly decreasing with the denominator of the right-hand-side being positive for all $\forall k\left(\ge k_o\right)\in {\mathit{N}}_0$. Then, either $\left(x\left(k\right)-K\left(k\right)\right)\to 0$ as $k\to \infty$, or $x\left(k\right)\to 0$ as $k\to \infty$; furthermore,

$$x\left(k\right)<\mathit{min}\left(K\left(k\right),x\left(k-1\right)\right)<\dots <\underset{k\ge j\ge 0}{\mathit{inf}}K\left(j\right);\forall k\left(\ge k_0\right)\in {\mathit{N}}_0$$

Since ${\left\{K\left(k\right)\right\}}_{j=k_0}^{\infty }$ is non-decreasing, then $\underset{k_0\ge k\ge 0}{\mathit{inf}}K\left(k\right)=\underset{\infty \ge k\ge 0}{\mathit{inf}}K\left(k\right)\ge \underset{\infty \ge k\ge k_0}{\mathit{inf}}K\left(k\right)$, so that

$$x\left(k\right)<\mathit{min}\left(\underset{k\ge j\ge 0}{\mathit{inf}}K\left(j\right),x\left(k-1\right)\right)\ge \underset{\infty \ge k\ge k_0}{\mathit{inf}}K\left(k\right)\ge K\left(k_0\right);\forall j\left(\ge k_0\right)\in {\mathit{N}}_0$$

Therefore, $\left(x\left(k\right)-K\left(k\right)\right)\to 0$ as $k\to \infty$ is not possible, so $x\left(k\right)\to 0$ as $k\to \infty$. Since $k_0$ is finite and ${\left\{x\left(k\right)\right\}}_{k_0}^{\infty }\subset {\mathit{R}}_{0+}$ is strictly decreasing and converges asymptotically to zero, then there is some finite $k_1\in \mathit{N}$ such that $x\left(k_0+k_1-1\right)<2$ and the species reproduction is not feasible for the next samples, so that extinction happens in finite time $k_0+k_1$.

If the assumption of ${\left\{K\left(k\right)\right\}}_{k=k_0}^{\infty }$ being non-decreasing is replaced by ${\left\{K\left(k\right)\right\}}_{j=k_0}^{\infty }\subset \left(0,2\right)$, then the result still holds, since $x\left(k\right)<K\left(k\right)<2$; $\forall k\left(\ge k_0\right)\in {\mathit{N}}_0$ so that, in the event that $\left(x\left(k\right)-K\left(k\right)\right)\to 0$ as $k\to \infty$, the number of individuals becomes zero after a finite time. □

Lemma 2.

Let us assume that ${\left\{d\left(k\right)\right\}}_{k=0}^{\infty }\equiv 0$, ${\left\{b\left(k\right)\right\}}_{k=0}^{\infty }\equiv 1$ and that $x\left(0\right)>0$. Let us also assume that, for some finite $k\in {\mathit{N}}_0$, ${\left\{\mu \left(j\right)\right\}}_k^{\infty }\subset \left(0,1\right]$, $card\left\{j\left(\ge k\right)\in {\mathit{N}}_0\text{:}\mu \left(j\right)<1\right\}<\infty$ and ${\left\{x\left(j\right)\right\}}_k^{\infty }\subset {\mathit{R}}_{0+}$ is bounded. Then, $x\left(k\right)>0$, that is, there is no extinction in finite time and $x\left(k\right)=x\left(>0\right)$; $\forall k\ge k_0\left(\in {\mathit{N}}_0\right)$ with finite $k_0$, so that a non-extinction equilibrium point is reached in finite time.

In Lemma 2, note that the condition $card\left\{j\left(\ge k\right)\in {\mathit{N}}_0\text{:}\mu \left(j\right)<1\right\}<\infty$ implies that $card\left\{j\left(\ge k\right)\in {\mathit{N}}_0\text{:}\mu \left(j\right)=1\right\}={\chi }_0$, that is an infinity denumerable cardinal. In other words, there is only a finite number of samples in the infinite subset of the natural numbers $\left\{k,k+1,\dots ,+\infty \right\}$ for which the intrinsic growth rate is strictly less than unity. This condition guarantees that, contrarily to Lemma 1, there is no extinction at the $k-th$ sample. Additionally, it turns out that, since the intrinsic growth rate sequence is less than one for a finite number of samples, there exists a finite non-negative integer number $k_0$ such that $\mu \left(k\right)=1$: $\forall k\ge k_0$ implying that $x\left(k_0+j\right)=x\left(k_0\right)$; $\forall j\in {\mathit{N}}_0$ leading to the existence of an equilibrium point. It is addressed, in Section 5, how it is possible to achieve asymptotic extinction in the single species and in the competition impulsive Beverton–Holt equations under certain trade-offs between the independent consumption sequence and the harvesting quota, even if the intrinsic growth rate is under unity.

2.2. The Competition Impulsive Beverton–Holt Equation

The class of impulsive discrete Beverton–Holt Equation of $n$ competing species proposed for further analysis is a generalization of the discrete Beverton–Holt Equation (1) for the particular case of a single species, i.e., for $n=1$, with a constant parameterization of intrinsic growth rates and carrying capacities through time being expressed for $n$ competing species as

$$x_i^{-}\left(k+1\right)=\frac{{\mu }_i{K}_i{x}_i\left(k\right)}{K_i+{\displaystyle {\sum }_{j=1}^n{c}_{ji}}\left({\mu }_i-1\right)x_j\left(k\right)}$$

(2)

$$x_i\left(k+1\right)=b_i\left(k+1\right)x_i^{-}\left(k+1\right)-d_i\left(k+1\right);\forall i\in \overline{n}=\left\{1,2,\dots ,n\right\},\forall k\in {\mathit{N}}_0$$

(3)

with given finite initial conditions $x_i\left(0\right)\ge 0$. For some coupling coefficients $c_{ij}\ge 0$; $\forall i,j\in \overline{n}$ with $c_{ii}=1$; $\forall i\in \overline{n}$. The subscripts stand for the populations and model parameters of the various competing species, while each current sample is denoted in parenthesis. The superscript “-” stands for the population values to the left of a sampling instant, while the absence of superscript indicates its value to the right of sampling instant. Note that it was assumed, for the sake of exposition simplicity, that the intrinsic growth rate, carrying capacity and inter-species coupling dynamics coefficients are constant through time for each one of the species. The impulsive control parameters are the members of the real sequences ${\left\{b_i\left(k\right)\right\}}_{k=1}^{\infty }$ and ${\left\{d_i\left(k\right)\right\}}_{k=1}^{\infty }$; $\forall i\in \overline{n}$. Those sequences may modify the levels of populations to the right of the sampling instants. If those sequences are identically zero for any population at a sampling instant, then its value after sampling remains unaltered. The combination of (2) and (3) yields

$$x_i\left(k+1\right)=\frac{\left[b_i\left(k+1\right){\mu }_i{K}_i-d_i\left(k+1\right)\left({\mu }_i-1\right)\right]x_i\left(k\right)-d_i\left(k+1\right)\left(K_i\left(k\right)+{\displaystyle {\sum }_{j\left(\ne i\right)=1}^n{c}_{ji}}\left(k\right)\left({\mu }_i-1\right)x_j\left(k\right)\right)}{K_i\left(\right)+{\displaystyle {\sum }_{j=1}^n{c}_{ji}}\left({\mu }_i-1\right)x_j\left(k\right)};\forall k\in {\mathit{N}}_0,\forall i\in \overline{n}.$$

(4)

It is of interest to summarize, first, some basic properties of the impulsive time-invariant single Beverton–Holt equation for only one species to then interpret some parallel properties associated with a tandem of competing species. It is apparent that the equilibrium point exists also if the left and right values at the sampling time instants are non-negative and finite, even if they are distinct. In the case that they are distinct, there is an oscillatory equilibrium solution switching among those left and right values at the sampling time instants. In the case that the four parameters are potentially time-varying, the mentioned impulsive Beverton–Holt equation for a single species $\left(\mathrm{that}\mathrm{is},n=1\right)$ is the following one:

$$x^{-}\left(k+1\right)=\frac{\mu \left(k\right)K\left(k\right)x\left(k\right)}{K\left(k\right)+\left(\mu \left(k\right)-1\right)x\left(k\right)};$$

$$x\left(k+1\right)=b\left(k+1\right)x^{-}\left(k+1\right)-d\left(k+1\right)$$

that, combined, yield

$$\begin{gathered} x\left(k+1\right)=b\left(k+1\right)x^{-}\left(k+1\right)-d\left(k+1\right) \\ =\frac{\left[\mu \left(k\right)b\left(k+1\right)K\left(k\right)-d\left(k+1\right)\left(\mu \left(k\right)-1\right)\right]x\left(k\right)-d\left(k+1\right)K\left(k\right)}{K\left(k\right)+\left(\mu \left(k\right)-1\right)x\left(k\right)} \end{gathered}$$

2.3. Equilibrium Points

The subsequent result holds for the case of one single species.

Theorem 1.

Let us assume that either the intrinsic growth rates, carrying capacities, harvesting quotas and independent consumptions are constant parameters, or that the related parameterizing sequences converge asymptotically to constant parameters. Then, the following properties hold:

(i) 

There exist equilibrium points (or, more properly, left and right limits of equilibrium points)

$$x_{1,2}=\frac{\mu bK-d\left(\mu -1\right)-K\pm \sqrt{{\left(\mu bK-d\left(\mu -1\right)-K\right)}^2-4\left(\mu -1\right)dK}}{2\left(\mu -1\right)}$$

$$x_{1,2}^{-}\ge \frac{x_{1,2}+d}{b}$$

with physical sense, or feasible, (i.e., being real non-negative) of the single-species impulsive Beverton–Holt equation if and only if

$$d\in \left[-x_1,\mathit{min}\left(\frac{{\left(\sqrt{\mu b}-1\right)}^{2}K}{\mu -1},\frac{\left(\mu b-1\right)K}{\mu -1}\right)\right]\cup \left[\frac{{\left(\sqrt{\mu b}+1\right)}^{2}K}{\mu -1},\infty \right)$$

If $\mu \ge \mathit{max}\left(1,b^{-1}\right)$, then the above constraint becomes

$$d\in \left[-x_1,\frac{{\left(\sqrt{\mu b}-1\right)}^{2}K}{\mu -1}\right]\cup \left[\frac{{\left(\sqrt{\mu b}+1\right)}^{2}K}{\mu -1},\infty \right)$$

(ii) 

If $d=0$ and $b=1$, then there are no impulses at the equilibrium steady-state, so that the equilibrium solution is not oscillatory between its left and right values at the sampling instants, that is, $x_1=x_1^{-}=0$ (extinction) and $x_2=x_2^{-}=K$.

If $d=0$, then the equilibrium points become $x_1=0$ (extinction) and $x_2=\frac{\left(\mu b-1\right)K}{\mu -1}>0$, provided that either $\mu >\mathit{max}\left(1,b^{-1}\right)$ or $\mu <\mathit{min}\left(1,b^{-1}\right)$. If, in addition, $\mu >1$ and $b={\mu }^{-1}$, then $x_1=x_2=0$.

(iii) 

If $d=\frac{\left(\mu b-1\right)K}{\mu -1}<0$, then there is only a non-negative equilibrium point $x_1=\sqrt{\left|\frac{d}{\mu -1}\right|}K>0$ with either $\mu >1$ and $d<0$ or $\mu <1$ and $d<0$.

(iv) 

If $d=\frac{\mu bK}{\mu -1}$, then there is only a non-negative equilibrium point $x_1=\frac{\sqrt{1+4\left(1-\mu b\right)}-1}{2\left(\mu -1\right)}K>0$ with $\mu >1$ and $b\in {\left[0,{\mu }^{-1}\right)}^{}$. Let us assume that negative harvesting quotas are allowed, then $x_1=\frac{1+\sqrt{4\mu b-3}}{2\left(1-\mu \right)}>0$, provided that $b>\mathit{max}\left({\mu }^{-1},\frac{3}{4}\mu \right)$.

Proof. 

The equilibrium point to the left and right of the sampling instants satisfies $x^{-}=\frac{x+d}{b}$ subject to the constraint

$$x=\frac{\left[\mu bK-d\left(\mu -1\right)\right]x-dK}{K+\left(\mu -1\right)x}$$

The above constraint may be rewritten as

$$\left(\mu -1\right)x^2-\left[\mu bK-d\left(\mu -1\right)-K\right]x+dk=0$$

whose zeros $x_1,x_2\ge x_1$ are

$$x_{1,2}=\frac{\mu bK-d\left(\mu -1\right)-K\pm \sqrt{{\left(\mu bK-d\left(\mu -1\right)-K\right)}^2-4\left(\mu -1\right)dK}}{2\left(\mu -1\right)},$$

which have to be real and non-negative for the equilibrium point to have a physical sense, so that two joint necessary conditions are

$$d\le d_0=\frac{\left(\mu b-1\right)K}{\mu -1};{\left(\mu bK-d\left(\mu -1\right)-K\right)}^2\ge 4\left(\mu -1\right)dK$$

The second constraint can be re-arranged in the form

$${\left(\mu -1\right)}^2{d}^2-2\left[\left(\mu b-1\right)+2\right]K\left(\mu -1\right)d+{\left(\mu b-1\right)}^2{K}^2\ge 0$$

Defining the auxiliary variable $f=\left(\mu -1\right)d$, the above inequality takes the form

$$g\left(f\right)=f^2-2\left(\mu b+1\right)Kf+{\left(\mu b-1\right)}^2{K}^2\ge 0$$

One obtains that the zeros of the left-hand-side of the above constraint are

$$f_{1,2}=\left(\mu b+1\pm \sqrt{{\left(\mu b+1\right)}^2-{\left(\mu b-1\right)}^2}\right)K=\left(\mu b+1\pm 2\sqrt{\mu b}\right)K$$

and the constraint $g\left(f\right)\ge 0$ holds, since $g\left(f\right)=0$ is a convex parabola of zeros $f_1,f_2\ge f_1$, if any of the two constraints below holds

$$d\ge d_2=\frac{{\left(\sqrt{\mu b}+1\right)}^{2}K}{\mu -1}\mathrm{or}d\le d_1=\frac{{\left(\sqrt{\mu b}-1\right)}^{2}K}{\mu -1}$$

In order that, in addition, $x_{1,2}^{-}\ge \frac{x_{1,2}+d}{b}\ge 0$ (in order for the equilibrium points to the left of the sampling instants to be non-negative as well), $d\ge -x_1$ since $0\le x_1\le x_2$. Furthermore, $d\in \left[-x_1,\min \left(d_0,d_1\right)\right]\cup \left[d_2+\infty \right)$. If $\mu \ge \max \left(1,b^{-1}\right)$, then ${\left(\sqrt{\mu b}-1\right)}^2\le \mu b-1$. Property (i) follows directly from the above constraints. Property (ii) follows directly from the corresponding particular cases of Property (i).

To prove Property (iii), note that, if $d=\frac{\left(\mu b-1\right)K}{\mu -1}<0$, then the equilibrium point satisfies the constraint $\left(\mu -1\right)x^2-Kd=0$, which yields $x=\sqrt{\left|\frac{d}{\mu -1}K\right|}>0$ for $\mu >1$ and $d>0$, or for $\mu <1$ and $d<0$. The equilibrium point is unfeasible for alternative combinations of values of $\mu$ and $d$.

To prove Property (iv), note that, if $d=\frac{\mu bK}{\mu -1}$, then the equilibrium point constraint $x=\frac{\left[\mu bK-d\left(\mu -1\right)\right]x-dK}{K+\left(\mu -1\right)x}$ becomes $x=\frac{\left|d\right|K}{K+\left(\mu -1\right)x}$ for $d=\frac{\left(\mu b-1\right)K}{\mu -1}<0$. Thus, the equivalent constraint $\left(\mu -1\right)x^2+Kx-\left|d\right|K=0$ has, as zeros,

$$x_{1,2}=\frac{-K\pm \sqrt{K^2+4\left(\mu -1\right)\left|d\right|K}}{2\left(\mu -1\right)}=\frac{-1\pm \sqrt{1+4\left(1-\mu b\right)}}{2\left(\mu -1\right)}K$$

Let us consider two cases for $d<0$, namely,

Case a: $\mu b>1$ and $\mu <1$ so that, if $b>{\mu }^{-1}>1$ is not admissible, so that $x_{1,2}<0$ (i.e., both unfeasible since negative). If $b>1$ is admissible, then $x_1=\frac{1+\sqrt{4\mu b-3}}{2\left(1-\mu \right)}>0$, provided that $b>\mathit{max}\left({\mu }^{-1},\frac{3}{4}\mu \right)$ and $x_2=\frac{1-\sqrt{4\mu b-3}}{2\left(1-\mu \right)}<0$ (i.e., unfeasible), since $\mu b>1$.

Case b: $\mu b<1$ and $\mu >1$, implying $b\in {\left[0,{\mu }^{-1}\right)}^{}$, leading to $x_2=\frac{-1-\sqrt{1+4\left(1-\mu b\right)}}{2\left(\mu -1\right)}K<0$ (unfeasible) and $x_1=\frac{-1+\sqrt{1+4\left(1-\mu b\right)}}{2\left(\mu -1\right)}K>0$.

Therefore, only one equilibrium point is non-negative. Property (iii) has been proved. □

Note that Theorem 1(iii) establishes the existence of a non-negative equilibrium point with intrinsic growth rates exceeding unity and positive harvesting quotas subject to a prescribed upper-bound. The physical interpretation is that there is a certain migration flux (either spontaneous or due to a monitored re-population intervention) of adult individuals from the habitat environment entering the habitat under study. Note that Theorem 1(iii) was also extended by first considering that Case a is non-negative with $b>{\mu }^{-1}>1$, with $\mu <1$ and $d<0$. This implies that there is a negative migration flux (i.e., a supply of individuals from the environment to the habitat, either spontaneous or via intervention) and a negative harvesting quota, namely, a monitored supply of larvae to the habitat with associated complementary harvesting quota in a proportion greater than unity related to its natural stock within the habitat. In this case, $x_2=\frac{1-\sqrt{4\mu b-3}}{2\left(1-\mu \right)}<0$ (unfeasible) and $x_1=\frac{1+\sqrt{4\mu b-3}}{2\left(1-\mu \right)}>0$, provided that $b>\mathit{max}\left({\mu }^{-1},\frac{3}{4}\mu \right)$.

2.4. Non-Negativity and Boundedness of the Solutions

The subsequent assumptions are eventually made in the sequel in some of the technical results.

Assumption 1.

The carrying capacities, intrinsic growth rates and inter-species coupling dynamics are constant, i.e., $K_i>0$, ${\mu }_i>1$, $c_{ii}=1$, $c_{ij}\ge 0$; $\forall i,j\left(\ne i\right)\in \overline{n}$.

Assumption 2.

The complementary harvesting quotas and independent consumption sequences satisfy the upper-bounding constraints $0\le b_i\left(k\right)\le {\overline{b}}_i<+\infty$; $-\infty <d_i\left(k\right)\le b_i\left(k\right)x_i^{-}\left(k\right)$; $\forall i\in \overline{n}$, $\forall k\in {\mathit{N}}_0$.

It can be pointed out that Assumption 1 can be extended directly to the case that the constant parameters are sequences depending on time. It can be also generalized for ${\mu }_i\le 1$ under the additional constraint $\frac{K_i}{1-{\mu }_i}\ge {\displaystyle {\sum }_{j=1}^n{c}_{ji}}{x}_j\left(k\right)$; $\forall i,j\left(\ne i\right)\in \overline{n}$ or for its extension to the case when carrying capacities, intrinsic growth rates and inter-species coupling dynamics are sequences depending on time. The interpretation is that, if the intrinsic growth rate is under unity, then the coupling sequences from the remaining populations to the $i-th$ have to be small enough related to the ratio $K_i\left(k\right)/\left(1-{\mu }_i\left(k\right)\right)$. Note that the populations stocks to the left and right limits of the sampling instants have to be non-negative for coherency of the model evolution. The constraints of Assumption 2 guarantee that the populations to the left limits of the sampling instants are non-negative if those to the right limits are non-negative.

The following result on the non-negativity of the solution is directly obtained from (2)–(3) and Assumptions 1–2.

Proposition 1.

Under Assumptions 1–2, for all $i\in \overline{n}$ and any given $k\in {\mathit{N}}_0$, if $x_i\left(k\right)\ge 0$, then $x_i^{-}\left(k+1\right)\ge 0$ and $x_i\left(k+1\right)\ge 0$. If $x_i\left(k\right)>0$, then $x_i^{-}\left(k+1\right)>0$ and, also, $x_i\left(k+1\right)>0$ if, furthermore, $d_i\left(k+1\right)<b_i\left(k+1\right)x_i^{-}\left(k+1\right)$.

Assumptions 1–2 also lead to the subsequent result on the dominance (or best fitness) of a certain population on another one for all samples.

Proposition 2.

Let us assume that, for any given $i,j\left(\ne i\right)\in \overline{n}$, ${\mu }_i\ge {\mu }_j$, $K_i\ge {\overline{K}}_j=\underset{\ell \in n}{\mathit{max}}\left(\frac{c_{\ell i}}{c_{\ell j}}\right)\frac{{\mu }_i\left({\mu }_i-1\right)}{{\mu }_j\left({\mu }_j-1\right)}{K}_j$, ${\left\{b_i\left(k\right)-b_j\left(k\right)\right\}}_{k=1}^{\infty }\subset {\mathit{R}}_{0+}$ and ${\left\{d_j\left(k\right)-d_i\left(k\right)\right\}}_{k=1}^{\infty }\subset {\mathit{R}}_{0+}$ and that Assumptions 1–2 hold. Thus, if $x_i\left(0\right)\ge x_j\left(0\right)$, then ${\left\{x_i^{-}\left(k\right)-x_j^{-}\left(k\right)\right\}}_{k=0}^{\infty }\subset {\mathit{R}}_{0+}$ and ${\left\{x_i\left(k\right)-x_j\left(k\right)\right\}}_{k=0}^{\infty }\subset {\mathit{R}}_{0+}$.

The above conditions may be relaxed as follows:

If $K_i\ge {\overline{K}}_j$, ${\mu }_i\ge {\mu }_j$ and $x_i\left(0\right)\ge \frac{{\mu }_j}{{\mu }_i}{x}_j\left(0\right)$, then ${\left\{x_i^{-}\left(k\right)-x_j^{-}\left(k\right)\right\}}_{k=1}^{\infty }\subset {\mathit{R}}_{0+}$ and ${\left\{x_i^{-}\left(k\right)-x_j^{-}\left(k\right)\right\}}_{k=1}^{\infty }\subset {\mathit{R}}_{0+}$, provided that $d_j\left(k\right)-d_i\left(k\right)\ge b_j\left(k\right)x_j^{-}\left(k\right)-b_i\left(k\right)x_i^{-}\left(k\right)$; $\forall k\in \mathit{N}$.

Proof. 

Note that

$$\begin{gathered} x_i^{-}\left(1\right)=\frac{{\mu }_i{x}_i\left(0\right)}{1+{\displaystyle {\sum }_{\ell =1}^n{c}_{\ell i}}\left({\mu }_i-1\right)K_i^{-1}{x}_{\ell }\left(0\right)} \\ \ge x_j^{-}\left(1\right)=\frac{{\mu }_j{x}_j\left(0\right)}{1+{\displaystyle {\sum }_{\ell =1}^n{c}_{\ell j}}\left({\mu }_j-1\right)K_j^{-1}{x}_{\ell }\left(0\right)} \end{gathered}$$

(5)

if $x_i\left(0\right)\ge x_j\left(0\right)$, ${\mu }_i\ge {\mu }_j$ and

$$0\le {\displaystyle {\sum }_{\ell =1}^n\left(c_{\ell i}\left({\mu }_i-1\right)K_i^{-1}-c_{\ell j}\left({\mu }_j-1\right)K_j^{-1}\right)}{x}_{\ell }\left(0\right)\le 0$$

which holds if $K_i\ge {\overline{K}}_j$ and ${\mu }_i{x}_i\left(0\right)\ge {\mu }_j{x}_j\left(0\right)$, which leads to $x_i^{-}\left(1\right)\ge x_j^{-}\left(1\right)$. Furthermore, $x_i\left(1\right)\ge x_j\left(1\right)$ since $x_i\left(0\right)\ge x_j\left(0\right)$, $b_i\left(1\right)-b_j\left(1\right)\ge 0$ and $d_j\left(1\right)-d_i\left(1\right)\ge 0$. Then, one obtains recursively that ${\left\{x_i^{-}\left(k\right)-x_j^{-}\left(k\right)\right\}}_{k=0}^{\infty }\subset {\mathit{R}}_{0+}$ and ${\left\{x_i\left(k\right)-x_j\left(k\right)\right\}}_{k=0}^{\infty }\subset {\mathit{R}}_{0+}$, as claimed in the first part of the proposition. The second part is direct, since, under the assumptions that $K_i\ge K_j$ and $x_i\left(0\right)\ge \frac{{\mu }_j}{{\mu }_i}{x}_j\left(0\right)$, one obtains ${\mu }_i{K}_i{x}_i\left(0\right)\ge {\mu }_j{K}_j{x}_j\left(0\right)$ (not necessarily under the joint constraints $x_i\left(0\right)\ge x_j\left(0\right)$, ${\mu }_i\ge {\mu }_j$ and $K_i\ge K_j$). This implies that $x_i^{-}\left(1\right)\ge x_j^{-}\left(1\right)$, which, together with $d_j\left(1\right)-d_i\left(1\right)\ge b_j\left(1\right)x_j^{-}\left(1\right)-b_i\left(1\right)x_i^{-}\left(1\right)$ (not necessarily with $d_j\left(1\right)\ge d_1\left(1\right)$), implies that $x_i\left(1\right)\ge x_j\left(1\right)$. The result for $k\ge 1$ follows recursively. □

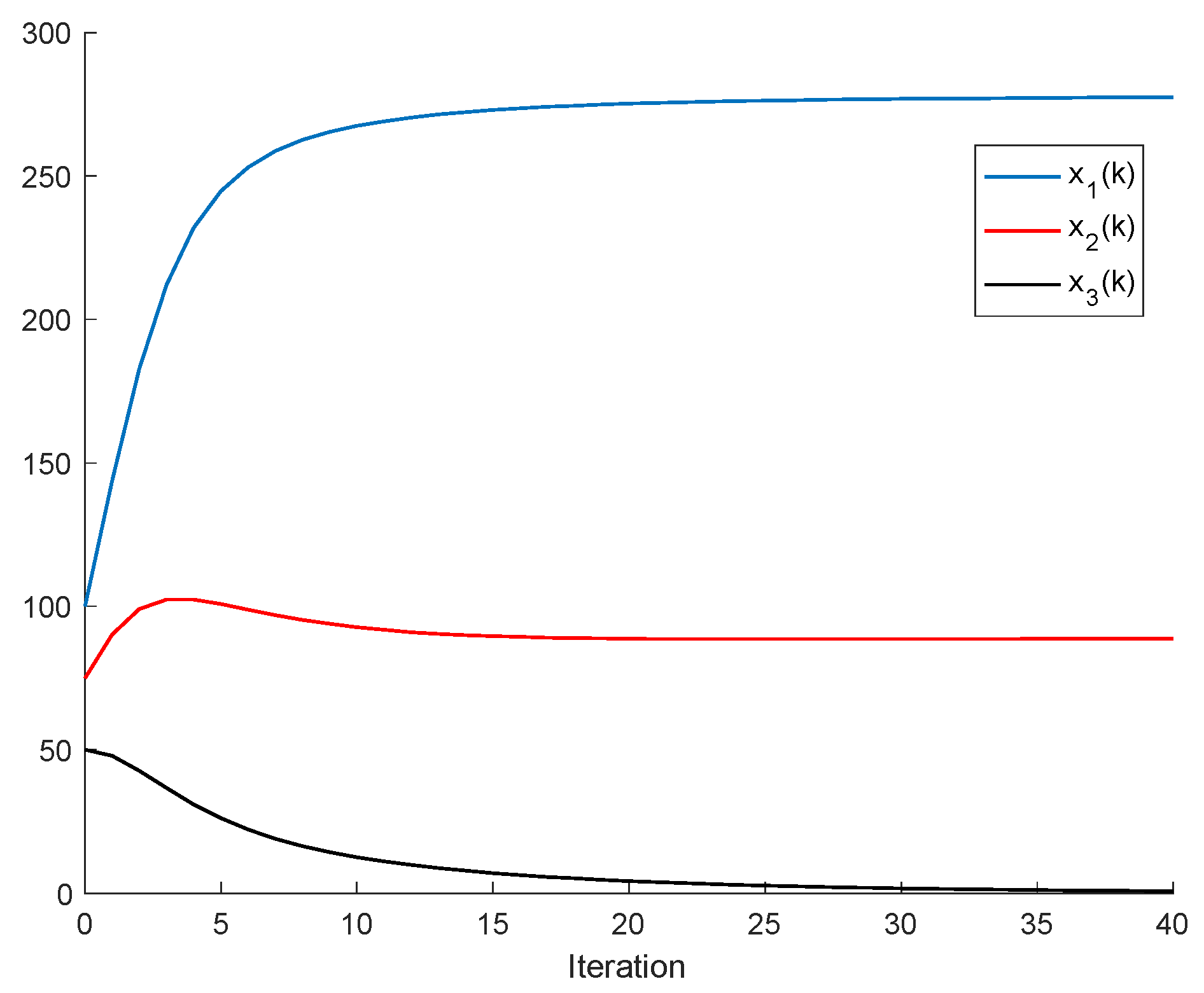
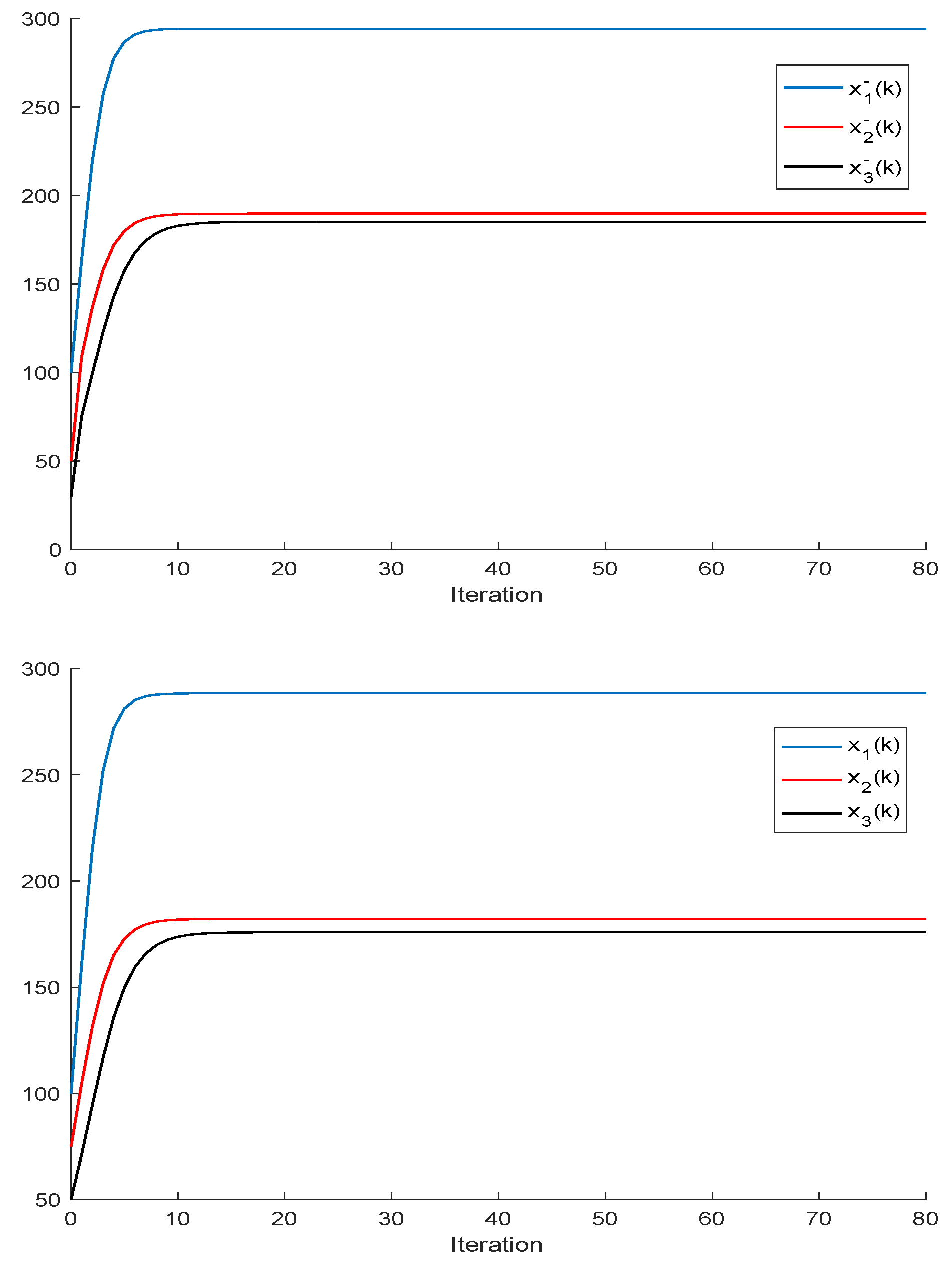
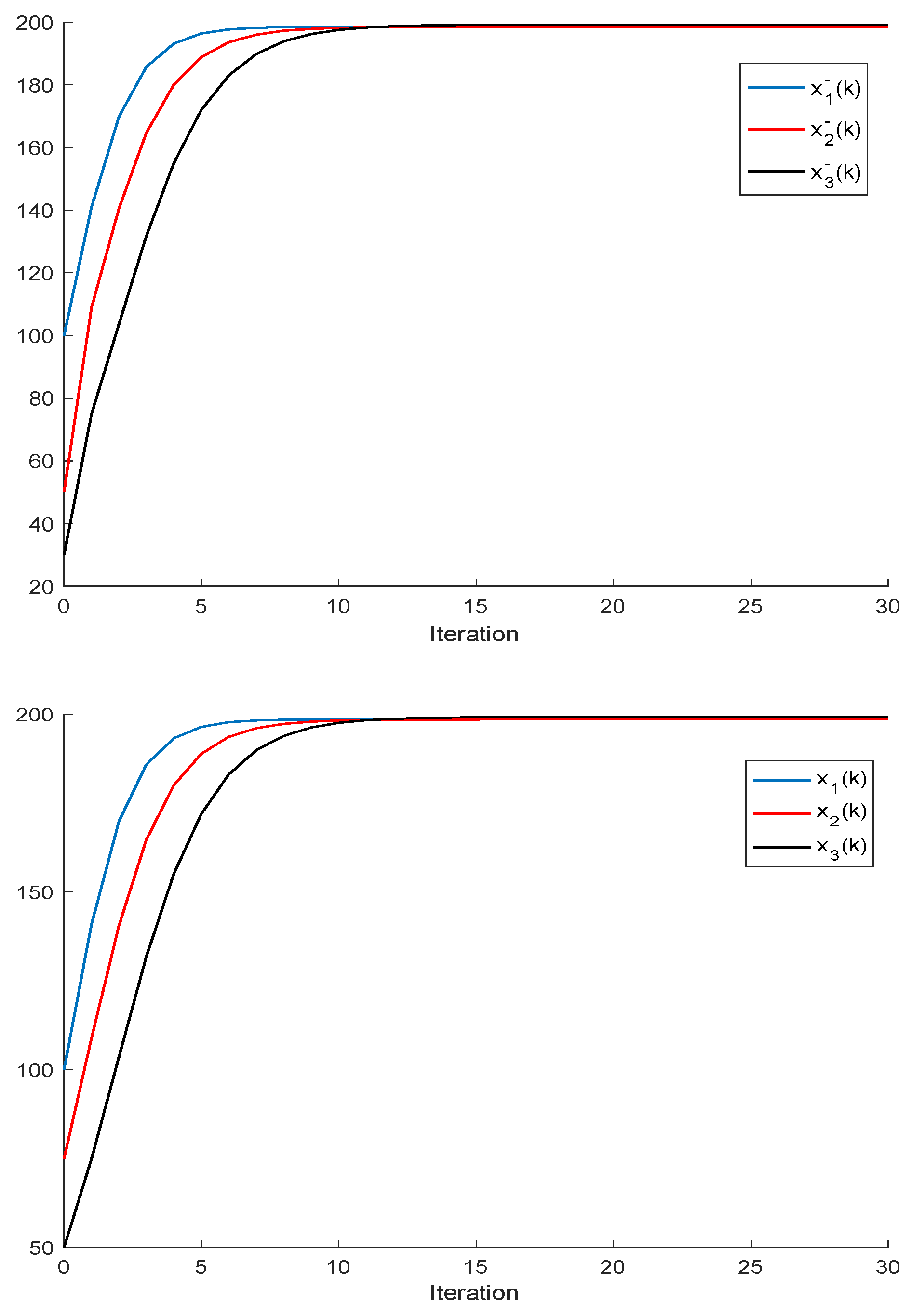
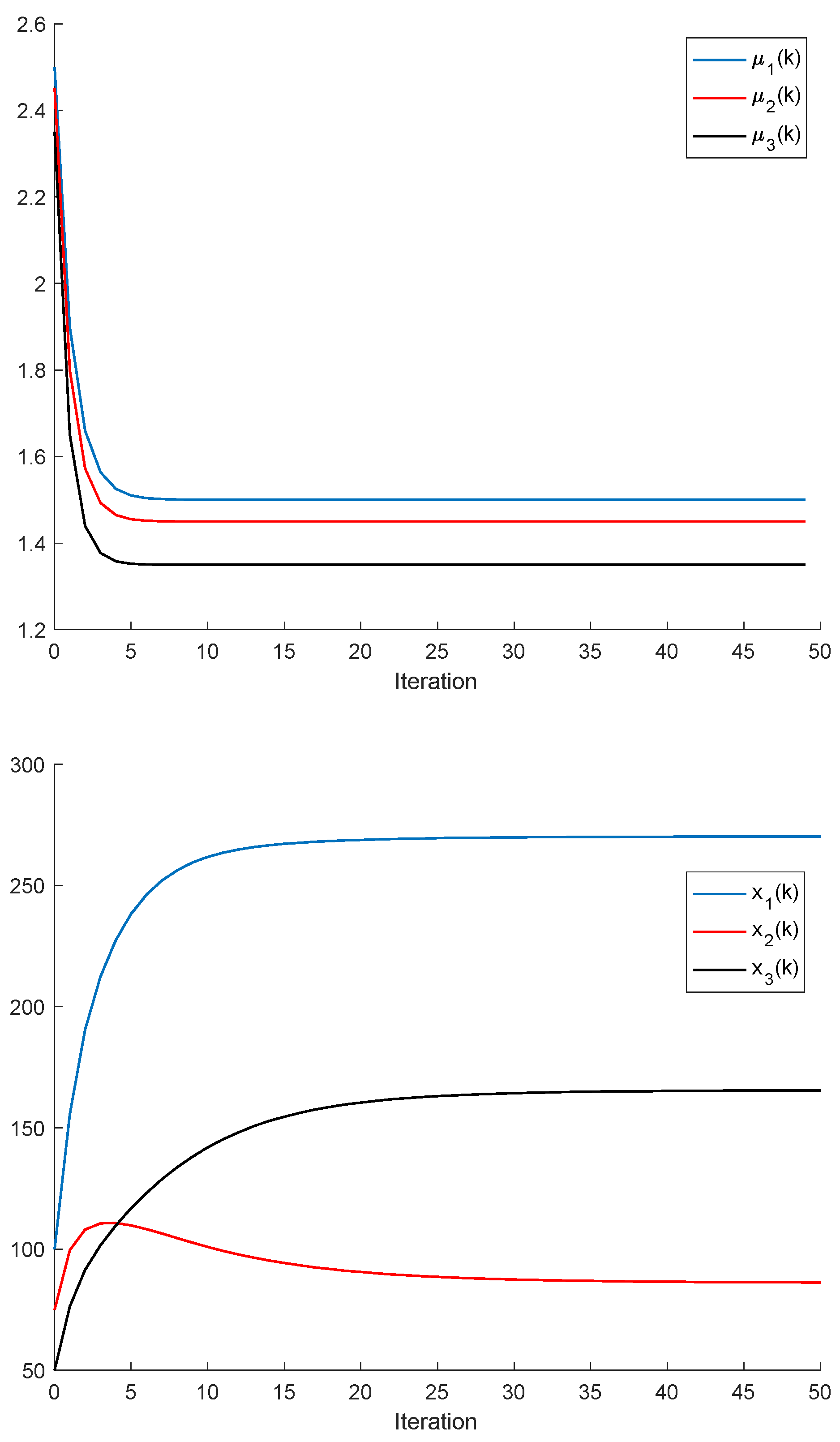
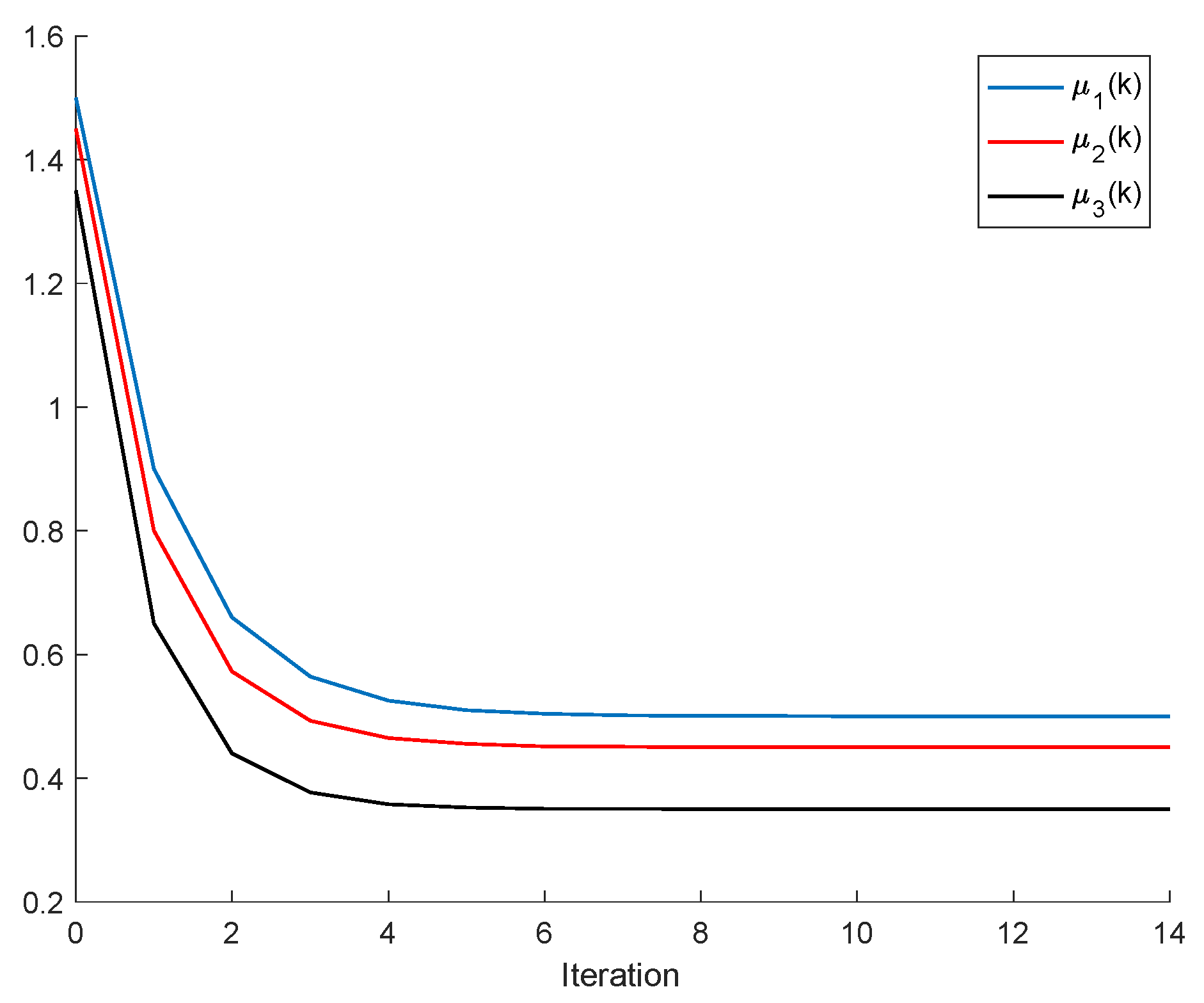
Remark 2.

It follows, from Proposition 2, that a population $i\in \overline{n}$ is dominant on the remaining ones, or, in other words, it has the best fitness, for all $j\left(\ne i\right)\in \overline{n}$ and the respective left and right sampled values if $K_i\ge \underset{j\left(\ne i\right)\in \overline{n}}{\mathit{max}}{\overline{K}}_j$, $x_i\left(0\right)\ge \frac{1}{{\mu }_i}\underset{j\left(\ne i\right)\in \overline{n}}{\mathit{max}}\left({\mu }_j{x}_j\left(0\right)\right)$ and $\underset{j\left(\ne i\right)\in \overline{n}}{\mathit{min}}\left(d_j\left(k\right)-b_j\left(k\right)x_j^{-}\left(k\right)\right)\ge d_i\left(k\right)-b_i\left(k\right)x_i^{-}\left(k\right)$; $\forall k\in \mathit{N}$. It turns out, furthermore, that an increase in an individual carrying capacity facilitates the increase in the corresponding species numbers, if all the remaining parameters remaining unchanged. The above constraints generalize Proposition 2, although at the expense of involving conditions on the left amounts of the population stocks. It can be pointed out that, eventually, there could exist more than one species with an identical best fitness within the set of competing species.

The following result is now proved on non-negativity, boundedness and eventual extinction of the species populations.

Theorem 2.

The following properties hold:

(i) 

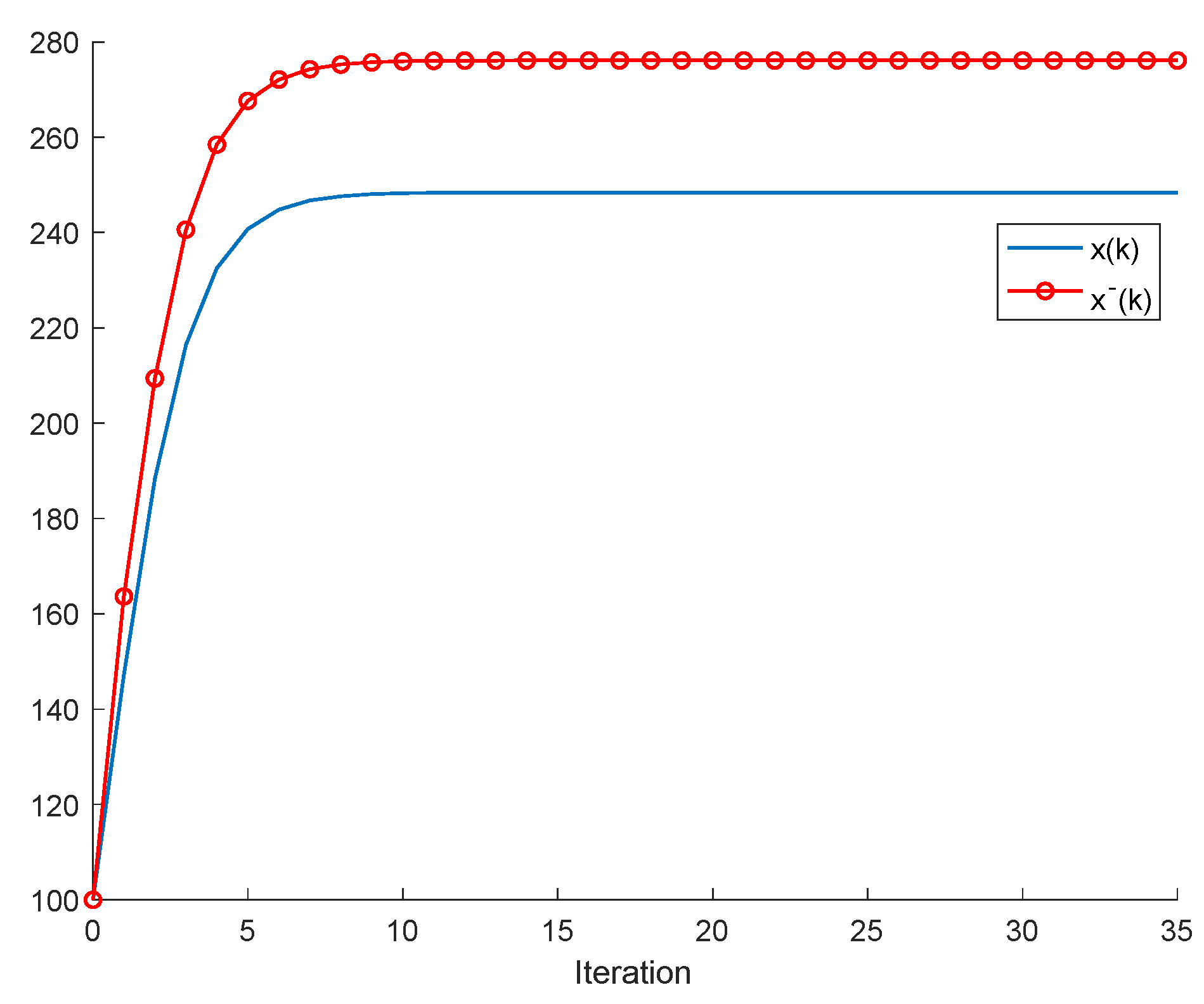
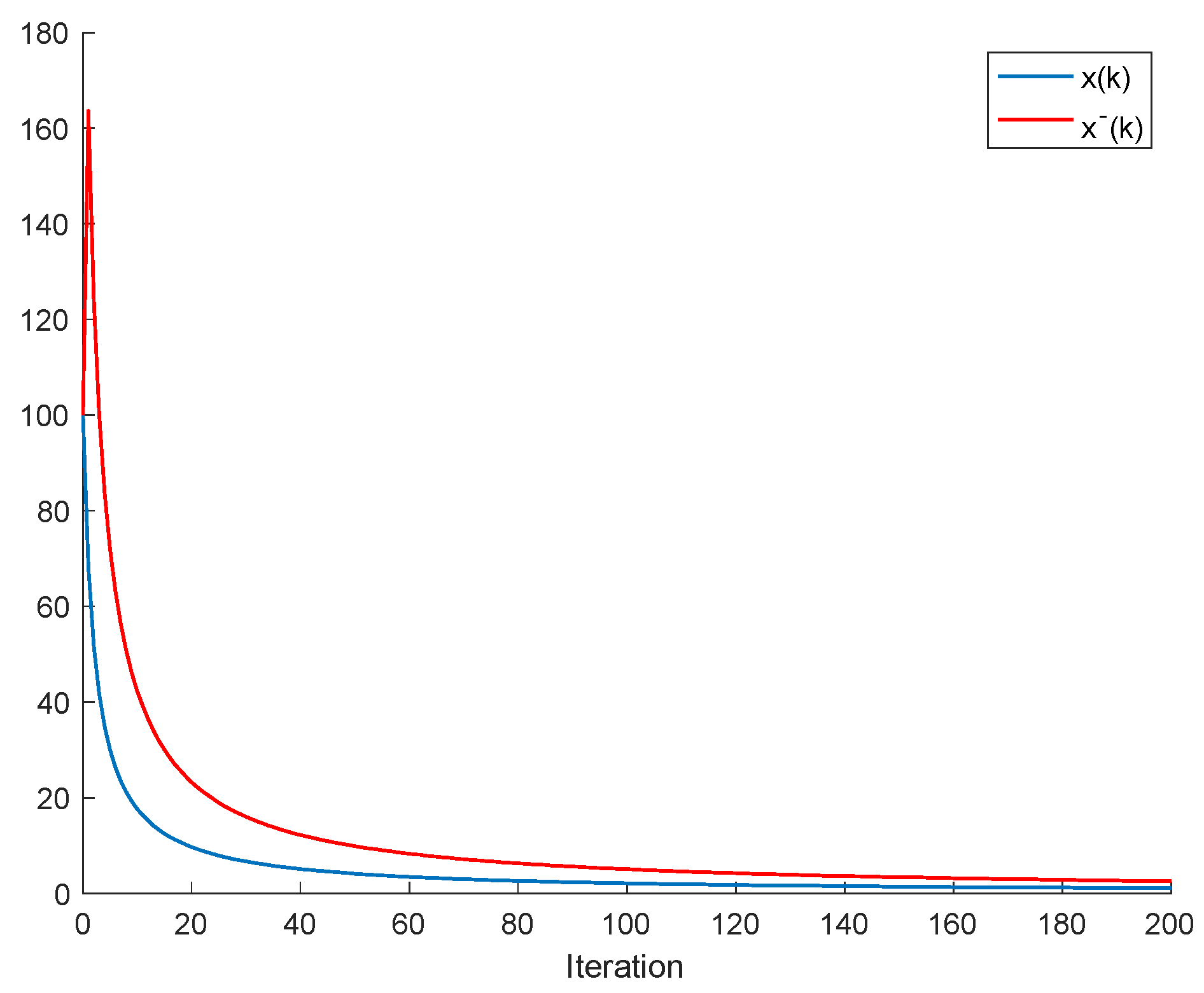
If $\infty >x_i\left(0\right)>0$; $\forall i\in \overline{n}$, Assumption 1 holds, ${\left\{b_i\left(k\right)\right\}}_0^{\infty }\equiv 1$ and ${\left\{d_i\left(k\right)\right\}}_0^{\infty }\equiv 0$; $\forall i\in \overline{n}$; then, ${\left\{x_i\left(k\right)\right\}}_{k=0}^{\infty }$ is non-negative and bounded; $\forall i\in \overline{n}$. Furthermore, if ${\left\{x_i\left(k\right)\right\}}_0^{\infty }\to 0$ (i.e., asymptotic extinction of the $ith$ species), then $\underset{k\to \infty }{\mathit{lim}\mathit{inf}}\underset{0\le k<\infty }{\mathit{min}}{K}_{ie}\left(k\right)=0$.

(ii) 

If $\infty >x_i\left(0\right)>0$; $\forall i\in \overline{n}$ and Assumptions 1 and 2 hold with ${\left\{d_i\left(k\right)\right\}}_{k=0}^{\infty }\subset {\mathit{R}}_{0+}$, then and it is a bounded non-negative sequence if ${\displaystyle {\prod }_{k=0}^{\infty }\left[{\mu }_i{b}_i\left(k\right)\right]}=0$; $\forall i\in \overline{n}$. This property holds, in particular, if $b_i\left(k\right)>{\mu }_i^{-1}$; $\forall k\in {\mathit{N}}_0$. If, furthermore, $0\le d_i\left(k\right)<b_i\left(k\right)x_i^{-}\left(k\right)$; $\forall k\in {\mathit{N}}_0$, then extinction in finite time does not occur for any $i\in \overline{n}$, so that extinction only happens asymptotically and ${\left\{x_i\left(k\right)\right\}}_{k=0}^{\infty }$ is a bounded non-negative sequence if ${\displaystyle {\prod }_{k=0}^{\infty }\left[{\mu }_i{b}_i\left(k\right)\right]}\le A<\infty$. In particular, if ${\displaystyle {\prod }_{k=j}^{j+a-1}\left[b_i\left(k\right)\right]}\le {\mu }_i^{-a}$; $\forall k\left(\ge j_0\right)\in {\mathit{Z}}_{0+}$ and some finite $j_0\in {\mathit{N}}_0$ and $a\in \mathit{N}$, then

$$x_i^{-}\left(k+1\right)=\frac{{\mu }_i{K}_i{x}_i\left(k\right)}{K_i+{\displaystyle {\sum }_{j=1}^n{c}_{ji}}\left({\mu }_i-1\right)x_j\left(k\right)}$$

(6)

If Assumptions 1 and 2 hold with ${\left\{d_i\left(k\right)\right\}}_{k=0}^{\infty }\subset {\mathsf{R}}_{}$, then ${\left\{x_i\left(k\right)\right\}}_{k=0}^{\infty }\to 0$ if ${\displaystyle {\prod }_{k=0}^{\infty }\left[{\mu }_i{b}_i\left(k\right)-d_i\left(k+1\right)\right]}=0$.

(iii) 

If Assumptions 1 and 2 hold, then ${\left\{x_i\left(k\right)\right\}}_{k=0}^{\infty }$ is bounded; $\forall i\in \overline{n}$.

Proof. 

One obtains that (2) is equivalent to

$$x_i^{-}\left(k+1\right)=\frac{{\mu }_i{x}_i\left(k\right)}{1+\frac{{\mu }_i-1}{K_i}{\displaystyle {\sum }_{j=1}^n{c}_{ji}}{x}_j\left(k\right)}=\frac{{\mu }_i{x}_i\left(k\right)}{1+\frac{{\mu }_i-1}{K_{ie}\left(k\right)}{x}_i\left(k\right)};\forall k\in {\mathit{N}}_0$$

(7)

where the equivalent $i-th$ carrying capacity $K_{ie}$ is given by

$$0\le K_{ie}\left(k\right)=\frac{K_i{x}_i\left(k\right)}{{\displaystyle {\sum }_{j=1}^n{c}_{ji}}{x}_j\left(k\right)}=\frac{K_i}{1+{\displaystyle {\sum }_{j\left(\ne i\right)=1}^n{c}_{ji}\frac{x_j\left(k\right)}{x_i\left(k\right)}}}\le K_i;\forall k\in {\mathit{N}}_0$$

(8)

since $c_{ii}=1$ and $c_{ij}\ge 0$; $\forall j\left(\ne i\right)\in \overline{n}$. By combining (7) and (8), one obtains

$$\begin{gathered} x_i^{-}\left(k+1\right)=\frac{{\mu }_i{x}_i\left(k\right)}{1+\frac{{\mu }_i-1}{K_{ie}\left(k\right)}{x}_i\left(k\right)}\le \frac{{\mu }_i{x}_i\left(k\right)}{1+\frac{{\mu }_i-1}{K_i}{x}_i\left(k\right)}=\frac{{\mu }_i{K}_i{x}_i\left(k\right)}{K_i+\left({\mu }_i-1\right)x_i\left(k\right)}; \\ \forall i\in \overline{n},\forall k\in {\mathit{N}}_0 \end{gathered}$$

(9)

If Assumption 1 holds, ${\left\{b_i\left(k\right)\right\}}_0^{\infty }\equiv 1$ and ${\left\{d_i\left(k\right)\right\}}_0^{\infty }\equiv 0$, then $x_i^{-}\left(k\right)=x_i\left(k\right)$; $\forall i\in \overline{n}$, $\forall k\in {\mathit{N}}_0$. Let us define $y_i\left(k\right)=1/\left(x_i^{-}\left(k\right)\right)$; $\forall i\in \overline{n}$, $\forall k\in {\mathit{N}}_0$. One obtains, from recursive calculations in (8) using (7),

$$\begin{gathered} 0<\frac{{\mu }_i-1}{{\mu }_i{K}_i}\le \frac{{\mu }_i-1}{{\mu }_i\underset{0\le k<\infty }{\mathit{max}}{K}_{ie}\left(k\right)}\le \frac{{\mu }_i-1}{{\mu }_i}{\displaystyle {\sum }_{j=0}^k\frac{{\mu }_i^{j-k}}{K_{ie}\left(j\right)}} \\ \le \frac{1}{x_i\left(k+1\right)}=y_i\left(k+1\right)=y_i^{-}\left(k+1\right)={\mu }_i^{-1}{y}_i\left(k\right)+\frac{{\mu }_i-1}{{\mu }_i{K}_{ie}\left(k\right)} \\ ={\mu }_i^{-\left(k+1\right)}{y}_i\left(0\right)+\frac{{\mu }_i-1}{{\mu }_i}{\displaystyle {\sum }_{j=0}^k\frac{{\mu }_i^{j-k}}{K_{ie}\left(j\right)}} \\ \le y_i\left(0\right)+\frac{{\mu }_i-1}{{\mu }_i\underset{0\le j\le k}{\mathit{min}}{K}_{ie}\left(j\right)}{\displaystyle {\sum }_{j=0}^k{\mu }_i^{j-k}} \\ \le \frac{1}{x_i\left(0\right)}+\frac{{\mu }_i-1}{{\mu }_i\underset{0\le j\le k}{\mathit{min}}{K}_{ie}\left(j\right)}{\displaystyle {\sum }_{j=0}^{\infty }{\mu }_i^{j-k}} \\ \le \frac{1}{x_i\left(0\right)}+\frac{{\mu }_i-1}{{\mu }_i\underset{0\le j\le \infty }{\mathit{min}}{K}_{ie}\left(j\right)}\frac{1-{\mu }_i^{-\left(k+1\right)}}{1-{\mu }_i^{-1}} \\ \le \frac{1}{x_i\left(0\right)}+\frac{1}{\underset{0\le k<\infty }{\mathit{min}}{K}_{ie}\left(k\right)}; \\ \forall i\in \overline{n},\forall k\in {\mathit{N}}_0 \end{gathered}$$

(10)

since $K_{ie}\left(k\right)\le K_i<\infty$. Since $\infty >x_i\left(0\right)>0$ and $\frac{1}{x_i\left(k+1\right)}>0$; $\forall i\in \overline{n}$, $\forall k\in {\mathit{N}}_0$, then ${\left\{x_i\left(k\right)\right\}}_0^{\infty }$ is bounded; $\forall i\in \overline{n}$. Note that ${\left\{x_i\left(k\right)\right\}}_0^{\infty }$ is a non-negative sequence for any given $i\in \overline{n}$ by construction and, furthermore, a positive sequence, unless $\underset{k\to \infty }{\mathit{lim}\mathit{inf}}\underset{0\le k<\infty }{\mathit{min}}{K}_{ie}\left(k\right)=0$, which would eventually imply, from (10), that ${\left\{1/x_i\left(k\right)\right\}}_0^{\infty }\to \infty$, so that ${\left\{x_i\left(k\right)\right\}}_0^{\infty }\to 0$. Since it has been already proved (Property (i)) that ${\left\{x_j\left(k\right)\right\}}_0^{\infty }$ is bounded for any $j\in \overline{n}$, then ${\left\{x_j\left(k\right)/x_i\left(k\right)\right\}}_0^{\infty }\to \infty$, which would translate into $\underset{k\to \infty }{\mathit{lim}\mathit{inf}}\underset{0\le k<\infty }{\mathit{min}}{K}_{ie}\left(k\right)=0$ from (8), if and only if ${\left\{x_i\left(k\right)\right\}}_0^{\infty }\to 0$. Property (i) has been proved. From Assumptions 1–2, with non-negative independent consumption, one directly obtains that $\frac{x_i\left(k+1\right)}{x_i\left(k\right)}\le b_i\left(k+1\right){\mu }_i$, which leads to the first part of Property (ii). If Assumptions 1 and 2 hold with non-necessarily non-negative independent consumption sequence, then ${\left\{x_i\left(k\right)\right\}}_{k=0}^{\infty }\to 0$ if ${\displaystyle {\prod }_{k=0}^{\infty }\left[{\mu }_i{b}_i\left(k\right)-d_i\left(k+1\right)\right]}=0$, which proves the second part of Property (ii).

Property (iii) is proved by contradiction arguments. Let us assume that Assumptions 1 and 2 hold and ${\left\{x_i\left(k\right)\right\}}_{k=0}^{\infty }$ is unbounded. Thus, there is a subsequence ${\left\{x_i\left(n_k\right)\right\}}_{k=0}^{\infty }\subset \left\{x_i\left(k\right)\right\}$, with $n_{k+1}-n_k<+\infty$, which is strictly increasing, so that ${\left\{x_i\left(n_k\right)\right\}}_{k=0}^{\infty }\to +\infty$ and then, from (7),

$$0\le \frac{x_i^{-}\left(k+1\right)}{x_i\left(k\right)}\le \frac{{\mu }_i{K}_{ie}\left(k\right)}{\left({\mu }_i-1\right)x_i\left(k\right)};\forall k\in {\mathit{N}}_0$$

then $\underset{k\to \infty }{\mathit{lim}}\frac{x_i^{-}\left(n_k+1\right)}{x_i\left(n_k\right)}=0$. Furthermore,

$$\begin{gathered} \frac{x_i^{-}\left(n_{k+1}\right)}{x_i\left(n_k\right)}=\left(\frac{x_i^{-}\left(n_{k+1}\right)}{x_i\left(n_{k+1}-1\right)}\right)\left(\frac{x_i\left(n_{k+1}-1\right)}{x_i^{-}\left(n_{k+1}-1\right)}\right) \\ \times \left(\frac{x_i^{-}\left(n_{k+1}-1\right)}{x_i\left(n_{k+1}-2\right)}\right)\left(\frac{x_i\left(n_{k+1}-2\right)}{x_i^{-}\left(n_{k+1}-2\right)}\right)\dots \left(\frac{x_i^{-}\left(n_k+1\right)}{x_i\left(n_k\right)}\right) \\ \le C\left(n_k,j\right)\frac{x_i^{-}\left(n_k+1\right)}{x_i\left(n_k\right)} \end{gathered}$$

(11)

where $C\left(n_k,j\right)$ is a positive real constant which is finite, since it is bounded to a finite number of iterations between $n_k$ and $n_{k+1}$, since $n_{k+1}-n_k<+\infty$ and since one has, from Assumption 2, that

$$x_i\left(k+1\right)=b_i\left(k+1\right)x_i^{-}\left(k+1\right)-d_i\left(k+1\right)\le M_i<+\infty ;\forall i\in \overline{n};\forall k\in {\mathit{N}}_0$$

and

$$0\le \frac{x_i\left(k+1\right)}{x_i^{-}\left(k+1\right)}=b_i\left(k+1\right)-\frac{d_i\left(k+1\right)}{x_i^{-}\left(k+1\right)}\le \frac{M_i}{x_i^{-}\left(k+1\right)}<+\infty$$

(12)

if $x_i^{-}\left(k+1\right)\ne 0$ and $\frac{x_i\left(k+1\right)}{x_i^{-}\left(k+1\right)}=\frac{0}{0}=+1<+\infty$ if $x_i^{-}\left(k+1\right)=0$, still from Assumption 2. Then, from (11) and (12), one obtains $\underset{k\to \infty }{\mathit{lim}}\frac{x\left(n_{k+1}\right)}{x_i\left(n_k\right)}=0$, since ${\left\{\frac{x_i^{-}\left(n_k+1\right)}{x_i\left(n_k\right)}\right\}}_{k=0}^{\infty }$ is bounded and ${\left\{x_i\left(n_k\right)\right\}}_{k=0}^{\infty }$ is strictly increasing from the contradiction argument hypothesis. Thus, there is a subsequence ${\left\{x_i\left(m_{n_k}\right)\right\}}_{k=0}^{\infty }\subset \left\{x_i\left(n_k\right)\right\}$ such that $\frac{x_i\left(m_{n_{k+1}}\right)}{x_i{\left(m_{n_k}\right)}^{}}<1$, so that one concludes, from D´Alembert criterion for convergence of sequences, that ${\left\{x_i{\left(m_{n_k}\right)}^{}\right\}}_{k=0}^{\infty }\to 0$. As a result, ${\left\{x_i\left(k\right)\right\}}_{k=0}^{\infty }$ is bounded. Property (iii) has been proved. □

Note that Theorem 2 (i) guarantees the boundedness of all the populations under Assumption 1, provided that the harvesting quota and the independent consumption are zero (so that there are no impulsive effects at sampling instants), while Theorem 2(iii) guarantees such a boundedness under Assumptions 1 and 2.

In the following, the limits of the convergent sequences are denoted with the same notation as the sequences of elements by suppressing the sample argument “k” for the sake of notation simplicity.

Theorem 3.

Let us assume that all the populations converge to equilibrium points, that is, ${\left\{x_i\left(k\right)\right\}}_0^{\infty }\to x_i$. Then, the following properties hold:

(i) 

Let us assume that Assumptions 1 and 2 hold and that ${\left\{b_i\left(k\right)\right\}}_0^{\infty }\to b_i\left(>{\mu }_i^{-1}\right)$, ${\left\{d_i\left(k\right)\right\}}_0^{\infty }\to d_i\in \left[0,{\overline{d}}_i\right]$, ${\left\{c_{ji}\left(k\right)\right\}}_0^{\infty }\to c_{ji}\in \left[0,{\overline{c}}_{ji}\right]$ for some ${\overline{d}}_i\in {\mathit{R}}_{0+}$, ${\overline{c}}_{ji}\in {\mathit{R}}_{0+}$; $\forall j\left(\ne i\right),i\in \overline{n}$. If ${\overline{d}}_i$ and ${\overline{c}}_{ji}$; $\forall j\left(\ne i\right),i\in \overline{n}$ are sufficiently small compared to $K_i\left(b_i{\mu }_i-1\right)$, then there are two equilibrium points $x_i\ge 0$; $\forall i\in \overline{n}$.

(ii) 

Let us assume that the quadruple $\left(K_i,{\mu }_i,b_i,d_i\right)$ satisfies the constraints

$$B_i=\left[K_i\left(b_i{\mu }_i-1\right)-\left({\mu }_i-1\right)d_i\right]\ge 0$$

$$C_i={\left(K_i\left(b_i{\mu }_i-1\right)-\left({\mu }_i-1\right)d_i\right)}^2-4\left({\mu }_i-1\right)d_i{K}_i\ge 0$$

Then, one of each $i-\mathrm{th}$ equilibrium point is feasible, that is, $x_i\ge 0$ under the subsequent stipulations:

(1) Either the coupling constraint ${\displaystyle {\sum }_{j\left(\ne i\right)=1}^n{c}_{ji}{x}_j}\in \left[\frac{B_i+\sqrt{B_i^2-C_i}}{{\mu }_i-1},\infty \right)$ from the remaining equilibrium points and, furthermore, any of the three conditions below:

$$\mathrm{C}1) b_i\ge {\mu }_i^{-1}\mathrm{and}0\le d_i\le \frac{K_i\left(b_i{\mu }_i-1\right)}{{\mu }_i-1}$$

$$\mathrm{C}2) {\mu }_i>1,b_i\in {\left({\mu }_i^{-1},5{\mu }_i^{-1}\right]}^{},d_i\in \left[\frac{K_i\left(b_i{\mu }_i-1\right)}{{\mu }_i-1},\frac{4K_i}{{\mu }_i-1}\right)$$

$$\mathrm{C}3) {\mu }_i<1,b_i\in {\left({\mu }_i^{-1},5{\mu }_i^{-1}\right]}^{},d_i\in \left[-\frac{4K_i}{1-{\mu }_i},-\frac{K_i\left(b_i{\mu }_i-1\right)}{1-{\mu }_i}\right);$$

(2) Or, the coupling constraint ${\displaystyle {\sum }_{j\left(\ne i\right)=1}^n{c}_{ji}{x}_j}\in \left[0,\infty \right)$ from the remaining equilibrium points together with $\mathit{sgn}\left(d_i\right)=\mathit{sgn}\left({\mu }_i-1\right)$ (which excludes the values ${\mu }_i=1$ and $d_i=0$).

Proof. 

Take any $i\in \overline{n}$. One obtains, from (2)–(3), by taking limits, that

$$x_i^{-}=\frac{{\mu }_i{K}_i{x}_i}{K_i+{\displaystyle {\sum }_{j=1}^n{c}_{ji}}\left({\mu }_i-1\right)x_j}$$

(13)

$$\begin{gathered} x_i=b_i{x}_i^{-}-d_i=\frac{b_i{\mu }_i{K}_i{x}_i}{K_i+{\displaystyle {\sum }_{j=1}^n{c}_{ji}}\left({\mu }_i-1\right)x_j}-d_i \\ =\frac{\left(b_i{\mu }_i{K}_i-d_i\left({\mu }_i-1\right)\right)x_i-d_i\left(K_i+\left({\mu }_i-1\right){\displaystyle {\sum }_{j\left(\ne i\right)=1}^n{c}_{ji}}{x}_j\right)}{K_i+{\displaystyle {\sum }_{j=1}^n{c}_{ji}}\left({\mu }_i-1\right)x_j} \end{gathered}$$

(14)

then

$$\left(\frac{\left(b_i{\mu }_i{K}_i-d_i\left({\mu }_i-1\right)\right)}{K_i+{\displaystyle {\sum }_{j=1}^n{c}_{ji}}\left({\mu }_i-1\right)x_j}-1\right)x_i=\frac{d_i\left(K_i+\left({\mu }_i-1\right){\displaystyle {\sum }_{j\left(\ne i\right)=1}^n{c}_{ji}}{x}_j\right)}{K_i+{\displaystyle {\sum }_{j=1}^n{c}_{ji}}\left({\mu }_i-1\right)x_j}$$

(15)

so that

$$\begin{gathered} x_i=\frac{d_i\left(K_i+\left({\mu }_i-1\right){\displaystyle {\sum }_{j\left(\ne i\right)=1}^n{c}_{ji}}{x}_j\right)}{b_i{\mu }_i{K}_i-d_i\left({\mu }_i-1\right)-K_i-{\displaystyle {\sum }_{j=1}^n{c}_{ji}}\left({\mu }_i-1\right)x_j} \\ =\frac{d_i\left(K_i+\left({\mu }_i-1\right){\displaystyle {\sum }_{j\left(\ne i\right)=1}^n{c}_{ji}}{x}_j\right)}{\left({\mu }_i-1\right)\left[\left(K_i-d_i-x_i\right)-{\displaystyle {\sum }_{j\left(\ne i\right)=1}^n{c}_{ji}}{x}_j\right]+\left(b_i-1\right)K_i{\mu }_i} \end{gathered}$$

(16)

by noting that the denominator of the above second identity balances that of the first one. Re-arranging terms in the above Equation (16) leads to

$$\left({\mu }_i-1\right)x_i^2-{\widehat{b}}_i{x}_i+{\widehat{c}}_i=0$$

(17)

where

$$\begin{gathered} {\widehat{b}}_i={\widehat{b}}_i\left(x_1,\dots ,x_{i-1},x_{i+1},\cdots ,x_n\right) \\ =\left({\mu }_i-1\right)\left(K_i-d_i-{\displaystyle {\sum }_{j\left(\ne i\right)=1}^n{c}_{ji}{x}_j}\right)+\left(b_i-1\right)K_i{\mu }_i \\ =K_i\left(b_i{\mu }_i-1\right)-\left({\mu }_i-1\right)\left(d_i+{\displaystyle {\sum }_{j\left(\ne i\right)=1}^n{c}_{ji}{x}_j}\right) \end{gathered}$$

(18)

$${\widehat{c}}_i={\widehat{c}}_i\left(x_1,\dots ,x_{i-1},x_{i+1},\cdots ,x_n\right)=d_i\left(K_i+\left({\mu }_i-1\right){\displaystyle {\sum }_{j\left(\ne i\right)=1}^n{c}_{ji}{x}_j}\right)$$

(19)

It is obvious, from the above equations, that if $b_i>1/{\mu }_i$ and ${\overline{d}}_i=0$ and ${\overline{c}}_{ji}=0$; $\forall j\left(\ne i\right)$, then ${\widehat{b}}_i=K_i\left(b_i{\mu }_i-1\right)$ and ${\widehat{c}}_i=0$; $\forall i\in \overline{n}$ and one obtains the equilibrium points $x_i=\frac{K_i\left(b_i{\mu }_i-1\right)}{{\mu }_i-1}>0$ and $x_i=0$ as zeros of (17). It turns out that, in the general case, the zeros of (17), namely,

$$x_i=\frac{{\widehat{b}}_i\pm \sqrt{{\widehat{b}}_i^2-4\left({\mu }_i-1\right){\widehat{c}}_i}}{2\left({\mu }_i-1\right)}$$

(20)

are both non-negative and real if ${\widehat{b}}_i>0$ and ${\widehat{b}}_i^2\ge 4\left({\mu }_i-1\right){\widehat{c}}_i$ which hold for each $i\in \overline{n}$ if ${\overline{d}}_i$ and ${\overline{c}}_{ji}$; $\forall j\left(\ne i\right)$ are sufficiently small in view of (18) and (19), such that ${\widehat{c}}_i$ is sufficiently small, compared to $K_i\left(b_i{\mu }_i-1\right)$ (that is, sufficiently small related to the first additive term of $\left|{\widehat{b}}_i\right|$) from the property of the continuity of the zeros of a polynomial with respect to its coefficients. Property (i) has been proved. Property (ii) is now proved by guaranteeing the validity of ${\widehat{b}}_i^2\ge 4\left({\mu }_i-1\right){\widehat{c}}_i$ depending on the coupling equilibrium dynamics from the remaining species $j\left(\ne i\right)\in \overline{n}$ to the $i-th$ one. First, let us define the auxiliary amount ${\Delta }_i=\left({\mu }_i-1\right){\displaystyle {\sum }_{j\left(\ne i\right)=1}^n{c}_{ji}{x}_j}$ so that, from (18) and (19),

$${\widehat{b}}_i=\left({\mu }_i-1\right)\left(K_i-d_i\right)-{\Delta }_i+\left(b_i-1\right)K_i{\mu }_i=K_i\left(b_i{\mu }_i-1\right)-\left({\mu }_i-1\right)d_i-{\Delta }_i$$

$${\widehat{c}}_i=d_i\left(K_i+{\Delta }_i\right)$$

then

$$\begin{array}{l}g\left({\Delta }_i\right)={\widehat{b}}_i^2-4\left({\mu }_i-1\right){\widehat{c}}_i={\left(K_i\left(b_i{\mu }_i-1\right)-\left({\mu }_i-1\right)d_i-{\Delta }_i\right)}^2-4\left({\mu }_i-1\right)\left(d_i\left(K_i+{\Delta }_i\right)\right)\\ ={\Delta }_i^2-2\left[K_i\left(b_i{\mu }_i-1\right)-\left({\mu }_i-1\right)d_i\right]{\Delta }_i+{\left(K_i\left(b_i{\mu }_i-1\right)-\left({\mu }_i-1\right)d_i\right)}^2-4\left({\mu }_i-1\right)d_i{K}_i-4\left({\mu }_i-1\right)d_i{\Delta }_i\\ ={\Delta }_i^2-2\left[K_i\left(b_i{\mu }_i-1\right)-\left({\mu }_i-1\right)d_i\right]{\Delta }_i+{\left(K_i\left(b_i{\mu }_i-1\right)-\left({\mu }_i-1\right)d_i\right)}^2-4\left({\mu }_i-1\right)d_i{K}_i\\ ={\Delta }_i^2-2B_i{\Delta }_i+C_i\ge 0\end{array}$$

(21)

holds, where

$$B_i=\left[K_i\left(b_i{\mu }_i-1\right)-\left({\mu }_i-1\right)d_i\right]$$

(22)

$$C_i={\left(K_i\left(b_i{\mu }_i-1\right)-\left({\mu }_i-1\right)d_i\right)}^2-4\left({\mu }_i-1\right)d_i{K}_i=B_i^2-4\left({\mu }_i-1\right)d_i{K}_i$$

(23)

Let us consider the subsequent two cases:

Case 1 ($g\left({\Delta }_i\right)=0$ has real zeros ${\Delta }_{i1,i2}$). For the above constraint (21) to be well-posed with real zeros ${\Delta }_{i1,i2}$ of $g\left({\Delta }_i\right)=0$, with ${\Delta }_{i2}=B_i+\sqrt{B_i^2-C_i}\ge {\Delta }_{i1}=B_i-\sqrt{B_i^2-C_i}$ (according to the definition of ${\Delta }_i$), so that $g\left({\Delta }_i\right)\ge 0$ if and only if ${\displaystyle {\sum }_{j\left(\ne i\right)=1}^n{c}_{ji}{x}_j}\in \left[\mathit{max}\left(0,\frac{B_i+\sqrt{B_i^2-C_i}}{{\mu }_i-1}\right),\infty \right)$, a necessary condition being that $B_i^2\ge C_i$, equivalently, $\left({\mu }_i-1\right)d_i\ge 0$. Provided that such a necessary condition holds, sufficient conditions for ${\Delta }_{i2}=$ $\ge 0$ are as follows:

(a) $B_i\ge 0$, equivalently, $0\le d_i\le \frac{K_i\left(b_i{\mu }_i-1\right)}{{\mu }_i-1}$, which, combined with the above necessary condition, also implies that $b_i\ge {\mu }_i^{-1}$;

(b) $B_i<0$ together with $C_i\le 0$. These two joint sufficiency-type conditions are respectively equivalent to $d_i>\frac{K_i\left(b_i{\mu }_i-1\right)}{{\mu }_i-1}$ and the implicit constraint $d_i\ge \underset{\_}{d_i}=\frac{B_i^2}{4\left({\mu }_i-1\right)K_i}=\frac{{\left({\lambda }_i-{\mu }_i+1\right)}^2{d}_i^2}{4\left({\mu }_i-1\right)K_i}$,obtained after defining the auxiliary parameter ${\lambda }_i=\frac{K_i\left(b_i{\mu }_i-1\right)}{d_i}$ for $d_i\ne 0$. Note that the particular case $d_i=0$ requires, for feasibility, that $B_i\ge 0$ (from the necessary condition $B_i^2\ge C_i$), so that it is included in the sufficient condition $B_i\ge 0$ (or $d_i\le \frac{K_i\left(b_i{\mu }_i-1\right)}{{\mu }_i-1}$), that is, it is included in (a). Since the given implicit constraint has to be checked for $d_i\ne 0$, it becomes identical to $1\ge \frac{{\left({\lambda }_i-{\mu }_i+1\right)}^2{d}_i}{4\left({\mu }_i-1\right)K_i}$, or equivalently identical to

$$d_i\le {\overline{d}}_i=\frac{4\left({\mu }_i-1\right)K_i}{{\left({\lambda }_i-{\mu }_i+1\right)}^2}=\frac{4\left({\mu }_i-1\right)K_i}{{\lambda }_i^2+{\left({\mu }_i-1\right)}^2-2\left({\mu }_i-1\right){\lambda }_i}$$

Note that $\left({\mu }_i-1\right){\lambda }_i=\frac{{\mu }_i-1}{d_i}{K}_i\left(b_i{\mu }_i-1\right)$, so that, under the given necessary conditions, $\mathit{sgn}\left[\left({\mu }_i-1\right){\lambda }_i\right]=sign\left[K_i\left(b_i{\mu }_i-1\right)\right]=\mathit{sgn}\left(b_i{\mu }_i-1\right)$, which is $+1$ if $b_i>{\mu }_i^{-1}$ and $-1$ if $b_i<{\mu }_i^{-1}$. Thus, if $b_i\ge {\mu }_i^{-1}$, then $d_i\le {\overline{d}}_i$ if $d_i\le \frac{4\left({\mu }_i-1\right)K_i}{{\lambda }_i^2+{\left({\mu }_i-1\right)}^2}$, which is, in turn, guaranteed if $d_i\le \frac{4K_i}{{\mu }_i-1}$. As a result, the sufficient condition (b) is guaranteed if $d_i\in \left(\frac{K_i\left(b_i{\mu }_i-1\right)}{{\mu }_i-1},\frac{4K_i}{{\mu }_i-1}\right]$, if $b_i\in {\left({\mu }_i^{-1},5{\mu }_i^{-1}\right]}^{}$.

On the other hand, if $b_i<{\mu }_i^{-1}$, then ${\overline{d}}_i=\frac{4\left({\mu }_i-1\right)K_i}{{\lambda }_i^2+\left|{\mu }_i-1\right|\left(\left|{\mu }_i-1\right|+2\left|{\lambda }_i\right|\right)}\le \frac{4K_i}{{\mu }_i-1}$ if, furthermore, ${\mu }_i>1$, implying again that the condition (b) is guaranteed if $d_i\in \left(\frac{K_i\left(b_i{\mu }_i-1\right)}{{\mu }_i-1},\frac{4K_i}{{\mu }_i-1}\right]$ and ${\overline{d}}_i=-\frac{4\left|{\mu }_i-1\right|K_i}{{\lambda }_i^2+\left|{\mu }_i-1\right|\left(\left|{\mu }_i-1\right|+2\left|{\lambda }_i\right|\right)}\ge -\frac{4K_i}{1-{\mu }_i}=\frac{4K_i}{{\mu }_i-1}$ if ${\mu }_i<1$.

Note that, in both,

Case 2 ($g\left({\Delta }_i\right)=0$ has complex conjugate zeros ${\Delta }_{i1,i2}$). This condition holds if and only if $B_i^2<C_i$ (which also trivially requires that $C_i>0$), which, in view of (23), requires that $\left({\mu }_i-1\right)d_i<0$, which holds if and only if $\mathit{sgn}\left(d_i\right)=\mathit{sgn}\left({\mu }_i-1\right)$. Since $g\left(0\right)=C_i>0$ and ${\Delta }_{i1,i2}$ are complex conjugate zeros, $g\left({\Delta }_i\right)>0$ in all its definition domain, that is, if ${\displaystyle {\sum }_{j\left(\ne i\right)=1}^n{c}_{ji}{x}_j}\in \left[0,\infty \right)$.

Property (ii) follows from Cases 1 and 2. □

Note, from Equation (20), that both equilibrium points of the $i-\mathrm{th}$ species are zero if $d_i=c_{ji}=0$; $\forall j\left(\ne i\right)\in \overline{n}$ and $b_i={\mu }_i^{-1}$; $\forall i\in \overline{n}$. Excluding this trivial case, also note from Equation (20) that, provided that the radicand is non-negative, a necessary condition for at least one of the equilibrium points to be non-negative is that either ${\widehat{b}}_i>0$ or ${\widehat{b}}_i<0$ and ${\widehat{c}}_i\ge 0$. The first case implies that

$$d_i+{\displaystyle {\sum }_{j\left(\ne i\right)=1}^n{c}_{ji}}{x}_j<\frac{K_i\left(b_i{\mu }_i-1\right)}{{\mu }_i-1}$$

The second case implies that ${\mu }_i<1$ and

$$d_i+{\displaystyle {\sum }_{j\left(\ne i\right)=1}^n{c}_{ji}}{x}_j>\frac{K_i\left(b_i{\mu }_i-1\right)}{{\mu }_i-1};$$

$$d_i\left(K_i-\left(1-{\mu }_i\right){\displaystyle {\sum }_{j\left(\ne i\right)=1}^n{c}_{ji}}{x}_j\right)\ge 0$$

while the second constraint above is fulfilled with $d_i\ge 0$ and ${\displaystyle {\sum }_{j\left(\ne i\right)=1}^n{c}_{ji}}{x}_j\le \frac{K_1}{1-{\mu }_i}$, or $d_i\le 0$ and ${\displaystyle {\sum }_{j\left(\ne i\right)=1}^n{c}_{ji}}{x}_j\ge \frac{K_1}{1-{\mu }_i}$.

Example 1

(Positive equilibrium points for $n=2$ and $n\ge 3$ with zero independent consumptions). The allocation and positivity of the equilibrium points is easy to deal with in an analytical way from a linear algebraic system in the absence of independent consumptions at the equilibrium state, as it is now discussed. If $n=2$ and $d_1=d_2=0$, then

$$x_i=\frac{{\mu }_i{b}_i{K}_i{x}_i}{K_i+\left({\mu }_i-1\right)\left(x_i+c_{ji}{x}_j\right)}\mathrm{for}i,j\left(\ne i\right)=1,2$$

(24)

which leads, for $x_i>0$ and for $i=1,2$, denoted also as $x={\left(x_1,x_2\right)}^T\succ \succ 0$, to

$$x_i+c_{ji}{x}_j=\frac{K_i\left(b_i{\mu }_i-1\right)}{{\mu }_i-1}\mathrm{for}i,j\left(\ne i\right)=1,2$$

(25)

leading to

$$\begin{array}{l}\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]={\left[\begin{array}{cc}1& c_{21}\\ c_{12}& 1\end{array}\right]}^{-1}\left[\begin{array}{c}\frac{K_1\left(b_1{\mu }_1-1\right)}{{\mu }_1-1}\\ \frac{K_2\left(b_2{\mu }_2-1\right)}{{\mu }_2-1}\end{array}\right]=\frac{1}{1-c_{12}{c}_{21}}{\left[\begin{array}{cc}1& -c_{21}\\ -c_{12}& 1\end{array}\right]}^{}\left[\begin{array}{c}\frac{K_1\left(b_1{\mu }_1-1\right)}{{\mu }_1-1}\\ \frac{K_2\left(b_2{\mu }_2-1\right)}{{\mu }_2-1}\end{array}\right]\\ =\frac{1}{1-c_{12}{c}_{21}}\left[\begin{array}{c}\frac{K_1\left(b_1{\mu }_1-1\right)}{{\mu }_1-1}-\frac{c_{21}{K}_2\left(b_2{\mu }_2-1\right)}{{\mu }_2-1}\\ \frac{K_2\left(b_2{\mu }_2-1\right)}{{\mu }_2-1}-\frac{c_{12}{K}_1\left(b_1{\mu }_1-1\right)}{{\mu }_1-1}\end{array}\right]\succ \succ 0\end{array}$$

(26)

provided that $K_i>0$ for $i=1,2$ and either ${\mu }_i>\mathit{max}\left(1,b_i^{-1}\right)$, or ${\mu }_i<\mathit{min}\left(1,b_i^{-1}\right)$, for $i=1,2$ and $c_{12}$ and $c_{21}$ are sufficiently small according to the relations

$$c_{ij}<\frac{K_j\left({\mu }_i-1\right)\left(b_j{\mu }_j-1\right)}{K_i\left({\mu }_j-1\right)\left(b_i{\mu }_i-1\right)};i,j\left(\ne i\right)=1,2$$

(27)

The equilibrium consensus, that is, the equilibrium points of both species are identical, $x=x_1=x_2=\frac{a}{1-c_{12}{c}_{21}}>0$ for some prefixed $a>0$ is achieved for the coupling coefficients satisfying

$$c_{ij}=\left(\frac{K_i\left(b_i{\mu }_i-1\right)}{{\mu }_i-1}-a\right)\frac{{\mu }_j-1}{K_j\left(b_j{\mu }_j-1\right)}\in \left[0,1\right);i,j\left(\ne i\right)=1,2$$

(28)

so that the parameter $a>0$ has to satisfy, furthermore,

$$\frac{K_i\left(b_i{\mu }_i-1\right)}{{\mu }_i-1}-a<\frac{K_j\left(b_j{\mu }_j-1\right)}{{\mu }_j-1};i,j\left(\ne i\right)=1,2$$

(29)

or

$$\begin{gathered} a>\mathit{max}\left(0,\underset{1\le i,j\left(\ne i\right)\le 2}{\mathit{max}}\left(\frac{K_j\left(b_j{\mu }_j-1\right)}{{\mu }_j-1}-\frac{K_i\left(b_i{\mu }_i-1\right)}{{\mu }_i-1},\frac{K_i\left(b_i{\mu }_i-1\right)}{{\mu }_i-1}-\frac{K_j\left(b_j{\mu }_j-1\right)}{{\mu }_j-1}\right)\right) \\ =\mathit{max}\left(0,\left|\frac{K_2\left(b_2{\mu }_2-1\right)}{{\mu }_2-1}-\frac{K_1\left(b_1{\mu }_1-1\right)}{{\mu }_1-1}\right|\right) \end{gathered}$$

(30)

The generalization to $n\ge 3$ species, if $d_i=0$; $\forall i\in N_0$, leads to a vector of equilibrium points given by

$$\begin{gathered} x=\left[\begin{array}{c}{x}_1\\ x_2\\ \cdots \\ x_n\end{array}\right]={\left[\begin{array}{cccc}1& c_{21}& \cdots & c_{n1}\\ c_{12}& 1& c_{32}& \cdots c_{n2}\\ \cdots & \cdots & \cdots & \cdots \\ c_{1n}& c_{2n}& \cdots & 1\end{array}\right]}^{-1}\left[\begin{array}{c}\frac{K_1\left(b_1{\mu }_1-1\right)}{{\mu }_1-1}\\ ⋮\\ ⋮\\ \frac{K_n\left(b_n{\mu }_n-1\right)}{{\mu }_n-1}\end{array}\right] \\ ={\left(I_n+o\left(\epsilon \right)\right)}^{-1}\left[\begin{array}{c}\frac{K_1\left(b_1{\mu }_1-1\right)}{{\mu }_1-1}\\ ⋮\\ ⋮\\ \frac{K_n\left(b_n{\mu }_n-1\right)}{{\mu }_n-1}\end{array}\right] \end{gathered}$$

(31)

provided that $K_i>0$, ${\mu }_i>\mathit{max}\left(1,b_i^{-1}\right)$; $\forall i\in \overline{n}$ with $c_{ij}\ge 0$; $\forall i,j\left(\ne i\right)\in \overline{3}$ and $\underset{1\le i,j\left(\ne i\right)\le n}{\mathit{max}}{c}_{ij}\le \epsilon$ for some $\epsilon \in {\mathit{R}}_{0+}$ so that, if $\epsilon$ is sufficiently small, then the inverse of $\left(I_n+o\left(\epsilon \right)\right)$ exists and $x\succ \succ 0$, i.e., all its components, that is, the equilibrium states of all the species, are positive.

The following technical result, which establishes equilibrium point upper-bounds when one of the species in the competing set is dominant to the left and right samples, holds.

Proposition 3.

Let us define the population inverses $y_i^{-}=1/x_i^{-}$ and $y_i=1/x_i$ at the equilibrium points and let us assume that the $i-th$ species is the dominant one in the set of $n$ competing species in the set that has the best fitness. Then, the following equilibrium constraints hold:

$$y_i^{-}\le \frac{b_i}{{\mu }_i{b}_i-1}\left[\frac{{\mu }_i-1}{K_i}+\frac{{\mu }_i-1}{K_i}{\displaystyle {\sum }_{j\left(\ne i\right)=1}^n{c}_{ji}\left(\frac{b_i-d_i{y}_i^{-}+d_i}{b_i\left(b_i-d_i{y}_i^{-}\right)}\right)+\frac{1}{b_i-d_i{y}_i^{-}}}\right]$$

(32)

$$\begin{gathered} y_i=\frac{b_i-d_i{y}_i^{-}+d_i}{b_i\left(b_i-d_i{y}_i^{-}\right)}{y}_i^{-}\le \frac{b_i-d_i{y}_i^{-}+d_i}{{\left(b_i-d_i{y}_i^{-}\right)}^{}\left({\mu }_i{b}_i-1\right)} \\ \times \left[\frac{{\mu }_i-1}{K_i}+\frac{{\mu }_i-1}{K_i}{\displaystyle {\sum }_{j\left(\ne i\right)=1}^n{c}_{ji}}\left(\frac{b_i-d_i{y}_i^{-}+d_i}{b_i\left(b_i-d_i{y}_i^{-}\right)}\right)+\frac{1}{b_i-d_i{y}_i^{-}}\right] \end{gathered}$$

(33)

If $d_i\le 0$ with $\left|d_i\right|\le \left(1-b_i\right)x_i^{-}$, then the following further upper-bounds for (32) and (33) are obtained:

$$\begin{gathered} y_i^{-}\le \frac{b_i}{{\mu }_i{b}_i-1}\left[\frac{{\mu }_i-1}{K_i}+\frac{{\mu }_i-1}{K_i}{\displaystyle {\sum }_{j\left(\ne i\right)=1}^n{c}_{ji}\left(\frac{\left(1-\left|d_i\right|\right)b_i^{-1}}{b_i+\left|d_i\right|y_i^{-}}\right)+\frac{1}{b_i+\left|d_i\right|y_i^{-}}}\right] \\ \le \frac{b_i}{{\mu }_i{b}_i-1}\left[\frac{{\mu }_i-1}{K_i}+\frac{{\mu }_i-1}{K_i}{\displaystyle {\sum }_{j\left(\ne i\right)=1}^n\frac{1}{b_i}\left(1+\frac{c_{ji}}{b_i}\right)}\right] \\ {y}_i\le \frac{{\mu }_i-1}{K_i}+\frac{{\mu }_i-1}{K_i}{\displaystyle {\sum }_{j\left(\ne i\right)=1}^n\frac{1}{b_i}\left(c_{ji}+\frac{1}{b_i}\right)} \end{gathered}$$

Proof. 

So that one obtains, from (2)–(3) the following equilibrium constraints, since $c_{ii}=1$; $\forall i\in \overline{n}$,

$$\begin{gathered} y_i^{-}=\frac{K_i+{\displaystyle {\sum }_{j=1}^n{c}_{ji}}\left({\mu }_i-1\right)x_j}{{\mu }_i{K}_i{x}_i} \\ ={\mu }_i^{-1}{y}_i+\frac{{\mu }_i-1}{{\mu }_i{K}_i}+\frac{{\mu }_i-1}{{\mu }_i{K}_i}{\displaystyle {\sum }_{j\left(\ne i\right)=1}^n{c}_{ji}}{y}_i{y}_j^{-1} \end{gathered}$$

(34)

$$y_i=\frac{1}{b_i{x}_i^{-}-d_i}=\frac{y_i^{-}}{b_i-d_i{y}_i^{-}}=b_i^{-1}{y}_i^{-}+{{\rm Y}}_i$$

(35)

where

$${{\rm Y}}_i=\left(\frac{1}{b_i-d_i{y}_i^{-}}-\frac{1}{b_i}\right)y_i^{-}=\frac{d_i{y}_i^{-}}{b_i\left(b_i-d_i{y}_i^{-}\right)}$$

(36)

Then, from (36) into (35), one obtains

$$y_i=\left(b_i^{-1}+\frac{d_i}{b_i\left(b_i-d_i{y}_i^{-}\right)}\right)y_i^{-}=\frac{b_i-d_i{y}_i^{-}+d_i}{b_i\left(b_i-d_i{y}_i^{-}\right)}{y}_i^{-}$$

(37)

Which, replaced in (34), yields

$$\begin{gathered} \left(1-{\mu }_i^{-1}\left(b_i^{-1}+\frac{d_i}{b_i\left(b_i-d_i{y}_i^{-}\right)}\right)\right)y_i^{-}=\frac{{\mu }_i-1}{{\mu }_i{K}_i}+\frac{{\mu }_i-1}{{\mu }_i{K}_i}{\displaystyle {\sum }_{j\left(\ne i\right)=1}^n{c}_{ji}}{y}_i{y}_j^{-1} \\ =\frac{{\mu }_i-1}{{\mu }_i{K}_i}+\frac{{\mu }_i-1}{{\mu }_i{K}_i}{\displaystyle {\sum }_{j\left(\ne i\right)=1}^n{c}_{ji}}{y}_j^{-1}\left(b_i^{-1}+\frac{d_i}{b_i\left(b_i-d_i{y}_i^{-}\right)}\right)y_i^{-} \end{gathered}$$

(38)

and then

$$\left(1-{\mu }_i^{-1}\left(b_i^{-1}+\frac{d_i}{b_i\left(b_i-d_i{y}_i^{-}\right)}\right)-\frac{{\mu }_i-1}{{\mu }_i{K}_i}{\displaystyle {\sum }_{j\left(\ne i\right)=1}^n{c}_{ji}}{y}_j^{-1}\left(b_i^{-1}+\frac{d_i}{b_i\left(b_i-d_i{y}_i^{-}\right)}\right)\right)y_i^{-}=\frac{{\mu }_i-1}{{\mu }_i{K}_i}$$

(39)

Note, from (3), that $x_i^{-}\ge \mathit{max}\left(0,d_i/b_i\right)$ (equivalently, $y_i^{-}\le b_i/d_i$) in order for the $i-th$ equilibrium point to be non-negative to the left of the sampling instants, provided that it is non-negative to the right of such sampling instants. Therefore, the last two additive terms on the left-hand-side of the above equation are necessarily negative under that stipulation.

Let us assume that the $i-th$ species is dominant so that $x_i\ge \underset{1\le j\left(\ne i\le n\right)}{\mathit{max}}{x}_j$, so that $y_i/y_j\le 1$; $\forall j(\ne i)\in \overline{n}$. Then,

$$\begin{gathered} \left(1-{\mu }_i^{-1}\left(b_i^{-1}+\frac{d_i}{b_i\left(b_i-d_i{y}_i^{-}\right)}\right)\right)y_i^{-} \\ \le \frac{{\mu }_i-1}{{\mu }_i{K}_i}+\frac{{\mu }_i-1}{{\mu }_i{K}_i}{\displaystyle {\sum }_{j\left(\ne i\right)=1}^n{c}_{ji}}\left(b_i^{-1}+\frac{d_i}{b_i\left(b_i-d_i{y}_i^{-}\right)}\right) \end{gathered}$$

(40)

and, since $\left(d_i/b_i\right)y_i^{-}\le 1$,

$$\begin{gathered} \frac{{\mu }_i{b}_i-1}{{\mu }_i{b}_i}{y}_i^{-}\le \frac{{\mu }_i-1}{{\mu }_i{K}_i}+\frac{{\mu }_i-1}{{\mu }_i{K}_i}{\displaystyle {\sum }_{j\left(\ne i\right)=1}^n{c}_{ji}}\left(b_i^{-1}+\frac{d_i}{b_i\left(b_i-d_i{y}_i^{-}\right)}\right)+\frac{{\mu }_i^{-1}{d}_i}{b_i\left(b_i-d_i{y}_i^{-}\right)}{y}_i^{-} \\ \le \frac{{\mu }_i-1}{{\mu }_i{K}_i}+\frac{{\mu }_i-1}{{\mu }_i{K}_i}{\displaystyle {\sum }_{j\left(\ne i\right)=1}^n{c}_{ji}}\left(\frac{b_i-d_i{y}_i^{-}+d_i}{b_i\left(b_i-d_i{y}_i^{-}\right)}\right)+\frac{1}{{\mu }_i\left(b_i-d_i{y}_i^{-}\right)} \end{gathered}$$

(41)

which is identical to (32); then, (33) is direct for the equilibrium values at the right of the sampling instants. The further two upper-bounds if $d_i\le 0$ inequalities follow directly from (32)–(33) and the proof is completed. □

The next definition relies on the concept of equilibrium consensus among the species in the sense that all of them reach the same equilibrium points.

Definition 1.

It is said that the $n\left(\ge 2\right)$ competing species set has a left/right equilibrium consensus if there exist at least two, non-necessarily distinct, non-negative real numbers $x^{-}$ and $x$ such that $x_i^{-}=x^{-}$ and $x_i=x$; $\forall i\in \overline{n}$, that is, the equilibrium point is common to all the species.

Some sufficient conditions for equilibrium consensus are found in the subsequent result.

Proposition 4.

The following parametric constraints hold:

(i) 

A right equilibrium consensus for a given common population $x$ is reached under the independent consumptions

$$d_i=\frac{\left(b_i{\mu }_i-1\right)K_i-\left({\mu }_i-1\right)\left({\displaystyle {\sum }_{j=1}^n{c}_{ji}}\right)x}{K_i+\left({\mu }_i-1\right)\left({\displaystyle {\sum }_{j=1}^n{c}_{ji}}\right)x}x;\forall i\in \overline{n}$$

(42)

(ii) 

A right equilibrium consensus for a common equilibrium population of value

$$x=\frac{\left(b_i{\mu }_i-1\right)K_i}{\left({\mu }_i-1\right)\left({\displaystyle {\sum }_{j=1}^n{c}_{ji}}\right)}$$

(43)

exists if $d_i=0$; $\forall i\in \overline{n}$ with either ${\mu }_i>\mathit{max}\left(1,b_i^{-1}\right)$ or ${\mu }_i<\mathit{min}\left(1,b_i^{-1}\right)$ for each $i\in \overline{n}$ for $x>0$, or, jointly, ${\mu }_i=b_i^{-1}\ne 1$; $\forall i\in \overline{n}$ for $x=0$ (that is, “extinction” consensus).

(iii) 

Let us assume that the competing species set has an equilibrium consensus and that there are no impulses at the equilibrium points, that is, $b_i=1$ and $d_i=0$; $\forall i\in \overline{n}$. Then, the equivalent carrying capacities $K_{ie}=K_e$; $\forall i\in \overline{n}$ are identical for all the species, the carrying capacities are $K_i=K_e{\displaystyle {\sum }_{j=1}^n{c}_{ji}}$; $\forall i\in \overline{n}$ and the nonzero common equilibrium point coincides with such a common equivalent carrying capacity, i.e.,

$$x=x^{-}=\frac{K_i}{{\displaystyle {\sum }_{j=1}^n{c}_{ji}}}=K_{ie}=K_e;\forall i\in \overline{n}.$$

Proof. 

One obtains, from (4), for $x_i=x$; $\forall i\in \overline{n}$ that

$$\begin{gathered} \left({\mu }_i-1\right)\left({\displaystyle {\sum }_{j=1}^n{c}_{ji}}\right)x^2 \\ =\left[\left(b_i{\mu }_i-1\right)K_i-d_i\left({\mu }_i-1\right)\left({\displaystyle {\sum }_{j=1}^n{c}_{ji}}\right)\right]x-d_i{K}_i;\forall i\in \overline{n} \end{gathered}$$

(44)

which proves Property (i). Property (ii) follows directly from Property (i), by making $d_i=0$; $\forall i\in \overline{n}$, which leads to $x=\frac{\left(b_i{\mu }_i-1\right)K_i}{\left({\mu }_i-1\right)\left({\displaystyle {\sum }_{j=1}^n{c}_{ji}}\right)}$; $\forall i\in \overline{n}$. Since $c_{ji}\ge 0$; $\forall i,j\in \overline{n}$ implies that $\frac{K_i}{{\displaystyle {\sum }_{j=1}^n{c}_{ji}}}=\frac{{\mu }_i-1}{b_i{\mu }_i-1}x\ge 0$, it follows that a necessary condition of fulfillment of those constraints for each $i\in \overline{n}$ is that either ${\mu }_i\ge \mathit{max}\left(1,b_i^{-1}\right)$ or ${\mu }_i\le \mathit{min}\left(1,b_i^{-1}\right)$, or, jointly, ${\mu }_i=b_i^{-1}\ne 1$; $\forall i\in \overline{n}$.

To prove Property (iii), note that, since $b_i=1$ and $d_i=0$; $\forall i\in \overline{n}$, one has, at the equilibrium points,

$$x^{-}=x=\frac{{\mu }_i{K}_{i}x}{K_i+{\displaystyle {\sum }_{j=1}^n{c}_{ji}}\left({\mu }_i-1\right)x}$$

(45)

whose solutions are $x=0$ and, after direct calculation for $x\ne 0$, one obtains

$$x^{-}=x=\frac{K_i}{{\displaystyle {\sum }_{j=1}^n{c}_{ji}}}=K_{ie}=K_e;\forall i\in \overline{n}.$$

(46)

□

Let us assume, for generalization purposes, that the intrinsic growth rates, the carrying capacities and inter-species coupling coefficients might also be time-varying, in general. Thus, one obtains, from the resulting generalized (2) and (3) and, provided that $x_i^{-}\left(k+1\right)\ne 0$ and ${\lambda }_{ji}\left(k\right)=x_j\left(k\right)/x_i\left(k\right)$, that

$$\begin{gathered} y_i^{-}\left(k+1\right)=\frac{1}{x_i^{-}\left(k+1\right)} \\ ={\mu }_i^{-1}\left(k\right)y_i\left(k\right)+\frac{{\mu }_i\left(k\right)-1}{K_i\left(k\right){\mu }_i\left(k\right)}+\frac{{\mu }_i\left(k\right)-1}{K_i\left(k\right){\mu }_i\left(k\right)}{\displaystyle {\sum }_{j(\ne )=1}^n{c}_{ji}}\left(k\right){\lambda }_{ji}\left(k\right) \end{gathered}$$

(47)

$$y_i\left(k+1\right)={\rho }_i^{-1}\left(k+1\right)y_i^{-}\left(k+1\right)$$

(48)

for any $i,j\left(\ne i\right)\in \overline{n}$, where

$${\rho }_i\left(k+1\right)=x_i\left(k+1\right)/x_i^{-}\left(k+1\right)=b_i\left(k+1\right)-d_i\left(k+1\right)y_i^{-}\left(k+1\right)>0$$

(49)

for non-negativity and non-extinction in finite-time of the solution sequence, so that $d_i\left(k+1\right)<b_i\left(k+1\right)x_i^{-}\left(k+1\right)$. Then, it follows, from (47) and (48), that

$$\begin{gathered} y_i\left(k+1\right)={\left({\rho }_i\left(k+1\right){\mu }_i\left(k\right)\right)}^{-1}{y}_i\left(k\right)+\frac{{\mu }_i\left(k\right)-1}{K_i\left(k\right){\mu }_i\left(k\right){\rho }_i\left(k+1\right)} \\ +\frac{{\mu }_i\left(k\right)-1}{K_i\left(k\right){\mu }_i\left(k\right){\rho }_i\left(k+1\right)}{\displaystyle {\sum }_{j(\ne )=1}^n{c}_{ji}}\left(k\right){\lambda }_{ji}\left(k\right) \end{gathered}$$

(50)

for any $i\in \overline{n}$. It can be proved that

$$\begin{gathered} x_i\left(k+1\right)>x_i^{-}\left(k+1\right) \\ \iff d_i\left(k+1\right)<\left(b_i\left(k+1\right)-1\right)x_i^{-}\left(k+1\right)\iff {\rho }_i\left(k+1\right)>1 \end{gathered}$$

(51)

$$\begin{gathered} x_i\left(k+1\right)<x_i^{-}\left(k+1\right) \\ \iff d_i\left(k+1\right)>\left(b_i\left(k+1\right)-1\right)x_i^{-}\left(k+1\right)\iff {\rho }_i\left(k+1\right)<1 \end{gathered}$$

(52)

$$\begin{gathered} x_i\left(k+1\right)=x_i^{-}\left(k+1\right) \\ \iff d_i\left(k+1\right)=\left(b_i\left(k+1\right)-1\right)x_i^{-}\left(k+1\right)\iff {\rho }_i\left(k+1\right)=1 \end{gathered}$$

(53)

for any $i\in \overline{n}$. We first prove (51) in detail by using contradiction arguments and logics of propositions rules as follows. Let us assume that ${\rho }_i\left(k+1\right)\le 1$ for some given $i\in \overline{n}$. Then, one obtains, from (49), that

$$b_i\left(k+1\right)x_i^{-}\left(k+1\right)>d_i\left(k+1\right)\ge \left(b_i\left(k+1\right)-1\right)x_i^{-}\left(k+1\right)$$

so that

$${\rho }_i\left(k+1\right)\le 1\Rightarrow d_i\left(k+1\right)\ge \left(b_i\left(k+1\right)-1\right)x_i^{-}\left(k+1\right)$$

which is the contrapositive logic proposition and then equivalent, logic proposition to the logic implication

$$d_i\left(k+1\right)<\left(b_i\left(k+1\right)-1\right)x_i^{-}\left(k+1\right)\Rightarrow {\rho }_i\left(k+1\right)>1$$

and the part “$\Rightarrow$” is proved in (51) for any $i\in \overline{n}$ if $x_i\left(k+1\right)>x_i^{-}\left(k+1\right)$. Now, let us assume that ${\rho }_i\left(k+1\right)>1$ and $d_i\left(k+1\right)\ge \left(b_i\left(k+1\right)-1\right)x_i^{-}\left(k+1\right)$. Then,

$${\rho }_i\left(k+1\right)=b_i\left(k+1\right)-d_i\left(k+1\right)y_i^{-}\left(k+1\right)\le b_i\left(k+1\right)-\left(b_i\left(k+1\right)-1\right)x_i^{-}\left(k+1\right)y_i^{-}\left(k+1\right)=b_i\left(k+1\right)-\left(b_i\left(k+1\right)-1\right)x_i^{-}\left(k+1\right)y_i^{-}\left(k+1\right)=1$$

which contradicts that ${\rho }_i\left(k+1\right)>1$. Then,

$${\rho }_i\left(k+1\right)>1\Rightarrow d_i\left(k+1\right)<\left(b_i\left(k+1\right)-1\right)x_i^{-}\left(k+1\right)$$

which proves the part “$\Leftarrow$” of (51) for any $i\in \overline{n}$. As a result, (51) has been proved for any $i\in \overline{n}$. The proofs of (52) and (53) are very close to the one above and were therefore omitted.

Now, note, from (49), that, for any given $i\in \overline{n}$,

$$\frac{1}{{\rho }_i\left(k+1\right){\mu }_i\left(k\right)}=\frac{1}{{\mu }_i\left(k\right)\left(b_i\left(k+1\right)-d_i\left(k+1\right)y_i^{-}\left(k+1\right)\right)}<1$$

(54)

if ${\mu }_i\left(k\right)\left(b_i\left(k+1\right)-d_i\left(k+1\right)y_i^{-}\left(k+1\right)\right)>1$, equivalently, if $x_i^{-}\left(k+1\right)>\frac{d_i\left(k+1\right){\mu }_i\left(k\right)}{{\mu }_i\left(k\right)b_i\left(k+1\right)-1}$ and, in a similar way, one has

$$\frac{1}{{\rho }_i\left(k+1\right){\mu }_i\left(k\right)}>1\mathrm{if}{x}_i^{-}\left(k+1\right)<\frac{d_i\left(k+1\right){\mu }_i\left(k\right)}{{\mu }_i\left(k\right)b_i\left(k+1\right)-1}$$

(55)

$$\frac{1}{{\rho }_i\left(k+1\right){\mu }_i\left(k\right)}=1\mathrm{if}{x}_i^{-}\left(k+1\right)=\frac{d_i\left(k+1\right){\mu }_i\left(k\right)}{{\mu }_i\left(k\right)b_i\left(k+1\right)-1}$$

(56)

Extinction at the limit as time tends to infinity needs some extra constraints, as follows, since $x_i\left(k+1\right)<\frac{d_i\left(k+1\right){\mu }_i\left(k\right)}{{\mu }_i\left(k\right)b_i\left(k+1\right)-1}$ does not hold at the limit with the left-hand side and right-hand side both converging to zero. So, the convergence to extinction of $x_i\left(k\right)$ as $k\to \infty$ implies that $x_i\left(k\right)=b_i\left(k\right)x_i^{-}\left(k\right)-d_i\left(k\right)\to 0$ as $k\to \infty$, then, equivalently, $x_i^{-1}\left(k\right)=y_i\left(k\right)\to \infty$ as $k\to \infty$ and we convey that also $x_i^{-}\left(k\right)\to 0$ (basically, the asymptotic convergences to the right and left of the sampling instants jointly hold), $b_i\left(k\right)\to 1$ and $d_i\left(k\right)\to 0$ as $k\to \infty$ with $\frac{d_i\left(k\right)}{x_i\left(k\right)}\to 0$ as $k\to \infty$ (so that $d_i\left(k\right)=o\left(x_i^{-1}\left(k\right)\right)$ as $k\to \infty$) and then ${\rho }_i\left(k\right)=b_i\left(k\right)-\frac{d_i\left(k\right)}{x_i\left(k\right)}\to 1$ as $k\to \infty$ from (49).

The following result, whose proof involves the use of the above considerations, is concerned with non-asymptotic and asymptotic extinction conditions.

Theorem 4.

The following properties hold:

(i) 

Let us assume that the $i-th$ species has the best fitness, $x_i\left(0\right)>0$ is finite, that the $i-th$ independent consumption fulfills $d_i\left(k+1\right)<b_i\left(k+1\right)x_i\left(k+1\right)$; $\forall k\in {\mathit{N}}_0$ and that there is a strict sequence of non-negative integer numbers ${\left\{k_{\ell }\right\}}_{\ell =0}^{\infty }\subset {\mathit{N}}_0$ with $k_{\ell +1}-k_{\ell }\le \overline{k}<+\infty$; $\forall \ell \in {\mathit{N}}_0$ such that ${\displaystyle {\prod }_{j=k_{\ell }}^{j=k_{\ell +1}}\left[{\rho }_i\left(k_{\ell +1}+1-j\right){\mu }_i\left(k_{\ell +1}-j\right)\right]}\ge \underset{\_}{\rho }>1$. Then, there is no asymptotic extinction of the $i-th$ species with the best fitness and its solution sequence is bounded for all time.

(ii) 

Let us assume that $\left(1-{\mu }_i\right){\displaystyle {\sum }_{j=1}^n{c}_{ji}}{x}_i\left(0\right)<1$, $b_i\left(k\right)\to 1$, $d_i\left(k\right)\to 0$ and $\frac{d_i\left(k\right)}{x_i\left(k\right)}\to 0$ as $k\to \infty$ and that $\underset{k\to \infty }{\mathit{lim}\mathit{inf}}{\mu }_i\left(k\right)\le 1$ with ${\displaystyle {\sum }_{k=1}^{\infty }\left({\mu }_i\left(k\right)-1\right)}=+\infty$. Then, there is asymptotic extinction of the i-th species with the best fitness and then that of all the remaining ones.

Proof. 

From recursive calculations by using (50), the inverse of the $i-th$ population is given by

$$\begin{gathered} y_i\left(k+1\right)={\displaystyle {\prod }_{j=0}^k\left[{\left({\rho }_i\left(k+1-j\right){\mu }_i\left(k-j\right)\right)}^{-1}\right]}{y}_i\left(0\right) \\ +{\sum }_{j=0}^k{\displaystyle {\prod }_{\ell =j}^{k-1}\left[\left({\rho }_i\left(\ell +2\right){\mu }_i\left(\ell +1\right)\right){}^{-1}\right]}\frac{{\mu }_i\left(j\right)-1}{K_i\left(j\right){\mu }_i\left(j\right){\rho }_i\left(j+1\right)}\left({\displaystyle {\sum }_{\ell =1}^n{c}_{\ell i}\left(j\right){\lambda }_{\ell i}\left(j\right)}\right) \end{gathered}$$

(57)

with the notation convention ${\displaystyle {\prod }_{\ell =j}^{k-1}\left[\left({\rho }_i\left(\ell +2\right){\mu }_i\left(\ell +1\right)\right){}^{-1}\right]}=1$ for $j=k$, ${\lambda }_{ii}\left(j\right)=1$, ${\lambda }_{\ell i}\left(j\right)\le 1$; $\forall \ell \left(\ne i\right)\in \overline{n}$ since the $i-th$ species has the best fitness. Since there exists a strictly increasing sequence ${\left\{k_{\ell }\right\}}_{\ell =0}^{\infty }\subset {\mathit{N}}_0$ with $k_{\ell +1}-k_{\ell }\le \overline{k}<+\infty$; $\forall \ell \in {\mathit{N}}_0$ such that

$$\begin{gathered} {\displaystyle {\prod }_{j=k_{\ell }}^{j=k_{\ell +1}}\left[{\rho }_i\left(k_{\ell +1}+1-j\right){\mu }_i\left(k_{\ell +1}-j\right)\right]}\ge \underset{\_}{\rho }>1 \mathrm{then} \\ \underset{k\to \infty }{\mathit{lim}}{\displaystyle {\prod }_{j=0}^k\left[{\rho }_i\left(k+1-j\right){\mu }_i\left(k-j\right){}^{-1}\right]} \end{gathered}$$

(58)

and

$$\begin{array}{l}{\displaystyle {\sum }_{j=0}^k{\displaystyle {\prod }_{\ell =j}^{k-1}\left[\left({\rho }_i\left(\ell +2\right){\mu }_i\left(\ell +1\right)\right){}^{-1}\right]}}\frac{{\mu }_i\left(j\right)-1}{K_i\left(j\right){\mu }_i\left(j\right){\rho }_i\left(j+1\right)}\\ \times \left({\displaystyle {\sum }_{\ell =1}^n{c}_{\ell i}\left(j\right){\lambda }_{\ell i}\left(j\right)}\right)<+\infty ;\forall k\in {\mathit{N}}_0\end{array}$$

(59)

since $x_i\left(0\right)>0$ is finite and then $y_i\left(0\right)>0$ is finite as well. Then, ${\left\{y_i\left(k\right)\right\}}_{k=0}^{\infty }<+\infty$ from (57) and ${\left\{x_i\left(k\right)\right\}}_{k=0}^{\infty }$ does not converge to zero. In addition, from that inverse sequence solution formula ${\left\{y_i\left(k\right)\right\}}_{k=0}^{\infty }\subset {\mathit{R}}_{+}$ and then ${\left\{x_i\left(k\right)\right\}}_{k=0}^{\infty }$ is bounded since it is convergent. Property (i) has been proved. To prove Property (ii), first note that the joint constraints $d_i\left(k+1\right)<b_i\left(k+1\right)x_i\left(k+1\right)$; $\forall k\in {\mathit{N}}_0$ and $\left(1-{\mu }_i\right){\displaystyle {\sum }_{j=1}^n{c}_{ji}}{x}_i\left(0\right)<1$, the second one implying also that $\left(1-{\mu }_i\right){\displaystyle {\sum }_{j=1}^n{c}_{ji}}{x}_j\left(0\right)<1$ since the $i-th$ species has the best fitness and being always guaranteed if ${\mu }_i\ge ;1$, guarantee that ${\left\{x_i\left(k\right)\right\}}_{k=0}^{\infty }\subset {\mathit{R}}_{0+}$ directly from the time-varying generalization of (2)–(3), even if ${\mu }_i<1$. The constraints $b_i\left(k\right)\to 1$, $d_i\left(k\right)\to 0$ and $\frac{d_i\left(k\right)}{x_i\left(k\right)}\to 0$ as $k\to \infty$ guarantee that eventual asymptotic extinction of the $i-th$ species jointly holds at the left and right of the sampling instants with ${\rho }_i\left(k\right)\to 1$, as $k\to \infty$, while the constraints, either $\underset{k\to \infty }{\mathit{lim}\mathit{inf}}{\mu }_i\left(k\right)<1$ or $\underset{k\to \infty }{\mathit{lim}\mathit{inf}}{\mu }_i\left(k\right)=1$ with ${\displaystyle {\sum }_{k=1}^{\infty }\left({\mu }_i\left(k\right)-1\right)}=+\infty$, guarantee that ${\left\{y_i\left(k\right)\right\}}_{k=0}^{\infty }\to \infty$ and then ${\left\{x_i\left(k\right)\right\}}_{k=0}^{\infty }\to 0$ so that ${\left\{x_j\left(k\right)\right\}}_{k=0}^{\infty }\to 0$, since the $i-th$ population has the best fitness; $\forall j\in \overline{n}$ from the formula which obtains the solution of the inverse population from the initial conditions. □

3. Stability Results Obtained by Lyapunov Method

It is now assumed that the Beverton–Holt equation is time-varying, in general, rather than parameterized by constant parameters. A Lyapunov sequence candidate is proposed for stability analysis around eventual non-extinction equilibrium points. From Assumption 2, an artificial auxiliary sequence ${\left\{{\nu }_i\left(k\right)\right\}}_{k\in \mathit{N}}\subset \mathit{R}$ is defined by ${\nu }_i\left(k\right)=\frac{d_i\left(k\right)}{x_i^{-}\left(k\right)}\in \left(-\infty ,b_i\left(k\right)\right]$; $\forall i\in \overline{n}$, $\forall k\in \mathit{N}$ (note that $d_i\left(k\right)$ is not defined for $k=0$). That definition, with the above constraint, guarantees that

$$d_i\left(k+1\right)={\nu }_i\left(k+1\right)x_i^{-}\left(k+1\right)\le b_i\left(k+1\right)x_i^{-}\left(k+1\right);\forall i\in \overline{n},\forall k\in \mathit{N}$$

(60)

Remark 3.

The above artificial sequence allows an easy integration of the eventual independent consumption contribution to the stability of non-extinction equilibrium points.

The above artificial sequence is not adequate to describe finite-time extinction $x_i\left(k\right)=x_i^{-}\left(k+1\right)=0$ with $d_i\left(k+1\right)<0$ (individuals of the species $i-th$ enter the habitat from outside) implying that the extinguished $i-th$ species to the left of the $\left(k+1\right)$ sampling instants recovers from previous extinction to the right of the $\left(k+1\right)$ sampling instant.

We can now describe the model to the right of the sampling instants as follows, if ${\left\{x_i^{-}\left(k\right)\right\}}_{k=0}^{\infty }\subset {\mathit{R}}_{+}$, $\forall i\in \overline{n}$,

$$x_i\left(k+1\right)=\frac{{\mu }_i\left(k\right)K_i\left(k\right)\left(b_i\left(k+1\right)-{\nu }_i\left(k+1\right)\right)}{K_i\left(k\right)+\left({\mu }_i\left(k\right)-1\right){\displaystyle {\sum }_{j=1}^n{c}_{ji}\left(k\right)x_j\left(k\right)}}{x}_i\left(k\right);\forall i\in \overline{n},\forall k\in \mathit{N}$$

(61)

for given initial finite conditions $x_i\left(0\right)>0$; $\forall i\in \overline{n}$, where ${\nu }_i\left(k\right)=\frac{d_i\left(k\right)}{x_i^{-}\left(k\right)}\in \left(-\infty ,b_i\left(k\right)\right]$. Let us define the $i-th$ population inverse $y_i\left(k\right)=x_i^{-1}\left(k\right)$; $\forall i\in \overline{n}$, $\forall k\in \mathit{N}$ so that

$$\begin{gathered} y_i\left(k+1\right)={\left({\mu }_i\left(k\right)\left(b_i\left(k+1\right)-{\nu }_i\left(k+1\right)\right)\right)}^{-1}{y}_i\left(k\right) \\ +\frac{{\mu }_i\left(k\right)-1}{{\mu }_i\left(k\right)K_i\left(k\right)\left(b_i\left(k+1\right)-{\nu }_i\left(k+1\right)\right)}\left({\displaystyle {\sum }_{j=1}^n{c}_{ji}\left(k\right)x_j\left(k\right)}\right)y_i\left(k\right) \end{gathered}$$

(62)

which can be rewritten as

$$\begin{gathered} y_i\left(k+1\right)=\left(a_i\left(k\right)+h_i\left(k\right)\right)y_i\left(k\right)=a_i\left(k\right)\left(1+\frac{{\mu }_i\left(k\right)-1}{K_i\left(k\right)}\left({\displaystyle {\sum }_{j=1}^n{c}_{ji}\left(k\right)x_j\left(k\right)}\right)\right)y_i\left(k\right) \\ =a_i\left(k\right)\left(1+\frac{{\mu }_i\left(k\right)-1}{K_i\left(k\right)}+\frac{{\mu }_i\left(k\right)-1}{K_i\left(k\right)}\left({\displaystyle {\sum }_{j\left(\ne i\right)=1}^n{c}_{ji}\left(k\right)x_j\left(k\right)}\right)\right)y_i\left(k\right) \end{gathered}$$

(63)

where

$$a_i\left(k\right)={\left({\mu }_i\left(k\right)\left(b_i\left(k+1\right)-{\nu }_i\left(k+1\right)\right)\right)}^{-1}$$

(64)

$$\begin{gathered} h_i\left(k\right)=\frac{{\mu }_i\left(k\right)-1}{{\mu }_i\left(k\right)K_i\left(k\right)\left(b_i\left(k+1\right)-{\nu }_i\left(k+1\right)\right)}\left({\displaystyle {\sum }_{j=1}^n{c}_{ji}\left(k\right)x_j\left(k\right)}\right) \\ =\frac{\left({\mu }_i\left(k\right)-1\right)a_i\left(k\right)}{K_i\left(k\right)}\left({\displaystyle {\sum }_{j=1}^n{c}_{ji}\left(k\right)x_j\left(k\right)}\right) \end{gathered}$$

(65)

The following result relies on the asymptotic stability of the non-extinction equilibrium point of the competition impulsive Beverton–Holt equation.

Theorem 5.

Let us assume that all the competing species have non-zero equilibrium points $x_i\in {\mathit{R}}_{+}$. Those equilibrium points are asymptotically stable, provided that the following constraints hold:

$$\begin{gathered} (\mathrm{a})a_i\left(k\right)+h_i\left(k\right)=a_i\left(k\right)\left(1+\frac{{\mu }_i\left(k\right)-1}{K_i\left(k\right)}\left({\displaystyle {\sum }_{j=1}^n{c}_{ji}\left(k\right)x_j\left(k\right)}\right)\right)<1; \\ \forall k\in {\mathit{N}}_0 \\ (\mathrm{b})\underset{k\to \infty }{\mathit{lim}\mathit{sup}}\left[a_i\left(k\right)\left(1+\frac{{\mu }_i\left(k\right)-1}{K_i\left(k\right)}\left({\displaystyle {\sum }_{j=1}^n{c}_{ji}\left(k\right)x_j\left(k\right)}\right)\right)\right]\le 1 \end{gathered}$$

and that, furthermore, at least one of the subsequent four constraints hold for some set of real parameters ${\theta }_i>0$; $\forall i\in \overline{n}$:

$$\begin{gathered} (\mathrm{c}) x_i\left(k\right)<{\left(1+a_i\left(k\right)+h_i\left(k\right)\right)}^{}\frac{x_i}{2};\forall k\in {\mathit{N}}_0 \\ (\mathrm{d}){\displaystyle {\sum }_{i=1}^n\frac{{\theta }_i}{x_i\left(k\right)}}\left(1+a_i\left(k\right)+h_i\left(k\right)\right)>2{\displaystyle {\sum }_{i=1}^n\frac{{\theta }_i}{x_i}};\forall k\in {\mathit{N}}_0 \\ (\mathrm{e})\frac{\underset{1\le i\le n}{\mathit{max}} x_i^2\left(k\right)}{\underset{1\le i\le n}{\mathit{min}} x_i\left(k\right)}<\frac{{\displaystyle {\sum }_{i=1}^n{\theta }_i{\left(1-{\left(a_i\left(k\right)+h_i\left(k\right)\right)}^2\right)}^{}}}{2{\displaystyle {\sum }_{i=1}^n{\theta }_i\left[1-a_i\left(k\right)-h_i\left(k\right)\right]}}{x}_i^{} \\ (\mathrm{f})\frac{{\displaystyle {\sum }_{i=1}^n{\theta }_i{x}_i^2\left(k\right)}}{{\displaystyle {\sum }_{i=1}^n{\theta }_i{x}_i\left(k\right)}}<\frac{\underset{1\le i\le n}{\mathit{min}}\left(1-\left(a_i\left(k\right)+h_i\left(k\right)\right){}^2\right)}{2 \underset{1\le i\le n}{\mathit{max}}\left(1-a_i\left(k\right)-h_i\left(k\right)\right)}{x}_i \end{gathered}$$

Proof. 

Let us define $y_i=x_i^{-1}$; $\forall i\in \overline{n}$ with $x_i$ being a nonzero equilibrium point of the $i$-th species and ${\tilde{y}}_i\left(k\right)=y_i\left(k\right)-y_i$; $\forall i\in \overline{n}$, $\forall k\in {\mathit{N}}_0$. Let us consider the Lyapunov sequence candidate $V\left(k\right)={\displaystyle {\sum }_{i=1}^n{\theta }_i}{\left(y_i\left(k\right)-y_i\right)}^2$; $\forall k\in {\mathit{N}}_0$ for some set of design scalar coefficients ${\theta }_i>0$; $\forall i\in \overline{n}$. Then, the one-step incremental Lyapunov sequence candidate verifies the subsequent chain of relations:

$$\begin{gathered} \Delta V\left(k\right)=V\left(k+1\right)-V\left(k\right)={\displaystyle {\sum }_{i=1}^n{\theta }_i\left({\tilde{y}}_i^2\left(k+1\right)-{\tilde{y}}_i^2\left(k\right)\right)} \\ ={\displaystyle {\sum }_{i=1}^n{\theta }_i\left({\tilde{y}}_i\left(k+1\right)+{\tilde{y}}_i\left(k\right)\right)}\left({\tilde{y}}_i\left(k+1\right)-{\tilde{y}}_i\left(k\right)\right) \\ ={\displaystyle {\sum }_{i=1}^n{\theta }_i\left(\left[a_i\left(k\right)+h_i\left(k\right)\right]y_i\left(k\right)-y_i+y_i\left(k\right)-y_i\right)} \\ \times \left(\left[a_i\left(k\right)+h_i\left(k\right)\right]y_i\left(k\right)-y_i-y_i\left(k\right)+y_i\right) \\ ={\displaystyle {\sum }_{i=1}^n{\theta }_i\left(\left[a_i\left(k\right)+h_i\left(k\right)+1\right]y_i\left(k\right)-2y_i\right)}\left(\left[a_i\left(k\right)+h_i\left(k\right)-1\right]y_i\left(k\right)\right) \\ ={\displaystyle {\sum }_{i=1}^n{\theta }_i\left[a_i\left(k\right)+h_i\left(k\right)+1\right]\left[a_i\left(k\right)+h_i\left(k\right)-1\right]y_i^2\left(k\right)} \\ -2{\displaystyle {\sum }_{i=1}^n{\theta }_i{y}_i\left[a_i\left(k\right)+h_i\left(k\right)-1\right]y_i\left(k\right)} \\ =-{\displaystyle {\sum }_{i=1}^n{\theta }_i\left({\left(1+a_i\left(k\right)+h_i\left(k\right)\right)}^{}{y}_i\left(k\right)-2y_i\right)\left(1-a_i\left(k\right)-h_i\left(k\right)\right)y_i\left(k\right)} \\ \le -{\displaystyle {\sum }_{i=1}^n\left({\left(1+a_i\left(k\right)+h_i\left(k\right)\right)}^{}{y}_i\left(k\right)-2y_i\right)\underset{1\le i\le n}{\min }\left[{\theta }_i\left(1-a_i\left(k\right)-h_i\left(k\right)\right)y_i\left(k\right)\right]}; \\ \forall k\in {\mathit{N}}_0 \end{gathered}$$

(66)

Other upper-bounds of $\Delta V\left(k\right)$ are clearly the following ones:

$$\begin{gathered} -\left({\displaystyle {\sum }_{i=1}^n{\theta }_i{\left[1-{\left(a_i\left(k\right)+h_i\left(k\right)\right)}^2\right]}^{}}\right)\underset{1\le i\le n}{\mathit{min}} y_i^2\left(k\right) \\ +2\left({\displaystyle {\sum }_{i=1}^n{\theta }_i{y}_i\left[1-a_i\left(k\right)-h_i\left(k\right)\right]}\right)\underset{1\le i\le n}{\mathit{max}} y_i\left(k\right) \end{gathered}$$

(67)

and

$$\begin{gathered} -\underset{1\le i\le n}{\mathit{min}}\left(1-\left(a_i\left(k\right)+h_i\left(k\right)\right){}^2\right)\left({\displaystyle {\sum }_{i=1}^n{\theta }_i{y}_i^2\left(k\right)}\right) \\ +2 \underset{1\le i\le n}{\mathit{max}}\left(1-a_i\left(k\right)-h_i\left(k\right)\right)\left({\displaystyle {\sum }_{i=1}^n{\theta }_i{y}_i\left(k\right)y_i}\right) \end{gathered}$$

(68)

Thus, if the constraints (a) and (b) and one of the constraints from (c) to (f) hold, then ${\left\{-\Delta V_k\right\}}_{k=0}^{\infty }\subset {\mathit{R}}_{+}$, so that ${\left\{V_k\right\}}_{k=0}^{\infty }$ is bounded and strictly decreasing, so that ${\left\{V_k\right\}}_{k=0}^{\infty }\to 0$ so that $y_i\left(k\right)\to y_i=x_i^{-1}$, equivalently, $x_i\left(k\right)\to x_i$; $\forall i\in \overline{n}$; $\forall k\in {\mathit{N}}_0$. □

Remark 4.

Note that the constraint (a) of Theorem 5 requires, as a necessary condition, ${\mu }_i\left(k\right)\left(b_i\left(k+1\right)-{\nu }_i\left(k+1\right)\right)>1$; $\forall i\in \overline{n}$; $\forall k\in {\mathit{N}}_{0+}$.

Note also that a sufficient condition for Theorem 5 to hold is

$$\begin{gathered} {\displaystyle {\sum }_{i=1}^n{\theta }_i\left({\left(1+a_i\left(k\right)+h_i\left(k\right)\right)}^{}{y}_i\left(k\right)-2y_i\right)\left(1-a_i\left(k\right)-h_i\left(k\right)\right)}>0; \\ \forall i\in \overline{n}, \forall k\in {\mathit{N}}_0 \end{gathered}$$

(69)

although it is not as easy to test as the conditions given in the theorem statement.

Note that stability around the zero equilibrium implies the asymptotic extinction of all the species, This also implies that the inverse populations diverge asymptotically to $+\infty$. Note that

$$\begin{gathered} y_i\left(k+1\right)=\frac{1}{{\mu }_i\left(k\right)K_i\left(k\right)\left(b_i\left(k+1\right)-d_i\left(k+1\right)y_i^{-}\left(k+1\right)\right)}\left(K_i\left(k\right)y_i\left(k\right)+{\mu }_i\left(k\right)-1\right) \\ +\frac{{\mu }_i\left(k\right)-1}{{\mu }_i\left(k\right)K_i\left(k\right)\left(b_i\left(k+1\right)-d_i\left(k+1\right)y_i^{-}\left(k+1\right)\right)}\left({\displaystyle {\sum }_{j\left(\ne i\right)=1}^n{c}_{ji}\left(k\right)\frac{y_i\left(k\right)}{y_j\left(k\right)}}\right) \end{gathered}$$

(70)

The asymptotic extinction is formalized through the subsequent result.

Theorem 6.

Let us assume that the following conditions hold:

(a) ${\left\{K_i\left(k\right)\right\}}_{k=0}^{\infty }\subset \left(0,\overline{K}\right)$, ${\left\{{\mu }_i\left(k\right)\right\}}_{k=0}^{\infty }\subset \left(1,\overline{\mu }\right)$, $\left\{b_i\left(k\right)\right\}{}_{k=0}^{\infty }\subset \left[0,\overline{b}\right]$, $c_{ii}\left(k\right)=1$, ${\left\{c_{ji}\left(k\right)\right\}}_{k=0}^{\infty }\subset \left[0,1\right]$ and $d_i\left(k\right)\in {\left(-\infty ,b_i\left(k\right)x_i^{-}\left(k\right)\right]}^{}$; $\forall i\in \overline{n}$, $\forall k\in {\mathit{N}}_0$.

(b) If there is some finite $k\in {\mathit{N}}_0$ such that $x_i\left(k\right)=0$, then $x_i\left(k+1\right)=-d_i\left(k+1\right)=0$

(c) $\underset{k\to \infty }{\lim }\left({\displaystyle {\prod }_{j=0}^k\left[{\alpha }_i\left(j\right)\right]}\right)=+\infty$

Then, ${\left\{x_i\left(k\right)\right\}}_{k=0}^{\infty }\to 0$; $\forall i\in \overline{n}$ if

$$\underset{k\to \infty }{\mathit{lim}}\mathit{inf}\frac{K_i\left(k\right)y_i\left(k\right)+{\mu }_i\left(k\right)-1}{{\mu }_i\left(k\right)K_i\left(k\right)\left(b_i\left(k+1\right)-d_i\left(k+1\right)y_i^{-}\left(k+1\right)\right)}>1$$

Proof. 

Note that the assumption $d_i\left(k\right)\le b_i\left(k\right)x_i^{-}\left(k\right)$ is equivalent to $b_i\left(k\right)-d_i\left(k\right)y_i^{-}\left(k\right)\ge 0$; $\forall i\in \overline{n}$, $\forall k\in {\mathit{N}}_{0+}$ and implies that $x_i\left(k\right)\ge 0$ and $y_i\left(k\right)\ge 0$; $\forall i\in \overline{n}$, $\forall k\in {\mathit{N}}_0$. Let us define the auxiliary variables for $i\in \overline{n}$, $k\in {\mathit{N}}_0$ as

$${\alpha }_i\left(k\right)=\frac{K_i\left(k\right)y_i\left(k\right)+{\mu }_i\left(k\right)-1}{{\mu }_i\left(k\right)K_i\left(k\right)\left(b_i\left(k+1\right)-d_i\left(k+1\right)y_i^{-}\left(k+1\right)\right)}$$

(71)

$${\beta }_i\left(k\right)=\frac{{\mu }_i\left(k\right)-1}{{\mu }_i\left(k\right)K_i\left(k\right)\left(b_i\left(k+1\right)-d_i\left(k+1\right)y_i^{-}\left(k+1\right)\right)}$$

(72)

$${\gamma }_i\left(k\right)={\displaystyle {\sum }_{j\left(\ne i\right)=1}^n{c}_{ji}\left(k\right)\frac{y_i\left(k\right)}{y_j\left(k\right)}}$$

(73)

so that

$$y_i\left(k+1\right)={\alpha }_i\left(k\right)y_i\left(k\right)+{\beta }_i\left(k\right){\gamma }_i\left(k\right);\forall i\in \overline{n},\forall k\in {\mathit{N}}_0$$

(74)

One obtains, via recursive calculations with the above relation, that

$$\begin{gathered} y_i\left(k+1\right)-{\displaystyle {\sum }_{j=0}^k\left({\displaystyle {\prod }_{j=0}^k\left[{\alpha }_i(\ell )\right]{}^{k-j}{\beta }_i\left(j\right){\gamma }_i\left(j\right)}\right)}=\left({\prod }_{j=0}^k\left[{\alpha }_i\left(j\right)\right]\right)y_i\left(0\right); \\ \forall i\in \overline{n},\forall k\in {\mathit{N}}_0 \end{gathered}$$

(75)

And, if $y_i\left(0\right)>0$ and finite (equivalently, $0<x_i\left(0\right)<+\infty$) for all $i\in \overline{n}$, then

$$\underset{k\to \infty }{\mathit{lim}}\left(y_i\left(k+1\right)-{\displaystyle {\sum }_{j=0}^k\left({\displaystyle {\prod }_{j=0}^k\left[{\alpha }_i(\ell )\right]{}^{k-j}{\beta }_i\left(j\right){\gamma }_i\left(j\right)}\right)}\right)=+\infty ;\forall i\in \overline{n}$$

(76)

The following cases can arise:

Case 1: ${\left\{y_i\left(k\right)\right\}}_{k=0}^{\infty }\to +\infty$; $\forall i\in \overline{n}$, equivalently, ${\left\{x_i\left(k\right)\right\}}_{k=0}^{\infty }\to 0$; $\forall i\in \overline{n}$. The proof follows directly.

Case 2: ${\left\{y_i\left(k\right)\right\}}_{k=0}^{\infty }$ is bounded and $\underset{k\to \infty }{\mathit{lim}}\left({\displaystyle {\sum }_{j=0}^k\left({\displaystyle {\prod }_{j=0}^k\left[{\alpha }_i(\ell )\right]{}^{k-j}{\beta }_i\left(j\right){\gamma }_i\left(j\right)}\right)}\right)=+\infty$ for some $i\in \overline{n}$.

Case 2 can hold through several sub-cases as follows:

a) Sub-case 2a: Either ${\left\{{\alpha }_i\left(k\right)\right\}}_{k=0}^{\infty }\to +\infty$ or ${\left\{{\beta }_i\left(k\right)\right\}}_{k=0}^{\infty }\to +\infty$. Since the numerators of their respective general terms are finite, then either the denominators converge to zero or they have some element which is zero, that is, either $b_i\left(k\right)-d_i\left(k\right)y_i^{-}\left(k\right)\left(\ge 0\right)\to 0$ as $k\to \infty$ for some $i\in \overline{n}$ or there are some $k\in {\mathit{N}}_0$ and some $i\in \overline{n}$, such that $b_i\left(k\right)-d_i\left(k\right)y_i^{-}\left(k\right)=0$. However, these two sub-cases imply, respectively, ${\left\{x_i\left(k\right)\right\}}_{k=0}^{\infty }\to 0$ and $x_i\left(k\right)=0$, which implies that $x_i^{-}\left(k+1\right)=0$ and $x_i\left(k+1\right)=-d_i\left(k+1\right)=0$ from the assumption (b). In both cases, extinction is achieved either asymptotically or in a finite time and the claim of Case 2 that ${\left\{y_i\left(k\right)\right\}}_{k=0}^{\infty }$ is bounded cannot hold for any $i\in \overline{n}$ so that ${\left\{y_i\left(k\right)\right\}}_{k=0}^{\infty }\to +\infty$; $\forall i\in \overline{n}$. Thus, Case 2, supported by Sub-case 2a, cannot hold.

b) Sub-case 2b: Either ${\left\{{\gamma }_i\left(k\right)\right\}}_{k=0}^{\infty }\to +\infty$ or ${\left\{{\gamma }_j\left(k\right)\right\}}_{k=0}^{\infty }\to +\infty$ for some given $i\in \overline{n}$ and some $j\left(\ne i\right)\in \overline{n}$. Since the sequences ${\left\{c_{ji}\left(k\right)\right\}}_{k=0}^{\infty }\subset \left[0,1\right]$ then either ${\left\{\frac{y_i\left(k\right)}{y_j\left(k\right)}\right\}}_{k=0}^{\infty }\to \infty$, or ${\left\{\frac{y_i\left(k\right)}{y_j\left(k\right)}\right\}}_{k=0}^{\infty }=+\infty$, for $j\left(\ne i\right)\in \overline{n}$. Since ${\left\{y_i\left(k\right)\right\}}_{k=0}^{\infty }$ is claimed to be bounded, then the denominators of the quotients defining the general terms of the above sequence either converge to zero as $k\to \infty$ or are zero for some finite $k\in {\mathit{N}}_0$. However, this would imply the unboundedness of some of the subpopulations contradicting the boundedness property of Theorem 2, which still holds for the extended Beverton–Holt evolving under the time-varying parameterizing sequences ${\left\{K_i\left(k\right)\right\}}_{k=0}^{\infty }$, ${\left\{{\mu }_i\left(k\right)\right\}}_{k=0}^{\infty }$, ${\left\{b_i\left(k\right)\right\}}_{k=0}^{\infty }$ and ${\left\{d_i\left(k\right)\right\}}_{k=0}^{\infty }$, fulfilling the assumption (a) of this theorem. Therefore, Case 2 cannot hold when being supported by Sub-case 2b.

c) Sub-case 2c: $\underset{k\to \infty }{\mathit{lim}}\left({\displaystyle {\sum }_{j=0}^k\left({\displaystyle {\prod }_{j=0}^k\left[{\alpha }_i(\ell )\right]{}^{k-j}{\beta }_i\left(j\right){\gamma }_i\left(j\right)}\right)}\right)=+\infty$ with $\underset{k\to \infty }{\mathit{lim}}\left({\displaystyle {\sum }_{j=0}^k\left({\displaystyle {\prod }_{j=0}^k\left[{\alpha }_i(\ell )\right]{}^{k-j}}\right)}\right)=+\infty$ and ${\left\{{\beta }_i\left(j\right){\gamma }_i\left(j\right)\right\}}_{j=0}^{\infty }$ being bounded for any $i\in \overline{n}$. Since $\underset{k\to \infty }{\mathit{lim}}\left({\displaystyle {\prod }_{j=0}^k\left[{\alpha }_i\left(j\right)\right]}\right)=+\infty$ and since the above partial sum diverges to $+\infty$ as $k\to \infty$, one also concludes, from the assumed condition (c), i.e., $\underset{k\to \infty }{\mathit{lim}}\left({\displaystyle {\prod }_{j=0}^k\left[{\alpha }_i\left(j\right)\right]}\right)=+\infty$, that the Sub-case 2c reduces to Case 1. As a conclusion, only Case 1, including Sub-Case 2c, is possible, which implies the asymptotic extinction of all the subspecies. □

Remark 5.

As it could be expected from intuition, a large hunting/fishing quota or a certain level of positive independent consumption might lead to extinction. Such conclusions arise from inspecting either the zeroing in finite time or the asymptotic convergence to zero of the amount $b_i\left(k+1\right)-d_i\left(k+1\right)y_i^{-}\left(k+1\right)$. In a parallel way, sufficiently small hunting/fishing quotas or small positive independent consumption can keep the populations free of extinction.

4. About Extinction Conditions under Small Intrinsic Growth Rates

Note that Theorem 6 gives extinction conditions for intrinsic growth rates exceeding unity, which is an usual condition in the background literature on Beverton–Holt equations [5,6,7,8,9,10,11,12,18,26,27,28,29,33]. In this section, the asymptotic extinction is studied for the case of intrinsic growth rates being less than unity.

Remark 6.

Note that extinction at the right of the $k-th$ sampling instant of the $i-th$ species occurs if $d_i\left(k\right)=b_i\left(k\right)x_i^{-}\left(k\right)$ and it occurs asymptotically if $\left(d_i\left(k\right)-b_i\left(k\right)x_i^{-}\left(k\right)\right)\to 0$ as $k\to \infty$. This can happen irrespective if the intrinsic growth rate exceeds unity or is less than unity. The first case, which is the typical situation in the Beverton–Holt equation, might be addressed as a particular case included in Theorem 6. The condition is difficult to achieve in practical cases, since it requires an exact monitoring of the independent consumption through time. In the following and for the case of intrinsic growth rates below unity, this case is excluded from the analysis.

To fix ideas, we first discuss the case when just a single species is involved. For this purpose, we establish two preliminary necessary technical results for possible extinction either in finite time or asymptotic extinction, while keeping the solution sequence non-negative and bounded for all time under non-negative initial conditions.

Proposition 5.

Let us consider one single-species impulsive Beverton–Holt equation, Equation (1). Let us assume that ${\left\{\mu \left(k\right)\right\}}_{k=0}^{\infty }\subset \left(0,1\right]$, ${\left\{b\left(k\right)\right\}}_{k=1}^{\infty }\subset \left(0,1\right]$ and ${\left\{d\left(k\right)\right\}}_{k=1}^{\infty }\subset \left(-\infty ,+\infty \right)$ Then, for any given $k\in {\mathit{N}}_0$, $x\left(k\right)=0$ $\Rightarrow x^{-}\left(k+1\right)=0$ and, furthermore, $x\left(k+1\right)=0$ if and only if $d\left(k+1\right)=0$. If ${\left\{x\left(k\right)\right\}}_{k=0}^{\infty }\to 0$, then ${\left\{d\left(k\right)\right\}}_{k=1}^{\infty }\to 0$ and, if, in addition, ${\left\{b\left(k\right)\right\}}_{k=1}^{\infty }\subset {\mathit{R}}_{+}$, then ${\left\{x^{-}\left(k\right)\right\}}_{k=0}^{\infty }\to 0$.

Proof. 

One obtains, from (1), that

$$\begin{gathered} x\left(k+1\right)=\frac{\left[b\left(k+1\right)\mu \left(k\right)K\left(k\right)+d\left(k+1\right)\left(1-\mu \left(k\right)\right)\right]x\left(k\right)-d\left(k+1\right)K\left(k\right)}{K\left(k\right)-\left(1-\mu \left(k\right)\right)x\left(k\right)}; \\ \forall k\in {\mathit{N}}_0 \end{gathered}$$

(77)

Since $K\left(k\right)>0$, $x\left(k\right)=0\Rightarrow x^{-}\left(k+1\right)=0$ from (1) and $x\left(k+1\right)=0$ if and only if $d\left(k+1\right)=0$ and, if $b\left(k+1\right)>0$, then $x^{-}\left(k+1\right)=\frac{x\left(k+1\right)+d\left(k+1\right)}{b\left(k+1\right)}=0$. Note that, if ${\left\{x\left(k\right)\right\}}_{k=0}^{\infty }\to 0$, then

$d\left(k+1\right)=\frac{b\left(k+1\right)\mu \left(k\right)K\left(k\right)x\left(k\right)}{K\left(k\right)-\left(1-\mu \left(k\right)\right)x\left(k\right)}-x\left(k+1\right)\to 0$ as $k\to \infty$ and also $x^{-}\left(k+1\right)=\frac{x\left(k+1\right)+d\left(k+1\right)}{b\left(k+1\right)}\to 0$ as $k\to \infty$ if ${\left\{b\left(k\right)\right\}}_{k=1}^{\infty }\subset {\mathit{R}}_{+}$ since ${\left\{x\left(k\right)\right\}}_{k=0}^{\infty }\to 0$ and ${\left\{d\left(k\right)\right\}}_{k=1}^{\infty }\to 0$. □

Proposition 6.

Let us consider a Beverton–Holt equation for one single species. Let us assume that ${\left\{\mu \left(k\right)\right\}}_{k=0}^{\infty }\subset \left(0,1\right]$, ${\left\{b\left(k\right)\right\}}_{k=1}^{\infty }\subset \left(0,1\right]$ and ${\left\{d\left(k\right)\right\}}_{k=1}^{\infty }\subset \left(-\infty ,+\infty \right)$. Then, for any given $k\in {\mathit{N}}_0$, $x\left(k+1\right)\in \left[0,+\infty \right)$, with $x\left(k\right)\ge 0$, if and only if

$$\begin{gathered} x\left(k\right)\in \left[\mathit{min}\left(0,\frac{d\left(k+1\right)K\left(k\right)}{b\left(k+1\right)\mu \left(k\right)K\left(k\right)+d\left(k+1\right)\left(1-\mu \left(k\right)\right)}\right),\frac{K\left(k\right)}{1-\mu \left(k\right)}\right); \\ \forall k\in {\mathit{N}}_0 \end{gathered}$$

(78)

Proof. 

Let us consider several cases in (77) with the given assumptions, namely,

Case a: $x\left(k+1\right)\ge 0$, if $x\left(k\right)\in \left[\frac{d\left(k+1\right)K\left(k\right)}{b\left(k+1\right)\mu \left(k\right)K\left(k\right)+d\left(k+1\right)\left(1-\mu \left(k\right)\right)},\frac{K\left(k\right)}{1-\mu \left(k\right)}\right)$. Note that the limits of the admissible domain of $x\left(k\right)$ are mutually compatible, since

$$\begin{gathered} \frac{d\left(k+1\right)}{b\left(k+1\right)\mu \left(k\right)K\left(k\right)+d\left(k+1\right)\left(1-\mu \left(k\right)\right)}<\frac{1}{1-\mu \left(k\right)} \\ \iff d\left(k+1\right)<d\left(k+1\right)+\frac{b\left(k+1\right)\mu \left(k\right)K\left(k\right)}{1-\mu \left(k\right)} \end{gathered}$$

which trivially holds, since $\frac{b\left(k+1\right)\mu \left(k\right)K\left(k\right)}{1-\mu \left(k\right)}>0$. Since $x\left(k\right)$ is also requested to be non-negative, then (78) is used. It was proved that (78) implies that $x\left(k+1\right)\ge 0$. Now, note that the conditions ${\left\{\mu \left(k\right)\right\}}_{k=0}^{\infty }\subset \left(0,1\right]$, ${\left\{b\left(k\right)\right\}}_{k=1}^{\infty }\subset \left(0,1\right]$ and ${\left\{d\left(k\right)\right\}}_{k=1}^{\infty }\subset \left(-\infty ,+\infty \right)$ also imply that the domain of $x\left(k\right)$ is bounded and, from (77), $x\left(k+1\right)$ is also bounded. Thus, Case a fully verifies the statement claim.

Case b: $x\left(k+1\right)\ge 0$, if $x\left(k\right)\in \left(\frac{K\left(k\right)}{1-\mu \left(k\right)},\frac{d\left(k+1\right)K\left(k\right)}{b\left(k+1\right)\mu \left(k\right)K\left(k\right)+d\left(k+1\right)\left(1-\mu \left(k\right)\right)}\right)$. However, a necessary condition for the above domain of values of $x\left(k\right)$ to be well-posed is that

$$\begin{gathered} \frac{1}{1-\mu \left(k\right)}<\frac{d\left(k+1\right)}{b\left(k+1\right)\mu \left(k\right)K\left(k\right)+d\left(k+1\right)\left(1-\mu \left(k\right)\right)} \\ \iff d\left(k+1\right)>d\left(k+1\right)+\frac{b\left(k+1\right)\mu \left(k\right)K\left(k\right)}{1-\mu \left(k\right)} \end{gathered}$$

which is a contradiction. Then, Case b does not verify the statement claim.

Case c: $x\left(k+1\right)\ge 0$, if $x\left(k\right)=\frac{K\left(k\right)}{1-\mu \left(k\right)}=\frac{d\left(k+1\right)K\left(k\right)}{b\left(k+1\right)\mu \left(k\right)K\left(k\right)+d\left(k+1\right)\left(1-\mu \left(k\right)\right)}$ and the indetermination $0/0$, resulting from (77), is solvable with a positive limit, as the numerator and denominator converge to zero. However, the identity of both confluent values of $x\left(k\right)$ leads to the following contradiction:

$$0=d\left(k+1\right)-d\left(k+1\right)=\frac{b\left(k+1\right)\mu \left(k\right)K\left(k\right)}{1-\mu \left(k\right)}>0$$

so that Case c does not verify the statement claim. As a result, only Case a satisfies the statement claim and the proof is complete.□

The next main result of this section concerned with the case in which one single species relies on the asymptotic convergence of the solution to extinction when the solution to the right of the sampling instants is a non-negative strictly decreasing sequence, that is, ${\left\{x\left(k\right)-x\left(k+1\right)\right\}}_{k=0}^{\infty }\subset {\mathit{R}}_{+}$ and ${\left\{x\left(k\right)\right\}}_{k=0}^{\infty }\left(\subset {\mathit{R}}_{+}\right)\to 0$.

Theorem 7.

Let us consider the Beverton–Holt equation for one single species. Let us assume that, if $x\left(k_0\right)=0$ for any finite $k_0\in {\mathit{N}}_0$, then $d\left(k_0+1\right)=0$. Let us also assume that $0<x\left(0\right)=x^{-}\left(0\right)<\frac{K\left(0\right)}{1-\mu \left(0\right)}$, ${\left\{\mu \left(k\right)\right\}}_{k=0}^{\infty }\subset \left(0,1\right]$, ${\left\{K\left(k\right)\right\}}_{k=1}^{\infty }\subset \left(0,\overline{K}\right)$ with $\overline{K}<+\infty$, ${\left\{b\left(k\right)\right\}}_{k=1}^{\infty }\subset \left(0,1\right]$.

Let us also assume that

$$\begin{gathered} d\left(k+1\right)\in \left(\frac{\left[\left(b\left(k+1\right)\mu \left(k\right)-1\right)K\left(k\right)+\left(1-\mu \left(k\right)\right)x\left(k\right)\right]x\left(k\right)}{K\left(k\right)-\left(1-\mu \left(k\right)\right)x\left(k\right)},\frac{b\left(k+1\right)\mu \left(k\right)K\left(k\right)x\left(k\right)}{K\left(k\right)-\left(1-\mu \left(k\right)\right)x\left(k\right)}\right]; \\ \forall k\in {\mathit{N}}_0 \end{gathered}$$

(79)

Then, ${\left\{x\left(k\right)\right\}}_{k=0}^{\infty }\subset {\mathit{R}}_{0+}$, ${\left\{x^{-}\left(k\right)\right\}}_{k=0}^{\infty }\subset {\mathit{R}}_{0+}$, ${\left\{d\left(k\right)\right\}}_{k=1}^{\infty }\subset {\mathit{R}}_{}$ are bounded, with ${\left\{x^{-}\left(k\right)\right\}}_{k=0}^{\infty }\to 0$ and ${\left\{x\left(k\right)\right\}}_{k=0}^{\infty }\to 0$ being strictly decreasing and ${\left\{d\left(k\right)\right\}}_{k=1}^{\infty }\to 0$.

Proof. 

Let us consider the Lyapunov sequence candidate $V\left(k\right)=x\left(k\right)$; $\forall k\in {\mathit{N}}_0$ so that $\Delta V\left(k\right)=V\left(k+1\right)-V\left(k\right)=x\left(k+1\right)-x\left(k\right)$. Then, from Proposition 6, $0<x\left(k\right)<\frac{K\left(k\right)}{1-\mu \left(k\right)}$ for any $k\in {\mathit{N}}_0$ implies that $x\left(k+1\right)\ge 0$, so that

$$\begin{gathered} \left(K\left(k\right)-\left(1-\mu \left(k\right)\right)x\left(k\right)\right)\Delta V\left(k\right)=\left(K\left(k\right)-\left(1-\mu \left(k\right)\right)x\left(k\right)\right)\left(V\left(k+1\right)-V\left(k\right)\right) \\ =\left[\left(b\left(k+1\right)\mu \left(k\right)-1\right)K\left(k\right)+d\left(k+1\right)\left(1-\mu \left(k\right)\right)+\left(1-\mu \left(k\right)\right)x\left(k\right)\right]x\left(k\right)-d\left(k+1\right)K\left(k\right) \\ =\left[\left(b\left(k+1\right)\mu \left(k\right)-1\right)K\left(k\right)+\left(1-\mu \left(k\right)\right)x\left(k\right)\right]x\left(k\right)-d\left(k+1\right)\left[K\left(k\right)-\left(1-\mu \left(k\right)\right)x\left(k\right)\right] \\ \le 0;\forall k\in {\mathit{N}}_0 \end{gathered}$$

(80)

and ${\left\{x\left(k\right)\right\}}_{k=0}^{\infty }\subset {\mathit{R}}_{0+}$ is bounded and non-increasing, since $0<x\left(0\right)<\frac{K\left(0\right)}{1-\mu \left(0\right)}$ if

$$d\left(k+1\right)\ge \frac{\left[\left(b\left(k+1\right)\mu \left(k\right)-1\right)K\left(k\right)+\left(1-\mu \left(k\right)\right)x\left(k\right)\right]x\left(k\right)}{K\left(k\right)-\left(1-\mu \left(k\right)\right)x\left(k\right)};\forall k\in {\mathit{N}}_0$$

(81)

which implies that $\Delta V\left(k\right)\le 0$; $\forall k\in {\mathit{N}}_0$. Since $K\left(k\right)>\left(1-\mu \left(k\right)\right)x\left(k\right)$, it follows, from (80), that $x\left(k+1\right)<x\left(k\right)$, so that ${\left\{x\left(k\right)\right\}}_{k=0}^{\infty }$ is strictly decreasing, if $x\left(k\right)>0$ and (81) is a strict inequality, $\Delta V\left(k\right)\to 0$ as $k\to \infty$ and that $x\left(k\right)\to 0$ as $k\to \infty$. If $x\left(k+1\right)\ge 0$, then

$$d\left(k+1\right)\le b\left(k+1\right)x^{-}\left(k+1\right)=\frac{b\left(k+1\right)\mu \left(k\right)K\left(k\right)x\left(k\right)}{K\left(k\right)-\left(1-\mu \left(k\right)\right)x\left(k\right)};\forall k\in {\mathit{N}}_0$$

(82)

and ${\left\{x^{-}\left(k\right)\right\}}_{k=0}^{\infty }\subset {\mathit{R}}_{0+}$ is also bounded, since $x\left(0\right)=x^{-}\left(0\right)$ is finite and ${\left\{d\left(k\right)\right\}}_{k=1}^{\infty }\subset \left(-\infty ,+\infty \right)$. Combining both inequalities, (81), in its strict version, and (82), yields (79). This also implies that $x\left(k\right)\to 0$ as $k\to \infty$ so that $d\left(k+1\right)\to 0$ and $x^{-}\left(k+1\right)\to 0$ as $k\to \infty$. □

Remark 7.

Note that Theorem 7 holds, in particular and as stated, if $b\left(k+1\right)=\mu \left(k\right)\equiv 0$ since it involves, for all $k\in {\mathit{N}}_0$ the condition $-x\left(k\right)<d\left(k+1\right)\le 0$, implying that $x\left(k+1\right)-x\left(k\right)=-d\left(k+1\right)-x\left(k\right)<x\left(k\right)-x\left(k\right)=0$ if $x\left(k\right)\ne 0$, so that the one-step increment of the Lyapunov sequence is negative.

Let us consider now the extended competition model from (4) for the extinction of some species $i\in \overline{n}$ in the competition model with possible time-varying parameterization to conclude that

$$\begin{gathered} \frac{x{}_i\left(k+1\right)}{x_i\left(k\right)} \\ =\left(\left[b_i\left(k+1\right){\mu }_i\left(k\right)K_i\left(k\right)+d_i\left(k+1\right)\left(1-{\mu }_i\left(k\right)\right)\right]-\frac{d_i\left(k+1\right)}{x_i\left(k\right)}\left(K_i\left(k\right)+{\displaystyle {\sum }_{j\left(\ne i\right)=1}^n{c}_{ji}\left(k\right)}\left({\mu }_i\left(k\right)-1\right)x_j\left(k\right)\right)\right) \\ \forall k\in {\mathit{N}}_0 \end{gathered}$$

(83)

$$\times \frac{1}{K_i\left(k\right)-\left(1-{\mu }_i\left(k\right)\right)x_i\left(k\right)+{\displaystyle {\sum }_{j\left(\ne i\right)=1}^n{c}_{ji}}\left(k\right)\left({\mu }_i\left(k\right)-1\right)x_j\left(k\right)}<1; \forall k\in {\mathit{N}}_0$$

with the positive denominator in (83) implying a non-negative numerator, implying, equivalently, that $0\le x_i\left(k+1\right)<x_i\left(k\right)$ if $x_i\left(k\right)>0$ for all $k\in {\mathit{N}}_0$ if the “ad-hoc” version of (79) holds in the form

$$\begin{gathered} d_i\left(k+1\right)\le \frac{b_i\left(k+1\right){\mu }_i\left(k\right)K_i\left(k\right)x_i\left(k\right)}{K_i\left(k\right)-\left(1-{\mu }_i\left(k\right)\right)x_i\left(k\right)+{\displaystyle {\sum }_{j\left(\ne i\right)=1}^n{c}_{ji}\left(k\right)}\left({\mu }_i\left(k\right)-1\right)x_j\left(k\right)}; \\ \forall k\in {\mathit{N}}_0 \end{gathered}$$

(84)

$$\begin{gathered} d_i\left(k+1\right)>\frac{\left(b_i\left(k+1\right){\mu }_i\left(k\right)-1\right)K_i\left(k\right)+\left(1-{\mu }_i\left(k\right)\right)x_i\left(k\right)-{\displaystyle {\sum }_{j\left(\ne i\right)=1}^n{c}_{ji}\left(k\right)}\left({\mu }_i\left(k\right)-1\right)x_j\left(k\right)}{K_i\left(k\right)-\left(1-{\mu }_i\left(k\right)\right)x_i\left(k\right)+{\displaystyle {\sum }_{j\left(\ne i\right)=1}^n{c}_{ji}\left(k\right)}\left({\mu }_i\left(k\right)-1\right)x_j\left(k\right)}{x}_i\left(k\right); \\ \forall k\in {\mathit{N}}_0 \end{gathered}$$

(85)

which leads to the subsequent result.

Theorem 8.

Let us consider a competition Beverton–Holt equation for $n$ species. Let us assume that, if $x_i\left(k_0\right)=0$ for any finite $k_0\in {\mathit{N}}_0$ and $i\in \overline{n}$ then $d_i\left(k_0+1\right)=0$. Let us also assume that

$$\begin{gathered} x_j\left(0\right)=x_j^{-}\left(0\right)\ge 0;\forall j\left(\ne i\right)\in \overline{n}; \\ 0<x_i\left(0\right)=x_i^{-}\left(0\right)<\frac{K_i\left(0\right)+{\displaystyle {\sum }_{j\left(\ne i\right)=1}^n{c}_{ji}\left(0\right)}\left({\mu }_i\left(0\right)-1\right)x_j\left(0\right)}{1-{\mu }_i\left(0\right)}>, \\ {\left\{{\mu }_i\left(k\right)\right\}}_{k=0}^{\infty }\subset \left(0,1\right],{\left\{{\mu }_{\ell }\left(k\right)\right\}}_{k=0}^{\infty }\subset \left(1,{\overline{\mu }}_{\ell }\right)\subset \left(1,+\infty \right),{\left\{b_j\left(k\right)\right\}}_{k=1}^{\infty }\subset \left(0,1\right], \\ {\left\{K_j\left(k\right)\right\}}_{k=1}^{\infty }\subset \left(0,{\overline{K}}_j\right)\subset \left(0,+\infty \right)\mathrm{and}{d}_j\left(k\right)\subset (-\infty ,b_j\left(k\right)x_j^{-}(k\left)\right)];\forall j,\ell (\ne i)\in \overline{n}; \\ \forall k\in \mathit{N}. \end{gathered}$$

Let us also assume that

$$\begin{gathered} d_i\left(k+1\right)\in (\frac{\left(b_i\left(k+1\right){\mu }_i\left(k\right)-1\right)K_i\left(k\right)+\left(1-{\mu }_i\left(k\right)\right)x_i\left(k\right)-{\displaystyle {\sum }_{j\left(\ne i\right)=1}^n{c}_{ji}}\left(k\right)\left({\mu }_i\left(k\right)-1\right)x_j\left(k\right)}{K_i\left(k\right)-\left(1-{\mu }_i\left(k\right)\right)x_i\left(k\right)+{\displaystyle {\sum }_{j\left(\ne i\right)=1}^n{c}_{ji}\left(k\right)}\left({\mu }_i\left(k\right)-1\right)x_j\left(k\right)}{x}_i\left(k\right), \\ \frac{b_i\left(k+1\right){\mu }_i\left(k\right)K_i\left(k\right)x_i\left(k\right)}{K_i\left(k\right)-\left(1-{\mu }_i\left(k\right)\right)x_i\left(k\right)+{\displaystyle {\sum }_{j\left(\ne i\right)=1}^n{c}_{ji}\left(k\right)}\left({\mu }_i\left(k\right)-1\right)x_j\left(k\right)}];\forall k\in {\mathit{N}}_0 \end{gathered}$$

(86)

Then, ${\left\{x_i\left(k\right)\right\}}_{k=0}^{\infty }\subset {\mathit{R}}_{0+}$, ${\left\{x_i^{-}\left(k\right)\right\}}_{k=0}^{\infty }\subset {\mathit{R}}_{0+}$, ${\left\{d_i\left(k\right)\right\}}_{k=1}^{\infty }\subset {\mathit{R}}_{}$ are bounded, with ${\left\{x_i^{-}\left(k\right)\right\}}_{k=0}^{\infty }\to 0$ and ${\left\{x_i\left(k\right)\right\}}_{k=0}^{\infty }\to 0$ being strictly decreasing and ${\left\{d_i\left(k\right)\right\}}_{k=1}^{\infty }\to 0$.

5. Numerical Experiments

This Section aims at illustrating, through numerical simulation examples, some of the theoretical results discussed in the previous Sections. In this way, this Section is organized into a number of examples concerned with the Theorems and results stated in Section 2, Section 3 and Section 4.

Example 2.

Let us consider the system (1) parameterized by b(k) = 1, d(k) = 0, K(k) = 300 and $\mu (k)=0.6+5\times {0.6}^k$ with x(0) = 100. The values of $\mu (k)$ with iteration along with the evolution of x(k) are displayed in Figure 1. Thus, Lemma 1 holds, since the growth rate converges to 0.6 and $\mu (k)\in (0,1)$ for all $k\ge 5$. It is observed, in Figure 1, how the population extinguishes in finite time, since x(j) = 0 for j> 30 according to Lemma 1. On the other hand, when $\mu (k)=1+{0.62}^k$, we have that $\mu (k)$ converges to unity (in fact $\mu (k)$ is forced to be exactly unity from j = 10 onwards) and we are in the condition of applying Lemma 2. Therefore, Figure 2 shows how the population remains strictly positive for all discrete time (and even converges to a positive constant value) as Lemma 2 claims.

Example 3.

Let us consider the system (1) parameterized by the constant values b(k) = 0.9, d(k) = 0.1, K(k) = 300 and $\mu (k)=2.4$ with x(0) = 100. The evolution of x(k) is displayed in Figure 3. It can be seen, in this figure, that the population converges to the equilibrium point given numerically by 248.385. This value is in accordance with the calculations in Theorem 1(i), since $\mu (k)=2.4>\mathit{max}(1,1/b(k))=1.11$ and d = 0.1 satisfies the constraint

$$\begin{gathered} 0.1=d\in \left[-x_1,\frac{{\left(\sqrt{\mu b}-1\right)}^{2}K}{\mu -1}\right]\cup \left[\frac{{\left(\sqrt{\mu b}+1\right)}^{2}K}{\mu -1},\infty \right) \\ =\left[-0.0863,47.2741\right]\cup \left[1307,\infty \right). \end{gathered}$$

Thus, Theorem 1(i) holds. Furthermore, Theorem 1(i) provides two equilibrium points given by $x_1=0.0863$ and $x_2=248.385$. Moreover, Figure 3 also depicts the left value of the population $x^{-}(k)$. It satisfies at the equilibrium $276.09=x^{-}(k)=\frac{x_2+d}{b}=\frac{248.385+0.1}{0.6}=276.09$, as Theorem 1(i) states. If we now consider the case when b(k) = 1 and d = 0, i.e., there is no harvesting nor independent consumption, then the left and right values of the population are the same, as Figure 4 shows, while the equilibrium point is in accordance with Theorem 1(ii), since $x_2=\frac{\left(\mu b-1\right)K}{\mu -1}=300$, as it can be readily seen in Figure 4. In addition, when $b={\mu }^{-1}$ (and d = 0), the trajectory of the population is depicted in Figure 5. It can be observed, in this figure, that the population ends up extinguishing, as predicted by Theorem 1(ii).

Example 4.

Let us consider the multi-species Beverton–Holt Equations (2) and (3) parameterized by the constant values $b_i\left(k\right)=1$, $d_i\left(k\right)=0$, $K_1\left(k\right)=300$, $K_2\left(k\right)=200$ and $K_3\left(k\right)=100$ and ${\mu }_1(k)=2.4$, ${\mu }_2(k)=2$ and ${\mu }_3(k)=1.8$ with $x_1\left(0\right)=100$, $x_2\left(0\right)=50$ and $x_3\left(0\right)=30$. The coupling matrix is given by

$$C=\left(\begin{array}{ccc}1& 0.4& 0.3\\ 0.25& 1& 0.4\\ 0.5& 0.35& 1\end{array}\right)$$

These parameters correspond to the case when the species 1 dominates the other two. Thus, we are in the condition of applying Propositions 1 and 2 and Theorem 2(i) to guarantee that all populations are non-negative and, furthermore, $x_1\left(k\right)>x_2\left(k\right)>x_3\left(k\right)$, as Proposition 2 ensures. These results can be observed in Figure 6, where the evolution of the three populations is displayed. In addition, Figure 7 displays the evolution of the three species when we consider the same parameters as before, but $b_1=0.98$, $b_2=0.96$ and $b_3=0.95$ with $d_1=0.01$, $d_2=0.02$ and $d_3=0.03$ (i.e., $b_1>b_2>b_3$ while $d_3>d_2>d_1$). It is checked, in this case, that both Propositions 1 and 2 hold when a harvesting quota, along with an external consumption, is included in the system. It can be also observed, in Figure 7, that species 3 extinguishes. This situation is also predicted by Theorem 2(ii), since $b_3=0.95>1/{\mu }_3=0.55$, making x₃(k) converge to zero asymptotically. Finally, Theorem 2(iii) is also verified, since, as it can be observed in Figure 6 and Figure 7, all populations are bounded for all time.

Example 5.

Let us consider the multi-species Beverton–Holt Equations (2) and (3) parameterized by the constant values $b_1\left(k\right)=0.98$, $b_2\left(k\right)=0.96$ and $b_3\left(k\right)=0.95$, $d_i\left(k\right)=0$, $K_1\left(k\right)=300$, $K_2\left(k\right)=200$ and, $K_e\left(k\right)=200$ and ${\mu }_1(k)=2.4$, ${\mu }_2(k)=2$ and ${\mu }_3(k)=1.8$ with $x_1\left(0\right)=100$, $x_2\left(0\right)=50$ and $x_3\left(0\right)=30$. The coupling matrix is given by

$$C=\left(\begin{array}{ccc}1& 0.004& 0.003\\ 0.0025& 1& 0.004\\ 0.005& 0.0035& 1\end{array}\right)$$

The evolution of the three species under this parameterization is displayed in Figure 8. It can be seen that the population of the three species converge to a positive equilibrium point given by x₁ = 288.41, x₂ = 182.23 and x₃ = 175.90, in accordance with Theorem 3, since Condition C1 of Theorem 3(ii) holds. Furthermore, these values are close to the ones calculated from (31) and given by x₁ = 288.46, x₂ = 182.58 and x₃ = 175.42, since the elements of the matrix C are sufficiently small and satisfy the conditions (27).

Example 6.

Let us consider the multi-species Beverton–Holt Equations (2) and (3) parameterized by the constant values b_i(k) = 1, d_i(k) = 0, K_i(k) = 200 and ${\mu }_1(k)=2.4$, ${\mu }_2(k)=2$ and ${\mu }_3(k)=1.8$ with x₁(0) = 100, x₂(0) = 50 and x₃(k) = 30. The coupling matrix is given by

$$C=\left(\begin{array}{ccc}1& 0.004& 0.005\\ 0.0025& 1& 0.004\\ 0.005& 0.0035& 1\end{array}\right)$$

The evolution of the three species under this parameterization is displayed in Figure 9. It can be observed, in Figure 9, that there exists a consensus equilibrium point in which the equilibrium points of all species converge to the same unique value. The numerical location of the equilibrium point is given by x = 198.50, which is close to the theoretically calculated one of 198.70 predicted by Proposition 4 in (43).

Example 7.

Let us consider the multi-species Beverton–Holt Equations (2) and (3) parameterized by the constant values b_i(k) = 1, d_i(k) = 0, K₁(k) = 300, K₂(k) = K₃(k) = 200 and ${\mu }_1(k)=1.5+{0.4}^k$, ${\mu }_2(k)=1.45+{0.35}^k$ and ${\mu }_3(k)=1.35+{0.3}^k$ with x₁(0) = 100, x₂(0) = 75 and x₃(k) = 50. The coupling matrix is given by

$$C=\left(\begin{array}{ccc}1& 0.4& 0.005\\ 0.25& 1& 0.4\\ 0.05& 0.035& 1\end{array}\right)$$

The evolution of the three species under this parameterization is displayed in Figure 10. Since we are in the condition of applying Theorem 4(i), because $0=d_i<b_i{x}_i$ and ${\displaystyle {\prod }_{j=k_{\ell }}^{j=k_{\ell +1}}\left[b_i\left(k_{\ell +1}+1-j\right){\mu }_i\left(k_{\ell +1}-j\right)\right]}\ge \underset{\_}{\rho }>1$, then there is no asymptotic extinction of the populations, as Figure 10 shows. Moreover, all the populations converge to an equilibrium point which is asymptotically stable, as established by Theorem 5. In addition, Figure 11 displays the populations of the three species when ${\mu }_1(k)=0.5+{0.4}^k<1$, ${\mu }_2(k)=0.45+{0.35}^k<1$ and ${\mu }_3(k)=0.35+{0.3}^k<1$. As it is claimed in Theorem 4(ii), the three species extinguish asymptotically, since $\left(1-{\mu }_i(0)\right){\displaystyle {\sum }_{j=1}^n{c}_{ji}}{x}_i\left(0\right)<1$.

In conclusion, this section illustrates, through numerical simulation examples, some of the theoretically discussed results.

6. Conclusions

This paper discusses extinction and non-extinction conditions obtained from an impulsive-type competition Beverton–Holt equation, which, in the most general case, is modeled under a time-varying parameterization. Some of the obtained results rely on the existence of one or more competing species within the studied habitat having a best fitness, which is interpreted as a dominance of its population stock. Such mentioned extinction/non-extinction conditions are easily testable constraints on the harvesting, typically being hunting/fishing quotas, or, alternatively, on the independent consumption, which are the relevant parameters in the discontinuities at sampling time instants of the population dynamics. The performed research includes the study of the existence of extinction and non-extinction equilibrium points, the conditions of non-negativity and boundedness of the solutions for any given set of finite non-negative initial conditions, as well as formal generic results related to sufficiency-type conditions for asymptotic stability to any equilibrium point and, in particular, for extinction. The case of intrinsic growth rates being less than unity and implying extinction is also discussed compared to the evolution of the independent consumptions and the harvesting quotas sequences. Several simulated examples are displayed and discussed.