2.1. The Single-Species Impulsive Beverton–Holt Equation
The subsequent impulsive discrete Beverton–Holt equation for a single species, [
26,
27,
33] extends the standard one, which has been described in the introduction:
with given finite initial conditions
, where
is the so-called
intrinsic growth rate of the population, determined by life cycle and demographic properties (such as, for instance, species growth rate, survivorship rate, etc.) and
is the so-called
carrying capacity, a characteristic of the habitat dependent on resource availability, temperature, humidity, etc. Typically, the constraints
and
for all
are assumed for the Beverton–Holt equation, since if, otherwise, the carrying capacity is zero, then the habitat is incompatible with the species evolution within it; if
, then the species stock remains constant through time; if
, then
, so that two special atypical situations can happen, namely, if
for the initial samples and there is a sufficiently small population stock, which keeps the right-hand-side positivity, then the species stock grows over time, but it can tend to negative values, making the model to be not well-posed for a sufficiently extended time. If, on the contrary,
for all samples, then the population asymptotically extinguishes.
On the other hand, the impulsive parameters, which can modify the stocks of population, to the right of the sampling instants related to their left-values are the harvesting quota ; , which depends on the authorities policy depending on the spawning stock and foreseen recruitments and the independent consumption ; that implies recruitment variations depending on unforeseen disturbances, artificial re-population actions and local migrations “towards” or “from” the studied habitat. For easy presentation of some of the technical results, the complementary harvesting quota ; is used. Some particular results in this paper are given for the case of intrinsic growth rates under unity and for negative harvesting quotas, or, equivalently, for complementary harvesting quotas exceeding unity. The physical interpretation of this situation is that a re-population with a number of adults exceeding to population stock is performed with a ratio larger than unity.
Remark 1. Note that the public regulations on fishing or hunting taking into account the stocks of population imply that ; . However, if a repopulation with adults is intended, which is sometimes the case, then it can be decided to increase the above coefficient exceeding unity in the case that the population stock is low. Therefore, we admit, at the level of a general formulation, that the complementary harvesting quota is non-negative and bounded. It turns out that the independent consumption is positive, if there is a net flux of individuals from the studied habitat to outside of it, so that the population stock decreases, and it is negative, if there is a net flux entering the habitat, so that the population stock increases. Finally, it is zero if there is no interchange of population of the habitat with the environment. The independent consumption can also take into account repopulation actions that are not linked to a proportion on the existing population stock.
Note that, if , or if and , then . It can be argued that, although it is a common hypothesis to assume that and , it is possible, under certain extra constraints on the state of sufficient smallness, related to information about the equation parameters, that could take values under unity. To clarify this concern, let us assume Equation (1) without impulsive effects, that is, and , so that ; . Thus, for any given , if , then if , and is, furthermore, finite if . Furthermore, if , then , so that extinction happens in finite time. If , then , so that the population remains constant and fixed to its value at the sample.
Now, let us assume that
and
, implying that
and finite. Let us also assume that
. Then,
for
and finite. One obtains
which implies that
so that the former non-negativity constraint
is amended by the stronger one
And, proceeding recursively in the same way, it follows that
has a strictly decreasing infinite sequence of bounded non-negative upper-bounds. However, note that, if
, then the upper-bound remains unaltered. Thus, we have the following results.
Lemma 1. Let us assume that and (namely, there is no impulsive effect). Let us also assume that, for some finite , , is bounded and either is non-decreasing or . Then, such that for (that is, there is extinction in finite time).
Proof. Note that, since
,
is strictly decreasing if and only if
If
for some finite
, then the result is already proved. Thus, let us assume that
;
. Note that
, if and only if
, since
, that is, since
, leading to
;
, in order for it to be jointly strictly decreasing with the denominator of the right-hand-side being positive for all
. Then, either
as
, or
as
; furthermore,
Since
is non-decreasing, then
, so that
Therefore, as is not possible, so as . Since is finite and is strictly decreasing and converges asymptotically to zero, then there is some finite such that and the species reproduction is not feasible for the next samples, so that extinction happens in finite time .
If the assumption of being non-decreasing is replaced by , then the result still holds, since ; so that, in the event that as , the number of individuals becomes zero after a finite time. □
Lemma 2. Let us assume that , and that . Let us also assume that, for some finite , , and is bounded. Then, , that is, there is no extinction in finite time and ; with finite , so that a non-extinction equilibrium point is reached in finite time.
In Lemma 2, note that the condition
implies that
, that is an infinity denumerable cardinal. In other words, there is only a finite number of samples in the infinite subset of the natural numbers
for which the intrinsic growth rate is strictly less than unity. This condition guarantees that, contrarily to Lemma 1, there is no extinction at the
sample. Additionally, it turns out that, since the intrinsic growth rate sequence is less than one for a finite number of samples, there exists a finite non-negative integer number
such that
:
implying that
;
leading to the existence of an equilibrium point. It is addressed, in
Section 5, how it is possible to achieve asymptotic extinction in the single species and in the competition impulsive Beverton–Holt equations under certain trade-offs between the independent consumption sequence and the harvesting quota, even if the intrinsic growth rate is under unity.
2.3. Equilibrium Points
The subsequent result holds for the case of one single species.
Theorem 1. Let us assume that either the intrinsic growth rates, carrying capacities, harvesting quotas and independent consumptions are constant parameters, or that the related parameterizing sequences converge asymptotically to constant parameters. Then, the following properties hold:
- (i)
There exist equilibrium points (or, more properly, left and right limits of equilibrium points)with physical sense, or feasible, (i.e., being real non-negative) of the single-species impulsive Beverton–Holt equation if and only if If , then the above constraint becomes - (ii)
If and , then there are no impulses at the equilibrium steady-state, so that the equilibrium solution is not oscillatory between its left and right values at the sampling instants, that is, (extinction) and .
If , then the equilibrium points become (extinction) and , provided that either or . If, in addition, and , then .
- (iii)
If , then there is only a non-negative equilibrium point with either and or and .
- (iv)
If , then there is only a non-negative equilibrium point with and . Let us assume that negative harvesting quotas are allowed, then , provided that .
Proof. The equilibrium point to the left and right of the sampling instants satisfies
subject to the constraint
The above constraint may be rewritten as
whose zeros
are
which have to be real and non-negative for the equilibrium point to have a physical sense, so that two joint necessary conditions are
The second constraint can be re-arranged in the form
Defining the auxiliary variable
, the above inequality takes the form
One obtains that the zeros of the left-hand-side of the above constraint are
and the constraint
holds, since
is a convex parabola of zeros
, if any of the two constraints below holds
In order that, in addition, (in order for the equilibrium points to the left of the sampling instants to be non-negative as well), since . Furthermore, . If , then . Property (i) follows directly from the above constraints. Property (ii) follows directly from the corresponding particular cases of Property (i).
To prove Property (iii), note that, if , then the equilibrium point satisfies the constraint , which yields for and , or for and . The equilibrium point is unfeasible for alternative combinations of values of and .
To prove Property (iv), note that, if
, then the equilibrium point constraint
becomes
for
. Thus, the equivalent constraint
has, as zeros,
Let us consider two cases for , namely,
Case a: and so that, if is not admissible, so that (i.e., both unfeasible since negative). If is admissible, then , provided that and (i.e., unfeasible), since .
Case b: and , implying , leading to (unfeasible) and .
Therefore, only one equilibrium point is non-negative. Property (iii) has been proved. □
Note that Theorem 1(iii) establishes the existence of a non-negative equilibrium point with intrinsic growth rates exceeding unity and positive harvesting quotas subject to a prescribed upper-bound. The physical interpretation is that there is a certain migration flux (either spontaneous or due to a monitored re-population intervention) of adult individuals from the habitat environment entering the habitat under study. Note that Theorem 1(iii) was also extended by first considering that Case a is non-negative with , with and . This implies that there is a negative migration flux (i.e., a supply of individuals from the environment to the habitat, either spontaneous or via intervention) and a negative harvesting quota, namely, a monitored supply of larvae to the habitat with associated complementary harvesting quota in a proportion greater than unity related to its natural stock within the habitat. In this case, (unfeasible) and , provided that .
2.4. Non-Negativity and Boundedness of the Solutions
The subsequent assumptions are eventually made in the sequel in some of the technical results.
Assumption 1. The carrying capacities, intrinsic growth rates and inter-species coupling dynamics are constant, i.e., , , , ; .
Assumption 2. The complementary harvesting quotas and independent consumption sequences satisfy the upper-bounding constraints ; ; , .
It can be pointed out that Assumption 1 can be extended directly to the case that the constant parameters are sequences depending on time. It can be also generalized for under the additional constraint ; or for its extension to the case when carrying capacities, intrinsic growth rates and inter-species coupling dynamics are sequences depending on time. The interpretation is that, if the intrinsic growth rate is under unity, then the coupling sequences from the remaining populations to the have to be small enough related to the ratio . Note that the populations stocks to the left and right limits of the sampling instants have to be non-negative for coherency of the model evolution. The constraints of Assumption 2 guarantee that the populations to the left limits of the sampling instants are non-negative if those to the right limits are non-negative.
The following result on the non-negativity of the solution is directly obtained from (2)–(3) and Assumptions 1–2.
Proposition 1. Under Assumptions 1–2, for all and any given , if , then and . If , then and, also, if, furthermore, .
Assumptions 1–2 also lead to the subsequent result on the dominance (or best fitness) of a certain population on another one for all samples.
Proposition 2. Let us assume that, for any given , , , and and that Assumptions 1–2 hold. Thus, if , then and .
The above conditions may be relaxed as follows:
If , and , then and , provided that ; .
Proof. Note that
if
,
and
which holds if
and
, which leads to
. Furthermore,
since
,
and
. Then, one obtains recursively that
and
, as claimed in the first part of the proposition. The second part is direct, since, under the assumptions that
and
, one obtains
(not necessarily under the joint constraints
,
and
). This implies that
, which, together with
(not necessarily with
), implies that
. The result for
follows recursively. □
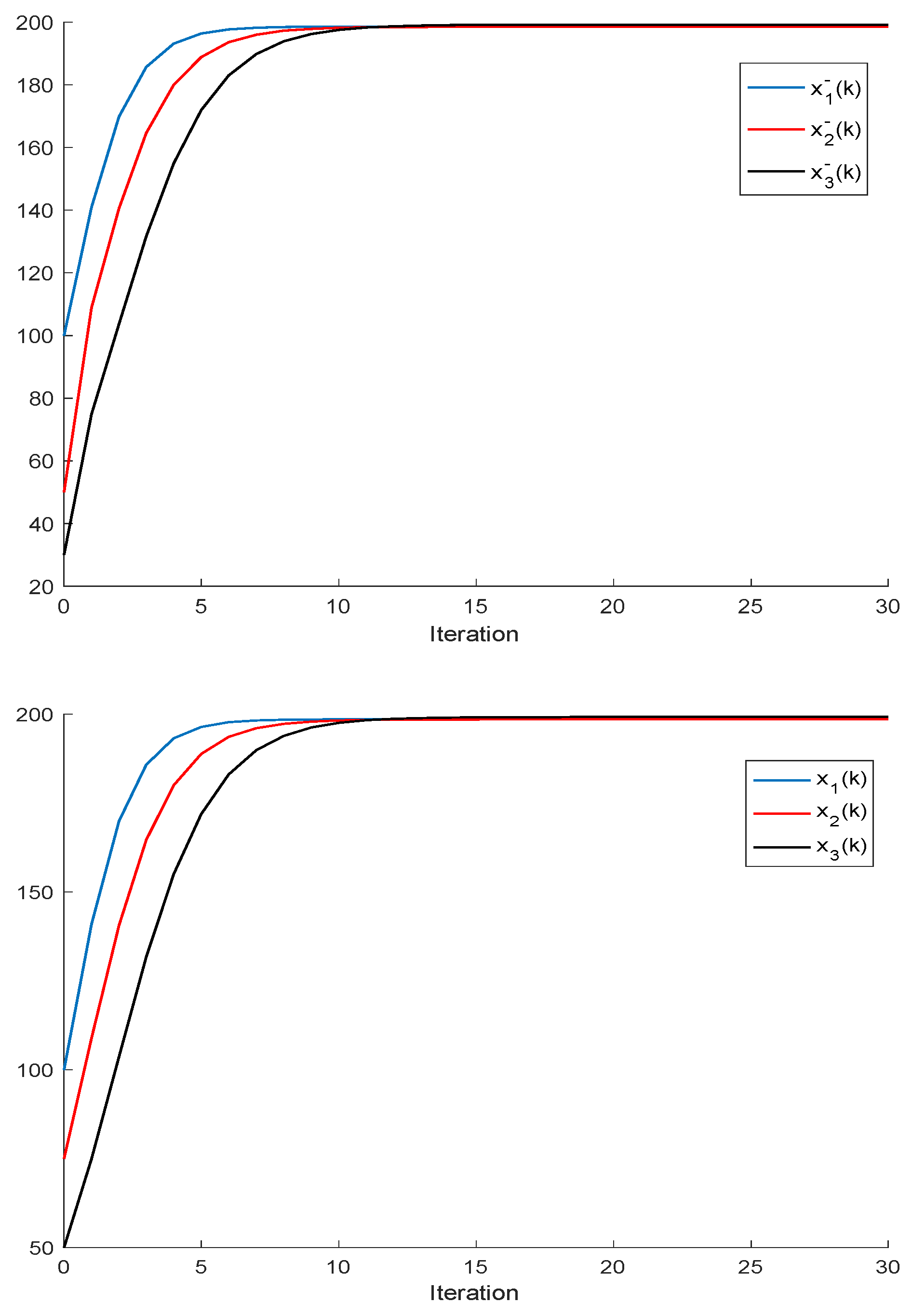
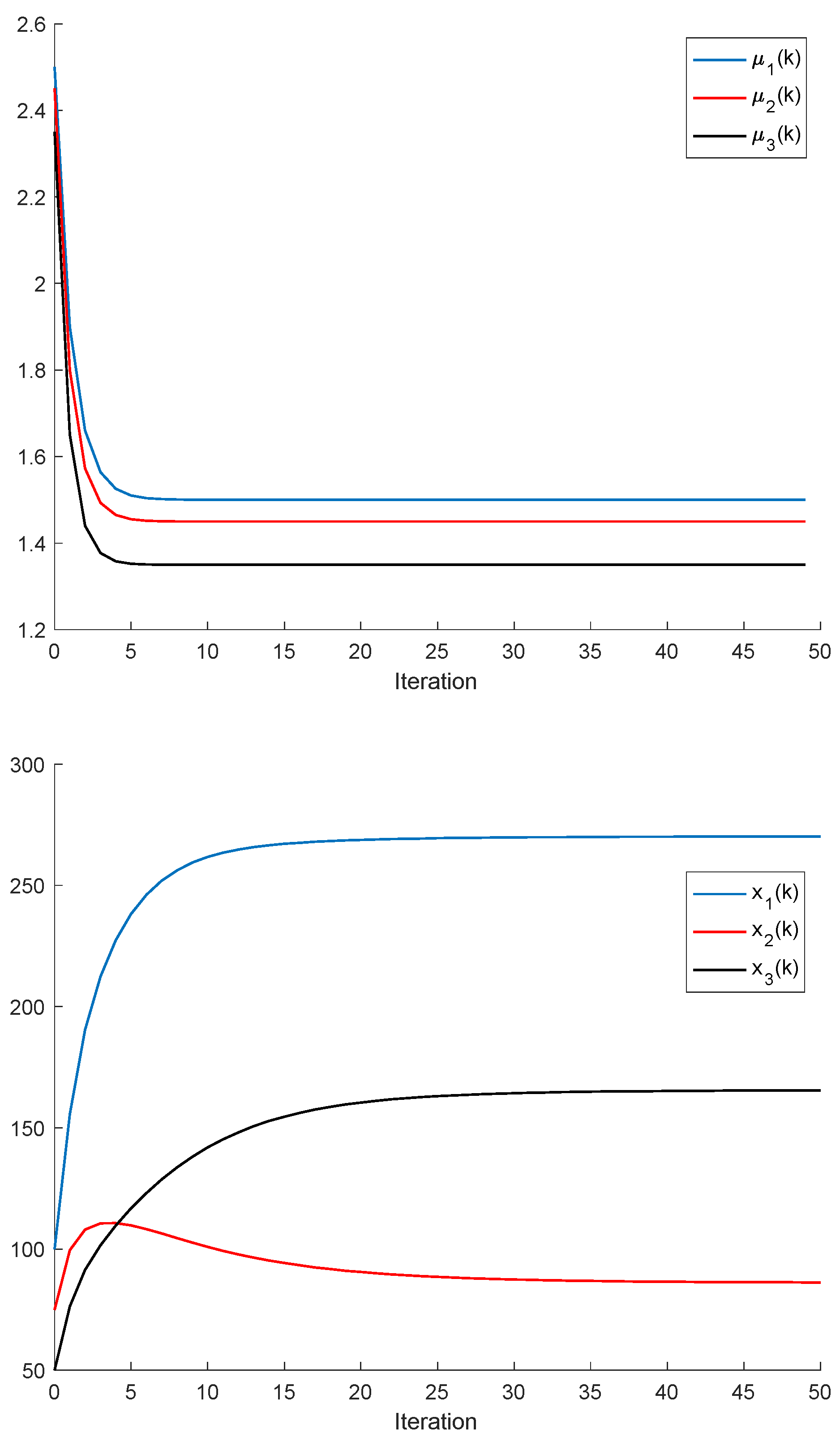
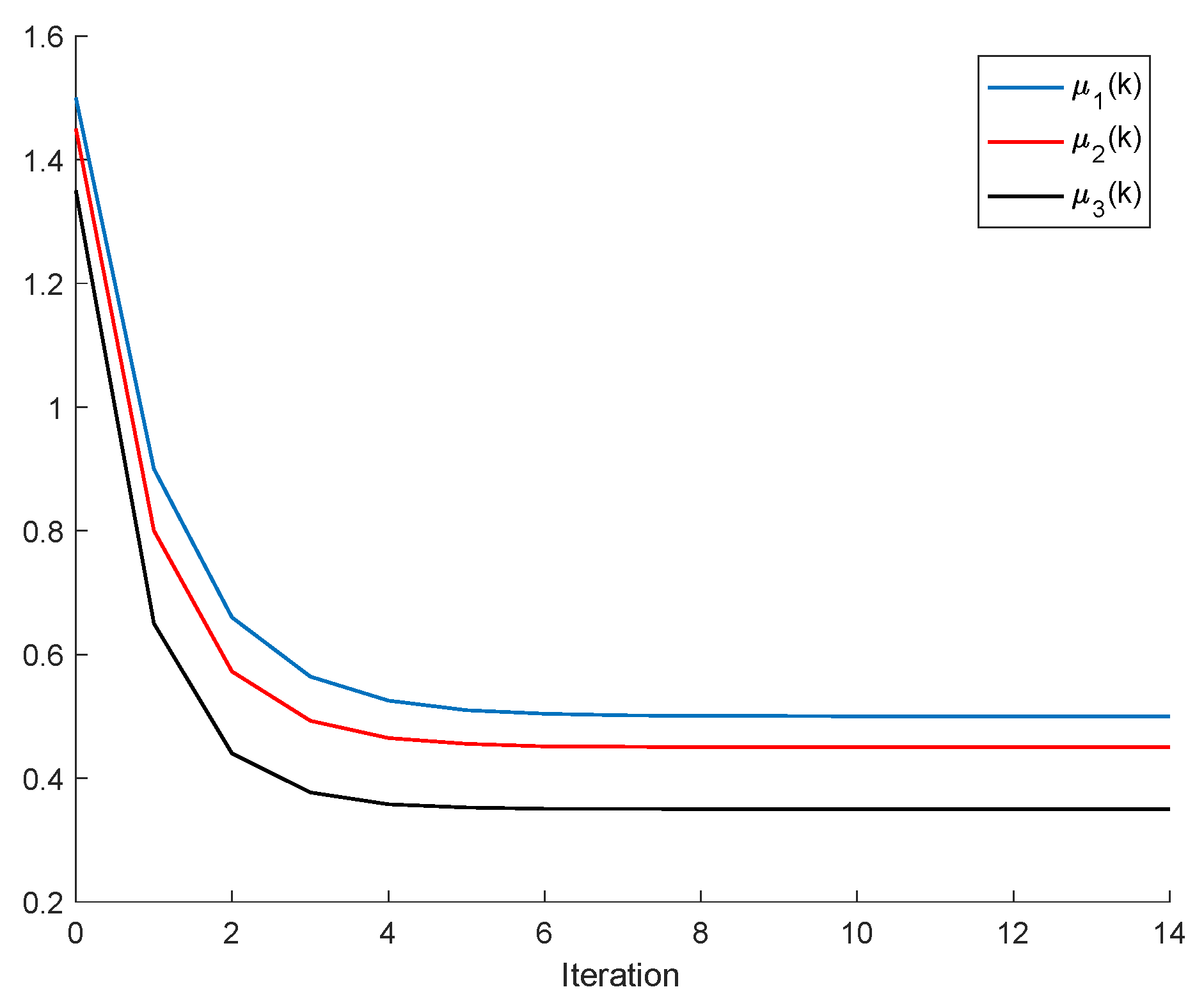
Remark 2. It follows, from Proposition 2, that a population is dominant on the remaining ones, or, in other words, it has the best fitness, for all and the respective left and right sampled values if , and ; . It turns out, furthermore, that an increase in an individual carrying capacity facilitates the increase in the corresponding species numbers, if all the remaining parameters remaining unchanged. The above constraints generalize Proposition 2, although at the expense of involving conditions on the left amounts of the population stocks. It can be pointed out that, eventually, there could exist more than one species with an identical best fitness within the set of competing species.
The following result is now proved on non-negativity, boundedness and eventual extinction of the species populations.
Theorem 2. The following properties hold:
- (i)
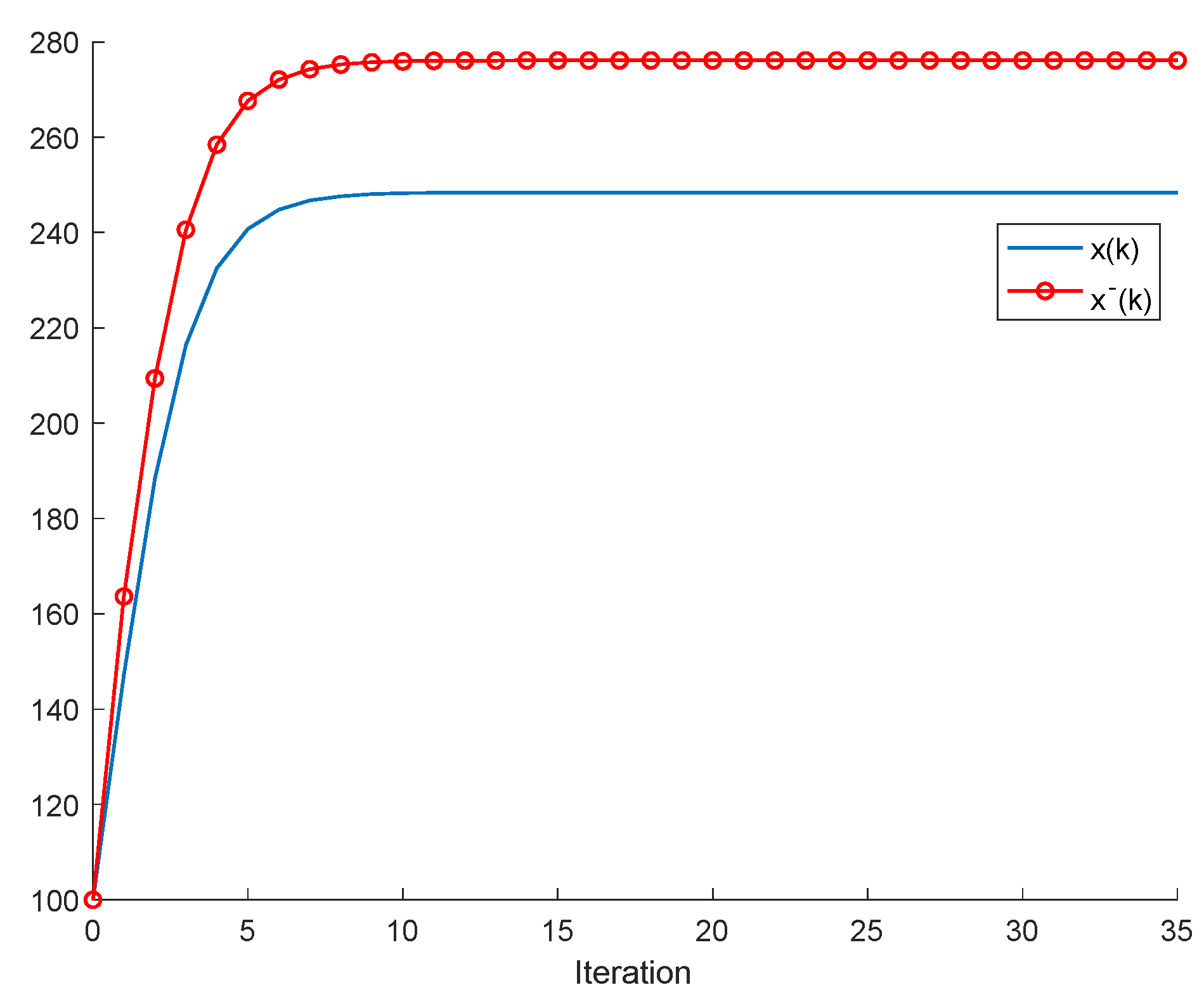
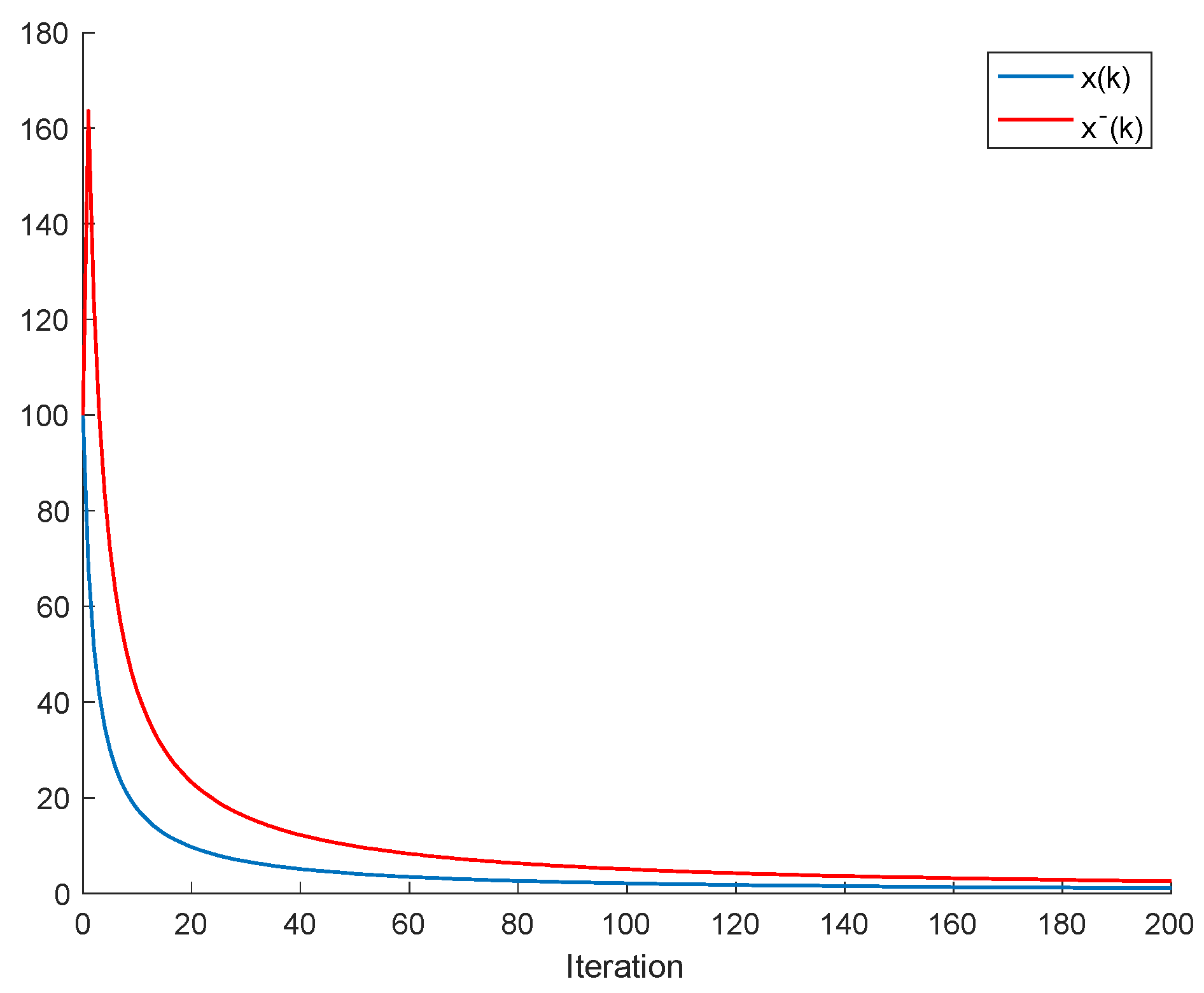
If ; , Assumption 1 holds, and ; ; then, is non-negative and bounded; . Furthermore, if (i.e., asymptotic extinction of the species), then .
- (ii)
If ; and Assumptions 1 and 2 hold with , then and it is a bounded non-negative sequence if ; . This property holds, in particular, if ; . If, furthermore, ; , then extinction in finite time does not occur for any , so that extinction only happens asymptotically and is a bounded non-negative sequence if . In particular, if ; and some finite and , then If Assumptions 1 and 2 hold with , then if .
- (iii)
If Assumptions 1 and 2 hold, then is bounded; .
Proof. One obtains that (2) is equivalent to
where the equivalent
carrying capacity
is given by
since
and
;
. By combining (7) and (8), one obtains
If Assumption 1 holds,
and
, then
;
,
. Let us define
;
,
. One obtains, from recursive calculations in (8) using (7),
since
. Since
and
;
,
, then
is bounded;
. Note that
is a non-negative sequence for any given
by construction and, furthermore, a positive sequence, unless
, which would eventually imply, from (10), that
, so that
. Since it has been already proved (Property (i)) that
is bounded for any
, then
, which would translate into
from (8), if and only if
. Property (i) has been proved. From Assumptions 1–2, with non-negative independent consumption, one directly obtains that
, which leads to the first part of Property (ii). If Assumptions 1 and 2 hold with non-necessarily non-negative independent consumption sequence, then
if
, which proves the second part of Property (ii).
Property (iii) is proved by contradiction arguments. Let us assume that Assumptions 1 and 2 hold and
is unbounded. Thus, there is a subsequence
, with
, which is strictly increasing, so that
and then, from (7),
then
. Furthermore,
where
is a positive real constant which is finite, since it is bounded to a finite number of iterations between
and
, since
and since one has, from Assumption 2, that
and
if
and
if
, still from Assumption 2. Then, from (11) and (12), one obtains
, since
is bounded and
is strictly increasing from the contradiction argument hypothesis. Thus, there is a subsequence
such that
, so that one concludes, from D´Alembert criterion for convergence of sequences, that
. As a result,
is bounded. Property (iii) has been proved. □
Note that Theorem 2 (i) guarantees the boundedness of all the populations under Assumption 1, provided that the harvesting quota and the independent consumption are zero (so that there are no impulsive effects at sampling instants), while Theorem 2(iii) guarantees such a boundedness under Assumptions 1 and 2.
In the following, the limits of the convergent sequences are denoted with the same notation as the sequences of elements by suppressing the sample argument “k” for the sake of notation simplicity.
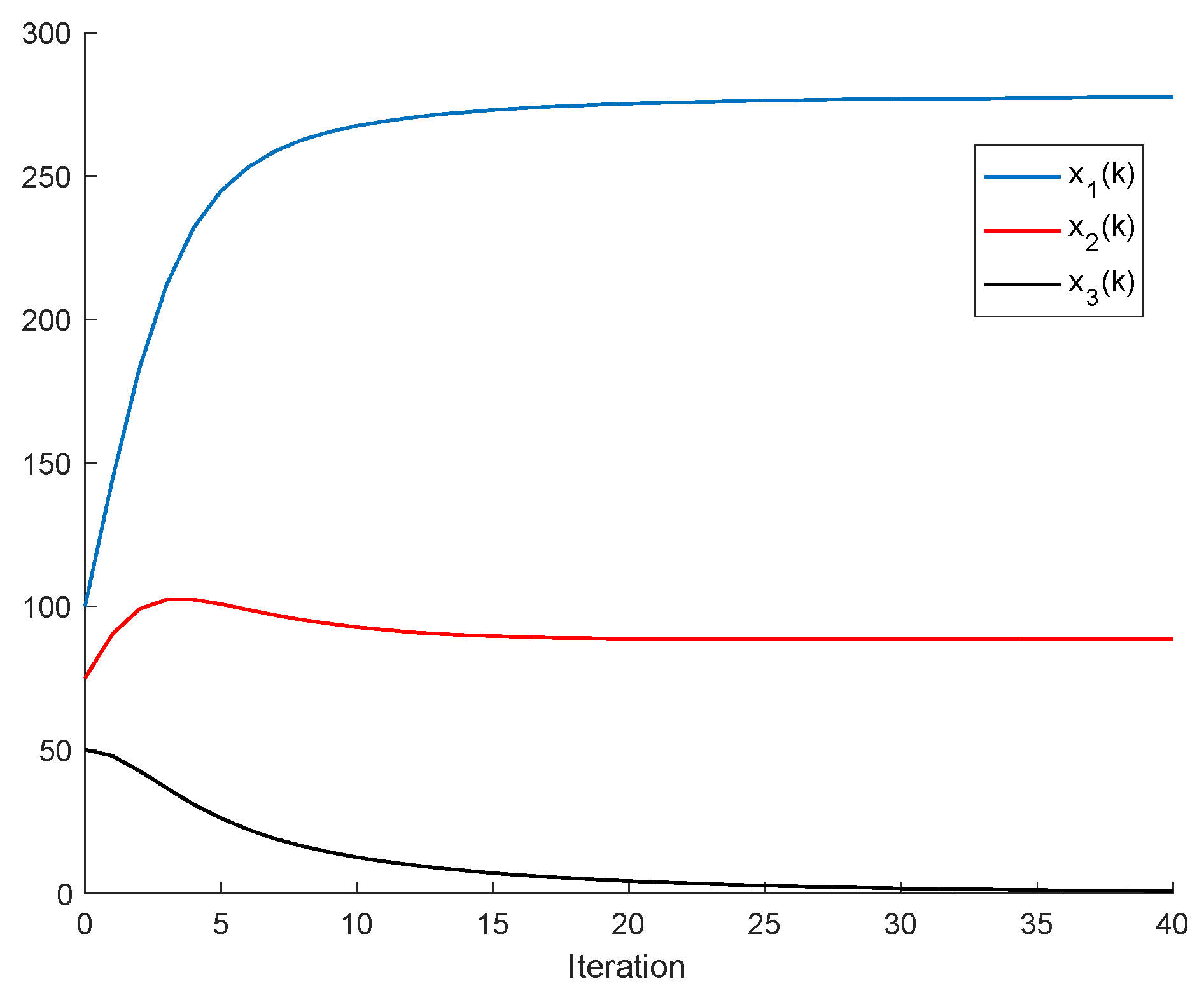
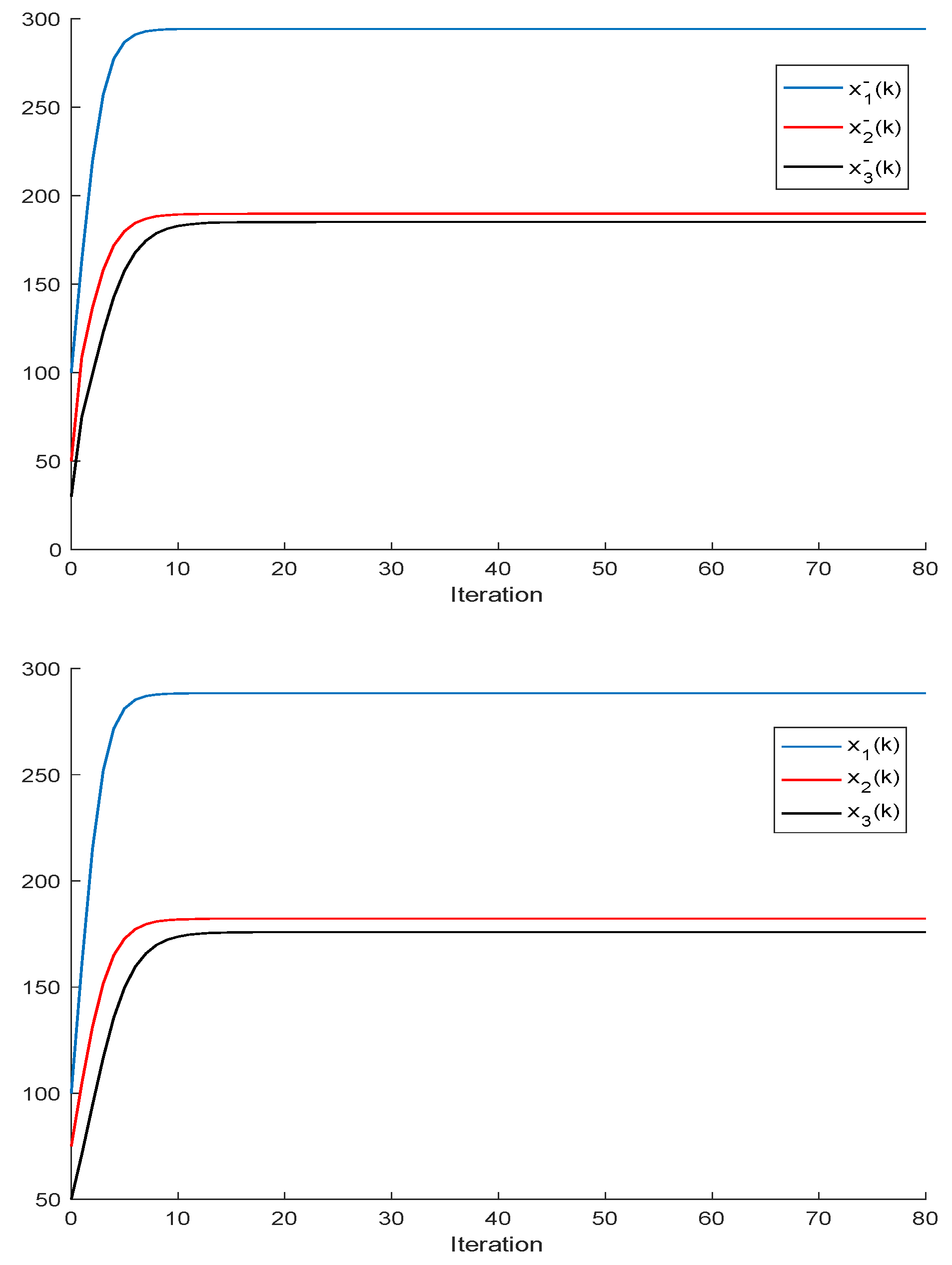
Theorem 3. Let us assume that all the populations converge to equilibrium points, that is, . Then, the following properties hold:
- (i)
Let us assume that Assumptions 1 and 2 hold and that , , for some , ; . If and ; are sufficiently small compared to , then there are two equilibrium points ; .
- (ii)
Let us assume that the quadruple satisfies the constraints
Then, one of each equilibrium point is feasible, that is, under the subsequent stipulations:
(1) Either the coupling constraint
from the remaining equilibrium points and, furthermore, any of the three conditions below:
(2) Or, the coupling constraint from the remaining equilibrium points together with (which excludes the values and ).
Proof. Take any
. One obtains, from (2)–(3), by taking limits, that
then
so that
by noting that the denominator of the above second identity balances that of the first one. Re-arranging terms in the above Equation (16) leads to
where
It is obvious, from the above equations, that if
and
and
;
, then
and
;
and one obtains the equilibrium points
and
as zeros of (17). It turns out that, in the general case, the zeros of (17), namely,
are both non-negative and real if
and
which hold for each
if
and
;
are sufficiently small in view of (18) and (19), such that
is sufficiently small, compared to
(that is, sufficiently small related to the first additive term of
) from the property of the continuity of the zeros of a polynomial with respect to its coefficients. Property (i) has been proved. Property (ii) is now proved by guaranteeing the validity of
depending on the coupling equilibrium dynamics from the remaining species
to the
one. First, let us define the auxiliary amount
so that, from (18) and (19),
then
holds, where
Let us consider the subsequent two cases:
Case 1 ( has real zeros ). For the above constraint (21) to be well-posed with real zeros of , with (according to the definition of ), so that if and only if , a necessary condition being that , equivalently, . Provided that such a necessary condition holds, sufficient conditions for are as follows:
(a) , equivalently, , which, combined with the above necessary condition, also implies that ;
(
b)
together with
. These two joint sufficiency-type conditions are respectively equivalent to
and the implicit constraint
,obtained after defining the auxiliary parameter
for
. Note that the particular case
requires, for feasibility, that
(from the necessary condition
), so that it is included in the sufficient condition
(or
), that is, it is included in (a). Since the given implicit constraint has to be checked for
, it becomes identical to
, or equivalently identical to
Note that , so that, under the given necessary conditions, , which is if and if . Thus, if , then if , which is, in turn, guaranteed if . As a result, the sufficient condition (b) is guaranteed if , if .
On the other hand, if , then if, furthermore, , implying again that the condition (b) is guaranteed if and if .
Note that, in both,
Case 2 ( has complex conjugate zeros ). This condition holds if and only if (which also trivially requires that ), which, in view of (23), requires that , which holds if and only if . Since and are complex conjugate zeros, in all its definition domain, that is, if .
Property (ii) follows from Cases 1 and 2. □
Note, from Equation (20), that both equilibrium points of the
species are zero if
;
and
;
. Excluding this trivial case, also note from Equation (20) that, provided that the radicand is non-negative, a necessary condition for at least one of the equilibrium points to be non-negative is that either
or
and
. The first case implies that
The second case implies that
and
while the second constraint above is fulfilled with
and
, or
and
.
Example 1 (
Positive equilibrium points for and with zero independent consumptions).
The allocation and positivity of the equilibrium points is easy to deal with in an analytical way from a linear algebraic system in the absence of independent consumptions at the equilibrium state, as it is now discussed. If and , thenwhich leads, for and for , denoted also as , toleading toprovided that for and either , or , for and and are sufficiently small according to the relations The equilibrium consensus, that is, the equilibrium points of both species are identical,
for some prefixed
is achieved for the coupling coefficients satisfying
so that the parameter
has to satisfy, furthermore,
or
The generalization to
species, if
;
, leads to a vector of equilibrium points given by
provided that
,
;
with
;
and
for some
so that, if
is sufficiently small, then the inverse of
exists and
, i.e., all its components, that is, the equilibrium states of all the species, are positive.
The following technical result, which establishes equilibrium point upper-bounds when one of the species in the competing set is dominant to the left and right samples, holds.
Proposition 3. Let us define the population inverses and at the equilibrium points and let us assume that the species is the dominant one in the set of competing species in the set that has the best fitness. Then, the following equilibrium constraints hold: If
with
, then the following further upper-bounds for (32) and (33) are obtained:
Proof. So that one obtains, from (2)–(3) the following equilibrium constraints, since
;
,
where
Then, from (36) into (35), one obtains
Which, replaced in (34), yields
and then
Note, from (3), that (equivalently, ) in order for the equilibrium point to be non-negative to the left of the sampling instants, provided that it is non-negative to the right of such sampling instants. Therefore, the last two additive terms on the left-hand-side of the above equation are necessarily negative under that stipulation.
Let us assume that the
species is dominant so that
, so that
;
. Then,
and, since
,
which is identical to (32); then, (33) is direct for the equilibrium values at the right of the sampling instants. The further two upper-bounds if
inequalities follow directly from (32)–(33) and the proof is completed. □
The next definition relies on the concept of equilibrium consensus among the species in the sense that all of them reach the same equilibrium points.
Definition 1. It is said that the competing species set has a left/right equilibrium consensus if there exist at least two, non-necessarily distinct, non-negative real numbers and such that and ; , that is, the equilibrium point is common to all the species.
Some sufficient conditions for equilibrium consensus are found in the subsequent result.
Proposition 4. The following parametric constraints hold:
- (i)
A right equilibrium consensus for a given common population is reached under the independent consumptions - (ii)
A right equilibrium consensus for a common equilibrium population of valueexists if ; with either or for each for , or, jointly, ; for (that is, “extinction” consensus). - (iii)
Let us assume that the competing species set has an equilibrium consensus and that there are no impulses at the equilibrium points, that is, and ; . Then, the equivalent carrying capacities ; are identical for all the species, the carrying capacities are ; and the nonzero common equilibrium point coincides with such a common equivalent carrying capacity, i.e.,
Proof. One obtains, from (4), for
;
that
which proves Property (i). Property (ii) follows directly from Property (i), by making
;
, which leads to
;
. Since
;
implies that
, it follows that a necessary condition of fulfillment of those constraints for each
is that either
or
, or, jointly,
;
.
To prove Property (iii), note that, since
and
;
, one has, at the equilibrium points,
whose solutions are
and, after direct calculation for
, one obtains
□
Let us assume, for generalization purposes, that the intrinsic growth rates, the carrying capacities and inter-species coupling coefficients might also be time-varying, in general. Thus, one obtains, from the resulting generalized (2) and (3) and, provided that
and
, that
for any
, where
for non-negativity and non-extinction in finite-time of the solution sequence, so that
. Then, it follows, from (47) and (48), that
for any
. It can be proved that
for any
. We first prove (51) in detail by using contradiction arguments and logics of propositions rules as follows. Let us assume that
for some given
. Then, one obtains, from (49), that
so that
which is the contrapositive logic proposition and then equivalent, logic proposition to the logic implication
and the part “
” is proved in (51) for any
if
. Now, let us assume that
and
. Then,
which contradicts that
. Then,
which proves the part “
” of (51) for any
. As a result, (51) has been proved for any
. The proofs of (52) and (53) are very close to the one above and were therefore omitted.
Now, note, from (49), that, for any given
,
if
, equivalently, if
and, in a similar way, one has
Extinction at the limit as time tends to infinity needs some extra constraints, as follows, since does not hold at the limit with the left-hand side and right-hand side both converging to zero. So, the convergence to extinction of as implies that as , then, equivalently, as and we convey that also (basically, the asymptotic convergences to the right and left of the sampling instants jointly hold), and as with as (so that as ) and then as from (49).
The following result, whose proof involves the use of the above considerations, is concerned with non-asymptotic and asymptotic extinction conditions.
Theorem 4. The following properties hold:
- (i)
Let us assume that the species has the best fitness, is finite, that the independent consumption fulfills ; and that there is a strict sequence of non-negative integer numbers with ; such that . Then, there is no asymptotic extinction of the species with the best fitness and its solution sequence is bounded for all time.
- (ii)
Let us assume that , , and as and that with . Then, there is asymptotic extinction of the i-th species with the best fitness and then that of all the remaining ones.
Proof. From recursive calculations by using (50), the inverse of the
population is given by
with the notation convention
for
,
,
;
since the
species has the best fitness. Since there exists a strictly increasing sequence
with
;
such that
and
since
is finite and then
is finite as well. Then,
from (57) and
does not converge to zero. In addition, from that inverse sequence solution formula
and then
is bounded since it is convergent. Property (i) has been proved. To prove Property (ii), first note that the joint constraints
;
and
, the second one implying also that
since the
species has the best fitness and being always guaranteed if
, guarantee that
directly from the time-varying generalization of (2)–(3), even if
. The constraints
,
and
as
guarantee that eventual asymptotic extinction of the
species jointly holds at the left and right of the sampling instants with
, as
, while the constraints, either
or
with
, guarantee that
and then
so that
, since the
population has the best fitness;
from the formula which obtains the solution of the inverse population from the initial conditions. □