Influence of the Flexible Tower on Aeroelastic Loads of the Wind Turbine
Abstract
:1. Introduction
2. Analytical Study
2.1. Equations of Motion for Vibrating Systems
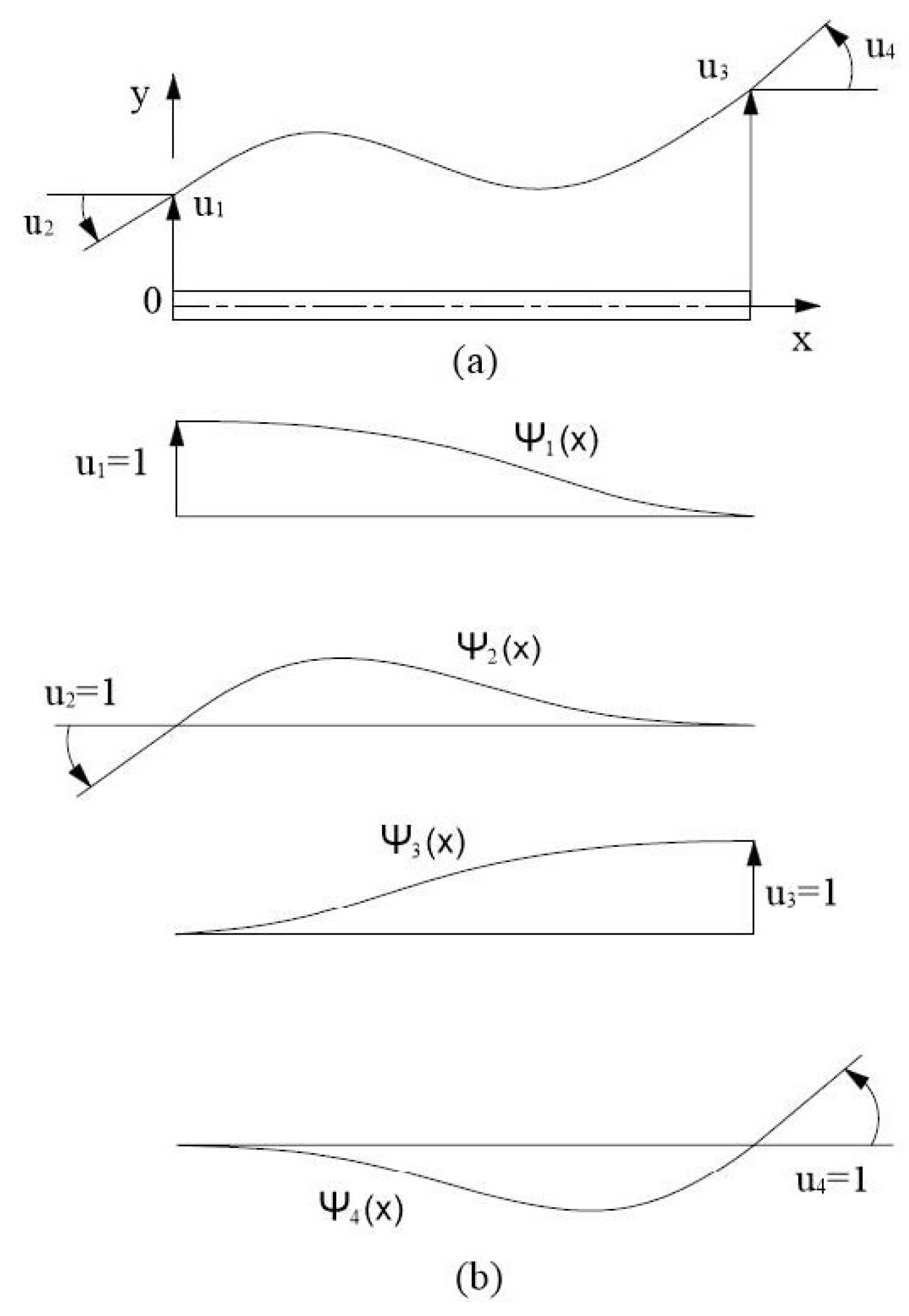
2.2. Tower Finite Element Modeling
2.3. Eigenvalue Analysis
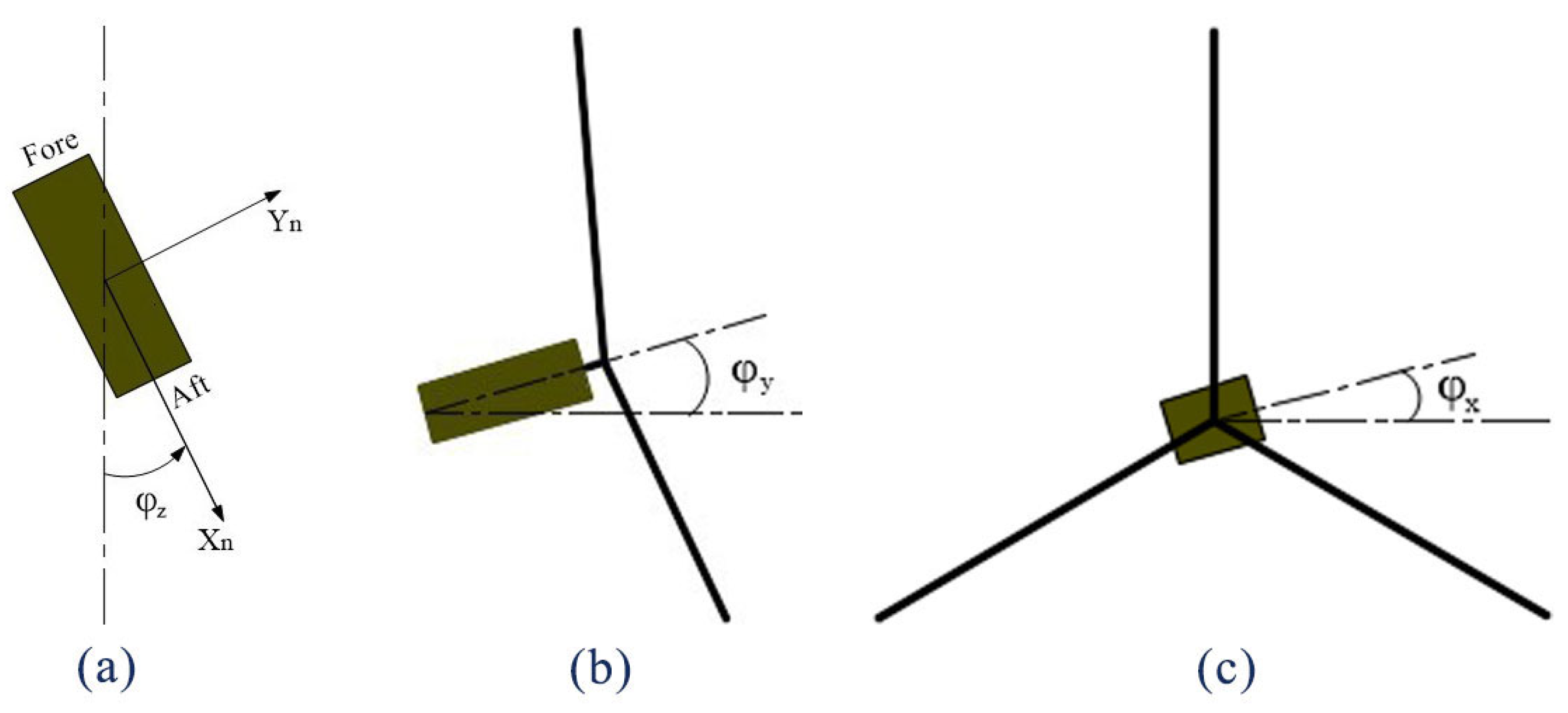
2.4. Solving the Nacelle Attitude Angle Using Euler Angles
3. Calculation Method
3.1. Calculation of Aerodynamic Loads under Consideration of NAF
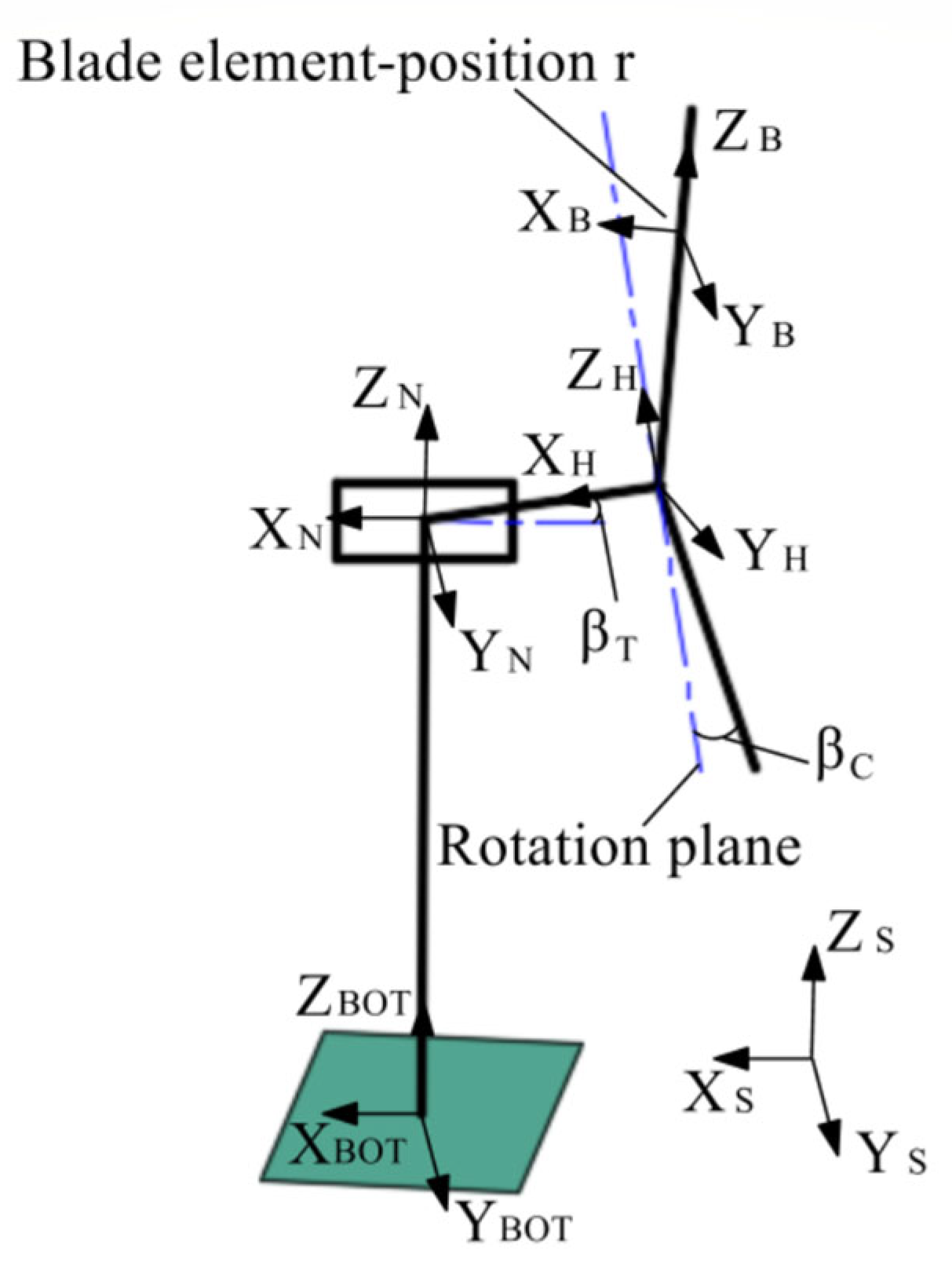
- The inertial coordinate system S coincides with the tower bottom coordinate system , and the nacelle coordinate system coincides with the tower top coordinate system .
- When the azimuth angle θ = 0, the wind turbine rotation plane coordinate system coincides with the hub coordinate system , and rotates with the azimuth angle θ.
- The tower height is L, and the horizontal distance from the top of the tower to the hub is .
- The spindle inclination angle and blade taper angle are and .
3.2. Tower Load Calculation
3.3. Solving Structural Equations of Motion
- Initial Calculation
- Firstly, the overall characteristic matrices K, M and C of the vibrating system are calculated.
- From the initial conditions and , is calculated.
- Step is selected with parameters , and calculate the integration constants.
- The equivalent stiffness matrix is calculated.
- For each time step
- The equivalent load vector at moment is determined.
- The displacement at moment is calculated.
- The velocity at time and the acceleration are solved.
3.4. Dynamic Response Analysis Process
4. Flexible Tower Vibration Feedback Analysis
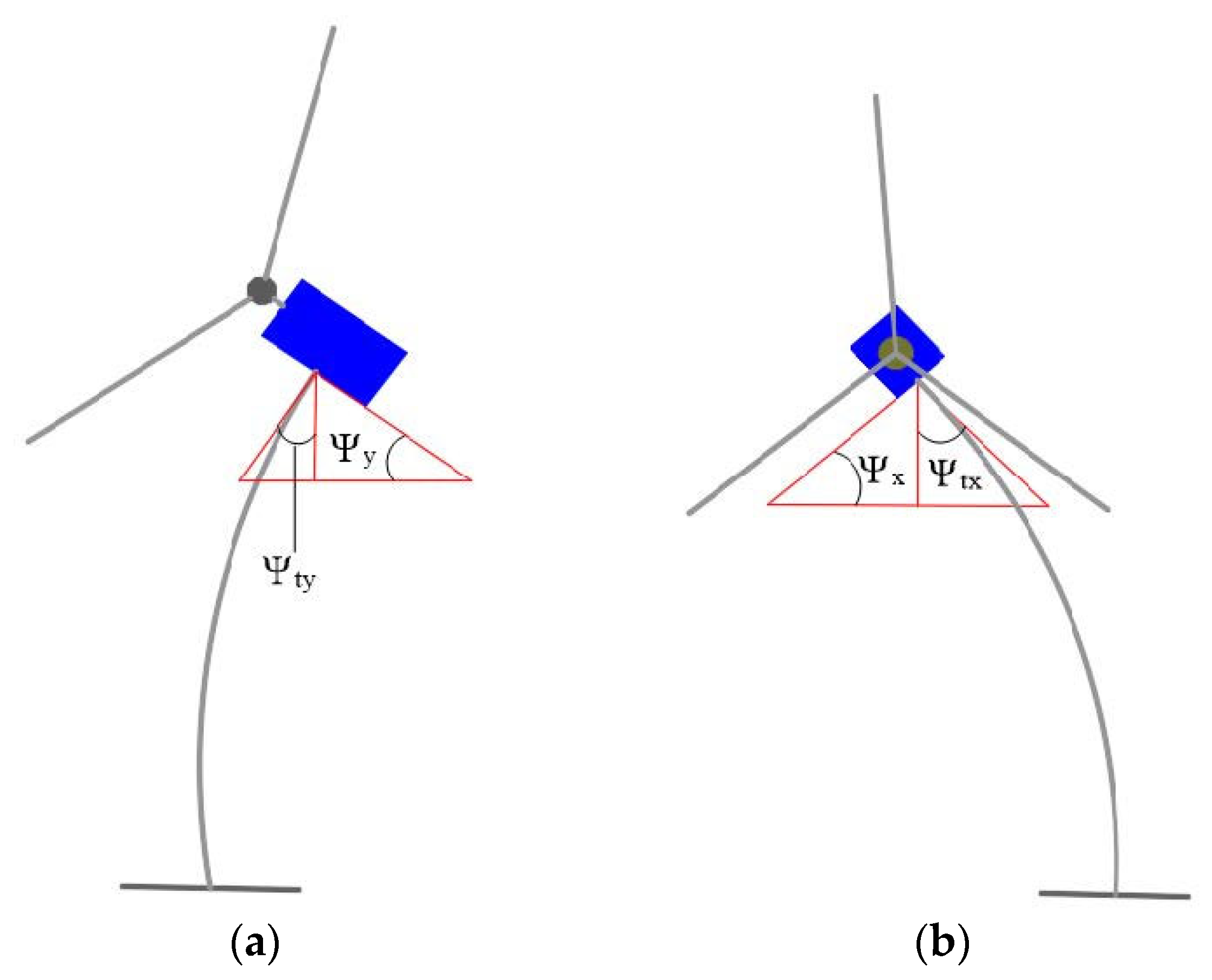
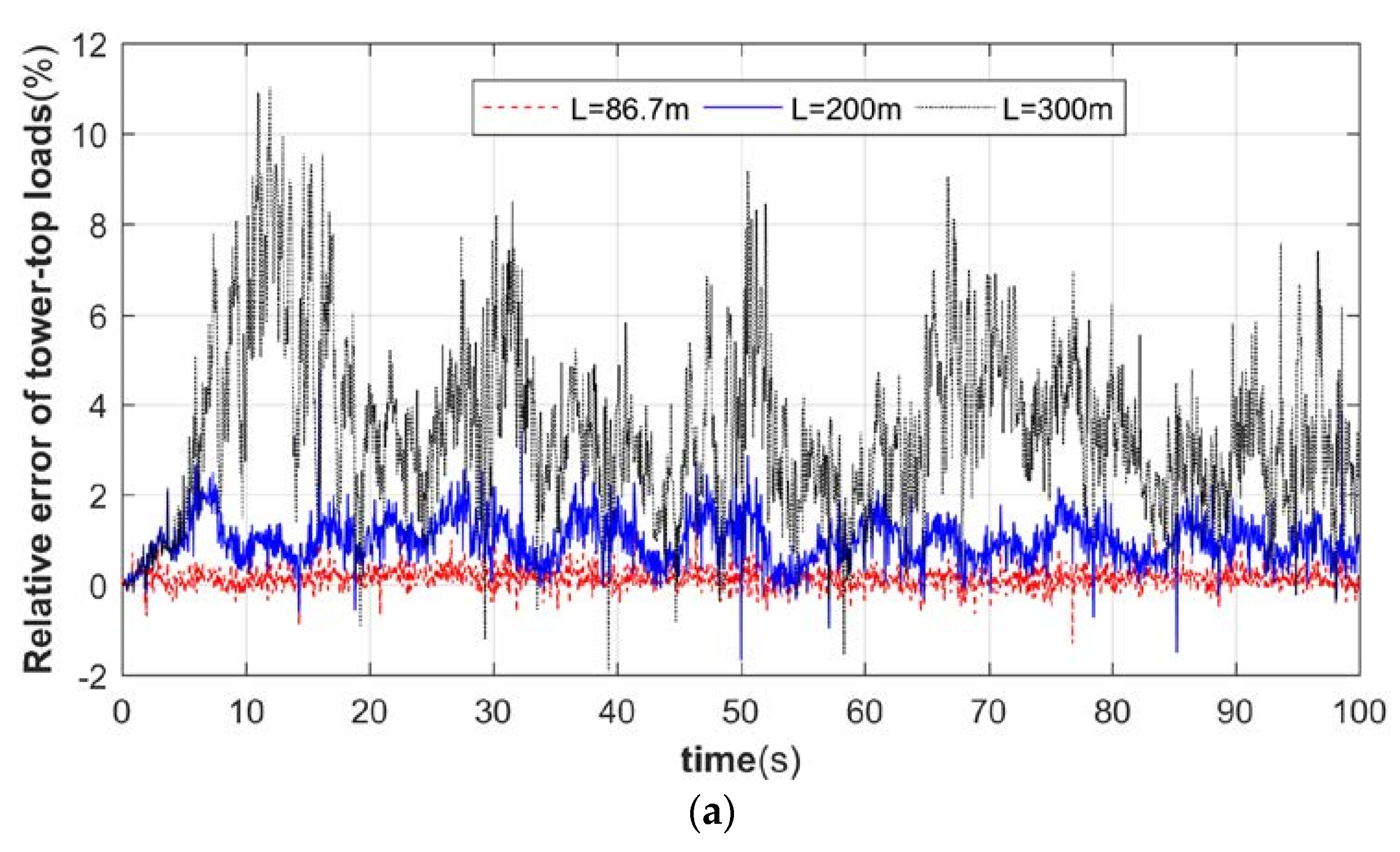
4.1. Tower Load Error Analysis
- The nacelle and the tower have only yaw motion.
- The center of mass of the nacelle coincides with the center of the tower top.
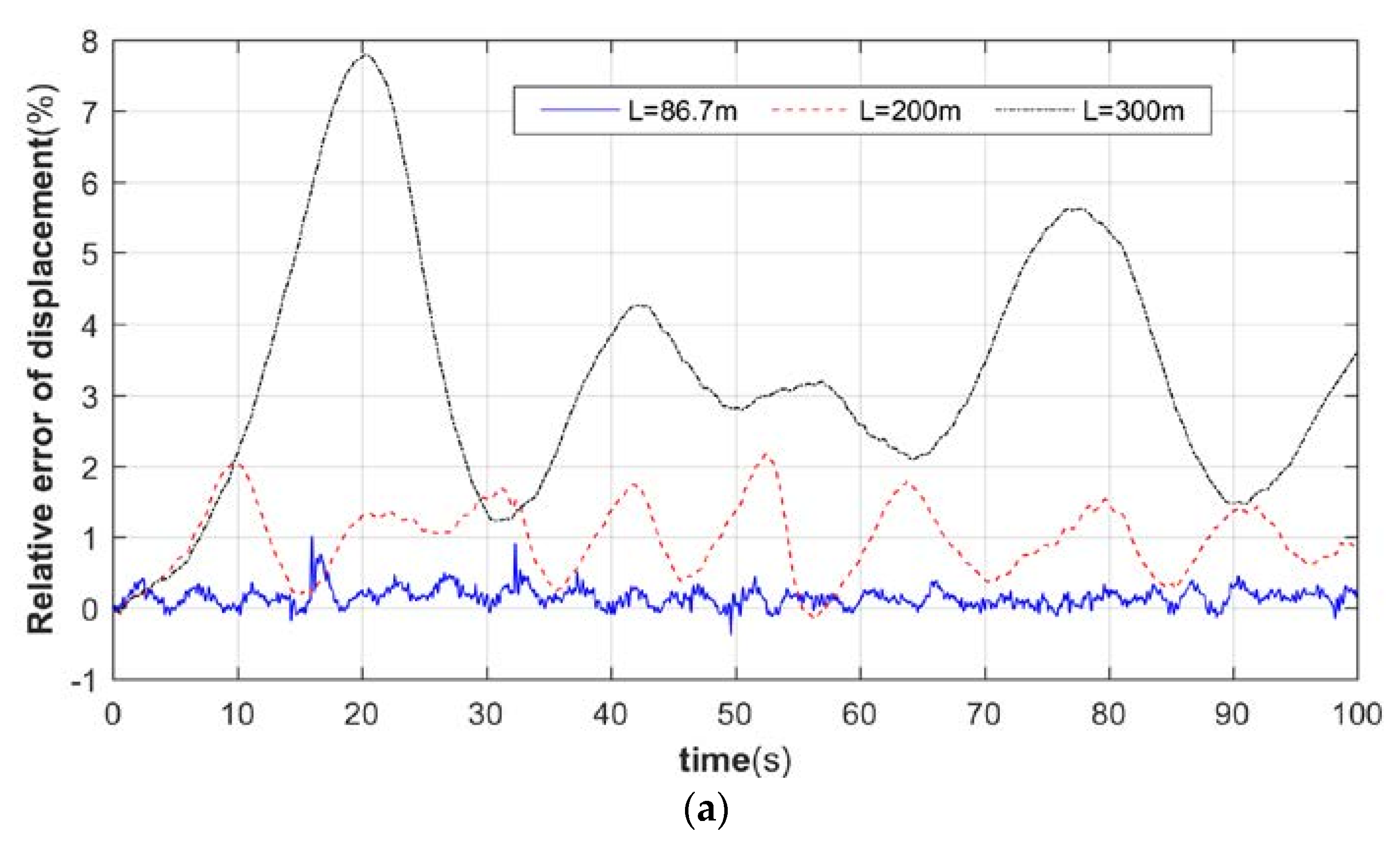
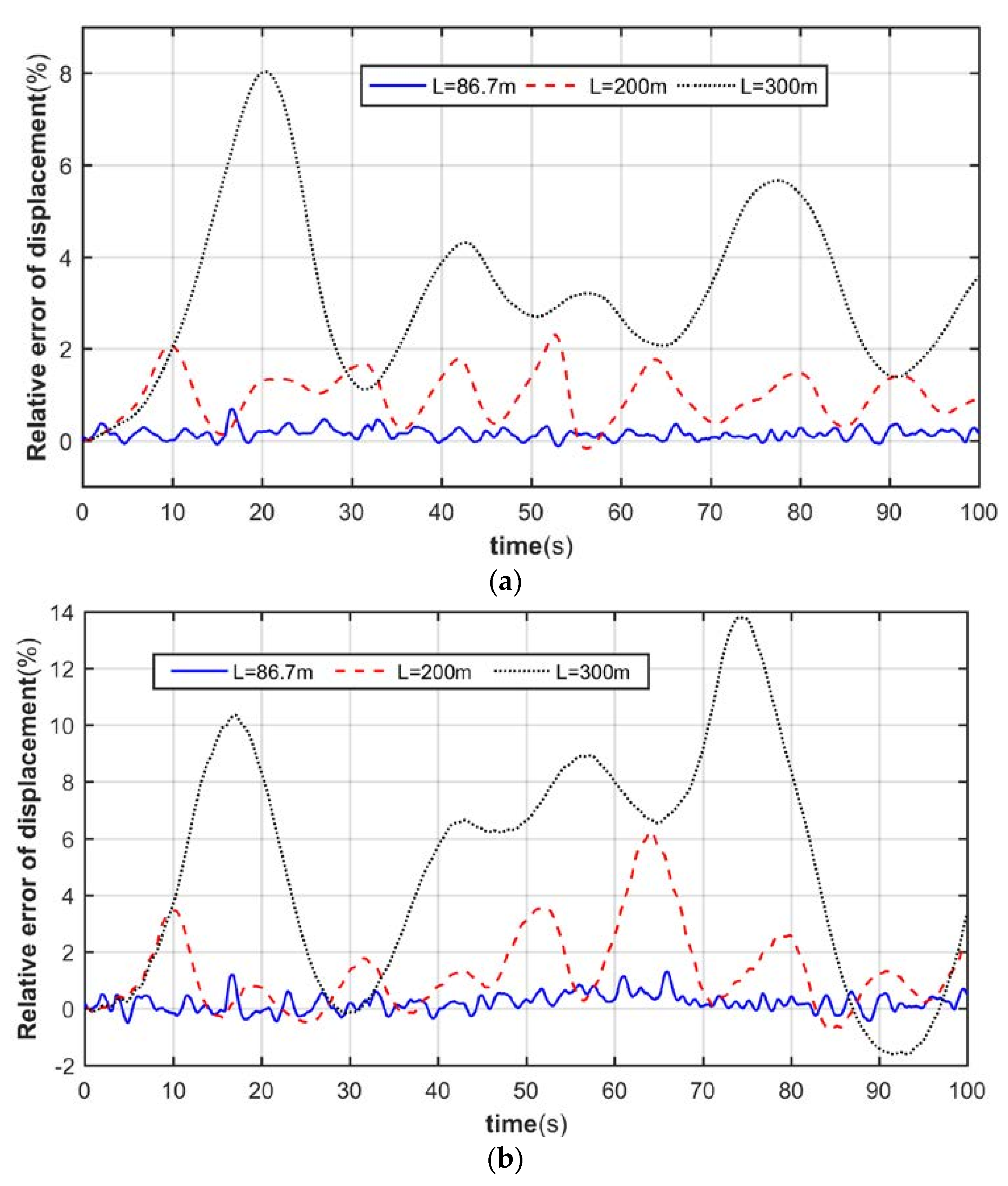
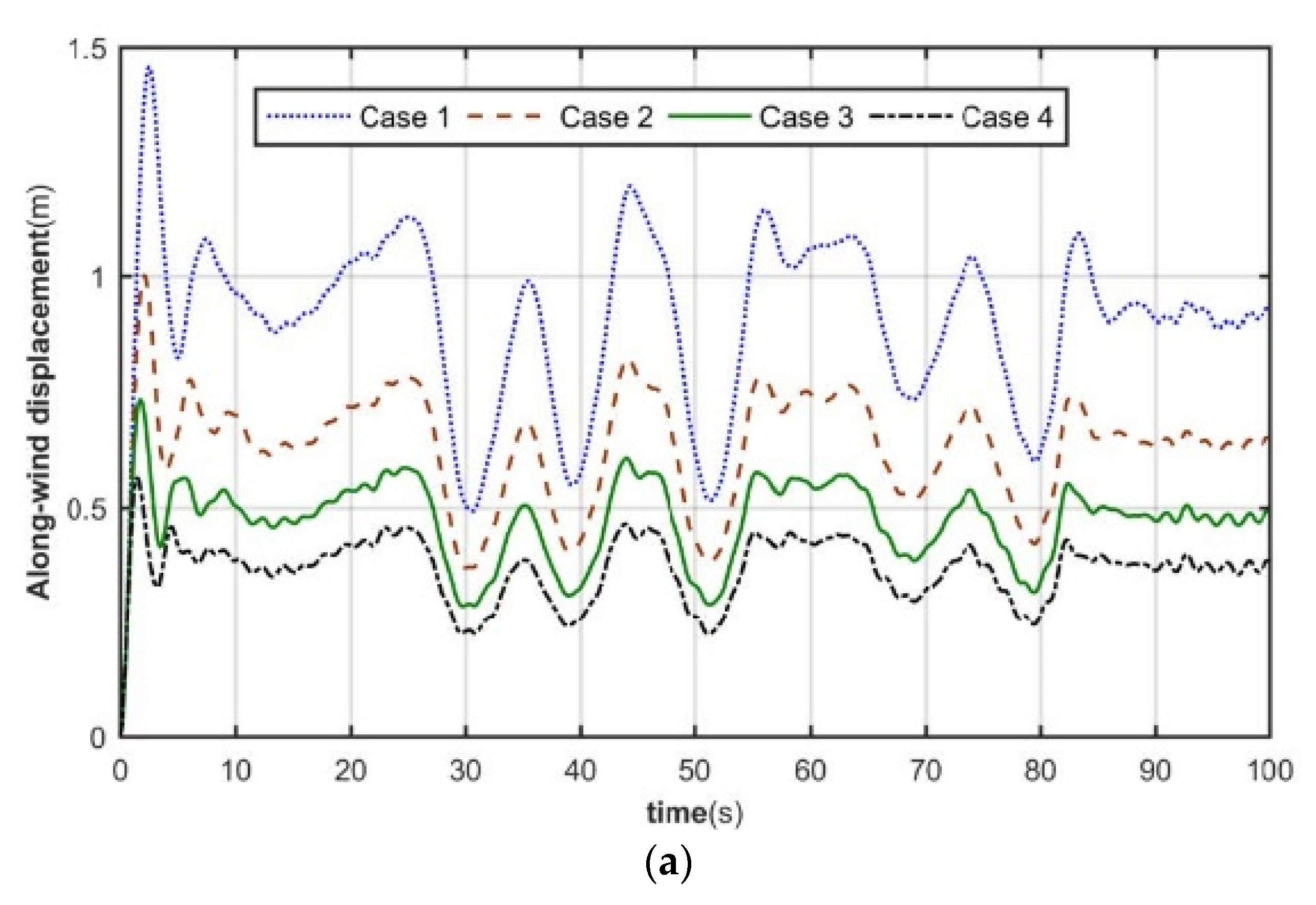
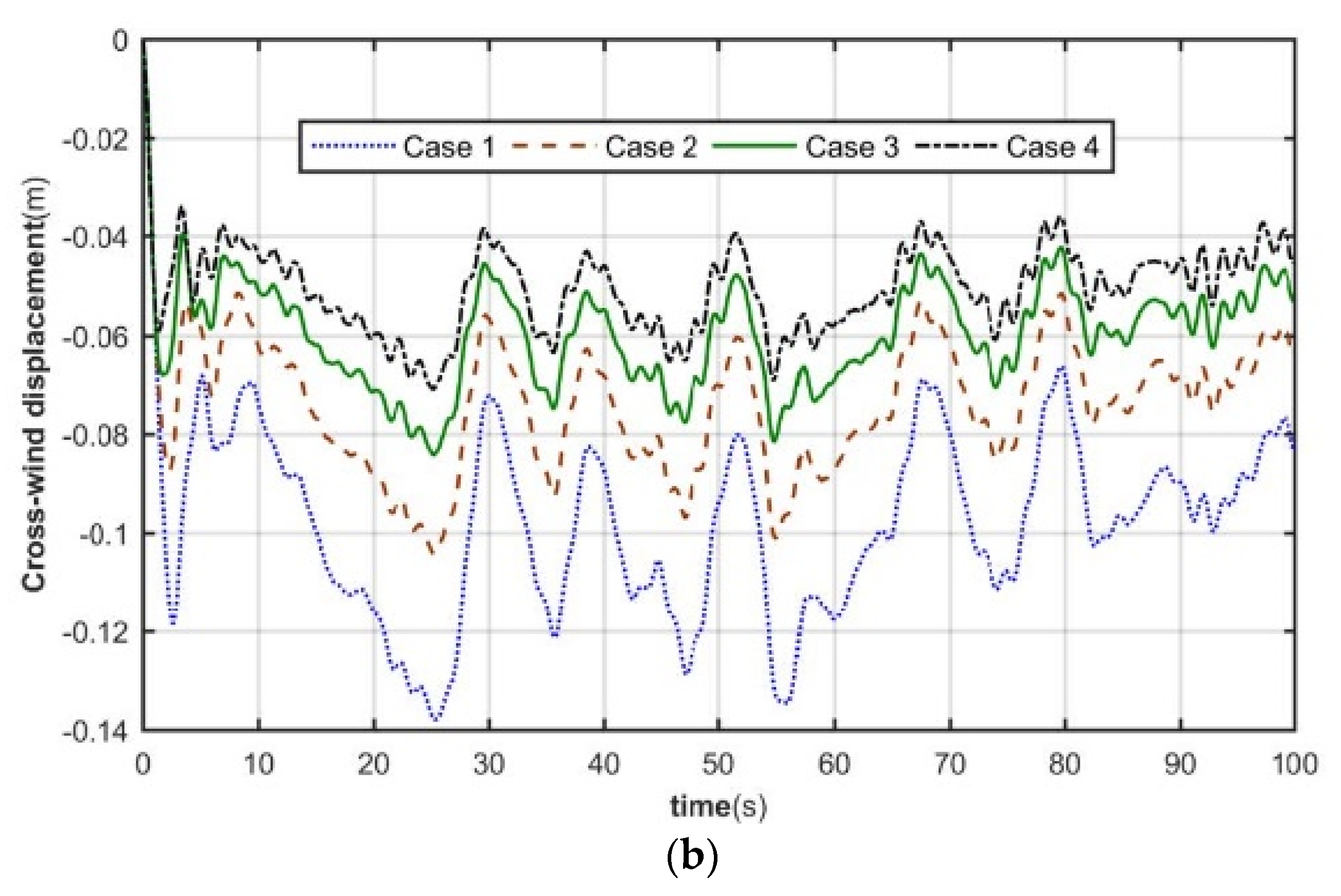
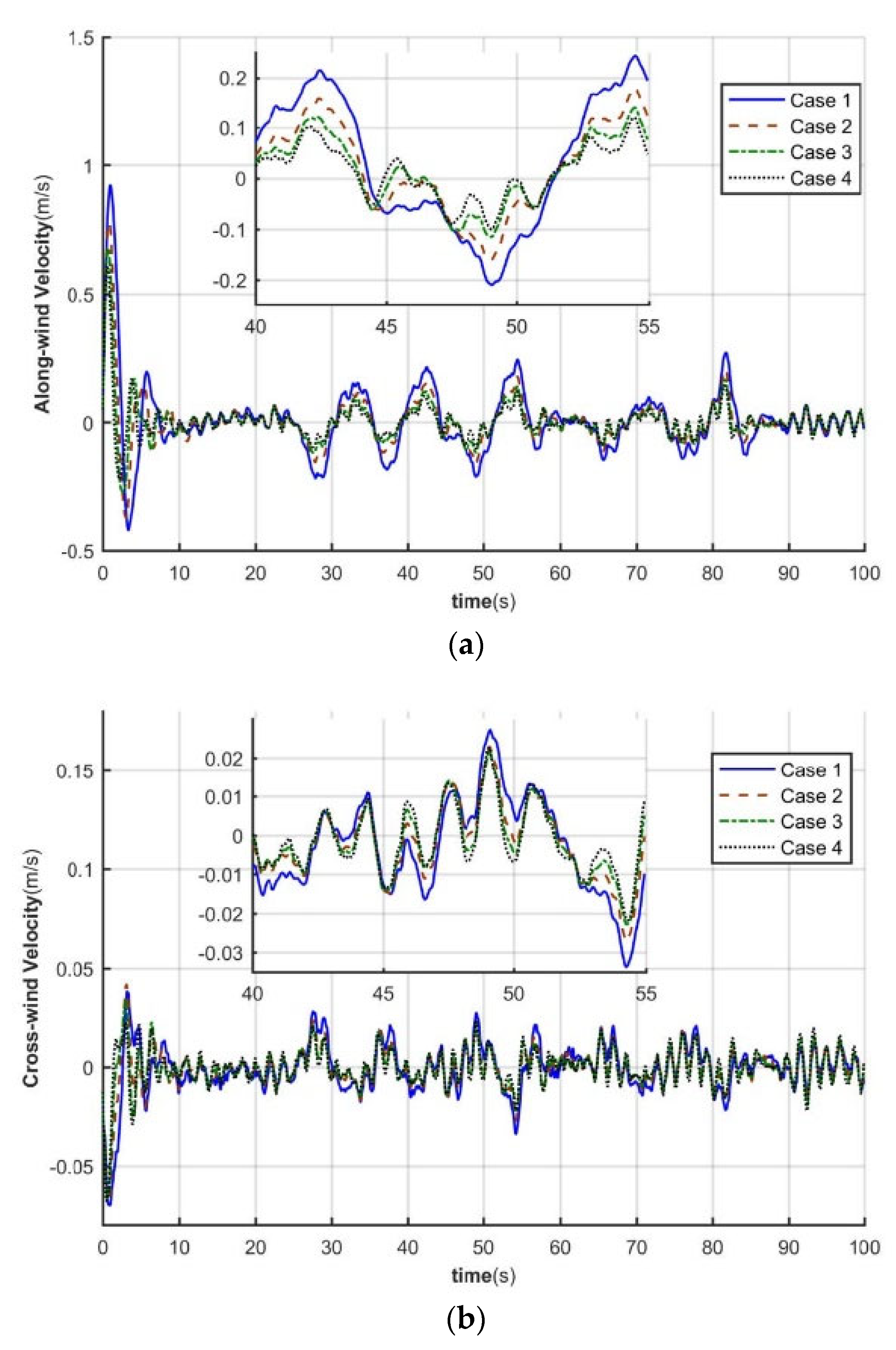
4.2. Dynamic Response Analysis of Tower System
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ciang, C.C.; Lee, J.R.; Bang, H.J. Structural health monitoring for a wind turbine system: A review of damage detection methods. Meas. Sci. Technol. 2008, 19, 122001. [Google Scholar] [CrossRef] [Green Version]
- Kang, N.; Park, S.C.; Park, J.; Atluri, S.N. Dynamics of flexible tower-blade and rigid nacelle system: Dynamic instability due to their interactions in wind turbine. J. Vib. Control. 2016, 22, 826–836. [Google Scholar] [CrossRef]
- Huo, T.; Tong, L.W. Wind-induced response analysis of wind turbine tubular towers with consideration of rotating effect of blades. Adv. Struct. Eng. 2020, 23, 289–306. [Google Scholar] [CrossRef]
- Adhikari, S.; Bhattacharya, S. Dynamic Analysis of Wind Turbine Towers on Flexible 465 Foundations. Shock. Vib. 2012, 19, 37–56. [Google Scholar] [CrossRef]
- Adhikari, S.; Bhattacharya, S. Vibration of wind-turbines considering soil-structure interaction. Wind. Struct. Int. J. 2011, 14, 85–112. [Google Scholar] [CrossRef] [Green Version]
- Spagnoli, A.; Montanari, L. Along-wind simplified analysis of wind turbines through a coupled blade-tower model. Wind. Struct. 2013, 17, 589–608. [Google Scholar] [CrossRef]
- Feliciano, J.; Cortina, G.; Calaf, M. Generalized analytical displacement model for wind turbine towers under aerodynamic loading. J. Wind. Eng. Ind. Aerodyn. 2018, 176, 120–130. [Google Scholar] [CrossRef]
- Hodges, D.H.; Dowell, E.H. Nonlinear equations of motion for the elastic bending and torsion of twisted nonuniform rotor blades.; NASA: Washington, DC, USA, 1974. [Google Scholar]
- Liu, X.; Li, G.; Chen, Y.; Ye, Z.; Tian, P. Dynamic response analysis of the tubular tower of horizontal axis wind turbines. Acta Energ. Sol. Sin. 2010, 3131, 412–417. [Google Scholar]
- Clough, R.W.; Penzien, J. Dynamic of Structures, Computers and Structures, 3rd ed.; CSI Computers & Structures, Inc.: Berkeley, CA, USA, 2003; pp. 169–359. [Google Scholar]
- Jonkman, J.; Butterfield, S.; Musial, W.; Scott, G. Definition of a 5-MW Reference Wind Turbine for Offshore 445 System Development. In National Renewable Energy Laboratory Technical Report; National Renewable 446 Energy Lab.(NREL): Golden, CO, USA, 2009. [Google Scholar]
- Diebel, J. Representing Attitude: Euler Angles, Unit Quaternions, and Rotation Vectors. Matrix 2006, 58, 1–35. [Google Scholar]
- Kallesøe, B.S. Equations of motion for a rotor blade, including gravity, pitch action and rotor speed variations. Wind Energy 2007, 10, 209–230. [Google Scholar] [CrossRef]
- Riesenfeld, R.F. Homogeneous Coordinates and Projective Planes in Computer Graphics. IEEE Comput. Graph. Appl. 1981, 1, 50–55. [Google Scholar] [CrossRef]
- Lloyd, G.; The Wind Energy Committee. Guideline for the Certification of Wind Turbines; Germanischer Lloyd: Hamburg, Germany, 2010; pp. 31–34. [Google Scholar]
- Burton, T.; Jenkins, N.; Sharpe, D.; Bossanyi, E. Wind Energy Handbook, 1st ed.; Wiley: New York, NY, USA, 2001; pp. 41–47. [Google Scholar]





| 1st | 2nd | 3rd | ||
|---|---|---|---|---|
| 10 | 0.5 | 0.20862 | 2.0824 | 6.8703 |
| 10 | 1 | 0.20874 | 2.0991 | 7.1053 |
| 10 | 5 | 0.20882 | 2.1124 | 7.2858 |
| 20 | 0.5 | 0.25229 | 2.2495 | 6.9903 |
| 20 | 1 | 0.25245 | 2.2725 | 7.2701 |
| 20 | 5 | 0.25249 | 2.2909 | 7.4874 |
| 50 | 0.5 | 0.29507 | 2.5064 | 7.2177 |
| 50 | 1 | 0.29533 | 2.5409 | 7.5925 |
| 50 | 5 | 0.29554 | 2.5683 | 7.8877 |
| 100 | 0.5 | 0.31463 | 2.6753 | 7.4038 |
| 100 | 1 | 0.31494 | 2.7180 | 7.8656 |
| 100 | 5 | 0.31519 | 2.7519 | 8.2307 |
| Modal | 1st | 2nd | 3rd |
|---|---|---|---|
| Natural frequency | 0.3391 | 3.0634 | 9.0983 |
| Name | Value | Name | Value |
|---|---|---|---|
| Rated power | 5000 KW | Cone angle | 2.5° |
| Rated wind speed | 11.4 m/s | Rated rotor speed | 12.1 rpm |
| Cut-in wind speed | 3 m/s | Rotor diameter | 126 m |
| Cut-out wind speed | 25 m/s | Tower mass density | 8500 kg/m³ |
| Blade length | 61.5 m | Tower’s modulus of elasticity | 2.1 × 1011 N/m2 |
| Blade mass | 17,740 kg | Structural-damping ratio | 1% |
| Blade number | 3 | Tower height | 86.7 m |
| Hub height | 90 m | Tower-base diameter | 6 m |
| Hub mass | 56,780 kg | Tower-base thickness | 0.0351 m |
| Nacelle mass | 240,000 kg | Tower-top diameter | 3.87 m |
| Shaft tilt | 5° | Tower-top thickness | 0.0247 |
| Height (m) | Diameter and Wall Thickness of Tower Top (m) | Diameter and Wall Thickness of Tower Bottom (m) | Structural Damping Ratio | |
|---|---|---|---|---|
| 86.7 | 2.1 × 1011 | 3.87, 0.247 | 6, 0.351 | 1% |
| 200 | 2.1 × 1011 | 3.87, 0.247 | 6, 0.351 | 1% |
| 300 | 2.1 × 1011 | 3.87, 0.247 | 6, 0.351 | 1% |
| Case 1 | 1 | 10 |
| Case 2 | 1 | 20 |
| Case 3 | 1 | 50 |
| Case 4 | Rigid foundation | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hao, J.; Wang, Z.; Yi, W.; Chen, Y.; Chen, J. Influence of the Flexible Tower on Aeroelastic Loads of the Wind Turbine. Appl. Sci. 2021, 11, 8876. https://doi.org/10.3390/app11198876
Hao J, Wang Z, Yi W, Chen Y, Chen J. Influence of the Flexible Tower on Aeroelastic Loads of the Wind Turbine. Applied Sciences. 2021; 11(19):8876. https://doi.org/10.3390/app11198876
Chicago/Turabian StyleHao, Junbo, Zedong Wang, Wenwu Yi, Yan Chen, and Jiyao Chen. 2021. "Influence of the Flexible Tower on Aeroelastic Loads of the Wind Turbine" Applied Sciences 11, no. 19: 8876. https://doi.org/10.3390/app11198876
APA StyleHao, J., Wang, Z., Yi, W., Chen, Y., & Chen, J. (2021). Influence of the Flexible Tower on Aeroelastic Loads of the Wind Turbine. Applied Sciences, 11(19), 8876. https://doi.org/10.3390/app11198876





