Optimization of the Electrical Demand of an Existing Building with Storage Management through Machine Learning Techniques
Abstract
:Featured Application
Abstract
1. Introduction
2. Models and Methods
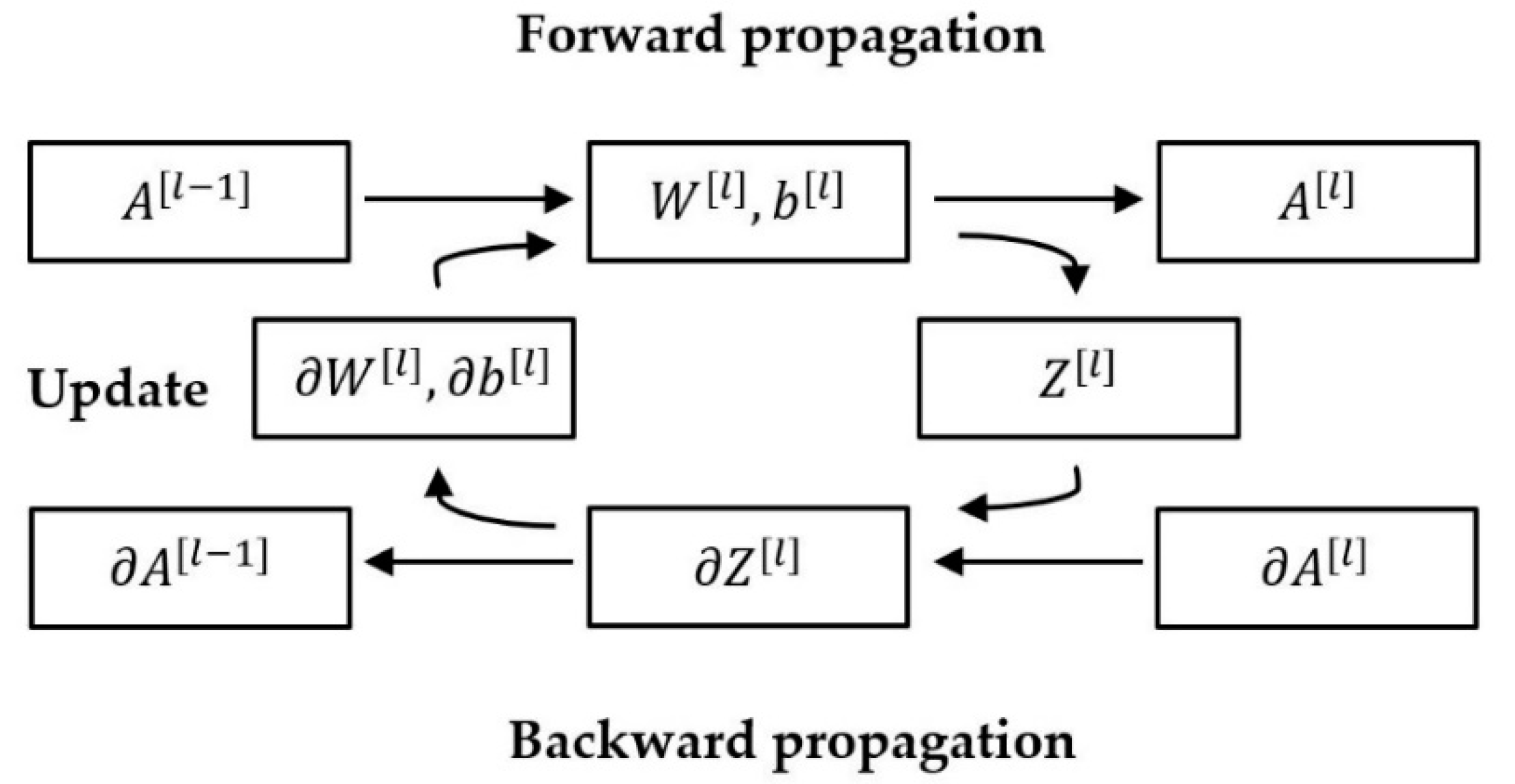
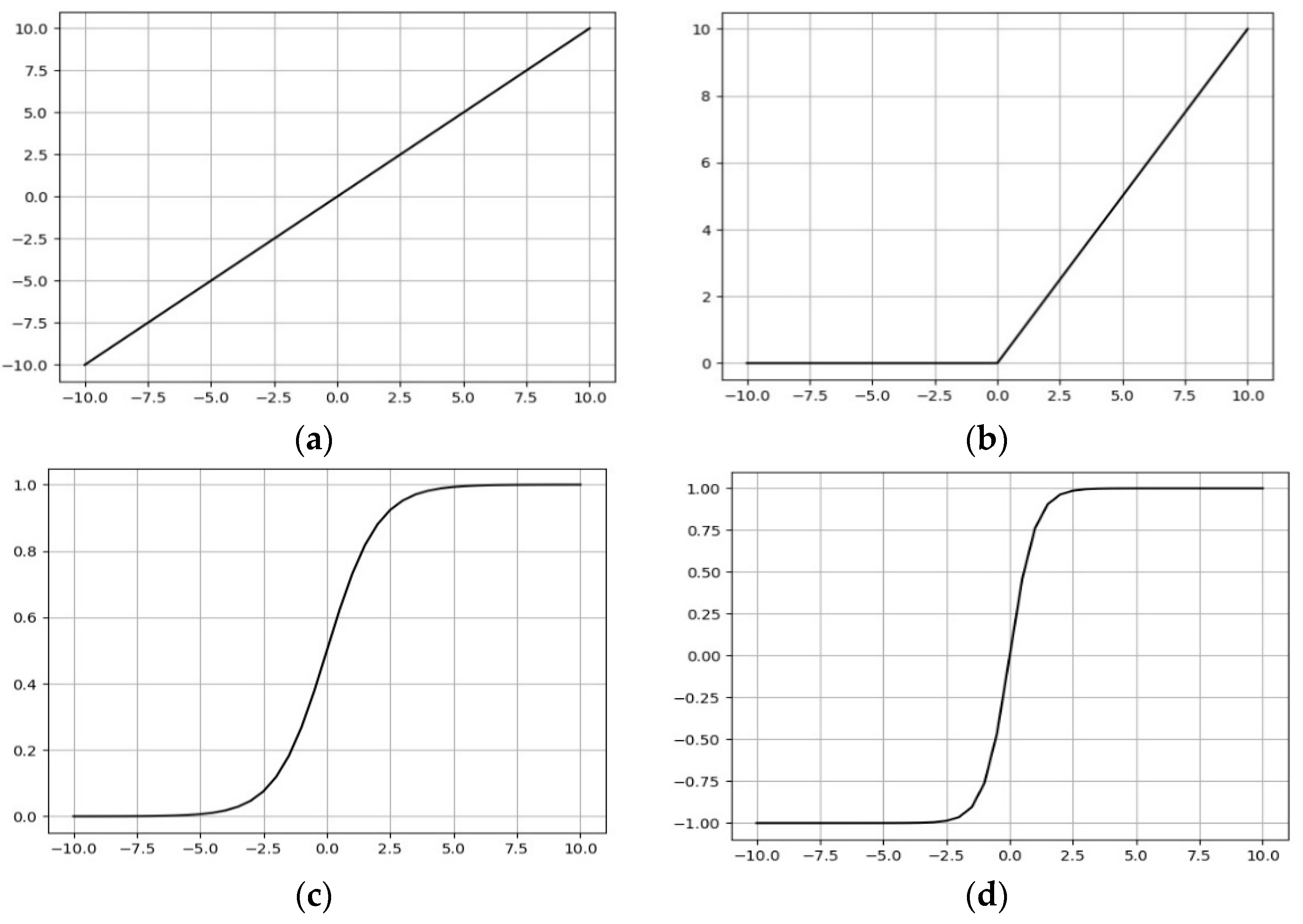
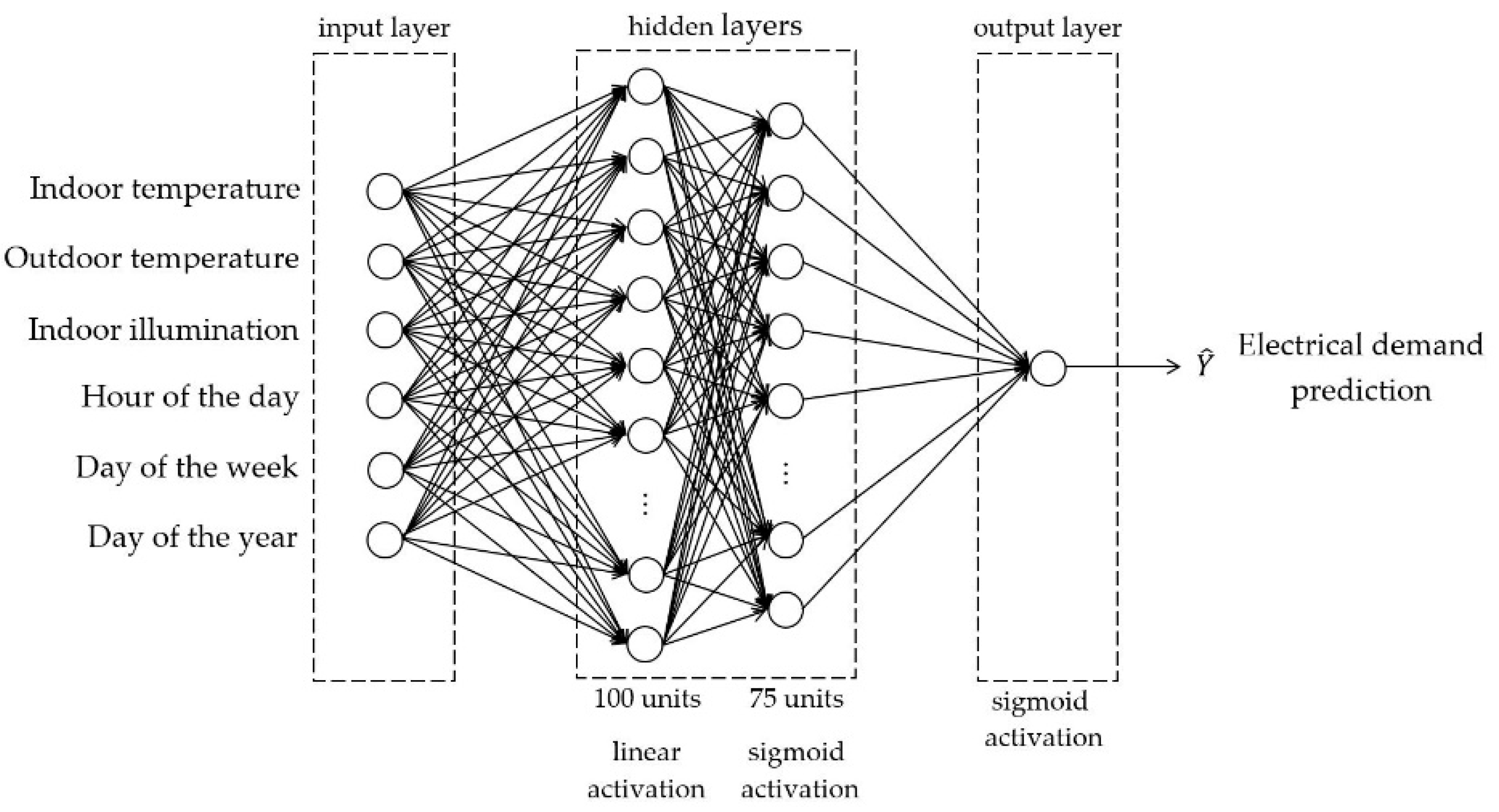
2.1. Machine Learning Prediction
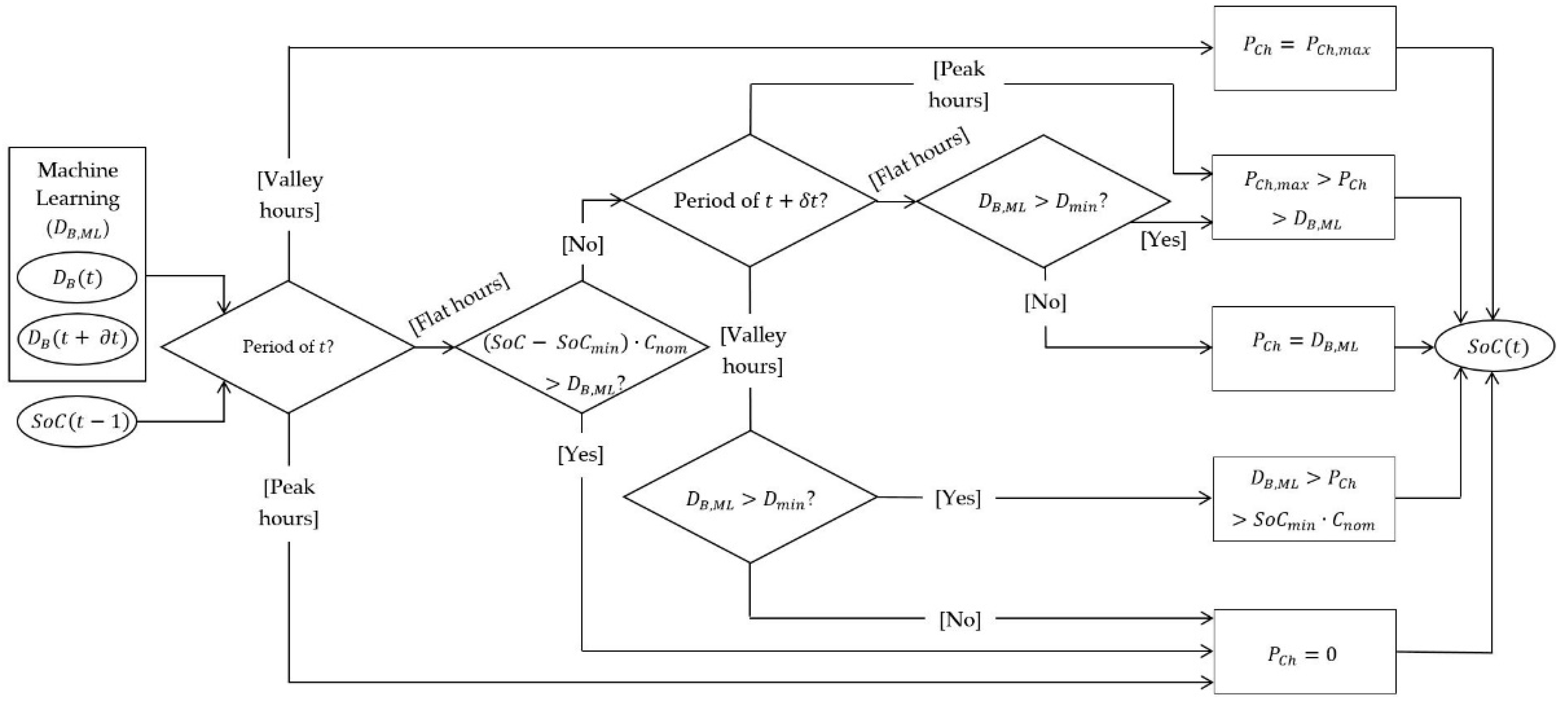
2.2. Battery Management Optimization
3. Case Study and Results
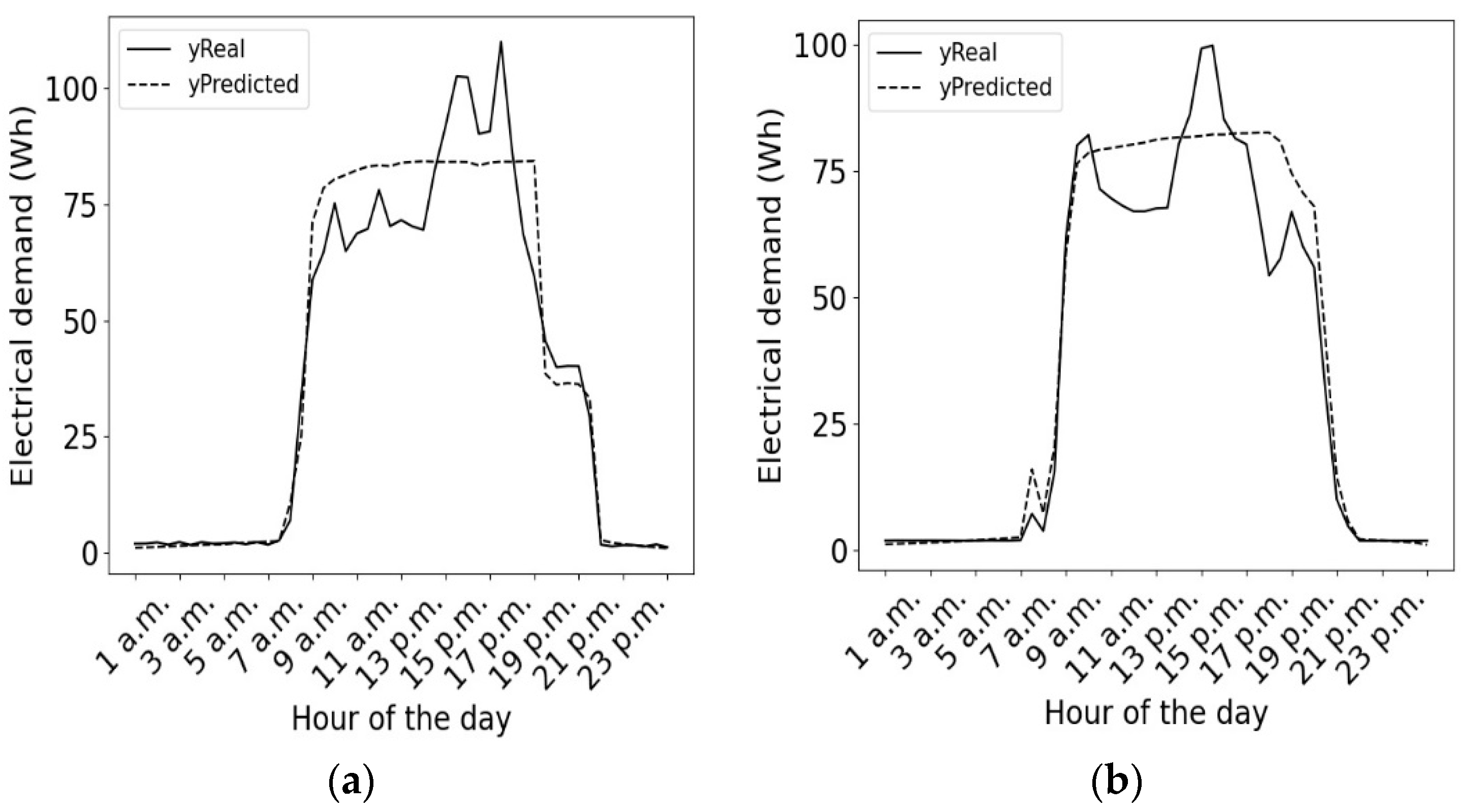
3.1. Machine Learning
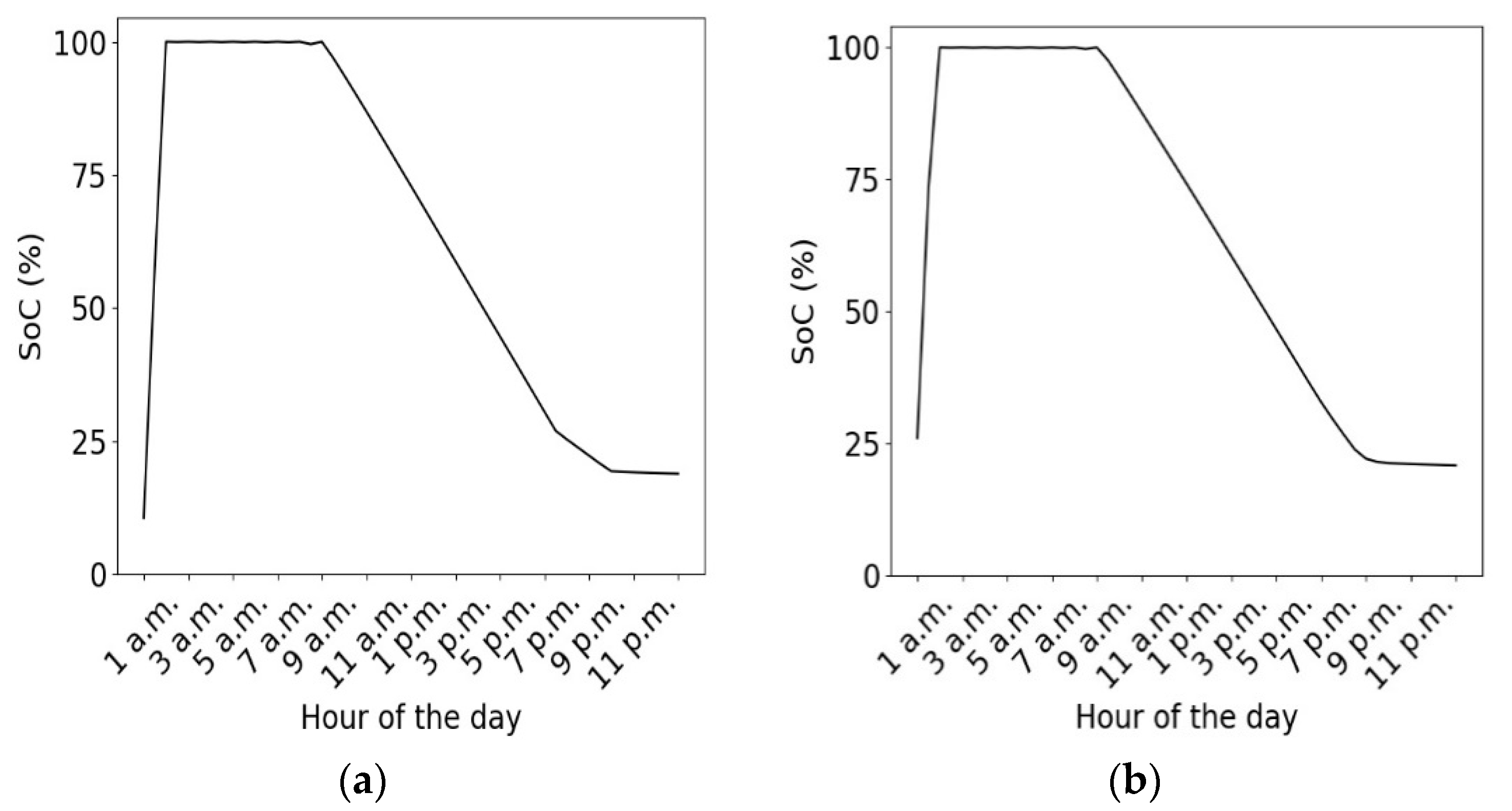
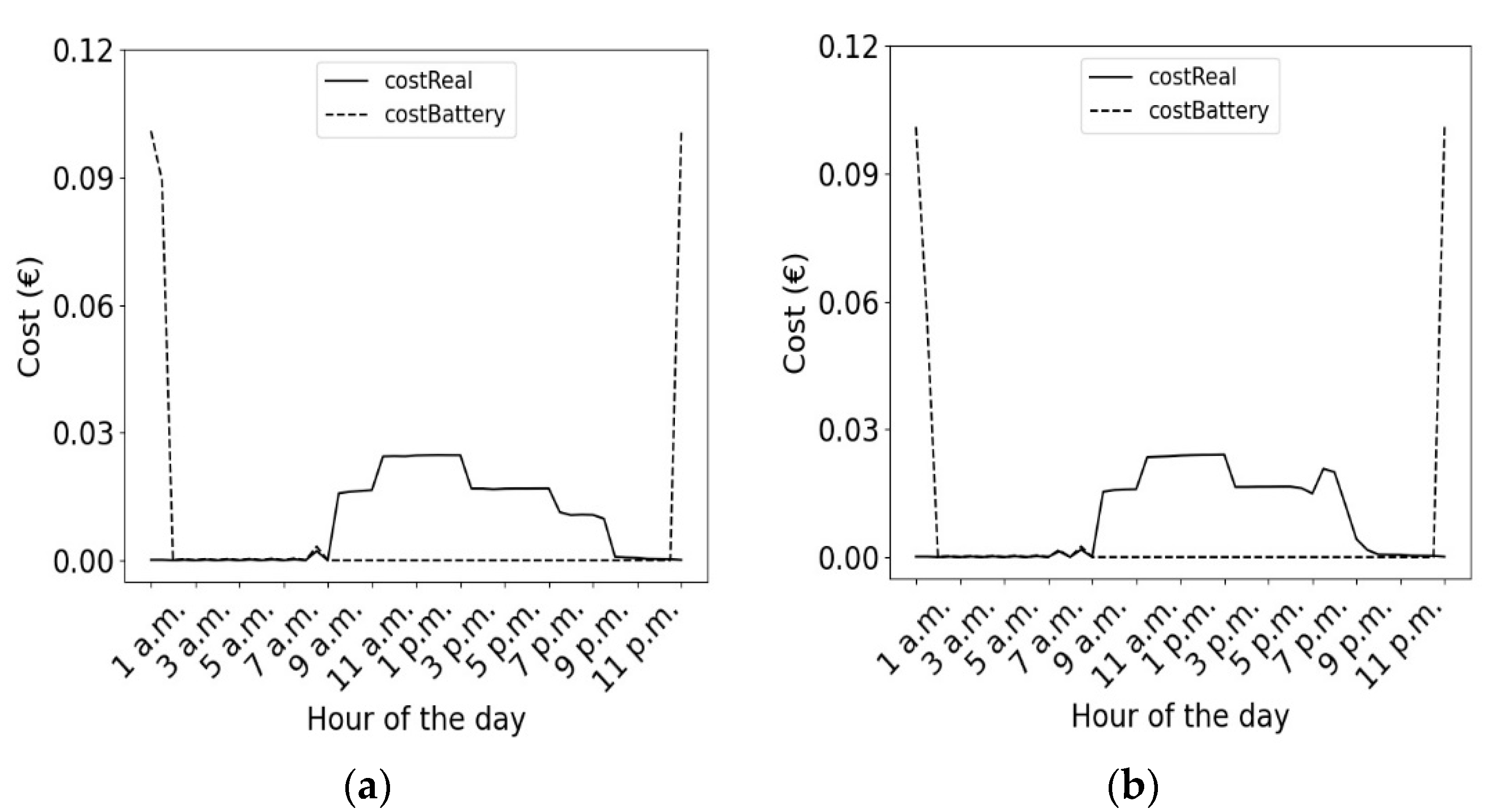
3.2. Management Storage
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- European Union. Regulation 2018/842; European Union: Brussels, Belgium, 2018. [Google Scholar]
- Official Journal of the European Union. Directive 2018/844 of the European Parliament and of the Council of 30 May 2018; EU: Brussels, Belgium, 2018. [Google Scholar]
- Li, D.H.W.; Yang, L.; Lam, J.C. Zero energy buildings and sustainable development implications—A review. Energy 2013, 54. [Google Scholar] [CrossRef]
- European Commission. 100 Climate-Neutral Cities by 2030—By and for the Citizens; EU: Brussels, Belgium, 2020. [Google Scholar]
- Nematchoua, M.K.; Sadeghi, M.; Reiter, S. Strategies and scenarios to reduce energy consumption and CO2 emission in the urban, rural and sustainable neighbourhoods. Sustain. Cities Soc. 2021, 72, 103053. [Google Scholar] [CrossRef]
- Nematchoua, M.K.; Marie-Reine Nishimwe, A.; Reiter, S. Towards nearly zero-energy residential neighbourhoods in the European Union: A case study. Renew. Sustain. Energy Rev. 2021, 135, 110198. [Google Scholar] [CrossRef]
- Brozovsky, J.; Gustavsen, A.; Gaitani, N. Zero emission neighbourhoods and positive energy districts—A state-of-the-art review. Sustain. Cities Soc. 2021, 72, 103013. [Google Scholar] [CrossRef]
- European Commission. Report from the Commission to the European Parliament and the Council: On Progress of Clean Energy Competitiveness; EU: Brussels, Belgium, 2020. [Google Scholar]
- Belton, C.A.; Lunn, P. Smart choices? An experimental study of smart meters and time-of-use tariffs in Ireland. Energy Policy 2020, 140, 111243. [Google Scholar] [CrossRef] [Green Version]
- European Commission. Study on Energy Storage—Contribution to the Security of the Electricity Supply in Europe; EU: Brussels, Belgium, 2020. [Google Scholar]
- Van De Ven, P.M.; Hegde, N.; Massoulie, L.; Salonidis, T. Optimal control of end-user energy storage. IEEE Trans. Smart Grid 2013, 4, 6477197. [Google Scholar] [CrossRef] [Green Version]
- Uski, S.; Forssén, K.; Shemeikka, J. Sensitivity assessment of microgrid investment options to guarantee reliability of power supply in rural networks as an alternative to underground cabling. Energies 2018, 11, 2831. [Google Scholar] [CrossRef] [Green Version]
- Banos, R.; Manzano-Agugliaro, F.; Montoya, F.G.; Gil, C.; Alcayde, A.; Gomez, J. Optimization methods applied to renewable and sustainable energy: A review. Renew. Sustain. Energy Rev. 2011, 15, 1753–1766. [Google Scholar] [CrossRef]
- Gao, Y.; Li, S.; Dong, W. A learning-based load, PV and energy storage system control for nearly zero energy building. In Proceedings of the 2020 IEEE Power & Energy Society General Meeting (PESGM), Montreal, QC, Canada, 2–6 August 2020; p. 9281924. [Google Scholar] [CrossRef]
- Codemo, C.G.; Erseghe, T.; Zanella, A. Energy storage optimization strategies for Smart grids. In Proceedings of the 2013 IEEE International Conference on Communications (ICC), Budapest, Hungary, 9–13 June 2013; p. 6655201. [Google Scholar] [CrossRef]
- Villanueva, D.; Cordeiro, M.; Feijoó, A.; Míguez, E.; Fernández, A. Effects of adding batteries in household installations: Savings, efficiency and emissions. Appl. Sci. 2020, 10, 5891. [Google Scholar] [CrossRef]
- Chauhan, R.K.; Chauhan, K. Building automation system for grid-connected home to optimize energy consumption and electricity bill. J. Build. Eng. 2019, 21, 409–420. [Google Scholar] [CrossRef]
- Bingham, R.D.; Angelin-Chaab, M.; Rosen, M.A. Whole building optimization of a residential home with PV and battery storage in The Bahamas. Renew. Energy 2019, 132, 1088–1103. [Google Scholar] [CrossRef]
- Mason, I.G.; Miller, A.J.V. Energetic and economic optimization of islanded household-scale photovoltaic-plus-battery systems. Renew. Energy 2016, 96, 559–573. [Google Scholar] [CrossRef]
- Ozoe, S.; Tanaka, Y.; Fukushima, M. A two-stage stochastic mixed-integer programming approach to the smart house scheduling problem. Electr. Eng. Jpn. 2014, 186, 48–58. [Google Scholar] [CrossRef]
- Mazzoni, S.; Ooi, S.; Nastasi, B.; Romagnoli, A. Energy storage technologies as techno-economic parameters for master-planning and optimal dispatch in smart multi energy systems. Appl. Energy 2019, 254, 113682. [Google Scholar] [CrossRef]
- Zhao, Y.; Lu, Y.; Yan, C.; Wang, S. MPC-based optimal scheduling of grid-connected low energy buildings with thermal energy storages. Energy Build. 2015, 86, 415–426. [Google Scholar] [CrossRef]
- Lu, Y.; Wang, S.; Sun, Y.; Yan, C. Optimal scheduling of buildings with energy generation and thermal energy storage under dynamic electricity pricing using mixed-integer nonlinear programming. Appl. Energy 2015, 147, 49–58. [Google Scholar] [CrossRef]
- Wu, X.; Hu, X.; Yin, X.; Zhang, C.; Qian, S. Optimal battery sizing of smart home via convex programming. Energy 2017, 140, 444–453. [Google Scholar] [CrossRef]
- Vazquez-Canteli, J.R.; Nagy, Z. Reinforcement learning for demand response: A review of algorithms and modeling techniques. Appl. Energy 2019, 235, 1072–1089. [Google Scholar] [CrossRef]
- Martínez-Comesaña, M.; Febrero-Garrido, L.; Granada-Álvarez, E.; Martínez-Torres, J.; Martínez-Mariño, S. Heat Loss Coefficient Estimation Applied to Existing Buildings through Machine Learning Models. Appl. Sci. 2020, 10, 8968. [Google Scholar] [CrossRef]
- Lecun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Alom, M.Z.; Taha, T.M.; Yakopcic, C.; Westberg, S.; Sidike, P.; Nasrin, M.S.; Hasan, M.; Van Essen, B.C.; Awwal, A.A.S.; Asari, V.K. A state-of-the-art survey on deep learning theory and architectures. Electronics 2019, 8, 292. [Google Scholar] [CrossRef] [Green Version]
- Hutter, F.; Lücke, J.; Schmidt-Thieme, L. Beyond Manual Tuning of Hyperparameters. Künstl. Intell. 2015, 29, 329–337. [Google Scholar] [CrossRef]
- Yang, X.S. Nature-inspired optimization algorithms: Challenges and open problems. J. Comput. Sci. 2020, 46, 101104. [Google Scholar] [CrossRef] [Green Version]
- Ozcanli, A.K.; Yaprakdal, F.; Baysal, M. Deep learning methods and applications for electrical power systems: A comprehensive review. Int. J. Energy Res. 2020, 44, 7136–7157. [Google Scholar] [CrossRef]
- Bedi, J.; Toshniwal, D. Deep learning framework to forecast electricity demand. Appl. Energy 2019, 238, 1312–1326. [Google Scholar] [CrossRef]
- Alshehri, M.; Kumar, M.; Bhardwaj, A.; Mishra, S.; Gyani, J. Deep learning based approach to classify saline particles in sea water. Water 2021, 13, 1251. [Google Scholar] [CrossRef]
- Anjos, O.; Iglesias, C.; Peres, F.; Martínes, J.; García, Á.; Taboada, J. Neural networks applied to discriminate botanical origin of honeys. Food Chem. 2015, 175, 128–136. [Google Scholar] [CrossRef]
- Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Region-based convolutional networks for accurate object detection and segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 7112511. [Google Scholar] [CrossRef] [PubMed]
- Taigman, Y.; Yang, M.; Ranzato, M.; Wolf, L. Deepface: Closing the gap to human-level performance in face verification. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014. [Google Scholar]
- Al-Qizwini, M.; Barjasteh, I.; Al-Qassab, H.; Radha, H. Deep learning algorithm for autonomous driving using GoogLeNet. In Proceedings of the 2017 28th IEEE Intelligent Vehicles Symposium (Iv 2017), Los Angeles, CA, USA, 11–14 June 2017; p. 7995703. [Google Scholar]
- Chen, L.; Hu, X.; Xu, T.; Kuang, H.; Li, Q. Turn signal detection during nighttime by CNN detector and perceptual hashing tracking. IEEE Trans. Intell. Transp. Syst. 2017, 18, 7891988. [Google Scholar] [CrossRef]
- Graves, A.; Mohamed, A.; Hinton, G. Speech recognition with deep recurrent neural networks. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013. [Google Scholar]
- Zhang, H.; Li, J.; Ji, Y.; Yue, H. Understanding subtitles by character-level sequence-to-sequence learning. IEEE Trans. Ind. Inform. 2017, 13, 7547277. [Google Scholar] [CrossRef]
- Ding, Z.; Chen, W.; Hu, T.; Xu, X. Evolutionary double attention-based long short-term memory model for building energy prediction: Case study of a green building. Appl. Energy 2021, 288, 116660. [Google Scholar] [CrossRef]
- Deltetto, D.; Coraci, D.; Pinto, G.; Piscitelli, M.S.; Capozzoli, A. Exploring the potentialities of deep reinforcement learning for incentive-based demand response in a cluster of small commercial buildings. Energies 2021, 14, 2933. [Google Scholar] [CrossRef]
- Khan, A.-N.; Iqbal, N.; Rizwan, A.; Ahmad, R.; Kim, D.-H. An ensemble energy consumption forecasting model based on spatial-temporal clustering analysis in residential buildings. Energies 2021, 14, 3020. [Google Scholar] [CrossRef]
- Bhatt, D.; Danalakshmi, D.; Hariharasudan, A.; Lis, M.; Grabowska, M. Forecasting of Energy Demands for Smart Home Applications. Energies 2021, 14, 1045. [Google Scholar] [CrossRef]
- Hwang, J.S.; Fitri, I.R.; Kim, J.-S.; Song, H. Optimal ESS scheduling for peak shaving of building energy using accuracy-enhanced load forecast. Energies 2020, 13, 5633. [Google Scholar] [CrossRef]
- Martínez-Comesaña, M.; Febrero-Garrido, L.; Troncoso-Pastoriza, F.; Martínez-Torres, J. Prediction of Building’s Thermal Performance Using LSTM and MLP Neural Networks. Appl. Sci. 2020, 10, 7439. [Google Scholar] [CrossRef]
- López-Gómez, J.; Ogando-Martínez, A.; Troncoso-Pastoriza, F.; Febrero-Garrido, L.; Granada-Álvarez, E.; Orosa-García, J.A. Photovoltaic Power Prediction Using Artificial Neural Networks and Numerical Weather Data. Sustainability 2020, 12, 10295. [Google Scholar] [CrossRef]
- Banik, R.; Das, P.; Ray, S.; Biswas, A. Prediction of electrical energy consumption based on machine learning technique. Electr. Energy 2021, 103, 909–920. [Google Scholar] [CrossRef]
- Luo, X.J.; Oyedele, L.O.; Ajayi, A.O.; Akinade, O.O. Comparative study of machine learning-based multi-objective prediction framework for multiple building energy loads. Sustain. Cities Soc. 2020, 61, 102283. [Google Scholar] [CrossRef]
- Chae, Y.T.; Horesh, R.; Hwang, Y.; Lee, Y.M. Artificial neural network model for forecasting sub-hourly electricity usage in commercial buildings. Energy Build. 2016, 111, 184–194. [Google Scholar] [CrossRef]
- Thomas, D.; Deblecker, O.; Ioakimidis, C.S. Optimal operation of an energy management system for a grid-connected smart building considering photovoltaics’ uncertainty and stochastic electric vehicles’ driving schedule. Appl. Energy 2018, 210, 1188–1206. [Google Scholar] [CrossRef]
- Brahman, F.; Honarmand, M.; Jadid, S. Optimal electrical and thermal energy management of a residential energy hub, integrating demand response and energy storage system. Energy Build. 2015, 90, 65–75. [Google Scholar] [CrossRef]
- Orosz, T.; Rassõlkin, A.; Kallaste, A.; Arsénio, P.; Pánek, D.; Kaska, J.; Karban, P. Robust Design Optimization and Emerging Technologies for Electrical Machines: Challenges and Open Problems. Appl. Sci. 2020, 10, 6653. [Google Scholar] [CrossRef]
- Pipattanasomporn, M.; Chitalia, G.; Songsiri, J.; Aswakul, C.; Pora, W.; Suwankawin, S.; Audomvongseree, K.; Hoonchareon, N. CU-BEMS, smart building electricity consumption and indoor environmental sensor datasets. Sci. Data 2020, 7, 241. [Google Scholar] [CrossRef]
| Indoor Temperature | Ambient Illumination | Loads Consumption | Lighting Consumption | Outdoor Temperature | |
|---|---|---|---|---|---|
| Errors (%) | 1.56 | 1.56 | 0.15 | 0.15 | 0.66 |
| Peak Hours | Flat Hours | Valley Hours | |
|---|---|---|---|
| Energy prices (€/kWh) | 0.2061 | 0.1128 | 0.0777 |
| Power prices (€/kW-day) | 0.0875 | 0.0875 | 0.0073 |
| Charging Power (W) | Discharging Power (W) | Capacity (Wh) | Efficiency (%) |
|---|---|---|---|
| 2500 | 2500 | 2500 | 95 |
| Train | Dev | Test | Full Sample | |
|---|---|---|---|---|
| RMSE (%) | 5.44 | 5.59 | 5.28 | 5.47 |
| Without Battery | With Battery | Savings | |
|---|---|---|---|
| Electricity expenses (€) | 97.26 | 39.54 | 57.72 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cordeiro-Costas, M.; Villanueva, D.; Eguía-Oller, P. Optimization of the Electrical Demand of an Existing Building with Storage Management through Machine Learning Techniques. Appl. Sci. 2021, 11, 7991. https://doi.org/10.3390/app11177991
Cordeiro-Costas M, Villanueva D, Eguía-Oller P. Optimization of the Electrical Demand of an Existing Building with Storage Management through Machine Learning Techniques. Applied Sciences. 2021; 11(17):7991. https://doi.org/10.3390/app11177991
Chicago/Turabian StyleCordeiro-Costas, Moisés, Daniel Villanueva, and Pablo Eguía-Oller. 2021. "Optimization of the Electrical Demand of an Existing Building with Storage Management through Machine Learning Techniques" Applied Sciences 11, no. 17: 7991. https://doi.org/10.3390/app11177991
APA StyleCordeiro-Costas, M., Villanueva, D., & Eguía-Oller, P. (2021). Optimization of the Electrical Demand of an Existing Building with Storage Management through Machine Learning Techniques. Applied Sciences, 11(17), 7991. https://doi.org/10.3390/app11177991







