Abstract
Cracks are one of the main problems that plague road workers. A correct understanding of the internal crack propagation mechanism of asphalt pavement will help road workers evaluate the road’s working status more comprehensively and make more reasonable decisions in design, construction, and maintenance work. This paper established a three-dimensional asphalt pavement layered model using the software ABAQUS and fracture mechanics theory and the extended finite element method were used to explore the mechanical response of the pavement base layer’s preset reflective cracks. This paper investigated the influence of the modulus of each layer, vehicle load on the principal stress, shear stress, J-integral, and two stress intensity factors (K1, K2) during the predetermined crack propagation process of the pavement base layer, and the entropy method was used to analyze the above-mentioned mechanical response. The results show that the main factor affecting the propagation of reflective cracks on asphalt pavements is the modulus of the bottom surface layer. However, from a modeling perspective, the effect of increasing load on crack growth is obvious. Therefore, in terms of technical feasibility, the prevention of reflective cracks should still be achieved by controlling the driving load and prohibiting overloading.
1. Introduction
Cracking is a challenging topic which the researchers face. Insufficient and improper treatment of cracks often negatively impacts the pavement structure and its performance. Numerous studies on cracks’ behavior have been conducted to reveal their influences on pavement performance. Initial cracks usually exist in the pavement structure in the form of micro-cracks, and these cracks grow due to temperature change, traffic loads, and other environmental factors. So, research on the mechanism of cracking growth will help monitor the cracks’ behaviors from the beginning of their development and offer feasible ways of manufacturing and maintenance. Traditional fatigue methods explain the initiation and growth of cracks [1], but this only provides a rough approach that performs poorly while calculating longitudinal cracks. To solve this kind of problem, fracture mechanism theories were established. Paris established the approximate equation of crack growth rate under repeated load [2]. Majidzadeh expanded this theory, and normal forms of crack growth were obtained [3]. However, this equation needs four parameters related to material properties, which decrease its reliability and limit its usage. A life-related index was established based on engineering data, including traffic load, environment conditions, and embankment conditions [4]. Conditions included by this index are also limited, and it will take a long time to perform road surveys, which can be inconvenient. These methods are always based on numerous engineering data and cannot involve many working conditions. Correction factors are always acquired when using these methods, so a convenient way of researching crack behavior is needed.
Conventional research on crack behavior heavily relies on laboratory-scale experiments, which require considerable time and effort. These experiments always focused on the final status of cracks and pavement, and the processes of cracks’ growth were ignored due to testing methods. Over these years, the finite element method has become a popular approach to simulate the cracks’ behavior during their life cycle. During their growth, every kind of cracks’ behavior can be calculated using finite element software, requiring much less time than local experiments. The two-dimensional plane strain model was established by Myers using finite element software ABAQUS [5]. This model revealed the growth of pre-set cracks under traffic loads and the direction of cracks’ growth, which offered a mature way of pavement simulation. García used the finite element method combined with fracture mechanics theory to investigate the cracking behavior of the orthogonal layered pavement, and uses the method of preset interlayer cracks to predict the cracking of each layer of the pavement during use. The results show that the cracking performance of the orthogonal layered pavement is largely affected by the initial shape and location of the cracks. These initial cracks mostly occur at the joints between layers, thinner layers and the free boundaries of each layer [6]. Results show that behaviors of crack growth are related to the viscoelasticity and creep properties of asphalt deeply. However, compared with two-dimensional models, three-dimensional models always perform better, especially when the process of crack growth was taken into consideration [5]. Parameters of crack growth and their time history curve can be calculated using the finite element method and predictions of pavement life, degree of damage can be drawn. Road workers can also choose the appropriate asphalt mixture based on the finite element calculation results, thus promoting the development of the asphalt mixture.
J-integral and stress intensity factors are often used to describe the behaviors of crack growth, from which researchers can have a direct understanding of the process. Okada developed a 3D model to compute the J-integral of large deformation solids [7]. Results show that J-integral is unconditionally path independent, reflecting that it is not very important to set a specific path while simulating cracks using J-integral, thus decreasing the difficulties. Moreover, energy can be used to calculate the J-integral. Okada added the strain energy density into the J-integral formulation to calculate the deformation histories of the specimen [7]. Yu proposed a new model of calculating J-integral based on the energy density equivalence by introducing 3D constraint functions to describe the relationships between J-integral and load in mode-I cracks [8]. Sasan compared two criteria of stress intensity factor and fracture energy to investigate the behavior of asphalt mixtures under combined tensile shear loadings [9]. The SCB (Semi-Cycle Bending Test) fracture test results show that the fracture behavior of asphalt mixtures is significantly dependent on testing temperature and loading rate, which can reflect the working conditions of asphalt mixtures during engineering construction. Moreover, finite element calculation was conducted to verify the correctness of SCB tests. As for pavement structure, J-integral and stress intensity factors can be different from theoretical calculations and mechanical experiments due to the structural differences between theoretical calculation models or mechanical specimens and pavement structure. Researchers often use elastic layered continuum theory to describe the structure of asphalt pavement. Alae established a three-layer 3D model of asphalt pavement with top-down cracks [10]. Working temperature and vehicle speed were assumed to be the changing working conditions of the pavement structure. Results show that top-down cracks in pavement structure can be broken down into I + II fracture, and J-integral can be used to describe stress intensity on the crack tip. Ma developed a wave propagation-based analytical solution to calculate the mechanical responses of transversely isotropic viscoelastic multi-layered asphalt pavement subject to moving harmonic load [11]. This solution can be used for asphalt pavement design and analysis with consideration of realistic load and material parameters. However, a specimen of asphalt mixtures can only reveal the crack resistance of the material, but the mixtures’ behaviors in pavement structure are not widely studied. J-integral and stress intensity factors on the crack tip in pavement structures have not been researched systematically. Mechanical responses during the crack growth need to be calculated using the finite element method.
The research described in this paper is aimed to reveal the cracks’ behaviors during the pavement’s life cycle and under different working situations. The effects of traffic loads and Young’s modulus of layers on the crack extension were investigated. This paper uses finite element software ABAQUS to simulate the pre-set crack’s growth during the pavement’s life cycle. J-integral, stress intensity factors, absolute stress, and strains were calculated to describe how the cracks extend while working. Moreover, the entropy method was used to analyze the relationship between these influencing factors aiming to help to deal with cracking problems efficiently.
2. Methods
2.1. Method
Fracture mechanics were widely used in crack analysis for their high accuracy, and the development of computer technology offers the convenience of calculating. Thus fracture mechanics are commonly used in pavement engineering. Using the finite element method for digital modeling can calculate the behavior of cracks. Responses of cracks could be summarized by modifying mechanical parameters of finite element model such as working conditions, structure combination, material composition.
Fracture mechanics divide cracks into three species (open crack—type I, sliding crack—type II, tear-open crack—type III) and stress intensity factors (KI, KII, KIII) were used to describe the tendency of cracking [12]. Linear superposition of three kinds of cracks can be used to describe the stress field at the tip of cracks. Normal stress and shear stress of the tip of cracks can be calculated using the following equations.
where r represents the distance from the calculation point to the crack tip. θ represents the angle between the calculation point and the crack tip in the polar coordinate system and the polar axis. Analysis of the above formula shows that the key to determining the stress field at the crack tip is the stress intensity factor. These factors are mainly determined by the properties of external load, the shape of cracks, and the geometry of elastomer, which can be expressed by the equation below.
where Zm (r) is an analytic function related to the boundary conditions, which can be calculated using finite element method software ABAQUS. The stress intensity factor at the ultimate fracture of a material is called fracture toughness, usually expressed by KIC, which can be determined by experiments.
Compared with the stress intensity factor, J-integral is more suitable for analyzing fracture problems under elastoplastic conditions [13]. The J-integral is used to solve the situation that a certain range of plastic zone appears at the tip of the crack under the elastoplastic condition, which makes the problem very complicated. The J-integral can describe the stress and strain field strength in the crack tip area, and it can be easily determined by experiment. Use stress intensity factor and J-integral can reveal the crack behavior in pavement engineering. A plane crack problem was assumed when calculating J-integral. The integral is performed around the crack tip, starting from the lower crack surface, and stopping counterclockwise to the crack’s upper surface, thus forming an integral loop. This integral value obviously has nothing to do with the integral path, so J-integral can reflect the intensity of the stress field near the crack tip. Figure 1 is a schematic diagram of the calculation of J-integral.
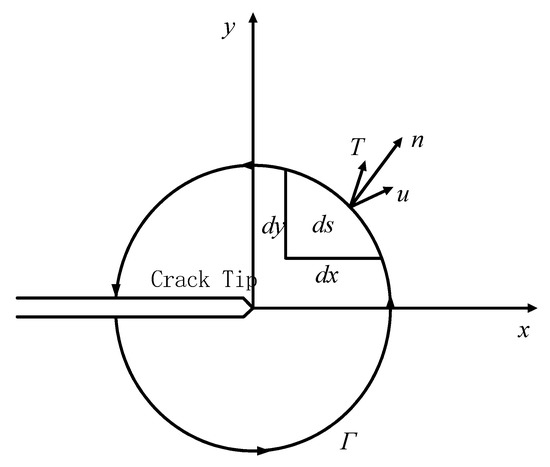
Figure 1.
Calculation of J-integral.
J-integral is defined as:
where ω represents the strain energy density on the loop. is the stress vector at any point on the loop. is the displacement vector at any point on the loop. In the case of linear elasticity (plane strain), the strain energy density ω is
where and respectively represent the stress tensor and strain tensor at the crack. Substitute (8) into (7), we have
If we take a loop Γ with the crack tip as the center and a radius of r,
As for stress vector
So
Substituting (10) and (12) into (7),
That is, the J-integral is the crack propagation energy release rate G in the linear elastic state. This is a constant and can be obtained through experiments or theoretical calculations. Therefore, the J-integral is used to establish the basis for the determination of cracks and is consistent with the establishment of the K value.
When using the traditional finite element method to simulate static non-propagating cracks, it is necessary to consider the singularity of the crack tip stress field according to the principles of fracture mechanics. Singular meshes were used to solve the problem, such as setting the meshes of the crack tip into M font or refining meshes in the crack tip area. Difficulties in computing were generated due to a large number of meshes, especially in three-dimensional models. It is hard to compute in crack tip areas due to the low quantity of meshes. Finite element method software ABAQUS offered Extended Finite Element Method (XFEM) to solve the problem, which uses shape functions to simulate crack areas in the pavement structure. Thus, it does not need to remesh and improves the efficiency of calculating. Based on the thought of unit decomposition, XFEM added functions that can reflect the discontinuous characteristics of the crack area [14,15]. The thought of unit decomposition thinks that any functions ψ(x) can be expressed using the equations below.
where is a parameter to be adjusted to make the expression reach the best approximation, is a function that satisfies the element decomposition, and Φ(x) is an extended function. As for crack simulation, XFEM uses the equations below to simulate.
where is the newly added degree of freedom and it has no meaning in physics. The only usage of is to adjust the function Φ(x) to achieve the best approximation. Compared with the traditional finite element method, XFEM added more freedom degrees, thus improving its accuracy.
XFEM and fracture mechanics were used in finite element method software ABAQUS, which can simulate the crack behavior during its growth with considerable accuracy. Crack behavior can be calculated by modifying properties of models and materials, which can make predictions on pavement life and different working conditions, thus saves much time and cost compared with local experiments.
2.2. Simulation
The finite element model was established using the software ABAQUS. Previous studies show that 6 m × 6 m × 5 m cube specimen was the most suitable kind of simulating the actual pavement structure [16,17]. C3D8R was selected as the grid type, and no lateral movement is chosen as the boundary condition to reveal the actual conditions of cracking. A three-dimensional model of pavement was established, and the pavement structure was assumed to be composed of five layers, from top to bottom as SMA asphalt mixture, AC-20, asphalt treated base (ATB), cement stabilized base (CTB), and soil ground (SG). The specific layer composition is shown in Figure 2, and the properties of different layers are shown in Table 1. The initial location of the crack was set in CTB is shown in Figure 2.
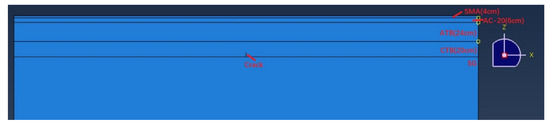
Figure 2.
Schematic of pavement structure and crack location.

Table 1.
Properties of layers.
The initial time of the analysis step was set to 0.1 s on the basis of previous studies, and the total time of the analysis step was 25 s in order to control the solution time and take the calculation accuracy into account. The load area of traffic was set as two rectangular areas with a width of 0.213 m, a length of 6m, and an interval of 0.1065 m based on Chinese standard traffic load. In the static analysis of the structure, the load changes with the type of vehicle load. This paper adopts 1.0~2.6 times of the standard axle load specified in the Chinese highway pavement design code for analysis. When it is 1 time, the load should be 700 kPa. Boundary conditions were set as no stress, no displacement at the edge of the side and bottom of the model based on elastic layered system theory. In this paper, the pavement structure load and boundary conditions were set as shown in Figure 3.
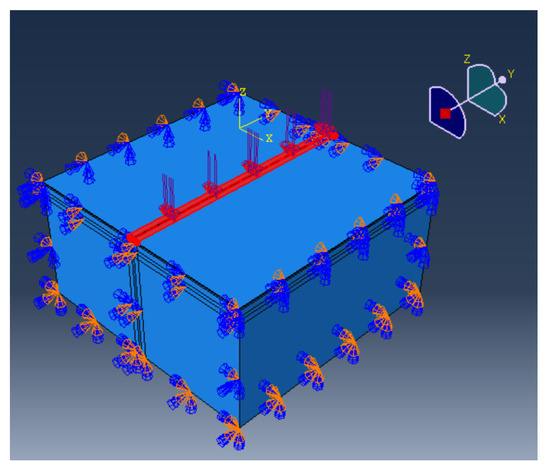
Figure 3.
Schematic of load and boundary conditions.
Stress intensity factor and J-integral of the crack can reveal the tendency of crack growth. In addition, the principal stress and shear stress intensity at the crack tip can also reflect the cracking situation. Grids at the crack tip were subdivided in order to guarantee the accuracy of simulation, and four typical grids were selected to investigate the principal stress and shear stress at the crack tip. The location of the grids was shown in Figure 4.

Figure 4.
Selection of typical grids.
3. Results and Discussion
3.1. Behavior of Crack Extension
The relevant Chinese regulations stipulate that the design of asphalt pavement adopts a sing-axle-two-wheel set axle load with an axle load of 100 kN as the design axle load. When the vehicle is parked on the road surface, the pressure on the contact area of the road surface is 0.7 MPa. Overloading and over-limit often occur while working, both of which will have an adverse effect on the pavement structure. This paper uses 0.2 times as the axle load gradient to explore the propagation of reflection cracks on the road surface under the action of 1.0 to 2.8 times axle load. There are 10 working conditions in total. The principal stress (S33 in ABAQUS) cloud diagram and the shear stress (S23 in ABAQUS) cloud diagram of the asphalt pavement under the action of 1.0 times the standard axle load are shown in Figure 5.
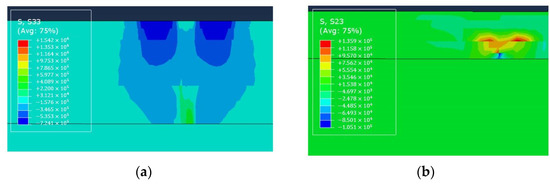
Figure 5.
(a) S33 diagram of crack area (b) S23 diagram of crack area.
Figure 5a indicates that the asphalt pavement structure bears vertical compressive stress under the vehicle load. The entire road surface is subject to greater compressive stress in the area of the surface layer directly in contact with the wheel under normal circumstances, which means that most areas of the pavement structure are compressed in the +z direction. However, due to the existence of reflective cracks in the base layer, an area with positive normal stress appears in the predetermined crack area, which indicates that the pavement structure is compressed in the −z-direction in the crack area due to the existence of crack. In addition, it can be seen that from the stress contour that the cracks do not grow strictly in the preset vertical direction during the expansion process. The normal stress of the crack area is obviously greater than the right on the left side of the preset vertical direction, and the crack continues to grow on the left. The growing process is affected by many factors, such as load, the thickness of each layer, the modulus of each layer, and the shape function of the crack area in ABAQUS. Figure 5a shows that there is a type I cracking in the crack growth process, and Figure 5b shows that there is also type II cracking in the process. Figure 5b indicates that there is a sliding trend between the different layers. The sliding trend between adjacent layers is caused by the existence of reflective cracks, the contact between the pavement structure layers is no longer stable. With the further action of the load, pavement cracks will spread around the entire pavement structure, causing serious damage to the pavement structure.
Crack development is a process, and ABAQUS believes that only when the mechanical parameters of the crack tip meet certain conditions, the cracks begin to develop. Meanwhile, the size of the three-dimensional layered structure of the pavement is considered to be infinite during the simulation process, and only the stress intensity factors and J-integral of the preset crack tip are calculated, that is, the destruction of the whole structure is not displayed for it was replaced by these mechanical factors. The J-integral and stress intensity factor time history curves of the crack tip were shown in Figure 6.
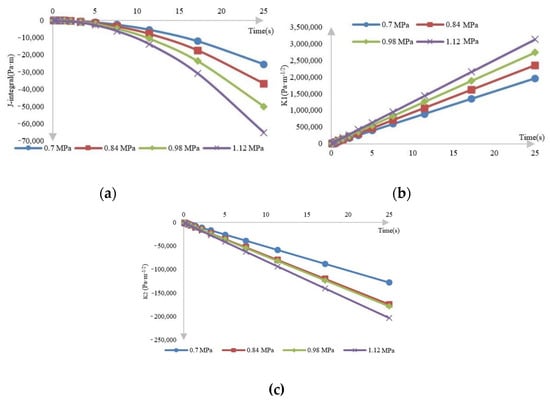
Figure 6.
(a) J-integral time history curve (b) K1 time history curve (c) K2 time history curve.
Figure 6 indicates that under the action of static load, the curve of J-integral is close to half of the quadratic curve, while the changing trend of the stress intensity factor is a straight line. The time history curve shows that as the load time increases, the values of the three are increasing, and the crack propagation trend is also increasing, and the crack propagation rate will increase at a fixed growth rate before the structure is completely destroyed. This is because pavement damage will continue to accumulate under the action of traffic load, but the load will not disappear. As the crack continues to grow, the rate of crack propagation will gradually become faster and eventually grow at a stable speed, indicating that the crack has fully cracked in the middle and late stages of crack propagation, which behave as mesh failure in ABAQUS, and gradually expand around until the structure is completely destroyed. If the size of the simulating specimen is infinite, the crack continues to grow at a steady growth rate. In addition, it is not difficult to know that the accumulation of road damage will accelerate under the action of overload, and the development trend will increase.
3.2. Traffic Loads
Pavement may bear different loads during usage, and different traffic loads can generate different stress in the pavement structure. The principal stress and shear stress of the crack tip under different loads are shown in Figure 7.
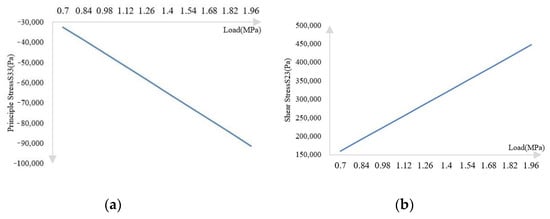
Figure 7.
(a) Principal stress change curve with load (b) Shear stress change curve with load.
The curve in Figure 7a satisfies Equation (16), where the value of R2 is 0.9999:
The curve in Figure 7b satisfies Equation (17), where the value of R2 is 0.9999:
The two curves indicate that the stress in pavement structure increases sharply with the increment of traffic loads. It can be seen that in the process of increasing the axle loads to 2.8 times the standard axle load, the principal stress increased by 181.29% and the shear stress increased by 180.82%, indicating that for every doubling of the load, the pavement structure will bear one more than the original standard axle load, especially in crack tips. The higher the stress, the faster the crack propagates, which leads to serious damage. The foregoing analysis also shows that the accumulation of road damage will accelerate under overloading, and the development trend will increase, which can be described using J-integral and stress intensity factors. Figure 8 shows the numerical changes of these mechanical factors related to crack growth under different overloads when the step time was set as 25 s.
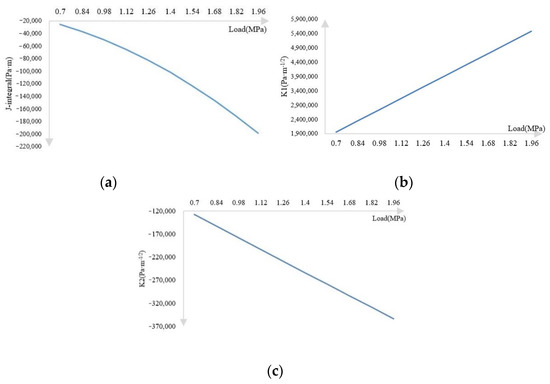
Figure 8.
(a) J-integral curve with load (b) K1 curve with load (c) K2 curve with load.
Consistent with the stress response, the J-integral and the stress intensity factors continue to increase when the traffic load increases. The J-integral increases by 681.83%, K1 increases by 179.43%, and K2 increases by 177.11%. The above curve and increase indicate that when the pavement load gradually increases to 2.8 times of the standard axle load, the mechanical factors related to the growth rate of pavement reflective cracks are also greatly enlarged, and the reflective pavement cracks develop more rapidly, indicating that overloading affects the pavement structure. The impact of this is huge, and road traffic loads should be strictly restricted.
3.3. Layers with Different Young’s Modulus
The mechanical response of pavement materials to traffic load is not the same, and its influence on crack growth is also different. In the pavement structure simulation process in ABAQUS, the difference in properties of various materials is mainly reflected in the difference in modules. This paper simulated the influence of different modulus of surface layer, middle surface layer, and bottom surface layer on the crack growth. Both the three-layer take 500 MPa as the modulus gradient, and the mechanical responses of the surface layer under 10 working conditions from 1400 MPa to 5900 MPa, the mechanical responses of the middle surface layer under 10 working conditions from 1200 MPa to 5700 MPa is explored, the mechanical responses of the bottom surface layer under 10 working conditions from 1000 MPa to 5500 MPa were analyzed. The influence of the modulus of the surface layer, middle surface layer, and the bottom surface layer of asphalt pavement on the principal stress S33 and shear stress S23 under the action of standard axle load were shown in Figure 9.
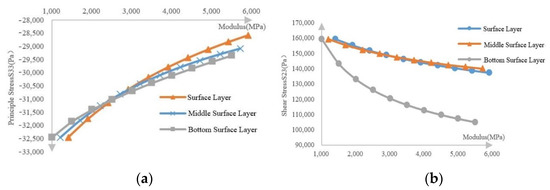
Figure 9.
(a) Influence of the modulus of each layer on the principal stress (b) influence of the modulus of each layer on the shear stress.
The simulation results show that the influence of the modulus of each layer of the road surface on the stress of the crack tip during the growth of the reflective crack satisfies the inverse proportional function. The surface layer modulus has the greatest influence on the principal stress, and the bottom surface layer modulus has the greatest influence on the shear stress. It can be seen from Figure 9a that the principal stress on the crack area decreases with the increase in the modulus of each surface layer, indicating that the increase in the modulus of each layer has a certain inhibitory effect on the crack growth. This is because as the structural layers gradually harden and their strength increases, the stress that they can withstand progressively increases. The working area of the pavement structure moves upward, and more traffic loads will be borne by the surface layer structure. For the reflective cracks of the base layer, its cracking behavior will be suppressed. In terms of shear stress, it can be seen from Figure 9b that as the layer structure of the road surface gradually hardens, the shear stress on the crack area becomes smaller. This is also because the structure layers above the crack become harder, which leads to the upward movement of the pavement work area. The surface structure bears more load, and less load is transmitted to the crack area, which has a certain restraining effect. When the bottom surface layer becomes hard, the energy required for cracking the bottom surface layer increases correspondingly, and the initial energy required for slipping becomes larger. From Figure 9b, it can be seen that the layers slide mutually, that is, the distribution of shear stress. The most concentrated area is between the bottom surface layer and the base layer, so the change of the bottom surface layer modulus has a relatively large influence on the shear stress in the crack tip. However, it should be noted that this suppression effect is not obvious. In the process of changing the modulus of each layer by 4500 MPa, the largest reduction in normal stress is only 11.93% of the surface layer, and the value is only about 40,000 Pa. The largest reduction in shear stress is the bottom surface layer, the amplitude is only 34.13%, and the value is about 400,000 Pa. Compared with the damage caused by overloading the pavement structure, such an improvement appears inadequate. In addition, the production of high modulus asphalt mixture often means discarding other aspects of the mixture, such as anti-rutting performance and water damage resistance, and the production cost is correspondingly increased. Therefore, it is not feasible to prevent reflection cracks by increasing the modulus of each structural layer of the pavement. It can only be used in areas with less overload and over-limit phenomena and low performance in other areas of the road.
In addition, the values of J-integral and stress intensity factor both decrease with the increase in the modulus of each layer, and during the change of the modulus of the three-layer pavement structure, the change of the modulus of the middle surface layer has the least influence on the three parameters and the modulus of the bottom surface layer has the greatest influence. Figure 10 shows the curves of J-integral and stress intensity factors while modulus is changing.
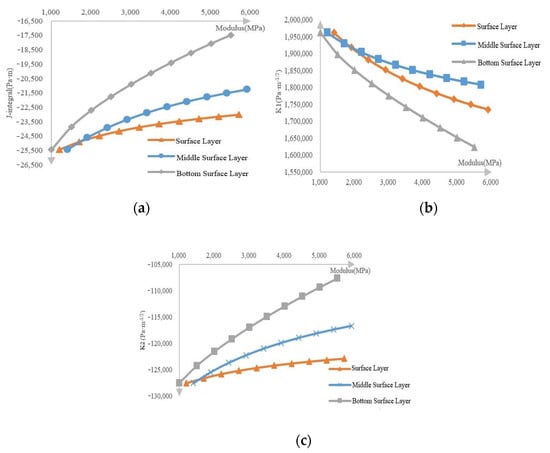
Figure 10.
(a) J-integral curve with modulus (b) K1 curve with modulus (c) K2 curve with modulus.
The J-integral is a parameter related to crack initiation, and the K value is a quantity related to the rate of crack propagation. The constant increase in the modulus of each layer of the pavement will make it difficult for the crack to initiate. It will take a longer load time to reach the crack initiation criterion. Specified maximum stress and crack initiation energy. After the stress and energy in the crack area reach the crack initiation criterion, the further development of the crack in the structure still requires greater stress and energy than when the modulus is lower. Therefore, with the gradual increase in the modulus of each layer, the crack propagation rate, and the severity are suppressed to a certain extent. In addition, the interfaces with the bottom surface layer are the first and the easiest to reach when the reflection cracks develop upward due to they are the closest to the base layer, where the reflective crack was set, so the effect of change of the bottom surface layer modulus on the crack growth rate is relatively more obvious. Same as the effect on stress, even if the bottom surface layer with the greatest impact becomes hard, its J-integral was reduced by 31.3%, and the absolute value was about 8000 Pa·s; the reduction of K1 is 17.26%, and the absolute value is about 0.34 MPa·m−1/2; the reduction degree of K2 is 15.60%, and the absolute value is about 20,000 Pa·m−1/2. The above value is too small compared with the effect of overload on J-integral and stress intensity factors. In actual road engineering, the method of increasing the modulus of each layer to suppress the development of reflection cracks does not have a good effect. Therefore, the vehicle load should be strictly limited.
3.4. Sensitivity of Various Influencing Factors on Asphalt Pavement
The entropy method was used to analyze the influence data of various working conditions on the mechanical response of the pavement crack tip in the foregoing three sections to obtain the primary and secondary relationship of the influence of various factors on the different mechanical responses. In the entropy analysis of this paper, the schemes to be evaluated are load effect, surface layer modulus, middle surface layer modulus, and bottom surface layer modulus. Each scheme has 10 working conditions. This paper counted the values of S33, S23, J-integral, K1, K2 under each working condition, taking the working condition as the vertical column and the evaluation plan as the horizontal row, and calculating the influence of each factor on them under 10 working conditions, and determined the weight of these influencing factors at the same time. The weight of the influence of various factors on S33, S23, K1, and K2 is shown in Table 2.

Table 2.
Weight of various factors.
It can be seen from the table above that among the factors that affect the J-integral, the modulus of the bottom surface layer of the surface layer is the most important factor, and the modulus of the surface layer and the middle surface layer modulus have the least influence. The factor that has the greatest influence on the four mechanical responses is the modulus of the bottom surface layer. This is because the bottom surface layer is the closest to the crack area. When the crack propagates to the bottom surface layer, the stress intensity and energy required for further expansion need to be accumulated at the contact between the bottom surface layer and the base layer. When the modulus of the bottom surface layer increases significantly, the cracking tendency becomes smaller, the cracks need to accumulate on the contact surface for a longer time, and the load needs to continue to act. Therefore, the most direct factor affecting the crack propagation process is the bottom surface layer modulus. However, the effects of several other factors need to be transmitted to the fracture area through the bottom surface layer, and the effect on the fracture area is not very direct. In addition, the analysis results also show that loads are not the most important factor affecting the mechanical response of the crack area, but from the foregoing analysis, it can be seen that they have a significant impact on the numerical value of the mechanical response of the crack area, far exceeding other working conditions. Therefore, special attention should be paid to controlling the traffic load.
4. Conclusions
Crack prevention and control is a long-term research field of road engineering. A correct understanding of the internal crack propagation mechanism of asphalt pavement will help road workers to evaluate road working conditions more comprehensively, and make better decisions in design, construction, and maintenance. In this study, the FEM software ABAQUS was used to establish a three-dimensional asphalt pavement layered model. Fracture mechanics theory and the extended finite element method were used to investigate the expansion behavior of preset cracks in the pavement base layer, and the following conclusions were obtained.
- A feasible three-dimensional pavement layered structure model was established, and numerical analysis was conducted using fracture mechanics theory and finite element software ABAQUS. The normal stress S33, shear stress S23, J-integral, and stress intensity factor K1 and K2 of the crack tip under different working conditions were calculated. Due to the existence of cracks, the difference between the positive and negative stresses between the base layer reached 2.209 × 105 Pa, and the difference between shear stress reached 4.018 × 104 Pa, indicating that the cracks showed a strong development trend both in the vertical and horizontal directions. The mechanical response of the crack tip is approximately a straight line when the vehicle load changes, and it is approximately an inverse proportional function when the modulus of each layer change. The R values of the fitted curves all reached over 0.99. In addition, the mechanical response of the stress and the stress intensity factor in some particular areas is high-order polynomial, generally second or third.
- Cracks will not strictly follow the preset path but will deviate from the preset vertical direction due to various factors. Therefore, in the actual monitoring of crack behavior, the normal stress and shear stress changes in the pavement structure should be monitored simultaneously in a larger area, and should not be limited to the crack tip.
- The load has a significant impact on the stress in the crack area. Under other conditions, the value of the stress change in the crack area is much smaller than under the load. In the process of increasing the load by 2.8 times, the principal stress increased by about 181.29%, and the shear stress increased by about 180.82%. In the process of increasing the modulus of each layer by 4500 MPa, the maximum reduction of normal stress is 11.93% of the surface layer, and the maximum shear stress is 34.13% of the ground layer. From a numerical point of view, the effect of increasing the modulus on crack propagation is relatively small compared with the effect of increasing load on cracking. Therefore, the vehicle load should be strictly limited to prevent road cracks.
- The entropy method was used to analyze the primary and secondary effects of various indicators in the process of reflecting crack propagation in asphalt pavement. The most important factor is the modulus of each layer, and the modulus of the bottom surface layer is the largest, followed by vehicle load. This shows that it is feasible to increase the modulus of each layer, especially the modulus of the bottom surface layer, to suppress the development of reflection cracks, but the impact of increasing the modulus on other road performance should not be ignored.
Author Contributions
Conceptualization, J.Y., Y.W., H.W. (Haopeng Wang) and H.W. (Houzhi Wang); methodology, J.Y., Y.W., H.W. (Haopeng Wang) and H.W. (Houzhi Wang); validation, Y.W. and H.W. (Houzhi Wang); formal analysis, Y.W. and H.W. (Houzhi Wang); investigation, Y.W. and H.W. (Houzhi Wang); data curation, Y.W. and H.W. (Houzhi Wang).; writing—original draft preparation, Y.W. and H.W. (Houzhi Wang); writing—review and editing, J.Y., Y.W., H.W. (Haopeng Wang) and H.W. (Houzhi Wang); visualization, Y.W. and H.W. (Houzhi Wang); supervision, J.Y. and H.W. (Houzhi Wang); project administration, J.Y. and H.W. (Houzhi Wang); funding acquisition, J.Y. and H.W. (Houzhi Wang). All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (No. 51778140, No. 52078130), Technology Research and Development Program of China State Railway Group Co., Ltd. (P2019G030), Postdoctoral Research Fund Program at Southeast University (1121002107).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Nemati, R.; Haslett, K.; Dave, E.V.; Sias, J.E. Development of a rate-dependent cumulative work and instantaneous power-based asphalt cracking performance index. Road Mater. Pavement Des. 2019, 20, S315–S331. [Google Scholar] [CrossRef]
- Isied, M.M.; Souliman, M. Integrated predictive artificial neural network fatigue endurance limit model for asphalt concrete pavements. Can. J. Civ. Eng. 2019, 46, 114–123. [Google Scholar] [CrossRef]
- Romeo, E.; Montepara, A. Characterization of Reinforced Asphalt Pavement Cracking Behavior using Flexural Analysis. Procedia-Soc. Behav. Sci. 2012, 53, 356–365. [Google Scholar] [CrossRef][Green Version]
- Hu, S.; Basheer, I.; Leidy, J.; Zhou, F. Development of a Universal Cracking Amount Model for Fatigue and Reflective Cracking of Asphalt Pavements. J. Perform. Constr. Facil. 2017, 31, 04017109. [Google Scholar] [CrossRef]
- Ann Myers, L.; Roque, R.; Birgisson, B. Propagation Mechanisms for Surface-Initiated Longitudinal Wheelpath Cracks. Transp. Res. Rec. 2001, 1778, 113–122. [Google Scholar] [CrossRef]
- García, I.G.; Carter, B.J.; Ingraffea, A.R.; Mantič, V. A numerical study of transverse cracking in cross-ply laminates by 3D finite fracture mechanics. Compos. Part B 2016, 95, 475–487. [Google Scholar] [CrossRef]
- Okada, H.; Ishizaka, T.; Takahashi, A.; Arai, K.; Yusa, Y. 3D J-integral evaluation for solids undergoing large elastic–plastic deformations with residual stresses and spatially varying mechanical properties of a material. Eng. Fract. Mech. 2020, 236, 107212. [Google Scholar] [CrossRef]
- Yu, S.-M.; Cai, L.-X. Analytical J-integral model for mode-I cracks in ductile materials with three-dimensional constraints. Eng. Fract. Mech. 2021, 252, 107801. [Google Scholar] [CrossRef]
- Mehdinejad, S.; Fazaeli, H.; Moniri, A.; Dabiri, A.S. Comparison of two criteria of stress intensity factor and fracture energy to investigate the behavior of asphalt mixtures under combined tensile-shear loading modes-A statistical approach. Constr. Build. Mater. 2021, 290, 123230. [Google Scholar] [CrossRef]
- Alae, M.; Ling, M.; Haghshenas, H.F.; Zhao, Y. Three-dimensional finite element analysis of top-down crack propagation in asphalt pavements. Eng. Fract. Mech. 2021, 248, 107736. [Google Scholar] [CrossRef]
- Ma, X.; Quan, W.; Si, C.; Dong, Z.; Dong, Y. Analytical solution for the mechanical responses of transversely isotropic viscoelastic multi-layered asphalt pavement subjected to moving harmonic load. Soil Dyn. Earthq. Eng. 2021, 147, 106822. [Google Scholar] [CrossRef]
- Gdoutos, E.E. Fracture Mechanics: An Introduction; Gewerbestrasse, Springer Nature: Heidelberg, Germany, 2020. [Google Scholar]
- Rice, J.R. A path-independent integral and the approximate analysis of strain concentration by notches and cracks. J. Appl. Mech. 1968, 35, 379–386. [Google Scholar] [CrossRef]
- Melenk, J.M.; Babuska, I. The partition of unity finite element method: Basic theory and applications. Comput. Methods Appl. Mech. Eng. 1996, 139, 289–314. [Google Scholar] [CrossRef]
- Melenk, J.M.; Babuska, I. Approximation With harmonic and generalized harmonic polynomials in the partition of unity method. Comput. Assist. Mech. Eng. Sci. 1997, 4, 607–632. [Google Scholar]
- Deng, Y.; Luo, X.; Gu, F.; Zhang, Y.; Lytton, R.L. 3D simulation of deflection basin of pavements under high-speed moving loads. Constr. Build. Mater. 2019, 226, 868–878. [Google Scholar] [CrossRef]
- Sui, X.; Cao, L.; Ma, X.; Wang, H.; Dong, Z. Research on transversely isotropic permeability of asphalt pavement: Laboratory tests and computational simulation. Constr. Build. Mater. 2020, 251, 118958. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).