An Intelligent Error Correction Algorithm for Elderly Care Robots
Abstract
:1. Introduction
2. Related Work
2.1. Gesture Recognition
2.2. Intelligent Error Correction
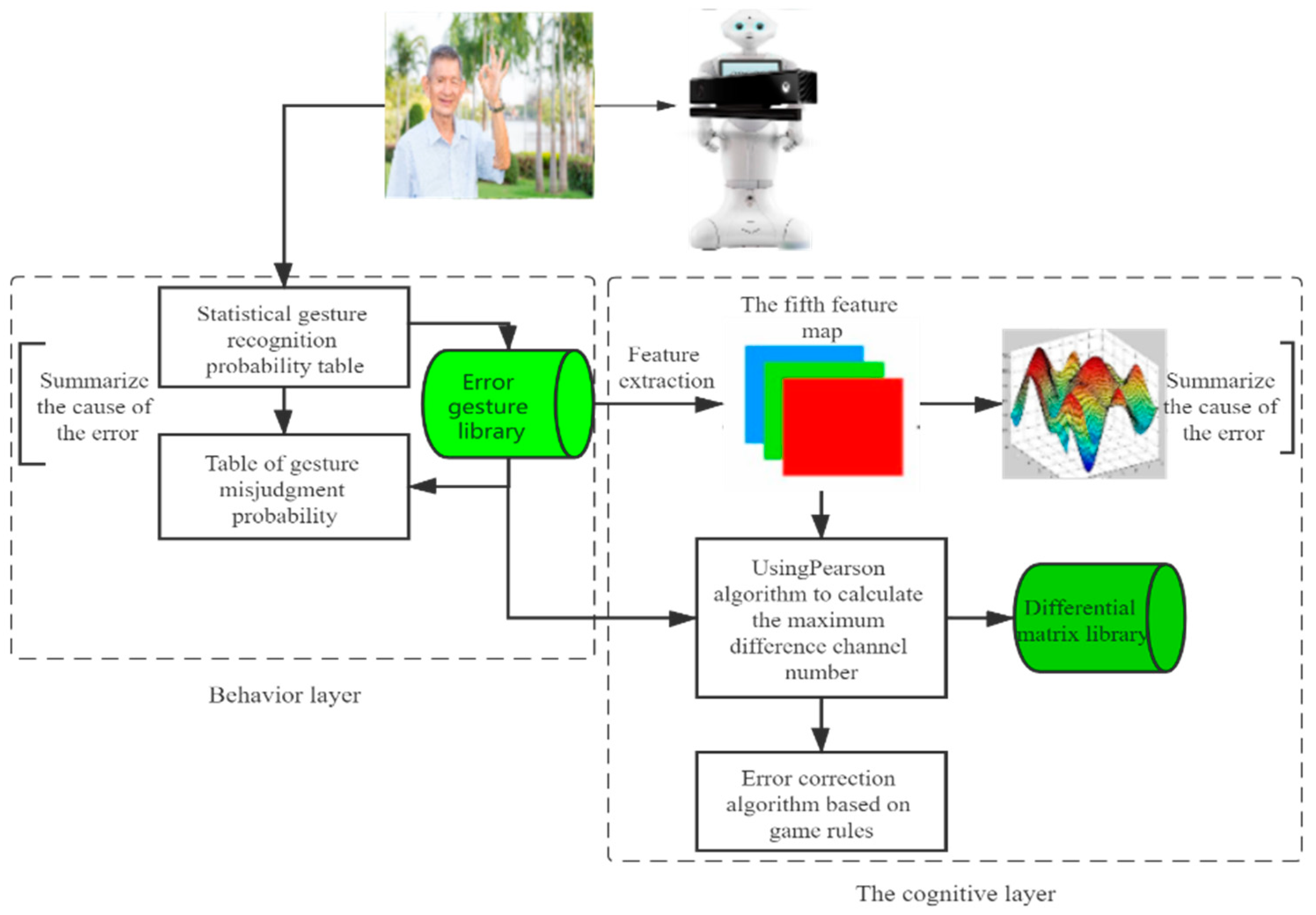
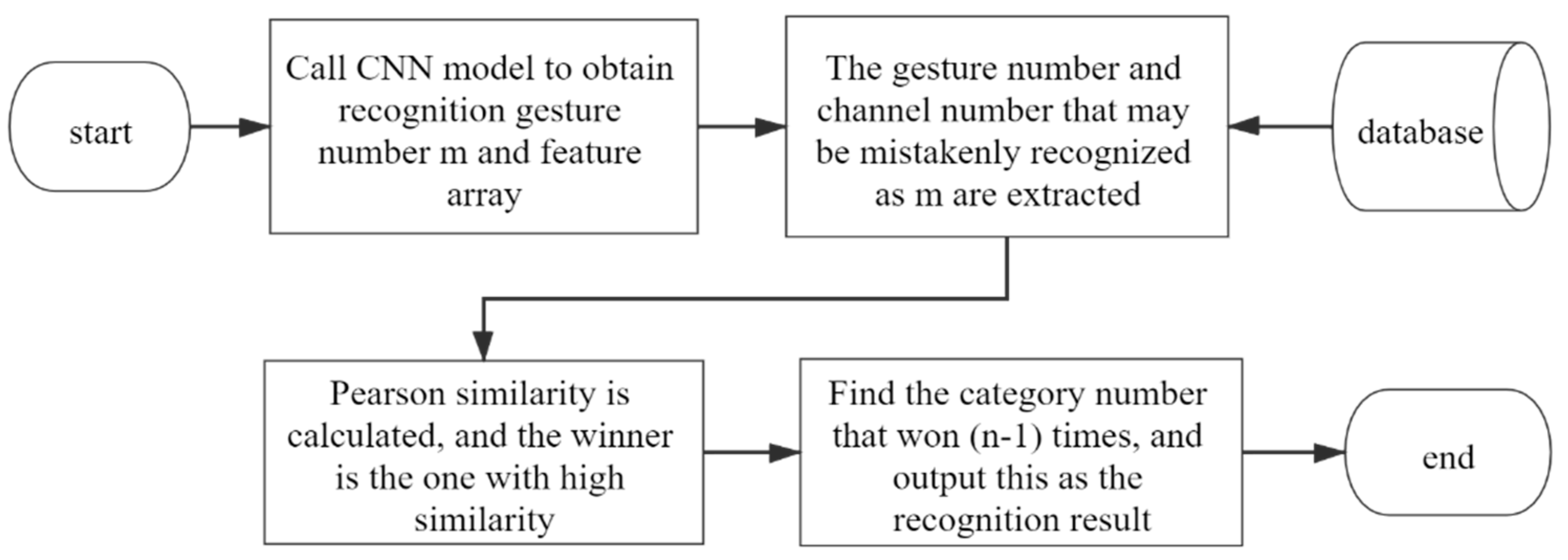
3. Intelligent Error Correction Algorithm
3.1. Reasons for Low Recognition Rate
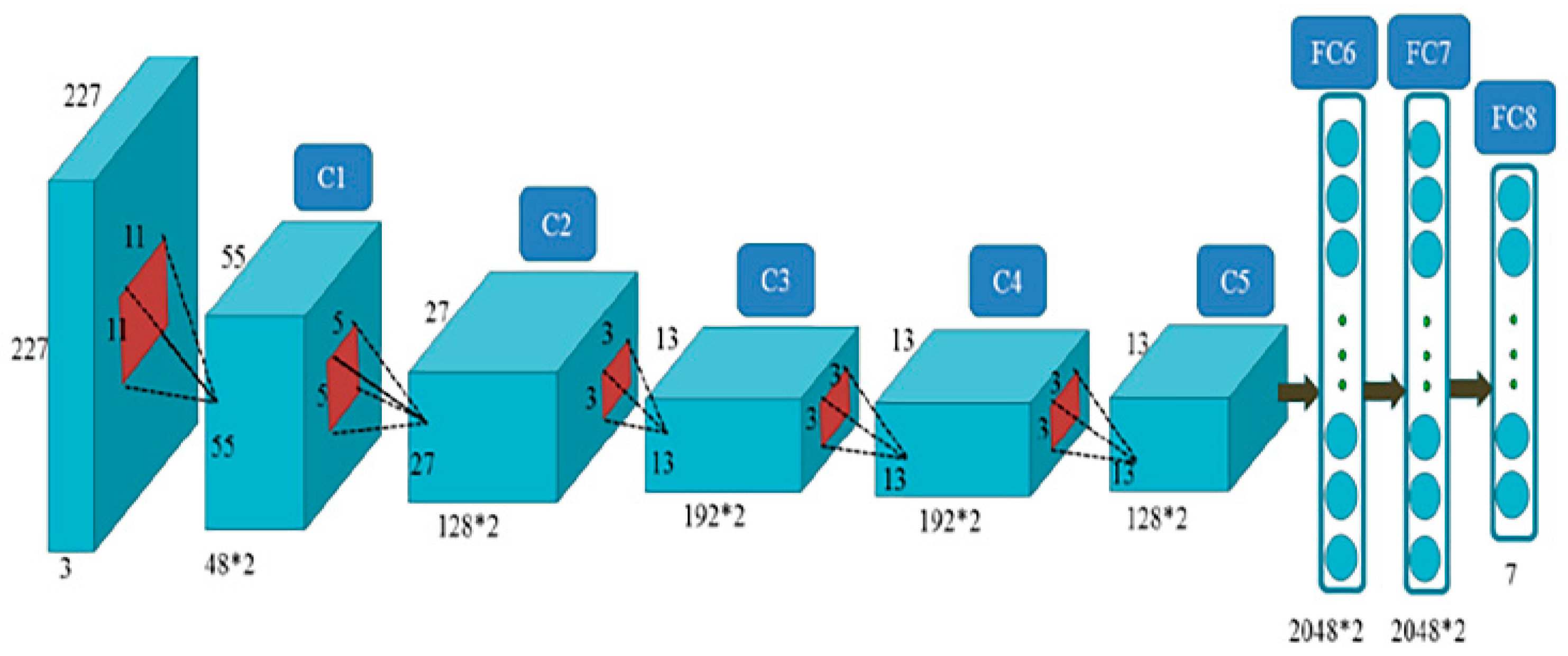
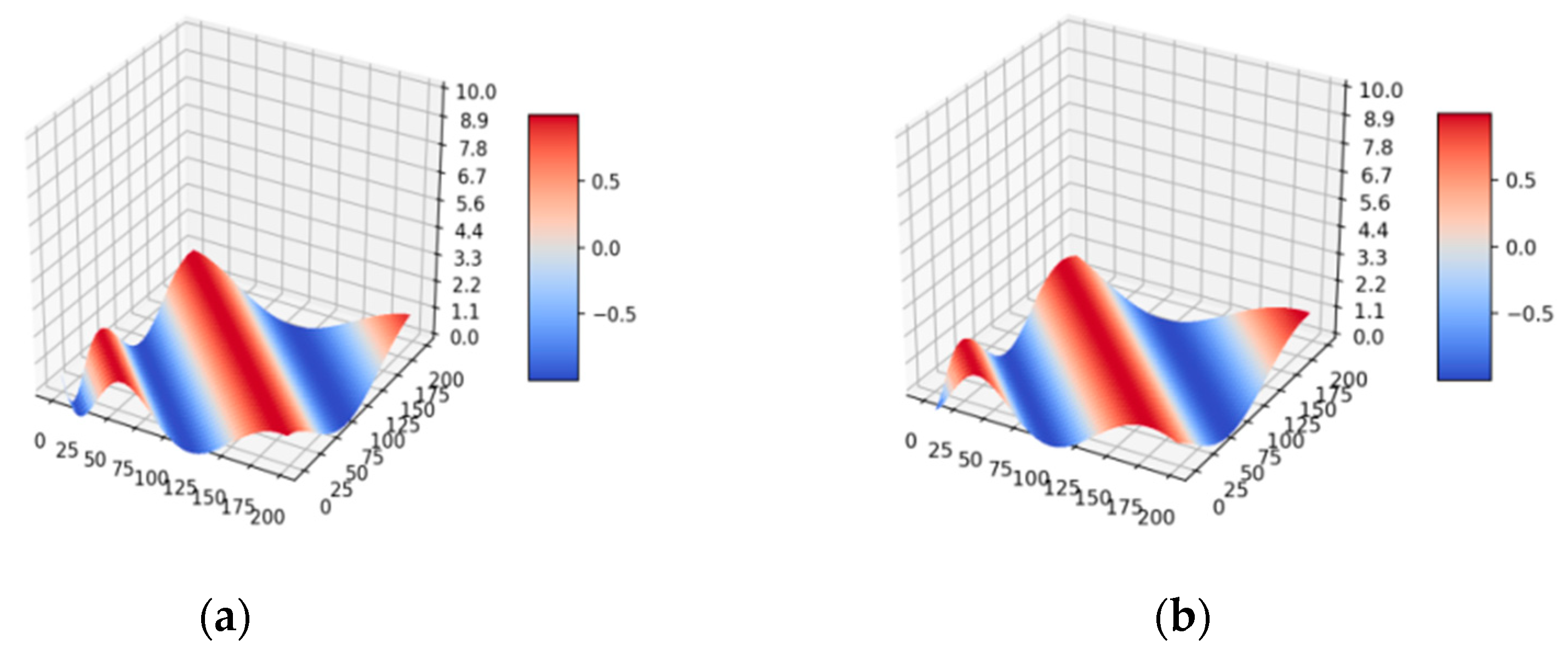
3.2. Error Correction Algorithm Based on Convolution Layer
| Algorithm 1 Error correction algorithm based on game rules | |
| 1: | Input: Gesture recognition number m*; Initialization n = 0. |
| 2: | Output: Correct gesture type number n. |
| 3: | If (Input (?) Output m*) |
| 4: | Search (?) = (m, p, q); |
| 5: | Search Matrix layer number with the largest difference from (m and p) = , (m and q) = , (p and q) = ; |
| 6: | getSimilarity (m*., m.);/* The similarity between layer channel of m* and layer channel of m is calculated. */ |
| 7: | getSimilarity (m*., p.); |
| 8: | If ( > ) M++; else P++;/* M is the number of times m wins, P is the number of times p wins, and if > , m wins. */ |
| 9: | getSimilarity (m*., m.); |
| 10: | getSimilarity (m*., q.); |
| 11: | If ( > ) M++; else Q++; |
| 12: | getSimilarity (m*., m.); |
| 13: | getSimilarity (m*., q.); |
| 14: | If ( > ) P++; else Q++; |
| 15: | For (M, P, Q) is 2/* Find out who won two games, because everyone can play two games at most. */ |
| 16: | If (M == 2) n = m;/* Correct the recognition gesture category to m. */ |
| 17: | If (P == 2) n = p; |
| 18: | If (Q == 2) n = q; |
| 19: | If (n == 0) Reenter gesture command;/* No best match template found. */ |
| 20: | Else output n; |
| 21: | end |
4. Experimental Results and Analysis
4.1. Experimental Environment Setting
4.2. Experimental Methods
- The experimenters should interact with natural gestures as in daily life, and the speed should not be too fast;
- The experimenters only make gestures related to tea drinking service to avoid affecting the experiment time;
- After each gesture instruction, the experimenter should make the second gesture instruction after the robot finishes;
- The experimenters conducted ten tea service experiments based on a behavior-mechanism-error-correction algorithm and tea service experiments based on a robot cognitive-error-correction algorithm.
4.3. Experiment Results
4.3.1. Demonstration of Experimental Results
4.3.2. Algorithm Feasibility Verification
4.4. Contrast Experiment
4.5. User Experience and Cognitive Load
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Qiannan, Z. Research on Gesture Recognition Technology Based on Computer Vision; Dalian University of Technology: Dalian, China, 2020. [Google Scholar]
- Yi, J.; Cheng, J.; Ku, X. Review of visual gesture recognition. Comput. Sci. 2016, 43, 103–108. [Google Scholar]
- Du, Y.; Yang, R.; Chen, Z.; Wang, L.; Weng, X.; Liu, X. A deep learning network-assisted bladder tumour recognition under cystoscopy based on Caffe deep learning framework and EasyDL platform. Int. J. Med Robot. Comput. Assist. Surg. 2020, 17, e2169. [Google Scholar] [CrossRef]
- Wu, H.; Ding, X.; Li, Q.; Du, L.; Zou, F. Classification of women’s trousers silhouette using convolution neural network CaffeNet model. J. Text. Res. 2019, 40, 117–121. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Dutta, A.; Islam, M.M. Detection of Epileptic Seizures from Wavelet Scalogram of EEG Signal Using Transfer Learning with AlexNet Convolutional Neural Network. In Proceedings of the 2020 23rd International Conference on Computer and Information Technology (ICCIT), Dhaka, Bangladesh, 19–21 December 2020. [Google Scholar]
- Gaur, A.; Yadav, D.P.; Pant, G. Morphology-based identification and classification of Pediastrum through AlexNet Convolution Neural Network. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1116, 012197. [Google Scholar] [CrossRef]
- Mitra, S.; Acharya, T. Gesture Recognition: A Survey. IEEE Trans. Syst. Man Cybern. Part C 2007, 37, 311–324. [Google Scholar] [CrossRef]
- Fang, W.; Ding, Y.; Zhang, F.; Sheng, J. Gesture Recognition Based on CNN and DCGAN for Calculation and Text Output. IEEE Access 2019, 7, 28230–28237. [Google Scholar] [CrossRef]
- Grimes, G.J. Digital Data Entry Glove Interface Device. U.S. Patent US4414537, 8 November 1983. [Google Scholar]
- Takahashi, T.; Kishino, F. Hand gesture coding based on experiments using a hand gesture interface device. ACM SIGCHI Bull. 1991, 23, 67–74. [Google Scholar] [CrossRef]
- Lee, J.; Lee, Y.; Lee, E.; Hong, S. Hand region extraction and gesture recognition from video stream with complex background through entropy analysis. In Proceedings of the 26th Annual International Conference of the IEEE, San Francisco, CA, USA, 1–5 September 2004; pp. 1513–1516. [Google Scholar]
- Marouane, H.; Abdelhak, M. Hand Gesture Recognition Using Kinect’s Geometric and HOG Features. In Proceedings of the 2nd international Conference on Big Data, Cloud and Applications, Tetouan, Morocco, 29–30 March 2017; p. 48. [Google Scholar]
- Hu, D.; Wang, C.; Nie, F.; Li, X. Dense Multimodal Fusion for Hierarchically Joint Representation. In Proceedings of the ICASSP 2019-2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019; pp. 3941–3945. [Google Scholar]
- Gao, Q.; Liu, J.; Ju, Z.; Li, Y.; Zhang, T.; Zhang, L. Static Hand Gesture Recognition with Parallel CNNs for Space Human-Robot Interaction International Conference on Intelligent Robotics & Applications; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Tewari, A.; Taetz, B.; Grandidier, F.; Stricker, D. A Probabilistic Combination of CNN and RNN Estimates for Hand Gesture Based Interaction in Car. In Proceedings of the IEEE International Symposium on Mixed & Augmented Reality IEEE International Symposium on Mixed & Augmented Reality IEEE, Nantes, France, 9–13 October 2017. [Google Scholar]
- Wu, Y.; Zheng, B.; Zhao, Y. Dynamic Gesture Recognition Based on LSTM-CNN. In Proceedings of the 2018 Chinese Automation Congress (CAC), Xi’an, China, 30 November–2 December 2018; pp. 2446–2450. [Google Scholar]
- Wang, M.; Yan, Z.; Wang, T.; Cai, P.; Gao, S.; Zeng, Y.; Wan, C.; Wang, H.; Pan, L.; Yu, J.; et al. Gesture recognition using a bioinspired learning architecture that integrates visual data with somatosensory data from stretchable sensors. Nat. Electron. 2020, 3, 563–570. [Google Scholar] [CrossRef]
- Aviles-Arriaga, H.H.; Sucar, L.E.; Mendoza, C.E. Visual Recognition of Similar Gestures. In Proceedings of the International Conference on Pattern Recognition IEEE, Hong Kong, China, 20–24 August 2006. [Google Scholar]
- Elmezain, M.; Al-Hamadi, A.; Michaelis, B. Hand gesture recognition based on combined features extraction. J. World Acad. Sci. Eng. Technol. 2009, 60, 395. [Google Scholar]
- Ding, Z.; Chen, Y.; Chen, Y.L.; Wu, X. Similar hand gesture recognition by automatically extracting distinctive features. Int. J. Control. Autom. Syst. 2017, 15, 1770–1778. [Google Scholar] [CrossRef]
- Sun, K. Research on Error Recognition Gesture Detection and Error Correction Algorithm Based on Convolutional Neural Network; University of Jinan: Jinan, China, 2019. (In Chinese) [Google Scholar]
- Stanceski, S.; Zhang, J. A Simple and Effective Learning Approach to Motion Error Correction of an Industrial Robot. In Proceedings of the 2019 International Conference on Advanced Mechatronic Systems (ICAMechS), Kusatsu, Japan, 26–28 August 2019; pp. 120–125. [Google Scholar]
- Akinola, I.; Wang, Z.; Shi, J.; He, X.; Lapborisuth, P.; Xu, J.; Watkins-Valls, D.; Sajda, P.; Allen, P. Accelerated Robot Learning via Human Brain Signals. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020. [Google Scholar]
- Bested, S.R.; de Grosbois, J.; Crainic, V.A.; Tremblay, L. The influence of robotic guidance on error detection and correction mechanisms. Hum. Mov. Sci. 2019, 66, 124–132. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.K.; Kirchner, E.A.; Stefes, A.; Kirchner, F. Intrinsic interactive reinforcement learning—Using error-related potentials for real world human-robot interaction. Sci. Rep. Nat. 2017, 7, 17562. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Brilliant. Detailed Explanation of Opencv Convolution Principle, Edge Filling Mode and Convolution Operation. Blog Garden. 2020. Available online: https://www.cnblogs.com/wojianxin/p/12597328.html (accessed on 30 March 2020).
- Abidi, A.; Nouira, I.; Assali, I.; Saafi, M.A.; Bedoui, M.H. Hybrid Multi-Channel EEG Filtering Method for Ocular and Muscular Artifact Removal Based on the 3D Spline Interpolation Technique. Comput. J. 2021, bxaa175. [Google Scholar] [CrossRef]
- Benesty, J.; Chen, J.; Huang, Y.; Cohen, I. Pearson Correlation Coefficient. Noise Reduction in Speech Processing; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–4. [Google Scholar]
- Kraft, D. Computing the Hausdorff Distance of Two Sets from Their Distance Functions. Int. J. Comput. Geom. Appl. 2020, 30, 19–49. [Google Scholar] [CrossRef]
- Biran, A.; Jeremic, A. Segmented ECG Bio Identification using Fréchet Mean Distance and Feature Matrices of Fiducial QRS Features. In Proceedings of the 14th International Conference on Bio-inspired Systems and Signal Processing, Vienna, Austria, 11–13 February 2021. [Google Scholar]



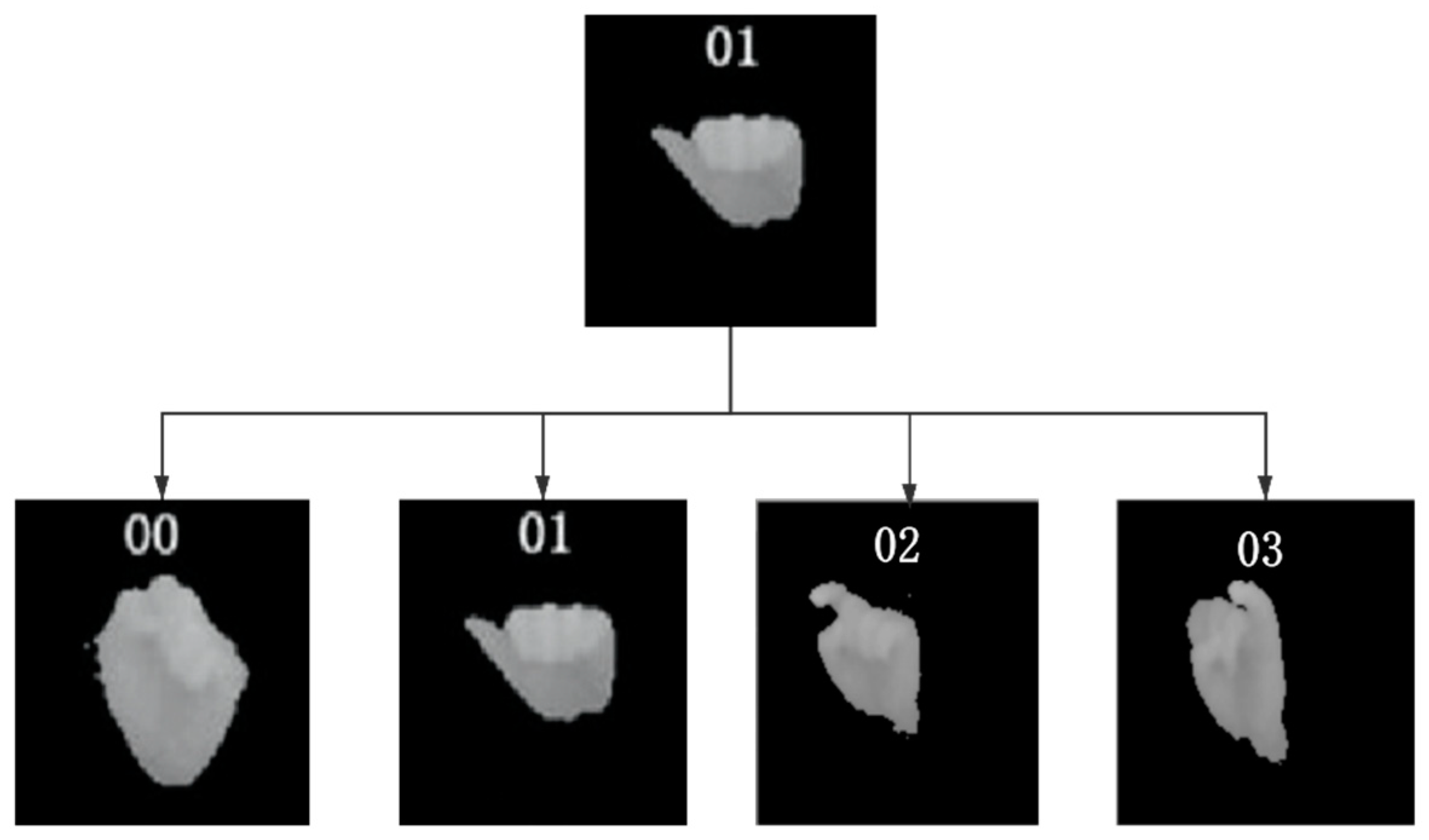





| Gestural Characteristics of the Elderly | Gesture Characteristics of Young People |
|---|---|
| 1: Fingers bend naturally | 1: Fingers are naturally straight |
| 2: Constant shaking of the palm | 2: The palm of a hand is steady |
| 3: Fingers have no power | 3: Fingers have high power |
| Signal Types (Number) | Fist (00) | Thumbs Out (01) | Index Finger Out (02) | Little Finger Out (03) | Five Fingers Merge (04) | Five Fingers Spread (05) | “Ok” Gesture (06) |
|---|---|---|---|---|---|---|---|
| Elderly (%) | 98.1 | 76.4 | 82.4 | 75.4 | 97.2 | 72.7 | 98.1 |
| Young (%) | 98.4 | 90.3 | 91.2 | 96.7 | 97.3 | 96.7 | 98.9 |
| Actual Number | ||||||
|---|---|---|---|---|---|---|
| Predicted Number | 00 | 01 | 02 | 03 | 04 | 05 |
| 00 | 0.805 | 0.103 | 0.008 | 0.084 | 0 | 0 |
| 01 | 0.016 | 0.765 | 0.105 | 0.114 | 0 | 0 |
| 02 | 0.001 | 0.108 | 0.888 | 0.003 | 0 | 0 |
| 03 | 0.002 | 0.012 | 0.074 | 0.872 | 0 | 0 |
| 04 | 0 | 0 | 0 | 0 | 0.781 | 0.219 |
| 05 | 0 | 0 | 0 | 0 | 0.037 | 0.962 |
| Some Important Gesture Instructions in Tea Service Experiment | |
|---|---|
| Experimenter: | Make gesture 01 (left turn command). |
| Pepper: | The robot turns left 90° without obstacles on the left. |
| Experimenter: | Make gesture 03 (right turn command) |
| Pepper: | The robot turns 90° to the right without obstacles on the right side. |
| Experimenter: | Make gesture 05 (forward command). |
| Pepper: | If there is an obstacle ahead, the robot will stop automatically to ensure absolute safety. |
| Experimenter: | Make gesture 06 (take the cup command). |
| Pepper: | The robot determines that the cup is in front of the robot through target detection, and then performs the grab operation. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Feng, Z.; Yang, X.; Xu, T.; Qiu, X.; Hou, Y. An Intelligent Error Correction Algorithm for Elderly Care Robots. Appl. Sci. 2021, 11, 7316. https://doi.org/10.3390/app11167316
Zhang X, Feng Z, Yang X, Xu T, Qiu X, Hou Y. An Intelligent Error Correction Algorithm for Elderly Care Robots. Applied Sciences. 2021; 11(16):7316. https://doi.org/10.3390/app11167316
Chicago/Turabian StyleZhang, Xin, Zhiquan Feng, Xiaohui Yang, Tao Xu, Xiaoyu Qiu, and Ya Hou. 2021. "An Intelligent Error Correction Algorithm for Elderly Care Robots" Applied Sciences 11, no. 16: 7316. https://doi.org/10.3390/app11167316
APA StyleZhang, X., Feng, Z., Yang, X., Xu, T., Qiu, X., & Hou, Y. (2021). An Intelligent Error Correction Algorithm for Elderly Care Robots. Applied Sciences, 11(16), 7316. https://doi.org/10.3390/app11167316







