1. Introduction
In the past few decades, enormous development in the field of robotics has resulted in replacing human tasks with robots. Similar advancement of technologies has also been observed in the development of delivery robots, such as packaging robots, autonomous driving robots, etc. One of the major aspects of today’s delivery system comprises door-to-door delivery. In order to achieve complete autonomy in such delivery systems, a robot must be capable of climbing the stairs (up and down) of a building.
Extensive research has been undertaken by many researchers to develop robots with climbing capabilities. These robots are broadly categorized into three groups: tracked, articulated leg and hybrid system. In a track based stair climbing system [
1], track belts are used to drive the robot. Lawn et al. proposed to replace single track belt system with a set of two track-belt system to improve the stability of a step climbing wheelchair [
2]. Research was conducted to develop a novel variable geometry tracked mechanism [
3]. Such systems are highly controllable and can successfully maneuver on rough terrains and stairs. However, these systems are slower as compared to the wheel based systems. On the other hand, systems based on articulate legs [
4] are highly effective in climbing stairs, although they are quite complex to control. Hence, many researchers tend to work towards the development of hybrid systems, which can be further classified into two categories: wheels with track [
5] and wheels with articulated legs [
6]. A hybrid shrimp mechanism consisting a front fork, a body and a parallel bogies was developed to maneuver in an unstructured environment for rescue operations [
7]. Woo et al. proposed a step climbing robot based on passive four bar linkage type locomotive motion [
8]. In an another hybrid mechanism, the use of two legs with seven degrees of freedom is discussed [
9]. In an interesting research study, a eight legged (four pair) hybrid step climbing robot was proposed. The step climbing is achieved by controlling the height of each pair of the legs [
10]. Zuniga et al. illustrated a novel step climbing robot consisting a pair of rotating links at the front and back of the robot [
11]. A hybrid leg-wheel robot termed as the Mantis robot was developed and the front links were used as clamps and pulled the main body of robot to overcome any obstacle [
12]. A novel step climbing robot consisting two pairs of half circled legs is proposed by Qiao et al. [
13]. In yet another case, a separate attachable stair climbing module has been developed, which can be attached or detached based on the requirement [
14]. The attached module consists of linear actuators that pushes the robot in an upward direction. Although this system is lightweight, it requires human assistance.
In [
15], powered linkage-based mechanisms along with clustered wheels for the purpose of achieving high step climbing capabilities have been proposed. While powered links help in pushing the robot, clustered wheels take care of obstacle avoidance. In another research study, a swing arm based linkage mechanism was proposed [
16]. Another interesting group of hybrid systems are available in the open literature [
17,
18,
19,
20,
21,
22], presented by Morales et al. The authors explain the usage of sliders to overcome obstacles. Clamps are fixed on a subsequent step and then sliders are used to lift the robot. This mechanism is stable and it keeps the robot vertical during ascending or descending motions. Furthermore, advanced robots have also been developed which are not only able to climb the stairs but are also capable of balancing on two wheels. Ghani et al. [
23] also proposed the use of two wheel clusters. In [
24] Shino et al. proposed to use sliding chair along with two wheel cluster. Research was conducted to develop stair climbing robots by using rotating multi-limb structure [
25]. Moreover, a mechanism based on four bar parallel links was developed [
26]. Furthermore, researchers have also worked on cluster based stair climbing robots in which a single wheel is replaced by a cluster of three wheels. These wheel clusters are connected to the body of the robot at the centroid of a triangle formed by those wheels. Through a series of articles, Quaglia et al. illustrated a step climbing robot which comprised two pairs of clustered wheels [
27,
28,
29]. In order to improve the mobility of the robot, a modular approach was implemented [
30,
31]. In order to improve stability of the climbing robot, the front pair of wheel cluster was replaced by a track-belt assembly [
32,
33,
34]. As we may notice, many stair climbing robots are developed and can climb up or down the stairs; however, these systems have their own shortcomings. Robots with track-belts are efficient in climbing the stairs but are relatively slower in planes in comparison to wheel-based systems. In cluster-based and hybrid robots, the inclination angle varies drastically, limiting the robot to carry objects possessing a low center of gravity. Maintaining the inclination angle of the robot parallel to the ground is important while carrying a liquid or semi-liquid product. Hence, in this article, a novel robot is proposed, wherein two motors are attached to the front wheels of the robot and another one to the rear wheel along with an actuator, which is responsible for controlling the variation in the inclination angle of the robot. While climbing up the stairs, maintaining a proper inclination angle results in establishing a better grip between the wheels and the edge of the stairs. This reduces the risk of slippage. On the other hand, maintaining a proper inclination angle during descending reduces the probability of toppling, resulting in the improved stability of the robot. The fundamental question that we wanted to address in this study is whether the performance of the system (stair climbing robot) improves in terms of stability and dynamic equilibrium by adding a minimalistic linkage mechanism. A qualitative comparison of existing step climbing mechanisms is presented in the
Table 1. Initial work towards the development of the proposed mechanism is available in the open literature [
35]. In [
36], the mathematical formulation and preliminary experiment results of the proposed mechanism were discussed. In the subsequent sections, details of the proposed mechanism, simulation and experimental results are explained.
This paper is organized in the following manner:
Section 2 explains the working principle;
Section 3 defines the design parameters and modeling of the robot. In
Section 4, the analysis of the effects of various parameters of a climbing robot is studied; in
Section 5, development of a prototype and the results of experiments on the prototype are discussed. In
Section 6, the importance of controlling the inclination angle of a robot while climbing a stair is explained.
Section 7 concludes the article.
2. Working Principle
This section explains the proposed mechanism of the stair-climbing robot.
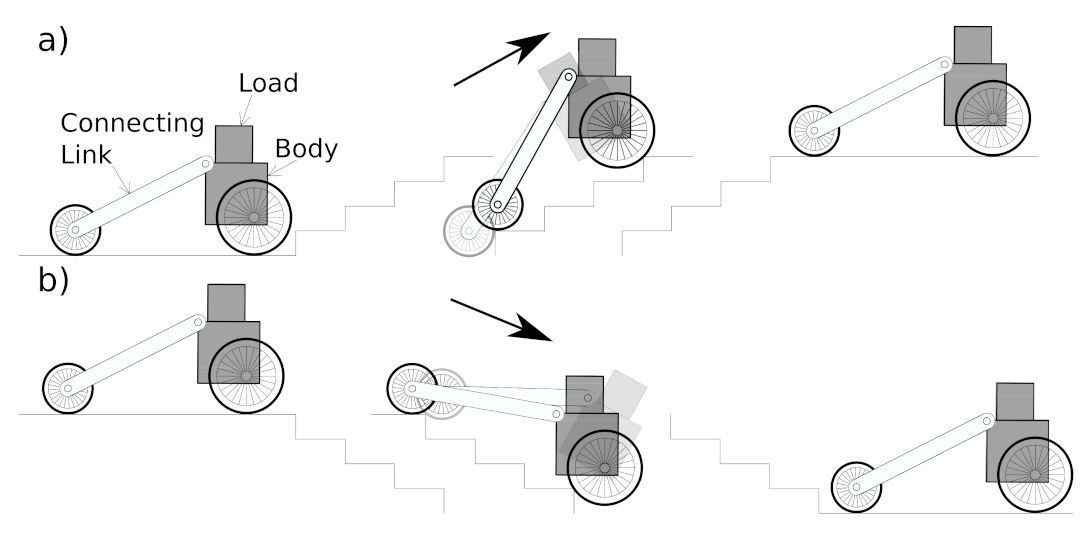
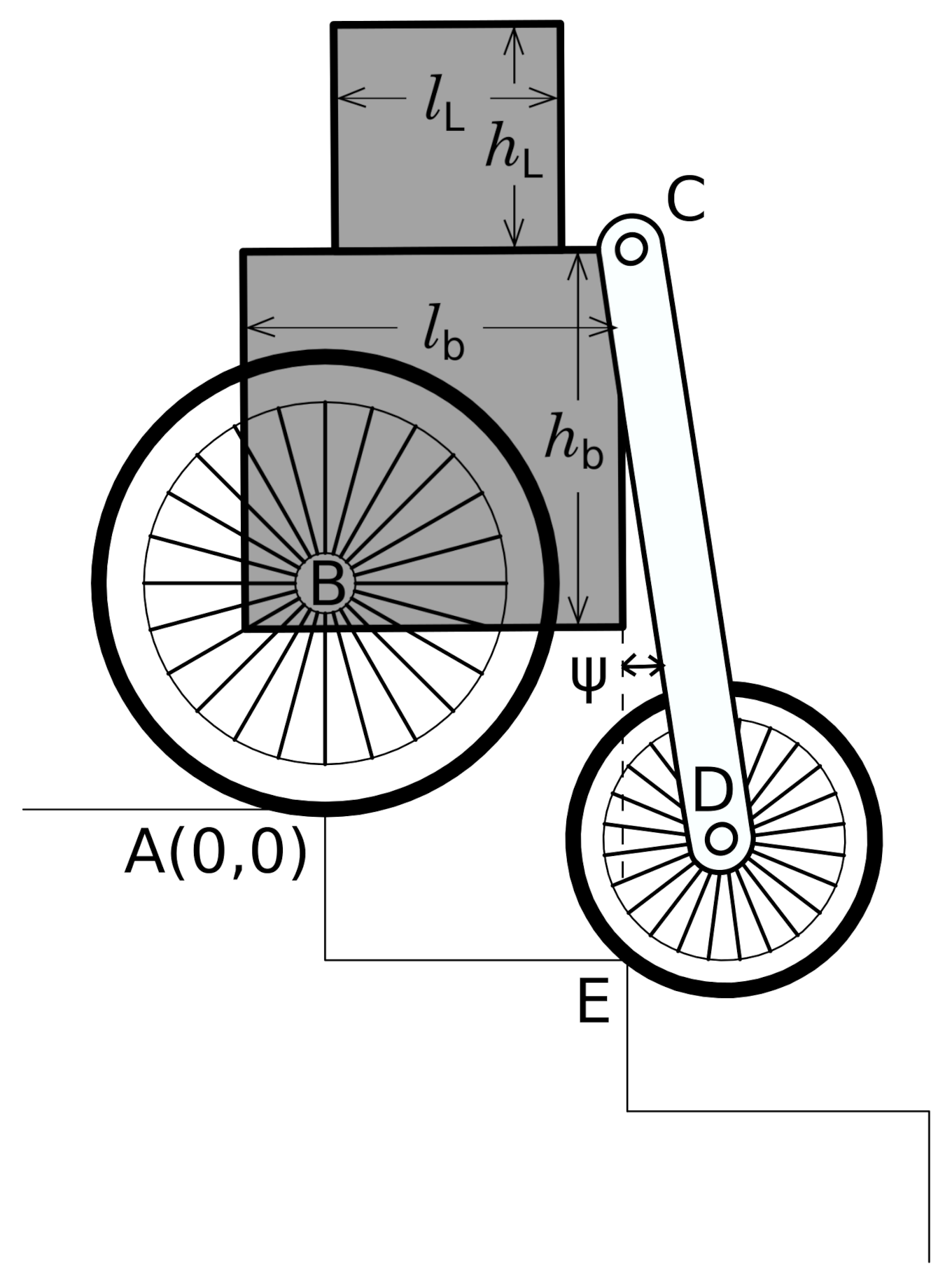
Figure 1a shows a schematic of a series of actions taken by the robot while ascending the stairs, whereas
Figure 1b describes the descending process of the robot of the stairs. The proposed robot has two large front wheels and one small rear wheel. The rear wheel is connected to the body of the robot by a connecting link and a revolute joint. The angle between the connecting link and the body is varied to maintain the inclination angle of the body while ascending or descending the stairs.
In
Figure 1a, the left image represents the condition when both rear and front wheels are on the ground, while the middle figure refers to the situation when the front wheels and rear wheels are on the step. The light shaded image of the robot represents the position of the robot in which the angle between the body and the connecting link is kept constant during the entire climbing operation. The right image on the figure shows the position of the robot after completion of the climbing operation. Similarly,
Figure 1b illustrates changes in the posture of the robot while descending the steps.
It may be noted, if the angle between the connecting link and the body of the robot remains constant, the inclination of the body with respect to the horizontal will vary as the robot progresses on the steps. During the ascent and descent, the inclination angle of the body will tend to increase and decrease, respectively. During the descent, depending on the configuration of the robot and steps, the inclination angle may reduce to a negative value which may cause the robot to topple. This situation can be avoided by controlling the angle between the connecting link and the body of the robot.
In order to compensate for the change in the inclination of the robot, an additional servo motor is used at the joint between the body and the connecting link while climbing on the steps. This servo motor is actuated by a microcontroller whenever a change in the inclination angle of the body is detected. An IMU is used to track any change in angle during the motion of the robot. These signals are fed to a microcontroller, which in turn controls the actuator. As a result, the inclination angle of the robot is properly maintained. In the following section, the design and modeling of the robot are discussed.
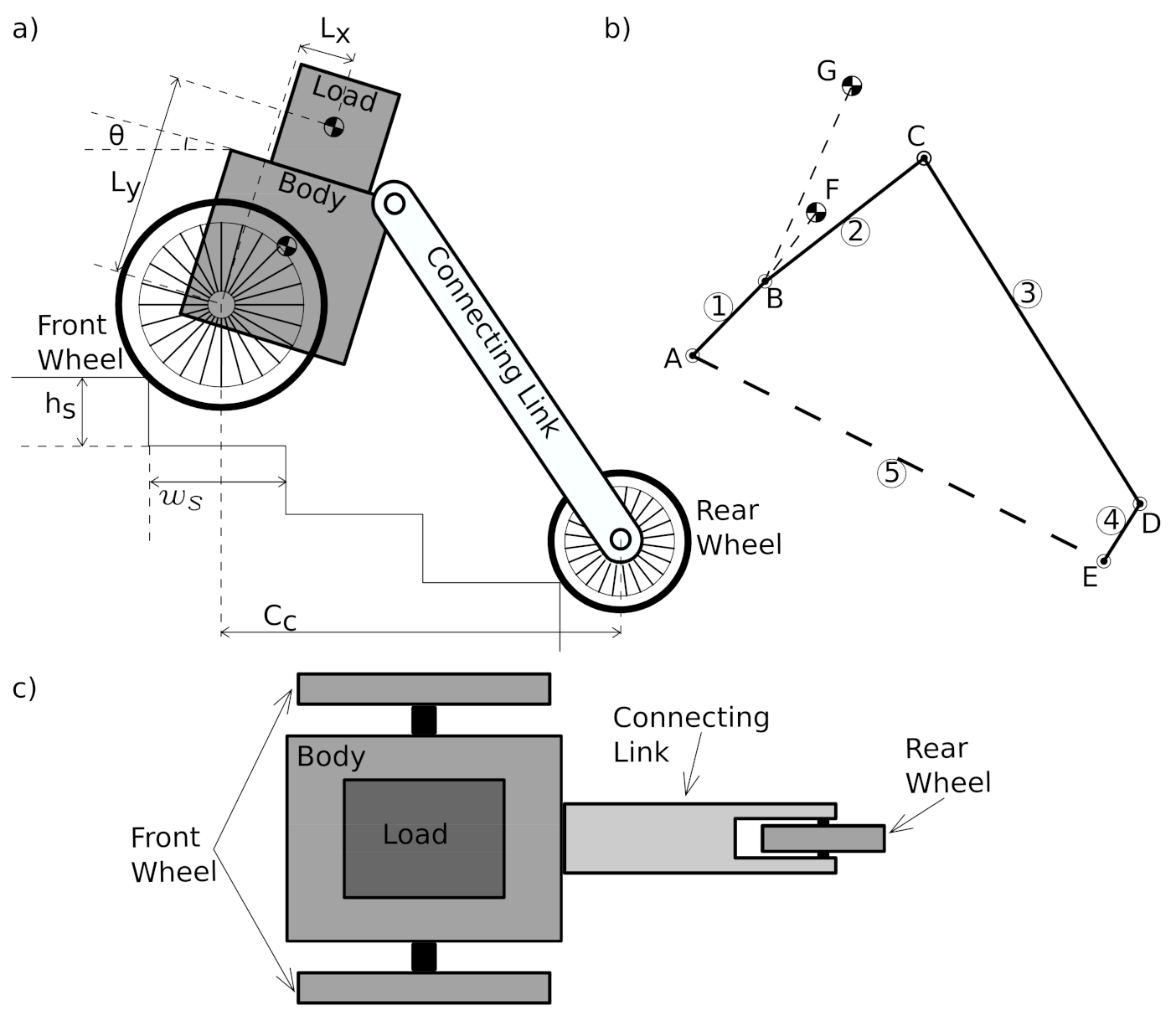
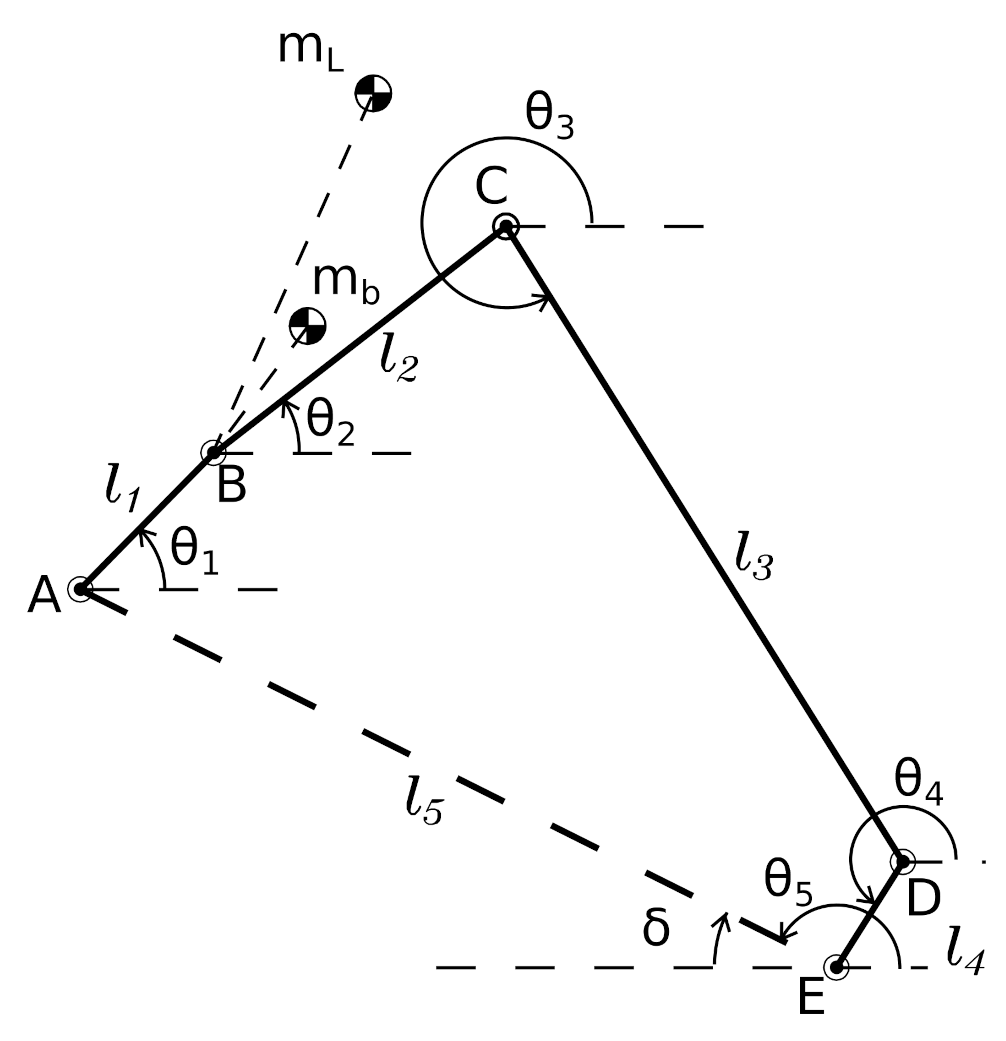
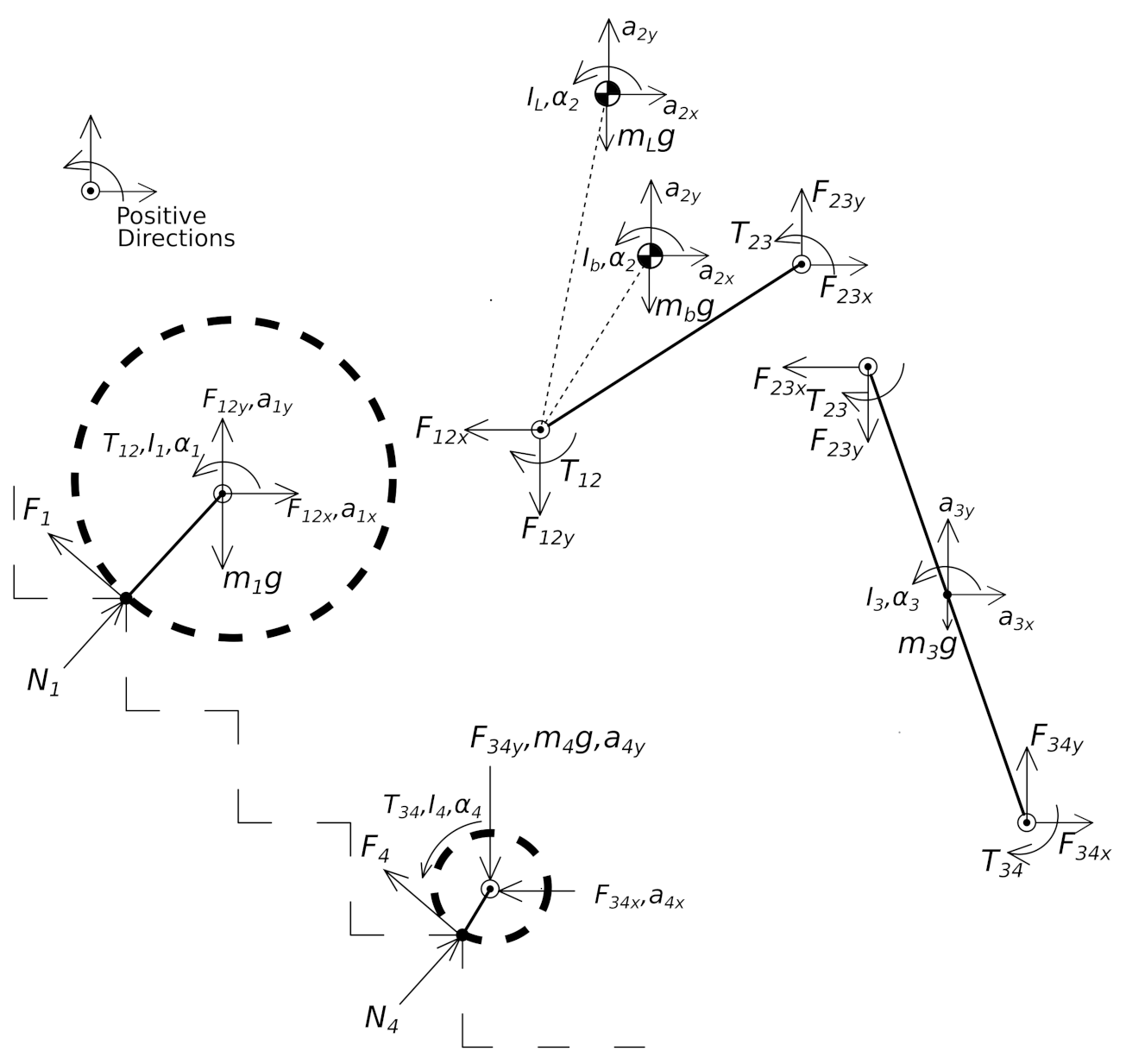
4. Design Analysis
In
Section 3, the equations for describing the mathematical model of the proposed robot are discussed. The contribution of various parameters of the robot must be studied for successful operation of the robot on the stairs. In this section, the contribution of the parameters of a robot on the stairs is illustrated. The dimensions of the robot and the stairs are shown in
Table 2. For the analysis, one of the parameters is varied while keeping the other parameters unchanged.
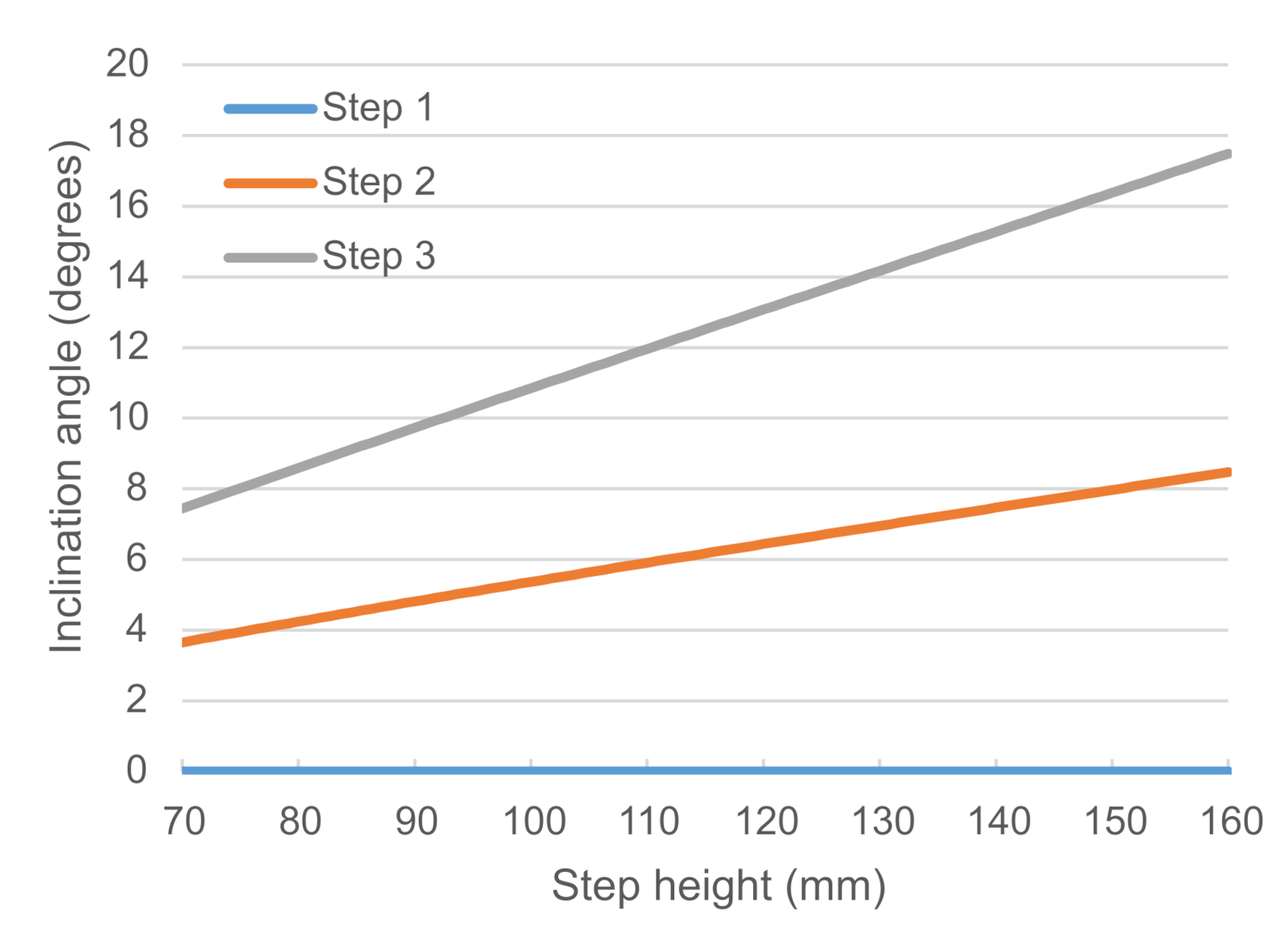
When the robot climb stairs, the inclination angle of the robot changes significantly. With little consideration, it may be observed that the change in inclination angle depends on various parameters of the robot and the stair. One of the parameters that influence the variation in the inclination angle is the height of the step of a stair.
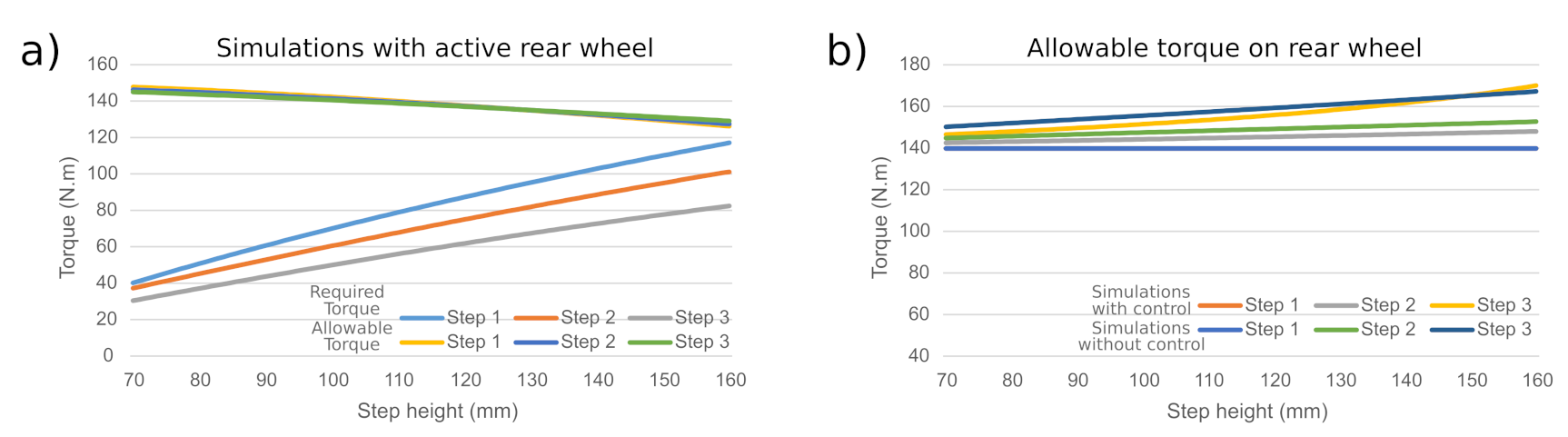
Figure 9 illustrates the change in inclination angle of the robot at three initial steps of the stairs when the height of the step is varied from 70 mm to 160 mm. The three plots, step 1, step 2 and step 3, represent the variation of inclination angle when the front wheel is at the first, second and third steps of the stair and the height of the step is varied from 70 mm to 160 mm, respectively. It may be noticed that, in step 1, although the contact point of the step edge with the front will raise with an increase in step height, the robot inclination angle remains unaffected. It is observed that with the increase in step number, the slope of the plot, which represents the change in inclination angle of the robot, also increases.
In
Figure 9, as the height of a step increases, the torque required by the front wheels to overcome the step will also increase. Although higher torque required by the front wheels may be achieved by selecting higher torque motors, the maximum allowable torque on the front wheel is directly proportional to the product of the coefficient of static friction and the normal reaction of the wheel at the contact point between the edge and the wheel (Equation (
12)). If the torque on the front wheels exceeds the maximum permissible limit, the front wheel will slip on the edge of the step, resulting in failure in climbing the stairs. The variations in the required torque and maximum allowable torque with respect to the change in step height at three initial steps are shown in
Figure 10. In
Figure 10a, the effect of step height on the torques of the front wheels is shown when the simulations are performed while controlling the inclination angle of the robot in climbing up the stairs, whereas
Figure 10b illustrates the simulations without controlling the inclination angle. It may be observed that in both the controlled and uncontrolled simulations, the required torque increases along with the height of the steps, whereas the maximum allowable torque decreases. However, in the controlled case, the torque required to overcome the step is lower than the maximum allowable torque, whereas the required torque is higher than the maximum allowable torque in the uncontrolled case. This will result in slippage of the front wheel during uncontrolled operations.
In
Figure 10, the uncontrolled simulations are performed with passive rear wheels, whereas controlled simulations are performed with active rear wheels. It may be noticed that during uncontrolled simulations, the maximum allowable torque on the front wheels is less than the required torque, resulting in the slippage of front wheels. In
Figure 11, the behavior of the climbing robot during uncontrolled and controlled simulations with active rear wheels is studied. The statistical analyses of variation in the difference of required and allowable torque in the front wheels during controlled and uncontrolled conditions with respect to change in height of step are shown in
Table 3. It may be observed that the mean values of required torque on step 1, 2 and 3 are 64.66 Nm, 63.68 Nm and 69.21 Nm, respectively. This implies that, during uncontrolled conditions, more torque is required to overcome a step as compared to the controlled condition. The standard deviation value for each step suggests that the required torque in the uncontrolled condition is always higher than the controlled condition, when simulations are performed with respect to the varying height of the stair. Similarly, negative mean values of allowable torque imply that the allowable torque in an uncontrolled condition is smaller as compared to the controlled condition. Moreover, standard deviation values show that the allowable torque always remain higher in the controlled condition. This reduces the probability of slipping during controlled conditions as compared to the uncontrolled condition.
Figure 11a illustrates the variation in allowable and required torque at three initial steps on the front wheels with a change in step height. By comparing the results of an uncontrolled simulation with the active rear wheel (as shown in
Figure 11a) and the controlled simulations with the active rear wheel (as shown in
Figure 10a), it may be observed that as the step number increases, the required torque to overcome the step in uncontrolled simulations become lesser than compared to the controlled conditions. In
Table 4, the mean values and standard deviation values of variation in difference of required and allowable torque in the front wheels during controlled and uncontrolled conditions with active rear wheel and with respect to change in height of step are shown. It may be observed that the mean values of difference in the required torque between uncontrolled and controlled condition are negative and the difference becomes smaller with the increase in step number. By Analyzing the mean values with standard deviation values implies that although the required torque in uncontrolled condition is smaller than the controlled condition at lower steps, as the step number increases, the required torque in the front wheels becomes smaller in the controlled condition as compared to the uncontrolled condition. This phenomenon is observed as the inclination angle of the robot increases with the step number. By analyzing the mean and standard deviation values of allowable torque, it may be observed that as the step number increases, the allowable torque in the controlled condition increases and deviates less than compared to lower step number. In order to understand this behavior, the variations in maximum allowable torque on the rear wheel in both controlled and uncontrolled conditions are plotted and shown in
Figure 11b. It may be observed that except for the condition where the front wheels are on the third step and the step height is over 150 mm (approximately), the maximum allowable torque on the rear wheel in the uncontrolled condition is greater than the controlled condition. The torque on the rear wheel pushes the robot, which in turn accounts for the decrease in torque requirement on the front wheels. Hence, the higher the rear wheel torque, the lower the torque will be that is required by the front wheels for climbing over an obstacle.
Table 5 shows the mean and standard deviation values of difference in allowable torque during the uncontrolled and controlled condition in the rear wheel with an increase in step number and change in height of the step. The decreasing value of mean and increasing value of standard deviation with higher step number implies that with the increase in the step number and the height of the step, the allowable torque in the controlled condition becomes higher than that of uncontrolled condition.
The simulation conditions for the results plotted in the
Figure 10 and
Figure 11 corresponds to a situation where the front wheel is considered on a step whereas the rear wheel in on a plane surface. Moreover, the height of the carried load is kept constant in the simulations. For a climbing robot, one of the most challenging conditions is when both the front and rear wheels overcome the steps simultaneously. In
Figure 12, the effect of the height of the center of gravity of load is illustrated when both the front and rear wheels are at the edge of the steps. The height of the center of gravity of the load is varied from 50 mm to 1300 mm. The simulations for the cases wherein the inclination angle is actively controlled are performed for step 2 and step 3, only as the simulations at step 4, to maintain the inclination angle of the robot; the rear wheel has already climbed over the step 1.
Figure 12a,b illustrates the variation in torque requirement in the front and rear wheels, respectively. It may be observed in
Figure 12a that the required torque to overcome the step decreases in the case of controlled simulations as the front wheels are placed on higher steps. This phenomenon occurs because the connecting link is rotated to maintain the inclination angle, which in turn reduces the horizontal center distance of the front and rear wheels. As the center distance decreases, the center of the load proceeds closer to the rear wheel and a higher percentage of vertical load is shared by the rear wheels as compared to the front wheels. Moreover, the required torque on front wheels remains constant even with the increase in the height of the center of gravity (of the load). However, in the case of uncontrolled conditions, the variations in the required torque (required by the front wheels to overcome a step with respect to the changing heights of the center of gravity of the load) possess a negative slope. Moreover, the slope decreases with every higher step number. Eventually, the torque reduces to a negative value at the fourth step, while the height of the center of gravity (of the load) is close to 1300 mm. The negative value of the torque signifies that the normal reaction on the front wheels has decreased to a negative value and the robot will topple due to the moment produced by the load. As the normal reaction on the front wheel during uncontrolled stimulation decreases, the normal reaction on the rear wheel will increase, which is shown in
Figure 12b. The statistical analyses of variation in the difference of required and allowable torque in the front wheels during controlled and uncontrolled conditions with respect to the height of the center of gravity of load are shown in
Table 6. The negative mean value for the difference in required torque implies that the required torque in the uncontrolled condition is less than controlled condition and the difference increases with an increase in step number as well as the height of the center of gravity of the load. The reason for this phenomenon is, as the step number increases in the uncontrolled condition, the inclination angle also increases, which results in a higher percentage of load shared by the rear wheel than compared to the front wheels. Hence, the difference between the required torque on the rear wheel increases with an increase in step number. This shows that the required torque in the rear wheels during the uncontrolled condition is higher than the controlled condition.
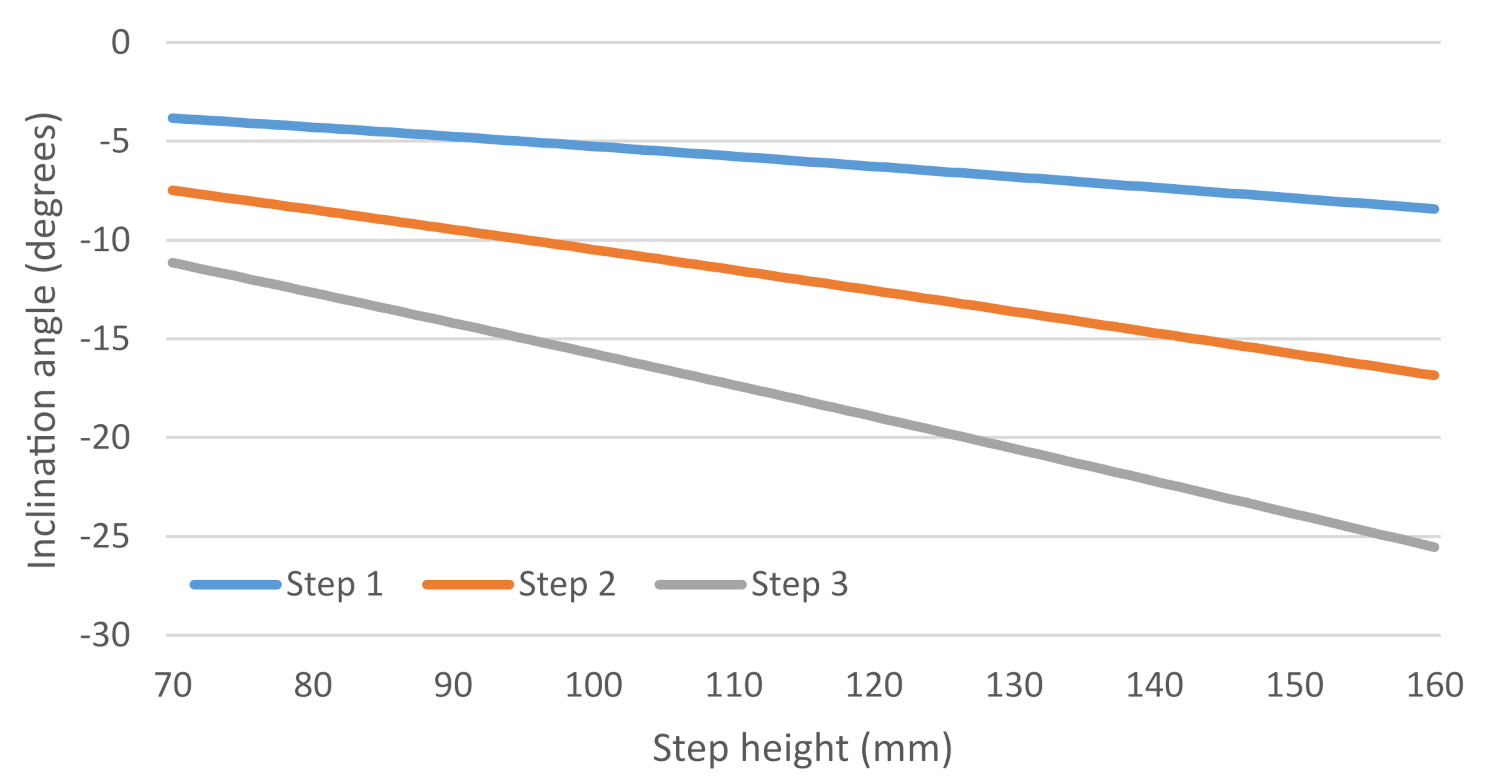
While the robot is climbing up the stairs, gravity acts against its motion which makes the ascending motion on the stairs difficult in comparison to the descending. However, while the robot is climbing down a stair, its inclination angle is an important parameter since, beyond a certain inclination angle, the robot may topple. In
Figure 13, the variation of the inclination angle (of the robot) with respect to the change in height of the steps at three initial steps (from the top) is plotted. The first step on the stair (after the top platform) is referred as textbf step 1, whereas textbf step 2 and textbf step 3 are the subsequent steps. It may be observed that as the height of the step increases, the inclination of the robot decreases. The slope of the plot showing variation in the inclination decreases with an increase in step number.
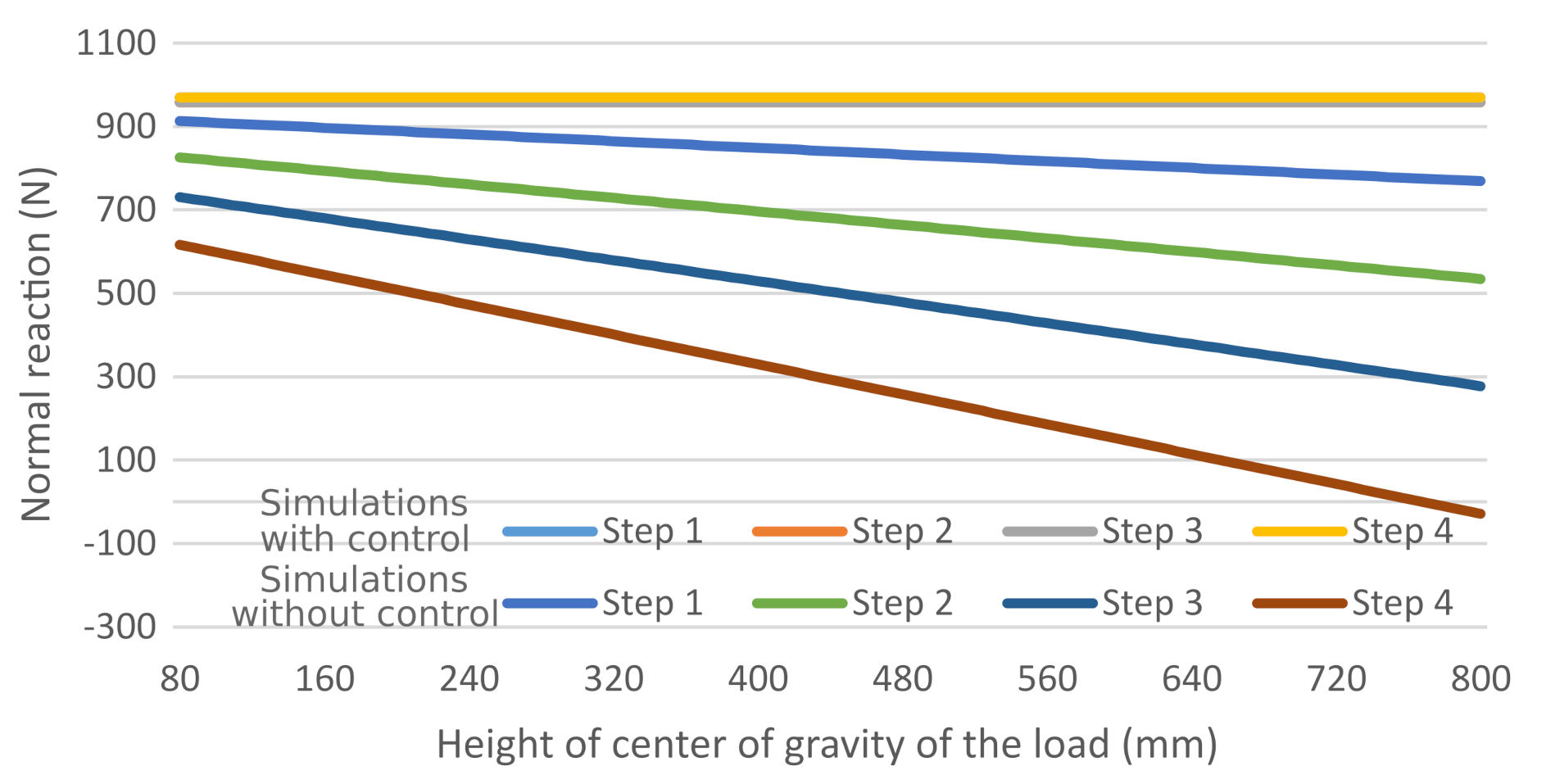
One of the important parameters for the successful descent of the robot is the height of the center of gravity of the load. In order to analyze the effect of height of the center of gravity of the load, the variation in the normal reaction on the rear wheel of the robot is illustrated in
Figure 14. It may be observed that, during the controlled simulation, the inclination angle of the robot remains unchanged and the variations in normal reaction have a constant slope. However, in an uncontrolled simulation, the inclination angle of the robot varies drastically with an increase in the center of gravity (of the load) due to the normal reaction on the rear wheel decreasing as well. This phenomenon is observed as the moment generated by the load increases with the decrease in inclination angle. It may be obesrved that during the uncontrolled simulation at step 4, if the height of the center of gravity (of the load) is more than 771 mm (approximately), the normal reaction on the rear wheels is reduced to a negative value. This will result in the toppling of the robot.
Table 7 shows the mean and standard deviation values of the difference in normal reaction in the rear wheel with an increase in step number and change in the height of the center of gravity. The increase in negative mean value imply that the normal reaction on the rear wheel during the uncontrolled condition becomes smaller than compared to the controlled condition as the step number increases. The standard deviation values imply that, in all the cases with increased height of the center of gravity, the normal reaction on the rear wheel is smaller in the uncontrolled condition than compared to the controlled condition.
5. Proof of Concept Model
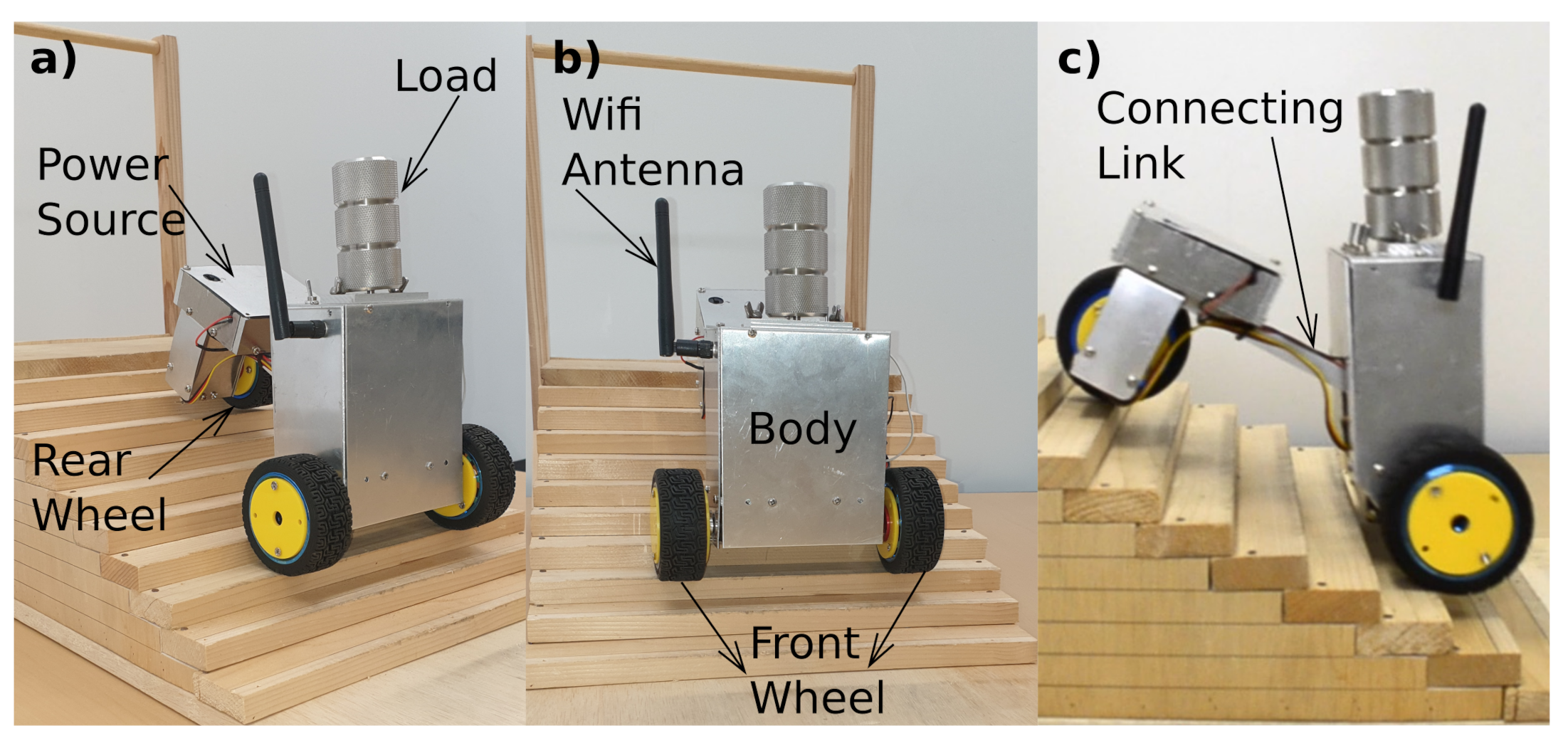
By using design analysis, it was found that robots with fixed center distance between the front and rear wheels fail to carry a load with a high center of gravity while climbing a stair. In order to realize the phenomenon, a scale-down prototype is developed and experiments are performed on steps. In
Figure 15, an image of the model is shown.
Table 8 describes different parts of the model. The prototype consists of two front wheels and a rear wheel. The rear wheel is connected to the body by a link termed as the connecting link.
The electronic components used to develop the prototype are shown in
Figure 16a. In the prototype, an Arduino Uno microcontroller is used as the brain of the robot. All the wheels are driven by continuous servo motors. In order to control the inclination angle, another servo motor is used which drives the connecting link of the robot. The prototype is powered by a 6V battery source. Three toggle switches are used in the robot. Switch 1 is used to connect the power source to the four motors of the robot. The power supply to the microcontroller is connected through switch 2. Switch 3 is responsible for toggling between the operating conditions of the prototype, i.e., operating with or without control.
MPU 6050 is used to sense the inclination angle of the model. The sensor consists of three Gyroscopes and three accelerometers for sensing three degrees of rotation and three dimensional spatial motions, respectively. The inclination angle of the robot is communicated to the monitor by using a wireless module. Experiments are performed for ascendance and descendance of the robot on the stairs.
Figure 17,
Figure 18,
Figure 19 and
Figure 20 show the snapshots of the videos of the experiment. In order to remotely monitor the change in inclination angle of the prototype, a wifi module is used.
Figure 16b shows the flow chart of the control system that is used to maintain the inclination angle of the proposed robot. The inclination angle sensed by the inertial measurement unit (IMU) is processed by the microcontroller. Depending upon the deviation of the current inclination angle of the robot from the desired value, the microcontroller sends the actuation signals to the actuator for rotating the connecting link. By rotating the connecting link, the inclination angle of the robot is maintained at a desired value.
Figure 17 and
Figure 18 show the images while the model is ascending the steps.
Figure 17 illustrates the case in which the inclination angle of the robot is controlled, whereas
Figure 18 shows the uncontrolled case. During the experiments, it is observed that when the inclination angle of the robot is not controlled, the robot slips on the fifth step. On the other hand, when the inclination angle is controlled, the robot successfully climb up the stairs.
Similarly,
Figure 19 and
Figure 20 show frames of the experiments, wherein the robot is descending the steps.
Figure 19 represents the descendance when the inclination angle of the robot is controlled, whereas the experiment is performed without controlling the inclination angle in
Figure 20. It is observed that the robot topples on the fourth step (from top) when the inclination angle is not controlled, whereas in the case of the controlled inclination angle, the robot successfully descends the stairs.
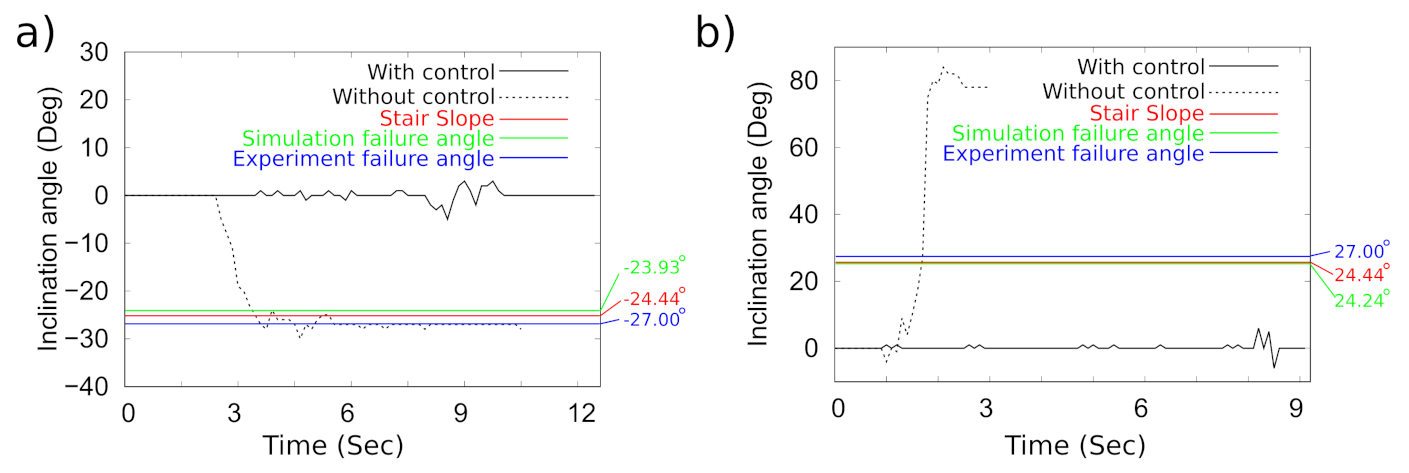
Figure 21a shows the comparison of inclination angles (of the robot) during its ascendance in controlled and uncontrolled conditions, respectively. The slope of the stair is 24.44
. It is observed that in the controlled condition, the maximum and minimum inclination angles are limited to 3
and
, respectively. The inclination angle of the robot drops to −30
during an uncontrolled setting. By using simulation, it was observed that at an inclination angle of −23.93
, the front wheels and the rear wheel touch the edge of the steps. At such inclination angles, the torque, due to the high center of gravity of the load, increases to an extent that the normal reaction at the front wheels reduces to 5.29 N, whereas the normal reaction at the rear wheel increases to 22.25 N. Since the normal reaction at front wheels is low, the probability of slipping increases. During the experiments, it is observed that the slipping of wheels occurs at an angle of −27
. Similarly,
Figure 21b illustrates the comparison of inclination angles (of the robot) during its descendance in controlled and uncontrolled conditions, respectively. It is observed that in the controlled condition the maximum and minimum inclination angle is limited to 6
and −6
, respectively. The inclination angle of the robot raises to 27
during an uncontrolled setting. Once the inclination angle reaches 27
, the robot topples down. By using simulation, it was found that the robot topples at an inclination angle of 24.24
. The difference may have happened as the inertia effect is ignored in the simulations.
Table 9 shows the mean and standard deviation values of difference in inclination angle of the prototype during ascending and descending experiments on the prototype with controlled and uncontrolled conditions. The negative mean value and standard deviation value during ascending show that, while climbing up without control, the inclination angle of the robot becomes negative and it decreases as the robot proceeds on the step. Similarly, the positive mean value and standard deviation value during descending show that, while climbing down without control, the inclination angle of the robot increases as the robot proceeds on the step.
6. Discussion
In this section, the reasons for the failure of the robot during its ascendance and descendance on the stairs when the inclination angle of the robot is not controlled are discussed.
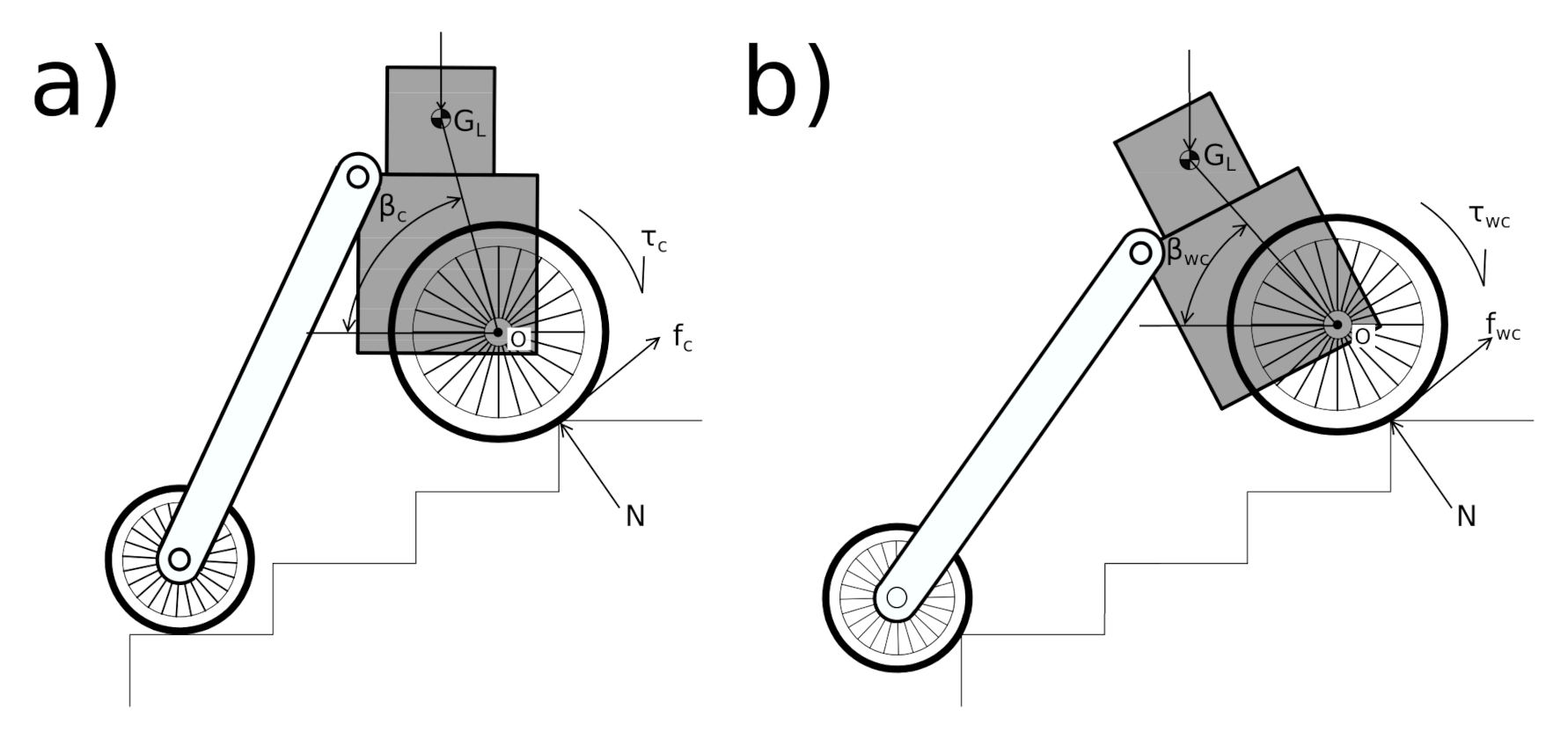
Figure 22 illustrates two situations of the robot while it is climbing up on the stairs.
Figure 22a shows the controlled situation while
Figure 22b shows the uncontrolled situation. In the schematic, point
indicates the center of gravity of the load.
represents the angle made by a line joining the center of gravity of load and the center of front wheel (
O) with the horizontal. The subscripts of angle
, ‘c’ and ‘wc’ indicate the controlled and without control conditions.
is the torque of the motor at the front wheel. ‘f’ and ‘N’ are the frictional forces and normal reactions of the front wheel on the edge of the step, respectively.
It may be observed that the following is the case.
Hence, the counterclockwise moment in the uncontrolled condition (due to the center of gravity of the load) about the point
O is more than that of the controlled condition. Therefore, the following is the case.
Since the frictional force on the front wheel during the uncontrolled condition is greater than that of the controlled condition, the probability of slippage during the uncontrolled condition is greater than that of the controlled condition. Similar behavior has also been observed during the experiments.
In
Figure 23, the schematic of the two situations of robot is shown while the robot is descending the stairs.
Figure 23a illustrates the controlled situation while
Figure 23b shows the uncontrolled situation. ‘M’ is the moment due to the center of gravity of load with respect to the front wheel center (
O). It may be observed from
Figure 23 that the moment due to the center of gravity of the load (about
O) is in the counterclockwise direction during the controlled condition, whereas the moment is in the clockwise direction during the uncontrolled condition. This will result in the toppling of the robot in the uncontrolled condition, which is also observed during the experiments.
7. Conclusions
In this article, a new mechanism for a step climbing robot is discussed and consists of two front wheels, a rear wheel and an actuator (to control the center distance between the front and rear wheels). In order to compensate for the drastic variation in the inclination angle, which can result in instability, the angle between the connecting link and the body is varied. A dynamic model (of the proposed system) is developed and various simulations are performed. During the analysis of the model, it is found that the difference between allowable and required torque on the front wheels increases by 108.5% in the controlled condition than compared to the uncontrolled condition. This reduces the probability of slipping and improved the stability of the proposed system. It is observed that the robot carrying a load with a low center of gravity and for which its front and rear wheels are connected with a rigid frame is capable of climbing up or down the stairs. On the other hand, the robot fails to climb up and down when it is carrying a load possessing a higher center of gravity. During ascending simulations with control, the required torque on rear wheel is reduced by 26.3% than compared to uncontrolled simulations. Furthermore, the normal reaction of the rear wheel during descending simulation has increased by 170.9% by controlling the inclination angle, which reduced the probability of toppling of the proposed robot. Experiments on a scaled-down prototype also reveals that the robot is unable to climb up the stairs during uncontrolled conditions whereas in controlled conditions, it can successfully climb up the stairs. By controlling the inclination angle of the prototype, the variation of inclination angle during ascending is reduced by 77.8%, whereas the variation is reduced by 92.8% during descending. Similarly, during descending experiments, it was found that the robot topples when operated without control and the robot successfully climbs down the stairs when the inclination angle was controlled.
As observed from the configuration of the system, the length of the proposed system will increase significantly due to the connecting link, which in turn will restrict such robots to operate in a confined space. In order to overcome such limitations, the connecting link should be replaced by a linear actuator. Moreover, a robust control method may be designed to enhance the performance of the robot during an external disturbance. Since cost is also a very important parameter, optimization should be performed without compromising the stability and strength of the robot. Furthermore, these models should be tested against external disturbances. Finally, full-size prototypes should be developed and experiments should be carried out to ensure the safe and stable operations of the robot.