3.1. Solving the Multi-Objective Optimization Problem
The multi-objective optimization model was applied to the test case adjusted from Reference [
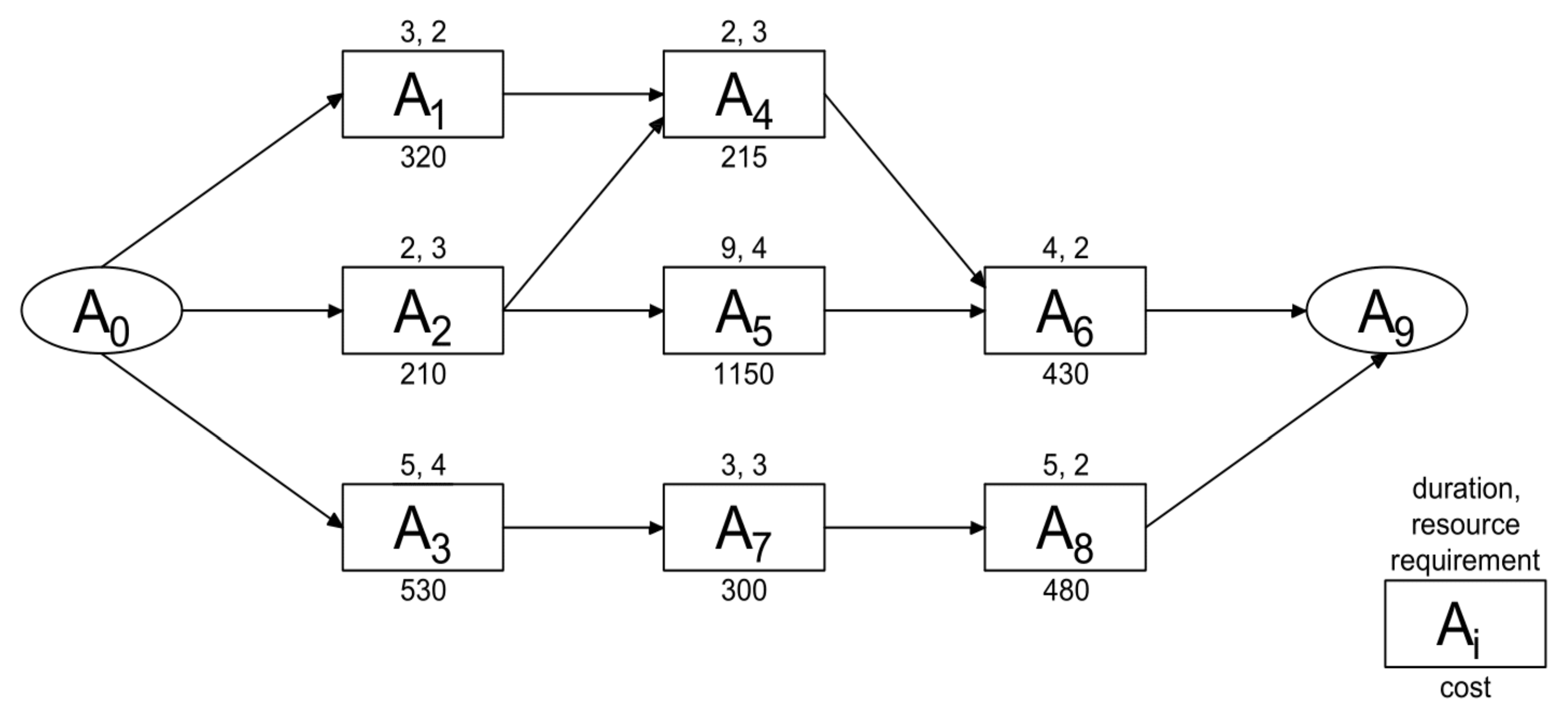
30] to provide a detailed description of the solving process for the multi-objective optimization problem on a single problem instance. The activity list for the problem instance is given in
Table 5. The project network is shown in
Figure 3, along with activities’ durations in months, their resource requirement per activity, and activities’ direct costs in thousand of financing units. Only one resource type is required during project execution, of which 7 units are available at any time. Since the model proposed herein requires cash-flow analysis, financial data, and contract terms are provided in
Table 6. All integer values considering financial input are given in thousand of financial units.
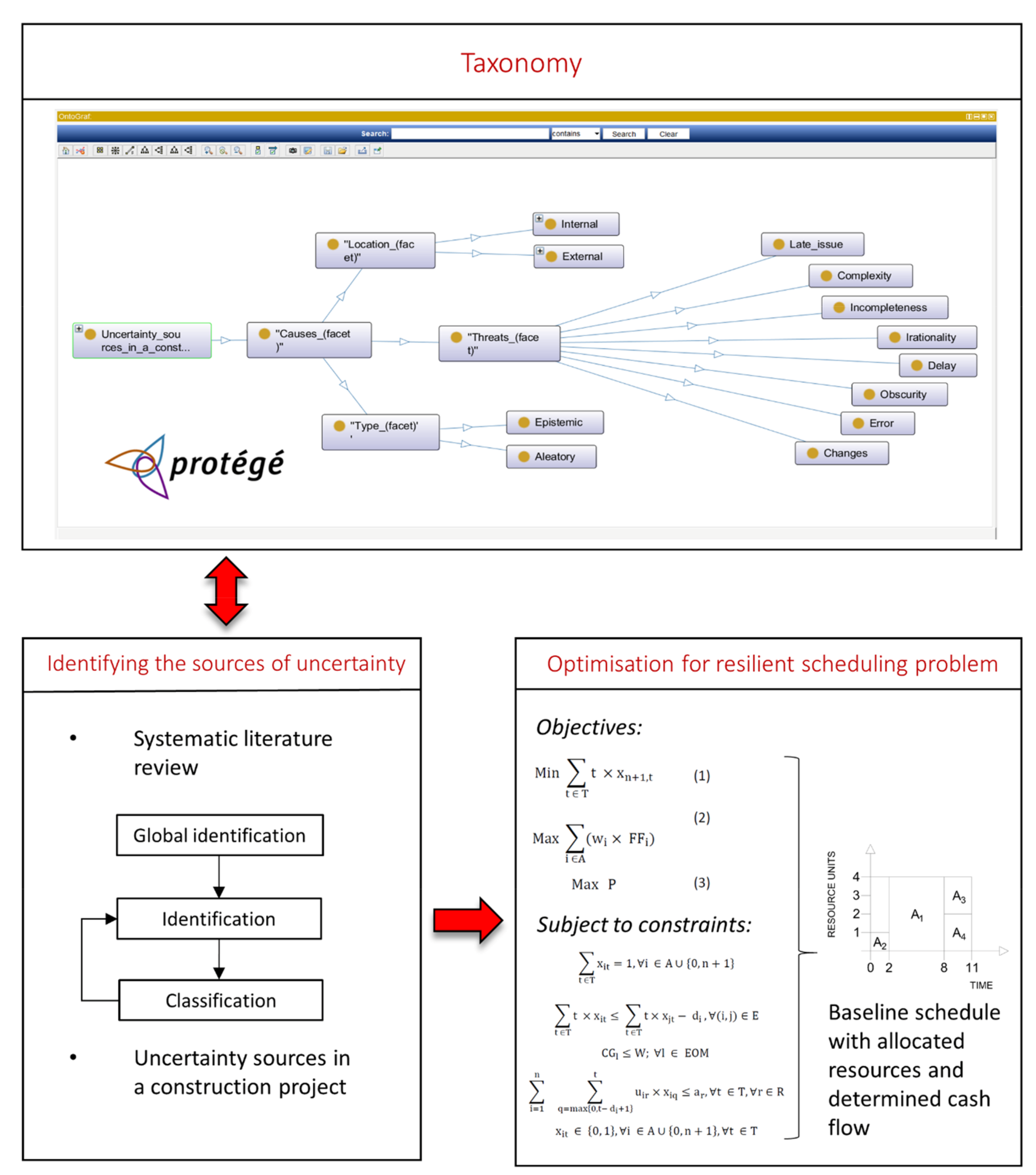
In the test case, we assume recognized uncertainty sources as follows:
Unfavorable weather conditions might interfere with the execution of Activity 2, which is performed on the construction site;
Architectural innovation involves an element of uncertainty while implementing the Activity 4;
Change orders in Activity 6 might cause technical difficulty for accomplishing the execution in the estimated time frame.
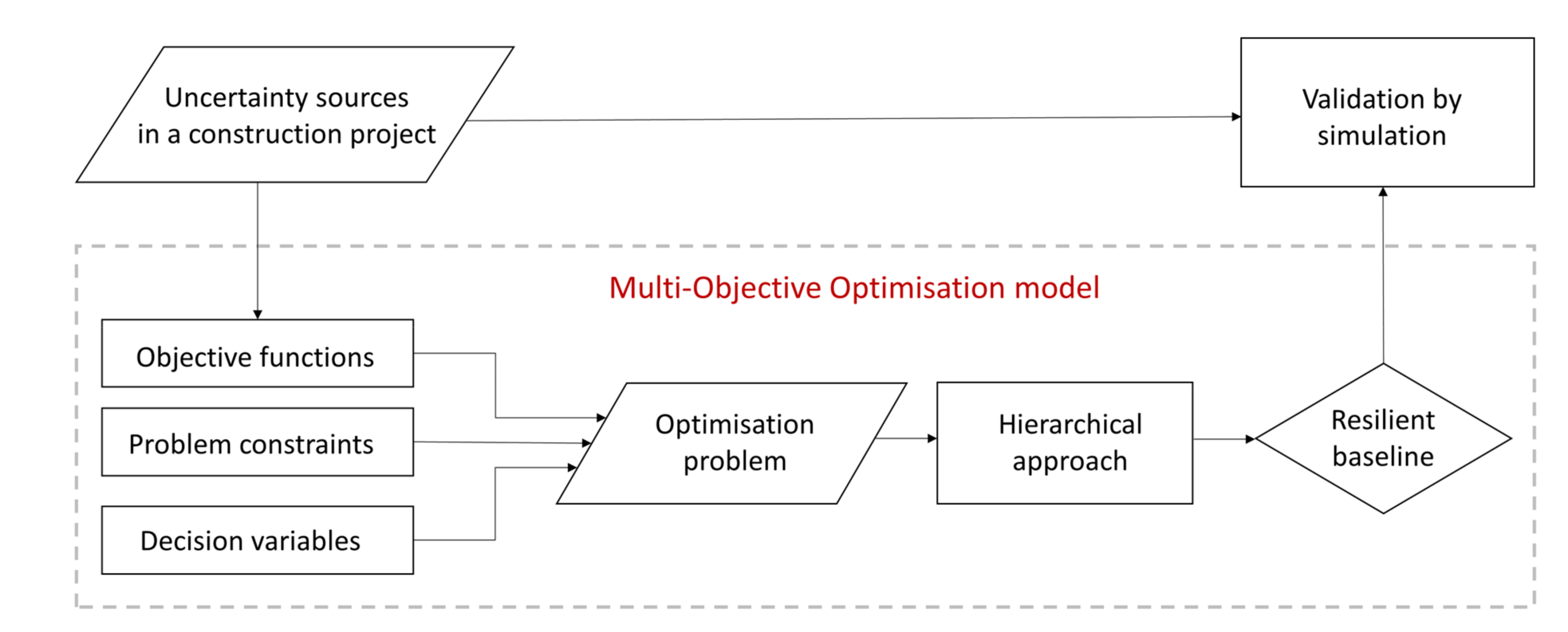
Having in mind optimization problems with multiple objectives, a single optimal solution cannot always be found in an unambiguous manner. For example, one baseline schedule may provide a shorter makespan, with lower values considering resilience surrogate measure and profit, while another baseline schedule may have a longer duration and significantly higher values of surrogate measure and profit. Therefore, from the mathematical point of view, one optimal solution generally is not guaranteed when solving optimization problems with more than one objective function.
To date, different methods have been introduced to solve the MOO problems. One of them is to combine or weigh different objective functions [
67], so the range of solutions can be found as Pareto optimal points. Following this approach, it is hard to obtain a single optimal schedule, since neither of the Pareto solutions can be improved without compromising other objective values [
68]. As can be seen in Reference [
69], although Pareto solutions can be considered broadly comparable, it is not possible to select only one dominant solution. Another problem then arises, as it is not always clear how to combine objective functions with different measurement units. For these reasons, a hierarchical approach was used to proceed with the solving process in the current study.
Since the initial assumption was that the decision-maker’s preferences in obtaining the final solution were known in advance, a hierarchical approach is employed to find a single baseline solution that can be implemented for a construction project. Priorities for all objectives are assigned in decreasing order of importance as follows: timeline minimization, surrogate measure maximization, and profit maximization. This way, project duration is optimized on the uppermost level of the solving process, and the following preference is to find the highest surrogate measure value amongst all solutions that satisfy the first hierarchical objective. At the final step of solving process, a profit value is maximized for the baseline schedule, without causing degradation in earlier objective functions.
The test problem was solved to optimality with an exact algorithm written in the Mathematica programming language. The overall process led to obtaining a single baseline schedule, with a makespan duration of 18 months, SM value of 0.487, and deterministic profit value evaluating to 904.12 thousand of financial units. This way, the stable baseline schedule, which is considered to be resilient under the impact of uncertainty, was produced as a result of the optimization process.
3.2. Validating Resilient Scheduling Process
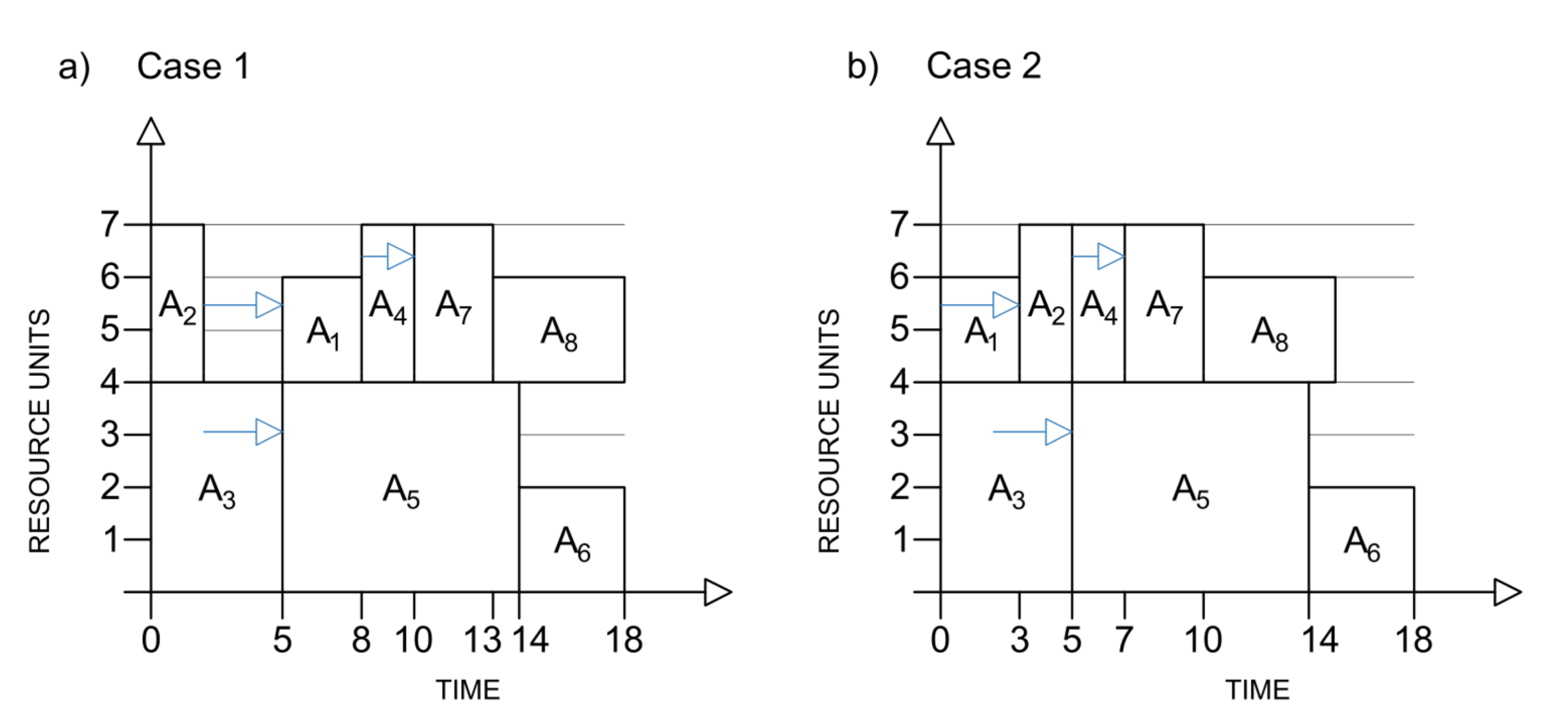
To validate the resilience of the proposed scheduling process, a probabilistic simulation analysis was conducted for different baseline solutions of the previously presented test problem. Due to the computational complexity of the underlying scheduling problem, the simulation analysis was bounded on two distinctive instances. The first baseline schedule refers to the single makespan instance obtained by solving the MOO test problem as previously described, while the other solution is found when the second and the third objective function were shifted in their hierarchy. For the second case, timeline minimization is still on the highest level of hierarchy in the optimization process; however, the profit maximization is in the second place of importance, and the surrogate measure maximization is at the bottom considering the hierarchical importance of objective functions. This way, the evaluation is made to compare the simulated behavior of two different baseline schedules: both of them have a duration of globally optimal 18 months, but in the first case, the SM value is higher and the baseline profit value is lower compared to SM value and baseline profit value from the second case. Objective function values for both cases are given in
Table 7, along with the baseline start times for all activities, including dummy start and dummy end. The credit limit was set to 280 thousand of financial units in both cases.
Since the goal of the simulation process is to analyse the project behavior under the impact of uncertainty, some of the activities’ durations in the process of validation are allowed to take stochastic values. For this reason, the duration of activities 2, 4, and 6 in the project network are allowed to take stochastic values. Uncertain activity times are modeled with beta distribution, where shape parameters are set to
and
in order to calculate realised activity durations in the Monte Carlo analysis. Stochastic activity durations in the simulation process are bounded between 0.7 and 2.2 of their estimated length, while the mode of the simulated activities is equal to the planned duration,
. Considering the simulated direct cost for each activity, it is assumed that the new cost is proportionally related to the realized duration of activity at a ratio, R, which is used to delineate if the cost of activity (C
a) at a simulated duration (T
a) consists mainly of material or equipment and labour. For example, if the cost of activity consists mainly of material, it will have a lower ratio value, R, while higher dependence on equipment and labour will be represented with a higher R-value [
70]. In the simulation analysis, R is set to 0.6 for all activities. To calculate activities’ cost C
a at a simulated duration T
a, Equation (14) is employed from the Reference [
70]:
where C
m represents the original cost of activity at the deterministic duration, T
m.
In the simulation analysis, additional resource relations are appended to accompany existing precedence connections between activities, so the baseline resource flow can be preserved throughout the entire simulation process. This way, resource conflicts are avoided through the simulation process where activities’ durations take stochastic values. Additional resource relations are shown for each baseline schedule in
Figure 4. Finally, the enhanced Monte Carlo simulation approach, which takes into consideration resource constraints, is taken on 10,000 iterations for each baseline case.
Equilibrium state was examined throughout 6 resilience dimensions: (
Eq i) probability of reaching baseline due date, (
Eq ii) probability of reaching baseline due date multiplied with coefficient 1.1, (
Eq iii) average tardiness amount for the proposed baseline, (
Eq iv) average tardiness amount for activities’ start times, (
Eq v) the percentage of simulations where credit limit was broken, and (
Eq vi) probability of reaching or exceeding the baseline profit. The last equilibrium dimension (
Eq vi) is calculated by considering only those simulations for which credit limit, W, was not broken. From the simulation results, as shown in
Table 8, it is evident that the first case (single optimal solution from the previous section) generates better results in all equilibrium calculations than the second case, for which profit maximization was considered as a more important objective than maximizing SM value. With an increase in
SM value, there is a constant rise in the probability of reaching both strict (
Eq i) and relaxed (
Eq ii) baseline duration, as well as a constant decrease of average project tardiness (
Eq iii), and a decrease of average tardiness for activities’ start times (
Eq iv). Moreover, the percentage of simulations for which the credit limit is broken (
Eq v) is slightly lower in the first case, where the SM value was higher. Finally, the probability of reaching baseline profit or attaining even higher profit values (
Eq vi) is significantly better for the test case with a higher SM value.
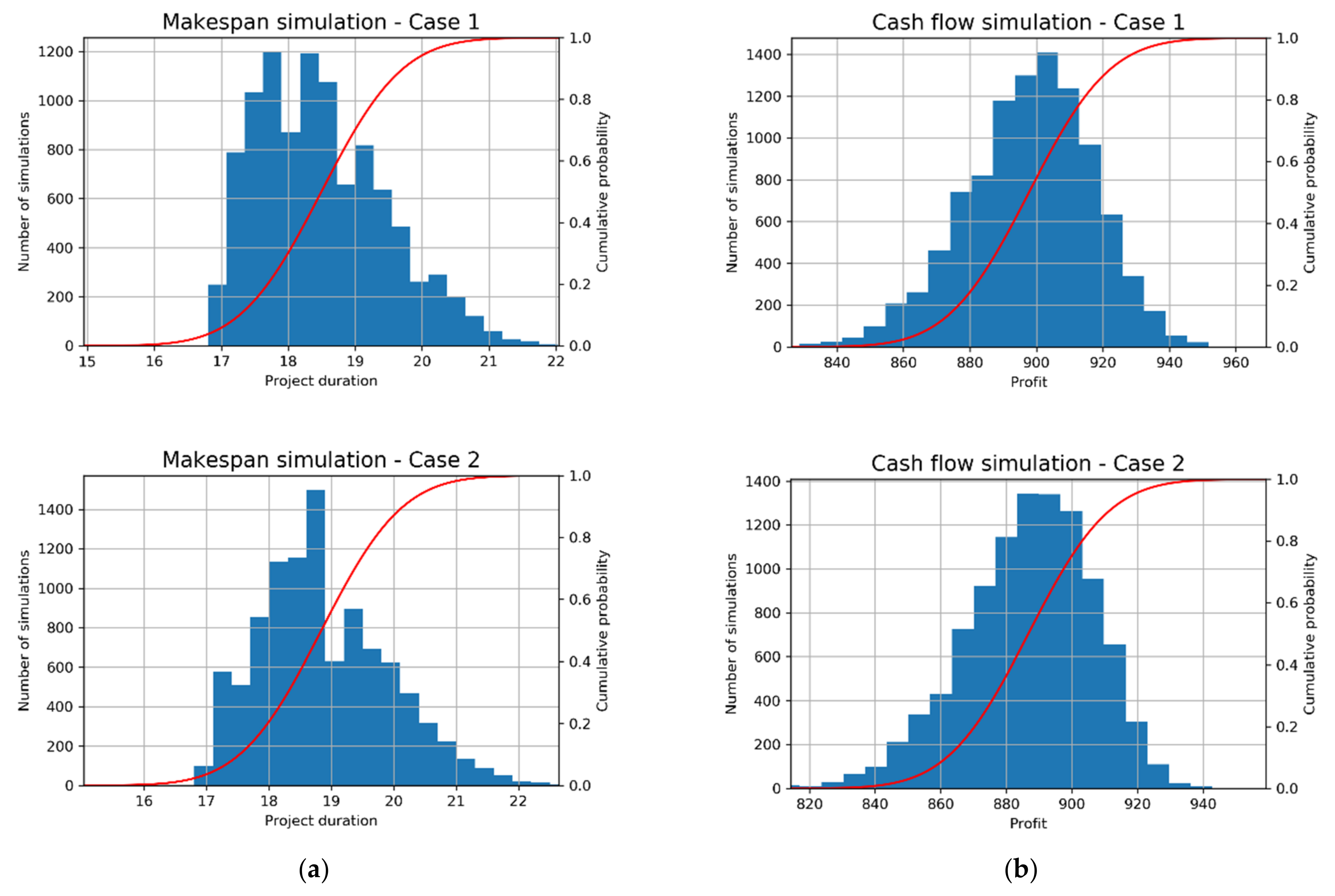
According to the simulation results, the initially suggested approach, where SM value maximization was taken as a more important objective function than maximizing the baseline profit, leads to better results considering the overall resilience of the baseline solution. Validation results indicate a positive correlation between increased SM value and resilience of baseline schedule with allocated resources. As a result of enhanced Monte Carlo analysis, probability distribution charts for makespan duration, considering both cases, are shown in
Figure 5a. Probability distribution charts for final profit are shown in
Figure 5b.
Since the average deviation of the maximal cash gap is negligible in both baseline cases (average deviation from the negotiated CL was around 0.01% in the simulations where the CL was broken), the probability distribution for profit is shown by considering all simulations, including those where violation of credit limit has occurred. After simulating two different baseline schedules with the Monte Carlo approach, where additional resource relations were appended, it was shown that a schedule with a higher SM value produces a better response to uncertainty.
The results of the equilibrium analysis showed improved performances in all equilibrium dimensions (Eq i – Eq vi) when comparing the baseline schedule with higher SM value to another solution in which profit maximization dominated SM improvement. The optimal trade-off between project duration, stability, and profit is obtained for a baseline schedule calculated as a result of the resilient scheduling approach presented in this study. According to validation results, it can be stated that the contractor will benefit from the enhanced resilience of the baseline schedule, since its schedule is improved for the case with the higher SM value. Therefore, this research contributes to the project-management body of knowledge by exploring an approach to develop resilient baseline schedules which will maximize the probability of reaching project goals. With the introduction of the financing aspects in the underlying resilience scheduling problem, the essential issues in construction-management reality are considered. The final output of the MOO problem is given in a form of a baseline schedule which simultaneously minimizes duration of a project, maximizes its resilience, and maximizes final profit from for a contractor. This way, project performances are improved, since the baseline calculations can be accepted with improved confidence levels.