Abstract
Both the calculation of ground slopes at points on the map and the elevation estimation for these points bear significant importance and also have applications in various domains, such as civil engineering, road and railway design. The paper presents two methods that use level curves: one that is fast and approximate and another which is slower, but more precise. The running speed of the two proposed methods and their results are compared by performing 100 million experiments. The paper also presents how these methods can be applied to optimize embankments. An accurate method to calculate the horizontal plane of the excavation/filling when building a new house is also presented.
1. Introduction
The possibility of calculating the slope and elevation using level curves has practical applicability in several fields of activity, such as civil engineering [1], architecture [2,3], railway [4], road and bridge engineering [5,6,7,8], topography [9], etc. Although the results found can be used in various areas, this article is limited to solving two problems related to civil engineering and to railways, roads, and bridges, both ultimately related to the embankments optimization. The problem is well known, but it was not closely examined by design engineers, who preferred an intuitive, approximate solution. The current article presents a rigorous and mathematically accurate solution to find the optimum between excavations and fillings, resulting in a reduction of the embankments related costs. The article presents in detail the solutions of two concrete problems in two different fields of activity.
The first problem investigated is in the field of civil engineering and consists of determining the optimal elevation corresponding to the finished floor of the ground level, when the building has to be positioned on a slope [1,2,3]. The second problem investigated is in the design of a new railway or road when there are several fixed points on the topographic map through which the new road [10,11,12,13] or the new railway [4,11] will pass.
The designer has to know the slope and elevation in each of these points as accurately as possible. Using the methods proposed in this paper, the two parameters (slope and elevation) can be determined fast and with a high level of accuracy using the level curves of the map, without the need for direct measurement on the spot. Furthermore, when designing roads or railways, the risk of failure, the frictional resistance, the safety factor against sliding or failure, the translational fill failure, or the cut volume and the road fill per meter require knowing the slopes (side slope, cut slope, or fill slope).
The paper is organized as follows: an algorithm to calculate the ground slope at a given point, using level curves, is deduced in Section 2. This problem is reduced to estimating the shortest segment that connects two lines through a point. Two methods are proposed, a fast and approximate one and a more exact one, respectively. The two methods are compared, and it is shown that the errors of the first method are low. In Section 3, the optimum excavation/filling plane is calculated when a new house is built. Two methods are proposed and discussed in Section 4, where they are compared. To finalize the paper, conclusions will be drawn based on the arguments presented.
2. Materials and Methods
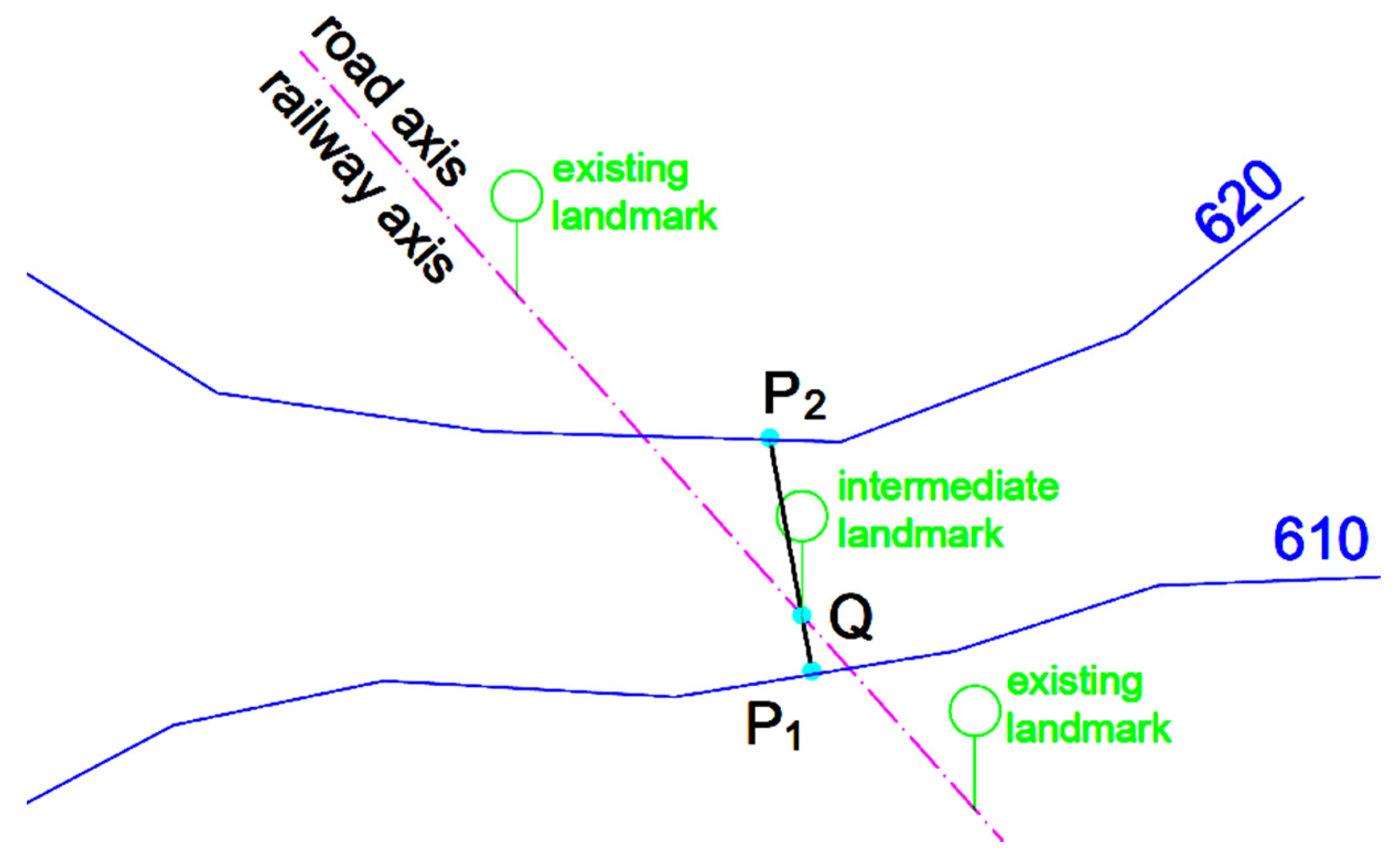
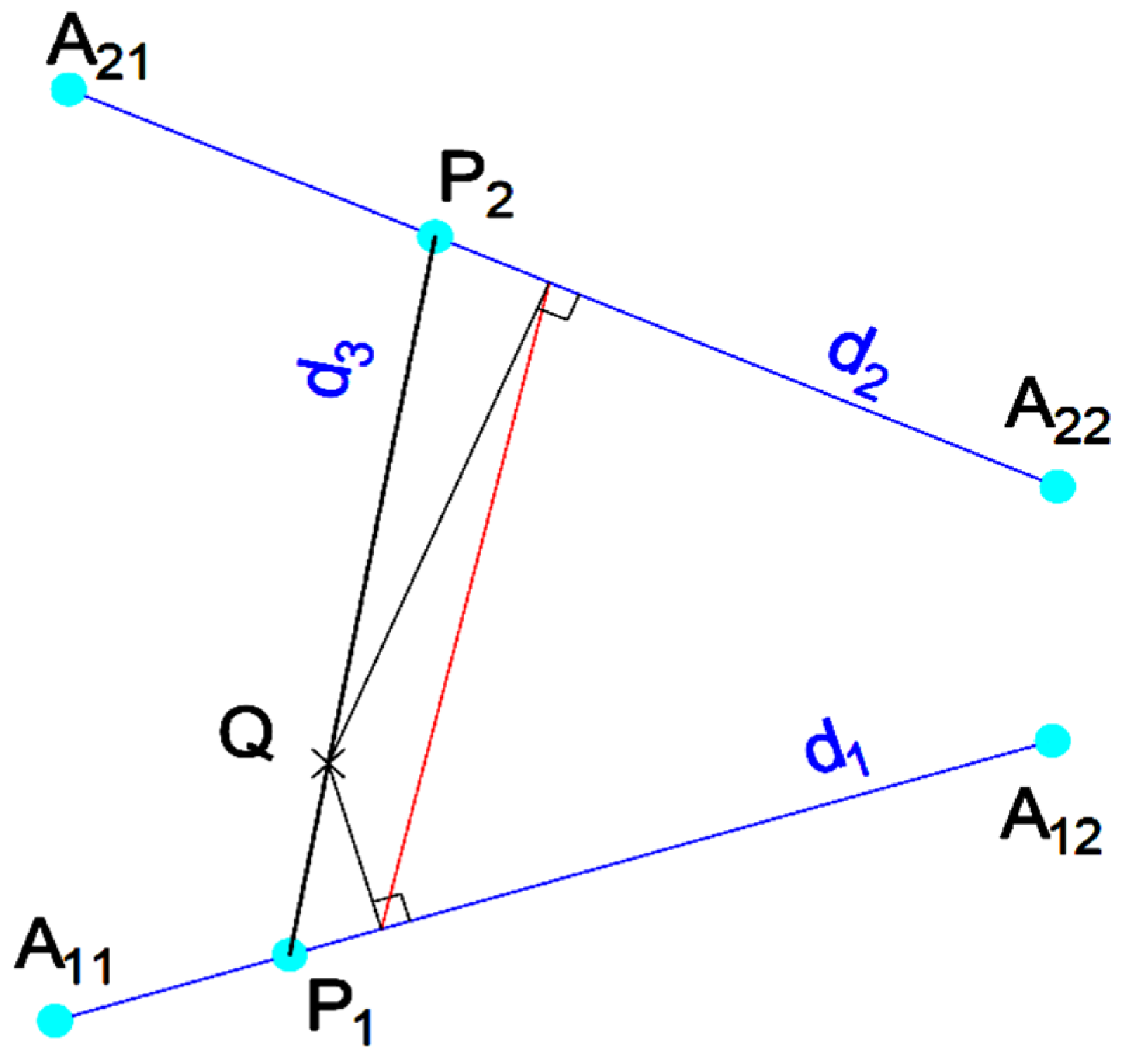
A method of calculating the soil slope through a given point is being introduced. The input data are: the level curves, in Figure 1, the two level curves located at elevation 610 and, respectively, 620, and the 2D coordinates of a point Q on the topographic map. The direction of the Ox axis is considered from west to east, the direction of the Oy axis is south-north. The output is the slope calculated at point Q. The slope can be determined using two other points collinear with Q for which the elevation is known. The points on the map for which the elevation is known are located on level curves. Therefore, it is enough to find two points collinear with Q located on two different level curves. Of course, for accuracy reasons, it is preferable that Q is located between these 2 points and the distance between the chosen 2 points is minimum. Consequently, the problem can be accurately solved if we determine the closest two level curves to Q (Q is located in between these curves) and two points P1 and P2, each located on one of the level curves, and the distance between P1 and P2 is minimum (see Figure 1).
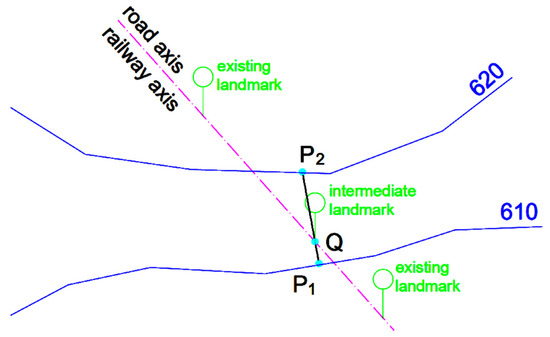
Figure 1.
Finding the slope at a point using level curves.
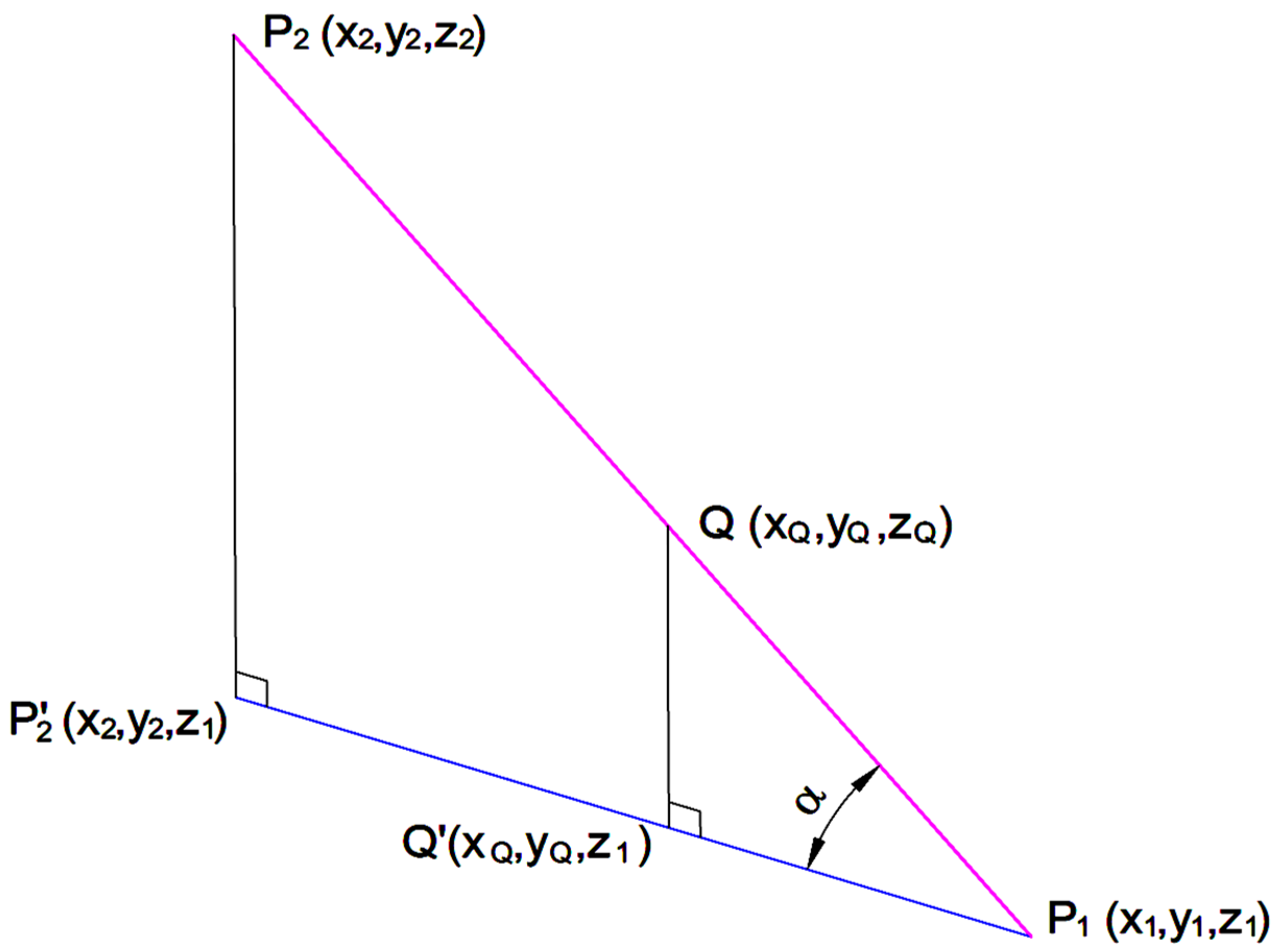
Since a level curve is approximated with consecutive coplanar segments of straight lines, our problem can be reduced to finding the shortest length segment |P1P2| that connects two coplanar line segments located on two consecutive level curves. When the two 2D points P1(x1,y1) and P2(x2,y2) are determined, they are transformed into 3D points by adding the elevations z1 and, respectively, z2 of the level curves on which each of the points are located. Using the 3D coordinates of these 2 points, the slope m = tan(α) at point Q (see Figure 2) can be calculated as follows:
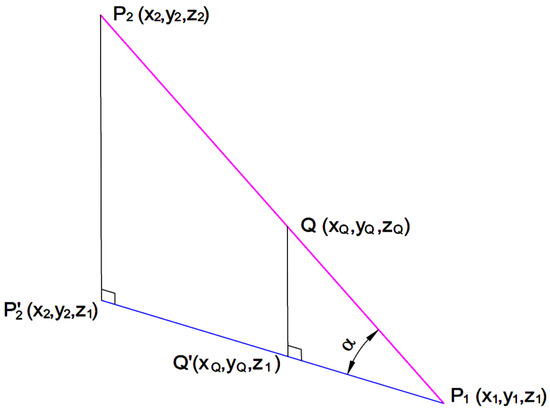
Figure 2.
Determining the slope at Q using P1 and P2.
The first problem (denoted IPS) intended to be solved is to identify the pair of segments (located on two level curves) to which the finding of the shortest length segment should be applied. Of course, for each of the two level curves, the candidates are the closest segments to point Q. Let us denote by Si the set of candidates (segments) for curve i (i = 1, 2). For each pair of segments s1 ∈ S1 and s2 ∈ S2, respectively, the corresponding shortest length segment [P1P2] between s1 and s2 is calculated. If s1 contains P1 and s2 contains P2, then the pair (s1, s2) is added to the set (denoted C) of solution candidates for IPS (Figure 3).
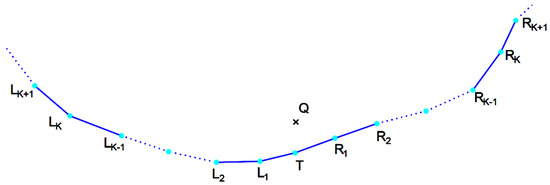
Figure 3.
Finding the closest line segments to Q.
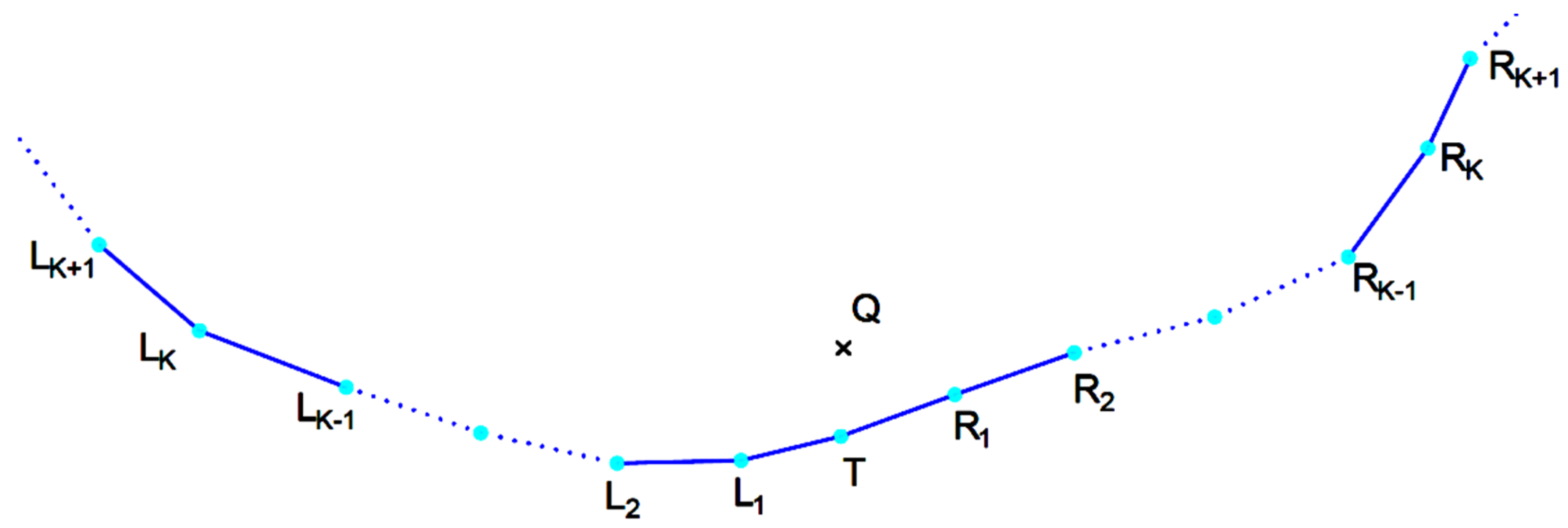
The set Si (i = 1, 2) can be built as follows: first, we find the point T belonging to the level curve i that is closest to Q. We consider then k ≥ 1 points (L1, L2, …, Lk) to the left of T on the level curve and k points (R1, R2, …, Rk) located to right (see Figure 4). Finally, the set Si consists of 2k segments of straight lines given by the consecutive points on the level curve i: Lk, Lk-1, …, L1, T, R1, R2, …, Rk, i.e.,:
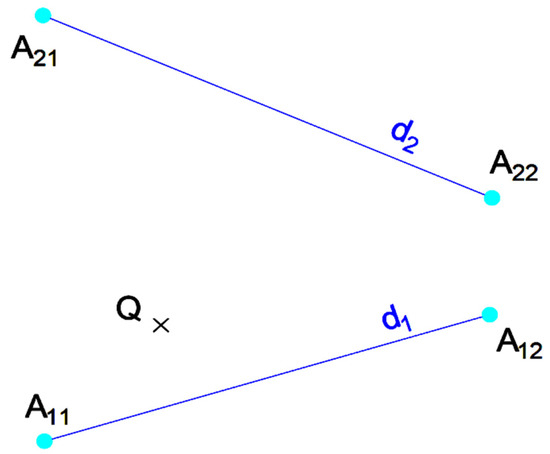
Figure 4.
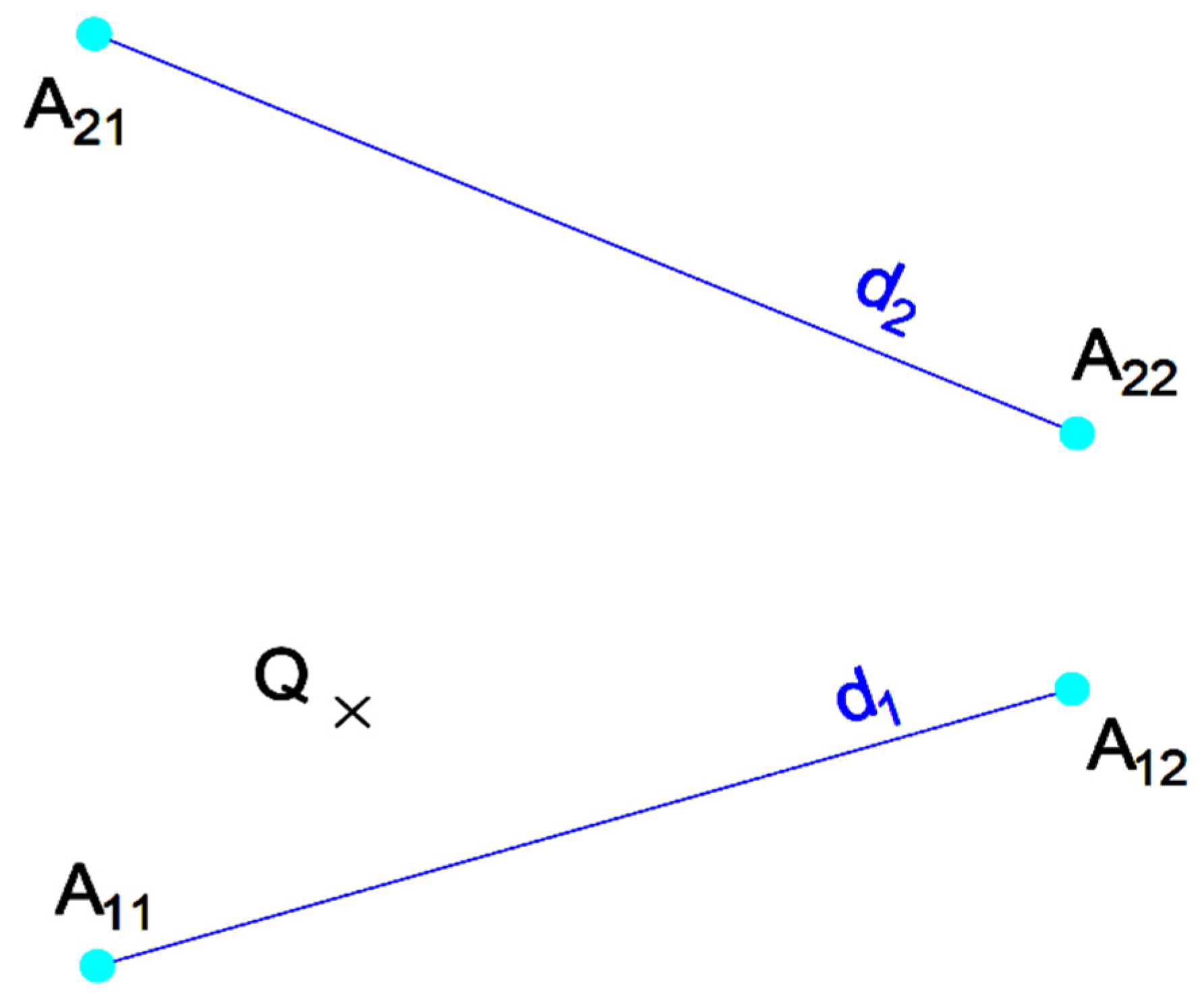
Connecting the point Q to the lines d1 and d2.
Now, let us see how k (giving the number of points in the vicinity of T) is considered. Usually (in real tests), k is enough to be 1. In few cases k is found to be greater. So, the calculations are started with k = 1 and, if necessary, it is increased.
The Algorithm 1 for solving IPS (denoted AIPS) is:
| Algorithm 1 Solving IPS (denoted AIPS) |
| AIPS: Input: the points of the closest two level curves to Q Output: the shortest line segment [P1P2] that connects the given two level curves finished = false; While not finished do C = ϕ (empty set); Build the sets of line segments S1 and S2 (see Equation (2)); For each segment s1 from S1 do For each segment s2 from S2 do Calculate the shortest length segment P1P2 that connects s1 and s2 and passes through Q; If P1 ∈ s1 and P2 ∈ s2 then Add [P1P2] to C; End if; End for; End for; If C not is empty then finished = true; else k = k+1; End if; End while; |
The shortest line segment that connects both level curves is the shortest segment [P1P2] from C.
After applying AIPS, the problem is reduced to calculating the shortest segment that passes through a given point Q and connects two coplanar lines d1 and d2 (Figure 4). We shall denote this problem as SSTPC2L (shortest segment through a point that connects 2 lines). In Figure 4 the points A11 and A12 determine the line d1, and the points A21 and A22 determine the line d2.
We present two methods of solving SSTPC2L: an approximate method and an exact mathematical method. These two methods (presented in Section 2.1 and Section 2.2) were partially described in [7].
2.1. Heuristic (Approximate) Method for SSTPC2L
From the topographic map, the point Q is known and two segments A11A12 and A21A22 are determined belonging to the level curves from Figure 1 (A11A12 on curve 610 and A21A22 on curve 620). These two segments are found according to Figure 3. The method consists of drawing the perpendiculars from the given point Q on the two given lines d1 and, respectively, d2 (Figure 5). We construct a line passing through Q which is parallel to the line determined by the feet of the two perpendiculars. The obtained line is denoted by d3, and its intersection with the lines d1 and d2 is the searched segment [P1P2] (approximate solution of SSTPC2L).
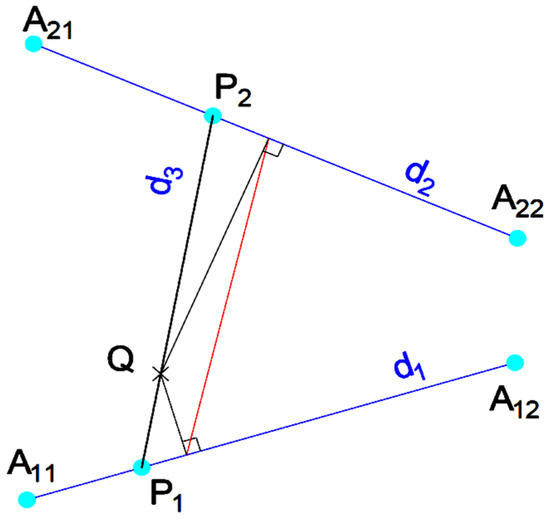
Figure 5.
Approximate method of finding points P1 and P2.
Now, let’s present how the points P1 and P2 are calculated.
The equation of the line di (i = 1, 2) starting from the points Ai1 and Ai2 is:
The perpendicular from Q on di (i = 1, 2) is:
The foot (i = 1, 2) of the perpendicular on di is obtained by solving the system of Equations (3) and (4).
The slope of the line Q1Q2 is:
Since is the slope of , then the parallel through the point is:
Finally, the points Pi (i = 1, 2) are obtained by solving the system of Equations (3) and (6).
The following Algorithm 2 (denoted A1SSTPC2L) is obtained to solve the problem SSTPC2L:
| Algorithm 2 Solving the problem SSTPC2L |
| A1SSTPC2L: Input: Q and the points of the closest two level curves to Q Output: The slope at point Q Apply AIPS to find A11, A12, A21, A22; Calculate the point Pi by solving system of Equations (3) and (6) (i = 1, 2). Calculate the slope at point Q using Equation (1). |
2.2. The Exact (Mathematical) Method for SSTPC2L
For this method, in order to simplify calculus, we apply some initial transformations (rotations and translations) to the points A11, A12, A21, A22, and Q so that the bisector of the angle between the lines d1 and d2 becomes parallel to Oy axis and the point Q is in the origin O, i.e., Q = O (0,0). To do so, we first calculate the intersection I of d1 and d2:
by solving the system of linear equations:
The following transformations to A11, A12, A21, A22 and Q are applied:
- Translation with (−xI, −yI) (I is moved into origin O)
- Rotation with sin(−u) = −sin(u) and cos(−u) = cos(u), where:
After this rotation, the line d1 is over Ox axis of the map’s system of coordinates.
- 3.
- Rotation with sin(v) and cos(v), where:
After this rotation, the bisector of the angle given by lines d1 and d2 is over Oy.
- 4.
- Translation with (−xQ, −yQ) (Q is moved into origin O)
The following 2 systems of equations have to be solved in order to find the points Pi(xi,yi) (i = 1,2) where the lines di (i = 1,2) intersect the line d:
Since Ai1, Ai2 define the line di (i = 1,2) in (10) we have:
Solving the 2 systems of equations, the points Pi(xi,yi) (i = 1,2) are found, where:
The distance between P1 and P2 must be minimized, i.e.,:
where:
By replacing (13) and (14) in (16) the following formula for f(a) is obtained:
We make the following notations:
It is easy to see that the function f is decreasing for , and is increasing for , since f is continuous, and are the slopes of the perpendiculars QQ1 and QQ2 from Q on the lines d1 and, respectively, d2, and “a” is the slope of the line d3. Consequently, there is a minimum of the function f denoted amin in the interval . So, the value amin is one of the solutions of the equation:
on the interval , where:
Remark 1.
Since the bisector of the angle between d1 and d2 is parallel to Oy axis, it is not difficult to see that:
In order to obtain the solution amin of the Equation (20), a numerical method [14] can be used such as bisection method [15], or tangent method. Since and , the bisection method is suitable to be applied on the interval:
After amin is calculated, the points Pi (i = 1, 2) are obtained using (13) and (14) and the distance between these two points is:
In order to go back to the initial system of coordinates, the inverse initial transformations must be applied in reverse order to the points P1 and P2, i.e.,:
- Translation with (−xQ, −yQ)
- Rotation with sin(u) and cos(u) (were calculated in (8))
- Rotation with sin(-v) = sin(v) and cos(-v) = cos(v) (calculated in (9))
- Translation with (xI, yI).
The following Algorithm 3 (denoted A2SSTPC2L) is obtained to solve SSTPC2L:
| Algorithm 3 Solving SSTPC2L |
| A2SSTPC2L: Input: Q and the points of the closest two level curves to Q Output: The slope at point Q Apply AIPS to find A11, A12, A21, A22; Transform the points A11, A12, A21, A22 and Q so that the bisector of the angle between the lines d1 and d2 is parallel to Oy axis and the point Q is in the origin O; Find the solution amin of the equation using bisection method on the interval (see Equations (19) and (20)); Calculate the coordinates of the points Pi (i = 1,2) using (13) and (14), where a = amin; Apply the inverse initial transformations in reverse order to the points P1 and P2; Calculate the slope at point Q using (1). |
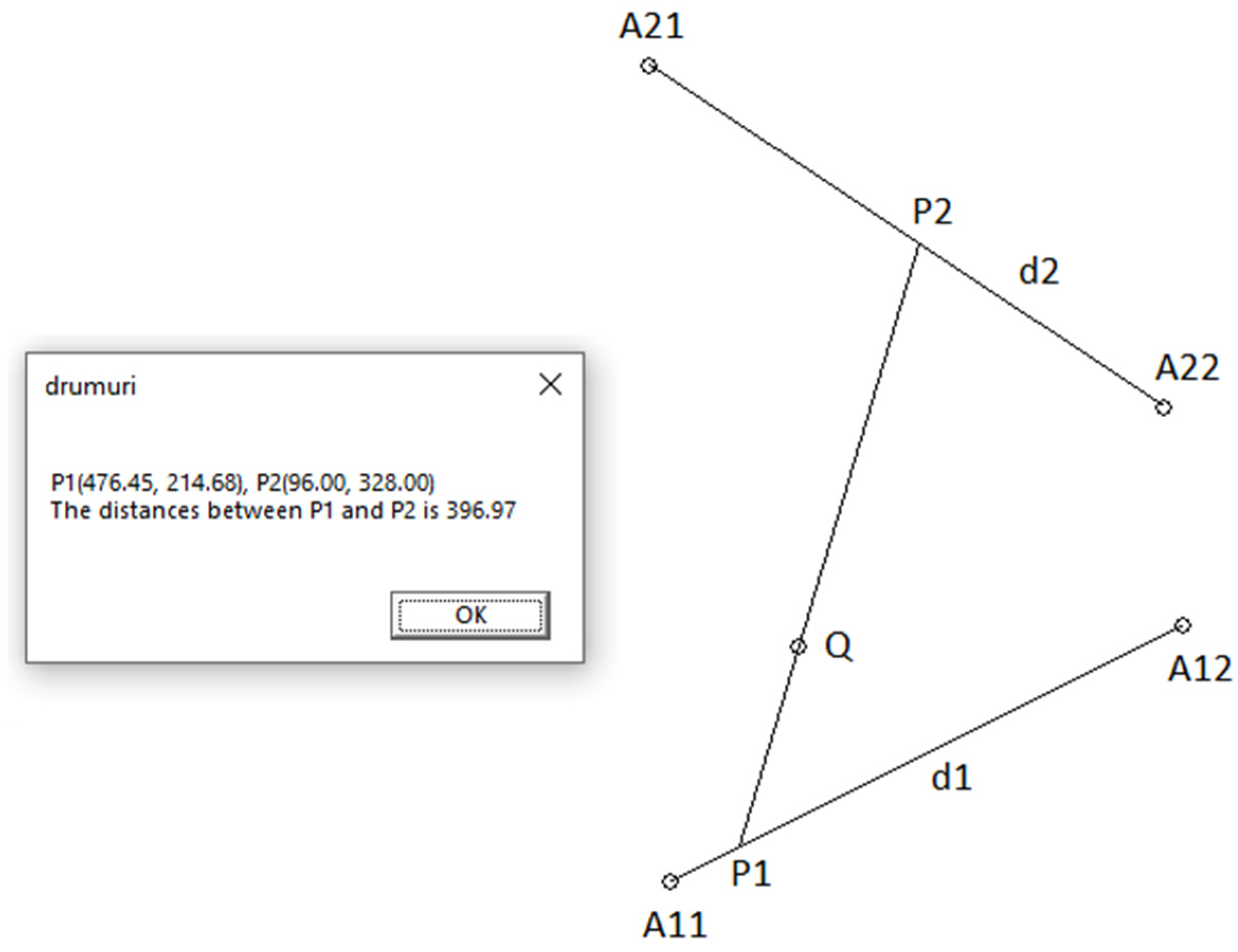
We implemented the above algorithm in Visual C++ and in the bisection method we set the error err = 0.0001 for finding the value amin. In Figure 6, a graphical output of our program is presented.
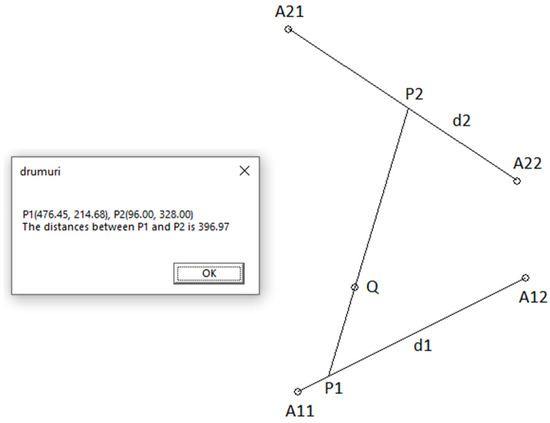
Figure 6.
Output of the Visual C++ program.
3. Results
Besides estimation of the ground slope for a given point, other two possible problems can be solved since we have now obtained a method to calculate the points P1, and P2 on the closest two level curves to a given point Q so that P1, Q, and P2 are collinear and the distance between P1 and P2 is minimum.
3.1. Elevation Estimation at a Point
The challenge is to estimate as well as possible the elevation z of a point Q. Assuming that z1 < z2 (see Figure 3) and since QQ’ is parallel to P2P′2, in the triangle P1P2P′2 we have:
From (25) we obtain the elevation of Q:
It is immediate that, without the assumption of z1 < z2, the following formula can be used to estimate the elevation of Q:
3.2. The Slope between Two Points
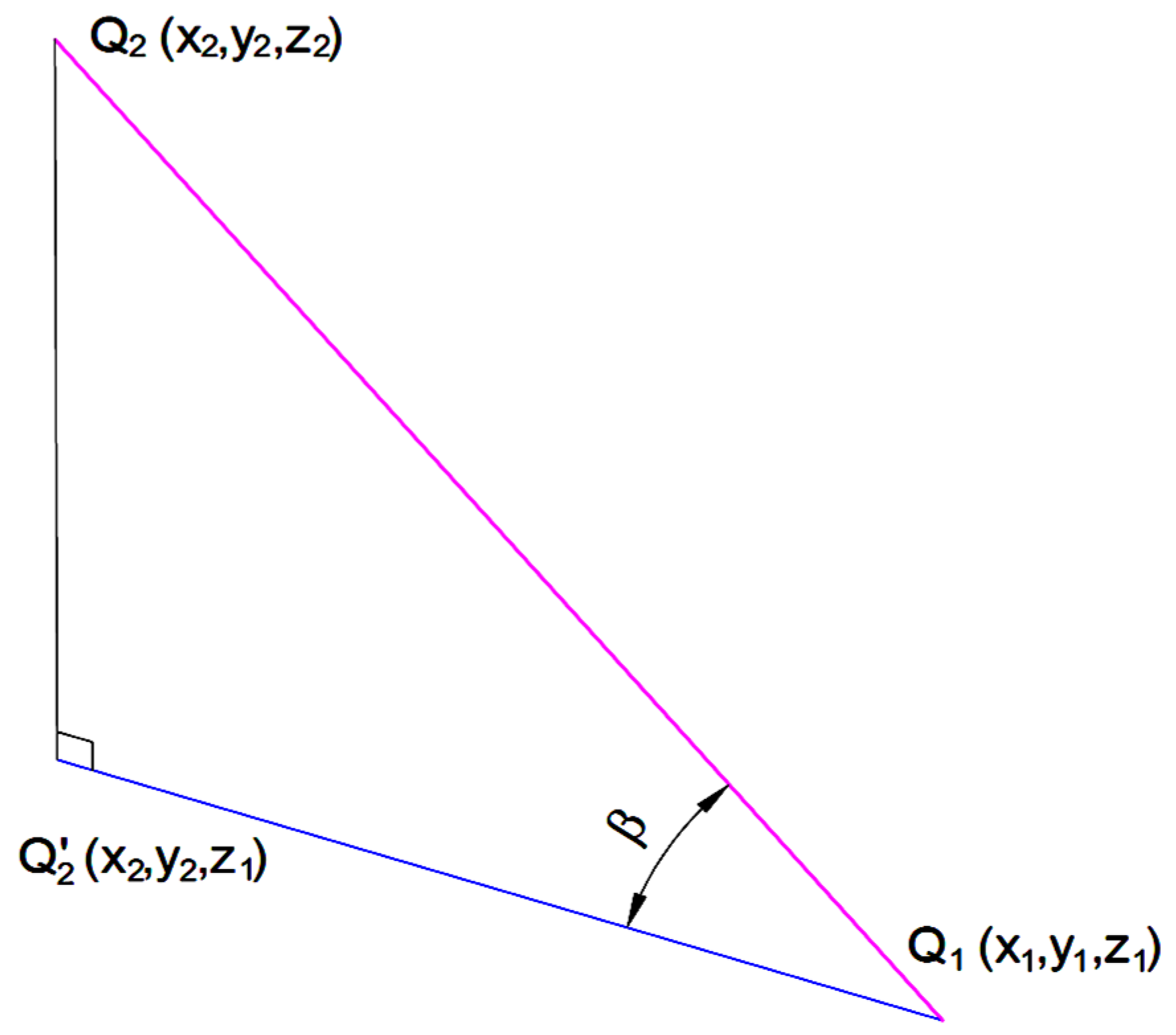
The problem of estimating the slope between two points is significant, seeing that when designing roads, the slope between any two points on a road cannot exceed a given maximum slope, e.g., for highways this value has to be less than 6% or 7%. Therefore, the chosen points from the future road can be tested for this eligibility. To do that, we consider the elevations of the points Q1 and Q2 calculated using formula (26) and we can estimate the slope m(Q1,Q2) of the road passing through Q1(x1,y1,z1) and Q2(x2,y2,z2) using the following formula (see Figure 7):
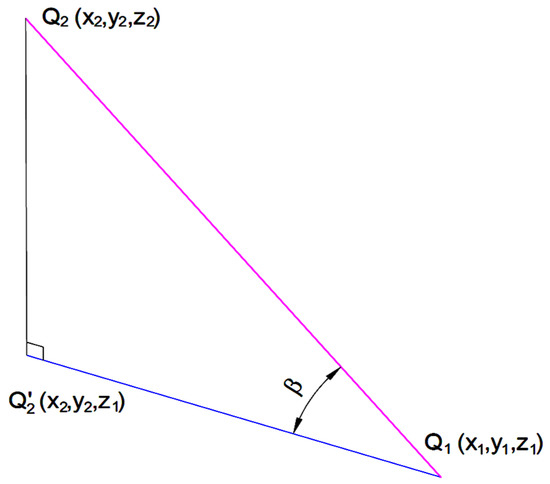
Figure 7.
The slope of the road passing through Q1 and Q2.
3.3. Optimum Excavation/Filling
When a house is built on sloping land and/or with elevations and depressions, the elevation of a horizontal plane must be calculated so that the excavations over the plane would fill the space below the plane resulting in a horizontal platform on which a house can be built. In such a manner, the optimal solution between excavations and fillings is calculated, resulting in a reduction in the costs of embankments. We shall follow up with a presentation of a method to accurately calculate the elevation of this plane. The well-known “flood fill” algorithm [16] from computer graphics is adapted to deal with this problem. Since the algorithm runs in a discrete space, the coordinates will be transformed into their discrete counterparts.
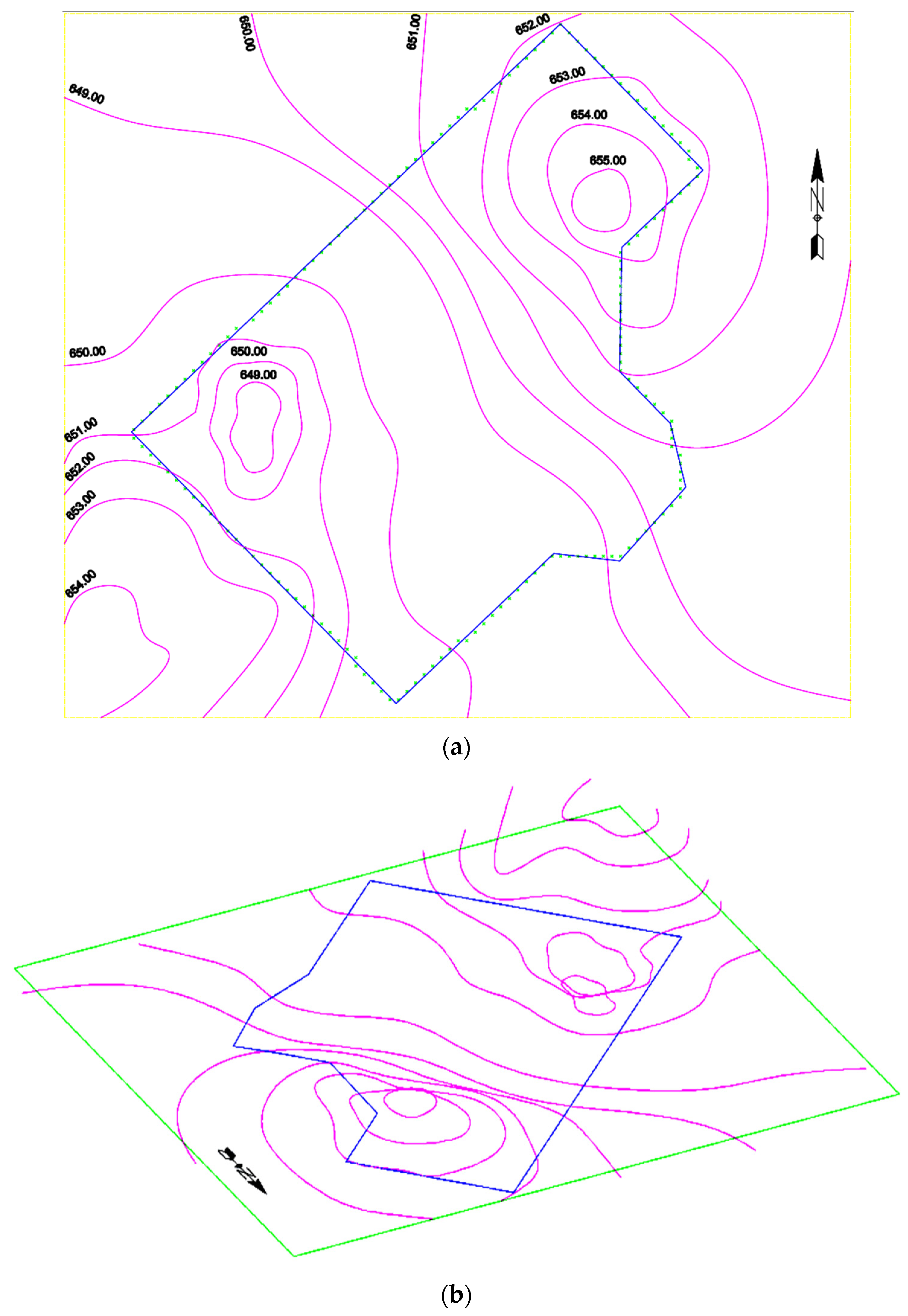
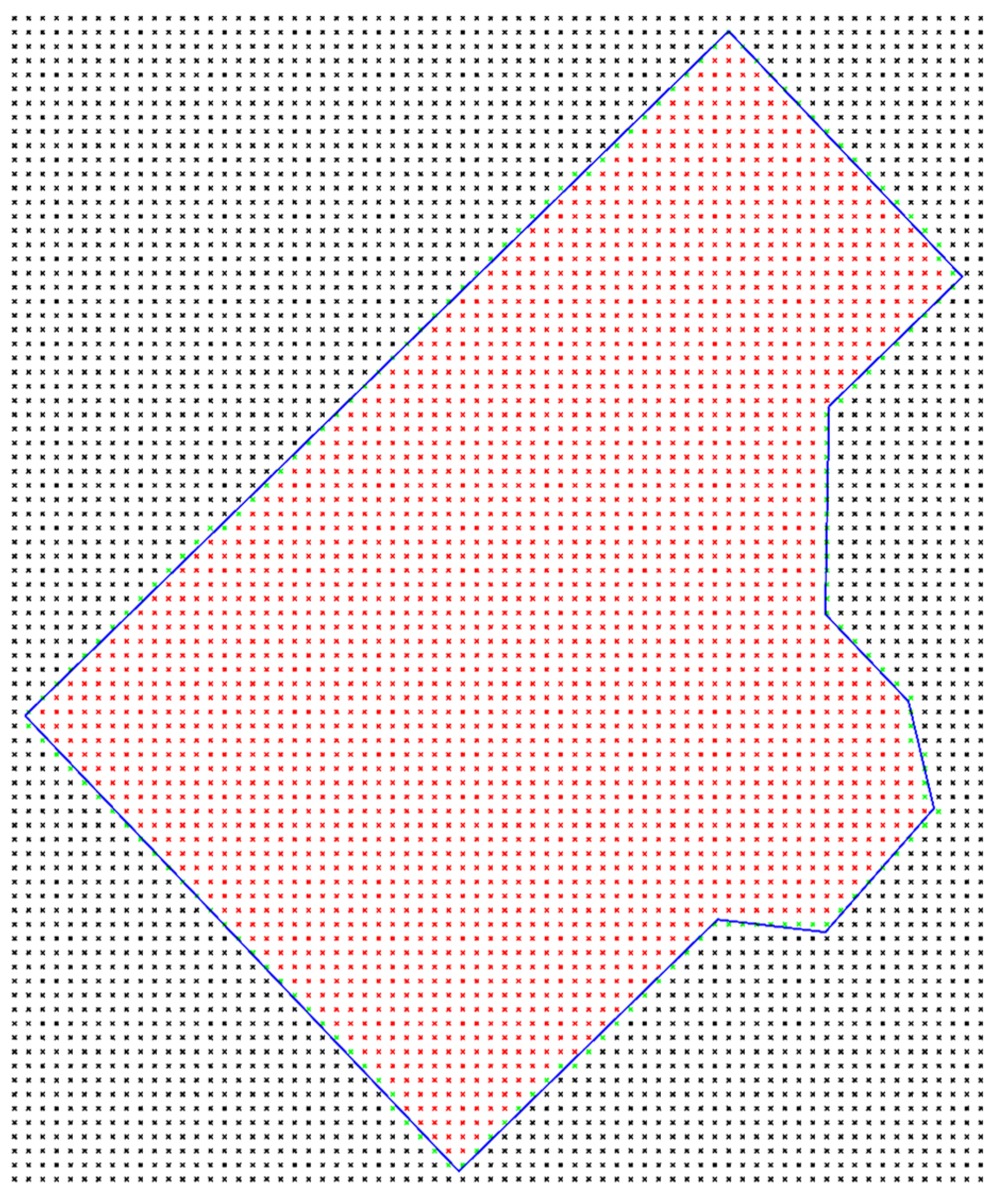
We start with the level curves from the vicinity of the house (Figure 8). Then a discretization is applied (Figure 9), meaning that the plane is divided into equidistant 2D points, e.g., in Figure 9, the distance of 40 cm between points was considered. The points of the contour of the house are transformed into their discrete counterparts (for each such a point, the closest discrete point is determined). Using Bresenham’s algorithm [17], the discrete points of the contour are found (green points in Figure 9). Using a flood fill algorithm [16] in the discrete plane of the house, the discrete points inside the contour are determined (red points from Figure 9). The elevation of each red or green point is calculated using the level curves. Using these elevations, the optimal elevation of the excavation/filling plane is computed. So, the following algorithm denoted AOEF is obtained.
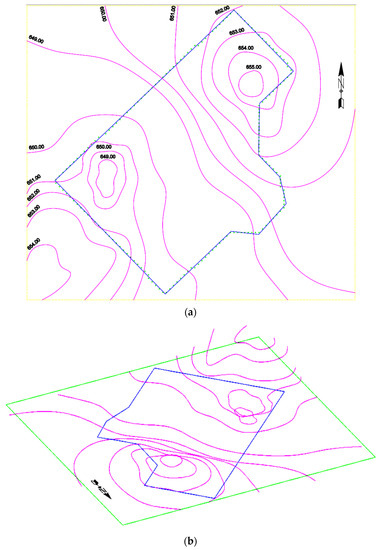
Figure 8.
Level curves (pink lines) in the vicinity of the house (blue lines): (a) 2D view; (b) 3D view.
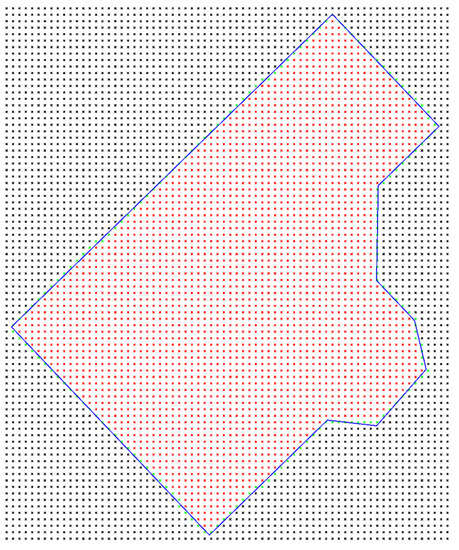
Figure 9.
Discretization of the plane of the house. Black points are outside the house, green points give the contour of the house, red points are inside.
Algorithm 4 Optimum Excavation/Filling (AOEF):
| Algorithm 4 Optimum Excavation/Filling (AOEF) |
| Input: the points Pi (i = 1, 2, ..., n) of the contour; for each point Pi do Find the closed discrete point P’i; end for; for i = 1 to n − 1 do Find the set of points Ci using Bresenham’s algorithm from point Pi to point Pi+1; end for; Using Bresenham’s algorithm from point Pn to point P1, find the set of points Cn; Find the points Qi (i = 1, 2, …, m) inside the contour given by C1 ∪ C1 ∪ … ∪ Cn; for each point Qi do Apply A2SSTPC2L to find the elevation zi of Qi; end for; |
Using the elevations zi, calculate the elevation of the optimal excavation/filling plane (see AHEFP).
Applying the elevations zi of the discrete points Qi inside the contour of the house, the elevation of the optimal excavation/filling plane can be determined as follows. The elevations are sorted ascendingly. A horizontal plane π(h) (h is the height/elevation of the plane) is placed consecutively starting with the first (the lowest) elevation, continuing with the second, and ending with the last one (the highest). The following algorithm is obtained:
Algorithm 5 Height of Excavation/Filling Plane (AHEFP):
| Algorithm 5 Height of Excavation/Filling Plane (AHEFP) |
| Input: vector of elevations z = (zi)i = 1, 2, …, m; Sort ascending the vector z; S = 0; for i = 2 to n do S = S + zi − z1; end for; S1 = 0; S2 = S; for i = 2 to n − 1 do S1 = S1 + (i − 1) ⋅ (zi − zi-1); S2 = S2 − (n − i + 1) ⋅ (zi − zi-1); if S2 ≤ S1 then opt = i; break; end if; end for; |
At each iteration of the last “for” loop from AFHEFP, the height of the plane is considered equal to zi, S1 is the sum of the distances between the elevation of zi the plane and the elevations below the plane, and S2 is the sum of the distances between the elevations over the plane and the elevation zi of the plane, i.e.,:
when starting a new iteration, S1 is the sum of i-1 components of z and was calculated in the previous iteration. The new sum S1 can be obtained from the previous by adding (i − 1) ⋅ (zi − zi-1).
At the beginning of each iteration, S2 is the sum of n-i+1 components of z and was calculated in the previous iteration. Thus, using the value of the previous S2, the new sum can be obtained from the previous by subtracting (n − i + 1) ⋅ (zi − zi-1).
Since S1 is increasing from 0 to S and S2 is decreasing from S to 0, the optimum is reached when S2 becomes less or equal to S1. More exactly, the optimum height of the plane is inside the interval [zopt-1, zopt]. If the values zopt-1 and zopt are close enough, i.e., zopt − zopt-1 < ε, where ε > 0 is the fixed maximum distance to the optimum, e.g., ε = 5 cm, then any of the values zopt-1 and zopt are good approximations of the optimum. If zopt − zopt-1 ≥ ε, then a divide and conquer strategy is applied to get closer to optimum. To do that, two initial planes π(zopt-1) and π(zopt) are considered. A new plane is placed in the middle. If the distance between S2 calculated for π((zopt-1+zopt)/2) and S1 for π(zopt-1) is less than the distance between S2 for π(zopt) and S1 for π((zopt-1+zopt)/2), then the optimum is further calculated in the interval [zopt-1, (zopt-1+zopt)/2]. Otherwise, the optimum is calculated in the interval [(zopt-1+zopt)/2, zopt] and so on.
Algorithm 6 divide and conquer for optimum excavation/filling plane (ADCOEFP):
| Algorithm 6 Divide and conquer for optimum excavation/filling plane (ADCOEFP) |
| a = zopt-1; b = zopt; Sa,1 = S1 − (opt − 1) ⋅ (zopt − zopt-1); Sa,2 = S2 + (n – opt + 1) ⋅ (zopt − zopt-1); Sb,1 = S1; Sb,2 = S2; while b − a ≥ ε do c = (a+b)/2; Sc,1 = Sa,1 + (opt − 1) ⋅ (c − a); Sc,2 = Sa,2 − (n − opt + 1) ⋅ (c − a); if |Sc,2 − Sa,1| < |Sb,2 − Sc,1| then a = c; Sa,1 = Sc,1; else b = c; Sb,2 = Sc,2; end if; end while; S1 = Sa,1; S2 = Sa,2; |
At the end of the while loop, any of the values, a or b are good approximations of the optimum. We considered a as the optimal solution. The approximate excavation volume is Ve = S2 ⋅ d2, and the filling volume is Vf = S1 ⋅ d2. Consequently, the difference between the two volumes is:
So, the two volumes are very similar.
3.4. Numerical Example
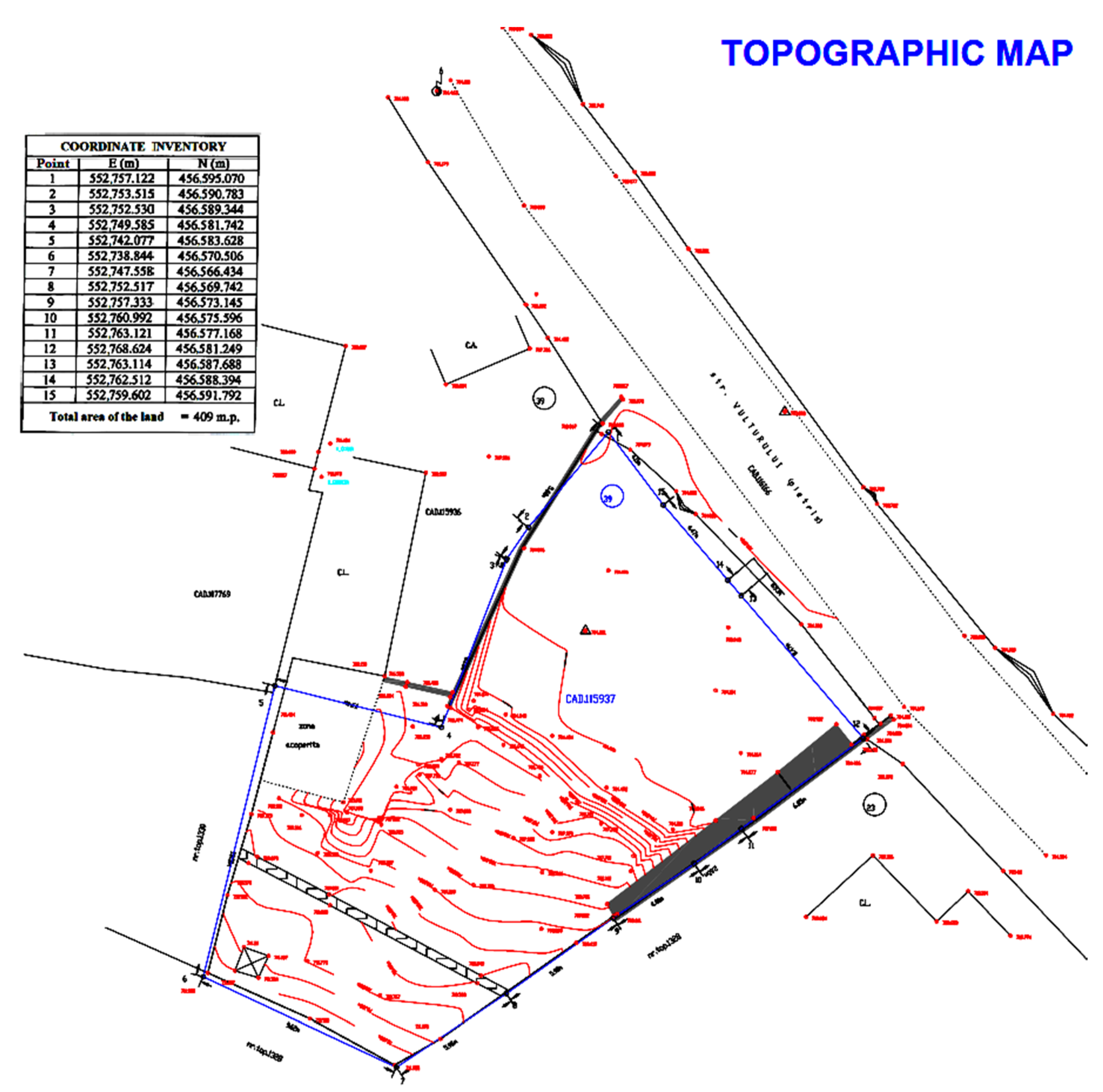
Figure 10 shows a real topographic map for a plot of land on which a house is to be built. The topographic map of the land was drawn up by a topometric engineer, with specific high-precision equipment, called in specialized terms “station.” For small areas of land, the station is successively placed and GPS 3D coordinates are measured relative to a fixed position (in our situation it is a terminal in the Black Sea area located at a distance of approximately 717 km). The first chosen points of the topographic survey are those that describe the contour of the plot of land. In our case, the terrain contour is described by the 15 points (numbered in black). These points are inventoried and noted in a table (coordinate inventory) located on the topographic map. The following points will describe the contour of the level elevations, the positioning of the access road, the position of the neighboring houses (they are marked on the map in red together with the elevation), etc. In the case of lands with a high slope, such as the one exemplified, the measured points must be thickened for a greater accuracy of tracing the level curves (in total we have over 100 such points).
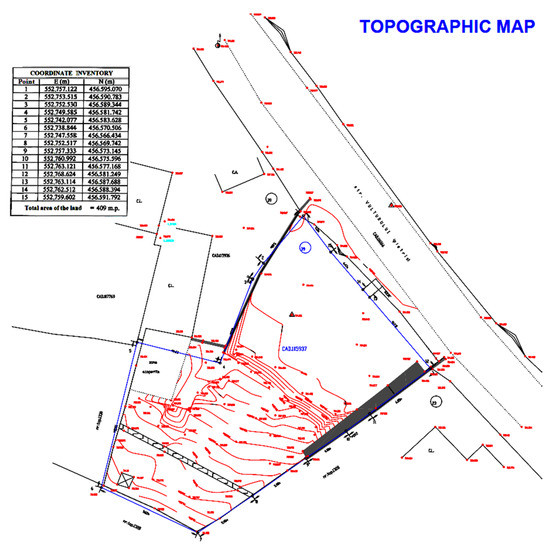
Figure 10.
Topographic map.
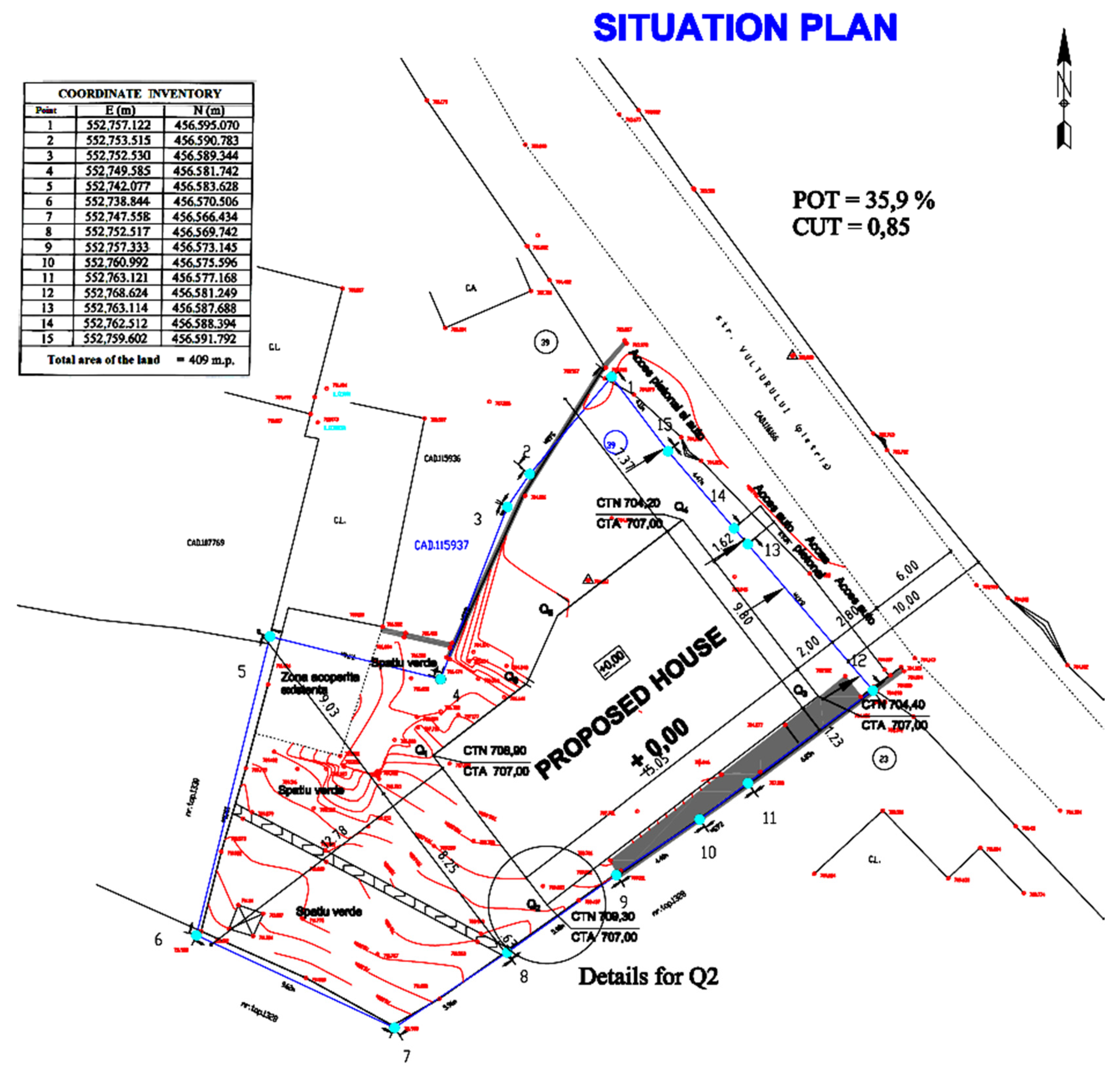
The designer receives in electronic format a topographic map similar to the one in Figure 10. On this topographic support, the designer will place the designed building on the scale, having to respect a series of rigors imposed by law, among which: the minimum distance from the property limit and/or from the road axis as in Figure 11. Once the construction is located, the new contour will appear on the topographic map described by a few new points (minimum 4, in the example, for the description of the contour, 6 points are used). A situation plan is drawn up in which, according to the legislation, the 2D coordinates of the corners of the construction must be specified (see Table 1) together with the elevation of the horizontal excavation/filling plane. In Figure 11, this elevation is denoted by CTA and is estimated at 707 m by the designer. A good determination of this elevation is not easy, especially if the terrain has a high slope.
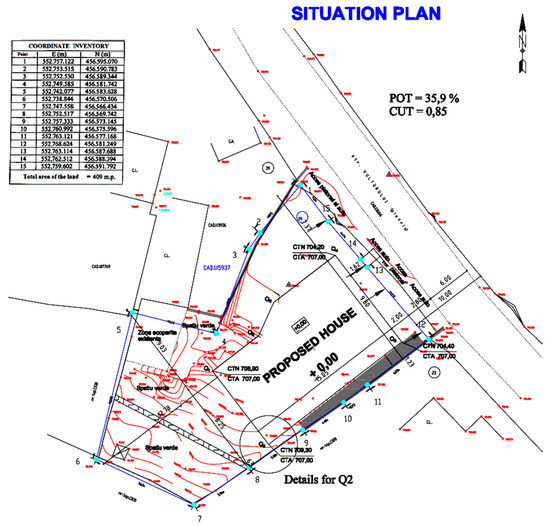
Figure 11.
Situation plan.

Table 1.
The x and y coordinates of the Q points.
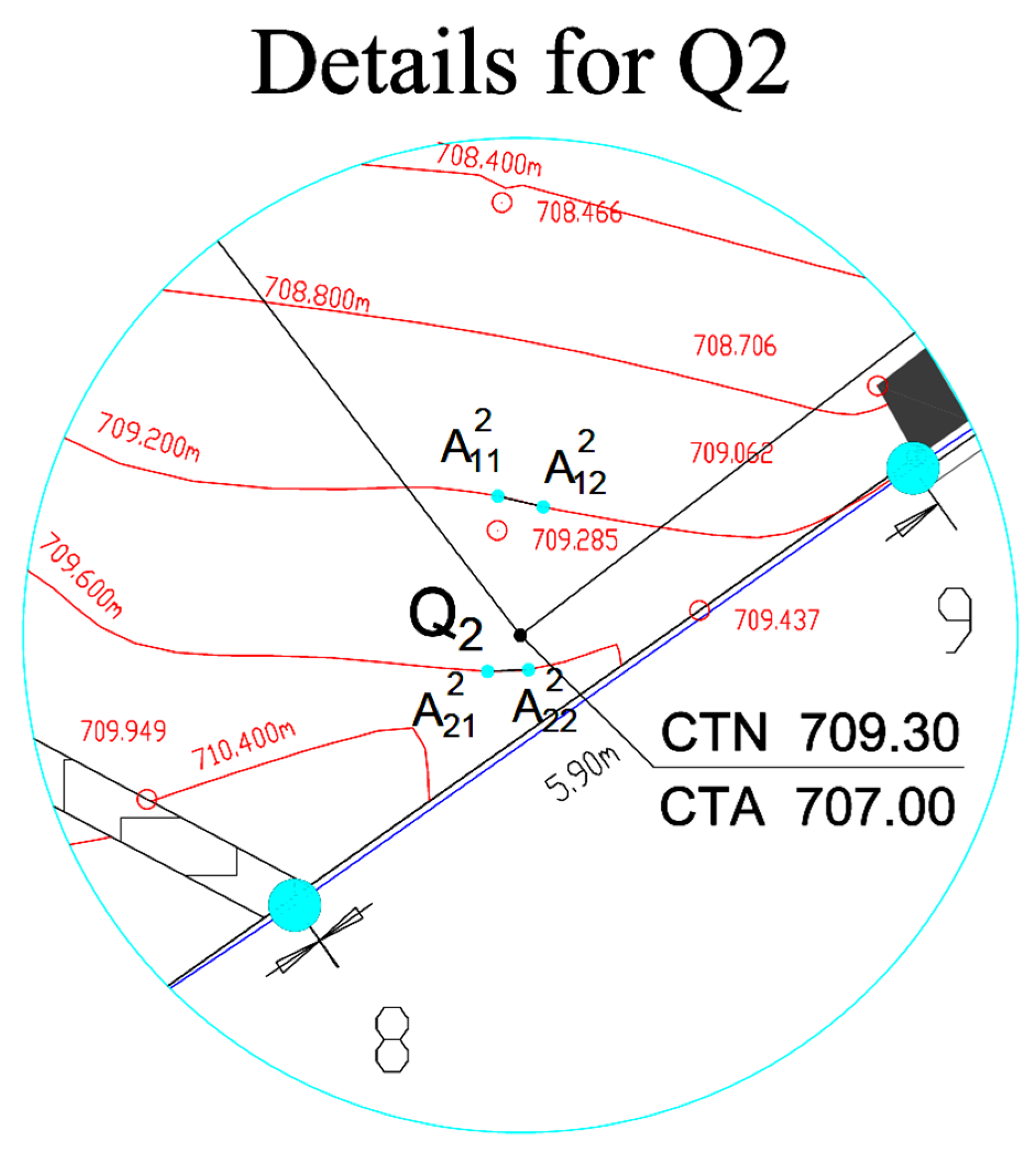
A detail of Figure 11 is presented in Figure 12 illustrating the points found using the algorithm AIPS.
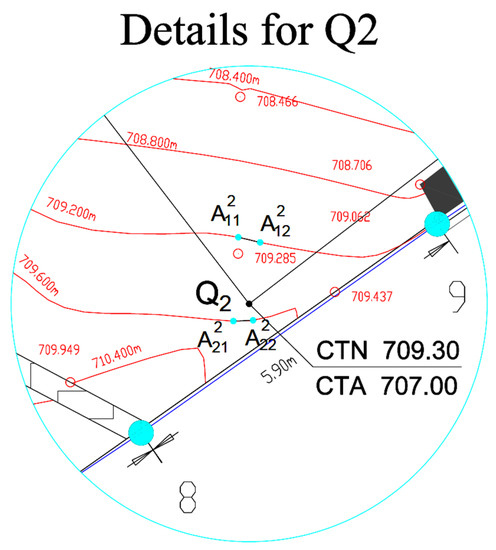
Figure 12.
Detail of Figure 11 for Q2.
Table 2 presents the coordinates of the points calculated for each point Qk (k = 1, 2, …, 6) by applying AIPS. Using A2SSTPC2L and (26), the elevation for each point Qk (k = 1, 2, …, 6) is calculated.

Table 2.
3D coordinates of the Q points.
Usually, for the dimensions of the project to be in accordance with the real construction, before commencing all the construction works, a plot is made on the field of the future building. For this purpose, the ground tracing is performed. The corners of the house are very precisely marked (the Q points). In our example, the provided measured elevations of the 6 points are presented in Table 3.

Table 3.
The estimated and the measured z-coordinates of the Q points.
As seen in Table 3, the estimated elevation and the measured one for each Q point are very close. The difference between them is less than 2 cm.
Using the coordinates of the points Qk (k = 1, 2, …, 6) from Table 1, Bresenham, and, then flood fill algorithms were applied resulting in 803 points located inside the perimeter of the house. The elevations of these points were calculated using A2SSTPC2L and (26). The algorithm AHEFP was applied for these 803 elevations and the height of the horizontal excavation/filling plane was accurately estimated as 706.2571 m, instead of the value 707 m proposed by the designer. Out of the 803 points, 412 were located below the horizontal plane, and 391 had the elevation over this plane.
4. Discussion
In order to compare the two proposed methods (from Section 2.1 and Section 2.2) for determining the points P1 and P2 100 million experiments were performed. For each experiment, two random lines d1 and d2 were selected and the point Q was also randomly chosen. The tests were performed using an ASUS ROG GL752VW-T4015D laptop with Intel® Core™ i7-6700HQ 2.60 GHz processor, and 8 GB of RAM.
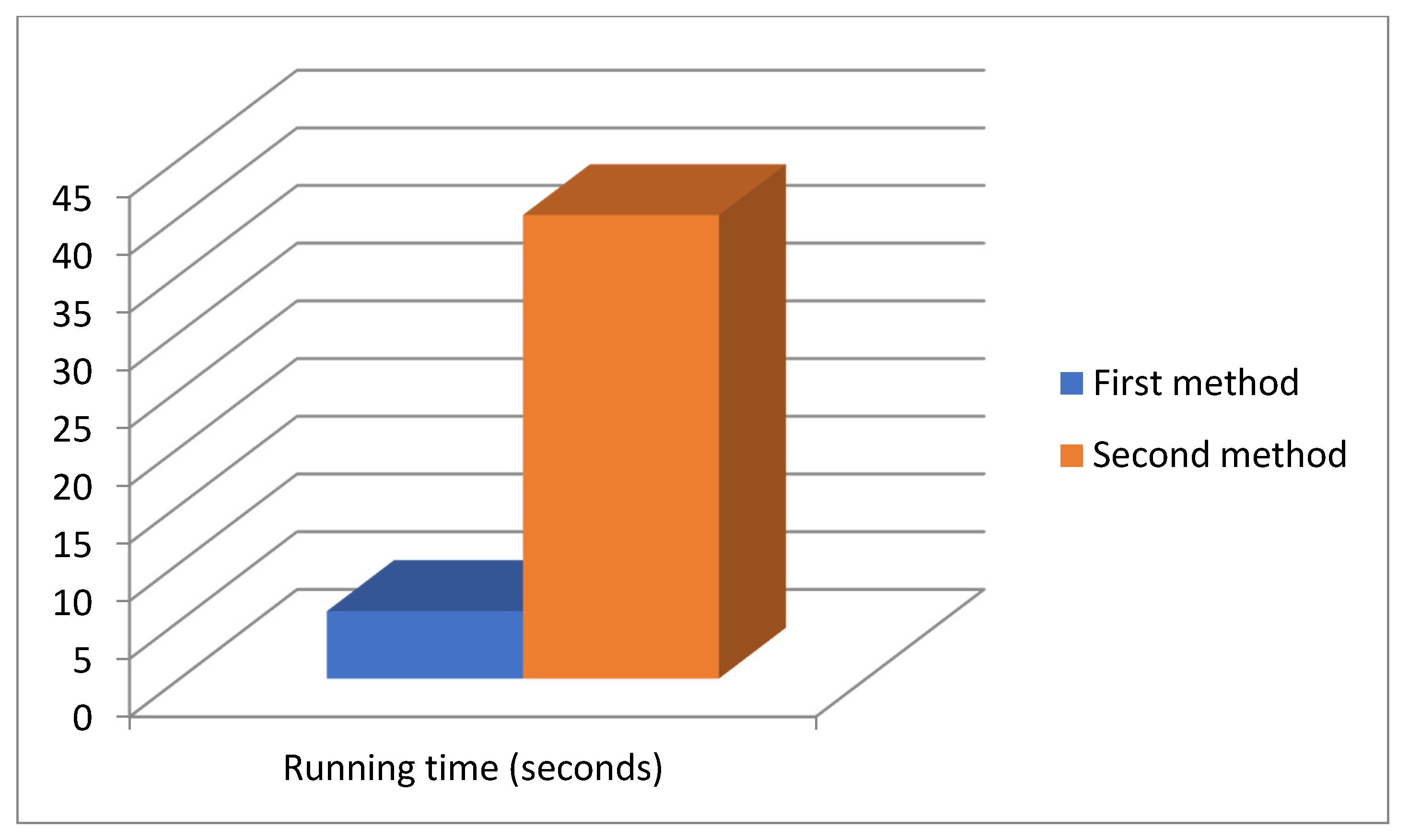
First, we analyzed the speed of the proposed methods. The total running time of the first method was 5.82 s. The total running time of the second method was 40.14 s. So, the first method is almost 7 times faster than the second one (see Figure 13). The first method is considerably faster because it requires elementary calculations, while the second one runs an iterative algorithm to solve the Equation (18).
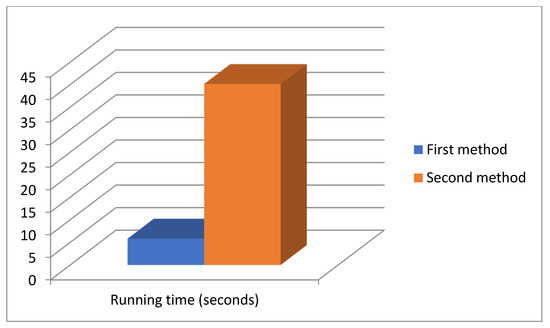
Figure 13.
Running time comparison of the two methods (100 million experiments).
We also calculated the accuracy of the first method against the second method since the error for the second method can be set as low as desired. An average error of 0.61% was obtained, the lowest error being 0 and the highest 1.17% (Table 4). So, we concluded that the accuracy of the approximate first method is good enough.

Table 4.
Errors of the first method obtained from 100 million experiments.
The steps of positioning the house will be next discussed, and the utility of the methods proposed in this paper will be shown. The designer receives a topographic map in electronic format. On this topographic support, the designer will place the designed building on the scale, having to comply with a series of rigors imposed by law, among which: the minimum distance from the property limit and/or from the road axis, etc. Once the construction is located, the outline of the house described by several new points will appear on the topographic map (minimum 4). At these new points, it is necessary to specify: the coordinates on the three dimensions according to which the elevation is specified, and the distances of the construction location from the property limits. The determination of the coordinates in the plan does not raise any concerns, but there are difficulties in obtaining the real vertical elevation especially if the terrain has a high slope. The article proposes a method for determining the exact elevation of the land at the corners of the building, and in fact for the entire contour. Depending on the contour dimensions, the designer establishes a position of the horizontal plane, a plane that corresponds to the finished floor of the ground level. The decision to establish this quota should be contingent on the volumes of embankments that will be made. The optimum is obtained when the excavation volume is approximately equal to the filling volume. The article solves this problem in Section 3.3.
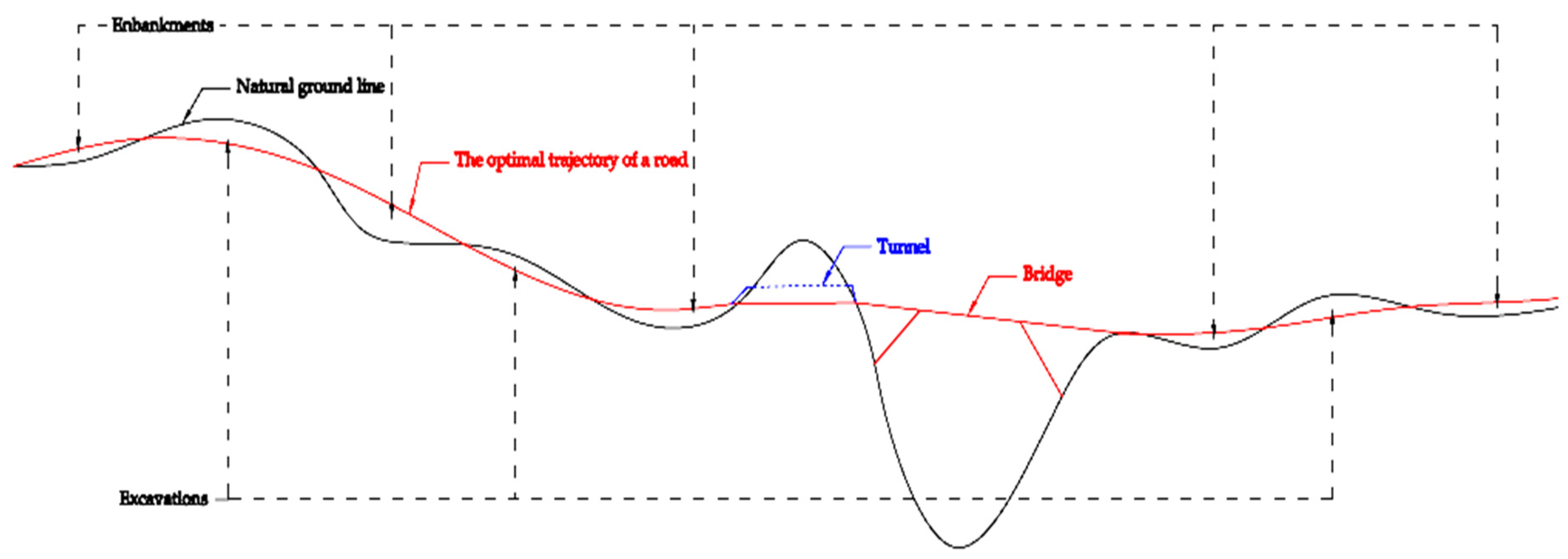
For the design of a road, a primary route of the road is made on a topographic map and road recognition is performed. A final design of the road follows both along its entire length and on its cross-sections. Figure 14 shows with a red line the optimal trajectory of a road depending on the elevation of the natural land. Because the considered road is a highway, the rules impose stricter restrictions on the slopes. If the allure of the natural terrain in certain areas is followed, the maximum allowed inclination of the road will inevitably be exceeded. As it can be seen in Figure 14, in these areas, measures must be taken to straighten the slope, such as fillings, excavations or the provision of bridges and viaducts, tunnels respectively. Through detailed awareness of the elevations and the inclination of the land in the points near the road, an optimal vertical tracing of the road can be established so that we have minimum excavations and fillings for an imposed road slope, or we can optimize the lengths of the bridges, respectively tunnels [12].
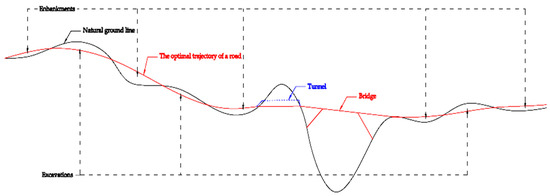
Figure 14.
The optimal trajectory of a road depending on the elevation of the natural land.
When designing a new road or railway, a number of initial design factors must be taken into account, such as: road category, design speed, width of a traffic lane, number of lanes, traffic frequency, equipment size, etc. Depending on the route imposed on the road, there are also other specific aspects that must be taken into account:
- Avoid high erosion hazard sites, particularly where mass failure is a possibility.
- Utilize natural terrain features such as stable benches, ridgetops, and low gradient slopes to minimize the area of road disturbance.
- If necessary, include short road segments with steeper gradients to avoid problem areas or to utilize natural terrain features.
- Avoid midslope locations on long, steep, or unstable slopes.
- Locate roads on well-drained soils and rock formations which dip into slopes rather than areas characterized by seeps, highly plastic clays, concave slopes hummocky topography, cracked soil and rock strata dipping parallel to the slope.
- For logging road, utilize natural log landing areas (flatter, benched, well-drained land) to reduce soil disturbance associated with log landings and skid roads.
- Avoid undercutting unstable, moist toe slopes when locating roads in or near a valley bottom.
- Roll or vary road grades where possible to dissipate flow in road drainage ditches and culverts and to reduce surface erosion.
- Select drainage crossings to minimize channel disturbance during construction and to minimize approach cuts and fills.
- Locate roads far enough above streams to provide an adequate buffer, or provide structure or objects to intercept sediment moving down slope below the road.
- If an unstable area such as a headwall must be crossed, consider end hauling excavated material rather than using sidecast methods. Avoid deep fills and compact all fills to accepted engineering standards. Design for close culvert and cross drain spacing to effectively remove water from ditches and provide for adequate energy dissipators below culvert outlets. Horizontal drains or interceptor drains may be necessary to drain excess groundwater [13].
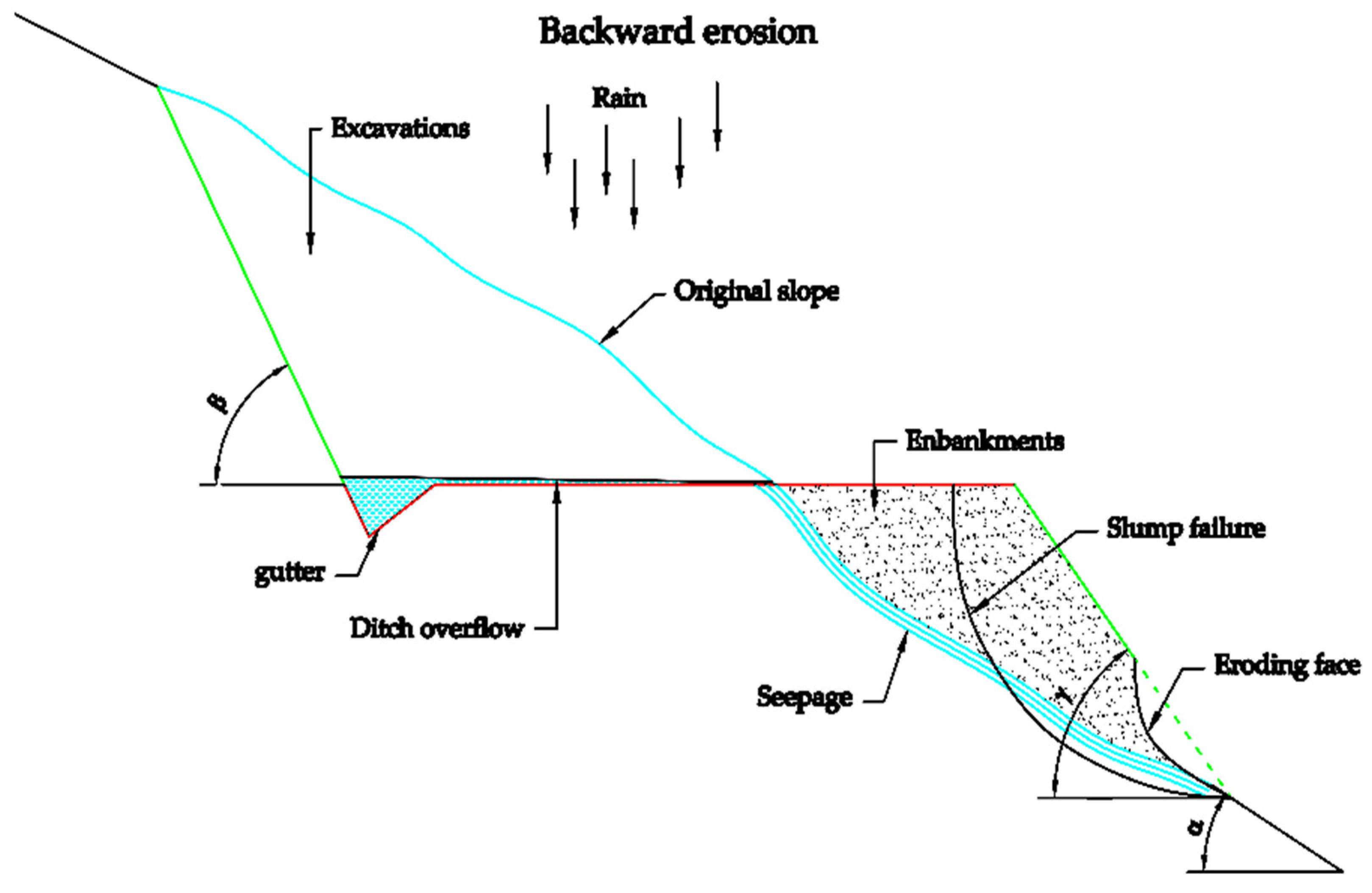
As seen in Figure 15, the angle of inclination of the terrain is an important parameter to know in order to avoid erosion and then landslides [18,19].
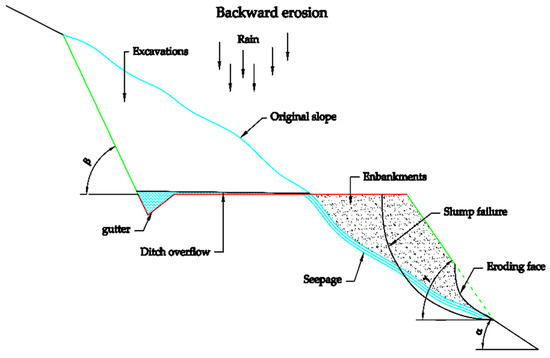
Figure 15.
Draining excess water to prevent landslides.
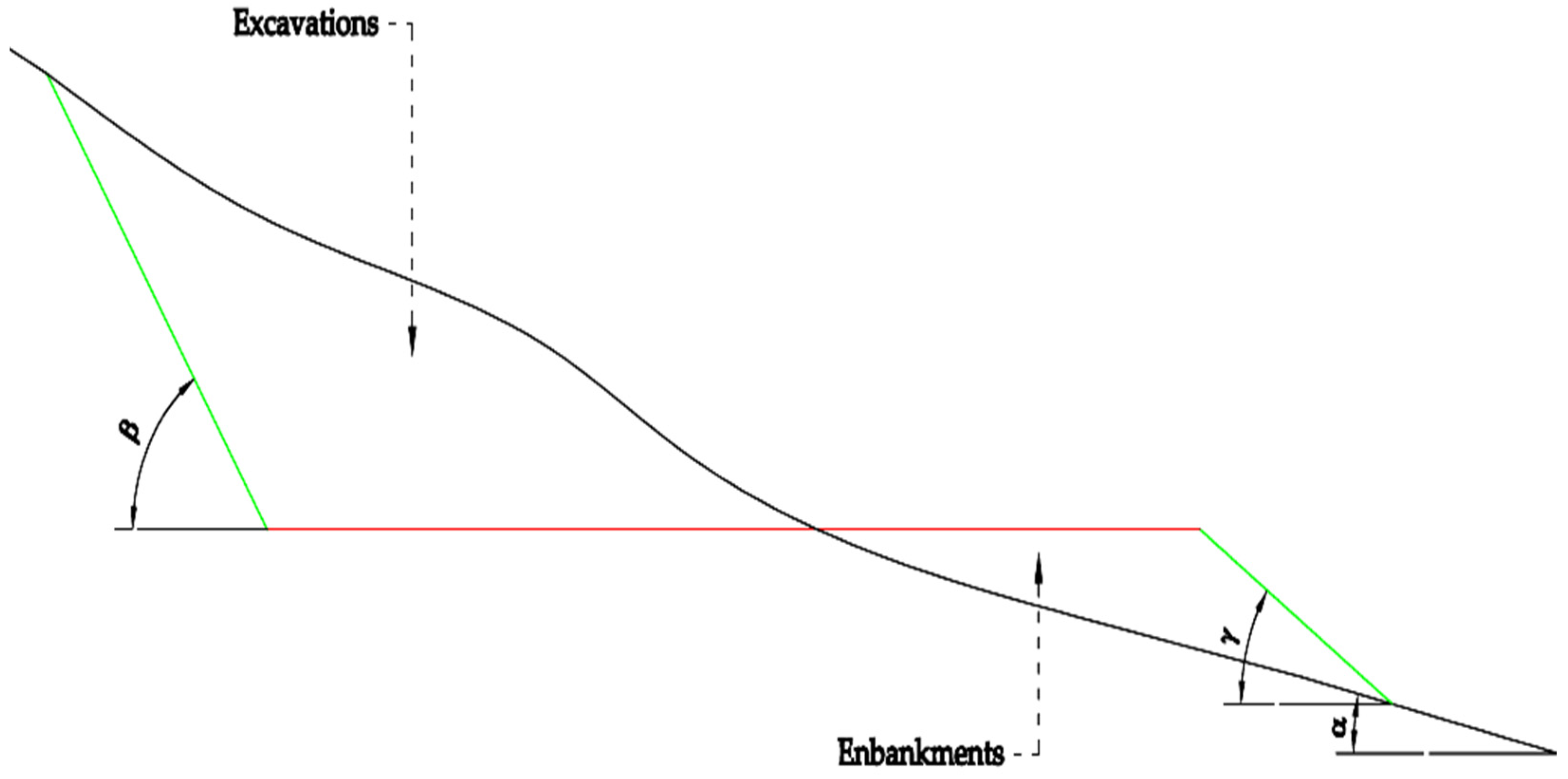
From the point of view of the cross-sections, the position of the road in relation to the terrain slope must take into account the above constraints. By the same token, knowing the slope of the land is essential for establishing the position both horizontally and especially vertically of the road, and for achieving a low cost related to the embankment works. This position is established according to the Full Bench Road Prism, which contains the elements in Figure 16.
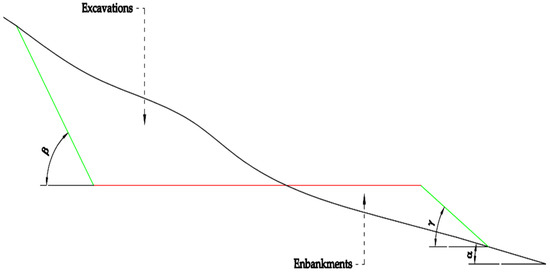
Figure 16.
Elements of road prism geometry.
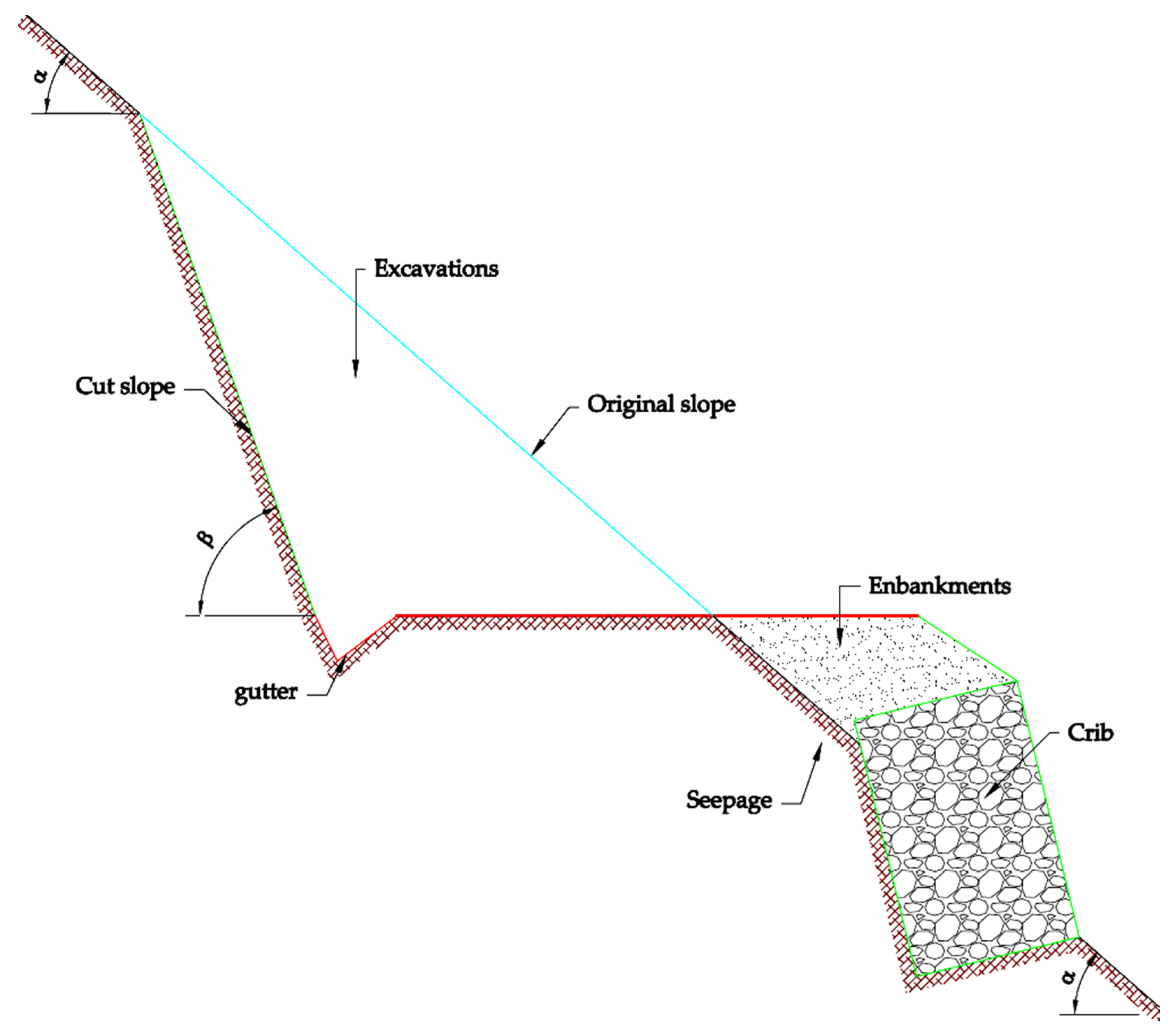
For very steep road areas such as the one in Figure 17, knowing the slope is imperative because substantial savings in embankment volumes can be made, resulting in decreasing the quantities of gabions or excavations [13].
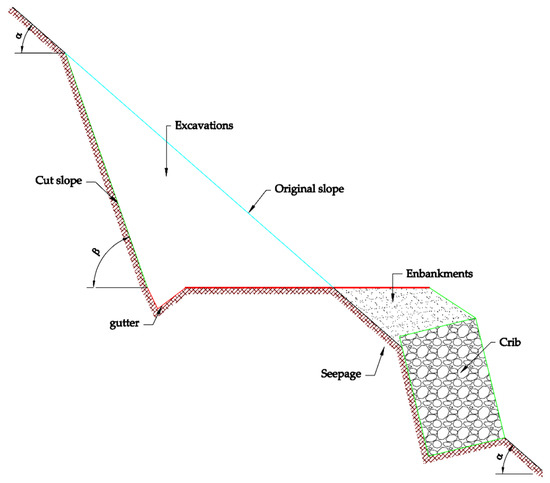
Figure 17.
Reduction in excavation made possible on a steep slope by the use of cribbing.
The problem related to determining the slope of natural land at a point on the topographic map is necessary both in the longitudinal section and in the cross-section of roads or railways and have the same solution described in Section 3.1 and Section 3.2.
The proposed methods can also be applied in environment protection, and hydrotechnical engineering [18,19]. The evaluation of the slope is also necessary for river levees. Slope stability analyses are conducted with rising water levels until certain failure is reached. Discharge occurs at a water height of around 7 cm above the crown, which means the slope would actually fail before reaching the hydraulic heads used for slope stability calculation during the overflow [20].
5. Conclusions
To conclude, the correct estimation of elevation at points has a practical application to calculate the optimum excavation/filling plane when a new house is built. The article presented a method to estimate accurately the elevation of this plane which reduces the costs of embankments.
When designing a new road or railway, designers need to know the ground slope at some points of the future road or rail as exactly as possible, as well as the elevation of each considered point, and, also, the slope of each consecutive two points. Instead of sending workers on the field to perform measurements, these values can be calculated with very good accuracy using the methods described in Section 2.1, and Section 2.2. Two algorithms to solve SSTPC2L are presented, a fast and approximate one and an exact but slower one. The error of the first method is low (see Table 1). It has the advantage of being very fast and accurate enough. Thus, if there are many points for which SSTPC2L is applied, the first method can be preferred. However, if we look for a more accurate solution, the second method is more suitable.
Author Contributions
Conceptualization, A.M.D. and O.D.; methodology, A.M.D. and O.D.; software, A.M.D.; validation, O.D.; formal analysis, A.M.D.; investigation, O.D.; resources, A.M.D. and O.D. data curation, A.M.D. and O.D.; writing—original draft preparation, A.M.D. and O.D.; writing—review and editing, A.M.D. and O.D.; supervision, A.M.D.; funding acquisition, A.M.D. and O.D. Both authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by University Transilvania of Brașov.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Levin, A.H. Hillside Building: Design and Construction, US 2nd ed.; Builder’s Book Ink: Los Angeles, CA, USA, 1999. [Google Scholar]
- Tarbatt, J.; Tarbatt, C.S. The Urban Block—A Guide for Urban Designers, Architects and Town Planners; RIBA Publishing: London, UK, 2020; ISBN 9781859468746. [Google Scholar]
- Kicklighter, C.E.; Thomas, W.S. Architecture: Residential Drafting and Design; G-W Publisher: Tinley Park, IL, USA, 2018. [Google Scholar]
- Pyrgidis, C.N. Railway Transportation Systems: Design, Construction and Operation; CRC Press: Boca Raton, FL, USA, 2019; ISBN 9780367027971. [Google Scholar]
- Ellis, P. Guide to Road Design Part 1: Introduction to Road Design; Austroads Ltd.: Sydney, Australia, 2015. [Google Scholar]
- Fannin, R.J.; Lorbach, J. Guide to Forest Road Engineering in Mountainous Terrain; Rome (Italy) FAO: Rome, Italy, 2007. [Google Scholar]
- Deaconu, O.; Deaconu, A. Numerical methods to find the slope at a point on map using level curves. In IOP Conf. Series: Materials Science and Engineering, Proceedings of the Application in Road Designing, International Conference CIBv2019 Civil Engineering and Building Services, Brașov, Romania, 1–2 November 2019; IOP Publishing: Philadelphia, PA, USA, 2020; p. 789. [Google Scholar]
- Aruga, K.; Sessions, J.; Akay, A.E.; Ching, W. Forest Road Deisign and Construction in Mountain Terrain. In Proceedings of the Conference of IUFRO, Vancouver, BC, Canada, 13–16 June 2004. [Google Scholar]
- Sutton, R. An Introduction to Topography; Larsen and Keller Education: New York, NY, USA, 2017; ISBN 13 978-1635492774. [Google Scholar]
- Suresh, N.; Akhilesh, K.M.; Avijit, M.; Prasanta, S.; Praveen, E. Review of Alignment design consistency in Mountainous/Hilly Roads. In Proceedings of the 3rd Conference of Transportation Research Group of India, Kolkata, India, 17–20 December 2015. [Google Scholar]
- Jin, X.; Wei, L.; Yiming, S. New design method for horizontal alignment of complex mountain highways based on “trajectory–speed” collaborative decision. Adv. Mech. Eng. 2017, 9, 1–18. [Google Scholar]
- Siviero, L. Roads and Verticality Strategy and Design in Mountain Landscape. Ph.D. Thesis, Faculty of Engineering, University of Trento, Trento, Italy, 2012. [Google Scholar]
- Sheng, T.C. Watershed Management Field Manual, Food and Agriculture Organization of the United Nations; Rome (Italy) FAO: Rome, Italy, 1998. [Google Scholar]
- Quarteroni, A.; Sacco, R.; Saleri, F. Numerical Mathematics; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Burden, R.L.; Faires, J.D. 2.1 The Bisection Algorithm, Numerical Analysis, 3rd ed.; PWS Publishers: Boston, MA, USA, 1985; ISBN 0-87150-857-5. [Google Scholar]
- Smith, A.R. Tint Fill. In SIGGRAPH ‘79: Proceedings of the 6th Annual Conference on Computer Graphics and Interactive Techniques; Association for Computing Machinery: New York, NY, USA, 1979; pp. 276–283. ISBN 978-0-89791-004-0. [Google Scholar]
- Bresenham, J.E. Algorithm for computer control of a digital plotter. IBM Syst. J. 1965, 4, 25–30. [Google Scholar] [CrossRef]
- Jadid, R.; Montoya, B.M.; Gabr, M.A. Strain-based Approach for Stability Analysis of Earthen Embankments. In Proceedings of the Dam Safety Conference, Online, Palm Springs, CA, USA, 21 September 2020–31 December 2020. [Google Scholar]
- Jiang, S.; Liu, X.; Huang, J. Non-intrusive reliability analysis of unsaturated embankment slopes accounting for spatial variabilities of soil hydraulic and shear strength parameters. Eng. Comput. 2020, 333, 1–14. [Google Scholar] [CrossRef]
- Rossi, N.; Bačić, M.; Kovačević, M.S.; Librić, L. Development of Fragility Curves for Piping and Slope Stability of River Levees. Water 2021, 13, 738. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).