1. Introduction
In a noisy real-time environment, the performance efficiency of Blind Source Separation (BSS) applications is degraded by background noise and interfering signals. The classical methods used for speech enhancement have reached their saturation level in terms of enhancement and performance. The estimation of the desired source signal from a mixture with noise, especially for non-stationary noisy conditions, is a bottleneck for these techniques. Therefore, the BSS applications require a solution that can suppress the noise according to the nature of the environment.
The speech signal enhancement problem has been well-studied in recent decades. Different solutions are provided to enhance the intelligibility and quality of the speech signals and improve the performance of the BSS systems. The classical techniques overcome this problem by using adaptive techniques such as minimum means square error (MMSE) [
1,
2,
3,
4,
5,
6,
7]. The MMSE adjusts itself according to the observed convolutive mixture. Another solution uses statistical models which accurately diagonalize the second-order statistical properties of the noisy reverberant mixture. This approach uses an auto-correlation covariance matrix and its one-sample delayed matrix, forming two positive definite symmetry matrices. Then, the matrices’ diagonalization can be exploited accurately by computing a generalized singular value decomposition (GSVD) using the tangent algorithm [
8].
The BSS methods extract the desired source speech signal from the convolutive mixture in the presence of noise. Various BSS methods such as Independent Component Analysis (ICA) and FASTICA extract the source speech signals in a noisy reverberant environment. First, the ICA de-noises the noisy reverberant mixture followed by the FASTICA algorithm to separate the de-noised estimated speech signal from the observed convolutive mixture [
9]. Additionally, in an undermined scenario, ICA is combined with a speech recognition system (SRS) to extract the desired targeted speech signal [
10]. However, these methods require prior knowledge of the mixing process and a number of source signals. Therefore, the advantage of our proposed BSS methods is that it separates the targeted source speech signal from the reverberant mixture without prior knowledge of the mixing process nor the number of source signals. This gives our approach an additional efficiency over existing speech processing methods that require prior knowledge or training. Unlike the existing models, we have used multivariate generalized Gaussian and super-Gaussian source priors as a hybrid source prior model. In this hybrid model, the generalized Gaussian source prior exploits higher-order statistical properties while multivariate super-Gaussian models use other related information.
The main problem encountered by BSS techniques is the permutation and scaling ambiguities after the speech separation process. Therefore, in [
11], the authors proposed a solution that can easily recognize the desired source speech signal in a noisy environment by looking at the speaker’s face. An audiovisual coherence is used to estimate the speech signals using statistical methods where statistical tools model the audio and visual information in the frequency domain (FD).
Furthermore, in multiple audio sources with scenarios with multiple microphones, the performance of the BSS separation process is improved by using the BSS output to generate the Wiener filter coefficients and applying them to the desired speech signals [
12]. Moreover, adaptive filtering with BSS can also reduce the noise, leading to speech enhancement and noise reduction. Forward Blind Source Separation (FBSS) combined with the Simplified Fast transversal filter (SFTF) method results in adoption gain from forwarding prediction [
13]. Nevertheless, adaptive filtering methods face problems while canceling or suppressing the acoustic noise. This issue is tackled using the Modified Predator–prey particle swarm optimization (MPPPSO) approach. It also solves the problem of steady-state error of PPPSO for non-stationary inputs and a large filter length [
14].The acoustic noise can also be suppressed by introducing variable step size in a two-channel sub-band forward algorithm (2CSF) that improves the convergence speed and overcomes the fixed step size problem in the traditional 2CSF method [
15]. Another approach using variable step sizes is adaptive blind source separation through a two-channel forward–backward structure based on the normalized least-mean square (NLMS) method that uses variable step sizes for steady-state conditions [
16]. The estimated source signal enhancement in the presence of acoustic noise is performed by Threshold Wavelet-based Forward Blind Source Separation (TWFBSS). This approach reduces the computational complexity from the Wavelet-based Forward Blind Source Separation (WFBSS) method [
17].
Kalman filters can also be used with BSS techniques to deal with the noisy convolutive mixture. First, the BSS approach extracts the estimated source speech signal from the non-stationary noisy reverberant mixture. Then, Kalman filtering suppresses the noise components in the estimated speech signal [
18]. Recently, new evolving techniques such as deep learning are also applied with the BSS approach in the reverberant noisy environment [
19]. In general, the BSS methods are tested under non-Gaussian noise modeled by the fourth-order cumulant, and the singular value decomposition-total least square method [
20]. Moreover, the speech signals are often corrupted by different types of noise produced in the surrounding environment that can be tackled by the Dual Recursive non-Quadratic (DRNQ) adaptive method combined with FBSS to enhance the speech quality [
21].
1.1. Background
The BSS methods estimate the desired source speech signals from the observed convolutive mixture containing noise. However, accurate identification of the targeted speech signal in a noisy reverberant environment is the fundamental goal of the speech processing systems. The traditional BSS methods are limited to multiple speech signals and sensors, where the de-noising process is challenging. Nevertheless, various signal processing methods, such as Single-channel Blind Source Separation (SBSS), Sparse Component Analysis (SCA), and Variation Mode Decomposition (VMD), can tackle this issue. The VMD method is applied to decompose a single channel into two channels, and then SCA separates the speech signals. This approach shows enhancement of speech signal in under-determined conditions [
22].
Another approach, AdaGrade, is proposed in [
23] for blind audio speech extraction that uses the gradient-based algorithm. The gradient learning rule is modified by pre-conditioning the input signal and using the AdaGrade update. In this method, the natural gradient method with two-step pre-processing suppresses the noise in the receiving reverberant mixture. First, the bias removal method followed by the least-square method is applied to de-noise the noisy convolutive mixture. Then, a joint algorithm with a gradient method estimates the noisy signals and the mixing matrix [
24]. Moreover, in [
25], the BSS involves Eigen filtering, which receives the dominant frequencies of the signal, and then Wavelet de-noising is applied. It suppresses the noise components and retains the speech signal regardless of its frequency components. The authors of [
26] propose an alternate method based on temporal predictability to obtain the individual independent noise signal where a non-negative matrix factorization algorithm enhances the speech signal. The performance is improved by adding time-correlation to the objective function, which restricts the time-varying gain of the noise [
27]. Moreover, masking techniques can also be applied to separate the desired speech signal from the received mixture, where the time-frequency masking rule can define the BSS method [
28]. In [
29], the authors propose an EM algorithm to suppress the noise in the convolutive mixture for the complex-Gaussian signal model and the unknown deterministic model. The statistical model is defined for both models, and the EM algorithm is developed for these models to estimate the speech signal and its acoustic parameters.
Recently, unsupervised speech enhancement algorithms are gaining interest that use a Real-Time (RT) two-channel BSS algorithm. In this method, a non-negative matrix factorization (NMF) dictionary is combined with a generalized cross-correlation (GCC) spatial localization approach. The RT-GCC-NMF operates in a frame-by-frame manner, comparing individual dictionary atoms with the desired speech signal or interfering noise based on the time-delay arrivals [
30].
1.2. Contributions
The BSS approach separation gain depends on the selection of an appropriate source prior function for extracting the desired speech signals [
31,
32]. For example, [
33] proposes a mixed source prior model comprised of super-Gaussian and Student’s T to enhance the performance of the BSS. Consequently, in [
34], the performance is improved by using a hybrid model, consisting of multivariate super-Gaussian and generalized Gaussian source priors. This approach models the higher amplitudes of the observed convolutive mixture by a multivariate generalized Gaussian source prior, and the low amplitudes are exploited by a multivariate Gaussian source prior. Unlike these existing works, we propose an efficient multistage BSS method. In this method, multivariate generalized Gaussian and super-Gaussian source priors are combined as a hybrid source prior model. The generalized Gaussian one exploits higher-order statistical properties while other related information is modeled by the multivariate super-Gaussian one. The contributions of this research work are as follows:
We propose a novel efficient multistage approach for BSS applications. This method concatenates the hybrid approach. Our proposed hybrid models combine multivariate generalized Gaussian and super-Gaussian source priors.
Based on the hybrid model, two different schemes are introduced, i.e., first BSS followed by de-noising and second de-noising in the first stage followed by BSS.
The performance of the proposed multistage hybrid model is evaluated with other multistage BSS methods having single source priors.
The performance of the proposed models are investigated via extensive simulations in a noisy reverberant environment.
1.3. Organization
The article is organized into the following sections.
Section 2 describes the hybrid source prior signal model for the Independent Vector Analysis (IVA).
Section 3 provides a detailed description of the proposed multistage approach for speech enhancement, followed by the results and discussion in
Section 4. In
Section 5, we evaluate the performance of the proposed multistage model.
Section 6 presents the conclusion and future works.
2. Signal Model
Consider a clean source speech signal
, noise signal
, mixing matrix
A, and received speech signal
contaminated by noise. It can be mathematically modeled as
The clean speech source signal, noise signal and the received noisy speech signal are transformed to the FD domain and these parameters are denoted by
,
, and
, respectively, while
k denotes the position index of the coefficient in the transformed domain. The design criteria of the estimator for the observation are to minimize the MSE given by
where
is the expectation operator and
is the estimated source signal. Minimum Mean Square Error (MMSE) filter can be used to minimize the mean square error (MSE) in (
2).
In a given noisy observation
with received signal
. The estimated
can be obtained by [
35],
Equation (
3) can be rewritten by Baye’s theorem [
35,
36,
37],
where
is the probability density function (pdf) and
denotes the dummy variable representing all possible values of
. Assuming a Gaussian distribution model, then
and
can mathematically written as
and
where
and
are the variances of the noisy signal and clean signal, respectively. Putting (
5) and (
6) in (
4), then
can be rewritten as [
35,
36],
where
is the a priori SNR and
. The values of
and
must be known. [
38,
39] shows the detailed method for estimating
. A decision directed estimating method was developed to estimate
[
36]. The equation of estimating
for
is given by [
35]
where
is the maximum function. It is used to obtain non-negative values.
is the estimated value of
of the previous frame.
is the constant tuned for the best results. The value of parameter
is set to
. If
is set to 1, it deteriorates the speech signal and smaller values result in high musical noise.
3. Proposed Multistage BSS Approach
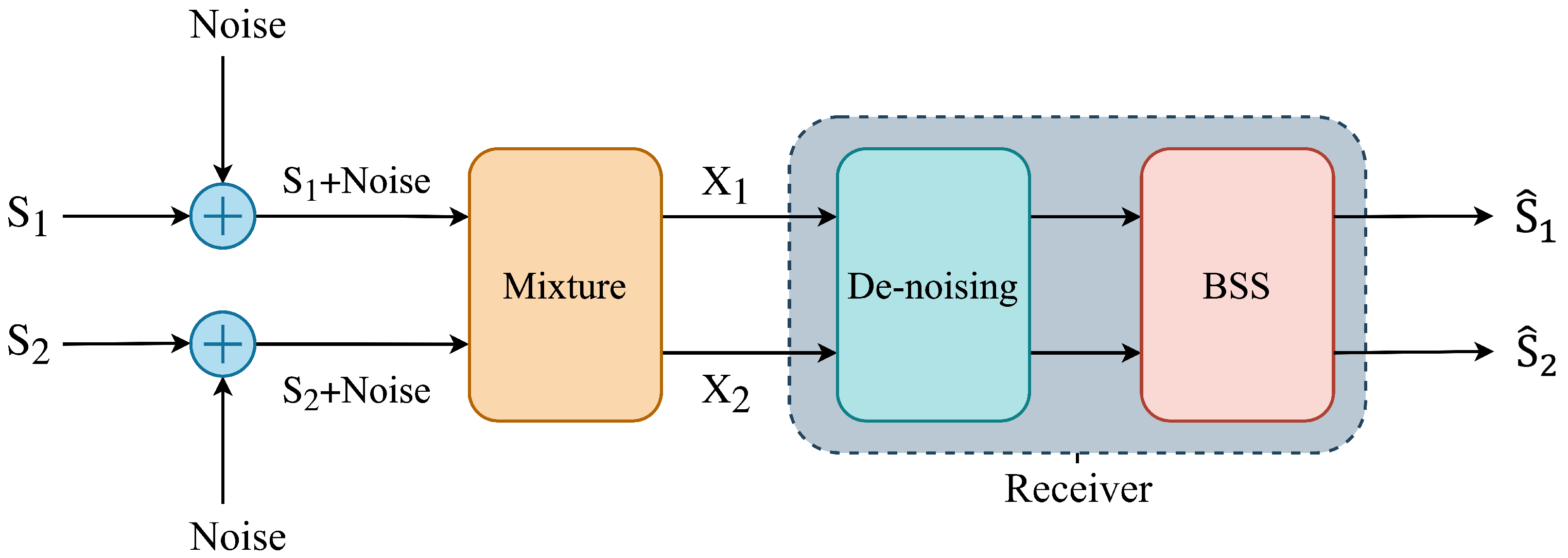
This section presents the proposed multistage approach for BSS and speech enhancement in a noisy reverberant environment. The multistage method comprises the BSS stage and de-noising stage using MMSE filtering as shown in
Figure 1 and
Figure 2, respectively. The proposed scheme evaluates different combinations of the BSS hybrid model and the de-noising MMSE method. In the first model (
Figure 1), the observed convolutive mixture speech signal is first processed by the BSS stage with a hybrid source prior model for the extraction of estimated speech signals from the reverberant mixture. The de-noising module processes the resultant noisy extracted speech signals where the noisy elements in the separated speech signals are suppressed to improve the quality of the estimated signals. In the second model (
Figure 2), the received reverberant observed speech mixture is de-noised by the MMSE filtering method in the first stage. In the second stage, the enhanced convolutive speech mixture is processed by the BSS stage with a hybrid source prior model to extract the de-noised estimated source speech signal from the enhanced reverberant mixture.
Multivariate generalized Gaussian and super-Gaussian source priors are combined into the hybrid source prior model in the BSS stage. The generalized Gaussian model exploits higher-order statistical properties while multivariate super-Gaussian models use other related information in the hybrid source prior model approach. The weights of the source priors in the hybrid model are adopted following the energy components of the received convolutive mixture [
34]. In the de-noising stage, the MMSE filtering method is used to suppress the noisy component in the received convolutive mixture signal.
The hybrid source prior model provides a better separation performance and preserves the frequency dependencies between different frequency blocks for the IVA algorithm. Instead of using a single source prior distribution, a combination of multivariate generalized Gaussian and super-Gaussian models is used for source priors for the IVA to preserve the frequency dependencies. By using the Kullback–Leibler (KL) divergence cost function to preserve the dependencies within the source speech signal while removing the dependencies among different source signals [
40]. Mathematically the non-linear cost function for the hybrid model can be written as [
31]
where
is the
k-th separating matrix and
is the source prior of
i-th estimated source signal. The multivariate cost function in (
9) is minimized by the gradient descent algorithm to remove the dependencies among different source signals and mathematically can be expressed as [
31]
where
I is the identity matrix and
is the non-linear score function which can be mathematically expressed as [
34]
The non-linear score function retains the dependency between different frequency bins, which is the main theme of the IVA algorithm and plays a vital role in the separation process. Fundamentally, the IVA method [
31] uses a multivariate super-Gaussian distribution source prior to model the different frequency bin inter-frequency dependencies, which are expressed as,
where
represents the standard deviation of
i-th source at
k-th frequency block. Using Equation (
11) to determine the score function of Equation (
12), we obtain
Equation (
13) shows the non-linear score function of the fundamental IVA algorithm and is used for inter-frequency dependencies between source signals. However, the non-linear score function is not unique and is strongly dependent on the source prior. Therefore, we can use different source priors to exploit higher-order statistics. The generalized multivariate Gaussian can also be used as a source prior distribution to retain inter-frequency dependencies between different frequency blocks. Due to its heavy tails, it exploits higher-order statistical properties between the source signal and can be expressed as [
32]
We assume the mean
and covariance
equal to identity. Then, using Equation (
11) for Equation (
14), the score function will be
In a noisy real-time environment, the non-stationary nature of the observed convolutive mixture contains high- as well as low-energy components. Hence, it is difficult for a single source prior to model the statistical properties of a non-stationary convolutive mixture. Therefore, a hybrid model is proposed containing multivariate generalized Gaussian and super-Gaussian source priors. The hybrid source prior model can better model low and higher amplitudes [
34]. The super-Gaussian source prior function models low-energy amplitude, and the high-energy amplitude is modeled by a multivariate generalized Gaussian source prior. The weights between these source priors in the hybrid source prior model are adopted based on the energy of a noisy convolutive mixture. The hybrid model can be expressed as
is the multivariate generalized Gaussian source prior distribution and
is the super-Gaussian source prior distribution. The non-linear hybrid score function is mathematically written as
where
is the weighting parameter, which depends on the normalized energy of the received noisy convolutive mixture. The weights of the non-linear score functions and
are adjusted by the normalized energy of the mixture at every frequency block.
5. Performance Evaluation
In this section, the separation performance of the proposed model is compared with various multistage BSS approaches with different source priors such as multivariate super-Gaussian [
31], Student’s T [
42], and generalized Gaussian distributions [
32]. The two proposed multistage models use the BSS approach to separate the estimated speech signals from the noisy convolutive mixture followed by the MMSE filtering technique to de-noise the signals.
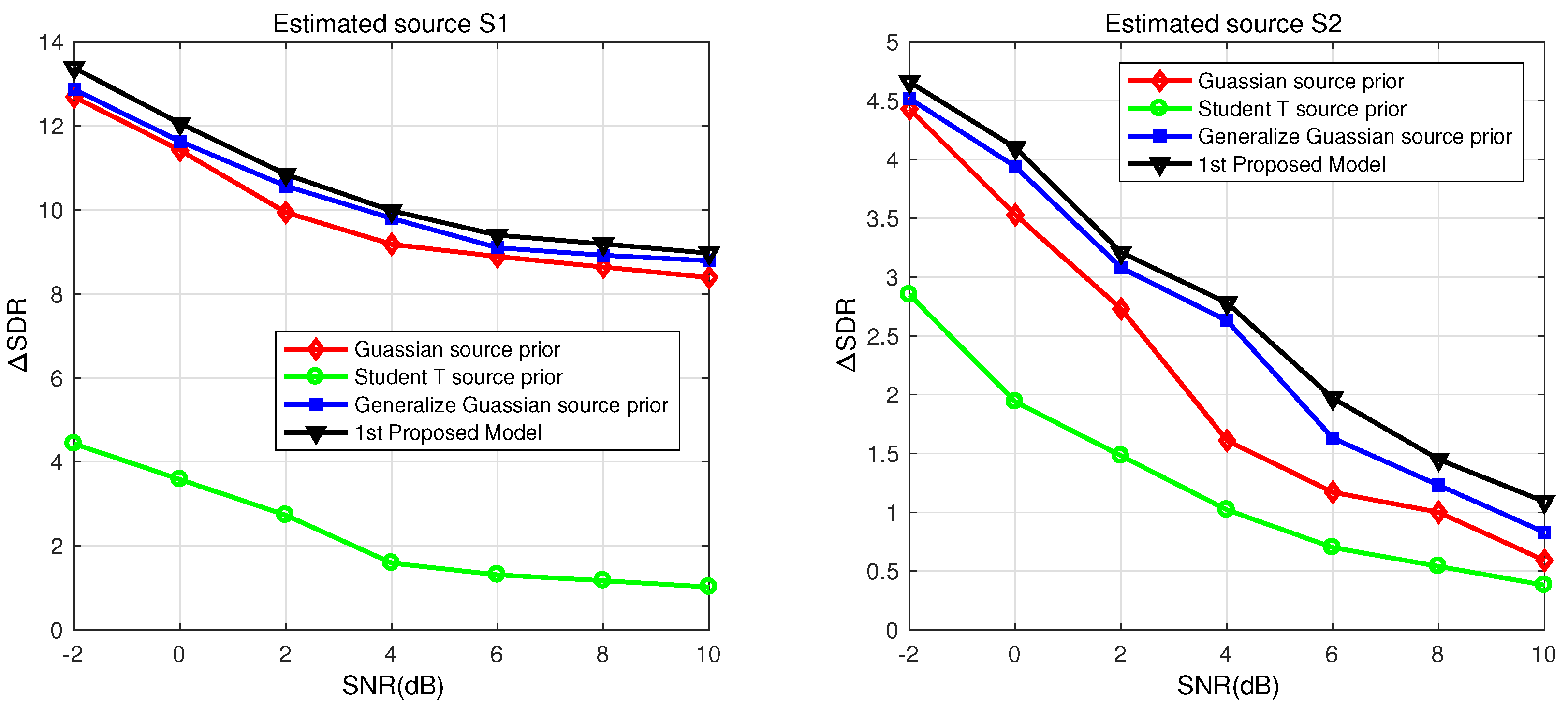
For the performance evaluation of first model, we generated 20 different noisy convolutive speech mixtures with the help of a simulated room model by randomly selecting speech signals from a pool of 10 source speech signals (five male and five female). We varied SNR and RT to obtain the average results where the SNR varies between −2 to 10 dB with window length = 512, NFFT = 1024, and RT = 100 msec. The average results are presented in
Table 1 in terms of SDR, showing that the proposed model gains an enhancement of 0.3 dB for
and 0.5 dB for
. Moreover, the proposed model is compared with the literature, showing its effectiveness with optimum gains of 0.2 and 1 dB for both estimated speech signal
and
, respectively.
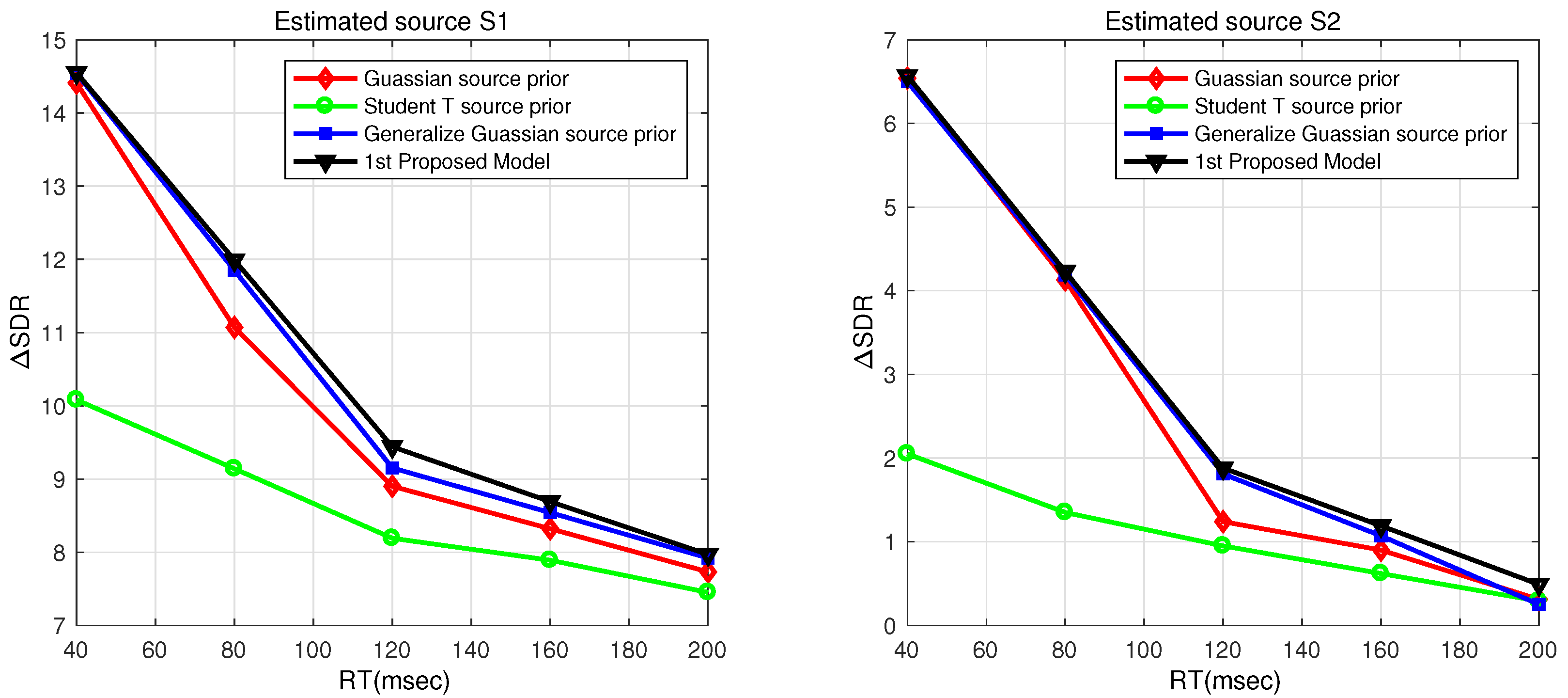
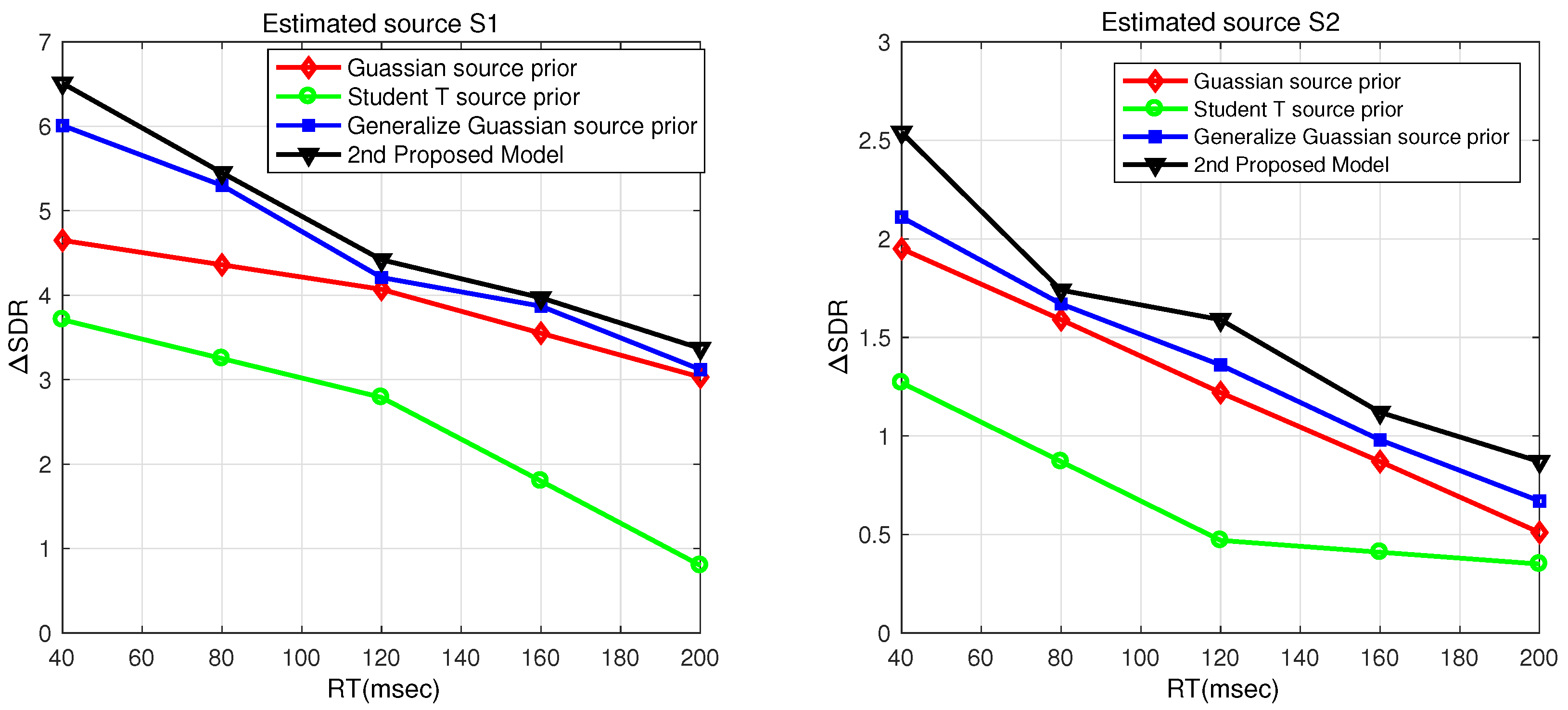
Additionally, RT was varied from 40 to 200 msec with a window length = 512, FFT frame length = 1024, and SNR = 4 dB. The noisy reverberant mixtures were fed to the proposed model and the other multistage BSS methodologies [
31,
32,
42]. The average objective analysis results are presented in
Table 2, which shows performance gains for the proposed model of 0.3 and 0.4 dB for
and
in comparison with other BSS approaches. The proposed approach also shows significant performance improvements of 3.81 and 2.9 dB for the estimated source signals
and
, respectively, from the multistage BSS having a source prior [
42]. The objective analysis is also compared with [
32], in which the proposed method shows optimum improvements of 0.16 and 0.2 dB for
and
, respectively.
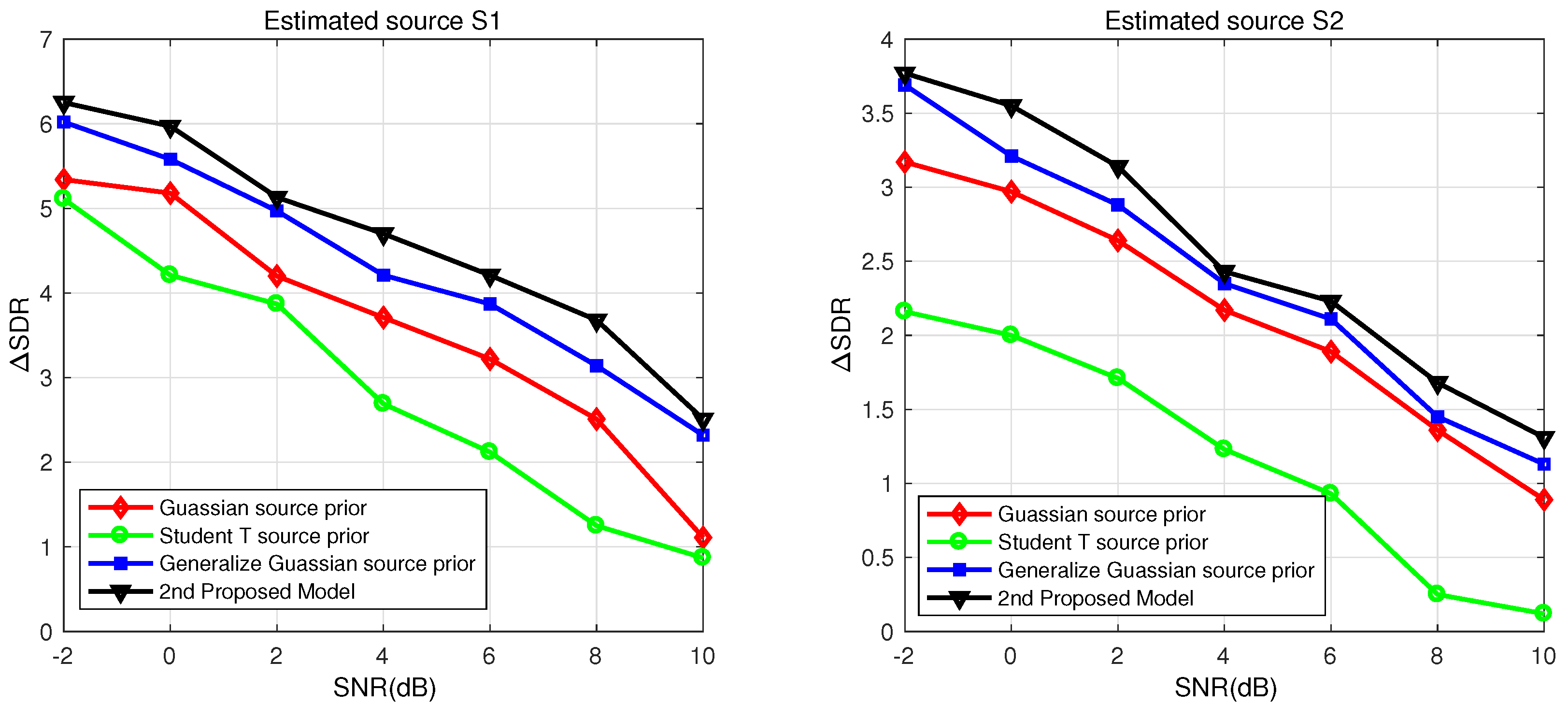
For the performance evaluation of the second model, the noisy reverberant mixtures were de-noised by using the MMSE filtering technique in the first stage. In the second stage, the estimated speech signals were separated from the de-noised mixture using the BSS method. The average results based on objective analysis by varying SNR are shown in
Table 3. It can be seen in
Table 3 that the proposed model shows a performance improvement of 0.2 dB for both
and
in comparison with other multistage BSS approaches. The results in
Table 3 show that the proposed approach achieved significant performance improvements of 0.7 and 0.8 dB in comparison with the Student’s T method [
42] for estimated source signals
and
, respectively. Moreover,
Table 3 demonstrates that the proposed approach shows 0.1 and 0.4 dB gains from [
32] for
and
, respectively. The objective evaluations with variable RT, having a window size = 512, FFT = 1024, and SNR = 4 dB, are provided in
Table 4. From
Table 4, the proposed model shows performance gains of 1.7, 2.14, and 0.21 dB for
and 0.6, 1.63, and 0.4 dB for
in comparison with [
31,
32,
42], respectively.
Experiments were also performed to cross verify the simulations where the window length, NFFT, and RT parameters were set to 512, 1024, and 100 msec, respectively. The five participants were asked to mark the MOS of the estimated speech signals extracted from the multistage BSS model with source prior [
31,
32,
42] and the two proposed methods. The average MOS results from the first model are presented in
Table 5 and
Table 6, with variable SNR and RT, respectively. In
Table 5 with variable SNR, it can be observed that the proposed approach achieved performance gains of 0.5, 0.8, and 0.2 in terms of MOS for estimated source
and 0.4, 0.6, 0.12 for estimated source
in comparison with other multistage BSS methods, respectively. For varying the RT parameter, having a fixed window length = 512, FFT = 1024, and SNR = 4 dB, the average MOS are shown in
Table 6 with gains of 0.4, 0.6, and 0.2 for
and 0.5, 0.7, 0.2 for
. The same procedure was followed to verify the second proposed model and the results are displayed in
Table 7 and
Table 8. For varying the SNR, it can be observed in
Table 7 that the proposed model achieves MOS gains of 0.4,0.7, and 0.2 for
and 0.3, 0.7, and 0.2 for
. Similarly, in
Table 8, results are provided by varying RT that show the MOS gains of the proposed model, i.e., 0.4, 0.6, and 0.2 for
and 0.2, 0.5, and 0.1 for
.
Comparative Analysis of the Proposed Models
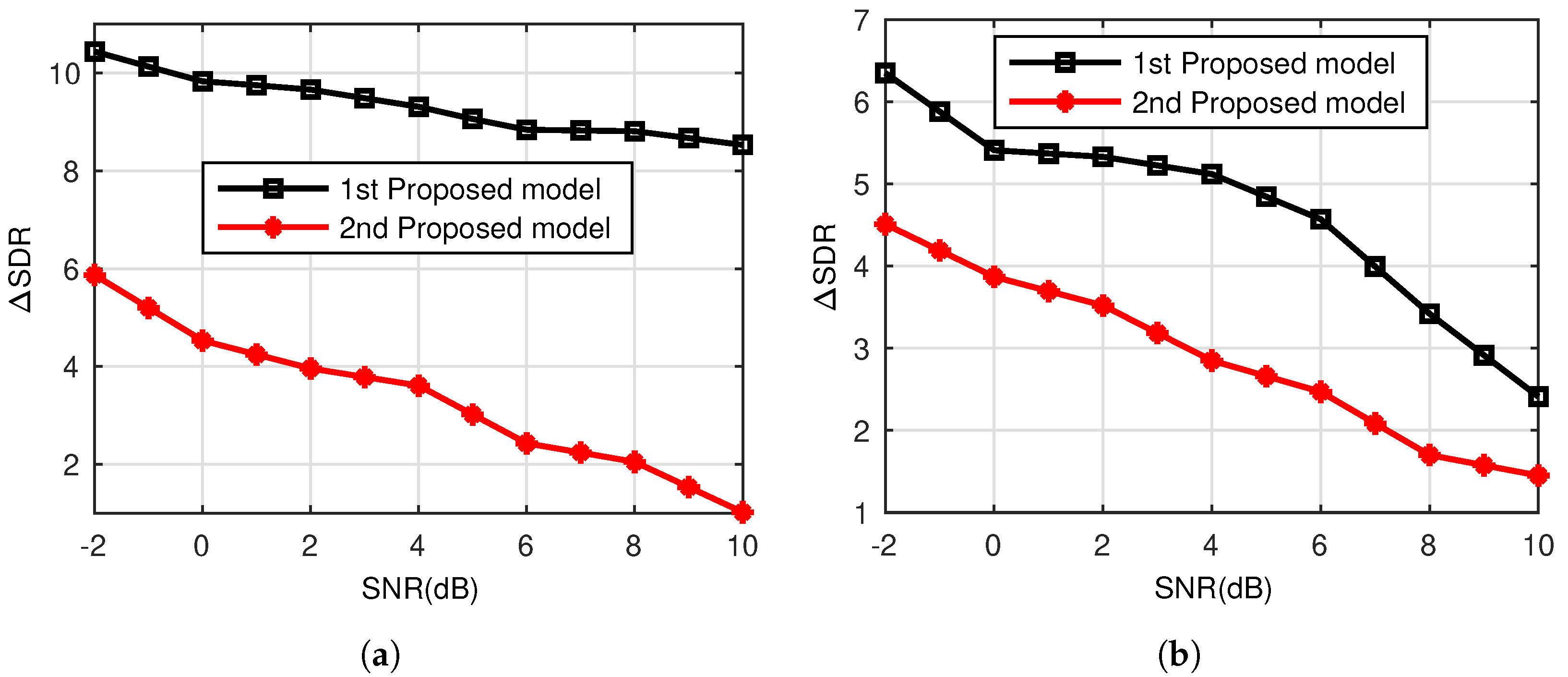
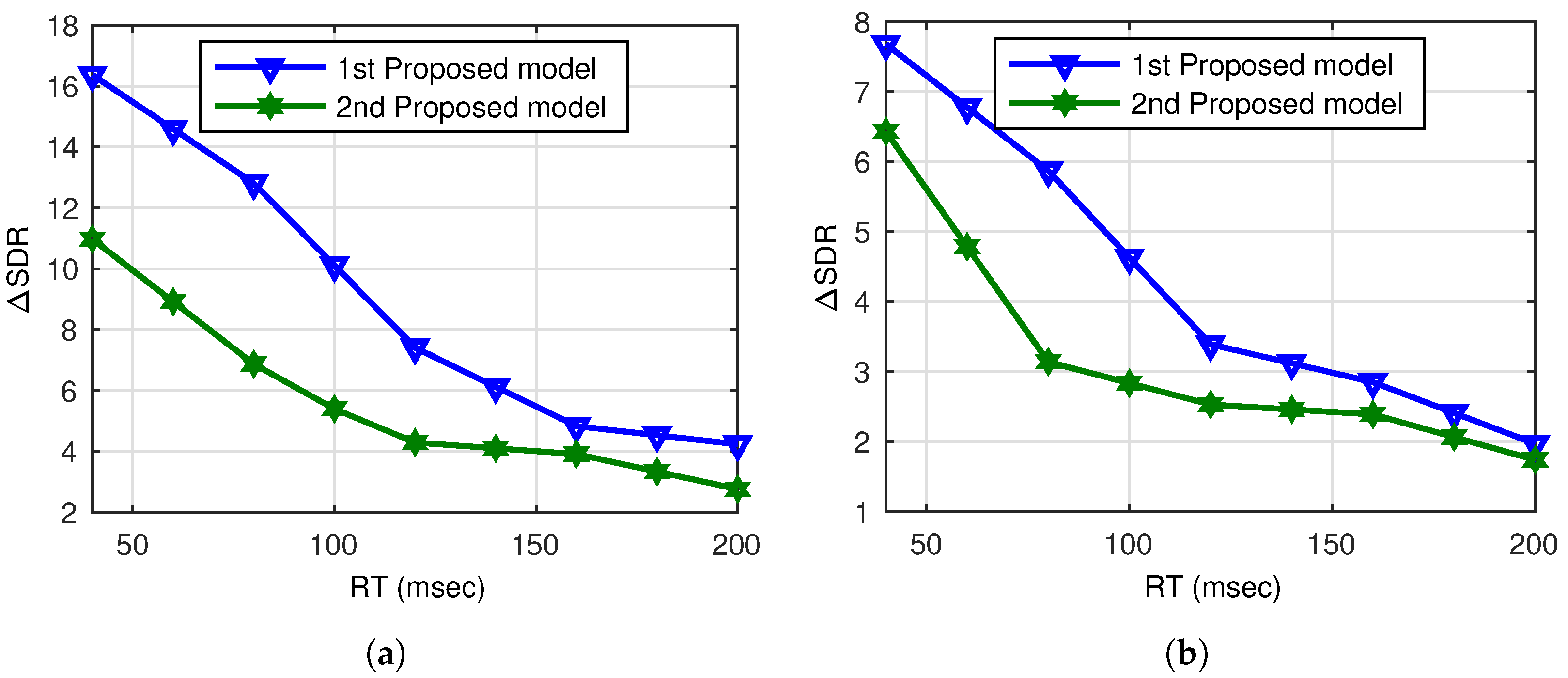
A comparative analysis of the two proposed models are presented in
Figure 9a and
Figure 10b for estimated speech signals
and
. The results of these figures are deduced from objective evaluations in
Table 1,
Table 2,
Table 3 and
Table 4 for variable SNR and RT.
From
Figure 9a,b, it is clear that the first model provides significant improvements in comparison to the second model for estimated source signals
and
with variable SNR. Similarly, for varying RT, it can be observed in
Figure 10a,b that the first model shows considerable performance gains in comparison to the second model for
and
. The performance of the first model (
Figure 1) is better than the second model (
Figure 2) for both RT and SNR because the first model suppresses the noise in the estimated source signal extracted from the noisy convolutive mixture, while in the second model, the de-noising technique suppresses noise and estimated source signals mixed in the noisy convolutive mixture. The de-noising module considers the other estimated signals in the noisy convolutive mixture as noise resulting from performance degradation.
6. Conclusions and Future Work
This paper proposes an efficient hybrid multistage approach for blind source separation (BSS) of noisy convolutive speech mixtures. In the BSS stage, a hybrid source prior model consisting of multivariate super-Gaussian and generalized Gaussian distribution models of the source signals is used in the observed noisy reverberant mixture. The weights are assigned between the source priors following the energy of the observed convolutive mixture. In the de-noising stage, the noise is suppressed by the MMSE filtering technique using two different proposed models. In the first model, the BSS module is followed by the de-noising stage. In the second model, the de-noising module is followed by the BSS stage. Both proposed models are compared with the literature, where the results clearly show the performance improvement of the proposed schemes. Furthermore, it was observed from the results that the proposed model with a BSS module followed by de-noising stage shows a significant gain in comparison with the model with first de-noising followed by the BSS stage.
In future work, we will perform experimental measurements in a real-time setup and compare the simulation and practical results both in terms of SNR, energy distribution, and error performance.