Study on Coupled Vertical Vehicle-Bridge Dynamic Performance of Medium and Low-Speed Maglev Train
Abstract
:1. Introduction
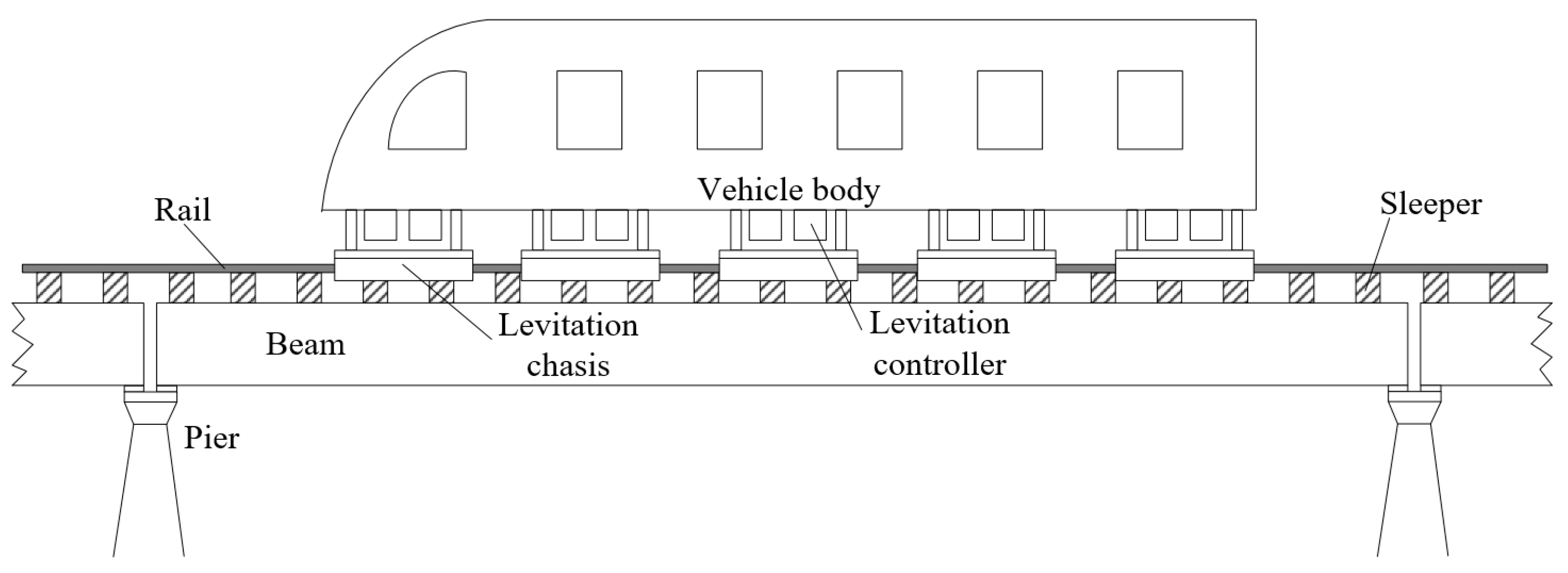
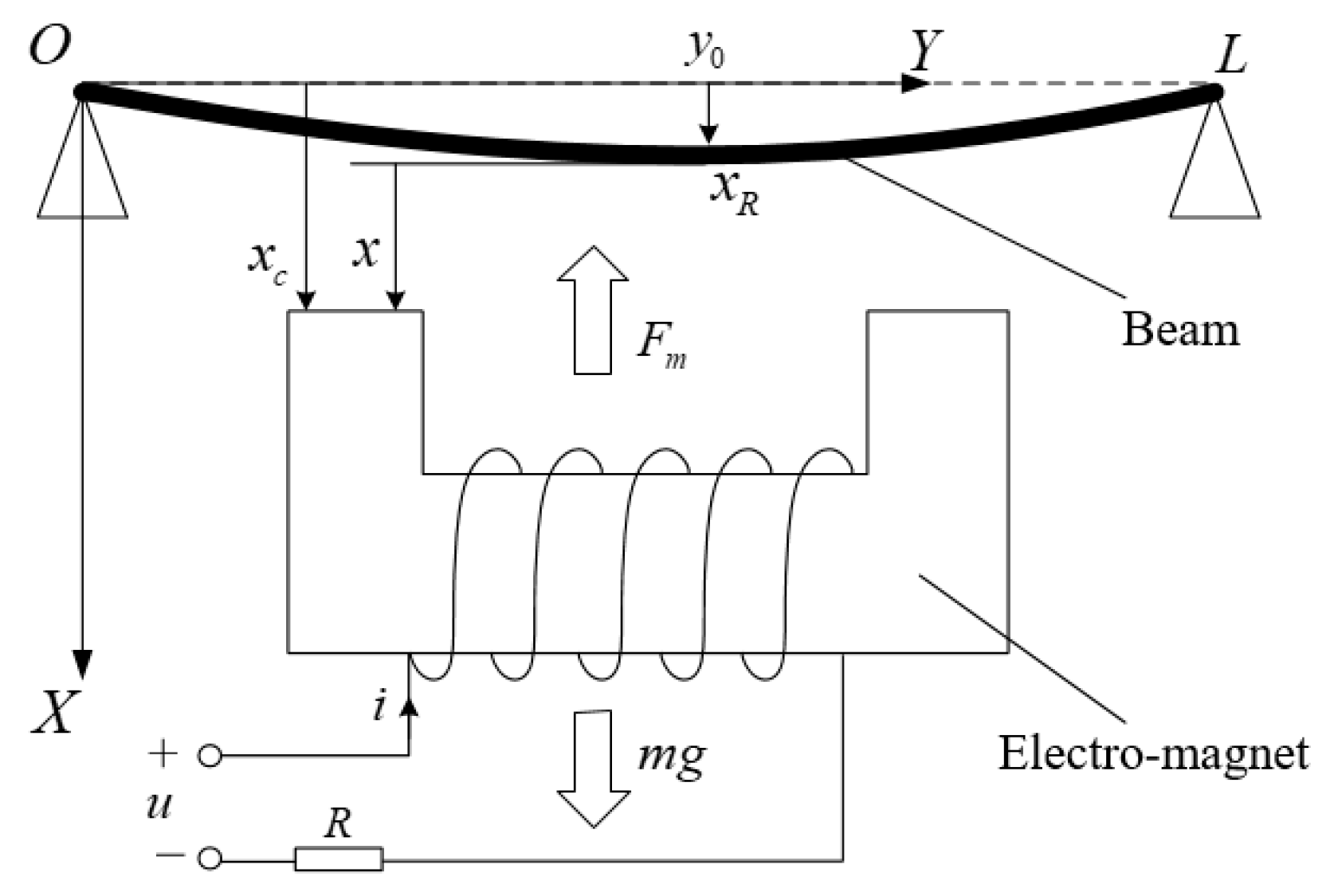
2. Coupled Vehicle-Bridge System Considering Elastic Beam
3. Numerical Simulations
4. Test Results and Analysis
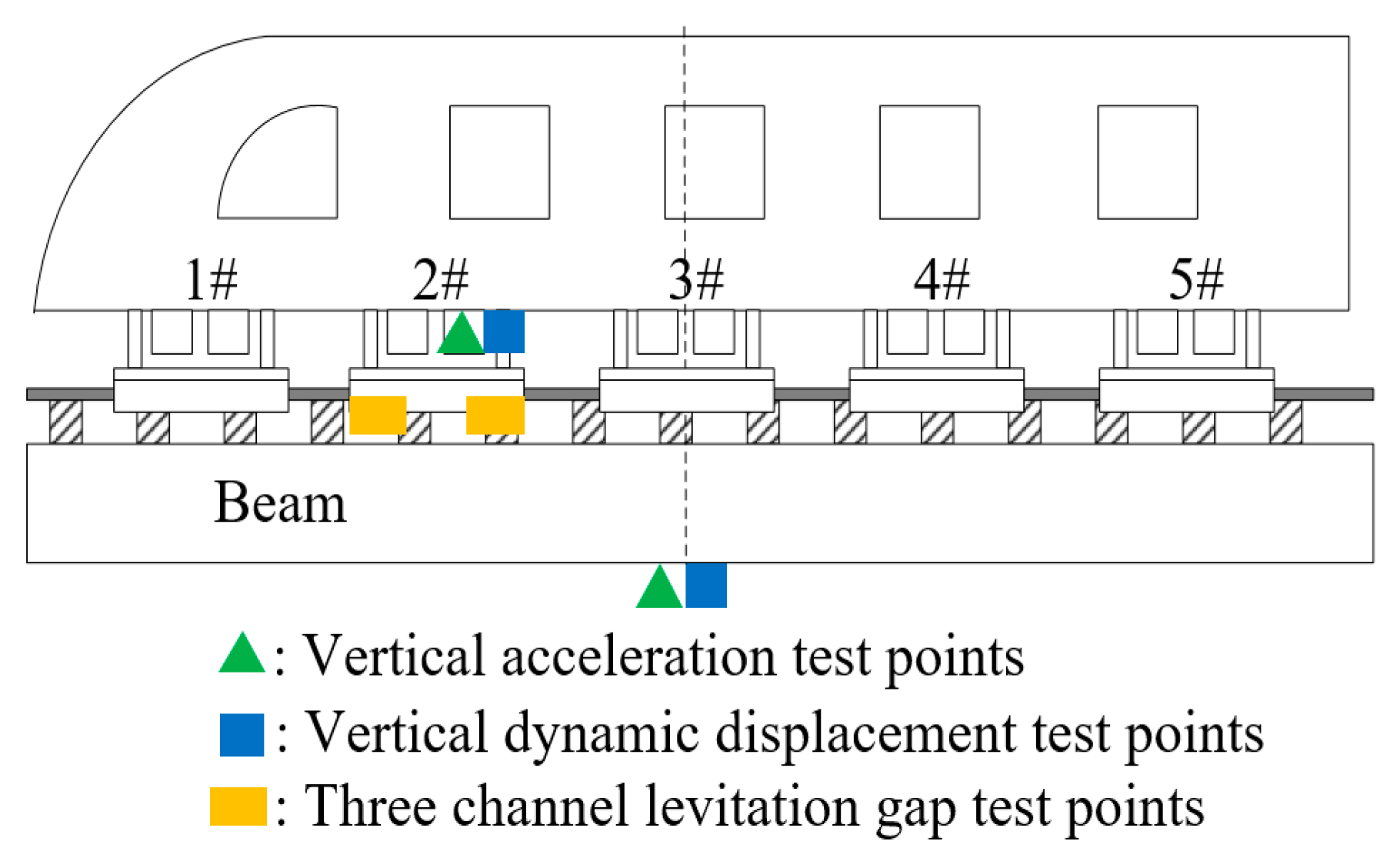
4.1. Test Scheme
4.2. Parametric Analysis
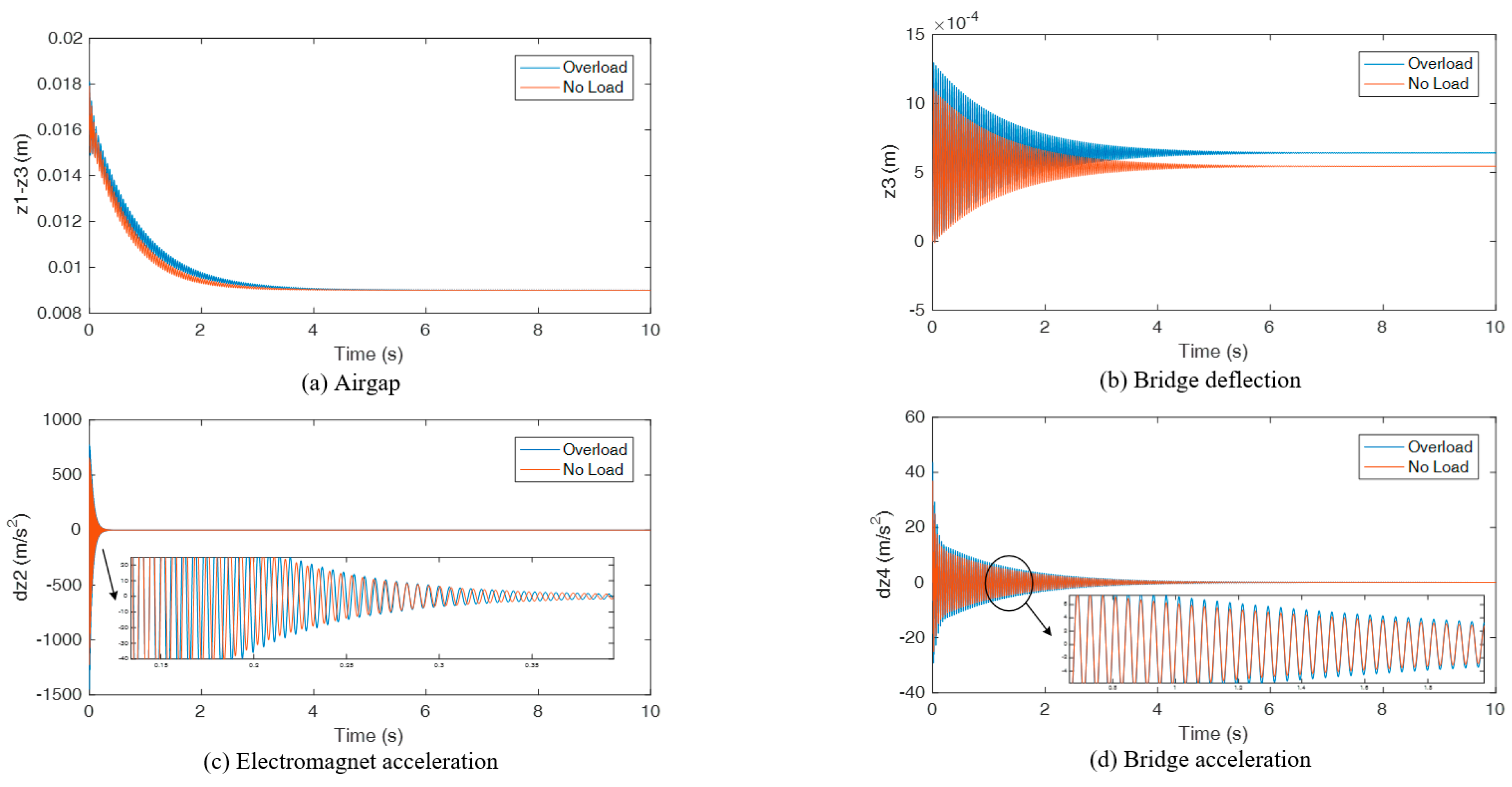
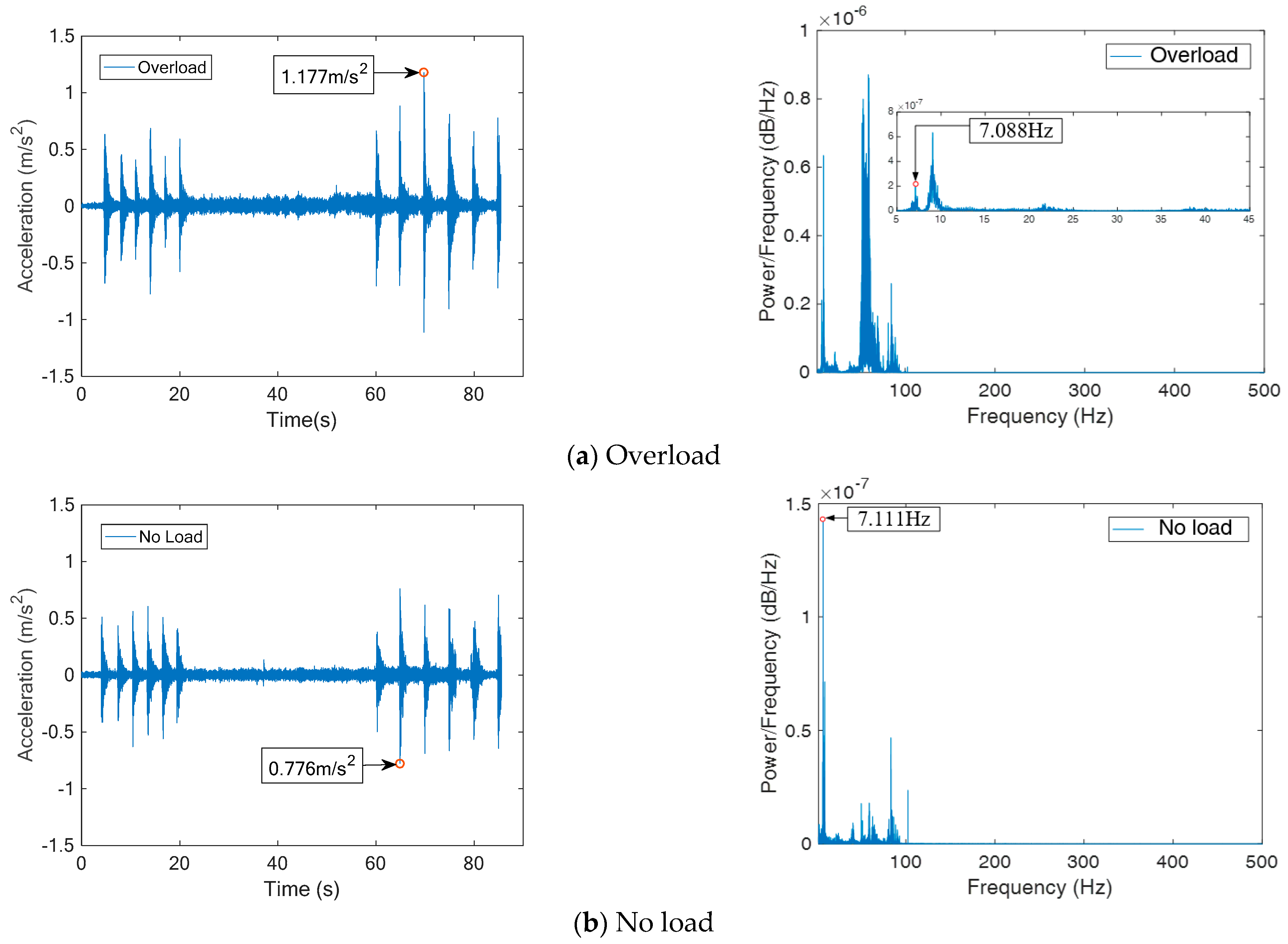
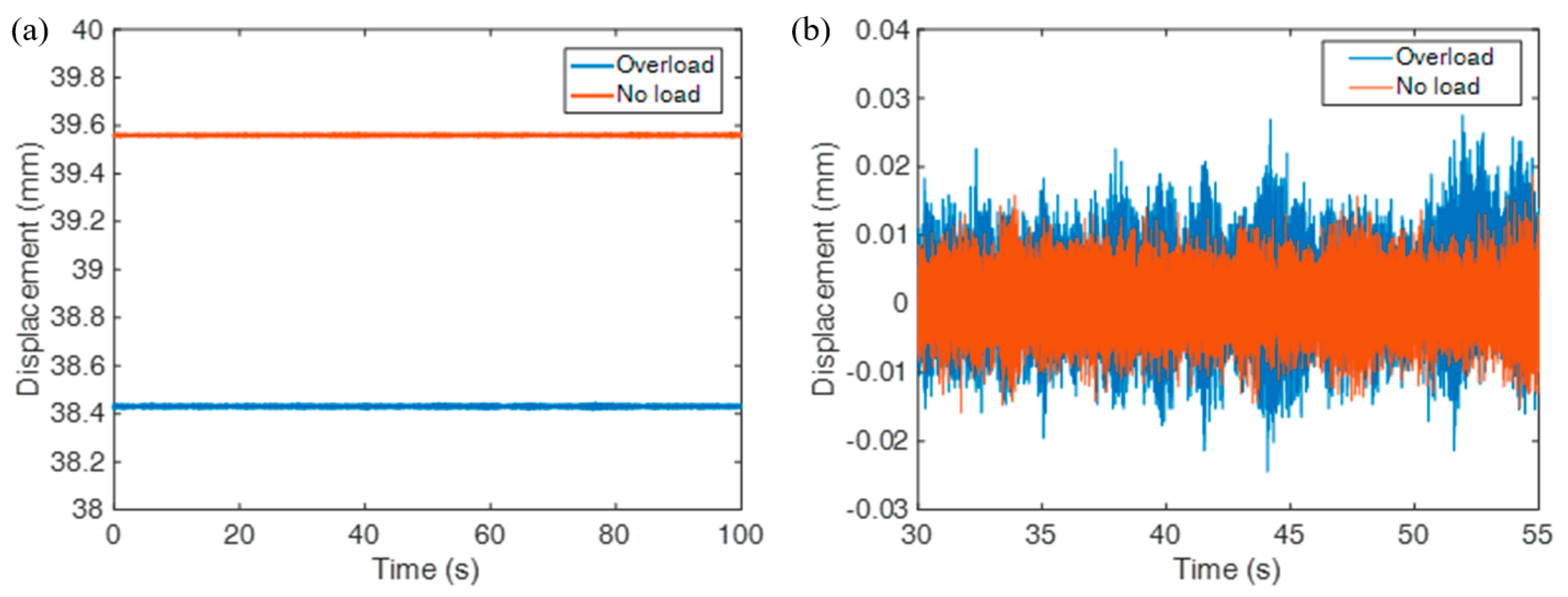
4.2.1. Vehicle Load
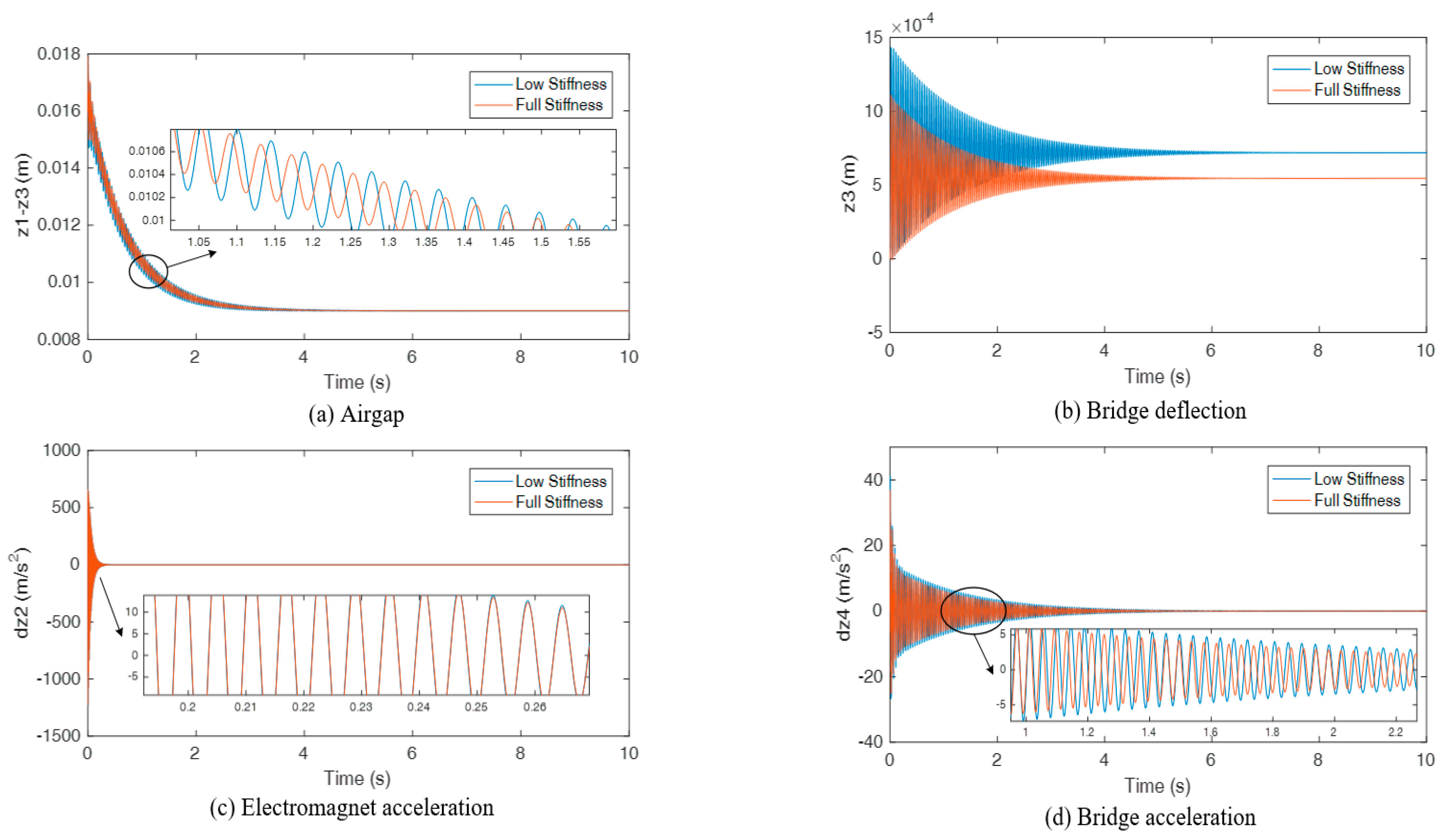
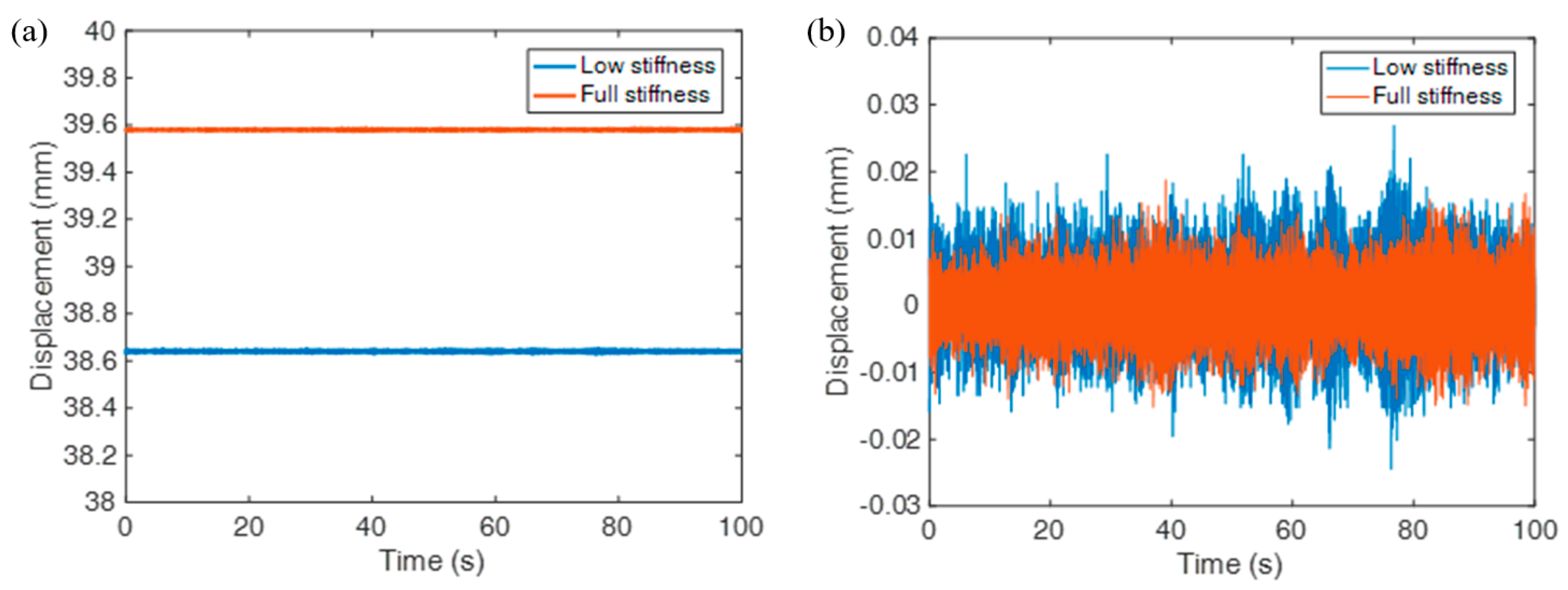
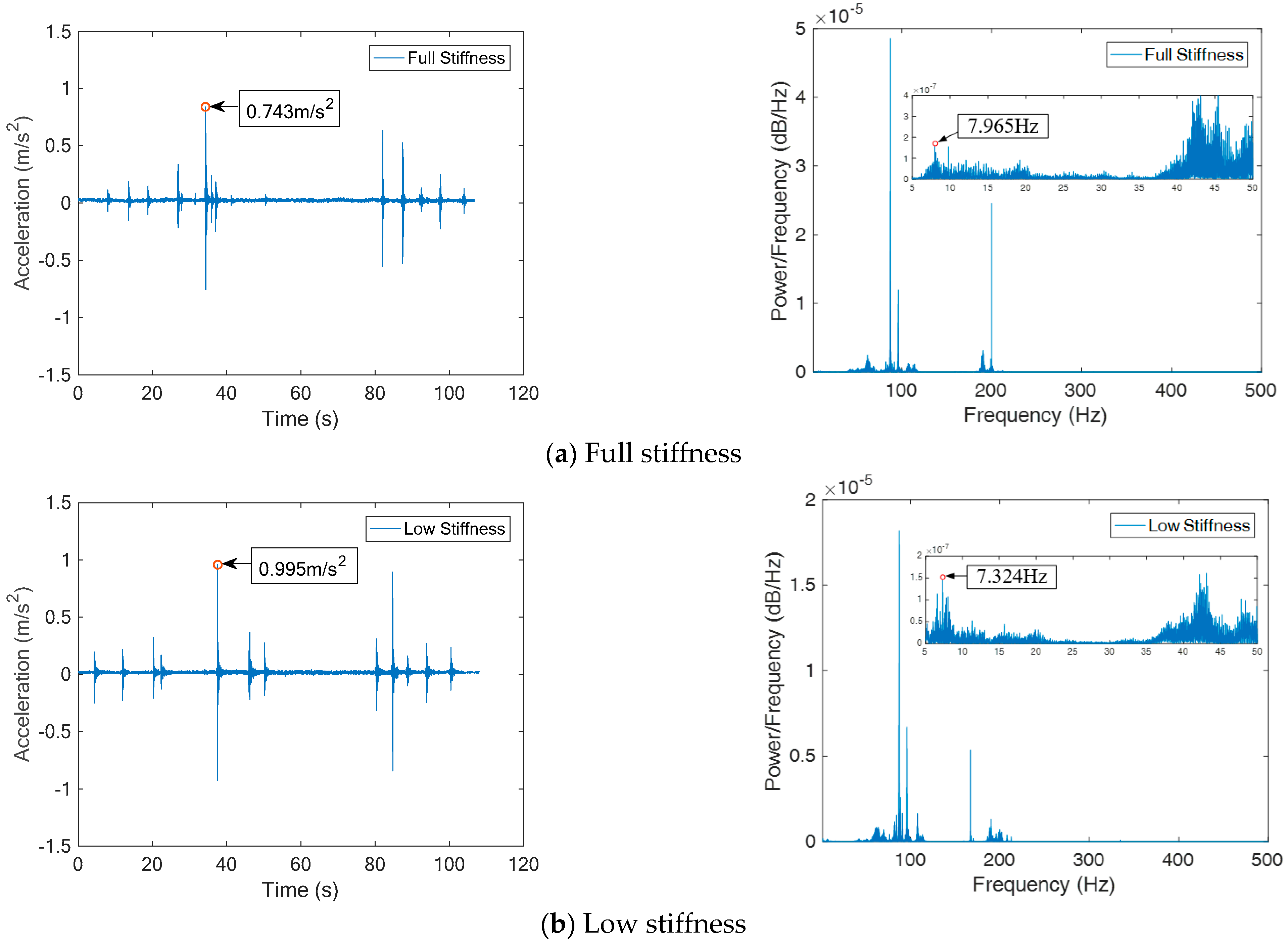
4.2.2. Bridge Stiffness
5. Conclusions
- (1)
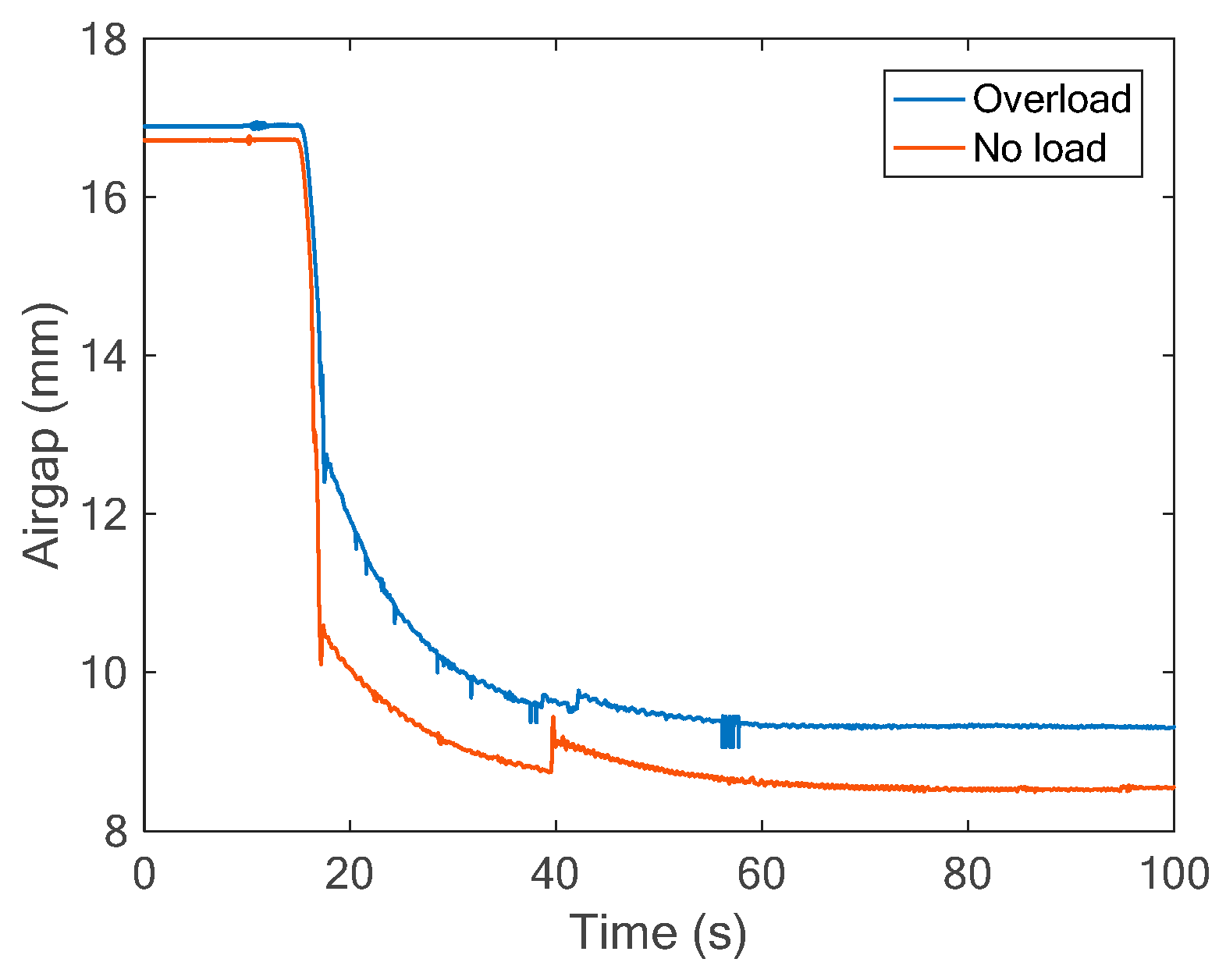
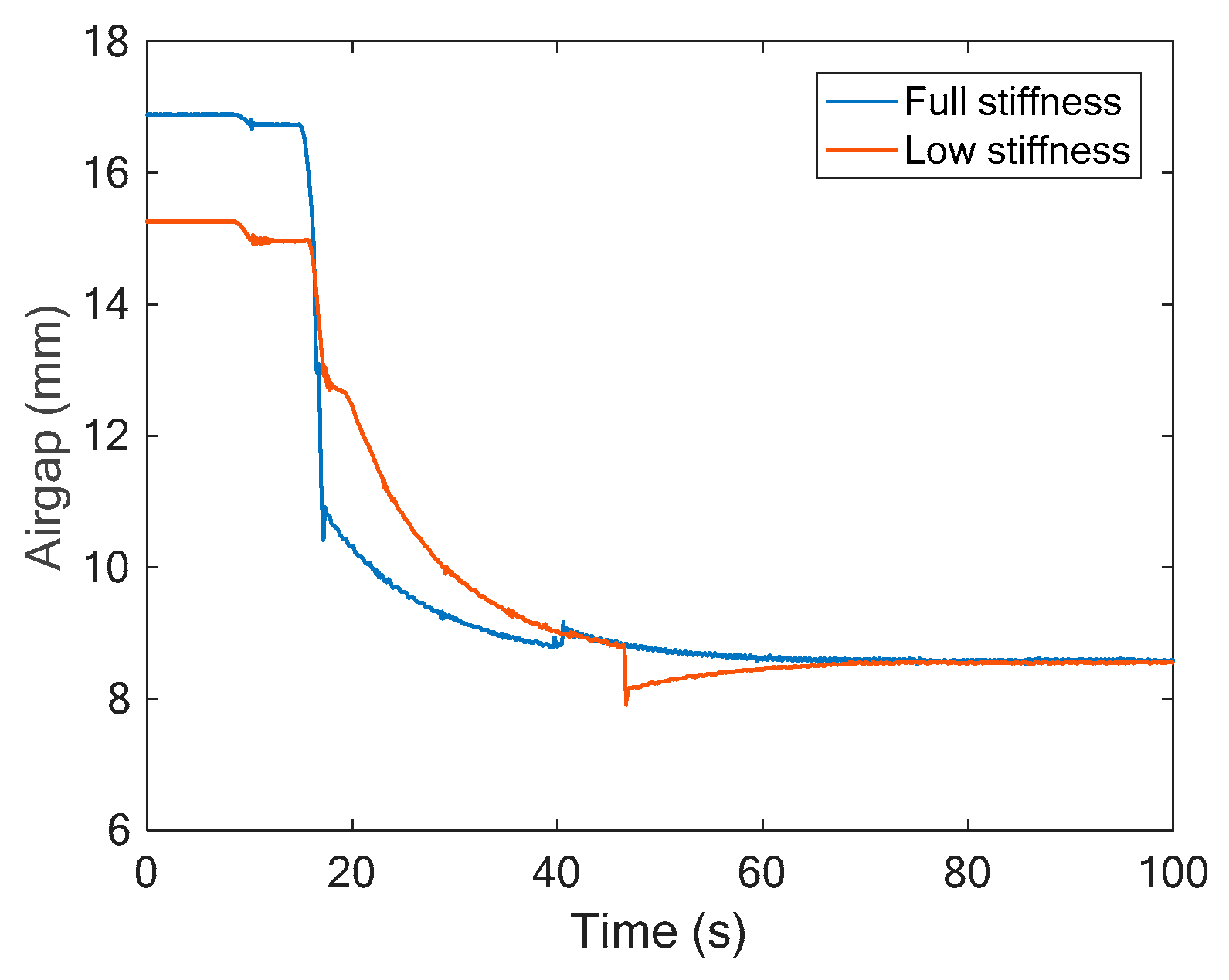
- The levitation gap was significantly affected by the change of load and stiffness. When the load increased, or the stiffness decreased, the response speed of the gap became slower, and there was a steady-state error of about 1 mm under overloaded conditions;
- (2)
- Based on the test analysis of various conditions, the deflection of the bridge varied from 2.41 mm to 3.59 mm. At full stiffness, the load increased by 6 tons, and the deflection increased by 1.18 mm. Under no load, the beam height decreased by 20 cm, and the deflection increased by 0.94 mm;
- (3)
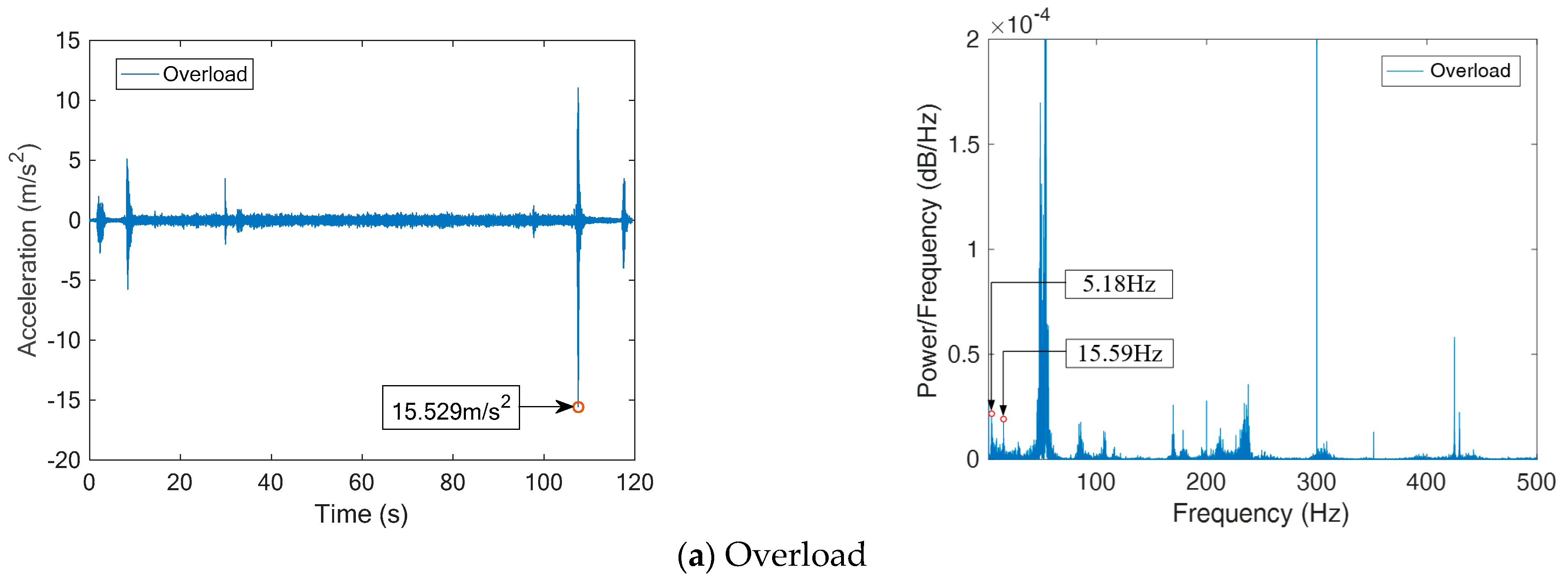
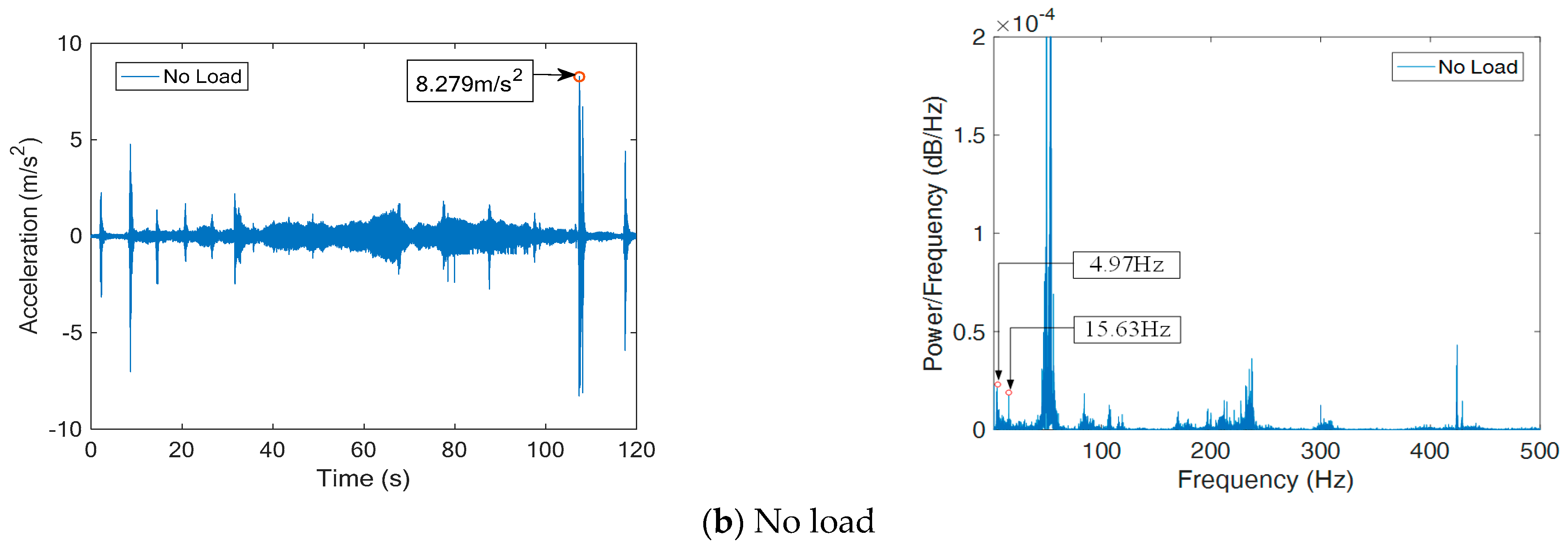
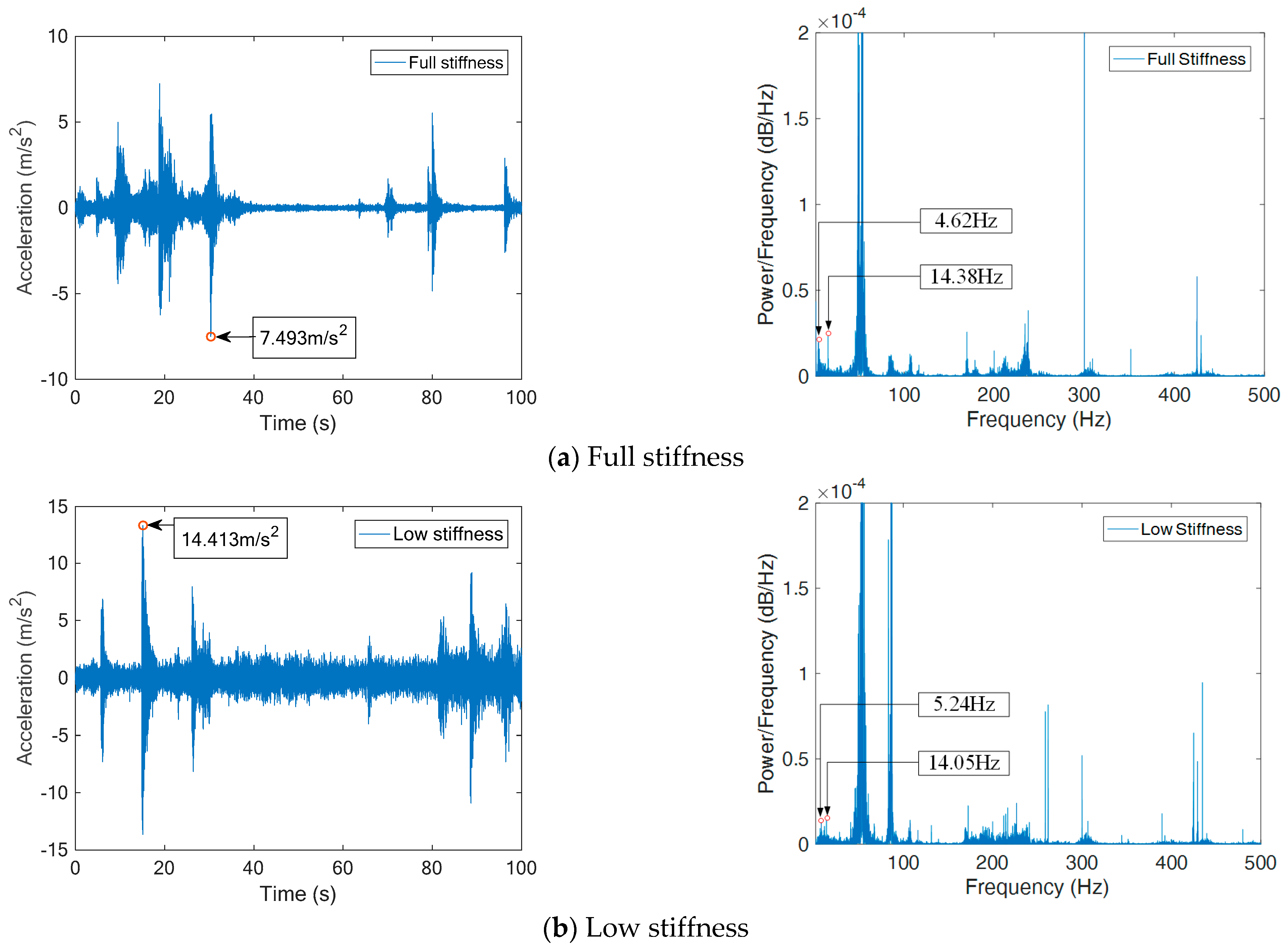
- The vertical vibration of suspension bogie and bridge increased with an increase in load or decrease in stiffness. At full stiffness, the load increased by 6 tons, and the maximum vertical acceleration of the suspension bogie and bridge increased by 7.25 m/s2 (87.6%) and 0.401 m/s2 (51.7%), respectively. Under no-load conditions, the beam height decreased by 20 cm, and the maximum vertical acceleration of suspension bogie and bridge increased by 6.92 m/s2 (92.3%) and 0.252 m/s2 (33.9%), respectively. The dynamic response of the suspension bogie changed more obviously;
- (4)
- The load had no effect on the first natural frequency of the bridge (about 7.1 Hz) or the suspension bogie (about 5 Hz). However, the stiffness had little influence on the first natural frequency of the bridge, and the low stiffness reduced by 0.6 Hz than the full stiffness and had no effect on the suspension bogie;
- (5)
- The frequency band of bridge vibration was in the range of 200 Hz, and that of suspension bogie was in the range of 400 Hz. The vertical vibration of the suspension bogie had more high-frequency components. In addition to the first-order vibration frequency, other frequencies with high energy were mostly caused by forced vibration. However, electromagnetic interference was more serious at 50 Hz and multiple frequencies (power frequency signal);
- (6)
- The time-domain law above was consistent with the simulation result, which verifies the reliability of the system model. In addition, the test results could be used as a reference for the design of rail transit coupling systems. In the future, new levitation control algorithms will be applied to the field test to evaluate the dynamic performance under the above conditions so as to further overcome the problems of system stability degradation caused by stiffness reduction or load increase.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yau, J.D. Vibration control of maglev vehicles traveling over a flexible guideway. J. Sound Vib. 2009, 321, 184–200. [Google Scholar] [CrossRef]
- Chen, C.; Xu, J.Q.; Rong, L.J.; Pan, H.L.; Gao, D.G. Nonlinear dynamics characteristics of maglev vehicle under track random irregularities. J. Traffic Transp. Eng. 2019, 19, 115–124. [Google Scholar]
- Gao, D.G.; Ni, F.; Lin, G.B.; Luo, S.; Ji, W. Aerodynamic Analysis of Pressure Wave of High-Speed Maglev Vehicle Crossing: Modeling and Calculation. Energies 2019, 12, 3770. [Google Scholar] [CrossRef] [Green Version]
- Wang, D.; Li, X.; Liang, L.; Qiu, X. Influence of the track structure on the vertical dynamic interaction analysis of the low-to-medium-speed maglev train-bridge system. Adv. Struct. Eng. 2019, 22, 2937–2950. [Google Scholar] [CrossRef]
- Li, X.; Geng, J.; Wang, D. Dynamic Responses of Low-Medium Speed Maglev Train-Simply Supported Beam Interaction System. Urban Rail Transit 2017, 3, 136–141. [Google Scholar] [CrossRef] [Green Version]
- Li, M.; Luo, S.H.; Ma, W.H. Experimental study on dynamic performance of medium and low speed maglev train-track-bridge system. Int. J. Rail Transp. 2020, 9, 232–255. [Google Scholar] [CrossRef]
- Zhang, M.; Ma, W.; Luo, S. Application of levitation frame with mid-set air spring on maglev vehicles. In Proceedings of the International Symposium on Power Electronics and Control Engineering (ISPECE), Xi’an, China, 28–30 December 2018. [Google Scholar]
- Liang, X.; Luo, S.H.; Ma, W.H.; Wu, Q.; Xu, Z.Q. Coupling Vibration Study of Medium-low Speed Maglev Train Long Span Continuous Bridge System. J. Railw. Eng. Soc. 2017, 34, 53–57. [Google Scholar]
- Lu, H.; Han, X.; Li, Z.; He, X.; Liu, K.; Chen, Z. Analysis of Vibration Characteristics of Low-medium Speed Maglev Levitation Systems in Lifting Stages. China Mech. Eng. 2019, 30, 318–324. [Google Scholar]
- Kim, K.J.; Han, J.B.; Han, H.S.; Yang, S.J. Coupled vibration analysis of Maglev vehicle-guideway while standing still or moving at low speeds. Veh. Syst. Dyn. 2015, 53, 587–601. [Google Scholar] [CrossRef]
- Shi, J.; Wei, Q.C.; Feng, Y.W. Analysis of Random Vibration Responses Characteristics of Maglev and Elevated-beam Guideway. J. Syst. Simul. 2005, 7, 1577–1579. [Google Scholar]
- Yoo, Y.S.; Park, W.C.; Yhim, S.S. Analytical Study of Railroad Bridge for Maglev Propulsion Train with Dynamical Influence Variable. J. Korea Acad. Ind. Coop. Soc. 2018, 19, 532–542. [Google Scholar]
- Wang, D.; Li, X.; Wang, Y.; Hu, Q. Dynamic interaction of the low-to-medium speed maglev train and bridges with different deflection ratios: Experimental and numerical analyses. Adv. Struct. Eng. 2020, 23, 2399–2413. [Google Scholar] [CrossRef]
- Wang, D.; Li, X.; Liang, L.; Qiu, X. Dynamic interaction analysis of bridges induced by a low-to-medium-speed maglev train. J. Vib. Control 2020, 26, 2013–2025. [Google Scholar] [CrossRef]
- Geng, J. Theory and Experiment Research of Key Parameters Design on Simply-Supported Track Girders of Low to Medium Speed Maglev Line. Ph.D. Thesis, Southwest Jiaotong University, Chengdu, China, 2018. [Google Scholar]
- Li, X.; Jin, X.; Wang, D.; Xie, K.; Zhu, Y. Tests for coupled vibration of a train-bridge system on Changsha low-medium speed maglev line. J. Vib. Shock 2019, 38, 57–63. [Google Scholar]
- Lee, J.S.; Kwon, S.D.; Kim, M.Y.; Yeo, I.H. A parametric study on the dynamics of urban transit maglev vehicle running on flexible guideway bridges. J. Sound Vib. 2009, 328, 301–317. [Google Scholar] [CrossRef]
- Chen, C.; Xu, J.; Ji, W.; Chao, R.; Sun, Y. Adaptive levitation control for characteristic model of low-speed maglev vehicle. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2020, 234, 1456–1467. [Google Scholar] [CrossRef]
- Xu, J.; Chen, C.; Sun, Y.; Ji, W.; Lin, G. Nonlinear dynamic analysis of Maglev Vehicle Based on flexible guideway and random irregularity. Int. J. Appl. Electromagn. Mech. 2019, 60, 263–280. [Google Scholar] [CrossRef]
- She, L.H.; Wang, H.; Zou, D.S.; Zhang, Z.Z.; Chang, W.S. Hopf bifurcation of maglev system with coupled elastic guideway. In Proceedings of the 20th Conference on Magnetically Levirate Systems and Linear Drives, San Diego, CA, USA, 15–18 December 2008; pp. 1–7. [Google Scholar]
- Cui, K.; Qin, X. Virtual reality research of the dynamic characteristics of soft soil under metro vibration loads based on BP neural networks. Neural Comput. Appl. 2018, 29, 1233–1242. [Google Scholar] [CrossRef]
- Kong, E.; Song, J.S.; Kang, B.B.; Na, S. Dynamic response and robust control of coupled Maglev vehicle and guideway system. J. Sound Vib. 2011, 330, 6237–6253. [Google Scholar] [CrossRef]
- Hu, J.; Ma, W.; Luo, S. Coupled dynamic analysis of low and medium speed maglev vehicle-bridge interaction using SIMPACK. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2021, 235, 377–389. [Google Scholar] [CrossRef]
- Li, J.; Li, J.; Zhou, D.; Cui, P.; Wang, L.; Yu, P. The active control of Maglev stationary self-excited vibration with a virtual energy harvester. IEEE Trans. Ind. Electron. 2015, 62, 2942–2951. [Google Scholar] [CrossRef]
- Zhang, L.L. Research on Hopf Bifurcation and Sliding Mode Control for Suspension System of Maglev Train. Ph.D. Thesis, Hunan University, Changsha, China, 2010. [Google Scholar]
- Hu, S.S. Automatic Control Principle; National Defense Industry Press: Beijing, China, 2000. [Google Scholar]


| Symbol | Quantity | Value |
|---|---|---|
| Mass of electromagnet | 500 kg | |
| Target gap | 0.009 m | |
| Span of Beam | 24.94 m | |
| Elastic modulus | 206 GPa | |
| Magnetic resistance | 4 Ω | |
| Damping ratio of the bridge | 0.005 | |
| Vacuum permeability | ||
| electromagnetic pole area | 0.024 m2 | |
| Turn Ratio | 500 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, Y.; Lin, G.; Ni, F.; Xu, J.; Chen, C. Study on Coupled Vertical Vehicle-Bridge Dynamic Performance of Medium and Low-Speed Maglev Train. Appl. Sci. 2021, 11, 5898. https://doi.org/10.3390/app11135898
Song Y, Lin G, Ni F, Xu J, Chen C. Study on Coupled Vertical Vehicle-Bridge Dynamic Performance of Medium and Low-Speed Maglev Train. Applied Sciences. 2021; 11(13):5898. https://doi.org/10.3390/app11135898
Chicago/Turabian StyleSong, Yifeng, Guobin Lin, Fei Ni, Junqi Xu, and Chen Chen. 2021. "Study on Coupled Vertical Vehicle-Bridge Dynamic Performance of Medium and Low-Speed Maglev Train" Applied Sciences 11, no. 13: 5898. https://doi.org/10.3390/app11135898
APA StyleSong, Y., Lin, G., Ni, F., Xu, J., & Chen, C. (2021). Study on Coupled Vertical Vehicle-Bridge Dynamic Performance of Medium and Low-Speed Maglev Train. Applied Sciences, 11(13), 5898. https://doi.org/10.3390/app11135898






