Modeling of Tunneling Total Loads Based on Symbolic Regression Algorithm
Abstract
1. Introduction
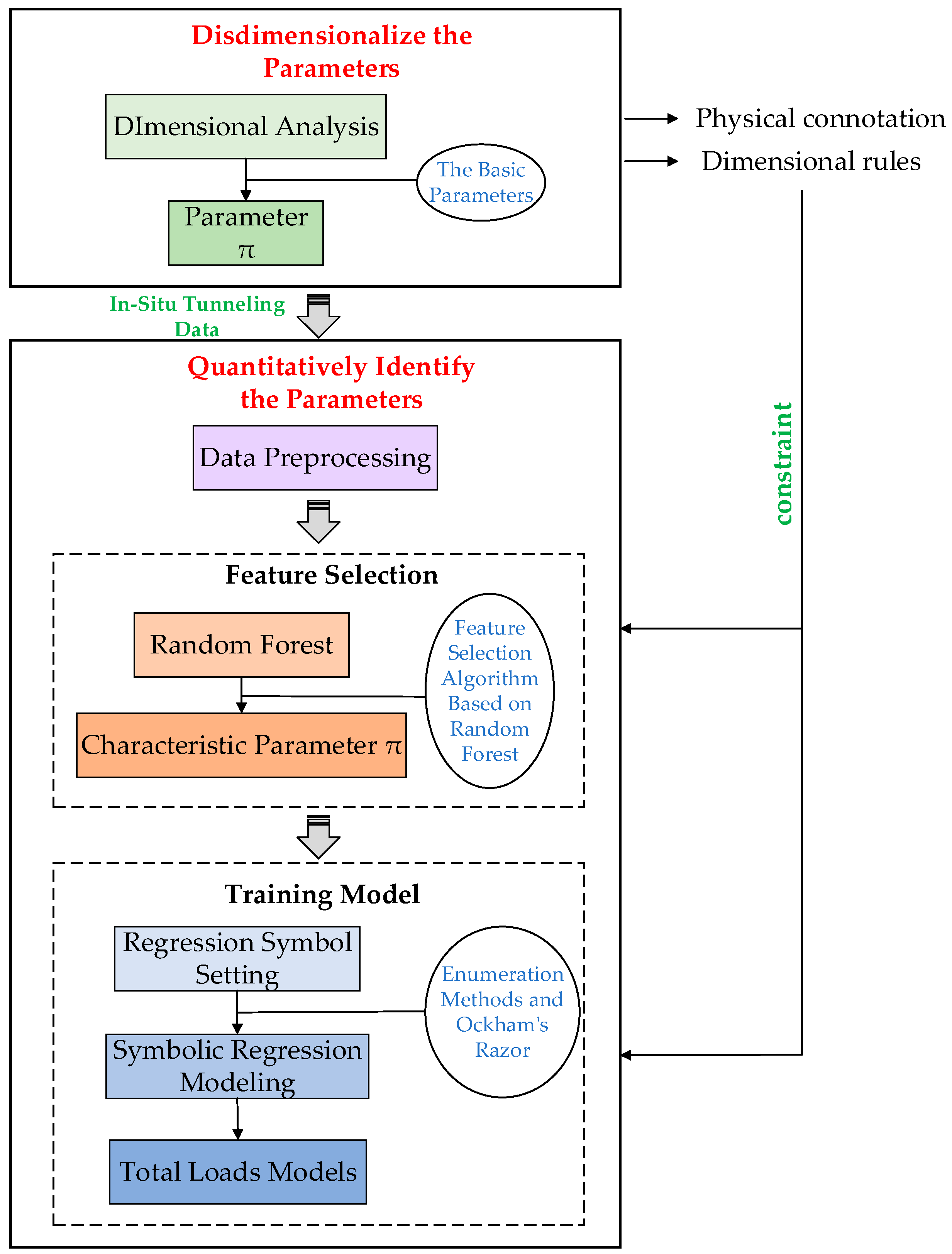
2. Modeling Method Based on Symbolic Regression Algorithm
3. Constructing π Quantities Based on Dimensional Analysis
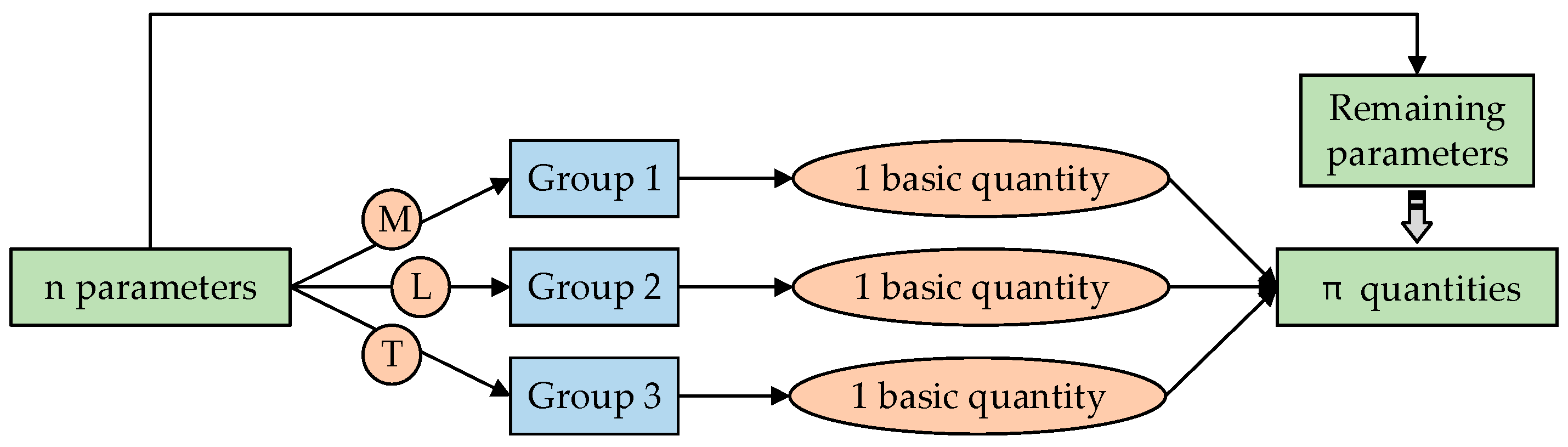
3.1. Selection of the Basic Quantities
3.2. Constructing π Quantities
4. Case Study
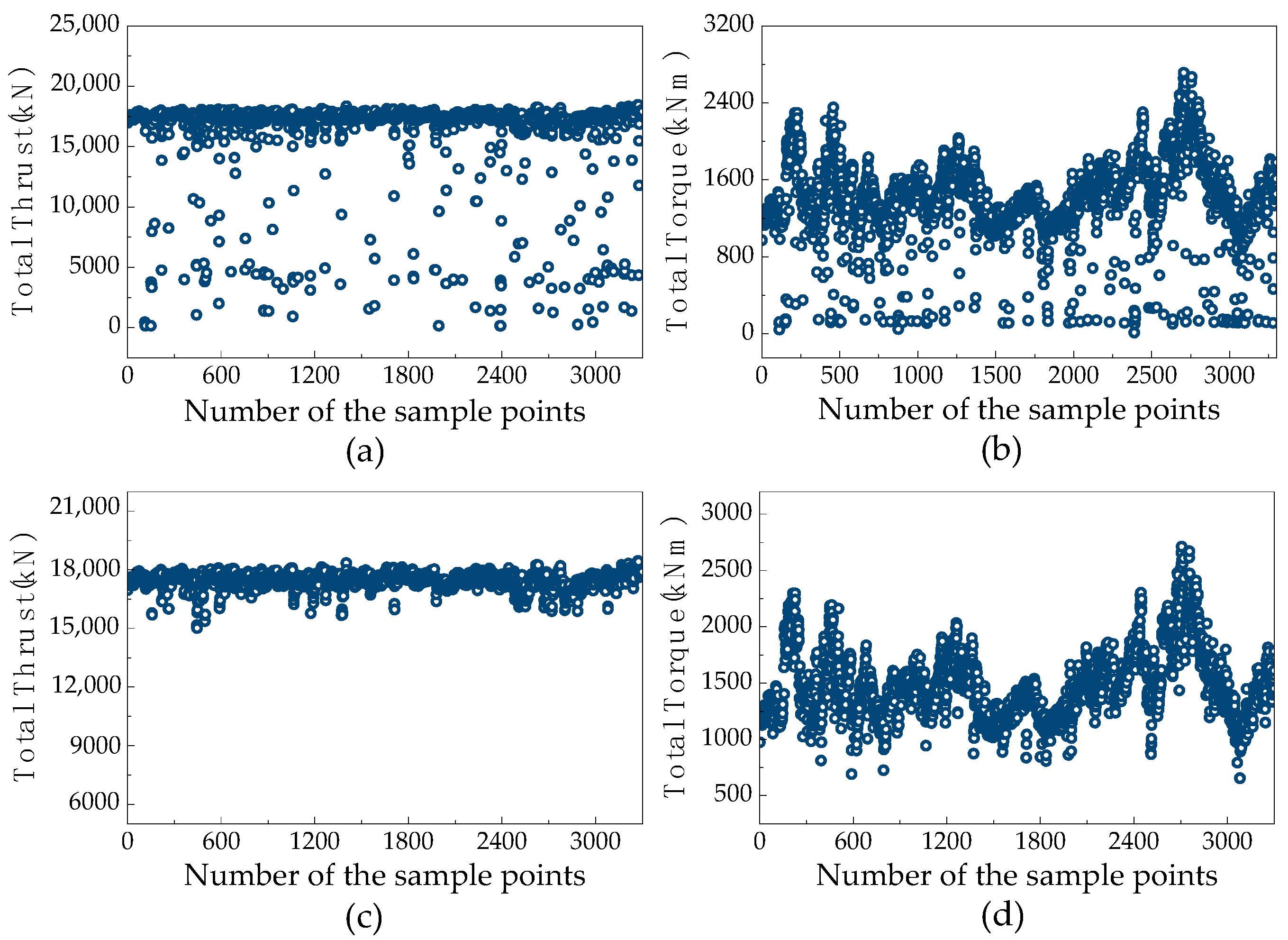
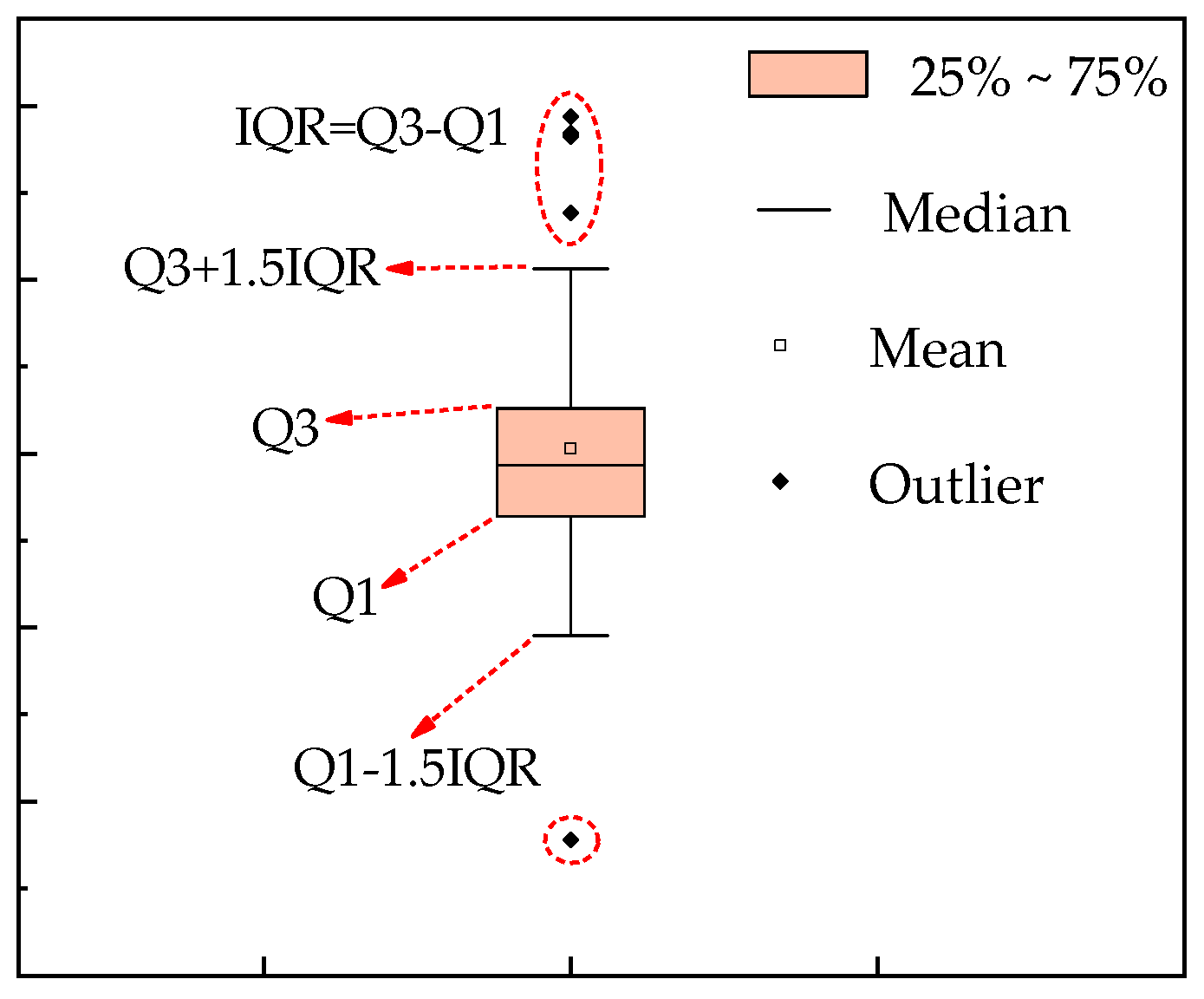
4.1. Preprocessing of In Situ Tunneling Data
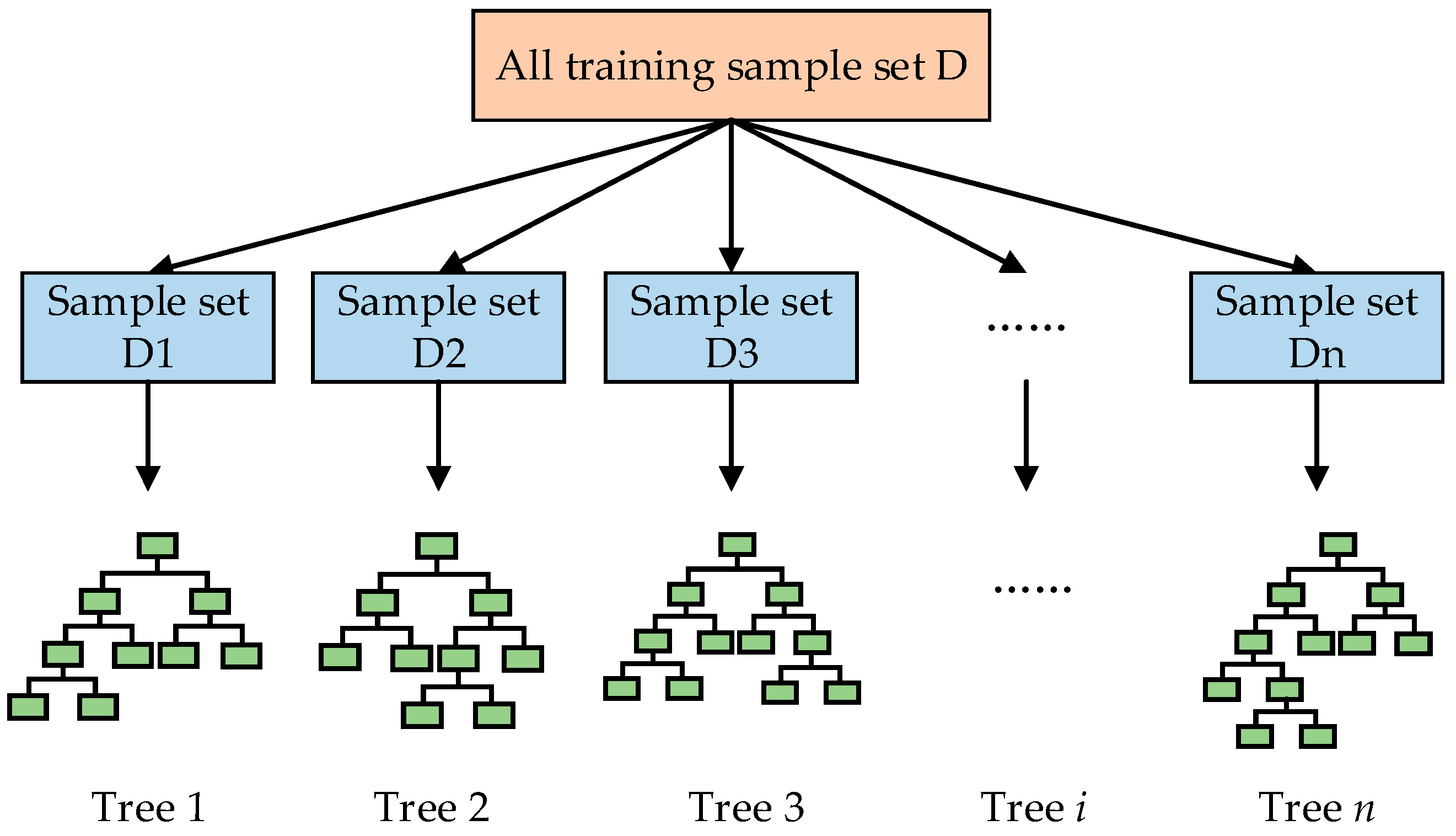
4.2. Feature Selection of Input Parameters
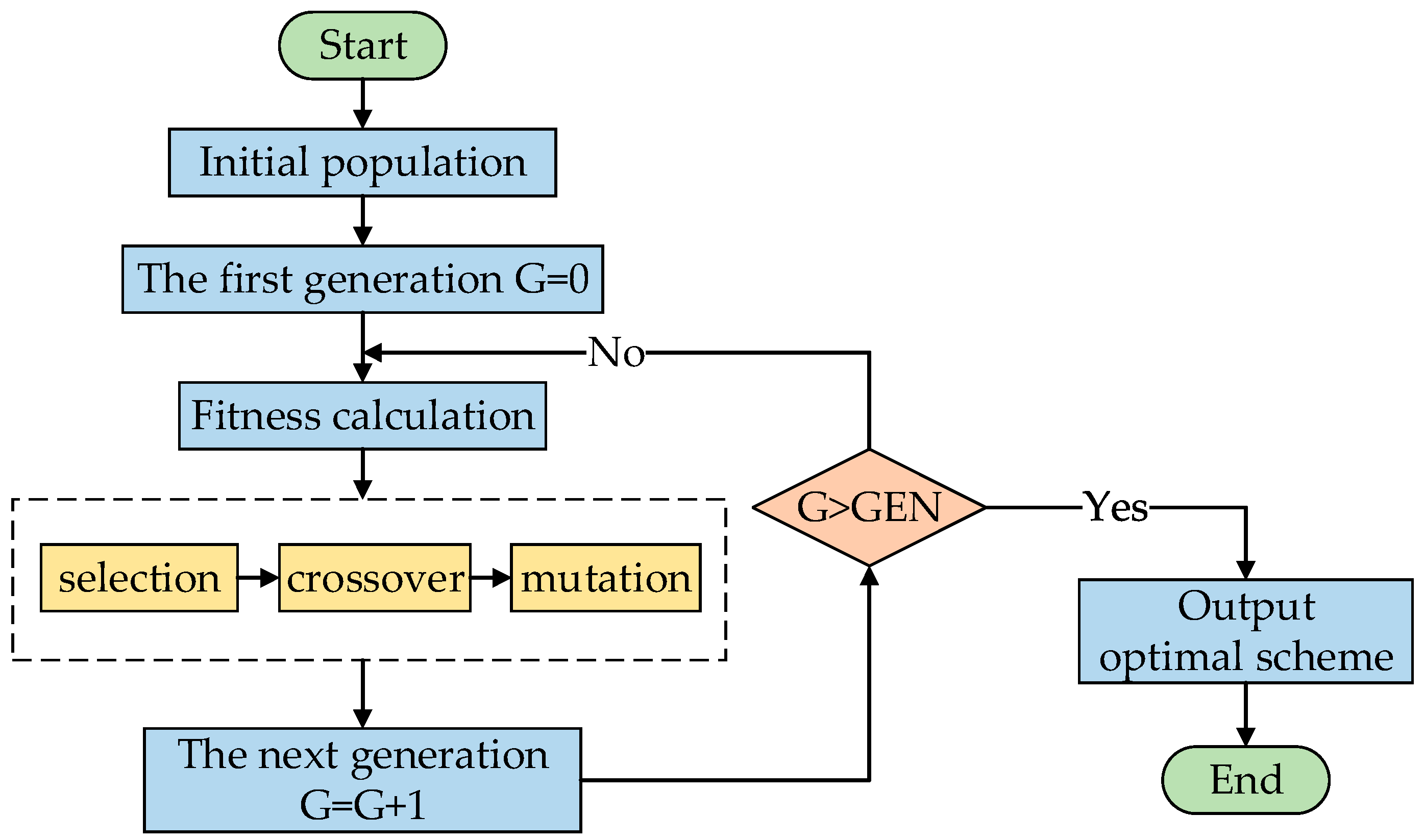
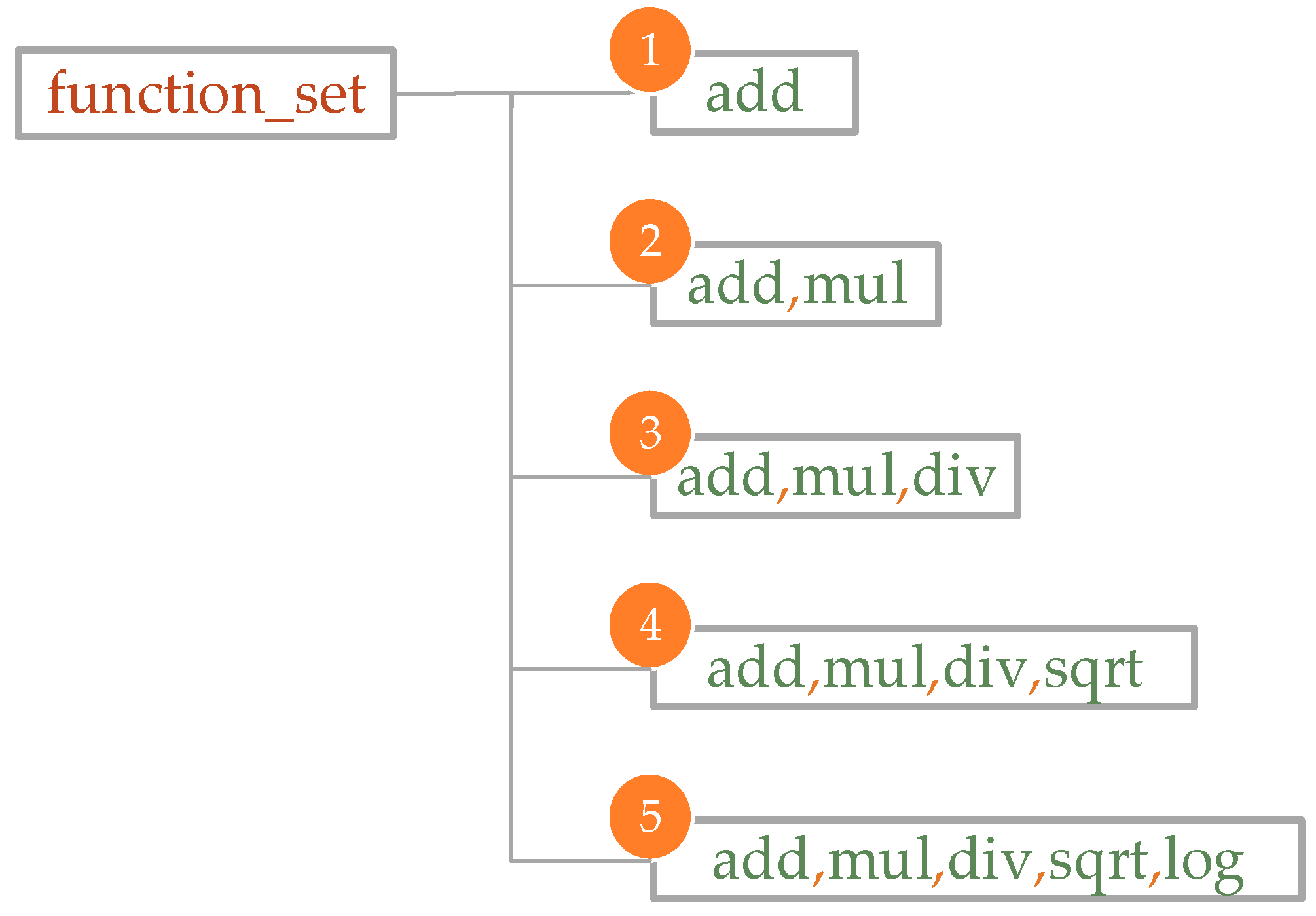
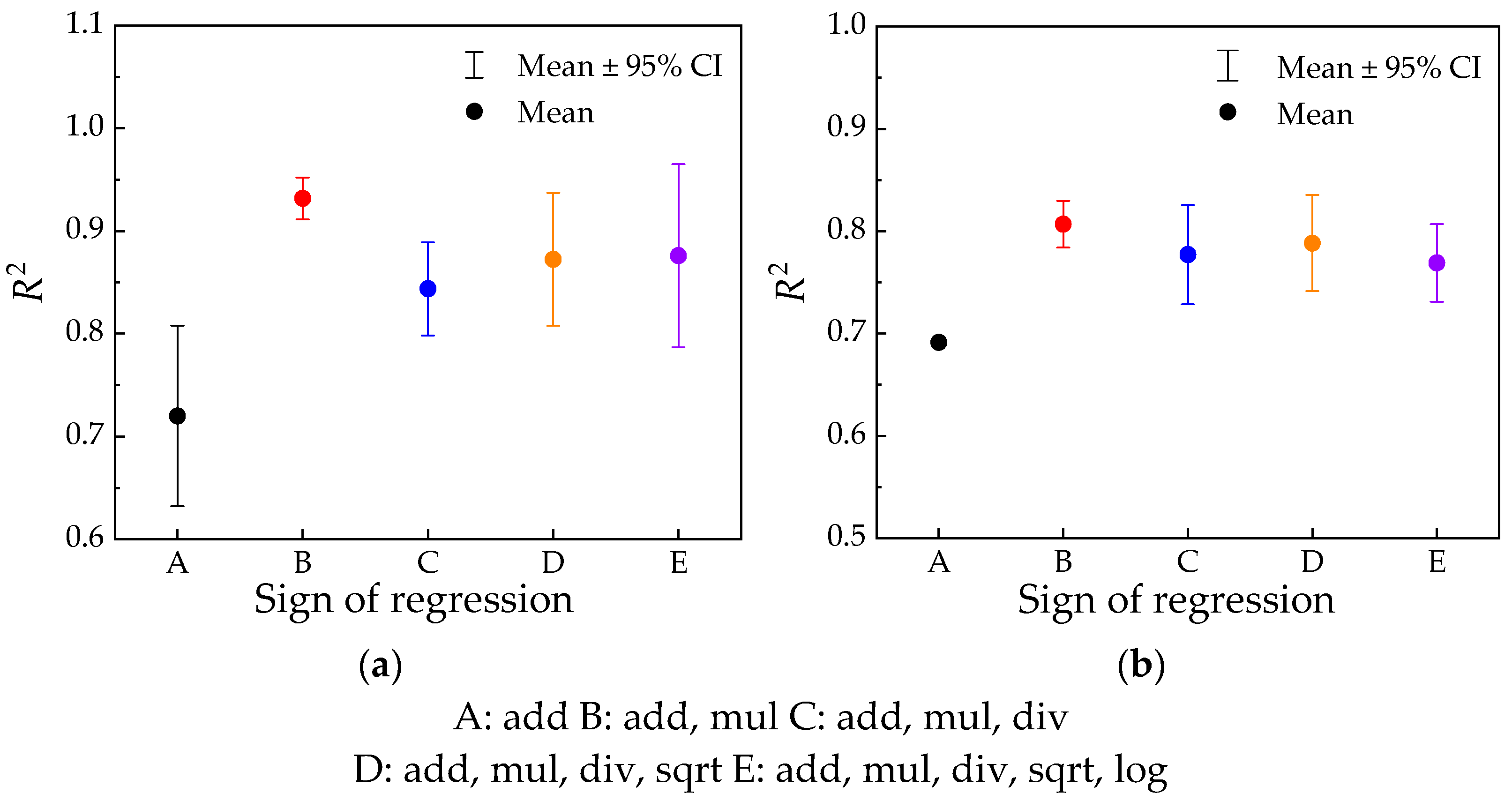
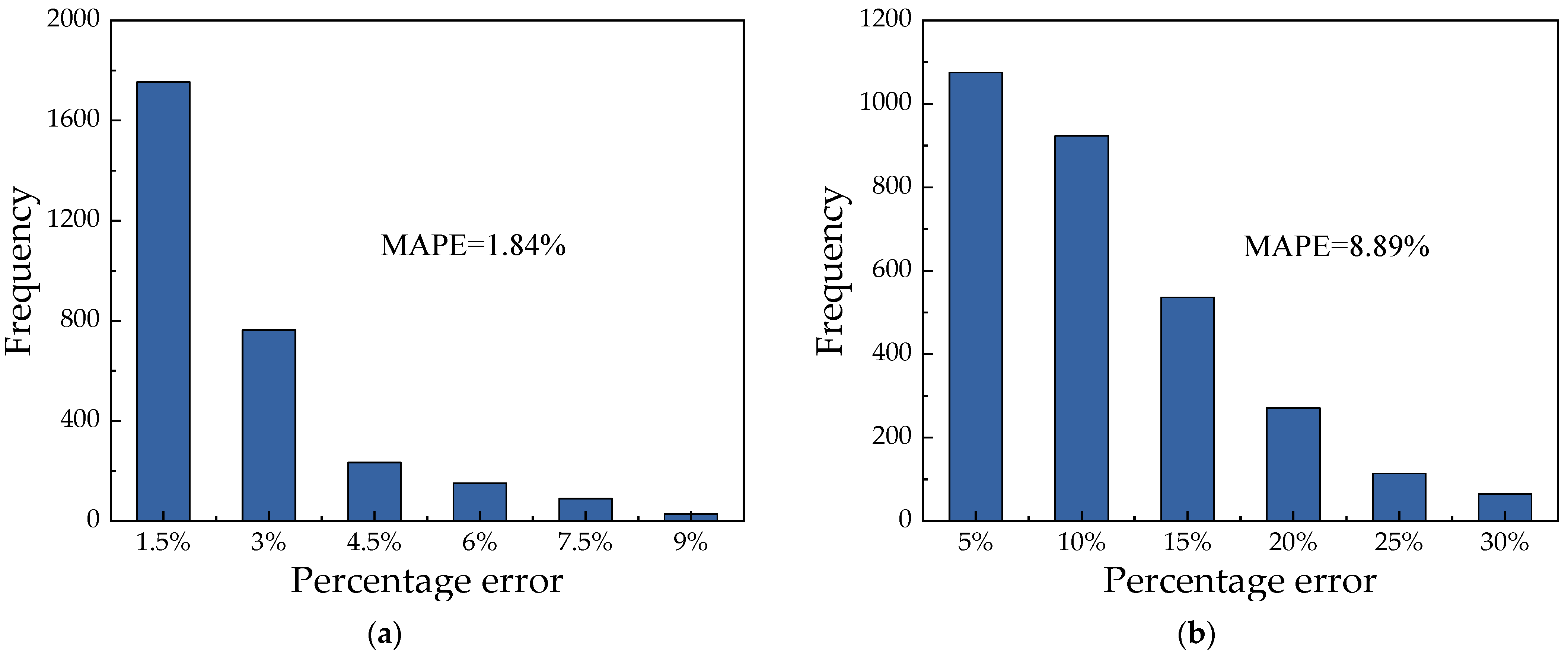
4.3. Modeling Based on Symbolic Regression Algorithm
4.4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Stachowiak, G.P.; Stachowiak, G.W.; Podsiadlo, P. Automated classification of wear particles based on their surface texture and shape features. Tribol. Int. 2008, 41, 34–43. [Google Scholar] [CrossRef]
- Hassanpour, J.; Ghaedi Vanani, A.A.; Rostami, J.; Cheshomi, A. Evaluation of common TBM performance prediction models based on field data from the second lot of Zagros water conveyance tunnel (ZWCT2). Tunn. Undergr. Space Technol. 2016, 52, 147–156. [Google Scholar] [CrossRef]
- Salimi, A.; Rostami, J.; Moormann, C.; Delisio, A. Application of non-linear regression analysis and artificial intelligence algorithms for performance prediction of hard rock TBMs. Tunn. Undergr. Space Technol. 2016, 58, 236–246. [Google Scholar] [CrossRef]
- Armaghani, D.J.; Koopialipoor, M.; Marto, A.; Yagiz, S. Application of several optimization techniques for estimating TBM advance rate in granitic rocks. J. Rock Mech. Geotech. Eng. 2019, 11, 779–789. [Google Scholar] [CrossRef]
- Koopialipoor, M.; Tootoonchi, H.; Jahed Armaghani, D.; Tonnizam Mohamad, E.; Hedayat, A. Application of deep neural networks in predicting the penetration rate of tunnel boring machines. Bull. Eng. Geol. Environ. 2019, 78, 6347–6360. [Google Scholar] [CrossRef]
- Dalong, J.; Zhichao, S.; Dajun, Y. Effect of Spatial Variability on Disc Cutters Failure During TBM Tunneling in Hard Rock. Rock Mech. Rock Eng. 2020, 53, 4609–4621. [Google Scholar] [CrossRef]
- Rispoli, A.; Ferrero, A.M.; Cardu, M. From Exploratory Tunnel to Base Tunnel: Hard Rock TBM Performance Prediction by Means of a Stochastic Approach. Rock Mech. Rock Eng. 2020, 53, 5473–5487. [Google Scholar] [CrossRef]
- Wei, M.; Song, Y.; Wang, X.; Peng, J. Safety diagnosis of TBM for tunnel excavation and its effect on engineering. Neural Comput. Appl. 2021, 33, 997–1005. [Google Scholar] [CrossRef]
- Ates, U.; Bilgin, N.; Copur, H. Estimating torque, thrust and other design parameters of different type TBMs with some criticism to TBMs used in Turkish tunneling projects. Tunn. Undergr. Space Technol. 2014, 40, 46–63. [Google Scholar] [CrossRef]
- Zhou, X.P.; Zhai, S.F. Estimation of the cutterhead torque for earth pressure balance TBM under mixed-face conditions. Tunn. Undergr. Space Technol. 2018, 74, 217–229. [Google Scholar] [CrossRef]
- Zhang, Q.; Su, C.; Qin, Q.; Cai, Z.; Hou, Z.; Kang, Y. Modeling and prediction for the thrust on EPB TBMs under different geological conditions by considering mechanical decoupling. Sci. China Technol. Sci. 2016, 59, 1428–1434. [Google Scholar] [CrossRef]
- Rostami, J.; Ozdemir, L. A new model for performance prediction of hard rock TBMs. Rect Proc. 1993, 50, 793–809. [Google Scholar]
- Rostami, J.; Ozdemir, L.; Nilson, B. Comparison between CSM and NTH hard rock TBM performance prediction models. In Proceedings of the Annual Technical Meeting of the Institute of Shaft Drilling Technology, Las Vegas, NV, USA, 1–3 May 1996; pp. 1–10. Available online: https://www.researchgate.net/publication/237801456 (accessed on 15 June 2021).
- Liu, H.P. Study on TBM Cutterhead Working Principle. Appl. Mech. Mater. 2012, 152–154, 1612–1618. [Google Scholar] [CrossRef]
- Young, K.T.; Jin, Y.H.; Jin, S.Y. A comparative study on the TBM disc cutter wear prediction model. J. Korean Tunn. Undergr. Space Assoc. 2014, 16. [Google Scholar] [CrossRef][Green Version]
- Shi, H.; Yang, H.; Gong, G.; Wang, L. Determination of the cutterhead torque for EPB shield tunneling machine. Autom. Constr. 2011, 20, 1087–1095. [Google Scholar] [CrossRef]
- Wang, L.; Gong, G.; Shi, H.; Yang, H. Modeling and analysis of thrust force for EPB shield tunneling machine. Autom. Constr. 2012, 27, 138–146. [Google Scholar] [CrossRef]
- Zhang, Q.; Huang, T.; Huang, G.Y.; Cai, Z.X.; Kang, Y.L. Theoretical model for loads prediction on shield tunneling machine with consideration of soil-rock interbedded ground. Sci. China Technol. Sci. 2013, 56, 2259–2267. [Google Scholar] [CrossRef]
- Zhang, Q.; Qu, C.Y.; Cai, Z.X.; Kang, Y.L.; Huang, T. Modeling of the thrust and torque acting on shield machines during tunneling. Autom. Constr. 2014, 40, 60–67. [Google Scholar] [CrossRef]
- Zhang, H.M.; Wu, X.G.; Zeng, W.H. Experimental study on earth pressure balance shield tunneling and mathematical model. Chin. J. Rock Mech. Eng. 2005, S2, 5762–5766. (In Chinese) [Google Scholar]
- Entacher, M.; Lorenz, S.; Galler, R. Tunnel boring machine performance prediction with scaled rock cutting tests. Int. J. Rock Mech. Min. 2014, 70, 450–459. [Google Scholar] [CrossRef]
- Zhang, Z.Q.; Li, T.; Han, A.M. Prediction Model of Shield Driving Rate and Cutterhead Torque and Its Formation Adaptability in Complex Strata. Tunn. Constr. 2016, 36, 1449–1455. (In Chinese) [Google Scholar]
- Yagiz, S. New equations for predicting the field penetration index of tunnel boring machines in fractured rock mass. Arab. J. Geosci. 2017, 10, 33. [Google Scholar] [CrossRef]
- Li, J.; Li, P.; Guo, D.; Li, X.; Chen, Z. Advanced prediction of tunnel boring machine performance based on big data. Geosci. Front. 2021, 12, 331–338. [Google Scholar] [CrossRef]
- Sun, W.; Shi, M.; Zhang, C.; Zhao, J.; Song, X. Dynamic load prediction of tunnel boring machine (TBM) based on heterogeneous in-situ data. Autom. Constr. 2018, 92, 23–34. [Google Scholar] [CrossRef]
- Zheng, Z.; Chen, K.; Zhang, Q. Identification of Loads on Shield Tunneling Machines Based on PSO-SVM Method. Appl. Mech. Mater. 2013, 392, 746–749. [Google Scholar] [CrossRef]
- Yagiz, S.; Karahan, H. Prediction of hard rock TBM penetration rate using particle swarm optimization. Int. J. Rock Mech. Min. 2011, 48, 427–433. [Google Scholar] [CrossRef]
- Zhang, Q.L.; Liu, Z.; Tan, J. Prediction of geological conditions for a tunnel boring machine using big operational data. Autom. Constr. 2019, 100, 73–83. [Google Scholar] [CrossRef]
- Köktürk-Güzel, B.E.; Beyhan, S. Symbolic Regression Based Extreme Learning Machine Models for System Identification. Neural Process. Lett. 2021, 53, 1565–1578. [Google Scholar] [CrossRef]
- Nijhout, F. An introduction to genetic algorithms. Complexity 1997, 2, 39–40. [Google Scholar] [CrossRef]
- Zheng, Q.; Sha, J.; Fang, C. An effective genetic algorithm to VDA with discontinuous “on-off” switches. Sci. China Earth Sci. 2012, 55, 1345–1357. [Google Scholar] [CrossRef]
- Xing, X.; Liu, Y.; Garg, A.; Ma, X.; Yang, T.; Zhao, L. An improved genetic algorithm for determining modified water-retention model for biochar-amended soil. Catena 2021, 200, 105143. [Google Scholar] [CrossRef]
- Mahardhika, T. Hybrid Algorithm as alternative method for optimization, a combination Genetic Algorithm and Particle Swarm Optimization. J. Phys. Conf. Ser. 2021, 1764, 12040. [Google Scholar] [CrossRef]
- Rodriguez-Fernández, J. Ockham’s razor. Endeavour 1999, 23, 121–125. [Google Scholar] [CrossRef]
- Sonnergaard, J.M. Ockham’s Razor Applied on Pharmaceutical Powder Compaction Models. J. Pharm. Sci. 2021, 110, 989–996. [Google Scholar] [CrossRef]
- Stanhill, G. Total, global and surface solar radiation: The case for Ockham’s razor. Weather 2018, 73, 117. [Google Scholar] [CrossRef]
- Mirko, F.; Mazen, A. The Ockham’s razor applied to COVID-19 model fitting French data. Annu. Rev. Control 2021. prepublish. [Google Scholar]
- Buckingham, E. On physically similar systems. J. Wash. Acad. Sci. Wash. DC 1914, 4, 345–376. [Google Scholar]
- Hou, S.K.; Liu, Y.R.; Li, C.Y.; Qin, P.X. Dynamic Prediction of Rock Mass Classification in the Tunnel Construction Process based on Random Forest Algorithm and TBM in situ Operation Parameters. Iop Conf. Ser. Earth Environ. Sci. 2020, 570, 052056. [Google Scholar] [CrossRef]
- Li, A.; Feng, M.; Li, Y.; Liu, Z. Application of Outlier Mining in Insider Identification Based on Boxplot Method. Procedia Comput. Sci. 2016, 91, 245–251. [Google Scholar] [CrossRef]

| Physical Parameters | Dimension | |
|---|---|---|
| Machine Parameters | Cutterhead diameter | L |
| Operating Parameters | Driving speed | L T−1 |
| Cutterhead rotation speed | T−1 | |
| Geologic Parameters | Rock density | M L−3 |
| Shear modulus | M L−1 T−2 | |
| Poisson’s ratio | — | |
| Cohesive force | M L−1 T−2 | |
| Compressive strength | M L−1 T−2 | |
| Tensile strength | M L−1 T−2 | |
| Target Parameters | Total thrust | M L T−2 |
| Total torque | M L2 T−2 |
| Basic Dimensions M | Basic Dimensions L | Basic Dimensions T | |||
|---|---|---|---|---|---|
| Physical Parameters | Dimension | Physical Parameters | Dimension | Physical Parameters | Dimension |
| M L−3 | L | L T−1 | |||
| M L−1 T−2 | L T−1 | M L−1 T−2 | |||
| M L−1 T−2 | M L−3 | M L−1 T−2 | |||
| M L−1 T−2 | M L−1 T−2 | M L−1 T−2 | |||
| M L−1 T−2 | M L−1 T−2 | M L−1 T−2 | |||
| M L−1 T−2 | |||||
| M L−1 T−2 | |||||
| T−1 | |||||
| Physical Parameters | Maximum | Minimum | Average | |
|---|---|---|---|---|
| Operating Parameters | Driving speed | 81.00 | 1.00 | 18.04 |
| Cutterhead rotation speed | 7.00 | 0.24 | 5.75 | |
| Geologic Parameters | Rock density | 2.70 | 2.64 | 2.65 |
| Shear modulus | 7.15 | 3.75 | 4.04 | |
| Poisson’s ratio | 0.27 | 0.23 | 0.26 | |
| Cohesive force | 1.91 | 1.45 | 1.50 | |
| Compressive strength | 106.57 | 74.99 | 78.82 | |
| Tensile strength | 6.59 | 4.75 | 4.96 | |
| Target Parameters | Total thrust | 18,458.00 | 151.00 | 16,843.48 |
| Total torque | 2712.00 | 12.00 | 1408.90 |
| Total Thrust | Total Torque | |||||||
|---|---|---|---|---|---|---|---|---|
| R2 | MAPE | Model | Theoretical Relationship | R2 | MAPE | Model | Theoretical Relationship | |
| SR | 0.95 | 1.82% | Explicit | reasonable | 0.81 | 8.83% | explicit | reasonable |
| LR | 0.96 | 1.55% | Explicit | unreasonable | 0.84 | 8.13% | explicit | unreasonable |
| ANN | 0.95 | 1.71% | hidden layer | unknown | 0.81 | 8.33% | hidden layer | unknown |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Zhang, Q.; Zhou, S.; Liu, S. Modeling of Tunneling Total Loads Based on Symbolic Regression Algorithm. Appl. Sci. 2021, 11, 5671. https://doi.org/10.3390/app11125671
Zhang L, Zhang Q, Zhou S, Liu S. Modeling of Tunneling Total Loads Based on Symbolic Regression Algorithm. Applied Sciences. 2021; 11(12):5671. https://doi.org/10.3390/app11125671
Chicago/Turabian StyleZhang, Liting, Qian Zhang, Siyang Zhou, and Shanglin Liu. 2021. "Modeling of Tunneling Total Loads Based on Symbolic Regression Algorithm" Applied Sciences 11, no. 12: 5671. https://doi.org/10.3390/app11125671
APA StyleZhang, L., Zhang, Q., Zhou, S., & Liu, S. (2021). Modeling of Tunneling Total Loads Based on Symbolic Regression Algorithm. Applied Sciences, 11(12), 5671. https://doi.org/10.3390/app11125671





