Methods of Constructing Time Series for Predicting Local Time Scales by Means of a GMDH-Type Neural Network
Abstract
:1. Introduction
2. GMDH-Type Neural Network
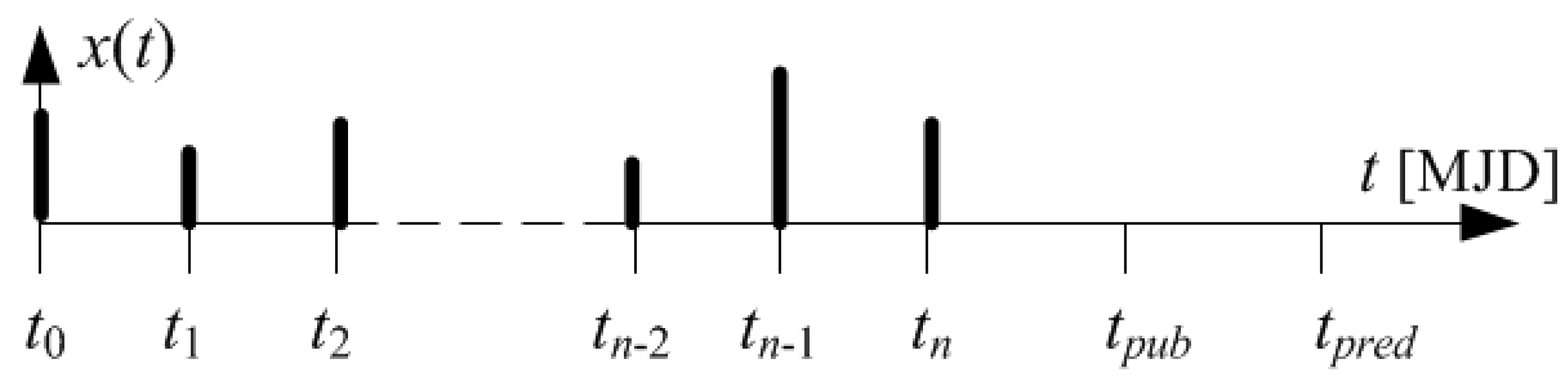
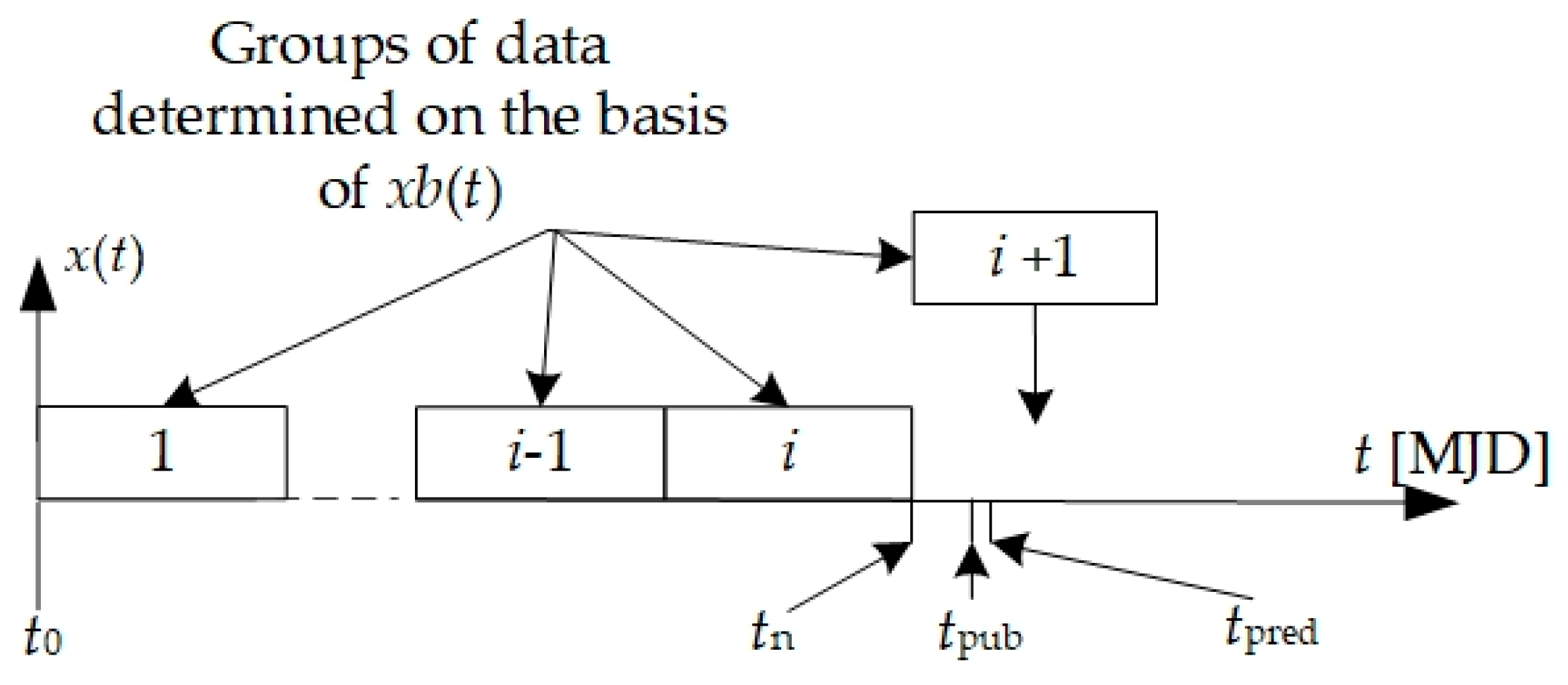
3. Construction of Time Series Based on the UTC Scale
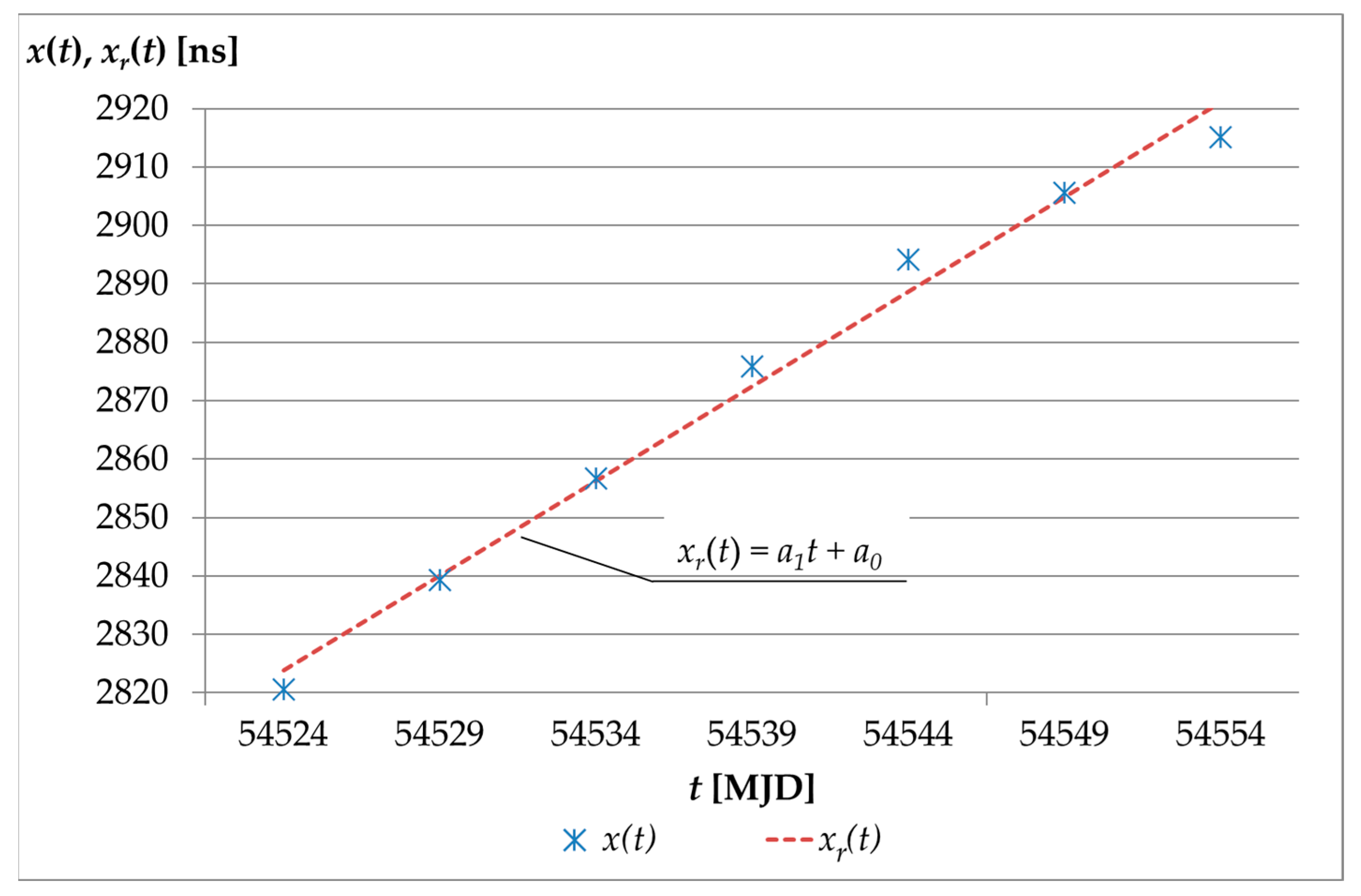
3.1. The Method of Constructing the TS1_5 and TS2_5 Time Series Prepared with the 5-Day Interval
- xa(t)—historical results of phase time measurements between 1 pps (pulse per second) signals from UTC(k) and the clock realizing UTC(k), determined with a one-day interval according to the relationship:
- xb(t)—values of [UTC-UTC(k)] deviations determined by BIPM for UTC(k) in relation to UTC, which are designated as MJD days that end in digits 4 and 9 according to the formula
3.2. The Method of Constructing the TS1_1, TS2_1, and TS3_1 Time Series Prepared with the 1-Day Interval
3.3. Assessment of the Construction Method of the Proposed Time Series Based on the UTC Scale
- -
- from −5.05 ns to 6.95 ns for TS1_5,
- -
- from −4.63 ns to 7.74 ns for TS2_5,
- -
- from −0.60 ns to 3.08 ns for TS1_1,
- -
- from −0.07 ns to 0.40 ns for TS2_1,
- -
- from −15.91 ns to 6.89 ns for TS3_1.
- (1)
- The smallest residual values have been obtained for the TS1_1 and TS2_1. This is due to the application of the PCHIP interpolation function, which makes it possible to prepare data for the GMDH-type NN with a one-day interval.
- (2)
- Comparison of ME, MAE, and MSE1 error values for all time series shows that for the TS3_1 time series the predictions are the most loaded.
- (3)
- The deviations predictions determined for TS1_1 and TS2_1 are characterized by small values of the MSE2 error component. This allows a good prediction of the variability of the predicted values in relation to the variability of the values observed for both time series, which results from the density of training data in a given month, thanks to application of the PCHIP function.
- (4)
- In the case of results obtained for TS2_1 time series, the smallest value of the MSE3 error component has been obtained in relation to the other time series. This is due to the decomposition of the TS1_1 time series, which resulted in a better compliance of the direction of changes in the prediction and the direction of changes in the predicted value for the TS2_1 time series.
- (5)
- The comparison of the obtained values of residuals and the values of all the prediction quality measures indicates, that the best quality of predicting the deviations has been obtained using the TS1_1 and TS2_1 time series. This is due to the application of xb(t) values determined with a one-day interval, thanks to the application of the PCHIP function. The research results for these time series for a longer period of time presented in [10,24] confirm that the TS1_1 and TS2_1 enable the best quality for predicting deviations. However, these studies show that the TS1_1 is more suitable for practical application. The TS2_1 is characterized by a slightly worse quality of prediction and is more time-consuming to prepare.
- (6)
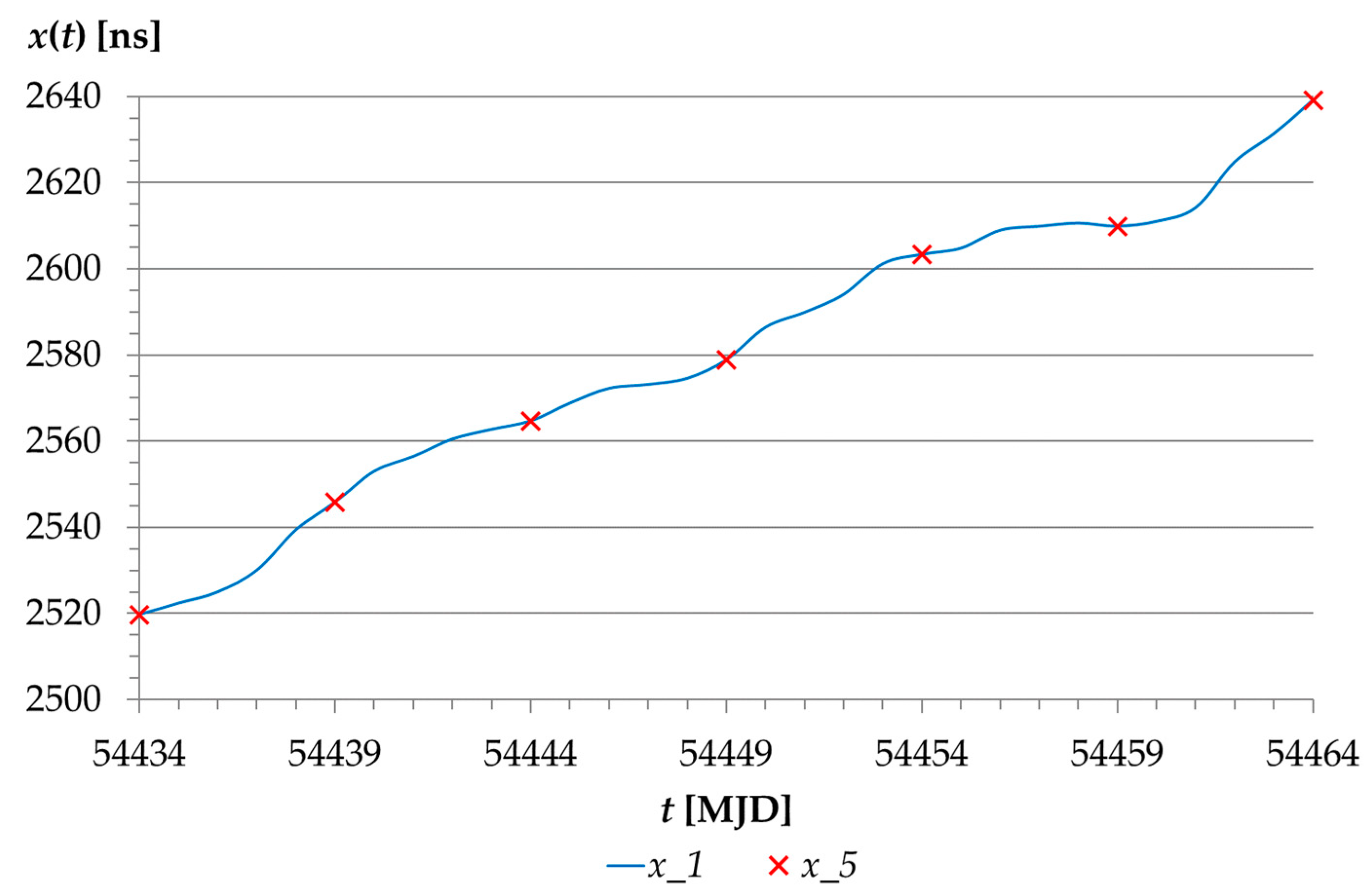
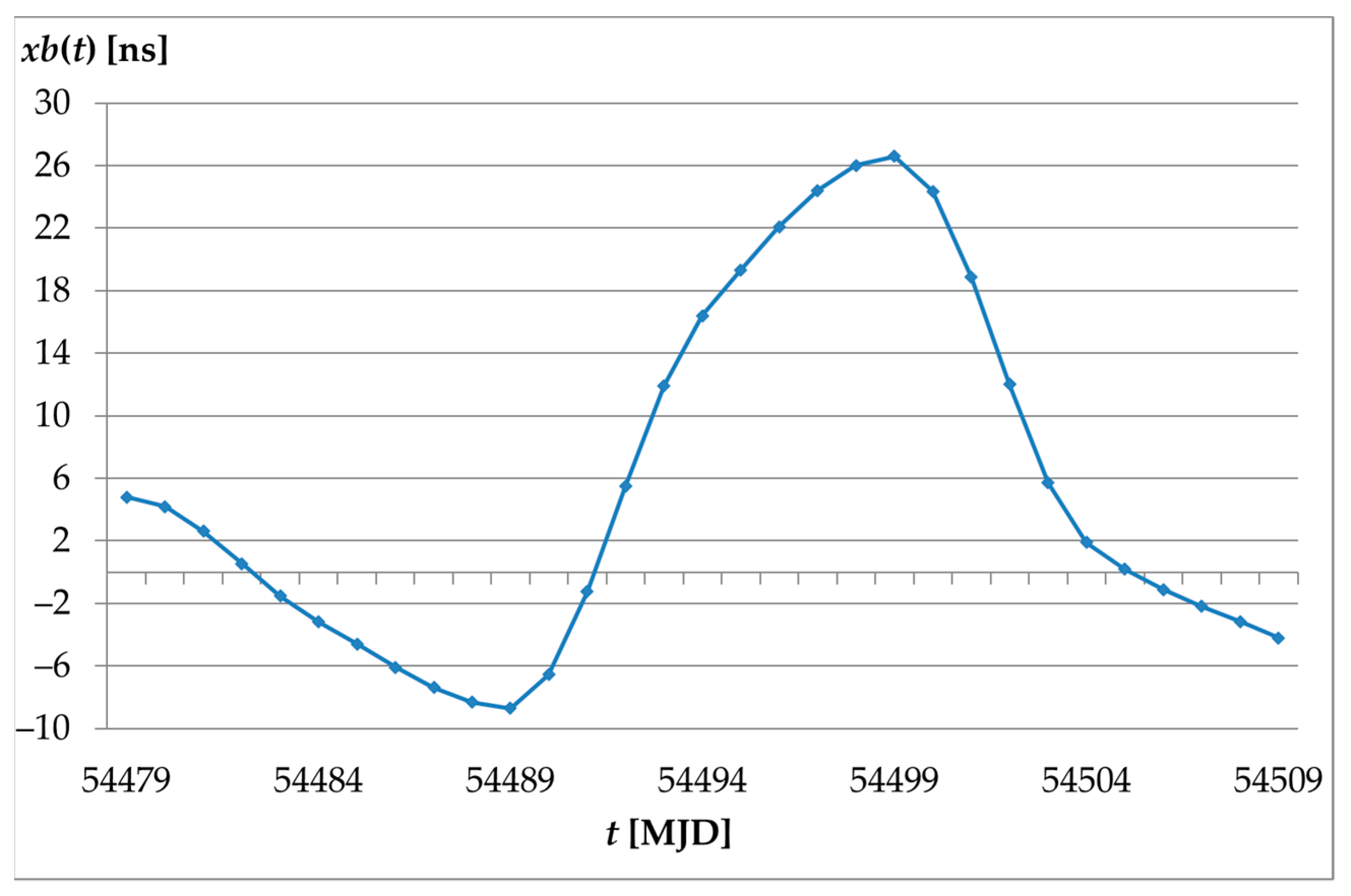
- The values of the TS3_1 are determined only on the basis of the xb(t) deviation values published by BIPM. The achieved unfavorable large value of xb(t) for the MJD 54499 day, amounting to 26.6 ns (Figure 7), directly influenced the large residual value for MJD 54509, as well as the MSE error and its components MSE1 and MSE3. Such a large residual value results from a large change in UTC-UTC(PL) deviations in the period from MJD 54479 to MJD 54509. The proposed TS3_1, despite the non-optimal residual values and the determined quality measures of prediction achieved, is a good alternative for predicting xb(tpred) in the case of absence of the xa(t) values due to a failure of the atomic clock or its replacement.
4. Construction of Time Series Based on the UTC and UTC Rapid Scale
4.1. The Method of Constructing the TS4_1 and TS5_1 Time Series Prepared with the 1-Day Interval
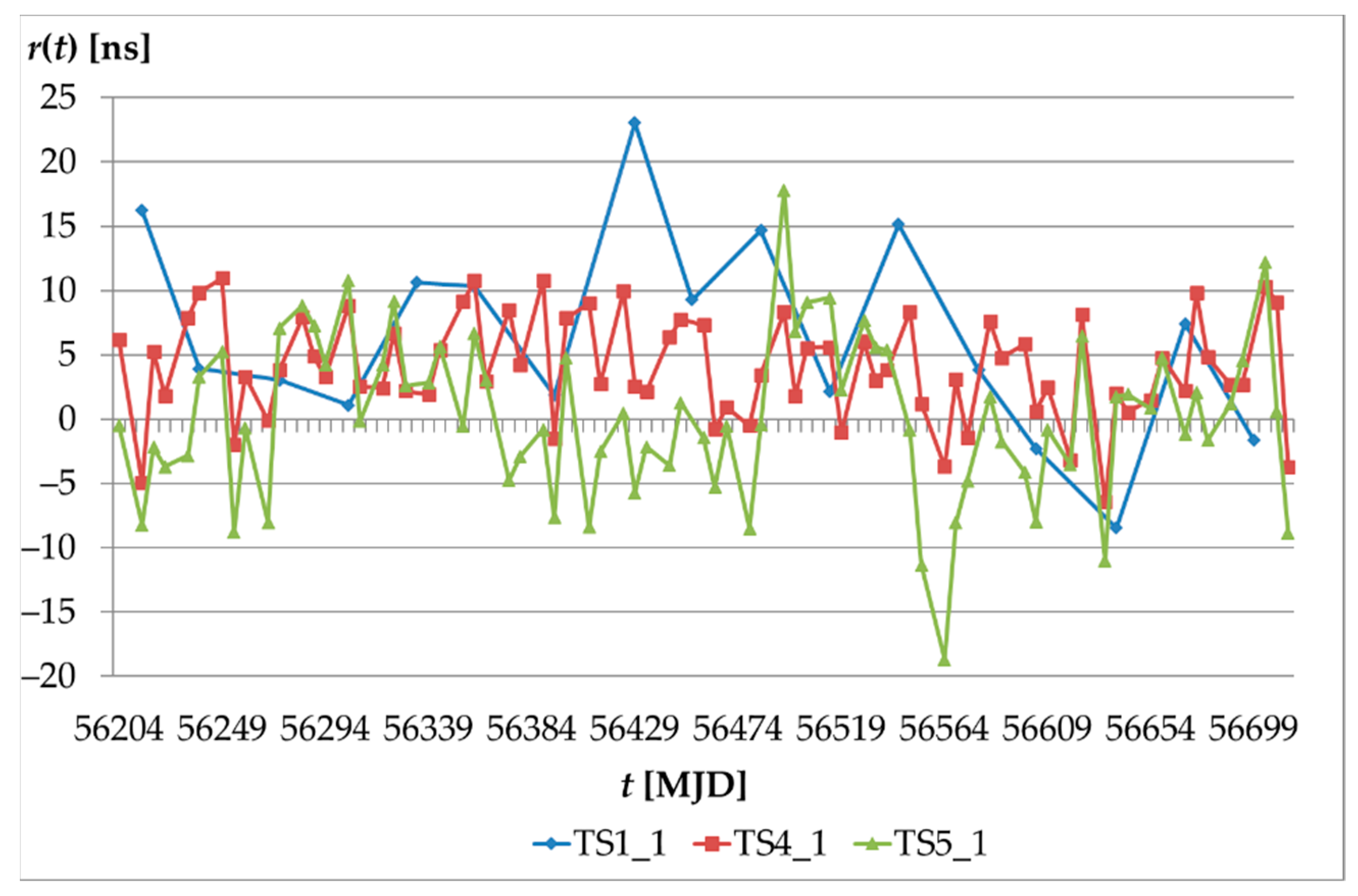
4.2. Assessment of the Construction Method of the Proposed Time Series Based on the UTC and UTC Rapid Scales
- -
- from −8.43 ns to 23.04 ns for TS1_1,
- -
- from −6.42 ns to 10.99 ns for TS4_1,
- -
- from −18.67 ns to 17.82 ns for TS5_1.
- (1)
- Comparison of ME, MAE, and MSE1 error values for three analyzed time series shows that for the TS5_1 time series, the predictions are the least loaded.
- (2)
- Predictions of the deviations determined by the GMDH-type NN for the TS4_1 time series are characterized by smaller MSE2 and MSE3 error values compared to the TS5_1 time series. This means better anticipation of fluctuations in the prediction variable and greater compliance of the direction of prediction changes in relation to the direction of changes in the predicted value. Hence, 64% of determined values of residuals for the TS4_1 time series are in the range of ±5 ns, and 96% of the determined residual values for this time series are in the range of ±10 ns. The remaining determined residual values (4%) are within ±11 ns.
- (3)
- From the group of TS1_1, TS4_1 and TS5_1 time series examined, the best prediction quality results were obtained for TS4_1 time series. This is due to the shorter prediction horizon, that has been achieved by introducing xbr(t) deviations determined by BIPM into the construction of these time series.
- (4)
- The introduction in the second method of constructing the time series of xbr(t) deviations determined by BIPM also makes it possible for TS5_1 to achieve better-quality predictions than for TS3_1
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Arias, E.F.; Panfilo, G.; Petit, G. Timescales at the BIPM. Metrologia 2011, 48, 145–153. [Google Scholar] [CrossRef]
- BIPM Time Department Data Base. Available online: https://webtai.bipm.org/database/clock.html (accessed on 15 April 2021).
- Panfilo, G.; Tavella, P. Atomic clock prediction based on stochastic differential equations. Metrologia 2008, 45, 108–116. [Google Scholar] [CrossRef]
- Bernier, L.G. Use of the Allan Deviation and Linear Prediction for the Determination of the Uncertainty on Time Calibrations Against Predicted Timescales. IEEE Trans. Instrum. Meas. 2003, 52, 483–486. [Google Scholar] [CrossRef]
- Davis, J.A.; Shemar, S.L.; Whibberley, P.B. A Kalman filter UTC(k) prediction and steering algorithm. In Proceedings of the Conference of the IEEE International Frequency Control Symposium/European Frequency and Time Forum Proceedings, San Francisco, CA, USA, 1–5 May 2011; pp. 779–784. [Google Scholar]
- Czubla, A.; Konopka, J.; Nawrocki, J. Realization of atomic SI second definition in context UTC(PL) and TA(PL). Metrol. Meas. Syst. 2006, 2, 149–159. [Google Scholar]
- Nelles, O. Nonlinear System Identification. From Classical Approaches to Neural Networks and Fuzzy Models; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Miczulski, W.; Sobolewski, Ł. Application of the GMDH neural networks in prediction of corrections of the national time scale. Electron. Des. Technol. Appl. 2011, 6, 45–47. [Google Scholar]
- Iwachnienko, A.G.; Wunsch, D.; Iwachnienko, G.A. Inductive Sorting-Out GMDH Algorithms with Polynomial Complexity for Active Neurons of Neural Network. In Proceedings of the International Joint Conference on Neural Networks (IJCNN), Washington, DC, USA, 10–16 July 1999; pp. 185–196. [Google Scholar]
- Sobolewski, Ł. Predicting the corrections for the Polish Timescale UTC(PL) using GMDH and GRNN neural networks. In Proceedings of the European Frequency Time Forum Proceedings, Neuchâtel, Switzerland, 23–26 June 2014; pp. 475–478. [Google Scholar]
- Miczulski, W.; Sobolewski, Ł. Algorithm for predicting [UTC-UTC(k)] by means of neural networks. IEEE Trans. Instrum. Meas. 2017, 66, 2136–2142. [Google Scholar] [CrossRef]
- Sobolewski, Ł. Predicting the Lithuanian Timescale UTC(LT) by means of GMDH neural network. Bull. Mil. Univ. Technol. 2017, 66, 31–41. [Google Scholar] [CrossRef]
- Sobolewski, Ł. Comparison of quality of UTC(PL) and UTC(NPL) scales prediction by means of GMDH neural network. In Measurement Systems in Theory and in Practice; Zielona Gora Press: Zielona Góra, Poland, 2020; pp. 229–242. [Google Scholar]
- Sobolewski, Ł. Application of GMDH Type Neural Network for Predicting UTC(K) Timescales Realized on the Basis of Hydrogen Masers. In Proceedings of the Conference of the European Frequency and Time Forum and IEEE International Frequency Control Symposium (EFTF/IFCS) proceedings, Besancon, France, 9–13 July 2017; pp. 42–46. [Google Scholar]
- Tanebe, T.; Ye, J.; Suzuyama, T.; Kobayashi, T.; Yamaguchi, Y.; Yasuda, M. Potential for improving the local realization of coordinated universal time with a convolutional neural network. Rev. Sci. Instrum. 2019, 90, 125111. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lei, Y.; Guo, M.; Hu, D.; Cai, H.; Zhao, D.; Hu, Z.; Gao, Y. Short-term prediction of UT1-UTC by combination of the grey model and neural networks. Adv. Space Res. 2017, 59, 524–531. [Google Scholar] [CrossRef]
- BIPM Annual Report on Time Activities 14; BIPM: Sevres, France, 2019.
- Kaczmarek, J.; Miczulski, W.; Kozioł, M.; Czubla, A. Integrated system for monitoring and control of the national time and frequency standard. IEEE Trans. Instrum. Meas. 2013, 62, 2828–2838. [Google Scholar] [CrossRef]
- Hecht-Nielsen, R. Neurocomputing; Adison-Wesley Publishing Co: New York, NY, USA, 1991. [Google Scholar]
- Mrugalski, M. Advanced Neural Network–Based Computational Schemes for Robust Fault Diagnosis; Springer International Publishing 510: Cham, Switzerland, 2014. [Google Scholar]
- Sobolewski, Ł. Application of the Neural Networks for Predicting the Corrections for the National Timescale UTC(PL); University of Zielona Gora Press: Zielona, Gora, 2016. [Google Scholar]
- Masters, T. Practical Neural Networks Recipes in C++; Academic Press Inc.: Boston, MA, USA, 1993. [Google Scholar]
- Miczulski, W.; Sobolewski, Ł. Influence of the GMDH neural network data preparation method on UTC(PL) correction prediction results. Metrol. Meas. Syst. 2012, 19, 123–132. [Google Scholar] [CrossRef] [Green Version]
- Pindyck, R.S.; Rubinfeld, D.C. Econometric Models and Economic Forecasts; McGraw Hill: Boston, MA, USA, 1998. [Google Scholar]
- Caldwell, R.B. Performance metrics for neural network-based trading system development. NeuroVest J. 1995, 3, 22–26. [Google Scholar]



| Measure of Quality of Prediction | TS1_5 | TS2_5 | TS1_1 | TS2_1 | TS3_1 |
|---|---|---|---|---|---|
| ME [ns] | 0.45 | 1.61 | 0.55 | 0.1 | −3.5 |
| MAE [ns] | 3.32 | 3.52 | 0.8 | 0.13 | 6.41 |
| MSE [ns2] | 16 | 19 | 2.0 | 0.04 | 74 |
| MSE1 [ns2] | 0.21 | 2.56 | 0.31 | 0.01 | 12.8 |
| MSE2 [ns2] | 5.15 | 6.73 | 0.01 | 0.01 | 2.25 |
| MSE3 [ns2] | 10.9 | 9.97 | 1.67 | 0.02 | 59.4 |
| RMSE [ns] | 4.04 | 4.39 | 1.41 | 0.19 | 8.6 |
| Measure of Quality of Prediction | TS1_1 | TS4_1 | TS5_1 |
|---|---|---|---|
| ME [ns] | 6.5 | 4.1 | 0.22 |
| MAE [ns] | 7.9 | 4.9 | 5.0 |
| MSE [ns2] | 102 | 33 | 40 |
| MSE1 [ns2] | 43 | 17 | 0.04 |
| MSE2 [ns2] | 5.8 | 0.01 | 1.5 |
| MSE3 [ns2] | 54 | 17 | 38 |
| RMSE [ns] | 11 | 5.8 | 6.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sobolewski, Ł.; Miczulski, W. Methods of Constructing Time Series for Predicting Local Time Scales by Means of a GMDH-Type Neural Network. Appl. Sci. 2021, 11, 5615. https://doi.org/10.3390/app11125615
Sobolewski Ł, Miczulski W. Methods of Constructing Time Series for Predicting Local Time Scales by Means of a GMDH-Type Neural Network. Applied Sciences. 2021; 11(12):5615. https://doi.org/10.3390/app11125615
Chicago/Turabian StyleSobolewski, Łukasz, and Wiesław Miczulski. 2021. "Methods of Constructing Time Series for Predicting Local Time Scales by Means of a GMDH-Type Neural Network" Applied Sciences 11, no. 12: 5615. https://doi.org/10.3390/app11125615
APA StyleSobolewski, Ł., & Miczulski, W. (2021). Methods of Constructing Time Series for Predicting Local Time Scales by Means of a GMDH-Type Neural Network. Applied Sciences, 11(12), 5615. https://doi.org/10.3390/app11125615







