Mechanics of Screw Joints Solved as Beams Placed in a Tangential Elastic Foundation
Abstract
1. Introduction
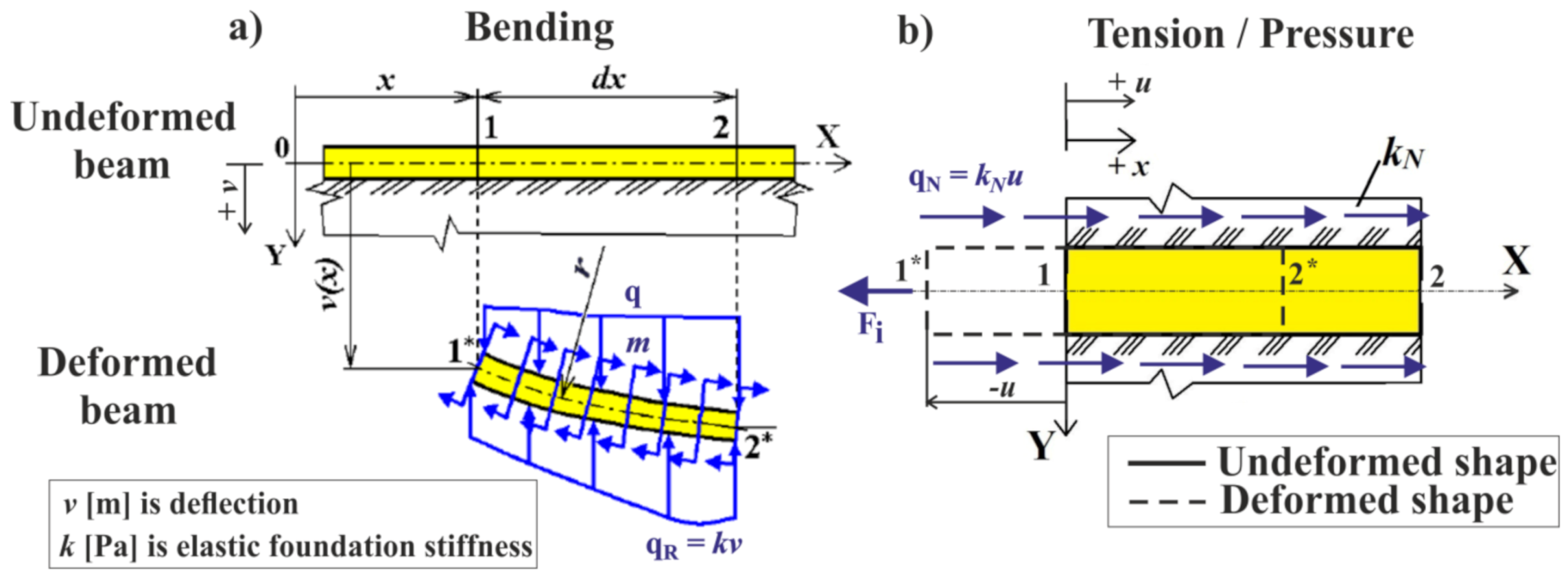
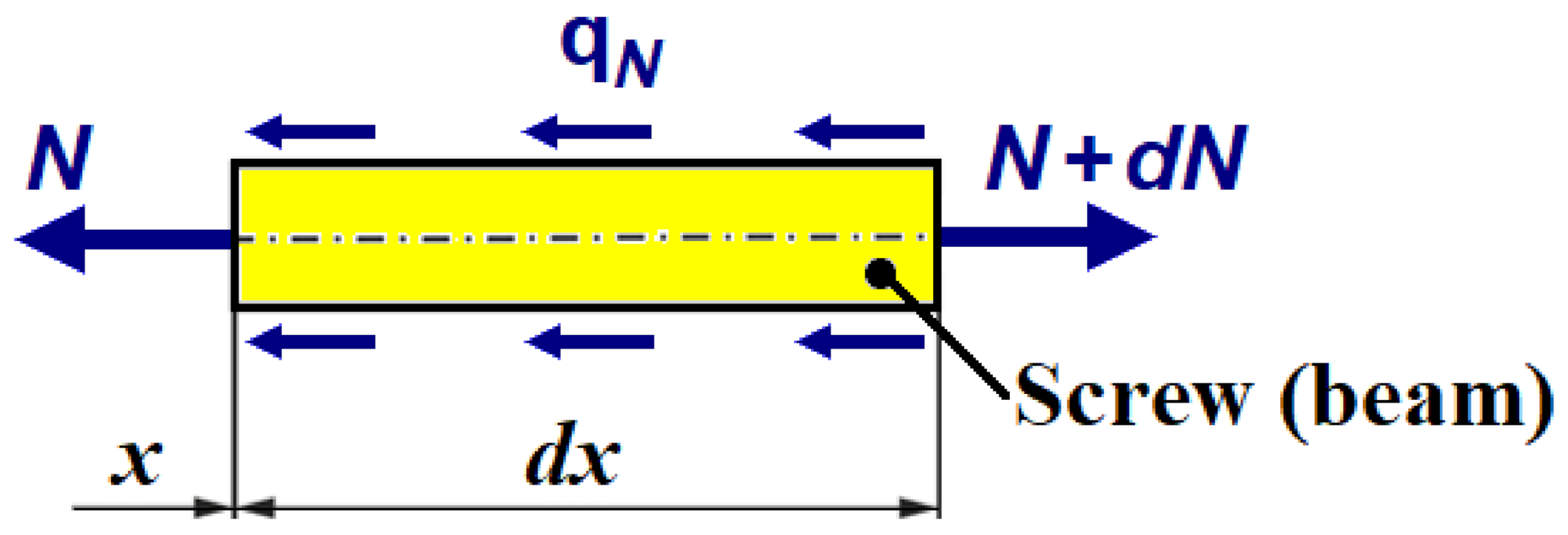
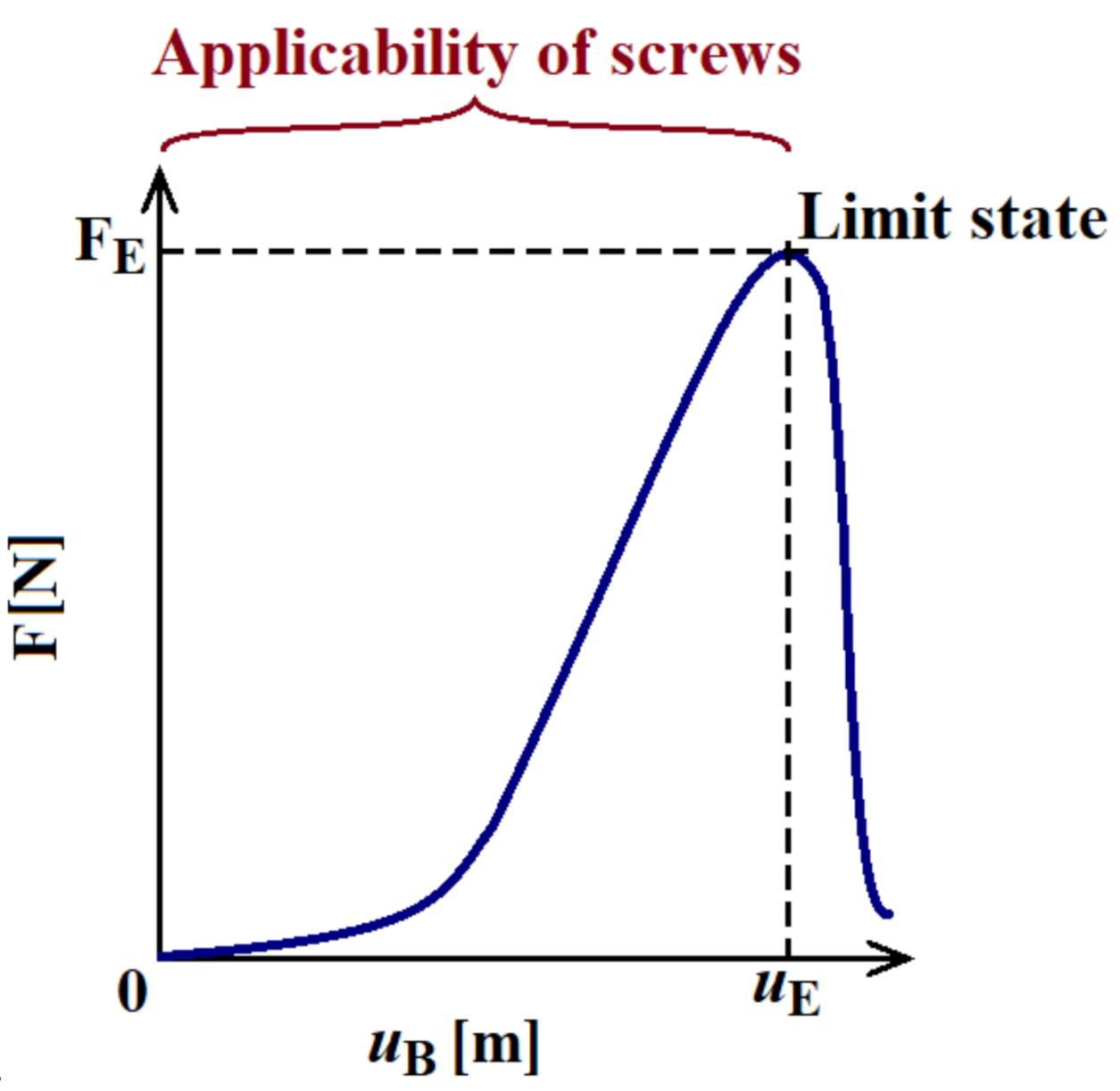
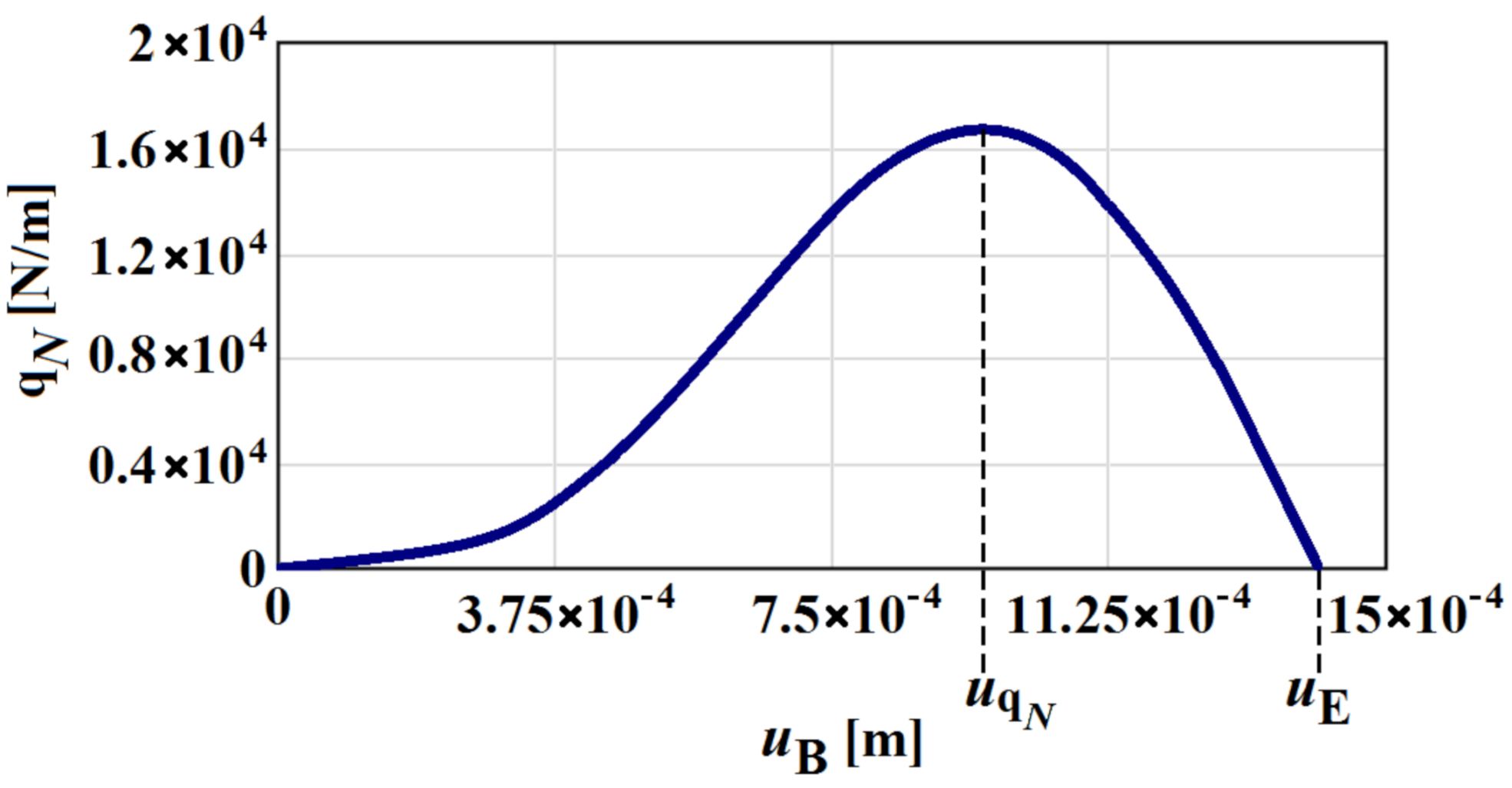
2. The Tangential (Tensile) Elastic Foundation
3. Material and Methods
- To prepare test samples for woodwork screw joints in the laboratory.
- To determine experimentally the dependence of pulling force in the laboratory (i.e., the pull-out test).
- To determine the appropriate shapes of the reaction force (i.e., to design a physical model of the tangential foundation) based on the evaluation of the experiment (laboratory measurements, regression methods, etc.).
- To solve differential Equation (3) based on the knowledge of the reaction force , i.e., to acquire the axial displacement .
- To compare the obtained results with experiments and to evaluate proposed models of the tangential foundation, including the correctness of theory and use.
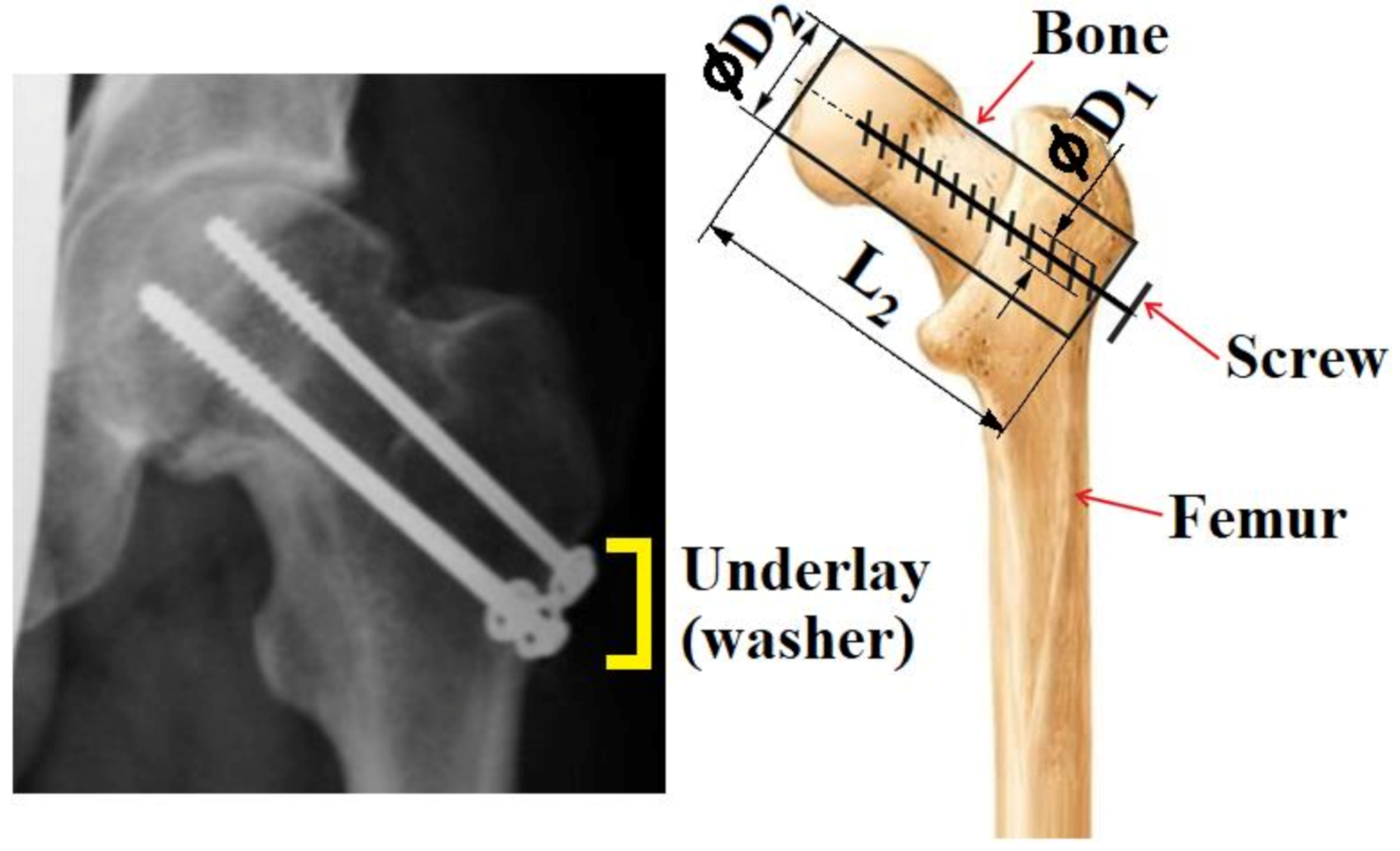
- To check dependencies on other materials such as bone (i.e., “similar” applications in biomechanics, traumatology and orthopaedics).
- To conduct a discussion, draw conclusions and suggest future possible applications and other possible solutions.
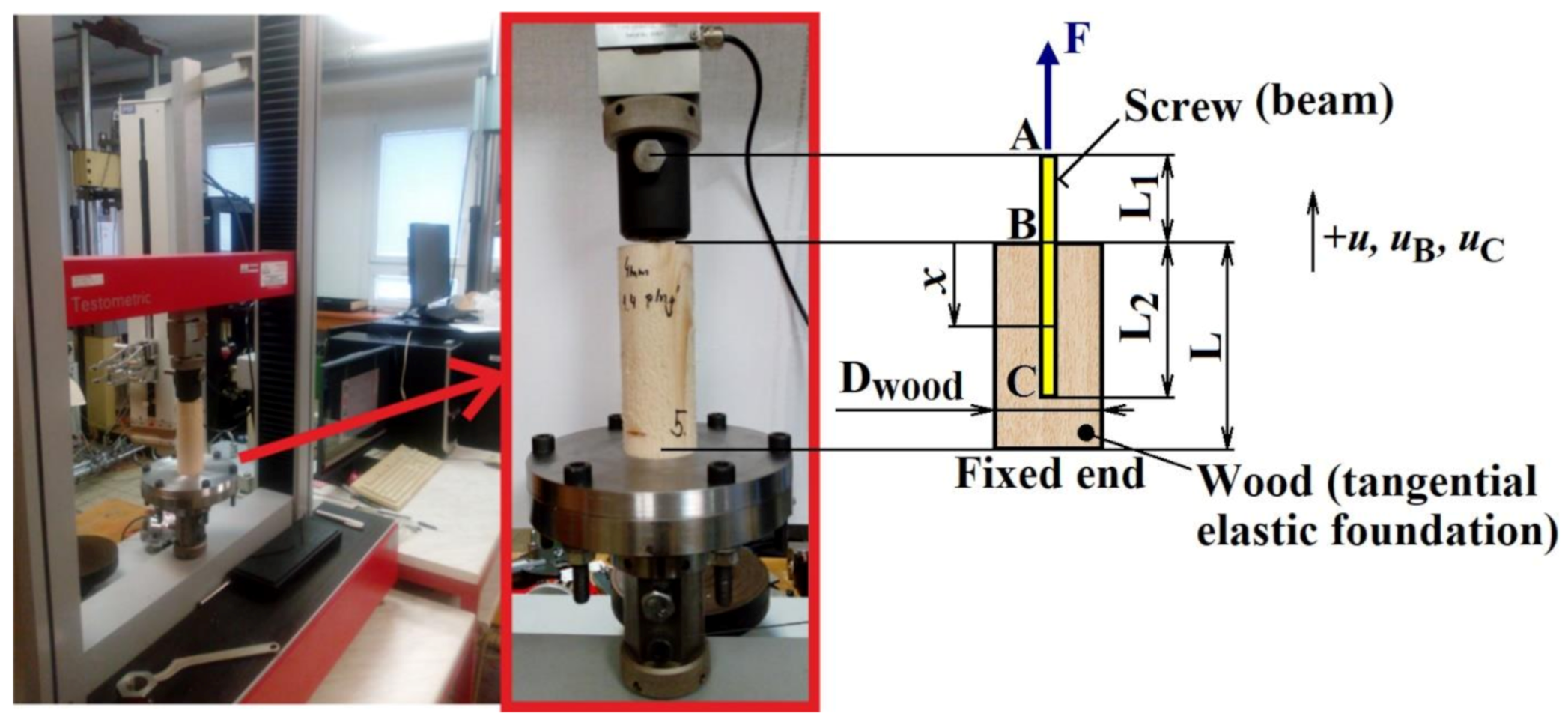
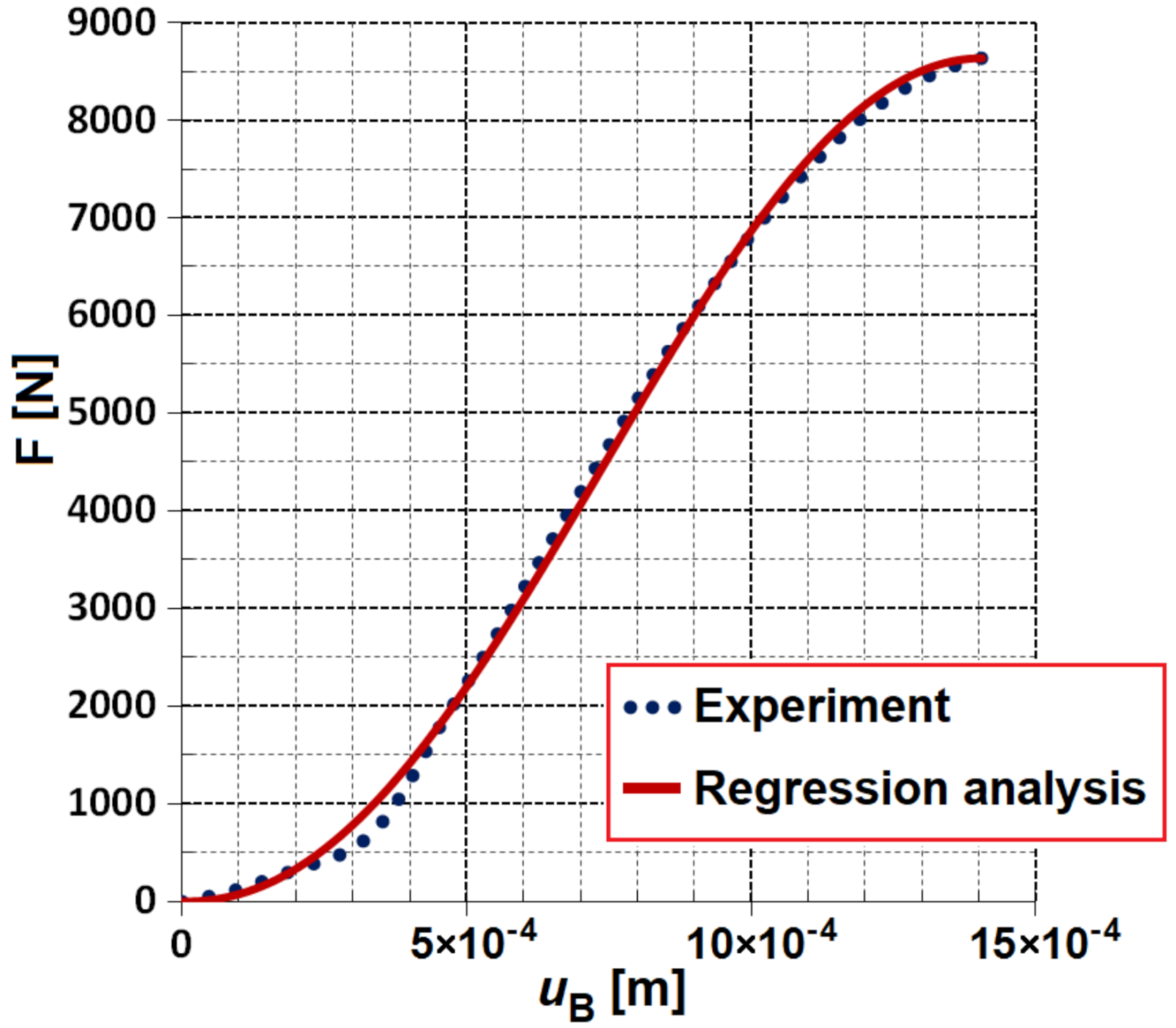
4. Experiment (Pull-Out Test for Screws) and Its Evaluation
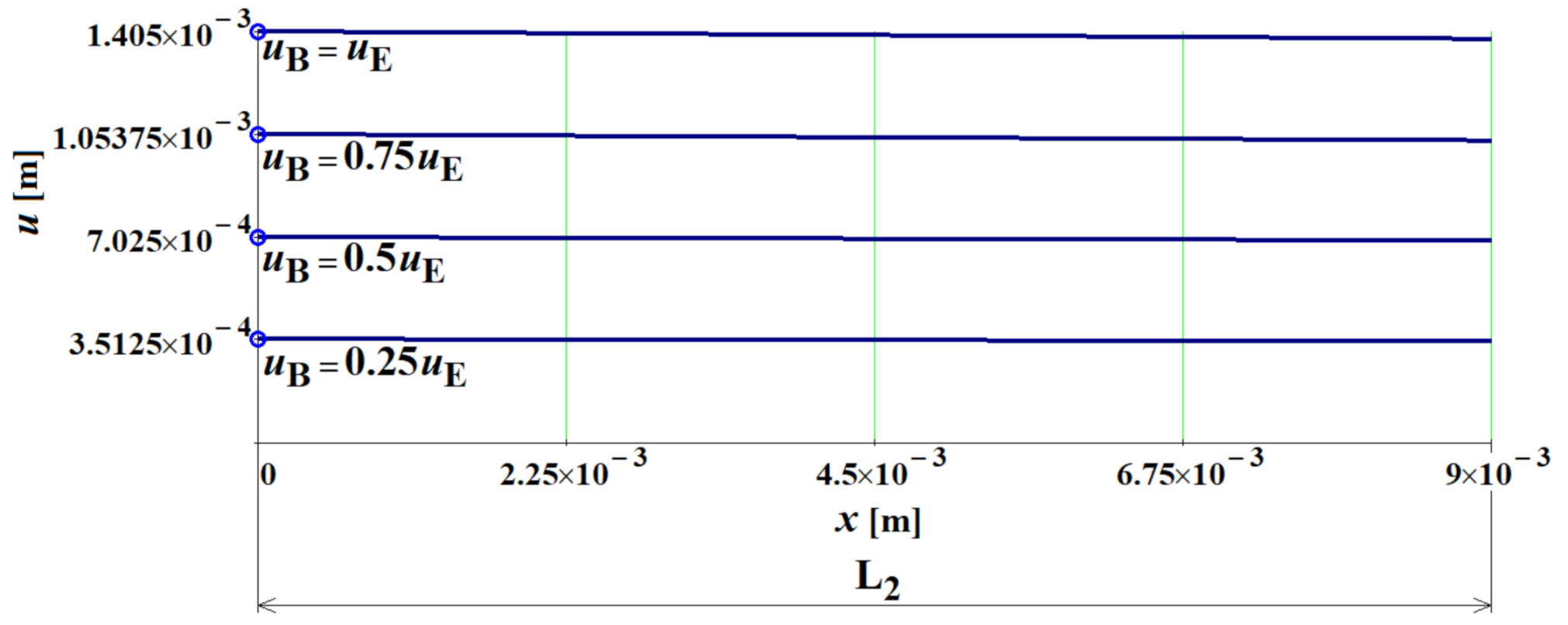
5. Determination of the Screw Elongation
6. Discussion
7. Results
- We have been able to derive the new theoretical solution of the differential equation of the screw joint using the tangential elastic foundation theory, including the determination of the boundary conditions and derivation of the analytical solution procedure.
- The screw (beam on the elastic foundation) is subjected to tension/compression loading in this article.
- Two types of screws (HB 6.5 and HB 7) were made of stainless steel 1.4441 (AISI 316L) and titanium alloy Ti6Al4V by machining technology and 3D printing + machining technology.
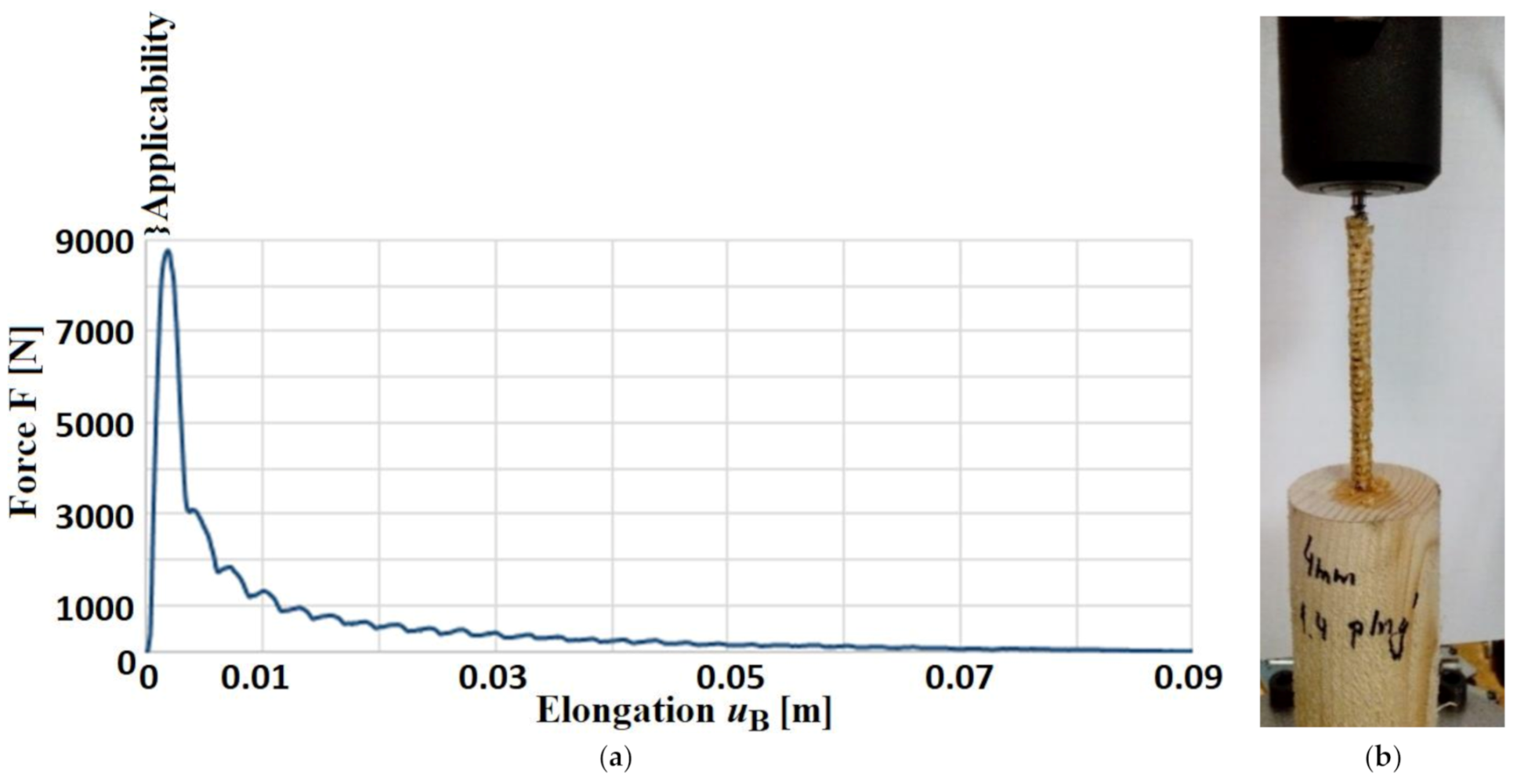
- Experimental tests (pull-out tests) for joining dry spruce wood and bovine and human bones (i.e., three types of generally anisotropic and non-homogeneous materials) were carried out using pull-out tests up to limit states (screw breakage, pulling the screw out of the fasteners). The , dependencies were obtained for 13 cases, and the limit failure states () were evaluated. Our experimental tests are in good agreement with different experiments with different materials (see [24,26,27,28]). However, it is advisable to perform more experiments.
- A sufficient regression analysis of a sufficiently determined dependence of the normal force on the elongation (displacement) of the screw was performed, i.e., the determination of the factor from the evaluation of the pull-out tests. Regression approximates the course of the experiment accurately enough for desired applicability (i.e., for interval ).
- Thus, the application of the tangential elastic foundation model can be generalized to the joining of diverse materials by different types of screws made of different materials (forming, 3D printing). The condition of such an application of the tangential foundation is the knowledge of the relationship for a given screw joint. However, this is only possible using the measurement evaluation.
- The obtained results confirm the correctness of the proposed tangential elastic foundation as an alternative and simpler solution of the complex 3D task of mechanical contact with friction, which is undoubtedly the case of the screw joint. Instead of the task of strongly non-linear mechanical contact, the simpler use of a suitable number of non-linear springs satisfying the relationships or can be applied. Such non-linear springs can be applied, for example, in nodes of the finite element mesh, etc. Thanks to the shortening of computational times, in addition to a simpler, more affordable and faster solution, it is also possible to apply the probabilistic approach very effectively in the design of the screw joint. Probabilistic approaches and probabilistic reliability assessments (based, e.g., on the Monte Carlo method and respecting the real variability of input and output variables) are in line with modern trends in science and technology (see [6,29,31,32,33]).
- It is clear from the first results and applications that the new tangential foundation model, which is also characterized by continuously distributed reaction force , or , offers a new alternative as a sufficiently accurate and relatively simple solution to the real complex interaction of the screw and the fasteners. It is also advantageous that large deformations, non-linearities, anisotropy or inhomogeneities can occur in this model of tangential foundation.
- It is also appropriate to focus on the future. In other models of elastic foundations, the influence of self-weight and dynamics (see [21]) can also be taken into account (however, this would lead to solving partial differential equations in the most complex tasks). The application of large deformations (logarithmic strains ) applied in Equation (1)), etc. is significant, as well as the combined bending + tension/pressure loads (see [15]) or torsion + bending + tension/pressure loads and impact loads [21], which are common, and not only in mechanical, building or biomechanical structures. This will be the subject of further research to follow up this article. Other complex biomechanical/mechanical applications are possible too, for example, see [12,14,26].
- After further experiments, our model can be applied as an alternative method in design codes, for example, see [3], etc.
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Aicher, S.; Gustafsson, P.J.; Wolf, M. Load Displacement and Bond Strength of Glued-in Rods in Timber Influenced by Adhesive, Wood Density, Rod Slenderness and Diameter. In Proceedings of the 1st International RILEM Symposium on Timber Engineering, Stockholm, Sweden, 13–15 September 1999; pp. 369–379. [Google Scholar]
- Breyer, D.E. Design of Wood Structures; McGraw-Hill: New York, NY, USA, 1988; pp. 1–680. ISBN 978-0070076754. [Google Scholar]
- European Standard EN 1995-1-1 Eurocode 5, 2004: Design of Timber Structures, Authority: The European Union Per Regulation 305/2011, Directive 98/34/EC, Directive 2004/18/EC. Available online: http://www.phd.eng.br/wp-content/uploads/2015/12/en.1995.1.1.2004.pdf (accessed on 21 April 2021).
- Hicks, T.G. Civil Engineering Formulas; McGraw-Hill: New York, NY, USA, 2010; pp. 1–395. ISBN 978-0-07-161470-2. [Google Scholar]
- Khurmi, R.S.; Gupta, J.K. Machine Design; Eurasia Publishing House: Kolkata, India, 2005; pp. 1–1230. ISBN 978-8121925372. [Google Scholar]
- Lokaj, A.; Vavrušová, K.; Rykalová, E. Application of Laboratory Tests Results of Dowel Joints in Cement-Splinter Boards VELOX into the Fully Probabilistic Methods (SBRA Method). Appl. Mech. Mater. 2012, 137, 95–99. [Google Scholar] [CrossRef]
- Mackerle, J. Finite element analyses in wood research: A bibliography. Wood Sci. Technol. 2005, 39, 579–600. [Google Scholar] [CrossRef]
- Vavrušova, K.; Mikolášek, D.; Lokaj, A.; Klajmonová, K.; Sucharda, O.; Pařenica, P. Determination of Carrying Capacity of Steel-Timber Joints with Steel Rods Glued-In Parallel to Grain; Wood Research: Karlova Ves, Slovakia, 2016; Volume 61, pp. 733–740. [Google Scholar]
- Sucharda, O.; Smirakova, M.; Vaskova, J.; MatečkovÁ, P.; Kubosek, J.; Cajka, R. Punching Shear Failure of Concrete Ground Supported Slab. Int. J. Concr. Struct. Mater. 2018, 12, 36. [Google Scholar] [CrossRef]
- Hu, Y.; Shen, L.; Nie, S.; Yang, B.; Sha, W. FE simulation and experimental tests of high-strength structural bolts under tension. J. Constr. Steel Res. 2016, 126, 174–186. [Google Scholar] [CrossRef]
- Začal, J.; Jančar, L. Effect of Temperature on Bolt Working Load of Pressure Vessels. In Advances in Mechanical Engineering; Springer: Berlin/Heidelberg, Germany, 2019; pp. 433–441. [Google Scholar]
- Bajtek, V.; Frydrysek, K.; Pleva, L. Stochastic Strength Analysis of Compression Headless Screw. MM Sci. J. 2020, 2020, 3837–3840. [Google Scholar] [CrossRef]
- Čada, R.; Frydrýšek, K.; Sejda, F.; Demel, J.; Pleva, L. Analysis of Locking Self-Taping Bone Screws for Angularly Stable Plates. J. Med. Biol. Eng. 2017, 37, 612–625. [Google Scholar] [CrossRef] [PubMed]
- Catapano, S.; Ferrari, M.; Mobilio, N.; Montanari, M.; Corsalini, M.; Grande, F. Comparative Analysis of the Stability of Prosthetic Screws under Cyclic Loading in Implant Prosthodontics: An In Vitro Study. Appl. Sci. 2021, 11, 622. [Google Scholar] [CrossRef]
- Frydrýšek, K.; Šír, M.; Pleva, L. Strength Analyses of Screws for Femoral Neck Fractures. J. Med. Biol. Eng. 2018, 38, 816–834. [Google Scholar] [CrossRef]
- Kwon, J.; Ha, M.H.; Lee, M.G. Alternative Pedicle Screw Design via Biomechanical Evaluation. Appl. Sci. 2020, 10, 4746. [Google Scholar] [CrossRef]
- Loi, F.; Córdova, L.A.; Pajarinen, J.; Lin, T.-H.; Yao, Z.; Goodman, S.B. Inflammation, fracture and bone repair. Bone 2016, 86, 119–130. [Google Scholar] [CrossRef]
- Michenková, Š. Nonlinear Problems of the Beams on Elastic Foundation (Nelineární úlohy nosníků na pružném podkladu). Ph.D. Thesis, VSB—Technical University of Ostrava, Faculty of Mechanical Engineering, Department of Applied Mechanics, , Ostrava, Czechia, 2017; pp. 1–170. (In Czech). [Google Scholar]
- Niculescu, B.; Faur, C.I.; Tataru, T.; Diaconu, B.M.; Cruceru, M. Investigation of Biomechanical Characteristics of Orthopedic Implants for Tibial Plateau Fractures by Means of Deep Learning and Support Vector Machine Classification. Appl. Sci. 2020, 10, 4697. [Google Scholar] [CrossRef]
- Available online: https://www.medin.cz/ (accessed on 21 April 2021).
- Marasová, D., Jr. Experimental Research on Dynamic Impact Loading Using Impact Rods. Int. Multidiscip. Sci. Geoconf. Sgem 2020, 20, 103–110. [Google Scholar]
- Van De Kamp, T.; Vagovič, P.; Baumbach, T.; Riedel, A. A Biological Screw in a Beetle’s Leg. Science 2011, 333, 52. [Google Scholar] [CrossRef]
- Autoritatea Pentru Administrarea Activelor Statului (AAAS). Karlsruhe Institute of Technology: Nature Uses Screws and Nuts. Available online: https://www.eurekalert.org/pub_releases/2011-07/haog-kio070111.php (accessed on 21 April 2021).
- Costa, F.; Ortolina, A.; Galbusera, F.; Cardia, A.; Sala, G.; Ronchi, F.; Uccelli, C.; Grosso, R.; Fornari, M. Pedicle screw cement augmentation. A mechanical pullout study on different cement augmentation techniques. Med. Eng. Phys. 2016, 38, 181–186. [Google Scholar] [CrossRef]
- Foley, W.L.; Frost, D.E.; Paulin, W.B., Jr.; Tucker, M.R. Uniaxial pullout evaluation of internal screw fixation. J. Oral Maxillofac. Surg. 1989, 47, 277–280. [Google Scholar] [CrossRef]
- Patel, P.S.D.; Shepherd, D.E.T.; Hukins, D.W.L. Axial and angled pullout strength of bone screws in normal and osteoporotic bone material. In Proceedings of the 13th International Conference on Biomedical Engineering, Singapore, 3–6 December 2008; pp. 1619–1622. [Google Scholar]
- Varghese, V.; Krishnan, V.; Kumar, G.S. Comparison of pullout strength of pedicle screws following revision using larger diameter screws. Med. Eng. Phys. 2019, 74, 180–185. [Google Scholar] [CrossRef] [PubMed]
- Zdero, R.; Aziz, M.S.; Nicayenzi, B. Pullout Force Testing of Cortical and Cancellous Screws in Whole Bone. In Experimental Methods in Orthopaedic Biomechanics; Elsevier BV: Amsterdam, The Netherlands, 2017; pp. 117–132. [Google Scholar]
- Frydrýšek, K.; Tvrdá, K.; Jančo, R.; Čajka, R.; Fries, J.; Michenková, S.; Nikodvm, M.; Theisz, G.; Pleva, L.; Manas, P.; et al. Handbook of Structures on Elastic Foundation; VSB—Technical University of Ostrava: Ostrava, Czech Republic, 2013; ISBN 978-80-248-3238-8. [Google Scholar]
- Morávkova, Z.; Tomečková, I.; Frydrýšek, K. Beam rested on unilateral elastic foundation—(Theory, experiments and finite element approach). Eng. Mech. 2017, 670–673. [Google Scholar]
- Frydrýšek, K.; Václavek, L. Stochastic Computer Approach Applied in the Reliability Assessment of Engineering Structures. Adv. Hum. Factorsbus. Manag. Train. Educ. 2016, 451, 121–129. [Google Scholar] [CrossRef]
- Marek, P.; Brozzetti, J.; Gustar, M.; Elishakoff, I. Probabilistic Assessment of Structures using Monte Carlo Simulations. Appl. Mech. Rev. 2002, 55, B31–B32. [Google Scholar] [CrossRef]
- Tvrdá, K. Foundation plate on the elastic half-space, deterministic and probabilistic approach. MATEC Web Conf. 2017, 107, 58. [Google Scholar] [CrossRef]
- Cárach, J.; Hloch, S.; Petrů, J.; Muller, M.; Hromasová, M.; Nag, A.; Čuha, D.; Hlaváček, P.; Hatala, M.; Kratochvíl, J.; et al. Evaluation of physical phenomena and surface integrity during hydroabrasive disintegration of the rotating workpiece with feedback loop control. Measurement 2019, 134, 586–594. [Google Scholar] [CrossRef]
- Kratochvíl, J.; Sadílek, M.; Musil, V.; Pagáč, M.; Stančeková, D. The Effectiveness of Strategies Printing Printer Easy 3D Maker. Adv. Sci. Technol. Res. J. 2018, 12, 197–205. [Google Scholar] [CrossRef]
- Losertová, M.; Štamborská, M.; Lapin, J.; Mareš, V. Comparison of Deformation Behavior of 316L Stainless Steel and Ti6Al4V Alloy Applied in Traumatology. Metalurgija 2016, 55, 667–670. [Google Scholar]
- Petrů, J.; Zlámal, T.; Špalek, F.; Čep, R. Surface Microhardening Studies on Steels After High Feed Milling. Adv. Sci. Technol. Res. J. 2018, 12, 222–230. [Google Scholar] [CrossRef]
- Slíva, A.; Brázda, R.; Procházka, A.; Martynková, G.S.; Barabaszová, K. Čech Investigation of Geometric Properties of Modified Titanium White by Fluidisation for Use in the Process of Transport, Handling, Processing and Storage. J. Nanosci. Nanotechnol. 2019, 19, 2997–3001. [Google Scholar] [CrossRef] [PubMed]
- Václav, Š.; Sivtsev, N.S.; Senderská, K. Investigation of Stress-Strain State of the Workpiece at Gauge Burnishing of its Holes. Adv. Sci. Technol. Res. J. 2017, 11, 211–222. [Google Scholar] [CrossRef]
- Winczek, J.; Gawronska, E.; Murčinková, Z.; Hatala, M.; Pavlenko, S.; Makles, K. Analysis of thermomechanical states in single-pass GMAW surfaced steel element. In Proceedings of the AIP Conference Proceedings, Bydgoszcz, Poland, 9–11 May 2017; Volume 1822, p. 020015. [Google Scholar]
- Hetényi, M. Beams on Elastic Foundation, 2nd ed.; University of Michigan Press: Ann Arbor, MI, USA, 1964. [Google Scholar]
- Liu, Q.; Ma, J. Analytical Model for Beams on Elastic Foundations Considering the Coupling of Horizontal and Vertical Displacements. J. Eng. Mech. 2013, 139, 1757–1768. [Google Scholar] [CrossRef]
- 50 kN Machines. Available online: https://www.testometric.co.uk/50kn/ (accessed on 21 April 2021).



| Material | Modulus of Elasticity E [Pa] | Yield Limit [MPa] | Fracture Limit [MPa] |
|---|---|---|---|
| 1.4441 | 2.1 × 1011 | 892 | 977 |
| Ti6Al4V | 1.06 × 1011 | 919 | 1034 |
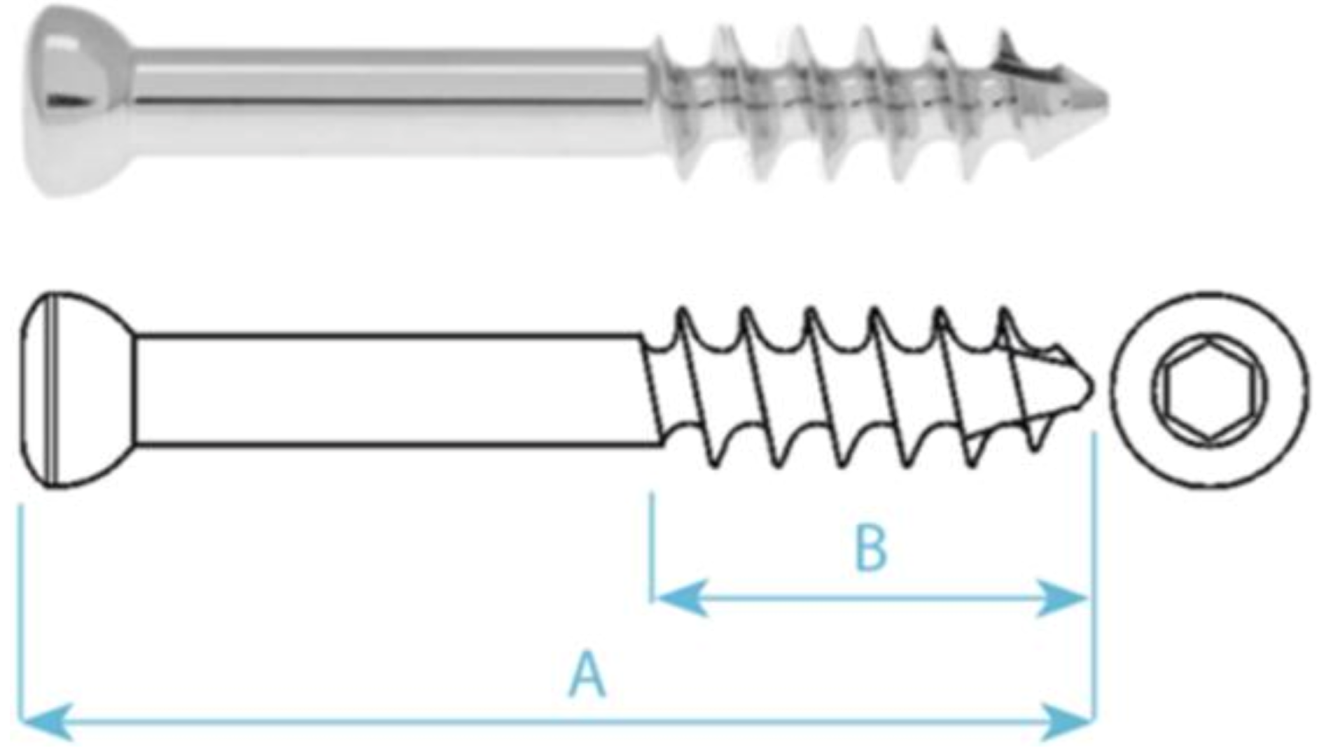
| Self-Tapping Cancellous Bone Screw HB6.5 | SSt | A | B |
 | 129796911 | 45 mm | 32 mm |
| 129796921 | 50 mm | ||
| 129796931 | 55 mm | ||
| 129796941 | 60 mm | ||
| 129796951 | 65 mm | ||
| 129796961 | 70 mm | ||
| 129796971 | 75 mm | ||
| 129796981 | 80 mm | ||
| 129796991 | 85 mm | ||
| Thread diameter 6.5 mm | 129797001 | 90 mm | |
| Shank diameter 4.5 mm | 129797011 | 95 mm | |
| Core diameter 3 mm | 129797021 | 100 mm | |
| Head diameter 8 mm | 129797031 | 105 mm | |
| Drill bit for threaded hole 3.2/3.75 mm | 129797041 | 110 mm | |
| Screwdriver Hex key 3.5 mm | 129797051 | 115 mm | |
| Material: Stainless steel AISI 316 L (DIN 1.4441/316 L medical) or titanium alloy (Ti6Al4V). Dimension “B” = . | 129797061 | 120 mm | |
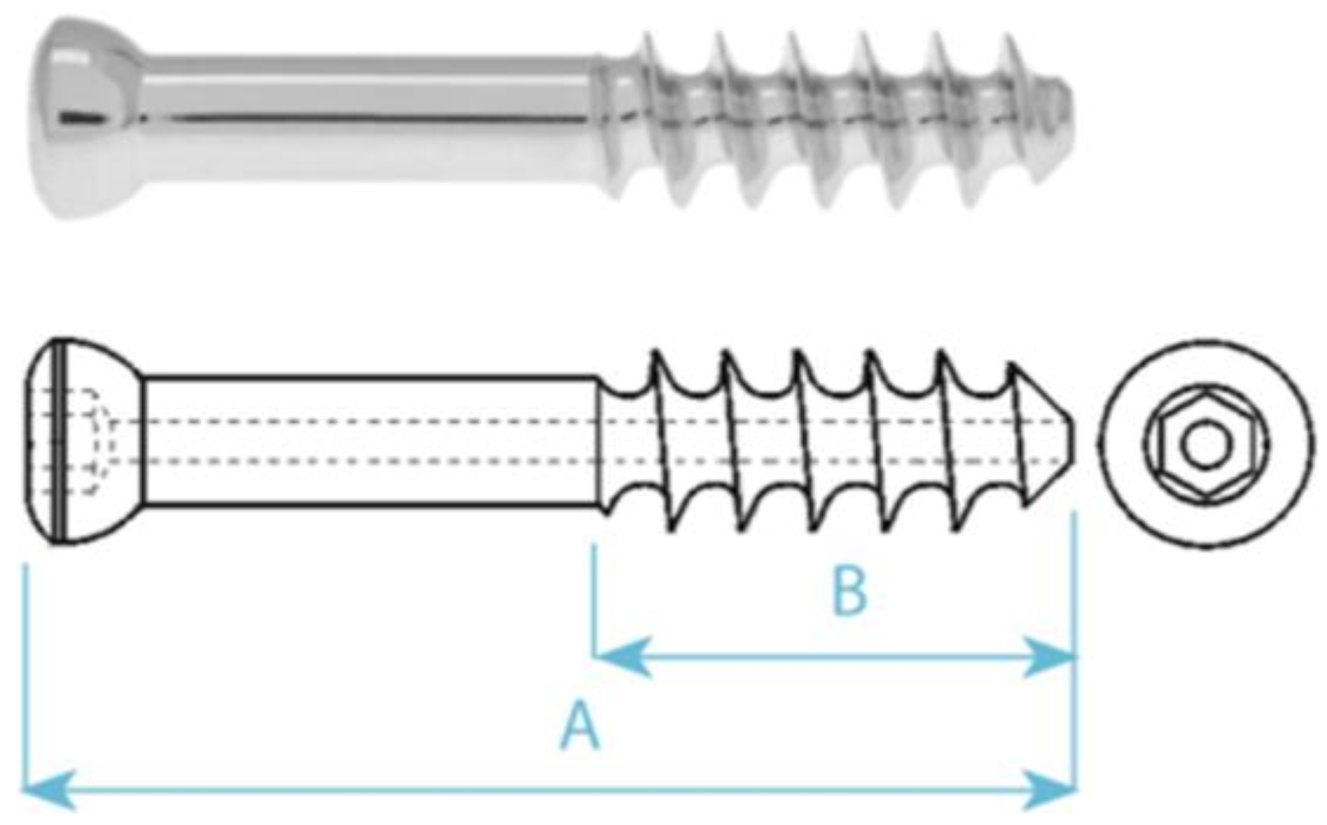
| Cancellous Bone Screw HB7 | SSt | A | B |
 | 129798210 | 40 mm | 32 mm |
| 129798220 | 45 mm | ||
| 129798230 | 50 mm | ||
| 129798240 | 55 mm | ||
| 129798250 | 60 mm | ||
| 129798260 | 65 mm | ||
| 129798270 | 70 mm | ||
| 129798280 | 75 mm | ||
| 129798290 | 80 mm | ||
| 129798300 | 85 mm | ||
| 129798310 | 90 mm | ||
| Thread diameter 7 mm | 129798320 | 95 mm | |
| Shank diameter 5 mm | 129798330 | 100 mm | |
| Core diameter 3.5 mm | 129798340 | 105 mm | |
| Head diameter 8 mm | 129798350 | 110 mm | |
| Drill bit for threaded hole 4 mm | 129798360 | 115 mm | |
| Screwdriver Hex key 3.5 mm | 129798370 | 120 mm | |
| Cannulation 1.8 mm | 129798380 | 125 mm | |
| Material: Stainless steel AISI 316 L (DIN 1.4441/316 L medical) or titanium alloy (Ti6Al4V). Dimension “B” = . | 129798390 | 130 mm |
| Measurement | ||||||
|---|---|---|---|---|---|---|
| Measurement Number | Screw Type | Screw Material | Pre-Drilled Hole Diameter [m] | Limit State | Damage Limit State Description | |
| 1 | HB 6.5 | 1.4441 (AISI 316L) | 0.0032 | 8634 | 0.001405 | Pulling the screw out of the wood |
| 2 | HB 6.5 | Ti6Al4V | 0.004 | 7475 | 0.001666 | |
| 3 | HB 7 | 1.4441 (AISI 316L) | 0.004 | 8541 | 0.001527 | Screw breakage |
| 4 | HB 7 | Ti6Al4V | 0.0045 | 8649 | 0.001638 | Pulling the screw out of the wood |
| 5 | HB 6.5 | 1.4441 (AISI 316L) | 0.004 | 8770 | 0.001707 | |
| 6 | HB 6.5 | 1.4441 (AISI 316L) | 0.004 | 8942 | 0.001468 | Screw breakage |
| 7 | HB 6.5 | 1.4441 (AISI 316L) | 0.004 | 8279 | 0.00114 | Pulling the screw out of the wood |
| 8 | HB 7 | 1.4441 (AISI 316L) | 0.005 | 7390 | 0.001385 | |
| 9 | HB 7 | 1.4441 (AISI 316L) | 0.005 | 7606 | 0.001544 | |
| 10 | HB 6.5 | Ti6Al4V | 0.005 | 7322 | 0.001906 | |
| 11 | HB 6.5 | Ti6Al4V | 0.005 | 7381 | 0.001339 | |
| 12 | HB 7 | Ti6Al4V | 0.0055 | 9105 | 0.001804 | |
| 13 | HB 7 | Ti6Al4V | 0.0055 | 9481 | 0.002157 | Screw breakage |
| Measurement Number | |||
|---|---|---|---|
| Regression | Measurement (Limit States), See also Table 3 | ||
| [1] | |||
| 1 | 1.078 | 8634 | 0.001405 |
| 2 | 0.5139 | 7475 | 0.001666 |
| 3 | 0.7876 | 8541 | 0.001527 |
| 4 | 0.5128 | 8649 | 0.001638 |
| 5 | 0.6739 | 8770 | 0.001707 |
| 6 | 0.7499 | 8942 | 0.001468 |
| 7 | 0.621 | 8279 | 0.00114 |
| 8 | 0.6648 | 7390 | 0.001385 |
| 9 | 0.7506 | 7606 | 0.001544 |
| 10 | 1.095 | 7322 | 0.001906 |
| 11 | 0.5122 | 7381 | 0.001339 |
| 12 | 0.6158 | 9105 | 0.001804 |
| 13 | 0.5347 | 9481 | 0.002157 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Frydrýšek, K.; Michenková, Š.; Pleva, L.; Koutecký, J.; Fries, J.; Peterek Dědková, K.; Madeja, R.; Trefil, A.; Krpec, P.; Halo, T.; et al. Mechanics of Screw Joints Solved as Beams Placed in a Tangential Elastic Foundation. Appl. Sci. 2021, 11, 5616. https://doi.org/10.3390/app11125616
Frydrýšek K, Michenková Š, Pleva L, Koutecký J, Fries J, Peterek Dědková K, Madeja R, Trefil A, Krpec P, Halo T, et al. Mechanics of Screw Joints Solved as Beams Placed in a Tangential Elastic Foundation. Applied Sciences. 2021; 11(12):5616. https://doi.org/10.3390/app11125616
Chicago/Turabian StyleFrydrýšek, Karel, Šárka Michenková, Leopold Pleva, Jan Koutecký, Jiří Fries, Kateřina Peterek Dědková, Roman Madeja, Antonín Trefil, Pavel Krpec, Tomáš Halo, and et al. 2021. "Mechanics of Screw Joints Solved as Beams Placed in a Tangential Elastic Foundation" Applied Sciences 11, no. 12: 5616. https://doi.org/10.3390/app11125616
APA StyleFrydrýšek, K., Michenková, Š., Pleva, L., Koutecký, J., Fries, J., Peterek Dědková, K., Madeja, R., Trefil, A., Krpec, P., Halo, T., Hrabovský, L., Bialy, L., Jančo, R., & Pokorný, J. (2021). Mechanics of Screw Joints Solved as Beams Placed in a Tangential Elastic Foundation. Applied Sciences, 11(12), 5616. https://doi.org/10.3390/app11125616









