SA-SVM-Based Locomotion Pattern Recognition for Exoskeleton Robot

Featured Application

This study is based on the self-developed wearable exoskeleton movement information acquisition system, which collects human movement information to identify locomotion patterns. The system is integrated into the wearable exoskeleton, allowing the exoskeleton to determine the current locomotion pattern based on movement information. The significance of this study is that the accurate locomotion pattern recognition can provide help for the compliance control of an exoskeleton robot.

Abstract

An exoskeleton robot is a kind of wearable mechanical instrument designed according to the shape and function of the human body. The main purpose of its design and manufacture is to enhance human strength, assist human walking and to help patients recover. The walking state of the exoskeleton robot should be highly consistent with the state of the human, so the accurate locomotion pattern recognition is the premise of the flexible control of the exoskeleton robot. In this paper, a simulated annealing (SA) algorithm-based support vector machine model is proposed for the recognition of different locomotion patterns. In order to improve the overall performance of the support vector machine (SVM), the simulated annealing algorithm is adopted to obtain the optimal parameters of support vector machine. The pressure signal measured by the force sensing resistors integrated on the sole of the shoe is fused with the position and pose information measured by the inertial measurement units attached to the thigh, shank and foot, which are used as the input information of the support vector machine. The max-relevance and min-redundancy algorithm was selected for feature extraction based on the window size of 300 ms and the sampling frequency of 100 Hz. Since the signals come from different types of sensors, normalization is required to scale the input signals to the interval (0,1). In order to prevent the classifier from overfitting, five layers of cross validation are used to train the support vector machine classifier. The support vector machine model was obtained offline in MATLAB. The finite state machine is used to limit the state transition and improve the recognition accuracy. Experiments on different locomotion patterns show that the accuracy of the algorithm is 97.47% ± 1.16%. The SA-SVM method can be extended to industrial robots and rehabilitation robots.

1. Introduction

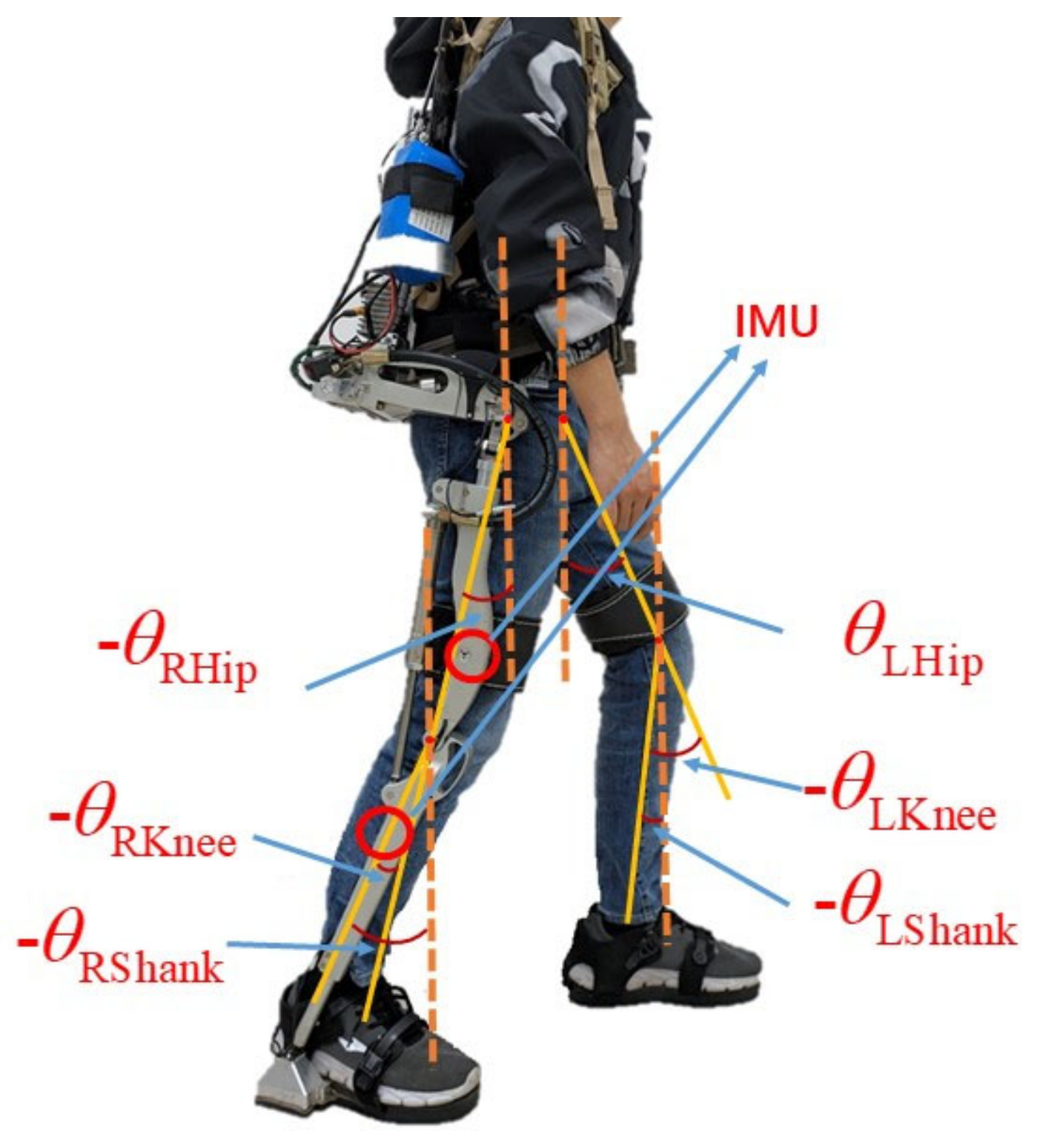
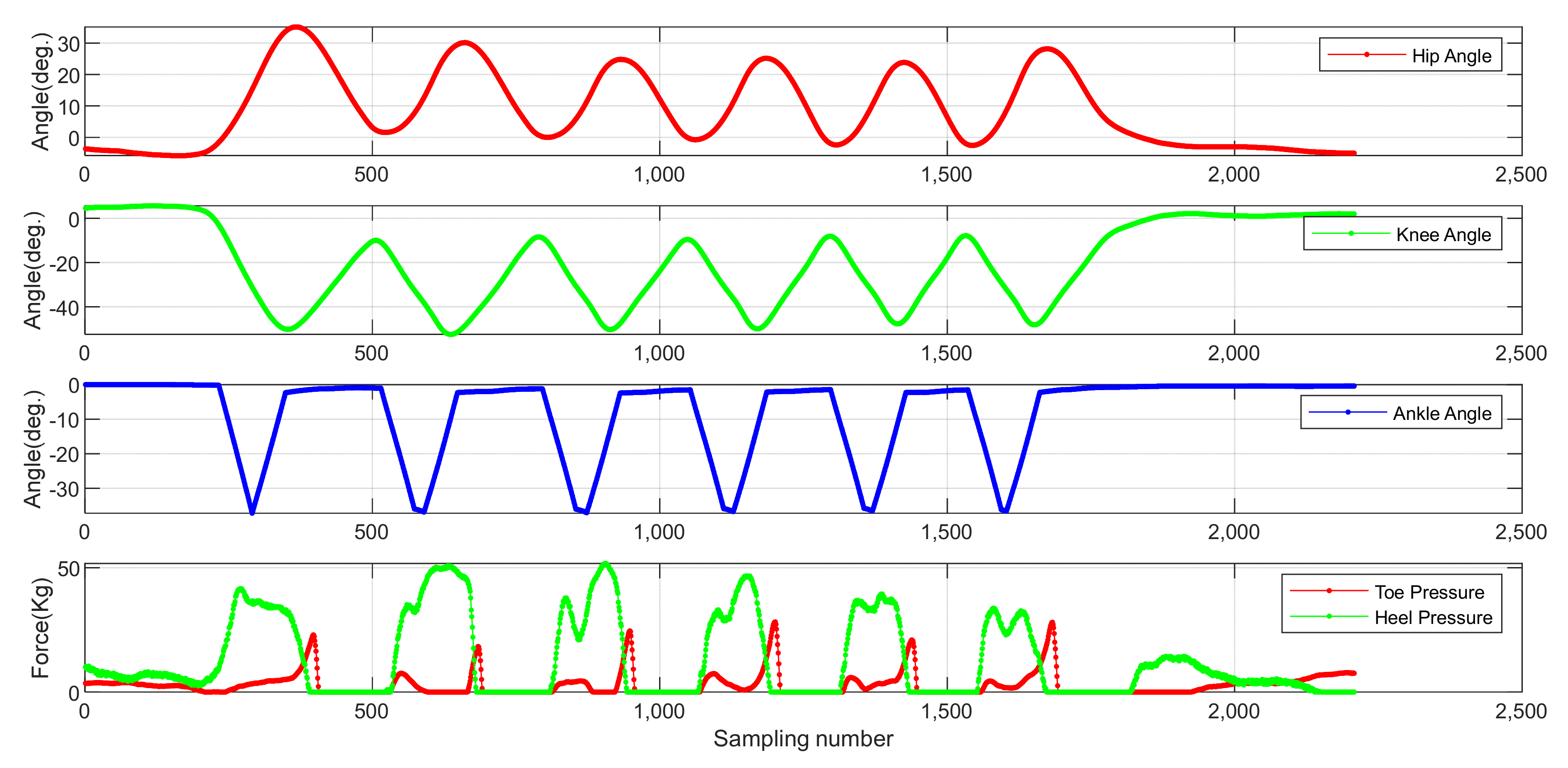
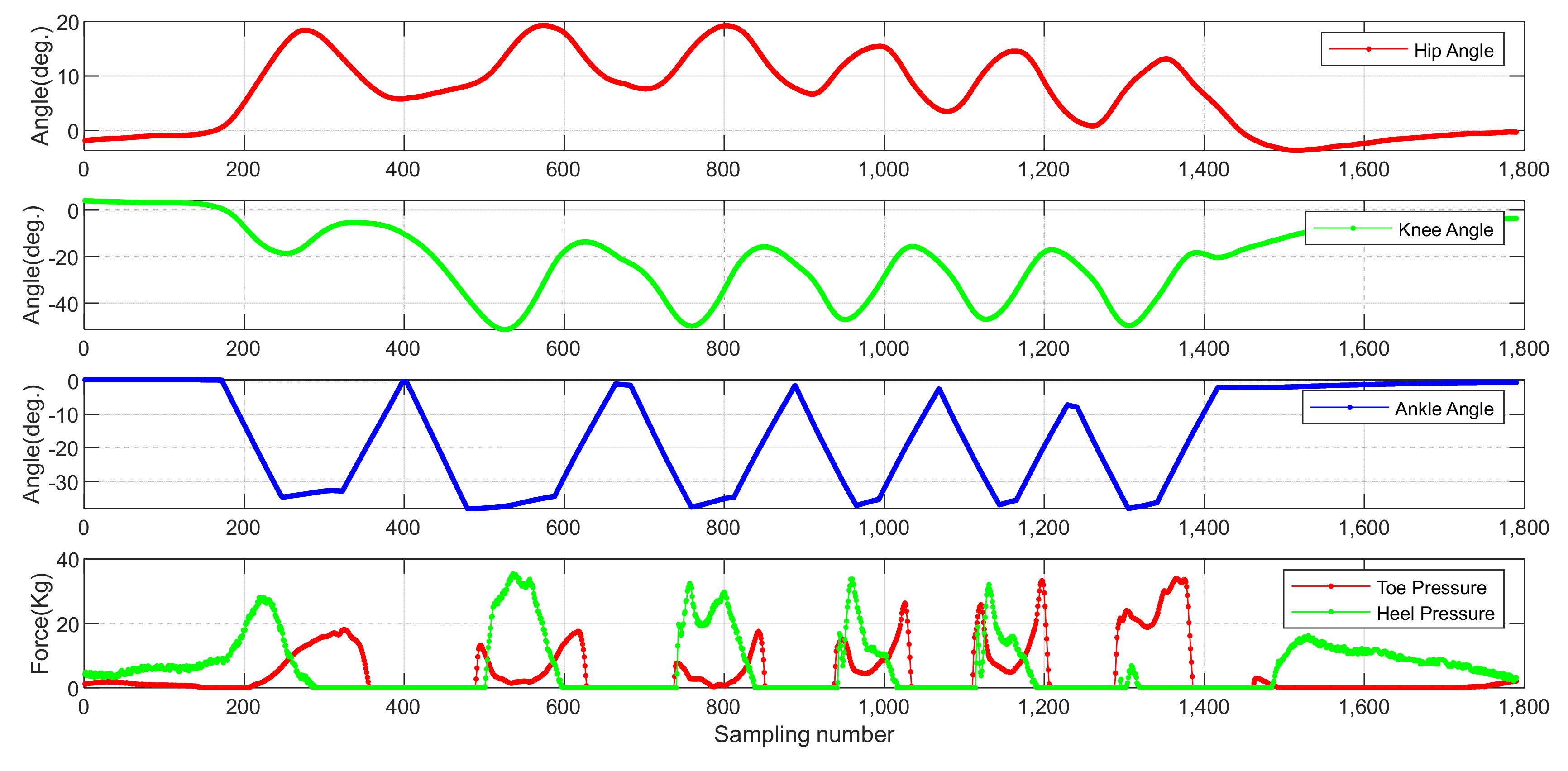
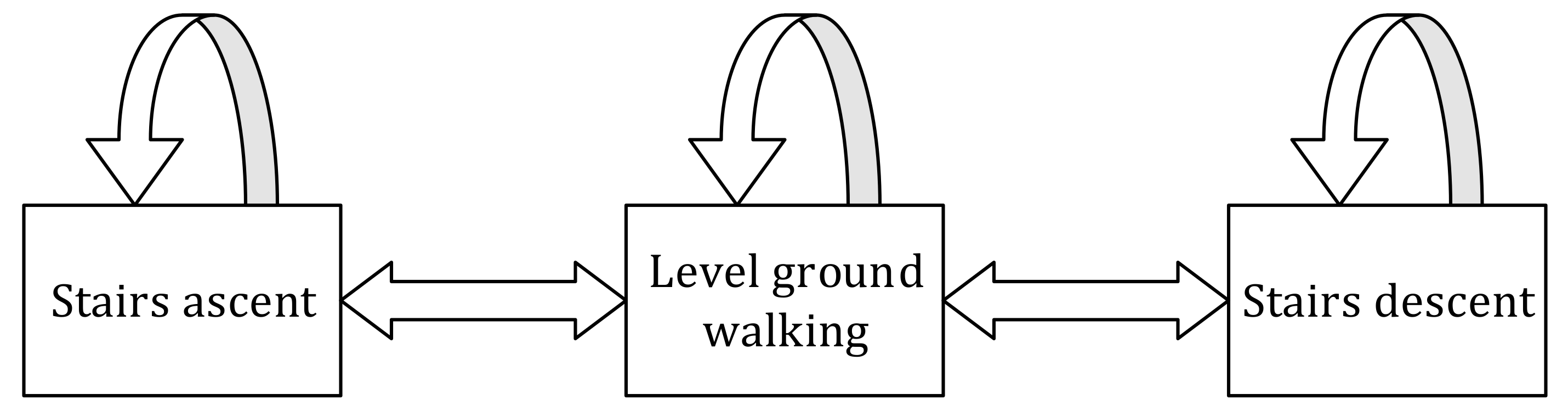
Locomotion pattern recognition plays an important role in the control of exoskeleton robots. In some practical situations, the exoskeleton robot often needs to understand the current locomotion pattern before it can make corresponding movements to complete the characteristic tasks. Accurate recognition of locomotion patterns is the premise of compliance control of exoskeleton robots.

Accurate locomotion pattern recognition is the basis of exoskeleton control. The accuracy of locomotion pattern recognition results is closely related to excellent human movement data. At the present time, there are many kinds of locomotion pattern recognition methods. The ways can be divided into image-based methods [1], biology-based methods [2,3] and sensor-based methods [4] according to the approaches of obtaining information. The first method is based on video image, which obtains the movement image sequence of human body through camera and analyzes the locomotion pattern after image processing. It is not suitable for wearable exoskeleton because this method has limitations on application scenes. The second is based on human physiological electrical signals. Human bioelectrical signals are electric potential signals that contain human behavioral intentions, which are transmitted to relevant tissues or organs by stimulation. The human body’s intentions can be sensed by identifying the triggered electrical signals. Electroencephalography (EEG) [5] and surface electromyography (seems) [6] come from the bioelectrical signal related to muscle contraction, which will not cause physical damage to the exoskeleton wearer. The signal acquisition technology is mature and easy to operate. However, the surface electrodes that collect electrical signals are susceptible to sweat on the skin surface, which will cause serious interference with the data and lead to errors in human locomotion pattern recognition. The third method based on locomotion sensors is mainly to acquire human locomotion intention by collecting movement information or force information of the users, such as angle, speed, acceleration, etc. These sensor data are not susceptible to external interference and have good stability, but there are also some problems such as signal delay, drift and error accumulation.

Usually, the human locomotion pattern recognition algorithm uses a single type of feature or a simple series of multiple features to achieve the fusion of multiple features. However, Shao et al. used a new spectrum coding algorithm called Kernelized Multiview Projection (KMP) [7] to better integrate heterogeneous feature representations used in human locomotion pattern recognition. They respectively use Histograms of Oriented Optical Flow (HOF) [8], Histogram of Gradient (HOG) [9], Local Binary Pattern (LBP) [10] and color histogram to represent features. KMP has demonstrated a leading position in human locomotion pattern recognition across five popular human locomotion data sets [7]. In terms of EEG research, at the university of Houston, a team led by Contreras-Vidal reduced the dimension of the characteristic matrix and combined it with local Fisher discriminant analysis data by extracting the characteristics of amplitude-modulated EEG signals. Additionally, a gaussian mixture model is used to change the exoskeleton robot state information and the mapping of the characteristic matrix, which finished the sit, stand, turn left, turn right research under the specific actions of brain electrical decoding technology [11]. The classification recognition rate can reach 97.7%. In terms of EMG research, Huang et al. sent 11 channels of EMG signals collected from the stump and hip of lower limb amputees into a linear discriminant classifier to dynamically identify seven movement patterns offline [12] with a recognition accuracy of 91.6%. To further investigate the effect of EMG signal activity, Harvey Grove et al. targeted the shank muscle nerves of a male thigh amputee and moved them to the thigh [13]. The average recognition rate was about 94% when the knee joint was flexed and extended, the ankle joint was dorsiflexed, and the tibia and femur were rotated. In the field of sensor signal research, Tong et al. used gyroscope signals to obtain joint angles and proposed the dynamic positioning system [14]. Young et al. collected sensing information of the lower limb exoskeleton itself, such as acceleration, angular velocity and pressure data. They manually selected features and used linear discriminant analysis classifier to solve the recognition problem of five movement modes and transformations of five modes [15]. The recognition rate reached 93.9%. Compared with bio-sensory sensors and physical interaction sensors alone, the method of multi-source information fusion can effectively increase the identification accuracy and reduce the prediction delay. Therefore, Young et al. proposed to use the dynamic Bayesian network method to integrate the sEMG signals and Inertial Measurement Unit (IMU) signals in the characteristic layer to identify the basic locomotion modes on the basis of the existing research. Subsequent studies that included a time history of exercise data reduced the steady-state pattern error recognition rate by 50% under deep belief network (DBN). It has a certain hysteresis, because the collected data is between the stance state before the locomotion transition and the swing state after the transition [16]. In addition, Chen et al. innovatively proposed and verified that 6 movement patterns can be recognized by collecting capacitive signals on the affected limbs of patients [17], the average identification accuracy can reach 93.4%. The image-based recognition method has scene limitation. EEG and sEMG sensors are not easy to wear and are easily affected by sweat, body temperature and other factors. Although the sensor information of the exoskeleton robot can intuitively judge the human locomotion pattern, the recognition result is not satisfactory.

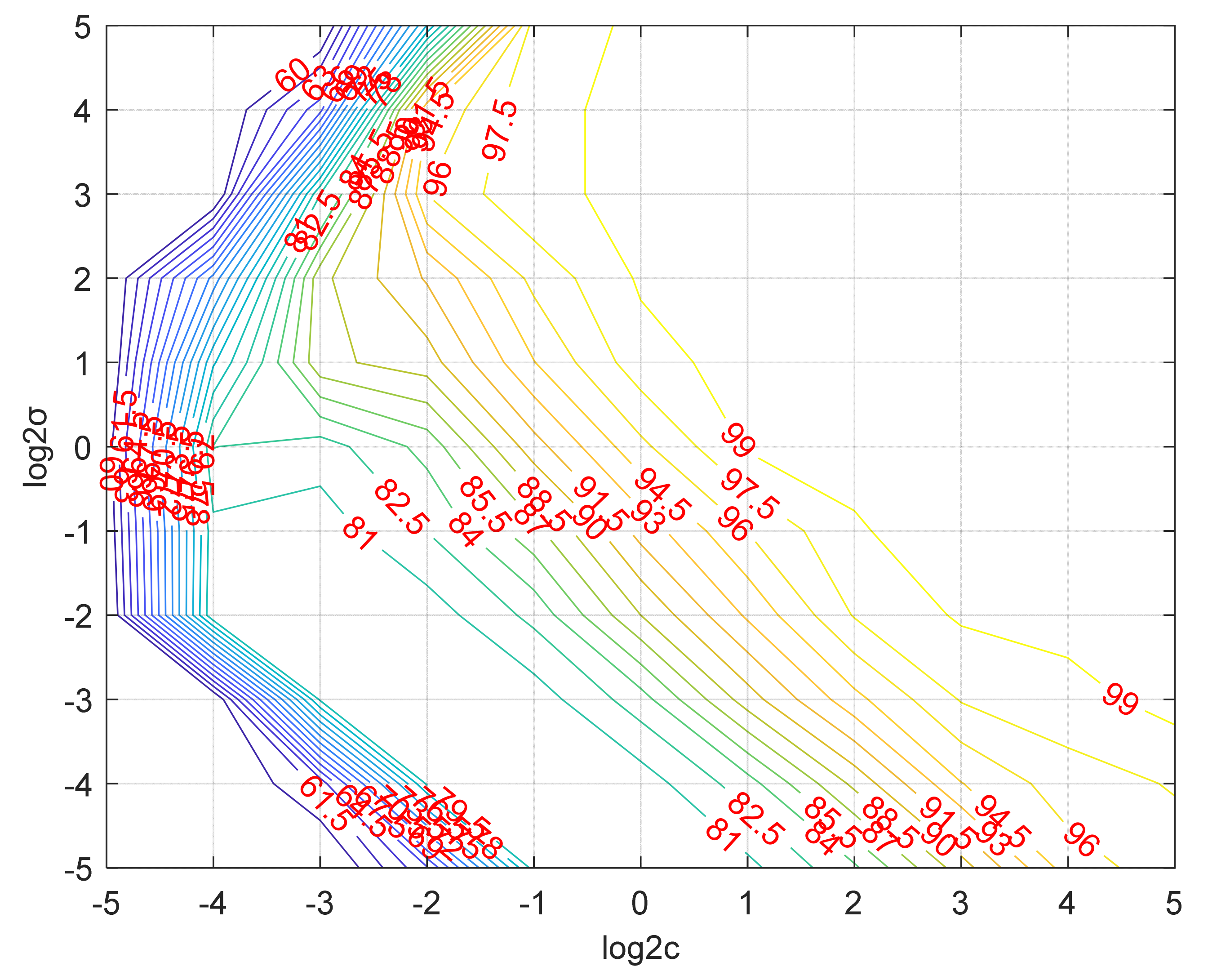
In order to solve the above effects, this paper proposes a locomotion pattern recognition method of exoskeleton robot based on SA-SVM. SA is one of the earliest and most popular meta-heuristic algorithms, which can effectively solve the parameter optimization problem of the SVM model. It introduces the natural mechanism of solid annealing as well as the appropriate random elements. The value of randomness in the whole solution neighborhood can avoid the algorithm falling into local optimum and improve the ability of global optimization.

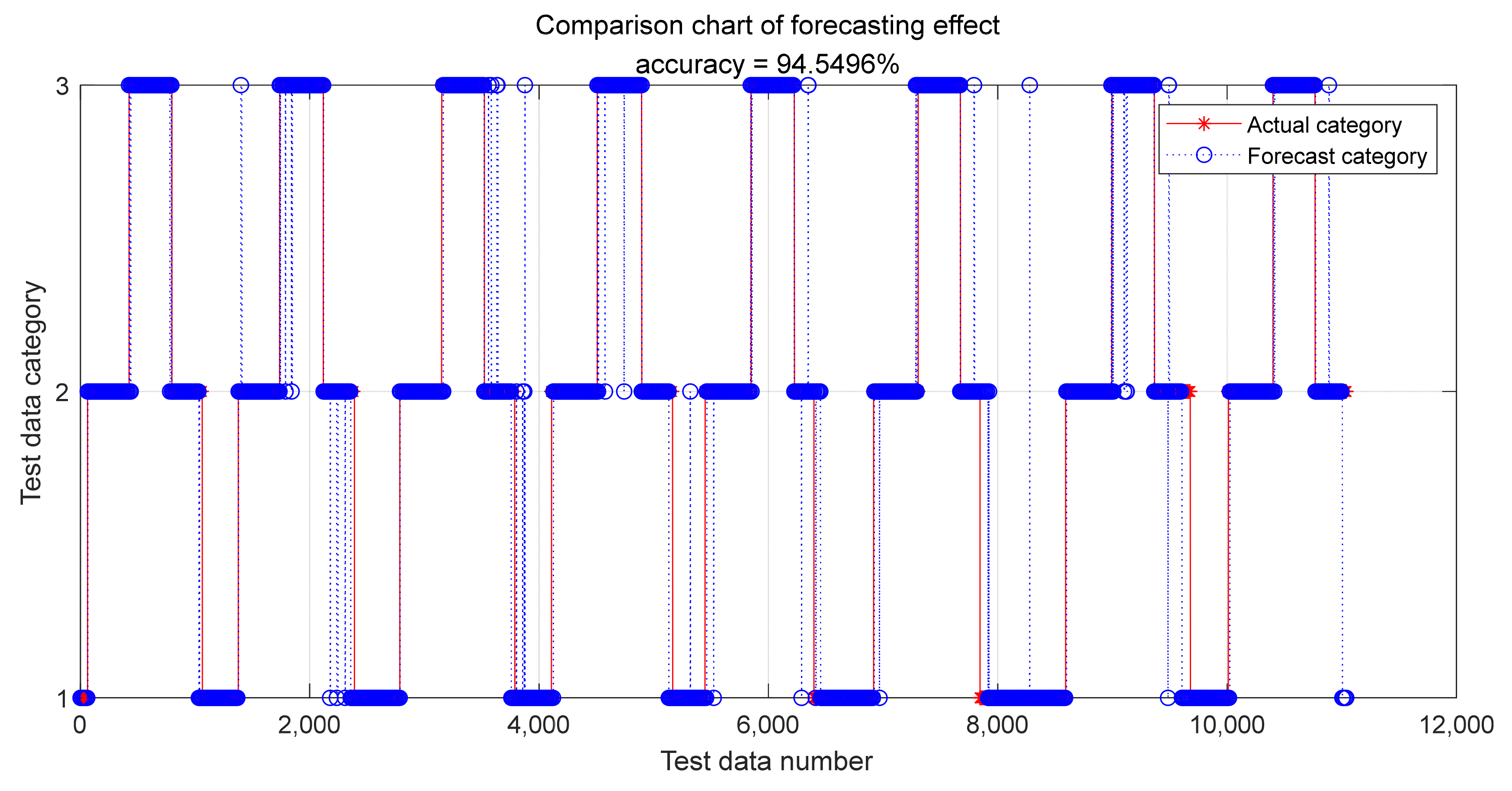
In order to identify the locomotion pattern stably and accurately, the SA-SVM model is adopted in this paper based on traditional SVM. Firstly, lower limb IMUs information, joint angle information and plantar pressure information were collected. Then, IMUs information, joint angle information and force sensing resistors (FSRs) data were combined as the input of SA-SVM model to further improve the overall locomotion pattern recognition model. The model effectiveness and accuracy of the multi-mode machine learning model are also verified.

2. Materials and Methods

2.1. Data Collection and Processing

The exoskeleton hardware system is based on ARM architecture. The core chip adopts 8-core A53 6818 processor, 2 GB RAM, 16 GB EMMC and supports HDMI. The main frequency is 2 GHz and the system uses RS485 high-speed 2 M transmission bus for data transmission, whose frequency is 100 Hz. After collecting the locomotion information of each part, the information is transmitted to the ARM main control computer through RS485 bus, so as to accomplish the drive and control of the exoskeleton robot.

The lower limb locomotion data were collected by the exoskeleton sensing system. There are two main types of sensors used to collect data, inertial measurement units (IMUs) and force sensitive resistors (FSRs). The lower limb locomotion data collected mainly included thigh angle, shank angle and plantar pressure. The angle of the hip joint is the angle between the vertical and thigh orientation. The angle of the knee joint is the angle between the thigh and the shank. Calculated from thigh angle and shank angle. The joint angles of the exoskeleton robot were defined according to clinical gait analysis (CGA), as shown in Figure 1.

Two pressure sensors FSRs (LOSON LSH-10) are placed on the heel and the ball of the foot respectively to detect the contact force between the sole and the ground, as shown in Figure 2. The measurement range of each FSR is 0–200 kg, the comprehensive accuracy is ±0.5%F·S, the diameter is 20 mm, the thickness is 12 mm. It is easy to install and carry as the size is small and the weight is light. Because the FSRs output electrical signal is relatively weak, it needs to be equipped with an amplifier circuit. The output FSRs signal can be amplified to 0–5 V through this circuit, which is corresponding to the measured 0–200 kg mass and showing good linear characteristics.

In order to improve the diversity of the experimental data and the generalization of the model, we selected six healthy men without gait defects as the study subjects. The subjects are 160 cm~180 cm in height and 50 kg~70 kg in weight. Before collecting the data of the subjects, the exoskeleton should be adjusted according to the height and weight of the subjects to ensure that each subject is wearing an independent exoskeleton and has adapted to the normal walking posture in a period of time. In addition, ensure that the sensor is in standard condition and calibrated. Exercise data were collected when the subjects were able to walk in a comfortable manner.

Each human subject wore an exoskeleton robot and carried out two experiments at a constant speed without weight. The first kind of experiment was to walk in different locomotion patterns, which consisted of level-ground walking, stairs ascent and stairs descent. Each locomotion pattern included 10 experimental trials for one human subject and each experiment lasted for about 20 s. The second kind of experiment is that each experimenter walked from the level ground walking to the other locomotion patterns and vice versa. The second kind of experiment includes 4 transitions. Each transition consisted of 5 experiments for one subject and the experiment lasted for 60 s. The stairs are 1.5 m wide, 40 cm deep and 15 cm high with a dip Angle of about 26°.

In order to filter out the noise and interference in the data we collected, a Butterworth low-pass filter was used to filter the data with a cut-off frequency of 10 Hz. Finally, we obtained IMUs and FSRs data from the sensor system. Some of the filtered data is shown in Figure 3, Figure 4 and Figure 5.

2.2. Feature Selection

Since the swing leg FSRs data is almost zero, the collected signals include standing FSRs, left and right leg joint angle information. The combined signal is expressed as:

$$x=\left[F_B,F_H,{\theta }_{LH},{\theta }_{LK},{\theta }_{LA},{\theta }_{RH},{\theta }_{RK},{\theta }_{RA}\right]$$

(1)

$F_B,F_H$ are the pressure of the foot palm and heel in the standing state. ${\theta }_{LH},{\theta }_{LK},{\theta }_{LA}$ are the angle of the left leg hip joint, knee joint and ankle joint. ${\theta }_{RH},{\theta }_{RK},{\theta }_{RA}$ are the angle of the right leg hip joint, knee joint and ankle joint. The FSRs of stance state and the lower limb angle were used as the classifier features based on the gait phase detection. Feature extraction is a process of selecting useful information from filtered signals. Useful features can be selected from the time series of sensor signals. A time series is a series of observations of the sensor, as shown below:

$$x_i\left(t\right),i=1,\dots ,m;t=1,\dots ,n$$

(2)

where $m$ is the number of sensor observations and $n$ is the data length of the window. We select features throughout the window and print them at the end of the window.

Traditional feature extraction algorithms are mostly based on whether they have strong correlation with the target variable to evaluate, but these features may also contain some redundant features. mRMR algorithm is used to ensure the maximum correlation while removing redundant features, which is equivalent to obtaining a set of purest feature subset. mRMR can be considered as an approximation to maximize the dependency between the joint distribution of feature subset and the target variable, which itself belongs to the feature selection method of filter. Maximum relevance is the search for features that meet the following formula:

$$maxD\left(S,c\right),D=\frac{1}{\left|S\right|}{\displaystyle \sum }_{x_i\in S}I\left(x_i;c\right)$$

(3)

The average value of mutual information among all features $x_i$ and classifications $c$ is used to approximate $D\left(S,c\right)$.

Features selected through Max-Relevance can be redundant and depend heavily on each other. When two features are redundant with each other, the classification results will not be significantly changed if one of them is removed. Therefore, the min-redundancy method can be used to eliminate redundant features:

$$minR\left(S\right),R=\frac{1}{{\left|S\right|}^2}{\displaystyle \sum }_{x_i,x_j\in S}I\left(x_i,x_j\right)$$

(4)

Maximum correlation $D$ and minimum redundancy $R$ are combined by defining operators $\Phi \left(D,R\right)$.

$$\max \Phi \left(D,R\right),\Phi =D-R$$

(5)

The mRMR algorithm is shown in Figure 6:

In each locomotion pattern, the results of feature selection by mRMR algorithm are shown in

Table 1. Comparison of the results of feature selection for level-ground walking.

Order	Name	Score
1	$F_B$	0.017
2	${\theta }_{LA}$	0.015
3	$F_H$	0.010
4	${\theta }_{RA}$	0.006
5	${\theta }_{LH}$	0.004
6	${\theta }_{RH}$	0.001
7	${\theta }_{RK}$	0.000
8	${\theta }_{LK}$	0.000

,

Table 2. Comparison of feature selection results for stairs ascent.

Order	Name	Score
1	$F_H$	0.027
2	${\theta }_{LK}$	0.021
3	${\theta }_{LA}$	0.019
4	$F_B$	0.011
5	${\theta }_{RA}$	0.006
6	${\theta }_{RH}$	0.003
7	${\theta }_{LH}$	0.001
8	${\theta }_{RK}$	0.002

and

Table 3. Comparison of feature selection results for stairs descent.

Order	Name	Score
1	${\theta }_{LH}$	0.023
2	$F_H$	0.016
3	$F_B$	0.014
4	${\theta }_{LA}$	0.012
5	${\theta }_{RA}$	0.007
6	${\theta }_{RH}$	0.003
7	${\theta }_{LK}$	0.000
8	${\theta }_{RK}$	0.002

.

Under the data sets of three locomotion patterns, the results of feature selection through mRMR algorithm are shown in

Table 4. Comparison of feature selection results of the three locomotion patterns.

Order	Name	Score
1	$F_H$	0.023
2	$F_B$	0.016
3	${\theta }_{LK}$	0.014
4	${\theta }_{RH}$	0.012
5	${\theta }_{LA}$	0.007
6	${\theta }_{LH}$	0.003
7	${\theta }_{RK}$	0.000
8	${\theta }_{RA}$	0.002

.

2.3. Locomotion Pattern Recognition

2.3.1. Support Vector Machine Classifier

SVM is an excellent supervised learning method for solving regression analysis and classification problems [18]. SVM is an efficient classifier, which can replace the existing multi-layer perceptron, RBF neural network, polynomial network and other learning algorithms [19]. The basic model of SVM is a linear classifier for binary classification problems. Its principle is to find the hyperplane that maximizes the distance between two kinds of features in the feature space. Binary classifiers can extend multiple classifiers. For the K-class classification problem, these methods design only one objective function to train all K-binary support vector machines simultaneously and maximize the boundary between each class and the rest of the class.

In the training of classification model, SVM introduces penalty factor $C$ to the constraint conditions so that the training model has the fault-tolerant ability. The larger the $C$, the lower the tolerance to the training sample error and the stronger the model fitting accuracy, but the poorer the generalization ability and the prone to over-fitting phenomenon. The smaller the $C$ is, the higher the tolerance to the error of training samples. Although the model has a strong generalization ability, the fitting accuracy of samples decreases, which increases the empirical risk and is prone to underfitting. The dimension of the characteristic subspace is related to the kernel function σ. The smaller the σ, the finer the classification and overfitting is easy to occur. On the contrary, the coarser the category, the less fit is likely to occur. To obtain the optimal SVM classification model, finding the optimal $C$ and σ is the key.

The optimization problem of solving SVM can be expressed as:

$$\begin{array}{c}\hfill \underset{\omega }{\min }J\left(\omega ,\xi \right)\frac{1}{2}{\left|\left|\omega \right|\right|}^2+C{\displaystyle \sum _{i=1}^m}{\xi }_i\\ \hfill \mathit{s.t.} y_i\left(\omega \Phi \left(x_i\right)+b\right)\ge 1-{\xi }_i,{\xi }_i\ge 0,i=1,2,\dots \end{array}$$

(6)

where $C$ is the penalty factor,$C>0$;${\xi }_i$ is the relaxation factor. In order to find the generalized optimal classification plane, it is necessary to consider the maximum classification interval and the minimum misclassification samples.

In order to better solve, the KKT optimality condition is used to transform the equation into a duality problem by introducing Lagrange multiplier [20].

$$\begin{array}{c}\underset{\omega ,b,\xi }{\min } \underset{\lambda ,\mu }{\max }L\left(\omega ,b,\xi ,\lambda ,\mu \right)=\frac{1}{2}{\left|\left|\omega \right|\right|}^2+C{\displaystyle \sum _{i=1}^m}{\xi }_i+\\ {\displaystyle \sum _{i=1}^n}{\lambda }_i\left[1-{\xi }_i-y_i\left({\omega }^T{x}_i+b\right)\right]-{\displaystyle \sum _{i=1}^n}{\mu }_i{\xi }_i\end{array}$$

(7)

where ${\lambda }_i,{\mu }_i$ is the Lagrange multiplier, $\omega ,b,{\xi }_i$ is the main problem parameter.

Take the partial derivatives of the main problem parameters respectively and put them into the Lagrange function to get (8).

$$\underset{\omega ,b,\xi }{\min }L\left(\omega ,b,\xi ,\lambda ,\mu \right)={\displaystyle \sum _{j=1}^n}{\lambda }_i-\frac{1}{2}{\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^n}{\lambda }_i{\lambda }_j{y}_i{y}_j\left(x_i·x_j\right)$$

(8)

Minimizing results with only $\lambda$ and no $\mu$ and results will maximize $\lambda$.

$$\begin{gathered} \underset{\lambda }{\max }\left[{\displaystyle \sum _{j=1}^n}{\lambda }_i-\frac{1}{2}{\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^n}{\lambda }_i{\lambda }_j{y}_i{y}_j\left(x_i·x_j\right)\right] \\ \mathit{s.t.}{\displaystyle \sum _{i=1}^n}{\lambda }_i{y}_i=0, {\lambda }_i\ge 0, C-{\lambda }_i-{\mu }_i=0 \end{gathered}$$

(9)

According to the above two formulae, we can find $\omega ,b$ as follows. The vectors from $S$ are the support vectors.

$$\omega ={\displaystyle \sum _{i=1}^m}{\lambda }_i{y}_i{x}_i$$

(10)

$$b=\frac{1}{\left|S\right|}{\displaystyle \sum }_{s\in S}\left(y_s-\omega x_s\right)$$

(11)

According to Equations (10) and (11), the optimal hyperplane can be obtained. In the classification model training of support vector machine, the appropriate kernel function is the one that can carry out nonlinear transformation in the input space. It can effectively avoid the complex inner product operation caused by nonlinear mapping in the high-dimensional feature space so as to eliminate the dimension disaster. Common forms of kernel function include polynomial function, multilayer perceptron kernel function, Gaussian radial basis kernel function (RBF), etc. RBF function is shown as Equation (12). It has wide convergence domain, few parameters and strong generality. In this paper, RBF function is adopted to establish SVM model.

$$K\left(x_i,x_j\right)=\exp \left(-\frac{\left|\left|x_i-x_j\right|\right|}{2{\mathsf{\sigma }}^2}\right)$$

(12)

2.3.2. Support Vector Machine Classifier Based on Simulated Annealing Algorithm

Simulated annealing algorithm is derived from the research results of statistical mechanics of materials. At high temperatures, particles have higher energies and are free to move and rearrange themselves. At low temperatures, the energy of the particles is low. In order for the particles to reach thermal equilibrium at each temperature, cooling (annealing) is carried out very slowly, starting at high temperatures.

Assume that the energy $E\left(i\right)$ of the material in the state is $i$, then the material will follow the following law when entering the state $j$ from the state $i$ at temperature $T$:

(1)

If $E\left(j\right)\le E\left(i\right)$, accept that the state is transitioned;

(2)

If$E\left(j\right)>E\left(i\right)$, the state transition is accepted with the following probabilities:

$$e^{\frac{E\left(i\right)-E\left(j\right)}{KT}}$$

(13)

where $K$ is the Boltzmann constant in physics; $T$ is material temperature.

When the material reaches thermal equilibrium after full conversion at a certain temperature, the probability of the material in the state $i$ satisfies the Boltzmann distribution.

$$P_T\left(X=i\right)=\frac{e^{-\frac{E\left(i\right)}{KT}}}{{{\displaystyle \sum }}_{j\in S}{e}^{-\frac{E\left(j\right)}{KT}}}$$

(14)

where $X$ is the random variable of the current state of the material; $S$ is the set of state spaces. Clearly,

$$\underset{T\to \infty }{\lim }\frac{e^{-\frac{E\left(i\right)}{KT}}}{e^{-\frac{E\left(j\right)}{KT}}}=\frac{1}{\left|S\right|}$$

(15)

where $\left|S\right|$ is the number of states in the set $S$.

This means that all the states have the same probability at high temperature.

$$\begin{array}{c}\underset{T\to 0}{\lim }\frac{e^{-\frac{E\left(i\right)-E_{min}}{KT}}}{{{\displaystyle \sum }}_{j\in S}{e}^{-\frac{E\left(j\right)-E_{min}}{KT}}}=\underset{T\to 0}{\lim }\frac{e^{-\frac{E\left(i\right)-E_{min}}{KT}}}{{{\displaystyle \sum }}_{j\in S_{min}}{e}^{-\frac{E\left(j\right)-E_{min}}{KT}}+{{\displaystyle \sum }}_{j\notin S_{min}}{e}^{-\frac{E\left(j\right)-E_{min}}{KT}}}\\ =\underset{T\to 0}{\lim }\frac{e^{-\frac{E\left(i\right)-E_{min}}{KT}}}{{{\displaystyle \sum }}_{j\in S_{min}}{e}^{-\frac{E\left(j\right)-E_{min}}{KT}}}=\left\{\begin{array}{c}\frac{1}{\left|S_{min}\right|}\\ 0, else\end{array}\right., i\in S_{min}\end{array}$$

(16)

where $E_{min}=minE\left(j\right)$ and $S_{min}=\left\{i|E\left(j\right)=E_{min}\right\}$.

The above equation indicates that when the temperature drops to a very low level, the material will enter a minimum energy state.

When the temperature drops to 0, the $E\left(i\right)$ distribution is

$$P_i^{*}=\left\{\begin{array}{c}\frac{1}{\left|S_{min}\right|}\\ 0, else\end{array}\right.,i\in S_{min}$$

(17)

and

$${\displaystyle \sum }_{x_i\in S_{min}}{P}_i^{*}=1$$

(18)

This means that the temperature drops very slowly and each temperature has a lot of state transitions so that each temperature to achieve thermal balance. It will find the global optimal solution with probability 1, so the simulated annealing algorithm can find the global optimal solution.

Selecting SVM parameters is essentially an optimization problem. In recent years, many experts and scholars have proposed many methods to optimize SVM parameters. Zhang et al. proposed a parameter selection algorithm for support vector machines based on ant colony optimization (ACO) [21]. Subasi et al. proposed parameter optimization of support vector machines based on particle swarm optimization (PSO) [22]. Wang et al. used genetic algorithm (GA) to optimize the parameters of support vector machines [23]. The convergence speed of ACO algorithm is slow and easy to fall into local optimal. The PSO algorithm is easy to converge in advance and has poor local optimization ability. GA algorithm needs to be encoded first and then decoded and the search speed is slow. To solve these problems, this paper proposes a SVM model optimized by simulated annealing algorithm. The flow chart of optimal SVM parameters for SA search is shown in Figure 7.

More than 40,000 sets of FSRs data and IMUs data processed by locomotion pattern labeling were used as data set in this experiment. It is divided into 70% training set and 30% test set. The completion process of SA-SVM model is shown in Figure 8, which can be summarized as follows:

(1)

In the training process, input a paragraph of unprocessed original data;

(2)

Data preprocessing and divide the test data;

(3)

Using SA to find the global optimal parameters and establish SA-SVM model;

(4)

Input test data into SA-SVM model to get classification results.

2.4. Finite State Machine

There will be no locomotion mutation because the human walking movement is smooth and continuous. Locomotion mutation means a rapid transition from the current locomotion pattern to another locomotion pattern during movement process. Similarly, the change of locomotion patterns in the human-machine system movement should also conform to the law of human movement. Unreasonable switching of locomotion patterns can easily cause the human-machine system to walk unsmoothly and even bring danger to the wearer. The finite state machine is mainly composed of a finite number of states, input signals and transition conditions between states. For each input signal, it is judged whether the state transition condition is met. If it is met, it will move to the next state, otherwise, it will still maintain the current state. The mathematical model of the locomotion recognition finite state machine is defined as follows:

$$\mathrm{M}=\left(\mathrm{Q},\mathrm{I},\mathrm{t},{\mathrm{q}}_0,\mathrm{F}\right)$$

(19)

In Formula (19), $Q=\left\{q_0,q_1,\dots ,q_n\right\}$ represents the set of states of a finite state machine, which includes level-ground walking, stair ascent and stair descent.$I$ is the input signal of finite state machine, including plantar pressure and joint angle signals. $t$ represents the transfer condition between each locomotion patterns. $q_0$ represents the initial state of the finite state machine. $F$ is the final state set.

The transition condition of the locomotion patterns are as follows: for the current locomotion pattern $q_{\mathrm{i}}$, whether $q_{\mathrm{i}+1}$, $q_{\mathrm{i}+2}$ and $q_{\mathrm{i}+3}$ are the same locomotion pattern and whether this locomotion pattern is the next. $q_{\mathrm{i}}$ transfers to the next state when it is true. $q_{\mathrm{i}+1}=q_{\mathrm{i}}$ means that the current locomotion pattern when it is false. The locomotion pattern states transition is shown in Figure 9.

The transfer conditions for the locomotion pattern are as follows: for the current locomotion pattern $q_i$, determine whether $q_{i+1}$,$q_{i+2}$ and $q_{i+3}$ are the same locomotion pattern and the locomotion pattern is $q_i$’s next locomotion pattern, if so, $q_i$ moves to the next locomotion pattern. If not, the current locomotion pattern remains unchanged.

3. Results

3.1. Experimental Results and Analysis

The parameter optimization results of the test set are shown in Figure 10. The abscissa is the parameter $C$, the ordinate is the parameter σ, the red number is the recognition accuracy of the test set, and the contour line indicates that the identification accuracy of the test set is the same under different parameter pairs ($C$,σ). As can be seen from the figure, from left to right, it represents the process of gradual improvement of SA parameter optimization accuracy. When the identification accuracy is 99%, the test set identification accuracy reaches the maximum. At this time, the SA-SVM model established by parameter pair ($C$,σ) has the highest identification accuracy.

The locomotion pattern recognition effect of level ground walking, stairs ascent and stairs descent are shown in Figure 11 and Figure 12. The abscissa represents the sample number and the ordinate 1 represents level ground walking, 2 represents stairs ascent and 3 represents stairs descent, * represents actual category, ○ represents forecast category. It is obvious from the figure that the locomotion pattern recognition effect is good in the movement process, but there are misjudgments when the locomotion patterns are switched. The SA-SVM classifier recognition accuracy rate is about 94%. The SA-SVM classifier with FSM recognition accuracy rate is about 97%.

3.2. Performance Evaluation

In order to verify the validity of SA-SVM locomotion pattern recognition model, confusion matrix is used to further evaluate the model performance based on the same locomotion data set. Here is an abbreviation for several patterns of movement, such as SDt: stairs descent; SAt: stairs ascent; LG: level ground walking. All subjects were asked to walk on different terrain at a natural walking speed.

Table 5. Confusion matrix of SVM experimental results without SA.

	LG	SAt	SDt
LG	91.04% ± 2.7%	2.14% ± 0.32%	8.5% ± 1.06%
SAt	1.7% ± 0.55%	89.64% ± 2.3%	0.9% ± 0.41%
SDt	7.96% ± 1.3%	1.3% ± 0.19%	87.04% ± 1.5%

and

Table 6. Confusion matrix of SA-SVM experimental results.

	LG	SAt	SDt
LG	95.9% ± 0.71%	1.63% ± 0.2%	5.1% ± 0.62%
SAt	1.85% ± 0.07%	96.4% ± 1.14%	1.35% ± 0.09%
SDt	5.44% ± 0.56%	1.17% ± 0.29%	92.1% ± 0.39%

shows two confusion matrices.

Table 5, Table 6 and

Table 7. Confusion matrix of SA-SVM with FSM experimental results.

	LG	SAt	SDt
LG	98.9% ± 0.85%	1.02% ± 0.37%	3.6% ± 0.44%
SAt	1.24% ± 0.05%	97.4% ± 1.75%	0.56% ± 0.12%
SDt	3.96% ± 0.2%	0.47% ± 0.18%	96.1% ± 0.88%

respectively report the confusion matrices of the SVM classifier, the SA-SVM combined model classifier and the SA-SVM combined model classifier with FSM on the test dataset. The elements of the confusion matrix are expressed in the form of mean error and standard error. As can be seen from Table 5, the SVM classifier has good test accuracy for each action. This shows that SVM can automatically extract valid features for classification. As can be seen from Table 6, the SA-SVM classifier further effectively improved the accuracy compared with Table 5, especially for the locomotion pattern of stairs descent. As can be seen from Table 7, the SA-SVM combined model classifier with FSM has higher identification accuracy. Since the degree of knee joint flexion is similar to that of level ground walking, it is more difficult to identify than other movement patterns. For the overall classification accuracy of all locomotion, the average classification accuracy of the SA-SVM combined model with FSM in all data was 97.47% ± 1.16%, much higher than the 89.24% ± 2.17% of the SVM classifier and the 94.8% ± 0.75% of the SA-SVM classifier.

4. Discussion

A SVM algorithm based on SA was proposed to recognize the different locomotion patterns of the exoskeleton robot. The finite state machine was used to improve the identification accuracy in the proposed algorithm. Experimental results on six healthy human subjects demonstrated the effectiveness of the proposed method for locomotion pattern recognition.

The proposed method needs two pressure sensors in the shoes and four inertial measurement units on the mechanical parts and there is no need to mount any sensors on the human body, which is very convenient in actual applications. In the proposed method, the three locomotion patterns of level-ground walking, stairs ascent and stairs descent were identified. The accuracy of locomotion patterns recognition used SA-SVM is 94.8 ± 0.75%, and the accuracy of locomotion patterns recognition used SA-SVM combined with FSM is 97.47% ± 1.16%. These sensors are placed on mechanical connecting rods to reduce fatigue for the subjects, which are suitable for long periods use. The results show that the proposed method can correctly identify the three locomotion patterns, and the average recognition delay is 26.43% ± 4.62% of one gait cycle, which is much less than one step. Generally speaking, the recognition results of locomotion patterns can be obtained in advance to allow sufficient reaction time for the subsequent control of the exoskeleton robot.

The proposed method needs to be improved to solve some problems. In the locomotion patterns transition state, the recognition accuracy is not high, which may lead to error of the exoskeleton control. The recognition delay of stairs descent and stairs descent transition state is about 30%, which may lead to the control lag of the exoskeleton robot. In practical application, we adopt the method of pre-control in the control part to solve the above problems of the locomotion pattern recognition, which ensures the stable control of the exoskeleton robot.

5. Conclusions

This paper presents a locomotion pattern recognition method based on SA-SVM. With the plantar pressure signals and joint angle signals, the mRMR algorithm was used to extract features from the combination locomotion time series signals. The experiments were performed on six healthy subjects in the laboratory and the results validated the proposed method. This paper proposed combination of the plantar pressure signals measured by force sensing resistors in the shoes and the posture information measured by inertial measurement units mounted on the mechanical structure of the thigh, shank and foot, which is used as the signal source for locomotion patterns recognition. The recognition accuracy of SVM optimized by SA is improved about 5.6% compared with SVM only. At the same time, accuracy improved nearly 3 % using FSM.