Dual Quaternion Embeddings for Link Prediction
Abstract
1. Introduction
- We introduce dual quaternions to knowledge graph embeddings.
- We propose a novel transformation based model DualQuatE to overcome the challenge of multiple relations between two entities.
- Our experiments denote that DualQuatE is effective compared to the existing state-of-the-art models.
2. Related Work
- DualQuatE, a transformation based model, measures score of triples by the distance between two entities. QuatE which is a semantic matching model measured the latent matching semantics of entities and relations.
- The purpose of the model is different. DualQuatE aims to address the challenge of having multiple relations between two entities. QuatE aims to utilize quaterion Hamilton product to encourage a more compact interaction between entities and relations.
- The geometric meaning is different. QuatE embeds entities and relations with quaterions to model relations as rotations. Our model firstly attempts to represent entities with pure quaternions and models relations as interaction of translation and rotation.
3. Preliminaries
- Quaternion: Quaternion [20], is a number system that extends complex numbers to four-dimensional numbers. Generally, a quaternion is a number of the form , where are real numbers and satisfy that .
- Quaternion conjugate: The definition of conjugate to a quaternion is .
- Quaternion Multiplication: Multiplication of two quaternions and is defined by:
- Rotation with quaternions in three-dimensional space: The point is rotated by the point along the unit vector (i.e., rotation axis), which can use quaternion multiplication to represent. We define and as pure quaternion, i.e., quaternions with real part being zero, is a unit quaternion, then
- Dual quaternion: Dual quaterion [21] is an eight-dimensional real algebra to combine with quaternions. Formally, a dual quaternion can be represented by , where is a dual unit with , both the real part and the dual part are quaternions. Therefore, a dual quaternion is of the form .
- Dual quaternion conjugate: The conjugate of the dual quaternion is defined as: , which can be represented by an 8-tuple: .
- Dual Quaternion Multiplication: Dual Quaternion Hamilton product between and is defined as follows:
- Unit Dual Quaternion: A dual quaternion is a unit dual quaternion, if , namely, satisfies the following conditions:where . In order to simplify the calculation process, we use another effective form to represent unit dual quaternion which defines as follows:where and is a pure quaterion. We prove that is a unit dual quaternion:We can easily verify , as shown below:
- Combination of Rotation and Translation: We define a point in the three-dimensional space as a pure quaterion and let be the translation. The point under the rotation followed by the translation becomes the point . It is straightforward to utilize unit dual quaternion multiplication to represent the transformation from to , as shown below:
4. Our DualQuatE Model
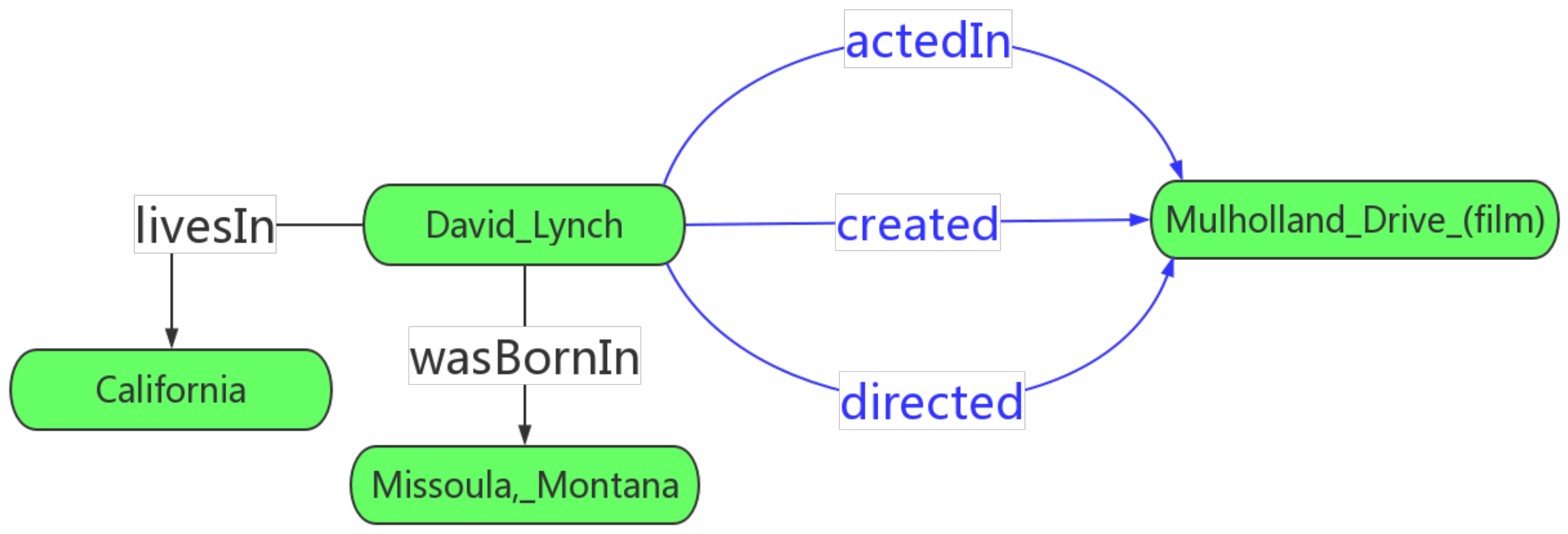
4.1. Multiple Relations between the Entities
4.2. Loss Function
| Algorithm 1DualQuatE. |
Input: Entity embeddings and relation embeddings . hyperparameters including margin , martrix dim k, negative sample size n.
|
4.3. Properties of DualQuatE
4.4. Variations
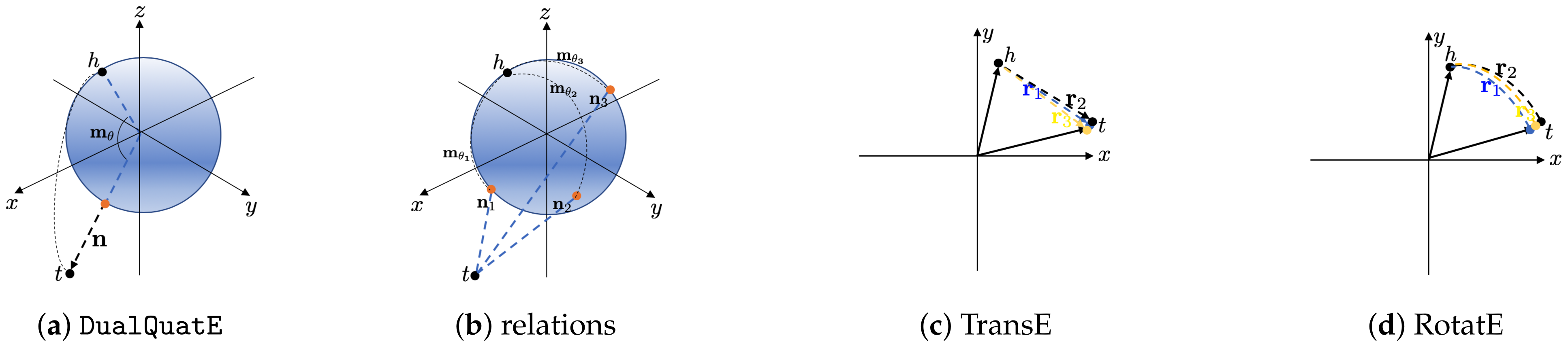
4.5. Connection to TransE and RotatE
5. Experiments
5.1. Experiment Settings
5.1.1. Datasets
5.1.2. Evaluation Metric
5.1.3. Baselines
5.1.4. Implementation Details
5.2. Results
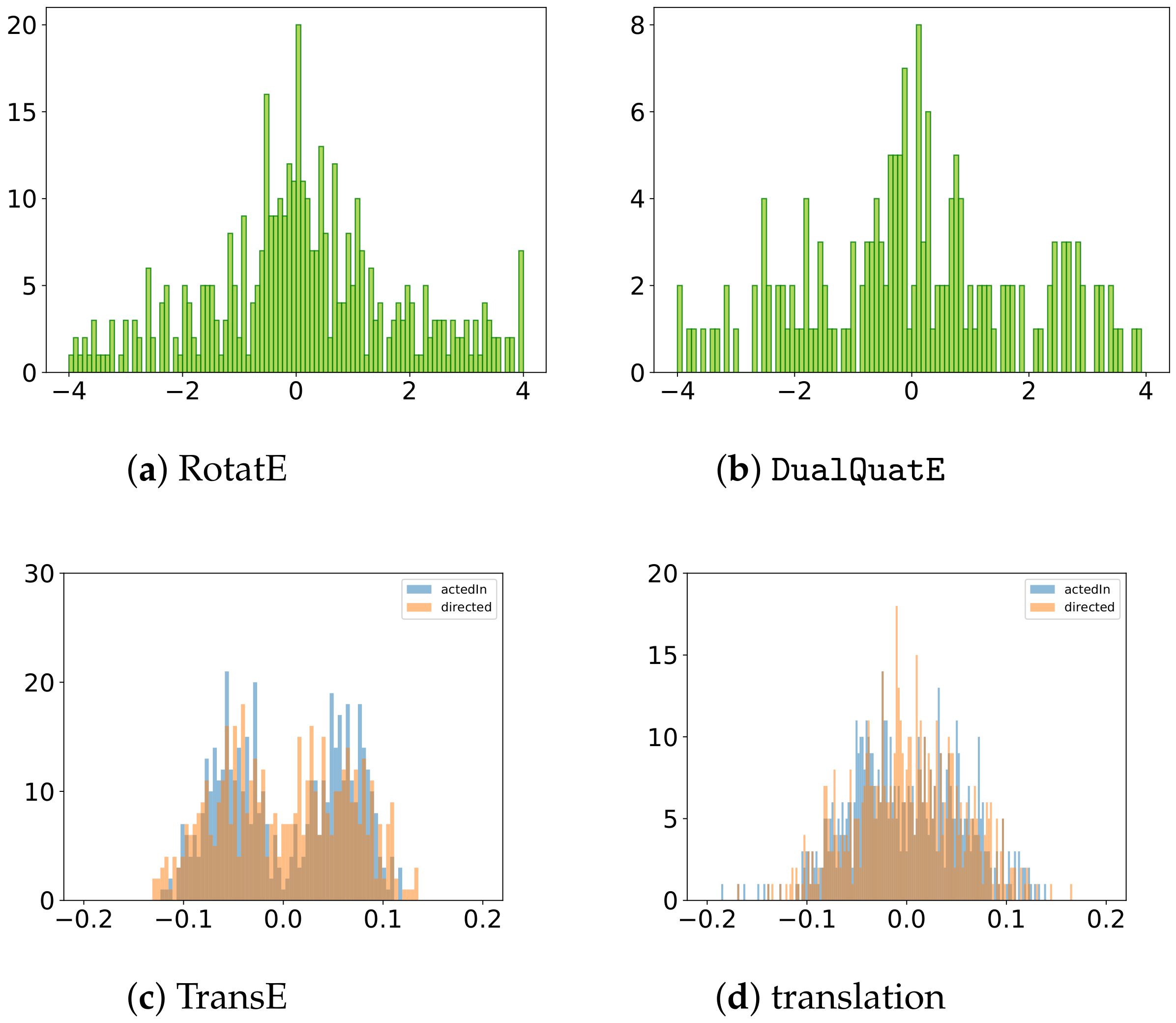
5.3. Relation Embeddings
5.4. Space and Time Complexity
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
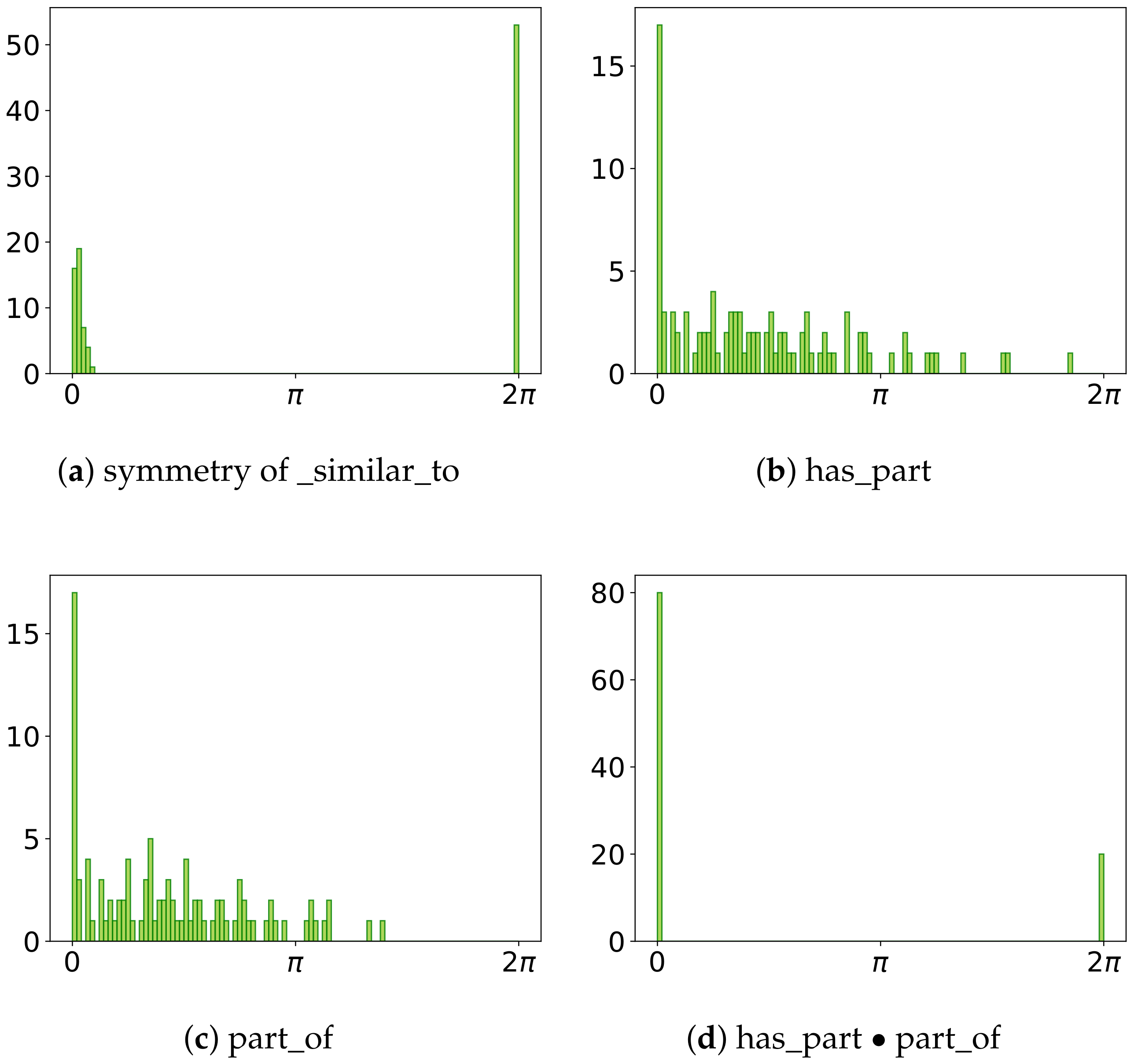
Appendix A. Proof of Relation Patterns
References
- Chen, Z.; Wang, X.; Xie, X.; Wu, T.; Bu, G.; Wang, Y.; Chen, E. Co-Attentive Multi-Task Learning for Explainable Recommendation; Kraus, S., Ed.; IJCAI: Macao, China, 2019; pp. 2137–2143. [Google Scholar]
- Kumar, V.; Hua, Y.; Ramakrishnan, G.; Qi, G.; Gao, L.; Li, Y. Difficulty-Controllable Multi-hop Question Generation from Knowledge Graphs. In Proceedings of the Semantic Web—ISWC 2019—18th International Semantic Web Conference, Auckland, New Zealand, 26–30 October 2019; Ghidini, C., Hartig, O., Maleshkova, M., Svátek, V., Cruz, I.F., Hogan, A., Song, J., Lefrançois, M., Gandon, F., Eds.; Part I; Lecture Notes in Computer Science. Springer: Cham, Switzerland, 2019; Volume 11778, pp. 382–398. [Google Scholar]
- Kanakaris, N.; Giarelis, N.; Siachos, I.; Karacapilidis, N. Shall I Work with Them? A Knowledge Graph-Based Approach for Predicting Future Research Collaborations. Entropy 2021, 23, 664. [Google Scholar] [CrossRef] [PubMed]
- Bordes, A.; Usunier, N.; Garcia-Duran, A.; Weston, J.; Yakhnenko, O. Translating embeddings for modeling multi-relational data. Adv. Neural Inf. Process. Syst. 2013, 26, 2787–2795. [Google Scholar]
- Sun, Z.; Deng, Z.; Nie, J.; Tang, J. RotatE: Knowledge Graph Embedding by Relational Rotation in Complex Space. arXiv 2019, arXiv:1902.10197. [Google Scholar]
- Zhang, S.; Tay, Y.; Yao, L.; Liu, Q. Quaternion Knowledge Graph Embeddings. In Advances in Neural Information Processing Systems 32: Annual Conference on Neural Information Processing Systems 2019, NeurIPS 2019, Vancouver, BC, Canada, 8–14 December 2019; Wallach, H.M., Larochelle, H., Beygelzimer, A., d’Alché-Buc, F., Fox, E.B., Garnett, R., Eds.; NeurIPS: Vancouver, BC, Canada, 2019; pp. 2731–2741. [Google Scholar]
- Zhang, Z.; Cai, J.; Zhang, Y.; Wang, J. Learning Hierarchy-Aware Knowledge Graph Embeddings for Link Prediction; AAAI Press: Palo Alto, CA, USA, 2020; pp. 3065–3072. [Google Scholar]
- Yang, B.; Yih, W.; He, X.; Gao, J.; Deng, L. Embedding Entities and Relations for Learning and Inference in Knowledge Bases; Bengio, Y., LeCun, Y., Eds.; ICLR: San Diego, CA, USA, 2015. [Google Scholar]
- Kazemi, S.M.; Poole, D. SimplE Embedding for Link Prediction in Knowledge Graphs; Bengio, S., Wallach, H.M., Larochelle, H., Grauman, K., Cesa-Bianchi, N., Garnett, R., Eds.; NeurIPS: Montréal, QC, Canada, 2018; pp. 4289–4300. [Google Scholar]
- Wang, Q.; Mao, Z.; Wang, B.; Guo, L. Knowledge Graph Embedding: A Survey of Approaches and Applications. IEEE Trans. Knowl. Data Eng. 2017, 29, 2724–2743. [Google Scholar] [CrossRef]
- Lin, Y.; Liu, Z.; Sun, M.; Liu, Y.; Zhu, X. Learning Entity and Relation Embeddings for Knowledge Graph Completion; Bonet, B., Koenig, S., Eds.; AAAI Press: Palo Alto, CA, USA, 2015; pp. 2181–2187. [Google Scholar]
- Nickel, M.; Rosasco, L.; Poggio, T.A. Holographic Embeddings of Knowledge Graphs; Schuurmans, D., Wellman, M.P., Eds.; AAAI Press: Palo Alto, CA, USA, 2016; pp. 1955–1961. [Google Scholar]
- Trouillon, T.; Welbl, J.; Riedel, S.; Gaussier, É.; Bouchard, G. Complex Embeddings for Simple Link Prediction; ICML: New York, NY, USA, 2016; pp. 2071–2080. [Google Scholar]
- Xu, C.; Li, R. Relation Embedding with Dihedral Group in Knowledge Graph; ACL: Florence, Italy, 2019; pp. 263–272. [Google Scholar]
- Dettmers, T.; Minervini, P.; Stenetorp, P.; Riedel, S. Convolutional 2D Knowledge Graph Embeddings. In Proceedings of the AAAI Conference on Artificial Intelligence; AAAI Press: Palo Alto, CA, USA, 2018; pp. 1811–1818. [Google Scholar]
- Schlichtkrull, M.S.; Kipf, T.N.; Bloem, P.; van den Berg, R.; Titov, I.; Welling, M. Modeling Relational Data with Graph Convolutional Networks. In Proceedings of the Semantic Web—15th International Conference, ESWC 2018, Heraklion, Crete, Greece, 3–7 June 2018; Gangemi, A., Navigli, R., Vidal, M., Hitzler, P., Troncy, R., Hollink, L., Tordai, A., Alam, M., Eds.; Lecture Notes in Computer Science. Springer: Cham, Switzerland, 2018; Volume 10843, pp. 593–607. [Google Scholar]
- Vashishth, S.; Sanyal, S.; Nitin, V.; Agrawal, N.; Talukdar, P.P. InteractE: Improving Convolution-Based Knowledge Graph Embeddings by Increasing Feature Interactions; AAAI Press: Palo Alto, CA, USA, 2020; pp. 3009–3016. [Google Scholar]
- Balazevic, I.; Allen, C.; Hospedales, T. Multi-relational poincaré graph embeddings. Adv. Neural Inf. Process. Syst. 2019, 32, 4463–4473. [Google Scholar]
- Chami, I.; Wolf, A.; Juan, D.; Sala, F.; Ravi, S.; Ré, C. Low-Dimensional Hyperbolic Knowledge Graph Embeddings. In Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics, ACL 2020, Online, 5–10 July 2020; Jurafsky, D., Chai, J., Schluter, N., Tetreault, J.R., Eds.; Association for Computational Linguistics: Beijing, China, 2020; pp. 6901–6914. [Google Scholar]
- Hamilton, W.R. LXXVIII. On quaternions; or on a new system of imaginaries in Algebra: To the editors of the Philosophical Magazine and Journal. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1844, 25, 489–495. [Google Scholar] [CrossRef]
- Kotelnikov, A.P. Screw calculus and some applications to geometry and mechanics. Annu. Imp. Univ. Kazan 1895, 24. [Google Scholar]
- Toutanova, K.; Chen, D. Observed versus latent features for knowledge base and text inference. In Proceedings of the 3rd Workshop on Continuous Vector Space Models and their Compositionality; Association for Computational Linguistics: Beijing, China, 2015; pp. 57–66. [Google Scholar]
- Mahdisoltani, F.; Biega, J.; Suchanek, F.M. YAGO3: A Knowledge Base from Multilingual Wikipedias. In Proceedings of the Seventh Biennial Conference on Innovative Data Systems Research (CIDR 2015), Asilomar, CA, USA, 4–7 January 2015. [Google Scholar]
- Ebisu, T.; Ichise, R. TorusE: Knowledge Graph Embedding on a Lie Group. In Proceedings of the AAAI Conference on Artificial Intelligence; AAAI Press: Palo Alto, CA, USA, 2018; pp. 1819–1826. [Google Scholar]
- Zhuo, H.H.; Muñoz-Avila, H.; Yang, Q. Learning hierarchical task network domains from partially observed plan traces. Artif. Intell. 2014, 212, 134–157. [Google Scholar] [CrossRef]
- Zhuo, H.H.; Yang, Q. Action-model acquisition for planning via transfer learning. Artif. Intell. 2014, 212, 80–103. [Google Scholar] [CrossRef]
- Zhuo, H.H.; Zha, Y.; Kambhampati, S. Discovering Underlying Plans Based on Shallow Models. ACM Trans. Intell. Syst. Technol. 2020, 11, 18:1–18:30. [Google Scholar] [CrossRef]
- Zhuo, H.H.; Kambhampati, S. Model-lite planning: Case-based vs. model-based approaches. Artif. Intell. 2014, 246, 1–21. [Google Scholar] [CrossRef]
- Zhuo, H.H. Recognizing Multi-Agent Plans When Action Models and Team Plans Are Both Incomplete. ACM Trans. Intell. Syst. Technol. 2019, 10, 30:1–30:24. [Google Scholar] [CrossRef]
- Feng, W.; Zhuo, H.H.; Kambhampati, S. Extracting Action Sequences from Texts Based on Deep Reinforcement Learning. In Proceedings of the International Joint Conferences on Artifical Intelligence (IJCAI), Stockholm, Sweden, 13–19 July 2018; pp. 4064–4070. [Google Scholar]
- Zhuo, H.H. Human-Aware Plan Recognition. In Proceedings of the AAAI Conference on Artificial Intelligence; AAAI Press: Palo Alto, CA, USA, 2017; pp. 3686–3693. [Google Scholar]
| Model | Symmetry | Antisymmetry | Inversion | Composition | Multiple Relations |
|---|---|---|---|---|---|
| TransE | 🗸 | 🗸 | 🗸 | 🗸 | × |
| RotatE | 🗸 | 🗸 | 🗸 | 🗸 | × |
| HAKE [7] | 🗸 | 🗸 | 🗸 | 🗸 | × |
| DistMult [8] | 🗸 | × | × | × | 🗸 |
| ComplEx [9] | 🗸 | 🗸 | 🗸 | × | 🗸 |
| QuatE | 🗸 | 🗸 | 🗸 | × | 🗸 |
| DualQuatE | 🗸 | 🗸 | 🗸 | 🗸 | 🗸 |
| Dataset | #E | #R | #TR | #V | #TE |
|---|---|---|---|---|---|
| FB15k | 14,951 | 1345 | 483,142 | 50,000 | 59,071 |
| FB15k-237 | 14,541 | 237 | 272,115 | 17,535 | 20,466 |
| WN8 | 40,943 | 18 | 141,442 | 5000 | 5000 |
| WN8RR | 40,943 | 11 | 86,835 | 3034 | 3134 |
| YOGA3-10 | 123,182 | 37 | 1,079,040 | 5000 | 5000 |
| YAGO3-10 | |||||
|---|---|---|---|---|---|
| Model | MR | MRR | Hit@1 | Hit@3 | Hit@10 |
| DistMult ♠ | 5926 | 0.34 | 0.24 | 0.38 | 0.54 |
| ComplEx ♠ | 6351 | 0.36 | 0.26 | 0.40 | 0.55 |
| ConvE ♠ | 1671 | 0.44 | 0.35 | 0.49 | 0.62 |
| RotatE | 1767 | 0.495 | 0.402 | 0.550 | 0.670 |
| InteractE | 2375 | 0.541 | 0.462 | - | 0.687 |
| HAKE | - | 0.545 | 0.462 | 0.596 | 0.694 |
| DualQuatE-1 | 1636 | 0.477 | 0.377 | 0.534 | 0.672 |
| DualQuatE-2 | 1889 | 0.503 | 0.411 | 0.557 | 0.676 |
| DualQuatE | 1210 | 0.534 | 0.445 | 0.591 | 0.695 |
| FB15k-237 | WN18RR | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Model | MR | MRR | Hit@1 | Hit@3 | Hit@10 | MR | MRR | Hit@1 | Hit@3 | Hit@10 |
| TransE ♣ | 357 | 0.294 | - | - | 0.465 | 3384 | 0.226 | - | - | 0.501 |
| ComplEx ♣ | 339 | 0.247 | 0.158 | 0.275 | 0.428 | 5261 | 0.44 | 0.41 | 0.46 | 0.51 |
| RotatE ♣ | 177 | 0.338 | 0.241 | 0.375 | 0.533 | 3340 | 0.476 | 0.428 | 0.492 | 0.571 |
| DihEdral | - | 0.32 | 0.23 | 0.353 | 0.502 | - | 0.48 | 0.452 | 0.491 | 0.536 |
| QuatE ¶ | 176 | 0.311 | 0.221 | 0.342 | 0.495 | 3472 | 0.481 | 0.436 | 0.500 | 0.564 |
| InteractE | 172 | 0.354 | 0.263 | - | 0.535 | 5202 | 0.463 | 0.430 | - | 0.528 |
| HAKE | - | 0.346 | 0.250 | 0.381 | 0.542 | - | 0.497 | 0.452 | 0.516 | 0.582 |
| DualQuatE-1 | 173 | 0.329 | 0.230 | 0.368 | 0.530 | 2989 | 0.463 | 0.408 | 0.484 | 0.571 |
| DualQuatE-2 | 174 | 0.345 | 0.246 | 0.384 | 0.545 | 3324 | 0.484 | 0.437 | 0.503 | 0.576 |
| DualQuatE | 171 | 0.342 | 0.245 | 0.381 | 0.535 | 2755 | 0.470 | 0.415 | 0.493 | 0.582 |
| FB15k | WN18 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Model | MR | MRR | Hit@1 | Hit@3 | Hit@10 | MR | MRR | Hit@1 | Hit@3 | Hit@10 |
| TransE ♣ | - | 0.463 | 0.297 | 0.578 | 0.749 | - | 0.495 | 0.113 | 0.888 | 0.943 |
| ComplEx | - | 0.692 | 0.599 | 0.759 | 0.840 | - | 0.941 | 0.936 | 0.945 | 0.947 |
| HolE | - | 0.524 | 0.402 | 0.613 | 0.739 | - | 0.938 | 0.930 | 0.945 | 0.949 |
| TorusE | - | 0.733 | 0.674 | 0.771 | 0.832 | - | 0.619 | 0.943 | 0.950 | 0.954 |
| SimplE | - | 0.727 | 0.660 | 0.773 | 0.838 | - | 0.942 | 0.939 | 0.944 | 0.947 |
| RotatE ♣ | 40 | 0.797 | 0.746 | 0.830 | 0.884 | 309 | 0.949 | 0.944 | 0.952 | 0.959 |
| DihEdral | - | 0.733 | 0.641 | 0.803 | 0.877 | - | 0.946 | 0.942 | 0.948 | 0.952 |
| QuatE ¶ | 41 | 0.770 | 0.700 | 0.821 | 0.878 | 388 | 0.949 | 0.941 | 0.954 | 0.960 |
| DualQuatE-1 | 31 | 0.751 | 0.659 | 0.825 | 0.884 | 241 | 0.947 | 0.939 | 0.952 | 0.959 |
| DualQuatE-2 | 50 | 0.766 | 0.696 | 0.818 | 0.877 | 220 | 0.948 | 0.942 | 0.953 | 0.961 |
| DualQuatE | 35 | 0.754 | 0.664 | 0.827 | 0.884 | 183 | 0.949 | 0.943 | 0.952 | 0.960 |
| Method | Space Complexity | Time Complexity |
|---|---|---|
| TransE | ||
| RotatE | ||
| HAKE | ||
| RESCAL | ||
| HolE | ||
| ComplEx | ||
| QuatE | ||
| DualQuatE |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, L.; Zhu, H.; Zhuo, H.H.; Xu, J. Dual Quaternion Embeddings for Link Prediction. Appl. Sci. 2021, 11, 5572. https://doi.org/10.3390/app11125572
Gao L, Zhu H, Zhuo HH, Xu J. Dual Quaternion Embeddings for Link Prediction. Applied Sciences. 2021; 11(12):5572. https://doi.org/10.3390/app11125572
Chicago/Turabian StyleGao, Liming, Huiling Zhu, Hankz Hankui Zhuo, and Jin Xu. 2021. "Dual Quaternion Embeddings for Link Prediction" Applied Sciences 11, no. 12: 5572. https://doi.org/10.3390/app11125572
APA StyleGao, L., Zhu, H., Zhuo, H. H., & Xu, J. (2021). Dual Quaternion Embeddings for Link Prediction. Applied Sciences, 11(12), 5572. https://doi.org/10.3390/app11125572





