Numerical and Experimental Assessment of a Novel Anchored for Intramedullary Telescopic Nails Used in Osteogenesis Imperfecta Fractures
Abstract
:Featured Application
Abstract
1. Introduction
2. Materials and Methods
2.1. Four-Bending Testing
2.2. Numerical Analysis of Four-Bending Testing
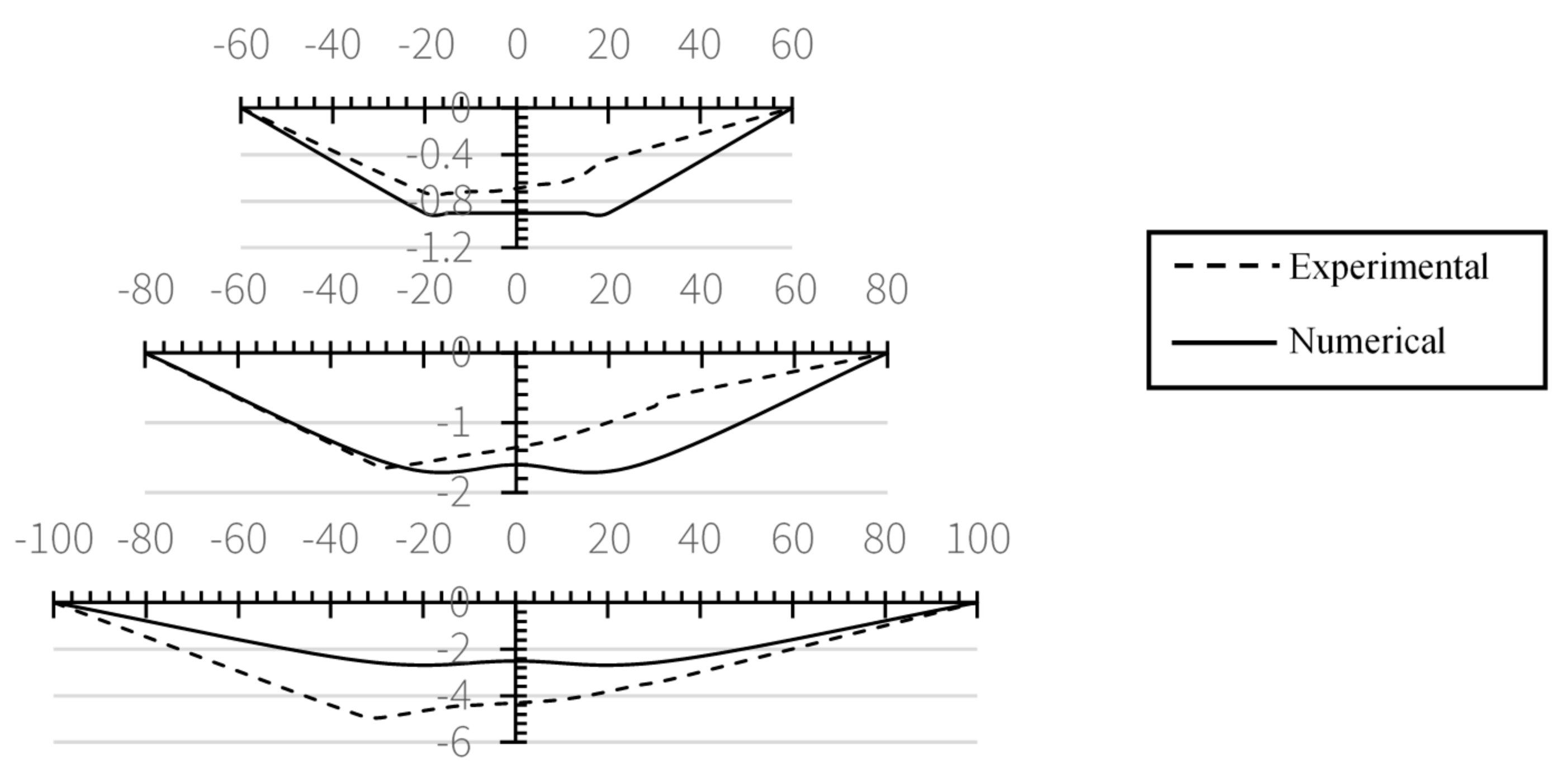
3. Experimental Results
4. Numerical Results
5. Discussion
6. Conclusions
7. Patents
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rueda, J.L.; Torres, C.R.; Ramírez, V.; Martínez, L.; Urriolagoitia, G. Design and comparative numerical analysis of designs of intramedular telescopic systems for the rehabilitation of patients with osteogenesis imperfecta (OI) type III. Adv. Struct. Mater. 2020, 113, 333–342. [Google Scholar]
- Garrido, I. Sistemas de Testeo Automático de Dispositivos Implantables. Bachelor’s Thesis, Universidad ORT, Montevideo, Uruguay, 2016. [Google Scholar]
- Küntscher, G. A new method of treatment of per trochanteric fractures. Proc. R. Soc. Med. 1970, 63, 1120–1121. [Google Scholar]
- Talijanovic, M.S.; Jones, M.D.; Ruth, J.T.; Benjamin, J.B.; Sheppard, J.E.; Hunter, T.B. Fracture fixation. Radiographics 2003, 23, 1569–1590. [Google Scholar] [CrossRef] [PubMed]
- Jay, L.R.; Paloski, M.D.; Sponseller, P.D.; Leet, A.I. Bent telescopic rod in patients with osteo-genesis imperfecta. J. Pediatr. Orthop. 2015, 36, 1–5. [Google Scholar]
- Reynders-Frederix, P.A.; Dobre, C.; Lengthening, L. Hydraulically Driven, Intramedullary Nailing: A Comprehensive Guide; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Zionts, L.E.; Bowen, R.E. Treatment of fractures and non-unions in children with osteogenesis imperfecta. Osteogenes. Imperfecta 2014, 1, 427–442. [Google Scholar]
- Wilkinson, J.M.; Scott, B.W.; Clarke, A.M.; Bell, M.J. Surgical stabilisation of the lower limb in osteogenesis imperfecta using the sheffield telescopic intramedullary rod system. J. Bone Jt. Surg. 1998, 80, 999–1004. [Google Scholar] [CrossRef]
- Biker, O.; Davies, N.; Latimer, M.; Graham, D.; Bellemore, M. Experience with the fassierduval telescopic rod; first 24 consecutive cases with a minimum of 1-year follow-up. J. Pediatr. Orthop. 2011, 31, 458–464. [Google Scholar]
- Martínez, L.; Reed, M.P.; García, A.; De Loma-Ossorio, M.; Torres, C.; Bueno, A. Crash impact dummies adapted to people affected by osteogenesis imperfecta IRCOBI Conference Proceedings. Int. Res. Counc. Biomech. Inj. 2016, 768–769. [Google Scholar]
- Cuautle-Estrada, A.; Torres-Sanmiguel, C.R.; Rivera-Hernández, M.A.; Ramírez, O.; Urriolagoitia-Calderón, G.M. Lower Limb Design for a Child Test Dummy, based on Osteogenesis Imperfecta characteristics. J. Phys. Conf. Ser. Vol. 2021, 1723, 012019. [Google Scholar] [CrossRef]
- Wyscoki, R.W.; Kapotas, J.S.; Virkus, W.W. Intramedullary nailing of proximal and distal one-third tibia shaft fractures with intraoperative tow- pin external fixation. J. Trauma Acute Care Surg. 2009, 66, 1135–1139. [Google Scholar] [CrossRef] [PubMed]
- Rosa, N.; Marta, M.; Vaz, M.; Tavares, S.M.O.; Simoes, R.; Magalhães, F.D.; Marques, A.T. Intramedullary nailing biomechanics: Evolution and challenges. J. Eng. Med. 2019, 233, 295–308. [Google Scholar] [CrossRef] [PubMed]
- Torres-San Miguel, C.R.; Hernández-Gómez, J.; Urriolagoitia-Sosa, G.; Romero-Ángeles, B.; Martínez-Sáez, L. Design and manufacture of a customised temporomandibular prosthesis. Rev. Int. Metodos Numer. Calc. Diseno Ing. 2019, 35, 1–22. [Google Scholar] [CrossRef]
- Hernández-Acosta, M.A.; Torres-San Miguel, C.R.; Piña-Díaz, A.J.; Paredes-Rojas, J.C.; Aguilar-Peréz, L.A.; Urriolagoitia-Sosa, G. Numerical study of a customized transtibial prosthesis based on an analytical design under a flex-foot® variflex® architecture. Appl. Sci. 2020, 10, 4275. [Google Scholar] [CrossRef]
- Laursen, T.A.; Simo, J.C. Continuum-based finite element formulation for the implicit solution of multibody, large deformation frictional contact problems. Int. J. Numer. Methods Eng. 1993, 36, 3451–3485. [Google Scholar] [CrossRef]
- Ramírez, V.; Torres, C.R.; Rueda, J.L.; Martínez, L.; Romero, B.; Urriolagoitia, G.M. Finite element analysis of 3D models of upper and lower limbs of mexican patients with osteogenesis imperfecta (OI) type III. Adv. Struct. Mater. 2020, 113, 343–354. [Google Scholar]
- Rueda-Arreguín, J.L.; Torres-San Miguel, C.R.; Ramírez-Vela, V.; Urriolagoitia-Sosa, G.; Martínez-Sáez, L. Simulation by finite element method of intramedullary telescopic systems for rehabilitation of patients with osteogenesis imperfecta. Rev. Mex. Ing. Biomed. 2019, 40, e201826. [Google Scholar]
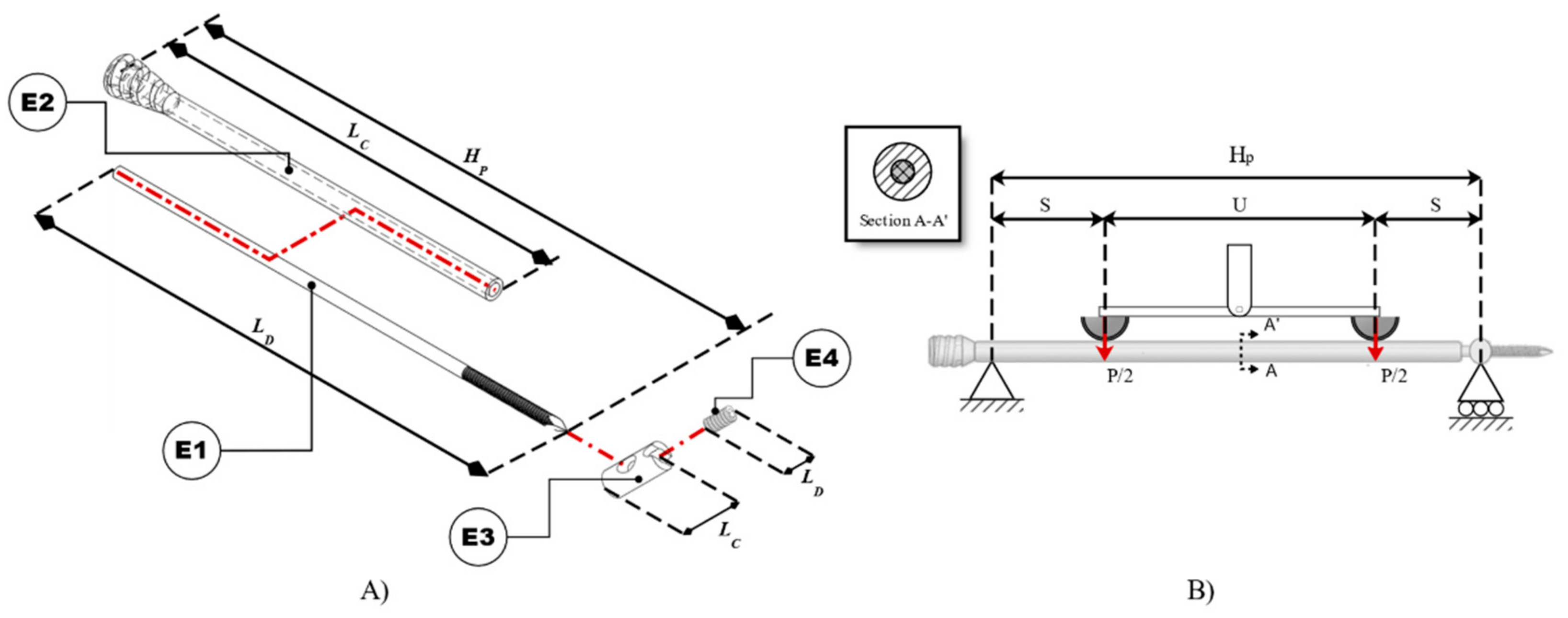
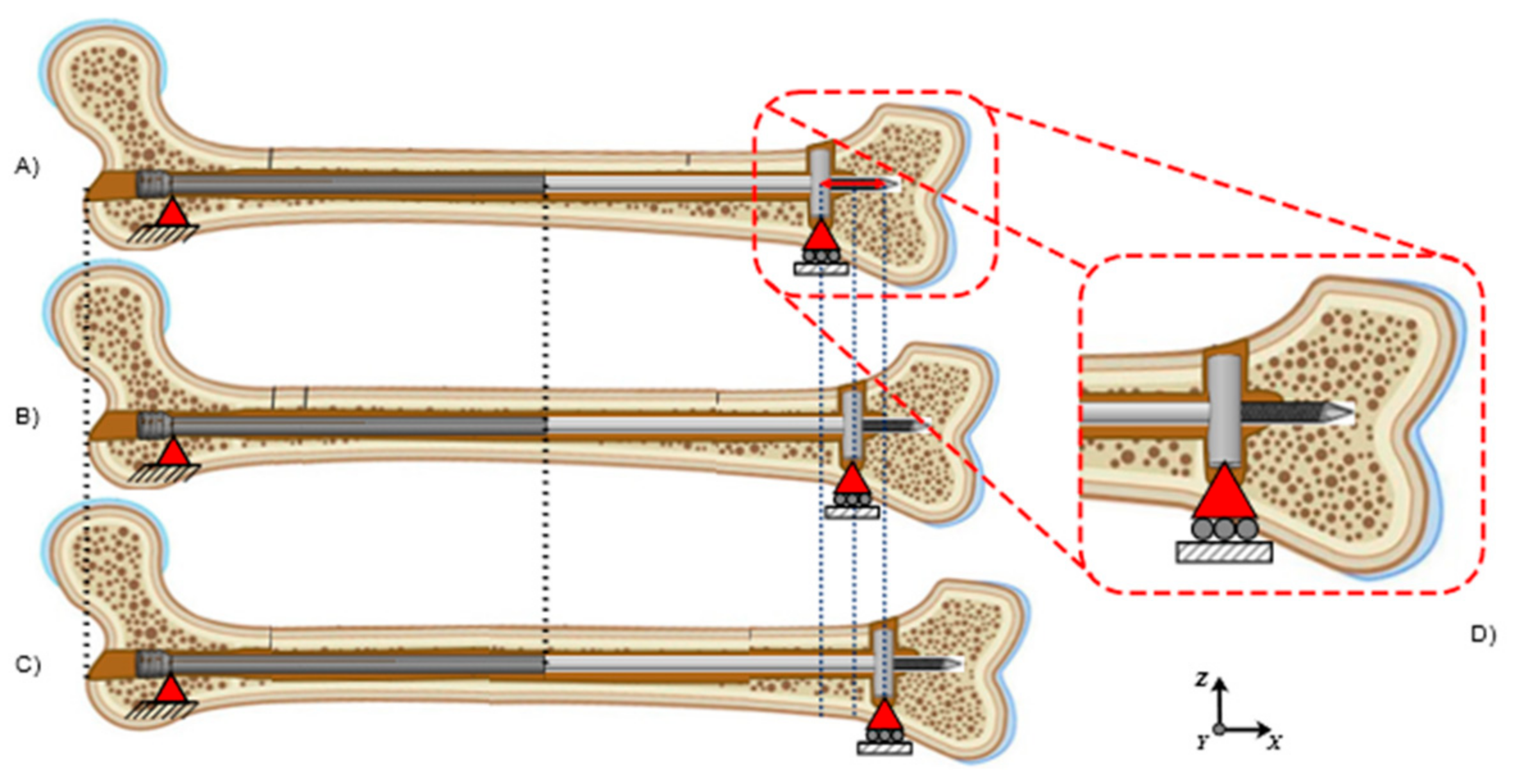
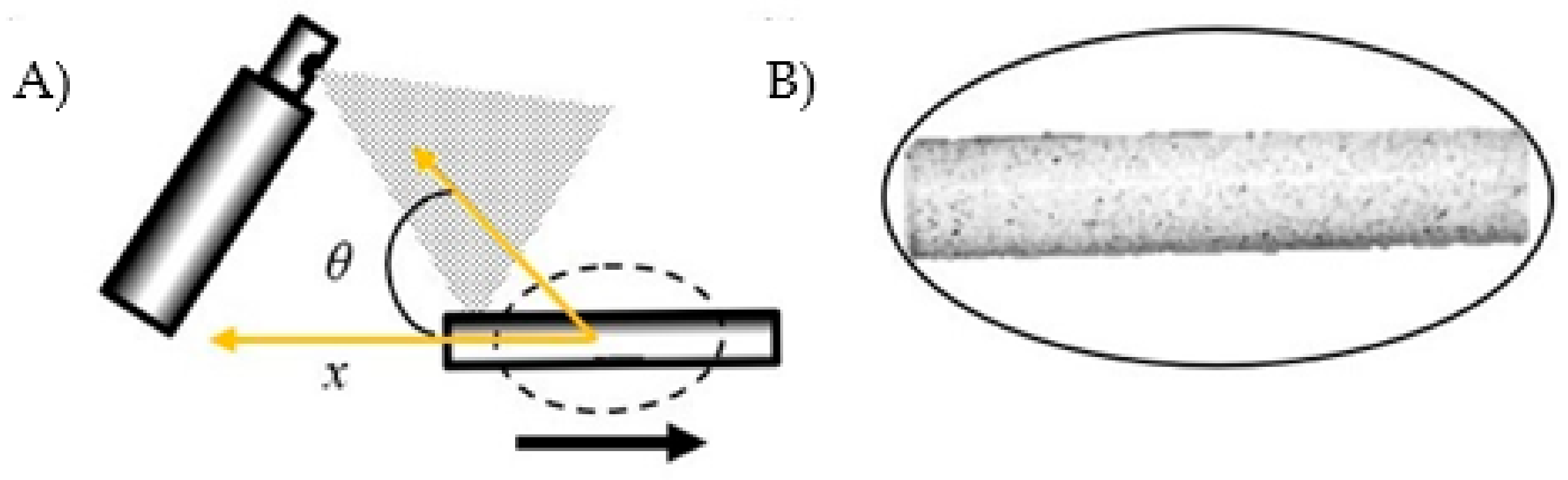

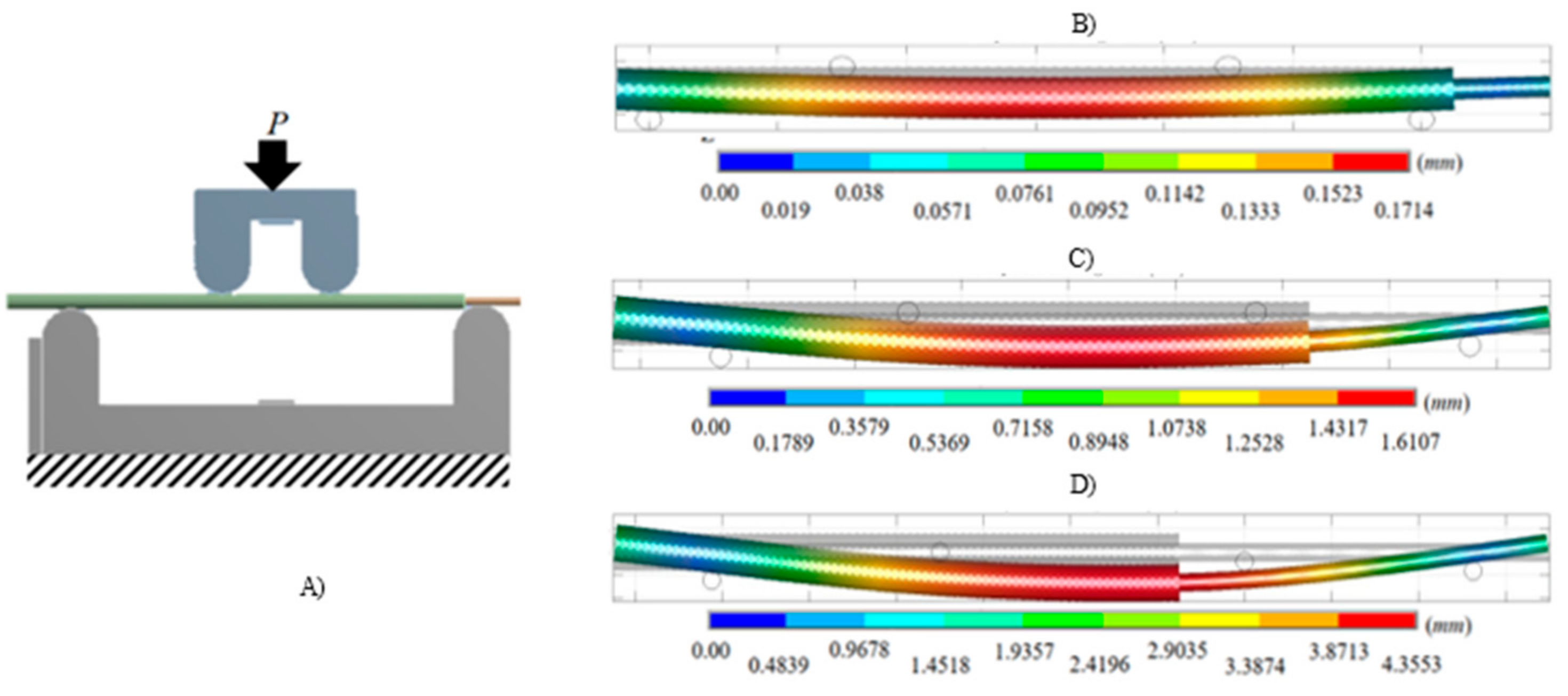
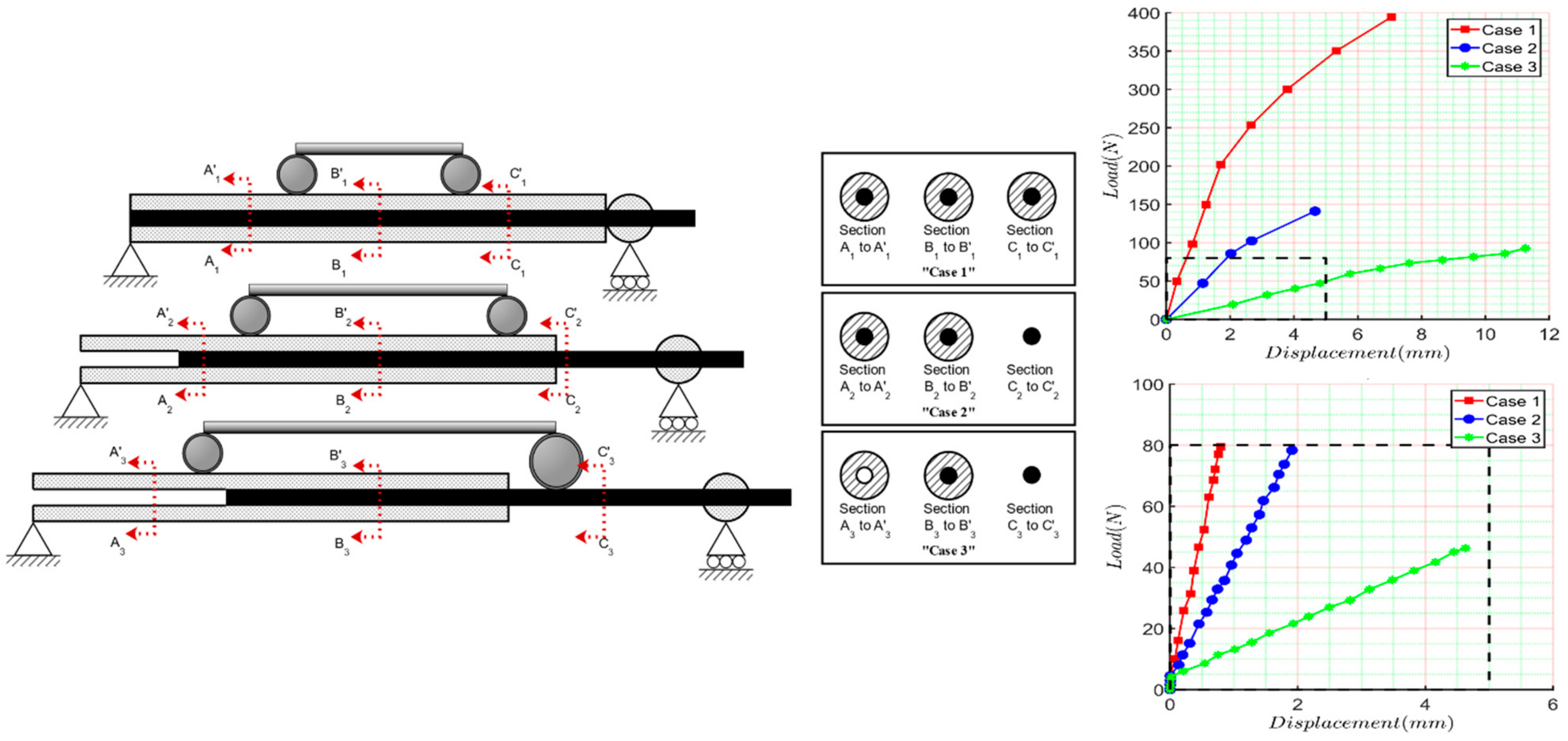
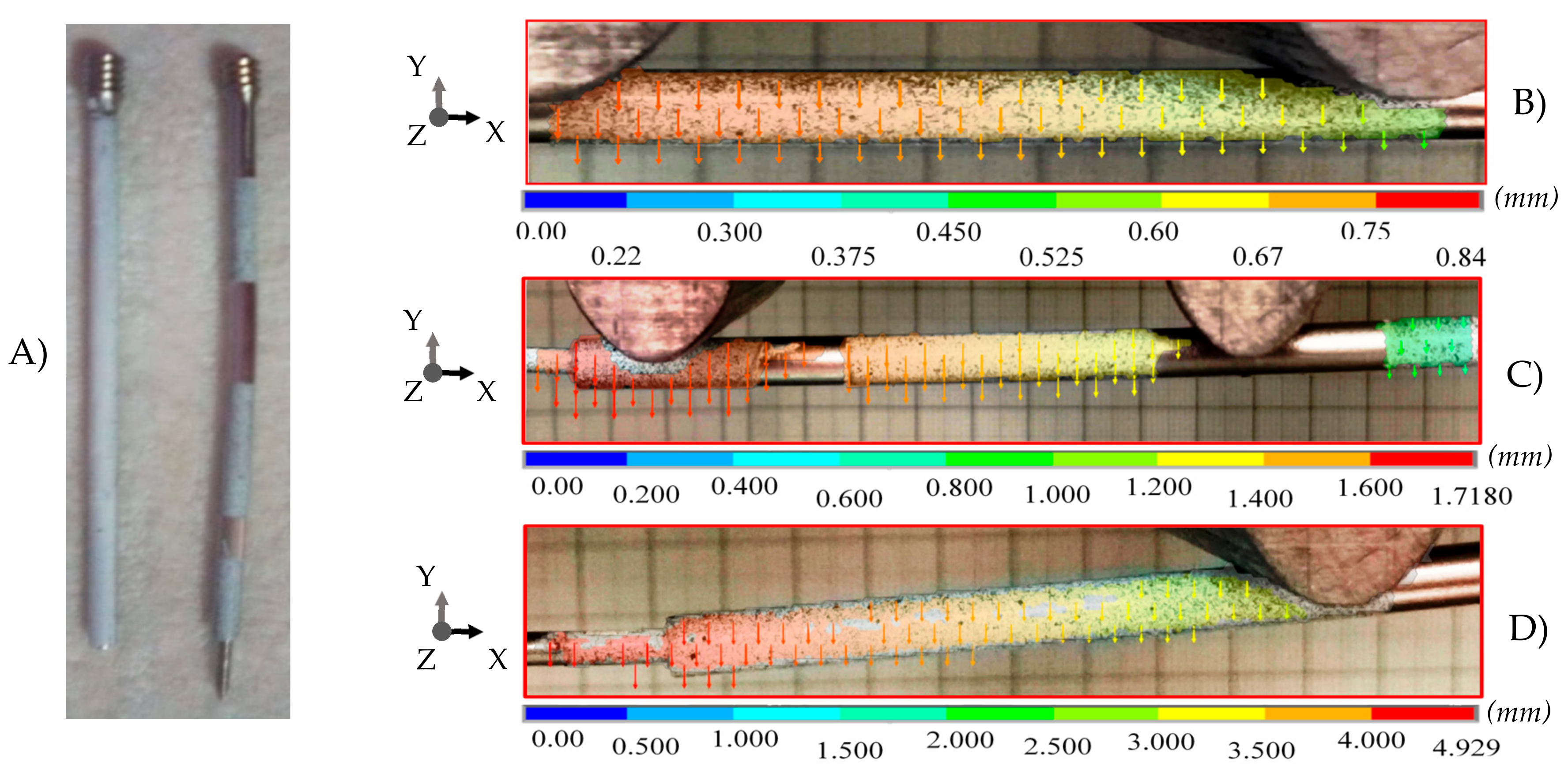
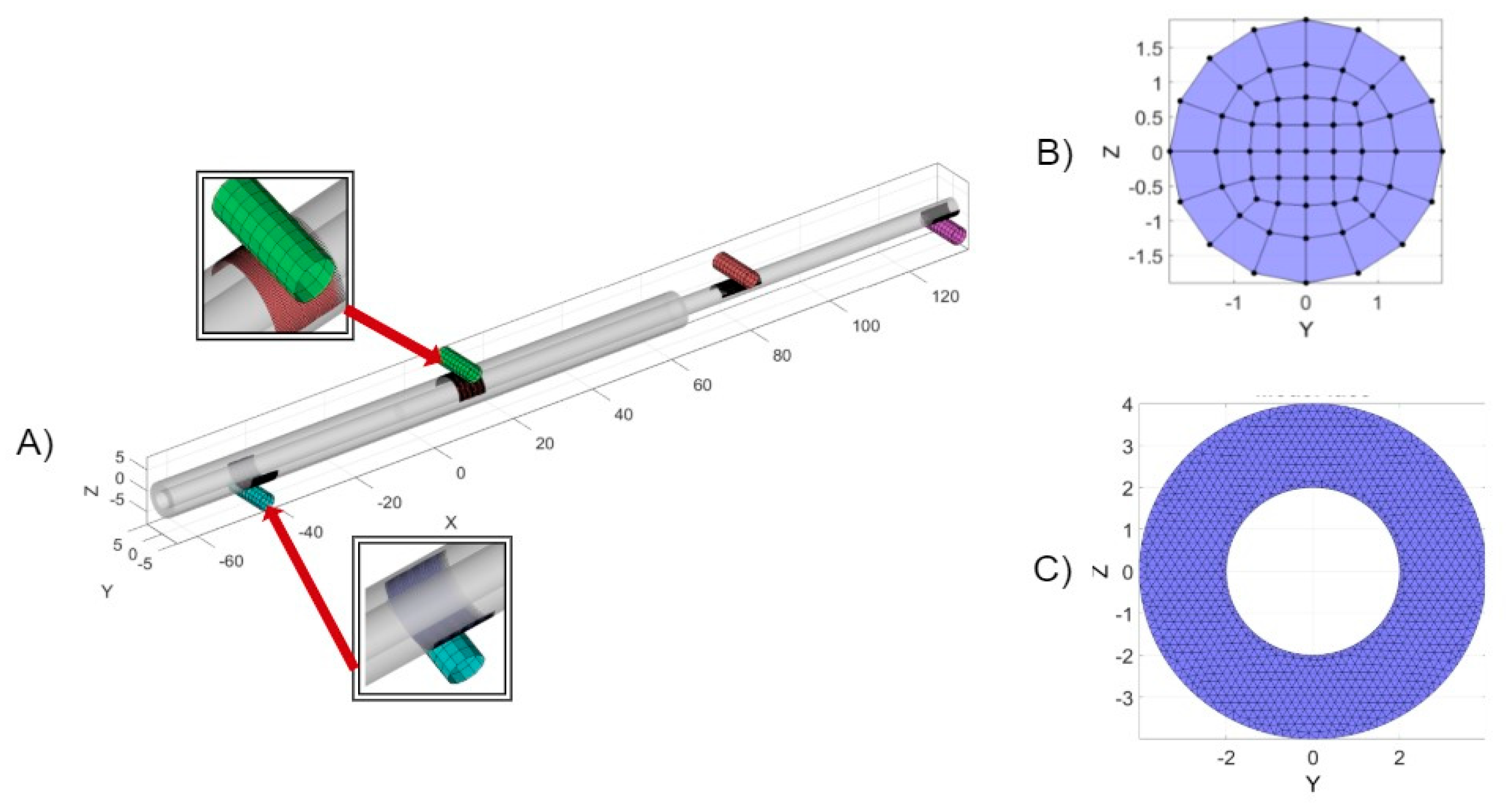
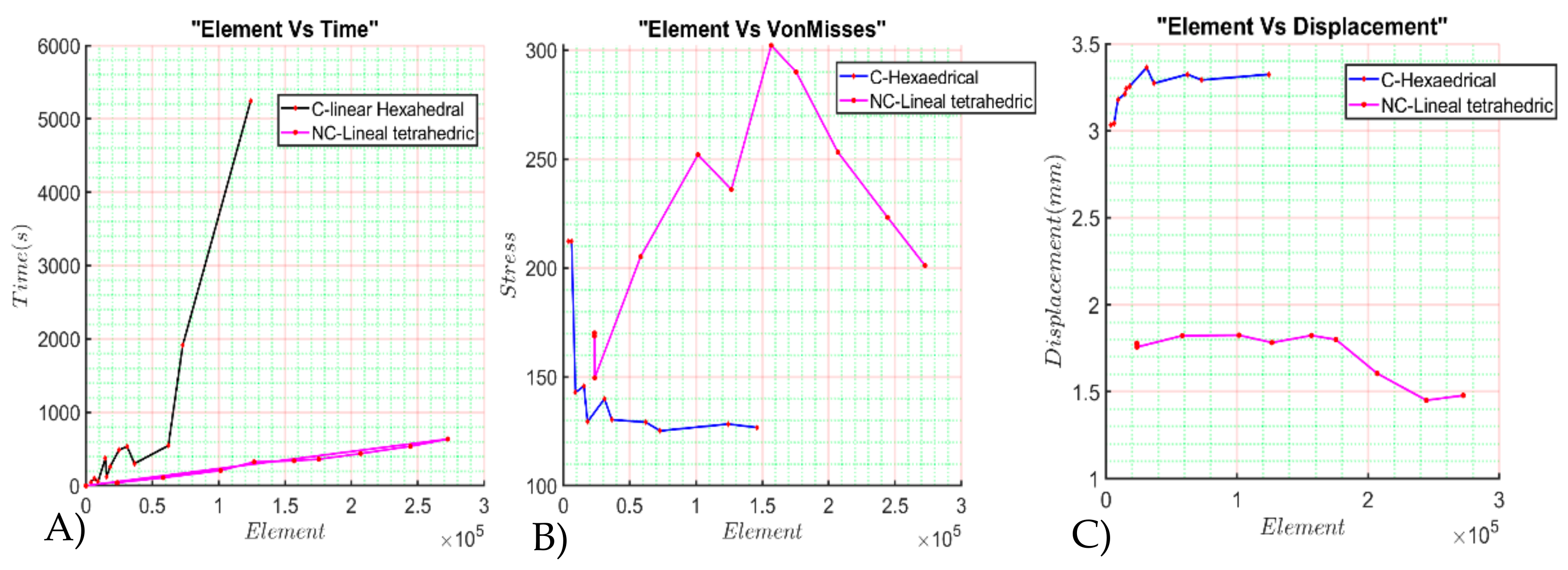

| Test | Elements | VM Value | Dz Mean | Time | Type of Element | Contact Condition |
|---|---|---|---|---|---|---|
| 1 | 3648.00 | 212.23 | 3.0329 | 44.81 | Hexahedrical linear | Sticky contact |
| 2 | 6208.00 | 212.18 | 3.0415 | 97.15 | ||
| 3 | 9120.00 | 142.86 | 3.1781 | 55.25 | ||
| 4 | 15,520.00 | 145.73 | 3.242 | 119.36 | ||
| 5 | 18,240.00 | 129.32 | 3.2561 | 261.61 | ||
| 6 | 31,040.00 | 139.91 | 3.3636 | 534.08 | ||
| 7 | 36,480.00 | 126.49 | 3.2719 | 300.91 | ||
| 8 | 62,080.00 | 129.19 | 3.3241 | 546.87 | ||
| 9 | 14,592.00 | 752.07 | 3.0163 | 374.70 | ||
| 10 | 24,832.00 | 784.86 | 2.817 | 486.77 | ||
| 11 | 36,480.00 | 130.28 | 3.2402 | 453.33 | ||
| 12 | 62,080.00 | 142.62 | 3.2824 | 1364.70 | ||
| 13 | 72,960.00 | 125.19 | 3.2912 | 1918.10 | ||
| 14 | 124,160.00 | 128.30 | 3.3238 | 5247.00 | ||
| 15 | 145,920.00 | 126.73 | 3.1404 | 960.00 | ||
| 16 | 24,640.00 | 332.84 | 2.6439 | 42.82 | Tetrahedral linear | Sticky contact |
| 17 | 49,280.00 | 432.53 | 2.8139 | 93.54 | ||
| 18 | 98,560.00 | 2184.20 | 4.1438 | 273.23 | ||
| 19 | 23,499.00 | 168.7178 | 1.7733 | 39 | Tetrahedral linear | Sliding elastic |
| 20 | 23,538.00 | 170.1108 | 1.7787 | 40.6458 | ||
| 21 | 23,646.00 | 149.4692 | 1.7566 | 41.33 | ||
| 22 | 58,274.00 | 205.1384 | 1.8222 | 109.2592 | ||
| 23 | 101,488.00 | 251.9337 | 1.8249 | 206.84 | ||
| 24 | 126,662.00 | 235.9668 | 1.7822 | 324.3423 | ||
| 25 | 147,773.00 | 209.373 | 1.6077 | 322.0232 | ||
| 26 | 206,997.00 | 253.1276 | 1.6049 | 437.8151 | ||
| 27 | 244,466.00 | 223.1868 | 1.4508 | 537.00791 | ||
| 28 | 272,644.00 | 201.0864 | 1.4787 | 635.524 | ||
| 29 | 339,645.00 | 439.0501 | 1.8002 | 762.511 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aguilar-Pérez, L.A.; Sánchez-Cruz, J.I.; Flores-Campos, J.A.; Torres-SanMiguel, C.R. Numerical and Experimental Assessment of a Novel Anchored for Intramedullary Telescopic Nails Used in Osteogenesis Imperfecta Fractures. Appl. Sci. 2021, 11, 5422. https://doi.org/10.3390/app11125422
Aguilar-Pérez LA, Sánchez-Cruz JI, Flores-Campos JA, Torres-SanMiguel CR. Numerical and Experimental Assessment of a Novel Anchored for Intramedullary Telescopic Nails Used in Osteogenesis Imperfecta Fractures. Applied Sciences. 2021; 11(12):5422. https://doi.org/10.3390/app11125422
Chicago/Turabian StyleAguilar-Pérez, Luis Antonio, José Israel Sánchez-Cruz, Juan Alejandro Flores-Campos, and Christopher René Torres-SanMiguel. 2021. "Numerical and Experimental Assessment of a Novel Anchored for Intramedullary Telescopic Nails Used in Osteogenesis Imperfecta Fractures" Applied Sciences 11, no. 12: 5422. https://doi.org/10.3390/app11125422
APA StyleAguilar-Pérez, L. A., Sánchez-Cruz, J. I., Flores-Campos, J. A., & Torres-SanMiguel, C. R. (2021). Numerical and Experimental Assessment of a Novel Anchored for Intramedullary Telescopic Nails Used in Osteogenesis Imperfecta Fractures. Applied Sciences, 11(12), 5422. https://doi.org/10.3390/app11125422







