Review of Convective Heat Transfer Modelling in CFD Simulations of Fire-Driven Flows
Abstract
:1. Introduction
2. Newton’s Law and CFD Equations
2.1. Newton’s Law of Cooling
- Natural or free convection: fluid motion results from heat transfer and its resulting density differences (i.e., buoyancy),
- Forced convection: flow motion produced by an external agent (e.g., fan, pump),
- Mixed convection: combination of both forced and natural convection.
- Flame spread: Under steady-state conditions, values of W/(m K) have been reported by Mitler et al. [17], in the order of – W/(m K) by Tewarson et al. [18] while an asymptotic value of W/(m K) was obtained from measurements conducted by Orloff et al. [15,16]. Finally, a value of W/(m K) (i.e., a typical value corresponding to natural convection) has been used by Quintiere [19] in his modelling of the burning behaviour of PMMA. During steady-state conditions, it has been reported that radiative heat transfer accounted for approximately 75–80% [20] (or 75–87% in [21]) of the total heat fluxes in scenarios involving upward flame spread over PMM slabs. This implies that convection is expected to contribute to approximately 15–20% in the total heat transfer.
2.2. CFD Governing Equations
- Continuity:
- Momentum:
- Chemical species:
- Sensible enthalpy:where is the density, u is the velocity, p is the pressure, is the effective dynamic viscosity, is the molecular viscosity, is the sub-grid scale viscosity, I is the identity tensor, g is the gravitational acceleration, is the species mass fraction, is the species mass diffusivity, is the turbulent Schmidt number, is the species reaction rate, is the number of chemical species (i.e., typically solving for species and obtaining from mass conservation), is the sensible energy, is the thermal diffusivity, is the turbulent Prandtl number, is the radiative heat flux, is the heat release rate per unit volume due to combustion and is the heat of combustion of the fuel.
3. Main Modelling Approaches
3.1. Experimental Correlations
3.1.1. Non-Dimensional Numbers
- Reynolds number:expressing the ratio of inertial forces to viscous forces, is typically used to characterize whether a flow is laminar or turbulent in forced convection problems. The critical Reynolds number (i.e., number above which the flow is turbulent) varies depending on the flow configuration (e.g., for flow over a plate) and can be used to calculate the critical distance, , from the leading edge of a surface, where the flow becomes turbulent.
- Grashof number:expressing the ratio of buoyancy forces to viscous forces, is typically used in natural convection problems.
- Prandtl number:expressing the ratio of molecular diffusivity of momentum to molecular diffusivity of heat across a fluid layer. The Prandtl number is used to characterize the relative thickness of the momentum and thermal boundary layers (e.g., thicker thermal boundary layer than momentum boundary layer for ).
- Nusselt number:expressing the ratio of convective to conductive heat transfer across a fluid layer. For forced convection while for natural convection .
- Rayleigh number:expressing the ratio of buoyancy and viscosity forces multiplied by the ratio of momentum and thermal diffusivities, is typically used to characterise whether a flow is laminar or turbulent in natural convection scenarios. The critical Rayleigh number varies depending on the flow configuration and can be used to calculate the critical distance, , from the leading edge of a surface, where the flow becomes turbulent.
3.1.2. Film Temperature
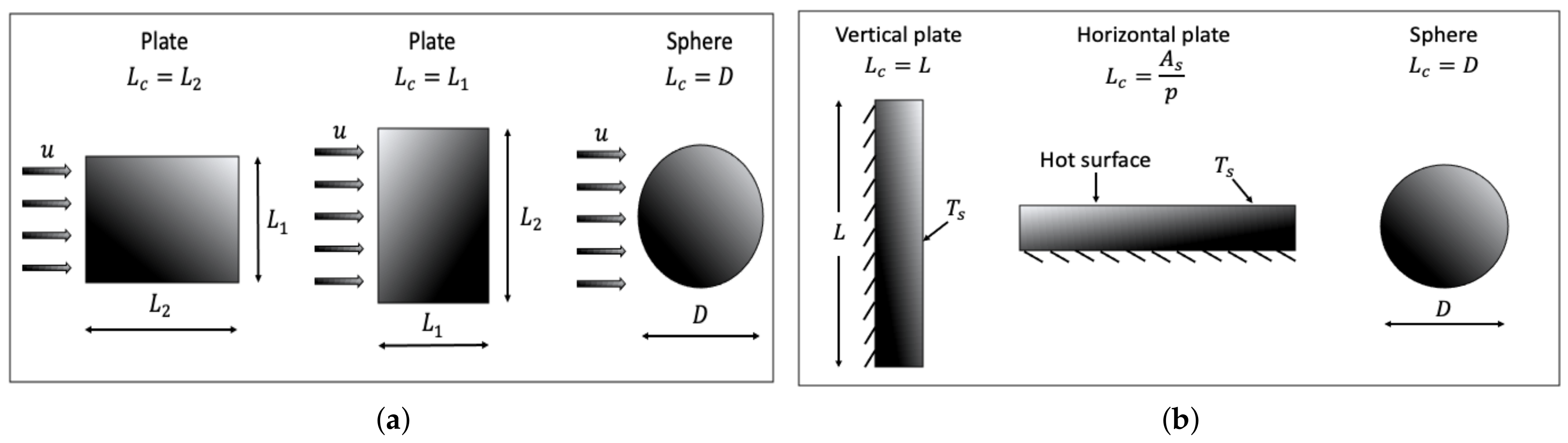
3.1.3. Characteristic Length
- Forced convection:For flow parallel to a plate: where L is the distance of the plate over which the fluid has to travel (i.e., in the direction of the flow). For flow around spheres: where D is the sphere diameter.
- Natural convection:For vertical plates: where L is the height of the plate. For horizontal plates: where and p are the surface area and perimeter of the plate, respectively. For spheres: where D is the sphere diameter.
3.1.4. Correlations
- Laminar flow: The flow is laminar over the entire surface.
- Turbulent flow: The flow is turbulent over the entire surface or when the laminar region is too small relative to the turbulent region.
- Combined flow: For cases when the surface is sufficiently long for the flow to become turbulent but not long enough to disregard the laminar region.
3.2. Law of the Wall
- Smooth wall:where is the von K rmn constant and . The viscous and inertial stresses are important in regions (i.e., called buffer layer) where . Following [48], the solution in this region is approximated by matching the viscous region and log regions at .
- Rough wall:where is the roughness length in viscous units and s is the dimensional roughness. The parameter can be estimated based on a piecewise function as:where and the parameter varies with but reaches a constant value of in the fully rough limit [46].
3.3. Wall-Resolved Approach
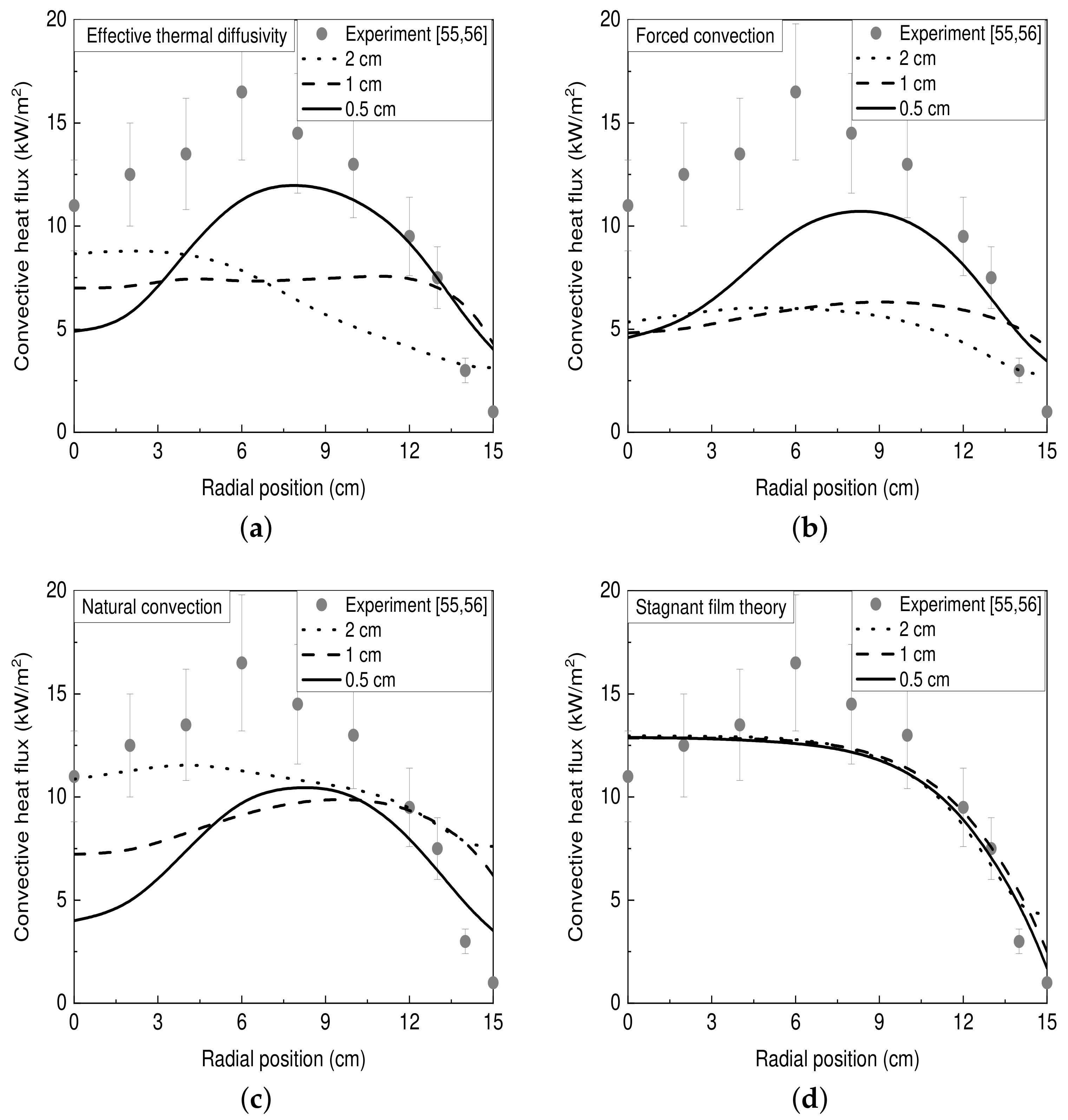
- Special case: The convective heat fluxes calculated with Equation (25) will typically start to be under-predicted with increasing grid size. To compensate for the reduction in the resolved heat fluxes, use of the effective thermal diffusivity can be made for calculating the convecting heat fluxes:where and are the effective and sub-grid scale thermal diffusivities, respectively. This approach considers sub-grid scale effects and attempts to model the convective heat transfer coefficient, h, without the explicit need of an empirical correlation through the use of a turbulence model.
4. Specific Treatment of Burning Surfaces
4.1. Convective Mass Transfer: Analogy with Convective Heat Transfer
- Natural convective burning over vertical plates [57]:withwhere is a modified Rayleigh number, is the latent heat of vaporization of the fuel, is the kinematic viscosity, is the mass fraction of the fuel, is the oxygen mass fraction in ambient air and r is the stoichiometric mass oxygen to fuel ratio.
- Forced convective burning of a flat plate [58]:where u is the flow velocity, is the kinematic viscosity of the fluid and B is the B-number of the fuel.
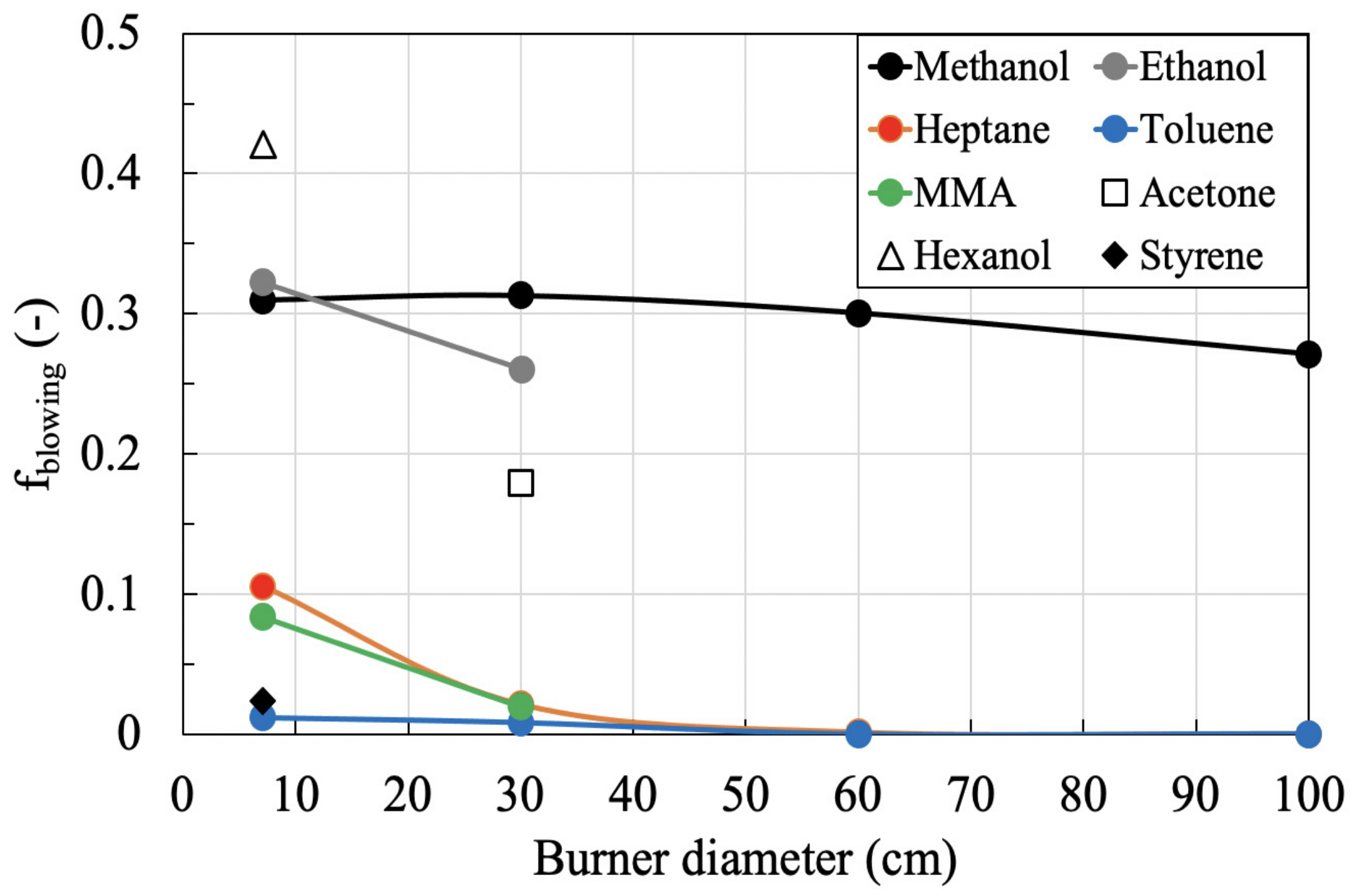
4.2. Blowing Effect
4.3. Modelling Approaches
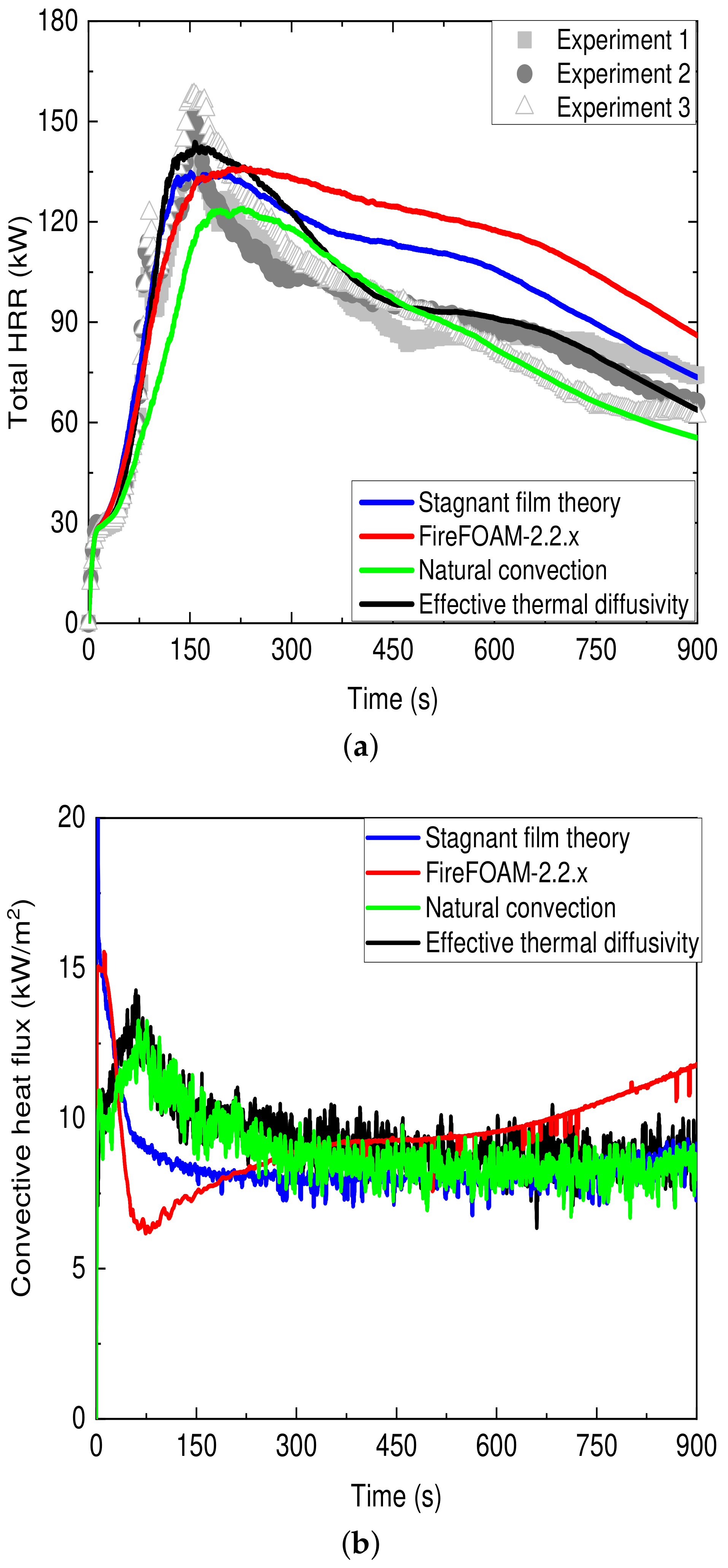
- The model is based on a 1D steady stagnant film approach and describes the gas-phase combustion process by considering known heat transfer relationships. The convective heat fluxes can be calculated as [9]:where is the combustion efficiency of the fuel, is the (global) radiative fraction, is the ambient oxygen mass fraction, is the heat of combustion per kg of consumed (i.e., approximately 13.1 MJ/kg for many hydrocarbon fuels), is the heat capacity, is the surface temperature which, in a fully developed fire, can be taken as the boiling point for a liquid or the ignition temperature for a solid, is the ambient temperature and is a correction for the ‘blowing’ effect (i.e., see Section 4.2). This expression stems from the classical B-number theory which describes liquid fuel evaporation due to convective heat transfer from nearby flames [9]. Estimation of the convection coefficients, h, can be made through the use of empirical experimental correlations based on the Nusselt number (e.g., Table 2 and Table 3). The calculation of the convective heat fluxes based on the stagnant film theory does not involve the flame temperature directly (i.e., Equation (40)) rather only indirectly through the temperature-dependent properties (e.g., convection coefficient h, heat capacity , thermal conductivity k, and Prandtl number ). For a detailed derivation of Equation (40) the reader is referred to [9]. It is interesting to note that Equation (40) can be re-written as:where is a global flame temperature calculated as:The concept of a global flame temperature is further discussed, in the context of liquid pool fires, in [42].Employing the stagnant film theory for modelling convective heat transfer has been considered in literature in the past e.g., for predicting the mass loss rates of pool fires (e.g., [16,42]), for determining the convective heat fluxes from pool fire experiments (e.g., [64]) and in numerical simulations involving liquid pool fires in mechanically ventilated compartments (e.g., [65,66]). The method based on stagnant film theory, previously shown to be both accurate and grid insensitive for pool fires [67], has had limited applicability on CFD simulations of flame spread until recently, e.g., [12] but has been employed in a global analytical model [68] for determining the convective heat feedback from the gas-phase combustion to the surface of charring materials.
- FireFOAM 2.2.x model:
- -
- If kg/(m s):
- -
- If kg/(m s):where is the mass loss rate due to pyrolysis of the solid fuel, is the convective heat flux calculated based on the molecular thermal diffusivity (positive for heating up of the wall, i.e., ), s is the direction normal to the wall, is a threshold value (e.g., in the range of kW/m [61]), is the maximum value (e.g., in the range of kW/m [61]) of the convective heat flux without mass transfer (i.e., calculated based on an average temperature difference and a convection coefficient value) and is a correction for the ‘blowing’ effect (i.e., see Section 4.2). This approach, does not directly take into account the local properties of the flow and considers that the convective heat fluxes remain relatively constant with elevation (i.e., the convective heat transfer coefficient, h, is not calculated). The first part of the wall function is employed in the early stages of flame spread when pre-heating of the virgin material occurs and there is no (substantial) burning. In this case, a linear function will assign a fraction of the a priori-determined convective heat flux in the fuel surface based on the fire intensity (i.e., determined by the resolved convective heat flux) in this area [61,62].The convective heat transfer approach used in FireFOAM 2.2.x has some deficiencies. More specifically, a constant value is employed and the convective heat fluxes only change due to mass transpiration effects, not directly accounting for local properties of the flow (i.e., in the determination of the ). Effectively, the main part of the convective heat transfer model (i.e., Equation (43)) does not explicitly consider the flame temperature for determining the convective heat transfer value, since is an a-priori determined value, rather it is only used for calculating .
4.4. Special Topic: Convective Heat Transfer within the Liquid
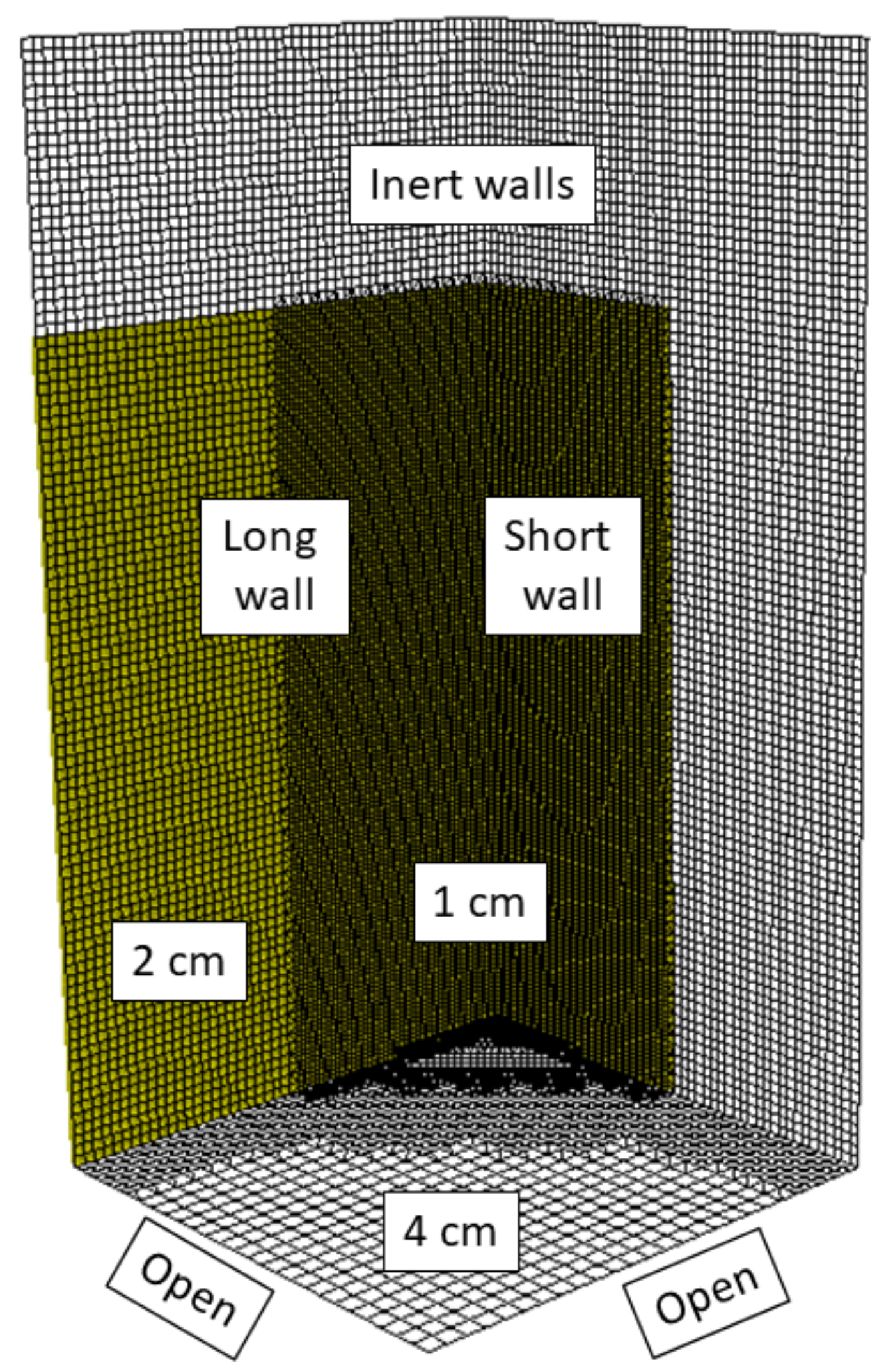
4.5. Special Topic: Influence of Grid Size
5. Applications
5.1. Pool Fires
5.2. Flame Spread
6. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Drysdale, D. An Introduction to Fire Dynamics; Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Tieszen, S.R. On the fluid mechanics of fires. Annu. Rev. Fluid Mech. 2001, 33, 67–92. [Google Scholar] [CrossRef] [Green Version]
- Joulain, P. Convective and radiative transport in pool and wall fires: 20 years of research in Poitiers. Fire Saf. J. 1996, 26, 99–149. [Google Scholar] [CrossRef]
- Joulain, P. The behavior of pool fires: State of the art and new insights. Proc. Comb. Inst. 1998, 27, 2691–2706. [Google Scholar] [CrossRef]
- Piomelli, U.; Balaras, E. Wall-layer models for large-eddy simulations. Annu. Rev. Fluid Mech. 2002, 34, 349–374. [Google Scholar] [CrossRef] [Green Version]
- Brown, A.; Bruns, M.; Gollner, M.; Hewson, J.; Maragkos, G.; Marshall, A.; McDermott, R.; Merci, B.; Rogaume, T.; Stoliarov, S.; et al. Proceedings of the first workshop organized by the IAFSS Working Group on Measurement and Computation of Fire Phenomena (MaCFP). Fire Saf. J. 2018, 101, 1–17. [Google Scholar] [CrossRef]
- Hamins, A.; Fischer, S.J.; Kashiwagi, T.; Klassen, M.E.; Gore, J.P. Heat Feedback to the Fuel Surface in Pool Fires. Combust. Sci. Technol. 1994, 97, 37–62. [Google Scholar] [CrossRef]
- Steinhaus, T.; Welch, S.; Carvel, R.O.; Torero, J.L. Large-scale pool fires. Therm. Sci. 2007, 11, 101–118. [Google Scholar] [CrossRef]
- Quintiere, J.G. Fundamentals of Fire Phenomena; Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Hu, L. A review of physics and correlations of pool fire behaviour in wind and future challenges. Fire Saf. J. 2017, 91, 41–55. [Google Scholar] [CrossRef]
- Ren, N.; Wang, Y. A Convective Heat Transfer Model for LES Fire Modeling. Proc. Comb. Inst. 2021, 38, 4535–4542. [Google Scholar] [CrossRef]
- Maragkos, G.; Zeinali, D.; Merci, B. Influence of convective heat transfer modelling in CFD simulations of upward flame spread. Fire Saf. J. 2021, 122, 103347. [Google Scholar] [CrossRef]
- Singh, A.V.; Gollner, M.J. A methodology for estimation of local heat fluxes in steady laminar boundary layer diffusion flames. Combust. Flame 2015, 162, 2214–2230. [Google Scholar] [CrossRef]
- Incropera, F.P.; DeWitt, D.P.; Bergman, T.L.; Lavine, A.S. Fundamentals of Heat and Mass Transfer, 6th ed.; John Wiley & Sons: New York, NY, USA, 2006. [Google Scholar]
- Orloff, L.; de Ris, J. Froude Modeling of Pool Fires; Technical Report No. RC81-BT-9; Factory Mutual Research: Norwood, MA, USA, 1982. [Google Scholar]
- Orloff, L.; de Ris, J. Froude Modeling of Pool Fires. Symp. Combust. 1982, 19, 885–895. [Google Scholar] [CrossRef]
- Mitler, H.E. Algorithm for the Mass-loss Rate of A Burning Wall. Fire Saf. Sci. 1989, 2, 179–188. [Google Scholar] [CrossRef] [Green Version]
- Tewarson, A. Smoke Point Height and Fire Properties of Materials; NIST-GCR-88-555; National Institute of Standards and Technology: Gaithersburg, MD, USA, 1988.
- Quintiere, J.G. A Semi-Quantitative Model for the Burning Rate of Solid Materials. Fire Saf. Sci. 1992, 1, 3–25. [Google Scholar]
- Orloff, L.; de Ris, J.; Markstein, G.H. Upward turbulent fire spread and burning of fuel surface. Symp. Combust. 1975, 15, 183–192. [Google Scholar] [CrossRef]
- Orloff, L.; Modak, A.T.; Alpert, R.L. Burning of large-scale vertical surfaces. Symp. Combust. 1977, 16, 1345–1354. [Google Scholar] [CrossRef]
- FireFOAM Code Website. Available online: https://github.com/fireFoam-dev (accessed on 14 March 2021).
- Fire Dynamics Simulator (FDS) Code. Available online: https://pages.nist.gov/fds-smv/ (accessed on 14 March 2021).
- Maragkos, G.; Beji, T.; Merci, B. Advances in modelling in CFD simulations of turbulent gaseous pool fires. Combust. Flame 2017, 181, 22–38. [Google Scholar] [CrossRef]
- Maragkos, G.; Beji, T.; Merci, B. Towards predictive simulations of gaseous pool fires. Proc. Comb. Inst. 2019, 37, 3927–3934. [Google Scholar] [CrossRef]
- Maragkos, G.; Merci, B. On the use of dynamic turbulence modelling in fire applications. Combust. Flame 2020, 26, 9–23. [Google Scholar] [CrossRef]
- Smagorinsky, J. General Circulation Experiments with the Primitive Equations. I. The Basic Experiment. Mon. Weather Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- Moin, P.; Squires, K.; Cabot, W.H.; Lee, S. A dynamic subgrid-scale model for compressible turbulence and scalar transport. Phys. Fluids A 1991, 3, 2746–2757. [Google Scholar] [CrossRef]
- Deardorff, J.W. Stratocumulus-capped mixed layers derived from a three-dimensional model. Bound. Layer Meteorol. 1980, 18, 495–527. [Google Scholar] [CrossRef]
- Magnussen, B.F.; Hjertager, B.H. On mathematical modeling of turbulent combustion with special emphasis on soot formation and combustion. Proc. Comb. Inst. 1977, 16, 719–729. [Google Scholar] [CrossRef]
- Modest, M.F. The Weighted-Sum-of-Gray-Gases Model for Arbitrary Solution Methods in Radiative Transfer. J. Heat Transf. 1991, 113, 650–656. [Google Scholar] [CrossRef]
- McAdams, W.H. Heat Transmission; McGraw-Hill Book Company: New York, NY, USA, 1957. [Google Scholar]
- Welty, J.; Rorrer, G.L.; Foster, D.G. Fundamentals of Momentum, Heat and Mass Transfer; John Wiley & Sons: New York, NY, USA, 2014. [Google Scholar]
- Holman, J.P. Heat Transfer, 10th ed.; McGraw-Hill: New York, NY, USA, 2010. [Google Scholar]
- Ranz, W.E.; Marshall, W.R. Evaporation from Drops. Chem. Eng. Prog. 1952, 48, 141–146. [Google Scholar]
- Churchill, S.W.; Chu, H.H.S. Correlating Equations for Laminar and Turbulent Free Convection from a Vertical Plate. Int. J. Heat Mass Transf. 1975, 18, 1323–1329. [Google Scholar] [CrossRef]
- Churchill, S.W. Free Convection around Immersed Bodies. In Heat Exchanger Design Handbook; Hemisphere Publishing: New York, NY, USA, 1983. [Google Scholar]
- Chen, Q.; Zhai, Z. The use of CFD tools for indoor environmental design. In Advanced Building Simulation; Spon Press: New York, NY, USA, 2004; pp. 119–140. [Google Scholar]
- Petrik, M.; Erdos, A.; Jarmai, K.; Szepesi, G. Optimum design of an air tank for fatigue and fire load. Acta Polytech. Hung. 2021, 18, 163–177. [Google Scholar] [CrossRef]
- Zhai, Z.; Chen, Q.Y. Numerical determination and treatment of convective heat transfer coefficient in the coupled building energy and CFD simulation. Build. Environ. 2004, 39, 1001–1009. [Google Scholar] [CrossRef]
- Beji, T.; Merci, B. Development of a numerical model for liquid pool evaporation. Fire Saf. J. 2018, 102, 48–58. [Google Scholar] [CrossRef]
- Hamins, A.P.; Yang, J.C.; Kashiwagi, T. Global Model for Predicting the Burning Rates of Liquid Pool Fires; NIST Interagency/Internal Report (NISTIR)-6381; National Institute of Standards and Technology: Gaithersburg, MD, USA, 1999.
- Sikanen, T.; Hostikka, S. Modelling and simulation of liquid pool fires with in-depth and heat transfer. Fire Saf. J. 2016, 80, 95–109. [Google Scholar] [CrossRef]
- Markus, E.; Snegirev, A.; Kuznetsov, E.; Tanklevskiy, L. Application of the thermal pyrolysis model to predict flame spread over continuous and discrete fire load. Fire Saf. J. 2019, 108, 102825. [Google Scholar] [CrossRef]
- Launder, B.E.; Spalding, D.B. The Numerical Computation of Turbulent Flows. Comput. Methods Appl. Mech. Eng. 1974, 3, 269–289. [Google Scholar] [CrossRef]
- McGrattan, K.; Hostikka, S.; Floyd, J.; McDermott, R.; Vanella, M. Fire Dynamics Simulator Technical Reference Guide Volume 1: Mathematical Model, 6th ed.; NIST Special Publication 1018-1; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2020.
- Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Werner, H.; Wengle, H. Large-eddy simulation of turbulent flow over and around a cube in a plate channel. In Proceedings of the 8th Symposium on Turbulent Shear Flows, Munich, Germany, 9–11 September 1991; pp. 155–168. [Google Scholar]
- Kader, B.A. Temperature and concentration profiles in fully turbulent boundary layers. Int. J. Heat Mass Transf. 1981, 24, 1541–1544. [Google Scholar] [CrossRef]
- Yan, Z.; Holmstedt, G. CFD Simulation of Upward Flame Spread over Fuel Surface. Fire Saf. Sci. 1997, 5, 345–356. [Google Scholar] [CrossRef] [Green Version]
- Ren, N.; Wang, Y.; Vilfayeau, S.; Trouvé, A. Large Eddy Simulation of Propylene Turbulent Vertical Wall Fires. In Proceedings of the Seventh International Seminar on Fire and Explosion Hazards, Providence, RI, USA, 5–10 May 2013. [Google Scholar]
- Ren, N.; Wang, Y.; Trouvé, A. Large Eddy Simulation of Vertical Turbulent Wall Fires. Procedia Eng. 2013, 33, 443–452. [Google Scholar] [CrossRef] [Green Version]
- Fukumoto, K.; Wang, C.; Wen, J. Large eddy simulation of upward flame spread on PMMA walls with a fully coupled fluid–solid approach. Combust. Flame 2018, 190, 365–387. [Google Scholar] [CrossRef] [Green Version]
- Ren, N.; Wang, Y.; Vilfayeau, S.; Trouvé, A. Large eddy simulation of turbulent vertical wall fires supplied with gaseous fuel through porous burners. Combust. Flame 2016, 169, 194–208. [Google Scholar] [CrossRef]
- Li, K.; Hostikka, S. Embedded flame heat flux method for simulation of quasi-steady state vertical flame spread. Fire Saf. J. 2019, 104, 117–129. [Google Scholar] [CrossRef] [Green Version]
- McDermott, R.J. Quality assessment in the fire dynamics simulator: A bridge to reliable simulations. In Proceedings of the Fire and Evacuation Modeling Technical Conference, Baltimore, MD, USA, 15–16 August 2011. [Google Scholar]
- Ahmad, T.; Faeth, G.M. Turbulent wall fires. Proc. Comb. Inst. 1979, 17, 1149–1160. [Google Scholar] [CrossRef]
- Glassman, I. Combustion; Academic Press: New York, NY, USA, 1977. [Google Scholar]
- Klassen, M.; Gore, J.P. Structure and Radiation Properties of Pool Fires; NIST GCR 94-651; National Institute of Standards and Technology: Gaithersburg, MD, USA, 1994.
- Kim, S.C.; Lee, K.Y.; Hamins, A. Energy Balance in Medium-Scale Methanol, Ethanol, and Acetone Pool Fires. Fire Saf. Sci. 2019, 107, 44–53. [Google Scholar]
- Zeinali, D.; Gupta, A.; Maragkos, G.; Agarwal, G.; Beji, T.; Chaos, M.; Wang, Y.; Degroote, J.; Merci, B. Study of the importance of non-uniform mass density in numerical simulations of fire spread over MDF panels in a corner configuration. Combust. Flame 2019, 200, 303–315. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Meredith, K.V.; Zhou, X.; Chatterjee, P.; Xin, Y.; Chaos, M.; Ren, N.; Dorofeev, S.B. Numerical Simulation of Sprinkler Suppression of Rack Storage Fires. Fire Saf. Sci. 2014, 11, 1170–1183. [Google Scholar] [CrossRef]
- Ren, N.; de Vries, J.; Zhou, X.; Chaos, M.; Meredith, K.V.; Wang, Y. Large-scale fire suppression modeling of corrugated cardboard boxes on wood pallets in rack-storage configurations. Fire Saf. J. 2017, 91, 695–704. [Google Scholar] [CrossRef]
- Hamins, A. Energetics of Small and Moderate-Scale Gaseous Pool Fires; NIST Technical Note 1926; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2016.
- Nasr, A.; Suard, S.; El-Rabii, H.; Gay, J.; Garo, J.-P. Fuel Mass-Loss Rate Determination in a Confined and Mechanically Ventilated Compartment Fire Using a Global Approach. Combust Sci. Technol. 2011, 183, 1342–1359. [Google Scholar] [CrossRef]
- Suard, S.; Nasr, A.; Melis, S.; Garo, J.P.; El-Rabii, H.; Gay, L.; Rigollet, L.; Audouin, L. Analytical Approach for Predicting Effects of Vitiated Air on the Mass Loss Rate of Large Pool Fire in Confined Compartments. Fire Saf. Sci. 2011, 10, 1513–1524. [Google Scholar] [CrossRef]
- Maragkos, G.; Merci, B. Grid insensitive modelling of convective heat transfer fluxes in CFD simulations of medium-scale pool fires. Fire Saf. J. 2020, 120, 103104. [Google Scholar] [CrossRef]
- Ritchie, S.J.; Steckler, K.D.; Hamins, A.; Cleary, T.G.; Yang, J.C.; Kashiwagi, T. The Effect of Sample Size on the Heat Release Rate of Charring Materials. Fire Saf. Sci. 1997, 5, 177–188. [Google Scholar] [CrossRef]
- Fukumoto, K.; Wen, J.X.; Li, M.; Yanming, D.; Changjian, W. Numerical simulation of small pool fires incorporating liquid fuel motion. Combust. Flame 2020, 213, 441–454. [Google Scholar] [CrossRef]
- Xu, B.; Wen, J. The effect of convective motion within liquid fuel on the mass burning rates of pool fires—A numerical study. Proc. Comb. Inst. 2021, 38, 4979–4986. [Google Scholar] [CrossRef]
- Vali, A.; Nobes, D.S.; Kostiuk, L.W. Fluid motion and energy transfer within burning liquid fuel pools of various thicknesses. Combust. Flame 2015, 162, 1447–1488. [Google Scholar] [CrossRef]
- Beji, T. Theoretical analysis of the liquid thermal structure in a pool fire. J. Fire Sci. 2021, 39, 36–52. [Google Scholar] [CrossRef]
- Ahmed, M.M.; Trouvé, A. Large eddy simulation of the unstable flame structure and gas-to-liquid thermal feedback in a medium-scale methanol pool fire. Combust. Flame 2021, 225, 237–254. [Google Scholar] [CrossRef]
- Zeinali, D.; Verstockt, S.; Beji, T.; Maragkos, G.; Degroote, J.; Merci, B. Experimental study of corner fires: Part II: Flame spread over MDF panels. Combust. Flame 2018, 189, 491–505. [Google Scholar] [CrossRef]
- Zeinali, D. Flame Spread and Fire Behavior in a Corner Configuration. Ph.D. Thesis, Ghent University, Ghent, Belgium, 2019. [Google Scholar]
- Sung, K.; Chen, J.; Bundy, M.; Hamins, A. The characteristics of a 1 m methanol pool fire. Fire Saf. Sci. 2021, 120, 103121. [Google Scholar] [CrossRef]

| Application | h |
|---|---|
| (W/(m K)) | |
| Natural convection | |
| Gases | 2–25 |
| Liquids | 100–1000 |
| Forced convection | |
| Gases | 25–250 |
| Liquids | 50–20,000 |
| Geometry | Range of Validity | ||
|---|---|---|---|
| Parallel to a plate | |||
| Laminar flow | L | [33] | |
| Turbulent flow | L | [33] | |
| Combined flow | L | [33] | |
| Around a sphere | D | [35] | |
| Geometry | Range of Validity | ||
|---|---|---|---|
| Vertical plate | |||
| Laminar flow | L | [32] | |
| Turbulent flow | L | [32] | |
| Any type of flow | L | [36] | |
| Horizontal plate | |||
| Laminar flow | [32] | ||
| Turbulent flow | [32] | ||
| Sphere | D | Ra | [37] |
| Geometry | Range of Validity | h | |
|---|---|---|---|
| Vertical plate | |||
| Laminar flow | L | ||
| Turbulent flow | - | ||
| Horizontal plate | |||
| Laminar flow | |||
| Turbulent flow | - |
| Geometry | Range of Validity | Sh | |
|---|---|---|---|
| Parallel to a plate | |||
| Laminar flow | L | [33] | |
| Turbulent flow | L | [33] | |
| Combined flow | L | [33] | |
| Around a sphere | D | [35] | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maragkos, G.; Beji, T. Review of Convective Heat Transfer Modelling in CFD Simulations of Fire-Driven Flows. Appl. Sci. 2021, 11, 5240. https://doi.org/10.3390/app11115240
Maragkos G, Beji T. Review of Convective Heat Transfer Modelling in CFD Simulations of Fire-Driven Flows. Applied Sciences. 2021; 11(11):5240. https://doi.org/10.3390/app11115240
Chicago/Turabian StyleMaragkos, Georgios, and Tarek Beji. 2021. "Review of Convective Heat Transfer Modelling in CFD Simulations of Fire-Driven Flows" Applied Sciences 11, no. 11: 5240. https://doi.org/10.3390/app11115240
APA StyleMaragkos, G., & Beji, T. (2021). Review of Convective Heat Transfer Modelling in CFD Simulations of Fire-Driven Flows. Applied Sciences, 11(11), 5240. https://doi.org/10.3390/app11115240






