Three-Dimensional Reconstruction-Based Vibration Measurement of Bridge Model Using UAVs
Abstract
:1. Introduction
2. Methods
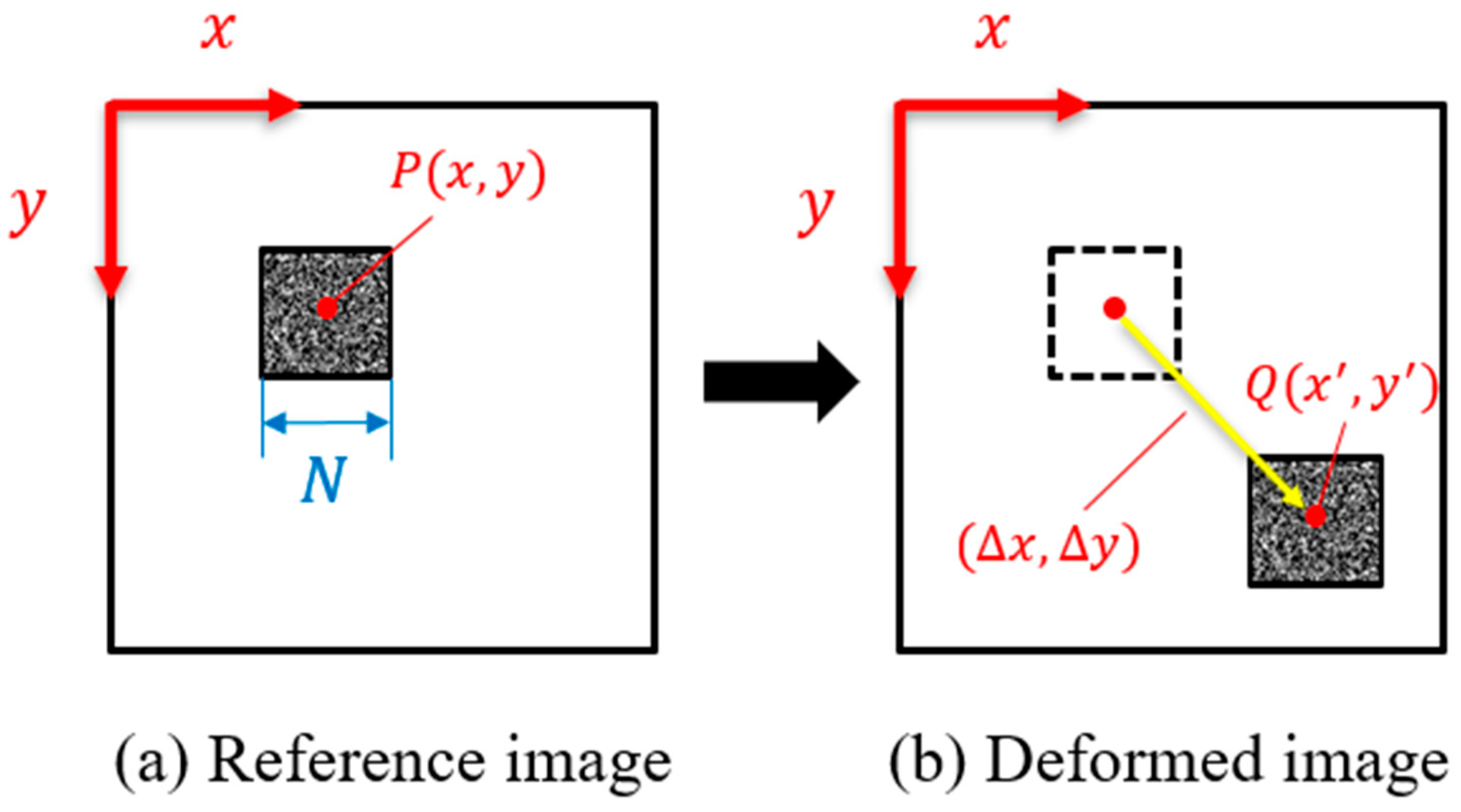
2.1. Displacement Tracked by DIC
2.2. Homography Transformation Method
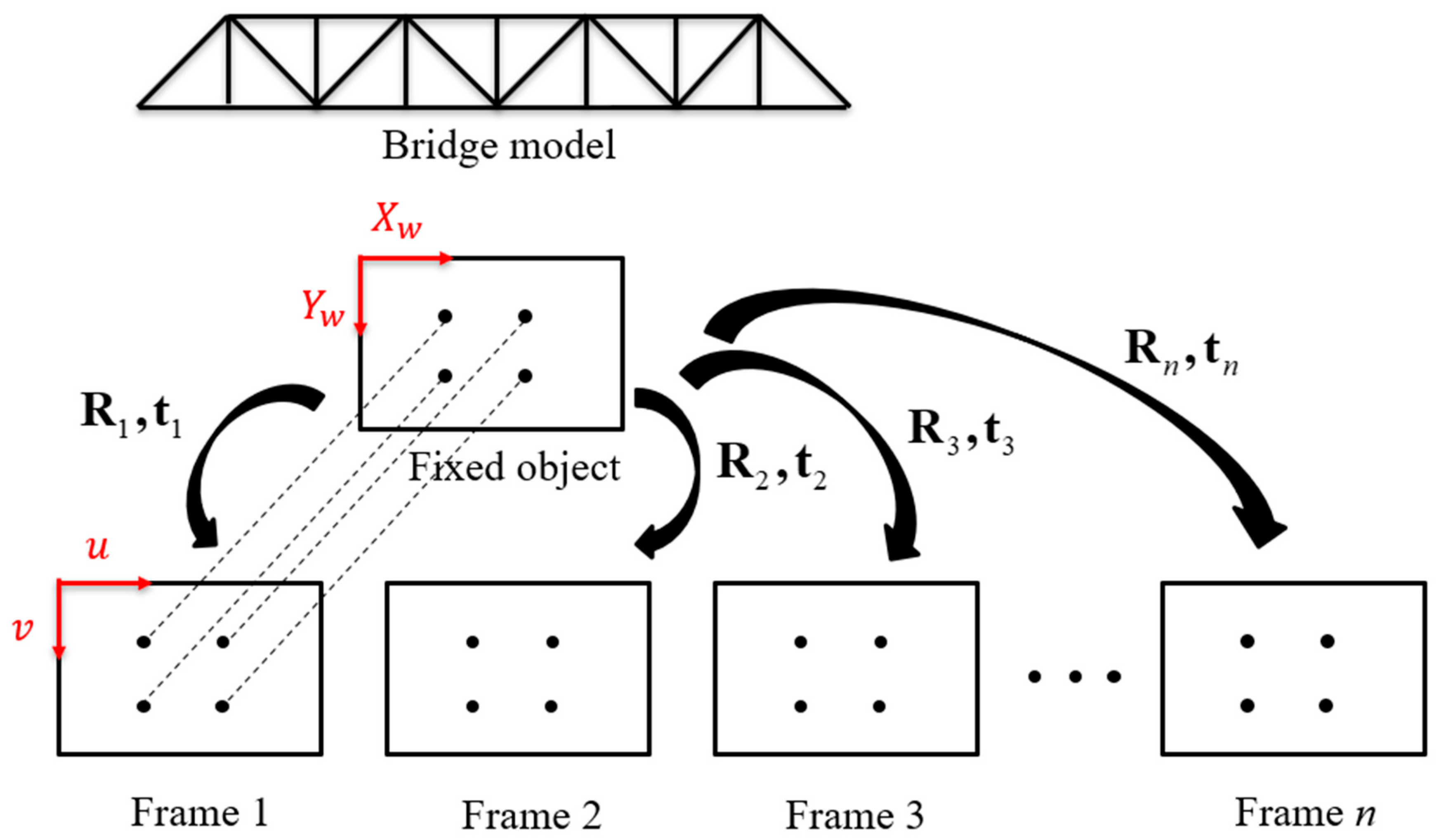
2.3. Three-Dimensional Reconstruction Method
2.3.1. Camera Calibration
2.3.2. Recovering the 3D Coordinates
2.4. Operational Modal Analysis (OMA)
3. Experiments
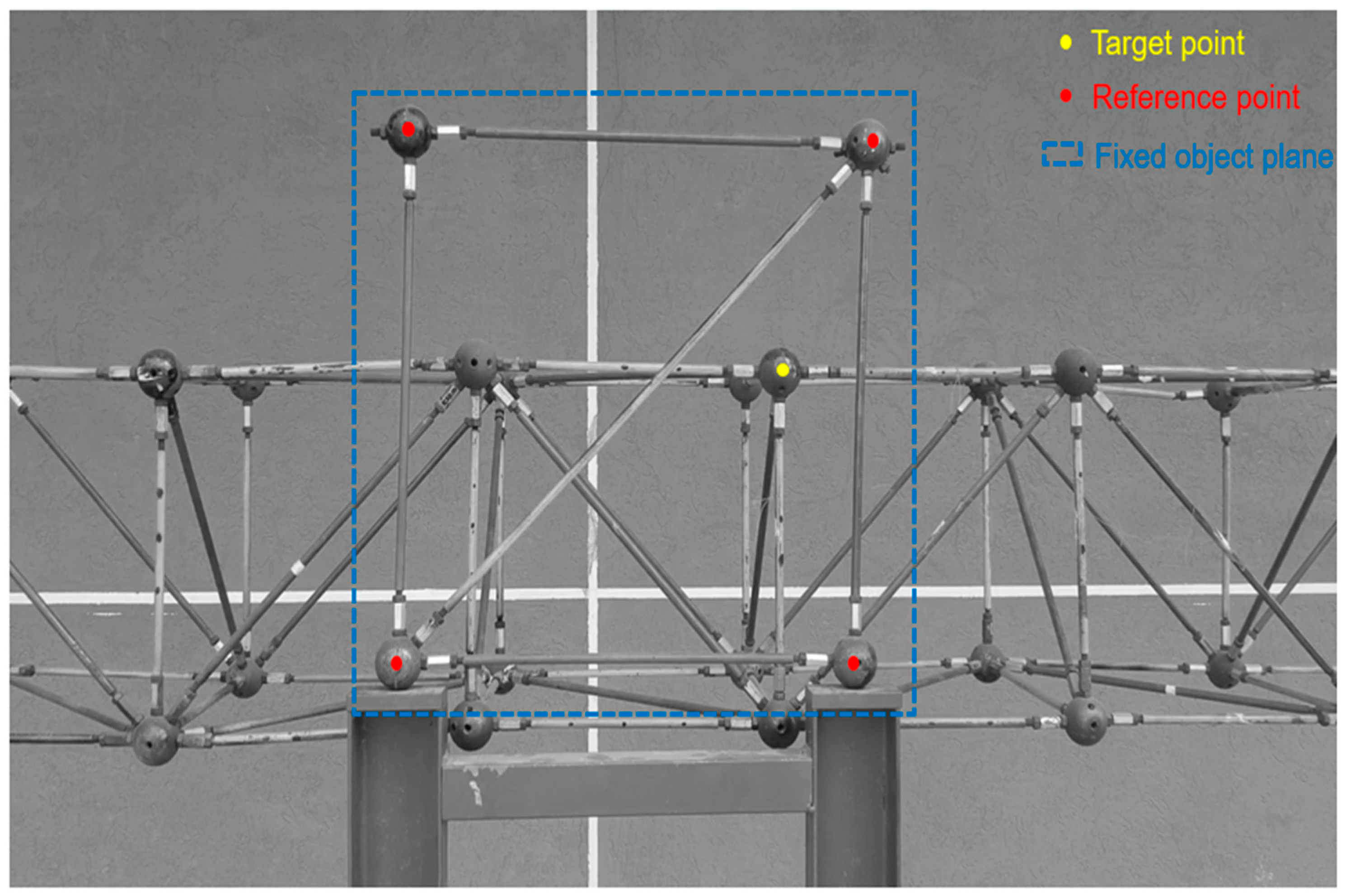
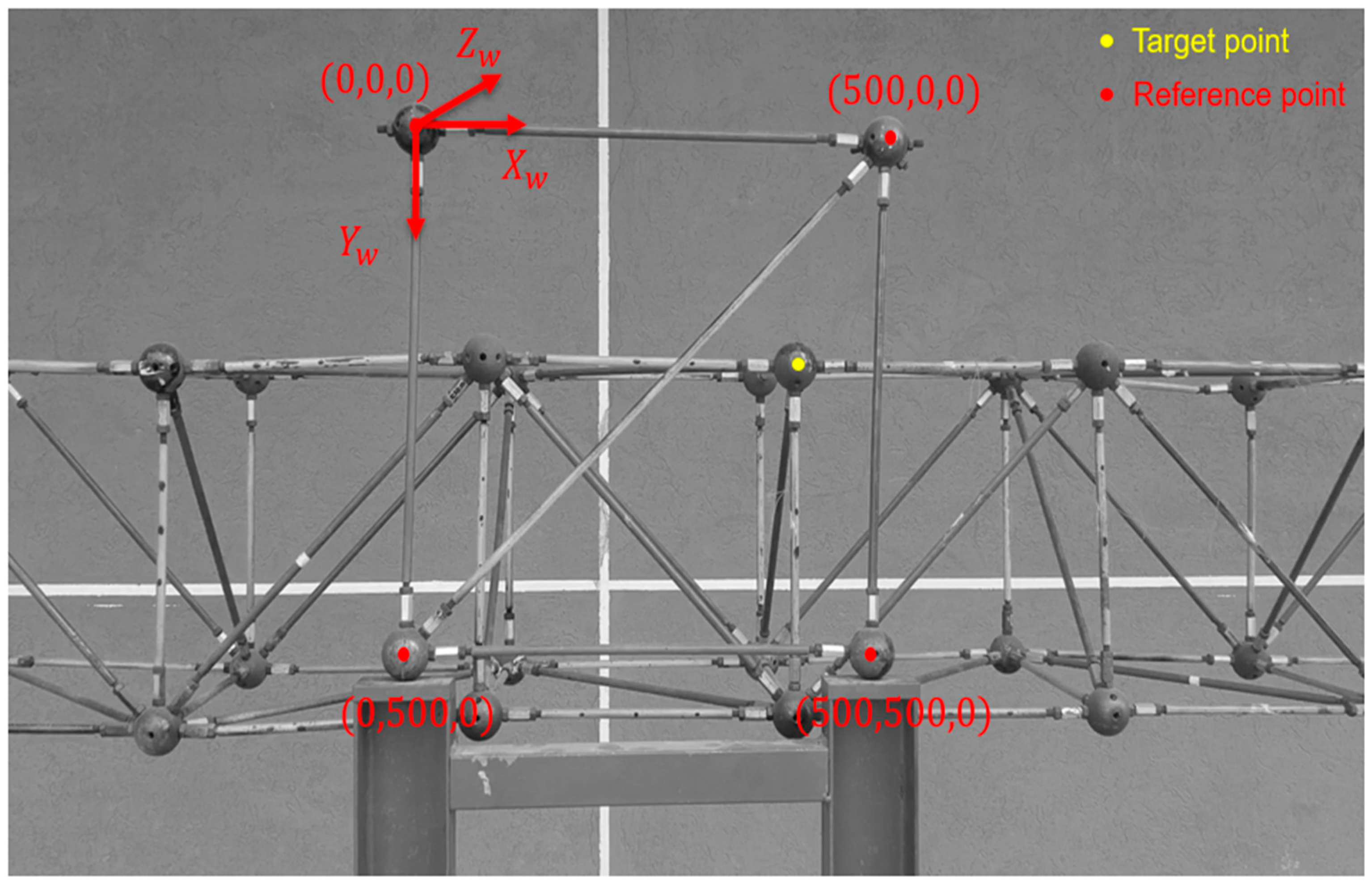
3.1. Experimental Setups
3.2. Experimental Schemes
4. Results
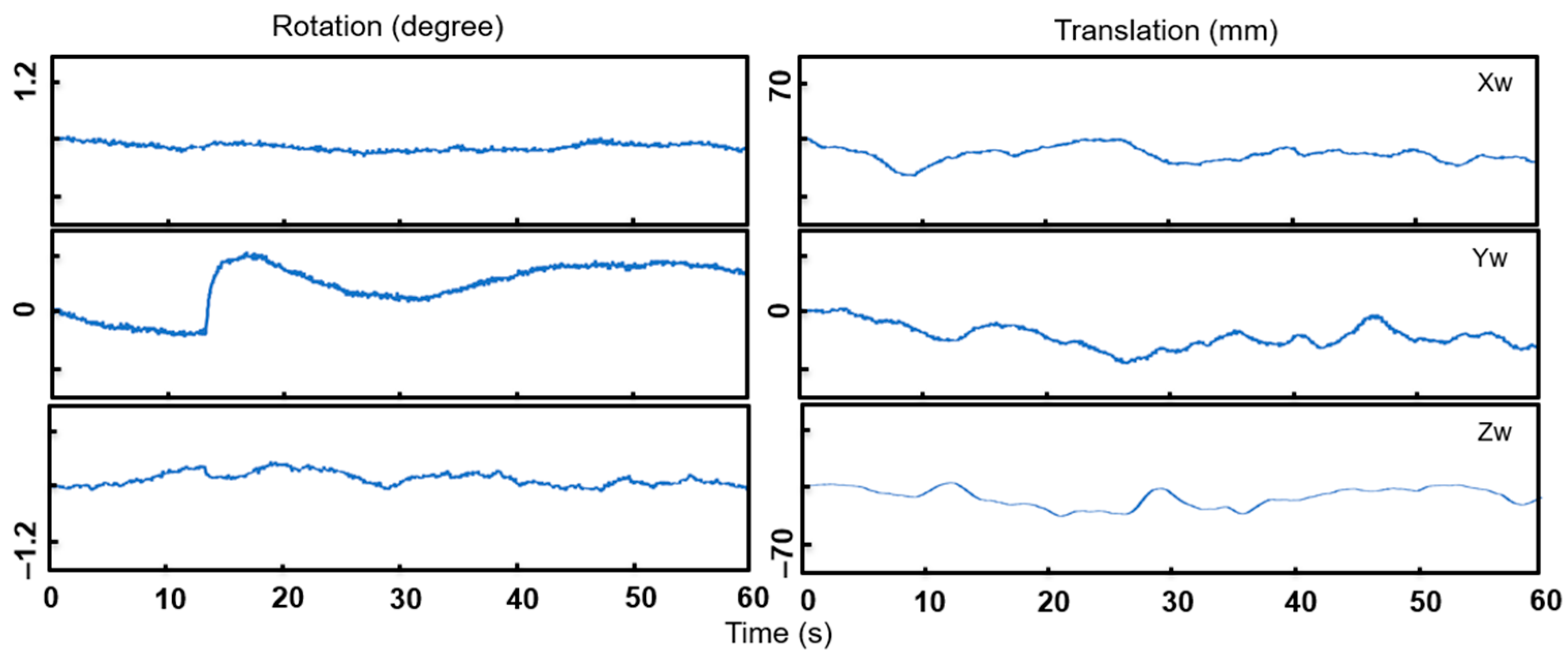
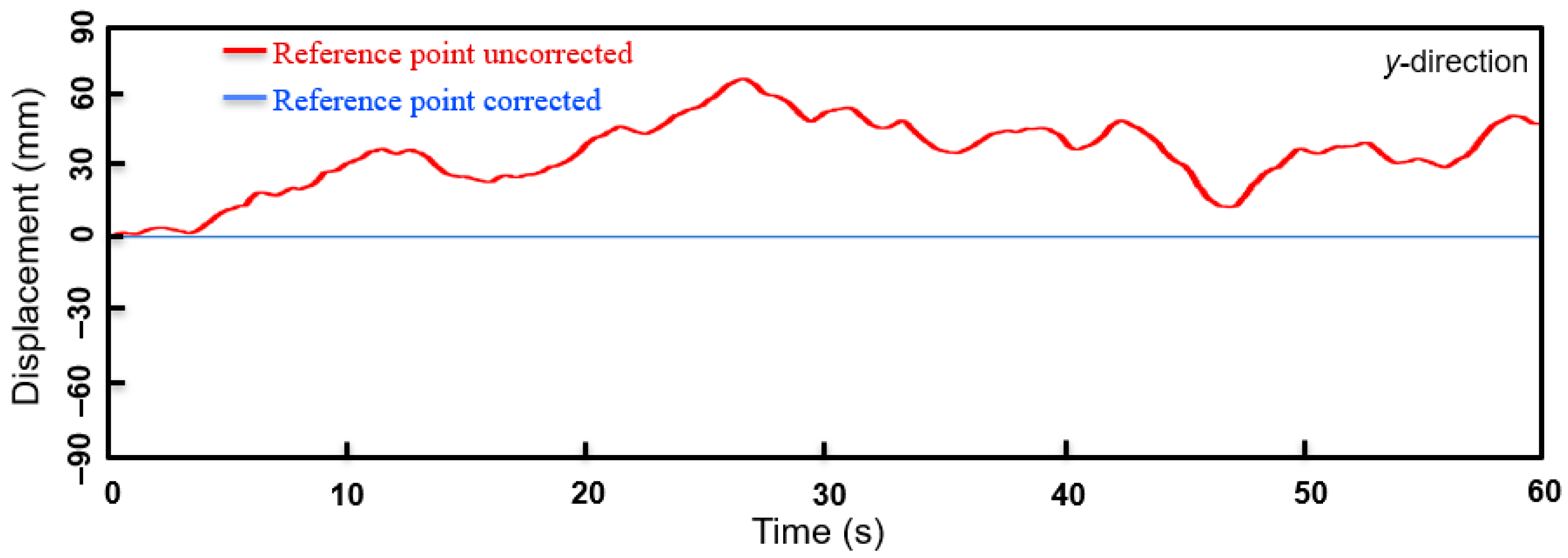
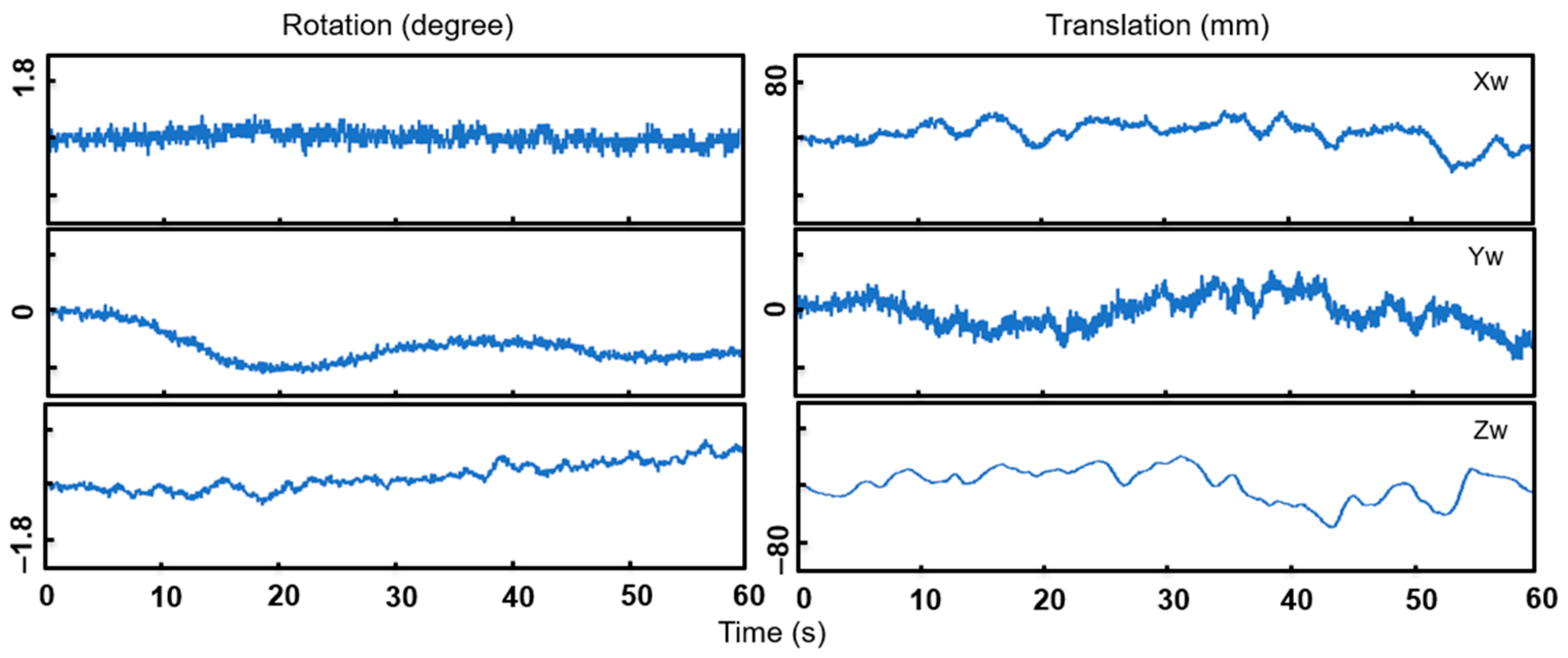
4.1. Correction through 3D Reconstruction
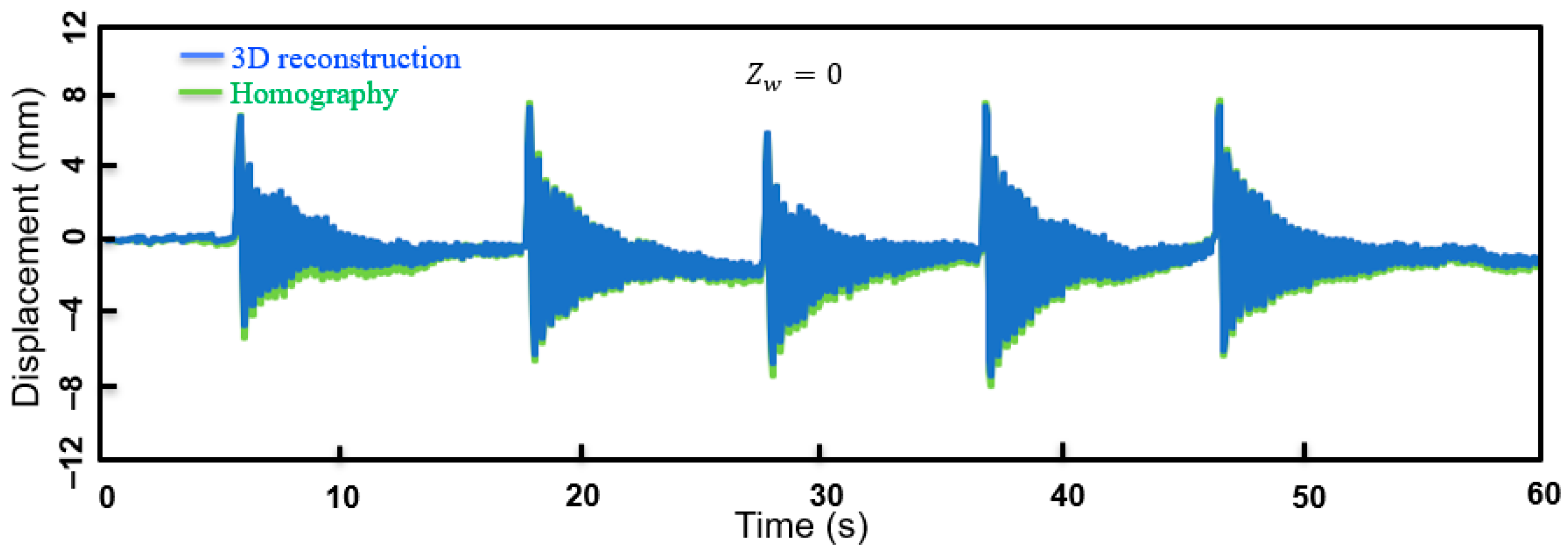
4.2. Comparison of Homography Transformation and 3D Reconstruction
5. Discussion and Conclusions
5.1. Discussion
- For the monocular camera, the value of is assumed to be constant, that is, the out-of-plane displacement (-direction) is ignored. In some structures with mainly in-plane displacement, the small change of can be ignored. Nevertheless, there will be an obvious error for the structures with large out-of-plane displacement if the change of is ignored. The structure-from-motion (SFM) technique can restore a bridge’s 3D model coordinates [31], including the Zw-direction, by processing high-resolution stereo-photogrammetric photos; it has been used for slow deformation monitoring. An image splitter system, which consisted of four fixed mirrors, is used to mimic four different views by using a single camera with a 45-degree horizontal angle with respect to the target [43]. However, it needs a large splitter and mirror to measure large bridges from a sufficient distance. Using two UAVs combined with a binocular vision principle to measure three-dimensional displacement needs further investigation.
- The experiment is carried out in a laboratory environment. Its conditions, including light, weather, reference points, etc. are in the ideal state. It is, however, inevitable that some negative factors may occur in the real bridge measurement, for example, difficulty in finding fixed reference objects. An artificial fixed object needs to be deployed under this situation. It is expected that this method can be realized in the real bridge measurement in the near future.
- In the current algorithm, the theory of planar homography is used to calculate the camera extrinsic matrix R and t. Hence, the four fixed reference points must be on the same plane with fixed-Zw. However, in some measurement circumstances, it is hard to guarantee that all four points are coplanar. Whether or not the reference points can be on different planes needs further study.
5.2. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhu, Y.; Ni, Y.-Q.; Jin, H.; Inaudi, D.; Laory, I. A temperature-driven MPCA method for structural anomaly detection. Eng. Struct. 2019, 190, 447–458. [Google Scholar] [CrossRef]
- Xu, X.; Ren, Y.; Huang, Q.; Fan, Z.Y.; Tong, Z.J.; Chang, W.J.; Liu, B. Anomaly detection for large span bridges during operational phase using structural health monitoring data. Smart Mater. Struct. 2020, 29, 045029. [Google Scholar] [CrossRef]
- Magalhães, F.; Cunha, Á.; Caetano, E. Vibration based structural health monitoring of an arch bridge: From automated OMA to damage detection. Mech. Syst Signal Process. 2012, 28, 212–228. [Google Scholar] [CrossRef]
- Fukuda, Y.; Feng, M.; Narita, Y.; Kaneko, S.; Tanaka, T. Vision-based displacement sensor for monitoring dynamic response using robust object search algorithm. IEEE Sens. 2010, 13, 1928–1931. [Google Scholar] [CrossRef] [Green Version]
- Xiong, C.; Lu, H.; Zhu, J. Operational Modal Analysis of Bridge Structures with Data from GNSS/Accelerometer Measurements. Sensors 2017, 17, 436. [Google Scholar] [CrossRef] [Green Version]
- Li, L.; Ohkubo, T.; Matsumoto, S. Vibration measurement of a steel building with viscoelastic dampers using acceleration sensors. Measurement 2020, 171, 108807. [Google Scholar] [CrossRef]
- Kovačič, B.; Kamnik, R.; Štrukelj, A.; Vatin, N. Processing of Signals Produced by Strain Gauges in Testing Measurements of the Bridges. Procedia Eng. 2015, 117, 795–801. [Google Scholar] [CrossRef] [Green Version]
- Pan, B.; Qian, K.; Xie, H.; Asundi, A. TOPICAL REVIEW: Two-dimensional digital image correlation for in-plane displacement and strain measurement: A review. Meas. Sci. Technol. 2009, 20, 152–154. [Google Scholar] [CrossRef]
- Psimoulis, P.; Pytharouli, S.; Karambalis, D.; Stiros, S. Potential of Global Positioning System (GPS) to measure frequencies of oscillations of engineering structures. J. Sound Vib. 2008, 318, 606–623. [Google Scholar] [CrossRef]
- Siringoringo, D.M.; Fujino, Y. Noncontact Operational Modal Analysis of Structural Members by Laser Doppler Vibrometer. Comput. Civ. Infrastruct. Eng. 2009, 24, 249–265. [Google Scholar] [CrossRef]
- Yi, T.-H.; Li, H.-N.; Gu, M. Experimental assessment of high-rate GPS receivers for deformation monitoring of bridge. Meas. 2013, 46, 420–432. [Google Scholar] [CrossRef]
- Reu, P.L.; Rohe, D.P.; Jacobs, L.D. Comparison of DIC and LDV for practical vibration and modal measurements. Mech. Syst. Signal Process. 2017, 86, 2–16. [Google Scholar] [CrossRef] [Green Version]
- Nassif, H.H.; Gindy, M.; Davis, J. Comparison of laser Doppler vibrometer with contact sensors for monitoring bridge deflection and vibration. NDT E Int. 2005, 38, 213–218. [Google Scholar] [CrossRef]
- Hyungchul, Y.; Hazem, E.; Hajin, C.; Mani, G.-F.; Spencer, B.F. Target-free approach for vision-based structural system identification using consumer-grade cameras. Struct. Control Health Monit. 2016, 23, 1405–1416. [Google Scholar] [CrossRef]
- Lydon, D.; Lydon, M.; Taylor, S.; Del Rincon, J.M.; Hester, D.; Brownjohn, J. Development and field testing of a vision-based displacement system using a low cost wireless action camera. Mech. Syst. Signal Process. 2019, 121, 343–358. [Google Scholar] [CrossRef] [Green Version]
- Xu, Y.; Brownjohn, J.M.W. Review of machine-vision based methodologies for displacement measurement in civil structures. J. Civ. Struct. Health Monit. 2018, 8, 91–110. [Google Scholar] [CrossRef] [Green Version]
- Vincenzo, F.; Ivan, R.; Angelo, T.; Roberto, R.; Gerardo, D.C. Motion Magnification Analysis for Structural Monitoring of Ancient Constructions. Measurement 2018, 129, 375–380. [Google Scholar] [CrossRef]
- Yoneyama, S. Basic principle of digital image correlation for in-plane displacement and strain measurement. Adv. Compos. Mater. 2016, 25, 105–123. [Google Scholar] [CrossRef]
- Chu, T.C.; Ranson, W.F.; Sutton, M.A. Applications of digital-image-correlation techniques to experimental mechanics. Exp. Mech. 1985, 25, 232–244. [Google Scholar] [CrossRef]
- Schreier, H.; Orteu, J.-J.; Sutton, M.A. Image Correlation for Shape, Motion and Deformation Measurements: Basic Concepts, Theory and Applications; Springer: New York, NY, USA, 2009. [Google Scholar] [CrossRef]
- Sousa, P.J.; Barros, F.; Lobo, P.; Tavares, P.; Moreira, P.M. Experimental measurement of bridge deflection using Digital Image Correlation. Procedia Struct. Integr. 2019, 17, 806–811. [Google Scholar] [CrossRef]
- Murray, C.; Hoag, A.; Hoult, N.A.; Take, W.A. Field monitoring of a bridge using digital image correlation. Proc. Inst. Civ. Eng. Bridg. Eng. 2015, 168, 3–12. [Google Scholar] [CrossRef]
- Busca, G.; Cigada, A.; Mazzoleni, P.; Zappa, E. Vibration Monitoring of Multiple Bridge Points by Means of a Unique Vision-Based Measuring System. Exp. Mech. 2014, 54, 255–271. [Google Scholar] [CrossRef]
- Dong, C.-Z.; Celik, O.; Catbas, F.N.; Obrien, E.; Taylor, S. A Robust Vision-Based Method for Displacement Measurement under Adverse Environmental Factors Using Spatio-Temporal Context Learning and Taylor Approximation. Sensors 2019, 19, 3197. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Reagan, D.; Sabato, A.; Niezrecki, C. Feasibility of using digital image correlation for unmanned aerial vehicle structural health monitoring of bridges. Struct. Heal. Monit. 2018, 17, 1056–1072. [Google Scholar] [CrossRef]
- Hoskere, V.; Park, J.W.; Yoon, H.; Spencer, B.F., Jr. Vision-Based Modal Survey of Civil Infrastructure Using Unmanned Aerial Vehicles. J. Struct. Eng. 2019, 145, 04019062. [Google Scholar] [CrossRef]
- Ellenberg, A.; Kontsos, A.; Moon, F.; Bartoli, I. Bridge related damage quantification using unmanned aerial vehicle imagery. Struct. Control. Health Monit. 2016, 23, 1168–1179. [Google Scholar] [CrossRef]
- Kim, H.; Lee, J.; Ahn, E.; Cho, S.; Shin, M.; Sim, S.H. Concrete Crack Identification Using a UAV Incorporating Hybrid Image Processing. Sensors 2017, 17, 2052. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zink, J.; Lovelace, B. Unmanned Aerial Vehicle Bridge Inspection Demonstration Project. 2015. Available online: https://trid.trb.org/view/1410491 (accessed on 7 June 2016).
- Yoon, H.; Shin, J.; Spencer, B.F. Structural Displacement Measurement Using an Unmanned Aerial System. Comput. Civ. Infrastruct. Eng. 2018, 33, 183–192. [Google Scholar] [CrossRef]
- Roselli, I.; Malena, M.; Mongelli, M.; Cavalagli, N.; Gioffrè, M.; De Canio, G.; De Felice, G. Health assessment and ambient vibration testing of the “Ponte delle Torri” of Spoleto during the 2016–2017 Central Italy seismic sequence. J. Civ. Struct. Heal. Monit. 2018, 8, 199–216. [Google Scholar] [CrossRef]
- Chen, G.; Liang, Q.; Zhong, W.; Gao, X.; Cui, F. Homography-based measurement of bridge vibration using UAV and DIC method. Meas 2021, 170, 108683. [Google Scholar] [CrossRef]
- Ribeiro, D.; Santos, R.; Cabral, R.; Saramago, G.; Montenegro, P.; Carvalho, H.; Correia, J.; Calçada, R. Calçada Non-contact structural displacement measurement using Unmanned Aerial Vehicles and video-based systems. Mech. Syst. Signal Process 2021, 160, 107869. [Google Scholar] [CrossRef]
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision, 2nd ed.; Cambridge University Press: New York, NY, USA, 2003. [Google Scholar]
- Yoneyama, S.; Ueda, H. Bridge Deflection Measurement Using Digital Image Correlation with Camera Movement Correction. Mater. Trans. 2012, 53, 285–290. [Google Scholar] [CrossRef] [Green Version]
- Zhai, Y.; Shah, M. Visual attention detection in video sequences using spatiotemporal cues. In Proceedings of the 14th annual ACM International Conference on Multimedia-MULTIMEDIA ’06, Barbara, CA, USA, 21–25 October 2006; pp. 815–824. [Google Scholar]
- Chen, G.; Wu, Z.; Gong, C.; Zhang, J.; Sun, X. DIC-Based Operational Modal Analysis of Bridges. Adv. Civ. Eng. 2021, 2021, 6694790. [Google Scholar] [CrossRef]
- Zhang, Z. A flexible new technique for camera calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1330–1334. [Google Scholar] [CrossRef] [Green Version]
- Sutton, M.; Mingqi, C.; Peters, W.; Chao, Y.; McNeill, S. Application of an optimized digital correlation method to planar deformation analysis. Image Vis. Comput. 1986, 4, 143–150. [Google Scholar] [CrossRef]
- Devriendt, C.; Guillaume, P. The use of transmissibility measurements in output-only modal analysis. Mech. Syst. Signal Process. 2007, 21, 2689–2696. [Google Scholar] [CrossRef]
- Yan, W.-J.; Ren, W.-X. Operational Modal Parameter Identification from Power Spectrum Density Transmissibility. Comput. Civ. Infrastruct. Eng. 2011, 27, 202–217. [Google Scholar] [CrossRef]
- Brincker, R.; Zhang, L.; Andersen, P. Modal identification of output-only systems using frequency domain decomposition. Smart Mater. Struct. 2001, 10, 441–445. [Google Scholar] [CrossRef] [Green Version]
- Yunus, E.H.; Utku, G.; Markus, H.; Eleni, C. A Novel Approach for 3D-Structural Identification through Video Recording: Magnified Tracking. Sensors 2019, 19, 1229. [Google Scholar] [CrossRef] [Green Version]









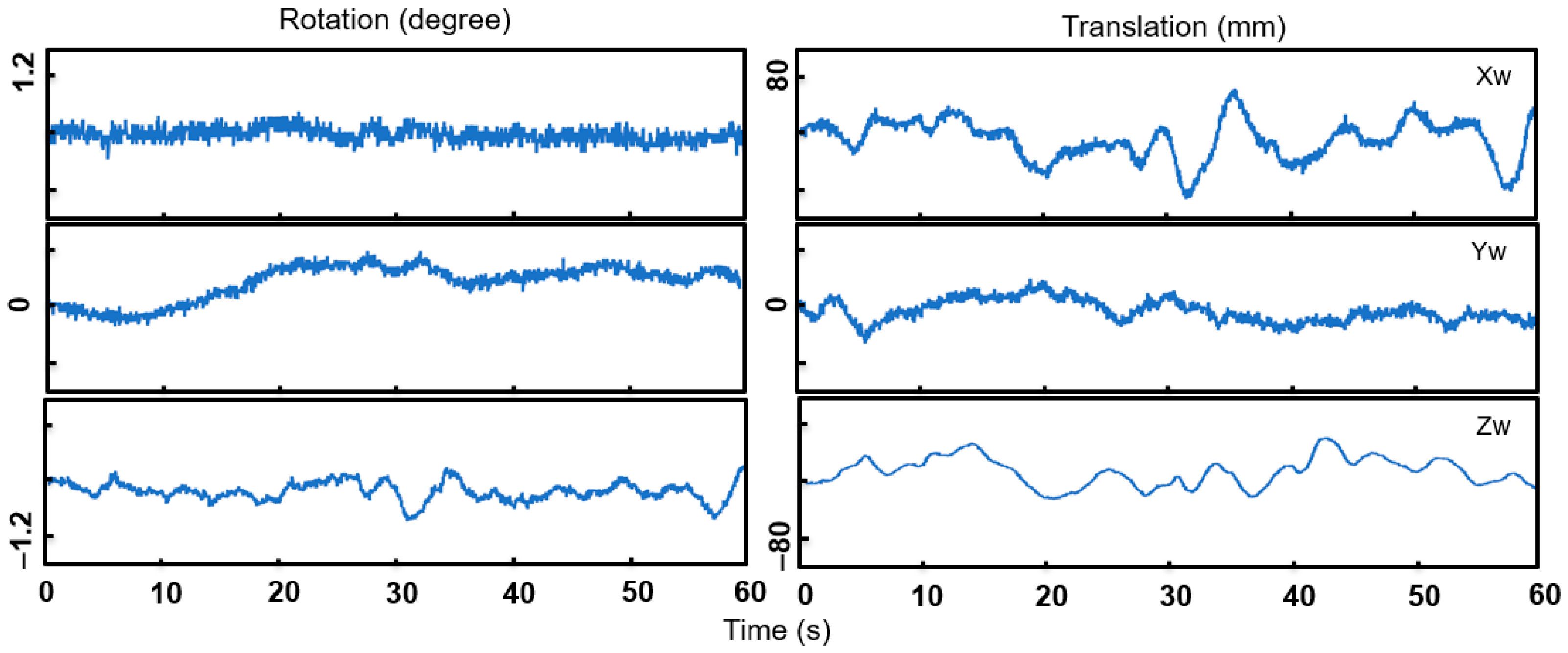

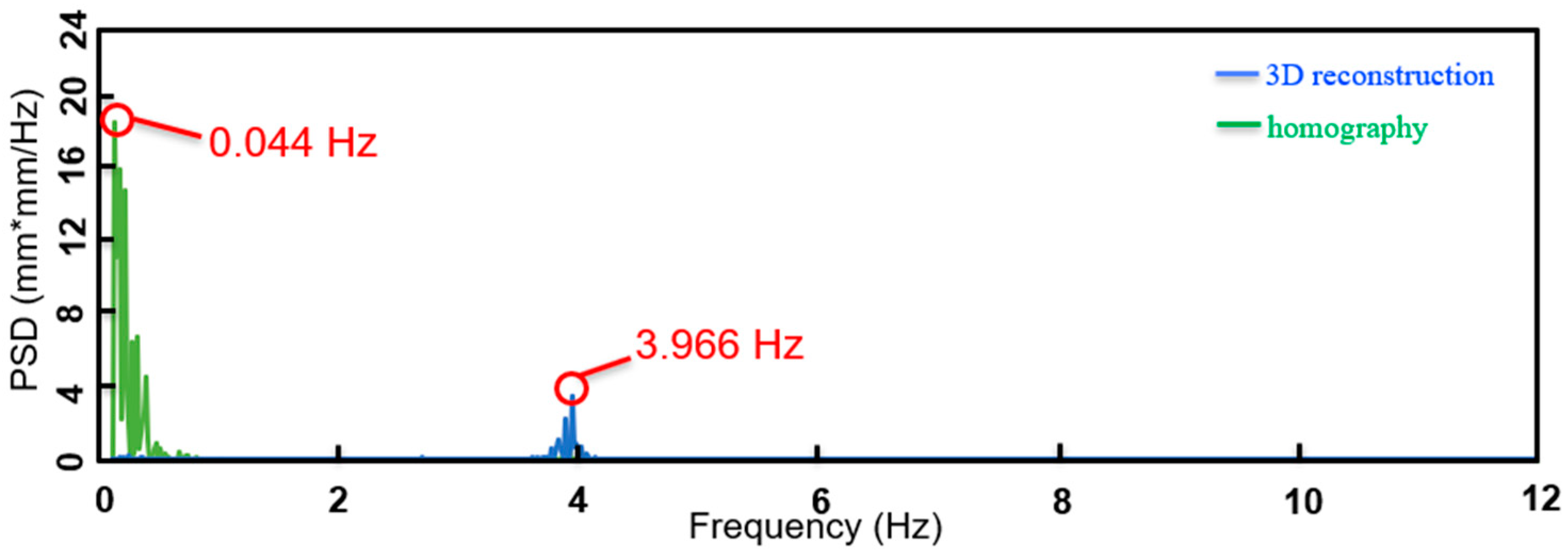
| Zw (m) | Homography | 3D Reconstruction | Homography | 3D Reconstruction |
|---|---|---|---|---|
| Frequency (Hz) | Frequency (Hz) | Relative Error (%) | Relative Error (%) | |
| 0 | 3.940 | 3.940 | 0 | 0 |
| 1 | 0.103 | 3.927 | 97.4 | 0.33 |
| −1 | 0.044 | 3.966 | 98.9 | 0.66 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Z.; Chen, G.; Ding, Q.; Yuan, B.; Yang, X. Three-Dimensional Reconstruction-Based Vibration Measurement of Bridge Model Using UAVs. Appl. Sci. 2021, 11, 5111. https://doi.org/10.3390/app11115111
Wu Z, Chen G, Ding Q, Yuan B, Yang X. Three-Dimensional Reconstruction-Based Vibration Measurement of Bridge Model Using UAVs. Applied Sciences. 2021; 11(11):5111. https://doi.org/10.3390/app11115111
Chicago/Turabian StyleWu, Zhihua, Gongfa Chen, Qiong Ding, Bing Yuan, and Xiaomei Yang. 2021. "Three-Dimensional Reconstruction-Based Vibration Measurement of Bridge Model Using UAVs" Applied Sciences 11, no. 11: 5111. https://doi.org/10.3390/app11115111
APA StyleWu, Z., Chen, G., Ding, Q., Yuan, B., & Yang, X. (2021). Three-Dimensional Reconstruction-Based Vibration Measurement of Bridge Model Using UAVs. Applied Sciences, 11(11), 5111. https://doi.org/10.3390/app11115111






