Multi-Area State Estimation: A Distributed Quasi-Static Innovation-Based Model with an Alternative Direction Method of Multipliers
Abstract
1. Introduction
- A distributed measurement model for non-linear multi-area state estimation which utilizes ADMM;
- Applying the Innovation Concept, which takes into account the masked error component in the Jacobian range space.
2. Background
2.1. State Estimation with the Innovation Concept
2.2. Alternating Direction Method of Multiplier (ADMM)
3. Multi-Area AC State Estimation Model Using ADMM
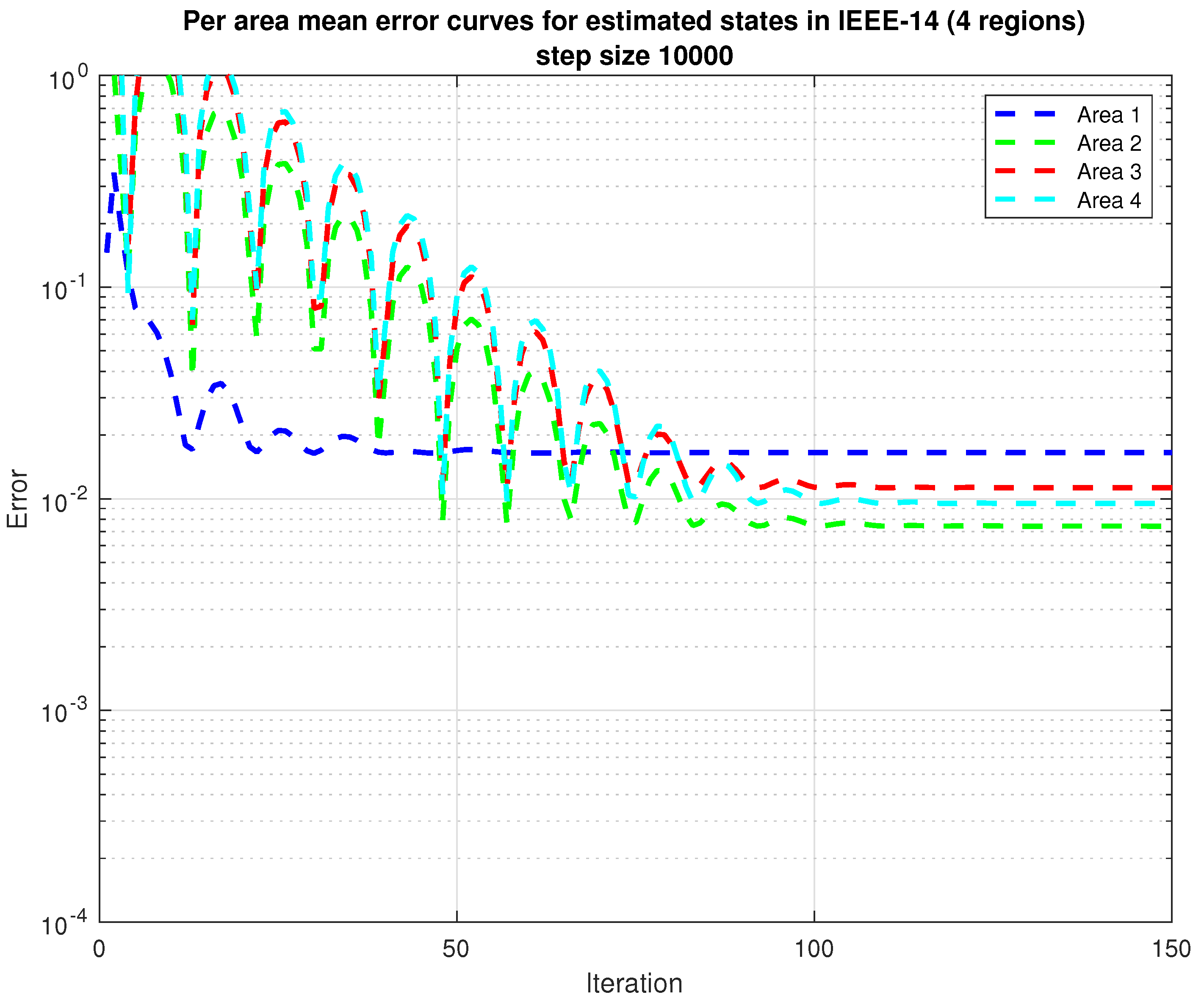
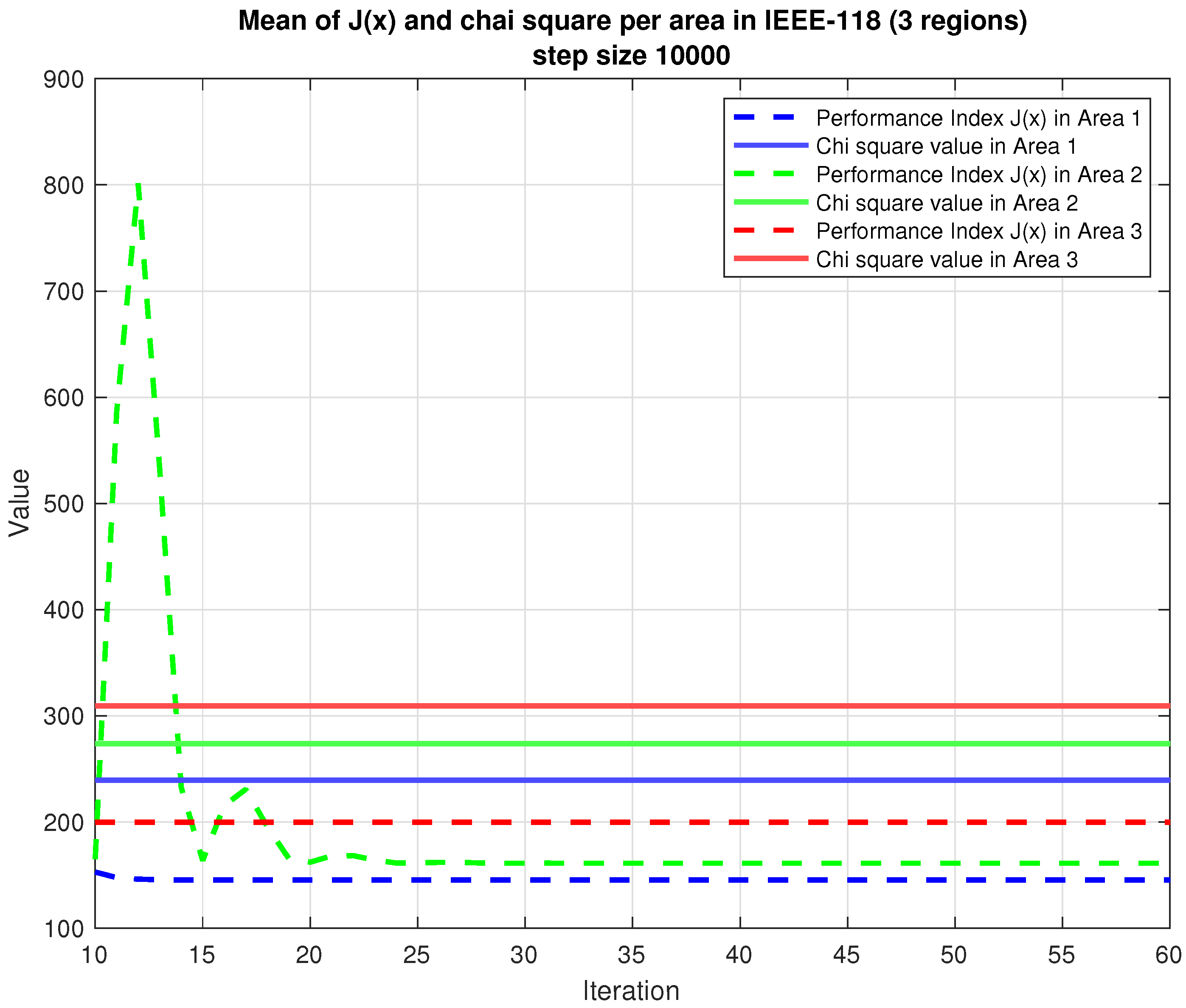
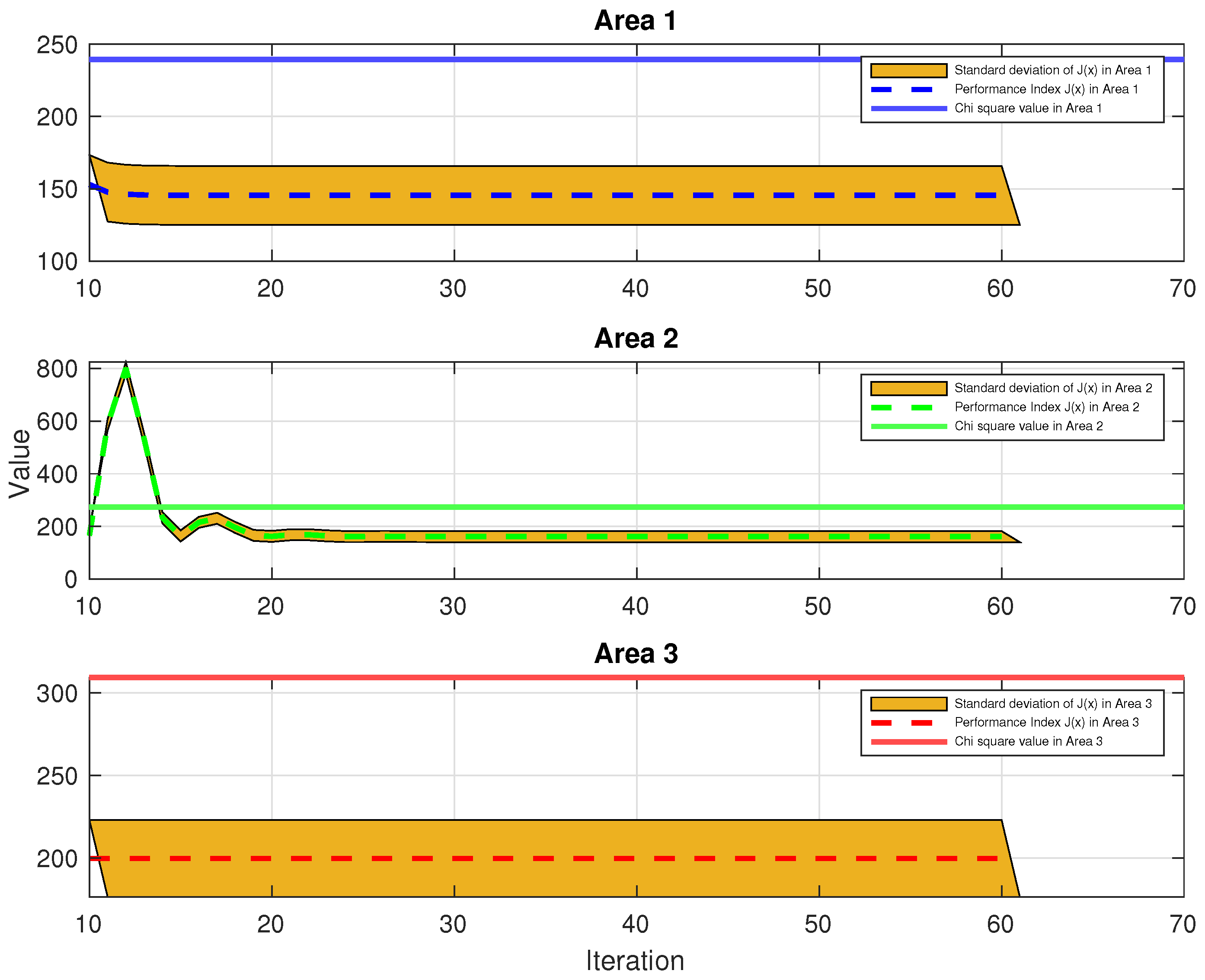
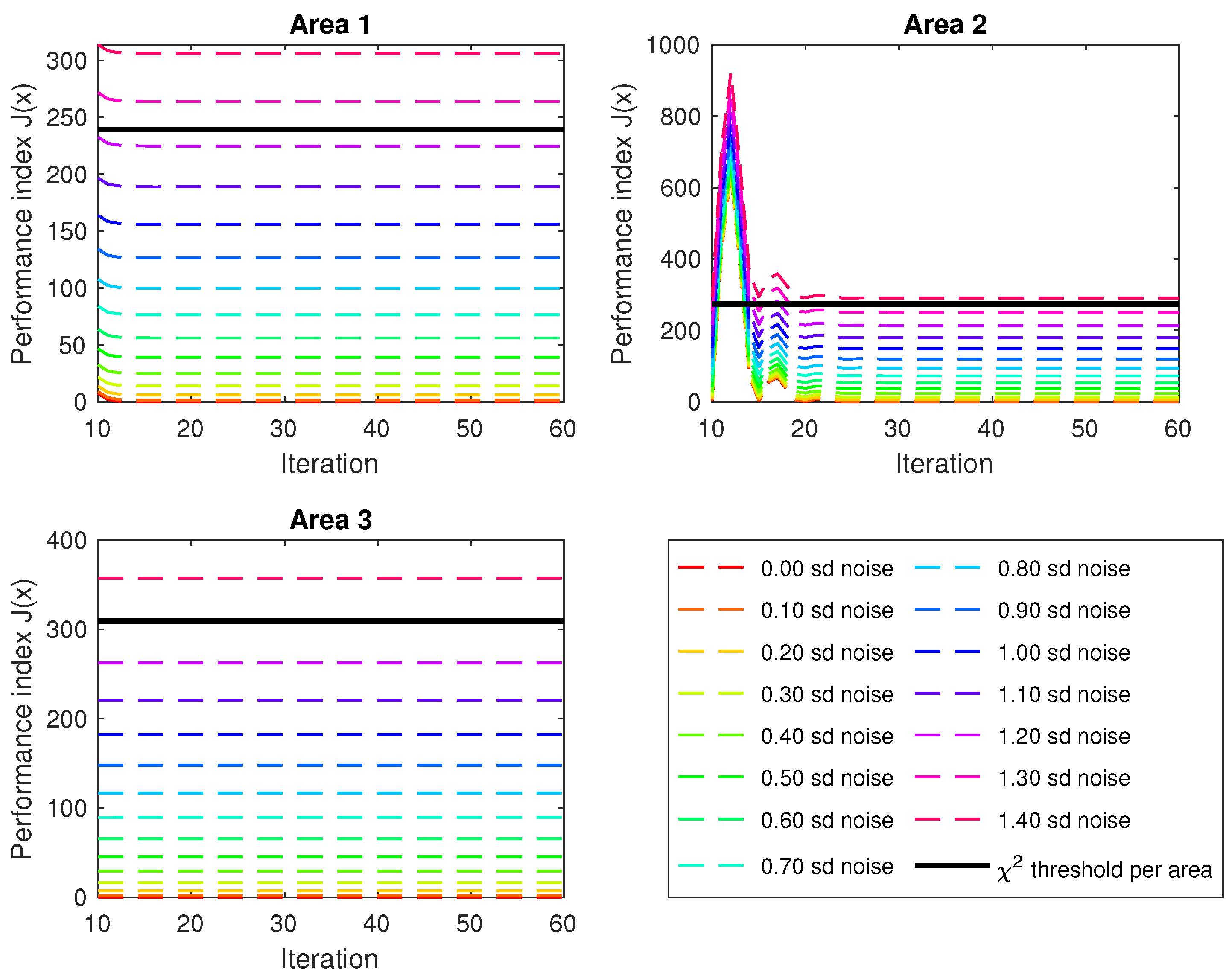
4. Case Study
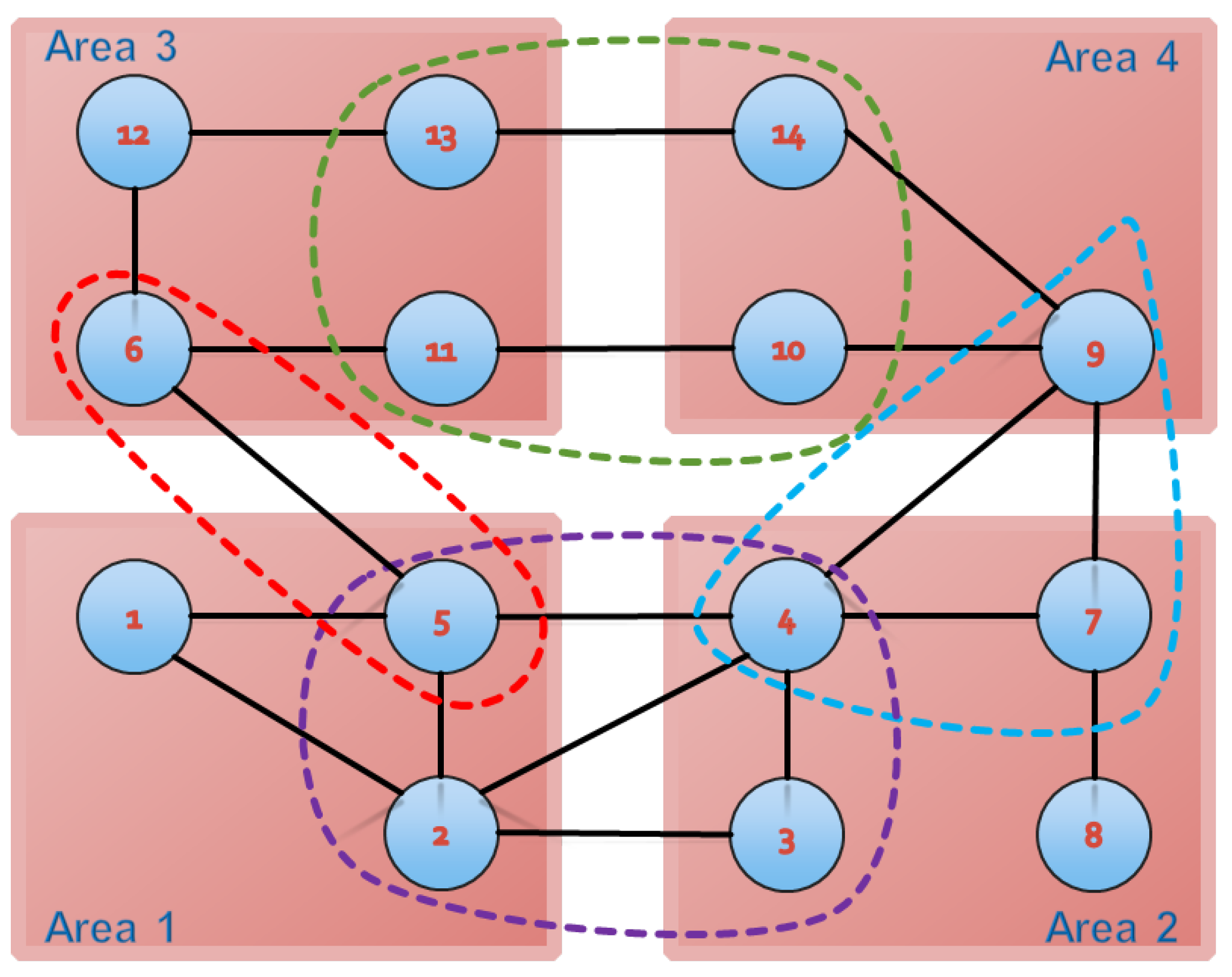
4.1. -14 Bus System
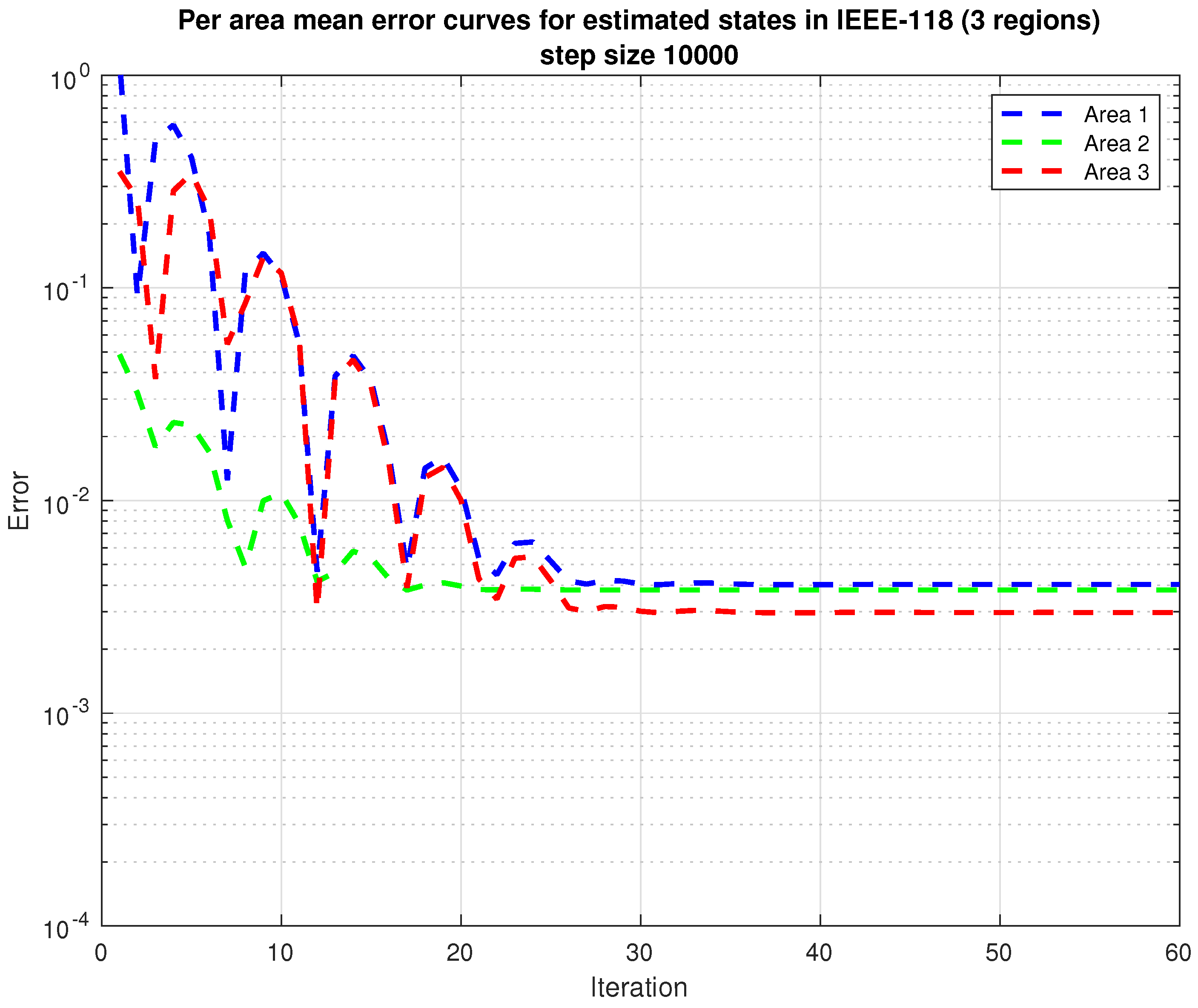
4.2. IEEE-118 Bus System
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Schweppe, F.C.; Wildes, J. Power system static-state estimation, Part I: Exact model. In IEEE Transactions on Power Apparatus and Systems; IEEE: Piscataway, NJ, USA, 1970; pp. 120–125. [Google Scholar]
- Cecati, C.; Mokryani, G.; Piccolo, A.; Siano, P. An overview on the smart grid concept. In Proceedings of the IECON 2010—36th Annual Conference on IEEE Industrial Electronics Society, Glendale, CA, USA, 7–10 November 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 3322–3327. [Google Scholar]
- McDaniel, P.; McLaughlin, S. Security and privacy challenges in the smart grid. IEEE Secur. Priv. 2009, 7, 75–77. [Google Scholar] [CrossRef]
- Korres, G.N. A distributed multiarea state estimation. IEEE Trans. Power Syst. 2010, 26, 73–84. [Google Scholar] [CrossRef]
- Korres, G.N.; Tzavellas, A.; Galinas, E. A distributed implementation of multi-area power system state estimation on a cluster of computers. Electr. Power Syst. Res. 2013, 102, 20–32. [Google Scholar] [CrossRef]
- Jiang, W.; Vittal, V.; Heydt, G.T. A distributed state estimator utilizing synchronized phasor measurements. IEEE Trans. Power Syst. 2007, 22, 563–571. [Google Scholar] [CrossRef]
- Gomez-Exposito, A.; Abur, A.; de la Villa Jaen, A.; Gomez-Quiles, C. A multilevel state estimation paradigm for smart grids. Proc. IEEE 2011, 99, 952–976. [Google Scholar] [CrossRef]
- Jiang, W.; Vittal, V.; Heydt, G.T. Diakoptic state estimation using phasor measurement units. IEEE Trans. Power Syst. 2008, 23, 1580–1589. [Google Scholar] [CrossRef]
- Zhao, L.; Abur, A. Multi area state estimation using synchronized phasor measurements. IEEE Trans. Power Syst. 2005, 20, 611–617. [Google Scholar] [CrossRef]
- Ebrahimian, R.; Baldick, R. State estimation distributed processing [for power systems]. IEEE Trans. Power Syst. 2000, 15, 1240–1246. [Google Scholar] [CrossRef]
- Zhu, H.; Giannakis, G.B. Power system nonlinear state estimation using distributed semidefinite programming. IEEE J. Sel. Top. Signal Process. 2014, 8, 1039–1050. [Google Scholar] [CrossRef]
- Xie, L.; Choi, D.H.; Kar, S.; Poor, H.V. Fully distributed state estimation for wide-area monitoring systems. IEEE Trans. Smart Grid 2012, 3, 1154–1169. [Google Scholar] [CrossRef]
- Min, L.; Abur, A. Total transfer computation for multi-area power systems. IEEE Trans. Power Syst. 2006, 21, 1141–1147. [Google Scholar] [CrossRef]
- Conejo, A.J.; de la Torre, S.; Canas, M. An optimization approach to multiarea state estimation. IEEE Trans. Power Syst. 2007, 22, 213–221. [Google Scholar] [CrossRef]
- Kekatos, V.; Giannakis, G.B. Distributed robust power system state estimation. IEEE Trans. Power Syst. 2012, 28, 1617–1626. [Google Scholar] [CrossRef]
- Monticelli, A. State Estimation in Electric Power Systems: A Generalized Approach; Springer Science & Business Media: Berlin, Germany, 1999; Volume 507. [Google Scholar]
- Abur, A.; Expósito, A. Power System State Estimation: Theory and Implementation; Power Engineering (Willis), CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Gómez-Expósito, A.; de la Villa Jaén, A.; Gómez-Quiles, C.; Rousseaux, P.; Van Cutsem, T. A taxonomy of multi-area state estimation methods. Electr. Power Syst. Res. 2011, 81, 1060–1069. [Google Scholar] [CrossRef]
- Bretas, N.G.; Bretas, A.S. A two steps procedure in state estimation gross error detection, identification, and correction. Int. J. Electr. Power Energy Syst. 2015, 73, 484–490. [Google Scholar] [CrossRef]
- Bretas, N.G.; Bretas, A.S. The Extension of the Gauss Approach for the Solution of an Overdetermined Set of Algebraic Non Linear Equations. IEEE Trans. Circ. Syst. II Express Briefs 2018, 65, 1269–1273. [Google Scholar] [CrossRef]
- Boyd, S.; Parikh, N.; Chu, E. Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers; Now Publishers Inc.: Delft, The Netherlands, 2011. [Google Scholar]
- Zimmerman, R.D.; Murillo-Sánchez, C.E.; Thomas, R.J. MATPOWER: Steady-state operations, planning, and analysis tools for power systems research and education. IEEE Trans. Power Syst. 2010, 26, 12–19. [Google Scholar] [CrossRef]
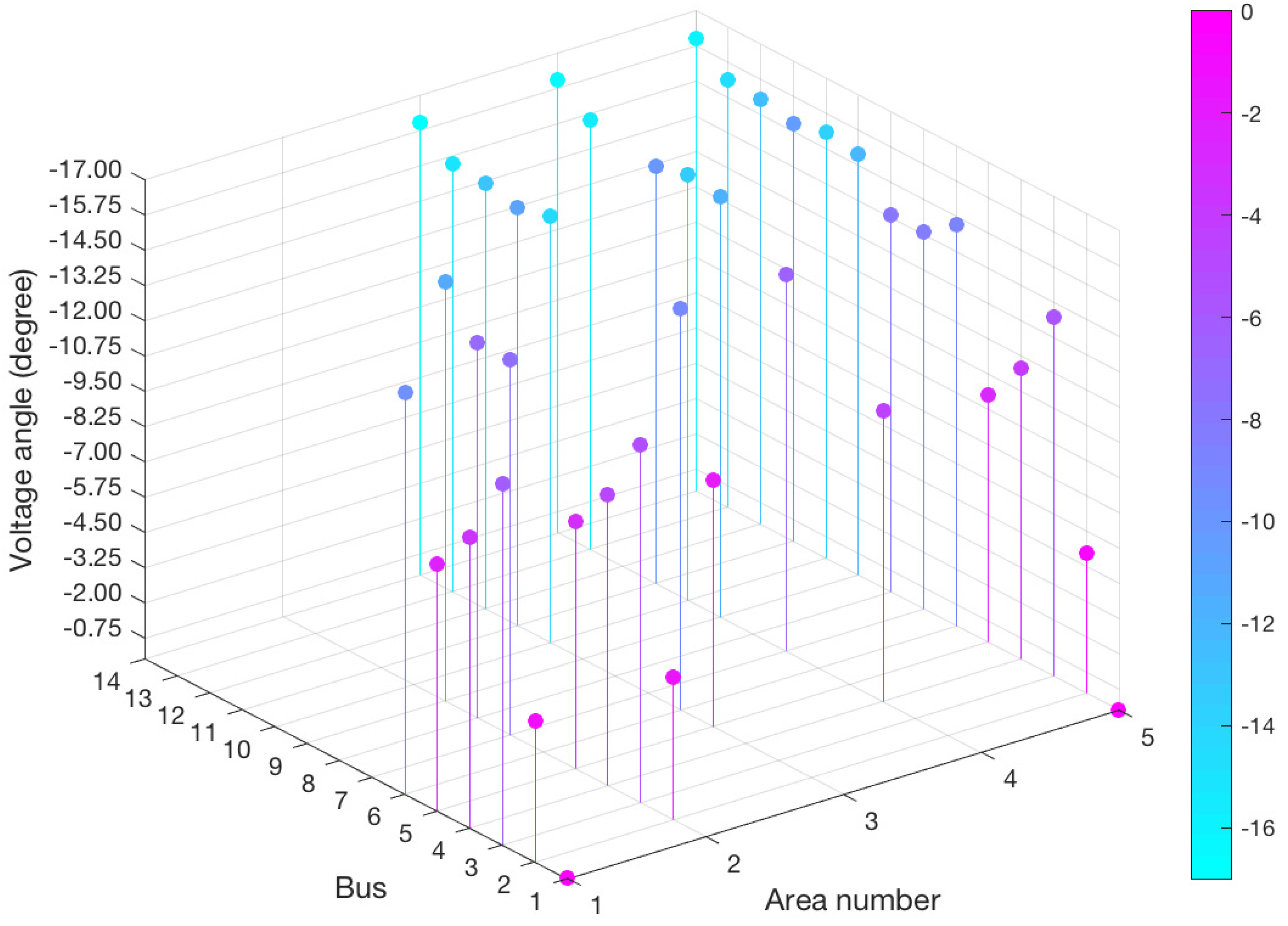
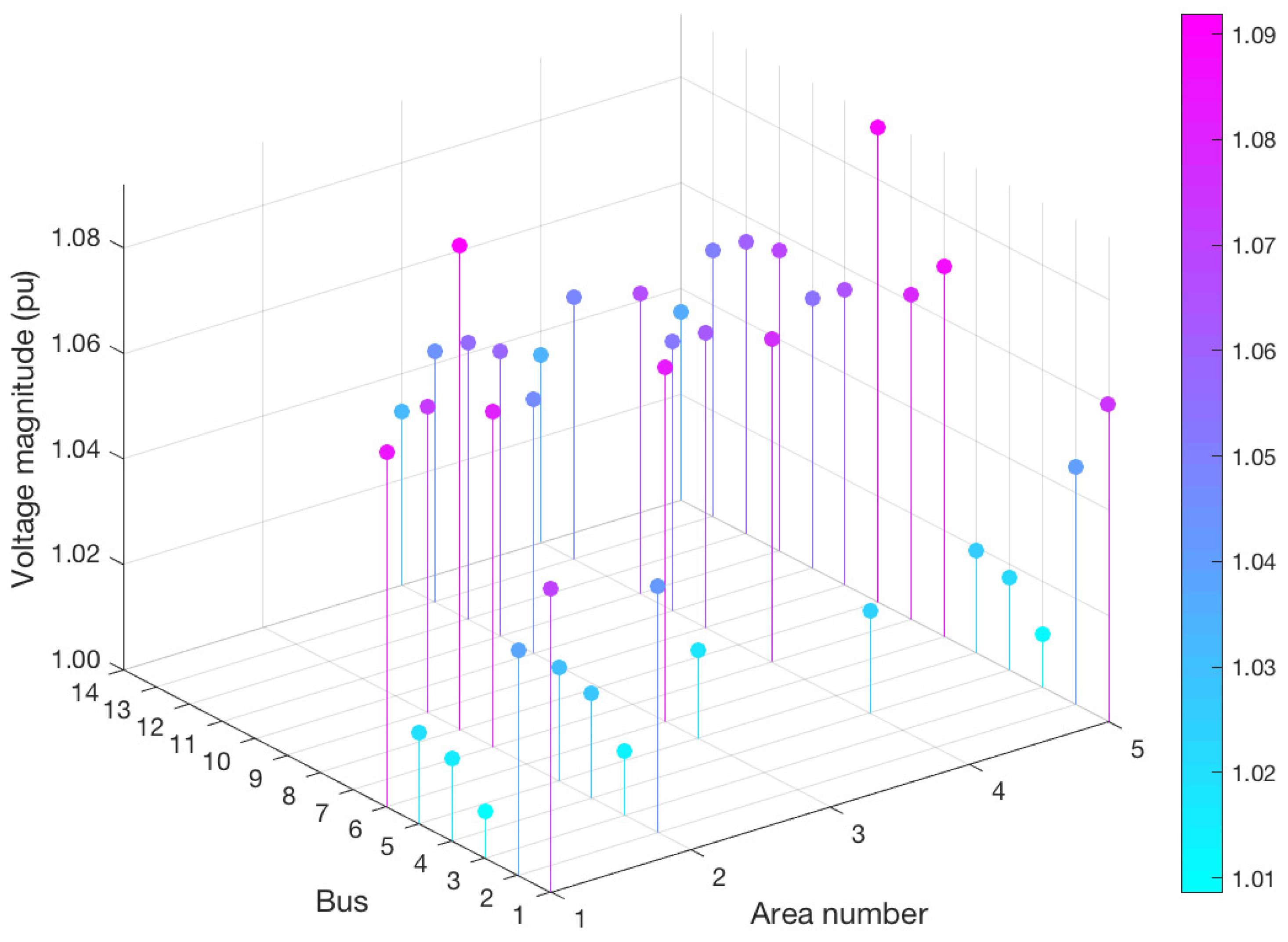
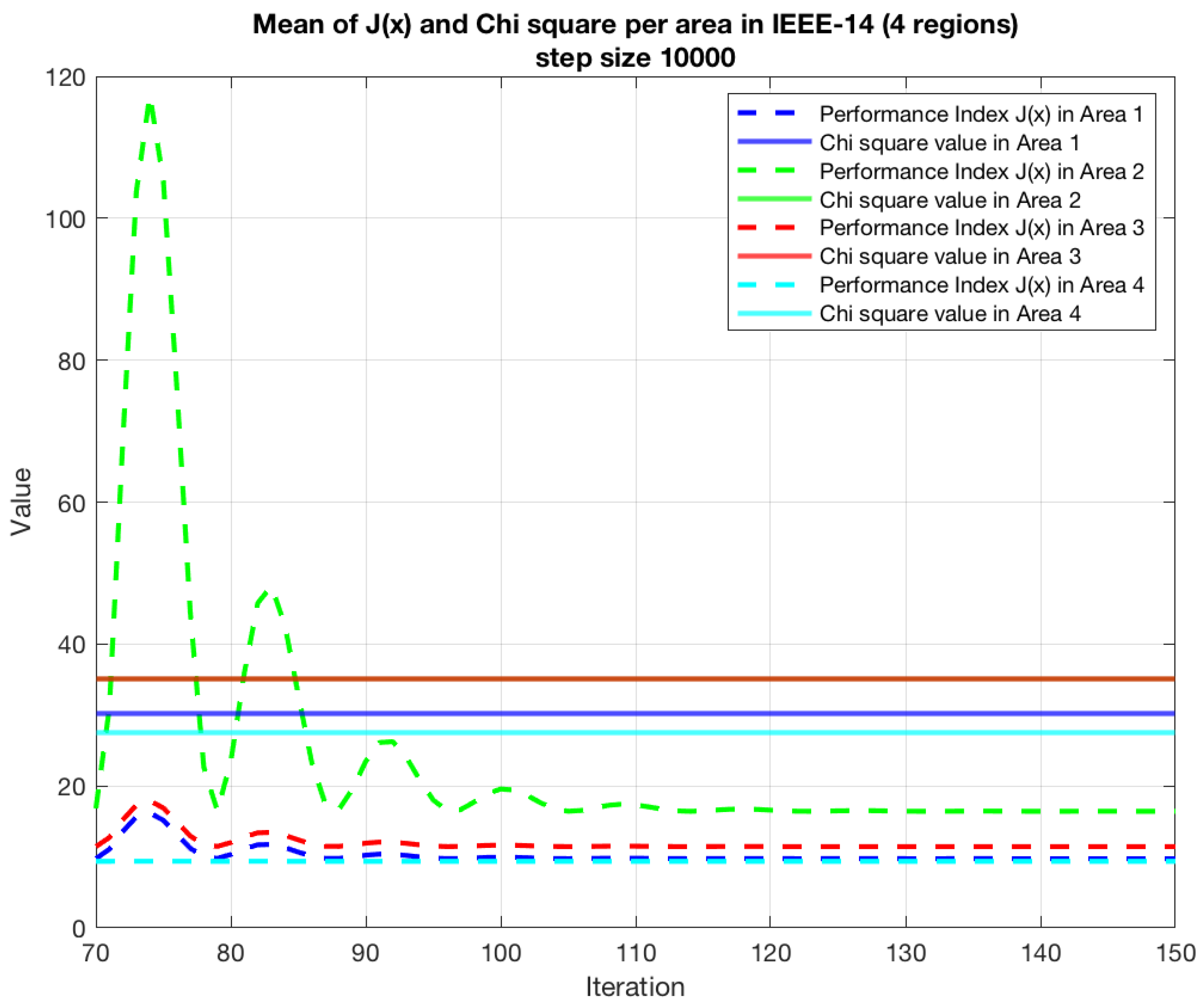
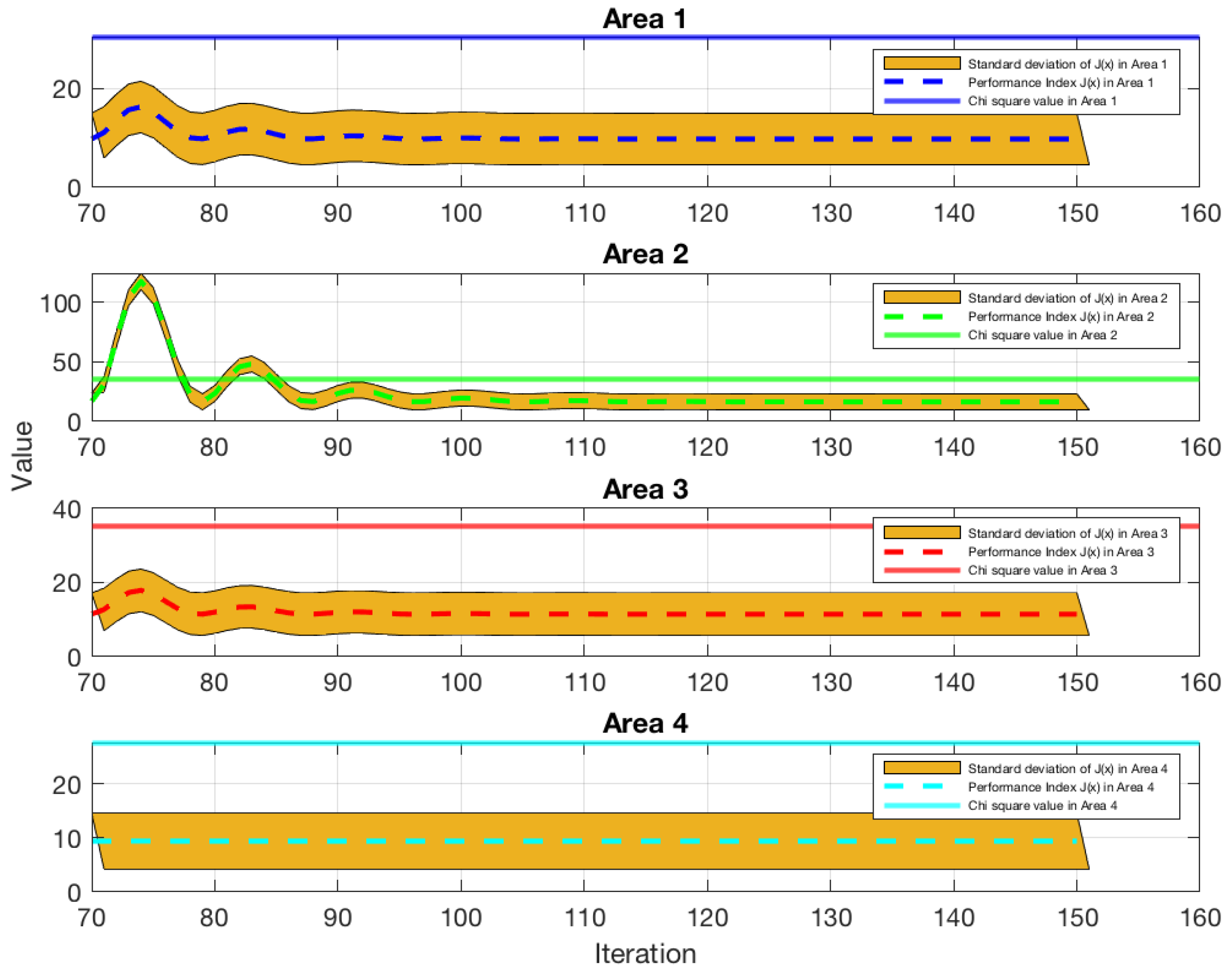
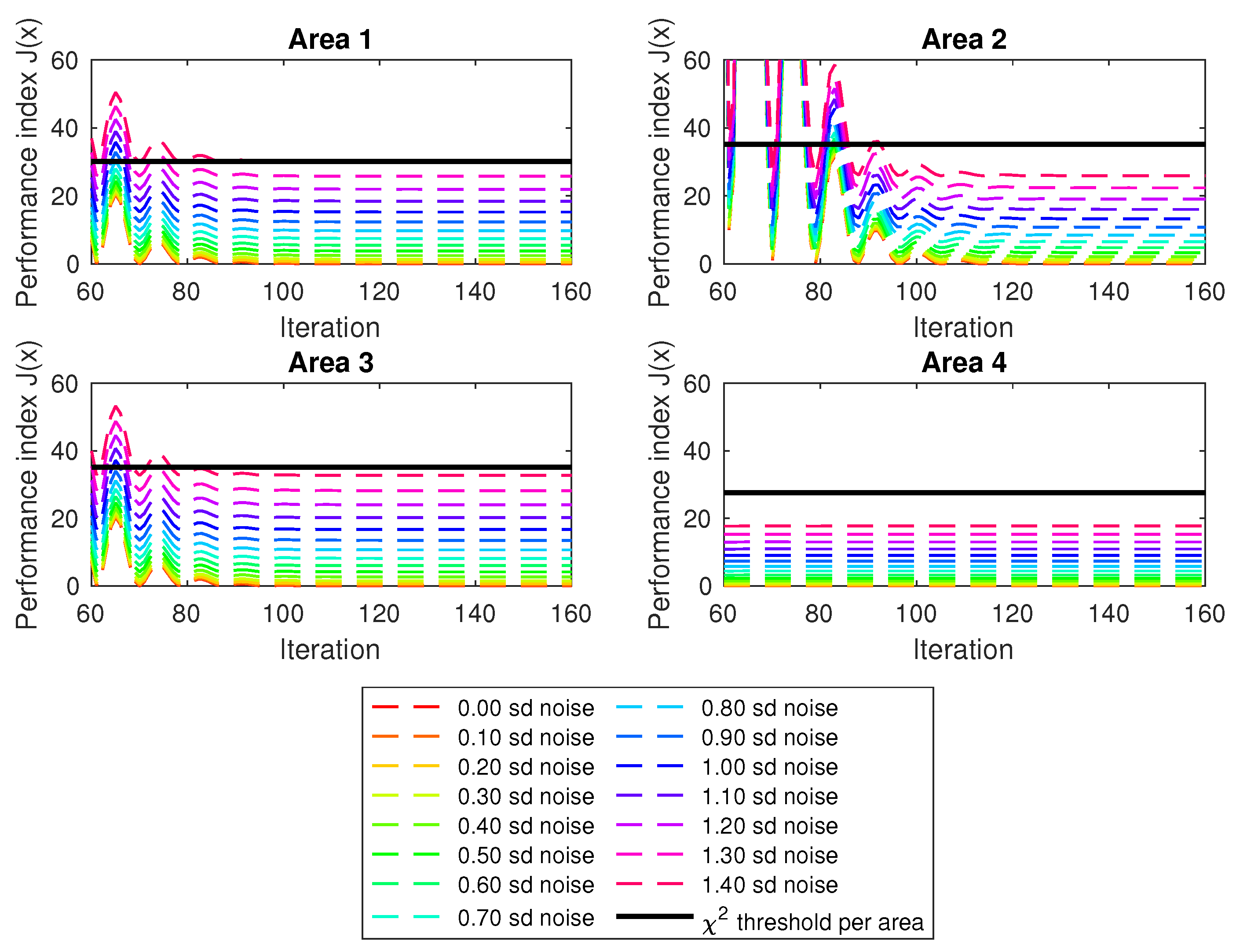
| State | Area 1 | Area 2 | Area 3 | Area 4 | |
|---|---|---|---|---|---|
| Mean | Angle (degree) | ||||
| Magnitude (pu) | |||||
| Average std. | Angle (degree) | ||||
| Magnitude (pu) |
| State | Area 1 | Area 2 | Area 3 | Area 4 | |
|---|---|---|---|---|---|
| Mean | Angle (degree) | ||||
| Magnitude (pu) | |||||
| Average std. | Angle (degree) | ||||
| Magnitude (pu) |
| State | Area 1 | Area 2 | Area 3 | |
|---|---|---|---|---|
| Mean | Angle (degree) | |||
| Magnitude (pu) | ||||
| Average std | Angle (degree) | |||
| Magnitude (pu) |
| State | Area 1 | Area 2 | Area 3 | |
|---|---|---|---|---|
| Mean | Angle (degree) | |||
| Magnitude (pu) | ||||
| Average std. | Angle (degree) | |||
| Magnitude (pu) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aljohani, N.; Zou, T.; Bretas, A.S.; Bretas, N.G. Multi-Area State Estimation: A Distributed Quasi-Static Innovation-Based Model with an Alternative Direction Method of Multipliers. Appl. Sci. 2021, 11, 4419. https://doi.org/10.3390/app11104419
Aljohani N, Zou T, Bretas AS, Bretas NG. Multi-Area State Estimation: A Distributed Quasi-Static Innovation-Based Model with an Alternative Direction Method of Multipliers. Applied Sciences. 2021; 11(10):4419. https://doi.org/10.3390/app11104419
Chicago/Turabian StyleAljohani, Nader, Tierui Zou, Arturo S. Bretas, and Newton G. Bretas. 2021. "Multi-Area State Estimation: A Distributed Quasi-Static Innovation-Based Model with an Alternative Direction Method of Multipliers" Applied Sciences 11, no. 10: 4419. https://doi.org/10.3390/app11104419
APA StyleAljohani, N., Zou, T., Bretas, A. S., & Bretas, N. G. (2021). Multi-Area State Estimation: A Distributed Quasi-Static Innovation-Based Model with an Alternative Direction Method of Multipliers. Applied Sciences, 11(10), 4419. https://doi.org/10.3390/app11104419







