Influence of θ′ Phase Cutting on Precipitate Hardening of Al–Cu Alloy during Prolonged Plastic Deformation: Molecular Dynamics and Continuum Modeling
Abstract
:Featured Application
Abstract
1. Introduction
2. Materials and Methods
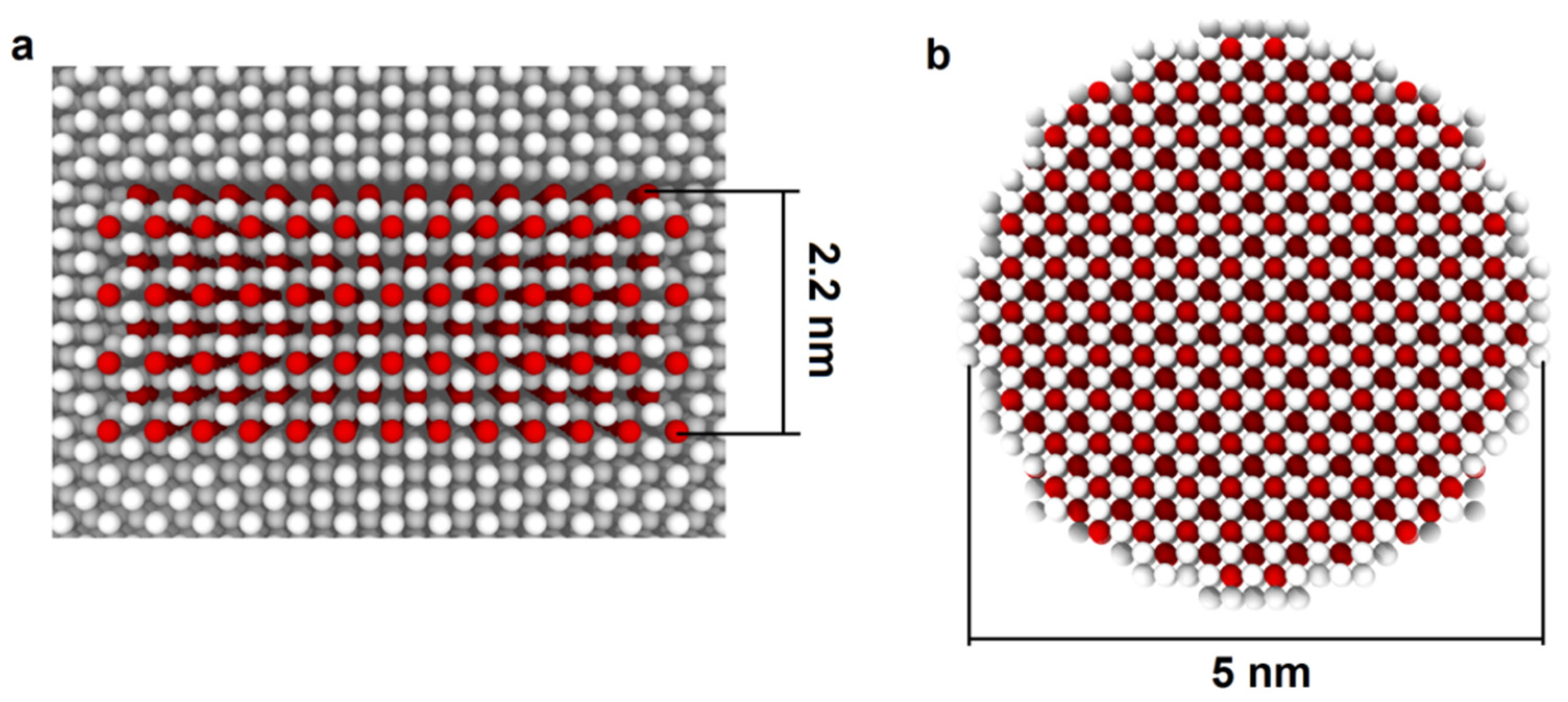
2.1. Statement of MD Task
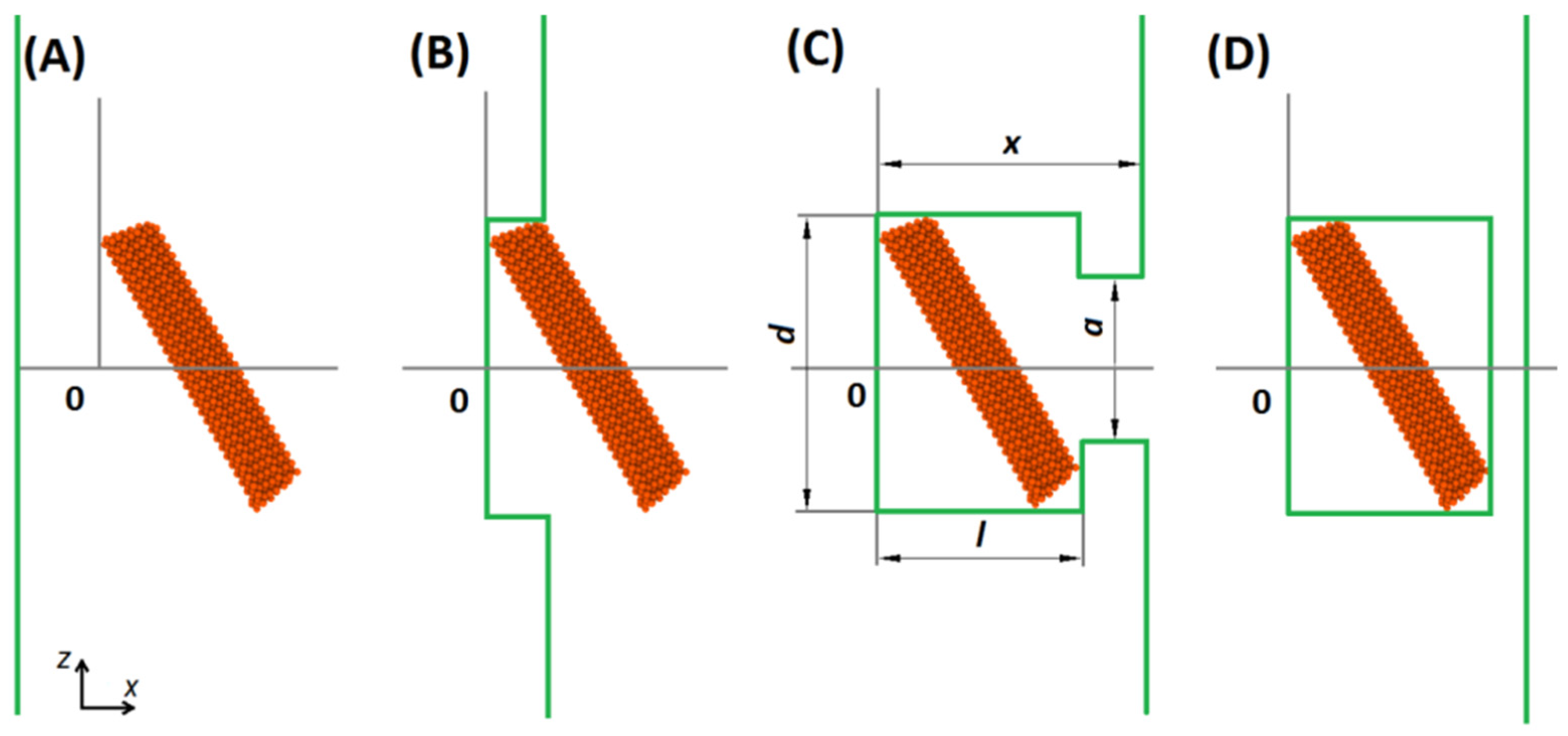
2.2. Model of Dislocation–Precipitate Interaction
2.3. Method of Discrete Dislocation Dynamics
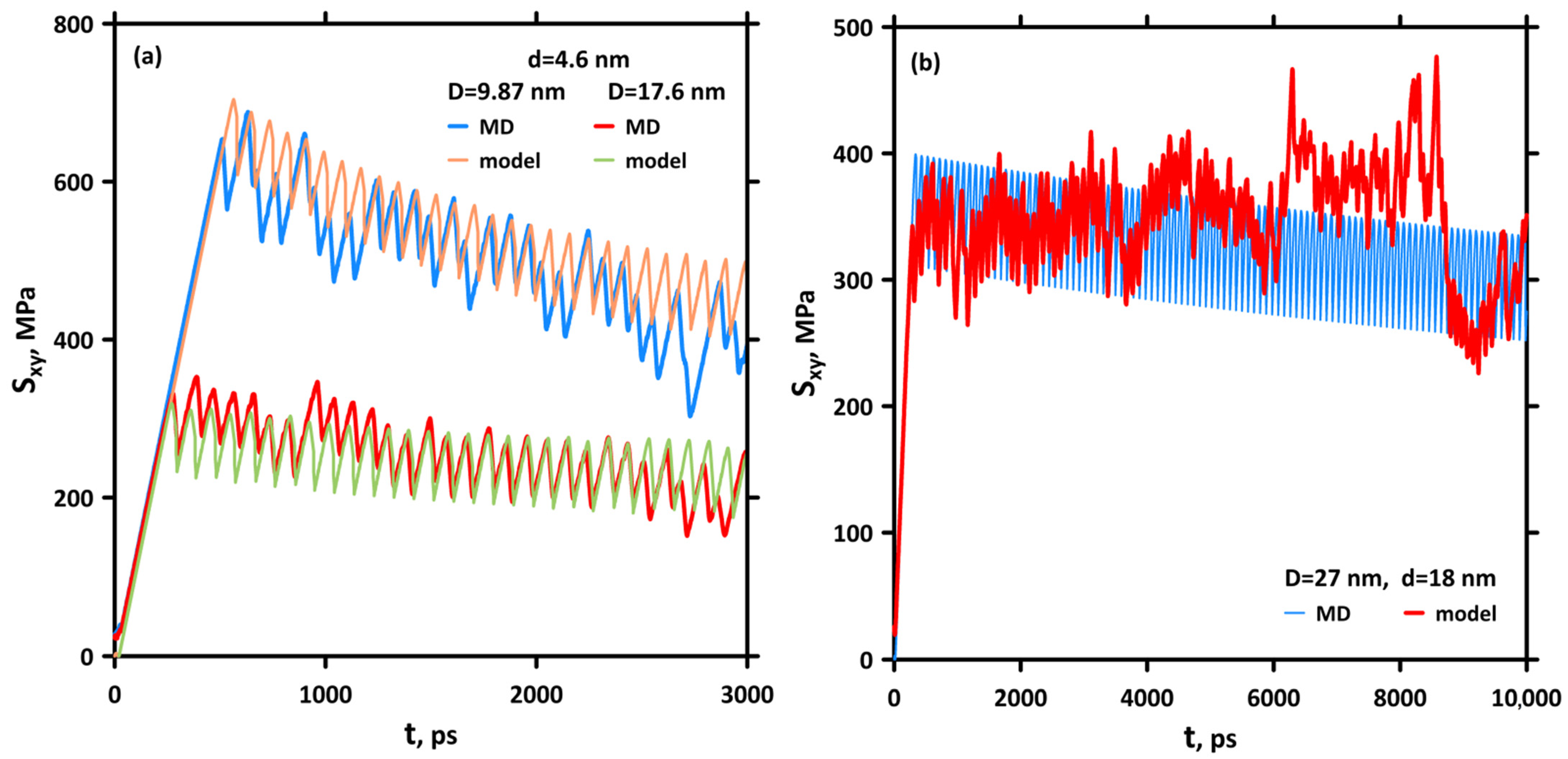
3. Results and Discussion
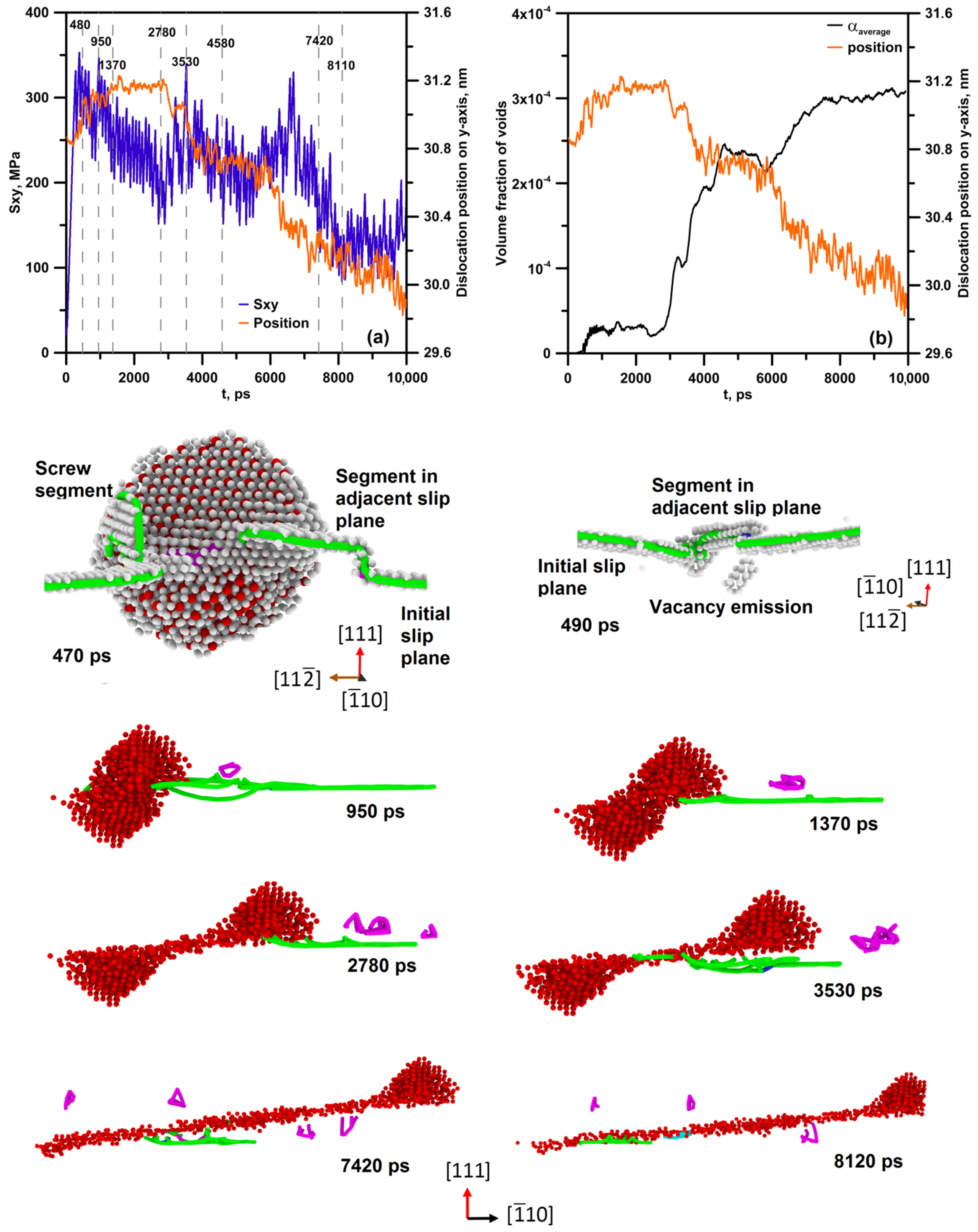
3.1. Mechanism of Interaction of Dislocation with Inclusion in MD
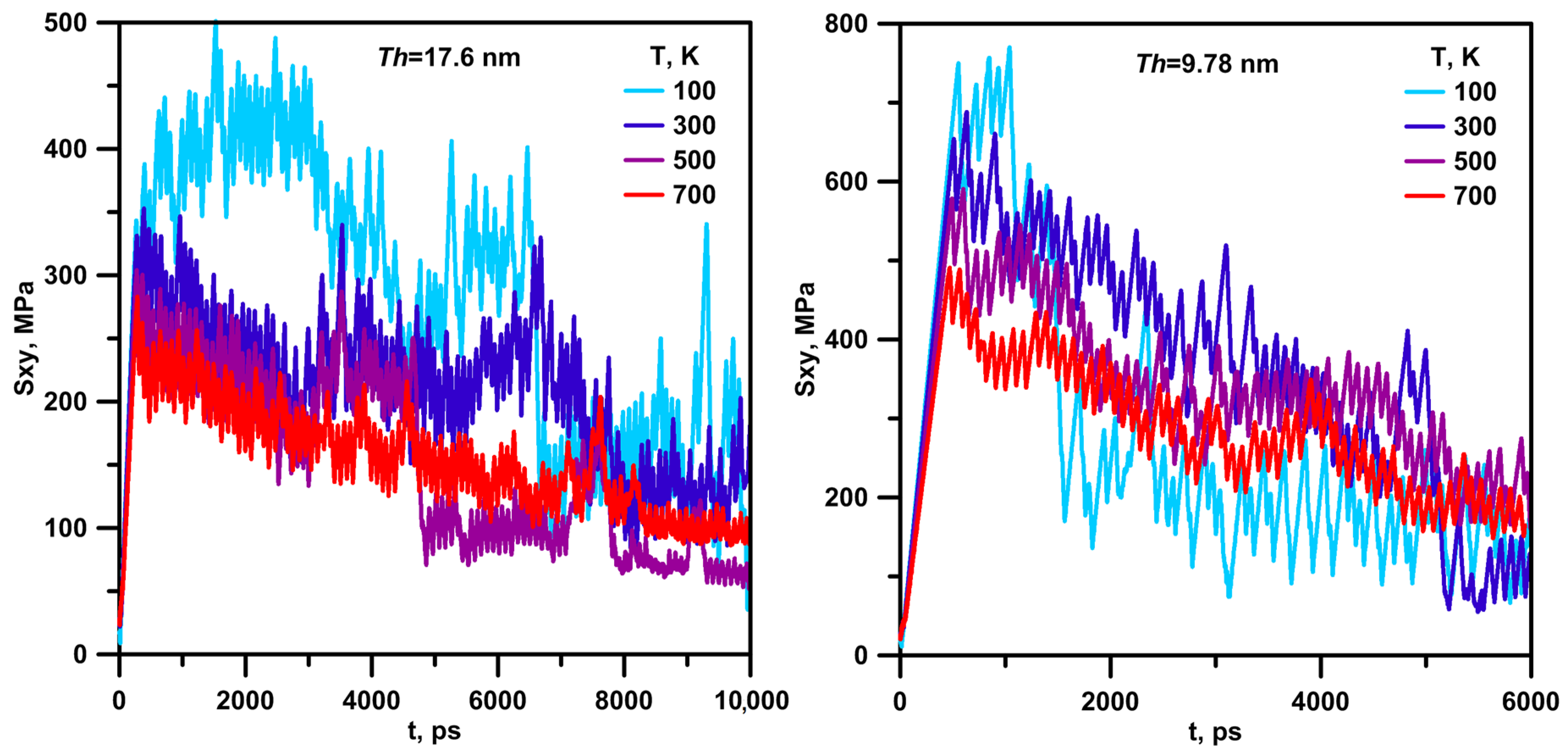
3.2. Influence of Multiple Interactions on the Structure of Inclusion and Stress State of the MD System
3.3. Accumulation of Vacancies in the MD System during Prolonged Deformation
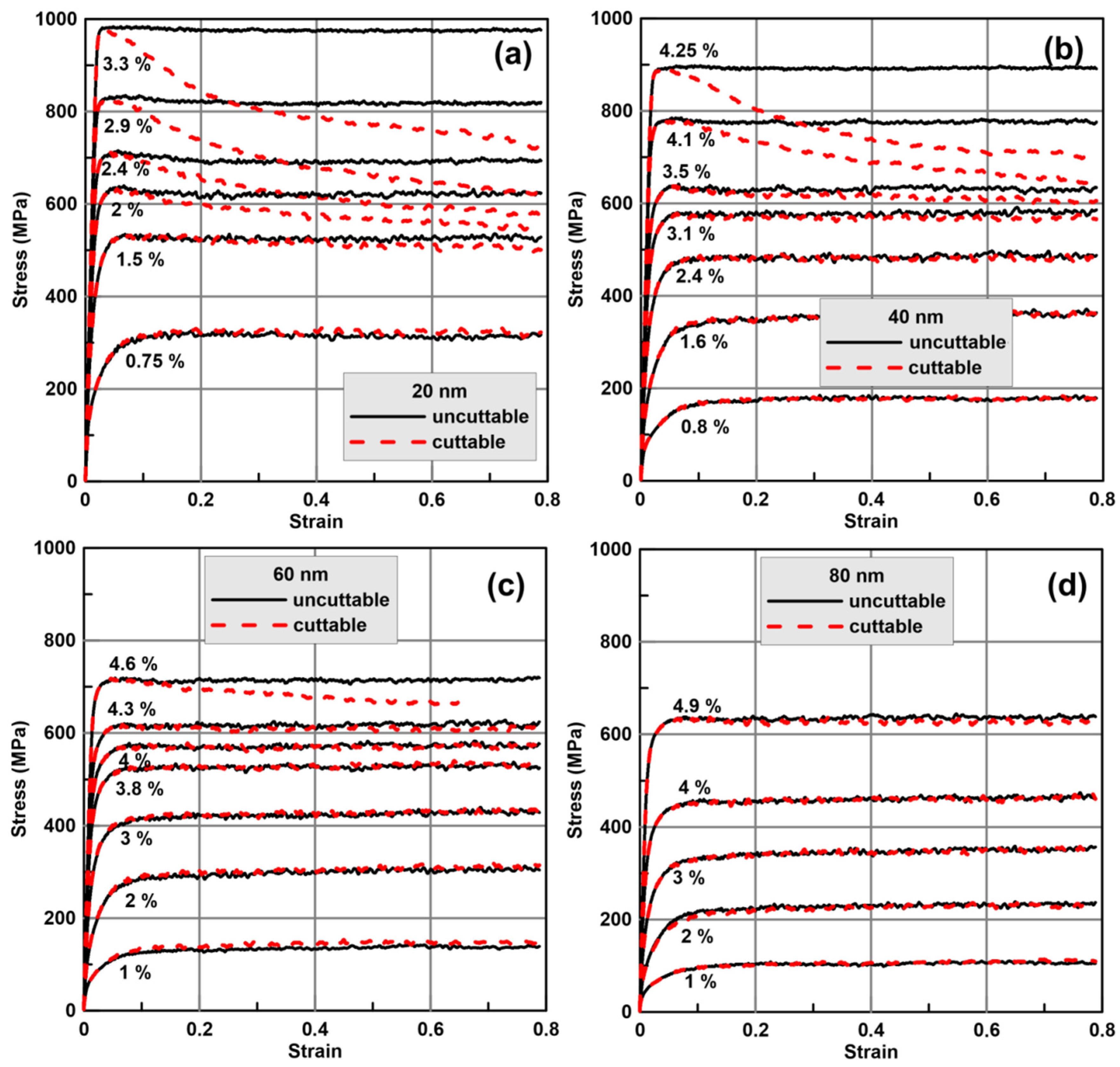
3.4. Accounting for Precipitate Softening in the Equation of Dislocation Motion
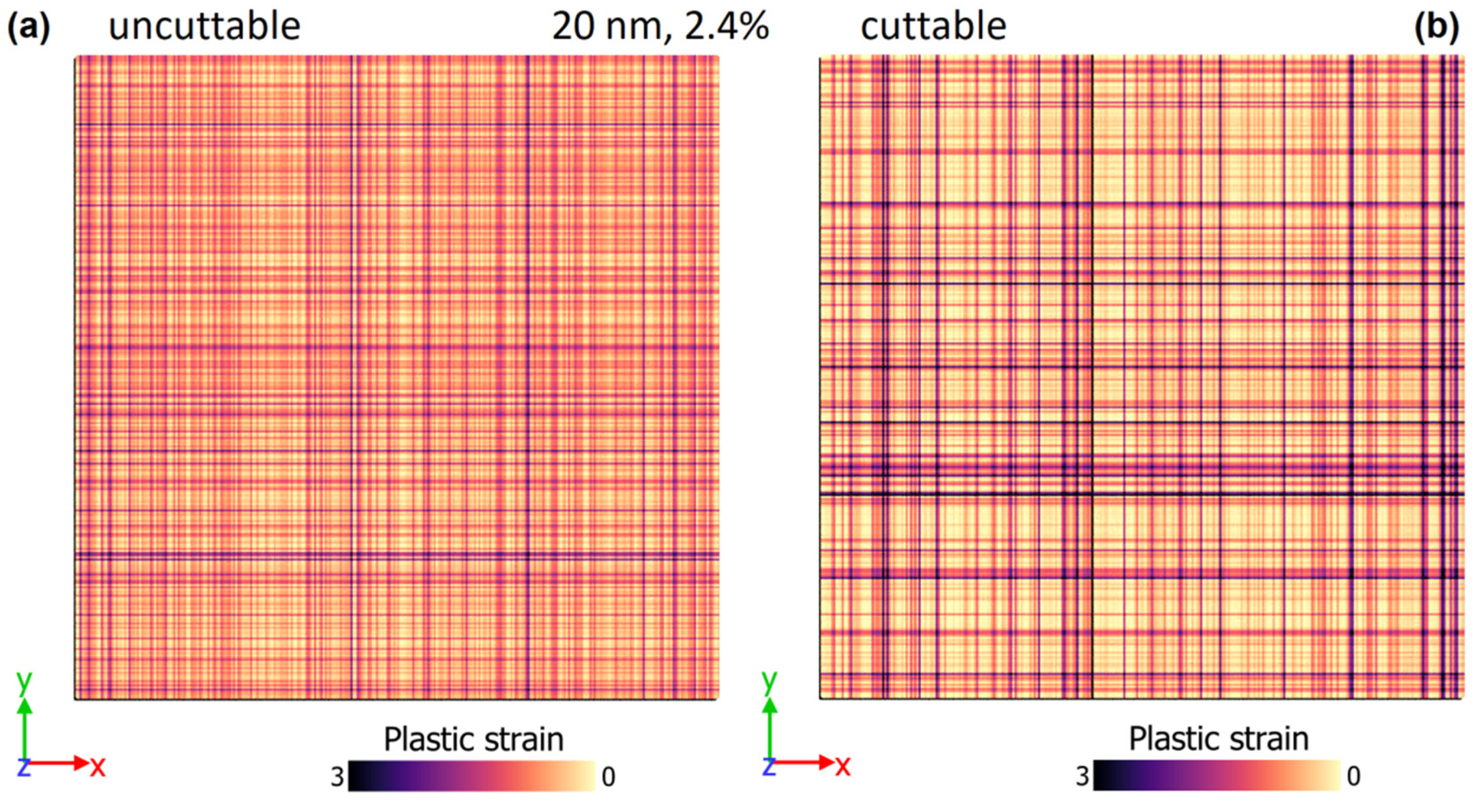
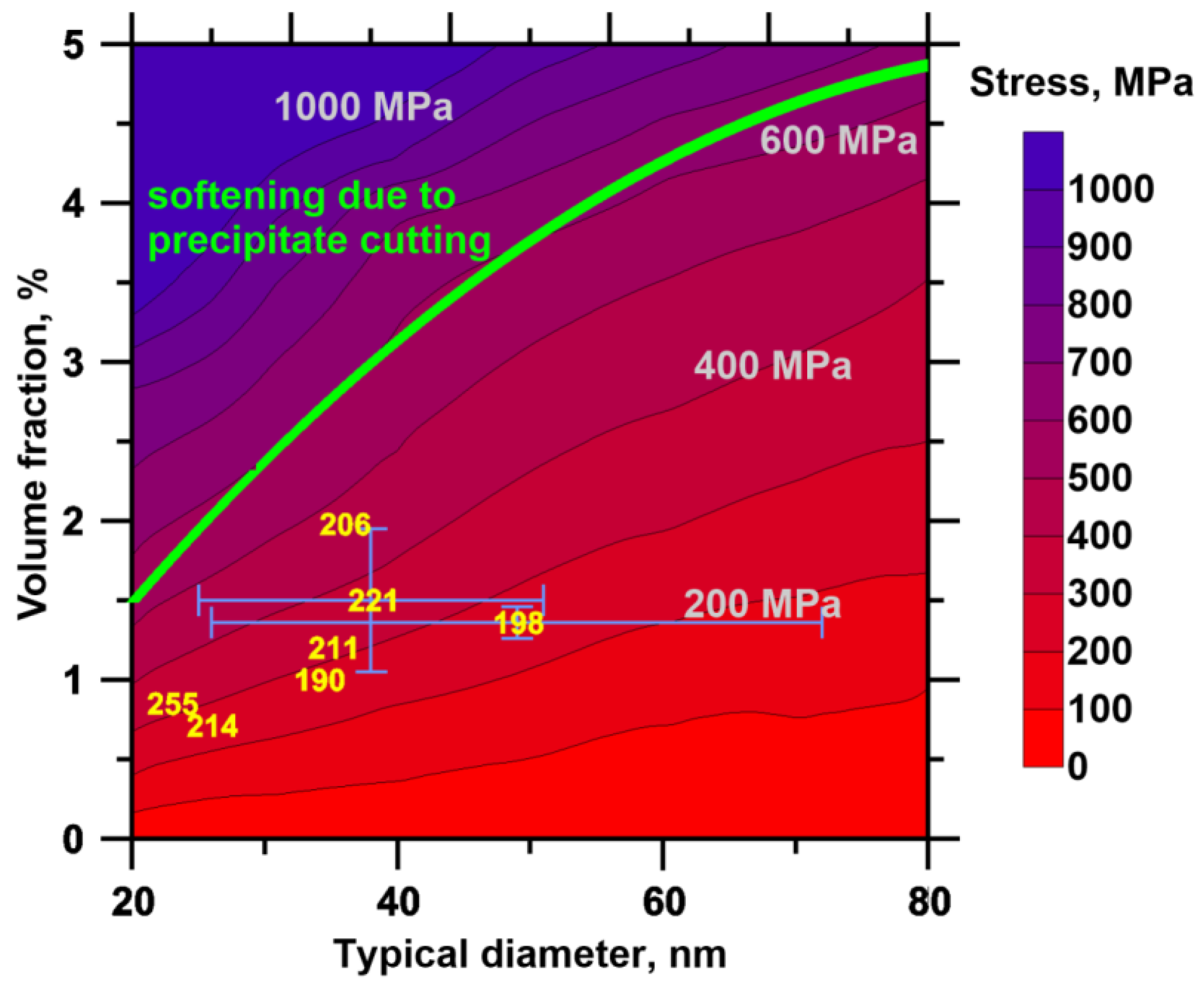
3.5. Strength of Alloys with Size-Distributed and Spatially Distributed Precipitates
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Zener, C.; Hollomon, J.H. Effect of Strain Rate upon Plastic Flow of Steel. J. Appl. Phys. 1944, 15, 22–32. [Google Scholar] [CrossRef]
- Bai, Y.; Dodd, B. Shear Localization: Occurrence Theories and Applications; Pergamon Press: Oxford, UK, 1992. [Google Scholar]
- Wright, T. The Physics and Mathematics of Adiabatic Shear Bands; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Walley, S.M. Shear Localization: A Historical Overview. Metall. Mater. Trans. A 2007, 38, 2629–2654. [Google Scholar] [CrossRef]
- Price, R.J.; Kelly, A. Deformation of age-hardened aluminium alloy crystals—I plastic flow. Acta Metall. 1964, 12, 159–169. [Google Scholar] [CrossRef]
- Asaro, R.J.; Rice, J.R. Strain localization in ductile single crystals. J. Mech. Phys. Solids 1977, 25, 309–338. [Google Scholar] [CrossRef] [Green Version]
- Medyanik, S.; Liu, W.; Li, S. On criteria for adiabatic shear band propagation. J. Mech. Phys. Solids 2007, 55, 1439. [Google Scholar] [CrossRef]
- Rittel, D.; Landau, P.; Venkert, A. Dynamic recrystallization as a potential cause for adiabatic shear failure. Phys. Rev. Lett. 2008, 101, 165501. [Google Scholar] [CrossRef] [Green Version]
- Clayton, J.D. Modeling effects of crystalline microstructure, energy storage mechanisms, and residual volume changes on penetration resistance of precipitate-hardened aluminum alloys. Compos. Part B 2009, 40, 443–450. [Google Scholar] [CrossRef]
- Mayer, A.E.; Borodin, E.N.; Mayer, P.N. Localization of plastic flow at high-rate simple shear. Int. J. Plast. 2013, 51, 188–199. [Google Scholar] [CrossRef]
- Osovski, S.; Rittel, D.; Venkert, A. The respective influence of microstructural and thermal softening on adiabatic shear localization. Mech. Mater. 2013, 56, 11–22. [Google Scholar] [CrossRef]
- Krasnikov, V.S.; Mayer, A.E. Modeling of plastic localization in aluminum and Al–Cu alloys under shock loading. Mater. Sci. Eng. A 2014, 619, 354–363. [Google Scholar] [CrossRef]
- Rodríguez-Martínez, J.A.; Vadillo, G.; Zaera, R.; Fernández-Sáez, J.; Rittel, D. An analysis of microstructural and thermal softening effects in dynamic necking. Mech. Mater. 2015, 80, 298–310. [Google Scholar] [CrossRef] [Green Version]
- Gurrutxaga-Lerma, B. Adiabatic shear banding and the micromechanics of plastic flow in metals. Int. J. Solids Struct. 2018, 132–133, 153–170. [Google Scholar] [CrossRef]
- Dorin, T.; De Geuser, F.; Lefebvre, W.; Sigli, C.; Deschamps, A. Strengthening mechanisms of T1 precipitates and their influence on the plasticity of an Al–Cu–Li alloy. Mater. Sci. Eng. A 2014, 605, 119–126. [Google Scholar] [CrossRef]
- Deschamps, A.; De Geuser, F.; Dorin, T.; Weyland, M. The influence of precipitation on plastic deformation of Al-Cu-Li alloys. Acta Mater. 2013, 61, 4010–4021. [Google Scholar] [CrossRef]
- Gazizov, M.; Kaibyshev, R. Low-cyclic fatigue behavior of an Al–Cu–Mg–Ag alloy under T6 and T840 conditions. Mater. Sci. Technol. 2017, 33, 688–698. [Google Scholar] [CrossRef]
- Azimi, A.; Owolabi, G.M.; Fallahdoost, H.; Kumar, N.; Warner, G. Dynamic Failure Investigation in Ultrafne Grained AA2219: Mechanical and Microstructural Analysis. Met. Mater. Int. 2019, 25, 900–911. [Google Scholar] [CrossRef]
- Kim, N.; Lee, E. Effect of T1 precipitate on the anisotropy of Al-Li alloy 2090. Acta Metall. Mater. 1993, 41, 941–948. [Google Scholar] [CrossRef]
- Gerold, V. On the structures of Guinier-Preston zones in Al-Cu alloys introductory paper. Scr. Metall. 1988, 22, 927–932. [Google Scholar] [CrossRef]
- Doherty, R.D. Physical Metallurgy; Cahn, R.W., Hassen, P., Eds.; Elsevier Science: New York, NY, USA, 1996. [Google Scholar]
- Starink, M.J.; Zahra, A.-M. Mechanisms of combined GP zone and θ′ precipitation in an Al-Cu alloy. J. Mater. Sci. Lett. 1997, 16, 1613–1615. [Google Scholar] [CrossRef]
- Ma, Z.; Zhan, L.; Liu, C.; Xu, L.; Xu, Y.; Ma, P.; Li, J. Stress-level-dependency and bimodal precipitation behaviors during creep ageing of Al-Cu alloy: Experiments and modeling. Int. J. Plast. 2018, 110, 183–201. [Google Scholar] [CrossRef]
- Zuiko, I.; Kaibyshev, R. Effect of plastic deformation on the ageing behaviour of an Al–Cu–Mg alloy with a high Cu/Mg ratio. Mater. Sci. Eng. A 2018, 737, 401–412. [Google Scholar] [CrossRef]
- Da Costa Teixeira, J.; Bourgeoisa, L.; Sinclaird, C.W.; Hutchinson, C.R. The effect of shear-resistant, plate-shaped precipitateson the work hardening of Al alloys: Towards a predictionof the strength–elongation correlation. Acta Mater. 2009, 57, 6075–6089. [Google Scholar] [CrossRef]
- Murayama, M.; Horita, Z.; Hono, K. Microstructure of two-phase Al–1.7 at% Cu alloy deformed by equal-channel angular pressing. Acta Mater. 2001, 49, 21–29. [Google Scholar] [CrossRef]
- Liu, Z.; Bai, S.; Zhou, X.; Gu, Y. On strain-induced dissolution of θ′ and θ particles in Al–Cu binary alloy during equal channel angular pressing. Mater. Sci. Eng. A 2011, 528, 2217–2222. [Google Scholar] [CrossRef]
- Dobromyslov, A.V.; Taluts, N.I.; Uksusnikov, A.N.; Kozlov, E.A. Effect of spherically converging shock waves on the phase and structural states of the artificially aged Al–4 wt % Cu alloy. Phys. Met. Metallogr. 2012, 113, 418–425. [Google Scholar] [CrossRef]
- Da-xiang, S.; Xin-ming, Z.; Ling-ying, Y.; Gang, G.; Hai-chun, J.; Xing-hui, G. Evolution of θ′ precipitate in aluminum alloy 2519A impacted by split Hopkinson bar. Mater. Sci. Eng. A 2015, 620, 241–245. [Google Scholar] [CrossRef]
- Olasumboye, A.T.; Owolabi, G.M.; Odeshi, A.G.; Yilmaz, N.; Zeytinci, A. Dynamic Response and Microstructure Evolution of AA2219-T4 and AA2219-T6 Aluminum Alloys. J. Dyn. Behav. Mater. 2018, 4, 151. [Google Scholar] [CrossRef]
- Chung, T.F.; Yang, Y.L.; Hsiao, C.N.; Li, W.C.; Huang, B.M.; Tsao, C.S.; Shi, Z.; Lin, J.; Fischione, P.E.; Ohmura, T.; et al. Morphological evolution of GP zones and nanometer-sized precipitates in the AA2050 aluminium alloy. Int. J. Lightweight Mater. Manuf. 2018, 1, 142–156. [Google Scholar] [CrossRef]
- Kaira, C.S.; Stannard, T.J.; De Andrade, V.; De Carlo, F.; Chawla, N. Exploring novel deformation mechanisms in aluminum-copper alloys using in situ 4D nanomechanical testing. Acta Mater. 2019, 176, 242–249. [Google Scholar] [CrossRef]
- Adlakha, I.; Garg, P.; Solanki, K.N. Revealing the atomistic nature of dislocation-precipitate interactions in Al-Cu alloys. J. Alloys Compd. 2019, 797, 325–333. [Google Scholar] [CrossRef]
- Krasnikov, V.S.; Mayer, A.E. Dislocation dynamics in aluminum containing θ′ phase: Atomistic simulation and continuum modeling. Int. J. Plast. 2019, 119, 21–42. [Google Scholar] [CrossRef]
- Zhang, P.; Bian, J.J.; Yang, C.; Zhang, J.Y.; Liu, G.; Weiss, J.; Sun, J. Plate-like precipitate effects on plasticity of Al-Cu micro-pillar: {100}-interfacial slip. Materialia 2019, 7, 100416. [Google Scholar] [CrossRef] [Green Version]
- Ma, P.P.; Liu, C.H.; Wu, C.L.; Liu, L.M.; Chen, J.H. Mechanical properties enhanced by deformation-modified precipitation of θ′-phase approximants in an Al-Cu alloy. Mater. Sci. Eng. A 2016, 676, 138–145. [Google Scholar] [CrossRef]
- Zuiko, I.; Kaibyshev, R. Ageing response of cold-rolled Al–Cu–Mg alloy. Mater. Sci. Eng. A 2020, 781, 139148. [Google Scholar] [CrossRef]
- Lumley, R.N.; Polmear, I.J.; Morton, A.J. Interrupted aging and secondary precipitation in aluminium alloys. Mater. Sci. Technol. 2003, 19, 1483–1490. [Google Scholar] [CrossRef]
- Fribourg, G.; Brechet, Y.; Deschamps, A.; Simar, A. Microstructure-based modelling of isotropic and kinematic strain hardening in a precipitation-hardened aluminium alloy. Acta Mater. 2011, 59, 3621–3635. [Google Scholar] [CrossRef]
- Anjabin, N.; Taheri, A.K.; Kim, H.S. Constitutive modeling of hot deformation behavior of the aa6063 alloy with different precipitates. Metall. Mater. Trans. A 2013, 44, 5853–5860. [Google Scholar] [CrossRef] [Green Version]
- De Vaucorbeil, A.; Poole, W.J.; Sinclair, C.W. The superposition of strengthening contributions in engineering alloys. Mater. Sci. Eng. A 2013, 582, 147–154. [Google Scholar] [CrossRef]
- Bardel, D.; Perez, M.; Nelias, D.; Dancette, S.; Chaudeta, P.; Massardier, V. Cyclic behaviour of a 6061 aluminium alloy: Coupling precipitation and elastoplastic modelling. Acta Mater. 2015, 83, 256–268. [Google Scholar] [CrossRef]
- Anjabin, N. Modeling the Anisotropic Flow Behavior of Precipitate-Hardened Al–Cu Alloys During Plane Strain Compression. Met. Mater. Int. 2019, 25, 159–167. [Google Scholar] [CrossRef]
- Li, Y.; Shi, Z.; Lin, J. Experimental investigation and modelling of yield strength and work hardening behaviour of artificially aged Al-Cu-Li alloy. Mater. Des. 2019, 183, 108121. [Google Scholar] [CrossRef]
- Bellon, B.; Haoualaa, S.; Lorca, J. An analysis of the influence of the precipitate type on the mechanical behavior of Al–Cu alloys by means of micropillar compression tests. Acta Mater. 2020, 194, 207–223. [Google Scholar] [CrossRef]
- Li, Y.L.; Kohar, C.P.; Mishra, R.K.; Inal, K. A new crystal plasticity constitutive model for simulating precipitation-hardenable aluminum alloys. Int. J. Plast. 2020, 132, 102759. [Google Scholar] [CrossRef]
- Chen, X.; Zhan, L.; Ma, Z.; Xu, Y.; Zheng, Q.; Cai, Y. Study on tensile/compressive asymmetry in creep ageing behavior of Al-Cu alloy under different stress levels. J. Alloys Compd. 2020, 843, 156157. [Google Scholar] [CrossRef]
- Ji, K.; Li, G.; Sun, Y.; Xu, J.; Chen, H.; Chen, K.; Zhu, Y.; Li, Y. A Constitutive Model for Yield Strength and Work Hardening Behaviour of Aluminium Alloys during Artificial Ageing. Metals 2020, 10, 1094. [Google Scholar] [CrossRef]
- Zhou, P.; Song, Y.; Hua, L.; Lin, J.; Lu, J. Using novel strain aging kinetics models to determine the effect of solution temperature on critical strain of Al-Zn-Mg-Cu alloy. J. Alloys Compd. 2020, 838, 155647. [Google Scholar] [CrossRef]
- Bahl, S.; Xiong, L.; Allard, L.F.; Michi, R.A.; Poplawsky, J.D.; Chuang, A.C.; Singh, D.; Watkins, T.R.; Shin, D.; Haynes, J.A.; et al. Aging behavior and strengthening mechanisms of coarsening resistant metastable θ′ precipitates in an Al–Cu alloy. Mater. Des. 2021, 198, 109378. [Google Scholar] [CrossRef]
- Zhang, Z.; Eakins, D.E.; Dunne, F.P.E. On the formation of adiabatic shear bands in textured HCP polycrystals. Int. J. Plast. 2016, 79, 196–216. [Google Scholar] [CrossRef] [Green Version]
- Lia, J.; Lia, Y.; Suo, T.; Wei, Q. Numerical simulations of adiabatic shear localization in textured FCC metal based on crystal plasticity finite element method. Mater. Sci. Eng. A 2018, 737, 348–363. [Google Scholar] [CrossRef]
- Zhou, Y.; Fan, Q.; Liu, X.; Wang, D.; Zhu, X.; Chen, K. Multi-scale crystal plasticity finite element simulations of the microstructural evolution and formation mechanism of adiabatic shear bands in dual-phase Ti20C alloy under complex dynamic loading. J. Mater. Sci. Technol. 2020, 59, 138–148. [Google Scholar] [CrossRef]
- Devincre, B.; Kubin, L.; Hoc, T. Physical analyses of crystal plasticity by DD simulations. Scr. Mater. 2006, 54, 741–746. [Google Scholar] [CrossRef]
- Santos-Güemes, R.; Bellón, B.; Esteban-Manzanares, G.; Segurado, J.; Capolungo, L.; LLorca, J. Multiscale modelling of precipitation hardening in Al–Cu alloys: Dislocation dynamics simulations and experimental validation. Acta Mater. 2020, 188, 475–485. [Google Scholar] [CrossRef] [Green Version]
- Santos-Güemes, R.; Esteban-Manzanares, G.; Papadimitriou, I.; Segurado, J.; Capolungo, L.; LLorca, J. Discrete dislocation dynamics simulations of dislocation-θ′ precipitate interaction in Al-Cu alloys. J. Mech. Phys. Solids 2018, 118, 228–244. [Google Scholar] [CrossRef] [Green Version]
- Krasnikov, V.S.; Mayer, A.E.; Pogorelko, V.V. Prediction of the shear strength of aluminum with θ phase inclusions based on precipitate statistics, dislocation and molecular dynamics. Int. J. Plast. 2020, 128, 102672. [Google Scholar] [CrossRef]
- Krasnikov, V.S.; Mayer, A.E.; Pogorelko, V.V.; Latypov, F.T.; Ebel, A.A. Interaction of dislocation with GP zones or θ″ phase precipitates in aluminum: Atomistic simulations and dislocation dynamics. Int. J. Plast. 2020, 125, 169–190. [Google Scholar] [CrossRef]
- Singh, C.V.; Warner, D.H. Mechanisms of Guinier–Preston zone hardening in the athermal limit. Acta Mater. 2010, 58, 5797–5805. [Google Scholar] [CrossRef]
- Yanilkin, A.V.; Krasnikov, V.S.; Kuksin, A.Y.; Mayer, A.E. Dynamics and kinetics of dislocations in Al and Al–Cu alloy under dynamic loading. Int. J. Plast. 2014, 55, 94–107. [Google Scholar] [CrossRef]
- Wu, B.; Bai, Z.; Misra, A.; Fan, Y. Atomistic mechanism and probability determination of the cutting of Guinier-Preston zones by edge dislocations in dilute Al-Cu alloys. Phys. Rev. Mater. 2020, 4, 020601. [Google Scholar] [CrossRef]
- Verestek, W.; Prskalo, A.P.; Hummel, M.; Binkele, P.; Schmauder, S. Molecular dynamics investigations of the strengthening of Al–Cu alloys during thermal ageing. Phys. Mesomech. 2017, 20, 291–304. [Google Scholar] [CrossRef]
- Esteban-Manzanares, G.; Martínez, E.; Segurado, J.; Capolungo, L.; LLorca, J. An atomistic investigation of the interaction of dislocations with Guinier-Preston zones in Al-Cu alloys. Acta Mater. 2019, 162, 189–201. [Google Scholar] [CrossRef] [Green Version]
- Hu, S.; Baskes, I.; Stan, M.; Chen, L.Q. Atomistic calculations of interfacial energies, nucleus shape and size of θ′ precipitates in Al–Cu alloys. Acta Mater. 2006, 54, 4699. [Google Scholar] [CrossRef]
- Hirel, P. Atomsk: A tool for manipulating and converting atomic data files. Comput. Phys. Commun. 2015, 197, 212–219. [Google Scholar] [CrossRef]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comp. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Apostol, F.; Mishin, Y. Interatomic potential for the Al-Cu system. Phys. Rev. B 2011, 83, 054116. [Google Scholar] [CrossRef] [Green Version]
- Kuksin, A.Y.; Yanilkin, A.V. Dislocation nucleation and motion in metals and alloys at high-rate deformation: Molecular dynamic simulation. Mech. Solids 2015, 50, 44–51. [Google Scholar] [CrossRef]
- Krasnikov, V.S.; Mayer, A.E. Influence of local stresses on motion of edge dislocation in aluminum. Int. J. Plast. 2018, 101, 170–187. [Google Scholar] [CrossRef]
- Marchand, D.; Jain, A.; Glensk, A.; Curtin, W.A. Machine learning for metallurgy I. A neural-network potential for Al-Cu. Phys. Rev. Mater. 2020, 4, 103601. [Google Scholar] [CrossRef]
- Kanel, G.I.; Zaretsky, E.B.; Razorenov, S.V.; Ashitkov, S.I.; Fortov, V.E. Unusual plasticity and strength of metals at ultra-short load durations. Phys. Uspekhi 2017, 60, 490–508. [Google Scholar] [CrossRef] [Green Version]
- Zuanetti, B.; McGrane, S.D.; Bolme, C.A.; Prakash, V. Measurement of elastic precursor decay in pre-heated aluminum films under ultra-fast laser generated shocks. J. Appl. Phys. 2018, 123, 195104. [Google Scholar] [CrossRef] [Green Version]
- Komarov, P.S.; Struleva, E.V.; Ashitkov, S.I. Generation of giant elastic ultrashort shock waves in chromium films by femtosecond laser pulses. J. Phys. Conf. Ser. 2019, 1147, 012023. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; Postma, J.P.M.; van Gunsteren, W.F.; DiNola, A.; Haak, J.R. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 1984, 81, 3684–3690. [Google Scholar] [CrossRef] [Green Version]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO—The Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2010, 18, 015012. [Google Scholar] [CrossRef]
- Kelchner, C.L.; Plimpton, S.J.; Hamilton, J.C. Dislocation nucleation and defect structure during surface indentation. Phys. Rev. B 1998, 58, 11085. [Google Scholar] [CrossRef]
- Stukowski, A.; Bulatov, V.V.; Arsenlis, A. Automated identification and indexing of dislocations in crystal interfaces. Model. Simul. Mater. Sci. Eng. 2012, 20, 085007. [Google Scholar] [CrossRef]
- Fomin, E.V.; Krasnikov, V.S. Interaction of edge dislocation with copper atoms in an aluminum crystal. J. Phys. Conf. Ser. 2020, 1556, 012050. [Google Scholar] [CrossRef]
- Sun, W.; Zhu, Y.; Marceau, R.; Wang, L.; Zhang, Q.; Gao, X.; Hutchinson, C. Precipitation strengthening of aluminum alloys by room-temperature cyclic plasticity. Science 2019, 363, 972–975. [Google Scholar] [CrossRef] [PubMed]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krasnikov, V.S.; Mayer, A.E.; Pogorelko, V.V.; Gazizov, M.R. Influence of θ′ Phase Cutting on Precipitate Hardening of Al–Cu Alloy during Prolonged Plastic Deformation: Molecular Dynamics and Continuum Modeling. Appl. Sci. 2021, 11, 4906. https://doi.org/10.3390/app11114906
Krasnikov VS, Mayer AE, Pogorelko VV, Gazizov MR. Influence of θ′ Phase Cutting on Precipitate Hardening of Al–Cu Alloy during Prolonged Plastic Deformation: Molecular Dynamics and Continuum Modeling. Applied Sciences. 2021; 11(11):4906. https://doi.org/10.3390/app11114906
Chicago/Turabian StyleKrasnikov, Vasiliy S., Alexander E. Mayer, Victor V. Pogorelko, and Marat R. Gazizov. 2021. "Influence of θ′ Phase Cutting on Precipitate Hardening of Al–Cu Alloy during Prolonged Plastic Deformation: Molecular Dynamics and Continuum Modeling" Applied Sciences 11, no. 11: 4906. https://doi.org/10.3390/app11114906
APA StyleKrasnikov, V. S., Mayer, A. E., Pogorelko, V. V., & Gazizov, M. R. (2021). Influence of θ′ Phase Cutting on Precipitate Hardening of Al–Cu Alloy during Prolonged Plastic Deformation: Molecular Dynamics and Continuum Modeling. Applied Sciences, 11(11), 4906. https://doi.org/10.3390/app11114906





