Systematic Review of Anomaly Detection in Hyperspectral Remote Sensing Applications
Abstract
:1. Introduction
2. Part A: Bibliometric Analysis
- RQ 1. What is the trend among scientific publications on hyperspectral image processing for anomaly detection in remote sensing applications?
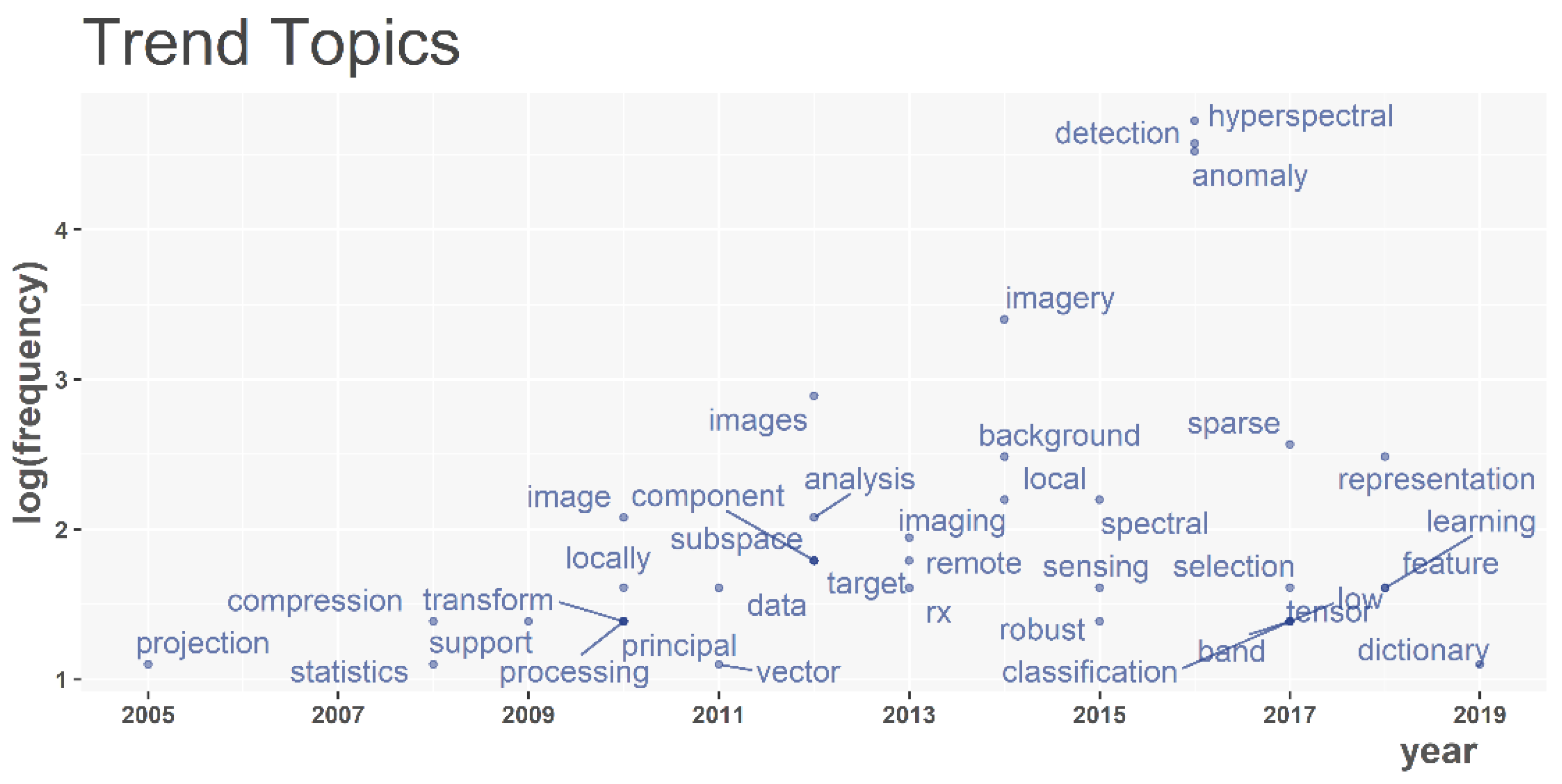
- RQ 2. What are future research directions in this scientific field?
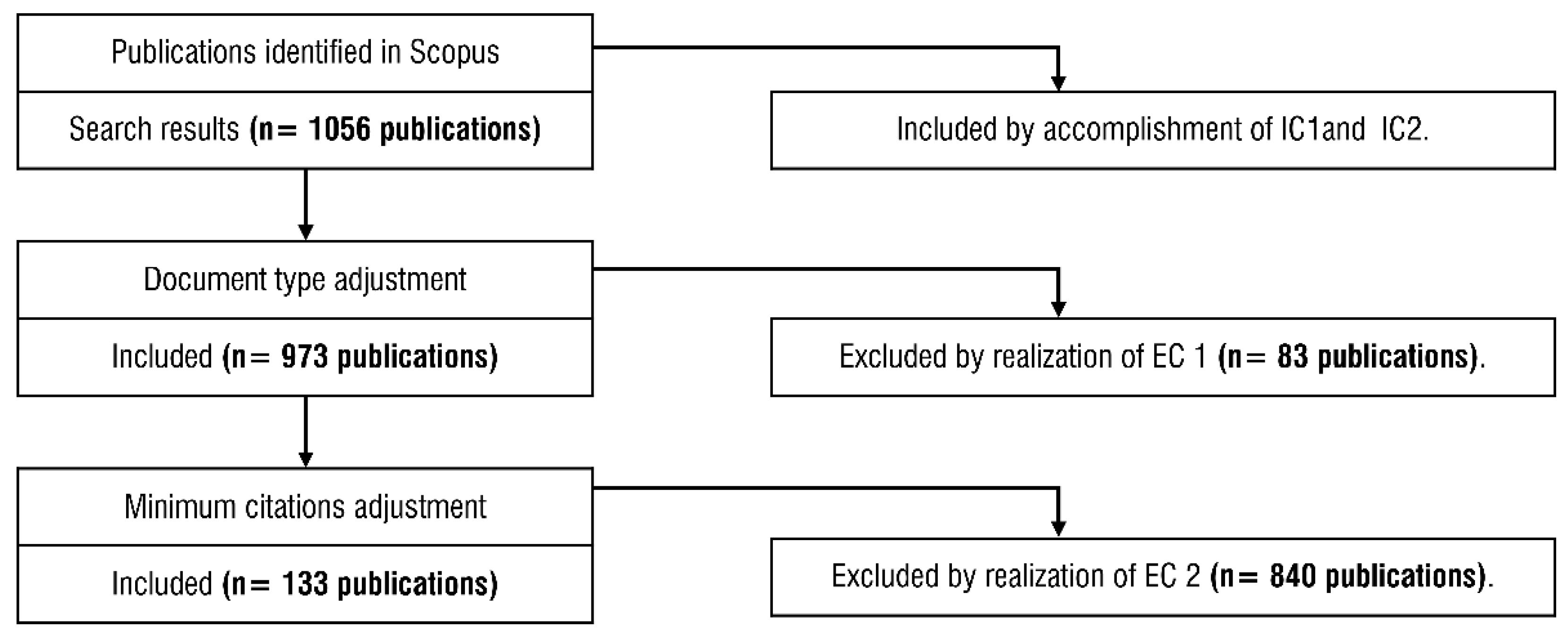
- IC 1. The search string (TITLE-ABS-KEY (hyperspectral AND anomaly AND detection))
- IC 2. The publications are written in English.
- EC 1. Reviews and conference reviews, books and book chapters, letters and notes.
- EC 2. Publications with less than three citations per year.
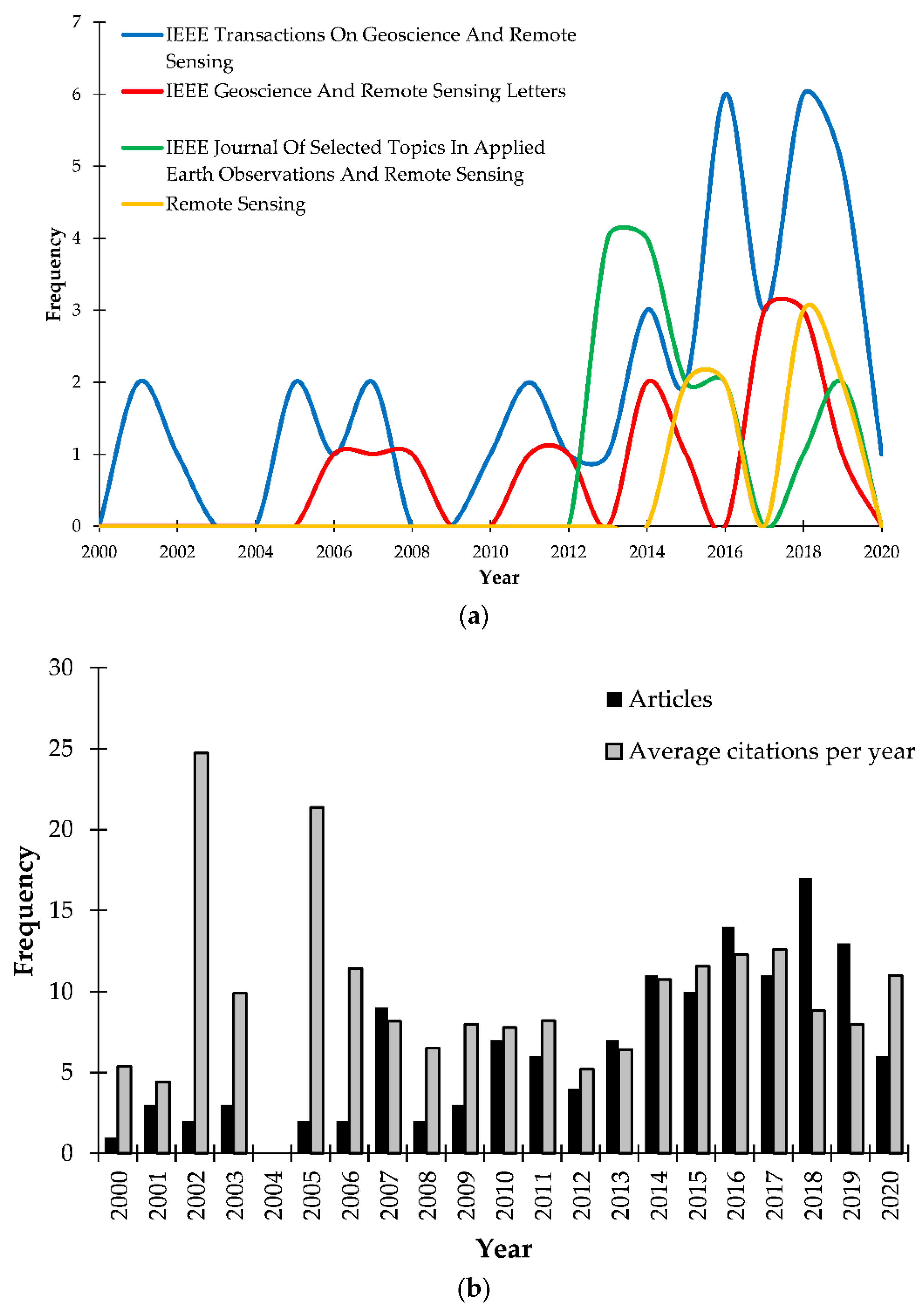
2.1. Descriptive Bibliometric Analysis
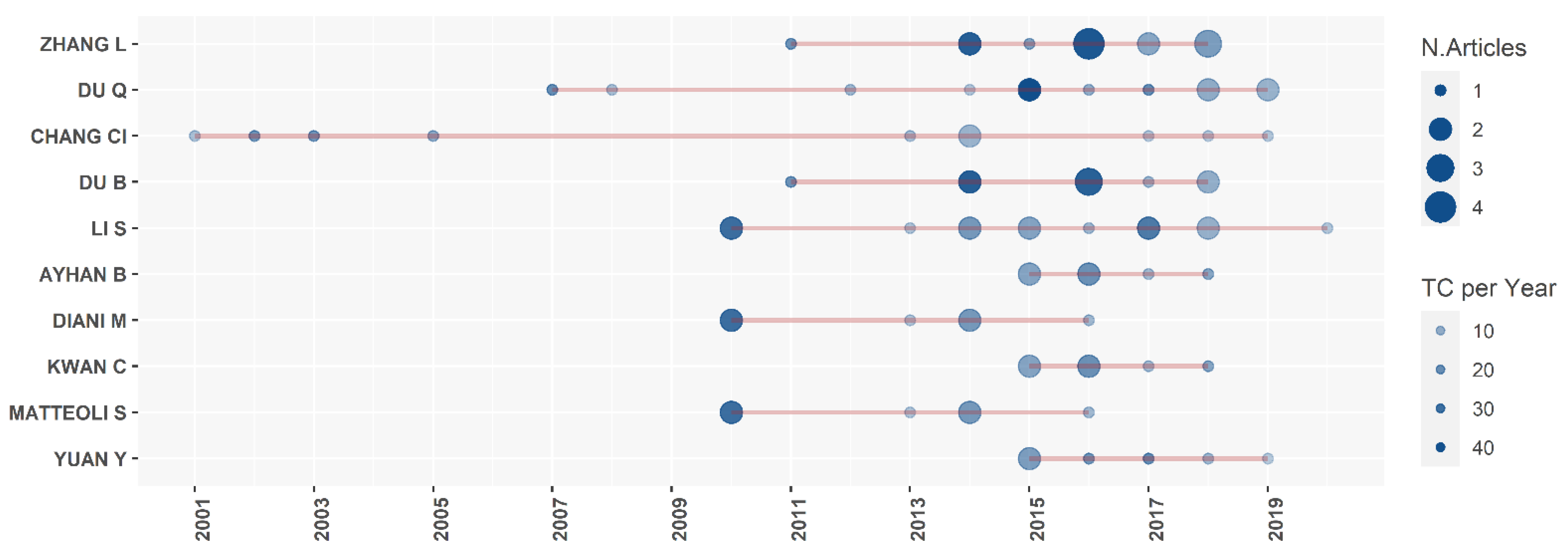
2.2. Authors Analysis
| Document | Reference | Global Citations | Local Citations |
|---|---|---|---|
| Stein, D.W.J.; Beaven, S.G.; Hoff, L.E.; Winter, E.M.; Schaum, A.P.; Stocker, A.D. Anomaly detection from hyperspectral imagery. IEEE Signal Process Mag 2002, 19, 58–69, doi:10.1109/79.974730 | [15] | 554 | 54 |
| Kwon, H.; Nasrabadi, N.M. Kernel RX-algorithm: A non-linear anomaly detector for hyperspectral imagery. IEEE Trans Geosci Remote Sens 2005, 43, 388–397, doi:10.1109/TGRS.2004.841487 | [26] | 470 | 56 |
| Chang, C.I.; Chiang, S.S. Anomaly detection and classification for hyperspectral imagery. IEEE Trans Geosci Remote Sens 2002, 40, 1314–1325, doi:10.1109/TGRS.2002.800280 | [28] | 386 | 51 |
| Ren, H.; Chang, C., I. Automatic spectral target recognition in hyperspectral imagery. IEEE Trans. Aerosp. Electron. Syst. 2003, 39, 1232–1249, doi:10.1109/TAES.2003.1261124. | [29] | 360 | 5 |
| Matteoli, S.; Diani, M.; Corsini, G. A tutorial overview of anomaly detection in hyperspectral images. IEEE Aerosp Electron Syst Mag 2010, 25, 5–27, doi:10.1109/MAES.2010.5546306. | [11] | 322 | 33 |
| Du, Q.; Fowler, J.E. Hyperspectral Image Compression Using JPEG2000 and Principal Component Analysis. IEEE Geoscience and Remote Sensing Letters 2007, 4, 201–205, doi:10.1109/LGRS.2006.888109. | [30] | 321 | 2 |
| Banerjee, A.; Burlina, P.; Diehl, C. A support vector method for anomaly detection in hyperspectral imagery. IEEE Trans Geosci Remote Sens 2006, 44, 2282–2291, doi:10.1109/tgrs.2006.873019. | [31] | 286 | 38 |
| Li, W.; Du, Q. Collaborative representation for hyperspectral anomaly detection. IEEE Trans Geosci Remote Sens 2015, 53, 1463–1474, doi:10.1109/tgrs.2014.2343955. | [27] | 251 | 42 |
| Penna, B.; Tillo, T.; Magli, E.; Olmo, G. Transform Coding Techniques for Lossy Hyperspectral Data Compression. IEEE Trans Geosci Remote Sens 2007, 45, 1408–1421, doi:10.1109/TGRS.2007.894565. | [32] | 241 | 3 |
| Du, B.; Zhang, L. A Discriminative Metric Learning Based Anomaly Detection Method. IEEE Trans Geosci Remote Sens 2014, 52, 6844–6857, doi:10.1109/TGRS.2014.2303895. | [33] | 220 | 27 |
| Document | Reference | Local Citations |
|---|---|---|
| Reed, I.S.; Yu, X. Adaptive Multiple-Band CFAR Detection of an Optical Pattern with Unknown Spectral Distribution. IEEE Trans. Acoust. Speech Sign. Proces. 1990, 38, 1760–1770, doi:10.1109/29.60107. | [34] | 90 |
| Carlotto, M.J. A cluster-based approach for detecting man-made objects and changes in imagery. IEEE Trans Geosci Remote Sens 2005, 43, 374–387, doi:10.1109/TGRS.2004.841481 | [35] | 32 |
| Manolakis, D.; Shaw, G. Detection algorithms for hyperspectral imaging applications. IEEE Signal Process Mag 2002, 19, 29–43, doi:10.1109/79.974724. | [9] | 32 |
| Nasrabadi, N.M. Hyperspectral target detection: An overview of current and future challenges. IEEE Signal Process Mag 2014, 31, 34–44, doi:10.1109/MSP.2013.2278992 | [18] | 21 |
| Harsanyi, J.C.; Chang, C.I. Hyperspectral Image Classification and Dimensionality Reduction: An Orthogonal Subspace Projection Approach. IEEE Trans Geosci Remote Sens 1994, 32, 779–785, doi:10.1109/36.298007 | [36] | 19 |
| Kerekes, J. Receiver operating characteristic curve confidence intervals and regions. IEEE Geoscience and Remote Sensing Letters 2008, 5, 251–255, doi:10.1109/lgrs.2008.915928. | [37] | 17 |
| Manolakis, D.; Marden, D.; Shaw, G.A. Hyperspectral Image Processing for Automatic Target Detection Applications. Lincoln laboratory journal 2003, 14, 79–116 | [38] | 16 |
| Nasrabadi, N.M. Regularization for spectral matched filter and RX anomaly detector. In Proceedings of Proc SPIE Int Soc Opt Eng, 2008 | [39] | 16 |
| Chen, Y.; Nasrabadi, N.M.; Tran, T.D. Sparse Representation for Target Detection in Hyperspectral Imagery. IEEE J. Sel. Top. Signal Process. 2011, 5, 629–640, doi:10.1109/jstsp.2011.2113170 | [40] | 16 |
| Chen, Y.; Nasrabadi, N.M.; Tran, T.D. Hyperspectral Image Classification Using Dictionary-Based Sparse Representation. IEEE Trans Geosci Remote Sens 2011, 49, 3973–3985, doi:10.1109/tgrs.2011.2129595. | [41] | 16 |
3. Part B: An Overview of Hyperspectral Image Processing for Anomaly Detection in Remote Sensing Applications
4. Mathematical Framework for Anomaly Detection
5. Unstructured Background Models
5.1. Reed-Xiaoli (RX) Algorithm
Improved Variants of the RX Detector
5.2. Nearest Neighbor Detectors
5.3. Kernel-Based Models
5.3.1. Kernel RX detector
5.3.2. Kernel Density Estimate of the Background Distribution Models
5.3.3. Support Vector Data Description (SVDD)
6. Structured Background Models
6.1. Subspace Models
6.1.1. Orthogonal Subspace Models
6.1.2. Signal Subspace Models
6.2. Cluster or Mixture-based Models
6.2.1. Gaussian-Mixture Model
6.2.2. Cluster or Segmentation Based Models
6.3. Representation-based Models
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Adao, T.; Hruska, J.; Padua, L.; Bessa, J.; Peres, E.; Morais, R.; Sousa, J.J. Hyperspectral Imaging: A Review on UAV-Based Sensors, Data Processing and Applications for Agriculture and Forestry. Remote Sens. 2017, 9, 1110. [Google Scholar] [CrossRef] [Green Version]
- Gowen, A.A.; O’Donnell, C.P.; Cullen, P.J.; Downey, G.; Frias, J.M. Hyperspectral imaging—An emerging process analytical tool for food quality and safety control. Trends Food Sci. Technol. 2007, 18, 590–598. [Google Scholar] [CrossRef]
- Bajić, M. Modeling and Simulation of Very High Spatial Resolution UXOs and Landmines in a Hyperspectral Scene for UAV Survey. Remote Sens. 2021, 13, 837. [Google Scholar] [CrossRef]
- Krtalić, A.; Bajić, M. Development of the TIRAMISU Advanced Intelligence Decision Support System. Eur. J. Remote Sens. 2019, 52, 40–55. [Google Scholar] [CrossRef] [Green Version]
- Lu, G.L.; Fei, B.W. Medical hyperspectral imaging: A review. J. Biomed. Opt. 2014, 19, 010901. [Google Scholar] [CrossRef]
- Eismann, M.T.; Stocker, A.D.; Nasrabadi, N.M. Automated Hyperspectral Cueing for Civilian Search and Rescue. Proc. IEEE 2009, 97, 1031–1055. [Google Scholar] [CrossRef]
- Krtalić, A.; Bajić, M.; Ivelja, T.; Racetin, I. The AIDSS Module for Data Acquisition in Crisis Situations and Environmental Protection. Sensors 2020, 20, 1267. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Govender, M.; Chetty, K.; Bulcock, H. A review of hyperspectral remote sensing and its application in vegetation and water resource studies. Water SA 2007, 33, 145–151. [Google Scholar] [CrossRef] [Green Version]
- Manolakis, D.; Shaw, G. Detection algorithms for hyperspectral imaging applications. IEEE Signal Process. Mag. 2002, 19, 29–43. [Google Scholar] [CrossRef]
- Manolakis, D. Taxonomy of detection algorithms for hyperspectral imaging applications. Opt. Eng. 2005, 44, 1–11. [Google Scholar] [CrossRef]
- Matteoli, S.; Diani, M.; Corsini, G. A tutorial overview of anomaly detection in hyperspectral images. IEEE Aerosp. Electron. Syst. Mag. 2010, 25, 5–27. [Google Scholar] [CrossRef]
- Elachi, C.; Van Zyl, J.J. Introduction to the Physics and Techniques of Remote Sensing; John Wiley & Sons: Hoboken, NJ, USA, 2006; Volume 28. [Google Scholar]
- Schowengerdt, R.A. Remote Sensing: Models and Methods for Image Processing; Academic Press: San Diego, CA, USA, 2006. [Google Scholar]
- Alpaydin, E. Introduction to Machine Learning; The MIT Press: Cambridge, MA, USA, 2010. [Google Scholar]
- Stein, D.W.J.; Beaven, S.G.; Hoff, L.E.; Winter, E.M.; Schaum, A.P.; Stocker, A.D. Anomaly detection from hyperspectral imagery. IEEE Signal Process. Mag. 2002, 19, 58–69. [Google Scholar] [CrossRef] [Green Version]
- Huck, A.; Guillaume, M. A CFAR algorithm for anomaly detection and discrimination in hyperspectral images. In Proceedings of the 2008 15th IEEE International Conference on Image Processing, San Diego, CA, USA, 12–15 October 2008; pp. 1868–1871. [Google Scholar]
- Matteoli, S.; Diani, M.; Theiler, J. An overview of background modeling for detection of targets and anomalies in hyperspectral remotely sensed imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2317–2336. [Google Scholar] [CrossRef]
- Nasrabadi, N.M. Hyperspectral target detection: An overview of current and future challenges. IEEE Signal Process. Mag. 2014, 31, 34–44. [Google Scholar] [CrossRef]
- Falagas, M.E.; Pitsouni, E.I.; Malietzis, G.A.; Pappas, G. Comparison of PubMed, Scopus, Web of Science, and Google Scholar: Strengths and weaknesses. FASEB J. 2008, 22, 338–342. [Google Scholar] [CrossRef] [PubMed]
- Mongeon, P.; Paul-Hus, A. The journal coverage of Web of Science and Scopus: A comparative analysis. Scientometrics 2016, 106, 213–228. [Google Scholar] [CrossRef]
- Elsevier. Scopus Content Coverage Guide. Available online: https://www.elsevier.com/__data/assets/pdf_file/0007/69451/Scopus_ContentCoverage_Guide_WEB.pdf (accessed on 24 April 2021).
- Moher, D.; Liberati, A.; Tetzlaff, J.; Altman, D.G.; Altman, D.; Antes, G.; Atkins, D.; Barbour, V.; Barrowman, N.; Berlin, J.A.; et al. Preferred reporting items for systematic reviews and meta-analyses: The PRISMA statement. Ann. Intern. Med. 2009, 151, 264–269. [Google Scholar] [CrossRef] [Green Version]
- Aria, M.; Cuccurullo, C. bibliometrix: An R-tool for comprehensive science mapping analysis. J. Informetr. 2017, 11, 959–975. [Google Scholar] [CrossRef]
- Elango, B.; Rajendran, P. Authorship trends and collaboration pattern in the marine sciences literature: A scientometric study. Int. J. Inf. Dissem. Technol. 2012, 2, 166–169. [Google Scholar]
- Bradford, S.C. Sources of information on specific subjects. Engineering 1934, 137, 85–86. [Google Scholar]
- Kwon, H.; Nasrabadi, N.M. Kernel RX-algorithm: A nonlinear anomaly detector for hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2005, 43, 388–397. [Google Scholar] [CrossRef]
- Li, W.; Du, Q. Collaborative representation for hyperspectral anomaly detection. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1463–1474. [Google Scholar] [CrossRef]
- Chang, C.I.; Chiang, S.S. Anomaly detection and classification for hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1314–1325. [Google Scholar] [CrossRef] [Green Version]
- Ren, H.; Chang, C.I. Automatic spectral target recognition in hyperspectral imagery. IEEE Trans. Aerosp. Electron. Syst. 2003, 39, 1232–1249. [Google Scholar] [CrossRef] [Green Version]
- Du, Q.; Fowler, J.E. Hyperspectral image compression using JPEG2000 and principal component analysis. IEEE Geosci. Remote Sens. Lett. 2007, 4, 201–205. [Google Scholar] [CrossRef]
- Banerjee, A.; Burlina, P.; Diehl, C. A support vector method for anomaly detection in hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2282–2291. [Google Scholar] [CrossRef]
- Penna, B.; Tillo, T.; Magli, E.; Olmo, G. Transform coding techniques for lossy hyperspectral data compression. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1408–1421. [Google Scholar] [CrossRef]
- Du, B.; Zhang, L. A discriminative metric learning based anomaly detection method. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6844–6857. [Google Scholar] [CrossRef]
- Reed, I.S.; Yu, X. Adaptive Multiple-Band CFAR Detection of an Optical Pattern with Unknown Spectral Distribution. IEEE Trans. Acoust. Speech Sign. Proces. 1990, 38, 1760–1770. [Google Scholar] [CrossRef]
- Carlotto, M.J. A cluster-based approach for detecting man-made objects and changes in imagery. IEEE Trans. Geosci. Remote Sens. 2005, 43, 374–387. [Google Scholar] [CrossRef]
- Harsanyi, J.C.; Chang, C.I. Hyperspectral Image Classification and Dimensionality Reduction: An Orthogonal Subspace Projection Approach. IEEE Trans. Geosci. Remote Sens. 1994, 32, 779–785. [Google Scholar] [CrossRef] [Green Version]
- Kerekes, J. Receiver operating characteristic curve confidence intervals and regions. IEEE Geosci. Remote Sens. Lett. 2008, 5, 251–255. [Google Scholar] [CrossRef] [Green Version]
- Manolakis, D.; Marden, D.; Shaw, G.A. Hyperspectral Image Processing for Automatic Target Detection Applications. Linc. Lab. J. 2003, 14, 79–116. [Google Scholar]
- Nasrabadi, N.M. Regularization for spectral matched filter and RX anomaly detector. SPIE Int. Soc. Opt. Eng. 2008. [Google Scholar] [CrossRef]
- Chen, Y.; Nasrabadi, N.M.; Tran, T.D. Sparse representation for target detection in hyperspectral imagery. IEEE J. Sel. Top. Signal Process. 2011, 5, 629–640. [Google Scholar] [CrossRef]
- Chen, Y.; Nasrabadi, N.M.; Tran, T.D. Hyperspectral image classification using dictionary-based sparse representation. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3973–3985. [Google Scholar] [CrossRef]
- Kay, S.M. Fundamentals of Statistical Signal Processing: Detection Theory; Prentice Hall: Hoboken, NJ, USA, 1998; p. 998. [Google Scholar]
- Neyman, J.; Pearson, E.S.; Pearson, K. IX. On the problem of the most efficient tests of statistical hypotheses. Philos. Trans. R. Soc. Lond. Ser. A Contain. Pap. Math. Phys. Character 1933, 231, 289–337. [Google Scholar] [CrossRef] [Green Version]
- Mahalanobis, P.C. On the Generalised Distance in Statistics; National Institute of Sciences: Calcutta, India, 1936; pp. 49–55. [Google Scholar]
- Veracini, T.; Matteoli, S.; Diani, M.; Corsini, G. An anomaly detection architecture based on a data-adaptive density estimation. In Proceedings of the 2011 3rd Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Lisbon, Portugal, 6–9 June 2011. [Google Scholar] [CrossRef]
- Ma, N.; Peng, Y.; Wang, S.; Leong, P.H.W. An unsupervised deep hyperspectral anomaly detector. Sensors 2018, 18, 693. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Su, H.; Wu, Z.; Du, Q.; Du, P. Hyperspectral Anomaly Detection Using Collaborative Representation with Outlier Removal. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 5029–5038. [Google Scholar] [CrossRef]
- Li, F.; Zhang, X.; Zhang, L.; Jiang, D.; Zhang, Y. Exploiting Structured Sparsity for Hyperspectral Anomaly Detection. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4050–4064. [Google Scholar] [CrossRef]
- Taghipour, A.; Ghassemian, H. Hyperspectral anomaly detection using spectral–spatial features based on the human visual system. Int. J. Remote Sens. 2019, 40, 8683–8704. [Google Scholar] [CrossRef]
- Kelly, E.J. An Adaptive Detection Algorithm. IEEE Trans. Aerosp. Electron. Syst. 1986, AES-22, 115–127. [Google Scholar] [CrossRef] [Green Version]
- Hunt, B.R.; Cannon, T.M. Nonstationary assumptions for gaussian models of images. IEEE Trans. Syst. Man. Cybern. 1976, SCM-6, 876–882. [Google Scholar]
- Margalit, A.; Reed, I.S.; Gagliardi, R.M. Adaptive Optical Target Detection Using Correlated Images. IEEE Trans. Aerosp. Electron. Syst. 1985, AES-21, 394–405. [Google Scholar] [CrossRef]
- Chen, J.Y.; Reed, I.S. A Detection Algorithm for Optical Targets in Clutter. IEEE Trans. Aerosp. Electron. Syst. 1987, AES-23, 46–59. [Google Scholar] [CrossRef]
- Swain, P.H.; Davis, S.M. Remote sensing: The quantitative approach. IEEE Trans. Pattern Anal. Mach. Intell. 1981, 713–714. [Google Scholar] [CrossRef]
- Molero, J.M.; Garzon, E.M.; Garcia, I.; Plaza, A. Analysis and optimizations of global and local versions of the RX algorithm for anomaly detection in hyperspectral data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 801–814. [Google Scholar] [CrossRef]
- Molero, J.M.; Garzón, E.M.; García, I.; Plaza, A. Anomaly detection based on a parallel kernel RX algorithm for multicore platforms. J. Appl. Remote Sens. 2012, 6, 061503. [Google Scholar] [CrossRef]
- Molero, J.M.; Garzon, E.M.; Garcia, I.; Quintana-Orti, E.S.; Plaza, A. Efficient implementation of hyperspectral anomaly detection techniques on GPUs and multicore processors. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2256–2266. [Google Scholar] [CrossRef] [Green Version]
- Molero, J.M.; Paz, A.; Garzón, E.M.; Martínez, J.A.; Plaza, A.; García, I. Fast anomaly detection in hyperspectral images with RX method on heterogeneous clusters. J. Supercomput. 2011, 58, 411–419. [Google Scholar] [CrossRef]
- Manolakis, D.; Marden, D. Non Gaussian models for hyperspectral algorithm design and assessment. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Toronto, ON, Canada, 24–28 June 2002; pp. 1664–1666. [Google Scholar]
- Marden, D.B.; Manolakis, D. Modeling Hyperspectral Imaging Data. In Proceedings of the Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral Imagery IX, Orlando, FL, USA, 23 September 2003; pp. 253–262. [Google Scholar]
- Niu, S.; Ingle, V.K.; Manolakis, D.; Cooley, T. On the modeling of hyperspectral imaging data with elliptically contoured distributions. In Proceedings of the 2010 2nd Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing, Reykjavik, Iceland, 14–16 June 2010; pp. 1–4. [Google Scholar]
- Caefer, C.E.; Silverman, J.; Orthal, O.; Antonelli, D.; Sharoni, Y.; Rotman, S.R. Improved covariance matrices for point target detection in hyperspectral data. Opt. Eng. 2008, 47, 076402. [Google Scholar] [CrossRef]
- Matteoli, S.; Diani, M.; Corsini, G. Improved covariance matrix estimation: Interpretation and experimental analysis of different approaches for anomaly detection applications. In Proceedings of the Image and Signal Processing for Remote Sensing XV, Berlin, Germany, 28 September 2009. [Google Scholar] [CrossRef]
- Gorelik, N.; Blumberg, D.; Rotman, S.R.; Borghys, D. Nonsingular approximations for a singular covariance matrix. In Proceedings of the Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral Imagery XVIII, Baltimore, MD, USA, 24 May 2012. [Google Scholar] [CrossRef]
- Huber-Lerner, M.; Hadar, O.; Rotman, S.R.; Huber-Shalem, R. Compression of hyperspectral images containing a subpixel target. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2246–2255. [Google Scholar] [CrossRef]
- Borghys, D.; Kasen, I.; Achard, V.; Perneel, C. Comparative evaluation of hyperspectral anomaly detectors in different types of background. In Proceedings of the Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral Imagery XVIII, Baltimore, MD, USA, 24 May 2012. [Google Scholar] [CrossRef]
- Friedman, J.H. Regularized discriminant analysis. J. Am. Stat. Assoc. 1989, 84, 165–175. [Google Scholar] [CrossRef]
- Hoffbeck, J.P.; Landgrebe, D.A. Covariance matrix estimation and classification with limited training data. IEEE Trans. Pattern Anal. Mach. Intell. 1996, 18, 763–767. [Google Scholar] [CrossRef]
- Kuo, B.C.; Landgrebe, D.A. A covariance estimator for small sample size classification problems and its application to feature extraction. IEEE Trans. Geosci. Remote Sens. 2002, 40, 814–819. [Google Scholar] [CrossRef] [Green Version]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer: New York, NY, USA, 2001. [Google Scholar]
- Manolakis, D.; Marden, D.; Kerekes, J.; Shaw, G. On the statistics of hyperspectral imaging data. In Proceedings of the Algorithms for Multispectral, Hyperspectral, and Ultraspectral Imagery VII, Orlando, FL, USA, 20 August 2001; pp. 308–316. [Google Scholar] [CrossRef] [Green Version]
- Hansen, P.C. Rank-Deficient and Discrete Ill-Posed Problems; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1999. [Google Scholar]
- Theiler, J. The incredible shrinking covariance estimator. In Proceedings of the Automatic Target Recognition XXII, Baltimore, MD, USA, 2 May 2012. [Google Scholar] [CrossRef] [Green Version]
- Davidson, C.E.; Ben-David, A. On the use of covariance and correlation matrices in hyperspectral detection. In Proceedings of the 2011 IEEE Applied Imagery Pattern Recognition Workshop (AIPR), Washington, DC, USA, 11–13 October 2011. [Google Scholar] [CrossRef]
- Rossi, A.; Acito, N.; Diani, M.; Corsini, G. RX architectures for real-time anomaly detection in hyperspectral images. J. Real-Time Image Process. 2014, 9, 503–517. [Google Scholar] [CrossRef]
- Zhao, C.; Wang, Y.; Qi, B.; Wang, J. Global and local real-time anomaly detectors for hyperspectral remote sensing imagery. Remote Sens. 2015, 7, 3966–3985. [Google Scholar] [CrossRef] [Green Version]
- Stellman, C.M.; Hazel, G.G.; Bucholtz, F.; Michalowicz, J.V.; Stocker, A.; Schaaf, W. Real-time hyperspectral detection and cuing. Opt. Eng. 2000, 39, 1928–1935. [Google Scholar] [CrossRef]
- Liu, W.M.; Chang, C.I. Multiple-window anomaly detection for hyperspectral imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 644–658. [Google Scholar] [CrossRef]
- Ren, L.; Zhao, L.; Wang, Y. A Superpixel-Based Dual Window RX for Hyperspectral Anomaly Detection. IEEE Geosci. Remote Sens. Lett. 2020, 17, 1233–1237. [Google Scholar] [CrossRef]
- Hu, X.; Hu, S.; Zhang, X.; Zhang, H.; Luo, L. Anomaly Detection Based on Local Nearest Neighbor Distance Descriptor in Crowded Scenes. Sci. World J. 2014, 2014, 632575. [Google Scholar] [CrossRef] [PubMed]
- Ming, Z.; Jingchao, C.; Yang, L. A Review of Anomaly Detection Techniques Based on Nearest Neighbor. In Proceedings of the 2018 International Conference on Computer Modeling, Simulation and Algorithm (CMSA 2018), Beijing, China, 22–23 April 2018; pp. 290–292. [Google Scholar] [CrossRef] [Green Version]
- Ahlberg, J.; Renhorn, I. Multi- and Hyperspectral Target and Anomaly Detection; Swedish Defence Research Agency, Division of Sensor Technology: Linköping, Sweden, 2004. [Google Scholar]
- Kruse, F.A.; Lefkoff, A.B.; Boardman, J.W.; Heidebrecht, K.B.; Shapiro, A.T.; Barloon, P.J.; Goetz, A.F.H. The spectral image processing system (SIPS)—interactive visualization and analysis of imaging spectrometer data. Remote Sens. Environ. 1993, 44, 145–163. [Google Scholar] [CrossRef]
- Krause, E.F. Taxicab Geometry: An Adventure in Non-Euclidean Geometry; Dover: New York, NY, USA, 1986. [Google Scholar]
- Cantrell, C.D. Modern Mathematical Methods for Physicists and Engineers; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Schlamm, A.; Messinger, D. A euclidean distance transformation for improved anomaly detection in spectral imagery. In Proceedings of the 2010 Western New York Image Processing Workshop, Rochester, NY, USA, 5 November 2010; pp. 26–29. [Google Scholar]
- Merkwirth, C.; Parlitz, U.; Lauterborn, W. Fast nearest-neighbor searching for nonlinear signal processing. Phys. Rev. E 2000, 62, 2089–2097. [Google Scholar] [CrossRef] [PubMed]
- Zhao, M.; Saligrama, V. Anomaly detection with score functions based on nearest neighbor graphs. In Proceedings of the Advances in Neural Information Processing Systems 22, Vancouver, BC, Canada, 7–10 December 2009; pp. 2250–2258. [Google Scholar]
- Schölkopf, B.; Smola, A.J. Learning with Kernels; The MIT Press: Cambridge, MA, USA, 2002. [Google Scholar]
- Zhao, C.; Yao, X.; Yan, Y. Modified Kernel RX Algorithm Based on Background Purification and Inverse-of-Matrix-Free Calculation. IEEE Geosci. Remote Sens. Lett. 2017, 14, 544–548. [Google Scholar] [CrossRef]
- Hotelling, H. Analysis of a complex of statistical variables into principal components. J. Educ. Psychol. 1933, 24, 417–441. [Google Scholar] [CrossRef]
- Hidalgo, J.A.P.; Pérez-Suay, A.; Nar, F.; Camps-Valls, G. Efficient Nonlinear RX Anomaly Detectors. IEEE Geosci. Remote Sens. Lett. 2021, 18, 231–235. [Google Scholar] [CrossRef]
- Scott, D. Multivariate Density Estimation; Wiley: New York, NY, USA, 1992. [Google Scholar]
- Silverman, B.W. Density Estimation for Statistics and Data Analysis; CRC Press: London, UK, 1986. [Google Scholar]
- Matteoli, S.; Veracini, T.; Diani, M.; Corsini, G. Background density nonparametric estimation with data-adaptive bandwidths for the detection of anomalies in multi-hyperspectral imagery. IEEE Geosci. Remote Sens. Lett. 2014, 11, 163–167. [Google Scholar] [CrossRef]
- Matteoli, S.; Veracini, T.; Diani, M.; Corsini, G. Models and methods for automated background density estimation in hyperspectral anomaly detection. IEEE Trans. Geosci. Remote Sens. 2013, 51, 2837–2852. [Google Scholar] [CrossRef]
- Matteoli, S.; Veracini, T.; Diani, M.; Corsini, G. A Locally Adaptive Background Density Estimator: An evolution for rx-based anomaly detectors. IEEE Geosci. Remote Sens. Lett. 2014, 11, 323–327. [Google Scholar] [CrossRef]
- Veracini, T.; Matteoli, S.; Diani, M.; Corsini, G. Nonparametric framework for detecting spectral anomalies in hyperspectral images. IEEE Geosci. Remote Sens. Lett. 2011, 8, 666–670. [Google Scholar] [CrossRef]
- Veracini, T.; Matteoli, S.; Diani, M.; Corsini, G.; De Ceglie, S.U. A non-parametric approach to anomaly detection in hyperspectral images. In Proceedings of the SPIE 7830, Image and Signal Processing for Remote Sensing XVI, Toulouse, France, 22 October 2010. [Google Scholar] [CrossRef]
- Ruiz, A.; López-de-Teruel, P.E. Nonlinear kernel-based statistical pattern analysis. IEEE Trans. Neural Netw. 2001, 12, 16–32. [Google Scholar] [CrossRef]
- Cremers, D.; Kohlberger, T.; Schnörr, C. Shape statistics in kernel space for variational image segmentation. Pattern Recognit. 2003, 36, 1929–1943. [Google Scholar] [CrossRef] [Green Version]
- Terrell, G.R.; Scott, D.W. Variable kernel density estimation. Ann. Stat. 1992, 20, 1236–1265. [Google Scholar] [CrossRef]
- Banerjee, A.; Burlina, P.; Meth, R. Fast hyperspectral anomaly detection via SVDD. In Proceedings of the International Conference on Image Processing, San Antonio, TX, USA, 16 September–19 October 2007; pp. IV101–IV104. [Google Scholar] [CrossRef]
- Schölkopf, B.; Platt, J.; Shawe-Taylor, J.; Smola, A.J.; Williamson, R.C. Estimating the support of a high-dimensional distribution. Tech. Rep. 2001, 13, 1443–1471. [Google Scholar] [CrossRef]
- Tax, D.; Duin, R. Data domain description by support vectors. ESANN 1999, 99, 251–256. [Google Scholar]
- Tax, D.M.J.; Ypma, A.; Duin, R.P.W. Support vector data description applied to machine vibration analysis. In Proceedings of the 5th Annual Conference of the Advanced School for Computing and Imaging, Delft, The Netherlands, 15–17 June 1999; pp. 398–405. [Google Scholar]
- Gualtieri, J.A.; Chettri, S.R.; Cromp, R.F.; Johnson, L.F. Support vector machine classifiers as applied to AVIRIS data. Summ. Eighth Jpl Airbrone Earth Sci. Workshop 1999, 217–227. Available online: http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.30.2656 (accessed on 24 April 2021).
- Gualtieri, J.A.; Cromp, R.F. Support vector machines for hyperspectral remote sensing classification. Proc. Spie Int. Soc. Opt. Eng. 1999, 3584, 221–232. [Google Scholar]
- Boltyanski, V.; Martini, H.; Soltan, V. Geometric Methods and Optimization Problems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 4. [Google Scholar]
- Golub, G.H.; Reinsch, C. Singular value decomposition and least squares solutions. In Linear Algebra; Springer: Berlin/Heidelberg, Germany, 1971; pp. 134–151. [Google Scholar]
- Comon, P. Independent component analysis, a new concept? Signal Process. 1994, 36, 287–314. [Google Scholar] [CrossRef]
- Chang, C.I. Orthogonal Subspace Projection (OSP) revisited: A comprehensive study and analysis. IEEE Trans. Geosci. Remote Sens. 2005, 43, 502–518. [Google Scholar] [CrossRef]
- Ranney, K.I.; Soumekh, M. Hyperspectral anomaly detection within the signal subspace. IEEE Geosci. Remote Sens. Lett. 2006, 3, 312–316. [Google Scholar] [CrossRef]
- Winter, E.M.; Winter, M.E. Autonomous hyperspectral end-member determination methods. In Proceedings of the Sensors, Systems, and Next-Generation Satellites III, Florence, Italy, 28 December 1999; pp. 150–158. [Google Scholar]
- Winter, M.E. N-FINDR: An algorithm for fast autonomous spectral end-member determination in hyperspectral data. In Proceedings of the SPIE’s International Symposium on Optical Science, Engineering, and Instrumentation, Denver, CO, USA, 27 October 1999; pp. 266–275. [Google Scholar]
- Bowles, J.; Gillis, D.; Palmadesso, P. New improvements in the ORASIS algorithm. In Proceedings of the 2000 IEEE Aerospace Conference, Big Sky, MT, USA, 25–25 March 2000; pp. 293–298. [Google Scholar]
- Boardman, J.W. Automating spectral unmixing of AVIRIS data using convex geometry concepts. In Proceedings of the Summaries 4th Annu. JPL Airborne Geosci. Workshop, Pasadena, CA, USA, 25 October 1993; pp. 11–14. [Google Scholar]
- Belouchrani, A.; Cardoso, J.-F. Maximum likelihood source separation by the expectation-maximization technique: Deterministic and stochastic implementation. In Proceedings of the International Symposium on Nonlinear Theory and Applications NOLTA’95, Las Vegas, NV, USA, 10–14 December 1995; pp. 49–53. [Google Scholar]
- Celeux, G.; Govaert, G. A classification EM algorithm for clustering and two stochastic versions. Comput. Stat. Data Anal. 1992, 14, 315–332. [Google Scholar] [CrossRef] [Green Version]
- Borghys, D.; Kåsen, I.; Achard, V.; Perneel, C. Hyperspectral anomaly detection: Comparative evaluation in scenes with diverse complexity. J. Electr. Comput. Eng. 2012. [Google Scholar] [CrossRef] [Green Version]
- Lloyd, S.P. Least Squares Quantization in PCM. IEEE Trans. Inf. Theory 1982, 28, 129–137. [Google Scholar] [CrossRef]
- Dunn, J.C. A fuzzy relative of the ISODATA process and its use in detecting compact well-separated clusters. J. Cybern. 1973, 3, 32–57. [Google Scholar] [CrossRef]
- Windham, M.P. Cluster Validity for the Fuzzy c-Means Clustering Algorithm. IEEE Trans. Pattern Anal. Mach. Intell. 1982, PAMI-4, 357–363. [Google Scholar] [CrossRef]
- Alruwaili, M.; Siddiqi, M.H.; Javed, M.A. A robust clustering algorithm using spatial fuzzy C-means for brain MR images. Egypt. Inform. J. 2020, 21, 51–66. [Google Scholar] [CrossRef]
- Togacar, M.; Ergen, B.; Comert, Z. COVID-19 detection using deep learning models to exploit Social Mimic Optimization and structured chest X-ray images using fuzzy color and stacking approaches. Comput. Biol. Med. 2020, 121, 103805. [Google Scholar] [CrossRef]
- Versaci, M.; Morabito, F.C. Image Edge Detection: A New Approach Based on Fuzzy Entropy and Fuzzy Divergence. Int. J. Fuzzy Syst. 2021, 1–19. [Google Scholar] [CrossRef]
- Stoica, P.; Selén, Y. A review of information criterion rules. IEEE Signal Process. Mag. 2004, 21, 36–47. [Google Scholar] [CrossRef]
- Kohonen, T. Self-organized formation of topologically correct feature maps. Biol. Cybern. 1982, 43, 59–69. [Google Scholar] [CrossRef]
- Duran, O.; Petrou, M. A time-efficient method for anomaly detection in hyperspectral images. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3894–3904. [Google Scholar] [CrossRef]
- Penn, B.S. Using self-organizing maps for anomaly detection in hyperspectral imagery. In Proceedings of the IEEE Aerospace Conference Proceedings, Big Sky, MT, USA, 9–16 March 2002; pp. 1531–1535. [Google Scholar]
- Baraniuk, R.G. Compressive sensing. IEEE Signal Process. Mag. 2007, 24, 118–120+124. [Google Scholar] [CrossRef]
- Candes, E.J.; Wakin, M.B. An introduction to compressive sampling: A sensing/sampling paradigm that goes against the common knowledge in data acquisition. IEEE Signal Process. Mag. 2008, 25, 21–30. [Google Scholar] [CrossRef]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Li, J.; Zhang, H.; Zhang, L.; Ma, L. Hyperspectral anomaly detection by the use of background joint sparse representation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 2523–2533. [Google Scholar] [CrossRef]
- Li, W.; Du, Q. A survey on representation-based classification and detection in hyperspectral remote sensing imagery. Pattern Recognit. Lett. 2016, 83, 115–123. [Google Scholar] [CrossRef]
- Li, W.; Du, Q.; Zhang, B. Combined sparse and collaborative representation for hyperspectral target detection. Pattern Recognit. 2015, 48, 3904–3916. [Google Scholar] [CrossRef]
- Ling, Q.; Guo, Y.; Lin, Z.; An, W. A Constrained Sparse Representation Model for Hyperspectral Anomaly Detection. IEEE Trans. Geosci. Remote Sens. 2019, 57, 2358–2371. [Google Scholar] [CrossRef]
- Xu, Y.; Wu, Z.; Li, J.; Plaza, A.; Wei, Z. Anomaly detection in hyperspectral images based on low-rank and sparse representation. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1990–2000. [Google Scholar] [CrossRef]
- Zhang, Y.; Du, B.; Zhang, L. A sparse representation-based binary hypothesis model for target detection in hyperspectral images. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1346–1354. [Google Scholar] [CrossRef]
- Li, S.; Yin, H.; Fang, L. Remote sensing image fusion via sparse representations over learned dictionaries. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4779–4789. [Google Scholar] [CrossRef]
- Sun, X.; Nasrabadi, N.M.; Tran, T.D. Task-driven dictionary learning for hyperspectral image classification with structured sparsity constraints. IEEE Trans. Geosci. Remote Sens. 2015, 53, 4457–4471. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, J.; Song, S.; Liu, D. Hyperspectral Anomaly Detection via Dictionary Construction-Based Low-Rank Representation and Adaptive Weighting. Remote Sens. 2019, 11, 192. [Google Scholar] [CrossRef] [Green Version]
- Candès, E.J.; Li, X.; Ma, Y.; Wright, J. Robust principal component analysis? J. ACM 2011, 58, 11. [Google Scholar] [CrossRef]
- Xu, Y.; Wu, Z.; Chanussot, J.; Wei, Z. Joint Reconstruction and Anomaly Detection from Compressive Hyperspectral Images Using Mahalanobis Distance-Regularized Tensor RPCA. IEEE Trans. Geosci. Remote Sens. 2018, 56, 2919–2930. [Google Scholar] [CrossRef]
- Zhu, L.; Wen, G. Hyperspectral anomaly detection via background estimation and adaptive weighted sparse representation. Remote Sens. 2018, 10, 272. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Du, B.; Zhang, L.; Wang, S. A low-rank and sparse matrix decomposition-based mahalanobis distance method for hyperspectral anomaly detection. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1376–1389. [Google Scholar] [CrossRef]
- Tan, K.; Hou, Z.; Ma, D.; Chen, Y.; Du, Q. Anomaly detection in hyperspectral imagery based on low-rank representation incorporating a spatial constraint. Remote Sens. 2019, 11, 1578. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Ma, X.; Huyan, N.; Gu, J.; Tang, X.; Jiao, L. Spectral-Difference Low-Rank Representation Learning for Hyperspectral Anomaly Detection. IEEE Trans. Geosci. Remote Sens. 2021. [Google Scholar] [CrossRef]
- Liu, G.; Lin, Z.; Yu, Y. Robust subspace segmentation by low-rank representation. In Proceedings of the ICML 2010—27th International Conference on Machine Learning, Haifa, Israel, 21–24 June 2010; pp. 663–670. [Google Scholar]
- Niu, Y.; Wang, B. Hyperspectral anomaly detection based on low-rank representation and learned dictionary. Remote Sens. 2016, 8, 289. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.; Li, S.; Qi, H.; Ayhan, B.; Kwan, C.; Vance, S. Identify anomaly component by sparsity and low rank. In Proceedings of the Workshop on Hyperspectral Image and Signal Processing, Evolution in Remote Sensing, Tokyo, Japan, 2–5 June 2015. [Google Scholar] [CrossRef]
- Tropp, J.A.; Gilbert, A.C. Signal recovery from random measurements via orthogonal matching pursuit. IEEE Trans. Inf. Theory 2007, 53, 4655–4666. [Google Scholar] [CrossRef] [Green Version]
- Dai, W.; Milenkovic, O. Subspace pursuit for compressive sensing signal reconstruction. IEEE Trans. Inf. Theory 2009, 55, 2230–2249. [Google Scholar] [CrossRef] [Green Version]
- Donoho, D.L.; Tsaig, Y. Fast Solution of l1-Norm Minimization Problems When the Solution May Be Sparse. IEEE Trans. Inf. Theory 2008, 54, 4789–4812. [Google Scholar] [CrossRef]
- Kim, S.J.; Koh, K.; Lustig, M.; Boyd, S.; Gorinevsky, D. An interior-point method for large-scale ℓ1-regularized least squares. IEEE J. Sel. Top. Signal Process. 2007, 1, 606–617. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression shrinkage and selection via the lasso: A retrospective. J. R. Stat. Soc. Ser. B Stat. Methodol. 2011, 73, 273–282. [Google Scholar] [CrossRef]
- Chen, S.S.; Donoho, D.L.; Saunders, M.A. Atomic decomposition by basis pursuit. SIAM J. Sci. Comput. 1998, 20, 33–61. [Google Scholar] [CrossRef]
- Gill, P.R.; Wang, A.; Molnar, A. The in-crowd algorithm for fast basis pursuit denoising. IEEE Trans. Signal Process. 2011, 59, 4595–4605. [Google Scholar] [CrossRef]
- Ma, D.; Yuan, Y.; Wang, Q. Hyperspectral anomaly detection via discriminative feature learning with multiple-dictionary sparse representation. Remote Sens. 2018, 10, 745. [Google Scholar] [CrossRef] [Green Version]
- Zhao, R.; Du, B.; Zhang, L. Hyperspectral Anomaly Detection via a Sparsity Score Estimation Framework. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3208–3222. [Google Scholar] [CrossRef]
- Li, W.; Tramel, E.W.; Prasad, S.; Fowler, J.E. Nearest regularized subspace for hyperspectral classification. IEEE Trans. Geosci. Remote Sens. 2014, 52, 477–489. [Google Scholar] [CrossRef] [Green Version]
- Wu, Z.; Su, H.; Du, Q. Low-Rank and Collaborative Representation for Hyperspectral Anomaly Detection. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 1394–1397. [Google Scholar]
- Jiang, K.; Xie, W.; Li, Y.; Lei, J.; He, G.; Du, Q. Semisupervised spectral learning with generative adversarial network for hyperspectral anomaly detection. IEEE Trans. Geosci. Remote Sens. 2020, 58, 5224–5236. [Google Scholar] [CrossRef]
- Wang, S.; Wang, X.; Zhang, L.; Zhong, Y. Auto-AD: Autonomous Hyperspectral Anomaly Detection Network Based on Fully Convolutional Autoencoder. IEEE Trans. Geosci. Remote Sens. 2021. [Google Scholar] [CrossRef]

| Main Information | Result |
| Time span | 2000–2020 |
| Sources | 41 |
| Total number of documents | 133 |
| Average years from publication | 7.41 |
| Average citations per documents | 72.65 |
| Average citations per year per doc | 8.14 |
| References | 4276 |
| Document types | |
| Article | 118 |
| Conference paper | 15 |
| Authors and collaboration | |
| Authors | 299 |
| Authors of single-authored documents | 5 |
| Authors of multi-authored documents | 294 |
| Co-Authors per Documents | 3.71 |
| Collaboration Index | 2.3 |
| Rank | Source Name | Documents | Zone 1 |
|---|---|---|---|
| 1 | IEEE Transactions On Geoscience And Remote Sensing | 39 | 1 |
| 2 | IEEE Geoscience And Remote Sensing Letters | 15 | 1 |
| 3 | IEEE Journal Of Selected Topics In Applied Earth Observations And Remote Sensing | 15 | 2 |
| 4 | Remote Sensing | 9 | 2 |
| 5 | Proceedings Of SPIE - The International Society For Optical Engineering | 5 | 2 |
| 6 | Remote Sensing Of Environment | 3 | 2 |
| 7 | Eurasip Journal On Advances In Signal Processing | 2 | 2 |
| 8 | IEEE Access | 2 | 2 |
| Author | SCOPUS Author ID | H-index | Total Citations | Number of Publications | First Publication (Year) |
|---|---|---|---|---|---|
| Chang CI | 35253647700 | 10 | 1259 | 10 | 2001 |
| Du Q | 7202060063 | 11 | 1044 | 12 | 2007 |
| Zhang L | 8359720900 | 13 | 962 | 13 | 2011 |
| Du B | 55020400300 | 9 | 799 | 9 | 2011 |
| Nasrabadi NM | 7006312852 | 3 | 724 | 3 | 2003 |
| Stocker AD | 7006884172 | 2 | 698 | 2 | 2002 |
| Kwon H | 7401838362 | 3 | 611 | 3 | 2003 |
| Diani M | 7003735775 | 6 | 597 | 6 | 2010 |
| Matteoli S | 24076749300 | 6 | 597 | 6 | 2010 |
| Beaven SG | 57206689538 | 1 | 554 | 1 | 2002 |
| Hoff LE | 7005107977 | 1 | 554 | 1 | 2002 |
| Schaum AP | 57207501822 | 1 | 554 | 1 | 2002 |
| Stein DWJ | 7401616297 | 1 | 554 | 1 | 2002 |
| Winter EM | 7102040936 | 1 | 554 | 1 | 2002 |
| Fowler JE | 7402370679 | 4 | 513 | 4 | 2007 |
| Chiang SS | 7201472110 | 2 | 511 | 2 | 2001 |
| Li J | 24481713500 | 5 | 496 | 5 | 2014 |
| Corsini G | 7103074007 | 5 | 486 | 5 | 2010 |
| Li W | 56215159000 | 4 | 442 | 4 | 2015 |
| Plaza A | 7006613644 | 5 | 420 | 5 | 2010 |
| Year | Document |
|---|---|
| 2001 | Competitive Region Growth, Elliptically Contoured Distributions, Evolutional Algorithm, Kurtosis, Projection Pursuit, Spherically Invariant Random Vectors |
| 2002 | Causal RXD, Correlation Matched-Filter-Based Measure, Target Discrimination Measure |
| 2003 | Clustering Algorithms, Dual Window, Eigen Separation Transform, Embedded Computing |
| 2005 | Kernels, Linear Discriminant Analysis, Orthogonal Subspace Projection/AD, RX Detector, Signal Parameter Estimation |
| 2006 | Bhattacharyya Distance, Signal Subspace Processing, Support Vector Data Description (SVDD) |
| 2007 | Detection Index, Minimum Description Length, Real-Time (R-T) Processing, Self-Organising Maps, Separability Index, Signal-Subspace Rank, Singular Value Decomposition, Wavelets |
| 2008 | Karhunen-Love-Transform, Principal Component Analysis (PCA), Kernel PCA, Signal Detection, Spectral Decorrelation |
| 2009 | GPU Processing, Generalized Least Squares, Maximum Autocorrelation Factors, Multivariate Normal Mixture Model, Principal Autocorrelation Factors |
| 2010 | Cluster-Based Approach, Feature Selection, Kernel-Based Learning, Quasi-Local Covariance Matrix, Regularization, Robust Locally Linear Embedding |
| 2011 | Embedded Systems, Gaussian Kernel, Independent Component Analysis, ROC Space, Sparse Matrix Transform, Support vector machine (SVM) |
| 2012 | Clustering, Compressed Sensing, PCA, Segmentation-Based AD, Sparse Kernel-Based Ensemble Learning, Spectral Unmixing |
| 2013 | Bayesian Learning, Dual Window-Based Eigen Separation Transform, Finite Mixture Model, Kernel density estimation (KDE), Multicore Platforms, Multiple-Window AD, Nonlinear PCA |
| 2014 | Dimensionality Reduction, High-Order Statistics, Local Sparsity Divergence, Low-Rank (L-R) And Sparse, Matched Filter, Robust Regression Analysis, Superpixels, Variable Bandwidth KDE, Weighted-RXD |
| 2015 | Graph Theory, High Order Statistics, L-R Approximation, Manifold Learning, R-T processing, Residual Analysis, Robust Background Estimation |
| 2016 | Cluster Kernel RX, Dual Clustering, Kernel Collaborative Representation (CR), Local Summation Strategy, Locally Linear Embedding, ROC, Robust PCA, Sparse Representation (SR), Sparsity Divergence Index, Spectral-Spatial Integration, Tensor Representation |
| 2017 | 3-D ROC, Band Subset Selection, Convolutional Neural Network (NN), Differential Morphology, Edge-Preserving Filtering, Joint SR, K-SVD, Multiple Graphs, Autoencoders, Tensor Decomposition |
| 2018 | A Posteriori AD, Band Selection, Deep Learning, Feature Extraction, Inverse PCA, Iterative AD, L-R Representation, Multiple Dictionaries, R-T Applications, Sparse Coding, Structured SR |
| 2019 | Adaptive Weighting, Constrained SR, Deep Brief Network, Dictionary Learning, Fractional Fourier, Local Summation, Low Dimensional Manifold Model, Structure Tensor |
| 2020 | Density Peak Clustering, Isolation Forest, Radiative Transfer Modeling |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Racetin, I.; Krtalić, A. Systematic Review of Anomaly Detection in Hyperspectral Remote Sensing Applications. Appl. Sci. 2021, 11, 4878. https://doi.org/10.3390/app11114878
Racetin I, Krtalić A. Systematic Review of Anomaly Detection in Hyperspectral Remote Sensing Applications. Applied Sciences. 2021; 11(11):4878. https://doi.org/10.3390/app11114878
Chicago/Turabian StyleRacetin, Ivan, and Andrija Krtalić. 2021. "Systematic Review of Anomaly Detection in Hyperspectral Remote Sensing Applications" Applied Sciences 11, no. 11: 4878. https://doi.org/10.3390/app11114878
APA StyleRacetin, I., & Krtalić, A. (2021). Systematic Review of Anomaly Detection in Hyperspectral Remote Sensing Applications. Applied Sciences, 11(11), 4878. https://doi.org/10.3390/app11114878







