The Steelmaking Process Parameter Optimization with a Surrogate Model Based on Convolutional Neural Networks and the Firefly Algorithm
Abstract
:1. Introduction
- We addressed the interesting problem of steelmaking process parameter optimization by proposing a simplified VGG model to build a surrogate model and then compared it with four other machine-learning methods.
- We applied three different algorithms—PSO, the ABC, and the FA—to search for optimal process parameters and then evaluated their performance. Our experimental results demonstrated that the FA can achieve high performance and outperforms the other methods.
2. Related Works
2.1. Surrogate Model
2.2. Survey of Machine Learning Method
2.2.1. Linear Regression
2.2.2. Random Forests
2.2.3. Support Vector Regression
2.2.4. Multilayer Perception
2.3. Bio-Inspired Search Algorithms
2.3.1. Particle Swarm Optimization
2.3.2. Artificial Bee Colony Algorithm
2.3.3. Firefly Algorithm
3. Material and Methods
3.1. Materials and Experimental Setup
3.2. Simplified VGG-16 Convolutional Neural Networks
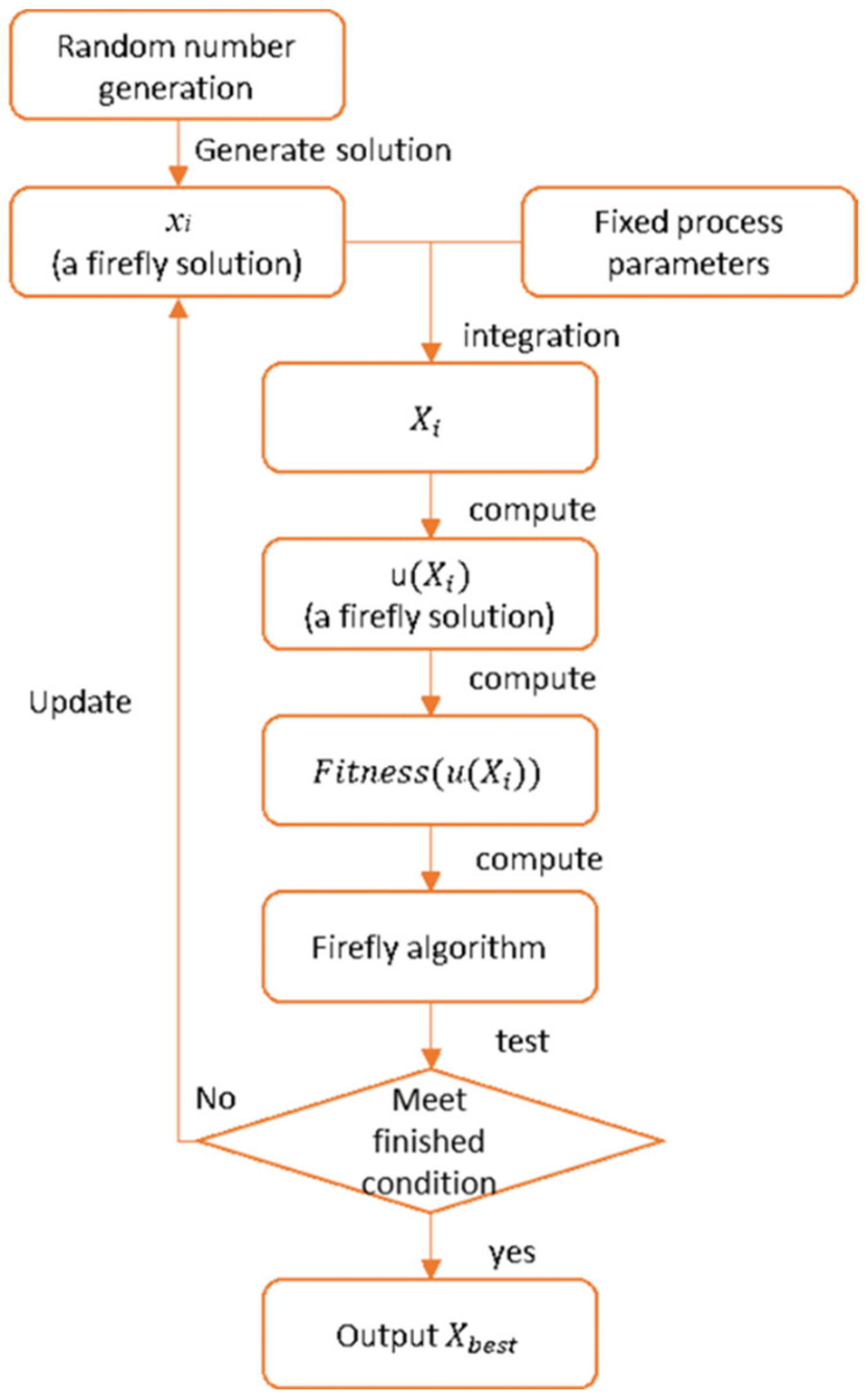
3.3. Process Parameter Optimization Using the Firefly Algorithm
- Step 1.
- Generate the initial solutions and the given hyper-parameters:
- Step 2.
- Firefly movement:
- Step 3.
- Select the current best solution:
- Step 4.
- Check the termination criterion:
4. Results and Discussion
4.1. Training Mechanism by Using ML Methods
4.2. Experimental Results of the Process Parameter Optimizations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Eric, M.; Stefanovic, M.; Djordjevic, A.; Stefanovic, N.; Misic, M.; Abadic, N.; Popović, P. Production process parameter optimization with a new model based on a genetic algorithm and ABC classification method. Adv. Mech. Eng. 2016, 8, 1–18. [Google Scholar] [CrossRef] [Green Version]
- Patil, V.D.; Sali, S.P. Process parameter optimization for computer numerical control turning on En36 alloy steel. In Proceedings of the 2017 International Conference on Nascent Technologies in Engineering (ICNTE), Navi Mumbai, India, 27–28 January 2017; pp. 1–5. [Google Scholar]
- Hoole, J.; Sartor, P.; Booker, J.D.; Cooper, J.E.; Gogouvitis, X.; Schmidt, R.K. Comparison of Surrogate Modeling Methods for Finite Element Analysis of Landing Gear Loads; Session: Surrogate Modeling for Uncertainty Quantification. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020. [Google Scholar]
- Salah, U.H.; Raman, P.S. Taguchi-based design of experiments in training POD-RBF surrogate model for in-verse material modelling using nanoindentation. Inverse Probl. Sci. Eng. 2017, 5, 363–381. [Google Scholar]
- Pfrommer, J.; Zimmerling, C.; Liu, J.; Kärger, L.; Henning, F.; Beyerer, J. Optimisation of manufacturing process parameters using deep neural networks as surrogate models. Procedia Cirp 2018, 72, 426–431. [Google Scholar] [CrossRef]
- Zhao, P.; Zhou, H.; Li, Y.; Li, D. Process parameters optimization of injection molding using a fast strip analysis as a surrogate model. Int. J. Adv. Manuf. Technol. 2010, 49, 949–959. [Google Scholar] [CrossRef]
- Forrester, A.I.; Keane, A.J. Recent advances in surrogate-based optimization. Prog. Aerosp. Sci. 2009, 45, 50–79. [Google Scholar] [CrossRef]
- Han, Z.-H.; Zhang, K.-S. Surrogate-Based Optimization. In Real-World Applications of Genetic Algorithms; IntechOpen: London, UK, 2012; pp. 343–362. [Google Scholar]
- Koziel, S.; Ciaurri, D.E.; Leifsson, L. Surrogate-Based Methods. In Computational Optimization, Methods and Algorithms; Springer: Berlin/Heidelberg, Germany, 2011; pp. 33–59. [Google Scholar]
- Simpson, T.; Poplinski, J.; Koch, P.N.; Allen, J. Metamodels for Computer-based Engineering Design: Survey and recommendations. Eng. Comput. 2001, 17, 129–150. [Google Scholar] [CrossRef] [Green Version]
- Cook, D.; Ragsdale, C.; Major, R. Combining a neural network with a genetic algorithm for process parameter optimization. Eng. Appl. Artif. Intell. 2000, 13, 391–396. [Google Scholar] [CrossRef]
- Thombansen, U.; Schuttler, J.; Auerbach, T.; Beckers, M.; Buchholz, G.; Eppelt, U.; Molitor, T. Model-based self-optimization for manufacturing systems. In Proceedings of the 2011 17th International Conference on Concurrent Enterprising, Aachen, Germany, 20–22 June 2011; pp. 1–9. [Google Scholar]
- Lovrić, M.; Meister, R.; Steck, T.; Fadljević, L.; Gerdenitsch, J.; Schuster, S.; Schiefermüller, L.; Lindstaedt, S.; Kern, R. Parasitic resistance as a predictor of faulty anodes in electro galvanizing: A comparison of machine learning, physical and hybrid models. Adv. Model. Simul. Eng. Sci. 2020, 7, 1–16. [Google Scholar] [CrossRef]
- Cemernek, D.; Cemernek, S.; Gursch, H.; Pandeshwar, A.; Leitner, T.; Berger, M.; Klösch, G.; Kern, R. Machine learning in continuous casting of steel: A state-of-the-art survey. J. Intell. Manuf. 2021. [Google Scholar] [CrossRef]
- Guo, S.; Yu, J.; Liu, X.; Wang, C.; Jiang, Q. A predicting model for properties of steel using the industrial big data based on machine learning. Comput. Mater. Sci. 2019, 160, 95–104. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Yan, C.; Yin, Z.; Shen, X.; Mi, D.; Guo, F.; Long, D. Surrogate-based optimization with improved support vector regression for non-circular vent hole on aero-engine turbine disk. Aerosp. Sci. Technol. 2020, 96, 105332. [Google Scholar] [CrossRef]
- Nauyen, T.H.; Nang, D.; Paustian, K. Surrogate-based multi-objective optimization of management options for agricultural landscapes using artificial neural networks. Ecol. Modeling 2019, 4, 1–13. [Google Scholar] [CrossRef]
- Jamshidi, M.B.; Lalbakhsh, A.; Alibeigi, N.; Soheyli, M.R.; Oryani, B.; Rabbani, N. Socialization of Industrial Robots: An Innovative Solution to improve Productivity. In Proceedings of the 2018 IEEE 9th Annual Information Technology, Electronics and Mobile Communication Conference (IEMCON), Vancouver, BC, Canada, 1–3 November 2018; pp. 832–837. [Google Scholar]
- Jamshidi, M.B.; Alibeigi, N.; Rabbani, N.; Oryani, B.; Lalbakhsh, A. Artificial Neural Networks: A Powerful Tool for Cognitive Science. In Proceedings of the 2018 IEEE 9th Annual Information Technology, Electronics and Mobile Communication Conference (IEMCON), Vancouver, BC, Canada, 1–3 November 2018; pp. 674–679. [Google Scholar]
- Jamshidi, M.B.; Lalbakhsh, A.; Talla, J.; Peroutka, Z.; Roshani, S.; Matousek, V.; Roshani, S.; Mirmozafari, M.; Malek, Z.; La Spada, L.; et al. Deep Learning Techniques and COVID-19 Drug Discovery: Fundamentals, State-of-the-Art and Future Directions. In Emerging Technologies during the Era of COVID-19 Pandemic; Springer: Berlin/Heidelberg, Germany, 2021; pp. 9–31. [Google Scholar]
- Xue, J.; Xiang, Z.; Ou, G. Predicting single freestanding transmission tower time history response during complex wind input through a convolutional neural network based surrogate model. Eng. Struct. 2021, 233, 111859. [Google Scholar] [CrossRef]
- Jia, X.J.; Liang, L.; Yang, Z.L.; Yu, M.Y. Muti-parameters optimization for electromagnetic acoustic transduces using surrogated-assisted particle swarm optimizer. Mech. Syst. Signal Process. 2021, 152, 107337. [Google Scholar] [CrossRef]
- Sun, L.; Sun, W.; Liang, X.; He, M.; Chen, H. A modified surrogate-assisted multi-swarm artificial bee colony for complex numerical optimization problems. Microprocess. Microsyst. 2020, 76, 103050. [Google Scholar] [CrossRef]
- Ewees, A.A.; Al-qaness, M.A.A.; Elaziz, M.A. Enhanced salp swarm algorithm based on firefly algorithm for unrelated parallel machine scheduling with set times. Appl. Math. Model. 2021, 94, 285–305. [Google Scholar] [CrossRef]
- Kiranyaz, S.; Avci, O.; Abdeljaber, O.; Ince, T.; Gabbouj, M.; Inman, D.J. 1D convolutional neural networks and applications: A survey. Mech. Syst. Signal Process. 2021, 151, 107398. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Zhang, M.; Long, D.; Qin, T.; Yang, J. A Chaotic Hybrid Butterfly Optimization Algorithm with Particle Swarm Optimization for High-Dimensional Optimization Problems. Symmetry 2020, 12, 1800. [Google Scholar] [CrossRef]
- Chao, C.-F.; Horng, M.-H.; Chen, Y.-C. Motion Estimation Using the Firefly Algorithm in Ultrasonic Image Sequence of Soft Tissue. Comput. Math. Methods Med. 2015, 343217. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, W.; Huang, Y.; Ye, Z.; Cai, W.; Yang, S.; Cheng, X.; Frank, I. Renyi’s Entropy Based Mutlilevel Thresholding Using a Novel Meta-Heuristic Algorithm. Appl. Sci. 2020, 10(9), 3225. [Google Scholar] [CrossRef]
- Horng, M.H. Multilevel thresholding selection based on the artificial bee colony algorithm for image segmentation. Expert Syst. Appl. 2011, 38, 13785–13791. [Google Scholar] [CrossRef]
- Kaminski, M. Neural Network Training Using Particle Swarm Optimization—A Case Study. In Proceedings of the 2019 24th International Conference on Methods and Models in Automation and Robotics (MMAR), Miedzyzdroje, Poland, 26–29 August 2019; pp. 115–120. [Google Scholar]
- Lalbakhsh, A.; Afzal, M.U.; Esselle, K.P. Multi-objective Particle Swarm Optimization to Design a Time-Delay Equalizer Metasurface for an Electromagnetic Band-Gap Resonator Antenna. IEEE Antennas Wirel. Propag. Lett. 2016, 16, 912–915. [Google Scholar] [CrossRef]
- Lalbkhsh, A.; Esselle, K.P. Directivity Improvement of a Fabry-Perot Cavity Antenna by enhancing Near Field Characteristic. In Proceedings of the 17th International Symposium on Antenna Technology and Applied Electromagnetics, Montreal, QC, Canada, 10–13 July 2016. [Google Scholar]
- Lalbakhsh, A.; Afzal, M.U.; Esselle, K. Simulation-driven particle swarm optimization of spatial phase shifters. In Proceedings of the 2016 International Conference on Electromagnetics in Advanced Applications (ICEAA), Cairns, QLD, Australia, 19–23 September 2016; pp. 428–430. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 6, pp. 1942–1948. [Google Scholar]
- Karaboga, D.; Basturk, B. On the performance of artificial bee colony (ABC) algorithm. Appl. Soft Comput. 2008, 8, 687–697. [Google Scholar] [CrossRef]
- Łukasik, S.; Żak, S. Firefly Algorithm for Continuous Constrained Optimization Tasks. In International Conference on Computational Collective Intelligence; Springer: Berlin/Heidelberg, Germany, 2009; pp. 97–106. [Google Scholar]
- Yang, X.-S. Firefly Algorithms for Multimodal Optimization. In International Symposium on Stochastic Algorithms; Springer: Berlin/Heidelberg, Germany, 2009; pp. 169–178. [Google Scholar]
- Yang, X.S. Nature-Inspired Metaheuristic Algorithms; Luniver Press: Frome, UK, 2008. [Google Scholar]
- Lalbakhsh, P.; Zaeri, B.; Lalbakhsh, A. An Improved Model of Ant Colony Optimization Using a Novel Pheromone Update Strategy. IEICE Trans. Inform. Syst. 2013, E96-D, 2309–2318. [Google Scholar] [CrossRef] [Green Version]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]


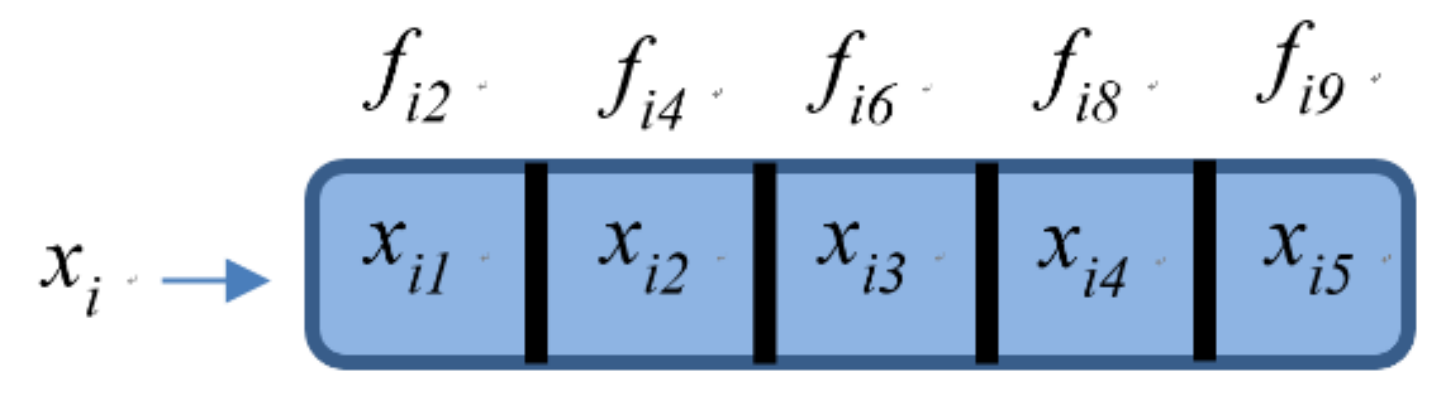
| Y1 | Y2 | Y3 | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 | X11 | X12 | X13 | X14 | X15 | X16 | X17 | X18 | X19 | X20 | X21 | X22 | X23 | X24 | X25 | X26 | X27 | X28 | X29 | X30 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 148 | 294 | 49 | 758 | 752 | 582 | 411 | 363 | 318 | 282 | 134 | 83 | 923 | 640 | 4.002723 | 0.0021 | 0.15 | 0.013 | 0.006 | 0.01 | 0.004 | 0.01 | 0.02 | 0 | 0.001 | 0.0027 | 0.003 | 0.039 | 0.033 | 0.032 | 0.0001 | 0.001 | 0.0001 |
| 146 | 294 | 50 | 748 | 747 | 574 | 403 | 361 | 318 | 288 | 150 | 124 | 915 | 643 | 3.99594 | 0.0014 | 0.12 | 0.017 | 0.005 | 0.01 | 0.005 | 0.01 | 0.01 | 0 | 0.001 | 0.0018 | 0.002 | 0.04 | 0.03 | 0.029 | 0.0001 | 0.001 | 0.0001 |
| 176 | 309 | 47 | 751 | 757 | 575 | 397 | 351 | 318 | 285 | 195 | 80 | 924 | 640 | 3.19883 | 0.0024 | 0.15 | 0.015 | 0.003 | 0 | 0.005 | 0.01 | 0.02 | 0 | 0.001 | 0.0027 | 0.003 | 0.044 | 0.036 | 0.035 | 0.0001 | 0 | 0.0001 |
| 139 | 288 | 51 | 754 | 754 | 575 | 397 | 351 | 313 | 291 | 195 | 80 | 928 | 647 | 3.198287 | 0.0012 | 0.14 | 0.014 | 0.003 | 0 | 0.006 | 0.01 | 0.02 | 0 | 0 | 0.0014 | 0 | 0.046 | 0.037 | 0.034 | 0.0001 | 0 | 0.0001 |
| 145 | 299 | 48 | 777 | 772 | 564 | 404 | 367 | 324 | 296 | 216 | 80 | 920 | 641 | 3.198613 | 0.0017 | 0.15 | 0.015 | 0.003 | 0 | 0.006 | 0.01 | 0.02 | 0 | 0.001 | 0.0016 | 0.003 | 0.042 | 0.041 | 0.04 | 0.0001 | 0.001 | 0.0001 |
| 150 | 302 | 49 | 768 | 757 | 580 | 411 | 358 | 320 | 292 | 194 | 107 | 922 | 648 | 3.500751 | 0.0014 | 0.16 | 0.015 | 0.005 | 0.01 | 0.005 | 0.01 | 0.02 | 0 | 0.001 | 0.0015 | 0.003 | 0.042 | 0.035 | 0.034 | 0.0001 | 0.001 | 0.0001 |
| 166 | 310 | 47 | 749 | 752 | 572 | 405 | 364 | 326 | 293 | 200 | 100 | 925 | 645 | 3.198607 | 0.0017 | 0.15 | 0.015 | 0.003 | 0 | 0.006 | 0.01 | 0.02 | 0 | 0.001 | 0.0016 | 0.003 | 0.042 | 0.041 | 0.04 | 0.0001 | 0.001 | 0.0001 |
| 153 | 303 | 47 | 748 | 752 | 572 | 402 | 360 | 325 | 294 | 206 | 80 | 923 | 647 | 3.198935 | 0.0017 | 0.15 | 0.015 | 0.003 | 0 | 0.006 | 0.01 | 0.02 | 0 | 0.001 | 0.0016 | 0.003 | 0.042 | 0.041 | 0.04 | 0.0001 | 0.001 | 0.0001 |
| 144 | 291 | 51 | 745 | 758 | 571 | 406 | 364 | 316 | 290 | 220 | 98 | 928 | 648 | 3.199251 | 0.0014 | 0.13 | 0.013 | 0.003 | 0 | 0.004 | 0.01 | 0.02 | 0 | 0.001 | 0.0016 | 0.003 | 0.045 | 0.037 | 0.036 | 0.0001 | 0.001 | 0.0001 |
| 148 | 295 | 49 | 758 | 752 | 575 | 401 | 361 | 315 | 288 | 220 | 88 | 927 | 641 | 2.600165 | 0.0014 | 0.13 | 0.012 | 0.004 | 0 | 0.005 | 0.01 | 0.01 | 0 | 0.001 | 0.0019 | 0.001 | 0.047 | 0.049 | 0.047 | 0.0002 | 0.001 | 0.0001 |
| 150 | 295 | 49 | 755 | 750 | 574 | 403 | 363 | 324 | 288 | 220 | 94 | 919 | 638 | 2.596573 | 0.0015 | 0.13 | 0.009 | 0.006 | 0 | 0.005 | 0.01 | 0.01 | 0 | 0.001 | 0.0026 | 0.001 | 0.047 | 0.04 | 0.039 | 0.0001 | 0.001 | 0.0001 |
| 154 | 304 | 47 | 762 | 764 | 575 | 406 | 365 | 320 | 293 | 204 | 82 | 921 | 645 | 3.000278 | 0.0014 | 0.17 | 0.018 | 0.004 | 0.01 | 0.004 | 0.01 | 0.02 | 0 | 0.001 | 0.0032 | 0.002 | 0.039 | 0.033 | 0.032 | 0.0001 | 0.001 | 0.0001 |
| 159 | 305 | 47 | 751 | 746 | 574 | 407 | 366 | 325 | 293 | 170 | 100 | 917 | 638 | 3.497113 | 0.0021 | 0.15 | 0.013 | 0.006 | 0.01 | 0.004 | 0.01 | 0.02 | 0 | 0.001 | 0.0027 | 0.003 | 0.039 | 0.033 | 0.032 | 0.0001 | 0.001 | 0.0001 |
| 162 | 308 | 47 | 756 | 749 | 574 | 407 | 365 | 323 | 289 | 170 | 96 | 914 | 648 | 3.50113 | 0.0014 | 0.16 | 0.014 | 0.005 | 0.01 | 0.005 | 0.01 | 0.02 | 0 | 0.001 | 0.0027 | 0.004 | 0.044 | 0.036 | 0.036 | 0.0002 | 0.001 | 0.0001 |
| 154 | 307 | 46 | 774 | 764 | 575 | 406 | 358 | 321 | 285 | 200 | 90 | 923 | 646 | 3.000014 | 0.0018 | 0.12 | 0.015 | 0.005 | 0 | 0.004 | 0.01 | 0.02 | 0 | 0 | 0.0016 | 0.001 | 0.043 | 0.038 | 0.035 | 0.0001 | 0.001 | 0.0001 |
| 150 | 297 | 49 | 762 | 756 | 575 | 406 | 365 | 315 | 290 | 200 | 90 | 921 | 641 | 3.199693 | 0.0017 | 0.13 | 0.012 | 0.006 | 0 | 0.004 | 0.01 | 0.02 | 0 | 0.001 | 0.0019 | 0 | 0.04 | 0.026 | 0.025 | 0.0002 | 0.001 | 0.0001 |
| 155 | 298 | 48 | 757 | 756 | 574 | 405 | 360 | 323 | 292 | 200 | 90 | 920 | 637 | 3.198027 | 0.0018 | 0.16 | 0.006 | 0.007 | 0 | 0.006 | 0.01 | 0.01 | 0 | 0.001 | 0.0043 | 0.002 | 0.048 | 0.051 | 0.05 | 0.0001 | 0.001 | 0.0001 |
| 149 | 300 | 49 | 764 | 762 | 575 | 405 | 357 | 314 | 290 | 200 | 90 | 922 | 645 | 3.200491 | 0.0017 | 0.14 | 0.014 | 0.005 | 0.01 | 0.005 | 0.01 | 0.02 | 0 | 0.001 | 0.0028 | 0.003 | 0.046 | 0.049 | 0.047 | 0.0002 | 0.001 | 0.0001 |
| 159 | 308 | 47 | 759 | 755 | 574 | 406 | 365 | 318 | 293 | 200 | 90 | 921 | 644 | 2.999876 | 0.0016 | 0.15 | 0.013 | 0.003 | 0 | 0.005 | 0.01 | 0.02 | 0 | 0.001 | 0.0039 | 0.002 | 0.044 | 0.031 | 0.03 | 0.0001 | 0 | 0.0001 |
| 152 | 302 | 49 | 764 | 762 | 575 | 407 | 364 | 323 | 291 | 175 | 80 | 915 | 647 | 3.498092 | 0.0021 | 0.15 | 0.013 | 0.006 | 0.01 | 0.004 | 0.01 | 0.02 | 0 | 0.001 | 0.0027 | 0.003 | 0.039 | 0.033 | 0.032 | 0.0001 | 0.001 | 0.0001 |
| Method | Batch Size | Training Epochs | Trainable Variables | Initial Learning Rate | Loss Function | Optimizer | Average Training Time (s) |
|---|---|---|---|---|---|---|---|
| Simplified VGG Model | 50 | 250 | 360,661 | 0.001 | MSE | Adam | 232.47 |
| Linear Regression | Random Forests | Support Vector Regression | Multilayer Perception | Simplified VGG Network | |
|---|---|---|---|---|---|
| Yield Stress, . | 5.052 ± 0.09 | 3.890 ± 0.11 | 4.057 ± 0.09 | 4.156 ± 0.09 | 3.781 ± 0.08 |
| Tensile Stress, | 4.094 ± 0.10 | 3.647 ± 0.09 | 3.761 ± 0.10 | 3.798 ± 0.10 | 3.621 ± 0.08 |
| Plastic Strain Ratio, | 1.032 ± 0.02 | 0.954 ± 0.02 | 0.993 ± 0.02 | 0.948 ± 0.02 | 0.946 ± 0.02 |
| Parameter | Value |
|---|---|
| Attractiveness, | 1.0 |
| Light Absorption Coefficient, γ | 1.0 |
| Number of Initial Firefly Solutions | 10 |
| MCL | 50 |
| σ | 0.1 |
| RF + PSO | RF + ABC | RF + Firefly | SVGG + PSO | SVGG + ABC | SVGG + Firefly |
|---|---|---|---|---|---|
| 96.89% | 97.99% | 98.99% | 97.32% | 97.99% | 100% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.-C.; Horng, M.-H.; Yang, Y.-Y.; Hsu, J.-H.; Chen, Y.-T.; Hung, Y.-C.; Sun, Y.-N.; Tsai, Y.-H. The Steelmaking Process Parameter Optimization with a Surrogate Model Based on Convolutional Neural Networks and the Firefly Algorithm. Appl. Sci. 2021, 11, 4857. https://doi.org/10.3390/app11114857
Liu Y-C, Horng M-H, Yang Y-Y, Hsu J-H, Chen Y-T, Hung Y-C, Sun Y-N, Tsai Y-H. The Steelmaking Process Parameter Optimization with a Surrogate Model Based on Convolutional Neural Networks and the Firefly Algorithm. Applied Sciences. 2021; 11(11):4857. https://doi.org/10.3390/app11114857
Chicago/Turabian StyleLiu, Yung-Chun, Ming-Huwi Horng, Yung-Yi Yang, Jian-Han Hsu, Yen-Ting Chen, Yu-Chen Hung, Yung-Nien Sun, and Yu-Hsuan Tsai. 2021. "The Steelmaking Process Parameter Optimization with a Surrogate Model Based on Convolutional Neural Networks and the Firefly Algorithm" Applied Sciences 11, no. 11: 4857. https://doi.org/10.3390/app11114857
APA StyleLiu, Y.-C., Horng, M.-H., Yang, Y.-Y., Hsu, J.-H., Chen, Y.-T., Hung, Y.-C., Sun, Y.-N., & Tsai, Y.-H. (2021). The Steelmaking Process Parameter Optimization with a Surrogate Model Based on Convolutional Neural Networks and the Firefly Algorithm. Applied Sciences, 11(11), 4857. https://doi.org/10.3390/app11114857






