Neural Network Control for Trajectory Tracking and Balancing of a Ball-Balancing Robot with Uncertainty
Abstract
:1. Introduction
- The trajectory tracking and balancing of the ball-balancing robot was achieved using a single-loop controller;
- It was possible to implement a control system without any knowledge of the upper bounds of uncertainties.
2. Materials and Methods
2.1. Dynamics of the Ball-Balancing Robot
2.2. Radial Basis Function Networks
2.3. Controller Design
3. Results
3.1. Stability Analysis
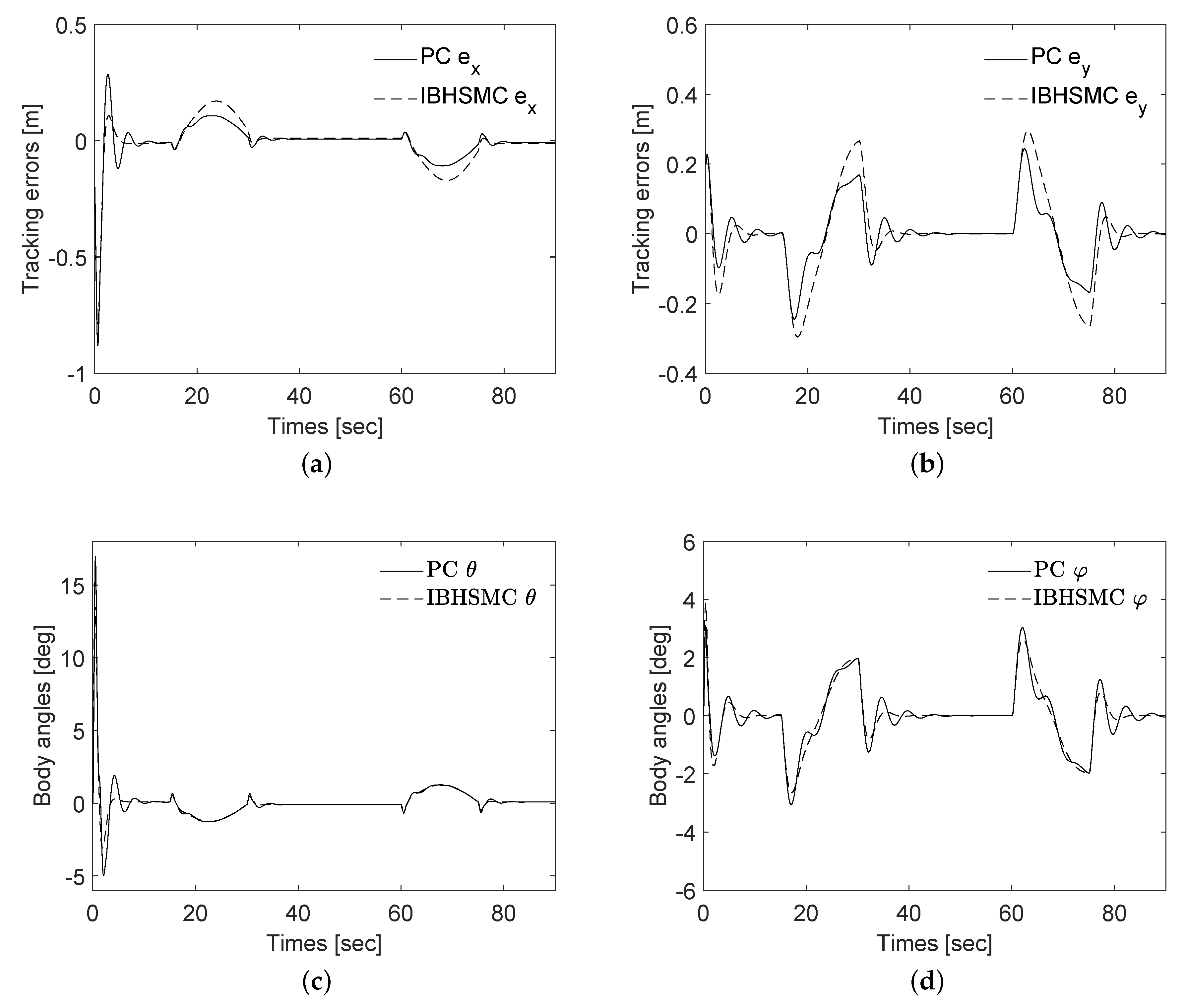
3.2. Simulation Results
4. Discussion
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix B
References
- Paszkiel, S. Using the Raspberry PI2 Module and the Brain-Computer Technology for Controlling a Mobile Vehicle. In Automation 2019; Szewczyk, R., Zieli ’nski, C., Kaliczy ’nska, M., Eds.; Springer International Publishing: Cham, Switzerland, 2020; Volume 920, pp. 356–366. [Google Scholar]
- Han, H.Y.; Han, T.Y.; Jo, H.S. Development of omnidirectional self-balancing robot. In Proceedings of the 2014 IEEE International Symposium on Robotics and Manufacturing Automation (ROMA), Kuala Lumpur, Malaysia, 15–16 December 2014; pp. 57–62. [Google Scholar]
- Tsai, C.C.; Chan, C.K.; Kau, L.C. LQR Motion Control of a Ball Riding Robot. In Proceedings of the 2012 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Tokyo, Japan, 11–14 July 2012; pp. 861–866. [Google Scholar]
- Lauwers, T.B.; Kantor, G.A.; Hollis, R.L. A dynamically stable single-wheeled mobile robot with inverse mouse-ball drive. In Proceedings of the 2006 IEEE International Conference on Robotics and Automation, Orlando, FL, USA, 15–19 May 2006; pp. 2884–2889. [Google Scholar]
- Nagarajan, U.; Kantor, G.; Hollis, R. The ballbot: An omnidirectional balancing mobile robot. Int. J. Robot. Res. 2014, 33, 917–930. [Google Scholar] [CrossRef]
- Pham, D.B.; Weon, I.S.; Lee, S.G. Partial feedback linearization double-loop control for a pseudo-2D ridable ballbot. Int. J. Control Autom. Syst. 2020, 18, 1310–1323. [Google Scholar] [CrossRef]
- Pham, D.B.; Kim, H.; Kim, J.; Lee, S.G. Balancing and transferring control of a ball segway using a double-loop approach [applications of control]. IEEE Control Syst. Mag. 2018, 38, 15–37. [Google Scholar]
- Wang, W.; Yi, J.; Zhao, D.; Liu, D. Design of a stable sliding-mode controller for a class of second-order underactuated systems. IEE Proc.-Control Theory Appl. 2004, 151, 683–690. [Google Scholar] [CrossRef] [Green Version]
- Pham, D.B.; Lee, S.G. Hierarchical sliding mode control for a two-dimensional ball segway that is a class of a second-order underactuated system. J. Vib. Control 2019, 25, 72–83. [Google Scholar] [CrossRef]
- Pham, D.B.; Lee, S.G. Aggregated hierarchical sliding mode control for a spatial ridable ballbot. Int. J. Precis. Eng. 2018, 19, 1291–1302. [Google Scholar] [CrossRef]
- Do, V.T.; Lee, S.G.; Kim, J.H. Robust integral backstepping hierarchical sliding mode controller for a ballbot system. Mech. Syst. Signal Process. 2020, 144, 106866. [Google Scholar] [CrossRef]
- Do, V.T.; Lee, S.G. Neural Integral Backstepping Hierarchical Sliding Mode Control for a Ridable Ballbot Under Uncertainties and Input Saturation. IEEE Trans. Syst. Man Cybern. Syst. 2021, 1–14. [Google Scholar] [CrossRef]
- Park, K.B. Comments on ‘design of a stable sliding-mode controller for a class of second-order underactuated Systems’. IET Control Theory Appl. 2012, 6, 1153. [Google Scholar] [CrossRef]
- Lee, S.M.; Park, B.S. Robust Control for Trajectory Tracking and Balancing of a Ballbot. IEEE Access 2020, 8, 159324–159330. [Google Scholar] [CrossRef]
- Sands, T. Development of Deterministic Artificial Intelligence for Unmanned Underwater Vehicles (UUV). J. Mar. Sci. Eng. 2020, 8, 578. [Google Scholar] [CrossRef]
- Fan, Y.; Huang, H.; Tan, Y. Robust adaptive path following control of an unmanned surface vessel subject to input saturation and uncertainties. Appl. Sci. 2019, 9, 1815. [Google Scholar] [CrossRef] [Green Version]
- Sands, T. Deterministic Artificial Intelligence; IntechOpen: London, UK, 2020; ISBN 978-1-78984-111-4. [Google Scholar]
- Tran, D.T.; Nguyen, M.N.; Ahn, K.K. RBF Neural Network Based Backstepping Control for an Electrohydraulic Elastic Manipulator. Appl. Sci. 2019, 9, 2237. [Google Scholar] [CrossRef] [Green Version]
- Swaroop, D.; Hedrick, J.K.; Yip, P.P.; Gerdes, J.C. Dynamic surface control for a class of nonlinear systems. IEEE Trans. Autom. Control 2000, 45, 1893–1899. [Google Scholar] [CrossRef] [Green Version]
- Ge, S.S.; Wang, C. Adaptive neural control of uncertain MIMO nonlinear systems. IEEE Trans. Neural Netw. 2004, 15, 674–692. [Google Scholar] [CrossRef] [PubMed]
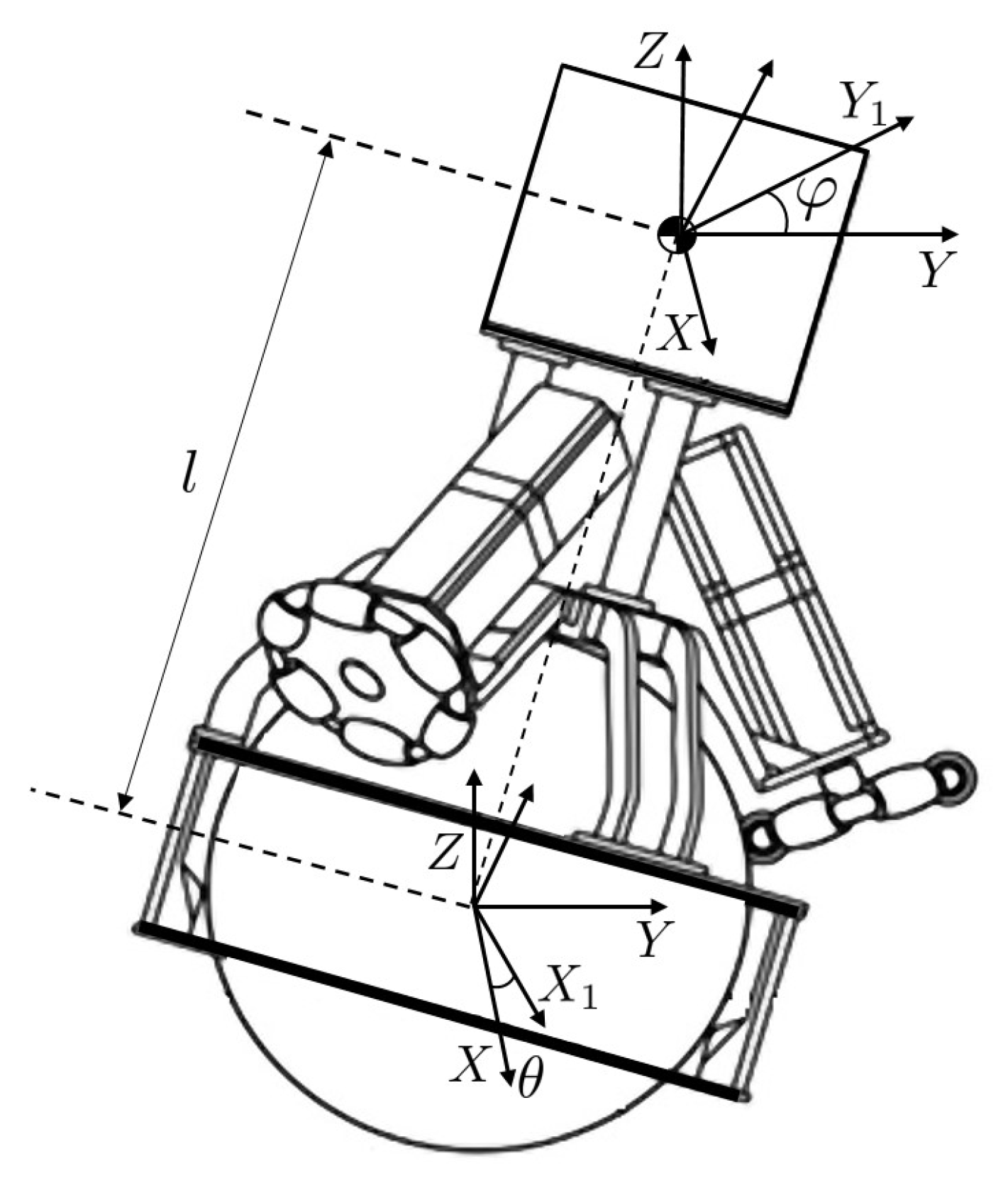


| Symbol | Parameter | Value |
|---|---|---|
| Body mass | ||
| l | Body length | |
| Moment of inertia of the body about the roll axis | ||
| Moment of inertia of the body about the pitch axis | ||
| Omnidirectional wheel radius | ||
| Omnidirectional wheel mass | ||
| Moment of inertia of the omnidirectional wheel | ||
| Ball mass | ||
| Ball radius | ||
| Moment of inertia of the ball | ||
| Zenith angle |
| Gain | Nominal | Perturbed |
|---|---|---|
| 0.1299 | 0.2108 | |
| 0.1278 | 0.1355 | |
| 0.1271 | 0.1244 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jang, H.-G.; Hyun, C.-H.; Park, B.-S. Neural Network Control for Trajectory Tracking and Balancing of a Ball-Balancing Robot with Uncertainty. Appl. Sci. 2021, 11, 4739. https://doi.org/10.3390/app11114739
Jang H-G, Hyun C-H, Park B-S. Neural Network Control for Trajectory Tracking and Balancing of a Ball-Balancing Robot with Uncertainty. Applied Sciences. 2021; 11(11):4739. https://doi.org/10.3390/app11114739
Chicago/Turabian StyleJang, Hyo-Geon, Chang-Ho Hyun, and Bong-Seok Park. 2021. "Neural Network Control for Trajectory Tracking and Balancing of a Ball-Balancing Robot with Uncertainty" Applied Sciences 11, no. 11: 4739. https://doi.org/10.3390/app11114739
APA StyleJang, H.-G., Hyun, C.-H., & Park, B.-S. (2021). Neural Network Control for Trajectory Tracking and Balancing of a Ball-Balancing Robot with Uncertainty. Applied Sciences, 11(11), 4739. https://doi.org/10.3390/app11114739







