Graph-Based Modeling in Shop Scheduling Problems: Review and Extensions
Abstract
:1. Introduction
- We proposed a novel subjective measurement to evaluate the quality of the references in review papers. This procedure and measurement have not been observed in any previous review papers. Analyzing the distribution of publications based on the quality of journals can indicate the research trend and hotspot, as well as verify the validation of the dataset.
- We proposed a novel categorization over the most common and efficient graph-based models being used in the shop scheduling problems.
- We presented a comprehensive statistical analysis of the current dataset using both visualization tools and master tables where references can be easily compared across different criteria/categories.
- The most important breakthrough of this study is that we generated a unique modeling approach from scratch to visualize both gaps and hotspots in the literature based on our findings/analysis in the dataset. This creative model puts theory into practice and show the functionality of different types of graphs to model any systems, including a review survey, which is defined as a system here.
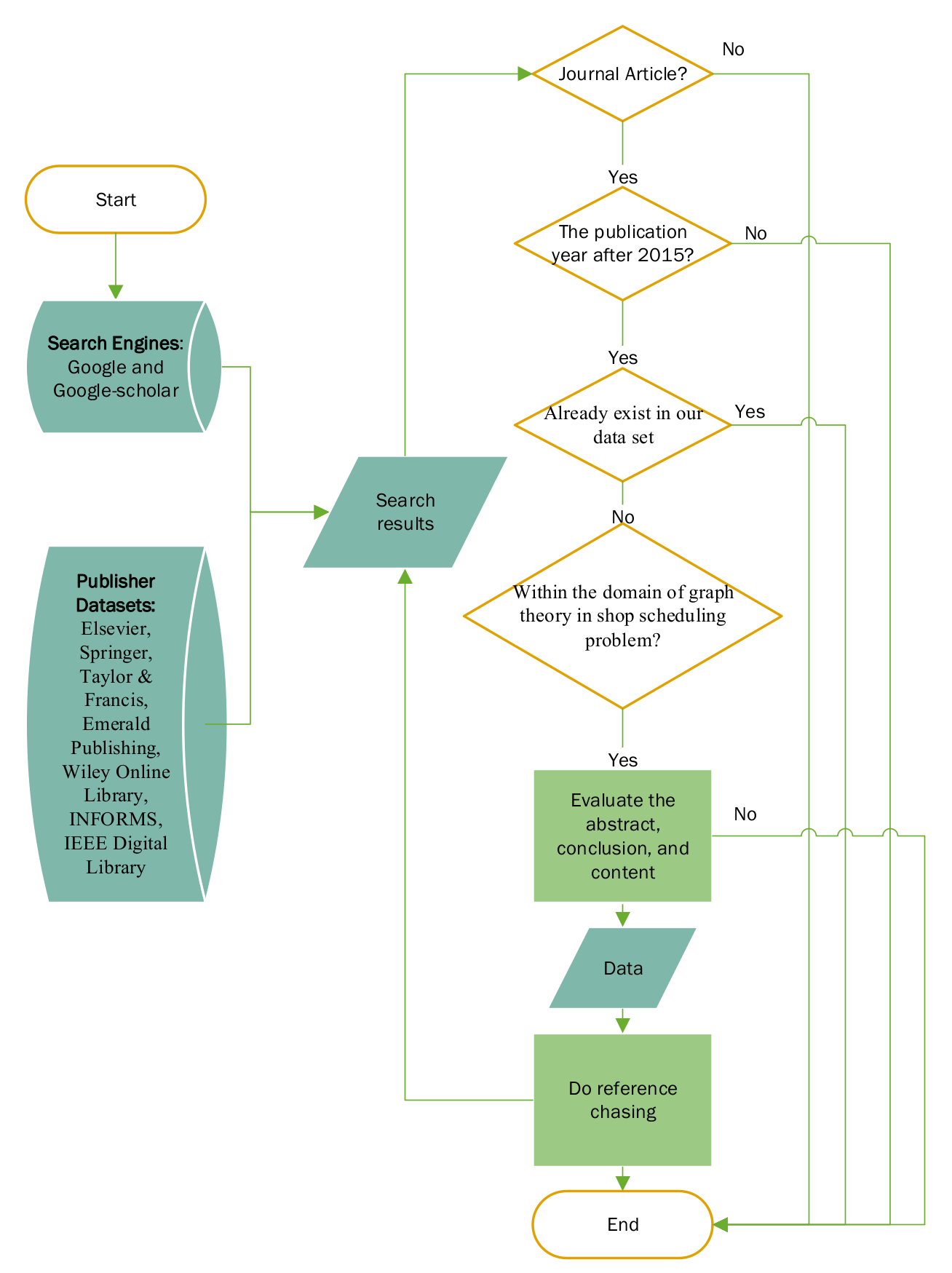
2. Materials and Methods
3. The Theory of Shop Scheduling Problems
3.1. Objectives of Scheduling Problems
3.2. Shop Layouts
3.2.1. Single-Stage System
3.2.2. Job Shop System
3.2.3. Flexible Manufacturing System (FMS)
3.2.4. Flow Shop System
3.2.5. Open Shop
3.2.6. Mixed Shop
3.2.7. Cellular Manufacturing System (CMS)
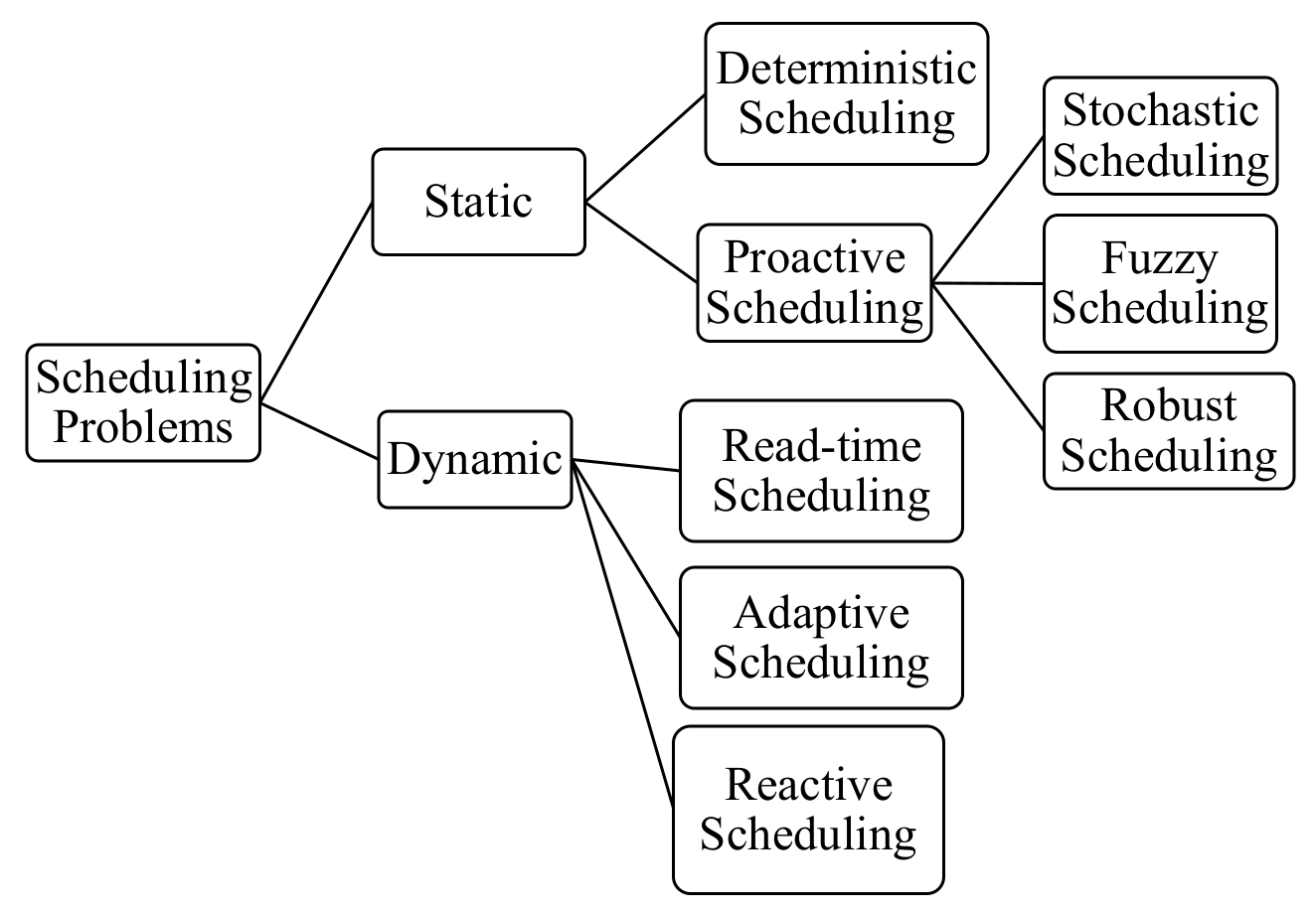
4. Classifications and Solutions of Scheduling Problems
4.1. Classification of Scheduling Problems
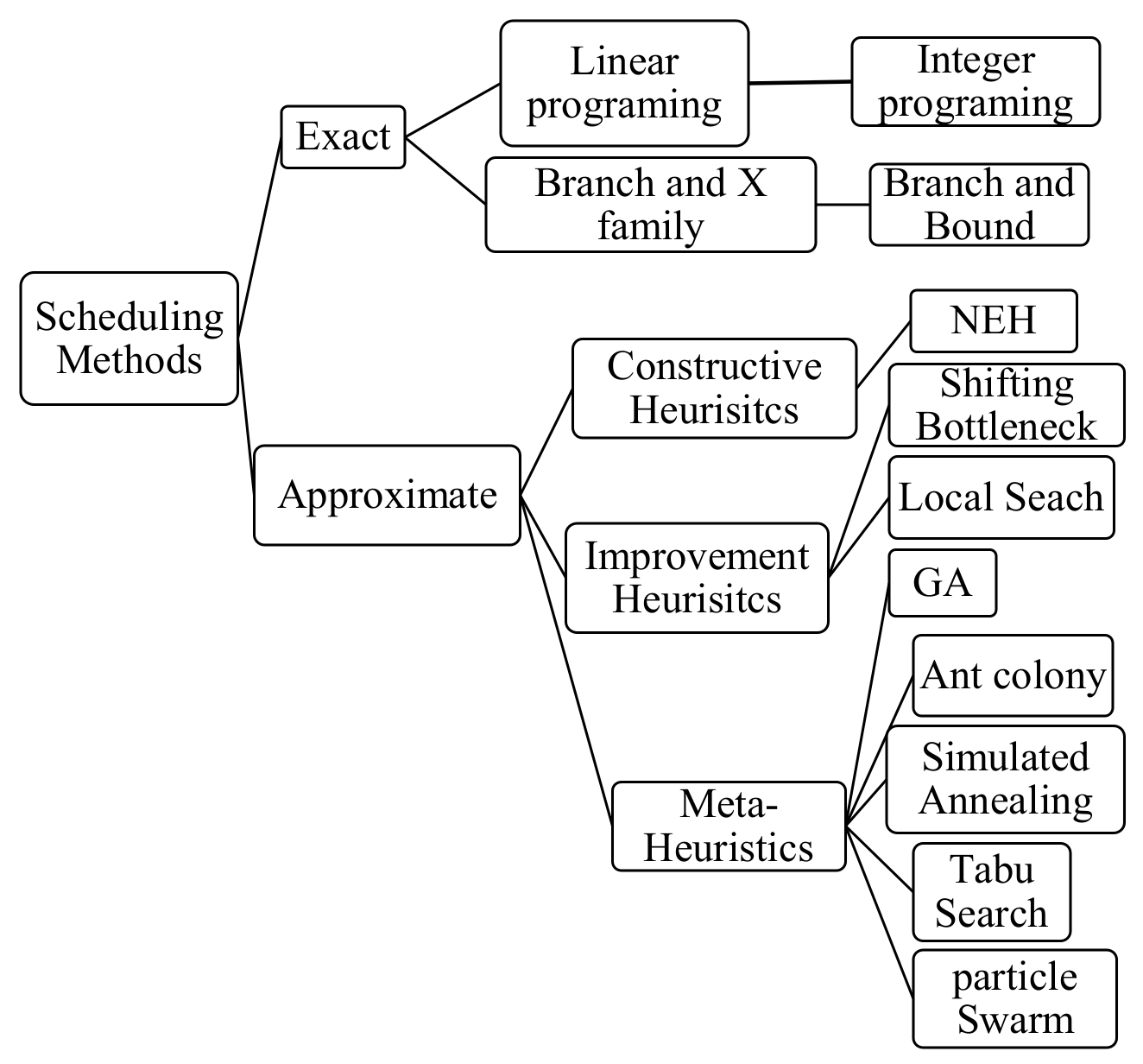
4.2. Methods to Solve Scheduling Problems
4.2.1. Exact Methods
4.2.2. Approximate Methods
| Algorithm 1 Solving a generic scheduling problem by an approximate method |
| 1: Start with a random schedule or use a constructive method to generate a base schedule. 2: Calculate the performance measure 3: While a good solution (ideally, the optimal solution) has not been reached: 4: Perturb the schedule 5: Recalculate the performance measure |
5. Theory and the Application of Different Types of Graphs
5.1. Clique
5.2. Graph Coloring
5.3. Social Network (Collaborative Network)
5.4. Agreement Graph and Bipartite Graph
5.5. Markov Random Fields
5.6. Traveling Salesman Graph
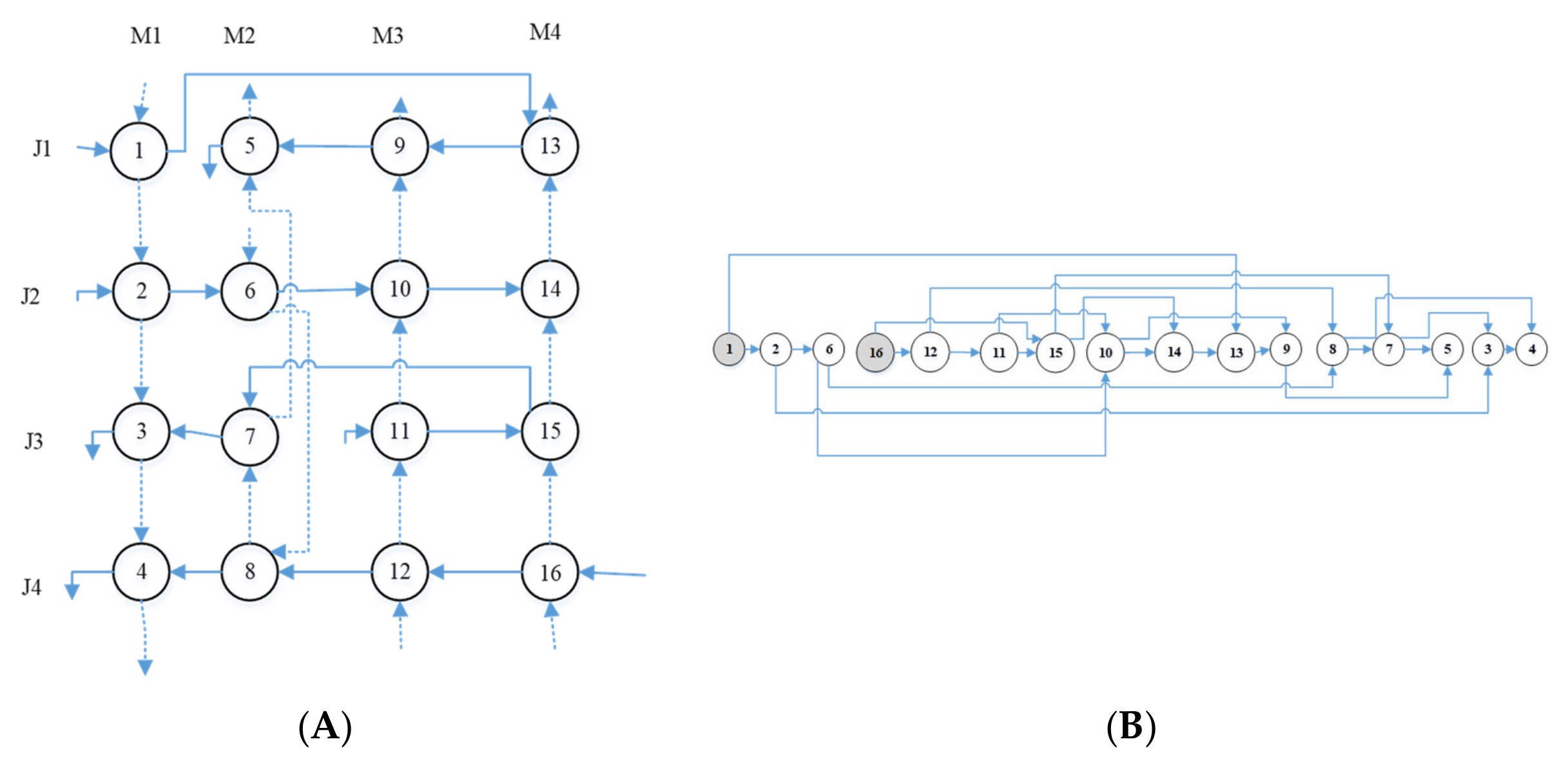
5.7. Directed Acyclic Graph (DAG)
5.7.1. Topologically Sorting a DAG
| Algorithm 2 Topological Sort Algorithm |
| Output T, the set of nodes which are topologically sorted |
| 1. Count the number of predecessors for all nodes using a counter Π 2. Insert all the first node with no predecessor in the dynamic set Q 3. While Q is not empty: 4. Remove a node from Q 5. Place the node in the topological set (T) 6. For all successors: 7. Decrement Π of the successor 8. If Π = 0 9. Insert the successor in Q |
5.7.2. Calculating the Longest Path in a DAG
| Algorithm 3: Finding the length of the longest path using Dynamic Programing Algorithm |
| Output ln the length of the longest path to node n Lmax, the length of the longest path |
| 1. For all nodes x on the topological sort (T): 2. Remove x from T 3. 4. |
5.7.3. DAGs for Manufacturing Systems
5.8. Precedence Graph (Conflict Graph)
5.9. Petri Net
5.10. Alternative Graph
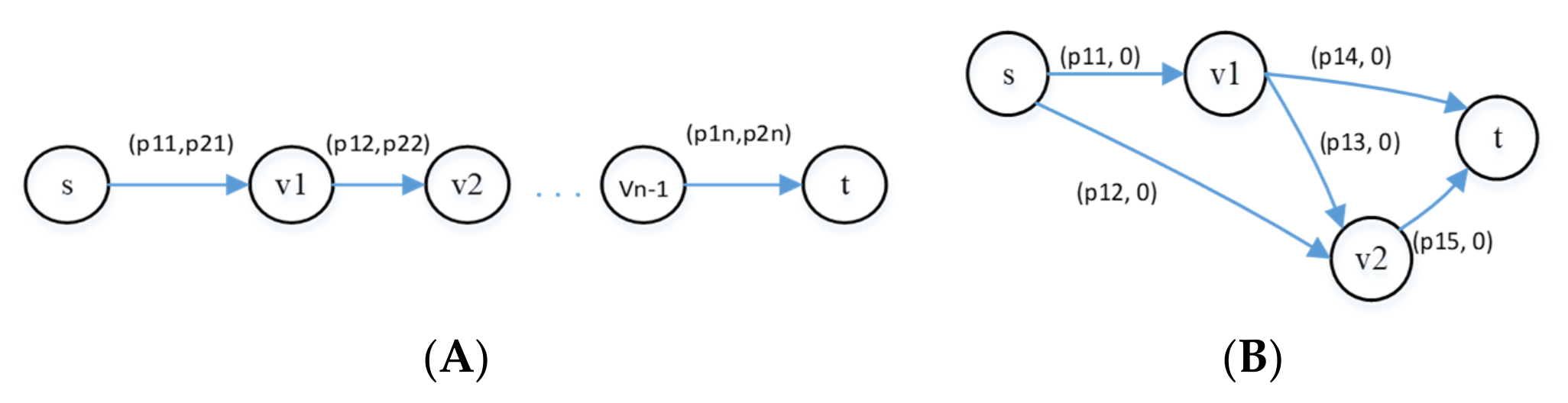
5.11. Multi-Stage Graph
5.12. Tree
5.12.1. Branch and Bound Algorithm/Tree
5.12.2. Hyper-Heuristic Tree
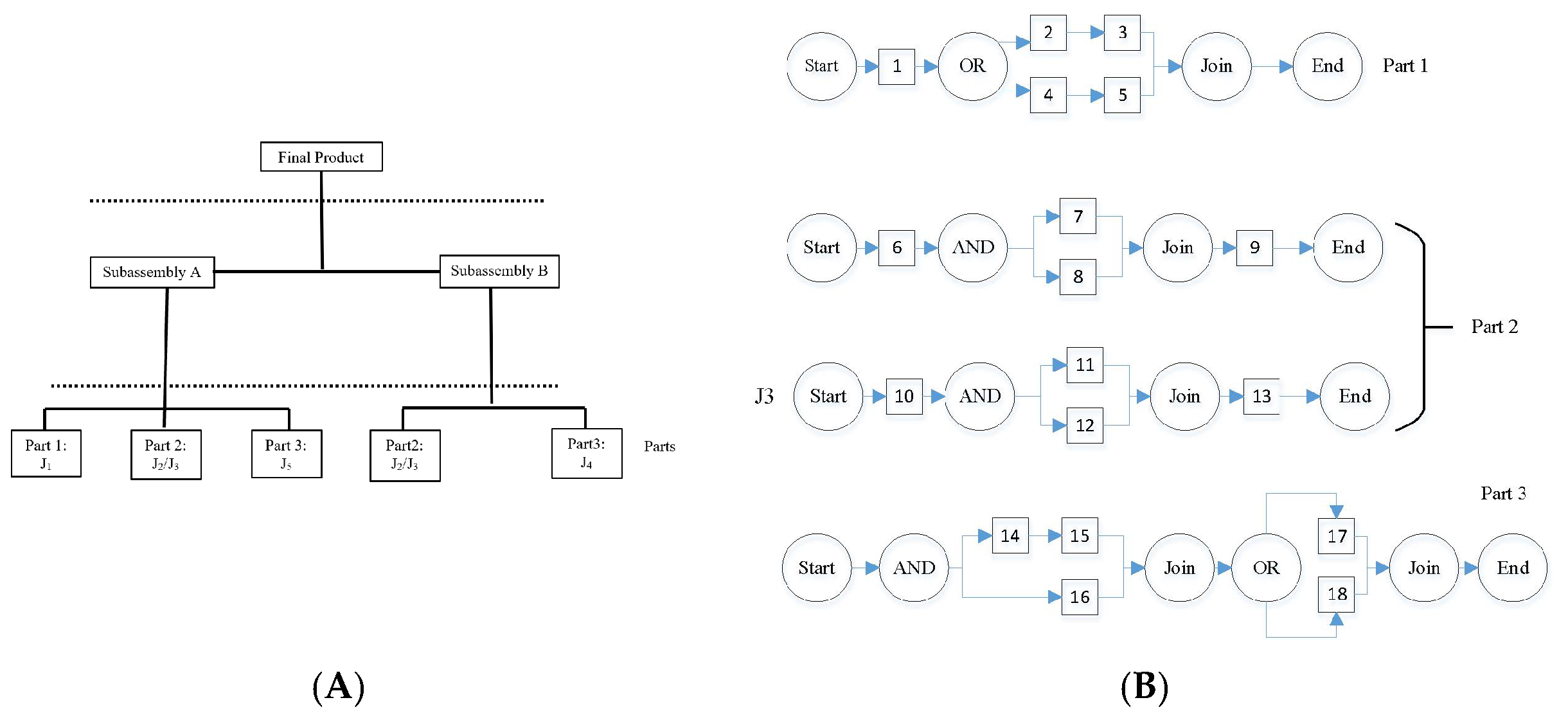
5.12.3. AND-OR Graph
5.12.4. Game Tree
5.12.5. Processing Operation Tree
5.13. Semantic Graph
5.14. A Mixed Graph
5.14.1. Disjunctive Graph
5.14.2. Ant Colony Graph
6. Overview of the Full Dataset
7. Analysis and Discussion
8. Summary of Our Results
9. Conclusions and Future Research Directions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Trudeau, R.J. Introduction to Graph. Theory; Courier Corporation: North Chelmsford, MA, USA, 2013. [Google Scholar]
- Carlson, S.C. Königsberg Bridge Problem, in Encyclopedia Britannica. 2010. Available online: https://www.britannica.com/science/Konigsberg-bridge-problem (accessed on 16 May 2021).
- Mehrani, R.; Sharma, S. Behavior of water confined between hydrophobic surfaces with grafted segments. Colloid Interface Sci. Commun. 2021, 40, 100355. [Google Scholar] [CrossRef]
- Madraki, Y.; Oakley, A.; Le, A.N.; Colin, A.; Ovarlez, G.; Hormozi, S. Shear thickening in dense non-Brownian suspensions: Viscous to inertial transition. J. Rheol. 2020, 64, 227–238. [Google Scholar] [CrossRef] [Green Version]
- Riaz, F.; Ali, K.M. Applications of Graph Theory in Computer Science. In Proceedings of the 2011 Third International Conference on Computational Intelligence, Communication Systems and Networks, Bali, Indonesia, 26–28 July 2011; pp. 142–145. [Google Scholar]
- Madraki, G.; Grasso, I.; Otala, J.; Liu, Y.; Matthews, J. Characterizing and Comparing COVID-19 Misinformation Across Languages, Countries and Platforms. arXiv 2020, arXiv:2010.06455. [Google Scholar]
- Amato, F.; Castiglione, A.; De Santo, A.; Moscato, V.; Picariello, A.; Persia, F.; Sperlí, G. Recognizing human behaviours in online social networks. Comput. Secur. 2018, 74, 355–370. [Google Scholar] [CrossRef]
- Amato, F.; Moscato, V.; Picariello, A.; Sperli, G. Multimedia Social Network Modeling: A Proposal. In Proceedings of the 2016 IEEE Tenth International Conference on Semantic Computing (ICSC), Laguna Hills, CA, USA, 4–6 February 2016; pp. 448–453. [Google Scholar]
- Otala, J.M.; Kurtic, G.; Grasso, I.; Liu, Y.; Matthews, J.; Madraki, G. 2021. Political Polarization and Platform Migration: A Study of Parler and Twitter Usage by United States of America Congress Members. In Companion Proceedings of the Web Conference 2021 (WWW ’21 Companion), April 19–23, 2021, Ljubljana, Slovenia; ACM: New York, NY, USA, 2021; p. 10. [Google Scholar] [CrossRef]
- La Gatta, V.; Moscato, V.; Postiglione, M.; Sperlì, G. CASTLE: Cluster-aided space transformation for local explanations. Expert Syst. Appl. 2021, 179, 115045. [Google Scholar] [CrossRef]
- Djakbarova, U.; Madraki, Y.; Chan, E.T.; Kural, C. Dynamic interplay between cell membrane tension and clathrin-mediated endocytosis. Biol. Cell 2021. [Google Scholar] [CrossRef]
- Mehrdad, S.; Mousavian, S.; Madraki, G.; Dvorkin, Y. Cyber-Physical Resilience of Electrical Power Systems Against Malicious Attacks: A Review. Curr. Sustain. Energy Rep. 2018, 5, 14–22. [Google Scholar] [CrossRef]
- Mousavian, S.; Conejo, A.J.; Sioshansi, R. Equilibria in investment and spot electricity markets: A conjectural-variations approach. Eur. J. Oper. Res. 2020, 281, 129–140. [Google Scholar] [CrossRef]
- Mousavian, S.; Erol-Kantarci, M.; Mouftah, H.T. Cyber-Security and Resiliency of Transportation and Power Systems in Smart Cities. In Transportation and Power Grid in Smart Cities; Wiley: Hoboken, NJ, USA, 2018; pp. 507–527. [Google Scholar]
- Hosseini, S.; Ivanov, D. Bayesian networks for supply chain risk, resilience and ripple effect analysis: A literature review. Expert Syst. Appl. 2020, 161, 113649. [Google Scholar] [CrossRef] [PubMed]
- Salmani, Y.; Partovi, F.Y.; Banerjee, A. Customer-driven investment decisions in existing multiple sales channels: A downstream supply chain analysis. Int. J. Prod. Econ. 2018, 204, 44–58. [Google Scholar] [CrossRef]
- La Gatta, V.; Moscato, V.; Postiglione, M.; Sperli, G. An Epidemiological Neural Network Exploiting Dynamic Graph Structured Data Applied to the COVID-19 Outbreak. IEEE Trans. Big Data 2021, 7, 45–55. [Google Scholar] [CrossRef]
- Caggiano, A. Manufacturing System. In CIRP Encyclopedia of Production Engineering; Laperrière, L., Reinhart, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 830–836. [Google Scholar]
- Fan, K.; Zhai, Y.; Li, X.; Wang, M. Review and classification of hybrid shop scheduling. Prod. Eng. 2018, 12, 597–609. [Google Scholar] [CrossRef]
- Singh, G.; Kaur, G.; Singh, G. Review of Graph Based Scheduling Algorithms. Int. Res. J. Eng. Technol. (IRJET) 2015, 2. [Google Scholar]
- Sachdeva, S.; Panwar, P. A review of multiprocessor directed acyclic graph (DAG) scheduling algorithms. Int. J. Comput. Sci. Commun. 2015, 66, 67–72. [Google Scholar]
- Weise, J.; Benkhardt, S.; Mostaghim, S. A Survey on Graph-based Systems in Manufacturing Processes. In Proceedings of the 2018 IEEE Symposium Series on Computational Intelligence (SSCI), Bangalore, India, 18–21 November 2018; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2018; pp. 112–119. [Google Scholar]
- Da Silva, E.C.; Gabriel, P.H. A Comprehensive Review of Evolutionary Algorithms for Multiprocessor DAG Scheduling. Computation 2020, 8, 26. [Google Scholar] [CrossRef]
- Blazewicz, J.; Kobler, D. Review of properties of different precedence graphs for scheduling problems. Eur. J. Oper. Res. 2002, 142, 435–443. [Google Scholar] [CrossRef]
- Tuncel, G.; Bayhan, G.M. Applications of Petri nets in production scheduling: A review. Int. J. Adv. Manuf. Technol. 2007, 34, 762–773. [Google Scholar] [CrossRef]
- Yadav, A.; Jayswal, S. Modelling of flexible manufacturing system: A review. Int. J. Prod. Res. 2018, 56, 2464–2487. [Google Scholar] [CrossRef]
- Panwalkar, S.S.; Koulamas, C. The evolution of schematic representations of flow shop scheduling problems. J. Sched. 2018, 22, 379–391. [Google Scholar] [CrossRef]
- Sotskov, Y.N. Mixed Graph Colorings: A Historical Review. Mathematics 2020, 8, 385. [Google Scholar] [CrossRef] [Green Version]
- West, J.; Bergstrom, C.; Bergstrom, T.; Althouse, B. Eigenfactor; University of Washington: Washington, DC, USA, 2007; Available online: http://eigenfactor.org/about.php (accessed on 16 April 2021).
- ABDC Journal Quality List. 2019. Available online: https://abdc.edu.au/wp-content/uploads/2020/03/abdc-2019-journal-quality-list-review-report-6-december-2019_2.pdf (accessed on 16 April 2021).
- Shen, L.; Dauzère-Pérès, S.; Neufeld, J.S. Solving the flexible job shop scheduling problem with sequence-dependent setup times. Eur. J. Oper. Res. 2018, 265, 503–516. [Google Scholar] [CrossRef]
- Lamorgese, L.; Mannino, C. A Noncompact Formulation for Job-Shop Scheduling Problems in Traffic Management. Oper. Res. 2019, 67, 1586–1609. [Google Scholar] [CrossRef]
- Sobeyko, O.; Mönch, L. Heuristic approaches for scheduling jobs in large-scale flexible job shops. Comput. Oper. Res. 2016, 68, 97–109. [Google Scholar] [CrossRef]
- Madraki, G.; Bahalkeh, E.; Judd, R. Efficient Algorithm to Find Makespan under Perturbation in Operation Times. In Proceedings of the IIE Annual Conference, Institute of Industrial and Systems Engineers (IISE), Nashville, TN, USA, 30 May–2 June 2015; Institute of Industrial and Systems Engineers (IISE): Norcross, GA, USA, 2015. [Google Scholar]
- Mei, Y.; Nguyen, S.; Xue, B.; Zhang, M. An Efficient Feature Selection Algorithm for Evolving Job Shop Scheduling Rules With Genetic Programming. IEEE Trans. Emerg. Top. Comput. Intell. 2017, 1, 339–353. [Google Scholar] [CrossRef]
- Nip, K.; Wang, Z.; Xing, W. A study on several combination problems of classic shop scheduling and shortest path. Theor. Comput. Sci. 2016, 654, 175–187. [Google Scholar] [CrossRef]
- Zhang, J.; Ding, G.; Zou, Y.; Qin, S.; Fu, J. Review of job shop scheduling research and its new perspectives under Industry 4. J. Intell. Manuf. 2019, 30, 1809–1830. [Google Scholar] [CrossRef]
- Cao, Z.; Zhou, L.; Hu, B.; Lin, C. An Adaptive Scheduling Algorithm for Dynamic Jobs for Dealing with the Flexible Job Shop Scheduling Problem. Bus. Inf. Syst. Eng. 2019, 61, 299–309. [Google Scholar] [CrossRef] [Green Version]
- El-Desoky, I.; El-Shorbagy, M.A.; Nasr, S.M.; Hedaqy, Z.M.; Mousa, A.A. A hybrid genetic algorithm for job shop scheduling problems. Int. J. Adv. Eng. Technol. Comput. Sci. 2016, 3, 6–17. [Google Scholar]
- Pinedo, M. Planning and Scheduling in Manufacturing and Services; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Clewett, A.J.; Baker, K.R. Introduction to Sequencing and Scheduling. Oper. Res. Q. 1977, 28, 352. [Google Scholar] [CrossRef]
- Wan, G.; Yen, B.P.-C. Tabu search for single machine scheduling with distinct due windows and weighted earliness/tardiness penalties. Eur. J. Oper. Res. 2002, 142, 271–281. [Google Scholar] [CrossRef]
- Guan, L.; Li, J.; Li, W.; Lichen, J. Improved approximation algorithms for the combination problem of parallel machine scheduling and path. J. Comb. Optim. 2019, 38, 689–697. [Google Scholar] [CrossRef]
- Behnamian, J. Graph colouring-based algorithm to parallel jobs scheduling on parallel factories. Int. J. Comput. Integr. Manuf. 2015, 29, 622–635. [Google Scholar] [CrossRef]
- Zabihzadeh, S.S.; Rezaeian, J. Two meta-heuristic algorithms for flexible flow shop scheduling problem with robotic transportation and release time. Appl. Soft Comput. 2016, 40, 319–330. [Google Scholar] [CrossRef]
- Mati, Y.; Dauzère-Pérès, S.; Lahlou, C. A general approach for optimizing regular criteria in the job-shop scheduling problem. Eur. J. Oper. Res. 2011, 212, 33–42. [Google Scholar] [CrossRef]
- Dabah, A.; Bendjoudi, A.; AitZai, A.; Taboudjemat, N.N. Efficient parallel tabu search for the blocking job shop scheduling problem. Soft Comput. 2019, 23, 13283–13295. [Google Scholar] [CrossRef]
- Pranzo, M.; Pacciarelli, D. An iterated greedy metaheuristic for the blocking job shop scheduling problem. J. Heuristics 2015, 22, 587–611. [Google Scholar] [CrossRef]
- Lange, J.; Werner, F. Approaches to modeling train scheduling problems as job-shop problems with blocking constraints. J. Sched. 2017, 21, 191–207. [Google Scholar] [CrossRef]
- Chaouch, I.; Driss, O.B.; Ghedira, K. A novel dynamic assignment rule for the distributed job shop scheduling problem using a hybrid ant-based algorithm. Appl. Intell. 2019, 49, 1903–1924. [Google Scholar] [CrossRef]
- AitZai, A.; Benmedjdoub, B.; Boudhar, M. Branch-and-bound and PSO algorithms for no-wait job shop scheduling. J. Intell. Manuf. 2014, 27, 679–688. [Google Scholar] [CrossRef]
- El Khoukhi, F.; Boukachour, J.; Alaoui, A.E.H. The “Dual-Ants Colony”: A novel hybrid approach for the flexible job shop scheduling problem with preventive maintenance. Comput. Ind. Eng. 2017, 106, 236–255. [Google Scholar] [CrossRef]
- Xie, J.; Gao, L.; Peng, K.; Li, X.; Li, H. Review on flexible job shop scheduling. IET Collab. Intell. Manuf. 2019, 1, 67–77. [Google Scholar] [CrossRef]
- Wu, J.; Wu, G.D.; Wang, J.J. Flexible Job-Shop Scheduling Problem Based on Hybrid ACO Algorithm. Int. J. Simul. Model. 2017, 16, 497–505. [Google Scholar] [CrossRef]
- Chen, J.C.; Wu, C.-C.; Chen, C.-W.; Chen, K.-H. Flexible job shop scheduling with parallel machines using Genetic Algorithm and Grouping Genetic Algorithm. Expert Syst. Appl. 2012, 39, 10016–10021. [Google Scholar] [CrossRef]
- Brucker, P.; Schlie, R. Job-shop scheduling with multi-purpose machines. Comput. 1990, 45, 369–375. [Google Scholar] [CrossRef]
- Dauzère-Pérès, S.; Paulli, J. An integrated approach for modeling and solving the general multiprocessor job-shop scheduling problem using tabu search. Ann. Oper. Res. 1997, 70, 281–306. [Google Scholar] [CrossRef]
- Zhao, B.; Gao, J.; Chen, K.; Guo, K. Two-generation Pareto ant colony algorithm for multi-objective job shop scheduling problem with alternative process plans and unrelated parallel machines. J. Intell. Manuf. 2018, 29, 93–108. [Google Scholar] [CrossRef]
- Prakash, A.; Chan, F.T.; Deshmukh, S. FMS scheduling with knowledge based genetic algorithm approach. Expert Syst. Appl. 2011, 38, 3161–3171. [Google Scholar] [CrossRef]
- Chan, F.T.S.; Chan, H.K. A comprehensive survey and future trend of simulation study on FMS scheduling. J. Intell. Manuf. 2004, 15, 87–102. [Google Scholar] [CrossRef]
- Błażewicz, J.; Ecker, K.H.; Pesch, E.; Schmidt, G.; Węglarz, J. Scheduling in Flexible Manufacturing Systems. In Scheduling Computer and Manufacturing Processes; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 1996; pp. 369–421. [Google Scholar]
- Baruwa, O.T.; Piera, M.A. A coloured Petri net-based hybrid heuristic search approach to simultaneous scheduling of machines and automated guided vehicles. Int. J. Prod. Res. 2016, 54, 4773–4792. [Google Scholar] [CrossRef]
- Gupta, J.N.; Stafford, E.F. Flowshop scheduling research after five decades. Eur. J. Oper. Res. 2006, 169, 699–711. [Google Scholar] [CrossRef]
- Ravindran, D.; Selvakumar, S.; Sivaraman, R.; Haq, A.N. Flow shop scheduling with multiple objective of minimizing makespan and total flow time. Int. J. Adv. Manuf. Technol. 2004, 25, 1007–1012. [Google Scholar] [CrossRef]
- Belabid, J.; Aqil, S.; Allali, K. Solving Permutation Flow Shop Scheduling Problem with Sequence-Independent Setup Time. J. Appl. Math. 2020, 2020, 1–11. [Google Scholar] [CrossRef]
- Motlagh, M.M.; Azimi, P.; Amiri, M.; Madraki, G. An efficient simulation optimization methodology to solve a multi-objective problem in unreliable unbalanced production lines. Expert Syst. Appl. 2019, 138, 112836. [Google Scholar] [CrossRef]
- Dallery, Y.; Gershwin, S. Manufacturing flow line systems: A review of models and analytical results. Queueing Syst. 1992, 12, 3–94. [Google Scholar] [CrossRef] [Green Version]
- Lee, C.-Y.; Cheng, T.C.E.; Lin, B.M.T. Minimizing the Makespan in the 3-Machine Assembly-Type Flowshop Scheduling Problem. Manag. Sci. 1993, 39, 616–625. [Google Scholar] [CrossRef]
- Wang, S.-Y.; Wang, L. An Estimation of Distribution Algorithm-Based Memetic Algorithm for the Distributed Assembly Permutation Flow-Shop Scheduling Problem. IEEE Trans. Syst. Man Cybern. Syst. 2016, 46, 139–149. [Google Scholar] [CrossRef]
- Gmys, J.; Mezmaz, M.; Melab, N.; Tuyttens, D. A computationally efficient Branch-and-Bound algorithm for the permutation flow-shop scheduling problem. Eur. J. Oper. Res. 2020, 284, 814–833. [Google Scholar] [CrossRef] [Green Version]
- Qian, B.; Li, Z.-C.; Hu, R. A copula-based hybrid estimation of distribution algorithm for m-machine reentrant permutation flow-shop scheduling problem. Appl. Soft Comput. 2017, 61, 921–934. [Google Scholar] [CrossRef]
- Ashrafi, M.; Davoudpour, H.; Abbassi, M. Investigating the efficiency of GRASP for the SDST HFS with controllable processing times and assignable due dates. In Handbook of Research on Novel Soft Computing Intelligent Algorithms: Theory and Practical Applications; IGI Global: Hershey, PA, USA, 2014; pp. 538–567. [Google Scholar]
- Lee, T.-S.; Loong, Y.-T. A review of scheduling problem and resolution methods in flexible flow shop. Int. J. Ind. Eng. Comput. 2019, 10, 67–88. [Google Scholar] [CrossRef]
- Dorndorf, U.; Pesch, E. Solving the open shop scheduling problem. J. Sched. 2001, 4, 157–174. [Google Scholar] [CrossRef]
- Tellache, N.E.H.; Boudhar, M.; Yalaoui, F. Two-machine open shop problem with agreement graph. Theor. Comput. Sci. 2019, 796, 154–168. [Google Scholar] [CrossRef]
- Tellache, N.E.H.; Boudhar, M. Open shop scheduling problems with conflict graphs. Discret. Appl. Math. 2017, 227, 103–120. [Google Scholar] [CrossRef]
- Pempera, J.; Smutnicki, C. Open shop cyclic scheduling. Eur. J. Oper. Res. 2018, 269, 773–781. [Google Scholar] [CrossRef]
- Shakhlevich, N.V.; Sotskov, Y.N.; Werner, F. Complexity of mixed shop scheduling problems: A survey. Eur. J. Oper. Res. 2000, 120, 343–351. [Google Scholar] [CrossRef]
- Wang, M.; Zhong, R.Y.; Dai, Q.; Huang, G.Q. A MPN-based scheduling model for IoT-enabled hybrid flow shop manufacturing. Adv. Eng. Inf. 2016, 30, 728–736. [Google Scholar] [CrossRef]
- Pasupuleti, V. Scheduling in Cellular Manufacturing Systems. Iberoam. J. Ind. Eng. 2012, 4, 231–243. [Google Scholar] [CrossRef]
- Zeng, C.; Tang, J.; Yan, C. Job-shop cell-scheduling problem with inter-cell moves and automated guided vehicles. J. Intell. Manuf. 2015, 26, 845–859. [Google Scholar] [CrossRef]
- Neufeld, J.S.; Gupta, J.N.; Buscher, U. A comprehensive review of flowshop group scheduling literature. Comput. Oper. Res. 2016, 70, 56–74. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, Y.; Long, C. Flexible robotic manufacturing cell scheduling problem with multiple robots. Int. J. Prod. Res. 2016, 54, 6768–6781. [Google Scholar] [CrossRef]
- Liu, C.; Wang, J.; Leung, J.Y.-T.; Li, K. Solving cell formation and task scheduling in cellular manufacturing system by discrete bacteria foraging algorithm. Int. J. Prod. Res. 2016, 54, 923–944. [Google Scholar] [CrossRef]
- Pinedo, M.; Hadavi, K. Scheduling: Theory, Algorithms and Systems Development. In Proceedings of the Operations Research Proceedings 1991; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 1992; pp. 35–42. [Google Scholar]
- Chen, B.; Potts, C.N.; Woeginger, G.J. A Review of Machine Scheduling: Complexity, Algorithms and Approximability. Handb. Comb. Optim. 1998, 1493–1641. [Google Scholar] [CrossRef]
- Stoop, P.P.; Wiers, V.C. The complexity of scheduling in practice. Int. J. Oper. Prod. Manag. 1996, 16, 37–53. [Google Scholar] [CrossRef]
- Lin, L.; Gen, M.; Liang, Y.; Ohno, K. A Hybrid EA for Reactive Flexible Job-shop Scheduling. Procedia Comput. Sci. 2012, 12, 110–115. [Google Scholar] [CrossRef] [Green Version]
- Amjad, M.K.; Butt, S.I.; Kousar, R.; Ahmad, R.; Agha, M.H.; Faping, Z.; Anjum, N.; Asgher, U. Recent Research Trends in Genetic Algorithm Based Flexible Job Shop Scheduling Problems. Math. Probl. Eng. 2018, 2018, 1–32. [Google Scholar] [CrossRef] [Green Version]
- Mokotoff, E. Parallel machine scheduling problems: A survey. Asia Pacif. J. Oper. Res. 2001, 18, 193. [Google Scholar]
- Martí, R.; Reinelt, G. The Linear Ordering Problem: Exact and Heuristic Methods in Combinatorial Optimization; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011; Volume 175. [Google Scholar]
- Kemmoé, S.; Lamy, D.; Tchernev, N. A Job-shop with an Energy Threshold Issue Considering Operations with Consumption Peaks. IFAC PapersOnLine 2015, 48, 788–793. [Google Scholar] [CrossRef]
- Sawik, T. Mixed integer programming for scheduling flexible flow lines with limited intermediate buffers. Math. Comput. Model. 2000, 31, 39–52. [Google Scholar] [CrossRef]
- Jourdan, L.; Basseur, M.; Talbi, E.-G. Hybridizing exact methods and metaheuristics: A taxonomy. Eur. J. Oper. Res. 2009, 199, 620–629. [Google Scholar] [CrossRef]
- Büyüktahtakin, I.E. Dynamic Programming Via Linear Programming. Wiley Encyclop. Oper. Res. Manag. Sci. 2010. [Google Scholar] [CrossRef]
- Williamson, D.P.; Shmoys, D.B. The Design of Approximation Algorithms. Design Approxim. Algorith. 2009. [Google Scholar]
- Bianchi, L.; Dorigo, M.; Gambardella, L.M.; Gutjahr, W.J. A survey on metaheuristics for stochastic combinatorial optimization. Nat. Comput. 2009, 8, 239–287. [Google Scholar] [CrossRef] [Green Version]
- Framinan, J.M.; Leisten, R.; Ruiz-Usano, R. Efficient heuristics for flowshop sequencing with the objectives of makespan and flowtime minimisation. Eur. J. Oper. Res. 2002, 141, 559–569. [Google Scholar] [CrossRef]
- Lunardi, W.T.; Birgin, E.G.; Ronconi, D.P.; Voos, H. Metaheuristics for the online printing shop scheduling problem. Eur. J. Oper. Res. 2020. [Google Scholar] [CrossRef]
- Afsar, H.; Lacomme, P.; Ren, L.; Prodhon, C.; Vigo, D. Resolution of a Job-Shop problem with transportation constraints: A master/slave approach. IFAC PapersOnLine 2016, 49, 898–903. [Google Scholar] [CrossRef]
- Mencía, R.; Sierra, M.R.; Mencía, C.; Varela, R. Memetic algorithms for the job shop scheduling problem with operators. Appl. Soft Comput. 2015, 34, 94–105. [Google Scholar] [CrossRef]
- Shi, F.; Zhao, S.; Meng, Y. Hybrid algorithm based on improved extended shifting bottleneck procedure and GA for assembly job shop scheduling problem. Int. J. Prod. Res. 2020, 58, 2604–2625. [Google Scholar] [CrossRef]
- Choo, W.M.; Wong, L.-P.; Khader, A.T. A modified bee colony optimization with local search approach for job shop scheduling problems relevant to bottleneck machines. Int. J. Adv. Soft Comput. Appl. 2016, 8, 52–78. [Google Scholar]
- Abdel-Kader, R.F. An improved PSO algorithm with genetic and neighborhood-based diversity operators for the job shop scheduling problem. Appl. Artif. Intell. 2018, 32, 433–462. [Google Scholar] [CrossRef]
- Nasiri, M.M. A modified ABC algorithm for the stage shop scheduling problem. Appl. Soft Comput. 2015, 28, 81–89. [Google Scholar] [CrossRef]
- Bahalkeh, E.; Madraki, G.; Judd, R. Efficient system matrix calculation for manufacturing systems. In Proceedings of the IIE Annual Conference, Nashville, TN, USA, 30 May–2 June 2015; Institute of Industrial and Systems Engineers (IISE): Norcross, GA, USA, 2015. [Google Scholar]
- Moon, J.W.; Moser, L. On cliques in graphs. Isr. J. Math. 1965, 3, 23–28. [Google Scholar] [CrossRef]
- Prosser, P. Exact Algorithms for Maximum Clique: A Computational Study. Algorithms 2012, 5, 545–587. [Google Scholar] [CrossRef] [Green Version]
- Mohabeddine, A.; Boudhar, M. New results in two identical machines scheduling with agreement graphs. Theor. Comput. Sci. 2019, 779, 37–46. [Google Scholar] [CrossRef]
- Even, G.; Halldórsson, M.M.; Kaplan, L.; Ron, D. Scheduling with conflicts: Online and offline algorithms. J. Sched. 2008, 12, 199–224. [Google Scholar] [CrossRef]
- Halldórsson, M.M.; Kortsarz, G. Multicoloring: Problems and Techniques. In Proceedings of the International Symposium on Mathematical Foundations of Computer Science, Prague, Czech Republic, 22–27 August 2004; Springer: Berlin/Heidelberg, Germany, 2004; Volume 3153, pp. 25–41. [Google Scholar]
- Furmańczyk, H.; Kubale, M. Scheduling of unit-length jobs with cubic incompatibility graphs on three uniform machines. Discret. Appl. Math. 2018, 234, 210–217. [Google Scholar] [CrossRef] [Green Version]
- Thevenin, S.; Zufferey, N.; Potvin, J.-Y. Graph multi-coloring for a job scheduling application. Discret. Appl. Math. 2018, 234, 218–235. [Google Scholar] [CrossRef]
- Furmańczyk, H.; Kubale, M. The complexity of equitable vertex coloring of graphs. J. Appl. Comput. Sci. 2005, 13, 95–106. [Google Scholar]
- Ganguli, R.; Roy, S. A study on course timetable scheduling using graph coloring approach. Int. J. Comput. Appl. Math. 2017, 12, 469–485. [Google Scholar]
- Reddy, M.S.; Ratnam, C.; Agrawal, R.; Varela, M.; Sharma, I.; Manupati, V. Investigation of reconfiguration effect on makespan with social network method for flexible job shop scheduling problem. Comput. Ind. Eng. 2017, 110, 231–241. [Google Scholar] [CrossRef] [Green Version]
- Bendraouche, M.; Boudhar, M. Scheduling with agreements: New results. Int. J. Prod. Res. 2015, 54, 1–15. [Google Scholar] [CrossRef]
- Bendraouche, M.; Boudhar, M.; Oulamara, A. Scheduling: Agreement graph vs resource constraints. Eur. J. Oper. Res. 2015, 240, 355–360. [Google Scholar] [CrossRef]
- Sun, L.; Lin, L.; Li, H.; Gen, M. Cooperative Co-Evolution Algorithm with an MRF-Based Decomposition Strategy for Stochastic Flexible Job Shop Scheduling. Mathematics 2019, 7, 318. [Google Scholar] [CrossRef] [Green Version]
- Rosenkrantz, D.J.; Stearns, R.E.; Lewis, P.M. Approximate algorithms for the traveling salesperson problem. 15th Ann. Sympos. Switch. Automata Theory 1974. [Google Scholar] [CrossRef]
- Bożejko, W.; Uchroński, M.; Wodecki, M. Block approach to the cyclic flow shop scheduling. Comput. Ind. Eng. 2015, 81, 158–166. [Google Scholar] [CrossRef]
- Bożejko, W.; Gnatowski, A.; Pempera, J.; Wodecki, M. Parallel tabu search for the cyclic job shop scheduling problem. Comput. Ind. Eng. 2017, 113, 512–524. [Google Scholar] [CrossRef]
- Madraki, G.; Judd, R. Accelerating the calculation of makespan used in scheduling improvement heuristics. Comput. Oper. Res. 2021, 130, 105233. [Google Scholar] [CrossRef]
- González, M.A.; Vela, M.D.C.R.; Varela, R. Scatter search with path relinking for the flexible job shop scheduling problem. Eur. J. Oper. Res. 2015, 245, 35–45. [Google Scholar] [CrossRef]
- Kahn, A.B. Topological sorting of large networks. Commun. ACM 1962, 5, 558–562. [Google Scholar] [CrossRef]
- Selvakumar, S.; Murthy, C.S.R. Scheduling precedence constrained task graphs with non-negligible intertask communication onto multiprocessors. IEEE Trans. Parallel Distrib. Syst. 1994, 5, 328–336. [Google Scholar] [CrossRef]
- Katriel, I.; Michel, L.; Van Hentenryck, P. Maintaining Longest Paths Incrementally. Constraints 2005, 10, 159–183. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Goebel, R.; Lin, G.; Su, B.; Zhang, A. Open-shop scheduling for unit jobs under precedence constraints. Theor. Comput. Sci. 2020, 803, 144–151. [Google Scholar] [CrossRef]
- Birgin, E.; Ferreira, J.; Ronconi, D. List scheduling and beam search methods for the flexible job shop scheduling problem with sequencing flexibility. Eur. J. Oper. Res. 2015, 247, 421–440. [Google Scholar] [CrossRef]
- Lunardi, W.T.; Birgin, E.G.; Laborie, P.; Ronconi, D.P.; Voos, H. Mixed Integer linear programming and constraint programming models for the online printing shop scheduling problem. Comput. Oper. Res. 2020, 123, 105020. [Google Scholar] [CrossRef]
- Tellache, N.E.H.; Boudhar, M. Flow shop scheduling problem with conflict graphs. Ann. Oper. Res. 2017, 261, 339–363. [Google Scholar] [CrossRef]
- Leake, C.; Baccelli, F.; Cohen, G.; Olsder, G.J.; Quadrat, J.-P. Synchronization and Linearity: An Algebra for Discrete Event Systems. J. Oper. Res. Soc. 1994, 45, 118. [Google Scholar] [CrossRef] [Green Version]
- Lee, T.-E.; Park, S.-H. An Extended Event Graph With Negative Places and Tokens for Time Window Constraints. IEEE Trans. Autom. Sci. Eng. 2005, 2, 319–332. [Google Scholar] [CrossRef]
- Cohen, G.; Gaubert, S.; Quadrat, J.-P. Max-plus algebra and system theory: Where we are and where to go now. Annu. Rev. Control. 1999, 23, 207–219. [Google Scholar] [CrossRef] [Green Version]
- Zhou, M.; Venkatesh, K. Modeling, Simulation, and Control. of Flexible Manufacturing Systems; World Scientific Pub Co Pte Lt: Singapore, 1999. [Google Scholar]
- Zhou, M.; Dicesare, F.; DesRochers, A. A hybrid methodology for synthesis of Petri net models for manufacturing systems. IEEE Trans. Robot. Autom. 1992, 8, 350–361. [Google Scholar] [CrossRef]
- Lusby, R.M.; Larsen, J.; Ehrgott, M.; Ryan, D. Railway track allocation: Models and methods. OR Spectr. 2011, 33, 843–883. [Google Scholar] [CrossRef]
- Dabah, A.; Bendjoudi, A.; AitZai, A.; El-Baz, D.; Taboudjemat, N.N. Hybrid multi-core CPU and GPU-based B&B approaches for the blocking job shop scheduling problem. J. Parallel Distrib. Comput. 2018, 117, 73–86. [Google Scholar] [CrossRef] [Green Version]
- Gholami, O.; Krasemann, J.T. A Heuristic Approach to Solving the Train Traffic Re-Scheduling Problem in Real Time. Algorithms 2018, 11, 55. [Google Scholar] [CrossRef] [Green Version]
- Corominas, A.; García-Villoria, A.; González, N.-A.; Pastor, R. A multistage graph-based procedure for solving a just-in-time flexible job-shop scheduling problem with machine and time-dependent processing costs. J. Oper. Res. Soc. 2018, 70, 620–633. [Google Scholar] [CrossRef]
- Wang, S.; Liu, M.; Chu, C. A branch-and-bound algorithm for two-stage no-wait hybrid flow-shop scheduling. Int. J. Prod. Res. 2014, 53, 1143–1167. [Google Scholar] [CrossRef]
- Nip, K.; Wang, Z.; Nobibon, F.T.; Leus, R. A combination of flow shop scheduling and the shortest path problem. J. Combin. Optim. 2015, 29, 36–52. [Google Scholar] [CrossRef] [Green Version]
- Bierwirth, C.; Kuhpfahl, J. Extended GRASP for the job shop scheduling problem with total weighted tardiness objective. Eur. J. Oper. Res. 2017, 261, 835–848. [Google Scholar] [CrossRef]
- Kim, H.-J.; Lee, J.-H. Three-machine flow shop scheduling with overlapping waiting time constraints. Comput. Oper. Res. 2019, 101, 93–102. [Google Scholar] [CrossRef]
- Zhang, F.; Mei, Y.; Nguyen, S.; Zhang, M. Evolving Scheduling Heuristics via Genetic Programming With Feature Selection in Dynamic Flexible Job-Shop Scheduling. IEEE Trans. Cybern. 2021, 51, 1797–1811. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Yang, J.-J.; Zheng, L.-Y. Hyper-Heuristic Coevolution of Machine Assignment and Job Sequencing Rules for Multi-Objective Dynamic Flexible Job Shop Scheduling. IEEE Access 2018, 7, 68–88. [Google Scholar] [CrossRef]
- Hart, E.; Sim, K. A hyper-heuristic ensemble method for static job-shop scheduling. Evolut. Comput. 2016, 24, 609–635. [Google Scholar] [CrossRef] [Green Version]
- Zhang, S.; Wang, S. Flexible Assembly Job-Shop Scheduling With Sequence-Dependent Setup Times and Part Sharing in a Dynamic Environment: Constraint Programming Model, Mixed-Integer Programming Model, and Dispatching Rules. IEEE Trans. Eng. Manag. 2018, 65, 487–504. [Google Scholar] [CrossRef]
- Rossi, A.; Lanzetta, M. Integration of hybrid additive/subtractive manufacturing planning and scheduling by metaheuristics. Comput. Ind. Eng. 2020, 144, 106428. [Google Scholar] [CrossRef]
- Liu, Q.; Li, X.; Gao, L.; Li, Y. A Modified Genetic Algorithm With New Encoding and Decoding Methods for Integrated Process Planning and Scheduling Problem. IEEE Trans. Cybern. 2020, 1–10. [Google Scholar] [CrossRef]
- Zhang, S.; Wong, T.N. Flexible job-shop scheduling/rescheduling in dynamic environment: A hybrid MAS/ACO approach. Int. J. Prod. Res. 2016, 55, 3173–3196. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, J.; Liu, Y. Game theory based real-time multi-objective flexible job shop scheduling considering environmental impact. J. Clean. Prod. 2017, 167, 665–679. [Google Scholar] [CrossRef]
- Rivest, R.L. Game tree searching by min/max approximation. Artif. Intell. 1987, 34, 77–96. [Google Scholar] [CrossRef]
- Lei, Q.; Guo, W.; Song, Y. Integrated scheduling algorithm based on an operation relationship matrix table for tree-structured products. Int. J. Prod. Res. 2018, 56, 5437–5456. [Google Scholar] [CrossRef]
- Zhu, Z.; Zhou, X.; Shao, K. A novel approach based on Neo4j for multi-constrained flexible job shop scheduling problem. Comput. Ind. Eng. 2019, 130, 671–686. [Google Scholar] [CrossRef]
- Grimes, D.; Hebrard, E. Solving Variants of the Job Shop Scheduling Problem Through Conflict-Directed Search. INFORMS J. Comput. 2015, 27, 268–284. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Cai, J.; Li, M.; Liu, Z. Flexible Job Shop Scheduling Problem Using an Improved Ant Colony Optimization. Sci. Program. 2017, 2017, 1–11. [Google Scholar] [CrossRef]
- Qin, W.; Zhuang, Z.; Liu, Y.; Tang, O. A two-stage ant colony algorithm for hybrid flow shop scheduling with lot sizing and calendar constraints in printed circuit board assembly. Comput. Ind. Eng. 2019, 138, 106115. [Google Scholar] [CrossRef]
- Ciro, G.C.; Dugardin, F.; Yalaoui, F.; Kelly, R. Open shop scheduling problem with a multi-skills resource constraint: A genetic algorithm and an ant colony optimisation approach. Int. J. Prod. Res. 2015, 54, 4854–4881. [Google Scholar] [CrossRef]
- Riahi, V.; Kazemi, M. A new hybrid ant colony algorithm for scheduling of no-wait flowshop. Oper. Res. 2016, 18, 55–74. [Google Scholar] [CrossRef] [Green Version]
- Başak, Ö.; Albayrak, Y.E. Petri net based decision system modeling in real-time scheduling and control of flexible automotive manufacturing systems. Comput. Ind. Eng. 2015, 86, 116–126. [Google Scholar] [CrossRef]
- Baruwa, O.T.; Piera, M.A. Identifying FMS repetitive patterns for efficient search-based scheduling algorithm: A colored Petri net approach. J. Manuf. Syst. 2015, 35, 120–135. [Google Scholar] [CrossRef]
- Marin, J.M.; Romero, N.H.; Mora, J.C.S.T.; Gomez, E.S.M. Modeling and simulation of flow shop scheduling problem through Petri net tools. World Acad. Sci. Eng. Technol. Int. J. Comput. Elect. Automat. Control. Inform. Eng. 2016, 10, 936–940. [Google Scholar]
- Al-Ahmari, A. Optimal robotic cell scheduling with controllers using mathematically based timed Petri nets. Inf. Sci. 2016, 329, 638–648. [Google Scholar] [CrossRef]
- Madraki, G.; Judd, R.P. Efficient algorithm to find makespan in manufacturing systems under multiple scheduling perturbations. Int. J. Prod. Res. 2017, 56, 5402–5418. [Google Scholar] [CrossRef]
- Samarghandi, H.; Behroozi, M. On the exact solution of the no-wait flow shop problem with due date constraints. Comput. Oper. Res. 2017, 81, 141–159. [Google Scholar] [CrossRef]
- Chamnanlor, C.; Sethanan, K.; Gen, M.; Chien, C.-F. Embedding ant system in genetic algorithm for re-entrant hybrid flow shop scheduling problems with time window constraints. J. Intell. Manuf. 2017, 28, 1915–1931. [Google Scholar] [CrossRef]
- Yu, L.; Zhu, C.; Shi, J.; Zhang, W. An Extended Flexible Job Shop Scheduling Model for Flight Deck Scheduling with Priority, Parallel Operations, and Sequence Flexibility. Sci. Program. 2017, 2017, 1–15. [Google Scholar] [CrossRef]
- Mejia, G.; Caballero-Villalobos, J.P.; Montoya, C. Petri Nets and Deadlock-Free Scheduling of Open Shop Manufacturing Systems. IEEE Trans. Syst. Man Cybern. Syst. 2018, 48, 1017–1028. [Google Scholar] [CrossRef]
- Bożek, A.; Werner, F. Flexible job shop scheduling with lot streaming and sublot size optimisation. Int. J. Prod. Res. 2017, 56, 6391–6411. [Google Scholar] [CrossRef]
- Shokouhi, E. Integrated multi-objective process planning and flexible job shop scheduling considering precedence constraints. Prod. Manuf. Res. 2017, 6, 61–89. [Google Scholar] [CrossRef] [Green Version]
- Lunardi, W.T.; Voos, H. An extended flexible job shop scheduling problem with parallel operations. ACM SIGAPP Appl. Comput. Rev. 2018, 18, 46–56. [Google Scholar] [CrossRef]
- Madraki, G.; Judd, R.P. Recalculating the Length of the Longest Path in Perturbed Directed Acyclic Graph. IFAC PapersOnLine 2019, 52, 1560–1565. [Google Scholar] [CrossRef]
- Liao, W.; Fu, Y. Min–max regret criterion-based robust model for the permutation flow-shop scheduling problem. Eng. Optim. 2019, 52, 687–700. [Google Scholar] [CrossRef]
- Billaut, J.-C.; Della Croce, F.; Salassa, F.; T’Kindt, V. No-idle, no-wait: When shop scheduling meets dominoes, Eulerian paths and Hamiltonian paths. J. Sched. 2018, 22, 59–68. [Google Scholar] [CrossRef]
- Kress, D.; Müller, D.; Nossack, J. A worker constrained flexible job shop scheduling problem with sequence-dependent setup times. OR Spectr. 2018, 41, 179–217. [Google Scholar] [CrossRef]
- Tian, S.; Wang, T.; Zhang, L.; Wu, X. Real-time shop floor scheduling method based on virtual queue adaptive control: Algorithm and experimental results. Measurement 2019, 147, 106689. [Google Scholar] [CrossRef]
- Wu, X.; Tian, S.; Zhang, L. The Internet of Things Enabled Shop Floor Scheduling and Process Control Method Based on Petri Nets. IEEE Access 2019, 7, 27432–27442. [Google Scholar] [CrossRef]
- Hu, L.; Liu, Z.; Hu, W.; Wang, Y.; Tan, J.; Wu, F. Petri-net-based dynamic scheduling of flexible manufacturing system via deep reinforcement learning with graph convolutional network. J. Manuf. Syst. 2020, 55, 1–14. [Google Scholar] [CrossRef]
- Vital-Soto, A.; Azab, A.; Baki, M.F. Mathematical modeling and a hybridized bacterial foraging optimization algorithm for the flexible job-shop scheduling problem with sequencing flexibility. J. Manuf. Syst. 2020, 54, 74–93. [Google Scholar] [CrossRef]
- Zhu, Z.; Zhou, X. An efficient evolutionary grey wolf optimizer for multi-objective flexible job shop scheduling problem with hierarchical job precedence constraints. Comput. Ind. Eng. 2020, 140, 106280. [Google Scholar] [CrossRef]
- Xie, Z.; Zhang, X.; Xia, Y.; Xin, Y. A Multi-Rule Algorithm for Multi-Shop Integrated Scheduling Problem. Design Eng. 2020, 968–979. [Google Scholar]
- Wang, Z.; Gombolay, M. Learning Scheduling Policies for Multi-Robot Coordination With Graph Attention Networks. IEEE Robot. Autom. Lett. 2020, 5, 4509–4516. [Google Scholar] [CrossRef]
- Mejía, G.; Lefebvre, D. Robust scheduling of flexible manufacturing systems with unreliable operations and resources. Int. J. Prod. Res. 2020, 58, 6474–6492. [Google Scholar] [CrossRef]
- Pan, L.; Yang, B.; Jiang, J.; Zhou, M. A Time Petri Net With Relaxed Mixed Semantics for Schedulability Analysis of Flexible Manufacturing Systems. IEEE Access 2020, 8, 46480–46492. [Google Scholar] [CrossRef]
- Tellache, N.E.H.; Boudhar, M. Two-machine flow shop problem with unit-time operations and conflict graph. Int. J. Prod. Res. 2014, 55, 1–16. [Google Scholar] [CrossRef]
- Tellache, N.E.H.; Boudhar, M. The two-machine flow shop problem with conflict graphs. IFAC PapersOnLine 2016, 49, 1026–1031. [Google Scholar] [CrossRef]
- Kouider, A.; Haddadène, H.A.; Ourari, S.; Oulamara, A. Mixed graph colouring for unit-time scheduling. Int. J. Prod. Res. 2014, 55, 1–10. [Google Scholar] [CrossRef]
- Ilani, H.; Shufan, E.; Grinshpoun, T. Partially concurrent open shop scheduling with integral preemptions. Ann. Oper. Res. 2017, 259, 157–171. [Google Scholar] [CrossRef]
- Grinshpoun, T.; Ilani, H.; Shufan, E. The representation of partially-concurrent open shop problems. Ann. Oper. Res. 2015, 252, 455–469. [Google Scholar] [CrossRef]
- Cheng, Y.; Bi, L.; Tao, F.; Ji, P. Hypernetwork-based manufacturing service scheduling for distributed and collaborative manufacturing operations towards smart manufacturing. J. Intell. Manuf. 2018, 31, 1707–1720. [Google Scholar] [CrossRef]
- Ilani, H.; Grinshpoun, T.; Shufan, E. Bounded colouring motivated by the limited resource partially concurrent open shop problem. Ann. Oper. Res. 2019, 1–16. [Google Scholar] [CrossRef]
- Shi, X.; Long, W.; Li, Y.; Deng, D.-S. Multi-population genetic algorithm with ER network for solving flexible job shop scheduling problems. PLoS ONE 2020, 15, e0233759. [Google Scholar] [CrossRef]
- Rossi, A.; Soldani, S.; Lanzetta, M. Hybrid stage shop scheduling. Expert Syst. Appl. 2015, 42, 4105–4119. [Google Scholar] [CrossRef]
- Ciro, G.C.; Dugardin, F.; Yalaoui, F.; Kelly, R. A fuzzy ant colony optimization to solve an open shop scheduling problem with multi-skills resource constraints. IFAC PapersOnLine 2015, 48, 715–720. [Google Scholar] [CrossRef]
- Cruz-Chávez, M.A. Neighbourhood generation mechanism applied in simulated annealing to job shop scheduling problems. Int. J. Syst. Sci. 2014, 46, 1–13. [Google Scholar] [CrossRef]
- Amirghasemi, M.; Zamani, R. An effective asexual genetic algorithm for solving the job shop scheduling problem. Comput. Ind. Eng. 2015, 83, 123–138. [Google Scholar] [CrossRef] [Green Version]
- Nouri, H.E.; Driss, O.B.; Ghédira, K. Hybrid metaheuristics for scheduling of machines and transport robots in job shop environment. Appl. Intell. 2016, 45, 808–828. [Google Scholar] [CrossRef]
- Kuhpfahl, J.; Bierwirth, C. A study on local search neighborhoods for the job shop scheduling problem with total weighted tardiness objective. Comput. Oper. Res. 2016, 66, 44–57. [Google Scholar] [CrossRef]
- Nouri, H.E.; Driss, O.B.; Ghédira, K. Simultaneous scheduling of machines and transport robots in flexible job shop environment using hybrid metaheuristics based on clustered holonic multiagent model. Comput. Ind. Eng. 2016, 102, 488–501. [Google Scholar] [CrossRef]
- Zhao, F.; Shao, Z.; Wang, J.; Zhang, C. A hybrid differential evolution and estimation of distribution algorithm based on neighbourhood search for job shop scheduling problems. Int. J. Prod. Res. 2015, 54, 1039–1060. [Google Scholar] [CrossRef]
- Shahzad, A.; Mebarki, N. Learning Dispatching Rules for Scheduling: A Synergistic View Comprising Decision Trees, Tabu Search and Simulation. Computers 2016, 5, 3. [Google Scholar] [CrossRef] [Green Version]
- Huang, S.; Tian, N.; Ji, Z. Particle swarm optimization with variable neighborhood search for multiobjective flexible job shop scheduling problem. Int. J. Model. Simul. Sci. Comput. 2016, 7, 1650024. [Google Scholar] [CrossRef]
- Ge, H.; Sun, L.; Chen, X.; Liang, Y. An Efficient Artificial Fish Swarm Model with Estimation of Distribution for Flexible Job Shop Scheduling. Int. J. Comput. Intell. Syst. 2016, 9, 917–931. [Google Scholar] [CrossRef] [Green Version]
- Yang, Q.; Liu, J.; Huang, Y.; Wang, Y.; Wang, T. The dynamic 4S auto maintenance shop scheduling in a multi-constraint machine environment based on the theory of constraints. Int. J. Adv. Manuf. Technol. 2015, 83, 1773–1785. [Google Scholar] [CrossRef]
- Elmi, A.; Topaloglu, S. Multi-degree cyclic flow shop robotic cell scheduling problem: Ant colony optimization. Comput. Oper. Res. 2016, 73, 67–83. [Google Scholar] [CrossRef]
- Jin, L.; Tang, Q.; Zhang, C.; Shao, X.; Tian, G. More MILP models for integrated process planning and scheduling. Int. J. Prod. Res. 2016, 54, 4387–4402. [Google Scholar] [CrossRef]
- Knopp, S.; Dauzère-Pérès, S.; Yugma, C. A batch-oblivious approach for Complex Job-Shop scheduling problems. Eur. J. Oper. Res. 2017, 263, 50–61. [Google Scholar] [CrossRef]
- Sotskov, Y.N.; Gholami, O. Mixed graph model and algorithms for parallel-machine job-shop scheduling problems. Int. J. Prod. Res. 2014, 55, 1–16. [Google Scholar] [CrossRef]
- Bürgy, R. A neighborhood for complex job shop scheduling problems with regular objectives. J. Sched. 2017, 20, 391–422. [Google Scholar] [CrossRef]
- Hao, X.; Gen, M.; Lin, L.; Suer, G.A. Effective multiobjective EDA for bi-criteria stochastic job-shop scheduling problem. J. Intell. Manuf. 2017, 28, 833–845. [Google Scholar] [CrossRef]
- Zuo, Y.; Gong, M.; Jiao, L. Adaptive multimeme algorithm for flexible job shop scheduling problem. Nat. Comput. 2016, 16, 677–698. [Google Scholar] [CrossRef]
- Xiong, H.; Fan, H.; Jiang, G.; Li, G. A simulation-based study of dispatching rules in a dynamic job shop scheduling problem with batch release and extended technical precedence constraints. Eur. J. Oper. Res. 2017, 257, 13–24. [Google Scholar] [CrossRef]
- Tamssaouet, K.; Dauzère-Pérès, S.; Yugma, C. Metaheuristics for the job-shop scheduling problem with machine availability constraints. Comput. Ind. Eng. 2018, 125, 1–8. [Google Scholar] [CrossRef]
- Yu, J.-M.; Lee, D.-H. Scheduling algorithms for job-shop-type remanufacturing systems with component matching requirement. Comput. Ind. Eng. 2018, 120, 266–278. [Google Scholar] [CrossRef]
- Xiong, W.; Fu, D. A new immune multi-agent system for the flexible job shop scheduling problem. J. Intell. Manuf. 2015, 29, 857–873. [Google Scholar] [CrossRef]
- Nagata, Y.; Ono, I. A guided local search with iterative ejections of bottleneck operations for the job shop scheduling problem. Comput. Oper. Res. 2018, 90, 60–71. [Google Scholar] [CrossRef]
- Zhang, S.; Wong, T.N. Integrated process planning and scheduling: An enhanced ant colony optimization heuristic with parameter tuning. J. Intell. Manuf. 2014, 29, 585–601. [Google Scholar] [CrossRef]
- Meolic, R.; Brezocnik, Z. Flexible job shop scheduling using zero-suppressed binary decision diagrams. Adv. Prod. Eng. Manag. 2018, 13, 373–388. [Google Scholar] [CrossRef]
- Liu, N.; Zhang, Y.F.; Lu, W.F. Improving Energy Efficiency in Discrete Parts Manufacturing System Using an Ultra-Flexible Job Shop Scheduling Algorithm. Int. J. Precis. Eng. Manuf. Technol. 2019, 6, 349–365. [Google Scholar] [CrossRef]
- Burdett, R.L.; Corry, P.; Yarlagadda, P.K.; Eustace, C.; Smith, S. A flexible job shop scheduling approach with operators for coal export terminals. Comput. Oper. Res. 2019, 104, 15–36. [Google Scholar] [CrossRef]
- Cruz-Chavez, M.A.; Rosales, M.H.C.; Zavala-Diaz, J.C.; Aguilar, J.A.H.; Rodriguez-Leon, A.; Avelino, J.C.P.; Ortiz, M.E.L.; Salinas, O.H. Hybrid Micro Genetic Multi-Population Algorithm With Collective Communication for the Job Shop Scheduling Problem. IEEE Access 2019, 7, 82358–82376. [Google Scholar] [CrossRef]
- Zhou, Y.; Yang, J.-J.; Zheng, L.-Y. Multi-Agent Based Hyper-Heuristics for Multi-Objective Flexible Job Shop Scheduling: A Case Study in an Aero-Engine Blade Manufacturing Plant. IEEE Access 2019, 7, 21147–21176. [Google Scholar] [CrossRef]
- Jun, S.; Lee, S.; Chun, H. Learning dispatching rules using random forest in flexible job shop scheduling problems. Int. J. Prod. Res. 2018, 57, 3290–3310. [Google Scholar] [CrossRef]
- Abedi, M.; Chiong, R.; Noman, N.; Zhang, R. A multi-population, multi-objective memetic algorithm for energy-efficient job-shop scheduling with deteriorating machines. Expert Syst. Appl. 2020, 157, 113348. [Google Scholar] [CrossRef]
- Fan, K.; Wang, M.; Zhai, Y.; Li, X. Scatter search algorithm for the multiprocessor task job-shop scheduling problem. Comput. Ind. Eng. 2019, 127, 677–686. [Google Scholar] [CrossRef]
- Vela, C.R.; Afsar, S.; Palacios, J.J.; González-Rodríguez, I.; Puente, J. Evolutionary tabu search for flexible due-date satisfaction in fuzzy job shop scheduling. Comput. Oper. Res. 2020, 119, 104931. [Google Scholar] [CrossRef]
- Ahmadian, M.M.; Salehipour, A.; Cheng, T. A meta-heuristic to solve the just-in-time job-shop scheduling problem. Eur. J. Oper. Res. 2021, 288, 14–29. [Google Scholar] [CrossRef]





















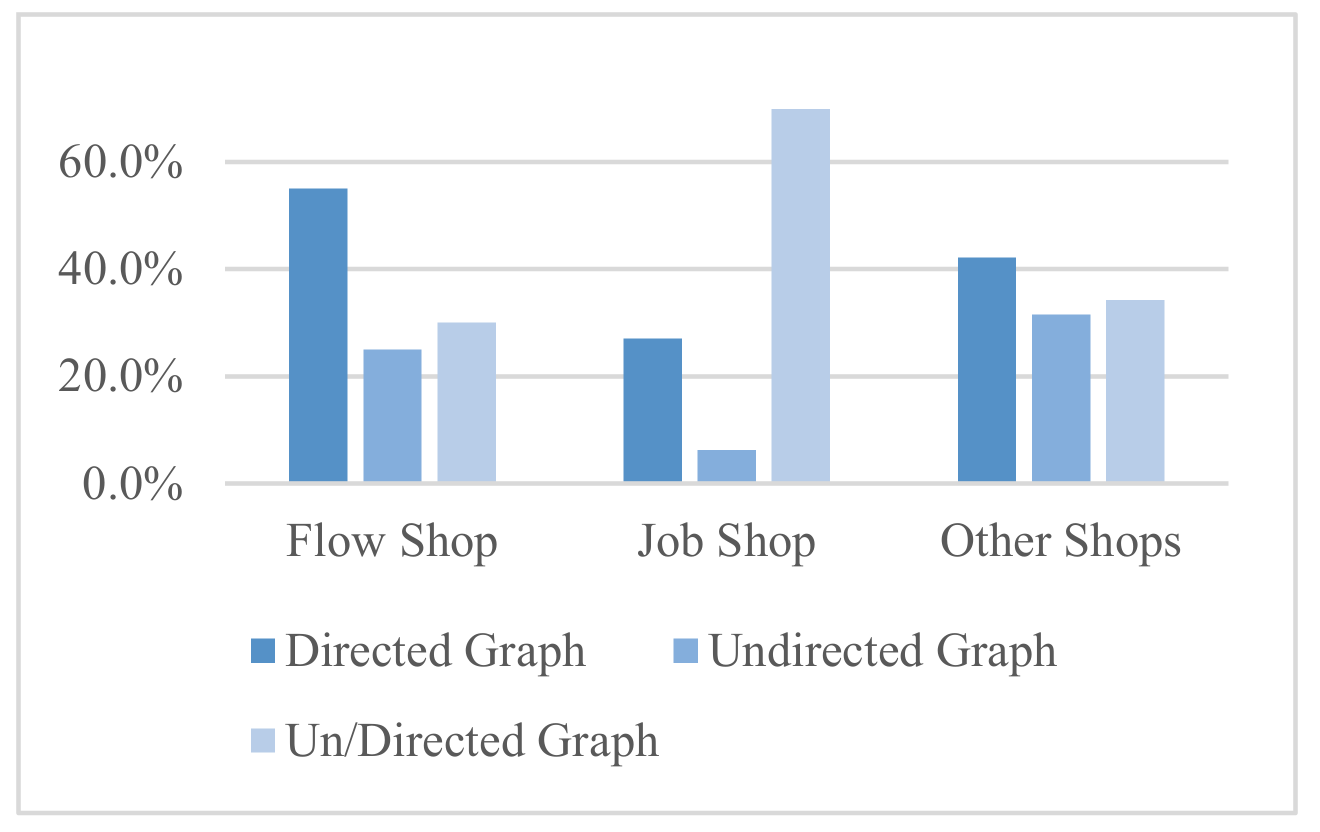
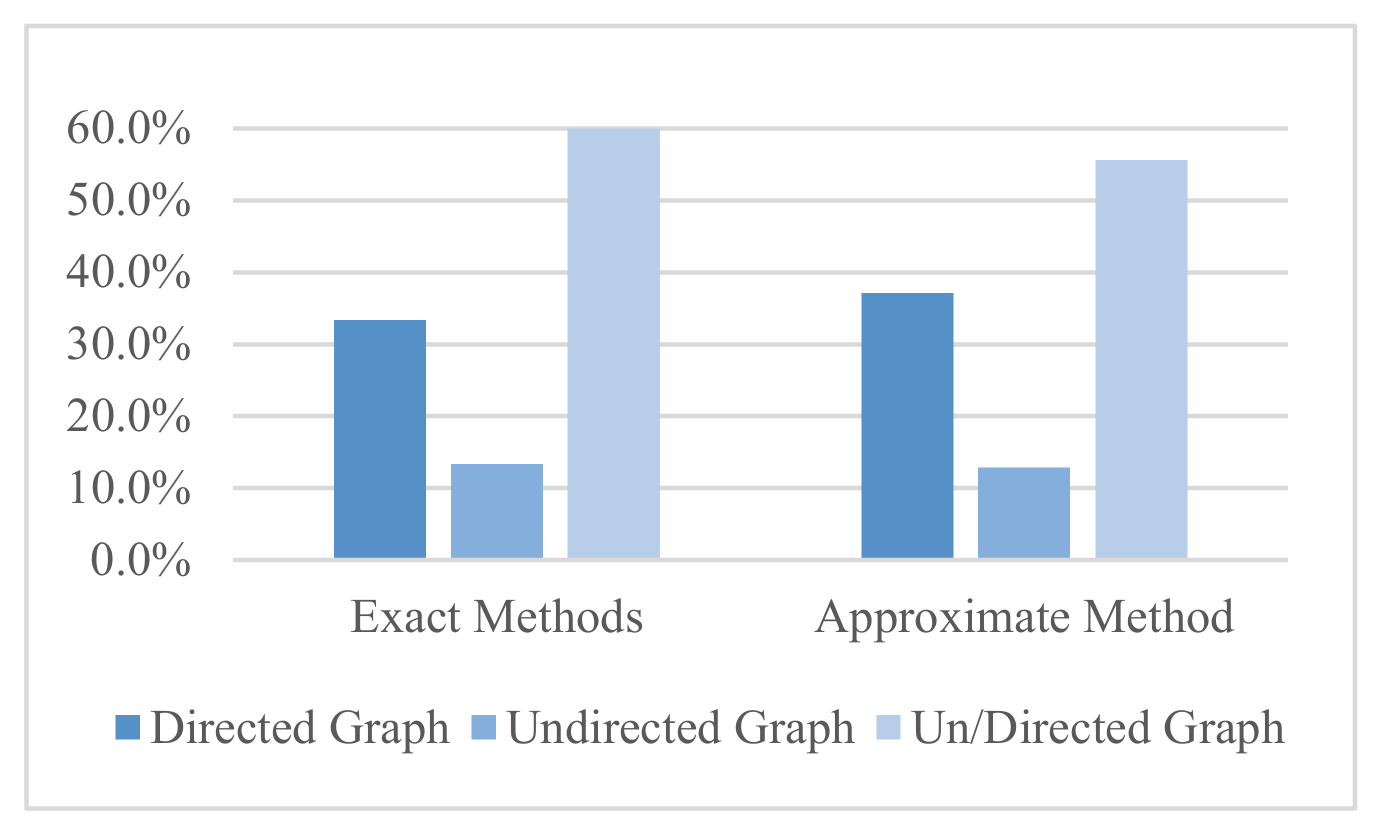

| Domain | Review Paper | Author-Year of Publication | Number of Reviewed Papers | The Time Period of Reviewed Papers | Targeted Topics | Additional Description |
|---|---|---|---|---|---|---|
| Computer Science | [20] | (Singh et al., 2015) | 14 | All before 1998 | The processor scheduling algorithms, DAG | Only DAG |
| [21] | (Sachdeva & Panwar, 2015) | 19 | 1979–2014 | DAG, Genetic Algorithm | Only DAG | |
| [22] | (Weise et al., 2018) | 67 | No time limit | Reviewing 9 graph-based systems, e.g., Ant colony, AND/OR, Social Networks, etc. | Investigating applications to manufacturing systems- Not scheduling problems | |
| [23] | (da Silva & Gabriel, 2020) | 56 | 1990–2020 | The processor scheduling algorithms, DAG | Only DAG | |
| Operation Management, Manufacturing systems | [24] | (Blazewicz & Kobler, 2002) | 26 | All before 1999 | Precedence graphs, unrelated parallel machines scheduling | Only Precedence graph |
| [25] | (Tuncel & Bayhan, 2007) | 20 | 1989–2005 | Petri nets, shop scheduling problem | Only Petri-net | |
| [26] | (Yadav & Jayswal, 2018) | 70 | No time limit | Flexible manufacturing systems, Multi-Criteria Decision Making, Petri Net, etc. | Only Petri-net | |
| [27] | (Panwalkar & Koulamas, 2019) | 56 | No time limit | Flow shop- Schematic representations | Not necessarily graph | |
| [28] | (Sotskov, 2020) | 88 | No time limit | Mixed Graph Colorings, Shop scheduling problem | Only mathematical theory of mixed graph coloring | |
| Our paper | Our paper (2021) | 143 | 2015–2021 | Graph theory, shop scheduling problem | All types of applied graphs |
| Total Citations for the Entire Dataset | 2729 |
|---|---|
| Average ‘citations per year’ for the collected papers | 5.5 |
| Most citations for a single paper per year [31] | 30.7 |
| Term | Description |
|---|---|
| Buffer | A waiting space for jobs between machines. Buffers avoids blocking situation |
| Blocking | This situation occurs when a machine cannot release a job due to lack of buffer. It halts further tasks until the buffer is restored |
| Start Time (Sij) | The time when job j starts being processed by machine i. |
| Processing Time (Pij) | is the time it takes for machine i to process job j |
| Travel Time | The time for a job to be transferred from one machine to another |
| Setup Time | The time required to prepare a system or machine for production |
| Bottleneck | The process that directly limits production capacity, i.e., the critical path. |
| Dispatching | Assigning resources to tasks, i.e., scheduling. |
| Assembly | A product of combined components. |
| Subassembly | A component that is built by combining several other components and used in a larger product. |
| Precedence | Job j can only start processing after jobs in set s have been completed. |
| Machine Eligibility | Machine i can only perform some subset of job j’s required processes. |
|
Machine Breakdown | Machines have non-continuous availability. |
| Routing | Job j’s operations must be completed in a specific order. |
| Incompatible jobs | Incompatible jobs cannot be processed by the same machine |
| Waiting Time | This situation occurs when the buffer between machines is too small blocking may occur, so, upstream machines cannot release jobs. |
| No-Wait | Consecutive operations of a job must be performed without wait-time on either machine. |
| No-Idle | Machines must continuously process jobs without overlap or pause. |
| Deadlock | This situation occurs when the order of operations creates a cycle, and the entire process stops under this situation. |
| Preemption | Jobs can be interrupted while being processed on machines. They can then be resumed on the same machine or a new one. |
| Objective | Description |
|---|---|
| Makespan | Total completion time: the time taken to complete all jobs. |
| Total workload of Machines | The total processing time across all machines. |
| Workload of most loaded machine | The machine(s) with the largest processing time(s). |
| Max lateness | The largest difference between a given job’s completion time and deadline. |
| Mean flow time | The average amount of time that a given job spends on the shop floor. |
| Tardiness | The difference between a given job’s completion time and deadline. |
| Total tardiness | The sum of each job’s tardiness. |
| Mean tardiness | The average of all jobs’ tardiness. |
| Weighted tardiness | The difference between a given job’s completion time and deadline multiplied by a weight (corresponding to cost). |
| Topic | Abbreviation | Description |
|---|---|---|
| FJS | Flexible Job Shop | |
| FFS | Flexible Flow Shop | |
| FMS | Flexible Manufacturing System | |
| Perm | Permutation Flow Shop | |
| Layout | CMS | Cellular Manufacturing System |
| Classic | Classic Job Shop | |
| Multi | Multi-stage Flow Shop | |
| Open | Open Shop | |
| Mixed | Mixed Shop | |
| Parallel | Parallel Machines (Single Stage) | |
| Scheduling | S | Static |
| Type | D | Dynamic |
| MS | Makespan | |
| Objectives | T | Tardiness related |
| BB | Branch and Bound | |
| LS | Local Search | |
| TS | Tabu Search | |
| GA | Genetic Algorithm | |
| ACO | Ant Colony Optimization | |
| NEH | Nawaz, Enscore, Ham algorithm | |
| Solutions | LP | Linear Programming |
| PSO | Particle Swarm Optimization | |
| SB | Shifting Bottleneck | |
| SA | Simulated Annealing | |
| Bench | Benchmark | |
| Case study | Num | Numerical example |
| RC | Real Case |
| References Using DIRECTED GRAPHS (1/2) | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Problem & Solution Characteristics | ||||||||||||||
| Type of Directed Graph | Layout | Scheduling Type | Objective | Solution Method | Case Study | |||||||||
| Ref. No. | References (Listed Chronologically) | Precedence | DAG | Petri Net | Alternative | Multi-Stage | Flow Shop | Job Shop | Other | Exact | Approximate | |||
| [124] | (González et al., 2015) | ✓ | FJS | S | MS | LS, TS | Bench | |||||||
| [141] | (Wang et al., 2015) | ✓ | Multi | S | MS | BB | Bench | |||||||
| [129] | (Birgin et al., 2015) | ✓ | FJS | S | MS | Other | Bench | |||||||
| [142] | (Nip et al., 2015) | ✓ | Multi | S | MS | Other | ||||||||
| [69] | (Wang & Wang, 2015) | ✓ | Perm | S | MS | LS, GA | Bench | |||||||
| [161] | (Başak & Albayrak, 2015) | ✓ | FMS | D | Other | RC | ||||||||
| [162] | (Baruwa & Piera, 2015) | ✓ | FMS | S | MS | Other | Bench | |||||||
| [79] | (Wang et al., 2016) | ✓ | Mixed | D | Other | ACO | Bench | |||||||
| [48] | (Pranzo & Pacciarelli, 2016) | ✓ | Classic | S | MS | Other | Bench | |||||||
| [36] | (Nip et al., 2016) | ✓ | Classic | Open | S | MS | Other | |||||||
| [163] | (Marin et al., 2016) | ✓ | FFS | S | MS | Other | ||||||||
| [164] | (Al-Ahmari, 2016) | ✓ | CMS | S | MS | Other | Num | |||||||
| [62] | (Baruwa & Piera, 2016) | ✓ | FMS | S | MS, Other | Other | Bench | |||||||
| [165] | (Madraki & Judd, 2018) | ✓ | Classic | S | MS | Other | Num | |||||||
| [131] | (Tellache & Boudhar, 2018) | ✓ | Multi | S | MS | NEH, Other | Num | |||||||
| [122] | (Bożejko et al., 2017) | ✓ | Classic | S | MS | TS, Other | Bench | |||||||
| [166] | (Samarghandi & Behroozi, 2017) | ✓ | Multi | S | MS | LP | Bench | |||||||
| [71] | (Qian et al., 2017) | ✓ | Perm | S | MS | LS, Other | Num RC | |||||||
| [167] | (Chamnanlor et al., 2017) | ✓ | FFS | S | MS | LS, GA, ACO | RC | |||||||
| [168] | (Yu et al., 2017) | ✓ | FJS | S | MS | LP | LS, Other | Num | ||||||
| [169] | (Mejía et al., 2017) | ✓ | Open | S | MS | Other | Num | |||||||
| [77] | (Pempera & Smutnicki, 2018) | ✓ | Open | S | MS | TS | Bench | |||||||
| [170] | (Bożek & Werner, 2018) | ✓ | FJS | S | MS | LP | TS | Bench | ||||||
| [171] | (Shokouhi, 2018) | ✓ | FJS | S | MS, Other | GA | Num | |||||||
| [138] | (Dabah et al., 2018) | ✓ | Classic | S | MS | BB | Bench | |||||||
| [172] | (Lunardi & Voos, 2018) | ✓ | FJS | S | MS | GA, Other | Bench | |||||||
| [139] | (Gholami & Törnquist Krasemann, 2018) | ✓ | Classic | D | T | LP | Other | Bench | ||||||
| [173] | (Madraki & Judd, 2019) | ✓ | Classic | S | MS | Other | Num | |||||||
| [140] | (Corominas et al., 2019) | ✓ | FJS, | S | T, Other | LP | Other | Bench | ||||||
| [38] | (Cao et al., 2019) | ✓ | FJS | D | MS | Other | Num | |||||||
| [27] | (Panwalkar & Koulamas, 2019) | ✓ | Multi | S | MS, Other | Other | ||||||||
| [174] | (Liao & Fu, 2019) | ✓ | Perm | S | MS, T | GA | Num | |||||||
| [47] | (Dabah et al., 2019) | ✓ | Classic | S | MS | TS | Bench | |||||||
| [175] | (Billaut et al., 2019) | ✓ | Multi | Classic | Open | S | MS | Other | ||||||
| [176] | (Kress et al., 2019) | ✓ | FJS | S | MS, T | Other | Bench RC | |||||||
| [177] | (Tian et al., 2019) | ✓ | FJS | D | MS | ACO | Bench | |||||||
| [43] | (Guan et al., 2019) | ✓ | Parallel | S | MS | Other | ||||||||
| [178] | (Wu et al., 2019) | ✓ | FJS | D | MS | ACO | Bench | |||||||
| [179] | (Hu et al., 2020) | ✓ | FMS | D | MS | Other | Num | |||||||
| [180] | (Vital-Soto et al., 2020) | ✓ | FJS | S | T | LP | LS, SA, Other | Bench RC | ||||||
| [130] | (Lunardi, Birgin, Laborie, et al., 2020) | ✓ | FJS | S | MS | LP | Num | |||||||
| [149] | (Rossi & Lanzetta, 2020) | ✓ | FJS | S | MS | ACO | Bench | |||||||
| [181] | (Zhu & Zhou, 2020) | ✓ | FJS | S | MS, Other | LP | Other | Num | ||||||
| [128] | (Chen et al., 2020) | ✓ | Open | S | MS | Other | ||||||||
| [99] | (Lunardi, Birgin, Ronconi, et al., 2020) | ✓ | FJS | S | MS | LS, GA, TS, Other | Bench | |||||||
| [182] | (Xie et al., 2020) | ✓ | Mixed | S | MS | Other | Num | |||||||
| [183] | (Wang & Gombolay, 2020) | ✓ | FMS | D | MS | Other | Bench | |||||||
| [184] | (Mejía & Lefebvre, 2020) | ✓ | FMS | S | MS | Other | Num RC | |||||||
| [185] | (Pan et al., 2020) | ✓ | FMS | S | MS | Other | Num | |||||||
| [123] | (Madraki & Judd, 2021) | ✓ | Classic | S | MS | SA, Other | Num | |||||||
| References Using UNDIRECTED GRAPHS (1/1) | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| References (Listed Chronologically) | Problem & Solution Characteristics | ||||||||||||||
| Type of Undirected Graph | Layout | Scheduling Type | Objective | Solution Method | Case Study | ||||||||||
| Ref. No. | Graph Coloring | Clique | Social Network | Markov Random Field | Traveling Salesman | Agreement (Bipartite) | Flow Shop | Job Shop | Other | Exact | Approximate | ||||
| [118] | (Bendraouche et al., 2015) | ✓ | Other | S | MS | ||||||||||
| [121] | (Bożejko et al., 2015) | ✓ | FFS | S | MS | TS | Num | ||||||||
| [162] | (Baruwa & Piera, 2015) | ✓ | FMS | S | MS | Other | Bench | ||||||||
| [186] | (Tellache & Boudhar, 2017b) | ✓ | Multi | S | MS | LP BB | Num | ||||||||
| [117] | (Bendraouche & Boudhar, 2016) | ✓ | Other | S | MS | ||||||||||
| [44] | (Behnamian, 2016) | ✓ | Parallel | S | MS | PSO | Bench | ||||||||
| [187] | (Tellache & Boudhar, 2016) | ✓ | Multi | S | MS | LP | Bench | ||||||||
| [62] | (Baruwa & Piera, 2016) | ✓ | FMS | S | MS, Other | Other | Bench | ||||||||
| [188] | (Kouider et al., 2017) | ✓ | Classic | S | MS | LP | TS | Bench | |||||||
| [131] | (Tellache & Boudhar, 2018) | ✓ | Multi | S | MS | NEH, Other | Num | ||||||||
| [76] | (Tellache & Boudhar, 2017a) | ✓ | Open | S | MS | Other | Num | ||||||||
| [189] | (Ilani et al., 2017) | ✓ | ✓ | Open | S | MS | Other | ||||||||
| [116] | (Reddy et al., 2017) | ✓ | FJS | S | MS | Other | Bench | ||||||||
| [190] | (Grinshpoun et al., 2017) | ✓ | Open | S | MS, T | Other | Bench | ||||||||
| [113] | (Thevenin et al., 2018) | ✓ | FJS | S | MS, Other | LP | NEH, LS | Num | |||||||
| [191] | (Cheng et al., 2018) | ✓ | Other | S | Other | RC | |||||||||
| [75] | (Tellache et al., 2019) | ✓ | ✓ | Open | S | MS | Other | ||||||||
| [119] | (Sun et al., 2019) | ✓ | FJS | S | MS, T | Other | Num | ||||||||
| [109] | (Mohabeddine & Boudhar, 2019) | ✓ | ✓ | Other | S | MS | Other | ||||||||
| [192] | (Ilani et al., 2019) | ✓ | Open | S | MS | Num | |||||||||
| [193] | (X. Shi et al., 2020) | ✓ | FJS | S | MS | GA | Bench | ||||||||
| [28] | (Sotskov, 2020) | ✓ | Multi | Classic | S | MS, T | |||||||||
| References Using UN/DIRECTED GRAPHS (1/2) | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| References (Listed Chronologically) | Problem & Solution Characteristics | ||||||||||||
| Type of Un/Directed Graph | Layout | Scheduling Type | Objective | Solution Method | Case Study | ||||||||
| Ref. No. | Semantic | Ant Colony | Disjunctive | Tree | Flow Shop | Job Shop | Other | Exact | Approximate | ||||
| [81] | (Zeng et al., 2015) | ✓ | FJS | CMS | S | MS | LS, GA | Num | |||||
| [194] | (Rossi et al., 2015) | ✓ | Mixed | S | MS | LP | NEH | RC | |||||
| [105] | (Nasiri, 2015) | ✓ | Mixed | S | MS | PSO, Other | Bench | ||||||
| [101] | (Mencia et al., 2015) | ✓ | Classic | S | MS | LS, GA, TS | Bench | ||||||
| [156] | (Grimes & Hebrard, 2015) | ✓ | Classic | Open | S | MS T | BB | Other | Bench | ||||
| [195] | (Ciro et al., 2015) | ✓ | Open | S | MS | LP | ACO | Num | |||||
| [196] | (Cruz-Chávez, 2015) | ✓ | Classic | S | MS | SA | Bench | ||||||
| [92] | (Kemmoé et al., 2015) | ✓ | Classic | S | MS | LP | Num | ||||||
| [197] | (Amirghasemi & Zamani, 2015) | ✓ | Classic | S | MS | GA, TS | Bench | ||||||
| [198] | (Nouri et al., 2016a) | ✓ | Classic | FMS | D | MS | GA, TS | Bench | |||||
| [51] | (AitZai et al., 2016) | ✓ | Classic | S | MS | BB | PSO | Bench | |||||
| [199] | (Kuhpfahl & Bierwirth, 2016) | ✓ | Classic | S | T | LS | Bench | ||||||
| [159] | (Campos Ciro et al., 2016) | ✓ | Open | S | MS | GA, ACO | Bench | ||||||
| [200] | (Nouri et al., 2016b) | ✓ | FJS | S | MS | GA, TS | Bench | ||||||
| [45] | (Zabihzadeh & Rezaeian, 2016) | ✓ | FFS | Parallel | S | MS, Other | LP | GA, ACO | Num | ||||
| [201] | (Zhao et al., 2016) | ✓ | Classic | S | MS | Other | Bench | ||||||
| [202] | (Shahzad & Mebarki, 2016) | ✓ | Classic | S | Other | TS | Bench | ||||||
| [100] | (Afsar et al., 2016) | ✓ | FMS | S | MS | LS, Other | Bench | ||||||
| [39] | (El-Desoky et al., 2016) | ✓ | Classic | S | MS | LS, GA | Bench | ||||||
| [103] | (Choo et al., 2016) | ✓ | Classic | S | MS | SB, LS, Other | Bench | ||||||
| [203] | (Huang et al., 2016) | ✓ | FJS | S | MS Other | SA, PSO | Bench | ||||||
| [83] | (Y. Yang et al., 2016) | ✓ | FJS | CMS | S | MS Other | LS, PSO | Bench | |||||
| [33] | (Sobeyko & Mönch, 2016) | ✓ | FJS | S | T | SB, LS, SA | Bench | ||||||
| [204] | (Ge et al., 2016) | ✓ | FJS | S | MS | PSO | Bench | ||||||
| [205] | (Q. Yang et al., 2016) | ✓ | FJS | D | T | Other | Bench | ||||||
| [206] | (Elmi & Topaloglu, 2016) | ✓ | FFS | CMS | S | Other | ACO | Num | |||||
| [207] | (Jin et al., 2016) | ✓ | FJS | S | MS | LP | Bench | ||||||
| [147] | (Hart & Sim, 2016) | ✓ | Classic | S | MS, T | Other | Bench | ||||||
| [188] | (Kouider et al., 2017) | ✓ | Classic | S | MS | LP | TS | Bench | |||||
| [208] | (Knopp et al., 2017) | ✓ | FJS | S | MS T Other | LS, SA | Bench | ||||||
| [52] | (El Khoukhi et al., 2017) | ✓ | FJS | S | MS | LP | ACO | Bench | |||||
| [54] | (Wu et al., 2017) | ✓ | FJS | S | MS Other | ACO | RC | ||||||
| [209] | (Sotskov & Gholami, 2017) | ✓ | FJS | S | MS | Other | Bench | ||||||
| [151] | (Zhang & Wong, 2017) | ✓ | ✓ | FJS | D | MS | ACO | Bench | |||||
| [210] | (Bürgy, 2017) | ✓ | Classic | S | MS T | TS | Bench | ||||||
| [211] | (Hao et al., 2017) | ✓ | Classic | S | MS T | Other | Bench | ||||||
| [157] | (Wang et al., 2017) | ✓ | FJS | S | MS | ACO | Bench | ||||||
| [168] | (Yu et al., 2017) | ✓ | FJS | S | MS | LP | LS, Other | Num | |||||
| [212] | (Zuo et al., 2017) | ✓ | FJS | S | MS | LS, GA | Bench | ||||||
| [213] | (Xiong et al., 2017) | ✓ | Classic | D | T | Other | Num Bench | ||||||
| [143] | (Bierwirth & Kuhpfahl, 2017) | ✓ | Classic | S | T | LS, Other | Bench | ||||||
| [35] | (Mei et al., 2017) | ✓ | Classic | D | MS, T | GA, Other | Num | ||||||
| [152] | (Zhang et al., 2017) | ✓ | FJS | D | MS, Other | Other | RC | ||||||
| [214] | (Tamssaouet et al., 2018) | ✓ | Classic | S | MS | TS, SA | Num | ||||||
| [31] | (Shen et al., 2018) | ✓ | FJS | S | MS | TS | Bench | ||||||
| [215] | (Yu & Lee, 2018) | ✓ | FJS | S | T | LP | Bench | ||||||
| [49] | (Lange & Werner, 2018) | ✓ | Classic | S | T | LP | Num | ||||||
| [58] | (Zhao et al., 2018) | ✓ | FJS | S | MS, T, Other | ACO | Num | ||||||
| [216] | (Xiong & Fu, 2018) | ✓ | FJS | S | MS | Other | Bench | ||||||
| [104] | (Abdel-Kader, 2018) | ✓ | Classic | S | MS | PSO | Bench | ||||||
| [217] | (Nagata & Ono, 2018) | ✓ | Classic | D | MS | LS, TS | Bench | ||||||
| [160] | (Riahi & Kazemi, 2018) | ✓ | Multi | S | MS | ACO, SA | Bench | ||||||
| [218] | (Zhang & Wong, 2018) | ✓ | ✓ | Classic | S | MS, Other | ACO | Bench | |||||
| [219] | (Meolic & Brezočnik, 2018) | ✓ | FJS | S | MS, Other | Other | Bench | ||||||
| [148] | (Zhang & Wang, 2018) | ✓ | FJS | D | MS | LP | Bench | ||||||
| [146] | (Zhou et al., 2018) | ✓ | FJS | D | MS, T | GA | Bench | ||||||
| [154] | (Lei et al., 2018) | ✓ | FJS | S | MS | GA | Bench | ||||||
| [32] | (Lamorgese & Mannino, 2019) | ✓ | ✓ | Classic | S | Other | LP | RC | |||||
| [50] | (Chaouch et al., 2019) | ✓ | Classic | S | MS | ACO | Bench | ||||||
| [220] | (Liu et al., 2019) | ✓ | FJS | S | T, Other | LP | GA | Num | |||||
| [221] | (Burdett et al., 2019) | ✓ | FJS | S | MS, Other | SA | Num | ||||||
| [222] | (Cruz-Chávez et al., 2019) | ✓ | Classic | S | MS | GA | Bench | ||||||
| [155] | (Zhu et al., 2019) | ✓ | FJS | S | MS | ACO | Num | ||||||
| [158] | (Qin et al., 2019) | ✓ | Mixed | S | MS | ACO | Bench | ||||||
| [223] | (Zhou et al., 2019) | ✓ | FJS | D | T, Other | GA | RC | ||||||
| [224] | (Jun et al., 2019) | ✓ | FJS | S | T | LP | GA | Num | |||||
| [144] | (Kim & Lee, 2019) | ✓ | Multi | S | MS | BB | Num | ||||||
| [102] | (F. Shi et al., 2020) | ✓ | FJS | S | MS | SB GA | Bench | ||||||
| [225] | (Abedi et al., 2020) | ✓ | Classic | S | T, Other | LS, GA | Num | ||||||
| [28] | (Sotskov, 2020) | ✓ | Multi | Classic | S | MS | |||||||
| [226] | (Fan et al., 2019) | ✓ | FJS | S | MS | LS, SA | Bench | ||||||
| [227] | (Vela et al., 2020) | ✓ | Classic | S | T | GA, TS | Bench | ||||||
| [185] | (Pan et al., 2020) | ✓ | FMS | S | MS | Other | Num | ||||||
| [149] | (Rossi & Lanzetta, 2020) | ✓ | FJS | S | MS | ACO | Bench | ||||||
| [150] | (Liu et al., 2020) | ✓ | FJS | S | MS | GA | Bench, RC | ||||||
| [70] | (Gmys et al., 2020) | ✓ | Perm | S | MS | BB | Bench | ||||||
| [145] | (Zhang et al., 2020) | ✓ | FJS | D | MS, Other | GA | Num | ||||||
| [228] | (Ahmadian et al., 2021) | ✓ | Classic | S | T | LS | Bench | ||||||
| Ref. No. | Reference | Graph Type | System | Objective | Scheduling | Solution | Case Study | Integration |
|---|---|---|---|---|---|---|---|---|
| [152] | (Zhang et al., 2017) | Game tree | 3 | 2 | 2 | 11 | 3 | 2 |
| [144] | (Kim & Lee, 2019) | B&B tree | 5 | 1 | 1 | 1 | 2 | 2 |
| [70] | (Gmys et al., 2020) | B&B tree | 4 | 1 | 1 | 1 | 1 | 2 |
| [154] | (Lei et al., 2018) | Processing operation tree | 1 | 1 | 1 | 6 | 1 | 1 |
| [149] | (Rossi & Lanzetta, 2020) | Multiple graphs: And-Or & precedence graphs | 3 | 1 | 1 | 7 | 1 | 2 |
| [218] | (Zhang & Wong, 2018) | Multiple graphs: AND-OR graph & disjunctive graph | 2 | 2 | 1 | 7 | 1 | 1 |
| [155] | (Zhu et al., 2019) | Semantic graph | 3 | 1 | 2 | 7 | 2 | 2 |
| [185] | (Pan et al., 2020) | Multiple graphs: Semantic graph & Petri Net | 10 | 1 | 2 | 11 | 2 | 2 |
| [193] | (X. Shi et al., 2020) | Social network | 3 | 1 | 1 | 6 | 1 | 1 |
| [119] | (Sun et al., 2019) | Markov Random Fields (MRFs) | 3 | 1 | 1 | 11 | 2 | 2 |
| [121] | (Bożejko et al., 2015) | Traveling salesman graph | 6 | 1 | 1 | 8 | 2 | 2 |
| Reference | Graph Type | System | Objective | Scheduling | Solution | Case Study | Integration | |
|---|---|---|---|---|---|---|---|---|
| [31] | (Shen et al., 2018) | Disjunctive graph | 3 | 1 | 1 | 8 | 1 | 2 |
| [179] | (Hu et al., 2020) | Petri-net | 10 | 1 | 2 | 11 | 2 | 2 |
| [218] | (Zhang & Wong, 2018) | Multiple graphs: AND-OR graph & disjunctive graph | 2 | 2 | 1 | 7 | 1 | 1 |
| [69] | (Wang & Wang, 2015) | DAG | 4 | 1 | 1 | 5,6 | 1 | 2 |
| [213] | (Xiong et al., 2017) | Disjunctive graph | 2 | 1 | 2 | 11 | 1,2 | 2 |
| [199] | (Kuhpfahl & Bierwirth, 2016) | Disjunctive graph | 2 | 1 | 1 | 5 | 1 | 2 |
| [152] | (Zhang et al., 2017) | Game tree | 3 | 2 | 2 | 11 | 3 | 2 |
| [180] | (Vital-Soto et al., 2020) | Precedence graph | 3 | 1 | 1 | 2,5,9,11 | 1,3 | 2 |
| [70] | (Gmys et al., 2020) | B&B tree | 4 | 1 | 1 | 1 | 1 | 2 |
| [145] | (Zhang et al., 2020) | Tree | 3 | 2 | 2 | 6 | 2 | 2 |
| [200] | (Nouri et al., 2016b) | Disjunctive graph | 3 | 1 | 1 | 6,8 | 1 | 2 |
| [216] | (Xiong & Fu, 2018) | Disjunctive graph | 3 | 1 | 1 | 11 | 1 | 2 |
| [52] | (El Khoukhi et al., 2017) | Ant colony graph | 3 | 1 | 1 | 2,7 | 1 | 2 |
| [124] | (González et al., 2015) | DAG | 3 | 1 | 1 | 5,8 | 1 | 2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Otala, J.; Minard, A.; Madraki, G.; Mousavian, S. Graph-Based Modeling in Shop Scheduling Problems: Review and Extensions. Appl. Sci. 2021, 11, 4741. https://doi.org/10.3390/app11114741
Otala J, Minard A, Madraki G, Mousavian S. Graph-Based Modeling in Shop Scheduling Problems: Review and Extensions. Applied Sciences. 2021; 11(11):4741. https://doi.org/10.3390/app11114741
Chicago/Turabian StyleOtala, Jacqueline, Alden Minard, Golshan Madraki, and Seyedamirabbas Mousavian. 2021. "Graph-Based Modeling in Shop Scheduling Problems: Review and Extensions" Applied Sciences 11, no. 11: 4741. https://doi.org/10.3390/app11114741
APA StyleOtala, J., Minard, A., Madraki, G., & Mousavian, S. (2021). Graph-Based Modeling in Shop Scheduling Problems: Review and Extensions. Applied Sciences, 11(11), 4741. https://doi.org/10.3390/app11114741






