Multi-Structural Optimization of Bearingless Permanent Magnet Slice Motor Based on Virtual Prototype in Ansoft Maxwell
Abstract
1. Introduction
- -
- Section 2 introduces the methodology, including the virtual prototype developed in Ansoft Maxwell and the optimization process architecture;
- -
- Section 3 presents the parameter assessment process for optimization, including performance evaluation and structural parameter sensitivity analysis;
- -
- Section 4 demonstrates the proposed multi-structural optimization method by utilizing a virtual prototype, and analyzes and discusses the optimization results;
- -
- Section 5 concludes the paper.
2. Methodology
2.1. Virtual Prototype of BPMSM
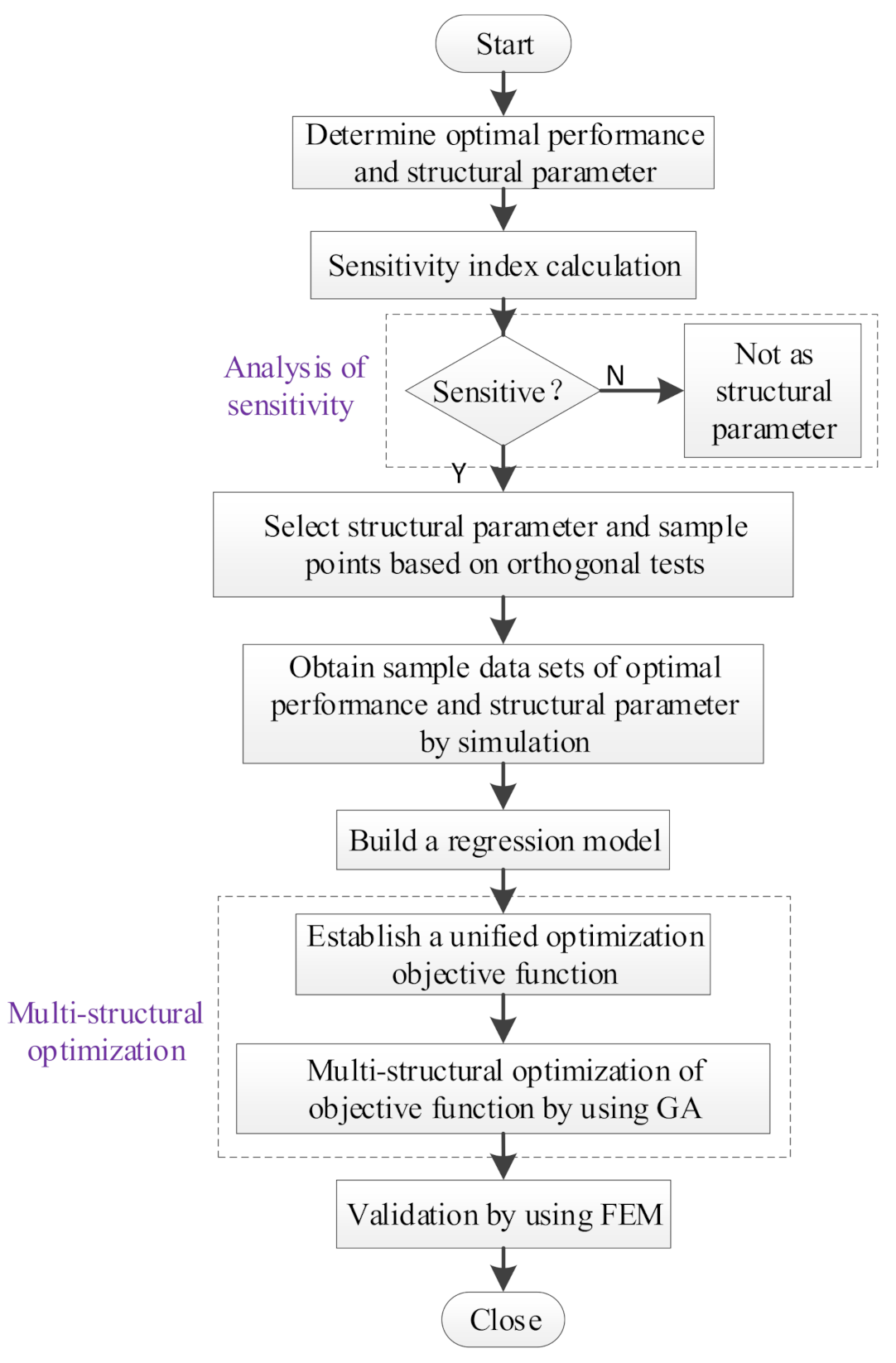
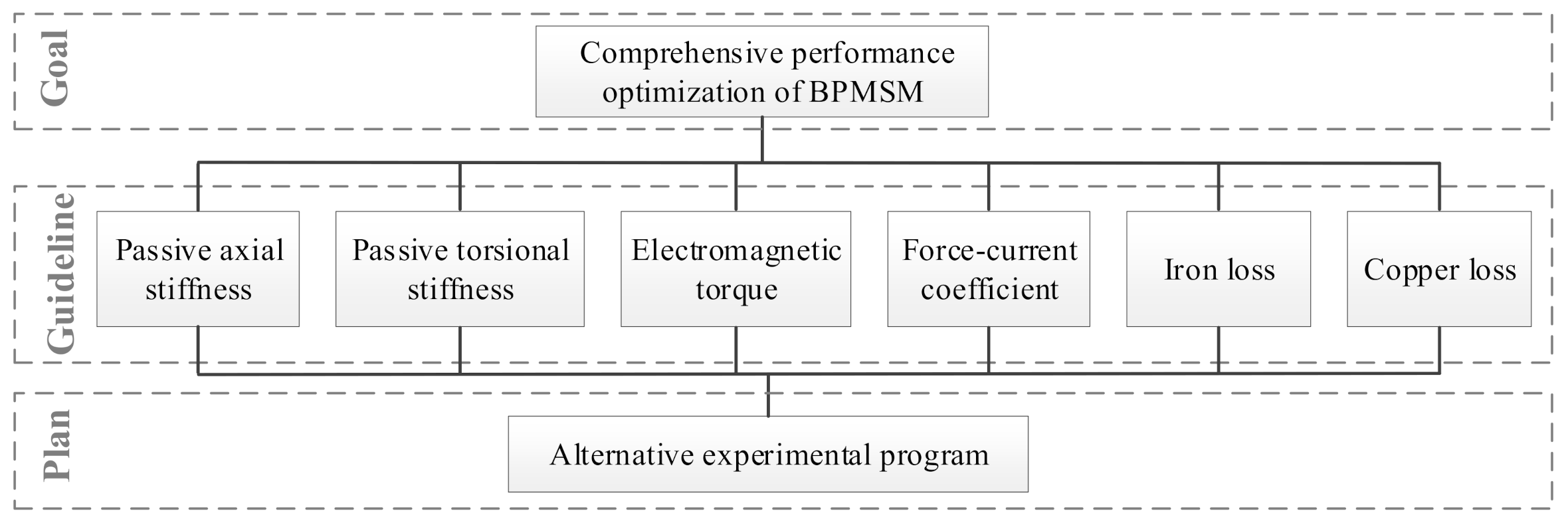
2.2. The Optimization Process Architecture
- -
- First, BPMSM performances, as the optimization objects and the structural parameter candidates to be optimized, are specified.
- -
- Second, a sensitivity index is proposed to judge the effects of the different structural parameters on the optimized performance of the BPMSM to avoid contradictions in the optimization process, and the searching range is determined according to the working conditions of the motor and the difficulty of assembly.
- -
- Third, the orthogonal test method [26] is used out to efficiently extract representative sample data.
- -
- Then, the linear relationship between individual BPMSM performance and the chosen structural parameter is derived by using the gradient descent method for parametric optimization modeling.
- -
- Finally, a dimensionless multi-structural optimization model is developed based on the regression model and solved using a GA.
3. Parameter Assessment for Optimization
3.1. BPMSM Performance Evaluation
- A.
- Levitation Performance
- -
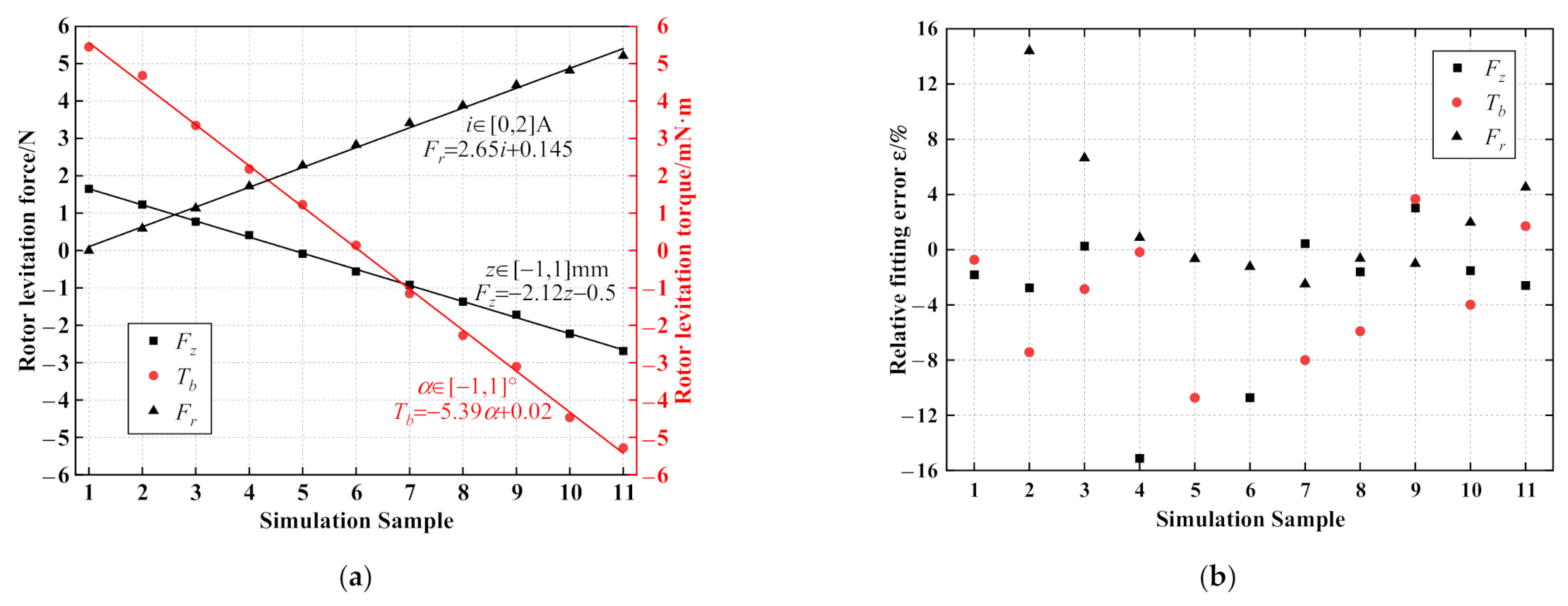
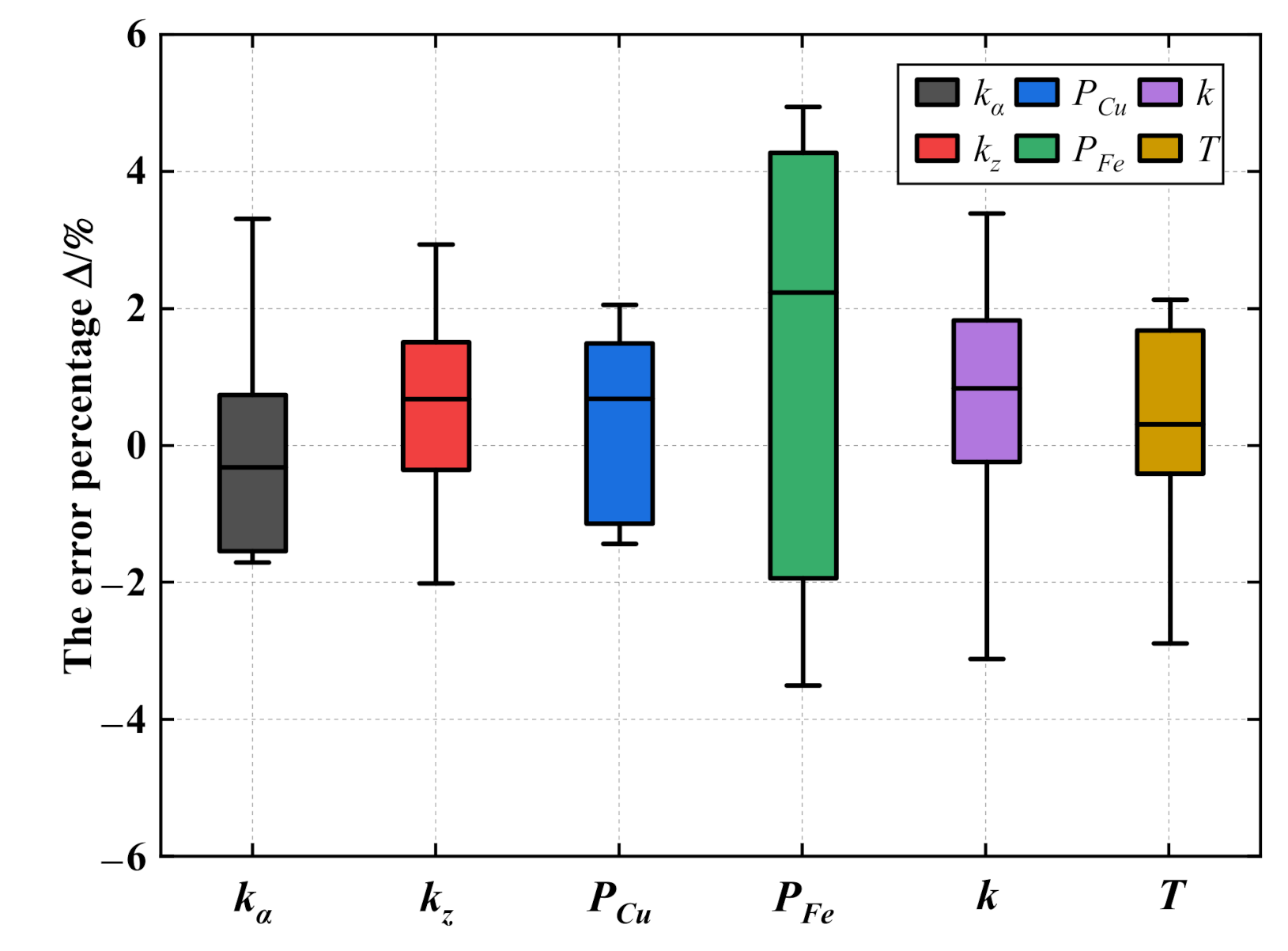
- For the fitted value near the excluded samples close to zero, involving sample Nos. 4 and 6 for the axial levitation force (Fz), sample Nos. 5 and 7 for the tilting levitation torque (Tb) and sample Nos. 2 and 3 for the rotor radial levitation force (Fr), their relative fitting errors are more significant (maximum 16%).
- -
- For other samples, the relative fitting error is comparatively small (most within 4%), indicating the linear fitting accuracy of BPMSM performance.
- B.
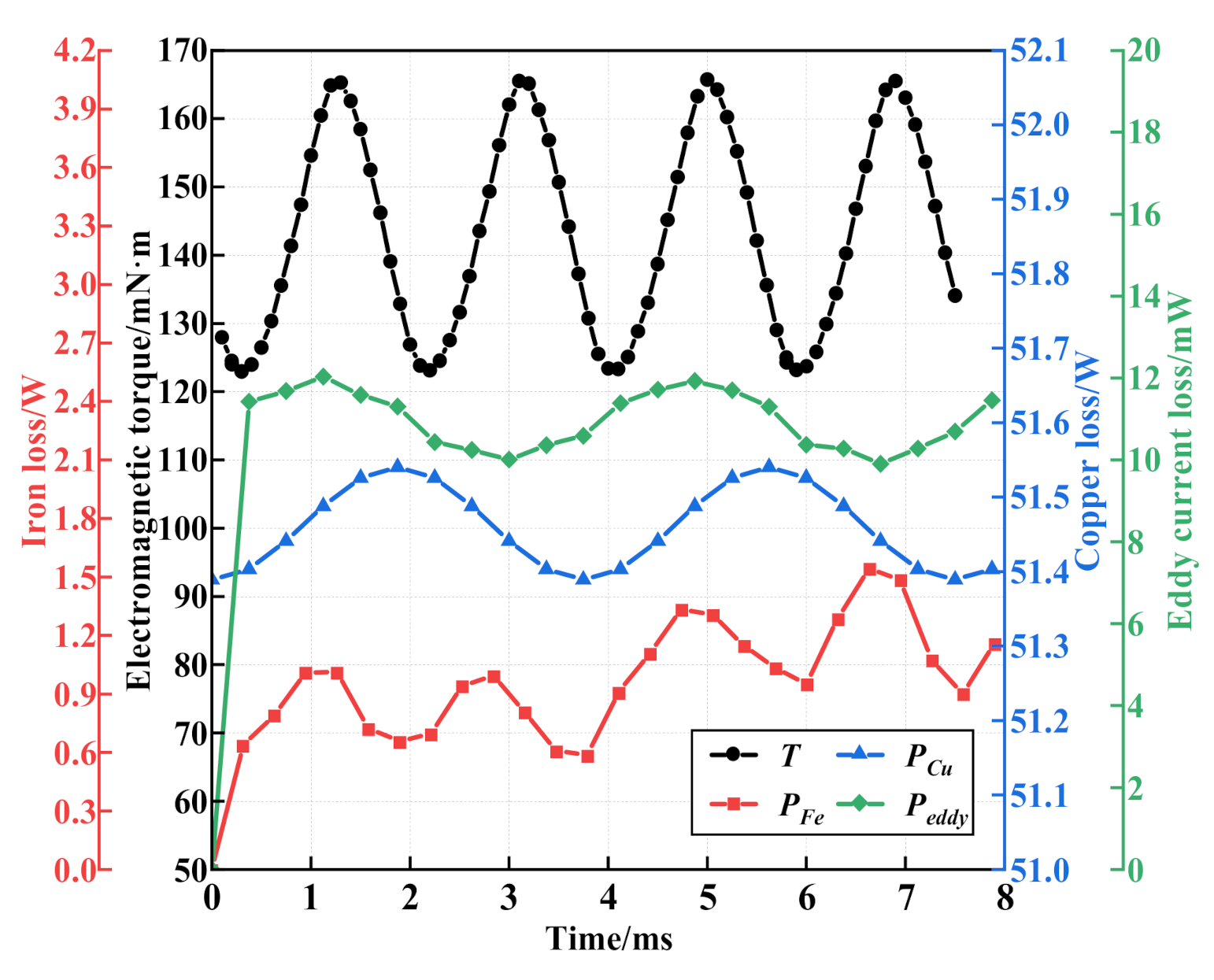
- Electromagnetic Torque
- C.
- Motor Efficiency
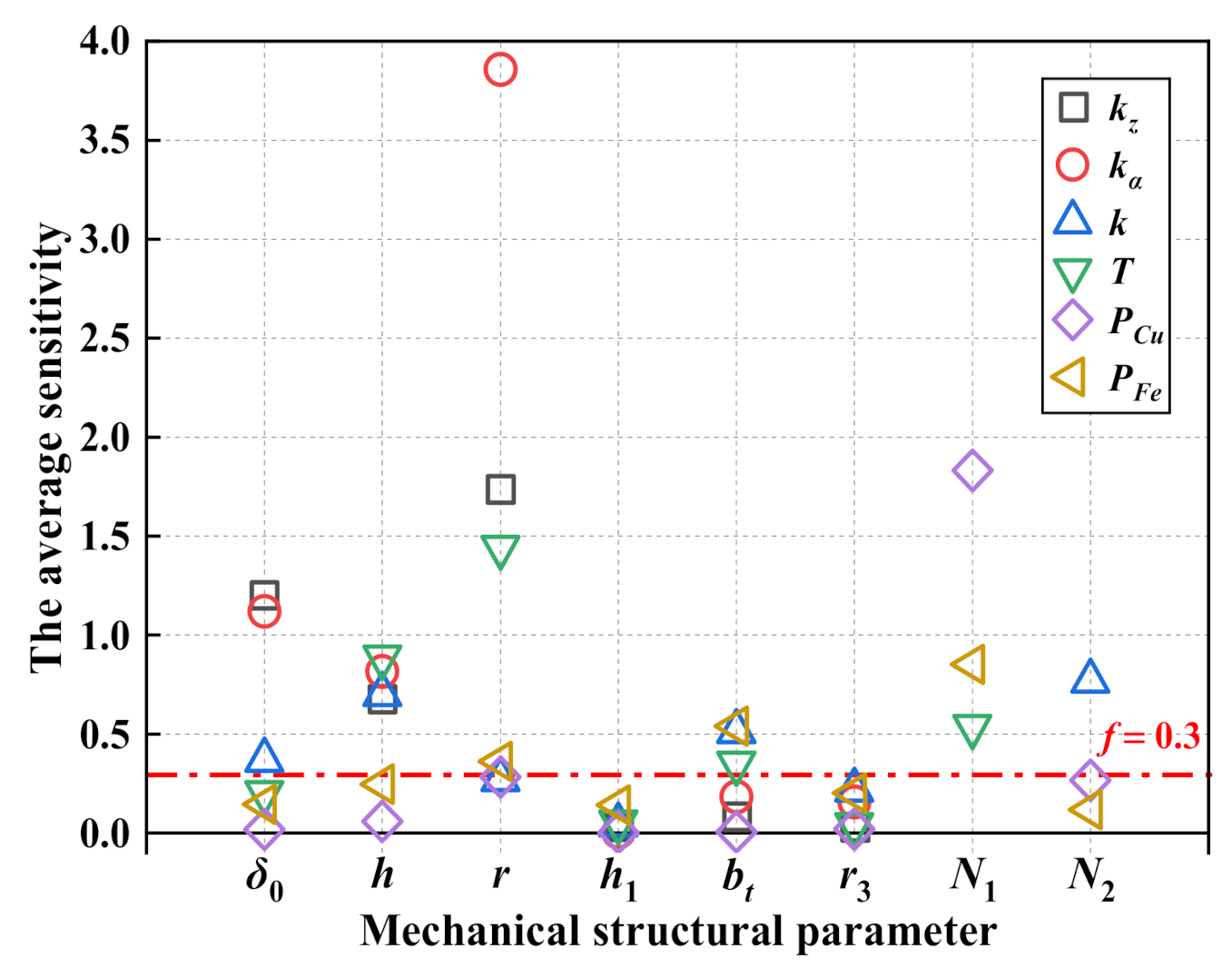
3.2. Sensitivity Analysis of Structural Parameters
- -
- When bt, ht, r3, N1, and N2 change individually, all other parameters remain unchanged;
- -
- When r, δ0, and h change individually, r4, d2, and ht will change accordingly.
4. Multi-Structural Optimization of BPMSM
4.1. Assess of Structural Parameter Sample Space
4.2. Single Performance Regression Model
4.3. Dimensionless Multi-Structural Optimization Model
- (1)
- The rotor diameter-to-height ratio is an important parameter that influences the axial levitation force and tilting levitation torque. In order to achieve a larger axial levitation force and tilting levitation torque, the optimal size of the BPMSM rotor diameter-to-height ratio satisfies .
- (2)
- Due to the power design requirement of the BPMSM, Pe = 120 W, the electromagnetic torque needs to meet
4.4. Multi-Structural Optimization of BPMSM by GA
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Silber, S.; Amrhein, W.; Bösch, P.; Schöb, R.; Barletta, N. Design aspects of bearingless slice motors. IEEE/ASME Trans. Mechatron. 1995, 10, 611–617. [Google Scholar] [CrossRef]
- Nussbaumer, T.; Karutz, P.; Zurcher, F. Magnetically levitated slice motors—An overview. IEEE Trans. Ind. Appl. 2011, 47, 754–766. [Google Scholar] [CrossRef]
- Sun, X.D.; Chen, L.; Yang, Z.B. Overview of bearingless permanent-magnet synchronous motors. IEEE Trans. Ind. Electron. 2013, 60, 5528–5538. [Google Scholar] [CrossRef]
- Zhu, Z.Q.; Pang, Y.; Howe, D.; Iwasaki, S.; Deodhar, R.; Pride, A. Analysis of electromagnetic performance of flux-switching permanent-magnet machines by nonlinear adaptive lumped parameter magnetic circuit model. IEEE Trans. Magn. 2005, 41, 4277–4287. [Google Scholar] [CrossRef]
- Gruber, W.; Amrhein, W.; Haslmayr, M. Bearingless segment motor with five stator elements—Design and optimization. IEEE Trans. Ind. Appl. 2009, 45, 1301–1308. [Google Scholar] [CrossRef]
- Reichert, T.; Nussbaumer, T.; Kolar, J.W. Novel bearingless brushless motor in exterior rotor construction for stirred bioreactors. In Proceedings of the IET Conference on Power Electronics, Machines and Drives, Brighton, UK, 19–21 April 2010; pp. 1–6. [Google Scholar]
- Gruber, W.; Briewasser, W.; Amrhein, W. Novel bearingless slice motor design with four concentrated coils featuring a unique operational behavior. In Proceedings of the 14th European Conference on Power Electronics and Applications, Birmingham, UK, 30 August 2011; pp. 1–10. [Google Scholar]
- Zürcher, F.; Nussbaumer, T.; Gruber, W.; Kolar, J.W. Design and development of a 26-pole and 24-slot bearingless motor. IEEE Trans. Magn. 2009, 45, 4594–4597. [Google Scholar] [CrossRef]
- Mitterhofer, H.; Mrak, B.; Gruber, W. Comparison of high-speed bearingless drive topologies with combined windings. IEEE Trans. Ind. Appl. 2015, 51, 2116–2122. [Google Scholar] [CrossRef]
- Gruber, W.; Nussbaumer, T.; Gruber, H.; Amrhein, W. Wide air gap and large-scale bearingless segment motor with six stator elements. IEEE Trans. Magn. 2010, 46, 2438–2441. [Google Scholar] [CrossRef]
- Sugimoto, H.; Uemura, Y.; Chiba, A.; Rahman, M.A. Design of homopolar consequent-pole bearingless motor with wide magnetic gap. IEEE Trans. Magn. 2013, 49, 2315–2318. [Google Scholar] [CrossRef]
- Bramerdorfer, G.; Jungmayr, G.; Amrhein, W.; Gruber, W.; Marth, E.; Reisinger, M. Bearingless segment motor with halbach magnet. In Proceedings of the 2010 International Symposium on Power Electronics, Electrical Drives, Automation and Motion, Pisa, Italy, 14–16 June 2010; pp. 1466–1471. [Google Scholar]
- Noh, M.; Trumper, D.L. Homopolar bearingless slice motor with flux-biasing halbach arrays. IEEE Trans. Ind. Electron. 2020, 67, 7757–7766. [Google Scholar] [CrossRef]
- Zhang, S.R.; Luo, F.L. Direct control of radial displacement for bearingless permanent-magnet-type synchronous motors. IEEE Trans. Ind. Electron. 2009, 56, 542–552. [Google Scholar] [CrossRef]
- Qiu, Z.J.; Deng, Z.Q.; Zhang, Y.J. Direct levitation force control of a consequent-pole permanent magnet bearingless motor. Trans. CES 2011, 26, 94–99. [Google Scholar]
- Zhu, S.M.; Zhu, H.Q. Suspension force control of bearingless permanent magnet slice motor based on flux linkage identification. ISA Trans. 2015, 57, 322–328. [Google Scholar] [CrossRef] [PubMed]
- Zhu, H.Q.; Zhu, S.M. Study on radial suspension forces of bearingless permanent magnet slice motor based on accurate inductance model. J. Microw. Optoelectron. Electromagn. Appl. 2014, 13, 240–253. [Google Scholar] [CrossRef]
- Zhang, T.; Ni, W.; Wang, X.H.; Zhang, C.; Jia, H.Y. Optimal design on bearingless permanent magnet synchronous motor to decrease losses and torque ripple. Sens. Transducers 2014, 182, 138–145. [Google Scholar]
- Sugimoto, H.; Miyoshi, M.; Chiba, A. Axial vibration suppression by field flux regulation in two-axis actively positioned permanent magnet bearingless motors with axial position estimation. IEEE Trans. Ind. Appl. 2018, 54, 1264–1272. [Google Scholar] [CrossRef]
- Zhang, W.; Zhu, H.Q.; Xu, Y.; Wu, M.Y. Direct control of bearingless permanent magnet slice motor based on active disturbance rejection control. IEEE Trans. Appl. Supercond. 2020, 30, 205–209. [Google Scholar] [CrossRef]
- Noh, M.; Gruber, W.; Trumper, D.L. Hysteresis bearingless slice motors with homopolar flux-biasing. IEEE/ASME Trans. Mechatron. 2017, 22, 2308–2318. [Google Scholar] [CrossRef]
- Ding, H.F.; Zhu, H.Q.; Hua, Y.Z. Optimization design of bearingless synchronous reluctance motor. IEEE Trans. Appl. Supercond. 2018, 28, 905–909. [Google Scholar] [CrossRef]
- Dini, P.; Saponara, S. Cogging torque reduction in brushless motors by a nonlinear control technique. Energies 2019, 12, 2224. [Google Scholar] [CrossRef]
- Dini, P.; Saponara, S. Design of an observer-based architecture and non-linear control algorithm for cogging torque reduction in synchronous motors. Energies 2020, 13, 2077. [Google Scholar] [CrossRef]
- Xia, K.; Ye, Y.H.; Ni, J.W.; Wang, Y.M.; Xu, P. Model predictive control method of torque ripple reduction for BLDC motor. IEEE Trans. Magn. 2019, 56, 1–6. [Google Scholar] [CrossRef]
- Genichi, T. Appendix A: Orthogonal Arrays and Linear Graphs: Tools for Quality Engineering; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2007; p. 1591. ISBN 9780470258354. [Google Scholar]
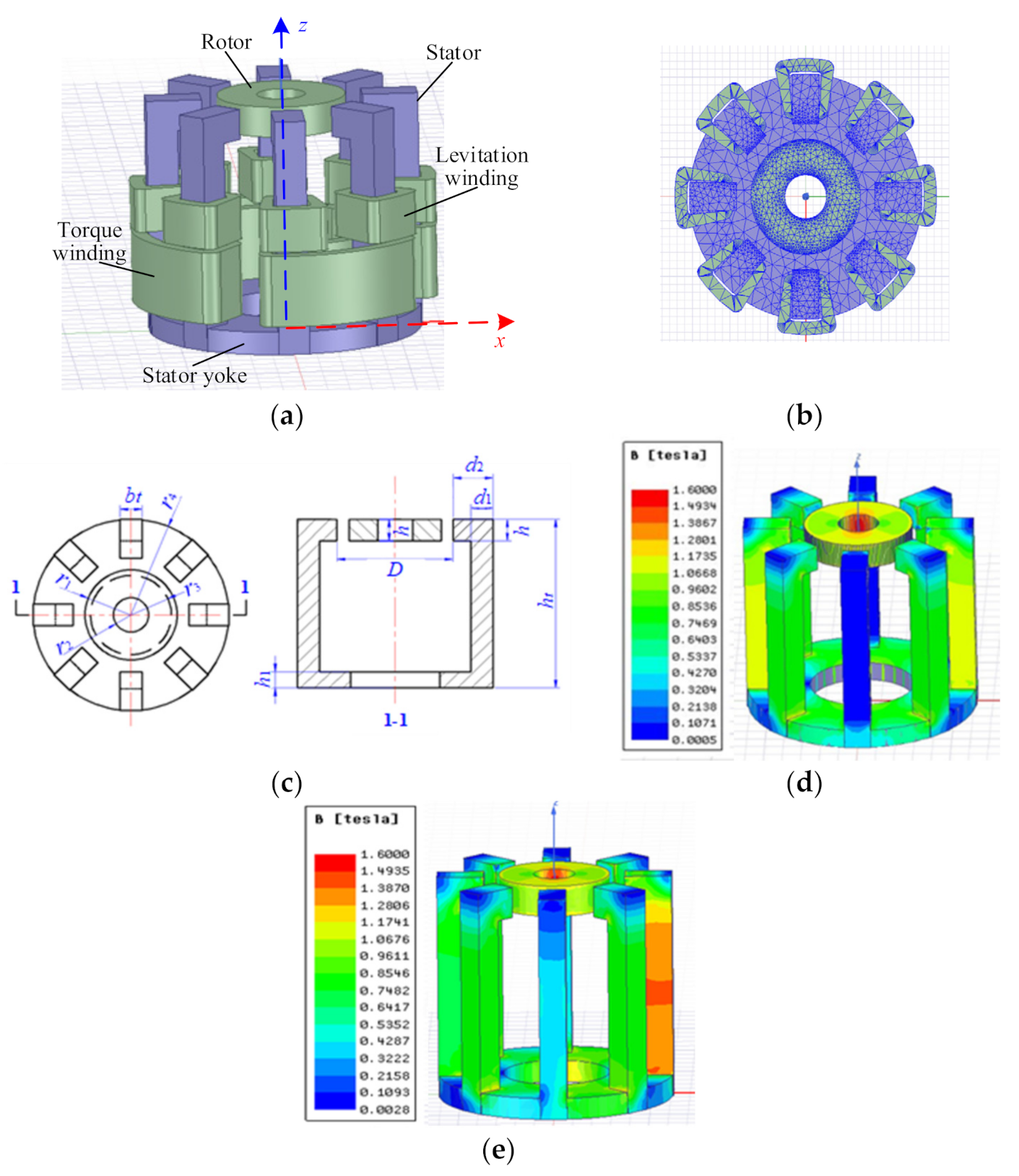

| Description | Symbol | Value |
|---|---|---|
| Pole number of torque winding | P1 | 1 |
| Pole number of levitation winding | P2 | 2 |
| Outer radius of rotor | r1 | 14.5 mm |
| Inner radius of rotor | r2 | 5.5 mm |
| Turn number of torque coil | N1 | 160 |
| Turn number of levitation coil | N2 | 520 |
| Height of yoke | h1 | 5.25 mm |
| Length of air gap | δ0 | 3.75 mm |
| Thickness of rotor | h | 7 mm |
| Diameter of armature | D | 36.5 mm |
| Inner radius of stator yoke | r3 | 14 mm |
| Outer radius of stator yoke | r4 | 30.75 mm |
| Height of stator tooth | ht | 54.26 mm |
| Width of stator tooth | bt | 7 mm |
| BPMSM Performance | δ0 | h | r | bt | h1 | r3 | N1 | N2 |
|---|---|---|---|---|---|---|---|---|
| kz | + | + | + | |||||
| kα | + | + | + | |||||
| k | + | + | + | + | ||||
| T | + | + | + | |||||
| PCu | + | + | + | |||||
| PFe | + | + | + | + |
| Factor | Level 1 | Level 2 | Level 3 | Level 4 | Level 5 |
|---|---|---|---|---|---|
| δ0 | 3 | 3.25 | 3.5 | 3.75 | 4 |
| r | 14.5 | 14.75 | 15 | 15.25 | 15.5 |
| h | 6 | 6.5 | 7 | 7.5 | 8 |
| N1 | 120 | 134 | 148 | 162 | 180 |
| N2 | 360 | 440 | 520 | 600 | 640 |
| Performance Rank | ω1 | ω2 | ω3 | ω4 | ω5 | ω6 |
|---|---|---|---|---|---|---|
| PCu > T = k > kz = kα > PFe | 0.107 | 0.107 | 0.064 | 0.332 | 0.195 | 0.195 |
| PCu = T > k > kz = kα > PFe | 0.098 | 0.098 | 0.059 | 0.288 | 0.169 | 0.288 |
| PCu > T > k > kz = kα > PFe | 0.088 | 0.088 | 0.054 | 0.375 | 0.151 | 0.244 |
| PCu = T = k > kz = kα > PFe | 0.122 | 0.122 | 0.069 | 0.229 | 0.229 | 0.229 |
| T > PCu > k > kz = kα > PFe | 0.088 | 0.088 | 0.054 | 0.244 | 0.151 | 0.375 |
| k > T = PCu > kz = kα > PFe | 0.107 | 0.107 | 0.064 | 0.195 | 0.332 | 0.195 |
| Group | x1 | x2 | x3 | x4 | x5 | fopt |
|---|---|---|---|---|---|---|
| A | 3.06 | 15.46 | 8 | 133.54 | 640 | −0.8264 |
| B | 3 | 15.5 | 8 | 146.59 | 640 | −0.8501 |
| C | 3 | 15.5 | 8 | 120 | 360 | −0.8125 |
| D | 3.05 | 15.46 | 8 | 146.89 | 640 | −0.8711 |
| E | 3 | 15.5 | 8 | 158.96 | 630.96 | −0.8889 |
| F | 3.09 | 15.33 | 8 | 146.47 | 640 | −0.9026 |
| BPMSM Performance | Before | After | Improvement/% |
|---|---|---|---|
| kz/(N/mm) | 2.12 | 3.3158 | 56.4 |
| kα/(N·m/rad) | 0.31 | 0.531 | 71.29 |
| k/(N/A) | 2.6527 | 3.1725 | 19.6 |
| T/(mN·m) | 143.08 | 173.3752 | 21.17 |
| η/% | 69 | 75 | 8.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, H.; Bian, F.; Yue, Y.; Li, B.; Yu, P.; Yang, L.; Chen, G.; Hu, L. Multi-Structural Optimization of Bearingless Permanent Magnet Slice Motor Based on Virtual Prototype in Ansoft Maxwell. Appl. Sci. 2021, 11, 4740. https://doi.org/10.3390/app11114740
Shen H, Bian F, Yue Y, Li B, Yu P, Yang L, Chen G, Hu L. Multi-Structural Optimization of Bearingless Permanent Magnet Slice Motor Based on Virtual Prototype in Ansoft Maxwell. Applied Sciences. 2021; 11(11):4740. https://doi.org/10.3390/app11114740
Chicago/Turabian StyleShen, Huimin, Feng Bian, Yang Yue, Bingchu Li, Ping Yu, Lihong Yang, Guangsheng Chen, and Liang Hu. 2021. "Multi-Structural Optimization of Bearingless Permanent Magnet Slice Motor Based on Virtual Prototype in Ansoft Maxwell" Applied Sciences 11, no. 11: 4740. https://doi.org/10.3390/app11114740
APA StyleShen, H., Bian, F., Yue, Y., Li, B., Yu, P., Yang, L., Chen, G., & Hu, L. (2021). Multi-Structural Optimization of Bearingless Permanent Magnet Slice Motor Based on Virtual Prototype in Ansoft Maxwell. Applied Sciences, 11(11), 4740. https://doi.org/10.3390/app11114740







