A Distributed Terahertz Metasurface with Cold-Electron Bolometers for Cosmology Missions
Abstract
1. Introduction
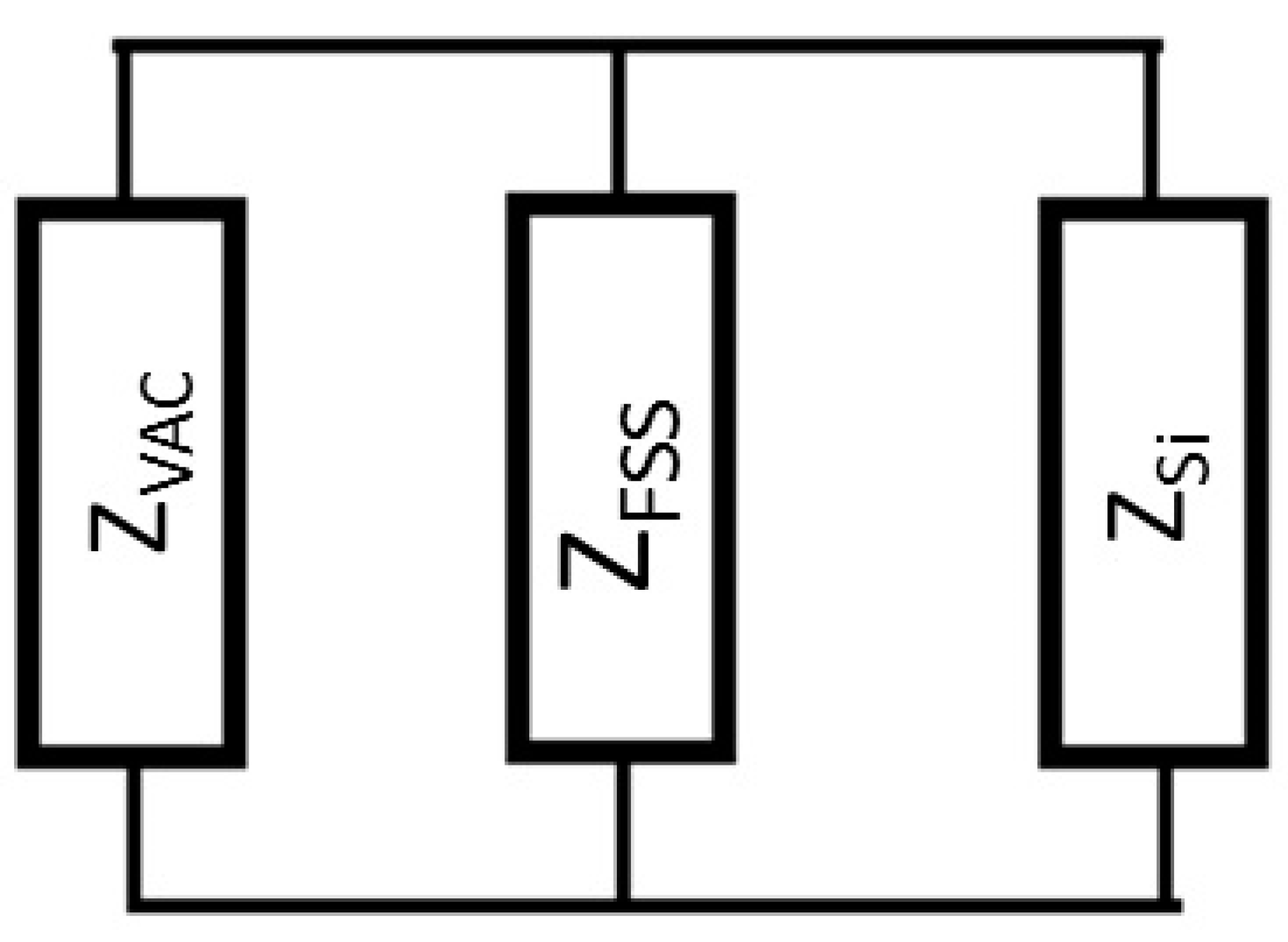
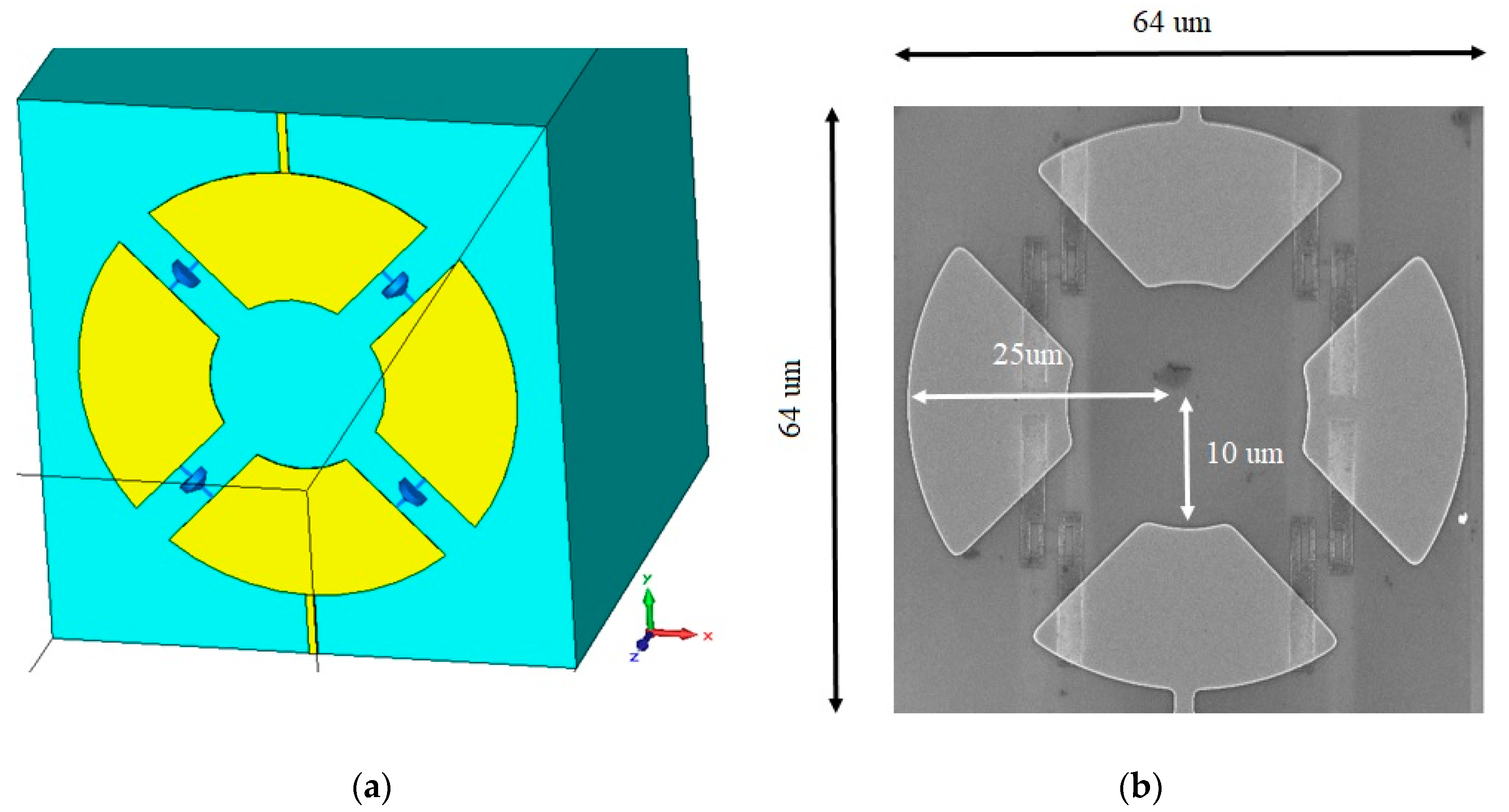
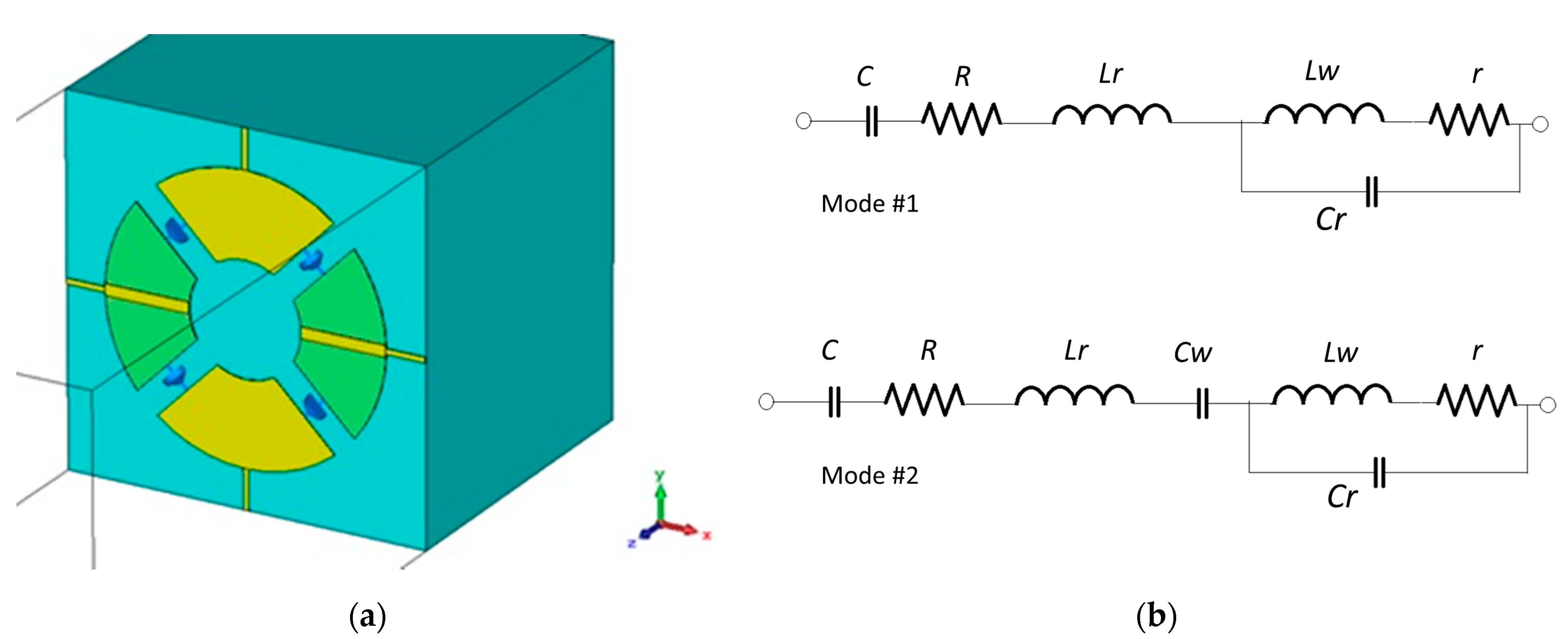
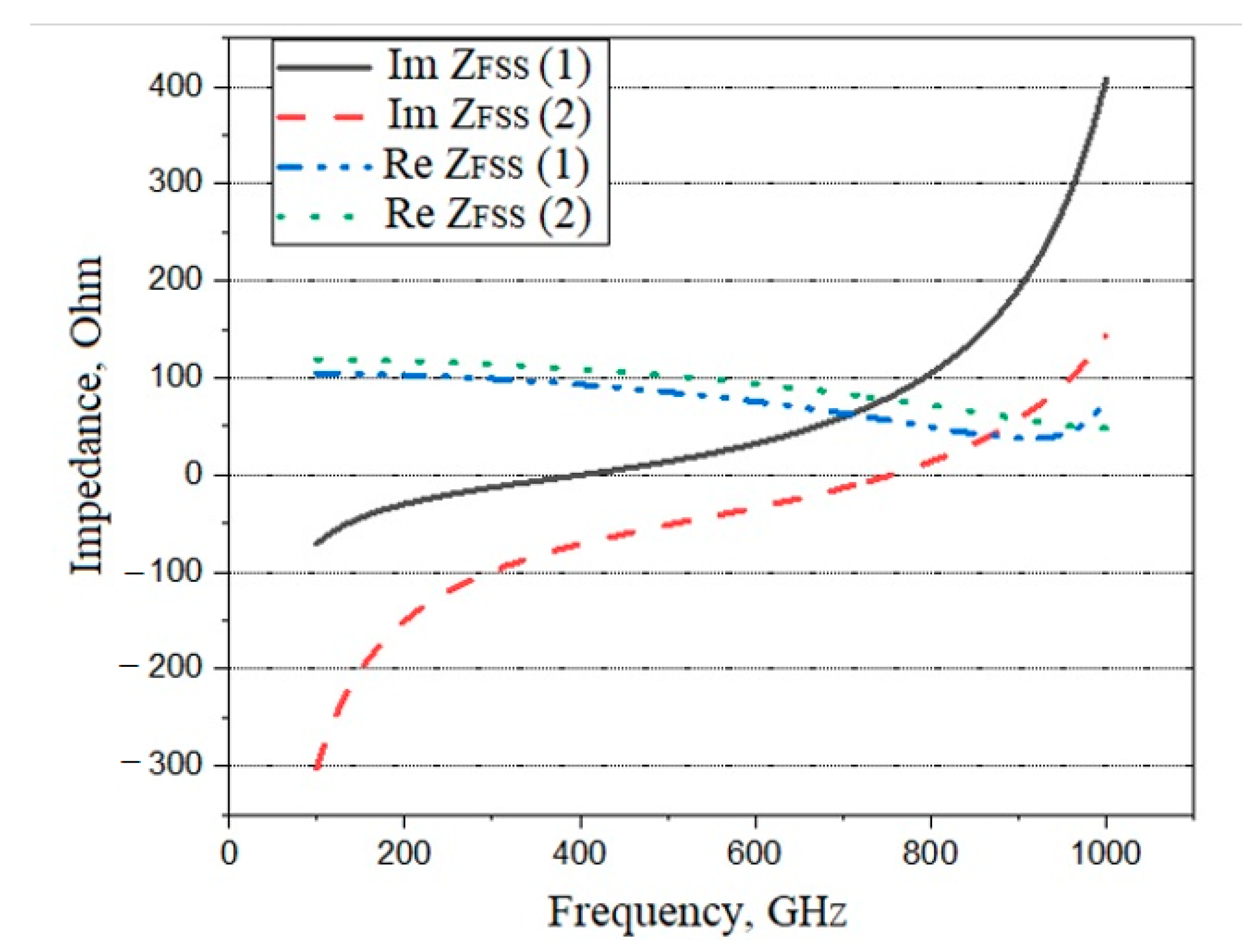
2. Numerical Model
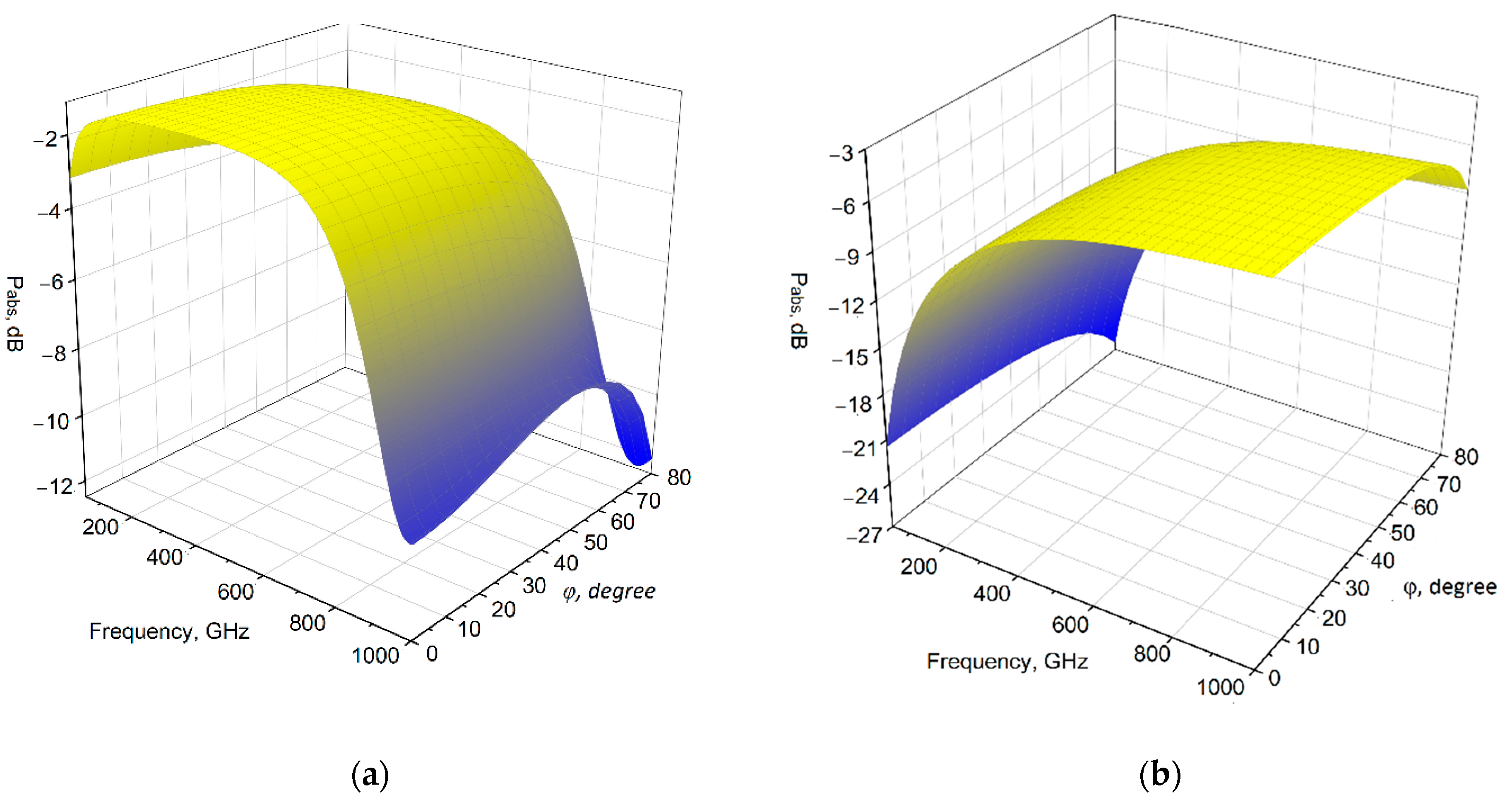
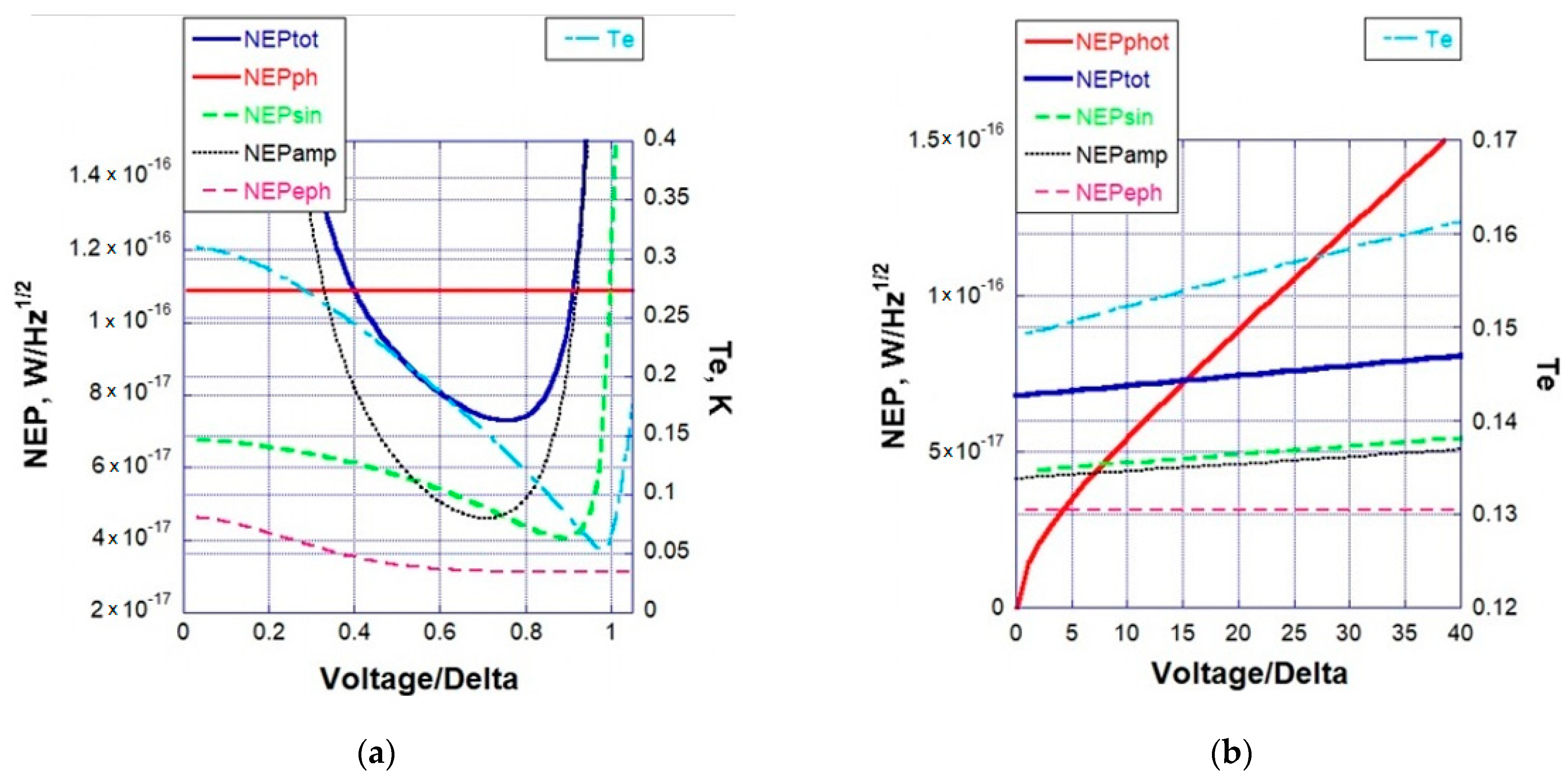
3. Noise Analysis
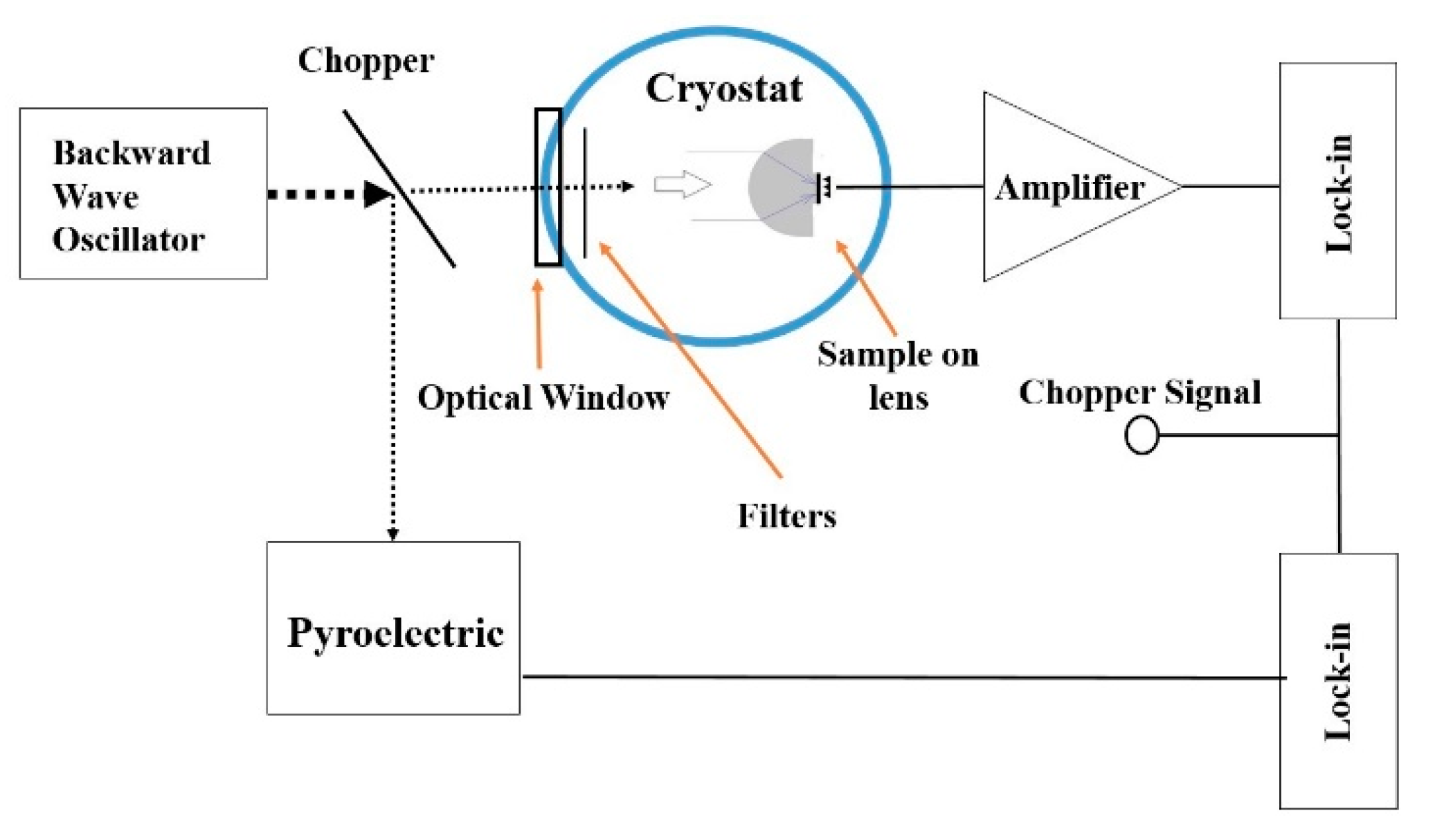
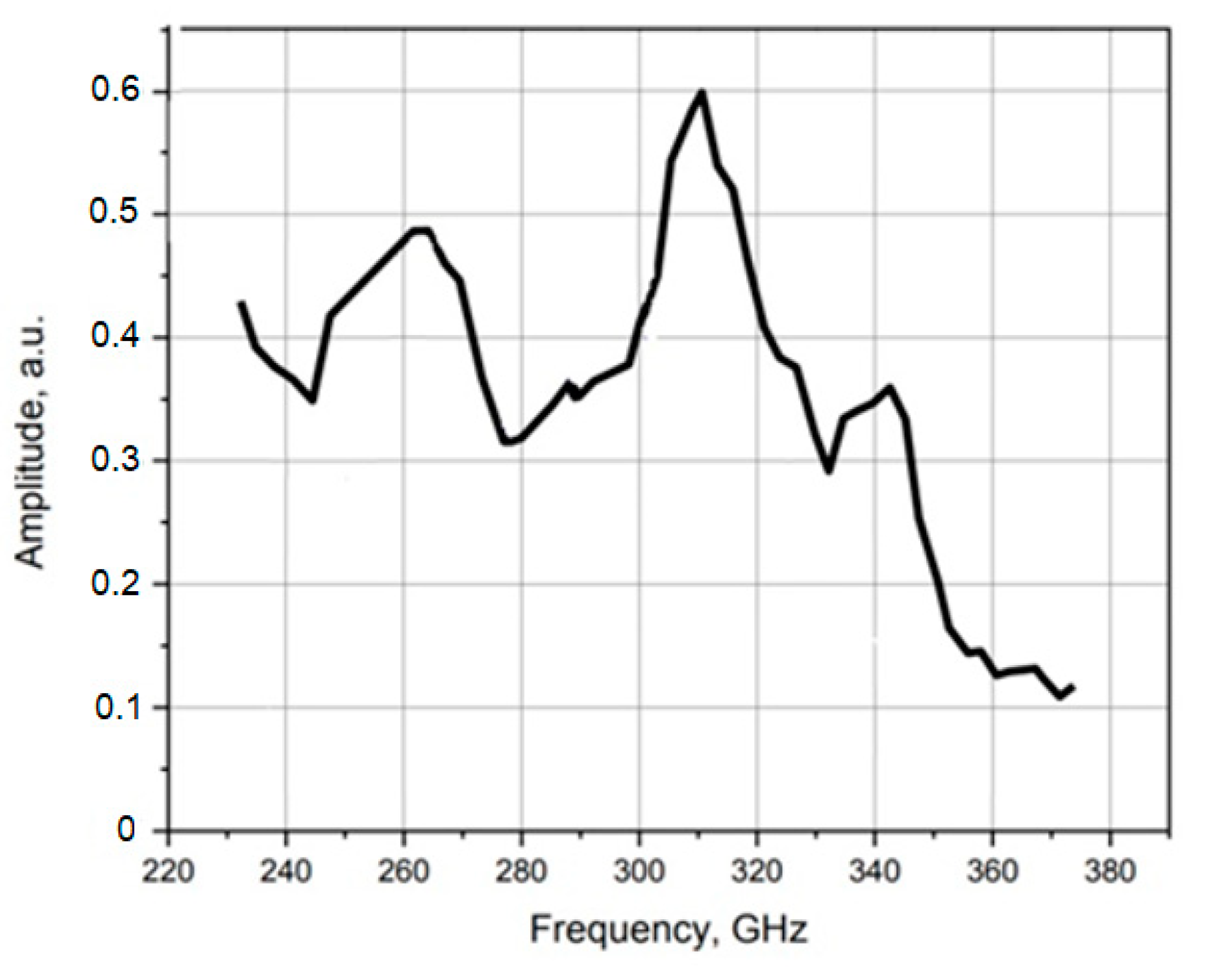
4. Experimental Check
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kuzmin, L.S. Cold-Electron Bolometer. In BOLOMETERS; Intechweb.org ed.; Perera, A.G.U., Ed.; Intech: Rijeka, Croatia, 2012; p. 77. ISBN 978-953-510235-9. [Google Scholar]
- Tarasov, M.A.; Kuzmin, L.S.; Edel’man, V.S.; Mahashabde, S.; de Bernardis, P. Optical Response of a Cold-Electron Bolometer Array Integrated in a 345-GHz Cross-Slot Antenna. IEEE Trans. Appl. Supercond. 2011, 21, 3635–3639. [Google Scholar] [CrossRef]
- Kuzmin, L. Ultimate cold-electron bolometer with strong electrothermal feedback. Proc. SPIE 2004, 5498, 349–361. [Google Scholar]
- Kuzmin, L.; Agulo, I.; Fominsky, M.; Savin, A.; Tarasov, M. Optimization of electron cooling by SIN tunnel junctions. Supercond. Sci. Technol. 2004, 17, s400–s405. [Google Scholar] [CrossRef]
- Gordeeva, A.V. Record electron self-cooling in cold-electron bolometers with a hybrid superconductor-ferromagnetic nanoabsorber and traps. Sci. Rep. 2020, 10, 21961. [Google Scholar] [CrossRef] [PubMed]
- Gordeeva, A.V.; Zbrozhek, V.O.; Pankratov, A.L.; Revin, L.S.; Shamporov, V.A.; Gunbina, A.A.; Kuzmin, L.S. Observation of photon noise by cold-electron bolometers. Appl. Phys. Lett. 2017, 110, 162603. [Google Scholar] [CrossRef]
- Kuzmin, L.S.; Pankratov, A.L.; Gordeeva, A.V.; Zbrozhek, V.O.; Shamporov, V.A.; Revin, L.S.; Blagodatkin, A.V.; Masi, S.; de Bernardis, P. Photon-noise-limited cold-electron bolometer based on strong electron self-cooling for high performance cosmology missions. Commun. Phys. 2019, 2, 1–8. [Google Scholar] [CrossRef]
- Aiola, S.; Amico, G.; Battaglia, P.; Battistelli, E.; Baù, A.; De Bernardis, P.; Bersanelli, M.; Boscaleri, A.; Cavaliere, F.; Coppolecchia, A.; et al. The Large-Scale Polarization Explorer (LSPE). Proc. SPIE 2012, 8446, 84467A. [Google Scholar]
- Kuzmin, L. 2D Array of Cold-Electron Nanobolometers with Double Polarization Cross-Dipole Antennae. Nanoscale Res. Lett. 2012, 7, 224. [Google Scholar] [CrossRef] [PubMed]
- Masi, S.; Ade, P.; Boscaleri, A.; De Bernardis, P.; De Petris, M.; De Troia, G.; Fabrini, M.; Iacoangeli, A.; Lamagna, L.; Lange, A.; et al. OLIMPO: A Balloon-Borne, Arcminute-Resolution Survey of the Sky at mm and Sub-mm Wavelengths. In Proceedings of the 16th ESA Symposium on European Rocket and Balloon Programmes and related Research, ESA-SP 530, Sankt Gallen, Switzerland, 2–5 June 2003. [Google Scholar]
- Mahashabde, S.; Sobolev, A.; Tarasov, M.; Tsydanzhapov, G.; Kuzmin, L. Planar frequency selective bolometric array at 350 GHz. IEEE Trans. Terahertz Sci. Technol. 2015, 5, 37–43. [Google Scholar] [CrossRef]
- Mahashabde, S.; Sobolev, A.; Bengtsson, A.; Andren, D.; Tarasov, M.A.; Salatino, M.; De Bernardis, P.; Masi, S.; Kuzmin, L.S. A Frequency Selective Surface Based Focal Plane Receiver for the OLIMPO Balloon-Borne Telescope. IEEE Trans. Terahertz Sci. Technol. 2015, 5, 145–152. [Google Scholar] [CrossRef]
- Mahashabde, S.; Tarasov, M.A.; Salatino, M.; Sobolev, A.; Masi, S.; Kuzmin, L.S.; de Bernardis, P. A distributed-absorber cold-electron bolometer single pixel at 95 GHz. Appl. Phys. Let. 2015, 107, 092602. [Google Scholar] [CrossRef]
- Sobolev, A.S.; Beiranvand, B.; Chekushkin, A.M.; Kudryashov, A.V.; Tarasov, M.A.; Yusupov, R.A.; Gunbina, A.; Vdovin, V.F.; Edelman, V. Wideband metamaterial-based array of SINIS bolometers. EPJ Web Conf. 2018, 195, 05009. [Google Scholar] [CrossRef][Green Version]
- Kuzmin, L. Optimization of the Hot-Electron Bolometer for Space Astronomy. In The International Workshop on Superconducting Nano-Electronics Devices; Pekola, J., Ruggiero, B., Silvestrini, P., Eds.; Springer: Boston, UK, 2002; pp. 145–154. [Google Scholar]
- Golubev, D.; Kuzmin, L. Nonequilibrium theory of a hot-electron bolometer with normal metal-insulator-superconductor tunnel junction. J. Appl. Phys. 2001, 89, 6464–6472. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Beiranvand, B.; Sobolev, A.S.; Larionov, M.Y.; Kuzmin, L.S. A Distributed Terahertz Metasurface with Cold-Electron Bolometers for Cosmology Missions. Appl. Sci. 2021, 11, 4459. https://doi.org/10.3390/app11104459
Beiranvand B, Sobolev AS, Larionov MY, Kuzmin LS. A Distributed Terahertz Metasurface with Cold-Electron Bolometers for Cosmology Missions. Applied Sciences. 2021; 11(10):4459. https://doi.org/10.3390/app11104459
Chicago/Turabian StyleBeiranvand, Behrokh, Alexander S. Sobolev, Michael Yu. Larionov, and Leonid S. Kuzmin. 2021. "A Distributed Terahertz Metasurface with Cold-Electron Bolometers for Cosmology Missions" Applied Sciences 11, no. 10: 4459. https://doi.org/10.3390/app11104459
APA StyleBeiranvand, B., Sobolev, A. S., Larionov, M. Y., & Kuzmin, L. S. (2021). A Distributed Terahertz Metasurface with Cold-Electron Bolometers for Cosmology Missions. Applied Sciences, 11(10), 4459. https://doi.org/10.3390/app11104459





