Independent Component Analysis Applied on Pulsed Thermographic Data for Carbon Fiber Reinforced Plastic Inspection: A Comparative Study
Abstract
1. Introduction
2. Literature Review
3. ICA and ICT
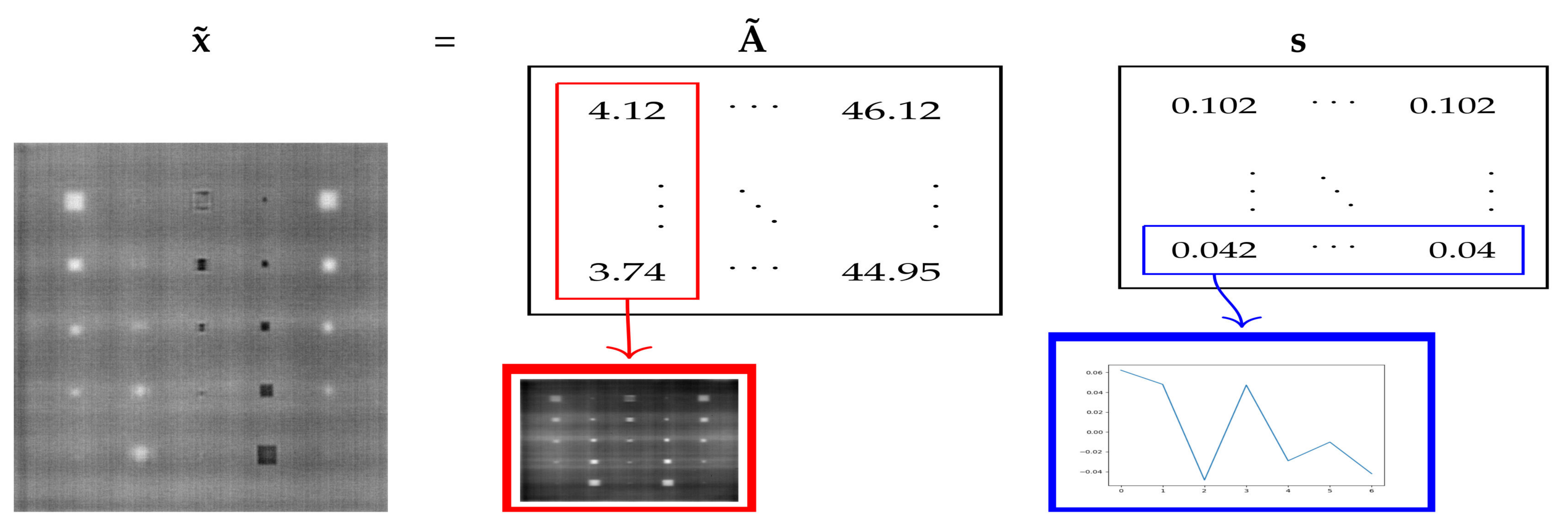
3.1. Independent Component Analysis
3.2. Related Work
3.2.1. Infomax-ICA
3.2.2. FastICA
3.2.3. Quasi-Newton ICA
3.2.4. Trust Region ICA
3.2.5. PICARD and PICARD-O
3.2.6. Miscellaneous
3.3. ICA in IRNDT
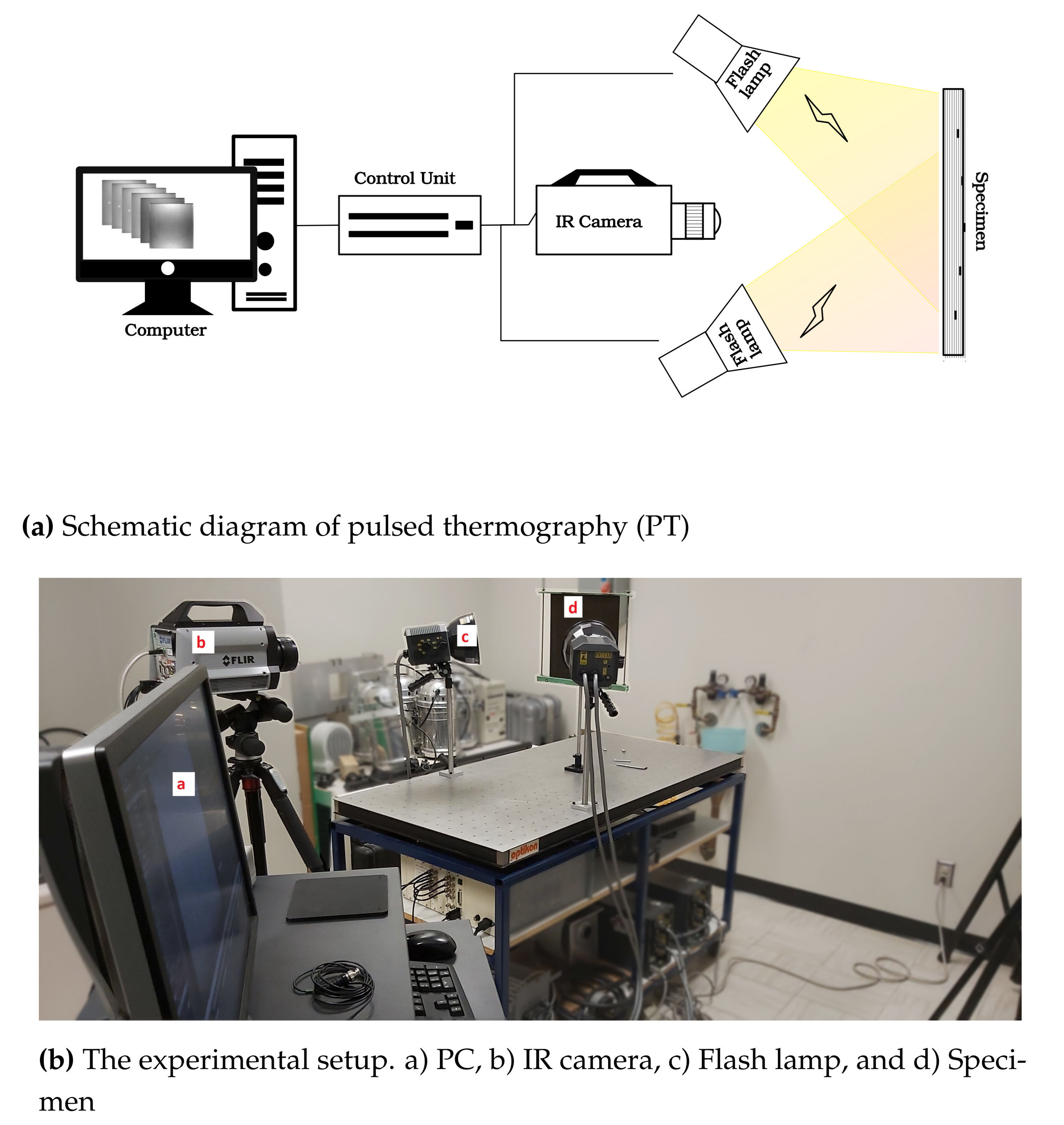
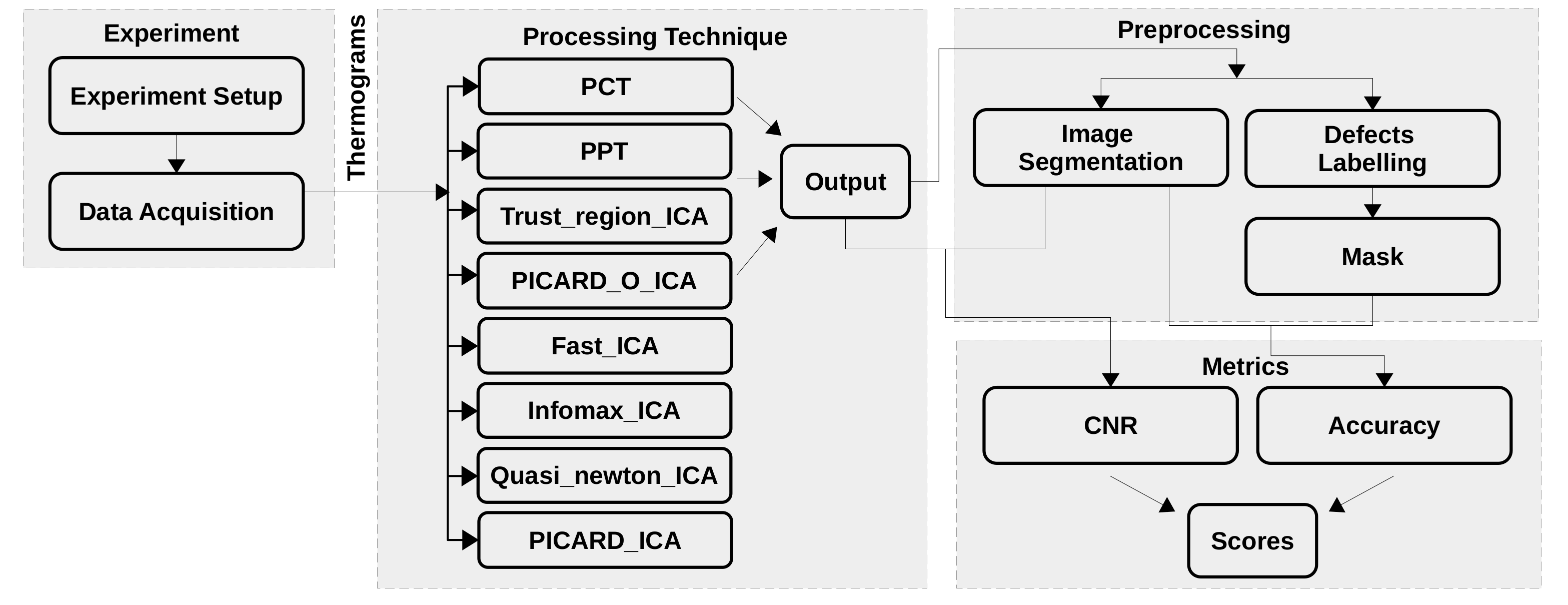
4. Materials and Methods
4.1. Data
4.2. Analysis
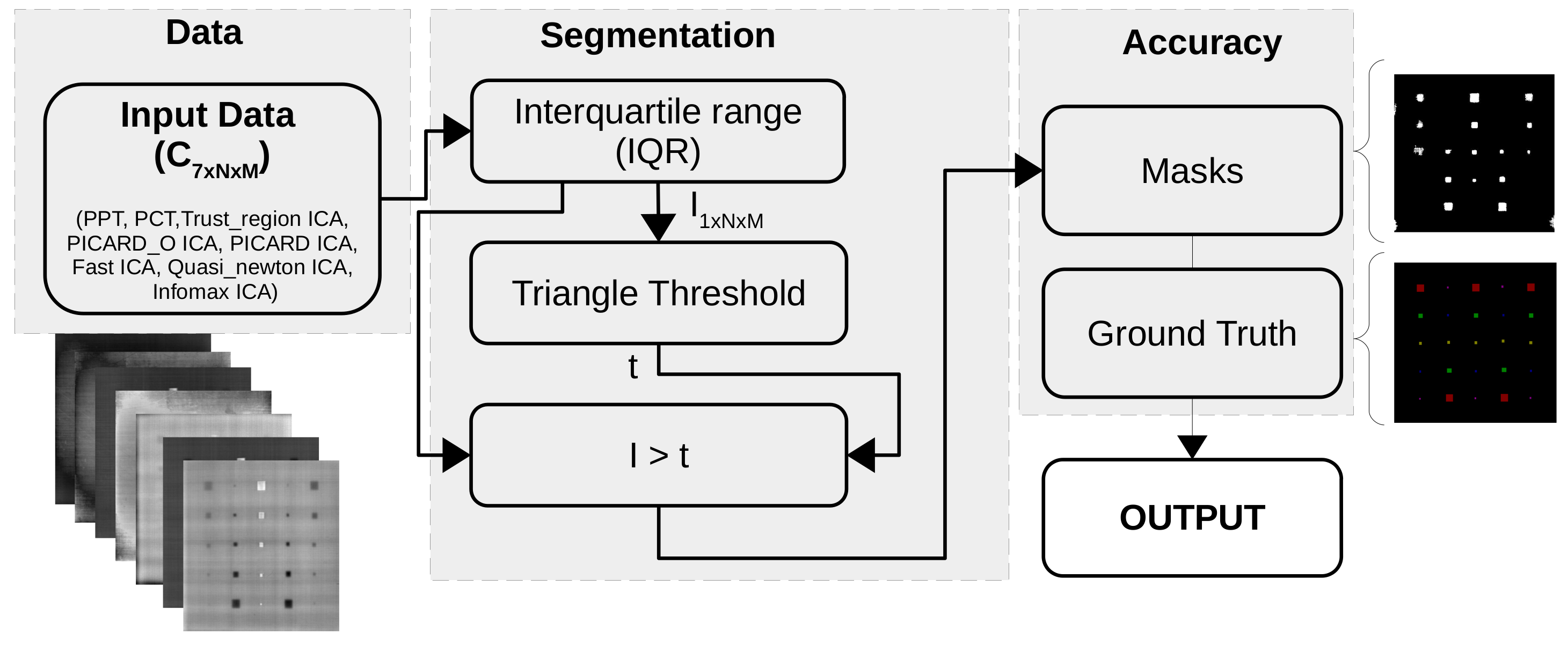
4.3. Figure of Merit
4.3.1. CNR
4.3.2. Accuracy
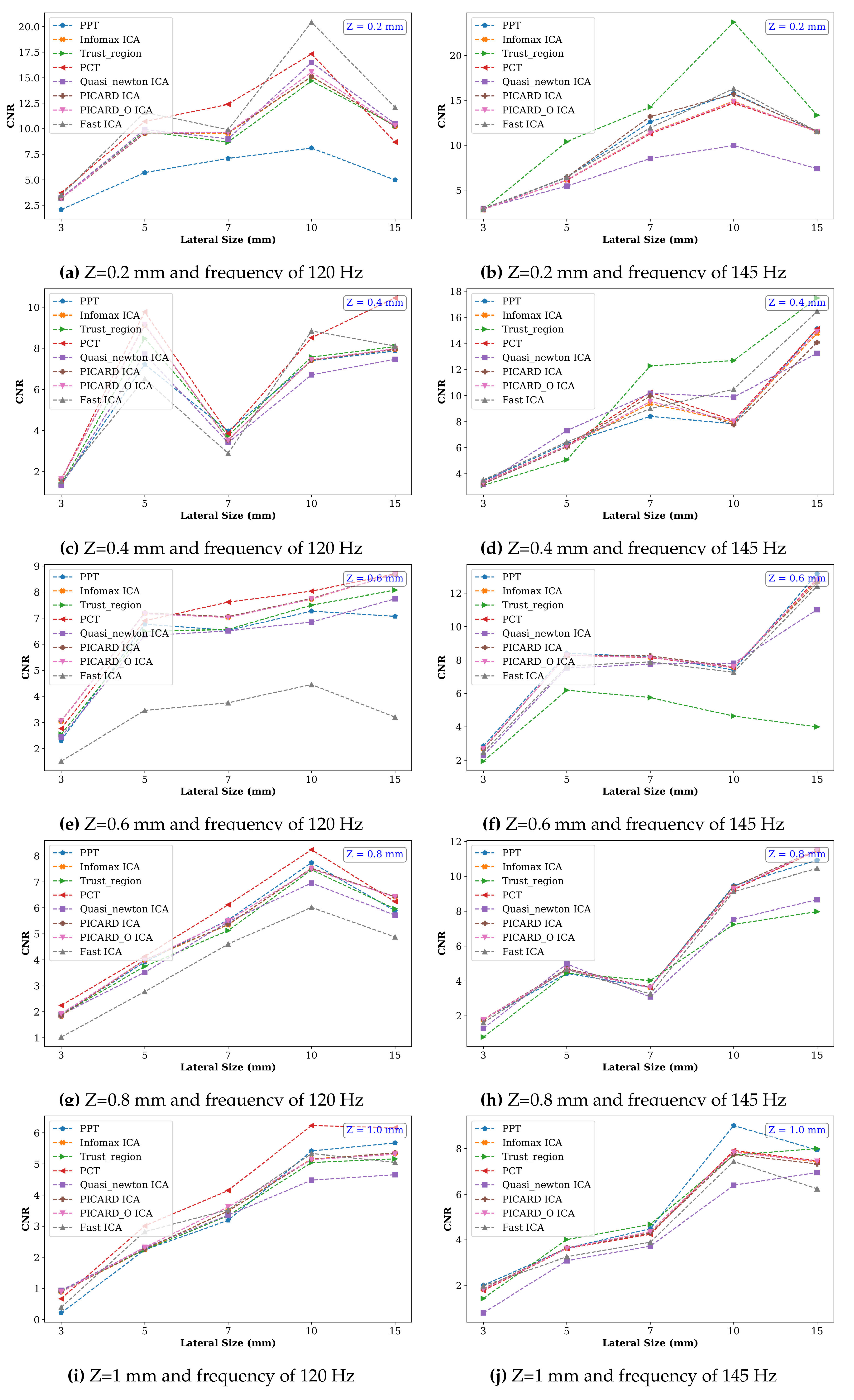
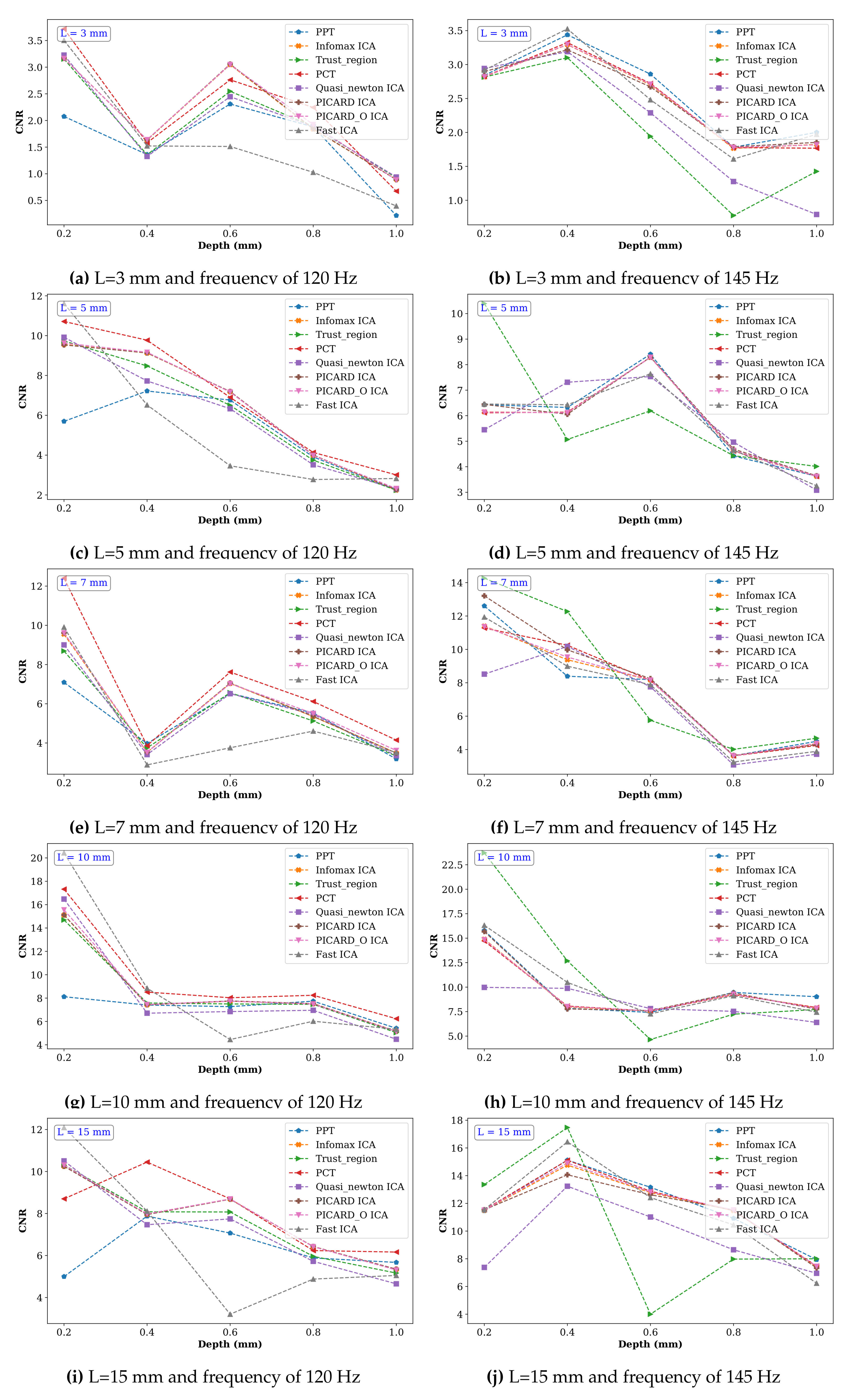
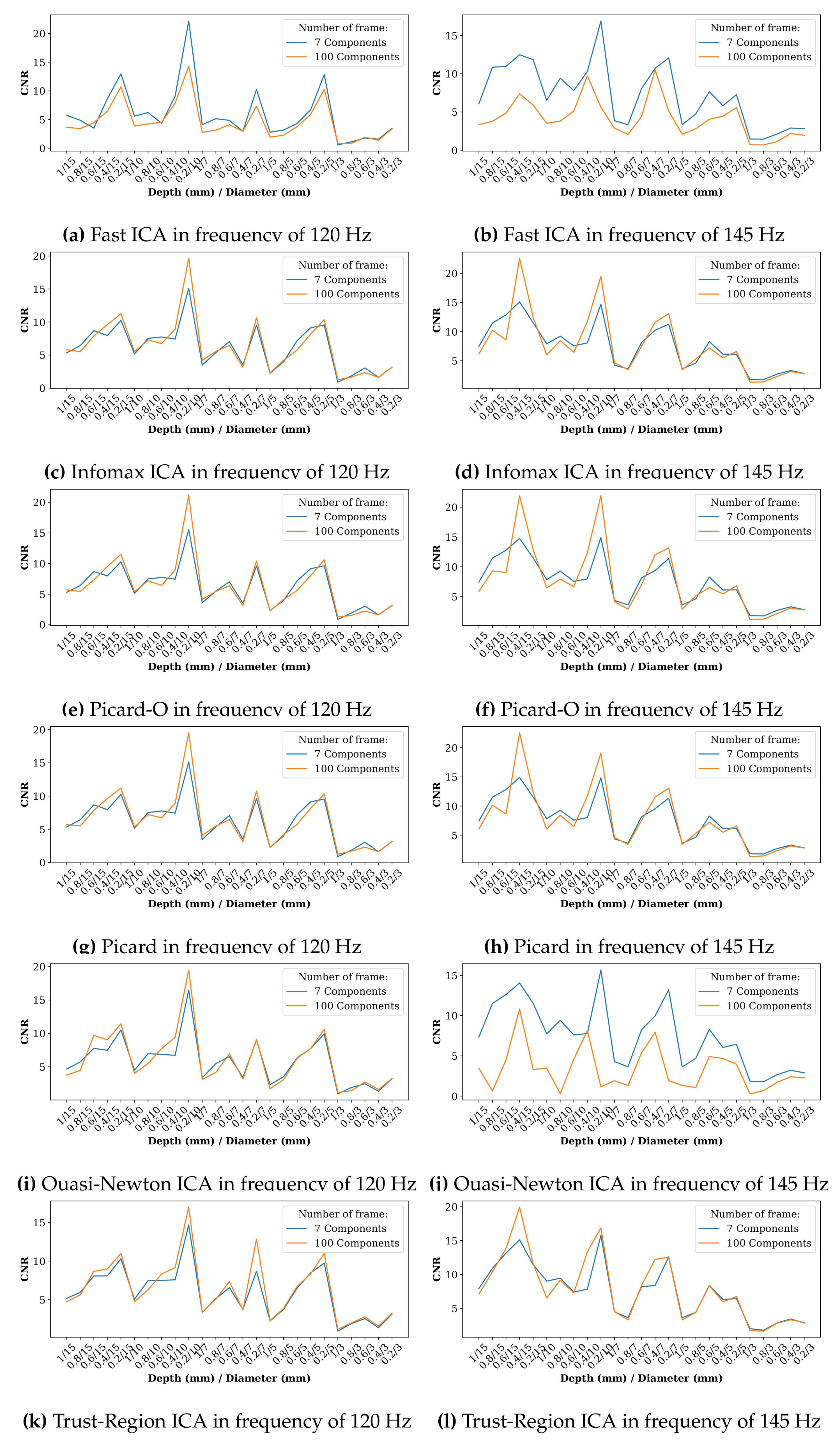
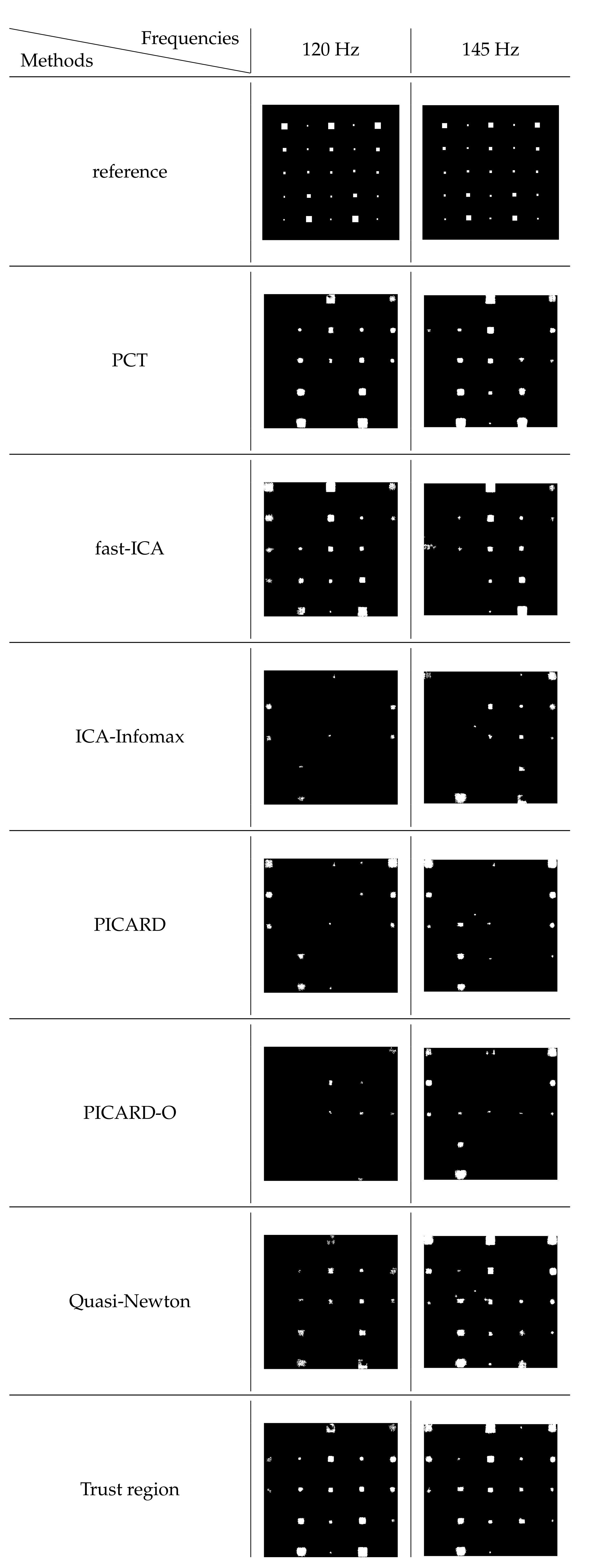
5. Results
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| NDT | Non Destructive Testing |
| IRT | InfraRed Thermography |
| PT | Pulsed Thermography |
| PPT | Pulsed Phase Thermography |
| PCA | Principal Component Analysis |
| PCT | Principal Component Thermography |
| ICA | Independent Component Analysis |
| ICT | Independent Component Thermography |
| BSS | Blind Signal Seperation |
| CFRP | Carbon Fiber Reinforced Plastic |
| CNR | Contrast over Noise Ration |
| MoG | Mixture of Gaussian |
| CCIPCA | Candid Covariance-free Incremental Principal Component Analysis |
| CCIPCT | Candid Covariance-free Incremental Principal Component Thermography |
| ESPCA | Edge-group Sparse Principal Component Analysis |
| ESPCT | Edge-group Sparse Principal Component Thermography |
| Sparse-PCA | Sparse Principal Component Analysis |
| SPCT | Sparse Principal Component Thermography |
| NMF | Non-negative Matrix Factorization |
| LatLRR | Latent Low Rank Representation |
| LatLRRT | Latent Low Rank Representation in Thermography |
| PLS | Partial Least Square |
| PLST | Partial Least Square Thermography |
| TSR | Thermographic Signal Reconstruction |
| SVM | Support Vector Machine |
| OLPPT | Orthogonal Locally Preserving Projection Thermography |
| ANN | Artificial Neural Network |
| DTT | Dynamic Thermal Tomography |
| GSA | Gapped Smoothing Algorithm |
| DAC | Difference of Absolute Contrast |
| MDAC | Modified Difference of Absolute Contrast |
| ATI | Apparent Thermal Inertia |
| TQ | Thermal Quadrupole |
| NLF | Non Linear Fitting |
| GAN | Generative Adversarial Network |
| LWIR | Long Wavelength InfraRed |
| MWIR | Mid Wavelength InfraRed |
| KPCA | Kernel-PCA |
| HOG | Histogram of Oriented Gradient. |
References
- Meola, C.; Boccardi, S.; Carlomagno, G.M. Infrared Thermography in the Evaluation of Aerospace Composite Materials: Infrared Thermography to Composites; Woodhead Publishing: Sawston, UK, 2016. [Google Scholar]
- Vavilov, V.; Burleigh, D. Infrared Thermography and Thermal Nondestructive Testing; Springer: Berlin, Germany, 2020. [Google Scholar]
- Houchin, J.S.; Parulski, K.A. Calibration System for a Raster Input Scanner. U.S. Patent 5,047,861, 10 September 1991. [Google Scholar]
- Harris, J.G.; Chiang, Y.M. Nonuniformity correction of infrared image sequences using the constant-statistics constraint. IEEE Trans. Image Process. 1999, 8, 1148–1151. [Google Scholar] [CrossRef]
- Ratliff, B.M.; Hayat, M.M.; Tyo, J.S. Radiometrically accurate scene-based nonuniformity correction for array sensors. JOSA A 2003, 20, 1890–1899. [Google Scholar] [CrossRef]
- Perenzoni, M.; Mosconi, D.; Stoppa, D. A 160 × 120-pixel uncooled IR-FPA readout integrated circuit with on-chip non-uniformity compensation. In Proceedings of the 2010 IEEE ESSCIRC, Seville, Spain, 14–16 September 2010; pp. 122–125. [Google Scholar]
- Cao, Y.; Tisse, C.L. Single-image-based solution for optics temperature-dependent nonuniformity correction in an uncooled long-wave infrared camera. Opt. Lett. 2014, 39, 646–648. [Google Scholar] [CrossRef]
- Maldague, X.; Marinetti, S. Pulse phase infrared thermography. J. Appl. Phys. 1996, 79, 2694–2698. [Google Scholar] [CrossRef]
- Rajic, N. Principal Component Thermography; Technical Report; Defence Science and Technology Organisation: Victoria, Australia, 2002. [Google Scholar]
- Hyvärinen, A.; Karhunen, J.; Oja, E. Independent Component Analysis. In Adaptive and Cognitive Dynamic Systems: Signal Processing, Learning, Communications and Control; Wiley: Hoboken, NJ, USA, 2004. [Google Scholar]
- Liu, Y.; Wu, J.Y.; Liu, K.; Wen, H.L.; Yao, Y.; Sfarra, S.; Zhao, C. Independent component thermography for non-destructive testing of defects in polymer composites. Measur. Sci. Technol. 2019, 30, 044006. [Google Scholar] [CrossRef]
- Fleuret, J.; Ebrahimi, S.; Maldague, X. Pulsed Thermography Signal Reconstruction Using Linear Support Vector Regression. In Proceedings of the 2020 International Conference on Quantitative InfraRed Thermography, Porto, Portugal, 6–10 July 2020. [Google Scholar] [CrossRef]
- Ahmed, J.; Gao, B.; Tian, G.Y.; Yang, Y.; Fan, Y.C. Sparse ensemble matrix factorization for debond detection in CFRP composites using optical thermography. Infrared Phys. Technol. 2018, 92, 392–401. [Google Scholar] [CrossRef]
- Zhang, X.; Saniie, J.; Heifetz, A. Neural learning based blind source separation for detection of material defects in pulsed thermography images. In Proceedings of the 2020 IEEE International Conference on Electro Information Technology (EIT), Chicago, IL, USA, 31 July–1 August 2020; pp. 112–116. [Google Scholar]
- Liu, K.; Tang, Y.; Lou, W.; Liu, Y.; Yang, J.; Yao, Y. A thermographic data augmentation and signal separation method for defect detection. Measur. Sci. Technol. 2021, 32, 045401. [Google Scholar] [CrossRef]
- Netzelmann, U.; Müller, D. Modified pulse-phase thermography algorithms for improved contrast-to-noise ratio from pulse-excited thermographic sequences. NDT E Int. 2020, 116, 102325. [Google Scholar] [CrossRef]
- Vavilov, V.P.; Shiryaev, V.V.; Kuimova, M.V. Time-and phase-domain thermal tomography of composites. Photonics 2018, 5, 31. [Google Scholar] [CrossRef]
- Poelman, G.; Hedayatrasa, S.; Segers, J.; Van Paepegem, W.; Kersemans, M. Adaptive spectral band integration in flash thermography: Enhanced defect detectability and quantification in composites. Compos. Part B Eng. 2020, 202, 108305. [Google Scholar] [CrossRef]
- Ahmed, J.; Baloch, G.A.; Tian, G.Y. Wavelet Domain Based Defect Detection using Optical Thermography. In Proceedings of the 2019 International Conference on Intelligent Medicine and Image Processing, Bali, Indonesia, 19–22 April 2019; pp. 83–87. [Google Scholar]
- Ahmed, J.; Gao, B.; Woo, W.L. Wavelet-integrated alternating sparse dictionary matrix decomposition in thermal imaging CFRP defect detection. IEEE Trans. Ind. Inf. 2018, 15, 4033–4043. [Google Scholar] [CrossRef]
- Ahmed, J.; Gao, B.; Woo, W.L.; Zhu, Y. Ensemble Joint Sparse Low-Rank Matrix Decomposition for Thermography Diagnosis System. IEEE Trans. Ind. Electron. 2020, 68, 2648–2658. [Google Scholar] [CrossRef]
- Liu, L.; Gao, B.; Wu, S.; Ahmed, J.; Woo, W.L.; Li, J.; Yu, Y. Structured iterative alternating sparse matrix decomposition for thermal imaging diagnostic system. Infrared Phys. Technol. 2020, 107, 103288. [Google Scholar] [CrossRef]
- Yousefi, B.; Sfarra, S.; Castanedo, C.I.; Maldague, X.P. Comparative Analysis on Thermal Non-Destructive Testing Imagery Applying Candid Covariance-Free Incremental Principal Component Thermography (CCIPCT). Infrared Phys. Technol. 2017, 85, 163–169. [Google Scholar] [CrossRef]
- Weng, J.; Zhang, Y.; Hwang, W.S. Candid Covariance-Free Incremental Principal Component Analysis. IEEE Trans. Pattern Anal. Mach. Intell. 2003, 25, 1034–1040. [Google Scholar] [CrossRef]
- Wu, J.Y.; Sfarra, S.; Yao, Y. Sparse principal component thermography for subsurface defect detection in composite products. IEEE Trans. Ind. Inf. 2018, 14, 5594–5600. [Google Scholar] [CrossRef]
- Yousefi, B.; Sharifipour, H.M.; Castanedo, C.I.; Maldague, X.P. Automatic IRNDT inspection applying sparse PCA-based clustering. In Proceedings of the 2017 IEEE 30th Canadian Conference on Electrical and Computer Engineering (CCECE), Windsor, ON, Canada, 30 April–3 May 2017; pp. 1–4. [Google Scholar]
- Wen, C.M.; Sfarra, S.; Gargiulo, G.; Yao, Y. Edge-Group Sparse Principal Component Thermography for Defect Detection in an Ancient Marquetry Sample. Proceedings 2019, 27, 7034. [Google Scholar] [CrossRef]
- Wen, C.M.; Sfarra, S.; Gargiulo, G.; Yao, Y. Thermographic Data Analysis for Defect Detection by Imposing Spatial Connectivity and Sparsity Constraints in Principal Component Thermography. IEEE Trans. Ind. Inf. 2020, 17, 3901–3909. [Google Scholar] [CrossRef]
- Min, W.; Liu, J.; Zhang, S. Edge-group sparse PCA for network-guided high dimensional data analysis. Bioinformatics 2018, 34, 3479–3487. [Google Scholar] [CrossRef]
- Yousefi, B.; Sfarra, S.; Sarasini, F.; Castanedo, C.I.; Maldague, X.P. Low-Rank Sparse Principal Component Thermography (Sparse-PCT): Comparative Assessment on Detection of Subsurface Defects. Infrared Phys. Technol. 2019, 98, 278–284. [Google Scholar] [CrossRef]
- Yousefi, B.; Castanedo, C.I.; Maldague, X.P. Low-rank Convex/Sparse Thermal Matrix Approximation for Infrared-based Diagnostic System. arXiv 2020, arXiv:2010.06784. [Google Scholar]
- Yousefi, B.; Castanedo, C.I.; Maldague, X.P.V. Measuring Heterogeneous Thermal Patterns in Infrared-Based Diagnostic Systems Using Sparse Low-Rank Matrix Approximation: Comparative Study. IEEE Trans. Instrum. Measur. 2021, 70, 1–9. [Google Scholar] [CrossRef]
- Fleuret, J.; Ibarra-Castanedo, C.; Ebrahimi, S.; Maldague, X. Latent Low Rank Representation Applied to Thermography. In Proceedings of the 2020 International Conference on Quantitative InfraRed Thermography, Porto, Portugal, 6–10 July 2020. [Google Scholar] [CrossRef]
- Liu, G.; Yan, S. Latent low-rank representation for subspace segmentation and feature extraction. In Proceedings of the 2011 IEEE International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 1615–1622. [Google Scholar]
- Lopez, F.; Nicolau, V.; Maldague, X.; Ibarra-Castanedo, C. Multivariate infrared signal processing by partial least-squares thermography. In Proceedings of the 16th International Symposium on Applied Electromagnetics and Mechanics, Québec, QC, Canada, 31 July–2 August 2013. [Google Scholar]
- Lopez, F.; Ibarra-Castanedo, C.; de Paulo Nicolau, V.; Maldague, X. Optimization of pulsed thermography inspection by partial least-squares regression. Ndt E Int. 2014, 66, 128–138. [Google Scholar] [CrossRef]
- Shepard, S.M.; Lhota, J.R.; Rubadeux, B.A.; Ahmed, T.; Wang, D. Enhancement and reconstruction of thermographic NDT data. In Proceedings of the Thermosense XXIV, Orlando, FL, USA, 1–4 April 2002; Maldague, X.P., Rozlosnik, A.E., Eds.; International Society for Optics and Photonics—SPIE: Orlando, FL, USA, 2002; Volume 4710, pp. 531–535. [Google Scholar] [CrossRef]
- Shepard, S.M.; Beemer, M.F. Advances in thermographic signal reconstruction. In Thermosense: Thermal Infrared Applications XXXVII; International Society for Optics and Photonics: Baltimore, MD, USA, 2015; Volume 9485, p. 94850R. [Google Scholar]
- Vapnik, V.N. The Nature of Statistical Learning Theory; Springer-Verlag: New York, NY, USA, 1995. [Google Scholar]
- Liu, K.; Tang, Y.; Yao, Y.; Liu, Y.; Yang, J. Orthogonal Locality Preserving Projections Thermography for Subsurface Defect Detection. In Proceedings of the IEEE 2019 CAA Symposium on Fault Detection, Supervision and Safety for Technical Processes (SAFEPROCESS), Xiamen, China, 5–7 July 2019; pp. 707–712. [Google Scholar]
- Liu, Y.; Liu, K.; Gao, Z.; Yao, Y.; Sfarra, S.; Zhang, H.; Maldague, X.P. Non-destructive defect evaluation of polymer composites via thermographic data analysis: A manifold learning method. Infrared Phys. Technol. 2019, 97, 300–308. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, K.; Yang, J.; Yao, Y. Spatial-neighborhood manifold learning for nondestructive testing of defects in polymer composites. IEEE Trans. Ind. Inf. 2019, 16, 4639–4649. [Google Scholar] [CrossRef]
- Yousefi, B.; Kalhor, D.; Usamentiaga Fernández, R.; Lei, L.; Castanedo, C.I.; Maldague, X.P. Application of deep learning in infrared non-destructive testing. In Proceedings of the QIRT 2018, Berlin, Germany, 21–28 June 2018. [Google Scholar]
- Xu, C.; Xie, J.; Wu, C.; Gao, L.; Chen, G.; Song, G. Enhancing the visibility of delamination during pulsed thermography of carbon fiber-reinforced plates using a stacked autoencoder. Sensors 2018, 18, 2809. [Google Scholar] [CrossRef] [PubMed]
- Saeed, N.; King, N.; Said, Z.; Omar, M.A. Automatic defects detection in CFRP thermograms, using convolutional neural networks and transfer learning. Infrared Phys. Technol. 2019, 102, 103048. [Google Scholar] [CrossRef]
- Vavilov, V.P. Dynamic thermal tomography: Recent improvements and applications. NDT E Int. 2015, 71, 23–32. [Google Scholar] [CrossRef]
- Galagan, R.M.; Momot, A.S. Analysis of application of neural networks to improve the reliability of active thermal NDT. Sci. News KPI 2019, 1, 7–14. [Google Scholar] [CrossRef][Green Version]
- Momot, A. Defect classification in active thermal testing with the use of neural networks. In Proceedings of the III Scientific and Technical Conference “NC in the context of Ukraine’s associate membership in the EU”, Kyiv, Ukraine, 17–19 September 2019. [Google Scholar]
- Momot, A.; Galagan, R. Influence of architecture and training dataset parameters on the neural networks efficiency in thermal nondestructive testing. Sci. Eur. 2019, 44, 1–44. [Google Scholar]
- Momot, A. Thermal defectometry of composite materials using artificial neural networks. In Proceedings of the XVIII International Scientific and Technical Conference “Instrument Manufacturing: State and perspectives”, Kyiv, Ukraine, 15–16 May 2019. [Google Scholar]
- Momot, A. Analysis of neural networks efficiency in active thermal defectometry depending on the number of thermograms. In Proceedings of the XIX International Scientific and Technical Conference “Instrument Manufacturing: State and prospects”, Kyiv, Ukraine, 13–14 May 2020. [Google Scholar]
- Chulkov, A.; Nesteruk, D.; Vavilov, V.; Moskovchenko, A.; Saeed, N.; Omar, M. Optimizing input data for training an artificial neural network used for evaluating defect depth in infrared thermographic nondestructive testing. Infrared Phys. Technol. 2019, 102, 103047. [Google Scholar] [CrossRef]
- Moskovchenko, A.; Vavilov, V.; Chulkov, A. Comparing the efficiency of defect depth characterization algorithms in the inspection of CFRP by using one-sided pulsed thermal NDT. Infrared Phys. Technol. 2020, 107, 103289. [Google Scholar] [CrossRef]
- Sun, J. Quantitative three-dimensional imaging of heterogeneous materials by thermal tomography. J. Heat Transf. 2016, 138, 112004. [Google Scholar] [CrossRef]
- Maillet, D.; Andre, S.; Batsale, J.C.; Degiovanni, A.; Moyne, C. Thermal Quadrupoles: Solving the Heat Equation through Integral Transforms; Wiley-Blackwell: Hoboken, NJ, USA, 2000. [Google Scholar]
- Bernegger, R.; Altenburg, S.J.; Roellig, M.; Maierhofer, C. Applicability of a 1D analytical model for pulse thermography of laterally heterogeneous semitransparent materials. Int. J. Thermophys. 2018, 39, 1–17. [Google Scholar] [CrossRef]
- Dudzik, S. Two-stage neural algorithm for defect detection and characterization uses an active thermography. Infrared Phys. Technol. 2015, 71, 187–197. [Google Scholar] [CrossRef]
- Duan, Y.; Liu, S.; Hu, C.; Hu, J.; Zhang, H.; Yan, Y.; Tao, N.; Zhang, C.; Maldague, X.; Fang, Q.; et al. Automated defect classification in infrared thermography based on a neural network. NDT E Int. 2019, 107, 102147. [Google Scholar] [CrossRef]
- Luo, Q.; Gao, B.; Woo, W.L.; Yang, Y. Temporal and spatial deep learning network for infrared thermal defect detection. NDT E Int. 2019, 108, 102164. [Google Scholar] [CrossRef]
- Ruan, L.; Gao, B.; Wu, S.; Tian, G. Deep Adversarial Network for CFRP Thermal Imaging Debond Diagnosis. In Proceedings of the 2019 Far East NDT New Technology Application Forum (FENDT), Qingdao, China, 24–27 June 2019; pp. 130–133. [Google Scholar] [CrossRef]
- Ruan, L.; Gao, B.; Wu, S.; Woo, W.L. DeftectNet: Joint loss structured deep adversarial network for thermography defect detecting system. Neurocomputing 2020, 417, 441–457. [Google Scholar] [CrossRef]
- Manzano, C.; Ngo, A.C.; Sivaraja, V.K.S. Intelligent infrared thermography inspection of subsurface defects. In Thermosense: Thermal Infrared Applications XLII; International Society for Optics and Photonics: Bellingham, WA, USA, 2020; Volume 11409, p. 114090V. [Google Scholar]
- He, K.; Gkioxari, G.; Dollár, P.; Girshick, R. Mask r-cnn. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2961–2969. [Google Scholar]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You only look once: Unified, real-time object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 779–788. [Google Scholar]
- Fang, Q.; Nguyen, B.D.; Castanedo, C.I.; Duan, Y.; Maldague, X., II. Automatic defect detection in infrared thermography by deep learning algorithm. In Thermosense: Thermal Infrared Applications XLII; International Society for Optics and Photonics: Bellingham, WA, USA, 2020; Volume 11409, p. 114090T. [Google Scholar]
- Redmon, J.; Farhadi, A. Yolov3: An incremental improvement. arXiv 2018, arXiv:1804.02767. [Google Scholar]
- Bang, H.T.; Park, S.; Jeon, H. Defect identification in composite materials via thermography and deep learning techniques. Compos. Struct. 2020, 246, 112405. [Google Scholar] [CrossRef]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster r-cnn: Towards real-time object detection with region proposal networks. arXiv 2015, arXiv:1506.01497. [Google Scholar] [CrossRef] [PubMed]
- Fang, Q.; Ibarra-Castanedo, C.; Maldague, X. Automatic defects segmentation and identification by deep learning algorithm with pulsed thermography: Synthetic and experimental data. Big Data Cognit. Comput. 2021, 5, 9. [Google Scholar] [CrossRef]
- Wei, Z.; Fernandes, H.; Herrmann, H.G.; Tarpani, J.R.; Osman, A. A Deep Learning Method for the Impact Damage Segmentation of Curve-Shaped CFRP Specimens Inspected by Infrared Thermography. Sensors 2021, 21, 395. [Google Scholar] [CrossRef] [PubMed]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In International Conference on Medical Image Computing and Computer-Assisted Intervention; Springer: Berlin, Germany, 2015; pp. 234–241. [Google Scholar]
- Feng, Q.; Gao, B.; Lu, P.; Woo, W.L.; Yang, Y.; Fan, Y.; Qiu, X.; Gu, L. Automatic seeded region growing for thermography debonding detection of CFRP. NDT E Int. 2018, 99, 36–49. [Google Scholar] [CrossRef]
- Marani, R.; Palumbo, D.; Renò, V.; Galietti, U.; Stella, E.; D’Orazio, T. Modeling and classification of defects in CFRP laminates by thermal non-destructive testing. Compos. Part B Eng. 2018, 135, 129–141. [Google Scholar] [CrossRef]
- Marani, R.; Palumbo, D.; Galietti, U.; Stella, E.; D’Orazio, T. Enhancing defects characterization in pulsed thermography by noise reduction. NDT E Int. 2019, 102, 226–233. [Google Scholar] [CrossRef]
- Liu, K.; Li, Y.; Yang, J.; Liu, Y.; Yao, Y. Generative principal component thermography for enhanced defect detection and analysis. IEEE Trans. Instrum. Measur. 2020, 69, 8261–8269. [Google Scholar] [CrossRef]
- Rajic, N. Principal component thermography for flaw contrast enhancement and flaw depth characterisation in composite structures. Compos. Struct. 2002, 58, 521–528. [Google Scholar] [CrossRef]
- Liu, K.; Ma, Z.; Liu, Y.; Yang, J.; Yao, Y. Enhanced Defect Detection in Carbon Fiber Reinforced Polymer Composites via Generative Kernel Principal Component Thermography. Polymers 2021, 13, 825. [Google Scholar] [CrossRef]
- Wang, Z.; Wan, L.; Xiong, N.; Zhu, J.; Ciampa, F. Variational level set and fuzzy clustering for enhanced thermal image segmentation and damage assessment. NDT E Int. 2021, 118, 102396. [Google Scholar] [CrossRef]
- Poelman, G.; Hedayatrasa, S.; Segers, J.; Tellez, J.A.C.; Paepegem, W.V.; Kersemans, M. Optical Infrared Thermography of CFRP with Artificial Defects: Performance of Various Post-Processing Techniques. Proceedings 2018, 2, 457. [Google Scholar] [CrossRef]
- Poelman, G.; Hedayatrasa, S.; Segers, J.; Van Paepegem, W.; Kersemans, M. A robust multi-scale gapped smoothing algorithm for baseline-free damage mapping from raw thermal images in flash thermography. In Proceedings of the 15th Quantitative InfraRed Thermography Conference, Porto, Portugal, 21–30 September 2020. [Google Scholar]
- Poelman, G.; Hedayatrasa, S.; Segers, J.; Van Paepegem, W.; Kersemans, M. Multi-scale gapped smoothing algorithm for robust baseline-free damage detection in optical infrared thermography. NDT E Int. 2020, 112, 102247. [Google Scholar] [CrossRef]
- Ratcliffe, C.P. Damage detection using a modified Laplacian operator on mode shape data. J. Sound Vib. 1997, 204, 505–517. [Google Scholar] [CrossRef]
- Ratcliffe, C.P.; Bagaria, W.J. Vibration technique for locating delamination in a composite beam. AIAA J. 1998, 36, 1074–1077. [Google Scholar] [CrossRef]
- Galagan, R.; Momot, A. Statistical analysis of thermal nondestructive testing data. Adv. Inf. Syst. 2019, 3, 58–62. [Google Scholar] [CrossRef]
- Vavilov, V.P.; Kuimova, M.V. Dynamic thermal tomography of composites: A comparison of reference and reference-free approaches. J. Nondestr. Eval. 2019, 38, 1–13. [Google Scholar] [CrossRef]
- Ahmadi, S.; Burgholzer, P.; Mayr, G.; Jung, P.; Caire, G.; Ziegler, M. Photothermal super resolution imaging: A comparison of different thermographic reconstruction techniques. NDT E Int. 2020, 111, 102228. [Google Scholar] [CrossRef]
- Ahmadi, S.; Hauffen, J.C.; Kästner, L.; Jung, P.; Caire, G.; Ziegler, M. Learned Block Iterative Shrinkage Thresholding Algorithm for Photothermal Super Resolution Imaging. arXiv 2020, arXiv:2012.03547. [Google Scholar]
- Kostroun, T.; Dvořák, M. Application of the Pulse Infrared Thermography Method for Nondestructive Evaluation of Composite Aircraft Adhesive Joints. Materials 2021, 14, 533. [Google Scholar] [CrossRef]
- Pilla, M.; Klein, M.; Maldague, X.; Salerno, A. New absolute contrast for pulsed thermography. In Proceedings of the QIRT, Dubrovnik, Croatia, 24–27 September 2002; Volume 5, pp. 53–58. [Google Scholar]
- Benítez, H.D.; Ibarra-Castanedo, C.; Bendada, A.; Maldague, X.; Loaiza, H.; Caicedo, E. Definition of a new thermal contrast and pulse correction for defect quantification in pulsed thermography. Infrared Phys. Technol. 2008, 51, 160–167. [Google Scholar] [CrossRef]
- Erazo-Aux, J.; Loaiza-Correa, H.; Restrepo-Giron, A.D. Histograms of oriented gradients for automatic detection of defective regions in thermograms. Appl. Opt. 2019, 58, 3620–3629. [Google Scholar] [CrossRef]
- Erazo-Aux, J.; Loaiza-Correa, H.; Restrepo-Giron, A.D.; Alfonso-Morales, W. Optimized Gaussian model for non-uniform heating compensation in pulsed thermography. Appl. Opt. 2020, 59, 4303–4313. [Google Scholar] [CrossRef]
- Erazo-Aux, J.; Loaiza-Correa, H.; Restrepo-Giron, A.D.; Ibarra-Castanedo, C.; Maldague, X. Thermal imaging dataset from composite material academic samples inspected by pulsed thermography. Data Brief 2020, 32, 106313. [Google Scholar] [CrossRef]
- Schager, A.; Zauner, G.; Mayr, G.; Burgholzer, P. Extension of the Thermographic Signal Reconstruction Technique for an Automated Segmentation and Depth Estimation of Subsurface Defects. J. Imaging 2020, 6, 96. [Google Scholar] [CrossRef]
- Muzika, L.; Švantner, M. Thermal Tomography Based on Time Transformation. 2019. Available online: https://dspace5.zcu.cz/handle/11025/34388 (accessed on 10 May 2021).
- Hedayatrasa, S.; Segers, J.; Calderon Tellez, J.A.; Van Paepegem, W.; Kersemans, M. On efficient FE simulation of pulse infrared thermography for inspection of CFRPs. In Proceedings of the 14th Quantitative InfraRed Thermography Conference, Berlin, Germany, 25–29 June 2018; pp. 748–756. [Google Scholar]
- Wang, M.; Gao, B.; Wu, T.; Hu, B.; Liu, L. Defect depth retrieval method based on nonlinear transformation for pulsed thermographic inspection. Int. J. Therm. Sci. 2020, 149, 106196. [Google Scholar] [CrossRef]
- Venegas, P.; Perán, J.; Usamentiaga Fernández, R.; Sáez de Ocáriz, I. Development of Virtual Illumination Functions for Thermographic NDT. In Proceedings of the 14th Quantitative InfraRed Thermography Conference, Berlin, Germany, 25–29 June 2018. [Google Scholar]
- Venegas, P.; Perán, J.; Usamentiaga, R.; de Ocáriz, I.S. Projected thermal diffusivity analysis for thermographic nondestructive inspections. Int. J. Therm. Sci. 2018, 124, 251–262. [Google Scholar] [CrossRef]
- Castellini, P.; Martarelli, M.; D’Antuono, A.; Paone, N. Soft-sensing reconstruction of in-depth defect geometry from active IR-thermography data. Measur. Sci. Technol. 2020, 31, 125902. [Google Scholar] [CrossRef]
- Dattoma, V.; Nobile, R.; Panella, F.; Pirinu, A.; Saponaro, A. Advanced NDT procedures and thermal data proceessing on CFRP aeronautical components. In Proceedings of the IRF 2018 of 6th International Conference Integrity-Reliability-Failure, Lisbon, Portugal, 22–26 July 2018; pp. 22–26. [Google Scholar]
- Popow, V.; Gurka, M. Full factorial analysis of the accuracy of automated quantification of hidden defects in an anisotropic carbon fibre reinforced composite shell using pulse phase thermography. NDT E Int. 2020, 116, 102359. [Google Scholar] [CrossRef]
- Grenyer, A.; Addepalli, S.; Zhao, Y.; Oakey, L.; Erkoyuncu, J.A.; Roy, R. Identifying challenges in quantifying uncertainty: Case study in infrared thermography. Procedia CIRP 2018, 73, 108–113. [Google Scholar] [CrossRef]
- Herault, J.; Jutten, C. Space or time adaptive signal processing by neural network models. In Proceedings of the AIP Conference Proceedings, Snowbird, UT, USA, 13–16 April 1986; American Institute of Physics: Snowbird, UT, USA, 1986; Volume 151, pp. 206–211. [Google Scholar]
- Tibaduiza, D.; Mujica, L.; Anaya, M.; Rodellar, J.; Güemes, A. Independent component analysis for detecting damages on aircraft wing skeleton. In Proceedings of the 5th European Conference on Structural Control (EACS 2012), Genoa, Italy, 18–20 June 2012; pp. 18–20. [Google Scholar]
- Hyvarinen, A. Fast and robust fixed-point algorithms for independent component analysis. IEEE Trans. Neural Netw. 1999, 10, 626–634. [Google Scholar] [CrossRef]
- Bell, A.J.; Sejnowski, T.J. An information-maximization approach to blind separation and blind deconvolution. Neural Comput. 1995, 7, 1129–1159. [Google Scholar] [CrossRef]
- Cardoso, J.F. Infomax and maximum likelihood for blind source separation. IEEE Signal Process. Lett. 1997, 4, 112–114. [Google Scholar] [CrossRef]
- Hyvärinen, A.; Oja, E. Independent Component Analysis: Algorithms and Applications. Neural Netw. 2000, 13, 411–430. [Google Scholar] [CrossRef]
- Zibulevsky, M. Blind source separation with relative newton method. In Proceedings of the ICA, Nara, Japan, 1–4 April 2003; Volume 2003, pp. 897–902. [Google Scholar]
- Choi, H.; Kim, S.; Choi, S. Trust-region learning for ICA. In Proceedings of the 2004 IEEE International Joint Conference on Neural Networks (IEEE Cat. No. 04CH37541), Budapest, Hungary, 24–29 July 2004; Volume 1, pp. 41–46. [Google Scholar]
- Choi, H.; Choi, S. Relative trust region learning for ICA. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP’05), Philadelphia, PA, USA, 23–25 March 2005; Volume 5, p. v-261. [Google Scholar]
- Choi, H.; Choi, S. A relative trust-region algorithm for independent component analysis. Neurocomputing 2007, 70, 1502–1510. [Google Scholar] [CrossRef]
- Ablin, P.; Cardoso, J.F.; Gramfort, A. Faster independent component analysis by preconditioning with Hessian approximations. IEEE Trans. Signal Process. 2018, 66, 4040–4049. [Google Scholar] [CrossRef]
- Ablin, P.; Cardoso, J.F.; Gramfort, A. Faster ICA under orthogonal constraint. In Proceedings of the 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018; pp. 4464–4468. [Google Scholar]
- Pfister, N.; Weichwald, S.; Bühlmann, P.; Schölkopf, B. Robustifying independent component analysis by adjusting for group-wise stationary noise. J. Mach. Learn. Res. 2019, 20, 1–50. [Google Scholar]
- Lipshutz, D.; Chklovskii, D.B. Bio-NICA: A biologically inspired single-layer network for Nonnegative Independent Component Analysis. arXiv 2020, arXiv:2010.12632. [Google Scholar]
- Hälvä, H.; Hyvarinen, A. Hidden Markov Nonlinear ICA: Unsupervised Learning from Nonstationary Time Series. In Proceedings of the Conference on Uncertainty in Artificial Intelligence PMLR, Toronto, ON, Canada, 3–6 August 2020; pp. 939–948. [Google Scholar]
- Rengifo, C.J.; Restrepo, A.D.; Nope, S.E. Method of selecting independent components for defect detection in carbon fiber-reinforced polymer sheets via pulsed thermography. Appl. Opt. 2018, 57, 9746–9754. [Google Scholar] [CrossRef]
- Lu, C.; Feng, J.; Chen, Y.; Liu, W.; Lin, Z.; Yan, S. Tensor robust principal component analysis with a new tensor nuclear norm. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 42, 925–938. [Google Scholar] [CrossRef] [PubMed]
- Fleuret, J.; Ibarra-Castanedo, C.; Ebrahimi, S.; Maldague, X. Independent Component Thermography Applied to Pulsed Thermographic Data. In Proceedings of the 3rd International Symposium on Structural Health Monitoring and Nondestructive Testing, Quebec-City, QC, Canada, 25–26 November 2020. [Google Scholar]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: Berlin, Germany, 2006. [Google Scholar]
- Carslaw, H.S.H.S. Conduction of Heat in Solids, 2nd ed.; Carslaw, H.S., Jaeger, J.C., Eds.; Clarendon Press: Oxford, UK, 1959. [Google Scholar]
- Zack, G.W.; Rogers, W.E.; Latt, S.A. Automatic measurement of sister chromatid exchange frequency. J. Histochem. Cytochem. 1977, 25, 741–753. [Google Scholar] [CrossRef] [PubMed]
- Usamentiaga, R.; Ibarra-Castanedo, C.; Maldague, X. More than Fifty Shades of Grey: Quantitative Characterization of Defects and Interpretation Using SNR and CNR. J. Nondestruct. Eval. 2018, 37, 25. [Google Scholar] [CrossRef]






| Features/Method | ICA | PCA |
|---|---|---|
| Linear transform | ✓ | ✓ |
| Goal of the transformation | maximizing the unmixing matrix as well as the independence of the components [10] | project the data into an orthogonal space while maximizing the variance of the projected data [122] |
| Matrix factorization | full rank to ensure the independence of the components. | low rank to ensure the non-correlation of the components. |
| Othrogonalize | not by default, however commonly a whitening step is computed beforethe ICA, which othogonalize the data. | ✓ |
| Ignore local data structure | ✓ | ✓[28,41] |
| Denoise | ✓ | ✓ |
| Remove uneven heating | ✓ |
| Method | Depth (mm) | Lateral Size (mm) | 145 Hz vs. 120 Hz | Lateral Size (mm) | 145 Hz vs. 120 Hz | Lateral Size (mm) | 145 Hz vs. 120 Hz | Lateral Size (mm) | 145 Hz vs. 120 Hz | Lateral Size (mm) | 145 Hz vs. 120 Hz | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 3 | 5 | 7 | 10 | 15 | ||||||||||||
| 120 Hz | 145 Hz | 120 Hz | 145 Hz | 120 Hz | 145 Hz | 120 Hz | 145 Hz | 120 Hz | 145 Hz | |||||||
| PCT | 0.2 | 3.718 | 2.917 | −22% | 10.711 | 6.456 | −40% | 12.402 | 11.938 | −4% | 17.323 | 16.317 | -6% | 8.699 | 11.544 | 33 % |
| 0.4 | 1.582 | 3.525 | 123% | 9.771 | 6.429 | −34% | 3.862 | 8.991 | 133% | 8.512 | 10.483 | 23% | 10.448 | 16.443 | 57% | |
| 0.6 | 2.762 | 2.481 | −10% | 6.898 | 7.639 | 11% | 7.617 | 7.885 | 3% | 8.030 | 7.273 | −9% | 8.697 | 12.417 | 43% | |
| 0.8 | 2.244 | 1.608 | −28% | 4.135 | 4.649 | 12% | 6.116 | 3.253 | −47% | 8.240 | 9.118 | 11% | 6.236 | 10.448 | 67% | |
| 1 | 0.673 | 1.972 | 193% | 3.008 | 3.253 | 8% | 4.147 | 3.892 | −6% | 6.234 | 7.443 | 19% | 6.163 | 6.234 | 1% | |
| PPT | 0.2 | 2.075 | 2.942 | 42% | 5.697 | 5.450 | −4% | 7.093 | 8.517 | 20% | 8.117 | 9.975 | 23% | 4.995 | 7.378 | 48 % |
| 0.4 | 1.360 | 3.190 | 134% | 7.220 | 7.310 | 1% | 3.974 | 10.177 | 156% | 7.404 | 9.879 | 33% | 7.875 | 13.238 | 68% | |
| 0.6 | 2.308 | 2.288 | −0.89% | 6.764 | 7.533 | 11% | 6.530 | 7.757 | 19% | 7.267 | 7.806 | 7% | 7.067 | 11.015 | 56% | |
| 0.8 | 1.880 | 1.276 | −32% | 3.912 | 4.964 | 27% | 5.536 | 3.081 | −44% | 7.737 | 7.528 | −3% | 5.884 | 8.649 | 47% | |
| 1 | 0.217 | 0.791 | 264% | 2.239 | 3.081 | 38% | 3.188 | 3.718 | 17% | 5.414 | 6.394 | 18% | 5.671 | 6.953 | 23% | |
| Fast-ICA | 0.2 | 3.474 | 2.802 | −19% | 12.840 | 7.261 | −43% | 10.259 | 12.078 | 18% | 22.184 | 16.903 | −24% | 12.983 | 11.848 | −9% |
| 0.4 | 1.576 | 2.899 | 84% | 6.721 | 5.813 | −13% | 2.940 | 10.698 | 264% | 9.077 | 10.296 | 13% | 8.632 | 12.486 | 45% | |
| 0.6 | 1.766 | 2.115 | 20% | 4.320 | 7.652 | 77% | 4.857 | 8.050 | 66% | 4.359 | 7.800 | 79% | 3.507 | 10.965 | 213% | |
| 0.8 | 1.112 | 1.443 | 30% | 3.165 | 4.736 | 50% | 5.145 | 3.333 | −35% | 6.219 | 9.421 | 51% | 4.871 | 10.856 | 123% | |
| 1 | 0.574 | 1.461 | 154% | 2.794 | 3.333 | 19% | 4.086 | 3.853 | −6% | 5.601 | 6.522 | 16% | 5.723 | 6.076 | 6% | |
| Infomax-ICA | 0.2 | 3.166 | 2.823 | −11% | 9.557 | 6.113 | −36% | 9.548 | 11.276 | 18% | 15.101 | 14.707 | −3% | 10.249 | 11.535 | 12 % |
| 0.4 | 1.633 | 3.323 | 103% | 9.127 | 6.140 | −33% | 3.520 | 10.247 | 191% | 7.424 | 8.068 | 9% | 7.960 | 15.113 | 90% | |
| 0.6 | 3.047 | 2.721 | −11% | 7.183 | 8.285 | 15% | 7.039 | 8.142 | 16% | 7.733 | 7.553 | −2% | 8.686 | 12.878 | 48% | |
| 0.8 | 1.837 | 1.775 | −3% | 3.988 | 4.617 | 16% | 5.348 | 3.619 | −32% | 7.524 | 9.230 | 23% | 6.424 | 11.475 | 79% | |
| 1 | 0.896 | 1.767 | 97% | 2.242 | 3.619 | 61% | 3.488 | 4.242 | 21% | 5.164 | 7.917 | 53 % | 5.338 | 7.472 | 40% | |
| Trust-region-ICA | 0.2 | 3.152 | 2.840 | −10% | 9.733 | 6.431 | −34% | 8.690 | 12.602 | 45% | 14.689 | 15.779 | 7% | 10.310 | 11.465 | 11% |
| 0.4 | 1.357 | 3.438 | 153% | 8.478 | 6.323 | −25% | 3.750 | 8.390 | 124% | 7.581 | 7.842 | 3% | 8.080 | 15.119 | 87% | |
| 0.6 | 2.547 | 2.859 | 12% | 6.499 | 8.408 | 29% | 6.564 | 8.191 | 25% | 7.498 | 7.414 | −1% | 8.072 | 13.161 | 63% | |
| 0.8 | 1.888 | 1.782 | −6% | 3.746 | 4.423 | 18% | 5.124 | 3.628 | −29% | 7.464 | 9.462 | 27% | 5.959 | 10.919 | 83% | |
| 1 | 0.926 | 2.000 | 116% | 2.239 | 3.628 | 62% | 3.336 | 4.491 | 35% | 5.046 | 9.019 | 79% | 5.164 | 7.938 | 54% | |
| Quasi-newton-ICA | 0.2 | 3.226 | 2.897 | −10% | 9.919 | 6.441 | −35% | 9.002 | 13.208 | 47% | 16.478 | 15.678 | −5% | 10.505 | 11.540 | 10% |
| 0.4 | 1.325 | 3.217 | 143% | 7.725 | 6.056 | −22% | 3.409 | 9.971 | 192% | 6.707 | 7.771 | 16% | 7.466 | 14.063 | 88% | |
| 0.6 | 2.446 | 2.671 | 9% | 6.330 | 8.295 | 31% | 6.513 | 8.248 | 27% | 6.846 | 7.605 | 11% | 7.743 | 12.621 | 63% | |
| 0.8 | 1.887 | 1.788 | −5% | 3.513 | 4.693 | 33% | 5.464 | 3.645 | −33% | 6.956 | 9.413 | 35% | 5.722 | 11.522 | 101% | |
| 1 | 0.939 | 1.853 | 97% | 2.307 | 3.645 | 58% | 3.353 | 4.295 | 28% | 4.477 | 7.747 | 73% | 4.651 | 7.335 | 58 % | |
| PICARD | 0.2 | 3.166 | 2.820 | −11% | 9.534 | 6.141 | −35% | 9.612 | 11.361 | 18% | 15.120 | 14.846 | −2% | 10.249 | 11.514 | 12 % |
| 0.4 | 1.636 | 3.296 | 101% | 9.134 | 6.117 | −33% | 3.525 | 9.539 | 171% | 7.428 | 8.019 | 8% | 7.948 | 14.907 | 87% | |
| 0.6 | 3.057 | 2.711 | −11% | 7.195 | 8.288 | 15% | 7.056 | 8.159 | 16% | 7.757 | 7.577 | −2% | 8.679 | 12.820 | 48% | |
| 0.8 | 1.847 | 1.778 | −4% | 4.003 | 4.641 | 16% | 5.360 | 3.622 | −32% | 7.522 | 9.277 | 23% | 6.429 | 11.526 | 79% | |
| 1 | 0.888 | 1.817 | 104% | 2.267 | 3.622 | 60% | 3.483 | 4.367 | 25% | 5.150 | 7.841 | 52% | 5.349 | 7.454 | 39% | |
| PICARD-O | 0.2 | 3.163 | 2.818 | −11% | 9.629 | 6.150 | −36% | 9.612 | 11.397 | 18% | 15.551 | 14.899 | −4% | 10.305 | 11.495 | 11 % |
| 0.4 | 1.640 | 3.293 | 101% | 9.163 | 6.114 | −33% | 3.518 | 9.378 | 166% | 7.452 | 7.971 | 7% | 7.983 | 14.761 | 85% | |
| 0.6 | 3.048 | 2.701 | −11% | 7.169 | 8.285 | 15% | 7.022 | 8.165 | 16% | 7.736 | 7.568 | −2% | 8.692 | 12.776 | 47% | |
| 0.8 | 1.923 | 1.764 | −8% | 3.981 | 4.628 | 16% | 5.508 | 3.625 | −34% | 7.489 | 9.276 | 24% | 6.418 | 11.477 | 79% | |
| 1 | 0.885 | 1.822 | 106% | 2.323 | 3.625 | 56% | 3.618 | 4.358 | 20% | 5.140 | 7.873 | 53% | 5.309 | 7.425 | 40% | |
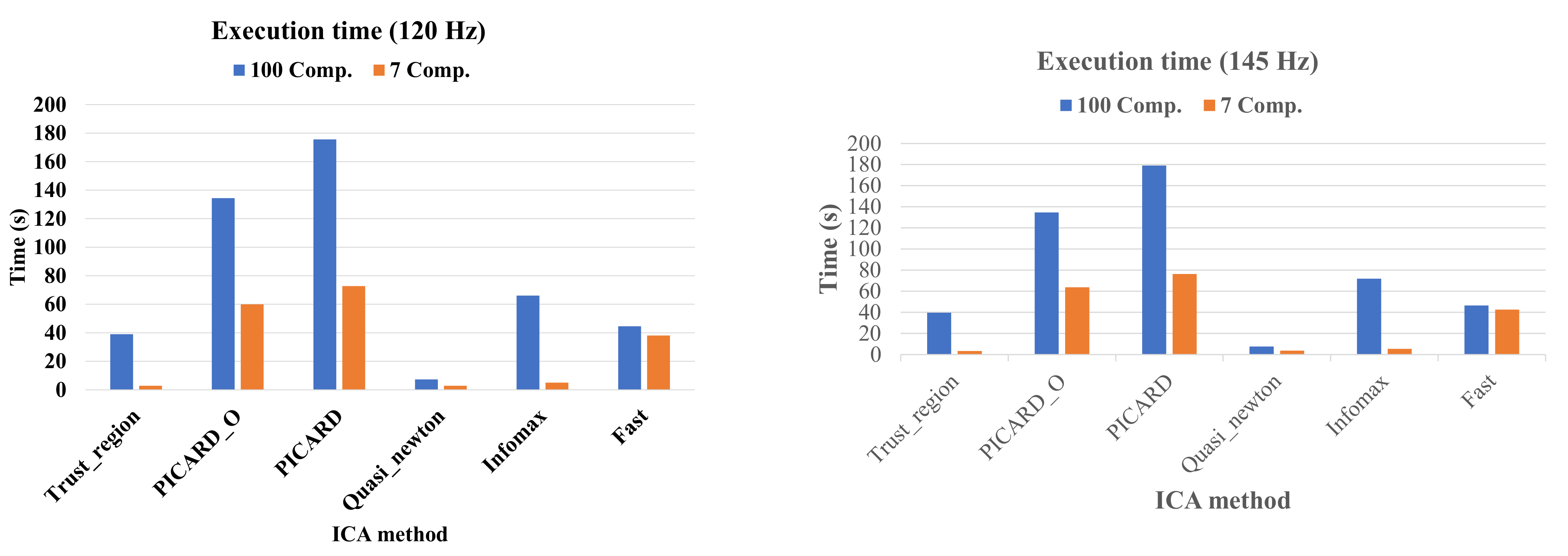
| Method | Execution Time (s) | 100 Comp. vs. 7 Comp. | Execution Time (s) | 100 Comp. vs. 7 Comp. | ||
|---|---|---|---|---|---|---|
| Frequency | Frequency | |||||
| 120 | 145 | |||||
| 7 Comp. | 100 Comp. | 7 Comp. | 100 Comp. | |||
| Trust region ICA | 2.8451 | 39.0860 | 13.74 | 3.3872 | 39.5966 | 11.69 |
| PICARD-O ICA | 59.9245 | 134.3624 | 2.24 | 63.8037 | 134.7053 | 2.11 |
| PICARD | 72.7453 | 175.5388 | 2.41 | 76.3144 | 179.1237 | 2.35 |
| Fast ICA | 38.1550 | 44.5424 | 1.17 | 42.6507 | 46.5227 | 1.09 |
| Infomax ICA | 5.0410 | 66.0711 | 13.11 | 5.4596 | 71.8660 | 13.16 |
| Quasi newton ICA | 2.8980 | 7.3608 | 2.54 | 3.7271 | 7.5612 | 2.03 |
| PCT | 8.7565 | 17.5889 | 2.0 | 9.2509 | 18.7692 | 2.02 |
| Method | Accuracy Score | |
|---|---|---|
| Frequency (Hz) | ||
| 120 | 145 | |
| PCT | 0.7310 | 0.8333 |
| Trust region ICA | 0.9340 | 0.767 |
| PICARD-O | 0.1270 | 0.6619 |
| PICARD | 0.4397 | 0.7959 |
| Fast ICA | 0.7319 | 0.8915 |
| Infomax ICA | 0.2279 | 0.4832 |
| Quasi newton ICA | 0.3758 | 0.7589 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fleuret, J.R.; Ebrahimi, S.; Ibarra-Castanedo, C.; Maldague, X.P.V. Independent Component Analysis Applied on Pulsed Thermographic Data for Carbon Fiber Reinforced Plastic Inspection: A Comparative Study. Appl. Sci. 2021, 11, 4377. https://doi.org/10.3390/app11104377
Fleuret JR, Ebrahimi S, Ibarra-Castanedo C, Maldague XPV. Independent Component Analysis Applied on Pulsed Thermographic Data for Carbon Fiber Reinforced Plastic Inspection: A Comparative Study. Applied Sciences. 2021; 11(10):4377. https://doi.org/10.3390/app11104377
Chicago/Turabian StyleFleuret, Julien R., Samira Ebrahimi, Clemente Ibarra-Castanedo, and Xavier P. V. Maldague. 2021. "Independent Component Analysis Applied on Pulsed Thermographic Data for Carbon Fiber Reinforced Plastic Inspection: A Comparative Study" Applied Sciences 11, no. 10: 4377. https://doi.org/10.3390/app11104377
APA StyleFleuret, J. R., Ebrahimi, S., Ibarra-Castanedo, C., & Maldague, X. P. V. (2021). Independent Component Analysis Applied on Pulsed Thermographic Data for Carbon Fiber Reinforced Plastic Inspection: A Comparative Study. Applied Sciences, 11(10), 4377. https://doi.org/10.3390/app11104377









