The Method of Production Scheduling with Uncertainties Using the Ants Colony Optimisation

Abstract

Production and maintenance tasks apply for access to the same resources. Maintenance-related machine downtime reduces productivity, but the costs incurred due to unplanned machine failures often outweigh the costs associated with predictive maintenance. Costs incurred due to unplanned machine failure include corrective maintenance, reworks, delays in deliveries, breaks in the work of employees and machines. Therefore, scheduling of production and maintenance tasks should be considered jointly. The problem of generating a predictive schedule with given constrains is considered. The objective of the paper is to develop a scheduling method that reflects the operation of the production system and nature of disturbances. The original value of the paper is the development of the method of a basic schedule generation with the application of the Ant Colony Optimisation. A predictive schedule is built by planning the technical inspection of the machine at time of the predicted failure-free time. The numerical simulations are performed for job/flow shop systems.

1. Introduction

The criteria of cost, quality and time availability are always contradictory. Entrepreneurs look for solutions that will not be reflected in the loss of quality or extension of deadlines for the implementation of tasks. Entrepreneurs are looking for organizational, technological and IT solutions that will allow for improvements in these areas.

Consider the problem of scheduling production tasks and planning technical inspections of machines. Production and maintenance tasks apply for access to the same resources, machines. Production and maintenance managers have divergent goals. Machines immobilization for maintenance decrease productivity. Boudjelida [1] investigated the robustness of joint production and maintenance scheduling in the problem of flow permutation and proved that the loss of efficiency due to the insertion of maintenance tasks into the production schedule increases. But costs incurred due to unplanned machine failure often outweigh the costs associated with predictive maintenance. Costs incurred due to unplanned machine failure include corrective maintenance, reworks, delays in deliveries, breaks in the work of employees and machines. Therefore, scheduling of production and maintenance tasks should be considered jointly.

The related literature distinguishes three approaches to production and maintenance planning in disturbance conditions: predictive, proactive and reactive. The goal of the predictive approach is to obtain a schedule that can absorb the disturbance without affecting planned external activities, while maintaining high system efficiency [2,3]. The proactive approach examines the influence of the disturbance on a schedule, using the criteria of stability. The schedule obtained for the best sequence of tasks related to maintenance and production is assumed for implementation [4]. The objective of the reactive approach is to adapt the schedule to the current situation [5].

There are two proactive approaches: proactive without or with prediction (Figure 1). In the first approach, only the impact of a disturbance on the schedule using robustness measures is examined. Researchers search for the best sequence of idle times between production tasks or batches taking the advantage of the simulation process [6,7]. Considering only the relationship between production and maintenance tasks as a conflict in management decisions may cause unmet demand or unexpected machine failures. A common objective is to maximize a system productivity and efficiency. Usually, the time interval for maintenance task and the number of maintenance tasks are fixed in advance. The mentioned deficiencies of proactive-reactive approaches are eliminated in predictive-reactive approaches.

The predictive-reactive approach is regarded as a combination of predictive and proactive scheduling techniques. Researchers predict maintenance time and then evaluate the effect of a disturbance on the predictive schedule using robustness measures [8,9]. Using the probability theory to describe machine conditions allows for more reliable maintenance planning. However, accepting the assumption that machine conditions are observable at the beginning of each period is not sufficient. Popular maintenance strategies are based on the periodic inspection of a machine and age dependent inspection and are also not sufficient. Attributes to describe the machine age and the influence of maintenance should be drawn from analysis of historical data on failure-free times and observation of dynamic machine conditions. The predictive-reactive method is considered in the presented paper.

Benbouzid-Sitayeb et al. [10] propose the joint production and preventive maintenance scheduling problem in permutation flowshops with the objective of minimizing the makespan. The insertion of the maintenance tasks is done according to several heuristics. Fei and Ma [11] propose a joint optimization on a hybrid flow shop system. A preventive maintenance strategy is based on reliability. The multi-objective is to minimize the makespan and total production cost. The authors proved that joint optimization is superior compared with independent decision-making. Nourelfath and Châtelet [12] present the integrating preventive maintenance and tactical production planning method for a parallel production system. The authors assume two possible causes for system failure: the independent failure of single components, and the simultaneous common cause failure of all components. The objective is to minimize the sum of preventive and corrective maintenance costs, setup costs, holding costs, backorder costs and production costs. Berrichi et al. [13] propose the Ant Colony Optimization algorithm to solve the joint production and maintenance scheduling problem. The trade-off solutions between objectives of production and maintenance is searched. Reliability models are used to take into account the maintenance aspect.

This paper faces the problem of generating a predictive schedule with given constrains in the conditions of disturbances for job shop/flow shop systems. The objective of the article is to develop an effective method of task scheduling, reflecting the operation of the production system and the nature of the disturbances. The method of estimation unknown system parameters such as Mean Time to Failure, Mean Time of Repaier is based on the theory of probability. The original value of the paper is the development of the method of a basic schedule generation with the application of the Ants Colony Optimisation (ACO). A predictive schedule is built by planning the technical inspection of the machine at time of the predicted failure-free time. Flexible operations are allocated to the machine during an increased risk of a failure. Three algorithms: genetic (GA) [14], immune (MOIA) [15] and clonal selection (CSA) [16] have been developed and compared for the presented problem of predictive schedules generation.

In this paper the concept of the ACO is presented and numerical examples are given for predictive scheduling. The ant colony optimization algorithm is applied to the problem of makespan minimization and schedule stability maksimisation. Comparative analyses of parameter variants of the ant colony optimization algorithm are performed.

The paper is organized as follows: The job shop scheduling problem for experimental study is presented in Section 2. The general concept of ACO is presented in Section 3. The application of ACO for the problem of production and maintenance task scheduling is described in Section 4. Section 5 contains numerical simulations and experimental test results related to the research. The paper concludes with a brief summary of the results (Section 6).

2. Production and Manitenance Scheduling Model

The scheduling problem in a job shop system where production tasks are allocated to resources with performance constraints due to maintenance is considered. Production systems are described by: (a) production tasks, (b) machines, (c) routes of production tasks, (d) operation times, (e) task completion dates. Production tasks are executed in exclusive-like mode and operations are not preempted. After a machine failure, the disrupted operations can be performed on parallel machines.

Data on the failure-free operation of the machine is collected. Knowledge about the machine reliability characteristics for the future planning horizon is acquired in five stages:

• Adoption of the hypothesis that the time of failure-free operation is described by the reliability distribution depending on the phase of the machine’s life cycle.
• Application of methods for estimating distribution parameters.
• Prediction of distribution parameters for the future planning period.
• Calculation of the reliability characteristics (e.g., mean time to failure (MTTF)) for the future planning period.
• Assessment of the impact of variable dates of failure on the values of stability and robustness criteria for given values of machine reliability characteristics.

The analyzed historical period is divided into i equal scheduling periods, $\left[\left(i-1\right)T,iT\right),i=1,...,m+1$. For each of them, N_i events are observed, i.e., machine failures with failure-free times $X_{i,1},...,X_{i,N_i}$. For each historical period i, the distribution parameters are estimated in order to describe the phenomenon of failure rate. Let us assume the hypothesis that the failure-free times $X_{i,1},...,X_{i,N_i}$ in period i $\left[\left(i-1\right)T,iT\right){,}_{}i=1,...,m+1$ are described by the exponential distribution with parameter ${\mu }_i>0$ with a density function:

$$f_i\left(t\right)=\{\begin{array}{l}{\mu }_i\exp \left(-{\mu }_{i}t\right){,}_{}t>0,\\ 0,t\le 0,\end{array}$$

(1)

Parameters ${\mu }_i$ are estimated in the second stage. Values of ${\mu }_i$ generally differ in subsequent historical periods i. Using the maximum likelihood method, the parameter $\widetilde{{\mu }_1}$ for the first period is estimated:

$$\widetilde{{\mu }_1}=\frac{n_1}{{\displaystyle {\sum }_{k=1}^{n_1}{x}_{1,k}^{}}}$$

(2)

In the empirical moment method, value $\widetilde{{\mu }_1}$ is determined comparing the equations:

$$\stackrel{}{m_1\left(x_1^{}\right)}=\frac{1}{n_1}{\displaystyle {\sum }_{k=1}^{n_1}{x}_{1,k}^{}}$$

(3)

where:

$$\stackrel{}{m_1\left(x_1^{}\right)}=\frac{1}{{\mu }_1}$$

(4)

and the formula for the estimated parameter $\widetilde{{\mu }_1}$ (2) is obtained.

After obtaining the estimated values of the distribution parameters for each historical period, parameter $\widetilde{{\mu }_{m+1}}$ is predicted for the future planning period using classical regression technique. Defining the function describing the parameters consists in eliminating fluctuations and identifying trends of the analyzed data on failure-free times. The least squares method is used for smoothing time series in linear and quadratic functions. To confirm the hypothesis that the scatter plot of a given function is the most reliable, two coefficients are calculated: (a) coefficient of determination (R2) which measures the trend fit to the failure-free data and (b) the function of losses (SSE) which is the sum of squared deviations residues. The hypothesis with the function with the highest R2 value and the lowest SSE value is selected.

In the fourth stage, we determine the reliability characteristics, such as [16]:

• Mean Time Between Failures = Mean Time To Failure + Mean Time of Repair, $\left(MTBF=MTTF+MTTR\right)$,

  $$MTBF=E\left\{X_{m+1,1}+Y_{m+1,1}\right\}=\frac{1}{{\mu }_{m+1}}+\frac{1}{{\alpha }_{m+1}},$$

  (5)

  where: ${\alpha }_{m+1}>0$ is predefined.
• Probability $P$ that in the interval $\left[f,g\right]\in \left[mT,\left(m+1\right)T\right)$ there occurs at least one failure,
• Period of increased risk of failure $\left[a,b+MTTR\right]$, where: a on the assumption that the probability of the failure-free time of the bottleneck is higher than a equalling 30%, b on the assumption that the probability of the failure-free time of the bottleneck is less than b equalling 70%.

In the fifth stage, the predictive schedule is generated for the reliability characteristics using the ant colony optimisation algorithm. The procedure of generating predictive schedules is presented in Section 4. The stability of schedule k is measured using the quality robustness and solution robustness criteria. The reactive schedule k* is generated in a situation where the predictive schedule k can not absorb the impact of the disturbance. The newly generated schedule should reproduce the previous one as much as possible according to the stability criterion:

$$SR\left(k*\right)={\displaystyle \sum _{j=1}^J{\displaystyle \sum _{v_j=1}^{V_j}\left|s{t}_{j,v_j}\left(k\right)-s{t}_{j,v_j}\left(k*\right)\right|}},$$

(6)

where: $s{t}_{j,v_j}\left(k\right)$ is start time of operation $v_j$ of task j in predictive schedule k; $s{t}_{j,v_j}\left(k*\right)$ is start time of operation $v_j$ of task j in reactive schedule k*.

After the disturbance, the value of the criterion used to evaluate the predictive schedule should not be significantly influenced. The quality robustness of schedule k is assessed by calculating the difference between the makespan criterion C before and after the machine failure:

$$QR\left(k*\right)=\left|C\left(k\right)-C\left(k*\right)\right|.$$

(7)

3. Basics on Ant Colony Optimization

Modeling how ants behave and interact helps solve many optimization problems. The first ant algorithm (Ant Colony Optimization) was presented by Marco Dore in 1992 [8]. The strength of ants lies in their numbers and the cooperation. The cooperation between individuals ensures the survival of the entire community. Each ant can find the shortest path from the anthill to the food source without analyzing the visible terrain that surrounds it. Ants easily adapt to new conditions. When the road is blocked by an obstacle, they can avoid it, when the place where the food was located becomes inaccessible, they will start looking for a new source of food.

An ant that has reached the food and returns to the anthill leaves a pheromone trail behind. Depending on what signal the ant wants to send to others, the smell and the intensity of the pheromone varies. Any other ant, sensing the pheromone in its immediate neighbourhood and analyzing its intensity, is able to determine which direction to go in order to reach the food. The more ants pass along the path from food to the anthill, the stronger the smell of the pheromone will remain on that path, making it the most attractive path. The paths that are less traveled are forgotten over time, and even if they led to food, the pheromone will not be enough to guide the ants to their destination.

The structure of the ant algorithm consists of three parts: main transition rule, global update rule, local update rule.

3.1. Main Transition Rule

Each ant follows the pseudo—random—proportional rule taking the next step. The rule determines whether the ant is focused on exploration (random path selection) or exploitation (determinism) moving from point r to point s (Equation (8)).

If an ant is focused on exploration, it does not react to the pheromone trace in its environment. This makes it more likely that the ant will pass over to an area that may be more attractive. If an ant is focused on exploitation, it only goes where it senses the pheromone trail, which makes the paths from the anthill to the food more abundant in pheromone.

$$S=\{\begin{array}{cc}\arg \underset{u\in N_k(r)}{\max }\{[\tau (r,u)]\cdot {[\eta (r,u)]}^{\beta }\},& \mathrm{for}q\le q_0\hfill \\ p_k(r,s),& \mathrm{for}q>q_{0,}\hfill \end{array}$$

(8)

where: q₀—a parameter, $q_0\in \langle 0,1\rangle$, q—a random number from $\langle 0,1\rangle$, $\tau$—size of the pheromone trace on the edge u, between points r and s, $\eta =\frac{1}{\delta }$—reciprocal of the distance $\delta (r,u)$ representing heuristics, $\beta$—the parameter of the relative importance between the pheromone trace and the reciprocal of the distance, $N_k(r)$—the set of those points that ant k (located at point r) has not yet visited, $p_k(r,s)$—a random variable selected according to the formula:

$$p_k(r,s)=\{\begin{array}{cc}\frac{[\tau (r,s)]\cdot {[\eta (r,s)]}^{\beta }}{{\displaystyle \sum _{u\in N_k(r)}[\tau (r,s)]\cdot {[\eta (r,s)]}^{\beta }}},& \mathrm{for}s\in N_k(r)\hfill \\ 0,& \mathrm{for}s\notin N_k(r)\hfill \end{array}$$

(9)

If parameter $q\le q_0$, the ant is driven by the desire to exploit already discovered areas. The most attractive point s for an ant is the one to which the distance from r is the shortest, and the pheromone value on the path from r to s is the highest.

If parameter $q>q_{0,}$, the ant is driven by the desire to discover new areas—exploration. In this case point s is a random point from all available points connected to point r. Each ant exploring a new area learns about it, which, if useful, passes on to other ants by means of the pheromone left behind. Any available point can be chosen, not only the best one.

Appropriate selection of parameter q₀ results in the quality improvement of solutions generated by the algorithm. By lowering parameter q₀, ants may start to pay too much attention to explore new areas. Already discovered routes leading to the target are quickly forgotten by other ants.

On the other hand, when parameter q₀ is overestimated, it is likely that ants focus on the suboptimal solution. There is not enough ants to explore new areas in search of a new, perhaps better solution.

3.2. Local Update of the Pheromone Trace

Local updating of the pheromone trace takes place every iteration, for each ant [8]. Looking for solutions, ants move between points on the edges connecting these points. At the same time, ants update the value of the pheromone, even if they have not found the best solution. Updating the pheromone trace locally aims to reduce the value of the pheromone on each visited edge in each iteration. Updating the pheromone trace locally prevents ants from accumulating on one path only, and introduces some variation in the results obtained:

$$\tau (r,s)\leftarrow (1-\rho )\cdot \tau (r,s)+\rho ·\mathsf{\Delta }\tau (r,s),$$

(10)

where: ρ—pheromone evaporation factor $\rho \in \langle 0,1\rangle$, $\tau (r,s)$—the amount of pheromone on the way from point r do s, $\mathsf{\Delta }{\tau }_K(r,s)$—reduction of the pheromone trace:

$$\mathsf{\Delta }{\tau }_K(r,s)={\tau }_0=\frac{1}{n·L_{nn}}$$

(11)

where: n—number of possible points to visit from the point r, L_nn—minimum distance between two adjacent points.

3.3. Global Pheromone Update

The global update of the pheromone consists in updating the pheromone value at the edges of the relatively optimal path from the anthill to the food. The relatively optimal path is the best solution to the problem from the beginning of the algorithm’s operation or determined for each iteration [8]:

$$\tau (r,s)\leftarrow (1-\alpha )·\tau (r,s)+\alpha ·{\displaystyle \sum _{k=1}^m\mathsf{\Delta }{\tau }_K(r,s),}$$

(12)

where: α—pheromone evaporation rate, (1 − α) ϵ <0,1> is the glow of the pheromone, $\tau (r,s)$—the amount of pheromone on the way from point r to s, m—the number of ants that have passed from point r to point s, $\mathsf{\Delta }{\tau }_K(r,s)$—the increase of the pheromone trace is calculated from:

$$\mathsf{\Delta }{\tau }_K(r,s)=\{\begin{array}{cc}\frac{1}{L_K},& \mathrm{for}(r,s)\in L_K\hfill \\ 0,& \mathrm{for}(r,s)\notin L_K\hfill \end{array}$$

(13)

where: $(r,s)\in L_K$—edge belonging to the global best solution, K—index of the ant that discovered the best solution, $L_K$—the length of the globally best solution.

4. ACO for Scheduling Production and Maintenance Tasks

The presented predictive-reactive method uses the advantage of computer simulation by repeating three steps:

(1)

generating a population of best ants,

(2)

conversion of basic schedules (represented by ants) into predictive schedules using the Minimal Impact of Disrupted Operation on the Schedule (MIDOS) rule.

(3)

assessment of the impact of a disruption on reactive schedule/s using criteria: solution robustness (SR) and quality robustness (QR) [15].

In the following the ACO implementation for generating basic schedules (first step) in job shop scheduling problems is presented.

Pheromone and heurisitic information initialization is inspired by Boudjelida [1]. The same ant coding procedure was presented in [1] as in this article. But the ACO algorithms differ in the procedure for improving the solution and the number of parameters controlling the intensity of the pheromone and the visibility of the pheromone. The main difference is also the approach to scheduling maintenance tasks. In this paper a predictive-reactive approach is considered, the author [1] proposes a proactive-reactive approach. Both articles also consider different types of scheduling problems.

4.1. Ants Coding

Ant k is positioned on a randomly selected task j from a randomly selected vector of tasks V_k. The selected task is placed on the ant taboo list T_k. The size of the taboo list is equal to the number of tasks J (j = 1, 2, ..., J) in a scheduling problem. The neighbourhood size for each selected task is two, n = 2. In other words, the ant can select two adjacent tasks of j from list V_k in the next step.

4.2. Solution Construction

Ant k selects a task to schedule by selecting parameter q and calculating a transition probability for exploration or exploitation (1 and 2). The task sekected from the neighbourhood is inserted in the Tabu list T_k. The selected task is scheduled. Ant k moving from task r to task s reduces the value of the pheromone information on the track (r, s) (3). In the scheduling problem, L_nn is the minimum deadline for completing a task after scheduling all neighborhood tasks and n is the number of tasks in the neighborhood. The process of a task selection is repeated until vector V_k is empty. The final solution achieved by ant k is presented by the production task sequence in Tabu list T_k.

4.3. The Best Solution Selection

The best solution selection is repeated after each ant has constructed a production task sequence. The best solution obtains the minimum value of makespan criterion C. Makespan represents the end time of the last operation in a schedule. The pheromone information is updated for each track that the best ant has followed (5). L_K is the value of criterion (C_max) in the presented scheduling problem.

4.4. The Predictive Schedule Generation

Predictive schedules take the advantage of prognostic analysis in the Minimal Impact of Disrupted Operation on the Schedule (MIDOS) rule. The MIDOS rule transforms schedules to be more robust and stable in the event of disruptions. In the MIDOS rule, the job which is predicted to be disturbed is rescheduled. The most flexible operation of the job is assigned to the bottleneck. The backward and forward scheduling are applied for remaining operations [12].

4.5. The Predictive-Reactive Schedule Generation

The predictive and reactive schedules are generated for the basic schedules achieved by the ACO. Predictive schedules are generated using the MIDOS rule. The MIDOS rule modifies the basic schedules so that they are more reliable and stable when there is a risk of disruption. Following the MIDOS rule, a task that is predicted to be disrupted is analyzed for the flexibility of its operations. The most flexible operations are assigned to the critical machine. For the remaining operations, the back and forth scheduling rule applies. There are two variants of the MIDOS rule. The MIDOS I rule uses a left-shifting heuristic of operations preceding a critical operation, and a right-shifting of operations following a critical operation. In the MIDOS II rule, forward and backward scheduling depends on the availability of parallel machines. Operations are scheduled appropriately on the earliest available parallel machines for the upstream and downstream operations of the critical operation, respectively.

After the disturbance, two rescheduling procedures are applied for disrupted operations: Right Shifting (RS) and Reschedule on Parallel Machines (RPM). SR assesses how much the current schedule differs from the previously adopted one. QR assesses how much the current value of the quality indicator differs from the value of the previously adopted schedule.

4.6. Update of the Pheromone Trace for Makespan Optimisation

The formula for updating the pheromone trace locally is modified in order to perform makespan optimisation. The reduction of the pheromone trace is calculated using.

$$\mathsf{\Delta }{\tau }_K(r,s)={\tau }_0=\frac{1}{n·C\left(nn\right)}$$

(14)

where: C(nn) is the end date of the last task in the schedule (makespan):

$$C\left(nn\right)=\max {\left[t{z}_{Vj}^{}\right]}^{}$$

(15)

$t{z}_{v_j}$ is the completion time of operation $v_j$ of job j, $v_j=1,\dots ,V_j$, $j=1,\dots ,J$.

The increase of the pheromone trace is calculated from

$$\mathsf{\Delta }{\tau }_{K^{**}}(r,s)=\{\begin{array}{cc}\frac{1}{C\left(nn\right)},& \mathrm{for}(r,s)\in L_{K^{**}}\hfill \\ 0,& \mathrm{for}(r,s)\notin L_{K^{**}}\hfill \end{array}$$

(16)

where: $(r,s)\in L_{K^{**}}$—job sequence belonging to the global best schedule, K**—index of the ant that discovered the best schedule.

The steps of the ACO are presented in Figure 2. The next Section presents a job shop (JS) scheduling problem for experimental study to better understood the steps of the ACO.

5. Predictive-Reactive Scheduling Case Study

This section introduces various ACO parameter data sets to verify the performance of ACO and MIDOS I or MIDOS II for predictive scheduling in various job shop sizes.

Job shop scheduling problems are investigated to fine-tune the parameters where 9 jobs have to be performed on 8 machines (9 × 8) and 11 jobs have to be performed on 10 machines (11 × 10). The first machine is the most heavily loaded. The failure-free time of the bottleneck MTTF equals 66. The repair time of the bottleneck MTTR equals 6. The increased probability of the bottleneck failure occurs in time horizon [a, b + MTTR] where: a = 60 and b = 72. The objective is to find an approach which is able to generate stable and robust schedules in the event of the bottleneck failure. The objective is to achieve a robust and stable schedule for the problem, C_max(k)→ min (15).

Computer simulation of the Ant Colony Optimisation is run for the parameter of the relative importance between the pheromone trace and the reciprocal of the distance $\beta =1$; pheromone evaporation factor $\alpha =\rho =\left\{0.2,0.4,0.6,0.8\right\};$ number of ants, K = {10, 15, 20, 25}; number of iterations, E = {10, 20, 30, 40} and parameter q₀ which decides abot exploration or exploatation selection by an ant, $q_0=\left\{0.3,0.4,0.5,0.6\right\}.$ The ACO is run 10 times for each set of input parameters {ρ, K, E, q₀}.

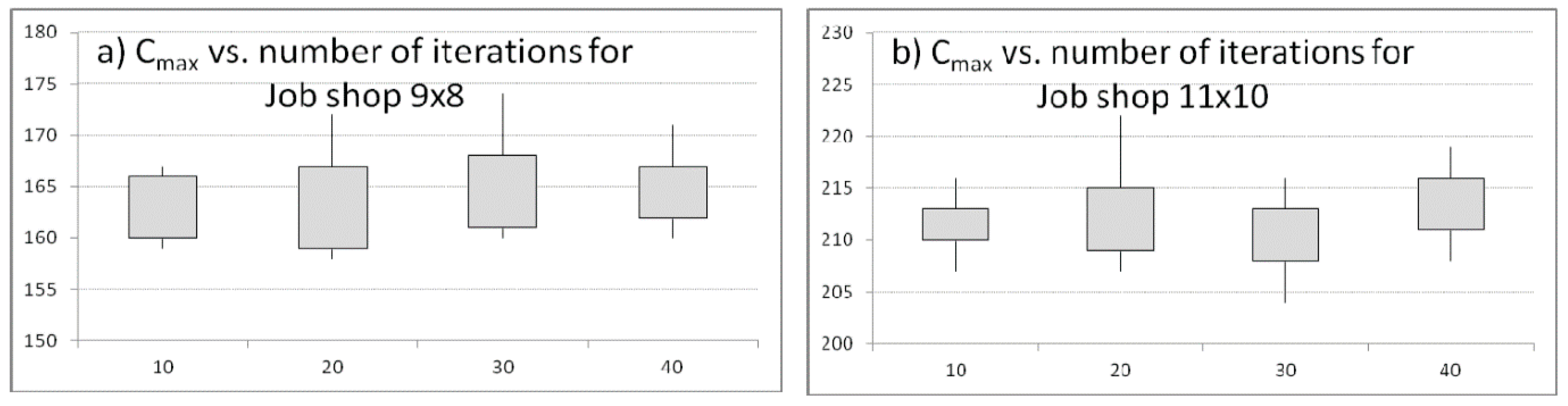
First, the influence of the number of iterations, E = {10, 20, 30, 40} over the quality of basic schedules generation for single criterion problem is investigated and for unchanging pheromone evaporation factor $\alpha =\rho =\left\{0.6\right\}$ and number of ants K = {10}. The parameter q₀ is equal to 0.5 to get an equal chance of choosing to explore and exploit by ants. By observing the first and third quartiles of C_max and the best schedules achieved the following conclusion can be drawn that a larger number of iteration is, the higher chances of achieving a better solution are in scheduling problem (11 × 10) (Figure 3b). By observing the first and third quartiles of C_max and the best schedules achieved for the scheduling problem (9 × 8), the opposite phenomenon can be observed. The smaller the number of iterations is, the greater the chances of achieving a better solution are (Figure 3a).

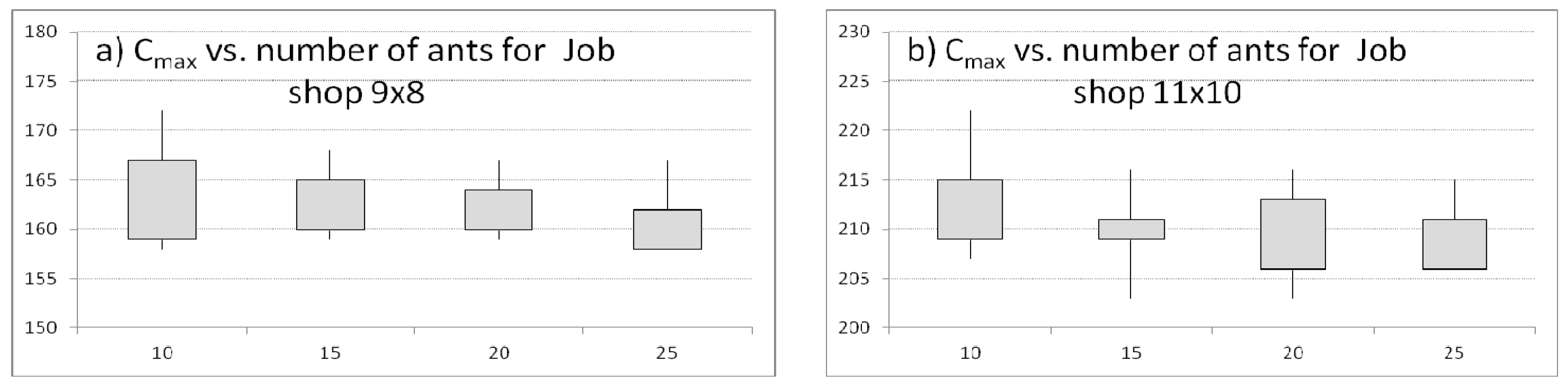
Next, the influence of the number of ants, K = {10, 15, 20, 25} over the quality of basic schedules generation for single criterion problem is investigated for unchanging pheromone evaporation factor $\alpha =\rho =\left\{0.6\right\}$, number of iterations E = {20}, parameter q₀ is equal to 0.5. Observing the results of the achieved value of the makespan criterion for the basic schedules (Figure 4), the following conclusion can be drawn that a larger the ant population is, the greater the chances of achieving a better solution are. This phenomenon is noticed for both sizes of scheduling problems (9 × 8) and (11 × 10).

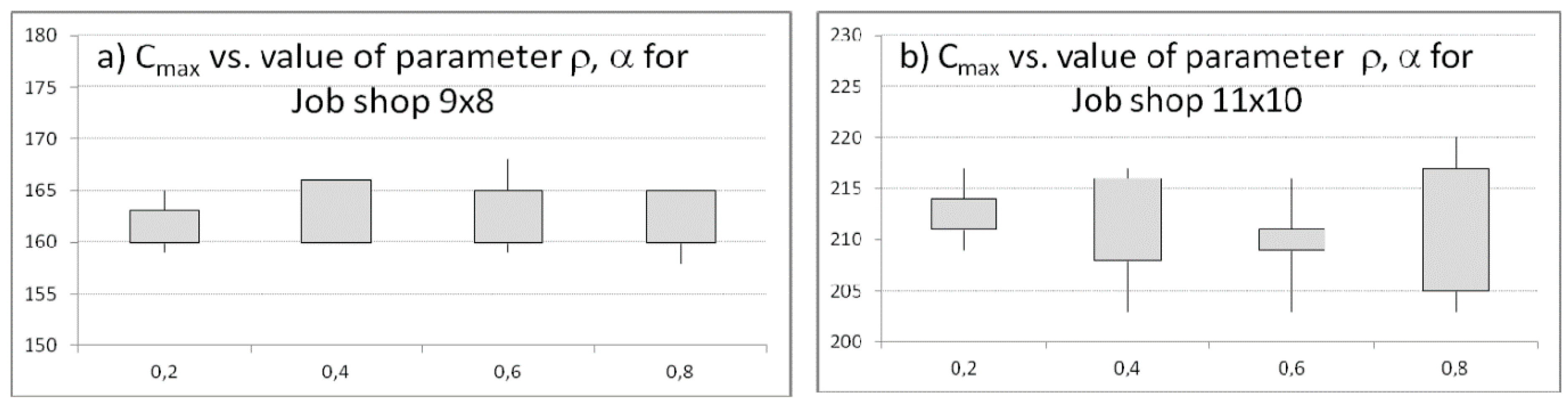
Then, the simulations are continued for the number of ants, K = {15}, iteration size, E = {20}, parameter q₀ = 0.5 and changing values of pheromone evaporation factor $\alpha =\rho =\left\{0.2,0.4,0.6,0.8\right\}.$ Observing average values of C_max and the best schedules achieved (Figure 5) the following conclusion can be drawn that the higher values of pheromone evaporation factors $\alpha =\rho$ are, the higer chances of achieving a better solution are. Algthough the average quality of population does not increase with the parameter values, better solutions are achieved for scheduling problem (9 × 8). The best scheduel is achieved for C_max equals 152 for scheduling problem (9 × 8), for the pheromone evaporation factor $\alpha =\rho$ = 0.8 (Figure 5a). The best scheduel is achieved for C_max equals 203 for scheduling problem (11 × 10), for the pheromone evaporation factor $\alpha =\rho$ = {0.4, 0.6, 0.8} (Figure 5b).

.

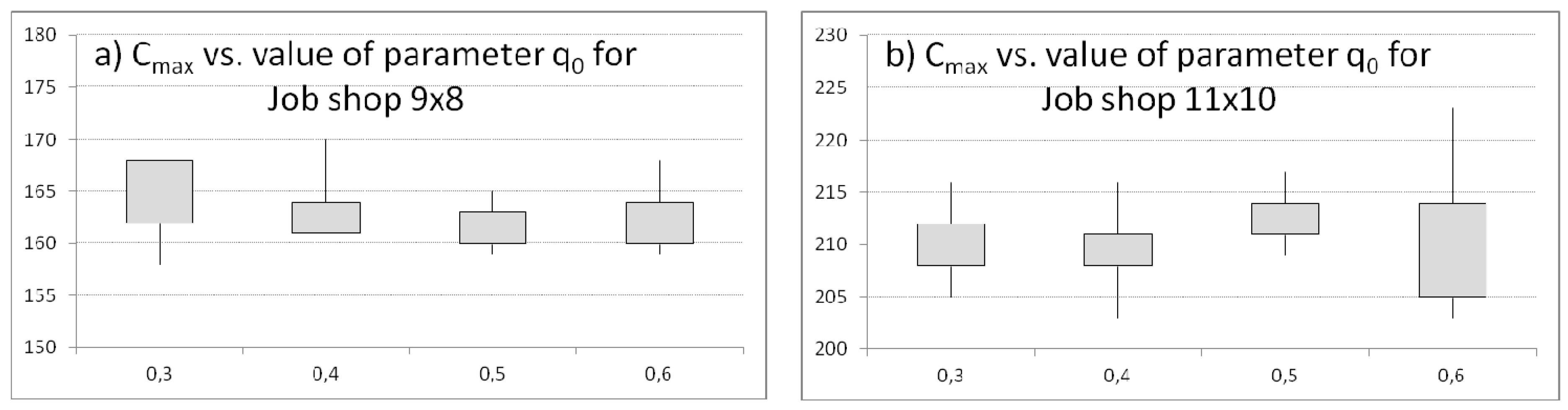
Then, the simulations are continued for the number of ants, K = {15}, iteration size, E = {20}, parameter $\alpha =\rho =\left\{0.2\right\}$ and changing values of parameter q₀ which decides abot exploration or exploatation selection by an ant, $q_0=\left\{0.3,0.4,0.5,0.6\right\}.$ Observing average values of C_max and the best schedules achieved (Figure 6) the following conclusion can be drawn that the lower values of parameter q₀ are, the higer chances of achieving a better solution are. The average quality of population does not increase with the parameter values for scheduling problems (9 × 8) and (11 × 10) (Figure 6a,b).

Next, the performance of the ACO and MIDOS I or MIDOS II is verified for predictive scheduling for different datasets of job shops. The predictive and reactive schedules are generated for the basic schedule achieved by the ACO for each set of input parameters {ρ, K, E, q₀}. Predictive schedules are generated using rules: the MIDOS I or MIDOS II.

For example, in the first simulation, the predictive and reactive schedules were generated for the basic schedule obtained by the ACO and MIDOS I for the sequence of tasks: {7 8 6 9 5 2 4 3 1} for scheduling problem (9 × 8) and {10 8 7 6 11 9 3 4 1 5 2} for scheduling problem (11 × 10) (

Table 1. The schedules generated using the MIDOS I and MIROS for the best basic schedules achieved by the ACO and input parameters {ρ, K, E, q₀}.

	Scheduling Problem (9 × 8)					Scheduling Problem (11 × 10)
{E, K, ρ, q0}	Cmax of Basic Schedule	Cmax of Predictive Schedule	Cmax of Reactive Schedule	SR	QR	Cmax of Basic Schedule	Cmax of Predictive Schedule	Cmax of Reactive Schedule	SR	QR
{10, 10, 0.6, 0.5}	159	141	141	48	0	207	177	177	0	0
{20, 10, 0.6, 0.5}	158	138	138	100	0	207	169	169	41	0
{30, 10, 0.6, 0.5}	160	144	144	75	0	204	168	168	97	0
{40, 10, 0.6, 0.5}	160	134	134	4	0	208	166	166	9	0
{20, 15, 0.6, 0.5}	159	140	140	2	0	207	175	175	8	0
{20, 20, 0.6, 0.5}	159	122	122	57	0	203	167	167	116	0
{20, 25, 0.6, 0.5}	158	136	136	2	0	206	174	174	14	0
{20, 15, 0.4, 0.5}	160	138	138	4	0	209	172	172	86	0
{20, 15, 0.6, 0.5}	159	130	130	61	0	203	165	165	156	0
{20, 15, 0.8, 0.5}	158	140	140	2	0	203	165	165	4	0
{20, 15, 0.2, 0.3}	158	147	147	23	0	205	174	174	12	0
{20, 15, 0.2, 0.4}	161	141	141	45	0	203	172	172	0	0
{20, 15, 0.2, 0.6}	159	140	140	2	0	203	174	174	4	0
average				32.69					42.077

). The makespan function of the predictive schedule generated using the MIDOS I was C_max(1) = 141. The makespan function of the reactive schedule generated using the MIROS was also C_max(1*) = 141. The solution robustness was SR(1) = 48 and the quality robustness was QR(1) = 0 for the first scheduling problem (9 × 8). Quality of the task sequences achieved for the remaining ants for scheduling problems (9 × 8) and (11 × 10) is described in Table 1. Also, computer simulations were run for generating predictive schedules using the MIDOS II. Quality of the predictive and reactive schedules for scheduling problems (9 × 8) and (11 × 10) is described in

Table 2. The schedules generated using the MIDOS II and MIROS for the best basic schedules achieved by the ACO and input parameters {ρ, K, E, q₀}.

	Scheduling Problem (9 × 8)					Scheduling Problem (11 × 10)
{E, K, ρ, q0}	Cmax of Basic Schedule	Cmax of Predictive Schedule	Cmax of Reactive Schedule	SR	QR	Cmax of Basic Schedule	Cmax of Predictive Schedule	Cmax of Reactive Schedule	SR	QR
{10, 10, 0.6, 0.5}	159	141	141	47	0	207	177	177	0	0
{20, 10, 0.6, 0.5}	158	138	138	100	0	207	169	169	6	0
{30, 10, 0.6, 0.5}	160	144	144	62	0	204	174	174	0	0
{40, 10, 0.6, 0.5}	160	134	134	4	0	208	166	166	9	0
{20, 15, 0.6, 0.5}	159	137	137	14	0	207	175	175	2	0
{20, 20, 0.6, 0.5}	159	122	122	56	0	203	167	167	182	0
{20, 25, 0.6, 0.5}	158	136	136	6	0	206	173	173	3	0
{20, 15, 0.4, 0.5}	159	138	138	4	0	209	172	172	13	0
{20, 15, 0.6, 0.5}	160	130	130	19	0	203	165	165	131	0
{20, 15, 0.8, 0.5}	158	139	139	47	0	203	165	165	4	0
{20, 15, 0.2, 0.3}	158	141	141	9	0	205	174	174	3	0
{20, 15, 0.2, 0.4}	161	141	141	45	0	203	172	172	0	0
{20, 15, 0.2, 0.6}	159	140	140	2	0	203	189	189	4	0
average				31.92					27.46

. The average solution robustness of predictive schedules generated using the ACO and MIDOS I was 32.69 for scheduling problem (9 × 8) and 42.07 for scheduling problem (11 × 10) (Table 1). The average solution robustness of predictive schedules generated using the ACO and MIDOS II was 31.92 for scheduling problem (9 × 8) and 27.46 for scheduling problem (11 × 10) (Table 2). 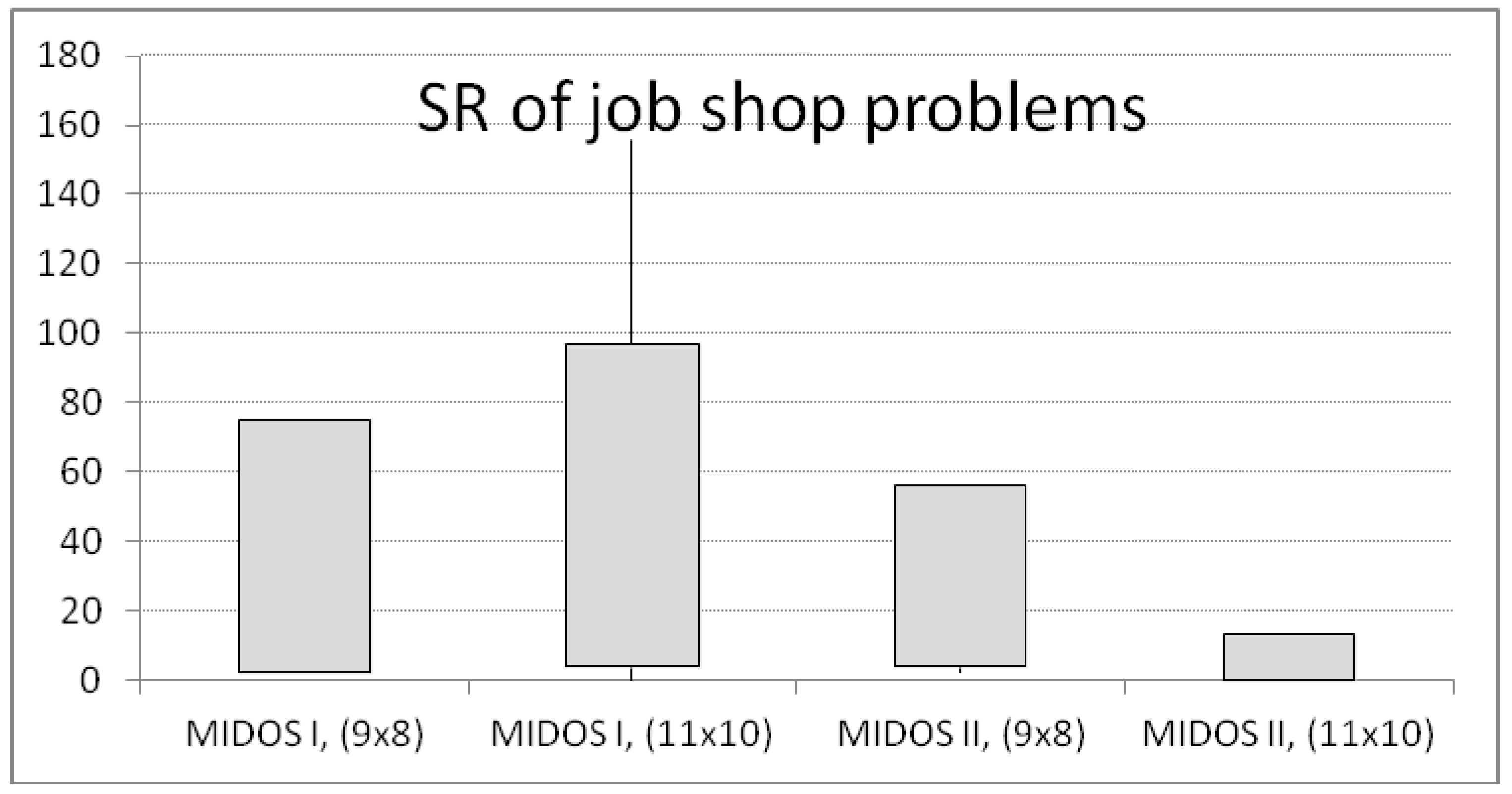All achieved schedules are robust taking into account the quality robustness criterion for both scheduling problems (9 × 8) (Table 1) and (11 × 10) (Table 2). By analyzing the minimum, maximum, first quantile, third quantile and the mean values of solution and quality robustness, the following conclusion can be drawn: the MIDOS II heuristic is better to apply to the basic schedules generated by ACO (Figure 7).

6. Conclusions

In the paper, the predictive-reactive (proactive with prediction) method for joint scheduling of production and maintenance tasks was presented. The presented method can improve the work of maintenance team. Machine failure causes great losses as a result of downtime, the need to replace parts or even modiffication of the production plan to take into account the fact that the given machine or device need to be repaired for a longer period. The analysis of historical data on the machine uptimes allowes one to plan the replacement of elements, machine inspection and may contribute to extending the machine uptime.

The original value of the paper was the development of the method of a basic schedule generation with the application of the Ant Colony Optimisation (ACO). A predictive schedule was built by planning the technical inspection of the machine at time of the predicted failure time. Flexible operations are allocated to the machine during an increased risk of failure. Next, the influence of the disturbance on the predictive schedule using robustness measures was examined.

In the future, the presented method for generating predictive schedules will be compared with the genetic algorithm, immune and clonal selection algorithms. ACO algorithms are alternative methods of searching the solution space for scheduling problems. The presented algorithm may, however, contribute to the development of a method that reflects the operation of the production system and the nature of disturbances, and improves the system operation.