Abstract
Recently, the study of analog optical computing raised renewed interest due to its natural advantages of parallel, high speed and low energy consumption over conventional digital counterpart, particularly in applications of big data and high-throughput image processing. The emergence of metamaterials or metasurfaces in the last decades offered unprecedented opportunities to arbitrarily manipulate the light waves within subwavelength scale. Metamaterials and metasurfaces with freely controlled optical properties have accelerated the progress of wave-based analog computing and are emerging as a practical, easy-integration platform for optical analog computing. In this review, the recent progress of metamaterial-based spatial analog optical computing is briefly reviewed. We first survey the implementation of classical mathematical operations followed by two fundamental approaches (metasurface approach and Green’s function approach). Then, we discuss recent developments based on different physical mechanisms and the classical optical simulating of quantum algorithms are investigated, which may lead to a new way for high-efficiency signal processing by exploiting quantum behaviors. The challenges and future opportunities in the booming research field are discussed.
1. Introduction
Exploring novel approaches to improve the computational capacity and efficiency is a goal that humans have been continuously pursuing. Early computers are constructed mechanically [1] or electronically [2,3,4] on the principle of analog, aiming to perform mathematical operations. Despite the impressive success achieved in the fields of weather prediction, aerospace and nuclear industry, these machines faced significant obstacles of slow response and large size [5]. In the 20th century, digital computing emerged with a rapid development of semiconductor technology and large-scale integrated circuits. It began to gradually substitute for their conventional analogue counterparts on the strength of easy programmability, high speed and flexibility. However, in solving specialized computational tasks, such as imaging-processing and edge detection, digital computers are often inefficient and hindered by high-power consumptions. As Moore’s law is approaching its physical limitations, the long-abandoned analog approach as an alternative paradigm has attracted renewed attention for its potential abilities to overcome these shortcomings [6,7,8].
Analog optical computing offers unique advantages of real-time, power-efficient, high-throughput imaging processing abilities originating from the wave-based nature [7,9,10,11]. Compared with standard digital processes, all-optical analog approaches do not refer to photoelectric converters but directly manipulate optical signals both temporally and spatially [12]. In the temporal domain, high-speed pulse waveform modulation enables numerous applications, including analog computing [13,14,15,16,17,18,19], differential equations solving [19,20,21,22,23], optical memory [24,25], photonic neural networks [26,27] and complex nonlinear system simulation [28,29,30]. In the spatial domain, the input functions are indicated by the spatial wavefronts which will be mathematically transformed with pre-designed optical systems. Therefore, this computing platform has intrinsic parallel characteristic, showing great potential for accelerating the processing of megalo-capacity datasets and images [31,32,33].
In addition to classical mathematical operations, researchers have also extended the concept of analog computing to quantum algorithms that promise an exponential speedup that is far beyond classical ones in solving problems of large integer factorization (Shor’s algorithm) [34] and combinatorial optimization (Grover’s algorithm) [35,36]. Some fundamental properties of quantum computing, including superposition principle and interference phenomena, are the essence of wave nature, which are not exclusive to quantum mechanical but are common to classical waves. By encoding quantum bit (qubits) into different degrees of freedom for the electromagnetic field (e.g., frequency, polarization, orbital angular momentum, space and time bins), many quantum computations can be efficiently simulated in optics [37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68].
However, traditional analog optical computing requires bulky optical components, such as diffractive lenses and spatial filters, which are inconvenient for miniaturization and integration of modern ultracompact optics. Empowered by recent development of nanofabrication technologies, metamaterial [69,70,71,72,73,74,75,76,77,78,79] or its two-dimensional counterpart, metasurface [80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99], is able to tailor subwavelength building blocks on the scales of micro- or nanometers, providing unprecedented flexibility to arbitrarily control the electromagnetic waves that are unattainable in the nature. Owning to their powerful wave manipulation abilities and deeply subwavelength characteristics, those meta-structures can significantly reduce the complexity and shrink the size of computing systems, making it possible to realize chip-level all-optical information processing systems [100,101].
In this review, we will focus on recent developments in both the physics and applications of the spatial analog optical computing. The paper is organized in four parts as described below. In Section 2 we overview the basic concept of computational metamaterials and the general principles for design and implementation for classical mathematical operations including integration, differentiation and integration equation solution. In Section 3 we introduce a type of wave-based signal processors that can mimic quantum mechanism with classical optical waves. These studies show that the quantum algorithms like Grover’s search algorithm and Deutsch-Jozsa algorithm can be simulated by cascading metamaterial functional blocks. In the last section, we conclude with an overview of computational metamaterials based on different mechanisms, the main challenges and the opportunities in the field for future research.
2. Computational Metamaterials
In 2014, Silva et al. [102] proposed a concept of “computational metamaterials” by locally tailoring the electromagnetic parameters of the metamaterials, the elaborately designed meta-structures can reshape the spatial profile of the input signal to perform mathematical operations including spatial differentiation, integration and convolution. The basic idea of computational metamaterials is schematically illustrated in Figure 1a as an example. The stacked multi-layered structure is functional as a first-order differentiator, for arbitrary input wavefronts f1(y) and f2(y), the corresponding output profiles are proportional to df1(y)/dy and df2(y)/dy, respectively. Compared with conventional analog signal processors and Fourier optics system, metamaterial-based approach provides more flexible mechanism for manipulation, more integrable volume and subwavelength thickness.
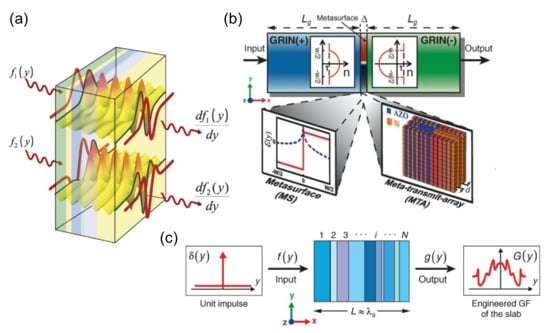
Figure 1.
(a) The conceptual sketch of computational metamaterials; schematic of the general protocol for (b) MS approach; and (c) GF approach; adapted with permission from [102], AAAS, 2014.
In general, there are two major protocols to realize metamaterial-based analog computing: metasurface (MS) approach and Green’s function (GF) approach. Similar to the classical 4f systems, the MS approach is based on spatial Fourier transformation, with a single-layered metasurface or multi-layered meta-transmit(reflect)-array to realize the desired transfer function, sandwiched between two subblocks performing the Fourier and inverse Fourier transform (see Figure 1b). In the GF approach, by optimizing the transmitted (reflected) response of the metamaterial slabs it can also act as certain mathematical operations without involving additional Fourier lenses. The former has the advantage of implementation simplicity and the latter has a more compact size. In the following sections, we will briefly review the design principle and recent progress pioneered by these two approaches.
2.1. Metasurface Approach
Initially, let us consider a pure mathematical transformation of convolution operation in Fourier domain. For an given input function f(x, y), the corresponding output function g(x, y) is the result of a desired mathematical operator which is indicated by the Green’s function h(x, y), x and y denote the spatial coordinates on the two-dimensional (2D) plane. By applying the linear convolution operation, g(x, y) can be described by
Based on convolution theorem, the Fourier transform of g(x, y) is equivalent to the multiplication of functions f and h in the Fourier domain:
where () represents the (inverse) Fourier transform, abbreviated (I)FT. kx and ky are frequency variables in the spatial Fourier space, is spatial FT of the transfer function h(x, y). It is actually easy to implement Equation (2) in the practical systems by simulating the input (output) function with a classical electric field Ein(x, y) (Eout(x, y)), in this case, the spatial variables (x, y) can play the role of (kx, ky). In wave-based computing system, Equation (2) can be rewritten as:
According to Equation (3), the optical computing system should comprise of three cascade metamaterial functional subblocks which are designed to accomplish FT, H(x, y) and IFT sequentially. In order to realize the FT subblock, an analog of traditional lenses is employed since the converging lenses can achieve 2D Fourier transform in the focal plane. In [102], a graded-index (GRIN) dielectric slab with a parabolic variation of permittivity is introduced to realize FT operator [103,104]. Besides of GRIN medium, meta-lens can also be applied to perform FT operator [105,106,107,108,109,110]. It worth nothing that, although we can define a GRIN(−) subblock to perform IFT in which the effective constitutive parameters should satisfy , it is not feasible for natural materials or practical for metamaterials to realize simultaneously negative permeability and permittivity. Therefore, as an alternative method, we can use additional FT subblock to approximate output profile according to the relation:
In this way, the electric field distribution is proportionate to the mirror image of the desired output function. Based on above discussion, the fundamental components of MS approach are represented in Figure 1b. Next, we will go to the details of how to design transfer functions when implementing different mathematical operations, such as differentiation, integration and convolution.
Firstly, for simplicity, we discuss the cases of one-dimensional nth derivation operators. Based on derivative property of the Fourier transform, , according to Equation (3), the expression is the required transfer function, where or . It means that the amplitude and phase of impinging optical wave will be modulated by when propagating through the transfer function subblock (suppose the thickness of transfer function subblock is ), where , with free space wavelength , and are relative permittivity and permeability of transfer function subblock. For the cases of integration and convolution operations, the transfer functions become to and , respectively. In addition, considering the limitation of lateral dimension, the transfer function H(y) has to be normalized to ensure the energy conservation (without gain materials) and keep the reflection (transmission) coefficient blow unity. Now, the question is, how to find a proper spatially-variant meta-structure that fulfills the required electromagnetic response. Here, we divide recent achievements of the MS approach into two categories according to the construction type.
2.1.1. Reflective Configurations of MS Approach
Plasmonic metasurfaces [83,111,112,113,114,115,116,117,118,119] promise the abilities to tailor the local phase and amplitude by exploiting the strong light-matter interactions due to the plasmonic resonances. In 2015, an inhomogeneous plasmonic metasurface approach, which consists of three-layer sandwich structure was introduced to optical analog computing for the first time by Anders Pors et al. [120]. A periodic arrangement of gold nanobrick arrays is on the top layer, an optically thick gold ground and subwavelength dielectric spacer is used to excite gap-surface plasmon (see Figure 2a). By properly designing the position and size of each nanobrick, this metal-insulator-metal structure can perform integration at visible wavelength with high efficiency. Similar to this work, in 2017, Chen et al. [121] used a dendritic structure instead of nanobrick to implement first-order differential operation. By varying the geometrical shapes, the desired reflection coefficients could be achieved (see Figure 2c). A different approach for reflectarray configuration is dielectric metasurface, which is composed of high refractive index dielectric nanoparticles supporting both magnetic and electric dipole-like resonances based on Mie theory. This approach can significantly reduce the ohmic losses caused by metallic structures in the optical spectrum. Motivate by this, Ata Chizari et al. [122] propose a dielectric meta-reflect-array where silicon nanobricks are placed on the silica spacer and silver substrate to manipulate amplitude and phase of reflected cross-polarized field by varying the lengths of nanobricks (see Figure 2b).
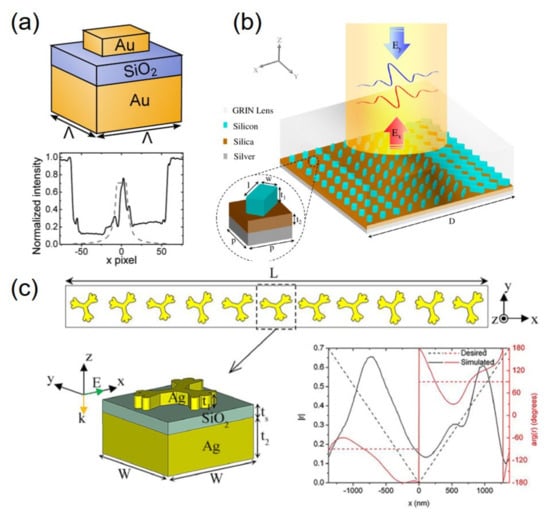
Figure 2.
(a) The unit cell of plasmonic metasurfaces consist of gold nanobrick atop a dielectric spacer and thick metal ground; adapted with permission from [120], ACS Publications, 2015. (b) Schematic representation of dielectric meta-reflect-array for the first-order derivation; adapted with permission from [122] © The Optical Society. (c) Top: eleven silver dendritic structure units with different parameters; left: the unit cell of plasmonic metasurfaces with dendritic structure instead of nanobrick; right: comparison of the theoretical and simulated results of the position-dependent reflection coefficient. Adapted with permission from [121] © The Optical Society.
2.1.2. Transmittive Configurations of MS Approach
Compared with reflective configurations, the optical computing systems with transmission mode are easily applied to optical devices, however most of them are facing the challenges of low transmission efficiency. In 2015, Amin Khavasi et al. [32] proposed a concept of “metalines” in which three symmetrically stacked graphene-based building blocks were utilized to perform differentiation and integration in the transmitted way (see Figure 3a). By manipulating plasmons surface wave via surface conductivity variation of the graphene, the amplitudes and phases of the transmitted wave could be controlled completely. While it was a proof-of-principle study, it opened up an avenue of the graphene-based structure which are designed to implement the mathematical operators with advantages of dynamic tunable and high-compact characteristics. Then, in 2016, Zhang et al. [123] introduced a more practical and flexible computing metamaterial system based on effective medium theory by drilling sub-wavelength hole-arrays with different radiuses, the desired effective permittivity distribution can be obtained to realized functional subblocks (see Figure 3b). To further improve the parallel processing abilities, a multi-way analog computing device combined with additional transformation optical subblock is investigated [124]. Two identical signals on the same input port propagate along opposite directions and perform first- and second-order differentiators simultaneously. Very recently, a one-dimensional high-contrast transmitarray (HCTA) metasurface was experimentally demonstrated by Zhang et al. [100] to realize Fourier transform and spatial differentiation with feature size of 140 nm. The on-chip meta-system provides low insertion loss and broad operating bands by tailoring widths and lengths of the rectangular slot arrays (see Figure 3c,d). Inspired by radial Hilbert transform filter, Huo et al. [125] proposed a spin-dependent dielectric metasurface, which can perform a spiral phase filtering operation in which a spiral phase profile is imprinted to the input wave. The tricky part in this proposal is to utilize the phase difference in opposite azimuth leading to a destructive interference when processing convolution transformation. The authors demonstrate that spiral phase filtering operation is equivalent to the 2D spatial differentiation of incident light field (see Figure 3e).
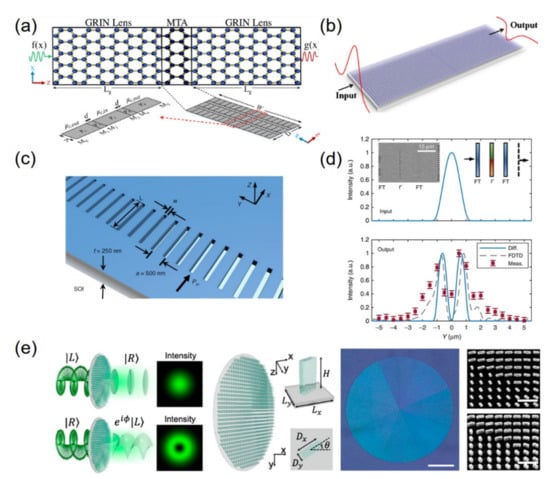
Figure 3.
(a) The sketch of graphene-based metaline; adapted with permission from [32] © The Optical Society. (b) Dielectric metamaterial with drilling hole arrays to solving second-order differential equation; adapted with permission from [123], IOP Publishing, 2016. (c) Schematic of on-chip 1D high-contrast transmitarray, the rectangular slot arrays are etched on the silicon-on-insulator (SOI) substrate with the period of 500 nm. (d) Comparison of the input (top) and output (bottom) intensity profile of an on-chip differentiator; adapted with permission from [100], Springer Nature, 2019. (e) Left: schematic of the concept for spin-dependent function control; middle: schematic of the dielectric metasurface spatial filter; right: photograph of the fabricated metasurface. Scale bar: 500 μm. Insets: scanning electron micrographs showing the top and oblique view of TiO2 nanopillar array. Scale bar: 1 μm. Adapted with permission from [125], ACS Publications, 2020.
2.2. Green’s Function Approach
In the original GF approach proposed by Silva et al. [102], the transmission or reflection coefficient of multi-layered stacked slabs with transversely homogenous and longitudinally inhomogeneous are engineered to approximate the desired transfer function without getting into the Fourier domain. Since additional Fourier lenses are not required, the GF approach has advantages over the MS approach with a more compact size and an easier fabrication process. The basic idea of the GF approach is to find the proper transmittance coefficient of the multi-layered slab to fit the desired GF kernel within , in which ky is the transverse wavevector, and k0 is the free space wavevector. A fast synthesis algorithm is adopted to minimize the difference between and , which can be expressed as:
where M is the number of layers, wr and wi are weight coefficients for real and imaginary parts. The optimized transmission spectrum is in good agreement with the desired GF which correspond to 2th spatial derivative provided that M = 10, wr = 2, wi = 1, and relative permeability of each layer keep at unity.
In recent years, extensive studies with resonant or non-resonant structures were proposed with the GF approach, such as multi-layered slabs [126,127], photonic crystal [128], diffraction gratings [15,31,129,130,131,132,133,134], surface plasmon-based devices [130,135,136,137], dielectric metasurfaces [138,139,140,141,142,143], nonlocal metasurfaces [144,145], random medium [146] and inverse-designed meta-structures [147]. Moreover, various physical mechanisms including Brewster effect [148], Goos-Hänchen effect [149] and spin hall effect [150] can also be applied to perform optical analog computing. Therefore, the GF approach can be generalized to a fundamental protocol for designing the particular transfer function (defined as ) which should be approximately proportional to the desired mathematical operations.
2.2.1. Diffraction Gratings
Diffraction gratings have been widely used in processing optical signals with integration or differentiation operations, most of them are based on Fano resonance or guided-mode resonance in which the reflection or transmission coefficient can approximate the transfer function in the vicinity of the resonance. In [131], Victor A. Soifer et al. experimentally demonstrate that a guided-mode resonant grating with period TiO2 slab waveguide on a quartz substrate can perform spatial differentiation with an obliquely incident beam. As shown in Figure 4a, the transverse profile of the incident wave Pinc(x, y) is formed by zeroth order diffraction to the transmitted profile of ptr(x, y). Figure 4b is the scanning electron microscopy image of the designed diffraction grating. A similar strategy is to adopt high-contrast grating, as illustrated in Figure 4c [132]. By observing the amplitude and phase (indicated by red dot and blue line in Figure 4d) of the spatial spectral transfer function evolving with different incident angle, it is found that the transfer function has a phase variation of around a certain angle . Within slight deviation of , the transfer function satisfies first-order differentiation. In a recent work, Alexios Parthenopoulos et al. [134] propose a novel dielectric subwavelength grating by employing high quality suspended Si3N4 films, where the first- and second-order spatial differentiation can be implemented at oblique and normal incidence, respectively. The even guided mode is excited with normal incident wavefront, and change dramatically to the odd guided mode as increasing the incidence angle. In addition to these dielectric gratings, metallic gratings are also investigated and experimentally demonstrated to realize analogue spatial differentiators. It is well-known that when a metallic grating is illuminated by an incident wave, at certain incident angle, the surface plasmon resonance will be excited. Yang et al. [133] found that by adjusting the geometric parameters of the subwavelength gratings, in the vicinity of surface plasmon resonance, the transfer function can be tailored to a linear function which satisfies the requirements of first-order differentiation.
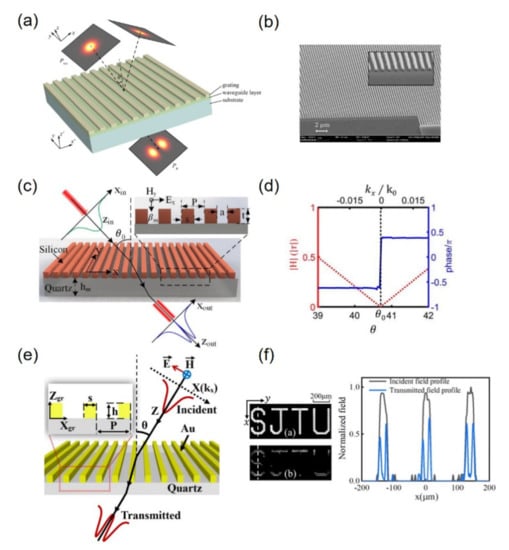
Figure 4.
(a) Schematic and (b) photograph of guided-mode resonant diffraction grating for first-order differentiation; adapted with permission from [131] © The Optical Society. (c) The schematic and (d) spatial spectral transfer function of the optical spatial differentiator based on subwavelength high-contrast gratings. Adapted with permission from [132], AIP Publishing, 2018. (e) Schematic of the first-order differentiator based on subwavelength metallic gratings. (f) The experimental results for the incident and transmitted images (left) and the normalized field profiles at the position of white dashed line. Adapted with permission from [133] © The Optical Society.
2.2.2. Plasmonic Structure
By exploiting the critical coupling condition of the surface plasmon polaritons (SPPs), many plasmonic analog computing devices have been realized. In 2017, Zhu et al. [135] introduced a classical Kretschmann prism configuration to realize the plasmonic spatial differentiation where the oblique incident wave (transverse profile of Sin(kx)) with TM-polarized are used to excite the surface plasmon between glass substrate and silver film, kx is the transverse component of the wavevector (see Figure 5a). In this case, the amplitude of reflected wave (transverse profile of Sout(kx)) is the result of the interference between the direct reflection and the leakage of SPPs. The spatial spectral transfer function around kx = 0 can be expressed as:
where is the phase change related to the process of the direct reflection at the glass–metal interface. and , where and are the radiative leakage rate of the SPP and the intrinsic material loss rate, respectively. When the critical coupling condition is satisfied (), Equation (6) can be simplified and approximated as , which corresponds to the first-order differentiation.
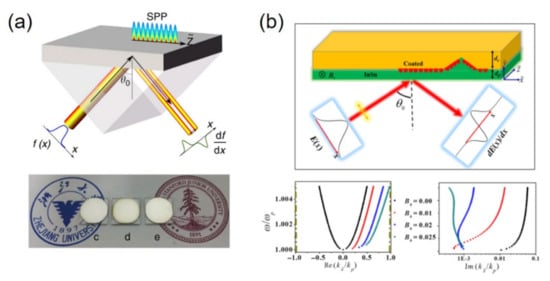
Figure 5.
(a) Top: schematic of the surface-plasmon-based scheme to perform spatial differentiation with the Kretschmann configuration. Bottom: photograph of the three samples with different thicknesses; adapted with permission from [135], Springer Nature, 2017. (b) Top: schematic of the backscattering-immune first-order spatial differentiator based on nonreciprocal plasmonic platform. Bottom: the simulated results of real and imaginary parts of the eigenvector with different external magnetic fields. Adapted with permission from [137], APS, 2019.
However, the SPPs is sensitive to the defect of the interface. As such, to further improve its robustness, Zhang et al. [137] proposed a unidirectional SPPs-based spatial differentiator which can avoid backscattering by applying an external static magnetic field (shown in Figure 5b). The magnetic field breaks the time-reversal symmetry and makes the system have a nonreciprocal property, which is critical to the unidirectional SPPs leaky mode. As shown in the bottom of Figure 5b, when applying external magnetic field, the SPPs surface mode changes from bidirectional to unidirectional. To verify the practicability when facing real-time image processing, the impact of plasmonic spatial differentiation under time-variant optical signals is analyzed by Zhang et al. [136]. By adopting similar setup described in [135], the reflected field profile with central frequency in the spatiotemporal coordinate can be expressed as:
where and are two constants where and , is phase change of direct reflection without excitation of SPP, , , , are the incident angle, the leakage rate, the group velocity of the SPP, and the speed of light in the prism at central frequency , respectively. The second term of Equation (7) indicates that the output field profile should consider the change rate of input time-modulated signals. As a conclusion, the authors estimate that the processing speed of plasmonic differentiator is up to the maximum of 1013 frame/s which is restricted by the time of establishing the SPP leaky radiation.
2.2.3. Two-Dimensional Dielectric Metasurfaces
The above discussions are mainly focused on 1D mathematical operations. However, anisotropic edge detection is not sufficient for real-time, high-throughput 2D image processing since multiple measurements are required. In this part, metasurfaces with symmetrically distributed dielectric nano-resonators are briefly reviewed to illustrate their capacity to reveal all information from the boundaries of objects. The basic physical mechanism of these 2D dielectric metasurfaces originates from the modal evolution where a bound state resonance mode with normal incident plane wave will change to a leaky waveguide mode at oblique incidence. The transmitted amplitudes encoded with information of spatial variation are sensitive to the transmission when increasing the incidence angle [151].
A type configuration is illustrated in Figure 6a [143], silicon nitride patch-arrays are embedded in a homogeneous medium of silicon dioxide. By tuning the height of patch-arrays, the spatial bandwidth and resolution of the edge detection can be modulated. The transmission coefficient of TE incident wave can be expressed as , where is the azimuthal angle, is the gain of the system, and . From Figure 6b, it can be seen that the transmission coefficient on the xoy plane formed the symmetric parabolic distribution due to the geometric symmetric, thereby it can be used to perform the second-order derivative with the quadratic approximation (see Figure 6c). In [142], a similar strategy is adopted to realize a 2D Laplace operator which can be combined with traditional imaging systems with a numerical aperture (NA) up to 0.32. However, since the quasi-guided leaky modes can only couple with p-polarized incident waves due to the modal symmetry, this scheme can only operate for one polarization. To overcome this limitation, Wan et al. [141] introduce a spatial differentiator can be performed for arbitrary polarized (unpolarized) wave by tailoring the spatial dispersion of electric dipole resonance supported by silicon nanodisks (see Figure 6d). Figure 6e shows that for both s- or p-polarized incident waves, the transfer function have similar parabolic shape which indicate the functionality of spatial differentiation for arbitrary polarization. The corresponding experiments verify the performance of this scheme (see Figure 6f).
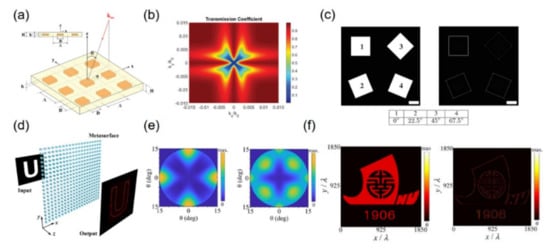
Figure 6.
(a) Schematic of the square patch-arrays metasurface for 2D edge detection; (b) 2D spatial transfer function spectrum; (c) edge detection of square-shaped input beams; adapted with permission from [143], IEEE, 2018. (d) Schematic of the basic configuration of dielectric metasurface for 2D spatial differentiation; (e) the transfer functions for or both linearly polarized light fields; (f) the output image of 2D edge detection for x polarization light waves. Adapted with permission from [141] © The Optical Society.
3. Other Emerging Approaches
3.1. Nonlocal Metasurface
Kwon et al. [144] introduce a new mechanism with increasing the nonlocal response of metasurfaces, which is generally considered to be undesirable and detrimental, by sinusoidally modulating the permittivity of each split-ring resonator (SRR) (Figure 7a). Within the modulation, the transmission formed a Fano response where a sharp variation of transmission coefficient emerges on the resonance frequency accompanied with the incident angle (see Figure 7b). By adding a horizontally misplaced metallic wire-arrays, the requirements of breaking both vertical and horizontal mirror symmetry are fulfilled to perform first-order derivative operation (see Figure 7c). Furthermore, 2D edge detection is demonstrated with combining the 1D computing metasurface and its 90° rotational symmetric structure (see Figure 7d–f).
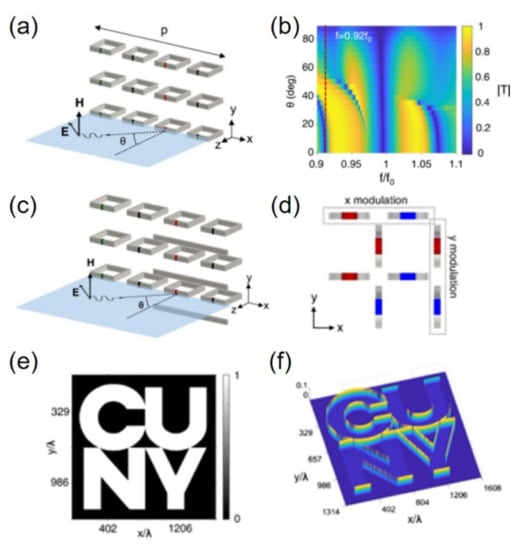
Figure 7.
(a) Schematic of sinusoidally modulated of split-ring resonators; (b) transmission spectrum with different incident angle; (c) schematic of asymmetric metasurface with a horizontally misplaced array of metallic wires for the first-derivative operation; (d) rotated metasurface for 2D second-derivative operation. (e) Input image and (f) output image of 2D edge detection for linear polarized wave. Adapted with permission from [144], APS, 2018.
3.2. Random Medium
Another counterintuitive approach is by employing random medium rather than deliberately designed structures with certain scattering properties to perform wave-based analog computing. In the study of Hougne et al. [146], it consists of two subsystems: a chaotic cavity as the random medium and a reflect-array metasurface playing the role of wavefront shaping device. As shown in Figure 8a, a plane impinging wave with input vector X is modulated by a wave front shaping device and subsequently propagating through a random medium to obtain the desired output wave front. For controlling spatial degree of freedom, the incident wave front is divided into four segments, marked by A to D (see Figure 8b). Here, an indoor cavity of irregular geometry is used as the random environment characterized with the Green’s function, which plays the key role of analog computing by enabling each segment of wave front to contribute to each output point. The reconfigurable metasurface contains 88 units whose reflection coefficient can be tuned from −1 to 1. Figure 8c shows the experimental configuration in which microwave absorbers are installed to limit the reverberation of the cavity.
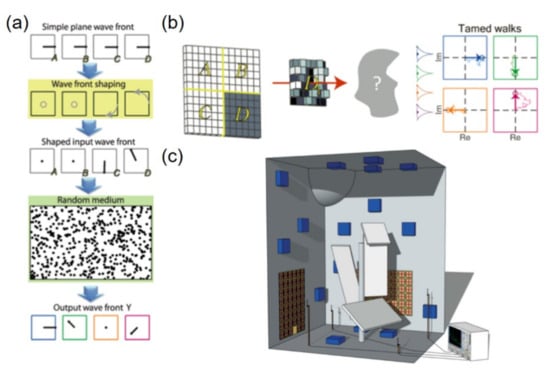
Figure 8.
(a) Schematic the random medium scheme for wave-based analog computation; (b) tamed contribution of segment D to observation points; (c) experimental setup in a metallic cavity of irregular geometry. Adapted with permission from [146], APS, 2018.
3.3. Inverse Design
Estakhri et al. [147] implement the discrete numerical method of solving integral equation in an optical way by using a recursive approach with a metamaterial block, feedback waveguides and coupling elements (see Figure 9a). The Fredholm integral equation of the second kind is expressed as: , where g(u) is the function to be solved, K(u,v) and Iin(u) are integral kernel and input signal. By sampling the complex values of electric fields on the input and output plane (with N points), the corresponding matrix equation can be established. To obtain the function g(u) is equivalent to calculate the inverse matrix (A), which can be realized by an inhomogeneous permittivity distributed metamaterial block. In the study, the authors adopt the objective-first optimization technique to approach the desired relative permittivity in each iteration constrained by criterion of transfer function I-A, where I is the identity matrix (the simulation results is shown in Figure 9b). The experiment of reflective configuration verifies that it is feasible to apply the inverse-designed metamaterial platform in solve integral equation (see Figure 9c,d).
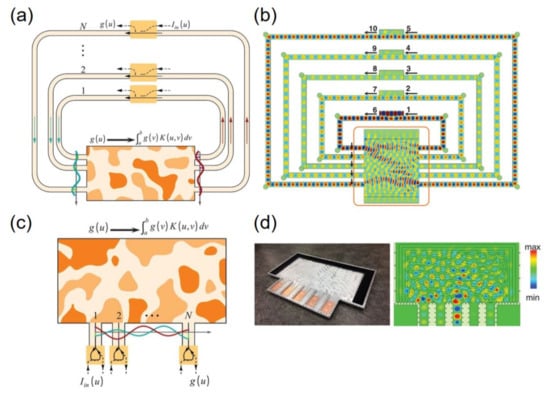
Figure 9.
(a) The conceptual sketch of the inverse-designed metamaterial platform in solve integral equation; (b) time snapshot of the simulation results for the transmissive configuration with external feedback network; (c) the reflective configuration of the internal feedback metamaterial system. (d) Left: the photograph of the constructed metamaterial system. Right: time snapshot of the simulation results for the reflective configuration with internal feedback network. Adapted with permission from [147], AAAS, 2019.
3.4. Brewster Effect
As mentioned above, the transversely homogenous multilayer slabs with even symmetry in the spatial Fourier domain cannot be applied to perform first-order derivative or integration operators since the odd symmetry is needed for these operations. In the study of Youssefi et al. [148], a rotated configuration is theoretically demonstrated to overcome this constraint by breaking the refection symmetry. The schematic of the rotated structure is shown in Figure 10a, when the oblique incident wave illuminating on the boundary of two dielectric medium (in this study, they are air and a dielectric substrate with different refractive indices of 1 and 2.1) at the Brewster angle, the GF around ky = 0 can be approximated with a linear function which is used to implement first-order derivative (see Figure 10b). The proposed simple structure enables effective implementation of the mathematical operations, however, there are some drawbacks in this configuration. The approximation requires the reflection spectrum of the interface to become equal to zero, which means only the signals around the Brewster angle can perform the derivation, leading to a relatively narrow spatial spectrum and small reflected energy.
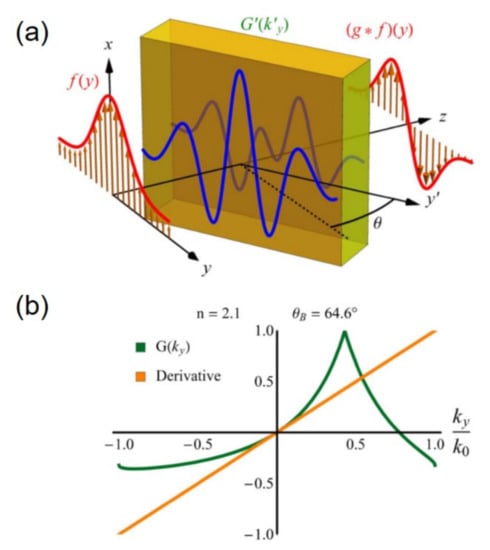
Figure 10.
(a) The schematic of the rotated structure for realizing an even or odd Green’s function; (b) the exact GF distribution and its approximation around ky = 0 based on the Taylor series. Adapted with permission from [148] © The Optical Society.
3.5. Goos-Hänchen Effect
Motivated by the high sensitivity of Goos-Hänchen (GH) effect for the interface of total internal reflection, Xu et al. [149] propose a GH-based approach where the kernel transfer function is acting on the air–glass interface to perform first-order derivative. After the total internal reflection, the reflected angular spectrum contains two linearly polarized components which are converted by a quarter-wave plate into two opposite circular-polarized components. The destructive interference of the reflected waves leads to the functionality of edge detection. The experimental setup is illustrated in Figure 11a, the phase distribution and spatial spectral transfer function are shown in Figure 11b. the results of edge detection for different images are shown in Figure 11c.
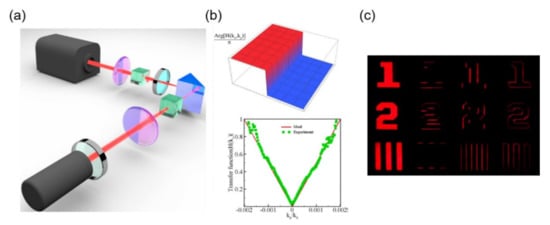
Figure 11.
(a) The experimental setup for measurement of the spatial spectral transfer function of the first order spatial differentiator based on GH effect; (b) top: the phase distribution for the spatial spectral transfer function. Bottom: the comparison of theoretical and experimental results for the spatial spectral transfer function for kx = 0; (c) output image of edge detection with different rotating angles. Adapted with permission from [149], AIP Publishing, 2020.
3.6. Spin Hall Effect
In the study of Zhu et al. [150], the authors demonstrate that realizing spatial differentiation is a natural effect of spin Hall effect (SHE) for the reflected or refracted wave at any planar interface. In this proposal, spin-dependent transverse shifts of and corresponding to parallel and antiparallel spin states, the destructive interference of the opposite shifts by selecting an orthogonally polarized reflected wave lead to the final output wave function, which can be expressed as: , where and denote the input and output wave functions. The limit of is approximately proportional to the first-order spatial differentiation when is much smaller than the initial wavefunction profile. As an example, Figure 12a shows that an obliquely incident paraxial beam illuminates on the interface of two isotropic media, two orthogonal polarizers are installed between the incident and reflected waves. The transfer function around ky = 0 is depicted in Figure 12b. the experimental results for 1D edge detection are shown in Figure 12c.
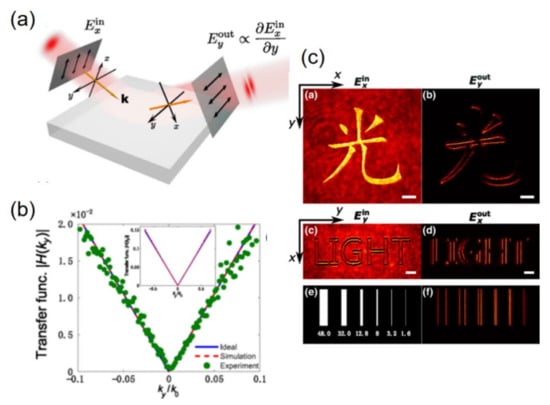
Figure 12.
(a) Schematic of spatial differentiation from the SHE of light on an optical planar interface between two isotropic materials; (b) the comparison of theoretical and experimental results for the spatial spectral transfer function for kx = 0; (c) the results of edge detection with different target images stored in Einx and Einy, respectively. Adapted with permission from [150], APS, 2019.
3.7. Quantum Computing with Metamaterials
Quantum computation [38], by employing the principles of quantum mechanics, such as superposition and entanglement, provides the basis for quantum algorithms that enable tremendous improvements over classical computing technology for certain complex tasks. For example, the large integer factorization problems are considered practically impossible for classical algorithms as the numbers get larger than 2048 bits. Therefore, it is essential for modern RSA encryption because the codes are virtually unbreakable. However, this cryptosystem is facing a daunting challenge by Shor’s algorithm [34], which promises the abilities of factoring integers in polynomial time. Another famous example is Grover’s search algorithm [35,36] in which searching an unsorted database only takes time compared with classical algorithm of , where N is the number of entries in the database. Although the quadratic speedup is slightly less impressive than other quantum algorithms with exponential acceleration capacities, the time saved is significant when N is considerably large. In fact, the extraordinary power of quantum computation comes from the smallest information carrier named quantum bits (or “qubits”). The quantum superposition phenomenon allows a single qubit to hold 0 and 1 states at the same time, as multiple qubits is coherently controlled, they process inherent parallel computing abilities that are far beyond the fastest classical computers.
However, despite these advantages over classical computers, up to now, to realize large-scale universal quantum computer is extreme difficult. Until 2016, a proof-of-principle demonstration of Shor’s algorithm can only be achieved to factor the number 15 [152]. Apparently, quantum computation still has a long way to go before it becomes practical. The biggest challenges that we faced were preparing, control and measurement of qubits, actions on qubits should be very carefully handled that even the slightest interaction with surrounding environments may leading to decoherence and destroy the quantum information. Among enormous numbers of experimental realizations of quantum algorithms in different physical systems (including nuclear magnetic resonance, quantum dots, trapped ions or QED cavities), the optical implementation is a promising way since the photons are more robust to external perturbation and thus corresponds to long decoherence times. In addition, the quantum optical system do not need extremely cold temperatures to function. The central idea of quantum optical computing is that quantum information can be encoded by different degrees of freedom of photons (e.g., polarization, orbital angular momentum, spatial and temporal modes), by utilizing the common properties shared by both classical optics and quantum mechanics, such as superposition and interference, it is possible to simulate certain quantum behaviors with classical light [37,39,40,42,43,45,48,49,50,51,52,53,55,56,57,58,59,62,67,153].
As a new platform for arbitrarily manipulating wavefront of light, metamaterials or metasurfaces can also be applied in simulating quantum algorithms with classical wave-based optics. In 2017, Zhang et al. [154] proposed a metamaterial-based quantum algorithm analog to perform Grover’s search algorithm. The designed metamaterial consisted of four cascade subblocks (an oracle subblock Um, two Fourier transform subblocks F, a phase plate subblock ) corresponding to the operators of oracle, Walsh–Hadamard transform and inversion-about-average (IAA) operation in Grover’s search algorithm (see Figure 13a). In this scheme, the quantum states are directly mapped onto classical optical fields. For instance, the incident electric field amplitude “E(y)” is the analogue of quantum probability amplitude, transversal coordinate “y” is used to label the item of the database and the maximum number of the database is depending on the full width at half-maximum of the beam “D” (listed in Table 1). When light occurs on the metamaterial, each functional subblock it passed is equivalent to performing a quantum operation; therefore, each roundtrip represents one iteration of the search algorithm. After multiple iterations in the metamaterial, the marked item is found by measuring the field distribution on the output plane (see Figure 13b). Recently, Cheng et al. [155] verified that Deutsch-Jozsa (DJ) algorithm could be simulated by using a similar strategy (see Figure 13c,d).
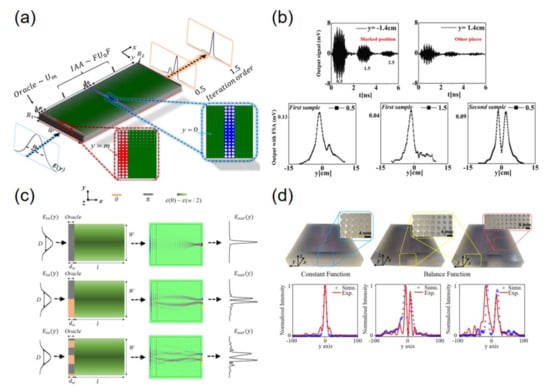
Figure 13.
(a) Schematic of the general protocol of simulating quantum search algorithm with metamaterials. (b) Experimental results of the time traces (top) and the field intensity (bottom) of the output with different iterations. Adapted with permission from [154], Wiley, 2017. (c) Simulation results of metamaterial-based DJ algorithm analogy with constant, simple balance and complex balance functions, respectively. (d) The photograph (top) and experimental results of three samples for simulating DJ algorithm. Adapted with permission from [155] © The Optical Society.

Table 1.
The general protocol of performing Grover’s search algorithm with metamaterial in quantum and classical realm.
In Table 1, we compare the general protocol of performing Grover’s search algorithm in quantum and classical realm to clarify the differences between the two strategies. As the spatial freedom of the optical field (cbit) is adopted to simulate the qubit, the classical wave-based architecture shows a simple and enlightening way to the field of signal processing. It should be mentioned that despite that it has been proved that entanglement is not necessary for the efficiency of some quantum algorithms [156], a lack of entanglement will essentially limit the physical resources for these classical analogies, leading to an exponential growth of the width of the beam as the numbers of qubits increase. In addition, the size of the database is also limited by the spatial resolution, diffraction effect and paraxial approximation of the optical system. With the rapid development of the field of artificial electromagnetism, we can expect more novel functionalities on simulating quantum behaviors, such as three-dimensional all-optical search and data classification.
4. Conclusions and Outlook
In this review, we have presented some of the most exciting developments in the field of analogous optical computing taking advantage of metamaterials, offering an integrated and miniaturized platform for image processing and edge detection to overcome the limitations of digital electronic computers. With continuous exploitation, tremendous novel approaches have been proposed based on different physical mechanisms, including Brewster effect, surface plasmonic, photonic spin Hall effect, local/excitation mode coupling to implement mathematical operations. Despite the promising unprecedent advances of meta-structures over traditional optical system for analog computing, to date, it is still extremely challenging to further improve the performance which is limited by spatial resolution, efficiency, operating bandwidth, strong polarization/angle/symmetry dependence. In general, computational metamaterials can be divided into two major categories: plasmonics and dielectrics. Leveraging highly confined surface plasmonic modes, plasmonic spatial differentiators process advantages of simplicity and ultracompact size. However, they suffer from some fundamental limitations, for instance, the critical coupling condition limits the incident angles, the presence of higher-order Taylor coefficients lead to a narrow spatial bandwidth and further effect the resolution of the computational system. In addition, the conversion efficiency is restricted by intrinsic material loss. To improve the efficiency and achieve high-resolution edge detection, all-dielectric metasurface is emerging as an alternative platform, which is a promising candidate for further broadening of the operational spatial bandwidth and reducing the absorption losses. It should be mentioned that dielectric metasurfaces also have some drawbacks—some of them only work for one polarization while the energy of other polarized waves is completely wasted, which may lead to relatively low signal-to-noise ratio. Moreover, determining how to balance the features of numerical aperture, efficiency and spatial resolution requires an elaborate design [157].
Although some limitations exist in this emerging field, we are pleased to see that many achievements have been proposed and demonstrated to overcome these drawbacks. Wang et al. [158] proposed a photonic crystal differentiator with improved robustness with incoherent light. Kwon et al. [145] designed a nonlocal metasurface by engineering nonlocality in momentum space that can perform both even- and odd-order differentiations. This study provides a high-quality, efficient and polarization-insensitive image processing platform for 2D edge detection. We believe that as it continuously evolves, the metamaterial-based analogous optical computing will be extensively applied in signal and image processing.
Author Contributions
Y.F. conceived the review; K.C., Y.F. wrote the manuscript; W.Z., Y.G., S.F., H.L. revised the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (No. 11774057, 12074314, 11674266), This research was funded by Funds for Equipment Advance Research during the 13th Five-Year Plan under Grant 61400030305.
Data Availability Statement
Data sharing not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Clymer, A.B. The mechanical analog computers of Hannibal Ford and William Newell. IEEE Ann. Hist. Comput. 1993, 15, 19–34. [Google Scholar] [CrossRef]
- Price, D.D.S. A History of Calculating Machines. IEEE Micro 1984, 4, 22–52. [Google Scholar] [CrossRef]
- Hausner, A. Analog and Analog/Hybrid Computer Programming; Prentice-Hall: Englewood Cliffs, NJ, USA, 1971. [Google Scholar] [CrossRef]
- Barrios, G.A.; Retamal, J.C.; Solano, E.; Sanz, M. Analog simulator of integro-differential equations with classical memristors. Sci. Rep. 2019, 9, 12928. [Google Scholar] [CrossRef] [PubMed]
- Tsividis, Y. Not your Father’s analog computer. IEEE Spectr. 2018, 55, 38–43. [Google Scholar] [CrossRef]
- Caulfield, H.J.; Dolev, S. Why future supercomputing requires optics. Nat. Photonics 2010, 4, 261–263. [Google Scholar] [CrossRef]
- The power of analogies. Nat. Photonics 2014, 8. [CrossRef]
- Passian, A.; Imam, N. Nanosystems, Edge Computing, and the Next Generation Computing Systems. Sensors 2019, 19, 4048. [Google Scholar] [CrossRef]
- Solli, D.R.; Jalali, B. Analog optical computing. Nat. Photonics 2015, 9, 704–706. [Google Scholar] [CrossRef]
- Karim, M.A.; Awwal, A.A. Optical Computing: An Introduction; Wiley, Inc.: New York, NY, USA, 1992. [Google Scholar]
- Herden, A.; Tschudi, T. Analog Optical Computing; Springer: Berlin/Heidelberg, Germany, 1986; pp. 369–383. [Google Scholar]
- Creasey, D.J. Digital Signal Processing: Principles, Devices and Applications. IEE Rev. 1990, 36, 275–276. [Google Scholar] [CrossRef]
- Park, Y.; Ahn, T.-J.; Dai, Y.; Yao, J.; Azaña, J. All-optical temporal integration of ultrafast pulse waveforms. Opt. Express 2008, 16, 17817–17825. [Google Scholar] [CrossRef]
- Quoc Ngo, N. Design of an optical temporal integrator based on a phase-shifted fiber Bragg grating in transmission. Opt. Lett. 2007, 32, 3020–3022. [Google Scholar] [CrossRef] [PubMed]
- Rutkowska, K.A.; Duchesne, D.; Strain, M.J.; Morandotti, R.; Sorel, M.; Azaña, J. Ultrafast all-optical temporal differentiators based on CMOS-compatible integrated-waveguide Bragg gratings. Opt. Express 2011, 19, 19514–19522. [Google Scholar] [CrossRef] [PubMed]
- Slavík, R.; Park, Y.; Kulishov, M.; Morandotti, R.; Azaña, J. Ultrafast all-optical differentiators. Opt. Express 2006, 14, 10699–10707. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.; Zhang, X.; Dong, J.; Liu, D.; Huang, D. High-speed all-optical differentiator based on a semiconductor optical amplifier and an optical filter. Opt. Lett. 2007, 32, 1872–1874. [Google Scholar] [CrossRef] [PubMed]
- Ferrera, M.; Park, Y.; Razzari, L.; Little, B.E.; Chu, S.T.; Morandotti, R.; Moss, D.J.; Azaña, J. On-chip CMOS-compatible all-optical integrator. Nat. Commun. 2010, 1, 29. [Google Scholar] [CrossRef] [PubMed]
- Zangeneh-Nejad, F.; Fleury, R. Topological analog signal processing. Nat. Commun. 2019, 10, 2058. [Google Scholar] [CrossRef]
- Chen, K.; Hou, J.; Huang, Z.; Cao, T.; Zhang, J.; Yu, Y.; Zhang, X. All-optical 1st- and 2nd-order differential equation solvers with large tuning ranges using Fabry-Pérot semiconductor optical amplifiers. Opt. Express 2015, 23, 3784–3794. [Google Scholar] [CrossRef]
- Yang, T.; Dong, J.; Lu, L.; Zhou, L.; Zheng, A.; Zhang, X.; Chen, J. All-optical differential equation solver with constant-coefficient tunable based on a single microring resonator. Sci. Rep. 2014, 4, 5581. [Google Scholar] [CrossRef]
- Karimi, A.; Zarifkar, A.; Miri, M. Design of a Miniaturized Broadband Silicon Hybrid Plasmonic Temporal Integrator for Ultrafast Optical Signal Processing. J. Lightwave Technol. 2020, 38, 2346–2352. [Google Scholar] [CrossRef]
- Wu, J.; Liu, B.; Peng, J.; Mao, J.; Jiang, X.; Qiu, C.; Tremblay, C.; Su, Y. On-Chip Tunable Second-Order Differential-Equation Solver Based on a Silicon Photonic Mode-Split Microresonator. J. Lightwave Technol. 2015, 33, 3542–3549. [Google Scholar] [CrossRef]
- Zhang, W.; Yao, J. Photonic integrated field-programmable disk array signal processor. Nat. Commun. 2020, 11, 406. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Guzzon, R.S.; Coldren, L.A.; Yao, J. Optical dynamic memory based on an integrated active ring resonator. Opt. Lett. 2018, 43, 4687–4690. [Google Scholar] [CrossRef] [PubMed]
- Brunner, D.; Soriano, M.C.; Mirasso, C.R.; Fischer, I. Parallel photonic information processing at gigabyte per second data rates using transient states. Nat. Commun. 2013, 4, 1364. [Google Scholar] [CrossRef]
- Moughames, J.; Porte, X.; Thiel, M.; Ulliac, G.; Larger, L.; Jacquot, M.; Kadic, M.; Brunner, D. Three-dimensional waveguide interconnects for scalable integration of photonic neural networks. Optica 2020, 7, 640–646. [Google Scholar] [CrossRef]
- Solli, D.R.; Herink, G.; Jalali, B.; Ropers, C. Fluctuations and correlations in modulation instability. Nat. Photonics 2012, 6, 463–468. [Google Scholar] [CrossRef]
- Donati, S.; Mirasso, C.R. Introduction to the feature section on optical chaos and applications to cryptography. IEEE J. Quantum Electron. 2002, 38, 1138–1140. [Google Scholar] [CrossRef]
- Turitsyna, E.G.; Smirnov, S.V.; Sugavanam, S.; Tarasov, N.; Shu, X.; Babin, S.A.; Podivilov, E.V.; Churkin, D.V.; Falkovich, G.; Turitsyn, S.K. The laminar–turbulent transition in a fibre laser. Nat. Photonics 2013, 7, 783–786. [Google Scholar] [CrossRef]
- Bykov, D.A.; Doskolovich, L.L.; Bezus, E.A.; Soifer, V.A. Optical computation of the Laplace operator using phase-shifted Bragg grating. Opt. Express 2014, 22, 25084–25092. [Google Scholar] [CrossRef]
- AbdollahRamezani, S.; Arik, K.; Khavasi, A.; Kavehvash, Z. Analog computing using graphene-based metalines. Opt. Lett. 2015, 40, 5239–5242. [Google Scholar] [CrossRef]
- Zangeneh-Nejad, F.; Khavasi, A.; Rejaei, B. Analog optical computing by half-wavelength slabs. Opt. Commun. 2018, 407, 338–343. [Google Scholar] [CrossRef]
- Shor, P.W. Algorithms for quantum computation: Discrete logarithms and factoring. In Proceedings of the 35th Annual Symposium on Foundations of Computer Science, Los Alamitos, CA, USA, 20–22 November 1994. [Google Scholar]
- Grover, L.K. A fast quantum mechanical algorithm for database search. In Proceedings of the 28th Annual ACM Symposium on Theory of Computing (STOC), Philadelphia, PA, USA, 6–8 July 1996; pp. 212–219. [Google Scholar]
- Grover, L.K. Quantum Computers Can Search Arbitrarily Large Databases by a Single Query. Phys. Rev. Lett. 1997, 79, 4709–4712. [Google Scholar] [CrossRef]
- Knill, E.; Laflamme, R.; Milburn, G.J. A scheme for efficient quantum computation with linear optics. Nature 2001, 409, 46–52. [Google Scholar] [CrossRef] [PubMed]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: New York, NY, USA, 2000. [Google Scholar]
- Spreeuw, R.J.C. A Classical Analogy of Entanglement. Found. Phys. 1998, 28, 361–374. [Google Scholar] [CrossRef]
- Spreeuw, R.J.C. Classical wave-optics analogy of quantum-information processing. Phys. Rev. A 2001, 63, 062302. [Google Scholar] [CrossRef]
- Collins, D.; Kim, K.W.; Holton, W.C. Deutsch-Jozsa algorithm as a test of quantum computation. Phys. Rev. A 1998, 58, R1633–R1636. [Google Scholar] [CrossRef]
- Kwiat, P.G.; Mitchell, J.R.; Schwindt, P.D.D.; White, A.G. Grover’s search algorithm: An optical approach. J. Mod. Opt. 2000, 47, 257–266. [Google Scholar] [CrossRef]
- Bhattacharya, N.; van Linden van den Heuvell, H.B.; Spreeuw, R.J.C. Implementation of Quantum Search Algorithm using Classical Fourier Optics. Phys. Rev. Lett. 2002, 88, 137901. [Google Scholar] [CrossRef]
- Dragoman, D. n-step optical simulation of the n-qubit state: Applications in optical computing. Optik 2002, 113, 425–428. [Google Scholar] [CrossRef]
- Puentes, G.; Mela, C.L.; Ledesma, S.; Iemmi, C.; Paz, J.P.; Saraceno, M. Optical simulation of quantum algorithms using programmable liquid-crystal displays. Phys. Rev. A 2004, 69, 042319. [Google Scholar] [CrossRef]
- Hijmans, T.W.; Huussen, T.N.; Spreeuw, R.J.C. Time and frequency domain solutions in an optical analogue of Grover’s search algorithm. J. Opt. Soc. Am. B 2006, 24, 214–220. [Google Scholar] [CrossRef]
- Luis, A. Coherence, polarization, and entanglement for classical light fields. Opt. Commun. 2009, 282, 3665–3670. [Google Scholar] [CrossRef]
- Zhang, P.; Liu, R.-F.; Huang, Y.-F.; Gao, H.; Li, F.-L. Demonstration of Deutsch’s algorithm on a stable linear optical quantum computer. Phys. Rev. A 2010, 82, 064302. [Google Scholar] [CrossRef]
- Lee, S.M.; Park, H.S.; Cho, J.; Kang, Y.; Lee, J.Y.; Kim, H.; Lee, D.-H.; Choi, S.-K. Experimental realization of a four-photon seven-qubit graph state for one-way quantum computation. Opt. Express 2012, 20, 6915–6926. [Google Scholar] [CrossRef] [PubMed]
- Marques, B.; Barros, M.R.; Pimenta, W.M.; Carvalho, M.A.D.; Ferraz, J.; Drumond, R.C.; Terra Cunha, M.; Pádua, S. Double-slit implementation of the minimal Deutsch algorithm. Phys. Rev. A 2012, 86, 032306. [Google Scholar] [CrossRef]
- Rohde, P.P. Optical quantum computing with photons of arbitrarily low fidelity and purity. Phys. Rev. A 2012, 86, 052321. [Google Scholar] [CrossRef]
- Goyal, S.K.; Roux, F.S.; Forbes, A.; Konrad, T. Implementing Quantum Walks Using Orbital Angular Momentum of Classical Light. Phys. Rev. Lett. 2013, 110, 263602. [Google Scholar] [CrossRef]
- Georgescu, I.M.; Ashhab, S.; Nori, F. Quantum simulation. Rev. Mod. Phys. 2014, 86, 153–185. [Google Scholar] [CrossRef]
- Goyal, S.K.; Roux, F.S.; Forbes, A.; Konrad, T. The Scalable Implementation of Quantum Walks using Classical Light. In Proceedings of the SPIE OPTO, San Francisco, CA, USA, 1–6 February 2014; Volume 8999, p. 8. [Google Scholar]
- Böhm, J.; Bellec, M.; Mortessagne, F.; Kuhl, U.; Barkhofen, S.; Gehler, S.; Stöckmann, H.-J.; Foulger, I.; Gnutzmann, S.; Tanner, G. Microwave Experiments Simulating Quantum Search and Directed Transport in Artificial Graphene. Phys. Rev. Lett. 2015, 114, 110501. [Google Scholar] [CrossRef]
- Goyal, S.K.; Roux, F.S.; Forbes, A.; Konrad, T. Implementation of multidimensional quantum walks using linear optics and classical light. Phys. Rev. A 2015, 92, 040302. [Google Scholar] [CrossRef]
- Hor-Meyll, M.; Tasca, D.S.; Walborn, S.P.; Ribeiro, P.H.S.; Santos, M.M.; Duzzioni, E.I. Deterministic quantum computation with one photonic qubit. Phys. Rev. A 2015, 92, 012337. [Google Scholar] [CrossRef]
- Perez-Garcia, B.; Francis, J.; McLaren, M.; Hernandez-Aranda, R.I.; Forbes, A.; Konrad, T. Quantum computation with classical light: The Deutsch Algorithm. Phys. Lett. A 2015, 379, 1675–1680. [Google Scholar] [CrossRef]
- Perez-Garcia, B.; Mclaren, M.; Goyal, S.K.; Hernandez-Aranda, R.I.; Forbes, A.; Konrad, T. Quantum computation with classical light: Implementation of the Deutsch–Jozsa algorithm. Phys. Lett. A 2015, 380, 1925–1931. [Google Scholar] [CrossRef]
- Zagoskin, A.M.; Felbacq, D.; Rousseau, E. Quantum metamaterials in the microwave and optical ranges. EPJ Quantum Technol. 2016, 3, 2. [Google Scholar] [CrossRef]
- Giri, P.R.; Korepin, V.E. A review on quantum search algorithms. Quantum Inf. Process. 2017, 16, 315. [Google Scholar] [CrossRef]
- Johansson, N.; Larsson, J.-Å. Efficient classical simulation of the Deutsch–Jozsa and Simon’s algorithms. Quantum Inf. Process. 2017, 16, 233. [Google Scholar] [CrossRef]
- Wei, H.-R.; Liu, J.-Z. Deterministic implementations of single-photon multi-qubit Deutsch–Jozsa algorithms with linear optics. Annals Phys. 2017, 377, 38–47. [Google Scholar] [CrossRef]
- Flamini, F.; Spagnolo, N.; Sciarrino, F. Photonic quantum information processing: A review. Rep. Prog. Phys. 2018, 82, 016001. [Google Scholar] [CrossRef] [PubMed]
- Perez-Garcia, B.; Hernandez-Aranda, R.I.; Forbes, A.; Konrad, T. The first iteration of Grover’s algorithm using classical light with orbital angular momentum. J. Mod. Opt. 2018, 65, 1942–1948. [Google Scholar] [CrossRef]
- Vianna, Y.; Barros, M.R.; Hor-Meyll, M. Classical realization of the quantum Deutsch algorithm. Am. J. Phys. 2018, 86, 914–923. [Google Scholar] [CrossRef]
- Zhang, S.; Li, P.; Wang, B.; Zeng, Q.; Zhang, X. Implementation of quantum permutation algorithm with classical light. J. Phys. Commun. 2019, 3, 015008. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, Y.; Sun, Y.; Sun, H.; Zhang, X. Quantum-inspired microwave signal processing for implementing unitary transforms. Opt. Express 2019, 27, 436–460. [Google Scholar] [CrossRef] [PubMed]
- Smith, D.R.; Pendry, J.B.; Wiltshire, M.C.K. Metamaterials and Negative Refractive Index. Science 2004, 305, 788–792. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Chan, C.T.; Sheng, P. Transformation optics and metamaterials. Nat. Mater. 2010, 9, 387. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Zhang, X. Metamaterials: A new frontier of science and technology. Chem. Soc. Rev. 2011, 40, 2494–2507. [Google Scholar] [CrossRef]
- Soukoulis, C.M.; Wegener, M. Past achievements and future challenges in the development of three-dimensional photonic metamaterials. Nat. Photonics 2011, 5, 523. [Google Scholar] [CrossRef]
- Cui, T.J.; Qi, M.Q.; Wan, X.; Zhao, J.; Cheng, Q. Coding metamaterials, digital metamaterials and programmable metamaterials. Light Sci. Appl. 2014, 3, e218. [Google Scholar] [CrossRef]
- Della Giovampaola, C.; Engheta, N. Digital metamaterials. Nat. Mater. 2014, 13, 1115. [Google Scholar] [CrossRef]
- Huo, P.; Zhang, S.; Liang, Y.; Lu, Y.; Xu, T. Hyperbolic Metamaterials and Metasurfaces: Fundamentals and Applications. Adv. Opt. Mater. 2019, 7, 1801616. [Google Scholar] [CrossRef]
- Fan, Y.; Wei, Z.; Li, H.; Chen, H.; Soukoulis, C.M. Low-loss and high-Q planar metamaterial with toroidal moment. Phys. Rev. B 2013, 87, 115417. [Google Scholar] [CrossRef]
- Chen, S.; Fan, Y.; Fu, Q.; Wu, H.; Jin, Y.; Zheng, J.; Zhang, F. A Review of Tunable Acoustic Metamaterials. Appl. Sci. 2018, 8, 1480. [Google Scholar] [CrossRef]
- Fan, Y.; Zhang, F.; Shen, N.-H.; Fu, Q.; Wei, Z.; Li, H.; Soukoulis, C.M. Achieving a high-Q response in metamaterials by manipulating the toroidal excitations. Phys. Rev. A 2018, 97, 033816. [Google Scholar] [CrossRef]
- Ziolkowski, R.W.; Engheta, N. Metamaterials: Two Decades Past and Into Their Electromagnetics Future and Beyond. IEEE Trans. Antennas Propag. 2020, 68, 1232–1237. [Google Scholar] [CrossRef]
- Yu, N.; Genevet, P.; Kats, M.A.; Aieta, F.; Tetienne, J.-P.; Capasso, F.; Gaburro, Z. Light Propagation with Phase Discontinuities: Generalized Laws of Reflection and Refraction. Science 2011, 334, 333–337. [Google Scholar] [CrossRef] [PubMed]
- Holloway, C.L.; Kuester, E.F.; Gordon, J.A.; Hara, J.O.; Booth, J.; Smith, D.R. An Overview of the Theory and Applications of Metasurfaces: The Two-Dimensional Equivalents of Metamaterials. IEEE Antennas Propag. Mag. 2012, 54, 10–35. [Google Scholar] [CrossRef]
- Kildishev, A.V.; Boltasseva, A.; Shalaev, V.M. Planar Photonics with Metasurfaces. Science 2013, 339, 1232009. [Google Scholar] [CrossRef]
- Meinzer, N.; Barnes, W.L.; Hooper, I.R. Plasmonic meta-atoms and metasurfaces. Nat. Photonics 2014, 8, 889–898. [Google Scholar] [CrossRef]
- Yu, N.; Capasso, F. Flat optics with designer metasurfaces. Nat. Mater. 2014, 13, 139. [Google Scholar] [CrossRef]
- Glybovski, S.B.; Tretyakov, S.A.; Belov, P.A.; Kivshar, Y.S.; Simovski, C.R. Metasurfaces: From microwaves to visible. Phys. Rep. 2016, 634, 1–72. [Google Scholar] [CrossRef]
- Hou-Tong, C.; Antoinette, J.T.; Nanfang, Y. A review of metasurfaces: Physics and applications. Rep. Prog. Phys. 2016, 79, 076401. [Google Scholar] [CrossRef]
- Zhang, L.; Mei, S.; Huang, K.; Qiu, C.-W. Advances in Full Control of Electromagnetic Waves with Metasurfaces. Adv. Opt. Mater. 2016, 4, 818–833. [Google Scholar] [CrossRef]
- Genevet, P.; Capasso, F.; Aieta, F.; Khorasaninejad, M.; Devlin, R. Recent advances in planar optics: From plasmonic to dielectric metasurfaces. Optica 2017, 4, 139–152. [Google Scholar] [CrossRef]
- Li, G.; Zhang, S.; Zentgraf, T. Nonlinear photonic metasurfaces. Nat. Rev. Mater. 2017, 2, 17010. [Google Scholar] [CrossRef]
- Chen, M.; Kim, M.; Wong Alex, M.H.; Eleftheriades George, V. Huygens’ metasurfaces from microwaves to optics: A review. Nanophotonics 2018, 7, 1207. [Google Scholar] [CrossRef]
- He, Q.; Sun, S.; Xiao, S.; Zhou, L. High-Efficiency Metasurfaces: Principles, Realizations, and Applications. Adv. Opt. Mater. 2018, 6, 1800415. [Google Scholar] [CrossRef]
- Hail, C.U.; Michel, A.-K.U.; Poulikakos, D.; Eghlidi, H. Optical Metasurfaces: Evolving from Passive to Adaptive. Adv. Opt. Mater. 2019, 7, 1801786. [Google Scholar] [CrossRef]
- Luo, X. Metamaterials and Metasurfaces. Adv. Opt. Mater. 2019, 7, 1900885. [Google Scholar] [CrossRef]
- Sun, S.; He, Q.; Hao, J.; Xiao, S.; Zhou, L. Electromagnetic metasurfaces: Physics and applications. Adv. Opt. Photonics 2019, 11, 380–479. [Google Scholar] [CrossRef]
- Fan, Y.; Shen, N.-H.; Zhang, F.; Zhao, Q.; Wei, Z.; Zhang, P.; Dong, J.; Fu, Q.; Li, H.; Soukoulis, C.M. Photoexcited Graphene Metasurfaces: Significantly Enhanced and Tunable Magnetic Resonances. ACS Photonics 2018, 5, 1612–1618. [Google Scholar] [CrossRef]
- Fan, Y.; Shen, N.-H.; Zhang, F.; Zhao, Q.; Wu, H.; Fu, Q.; Wei, Z.; Li, H.; Soukoulis, C.M. Graphene Plasmonics: A Platform for 2D Optics. Adv. Opt. Mater. 2018, 7, 1800537. [Google Scholar] [CrossRef]
- Cheng, K.; Wei, Z.; Fan, Y.; Zhang, X.; Wu, C.; Li, H. Realizing Broadband Transparency via Manipulating the Hybrid Coupling Modes in Metasurfaces for High-Efficiency Metalens. Adv. Opt. Mater. 2019, 7, 1900016. [Google Scholar] [CrossRef]
- Lou, J.; Liang, J.; Yu, Y.; Ma, H.; Yang, R.; Fan, Y.; Wang, G.; Cai, T. Silicon-Based Terahertz Meta-Devices for Electrical Modulation of Fano Resonance and Transmission Amplitude. Adv. Opt. Mater. 2020, 8, 2000449. [Google Scholar] [CrossRef]
- Zhu, W.; Fan, Y.; Li, C.; Yang, R.; Yan, S.; Fu, Q.; Zhang, F.; Gu, C.; Li, J. Realization of a near-infrared active Fano-resonant asymmetric metasurface by precisely controlling the phase transition of Ge2Sb2Te5. Nanoscale 2020, 12, 8758–8767. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Li, T.; Soman, A.; Mao, D.; Kananen, T.; Gu, T. On-chip wavefront shaping with dielectric metasurface. Nat. Commun. 2019, 10, 3547. [Google Scholar] [CrossRef] [PubMed]
- Abdollahramezani, S.; Hemmatyar, O.; Adibi, A. Meta-optics for spatial optical analog computing. Nanophotonics 2020, 9, 4075–4095. [Google Scholar] [CrossRef]
- Silva, A.; Monticone, F.; Castaldi, G.; Galdi, V.; Alù, A.; Engheta, N. Performing Mathematical Operations with Metamaterials. Science 2014, 343, 160. [Google Scholar] [CrossRef]
- Mendlovic, D.; Ozaktas, H.M. Fractional Fourier transforms and their optical implementation: I. J. Opt. Soc. Am. A 1993, 10, 1875–1881. [Google Scholar] [CrossRef]
- Ozaktas, H.M.; Mendlovic, D. Fractional Fourier transforms and their optical implementation. II. J. Opt. Soc. Am. A 1993, 10, 2522–2531. [Google Scholar] [CrossRef]
- Khorasaninejad, M.; Capasso, F. Metalenses: Versatile multifunctional photonic components. Science 2017, 358, eaam8100. [Google Scholar] [CrossRef]
- Lalanne, P.; Chavel, P. Metalenses at visible wavelengths: Past, present, perspectives. Laser Photonics Rev. 2017, 11, 1600295. [Google Scholar] [CrossRef]
- Wang, S.; Wu, P.C.; Su, V.-C.; Lai, Y.-C.; Hung Chu, C.; Chen, J.-W.; Lu, S.-H.; Chen, J.; Xu, B.; Kuan, C.-H.; et al. Broadband achromatic optical metasurface devices. Nat. Commun. 2017, 8, 187. [Google Scholar] [CrossRef]
- Yang, Q.; Gu, J.; Xu, Y.; Zhang, X.; Li, Y.; Ouyang, C.; Tian, Z.; Han, J.; Zhang, W. Broadband and Robust Metalens with Nonlinear Phase Profiles for Efficient Terahertz Wave Control. Adv. Opt. Mater. 2017, 5, 1601084. [Google Scholar] [CrossRef]
- Chen, W.T.; Zhu, A.Y.; Sanjeev, V.; Khorasaninejad, M.; Shi, Z.; Lee, E.; Capasso, F. A broadband achromatic metalens for focusing and imaging in the visible. Nat. Nanotechnol. 2018, 13, 220–226. [Google Scholar] [CrossRef] [PubMed]
- Shrestha, S.; Overvig, A.C.; Lu, M.; Stein, A.; Yu, N. Broadband achromatic dielectric metalenses. Light Sci. Appl. 2018, 7, 85. [Google Scholar] [CrossRef] [PubMed]
- Huang, L.; Chen, X.; Mühlenbernd, H.; Zhang, H.; Chen, S.; Bai, B.; Tan, Q.; Jin, G.; Cheah, K.-W.; Qiu, C.-W.; et al. Three-dimensional optical holography using a plasmonic metasurface. Nat. Commun. 2013, 4. [Google Scholar] [CrossRef]
- Li, G.; Kang, M.; Chen, S.; Zhang, S.; Pun, E.Y.-B.; Cheah, K.W.; Li, J. Spin-Enabled Plasmonic Metasurfaces for Manipulating Orbital Angular Momentum of Light. Nano Lett. 2013, 13, 4148–4151. [Google Scholar] [CrossRef]
- Lovera, A.; Gallinet, B.; Nordlander, P.; Martin, O.J.F. Mechanisms of Fano Resonances in Coupled Plasmonic Systems. ACS Nano 2013, 7, 4527–4536. [Google Scholar] [CrossRef]
- Ni, X.; Ishii, S.; Kildishev, A.V.; Shalaev, V.M. Ultra-thin, planar, Babinet-inverted plasmonic metalenses. Light Sci. Appl. 2013, 2, e72. [Google Scholar] [CrossRef]
- Pors, A.; Nielsen, M.G.; Eriksen, R.L.; Bozhevolnyi, S.I. Broadband Focusing Flat Mirrors Based on Plasmonic Gradient Metasurfaces. Nano Lett. 2013, 13, 829–834. [Google Scholar] [CrossRef]
- Chalabi, H.; Schoen, D.; Brongersma, M.L. Hot-Electron Photodetection with a Plasmonic Nanostripe Antenna. Nano Lett. 2014, 14, 1374–1380. [Google Scholar] [CrossRef]
- Saeidi, C.; van der Weide, D. Wideband plasmonic focusing metasurfaces. Appl. Phys. Lett. 2014, 105, 053107. [Google Scholar] [CrossRef]
- Qin, F.; Ding, L.; Zhang, L.; Monticone, F.; Chum, C.C.; Deng, J.; Mei, S.; Li, Y.; Teng, J.; Hong, M.; et al. Hybrid bilayer plasmonic metasurface efficiently manipulates visible light. Sci. Adv. 2016, 2. [Google Scholar] [CrossRef] [PubMed]
- Yue, F.; Wen, D.; Xin, J.; Gerardot, B.D.; Li, J.; Chen, X. Vector Vortex Beam Generation with a Single Plasmonic Metasurface. ACS Photonics 2016, 3, 1558–1563. [Google Scholar] [CrossRef]
- Pors, A.; Nielsen, M.G.; Bozhevolnyi, S.I. Analog Computing Using Reflective Plasmonic Metasurfaces. Nano Lett. 2015, 15, 791–797. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; An, D.; Li, Z.; Zhao, X. Performing differential operation with a silver dendritic metasurface at visible wavelengths. Opt. Express 2017, 25, 26417–26426. [Google Scholar] [CrossRef]
- Chizari, A.; Abdollahramezani, S.; Jamali, M.V.; Salehi, J.A. Analog optical computing based on a dielectric meta-reflect array. Opt. Lett. 2016, 41, 3451–3454. [Google Scholar] [CrossRef]
- Zhang, W.; Qu, C.; Zhang, X. Solving constant-coefficient differential equations with dielectric metamaterials. J. Opt. 2016, 18, 075102. [Google Scholar] [CrossRef]
- Wu, Y.; Zhuang, Z.; Deng, L.; Liu, Y.; Xue, Q.; Ghassemlooy, Z. Arbitrary Multi-way Parallel Mathematical Operations Based on Planar Discrete Metamaterials. Plasmonics 2018, 13, 599–607. [Google Scholar] [CrossRef]
- Huo, P.; Zhang, C.; Zhu, W.; Liu, M.; Zhang, S.; Zhang, S.; Chen, L.; Lezec, H.J.; Agrawal, A.; Lu, Y.; et al. Photonic Spin-Multiplexing Metasurface for Switchable Spiral Phase Contrast Imaging. Nano Lett. 2020, 20, 2791–2798. [Google Scholar] [CrossRef]
- Wu, W.; Jiang, W.; Yang, J.; Gong, S.; Ma, Y. Multilayered analog optical differentiating device: Performance analysis on structural parameters. Opt. Lett. 2017, 42, 5270–5273. [Google Scholar] [CrossRef]
- Zangeneh-Nejad, F.; Khavasi, A. Spatial integration by a dielectric slab and its planar graphene-based counterpart. Opt. Lett. 2017, 42, 1954–1957. [Google Scholar] [CrossRef]
- Guo, C.; Xiao, M.; Minkov, M.; Shi, Y.; Fan, S. Photonic crystal slab Laplace operator for image differentiation. Optica 2018, 5, 251–256. [Google Scholar] [CrossRef]
- Doskolovich, L.L.; Bezus, E.A.; Bykov, D.A.; Soifer, V.A. Spatial differentiation of Bloch surface wave beams using an on-chip phase-shifted Bragg grating. J. Opt. 2016, 18, 115006. [Google Scholar] [CrossRef]
- Fang, Y.; Lou, Y.; Ruan, Z. On-grating graphene surface plasmons enabling spatial differentiation in the terahertz region. Opt. Lett. 2017, 42, 3840–3843. [Google Scholar] [CrossRef]
- Bykov, D.A.; Doskolovich, L.L.; Morozov, A.A.; Podlipnov, V.V.; Bezus, E.A.; Verma, P.; Soifer, V.A. First-order optical spatial differentiator based on a guided-mode resonant grating. Opt. Express 2018, 26, 10997–11006. [Google Scholar] [CrossRef] [PubMed]
- Dong, Z.; Si, J.; Yu, X.; Deng, X. Optical spatial differentiator based on subwavelength high-contrast gratings. Appl. Phys. Lett. 2018, 112, 181102. [Google Scholar] [CrossRef]
- Yang, W.; Yu, X.; Zhang, J.; Deng, X. Plasmonic transmitted optical differentiator based on the subwavelength gold gratings. Opt. Lett. 2020, 45, 2295–2298. [Google Scholar] [CrossRef]
- Parthenopoulos, A.; Darki, A.A.; Jeppesen, B.R.; Dantan, A. Optical spatial differentiation with suspended subwavelength gratings. arXiv 2020, arXiv:2008.10945. [Google Scholar]
- Zhu, T.; Zhou, Y.; Lou, Y.; Ye, H.; Qiu, M.; Ruan, Z.; Fan, S. Plasmonic computing of spatial differentiation. Nat. Commun. 2017, 8, 15391. [Google Scholar] [CrossRef]
- Zhang, J.; Ying, Q.; Ruan, Z. Time response of plasmonic spatial differentiators. Opt. Lett. 2019, 44, 4511–4514. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, X. Backscattering-Immune Computing of Spatial Differentiation by Nonreciprocal Plasmonics. Phys. Rev. Appl. 2019, 11, 054033. [Google Scholar] [CrossRef]
- Cordaro, A.; Kwon, H.; Sounas, D.; Koenderink, A.F.; Alù, A.; Polman, A. High-Index Dielectric Metasurfaces Performing Mathematical Operations. Nano Lett. 2019, 19, 8418–8423. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Wu, W.; Chen, R.; Chen, W.; Chen, R.; Ma, Y. Analog Optical Spatial Differentiators Based on Dielectric Metasurfaces. Adv. Opt. Mater. 2020, 8, 1901523. [Google Scholar] [CrossRef]
- Zhou, J.; Qian, H.; Chen, C.-F.; Zhao, J.; Li, G.; Wu, Q.; Luo, H.; Wen, S.; Liu, Z. Optical edge detection based on high-efficiency dielectric metasurface. Proc. Natl. Acad. Sci. USA 2019, 116, 11137. [Google Scholar] [CrossRef] [PubMed]
- Wan, L.; Pan, D.; Yang, S.; Zhang, W.; Potapov, A.A.; Wu, X.; Liu, W.; Feng, T.; Li, Z. Optical analog computing of spatial differentiation and edge detection with dielectric metasurfaces. Opt. Lett. 2020, 45, 2070–2073. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Zheng, H.; Kravchenko, I.I.; Valentine, J. Flat optics for image differentiation. Nat. Photonics 2020, 14, 316–323. [Google Scholar] [CrossRef]
- Saba, A.; Tavakol, M.R.; Karimi-Khoozani, P.; Khavasi, A. Two-Dimensional Edge Detection by Guided Mode Resonant Metasurface. IEEE Photonics Technol. Lett. 2018, 30, 853–856. [Google Scholar] [CrossRef]
- Kwon, H.; Sounas, D.; Cordaro, A.; Polman, A.; Alù, A. Nonlocal Metasurfaces for Optical Signal Processing. Phys. Rev. Lett. 2018, 121, 173004. [Google Scholar] [CrossRef]
- Kwon, H.; Cordaro, A.; Sounas, D.; Polman, A.; Alù, A. Dual-Polarization Analog 2D Image Processing with Nonlocal Metasurfaces. ACS Photonics 2020, 7, 1799–1805. [Google Scholar] [CrossRef]
- Del Hougne, P.; Lerosey, G. Leveraging Chaos for Wave-Based Analog Computation: Demonstration with Indoor Wireless Communication Signals. Phys. Rev. X 2018, 8, 041037. [Google Scholar] [CrossRef]
- Mohammadi Estakhri, N.; Edwards, B.; Engheta, N. Inverse-designed metastructures that solve equations. Science 2019, 363, 1333. [Google Scholar] [CrossRef]
- Youssefi, A.; Zangeneh-Nejad, F.; Abdollahramezani, S.; Khavasi, A. Analog computing by Brewster effect. Opt. Lett. 2016, 41, 3467–3470. [Google Scholar] [CrossRef] [PubMed]
- Xu, D.; He, S.; Zhou, J.; Chen, S.; Wen, S.; Luo, H. Goos–Hänchen effect enabled optical differential operation and image edge detection. Appl. Phys. Lett. 2020, 116, 211103. [Google Scholar] [CrossRef]
- Zhu, T.; Lou, Y.; Zhou, Y.; Zhang, J.; Huang, J.; Li, Y.; Luo, H.; Wen, S.; Zhu, S.; Gong, Q.; et al. Generalized Spatial Differentiation from the Spin Hall Effect of Light and Its Application in Image Processing of Edge Detection. Phys. Rev. Appl. 2019, 11, 034043. [Google Scholar] [CrossRef]
- Yan, W.; Qiu, M. Two-dimensional optical edge detection. Nat. Photonics 2020, 14, 268–269. [Google Scholar] [CrossRef]
- Monz, T.; Nigg, D.; Martinez, E.A.; Brandl, M.F.; Schindler, P.; Rines, R.; Wang, S.X.; Chuang, I.L.; Blatt, R. Realization of a scalable Shor algorithm. Science 2016, 351, 1068. [Google Scholar] [CrossRef]
- Rakhmanov, A.L.; Zagoskin, A.M.; Savel’ev, S.; Nori, F. Quantum metamaterials: Electromagnetic waves in a Josephson qubit line. Phys. Rev. B 2008, 77, 144507. [Google Scholar] [CrossRef]
- Zhang, W.; Cheng, K.; Wu, C.; Wang, Y.; Li, H.; Zhang, X. Implementing Quantum Search Algorithm with Metamaterials. Adv. Mater. 2017, 3, 1703986. [Google Scholar] [CrossRef]
- Cheng, K.; Zhang, W.; Wei, Z.; Fan, Y.; Xu, C.; Wu, C.; Zhang, X.; Li, H. Simulate Deutsch-Jozsa algorithm with metamaterials. Opt. Express 2020, 28, 16230–16243. [Google Scholar] [CrossRef]
- Lloyd, S. Quantum search without entanglement. Phys. Rev. A 1999, 61, 010301. [Google Scholar] [CrossRef]
- Karimi, P.; Khavasi, A.; Mousavi Khaleghi, S.S. Fundamental limit for gain and resolution in analog optical edge detection. Opt. Express 2020, 28, 898–911. [Google Scholar] [CrossRef]
- Wang, H.; Guo, C.; Zhao, Z.; Fan, S. Compact Incoherent Image Differentiation with Nanophotonic Structures. ACS Photonics 2020, 7, 338–343. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).