Design and Modelling of a Novel Integrated Photonic Device for Nano-Scale Magnetic Memory Reading
Abstract
Featured Application
Abstract
1. Introduction
2. Materials and Methods
2.1. Optical Simulation and Device Concept
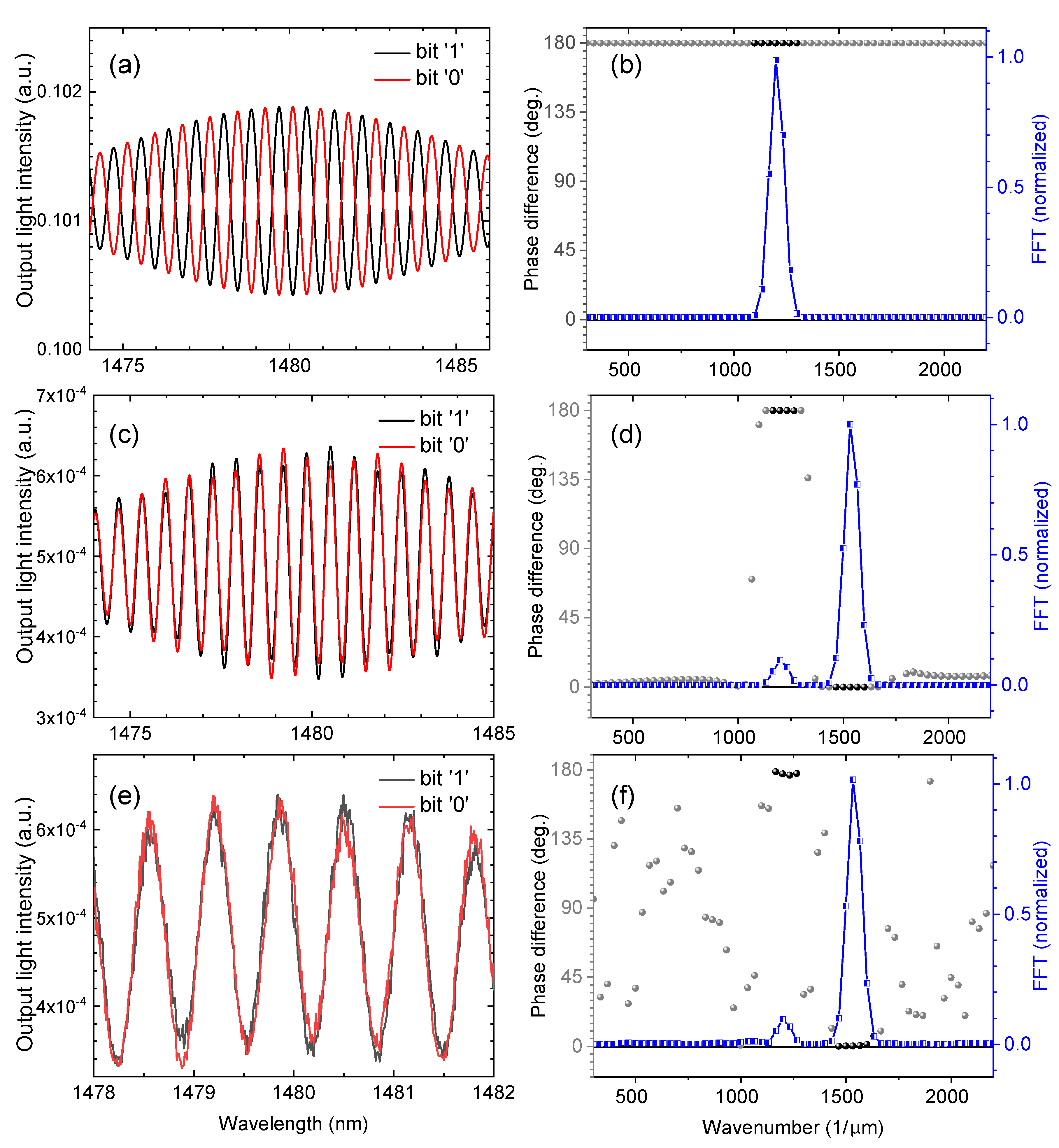
2.2. Mathematical Modelling and Fourier Transformation
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Goodman, J.W.; Leonberger, F.J.; Kung, S.-Y.; Athale, R.A. Optical interconnections for VLSI systems. Proc. IEEE 1984, 72, 850–866. [Google Scholar] [CrossRef]
- A Record Breaking Optical Chip. Available online: https://www.technologyreview.com/2008/06/25/219782/a-record-breaking-optical-chip/ (accessed on 11 November 2020).
- Intel Leverages Chip Might Etch Photonics Future. Available online: https://www.nextplatform.com/2016/08/17/intel-leverages-chip-might-etch-photonics-future/ (accessed on 11 November 2020).
- Kish, F.; Lal, V.; Evans, P.; Corzine, S.W.; Ziari, M.; Butrie, T.; Reffle, M.; Tsai, H.S.; Dentai, A.; Pleumeekers, J.; et al. System-on-chip photonic integrated circuits. IEEE J. Sel. Top. Quantum Electron. 2017, 24, 1–20. [Google Scholar] [CrossRef]
- Sun, C.; Wade, M.T.; Lee, Y.; Orcutt, J.S.; Alloatti, L.; Georgas, M.S.; Waterman, A.S.; Shainline, J.M.; Avizienis, R.R.; Lin, S.; et al. Single-chip microprocessor that communicates directly using light. Nature 2015, 528, 534–538. [Google Scholar] [CrossRef]
- Atabaki, A.H.; Moazeni, S.; Pavanello, F.; Gevorgyan, H.; Notaros, J.; Alloatti, L.; Wade, M.T.; Sun, C.; Kruger, S.A.; Meng, H.; et al. Integrating photonics with silicon nanoelectronics for the next generation of systems on a chip. Nature 2018, 556, 349–354. [Google Scholar] [CrossRef]
- Smit, M.; Williams, K.; Van Der Tol, J. Past, present, and future of InP-based photonic integration. APL Photonics 2019, 4, 050901. [Google Scholar] [CrossRef]
- Stanciu, C.; Hansteen, F.; Kimel, A.; Kirilyuk, A.; Tsukamoto, A.; Itoh, A.; Rasing, T. All-optical magnetic recording with circularly polarized light. Phys. Rev. Lett. 2007, 99, 047601. [Google Scholar] [CrossRef]
- Lalieu, M.; Peeters, M.; Haenen, S.; Lavrijsen, R.; Koopmans, B. Deterministic all-optical switching of synthetic ferrimagnets using single femtosecond laser pulses. Phys. Rev. B 2017, 96, 220411. [Google Scholar] [CrossRef]
- Van Hees, Y.; van der Tol, J.; Koopmans, B.; Lavrijsen, R. Periodically modulated ferromagnetic waveguide claddings with perpendicular magnetic anisotropy for enhanced mode conversion. IEEE Photonics Benelux Proc. 2017, 196–199. Available online: http://www.photonics-benelux.org/images/stories/media/proceedings/2017/s17p196.pdf (accessed on 21 November 2020).
- Kerr, J. On rotation of the plane of polarization by reflection from the pole of a magnet. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1877, 3, 321–343. [Google Scholar] [CrossRef]
- Freiser, M. A survey of magnetooptic effects. IEEE Trans. Magn. 1968, 4, 152–161. [Google Scholar] [CrossRef]
- Parkin, S.S.; Hayashi, M.; Thomas, L. Magnetic domain-wall racetrack memory. Science 2008, 320, 190–194. [Google Scholar] [CrossRef] [PubMed]
- Ryu, K.S.; Thomas, L.; Yang, S.H.; Parkin, S.S. Current induced tilting of domain walls in high velocity motion along perpendicularly magnetized micron-sized Co/Ni/Co racetracks. Appl. Phys. Express 2012, 5, 093006. [Google Scholar] [CrossRef]
- Yang, S.H.; Ryu, K.S.; Parkin, S. Domain-wall velocities of up to 750 m s- 1 driven by exchange-coupling torque in synthetic antiferromagnets. Nat. Nanotechnol. 2015, 10, 221–226. [Google Scholar] [CrossRef] [PubMed]
- Caretta, L.; Mann, M.; Büttner, F.; Ueda, K.; Pfau, B.; Günther, C.M.; Hessing, P.; Churikova, A.; Klose, C.; Schneider, M.; et al. Fast current-driven domain walls and small skyrmions in a compensated ferrimagnet. Nat. Nanotechnol. 2018, 13, 1154–1160. [Google Scholar] [CrossRef] [PubMed]
- Franken, J.; Swagten, H.; Koopmans, B. Shift registers based on magnetic domain wall ratchets with perpendicular anisotropy. Nat. Nanotechnol. 2012, 7, 499–503. [Google Scholar] [CrossRef]
- Wang, M.; Zhang, Y.; Zhao, X.; Zhao, W. Tunnel junction with perpendicular magnetic anisotropy: Status and challenges. Micromachines 2015, 6, 1023–1045. [Google Scholar] [CrossRef]
- Fiedler, S.; Stillrich, H.; Oepen, H.P. Magneto-optic properties of electron cyclotron resonance ion beam sputtered and magnetron sputtered Co/Pt multilayers. J. Appl. Phys. 2007, 102, 083906. [Google Scholar] [CrossRef]
- Krinchik, G.S.; Artemjev, V.A. Magneto-optic Properties of Nickel, Iron, and Cobalt. J. Appl. Phys. 1968, 39, 1276–1278. [Google Scholar] [CrossRef]
- Van der Tol, J.J.G.M.; Jiao, Y.; Van Engelen, J.P.; Pogoretskiy, V.; Kashi, A.A.; Williams, K. InP Membrane on Silicon (IMOS) Photonics. IEEE J. Quantum Electron. 2020, 56, 1–7. [Google Scholar] [CrossRef]
- Lavrijsen, R.; Hartmann, D.M.F.; van den Brink, A.; Yin, Y.; Barcones, B.; Duine, R.A.; Verheijen, M.A.; Swagten, H.J.M.; Koopmans, B. Asymmetric magnetic bubble expansion under in-plane field in Pt/Co/Pt: Effect of interface engineering. Phys. Rev. B 2015, 91, 104414. [Google Scholar] [CrossRef]
- Višňovskỳ, Š.; Jakubisová Lišková, E.; Nỳvlt, M.; Krishnan, R. Origin of magneto-optic enhancement in CoPt alloys and Co/Pt multilayers. Appl. Phys. Lett. 2012, 100, 232409. [Google Scholar] [CrossRef]
- Lumerical Solutions. Available online: https://www.lumerical.com/products/ (accessed on 29 October 2020).
- Atkinson, R.; Pahirathan, S.; Salter, I.W.; Grundy, P.J.; Tatnall, C.J.; Lodder, J.C.; Meng, Q. Fundamental optical and magneto-optical constants of CoPt and CoNiPt multilayered films. J. Magn. Magn. Mater. 1996, 162, 131–138. [Google Scholar] [CrossRef][Green Version]
- Pello, J.; van der Tol, J.; Keyvaninia, S.; van Veldhoven, R.; Ambrosius, H.; Roelkens, G.; Smit, M. High-efficiency ultrasmall polarization converter in InP membrane. Opt. Lett. 2012, 37, 3711–3713. [Google Scholar] [CrossRef] [PubMed][Green Version]
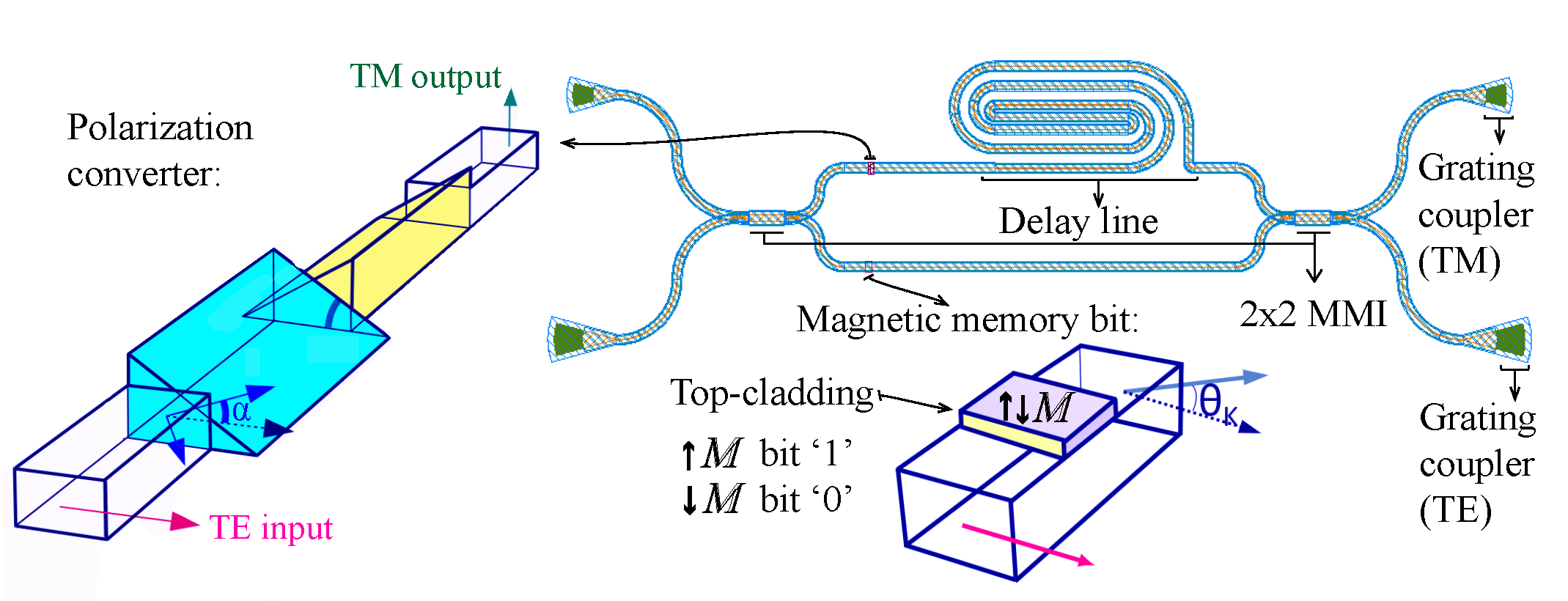
| Parameters | Definitions |
|---|---|
| Wavelength scanned (nm) | |
| Waveguide propagation loss (assumed to be the same for and ) | |
| Effective index of mode | |
| Effective index of mode | |
| Length of the upper branch (m) | |
| Length of the lower branch (m) | |
| Distance between polarization converter and left-hand side MMI splitter (m) | |
| Distance between memory bit (cladding) and left-hand side MMI splitter (m) | |
| Loss due to memory bit (cladding) | |
| Loss of -selective grating coupler for mode (dB) | |
| Kerr rotation | |
| Kerr ellipticity | |
| Angle of mode tilt induced by polarization converter (degree) | |
| Loss of -selective grating coupler for mode (dB) | |
| Extinction ratio of -selective grating coupler for mode (dB) | |
| Noise | Addition of a Gaussian distribution of random noise to the intensity |
| Parameter | Value |
| 1465–1495 nm | |
| 3 dB/cm | |
| 2.012 | |
| 1.809 | |
| Parameter | Value |
| 1386 m | |
| 462 m | |
| 200 m | |
| 100 m | |
| Parameter | Value |
| 0.13 dB/50 nm | |
| 1.5 dB | |
| ±0.2 | |
| ±0.2 |
| Parameter | Standard Device | Reduced Performance | Noise + Reduced Performance |
|---|---|---|---|
| 1.5 dB | 7 dB | 7 dB | |
| 50 dB | 28 dB | 28 dB | |
| Noise | none | none | 10.7 dB (SNR) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Demirer, F.E.; van den Bomen, C.; Lavrijsen, R.; van der Tol, J.J.G.M.; Koopmans, B. Design and Modelling of a Novel Integrated Photonic Device for Nano-Scale Magnetic Memory Reading. Appl. Sci. 2020, 10, 8267. https://doi.org/10.3390/app10228267
Demirer FE, van den Bomen C, Lavrijsen R, van der Tol JJGM, Koopmans B. Design and Modelling of a Novel Integrated Photonic Device for Nano-Scale Magnetic Memory Reading. Applied Sciences. 2020; 10(22):8267. https://doi.org/10.3390/app10228267
Chicago/Turabian StyleDemirer, Figen Ece, Chris van den Bomen, Reinoud Lavrijsen, Jos J. G. M. van der Tol, and Bert Koopmans. 2020. "Design and Modelling of a Novel Integrated Photonic Device for Nano-Scale Magnetic Memory Reading" Applied Sciences 10, no. 22: 8267. https://doi.org/10.3390/app10228267
APA StyleDemirer, F. E., van den Bomen, C., Lavrijsen, R., van der Tol, J. J. G. M., & Koopmans, B. (2020). Design and Modelling of a Novel Integrated Photonic Device for Nano-Scale Magnetic Memory Reading. Applied Sciences, 10(22), 8267. https://doi.org/10.3390/app10228267





