A Fast, Decentralized, Self-Aligned Carrier Method for Multicellular Converters †
Abstract
1. Introduction
2. Conventional Phase-Shifted Carrier Generation Method
3. Proposed Decentralized Self-Aligned Carrier Method
3.1. Proposed Decentralized Self-Aligned Phase-Shifted Carrier Method
3.2. Proposed Decentralized Self-Aligned Level-Shifted Carrier Method
4. Simulation Results
4.1. Simulation Models
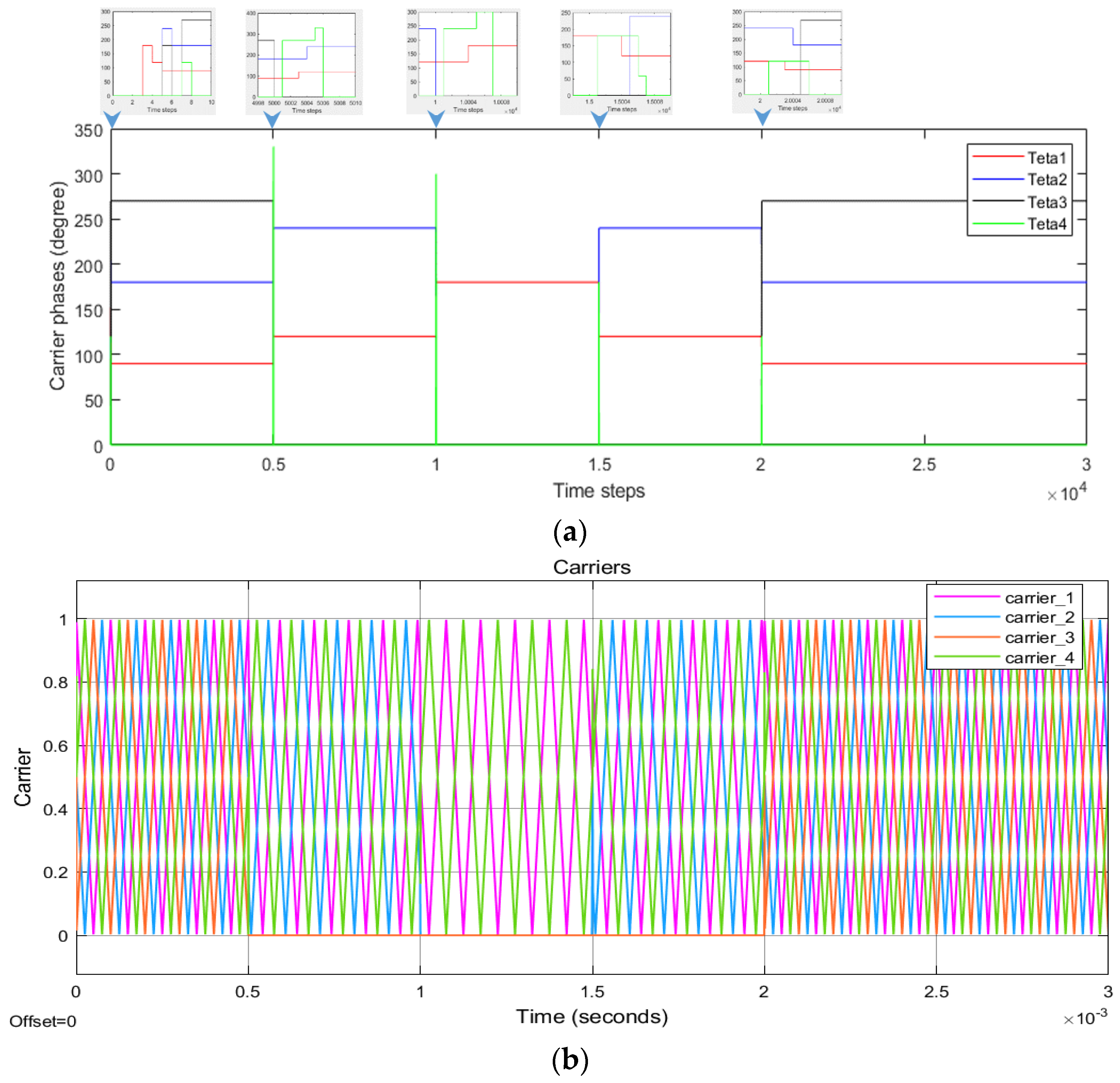
4.2. Evaluation of the Proposed DSA-PSC Method
4.3. Evaluation of the Proposed DSA-LSC Method
4.4. Evaluate the System Configuration Time
4.5. Evaluate the System Reconfiguration Time
5. Experimental Result
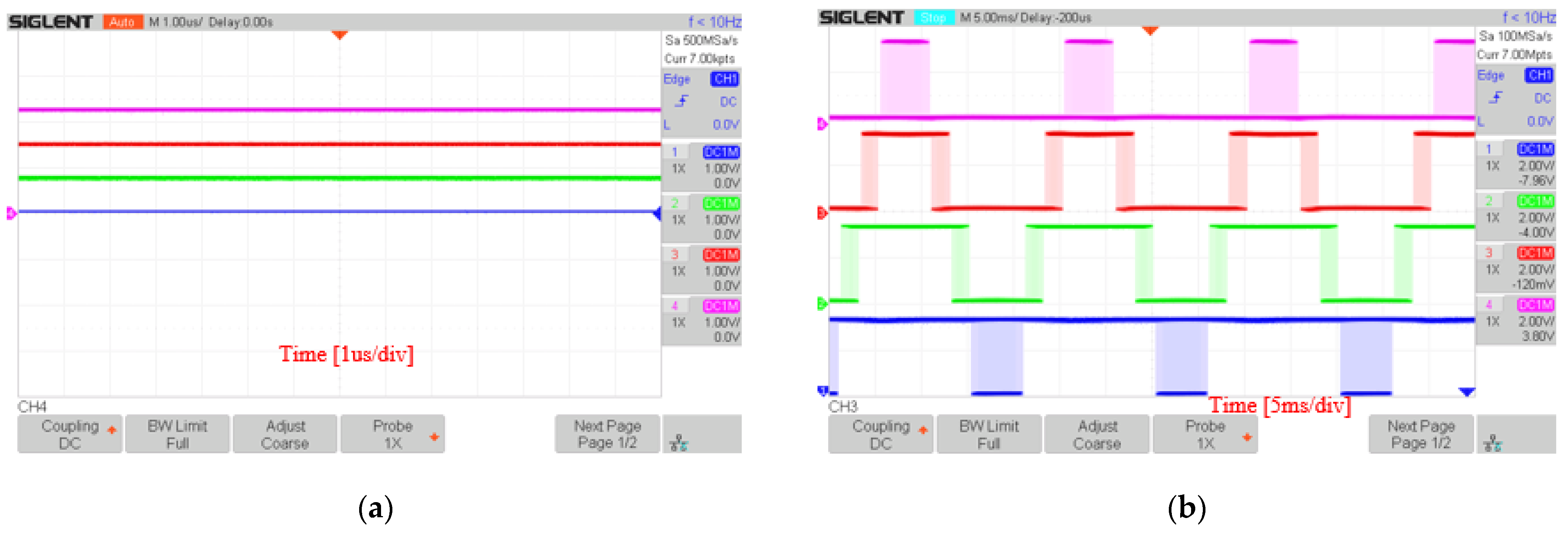
5.1. Experiment with DSA-PSC Method
5.2. Experiment with DSA-LSC Method
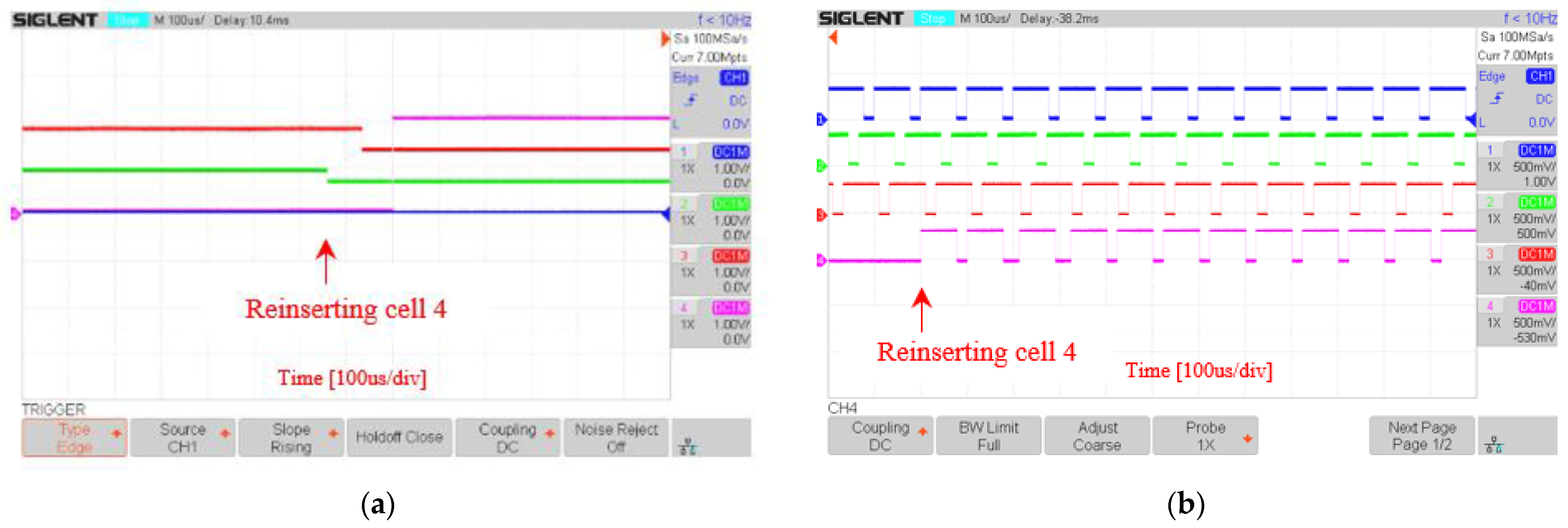
5.3. System Reconfiguration Speed
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Costabeber, A.; Mattavelli, P.; Saggini, S. Digital Time-Optimal Phase Shedding in Multiphase Buck Converters. IEEE Trans. Power Electron. 2010, 25, 2242–2247. [Google Scholar] [CrossRef]
- Roh, Y.-S.; Moon, Y.-J.; Park, J.; Jeong, M.-G.; Yoo, C. A Multiphase Synchronous Buck Converter with a Fully Integrated Current Balancing Scheme. IEEE Trans. Power Electron. 2015, 30, 5159–5169. [Google Scholar] [CrossRef]
- Rodriguez, J.; Lai, J.-S.; Peng, F.Z. Multilevel inverters: A survey of topologies, controls, and applications. IEEE Trans. Ind. Electron. 2002, 49, 724–738. [Google Scholar] [CrossRef]
- Rodriguez, J.; Bernet, S.; Wu, B.; Pontt, J.; Kouro, S. Multilevel Voltage-Source-Converter Topologies for Industrial Medium-Voltage Drives. IEEE Trans. Ind. Electron. 2007, 54, 2930–2945. [Google Scholar] [CrossRef]
- Kouro, S.; Malinowski, M.; Gopakumar, K.; Pou, J.; Franquelo, L.G.; Wu, B.; Rodriguez, J.; Perez, M.A.; Leon, J.I. Recent Advances and Industrial Applications of Multilevel Converters. IEEE Trans. Ind. Electron. 2010, 57, 2553–2580. [Google Scholar] [CrossRef]
- Lesnicar, A.; Marquardt, R. An innovative modular multilevel converter topology suitable for a wide power range. In Proceedings of the 2003 IEEE Bologna Power Tech Conference Proceedings, Bologna, Italy, 23–26 June 2003; Volume 3, p. 6. [Google Scholar] [CrossRef]
- Akagi, H. Classification, Terminology, and Application of the Modular Multilevel Cascade Converter (MMCC). IEEE Trans. Power Electron. 2011, 26, 3119–3130. [Google Scholar] [CrossRef]
- Poblete, P.; Pereda, J.; Nunez, F.; Aguilera, R.P. Distributed Current Control of Cascaded Multilevel Inverters. In Proceedings of the 2019 IEEE International Conference on Industrial Technology (ICIT), Melbourne, Australia, 13–15 February 2019; pp. 1509–1514. [Google Scholar]
- Xia, B.; Li, Y.; Li, Z.; Konstantinou, G.; Xu, F.; Gao, F.; Wang, P. Decentralized Control Method for Modular Multilevel Converters. IEEE Trans. Power Electron. 2019, 34, 5117–5130. [Google Scholar] [CrossRef]
- Gateau, G.; Dung, P.; Cousineau, M.; Do, P.T.; Nhan, L.H.; Le, H.N. Digital implementation of decentralized control for multilevel converter. In Proceedings of the 2017 International Conference on System Science and Engineering (ICSSE), Ho Chi Minh City, Vietnam, 21–23 July 2017; pp. 558–562. [Google Scholar] [CrossRef]
- Xu, B.; Tu, H.; Du, Y.; Yu, H.; Liang, H.; Lukic, S. A Distributed Control Architecture for Cascaded H-Bridge Converter. In Proceedings of the 2019 IEEE Applied Power Electronics Conference and Exposition (APEC), Anaheim, CA, USA, 17–21 March 2019; pp. 3032–3038. [Google Scholar] [CrossRef]
- Liu, J.; Yao, W.; Lu, Z.; Du, L.; Ji, Y. A distributed control structure and synchronization method for complex converter based on CAN. In Proceedings of the 2017 IEEE Southern Power Electronics Conference (SPEC), Puerto Varas, Chile, 4–7 December 2017; pp. 1–6. [Google Scholar] [CrossRef]
- McGrath, B.P.; Holmes, D.G.; Kong, W.Y. A Decentralized Controller Architecture for a Cascaded H-Bridge Multilevel Converter. IEEE Trans. Ind. Electron. 2014, 61, 1169–1178. [Google Scholar] [CrossRef]
- Wang, P.; Tang, Y.; Tu, P.; Wang, P. A fault-tolerant operation scheme for a modular multilevel converter with a distributed control architecture. In Proceedings of the 2017 IEEE Energy Conversion Congress and Exposition (ECCE), Cincinnati, OH, USA, 1–5 October 2017; pp. 4163–4170. [Google Scholar] [CrossRef]
- Yang, S.; Tang, Y.; Zagrodnik, M.; Amit, G.; Wang, P. A novel distributed control strategy for modular multilevel converters. In Proceedings of the 2017 IEEE Applied Power Electronics Conference and Exposition (APEC), Tampa, FL, USA, 26–30 March 2017; pp. 3234–3240. [Google Scholar] [CrossRef]
- Liu, J.; Yao, W.; Lu, Z.; Ma, J. Design and implementation of a distributed control structure for modular multilevel matrix converter. In Proceedings of the 2018 IEEE Applied Power Electronics Conference and Exposition (APEC), San Antonio, TX, USA, 4–8 March 2018; pp. 1934–1939. [Google Scholar] [CrossRef]
- Burlacu, P.D.; Mathe, L.; Teodorescu, R. Synchronization of the distributed PWM carrier waves for modular multilevel converters. In Proceedings of the 2014 International Conference on Optimization of Electrical and Electronic Equipment (OPTIM), Bran, Romania, 22–24 October 2014; pp. 553–559. [Google Scholar] [CrossRef]
- Huang, S.; Mathe, L.; Teodorescu, R. A new method to implement resampled uniform PWM suitable for distributed control of modular multilevel converters. In Proceedings of the IECON 2013—39th Annual Conference of the IEEE Industrial Electronics Society, Vienna, Austria, 10–13 November 2013; pp. 228–233. [Google Scholar] [CrossRef]
- Rong, Y.; Wang, J.; Shen, Z.; Burgos, R.; Boroyevich, D.; Zhou, S. Distributed Control and Communication System for PEBB-based Modular Power Converters. In Proceedings of the 2019 IEEE Electric Ship Technologies Symposium (ESTS), Washington, DC, USA, 14–16 August 2019; pp. 627–633. [Google Scholar] [CrossRef]
- Sinha, M.; Poon, J.; Johnson, B.B.; Rodriguez, M.; Dhople, S.V. Decentralized Interleaving of Parallel-connected Buck Converters. IEEE Trans. Power Electron. 2019, 34, 4993–5006. [Google Scholar] [CrossRef]
- Dutta, S.; Mallik, R.; Majmunovic, B.; Mukherjee, S.; Seo, G.-S.; Maksimovic, D.; Johnson, B. Decentralized Carrier Interleaving in Cascaded Multilevel DC-AC Converters. In Proceedings of the 2019 20th Workshop on Control and Modeling for Power Electronics (COMPEL), Toronto, ON, Canada, 16–19 June 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Phan, Q.D.; Gateau, G.; Nguyen, M.T.; Cousineau, M. 2D Decentralized Interleaving Principle for Multicell Serial-Parallel Converters. In Proceedings of the 2019 IEEE 13th International Conference on Power Electronics and Drive Systems (PEDS), Toulouse, France, 9–12 July 2019; pp. 1–7. [Google Scholar] [CrossRef]
- Cousineau, M.; le Bolloch, M.; Bouhalli, N.; Sarraute, E.; Meynard, T. Triangular carrier self-alignment using modular approach for interleaved converter control. In Proceedings of the 2011 14th European Conference on Power Electronics and Applications, Birmingham, UK, 30 August–1 September 2011; pp. 1–10. [Google Scholar]
- Xiao, Z.; Cousineau, M. Modular interleaved carrier generator using a straightforward implementation method. In Proceedings of the 2013 IEEE 11th International Workshop of Electronics, Control, Measurement, Signals and their application to Mechatronics, Toulouse, France, 24–26 June 2013; pp. 1–6. [Google Scholar] [CrossRef]
- Grégoire, L.-A.; Cousineau, M.; Seleme, I.S.; Ladoux, P. Real-Time Simulation of Interleaved Converters with Decentralized Control. In Proceedings of the International Conference on Renewable Energies and Power Quality (ICREPQ’16), Madrid, Spain, 4–6 May 2016; pp. 15–64. [Google Scholar]
- Gateau, G.; Cousineau, M.; Mannes-Hillesheim, M.; Dung, P. Digital Decentralized Current Control for Parallel Multiphase Converter. In Proceedings of the 2019 IEEE International Conference on Industrial Technology (ICIT), Melbourne, Australia, 13–15 February 2019; pp. 1761–1766. [Google Scholar] [CrossRef]
- Cousineau, M.; Xiao, Z. Fully decentralized modular approach for parallel converter control. In Proceedings of the 2013 Twenty-Eighth Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 17–21 March 2013; pp. 237–243. [Google Scholar] [CrossRef]
- Cousineau, M.; Xiao, Z. Fully masterless control of parallel converter. In Proceedings of the 2013 15th European Conference on Power Electronics and Applications (EPE), Lille, France, 2–6 September 2013; pp. 1–10. [Google Scholar] [CrossRef]
- Seleme, S.I.; Gregoire, L.A.; Cousineau, M.; Ladoux, P. Modular control with carrier auto-interleaving and capacitor-voltage balancing for MMCs. IET Power Electron. 2019, 12, 817–828. [Google Scholar] [CrossRef]
- Gao, H.; Wang, Y. On Phase Response Function Based Decentralized Phase Desynchronization. IEEE Trans. Signal Process. 2017, 65, 5564–5577. [Google Scholar] [CrossRef]
- Sinha, M.; Dorfler, F.; Johnson, B.; Dhople, S. Stabilizing Phase-balanced or Phase-synchronized Trajectories of Van der Pol Oscillators in Uniform Electrical Networks. In Proceedings of the 2018 56th Annual Allerton Conference on Communication, Control, and Computing (Allerton), Monticello, IL, USA, 2–5 October 2018; pp. 335–340. [Google Scholar] [CrossRef]
- Duma, R.; Dobra, P.; Abrudean, M.; Dobra, M. Rapid prototyping of control systems using embedded target for TI C2000 DSP. In Proceedings of the 2007 Mediterranean Conference on Control & Automation, Athens, Greece, 27–29 June 2007; pp. 1–5. [Google Scholar] [CrossRef]
- Dos Santos, B.; Araujo, R.E.; Varajao, D.; Pinto, C. Rapid Prototyping Framework for real-time control of power electronic converters using simulink. In Proceedings of the IECON 2013—39th Annual Conference of the IEEE Industrial Electronics Society, Vienna, Austria, 10–13 November 2013; pp. 2303–2308. [Google Scholar] [CrossRef]
- Katzir, L.; Loewenstern, Y.; Bishara, B.; Shmilovitz, D. Implementation of a high voltage power supply with the MATLAB/Simulink embedded coder. In Proceedings of the 2014 IEEE 28th Convention of Electrical & Electronics Engineers in Israel (IEEEI), Eilat, Israel, 3–5 December 2014; pp. 1–4. [Google Scholar] [CrossRef]















































| Input | Output | ||
|---|---|---|---|
| EN | Enable | ||
| teta_base | send_teta | ||
| count_in | Index from cell n−1, | count_out | Index from cell n, |
| number_in | Received total number from previous cells | number_out | Transmitted total number to next cell |
| Vrf_in | Received signal reference voltage from previous cell | Vrf_out | Transmitted signal reference voltage to next cell |
| clk_in | Received synchronous clock pulse from master cell | clk_out | Transmitted synchronous clock pulse to other cell |
| Input | Output | ||
|---|---|---|---|
| EN | Enable | ||
| ampl_base | ampl_min | ||
| count_in | Index from cell n−1, | count_out | Index from cell n, |
| number_in | Received total number of cells | number_out | Transmitted total number of cells to the next cell |
| Vrf_in | Received modulation index of referenced voltage from the previous cell | Vrf_out | Transmitted modulation index of referenced voltage to the next cell |
| Frf_in | Received referenced frequency from the previous cell | Frf_out | Transmitted frequency to the next cell |
| clk_in | Received synchronous clock pulse from the master cell | clk_out | Transmitted synchronous clock pulse to other cell |
| Parameter | Symbol | Unit | Value |
|---|---|---|---|
| Output inductor | L1 … L4, R1 … R4, | H Ω | 0.06 2.5 |
| Load resistor | R | Ω | 20 |
| Voltage source | E | V | 100 |
| Switching frequency | fsw | kHz | 10 |
| Sampling time | Ts | s | 1 × 10−7 |
| Duty_cycle | D | 0.8 |
| Parameter | Symbol | Unit | Value |
|---|---|---|---|
| Load resistor | R | Ω | 100 |
| Voltage source | Vdc1 …… Vdc8 | V | 40 |
| Switching frequency | fsw | kHz | 10 |
| Sampling time | Ts | s | 1 × 10−7 |
| Modulation index | M | 0.8 |
| Number of Cells in the System | Conventional Modified Updating Rule (K = 0.66; ε(Δθn, n+1) ≤ (10−4)0) | Proposed DSA-PSC Method (ε(Δθn, n+1) = 00) | |
|---|---|---|---|
| Number of time steps | 4 | 14 | 8 |
| 6 | 28 | 12 | |
| 13 | 170 | 26 |
| Actions | Conventional Modified Updating Rule (K = 0.66; ε(Δθn, n+1) ≤ (10−4)0) | Proposed DSA-PSC Method (ε(Δθn, n+1) = 00) | |
|---|---|---|---|
| Number of time steps | Removing cell 3 | 17 | 10 |
| Removing cell 5 | 24 | 8 | |
| Reinserting cell 5 | 15 | 8 | |
| Reinserting cell 3 | 24 | 10 |
| Component | Information |
|---|---|
| Controller board | C2000 Delfino MCUs F28379D LaunchPad Development Kit, Texas Instruments, Dallas, TX, USA |
| Power circuit | IGBT GW40N120KD |
| Driver circuit | Hybrid integrated IGBT driver MORNSUN QP12W08S-37, MORNSUN Guangzhou Science & Technology Co., Ltd. |
| Current sensor | Current Transducer LTS 15-NP IPN = 15 At, LEM Tektronix A622 AC/DC current probe |
| Parameter | Pin on DSP | Function |
|---|---|---|
| count_in | GPIO 97, 94, 65 | Get information of cell index from the previous cell |
| count_out | GPIO 130, 63, 64 | Send information of cell index to the next cell |
| number_in | GPIO 52, 41, 40 | Get information of total number of cell in the system |
| number_out | GPIO 26, 27, 25 | Send information of total number of cell in the system |
| EN | GPIO 66 | Enable to Activate/Deactivate the cell |
| clk_in | GPIO 14 | Receive synchronous clock pulse |
| clk_out | GPIO 04 | Send information of synchronous clock pulse to the next cell |
| teta_base | ADCA15 | Get information of carrier phase angle from the previous cell |
| send_teta | DACB | Send information of carrier phase angle to the next cell |
| Vrf_in | ADCA14 | Get information of modulation index of master cell |
| Vrf_out | DACA | Send information of modulation index to orther cell |
| B signal | GPIO 0 | IGBT control signal B (high-side switch) |
| H signal | GPIO 1 | IGBT control signal H (low-side switch) |
| Parameter | Symbol | Unit | Value |
|---|---|---|---|
| Output inductor | L1 … L4, R1 … R4, | H Ω | 0.06 2.5 |
| Load resistor | R | Ω | 20 |
| Voltage source | E | V | 100 |
| Switching frequency | fsw | Hz | 10,000 |
| Sampling time | Ts | s | 5 × 10−5 |
| Duty cycle | D | 0.8 |
| Parameter | Pin on DSP | Function |
|---|---|---|
| count_in | GPIO 97, 94, 65 | Get information of cell index from the previous cell |
| count_out | GPIO 130, 63, 64 | Send information of cell index to the next cell |
| number_in | GPIO 52, 41, 40 | Get information of total number of cells |
| number_out | GPIO 26, 27, 25 | Send information of total number of cells |
| EN | GPIO 66 | Enable to Activate/Deactivate a cell |
| clk_in | GPIO 14 | Receive synchronous clock pulse |
| clk_out | GPIO 04 | Send information of synchronous clock pulse to the next cell |
| Teta_base | ADCA15 | Get information of phase from the previous cell |
| Send_teta | DACB | Send information of phase to the next cell |
| Vrf_in | ADCA14 | Get information of modulation index from the previous cell |
| Vrf_out | DACA | Send information of modulation index to the next cell |
| Frf_in | GPIO 105, 104, 95, 139, 56, 10, 11 | Get information of frequency from the previous cell |
| Frf_out | GPIO 29, 131, 05, 24, 16, 06, 07 | Send information of frequency to the next cell |
| B signal | GPIO 0 | IGBT control signal B |
| H signal | GPIO 1 | IGBT control signal H |
| Parameter | Symbol | Unit | Value |
|---|---|---|---|
| Load resistor | R | Ω | 100 |
| Voltage source | Vdc1 …… Vdc8 | V | 40 |
| Switching frequency | fsw | Hz | 10,000 |
| Sampling time | Ts | s | 5 × 10−5 |
| Modulation index | M | 0.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Phan, Q.D.; Gateau, G.; Nguyen, P.C.; Cousineau, M.; To, H.P.; Nguyen, B.A.; Veit, L.; De Milly, R.; Hillesheim, M.M. A Fast, Decentralized, Self-Aligned Carrier Method for Multicellular Converters. Appl. Sci. 2021, 11, 137. https://doi.org/10.3390/app11010137
Phan QD, Gateau G, Nguyen PC, Cousineau M, To HP, Nguyen BA, Veit L, De Milly R, Hillesheim MM. A Fast, Decentralized, Self-Aligned Carrier Method for Multicellular Converters. Applied Sciences. 2021; 11(1):137. https://doi.org/10.3390/app11010137
Chicago/Turabian StylePhan, Quoc Dung, Guillaume Gateau, Phu Cong Nguyen, Marc Cousineau, Huu Phuc To, Bao Anh Nguyen, Lucas Veit, Romain De Milly, and M.Mannes Hillesheim. 2021. "A Fast, Decentralized, Self-Aligned Carrier Method for Multicellular Converters" Applied Sciences 11, no. 1: 137. https://doi.org/10.3390/app11010137
APA StylePhan, Q. D., Gateau, G., Nguyen, P. C., Cousineau, M., To, H. P., Nguyen, B. A., Veit, L., De Milly, R., & Hillesheim, M. M. (2021). A Fast, Decentralized, Self-Aligned Carrier Method for Multicellular Converters. Applied Sciences, 11(1), 137. https://doi.org/10.3390/app11010137






