Fast Simulation of Laser Heating Processes on Thin Metal Plates with FFT Using CPU/GPU Hardware
Abstract
1. Introduction
2. Literature Review
2.1. Laser Heating/Cutting Simulation
2.2. FFT-Based Laser Heating Simulation
2.3. Conclusions of the Literature Review
3. Methodology
3.1. Heat Transfer Equation for Laser Heating on Thin Plates
3.2. Analytic Solution
3.3. Discrete Fourier Transform (DFT) and Fast Fourier Transform (FFT)
3.4. Scheme 1—Discrete Sine Transform (DST)
| Algorithm 1 Retrieve temperature using a 2D DST |
| Require: Ensure:
|
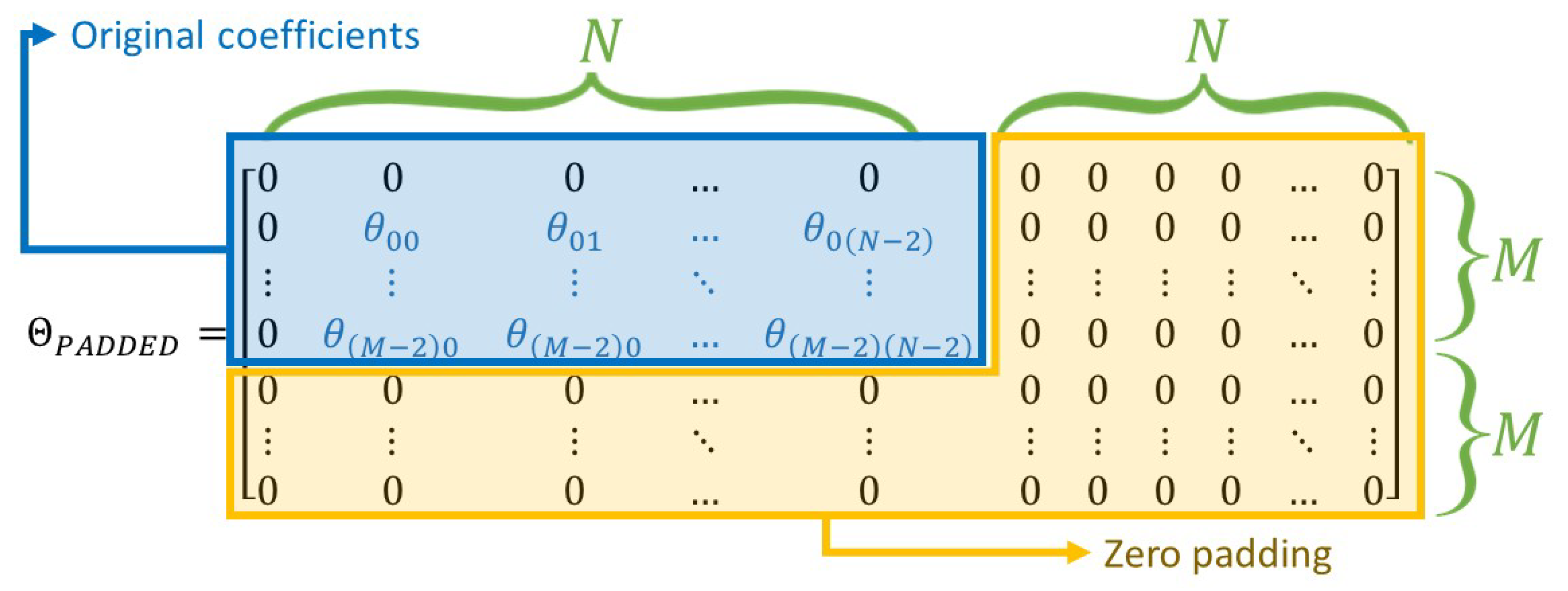
3.5. Scheme 2—FFT Padded with Zeros
| Algorithm 2 Retrieve temperature using a Fast Fourier Transform (FFT) with zero padding |
| Require: Ensure:
|
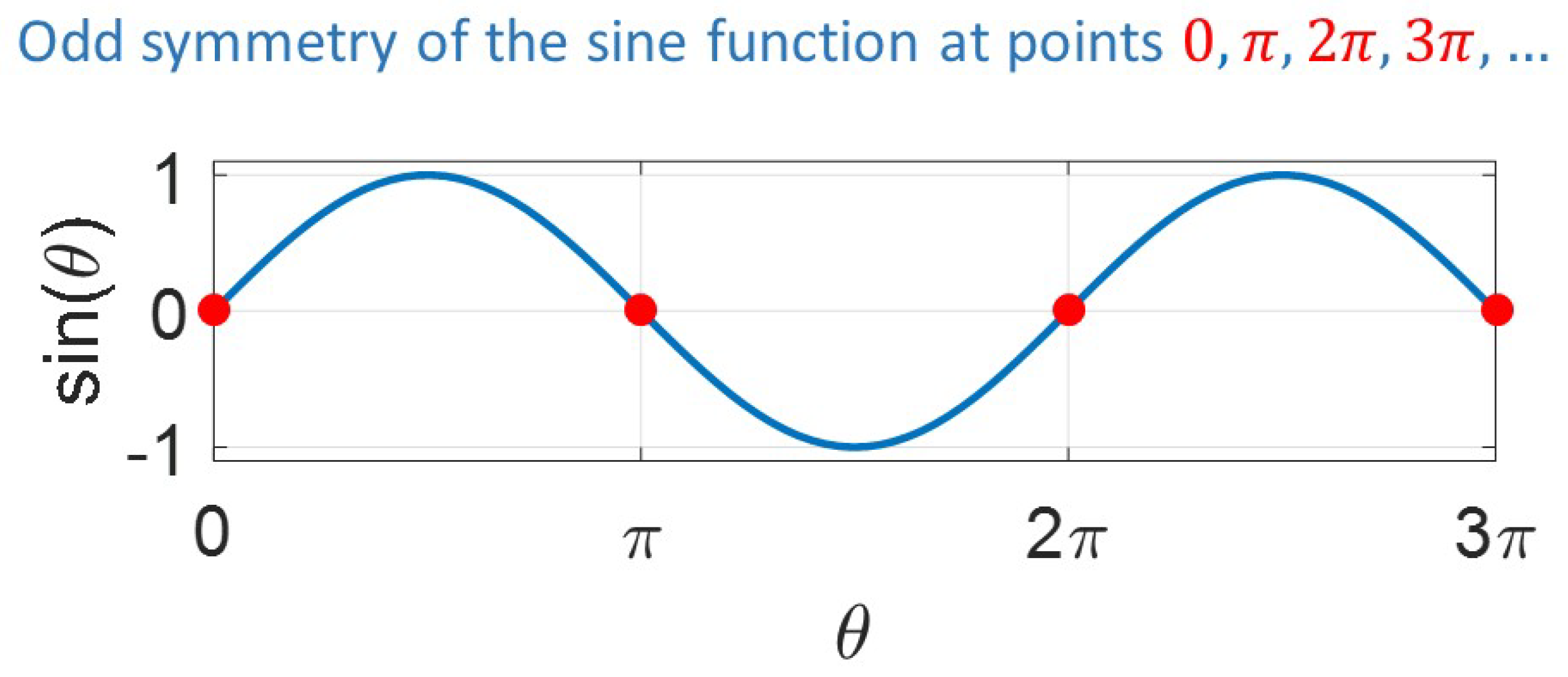
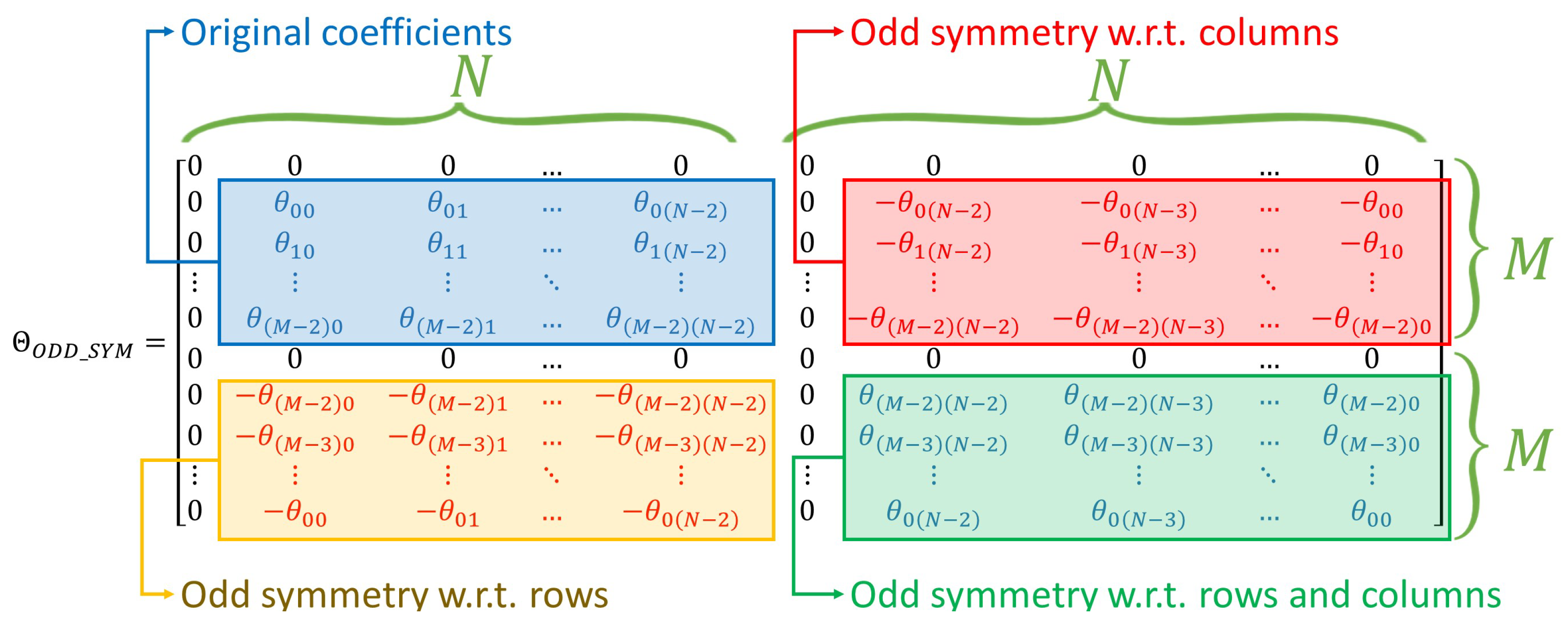
3.6. Scheme 3—Odd-Symmetry 1D FFT
| Algorithm 3 Retrieve temperature using 1D FFTs by applying odd symmetry to the original coefficients |
| Require: Ensure:
|
3.7. Scheme 4—Odd-Symmetry 2D FFT
| Algorithm 4 Retrieve temperature using 2D FFTs by applying odd sine symmetry and even cosine symmetry to the original coefficients |
| Require: Ensure:
|
3.8. Complexity Analysis
4. Results
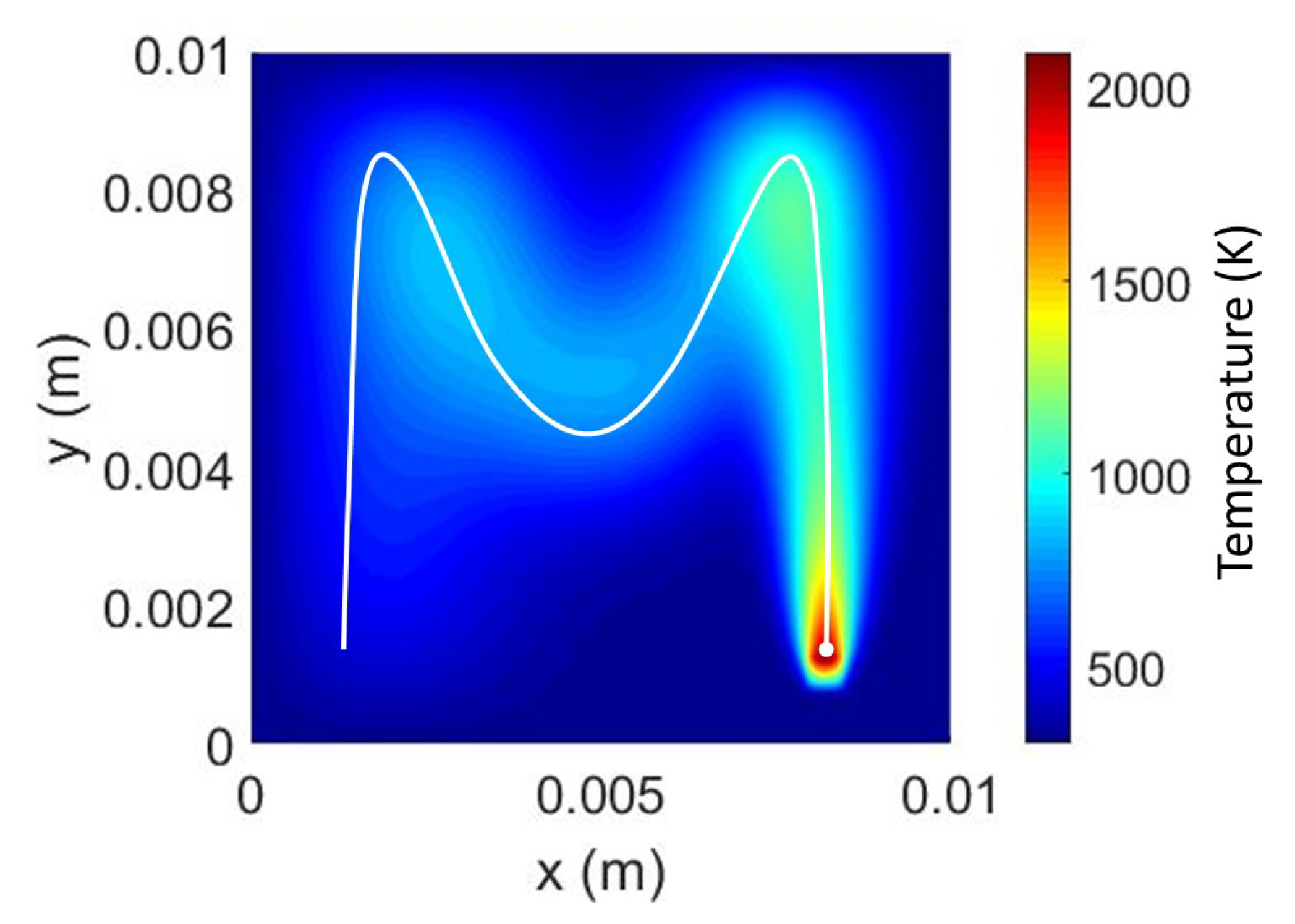
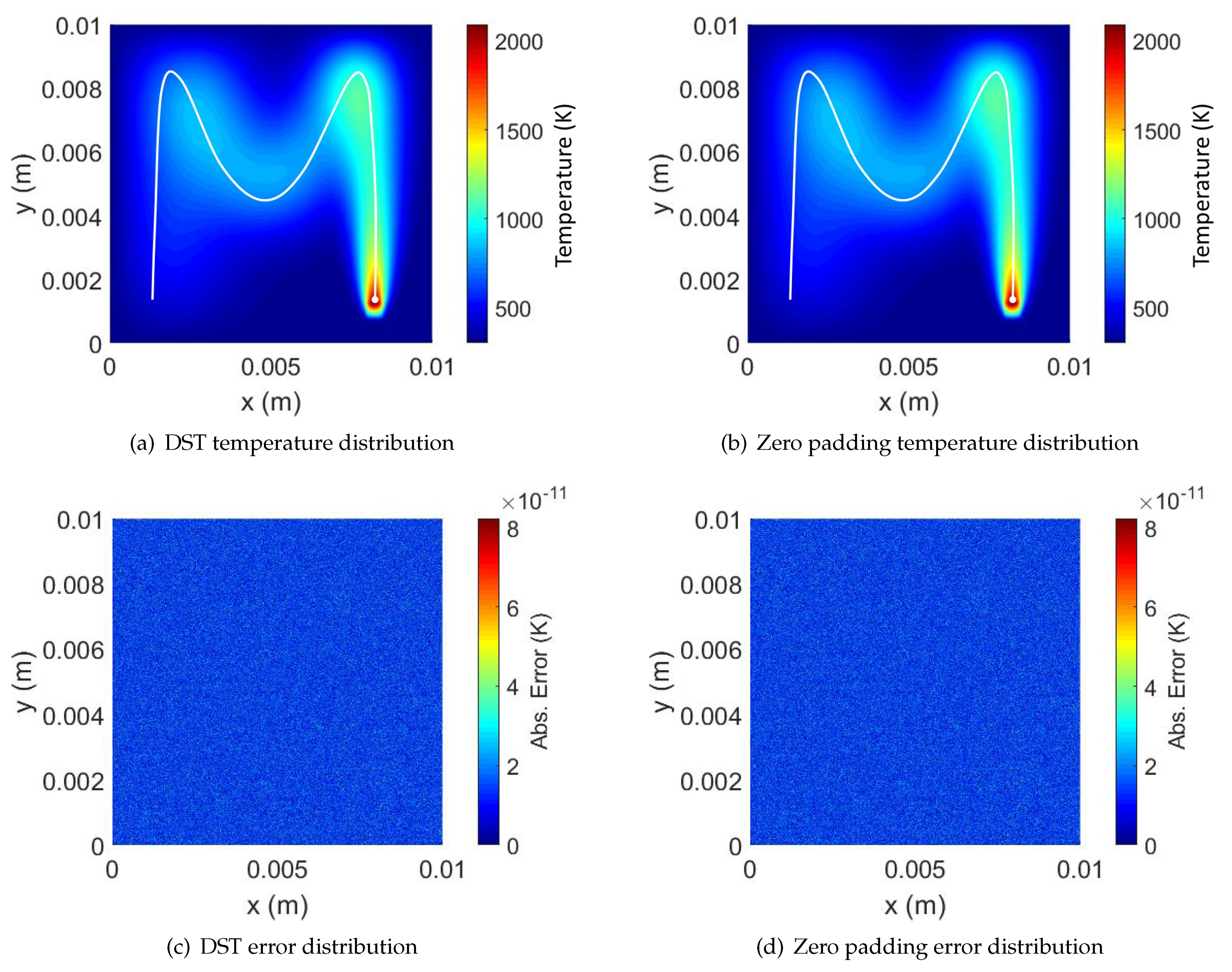
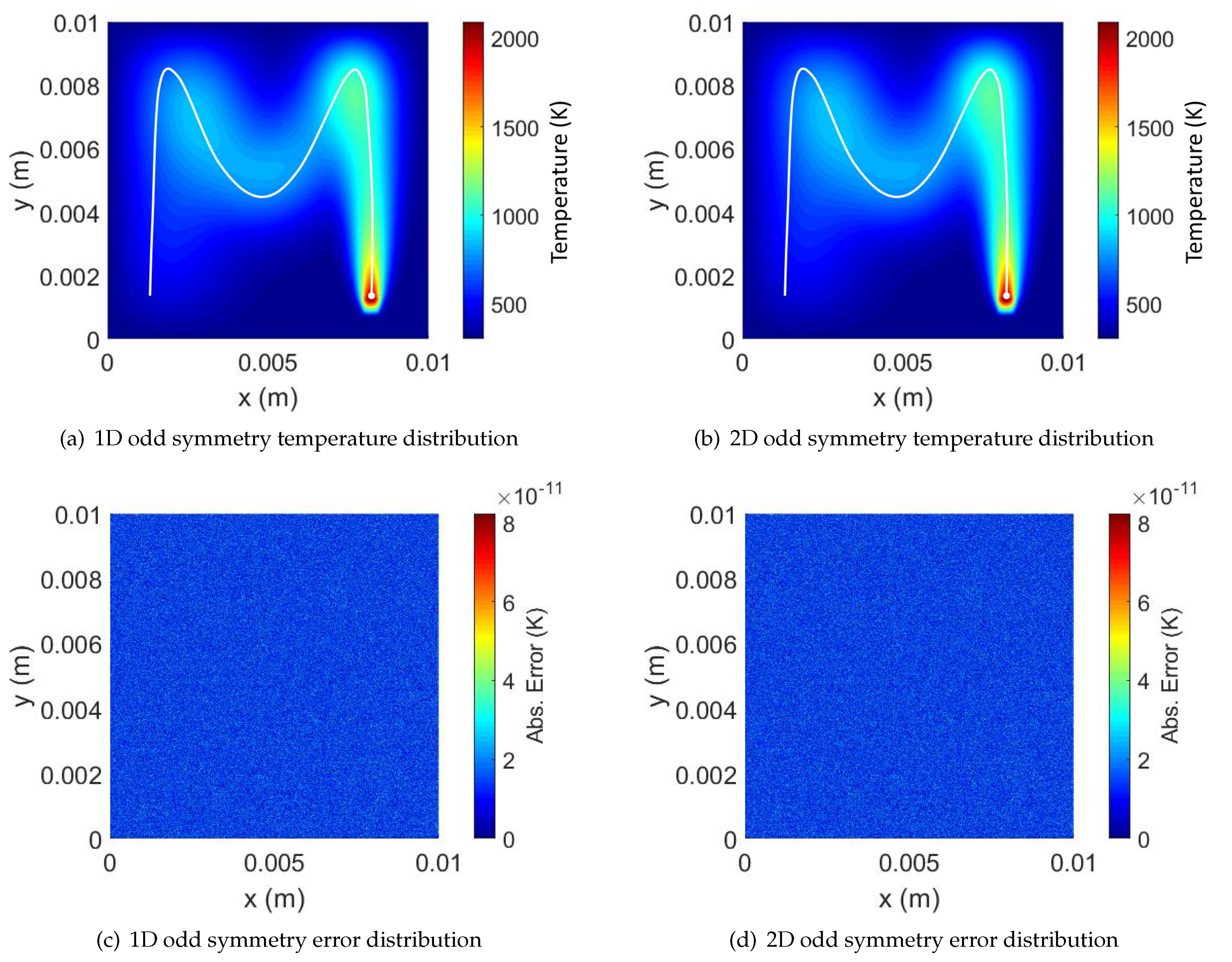
4.1. Numerical Validation
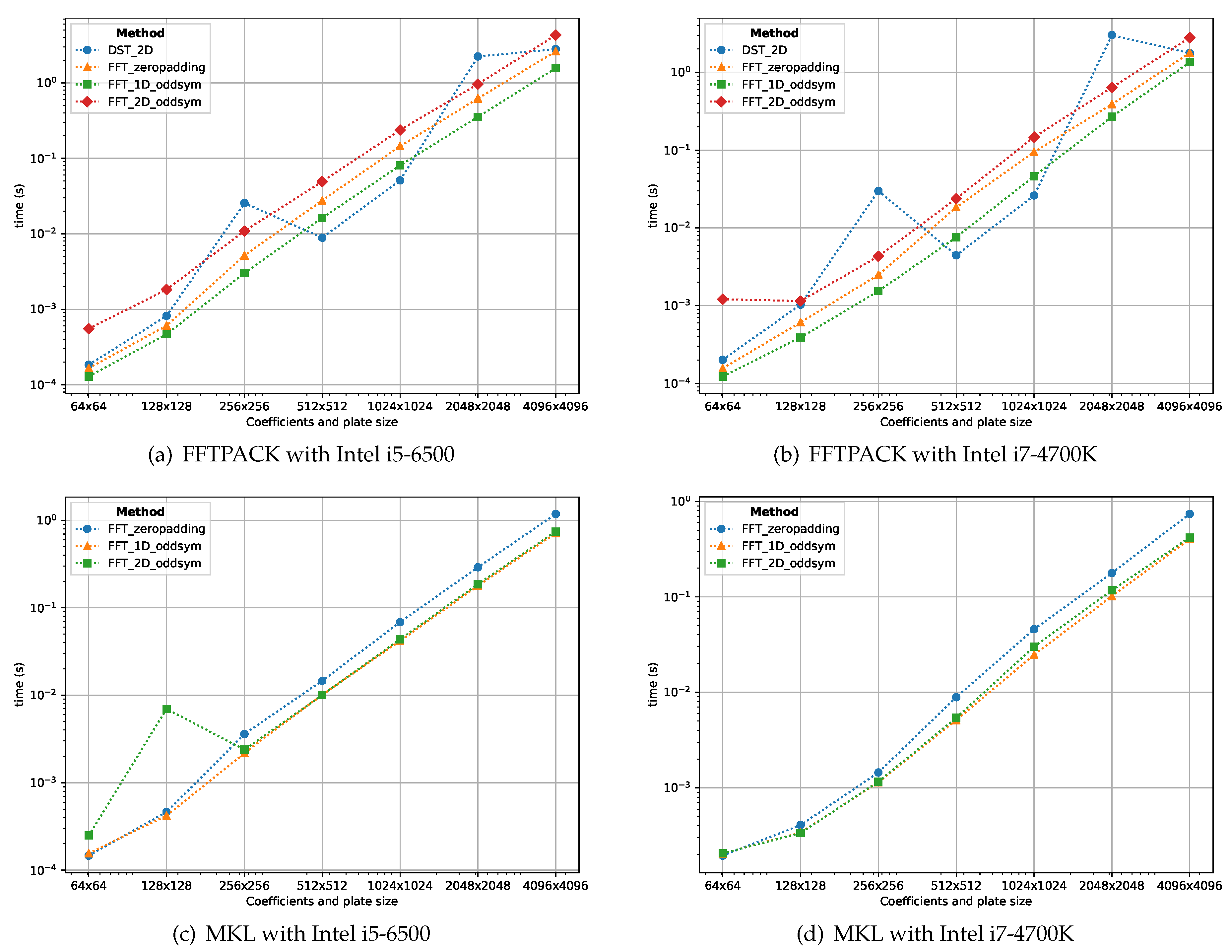
4.2. Computational Performance
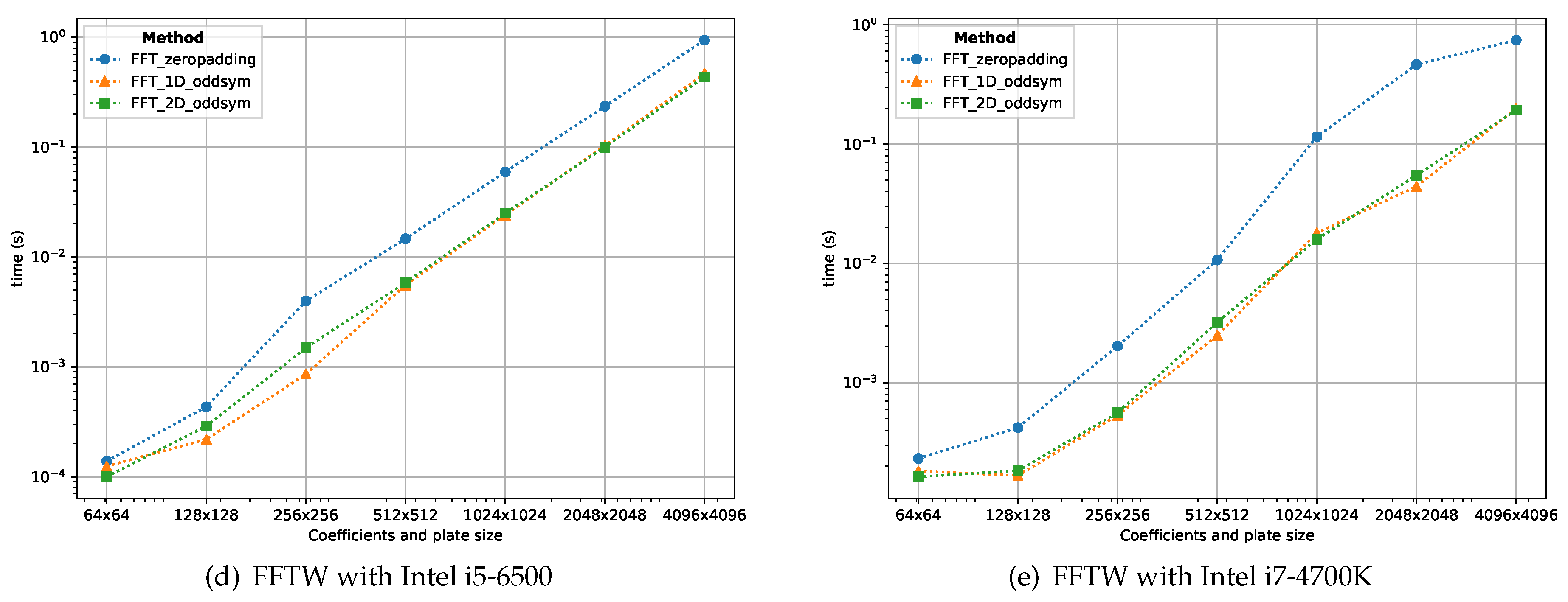
4.2.1. CPU Performance Measurements
4.2.2. GPU Performance Measurements
4.2.3. Comparison of CPU and GPU Performance
4.2.4. Comparison against State of the Art
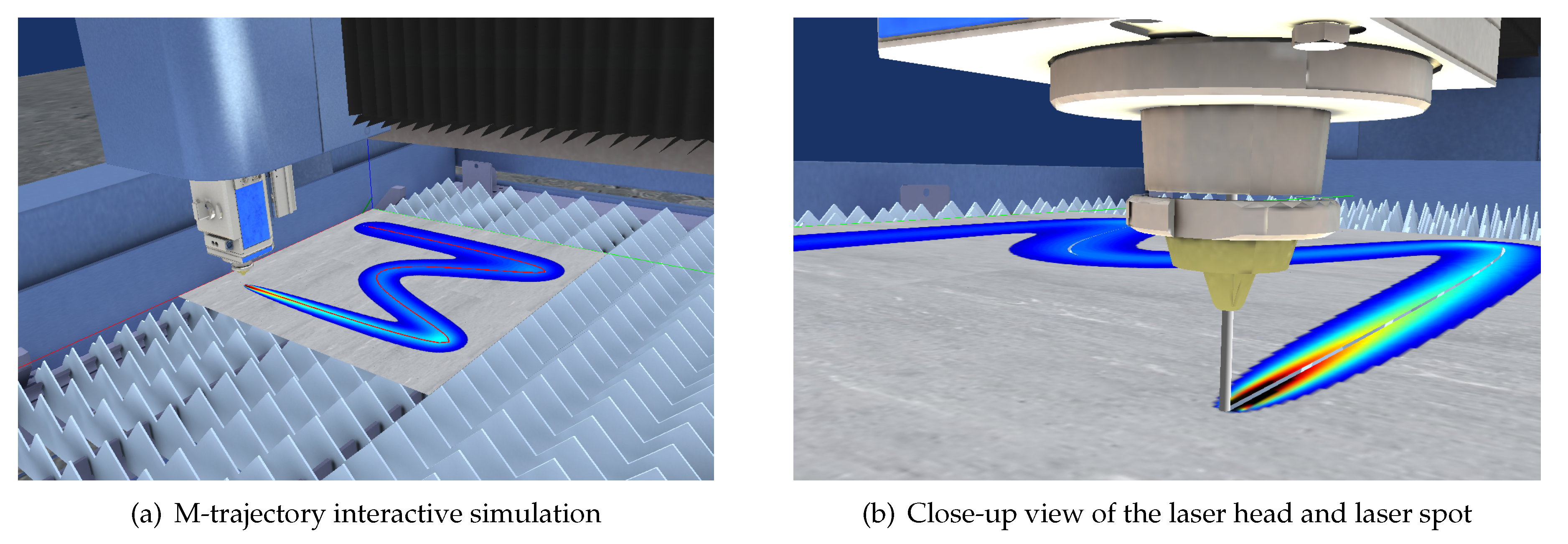
4.3. Interactive Simulator Prototype
5. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| PDE | Partial Differential Equation |
| DST | Discrete Sine Transform |
| DFT | Discrete Fourier Transform |
| FFT | Fast Fourier Transform |
| Width, height and thickness of the thin plate (m3). | |
| Total simulation time (s). | |
| Spatial and temporal coordinates. | |
| Temperature field on the metal plate (K). | |
| Plate density (kg/m3). | |
| Plate specific heat (J/kg K). | |
| Plate thermal conductivity (W/m K). | |
| R | Plate reflectivity (). |
| Temperature-dependent heat convection field (W/m2). | |
| h | Natural convection coefficient at the plate surface (W/(m2 K)) |
| Ambient temperature (K). | |
| Laser spot location at a given time . | |
| Power Density Field for the laser beam (W/m2). | |
| P | Laser power (W). |
| r | Laser spot radius (m). |
| 2D plate discretization size (). | |
| Fourier coefficient () for the temperature solution u at time t. | |
| Coefficients and for the Fourier basis in the X- and Y-axis, respectively. | |
| and are the discrete equivalent of () and (), respectively. | |
| eigenvalue of the heat (Laplace) operator defined on the rectangular plate. | |
| Piecewise linear discretization of the laser trajectory . |
Appendix A. Scheme 1—Discrete Sine Transform (DST)
Appendix B. Scheme 2—FFT Padded with Zeros
Appendix C. Scheme 3—Odd-Symmetry 1D FFT
Appendix D. Scheme 4—Odd-Symmetry 2D FFT
References
- Posada, J.; Toro, C.; Barandiaran, I.; Oyarzun, D.; Stricker, D.; de Amicis, R.; Pinto, E.B.; Eisert, P.; Döllner, J.; Vallarino, I. Visual Computing as a Key Enabling Technology for Industrie 4.0 and Industrial Internet. IEEE Comput. Graphics Appl. 2015, 35, 26–40. [Google Scholar] [CrossRef]
- Cooley, J.W.; Tukey, J.W. An algorithm for the machine calculation of complex Fourier series. Math. Comput. 1965, 19, 297–301. [Google Scholar] [CrossRef]
- Mejia-Parra, D.; Arbelaiz, A.; Moreno, A.; Posada, J.; Ruiz-Salguero, O. Fast Spectral Formulations of Thin Plate Laser Heating with GPU Implementations. In Proceedings of the 2nd International Conference on Mathematics and Computers in Science and Engineering (MACISE 2020), Madrid, Spain, 18–20 January 2020. to be Published. [Google Scholar]
- Yilbas, B.S.; Akhtar, S.; Keles, O. Laser cutting of triangular blanks from thick aluminum foam plate: Thermal stress analysis and morphology. Appl. Therm. Eng. 2014, 62, 28–36. [Google Scholar] [CrossRef]
- Akhtar, S.; Kardas, O.O.; Keles, O.; Yilbas, B.S. Laser cutting of rectangular geometry into aluminum alloy: Effect of cut sizes on thermal stress field. Opt. Lasers Eng. 2014, 61, 57–66. [Google Scholar] [CrossRef]
- Yilbas, B.; Akhtar, S.; Karatas, C. Laser cutting of rectangular geometry into alumina tiles. Opt. Lasers Eng. 2014, 55, 35–43. [Google Scholar] [CrossRef]
- Akhtar, S.S. Laser cutting of thick-section circular blanks: Thermal stress prediction and microstructural analysis. Int. J. Adv. Manuf. Technol. 2014, 71, 1345–1358. [Google Scholar] [CrossRef]
- Roberts, I.; Wang, C.; Esterlein, R.; Stanford, M.; Mynors, D. A three-dimensional finite element analysis of the temperature field during laser melting of metal powders in additive layer manufacturing. Int. J. Mach. Tools Manuf. 2009, 49, 916–923. [Google Scholar] [CrossRef]
- Shi, B.; Attia, H. Integrated Process of Laser-Assisted Machining and Laser Surface Heat Treatment. J. Manuf. Sci. Eng. 2013, 135, 061021. [Google Scholar] [CrossRef]
- Akarapu, R.; Li, B.Q.; Segall, A. A thermal stress and failure model for laser cutting and forming operations. J. Fail. Anal. Prev. 2004, 4, 51–62. [Google Scholar] [CrossRef]
- Nyon, K.Y.; Nyeoh, C.Y.; Mokhtar, M.; Abdul-Rahman, R. Finite element analysis of laser inert gas cutting on Inconel 718. Int. J. Adv. Manuf. Technol. 2012, 60, 995–1007. [Google Scholar] [CrossRef]
- Fu, C.; Sealy, M.; Guo, Y.; Wei, X. Finite element simulation and experimental validation of pulsed laser cutting of nitinol. J. Manuf. Process. 2015, 19, 81–86. [Google Scholar] [CrossRef]
- Modest, M.F. Three-dimensional, transient model for laser machining of ablating/decomposing materials. Int. J. Heat Mass Transf. 1996, 39, 221–234. [Google Scholar] [CrossRef]
- Han, G.-c.; Nas, S.-j. A Study on Torch Path Planning in Laser Cutting Processes Part 1: Calculation of Heat Flow in Contour Laser Beam Cutting. J. Manuf. Process. 1999, 1, 54–61, Special Issue of the Journal of Manufacturing Systems. [Google Scholar] [CrossRef]
- Xu, W.; Fang, J.; Wang, X.; Wang, T.; Liu, F.; Zhao, Z. A numerical simulation of temperature field in plasma-arc forming of sheet metal. J. Mater. Process. Technol. 2005, 164–165, 1644–1649, AMPT/AMME05 Part 2. [Google Scholar] [CrossRef]
- Kim, M.J. Transient evaporative laser-cutting with boundary element method. Appl. Math. Model. 2000, 25, 25–39. [Google Scholar] [CrossRef]
- Kim, M.J. Transient evaporative laser cutting with moving laser by boundary element method. Appl. Math. Model. 2004, 28, 891–910. [Google Scholar] [CrossRef]
- Kheloufi, K.; Hachemi Amara, E.; Benzaoui, A. Numerical Simulation of Transient Three-Dimensional Temperature and Kerf Formation in Laser Fusion Cutting. J. Heat Transf. 2015, 137, 112101. [Google Scholar] [CrossRef]
- Yuan, P.; Gu, D. Molten pool behaviour and its physical mechanism during selective laser melting of TiC/AlSi10Mg nanocomposites: Simulation and experiments. J. Phys. D Appl. Phys. 2015, 48, 035303. [Google Scholar] [CrossRef]
- Zimmer, K. Analytical solution of the laser-induced temperature distribution across internal material interfaces. Int. J. Heat Mass Transf. 2009, 52, 497–503. [Google Scholar] [CrossRef]
- Modest, M.F.; Abakians, H. Evaporative Cutting of a Semi-infinite Body With a Moving CW Laser. J. Heat Transf. 1986, 108, 602–607. [Google Scholar] [CrossRef]
- Jiang, H.J.; Dai, H.L. Effect of laser processing on three dimensional thermodynamic analysis for HSLA rectangular steel plates. Int. J. Heat Mass Transf. 2015, 82, 98–108. [Google Scholar] [CrossRef]
- Mejia, D.; Moreno, A.; Arbelaiz, A.; Posada, J.; Ruiz-Salguero, O.; Chopitea, R. Accelerated Thermal Simulation for Three-Dimensional Interactive Optimization of Computer Numeric Control Sheet Metal Laser Cutting. J. Manuf. Sci. Eng. 2017, 140, 031006. [Google Scholar] [CrossRef]
- Mejia-Parra, D.; Moreno, A.; Posada, J.; Ruiz-Salguero, O.; Barandiaran, I.; Poza, J.C.; Chopitea, R. Frequency-domain analytic method for efficient thermal simulation under curved trajectories laser heating. Math. Comput. Simul. 2019, 166, 177–192. [Google Scholar] [CrossRef]
- Mejia-Parra, D.; Montoya-Zapata, D.; Arbelaiz, A.; Moreno, A.; Posada, J.; Ruiz-Salguero, O. Fast Analytic Simulation for Multi-Laser Heating of Sheet Metal in GPU. Materials 2018, 11, 2078. [Google Scholar] [CrossRef] [PubMed]
- Ju, Y.; Farris, T.N. FFT Thermoelastic Solutions for Moving Heat Sources. J. Tribol. 1997, 119, 156–162. [Google Scholar] [CrossRef]
- Dillenseger, J.L.; Esneault, S. Fast FFT-based bioheat transfer equation computation. Comput. Biol. Med. 2010, 40, 119–123. [Google Scholar] [CrossRef]
- Berbenni, S.; Taupin, V.; Djaka, K.S.; Fressengeas, C. A numerical spectral approach for solving elasto-static field dislocation and g-disclination mechanics. Int. J. Solids Struct. 2014, 51, 4157–4175. [Google Scholar] [CrossRef]
- Djaka, K.S.; Villani, A.; Taupin, V.; Capolungo, L.; Berbenni, S. Field Dislocation Mechanics for heterogeneous elastic materials: A numerical spectral approach. Comput. Methods Appl. Mech. Eng. 2017, 315, 921–942. [Google Scholar] [CrossRef]
- Ma, R.; Truster, T.J. FFT-based homogenization of hypoelastic plasticity at finite strains. Comput. Methods Appl. Mech. Eng. 2019, 349, 499–521. [Google Scholar] [CrossRef]
- Paramatmuni, C.; Kanjarla, A.K. A crystal plasticity FFT based study of deformation twinning, anisotropy and micromechanics in HCP materials: Application to AZ31 alloy. Int. J. Plast. 2019, 113, 269–290. [Google Scholar] [CrossRef]
- Starn, J. A Simple Fluid Solver Based on the FFT. J. Graphics Tools 2001, 6, 43–52. [Google Scholar] [CrossRef]
- Taboada, J.M.; Landesa, L.; Obelleiro, F.; Rodriguez, J.L.; Bertolo, J.M.; Araujo, M.G.; Mouri no, J.C.; Gomez, A. High Scalability FMM-FFT Electromagnetic Solver for Supercomputer Systems. IEEE Antennas Propag. Mag. 2009, 51, 20–28. [Google Scholar] [CrossRef]
- Manolakis, D.; Ingle, V. Chapter 8—Computation of the Discrete Fourier Transform. In Applied Digital Signal Processing: Theory and Practice; Manolakis, D., Ingle, V., Eds.; Cambridge University Press: New York, NY, USA, 2011; pp. 434–484. [Google Scholar]
- Raaf, O.; Adane, A.E.H. Pattern recognition filtering and bidimensional FFT-based detection of storms in meteorological radar images. Digit. Signal Process. 2012, 22, 734–743. [Google Scholar] [CrossRef]
- Britanak, V.; Yip, P.C.; Rao, K. CHAPTER 1—Discrete Cosine and Sine Transforms. In Discrete Cosine and Sine Transforms; Britanak, V., Yip, P.C., Rao, K., Eds.; Academic Press: Oxford, UK, 2007; pp. 1–15. [Google Scholar] [CrossRef]
- Britanak, V.; Yip, P.C.; Rao, K. CHAPTER 4—Fast DCT/DST Algorithms. In Discrete Cosine and Sine Transforms; Britanak, V., Yip, P.C., Rao, K., Eds.; Academic Press: Oxford, UK, 2007; pp. 73–140. [Google Scholar] [CrossRef]
- Moreno, A.; Segura, Á.; Arregui, H.; Posada, J.; Ruíz de Infante, Á.; Canto, N. Using 2D Contours to Model Metal Sheets in Industrial Machining Processes. In Future Vision and Trends on Shapes, Geometry and Algebra; De Amicis, R., Conti, G., Eds.; Springer: London, UK, 2014; pp. 135–149. [Google Scholar]
- Velez, G.; Moreno, A.; Infante, A.R.D.; Chopitea, R. Real-time part detection in a virtually machined sheet metal defined as a set of disjoint regions. Int. J. Comput. Integr. Manuf. 2016, 29, 1089–1104. [Google Scholar] [CrossRef]





| Line | Description | Number of Operations | Dominant Term | Complexity Order |
|---|---|---|---|---|
| 1, 2 | Memory initialization | |||
| 4 | FFT of a column | |||
| 5 | Extract complex part | |||
| 3–6 | Loop through columns | |||
| 8 | FFT of a row | |||
| 9 | Extract complex part | |||
| 7–10 | Loop through rows | |||
| 11, 12 | Memory initialization | |||
| 13 | Sum of matrices | |||
| TOTAL |
| Parameter | Description | Value | Units |
|---|---|---|---|
| a | Plate width | m | |
| b | Plate height | m | |
| Plate thickness | m | ||
| Plate density | 8030 | kg/m3 | |
| Specific heat | 574 | J/(kg K) | |
| Thermal conductivity | 20 | W/(m K) | |
| R | Plate reflectivity | 0 | 1 |
| h | Convection coefficient | 20 | W/(m2 K) |
| Ambient temperature | 300 | K | |
| P | Laser power | 500 | W |
| r | Laser spot radius | m |
| Library | Python Package | Hardware |
|---|---|---|
| FFTPACK | scipy.fft | CPU |
| MKL | numpy.fft | CPU |
| FFTW | pyfftw | CPU |
| cuFFT | pyCUDA, scikit-cuda | GPU |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mejia-Parra, D.; Arbelaiz, A.; Ruiz-Salguero, O.; Lalinde-Pulido, J.; Moreno, A.; Posada, J. Fast Simulation of Laser Heating Processes on Thin Metal Plates with FFT Using CPU/GPU Hardware. Appl. Sci. 2020, 10, 3281. https://doi.org/10.3390/app10093281
Mejia-Parra D, Arbelaiz A, Ruiz-Salguero O, Lalinde-Pulido J, Moreno A, Posada J. Fast Simulation of Laser Heating Processes on Thin Metal Plates with FFT Using CPU/GPU Hardware. Applied Sciences. 2020; 10(9):3281. https://doi.org/10.3390/app10093281
Chicago/Turabian StyleMejia-Parra, Daniel, Ander Arbelaiz, Oscar Ruiz-Salguero, Juan Lalinde-Pulido, Aitor Moreno, and Jorge Posada. 2020. "Fast Simulation of Laser Heating Processes on Thin Metal Plates with FFT Using CPU/GPU Hardware" Applied Sciences 10, no. 9: 3281. https://doi.org/10.3390/app10093281
APA StyleMejia-Parra, D., Arbelaiz, A., Ruiz-Salguero, O., Lalinde-Pulido, J., Moreno, A., & Posada, J. (2020). Fast Simulation of Laser Heating Processes on Thin Metal Plates with FFT Using CPU/GPU Hardware. Applied Sciences, 10(9), 3281. https://doi.org/10.3390/app10093281






