Critical Temperature and Frequency Characteristics of GPLs-Reinforced Composite Doubly Curved Panel
Abstract
1. Introduction
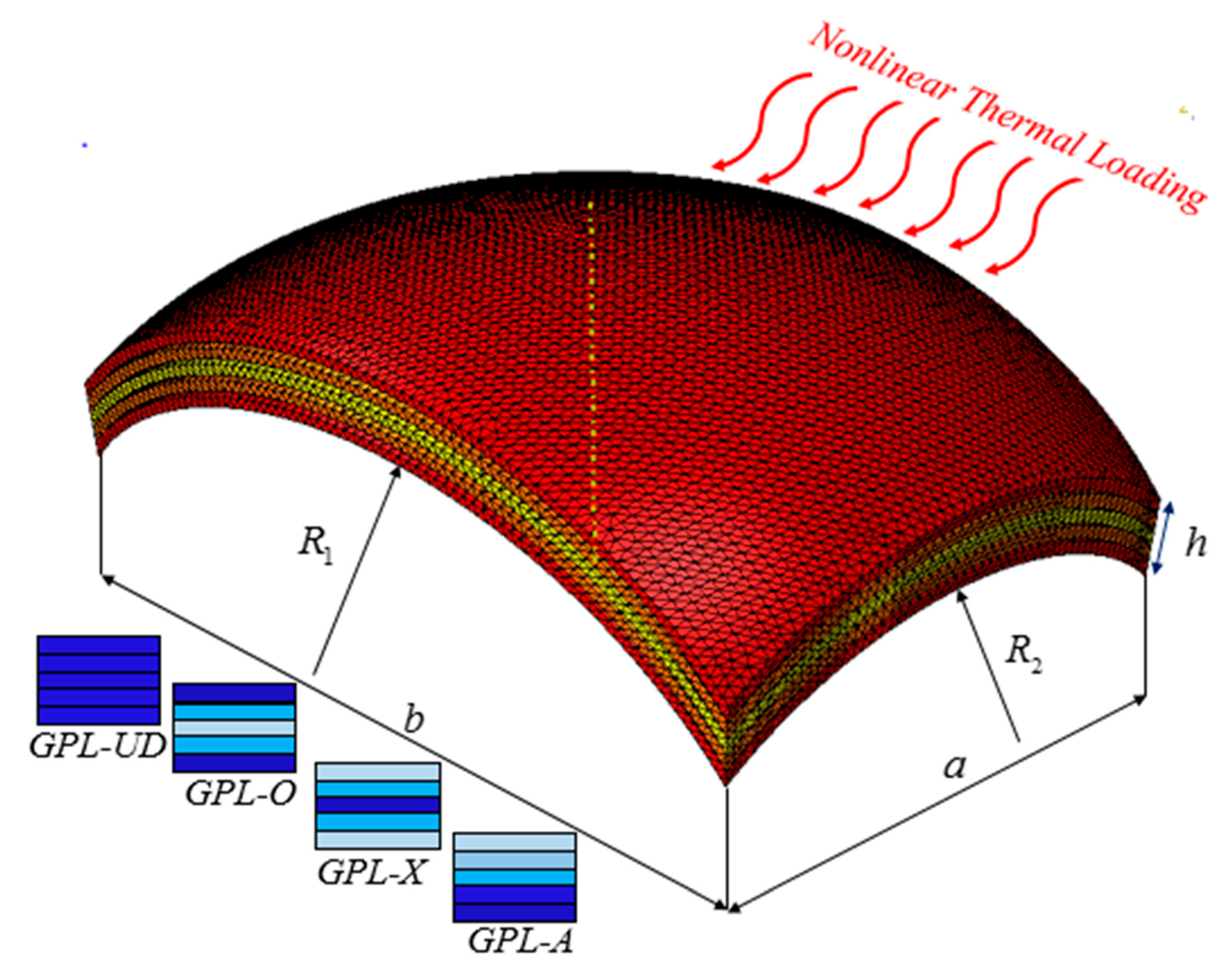
2. Theory and Formulation
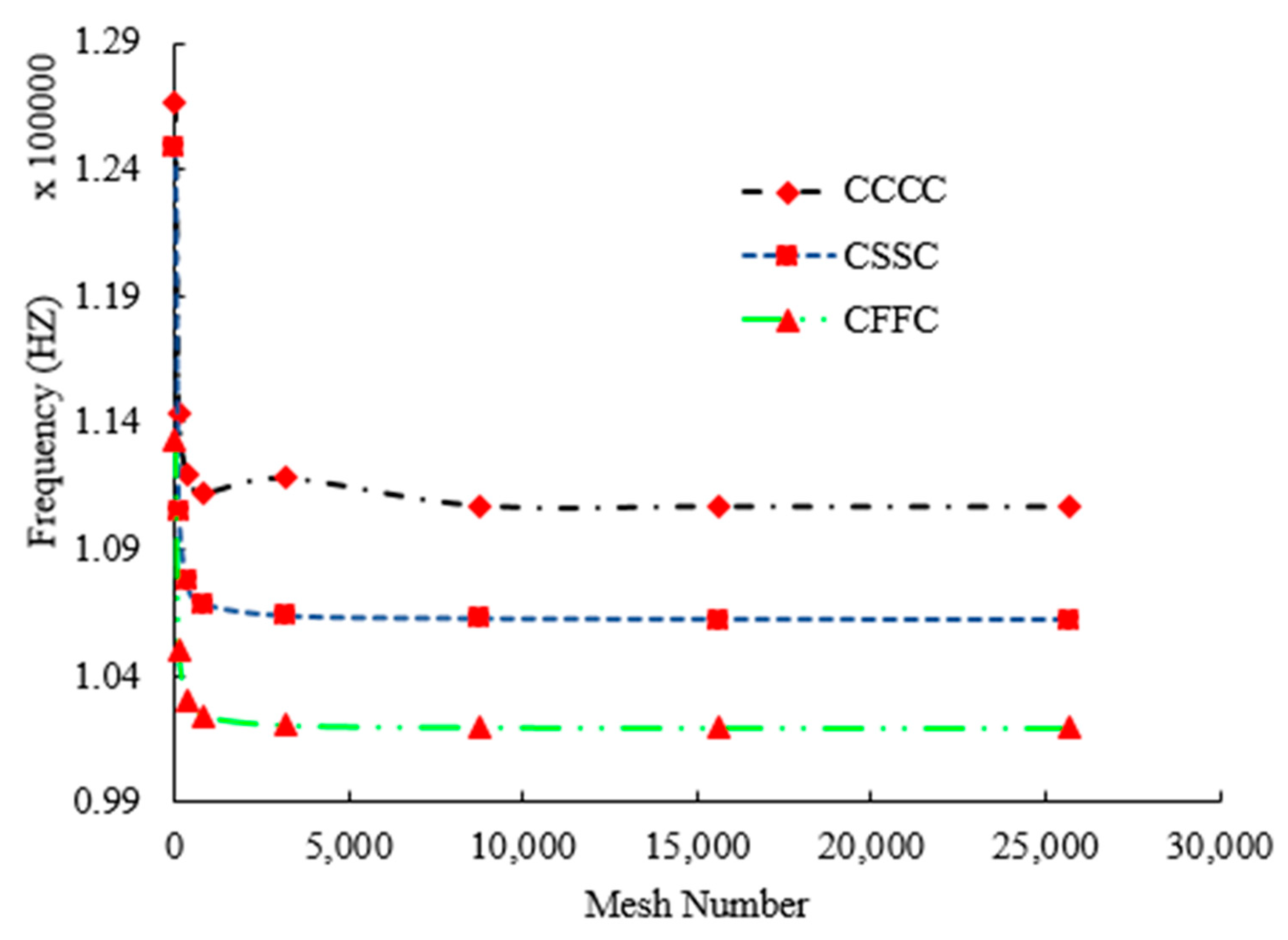
3. Solution Procedure
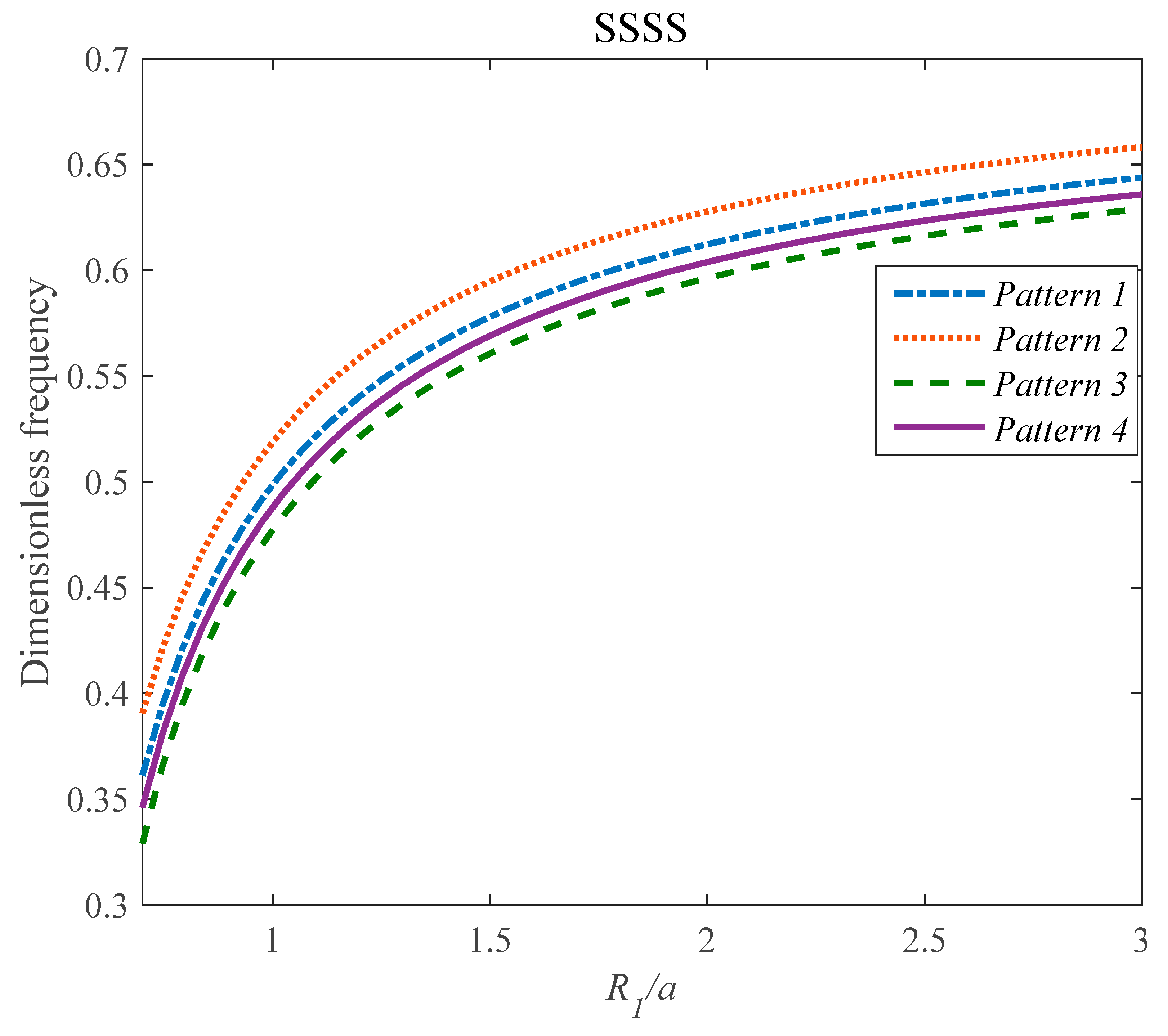
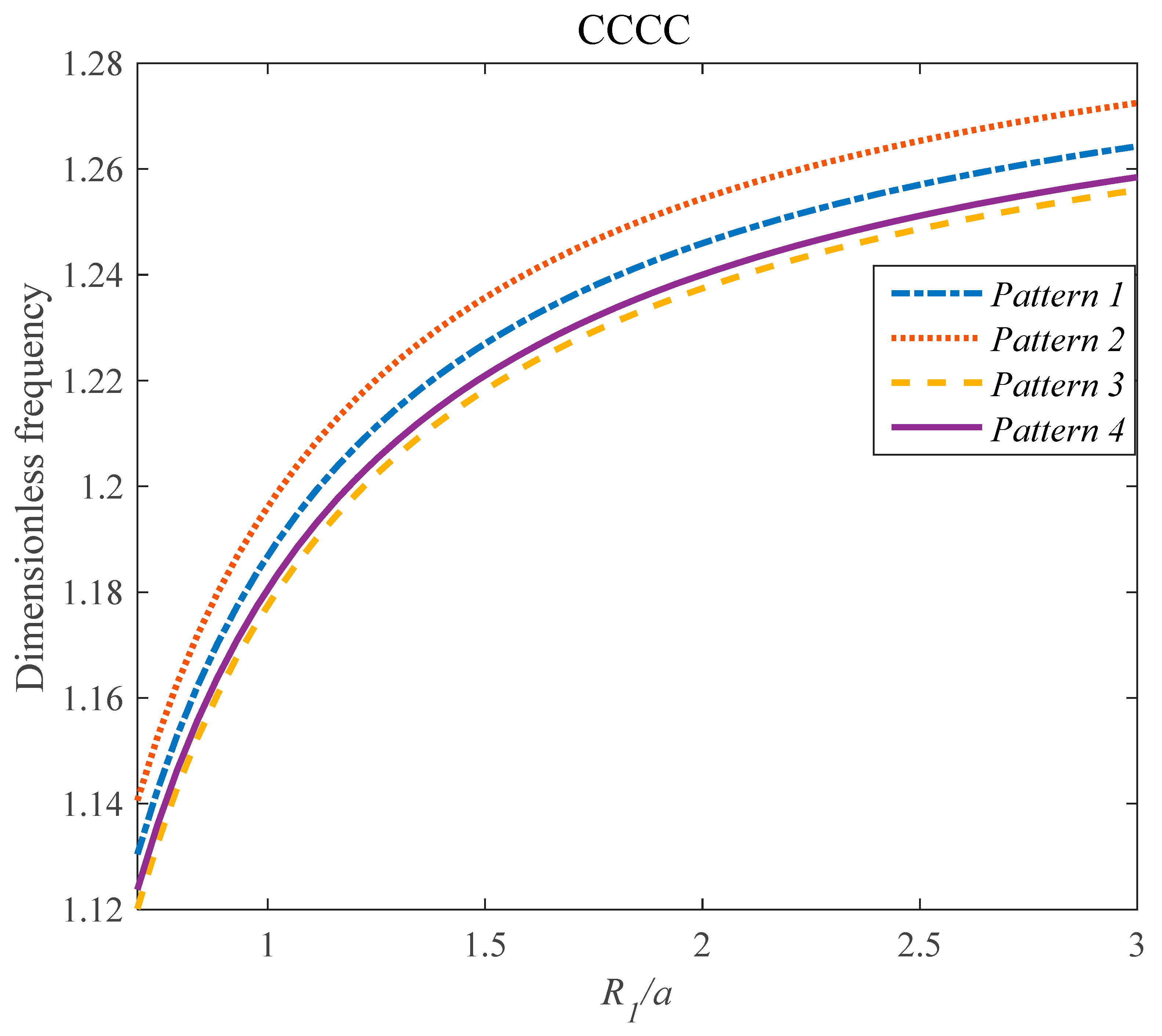
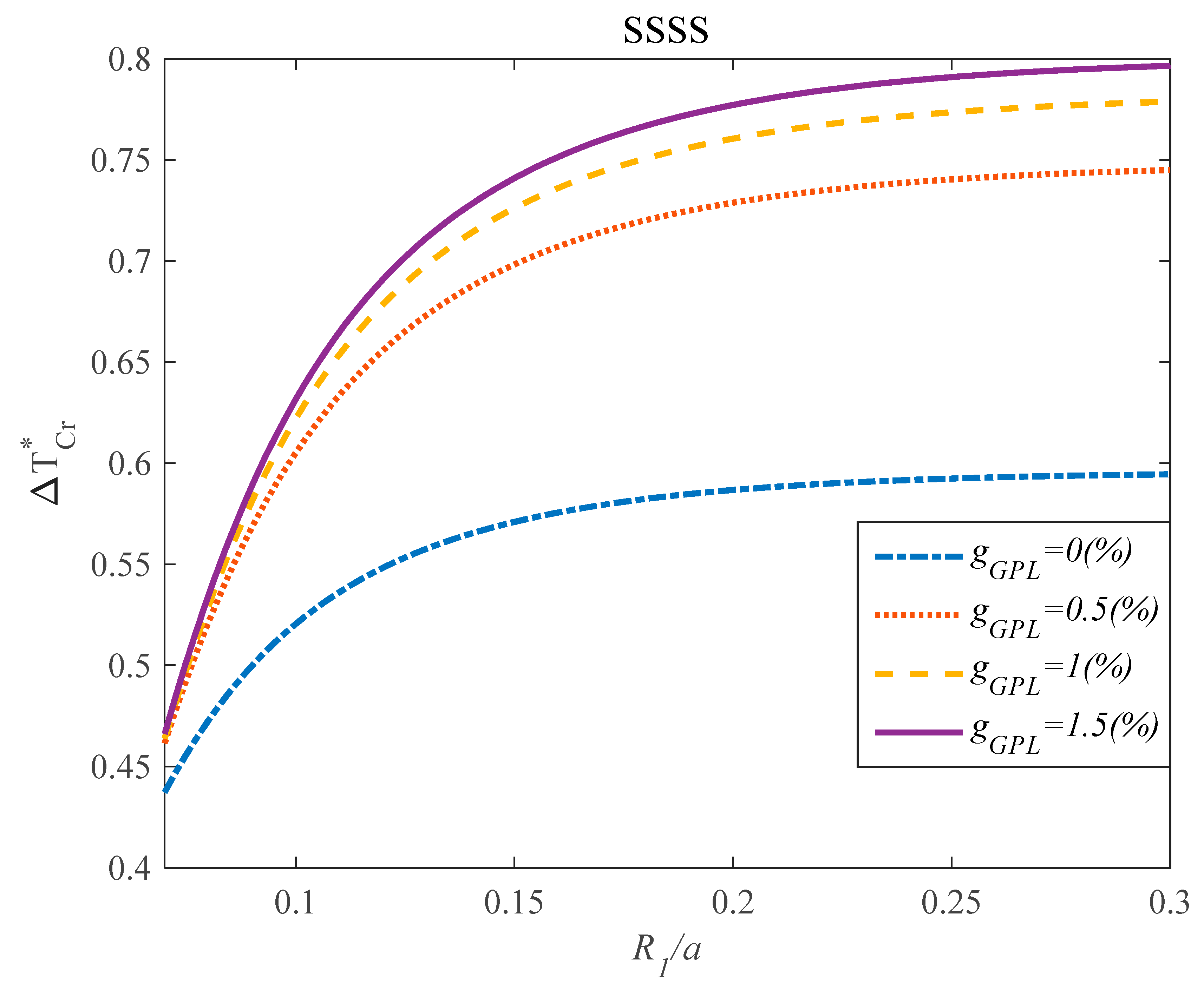
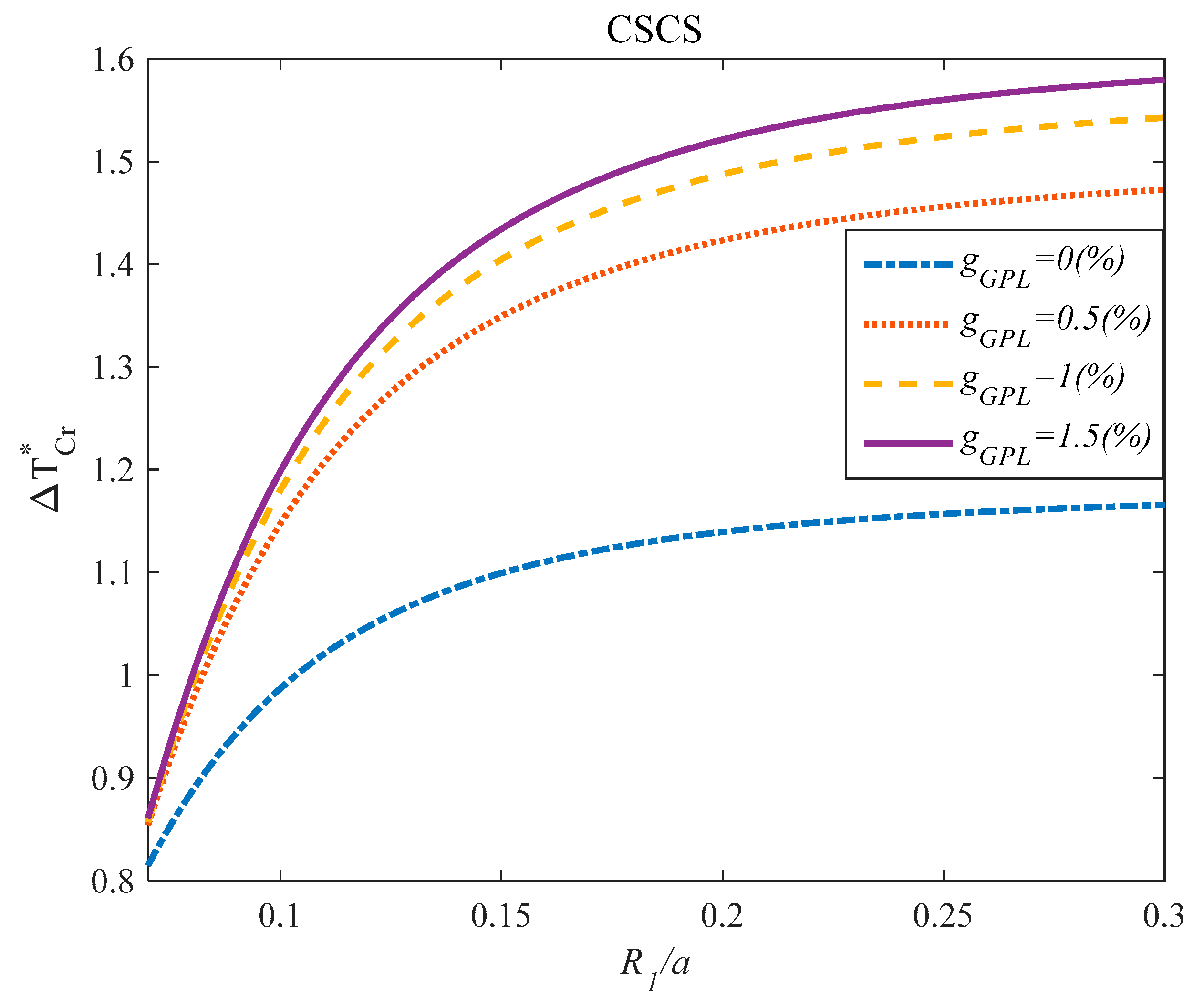
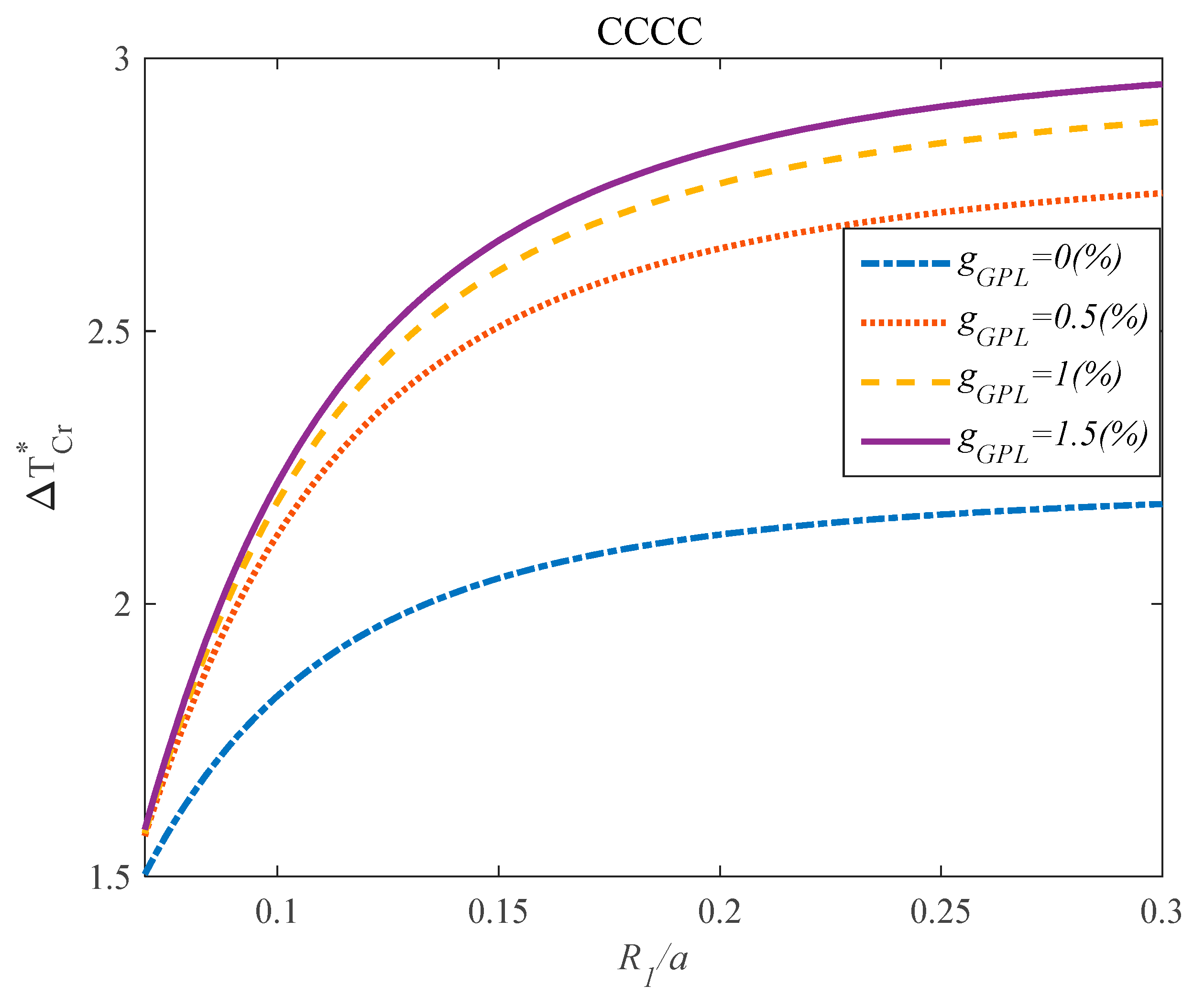
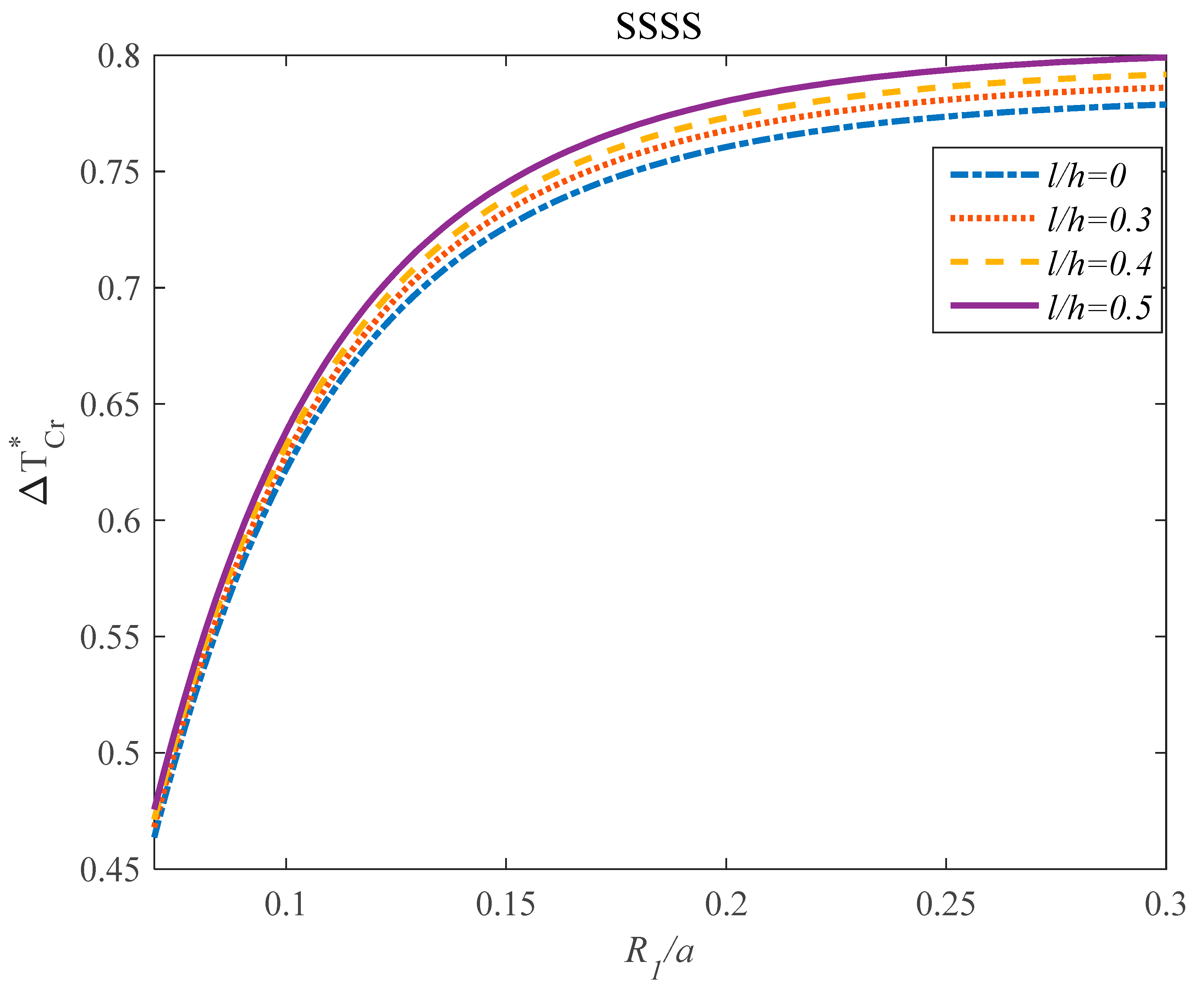
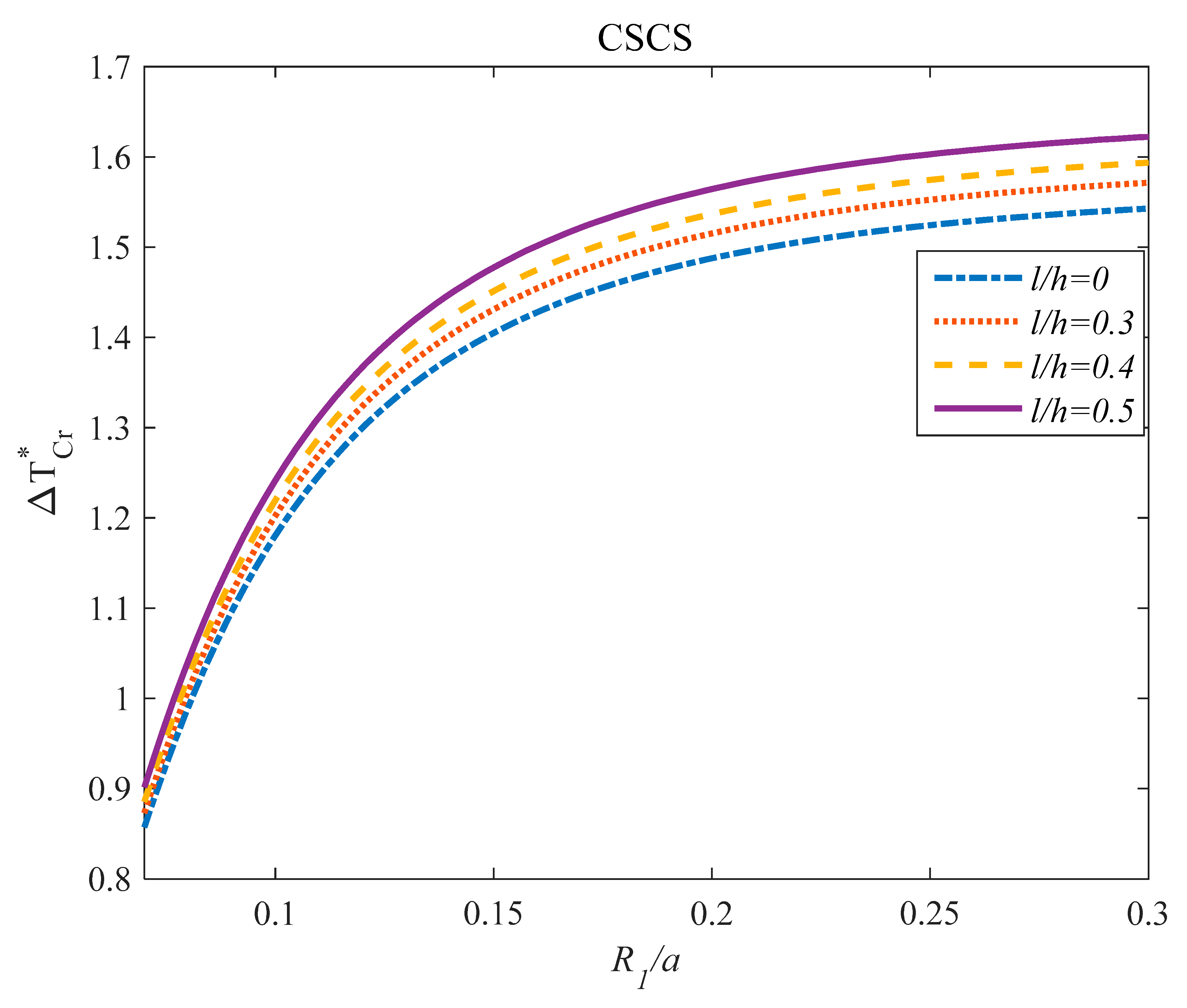
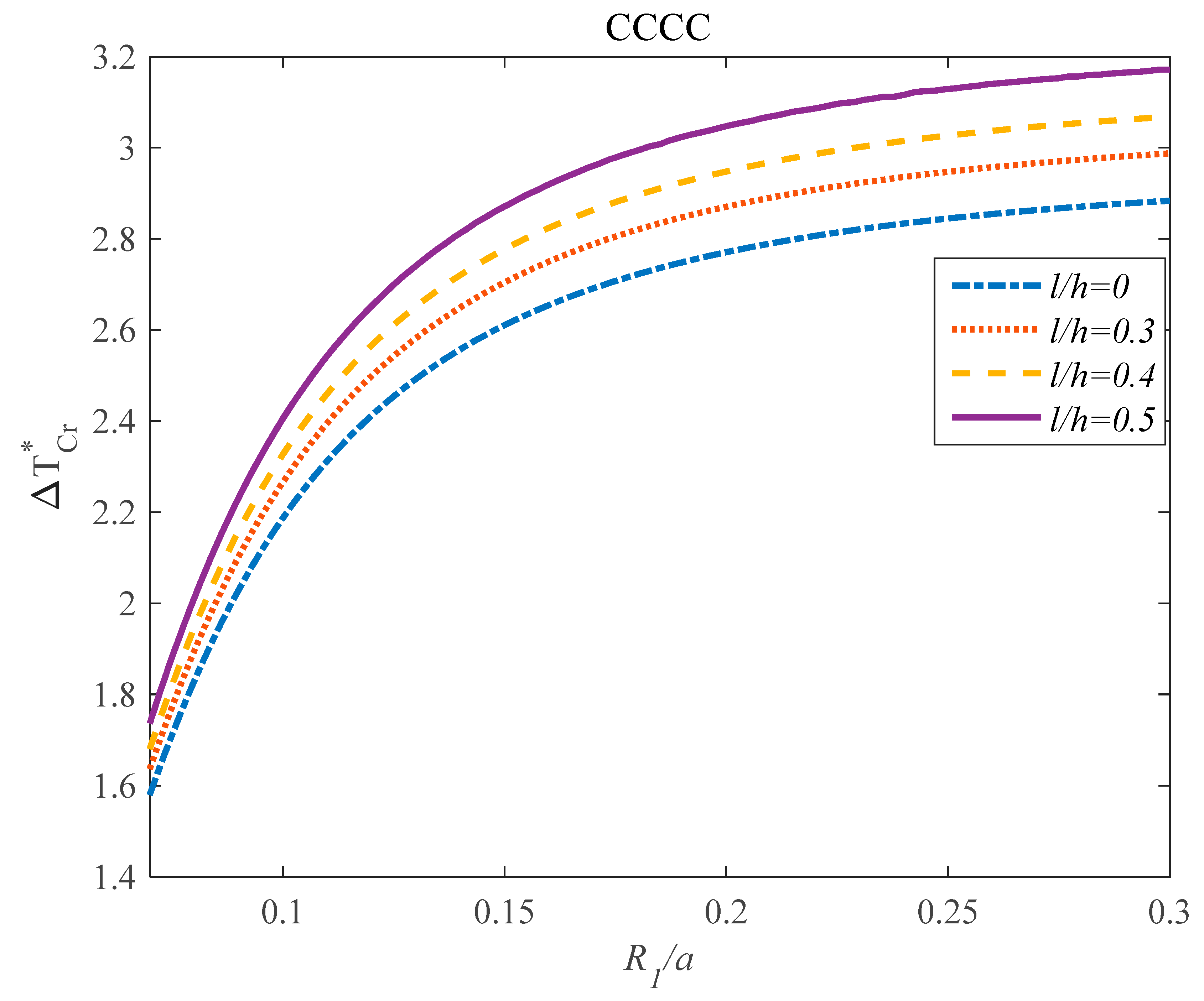
4. Results
5. Conclusions
- ⮚
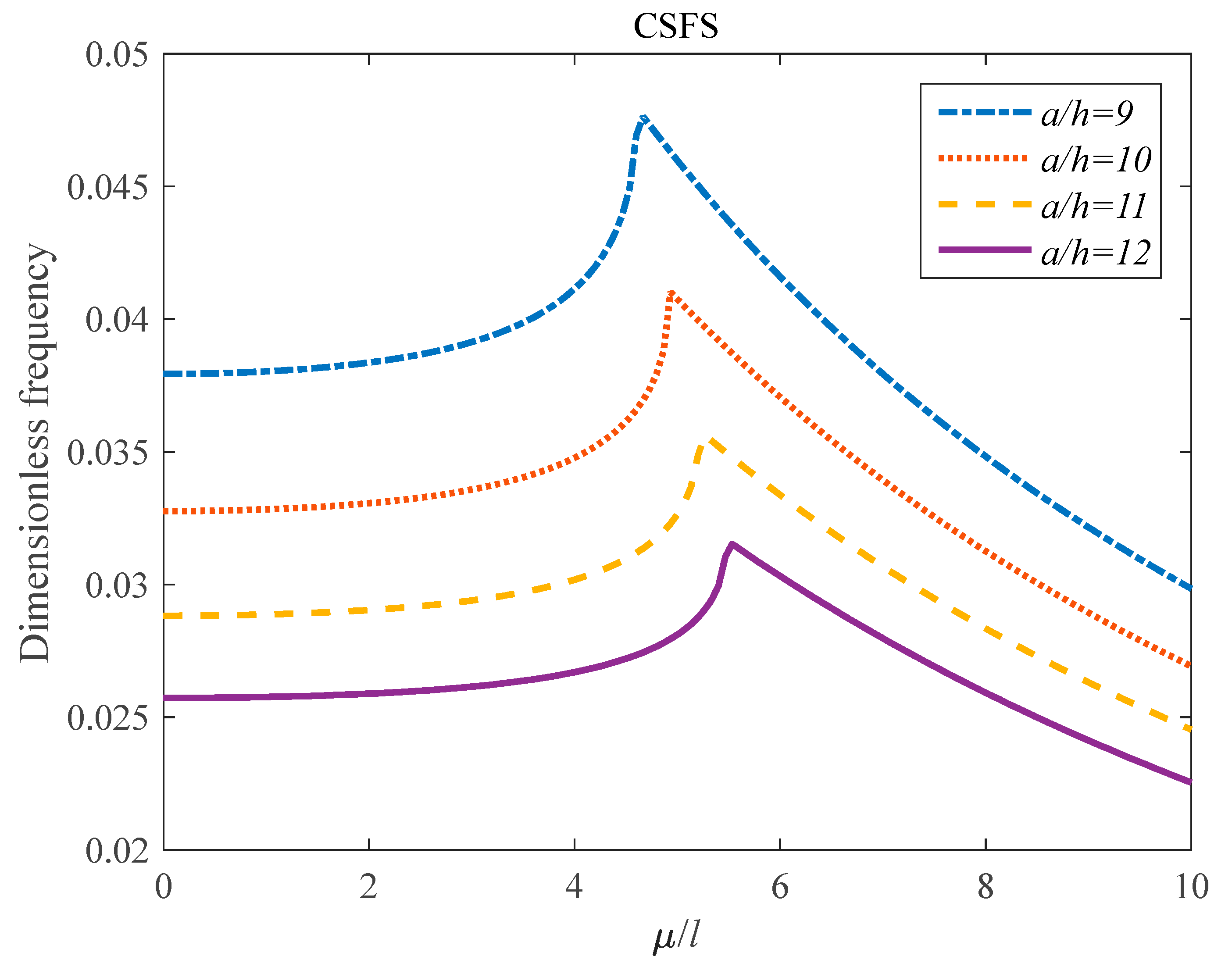
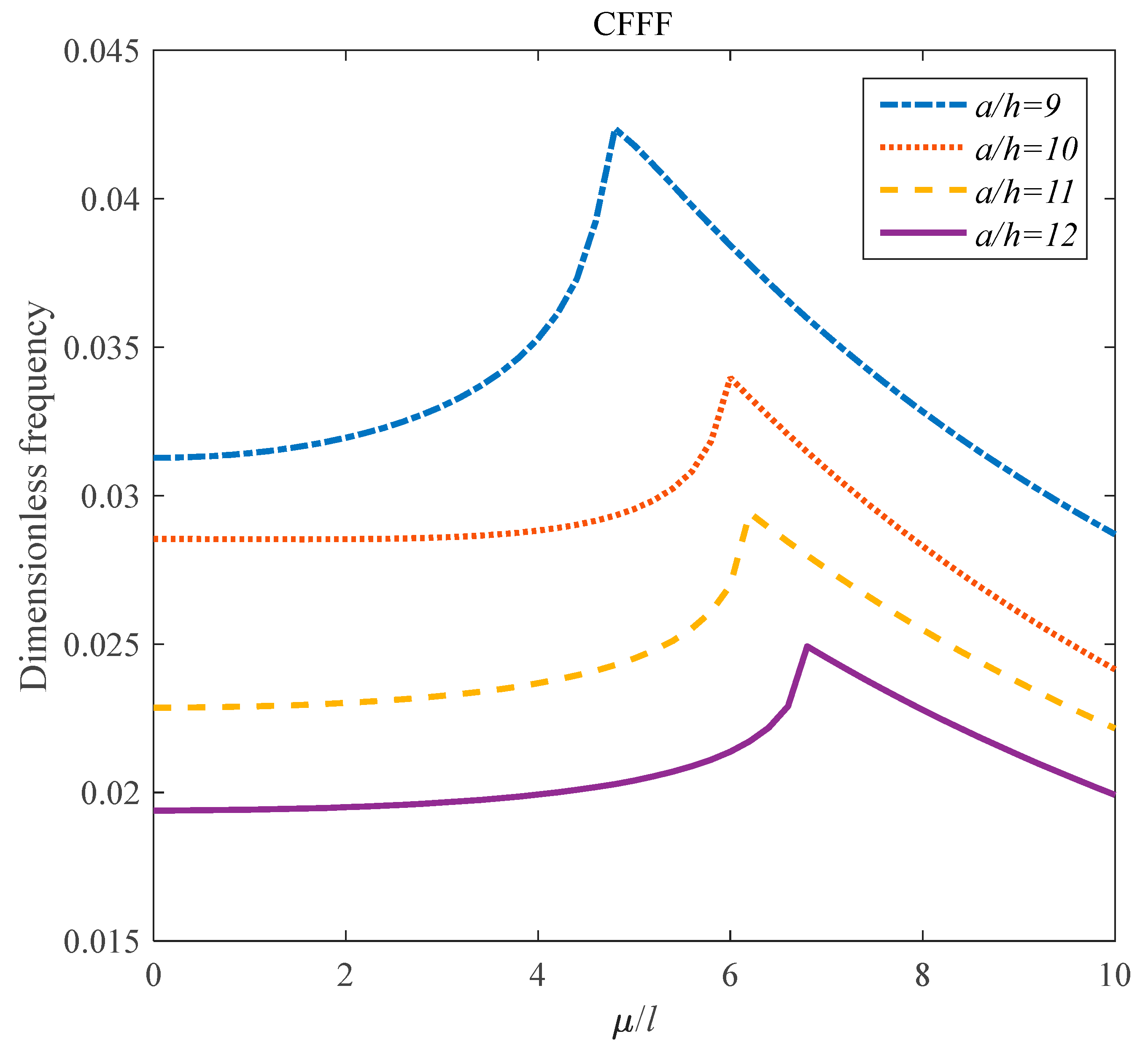
- The effects of the parameter on the frequency response of the GPLRC panel was dependent on the values of the l/h parameter.
- ⮚
- The dynamic stability of the system, unlike static stability, could be affected by the nonlocal parameter indirectly.
- ⮚
- At the high value of the effect of the on the dimensionless frequency of the composite panel was much more remarkable in comparison with the low value of it.
- ⮚
- The effect of the parameter on the critical temperature of the structures was hardly dependent on the values of the parameter.
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Zhao, X.; Li, D.; Yang, B.; Ma, C.; Zhu, Y.; Chen, H. Feature selection based on improved ant colony optimization for online detection of foreign fiber in cotton. Appl. Soft Comput. 2014, 24, 585–596. [Google Scholar] [CrossRef]
- Wang, M.; Chen, H. Chaotic multi-swarm whale optimizer boosted support vector machine for medical diagnosis. Appl. Soft Comput. 2020, 88, 105946. [Google Scholar] [CrossRef]
- Zhao, X.; Zhang, X.; Cai, Z.; Tian, X.; Wang, X.; Huang, Y.; Chen, H.; Hu, L. Chaos enhanced grey wolf optimization wrapped ELM for diagnosis of paraquat-poisoned patients. Comput. Biol. Chem. 2019, 78, 481–490. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.; Chen, H.-L. Adaptive computational chemotaxis based on field in bacterial foraging optimization. Soft Comput. 2014, 18, 797–807. [Google Scholar] [CrossRef]
- Shen, L.; Chen, H.; Yu, Z.; Kang, W.; Zhang, B.; Li, H.; Yang, B.; Liu, D. Evolving support vector machines using fruit fly optimization for medical data classification. Knowl. Based Syst. 2016, 96, 61–75. [Google Scholar] [CrossRef]
- Wang, M.; Chen, H.; Yang, B.; Zhao, X.; Hu, L.; Cai, Z.; Huang, H.; Tong, C. Toward an optimal kernel extreme learning machine using a chaotic moth-flame optimization strategy with applications in medical diagnoses. Neurocomputing 2017, 267, 69–84. [Google Scholar] [CrossRef]
- Xu, Y.; Chen, H.; Luo, J.; Zhang, Q.; Jiao, S.; Zhang, X. Enhanced Moth-flame optimizer with mutation strategy for global optimization. Inf. Sci. 2019, 492, 181–203. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, Q.; Luo, J.; Xu, Y.; Zhang, X. An enhanced Bacterial Foraging Optimization and its application for training kernel extreme learning machine. Appl. Soft Comput. 2020, 86, 105884. [Google Scholar] [CrossRef]
- Nadri, S.; Xie, L.; Jafari, M.; Alijabbari, N.; Cyberey, M.E.; Barker, N.S.; Lichtenberger, A.W.; Weikle, R.M. A 160 GHz frequency Quadrupler based on heterogeneous integration of GaAs Schottky diodes onto silicon using SU-8 for epitaxy transfer. In Proceedings of the 2018 IEEE/MTT-S International Microwave Symposium-IMS, Philadelphia, PA, USA, 10–15 June 2018; pp. 769–772. [Google Scholar]
- Shi, G.; Araby, S.; Gibson, C.T.; Meng, Q.; Zhu, S.; Ma, J. Graphene Platelets and Their Polymer Composites: Fabrication, Structure, Properties, and Applications. Adv. Funct. Mater. 2018, 28, 1706705. [Google Scholar] [CrossRef]
- Sun, J.; Zhao, J. Multi-layer graphene reinforced nano-laminated WC-Co composites. Mater. Sci. Eng. A 2018, 723, 1–7. [Google Scholar] [CrossRef]
- Rafiee, M.A.; Rafiee, J.; Wang, Z.; Song, H.; Yu, Z.-Z.; Koratkar, N. Enhanced mechanical properties of nanocomposites at low graphene content. Acs Nano 2009, 3, 3884–3890. [Google Scholar] [CrossRef] [PubMed]
- Safarpour, H.; Ghanizadeh, S.A.; Habibi, M. Wave propagation characteristics of a cylindrical laminated composite nanoshell in thermal environment based on the nonlocal strain gradient theory. Eur. Phys. J. Plus 2018, 133, 532. [Google Scholar] [CrossRef]
- Zeighampour, H.; Beni, Y.T.; Karimipour, I. Material length scale and nonlocal effects on the wave propagation of composite laminated cylindrical micro/nanoshells. Eur. Phys. J. Plus 2017, 132, 503. [Google Scholar] [CrossRef]
- Sahmani, S.; Fattahi, A.; Ahmed, N. Analytical mathematical solution for vibrational response of postbuckled laminated FG-GPLRC nonlocal strain gradient micro-/nanobeams. Eng. Comput. 2019, 35, 1173–1189. [Google Scholar] [CrossRef]
- Shokrgozar, A.; Ghabussi, A.; Ebrahimi, F.; Habibi, M.; Safarpour, H. Viscoelastic dynamics and static responses of a graphene nanoplatelets-reinforced composite cylindrical microshell. Mech. Based Des. Struct. Mach. 2020, 1–28. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Supeni, E.E.B.; Habibi, M.; Safarpour, H. Frequency characteristics of a GPL-reinforced composite microdisk coupled with a piezoelectric layer. Eur. Phys. J. Plus 2020, 135, 144. [Google Scholar]
- Ebrahimi, F.; Hashemabadi, D.; Habibi, M.; Safarpour, H. Thermal buckling and forced vibration characteristics of a porous GNP reinforced nanocomposite cylindrical shell. Microsyst. Technol. 2020, 26, 461–473. [Google Scholar] [CrossRef]
- Moayedi, H.; Aliakbarlou, H.; Jebeli, M.; Noormohammadi Arani, O.; Habibi, M.; Safarpour, H.; Foong, L. Thermal buckling responses of a graphene reinforced composite micropanel structure. Int. J. Appl. Mech. 2020, 12, 2050010. [Google Scholar] [CrossRef]
- Shokrgozar, A.; Safarpour, H.; Habibi, M. Influence of system parameters on buckling and frequency analysis of a spinning cantilever cylindrical 3D shell coupled with piezoelectric actuator. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2020, 234, 512–529. [Google Scholar] [CrossRef]
- Ghabussi, A.; Ashrafi, N.; Shavalipour, A.; Hosseinpour, A.; Habibi, M.; Moayedi, H.; Babaei, B.; Safarpour, H. Free vibration analysis of an electro-elastic GPLRC cylindrical shell surrounded by viscoelastic foundation using modified length-couple stress parameter. Mech. Based Des. Struct. Mach. 2019, 1–25. [Google Scholar] [CrossRef]
- Habibi, M.; Mohammadi, A.; Safarpour, H.; Ghadiri, M. Effect of porosity on buckling and vibrational characteristics of the imperfect GPLRC composite nanoshell. Mech. Based Des. Struct. Mach. 2019, 1–30. [Google Scholar] [CrossRef]
- Habibi, M.; Mohammadi, A.; Safarpour, H.; Shavalipour, A.; Ghadiri, M. Wave propagation analysis of the laminated cylindrical nanoshell coupled with a piezoelectric actuator. Mech. Based Des. Struct. Mach. 2019, 1–19. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Mohammadi, K.; Barouti, M.M.; Habibi, M. Wave propagation analysis of a spinning porous graphene nanoplatelet-reinforced nanoshell. Waves Random Complex Media 2019, 1–27. [Google Scholar] [CrossRef]
- Habibi, M.; Taghdir, A.; Safarpour, H. Stability analysis of an electrically cylindrical nanoshell reinforced with graphene nanoplatelets. Compos. Part B Eng. 2019, 175, 107125. [Google Scholar] [CrossRef]
- Mohammadgholiha, M.; Shokrgozar, A.; Habibi, M.; Safarpour, H. Buckling and frequency analysis of the nonlocal strain–stress gradient shell reinforced with graphene nanoplatelets. J. Vib. Control 2019, 25, 2627–2640. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Habibi, M.; Safarpour, H. On modeling of wave propagation in a thermally affected GNP-reinforced imperfect nanocomposite shell. Eng. Comput. 2019, 35, 1375–1389. [Google Scholar] [CrossRef]
- Ghanbari, B.; Ghadiri, M.; SafarPour, H. A modified strain gradient shell model for vibration analysis of DWCNT conveying viscous fluid including surface effects. Mech. Based Des. Struct. Mach. 2020, 21, 1–31. [Google Scholar] [CrossRef]
- Hashemi, H.R.; Alizadeh, A.A.; Oyarhossein, M.A.; Shavalipour, A.; Makkiabadi, M.; Habibi, M. Influence of imperfection on amplitude and resonance frequency of a reinforcement compositionally graded nanostructure. Waves Random Complex Media 2019, 1–27. [Google Scholar] [CrossRef]
- Esmailpoor Hajilak, Z.; Pourghader, J.; Hashemabadi, D.; Sharifi Bagh, F.; Habibi, M.; Safarpour, H. Multilayer GPLRC composite cylindrical nanoshell using modified strain gradient theory. Mech. Based Des. Struct. Mach. 2019, 47, 521–545. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Hajilak, Z.E.; Habibi, M.; Safarpour, H. Buckling and vibration characteristics of a carbon nanotube-reinforced spinning cantilever cylindrical 3D shell conveying viscous fluid flow and carrying spring-mass systems under various temperature distributions. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2019, 233, 4590–4605. [Google Scholar] [CrossRef]
- Mohammadi, A.; Lashini, H.; Habibi, M.; Safarpour, H. Influence of viscoelastic foundation on dynamic behaviour of the double walled cylindrical inhomogeneous micro shell using MCST and with the aid of GDQM. J. Solid Mech. 2019, 11, 440–453. [Google Scholar]
- Habibi, M.; Hashemabadi, D.; Safarpour, H. Vibration analysis of a high-speed rotating GPLRC nanostructure coupled with a piezoelectric actuator. Eur. Phys. J. Plus 2019, 134, 307. [Google Scholar] [CrossRef]
- Pourjabari, A.; Hajilak, Z.E.; Mohammadi, A.; Habibi, M.; Safarpour, H. Effect of porosity on free and forced vibration characteristics of the GPL reinforcement composite nanostructures. Comput. Math. Appl. 2019, 77, 2608–2626. [Google Scholar] [CrossRef]
- Habibi, M.; Mohammadgholiha, M.; Safarpour, H. Wave propagation characteristics of the electrically GNP-reinforced nanocomposite cylindrical shell. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 221. [Google Scholar] [CrossRef]
- Safarpour, H.; Pourghader, J.; Habibi, M. Influence of spring-mass systems on frequency behavior and critical voltage of a high-speed rotating cantilever cylindrical three-dimensional shell coupled with piezoelectric actuator. J. Vib. Control 2019, 25, 1543–1557. [Google Scholar] [CrossRef]
- Safarpour, M.; Ghabussi, A.; Ebrahimi, F.; Habibi, M.; Safarpour, H. Frequency characteristics of FG-GPLRC viscoelastic thick annular plate with the aid of GDQM. Thin-Walled Struct. 2020, 150, 106683. [Google Scholar] [CrossRef]
- Safarpour, M.; Ebrahimi, F.; Habibi, M.; Safarpour, H. On the nonlinear dynamics of a multi-scale hybrid nanocomposite disk. Eng. Comput. 2020, 1–20. [Google Scholar] [CrossRef]
- Moayedi, H.; Habibi, M.; Safarpour, H.; Safarpour, M.; Foong, L. Buckling and Frequency Responses of A Graphene Nanoplatelet Reinforced Composite Microdisk. Int. J. Appl. Mech. 2019, 11. [Google Scholar] [CrossRef]
- Sahmani, S.; Fattahi, A. Size-dependent nonlinear instability of shear deformable cylindrical nanopanels subjected to axial compression in thermal environments. Microsyst. Technol. 2017, 23, 4717–4731. [Google Scholar] [CrossRef]
- Sahmani, S.; Aghdam, M. Nonlocal electrothermomechanical instability of temperature-dependent FGM nanopanels with piezoelectric facesheets. Iran. J. Sci. Technol. Trans. Mech. Eng. 2019, 43, 579–593. [Google Scholar] [CrossRef]
- Sahmani, S.; Khandan, A. Size dependency in nonlinear instability of smart magneto-electro-elastic cylindrical composite nanopanels based upon nonlocal strain gradient elasticity. Microsyst. Technol. 2019, 25, 2171–2186. [Google Scholar] [CrossRef]
- Sarvestani, H.Y.; Akbarzadeh, A.; Mirabolghasemi, A. Structural analysis of size-dependent functionally graded doubly-curved panels with engineered microarchitectures. Acta Mech. 2018, 229, 2675–2701. [Google Scholar] [CrossRef]
- Zhou, S.; Zhang, R.; Zhou, S.; Li, A. Free vibration analysis of bilayered circular micro-plate including surface effects. Appl. Math. Model. 2019, 70, 54–66. [Google Scholar] [CrossRef]
- Gholami, R.; Darvizeh, A.; Ansari, R.; Pourashraf, T. Analytical treatment of the size-dependent nonlinear postbuckling of functionally graded circular cylindrical micro-/nano-shells. Iran. J. Sci. Technol. Trans. Mech. Eng. 2018, 42, 85–97. [Google Scholar] [CrossRef]
- Mohammadimehr, M.; Emdadi, M.; Afshari, H.; Rousta Navi, B. Bending, buckling and vibration analyses of MSGT microcomposite circular-annular sandwich plate under hydro-thermo-magneto-mechanical loadings using DQM. Int. J. Smart Nano Mater. 2018, 9, 233–260. [Google Scholar] [CrossRef]
- Mohammadimehr, M.; Atifeh, S.J.; Rousta Navi, B. Stress and free vibration analysis of piezoelectric hollow circular FG-SWBNNTs reinforced nanocomposite plate based on modified couple stress theory subjected to thermo-mechanical loadings. J. Vib. Control 2018, 24, 3471–3486. [Google Scholar] [CrossRef]
- Sajadi, B.; Alijani, F.; Goosen, H.; van Keulen, F. Effect of pressure on nonlinear dynamics and instability of electrically actuated circular micro-plates. Nonlinear Dyn. 2018, 91, 2157–2170. [Google Scholar] [CrossRef]
- Wang, Z.-W.; Han, Q.-F.; Nash, D.H.; Liu, P.-Q. Investigation on inconsistency of theoretical solution of thermal buckling critical temperature rise for cylindrical shell. Thin-Walled Struct. 2017, 119, 438–446. [Google Scholar] [CrossRef]
- Safarpour, H.; Hajilak, Z.E.; Habibi, M. A size-dependent exact theory for thermal buckling, free and forced vibration analysis of temperature dependent FG multilayer GPLRC composite nanostructures restring on elastic foundation. Int. J. Mech. Mater. Des. 2019, 15, 569–583. [Google Scholar] [CrossRef]
- Wang, K.; Wang, B.; Zhang, C. Surface energy and thermal stress effect on nonlinear vibration of electrostatically actuated circular micro-/nanoplates based on modified couple stress theory. Acta Mech. 2017, 228, 129–140. [Google Scholar] [CrossRef]
- Mahinzare, M.; Alipour, M.J.; Sadatsakkak, S.A.; Ghadiri, M. A nonlocal strain gradient theory for dynamic modeling of a rotary thermo piezo electrically actuated nano FG circular plate. Mech. Syst. Signal Process. 2019, 115, 323–337. [Google Scholar] [CrossRef]
- Mahinzare, M.; Ranjbarpur, H.; Ghadiri, M. Free vibration analysis of a rotary smart two directional functionally graded piezoelectric material in axial symmetry circular nanoplate. Mech. Syst. Signal Process. 2018, 100, 188–207. [Google Scholar] [CrossRef]
- Safarpour, H.; Barooti, M.; Ghadiri, M. Influence of Rotation on Vibration Behavior of a Functionally Graded Moderately Thick Cylindrical Nanoshell Considering Initial Hoop Tension. J. Solid Mech. 2019, 11, 254–271. [Google Scholar]
- Ebrahimi, F.; Safarpour, H. Vibration analysis of inhomogeneous nonlocal beams via a modified couple stress theory incorporating surface effects. Wind Struct. 2018, 27, 431–438. [Google Scholar]
- Mohammadi, K.; Barouti, M.M.; Safarpour, H.; Ghadiri, M. Effect of distributed axial loading on dynamic stability and buckling analysis of a viscoelastic DWCNT conveying viscous fluid flow. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 93. [Google Scholar] [CrossRef]
- SafarPour, H.; Hosseini, M.; Ghadiri, M. Influence of three-parameter viscoelastic medium on vibration behavior of a cylindrical nonhomogeneous microshell in thermal environment: An exact solution. J. Therm. Stresses 2017, 40, 1353–1367. [Google Scholar] [CrossRef]
- Safarpour, H.; Mohammadi, K.; Ghadiri, M.; Barooti, M.M. Effect of porosity on flexural vibration of CNT-reinforced cylindrical shells in thermal environment using GDQM. Int. J. Struct. Stab. Dyn. 2018, 18, 1850123. [Google Scholar] [CrossRef]
- Safarpour, H.; Mohammadi, K.; Ghadiri, M. Temperature-dependent vibration analysis of a FG viscoelastic cylindrical microshell under various thermal distribution via modified length scale parameter: A numerical solution. J. Mech. Behav. Mater. 2017, 26, 9–24. [Google Scholar] [CrossRef]
- SafarPour, H.; Ghanbari, B.; Ghadiri, M. Buckling and free vibration analysis of high speed rotating carbon nanotube reinforced cylindrical piezoelectric shell. Appl. Math. Model. 2019, 65, 428–442. [Google Scholar] [CrossRef]
- Shojaeefard, M.; Mahinzare, M.; Safarpour, H.; Googarchin, H.S.; Ghadiri, M. Free vibration of an ultra-fast-rotating-induced cylindrical nano-shell resting on a Winkler foundation under thermo-electro-magneto-elastic condition. Appl. Math. Model. 2018, 61, 255–279. [Google Scholar] [CrossRef]
- Ghadiri, M.; Safarpour, H. Free vibration analysis of embedded magneto-electro-thermo-elastic cylindrical nanoshell based on the modified couple stress theory. Appl. Phys. A 2016, 122, 833. [Google Scholar] [CrossRef]
- Ghadiri, M.; SafarPour, H. Free vibration analysis of size-dependent functionally graded porous cylindrical microshells in thermal environment. J. Therm. Stresses 2017, 40, 55–71. [Google Scholar] [CrossRef]
- Ghadiri, M.; Shafiei, N.; Safarpour, H. Influence of surface effects on vibration behavior of a rotary functionally graded nanobeam based on Eringen’s nonlocal elasticity. Microsyst. Technol. 2017, 23, 1045–1065. [Google Scholar] [CrossRef]
- SafarPour, H.; Ghadiri, M. Critical rotational speed, critical velocity of fluid flow and free vibration analysis of a spinning SWCNT conveying viscous fluid. Microfluid. Nanofluid. 2017, 21, 22. [Google Scholar] [CrossRef]
- Barooti, M.M.; Safarpour, H.; Ghadiri, M. Critical speed and free vibration analysis of spinning 3D single-walled carbon nanotubes resting on elastic foundations. Eur. Phys. J. Plus 2017, 132, 6. [Google Scholar] [CrossRef]
- SafarPour, H.; Mohammadi, K.; Ghadiri, M.; Rajabpour, A. Influence of various temperature distributions on critical speed and vibrational characteristics of rotating cylindrical microshells with modified lengthscale parameter. Eur. Phys. J. Plus 2017, 132, 281. [Google Scholar] [CrossRef]
- Ghadiri, M.; Safarpour, H. Free Vibration Analysis of a Functionally Graded Cylindrical Nanoshell Surrounded by Elastic Foundation Based on the Modified Couple Stress Theory. Amirkabir J. Mech. Eng. 2018, 49, 257–260. [Google Scholar]
- Song, M.; Kitipornchai, S.; Yang, J. Free and forced vibrations of functionally graded polymer composite plates reinforced with graphene nanoplatelets. Compos. Struct. 2017, 159, 579–588. [Google Scholar] [CrossRef]
- De Villoria, R.G.; Miravete, A. Mechanical model to evaluate the effect of the dispersion in nanocomposites. Acta Mater. 2007, 55, 3025–3031. [Google Scholar] [CrossRef]
- Karimiasl, M.; Ebrahimi, F.; Vinyas, M. Nonlinear vibration analysis of multiscale doubly curved piezoelectric composite shell in hygrothermal environment. J. Intell. Mater. Syst. Struct. 2019, 30, 1594–1609. [Google Scholar] [CrossRef]
- Moayedi, H.; Darabi, R.; Ghabussi, A.; Habibi, M.; Foong, L.K. Weld orientation effects on the formability of tailor welded thin steel sheets. Thin-Walled Struct. 2020, 149, 106669. [Google Scholar] [CrossRef]
- Ghazanfari, A.; Soleimani, S.S.; Keshavarzzadeh, M.; Habibi, M.; Assempuor, A.; Hashemi, R. Prediction of FLD for sheet metal by considering through-thickness shear stresses. Mech. Based Des. Struct. Mach. 2019, 1–18. [Google Scholar] [CrossRef]
- Alipour, M.; Torabi, M.A.; Sareban, M.; Lashini, H.; Sadeghi, E.; Fazaeli, A.; Habibi, M.; Hashemi, R. Finite element and experimental method for analyzing the effects of martensite morphologies on the formability of DP steels. Mech. Based Des. Struct. Mach. 2019, 1–17. [Google Scholar] [CrossRef]
- Hosseini, S.; Habibi, M.; Assempour, A. Experimental and numerical determination of forming limit diagram of steel-copper two-layer sheet considering the interface between the layers. Modares Mech. Eng. 2018, 18, 174–181. [Google Scholar]
- Habibi, M.; Hashemi, R.; Ghazanfari, A.; Naghdabadi, R.; Assempour, A. Forming limit diagrams by including the M–K model in finite element simulation considering the effect of bending. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2018, 232, 625–636. [Google Scholar] [CrossRef]
- Habibi, M.; Payganeh, G. Experimental and Finite Element Investigation of Titanium Tubes Hot Gas Forming and Production of Square Cross-Section Specimens. Aerosp. Mech. J. 2018, 14, 89–99. [Google Scholar]
- Habibi, M.; Hashemi, R.; Tafti, M.F.; Assempour, A. Experimental investigation of mechanical properties, formability and forming limit diagrams for tailor-welded blanks produced by friction stir welding. J. Manuf. Process. 2018, 31, 310–323. [Google Scholar] [CrossRef]
- Habibi, M.; Ghazanfari, A.; Assempour, A.; Naghdabadi, R.; Hashemi, R. Determination of forming limit diagram using two modified finite element models. Mech. Eng. 2017, 48, 141–144. [Google Scholar]
- Ghazanfari, A.; Assempour, A.; Habibi, M.; Hashemi, R. Investigation on the effective range of the through thickness shear stress on forming limit diagram using a modified Marciniak–Kuczynski model. Modares Mech. Eng. 2016, 16, 137–143. [Google Scholar]
- Habibi, M.; Hashemi, R.; Sadeghi, E.; Fazaeli, A.; Ghazanfari, A.; Lashini, H. Enhancing the mechanical properties and formability of low carbon steel with dual-phase microstructures. J. Mater. Eng. Perform. 2016, 25, 382–389. [Google Scholar] [CrossRef]
- Fazaeli, A.; Habibi, M.; Ekrami, A. Experimental and Finite Element Comparison of Mechanical Properties and Formability of Dual Phase Steel and Ferrite-Pearlite Steel With the Same Chemical Composition. Metall. Eng. 2016, 19, 84–93. [Google Scholar]
- Mahdi Alipour, S.; Mohammadi, K.; Mohammadi, A.; Habibi, M.; Safarpour, H. On dynamic of electro-elastic GNPRC cylindrical shell using modified length-couple stress parameter. Mech. Based Des. Struct. Mach. 2019, 1–20. [Google Scholar]
- Eyvazian, A.; Hamouda, A.M.; Tarlochan, F.; Mohsenizadeh, S.; Dastjerdi, A.A. Damping and vibration response of viscoelastic smart sandwich plate reinforced with non-uniform Graphene platelet with magnetorheological fluid core. Steel Compos. Struct. 2019, 33, 891. [Google Scholar]
- Motezaker, M.; Eyvazian, A. Post-buckling analysis of Mindlin Cut out-plate reinforced by FG-CNTs. Steel Compos. Struct. 2020, 34, 289–297. [Google Scholar]
- Derazkola, H.A.; Eyvazian, A.; Simchi, A. Modeling and experimental validation of material flow during FSW of polycarbonate. Mater. Today Commun. 2020, 22, 100796. [Google Scholar] [CrossRef]
- Eyvazian, A.; Hamouda, A.; Tarlochan, F.; Derazkola, H.A.; Khodabakhshi, F. Simulation and experimental study of underwater dissimilar friction-stir welding between aluminium and steel. J. Mater. Res. Technol. 2020. [Google Scholar] [CrossRef]
- Eyvazian, A.; Habibi, M.K.; Hamouda, A.M.; Hedayati, R. Axial crushing behavior and energy absorption efficiency of corrugated tubes. Mater. Des. (1980-2015) 2014, 54, 1028–1038. [Google Scholar] [CrossRef]
- Liu, W.; Zhang, Z.; Chen, J.; Jiang, D.; Fei, W.; Fan, J.; Li, Y. Feasibility evaluation of large-scale underground hydrogen storage in bedded salt rocks of China: A case study in Jiangsu province. Energy 2020, 198, 117348. [Google Scholar] [CrossRef]
- Liu, W.; Zhang, X.; Fan, J.; Li, Y.; Wang, L. Evaluation of Potential for Salt Cavern Gas Storage and Integration of Brine Extraction: Cavern Utilization, Yangtze River Delta Region. Nat. Resour. Res. 2020, 1–16. [Google Scholar] [CrossRef]
- Jafari, M.; Moradi, G.; SHIRAZI, R.S.; Mirzavand, R. Design and implementation of a six-port junction based on substrate integrated waveguide. Turk. J. Electr. Eng. Comput. Sci. 2017, 25, 2547–2553. [Google Scholar] [CrossRef]
- Shafiei, N.; Mirjavadi, S.S.; Afshari, B.M.; Rabby, S.; Hamouda, A. Nonlinear thermal buckling of axially functionally graded micro and nanobeams. Compos. Struct. 2017, 168, 428–439. [Google Scholar] [CrossRef]
- Żur, K.K.; Arefi, M.; Kim, J.; Reddy, J. Free vibration and buckling analyses of magneto-electro-elastic FGM nanoplates based on nonlocal modified higher-order sinusoidal shear deformation theory. Compos. Part B Eng. 2020, 182, 107601. [Google Scholar] [CrossRef]
- Gao, W.; Dimitrov, D.; Abdo, H. Tight independent set neighborhood union condition for fractional critical deleted graphs and ID deleted graphs. Discret. Contin. Dyn. Syst. Ser. 2018, 12, 711–721. [Google Scholar] [CrossRef]
- Gao, W.; Guirao, J.L.G.; Basavanagoud, B.; Wu, J. Partial multi-dividing ontology learning algorithm. Inf. Sci. 2018, 467, 35–58. [Google Scholar] [CrossRef]
- Gao, W.; Wang, W.; Dimitrov, D.; Wang, Y. Nano properties analysis via fourth multiplicative ABC indicator calculating. Arab. J. Chem. 2018, 11, 793–801. [Google Scholar] [CrossRef]
- Gao, W.; Wu, H.; Siddiqui, M.K.; Baig, A.Q. Study of biological networks using graph theory. Saudi J. Biol. Sci. 2018, 25, 1212–1219. [Google Scholar] [CrossRef] [PubMed]
- Gao, W.; Guirao, J.L.G.; Abdel-Aty, M.; Xi, W. An independent set degree condition for fractional critical deleted graphs. Discret. Contin. Dyn. Syst. Ser. 2019, 12, 877–886. [Google Scholar] [CrossRef]
- Shu, C. Differential Quadrature and Its Application in Engineering; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Moayedi, H.; Ebrahimi, F.; Habibi, M.; Safarpour, H.; Foong, L.K. Application of nonlocal strain–stress gradient theory and GDQEM for thermo-vibration responses of a laminated composite nanoshell. Eng. Comput. 2020, 1–16. [Google Scholar] [CrossRef]
- Cheshmeh, E.; Karbon, M.; Eyvazian, A.; Jung, D.; Tran, T.; Habibi, M.; Safarpour, M. Buckling and vibration analysis of FG-CNTRC plate subjected to thermo-mechanical load based on higher-order shear deformation theory. Mech. Based Des. Struct. Mach. 2020, 1–24. [Google Scholar] [CrossRef]
- Oyarhossein, M.A.; Alizadeh, A.A.; Habibi, M.; Makkiabadi, M.; Daman, M.; Safarpour, H.; Jung, D.W. Dynamic response of the nonlocal strain-stress gradient in laminated polymer composites microtubes. Sci. Rep. 2020, 10, 5616. [Google Scholar] [CrossRef]
- Najaafi, N.; Jamali, M.; Habibi, M.; Sadeghi, S.; Jung, D.W.; Nabipour, N. Dynamic instability responses of the substructure living biological cells in the cytoplasm environment using stress-strain size-dependent theory. J. Biomol. Struct. Dyn. 2020, 1–20. [Google Scholar] [CrossRef] [PubMed]
- Abdelmalek, Z.; Karbon, M.; Eyvazian, A.; Foroughi, A.; Safarpour, H.; Tlili, I. On the dynamics of a curved Microtubule-associated proteins by considering viscoelastic properties of the living biological cells. J. Biomol. Struct. Dyn. 2020, 1–26. [Google Scholar] [CrossRef] [PubMed]
- Wang, A.; Chen, H.; Hao, Y.; Zhang, W. Vibration and bending behavior of functionally graded nanocomposite doubly-curved shallow shells reinforced by graphene nanoplatelets. Results Phys. 2018, 9, 550–559. [Google Scholar] [CrossRef]
- Kumar, P.; Srinivas, J. Vibration, buckling and bending behavior of functionally graded multi-walled carbon nanotube reinforced polymer composite plates using the layer-wise formulation. Compos. Struct. 2017, 177, 158–170. [Google Scholar] [CrossRef]
- Nadri, S.; Xie, L.; Jafari, M.; Bauwens, M.F.; Arsenovic, A.; Weikle, R.M. Measurement and Extraction of Parasitic Parameters of Quasi-Vertical Schottky Diodes at Submillimeter Wavelengths. IEEE Microw. Wirel. Compon. Lett. 2019, 29, 474–476. [Google Scholar] [CrossRef]
- Simon, T.M.; Jackson, D.W. Articular cartilage: Injury pathways and treatment options. Sports Med. Arthrosc. Rev. 2018, 26, 31–39. [Google Scholar] [CrossRef]
- Shen, H.-S.; Xiang, Y.; Lin, F. Nonlinear vibration of functionally graded graphene-reinforced composite laminated plates in thermal environments. Comput. Methods Appl. Mech. Eng. 2017, 319, 175–193. [Google Scholar] [CrossRef]
- Wu, H.; Kitipornchai, S.; Yang, J. Thermal buckling and postbuckling of functionally graded graphene nanocomposite plates. Mater. Des. 2017, 132, 430–441. [Google Scholar] [CrossRef]



| N = M=7 | N = M = 9 | N = M = 11 | N = M = 13 | N = M = 15 | ||
|---|---|---|---|---|---|---|
| CFFF | Pure epoxy | 0.0152839 | 0.0171311 | 0.0122786 | 0.0184308 | 0.0185104 |
| Pattern 2 | 0.0320457 | 0.0333990 | 0.0379272 | 0.0340140 | 0.0340840 | |
| CSFS | Pure epoxy | 0.0245107 | 0.0279184 | 0.0205209 | 0.0205209 | 0.0205209 |
| Pattern 2 | 0.0411726 | 0.0410866 | 0.0407444 | 0.0407444 | 0.0407444 | |
| SSSS | Pure epoxy | 0.0328041 | 0.0328039 | 0.0328039 | 0.0328039 | 0.0328039 |
| Pattern 2 | 0.0685672 | 0.06850382 | 0.06844328 | 0.06839187 | 0.0683808 | |
| CSSS | Pure epoxy | 0.0551124 | 0.05553747 | 0.05366811 | 0.05552384 | 0.0555205 |
| Pattern 2 | 0.0971378 | 0.0989422 | 0.09917005 | 0.09929541 | 0.0992978 | |
| CCCC | Pure epoxy | 0.0763170 | 0.0763555 | 0.0763567 | 0.0763567 | 0.0763567 |
| Pattern 2 | 0.1388539 | 0.13889832 | 0.13889978 | 0.1389035 | 0.1389035 | |
| N = M = 7 | N = M = 9 | N = M = 11 | N = M = 13 | N = M = 15 | ||
|---|---|---|---|---|---|---|
| SSSS | /h = 0 | 1.449919 | 1.449102 | 1.449112 | 1.449111 | 1.449111 |
| /h = 0.4 | 1.463493 | 1.462706 | 1.462714 | 1.462714 | 1.462714 | |
| CSSS | /h = 0 | 2.466464 | 2.470683 | 2.470622 | 2.470649 | 2.470649 |
| /h = 0.4 | 2.512817 | 2.514689 | 2.514825 | 2.514884 | 2.514884 | |
| CCCC | /h = 0 | 4.292727 | 4.288484 | 4.288339 | 2.288339 | 2.288339 |
| /h = 0.4 | 4.468242 | 4.431111 | 4.435274 | 4.434809 | 4.434809 | |
| Resource | (n, m) | Pure Epoxy | Pattern 1 | Patter 2 | Patter 3 |
|---|---|---|---|---|---|
| Present | (1,1) | 0.0586 | 0.1221 | 0.0979 | 0.1417 |
| Wang et al. [105] | (1,1) | 0.0584 | 0.1216 | 0.1023 | 0.1365 |
| Song et al. [69] | (1,1) | 0.0584 | 0.1216 | 0.1020 | 0.1378 |
| ANSYS [106] | (1,1) | 0.0563 | 0.1171 | 0.0881 | 0.1319 |
| Present | (1,2) | 0.1405 | 0.2924 | 0.2369 | 0.3358 |
| Wang et al. [105] | (1,2) | 0.1391 | 0.2895 | 0.2469 | 0.3183 |
| Song et al. [69] | (1,2) | 0.1391 | 0.2895 | 0.2456 | 0.3248 |
| ANSYS [106] | (1,2) | 0.1361 | 0.2833 | 0.2162 | 0.4043 |
| a/h = 10 | a/h = 20 | ||||
|---|---|---|---|---|---|
| b/a = 1 | b/a = 2 | b/a = 1 | b/a = 2 | ||
| 0 | Ref. [93] | 0.0933 | 0.0590 | 0.0239 | 0.01500 |
| Presented study | 0.0927 | 0.0583 | 0.0234 | 0.01496 | |
| 1 | Ref. [93] | 0.0852 | 0.0557 | 0.0218 | -------- |
| Presented study | 0.0849 | 0.0545 | 0.0213 | 0.01474 | |
| H = a/15 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Numerical Results for | FEM Results for Pattern 4 | Numerical Results for | FEM Results for Pattern 3 | Numerical Results for | FEM Results for Pattern 2 | Numerical Results for | FEM Results for Pattern 1 | |
| Pattern 4 | Pattern 3 | Pattern 2 | Pattern 1 | |||||
| CCCC | 7.35 × 105 | 7.28 × 105 | 7.84 × 105 | 7.76 × 105 | 7.12 × 105 | 7.00 × 105 | 7.49 × 105 | 7.41 × 105 |
| CSSS | 5.28 × 105 | 5.21 × 105 | 5.71 × 105 | 5.63 × 105 | 5.15 × 105 | 5.07 × 105 | 5.43 × 105 | 5.33 × 105 |
| H = a/10 | ||||||||
| Numerical results for | FEM results for Pattern 4 | Numerical results for | FEM results for Pattern 3 | Numerical results for | FEM results for Pattern 2 | Numerical results for | FEM results for Pattern 1 | |
| Pattern 4 | Pattern 3 | Pattern 2 | Pattern 1 | |||||
| CCCC | 7.46 × 105 | 7.39 × 105 | 8.01 × 105 | 7.92 × 105 | 7.31 × 105 | 7.23 × 105 | 7.59 × 105 | 7.52 × 105 |
| CSSS | 5.43 × 105 | 5.38 × 105 | 5.98 × 105 | 5.90 × 105 | 5.26 × 105 | 5.20 × 105 | 5.65 × 105 | 5.60 × 105 |
| Material Properties: | GPL |
| Young’s modulus (GPa) | 1010 |
| Density (kg m−3) | 1062.5 |
| Poisson’s ratio | 0.186 |
| Thermal expansion coefficient (10−6/K) | 5 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adamian, A.; Hosseini Safari, K.; Sheikholeslami, M.; Habibi, M.; Al-Furjan, M.S.H.; Chen, G. Critical Temperature and Frequency Characteristics of GPLs-Reinforced Composite Doubly Curved Panel. Appl. Sci. 2020, 10, 3251. https://doi.org/10.3390/app10093251
Adamian A, Hosseini Safari K, Sheikholeslami M, Habibi M, Al-Furjan MSH, Chen G. Critical Temperature and Frequency Characteristics of GPLs-Reinforced Composite Doubly Curved Panel. Applied Sciences. 2020; 10(9):3251. https://doi.org/10.3390/app10093251
Chicago/Turabian StyleAdamian, Armen, Keivan Hosseini Safari, Mehdi Sheikholeslami, Mostafa Habibi, M. S. H. Al-Furjan, and Guojin Chen. 2020. "Critical Temperature and Frequency Characteristics of GPLs-Reinforced Composite Doubly Curved Panel" Applied Sciences 10, no. 9: 3251. https://doi.org/10.3390/app10093251
APA StyleAdamian, A., Hosseini Safari, K., Sheikholeslami, M., Habibi, M., Al-Furjan, M. S. H., & Chen, G. (2020). Critical Temperature and Frequency Characteristics of GPLs-Reinforced Composite Doubly Curved Panel. Applied Sciences, 10(9), 3251. https://doi.org/10.3390/app10093251






