Abstract
The discontinuities of a five-axis linear-segment toolpath result in fluctuation in the feedrate, acceleration and jerk commands that lead to machine tool vibration and poor surface finish. For path smoothing, with the global curve-fitting method it is difficult to control fitting error and the local corner-smoothing method has large curvature extreme. For path synchronization, the parameter synchronization method cannot ensure smooth rotary motion. Aiming at these problems, this paper proposes a double B-spline curve-fitting and synchronization-integrated feedrate scheduling method. Two C2-continuous and error-bounded B-spline curves are produced to fit tool-tip position and tool orientation, respectively. The fitting error is controlled by locally refining the curve segments that exceed the fitting tolerance. The tool-tip position trajectory is firstly planned to address axial kinematic constraints in the feedrate scheduling process. Then the feedrate is deformed for the tool orientation to guarantee smooth rotary motion as well as to share the same motion time with the tool-tip position segment by segment. The feasibility and effectiveness of the proposed method have been validated by simulations and experiments on the S-shape test piece. Simulations show that the proposed curve-fitting method can generate smooth toolpath and constrain fitting error. The proposed feedrate scheduling method can guarantee smooth rotary motion and keep axial motions under kinematic limits, compared with the method that does not consider axial kinematic constraints and the parameter synchronization method. Experimental results verify that the proposed curve-fitting method can generate smooth tool path under fitting tolerance, and the proposed feedrate scheduling method can produce smooth and restricted axial motions.
1. Introduction
To machine free-form parts used widely in aerospace, die and mould industries, cutter of the machine tool is required to follow the programmed toolpath under computer numerical control (CNC) commands [1,2]. The curvilinear toolpath generated by computer-aided manufacturing (CAM) software is usually approximated by successive linear segments (linear-segment toolpath or G01 blocks) [3]. However, the transition corners between adjacent linear segments lead to tangential and curvature discontinuities, which cause fluctuation in the feedrate, acceleration, and jerk commands in the feedrate scheduling process that generates machine tool vibration and poor surface finish [4]. To avoid this behavior, the continuity of the linear-segment toolpath needs to be improved. Several approaches have been proposed in the existing literature for three-axis linear-segment toolpath smoothing, which can be categorized as local corner-smoothing method and global curve-fitting method. The local corner-smoothing method utilizes parametric curves to locally replace the sharp corners, such as B-spline [5,6,7], Bezier [8,9,10], and Pythagorean-hodograph (PH) curves [11,12]. Zhang et al. [7] propose G4-continuous toolpath via a quintic B-spline curve. Optimized by curvature variation energy (CVE), the chord error is seriously constrained and curvature extrema can be analytically calculated. Then the jerk-smooth feedrate scheduling scheme is developed based on the bidirectional scanning algorithm. Fan et al. [10] generated a G4 interpolative trajectory model using a symmetric nine-degree Bezier curve with confined chord error and analytical curvature extrema for trajectory smoothing, and employs jerk-smooth feedrate mode to perform time-optimal feedrate scheduling. Shi et al. [12] adopt a curvature-continuous PH curve as a transition to blend sharp corners. The blending algorithm can guarantee the approximation error exactly. The control points, the arc length and the curvature of the transition curve also have analytical expressions. The high-order geometric continuity leads to high-smoothness toolpath and feedrate profile. But the rising complexity may prevent these methods from promoting to five-axis processing. On the other hand, the global curve-fitting method utilizes a parametric curve to smooth the linear-segment toolpath globally by interpolating or approximating G01 data points. However, this method suffers from below-standard fitting error. Bi et al. [13] propose a general, fast and robust B-spline fitting scheme with PIA method to generate G2 tool path under confined chord error for high speed interpolation of micro-line tool path. He et al. [14] propose a progressive and iterative approximation for least squares incorporating energy term (ELSPIA) to deal with chord error constraint. Lin et al. [15] derive the explicit expression for the Hausdorff distance between a line segment and a curve segment, then a time-parameterized curve-fitting algorithm is presented to combine path smoothing and trajectory planning.
Five-axis CNC machine tools provide better accessibility with the help of additional rotary axes [16,17]. The smoothing of five-axis linear-segment toolpath brings about extra difficulties compared to three-axis. First, the tool orientation must be smoothed to ensure smooth rotary motion in addition to the tool-tip position smoothing. Second, given that the tool-tip position and tool orientation are smoothed independently, the two smoothed trajectories must be synchronized [18]. The local corner-smoothing method and the global curve-fitting method mentioned above are extended and used to smooth tool-tip position and tool orientation respectively. The local corner-smoothing method applied to five-axis linear-segment toolpath can guarantee high-order continuity while respect error tolerance and synchronization of the tool-tip position and tool orientation is achieved by adjusting the joint points of the linear and curvilinear segments [19,20,21]. The global curve-fitting method applied to five-axis linear-segment toolpath can ensure toolpath smoothness, but the fitting error is hard to control and evaluate [22,23]. Moreover, the global curve-fitting method usually synchronizes two trajectories by sharing the same curve parameter (parameter synchronization). The parameter synchronization method [22,23] plans the tool-tip trajectory according to translational motion constraints and then makes the tool orientation follow the tool-tip in the curve parameter space. However, if the tool orientation is merely parameter synchronized with tool-tip position, the rotary motion may be discontinuous at certain locations.
After path smoothing and synchronization, the geometric information of toolpath is transferred to the feedrate, acceleration (the change rate of feedrate) and jerk (the change rate of acceleration) trajectories in CNC system [24]. The toolpath with high-order continuity can raise the feedrate at the sharp corner, decline the fluctuation of feedrate and acceleration, thus improve the machining quality. Many feedrate scheduling methods have been proposed in the literature, including the jerk-limited method [25,26,27], the optimization method [28], the linear programming method [29,30,31], and the time-synchronization method [32]. Du et al. [25] present a complete S-shape feedrate scheduling approach (CSFA) with limited jerk, acceleration and feedrate for the three-axis parametric toolpath. Beudaert et al. [28] propose a Velocity Profile Optimization (VPOp) algorithm which has been implemented for various toolpath format. Fan et al. [29] reduce the velocity planning problem to an equivalent linear programming problem with polynomial computational complexity O(N3.5) to find the optimal solution. Huang et al. [32] advise a real-time feed scheduling method for five-axis machining by simultaneously planning linear and angular trajectories (SLATP) considering axial kinematic constraints.
For path smoothing, the global curve-fitting method has difficulty in controlling fitting error and the local corner-smoothing method has large curvature extreme which decreases nominal velocity in feedrate scheduling. For path synchronization, the parameter synchronization method cannot guarantee smooth rotary motion. With the aim of resolving these problems, a double B-spline curve-fitting and synchronization-integrated feedrate scheduling method for five-axis linear-segment toolpath is presented in this paper. Two cubic B-spline curves are used for fitting the tool-tip position and tool orientation respectively. The data points are initially fitted by a B-spline curve and then the curve segments exceeding the fitting tolerance are locally refined to get the final curve. After curve-fitting, synchronization and feedrate scheduling is required to guarantee smooth motion and machining efficiency. Feedrate scheduling of the tool-tip position is conducted first to address the axial kinematic constraints. Then the feedrate of the tool orientation is deformed to share the same motion time with the tool-tip position so that the tool-tip position and tool orientation arrive at specific locations simultaneously.
The rest of the paper is organized as follows. The fitted curves for tool-tip position and tool orientation under fitting tolerance are generated in Section 2. The synchronization and feedrate scheduling of the tool-tip position and tool orientation are implemented in Section 3. Simulations and experiments are carried out in Section 4 to demonstrate the feasibility and effectiveness of the proposed method. Conclusions are drawn in Section 5.
2. Double B-Spline Curve-Fitting for Tool-Tip Position and Tool Orientation under Fitting Tolerance
In this section, a double B-spline curve-fitting method is proposed to smooth tool-tip position and tool orientation in different coordinate frames respectively. The overview of the proposed curve-fitting method is shown in Figure 1. Five-axis linear-segment toolpath is expressed as discrete cutter location (CL) data. CL data in the workpiece coordinate system (WCS) are defined as , where the Cartesian coordinate represents the tool-tip position, and the spherical coordinate represents the tool orientation. The tool orientation spherical coordinate can be mapped into plane, where and are two rotary angles in the machine coordinate system (MCS).
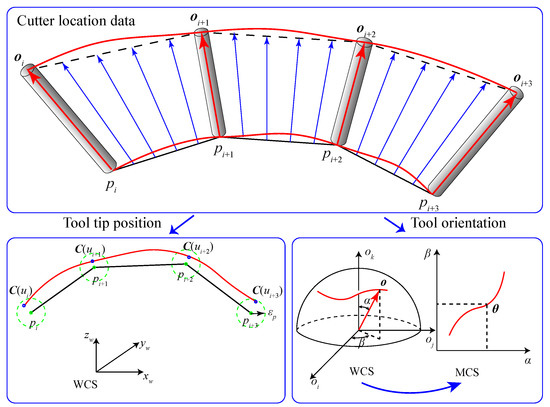
Figure 1.
Overview of double B-spline curve-fitting.
2.1. Tool-Tip Position Curve-Fitting
To fit successive linear segments, a cubic B-spline curve is used as the initial curve to guarantee C2-continuity (C2-continuity is necessary for continuous acceleration in feedrate scheduling). Besides geometric continuity, the fitting error and curvature are taken into consideration as criteria of a fitted curve. The fitting error affects the dimensional accuracy of the machined workpiece, hence must be regulated under fitting tolerance. The curvature, which affects the motion kinematics (the nominal velocity in feedrate scheduling), should be as small as possible but not under strict limitation.
The fitting error of tool-tip position is satisfied if the Hausdorff distance between the fitted curve and the tool-tip position polyline is not greater than the fitting tolerance in the WCS. For a curve segment and a line segment , the Hausdorff distance is [15]:
where is the Euclidean distance between and .
Since the explicit calculation of the Hausdorff distance by its definition between the fitted curve and the polyline is very computation-complex, the fitting error is classified into two categories. The first is called point error that indicates the approximation error between the fitting curve and the data points. The second is called chord error that represents the approximation error between the fitting curve and the linear segments.
To fit the tool-tip position data, we start with a cubic B-spline curve to satisfy point error. A cubic B-spline curve defined as linear combination of control points and cubic B-spline basis functions is given by [33]:
where d stands for degree of the curve and in this case . The B-spline basis functions defined on a non-descending knot vector are calculated recursively as follows [33]:
The cubic B-spline curve that passes through a set of tool-tip position data points is determined once the knot vector and control points are decided. The curve parameter value corresponding to data point and the knot vector are responsible for the shape and parameterization of the B-spline curve. is assigned using the cumulative chord length parameterization [33]:
where . The knot vector is built by averaging parameter values from Equation (3) as follows [33]:
Since the knot vector has been decided and each tool-tip position point has been assigned a parameter value, system of linear equations is established:
The control points are acquired by solving system of linear equations shown in Equation (6) using the inverse B-spline basis function matrix. Therefore, the initial curve interpolating all the data points defined by Equation (1) is resolved, and the point error is satisfied. However, the initial curve might exceed chord error at certain curve segments.
Assuming that the distance between the initial curve in the parameter interval and the corresponding line segment is greater than , the local refinement process is expected to be limited in the parameter interval so that the remaining portion of the curve is not affected.
In order to increase the flexibility of the local curve segment that needs to be refined, control points are added using knots insertion. Let be the knot inserted to , the new control points can be calculated as:
where .
Denote and as and after knot insertion. Denote the distance between the control point and as . and which must be not greater than due to strong convex hull property of B-spline curves [33], otherwise it is necessary to insert more knots to . To keep the portion outside unchanged, we can only adjust the control points . If , replace with where is the unit vector that points from to and is the distance moved along . Assign to the unit vector of the direction that is perpendicular to and to the value of . After all the local curve segments are refined, the final curve satisfies the fitting tolerance while maintaining C2-continuity. Flow of the proposed curve-fitting scheme is shown in Figure 2.
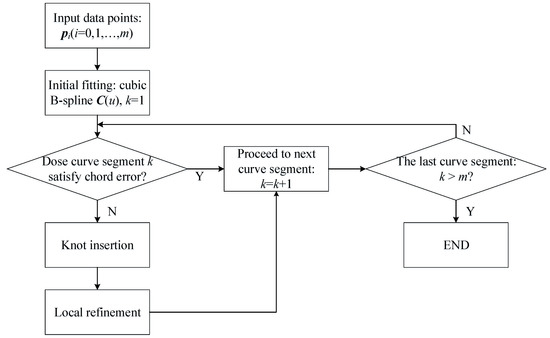
Figure 2.
Flowchart of the proposed curve-fitting scheme.
We present a planar example with five points and fitting tolerance of 0.05 mm as a numerical illustration of the proposed curve-fitting scheme. The result of the B-spline curve fitted to five data points is shown in Figure 3. The initial curve that satisfies point error exceeds chord error bound at segment 1 and segment 2, which are zoomed in to get a clearer view. Then the two segments is locally refined to obtain the final error-constrained curve. The fitting error and curvature results are demonstrated in Figure 4. As can be seen, the fitting error of the traditional global curve-fitting method exceeds the fitting tolerance. The proposed curve-fitting method, as an improvement of the global curve-fitting method, can get the fitting error strictly under the fitting tolerance. Compare to the local corner-smoothing method, the proposed method has smaller curvature extrema under the same geometric continuity. Notice that the local corner-smoothing method has lower fitting error in most areas because only the corner parts are replaced. The proposed curve-fitting method is more adaptive to micro linear segments whose adjacent corners are very close.
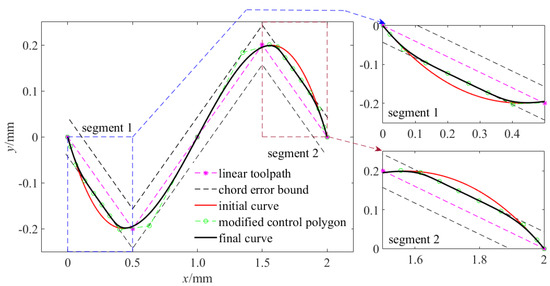
Figure 3.
Fitted curve of planar five-point example.
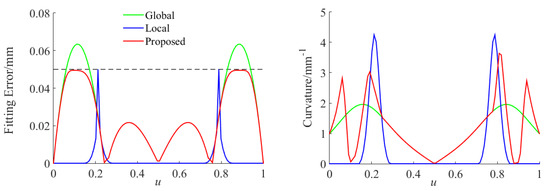
Figure 4.
Fitting error and curvature of planar five-point example.
2.2. Tool Orientation Curve-Fitting
The tool orientation data are expressed by the spherical coordinates in the WCS. Unlike curve-fitting of the tool-tip position, the tool orientation is fitted to the Cartesian coordinates that map from the given spherical coordinates to ensure that the magnitude of the orientation vector remains unity [22]. The mapping from the spherical coordinates to the Cartesian coordinates is obtained as follows:
where and are actually the rotary drive commands and in the MCS respectively. And the inverse mapping is in the following form:
The fitting tolerance of the tool orientation is given as in the WCS. Since the tool orientation is smoothed in the MCS, it is necessary to convert to which denotes the fitting tolerance of the tool orientation in the MCS.
As shown in Figure 5, we assume is the orientation position after O rotates in the WCS and is the transitional orientation position that rotates away from the -axis to reach . The lengths of edge , , and are obtained as:
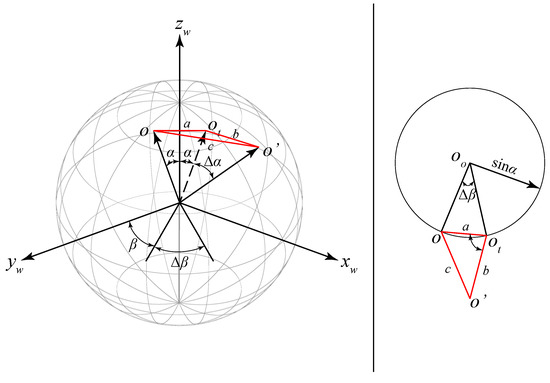
Figure 5.
Fitting error and curvature of planar five-point example.
Since , , and are extremely small, , , and are approximately collinear. Thus we have and Equation (10) can be simplified as:
Because , we have , that is which lead to . Since , the fitting error of the tool orientation is satisfied if . Without loss of generality, let .
The B-spline curve in the Cartesian plane is obtained with the input of the mapped tool orientation data and fitting tolerance according to the procedure in Section 2.1 as:
The tool orientation spline in the WCS is obtained using inverse mapping from Equation (9). It is noteworthy that the number of control points of the fitted curve depends on the initial curve and the fitting tolerance. Therefore the number of control points of the tool orientation is not necessarily the same as the tool-tip position.
3. Synchronization-Integrated Feedrate Scheduling
Since the tool-tip position and tool orientation are fitted independently in different coordinates, the synchronization and feedrate scheduling are necessary for curve interpolation. In this section, synchronization-integrated feedrate scheduling method is presented to ensure that the tool-tip position motion and tool orientation motion are synchronized and smooth. Feedrate scheduling of the tool-tip position is conducted firstly to address the axial kinematic constraints. Then the tool orientation feedrate is obtained by feedrate deformation method to guarantee smooth rotary motion as well as to share the same motion time with the tool-tip position segment by segment. Thus, the synchronization and feedrate scheduling is implemented in one procedure.
3.1. Feedrate Scheduling for Tool-Tip Position
The goal of feedrate scheduling is to find a smooth interpolation under machining constraints. Usually, the interpolation chord error, the axial kinematics and the tangential kinematics are important constraints for high speed and high accuracy machining. Under the circumstances, the interpolation error, the axial velocities and accelerations are considered to determine the allowable feedrate along the tool-tip position curve . Then the feedrate is scheduled using the S-shape jerk-limited method taking tangential acceleration and jerk into account.
The interpolation chord error along at the parameter value u can be approximated as [25]:
where T is the interpolation period, is the curvature radius, and is the feedrate at the parameter value u. Hence the interpolation chord error limited feedrate can be obtained as:
where is the defined limitation of interpolation error. Further, the feedrate in the curve parameter domain can be expressed as:
Denote as a representation of transition between time domain t and curve parameter domain u, and Equation (14) can be converted to:
The velocity of each axis can be calculated as:
where represents the drive displacement. If the maximum velocity of each axis is set as , the axial velocity constraint is written as:
The acceleration of each axis can be calculated as:
If the maximum velocity of each axis is set as , the axial velocity constraints can be written as:
The parameter interval of the tool-tip curve is divided into N equal sub-intervals at . Using the monotonic rational quadratic spline proposed by Fleisig and Spence [34], the discrete parameter value of the tool orientation corresponding to is computed. When N is large enough, the length of the parameter sub-interval is so small that in Equations (17) and (19) can be approximated using the finite differential method. We can address the interpolation chord error, the axial velocities and the axial acceleration constraints as an optimization problem with the objective of and constraints from Equations (16), (18) and (20). By solving the optimization problem, the allowable discrete feedrate values is acquired. Then the feedrate of the tool-tip position is generated utilizing the curve splitting and bi-directional scanning techniques.
3.2. Feedrate Deformation for Tool Orientation to Achieve Synchronization
The tool-tip position curve at the curve segment joint parameters and the tool orientation curve at the parameter are synchronized spontaneously. Since the feedrate scheduling of the tool-tip position is completed, the motion time along the tool-tip curve in the parameter interval is fixed. Thus the motion time along the tool orientation curve in the parameter interval must be equal to to achieve synchronization. The tangential acceleration and jerk are set to zero at the joint parameters so that the tool-tip position and tool orientation motion are smooth.
Based on these principles, a feedrate deformation method is presented to generate the feedrate of the tool orientation. We take the tool-tip feedrate profile with seven phases in as an illustration. The durations of the seven phases are computed by the start and end feedrate and , the maximum feedrate , the tangential acceleration and jerk and the arc-length :
where represents the acceleration time, represents the deceleration time. Denote the constant feedrate duration as . The feed displacement is calculated as:
The goal of feedrate deformation is to generate a tool orientation feedrate profile segment by segment with the same motion time as tool-tip position and nominal orientation displacement while keep tangential kinematics under constraint. Given the tool orientation start feedrate , the tool orientation segmented arc-length , the feedrate deformation begins with computing the new constant feedrate derived form Equation (22):
where is user-defined and , and are the same as tool-tip position. By adjusting k, different constant feedrates can be obtained to meet the tangential constraints. The updated tangential acceleration and jerk is calculated as:
If or still exceed the tangential constraint, we can consider stretching the acceleration time to and then compute a new constant feedrate so that and are reduced. The deceleration process can be handled in the same way. Figure 6 is an illustration of the feedrate deformation method. The orientation feedrate profile is obtained from deformation of the position feedrate profile so that they share the same motion time but get through respective displacements to reach a specific synchronized cutter location.
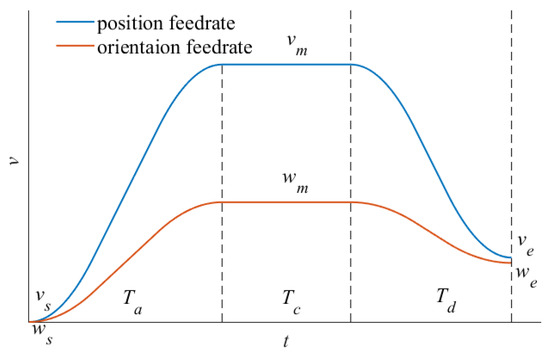
Figure 6.
Illustration of feedrate deformation method.
With the new constant feedrate, tangential acceleration and jerk, the tool orientation feed time is adjusted to match the tool-tip position feed time while the segmented arc-length remains the same. As a consequence, the tool-tip position and tool orientation arrive at specific points simultaneously where the two curves are synchronized.
4. Simulation and Experiment Validations
The feasibility and effectiveness of the proposed method is validated by simulations on a computer with 4.0 GHz CPU and 8GB RAM and experiments on a five-axis table-tilting machine tool (model of the machine tool) with two rotary axes of A and C whose configuration is illustrated in Figure 7.
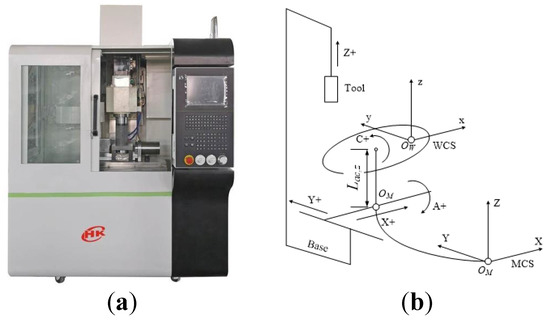
Figure 7.
Configuration of experimental five-axis computer numerical control (CNC) machine tool—(a) Real product. (b) Layout.
The inverse kinematic transformation of the experimental machine tool is:
where mm is the offset distance between A-axis and C-axis in the direction of z-axis. The machine is controlled by a TwinCAT-based CNC system with the sampling period of 1 ms. In order to formulate the feedrate profile to S-shape, we add the maximum allowable feedrate for tool-tip position and tool orientation respectively to the predefined constraints which are listed in Table 1.

Table 1.
Predefined constraints in the experiment.
The S-shape test piece is used to analyze the performance of the proposed method. The S-shape test piece is defined by two ruled surfaces and is usually used as a representation of the thin-wall workpiece in the aerospace industry. It requires an allowable range of final error from −0.05 mm to +0.05 mm [35]. We import the CAD model of the test piece shown in Figure 8a to UG NX 10 to plan the toolpath of the ruled surfaces using five-axis flank milling. The programmed toolpath shown in Figure 8b is approximated by a series of discrete G01 data points. The five-axis linear-segment toolpath of one of the four corners which consists of 12 G01 data points shown in Figure 8c is used to demonstrate the effectiveness for the proposed curve-fitting and feedrate scheduling method. The experimental 12 G01 data points is available in Appendix A Table A1. The tool-tip position fitting error tolerance is 0.05 mm and the tool orientation fitting error tolerance is 0.05°.
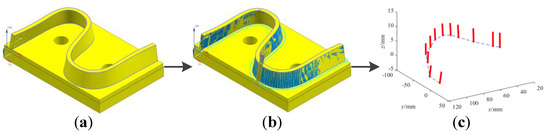
Figure 8.
Linear-segment toolpath generation for S-shape test piece—(a) computer-aided design (CAD) model. (b) Toolpath generated by computer-aided manufacturing (CAM). (c) Experimental G01 CL data.
The results of curve-fitting for the 12-point linear-segment toolpath are shown in Figure 9 and the corresponding fitting error calculated numerically in the curve parameter space is shown in Figure 10. From the data, it is evident that the fitting errors of the tool-tip position and of the tool orientation are both under fitting tolerance.
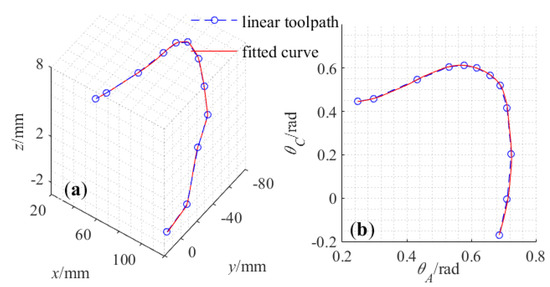
Figure 9.
Results of fitted curve for the experimental linear-segment toolpath—(a) Tool-tip position. (b) Tool orientation.
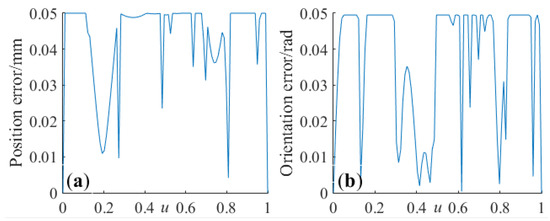
Figure 10.
Fitting error of tool-tip position and tool orientation—(a) Tool-tip position. (b) Tool orientation.
We assign to compute the discrete locations of the tool-tip position and tool orientation. Then the optimization problem proposed in Section 3.1 is established and solved using the solver in Matlab to get the allowable feedrate for the tool-tip position. The feedrate profile of the tool-tip position is obtained using the curve splitting and bi-directional scanning techniques and is shown in Figure 11. From the data we can tell that the scheduled feedrate profile is smooth and under feedrate restrictions.
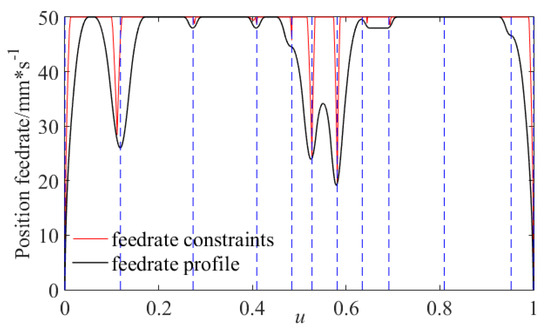
Figure 11.
Feedrate profile of the tool-tip position with respect to curve parameter.
The feedrate profiles of the original linear-segment toolpath and the smooth toolpath are compared to show that the total motion duration is reduced by 44.2% from 7.169 s to 3.999 s in Figure 12. It can also be seen that the tool orientation feedrate is generated sharing the same segmented motion time with the tool-tip position.
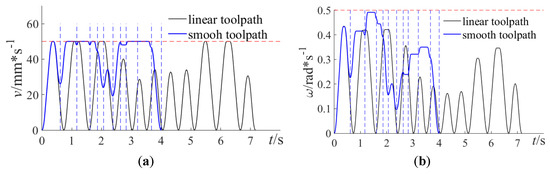
Figure 12.
Feedrate profile with respect to time—(a) Tool-tip position. (b) Tool orientation.
The interpolation is conducted to generate reference positions in the WCS, as shown in Figure 13. From the data, it is evident that the feed process is advanced at high rate except three obtrusive deceleration locations.
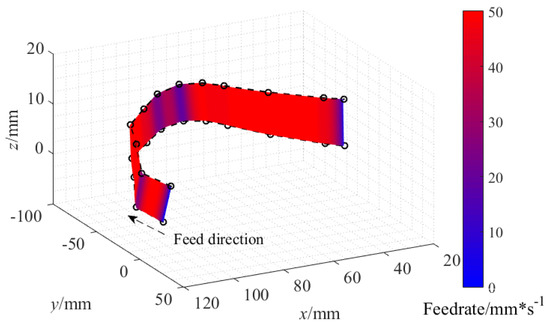
Figure 13.
Fitting error and curvature of planar five-point example.
The tangential kinematic profiles of the tool-tip position and tool orientation are illustrated in Figure 14. It can be spotted that all the tangential kinematic profiles meet with the tangential constraints. In Figure 14c,d, the results of the adjusting techniques mentioned in Section 3.2 is displayed in the feedrate deformation process.
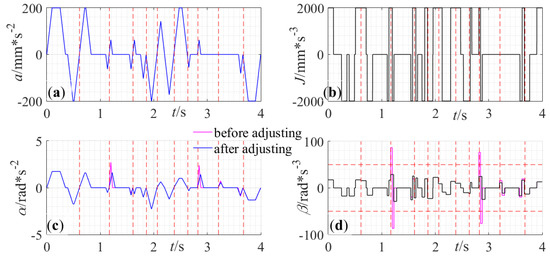
Figure 14.
Tangential kinematic profiles—(a) Tool-tip position acceleration. (b) Tool-tip position jerk. (c) tool orientation acceleration. (d) tool orientation jerk.
The traditional parameter synchronization method obtains the tool orientation feedrate after scheduling the tool-tip feedrate by simply sharing the curve parameter. It may cause wild fluctuation in the tool orientation kinematics, as shown in Figure 15.
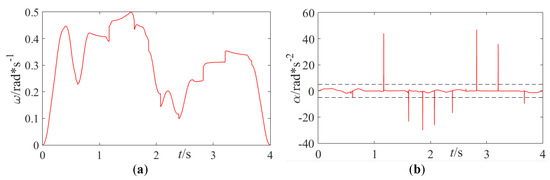
Figure 15.
Tool orientation kinematic profiles using parameter synchronization—(a) Feedrate profile. (b) Tangential acceleration profile.
Since the interpolation results of the tool-tip position and tool orientation are obtained, the reference axial positions are decided according to inverse kinematic transformation from Equation (25). Then the reference axial velocities and accelerations are calculated by differentiating the axial positions. The axial velocities and accelerations does not consider axial constraints are shown in Figure 16. It can be seen that despite a slight improvement of feed time (3.595 s), the acceleration of X-axis and velocity of C-axis exceed the corresponding constraints. The axial velocities and accelerations using the parameter synchronization [23] are demonstrated in Figure 17. The accelerations of all axes are far greater than the allowable values at certain locations. The axial velocities and accelerations using the proposed method is depicted in Figure 18. The data demonstrate that the axial velocities and accelerations are both under limitation. The maximum absolute axial velocities and accelerations using different methods are listed in Table 2 as an intuitive comparison and the anomalously great values are highlighted in bold, especially for axial accelerations using the parameter synchronization method. As can be seen, the large variations of axial accelerations of the traditional parameter synchronization method come from the wild fluctuation in the tool orientation acceleration as shown in Figure 15b.
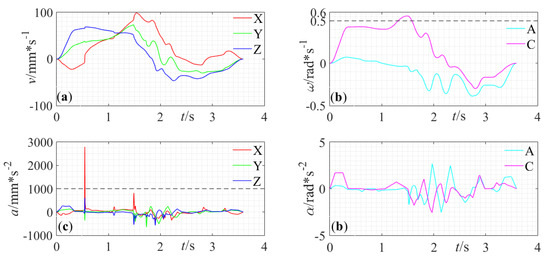
Figure 16.
Axial velocities and accelerations that does not consider axial kinematic constraints—(a) Translational axial velocities. (b) Rotary axial velocities. (c) Translational axial accelerations. (d) Rotary axial accelerations.
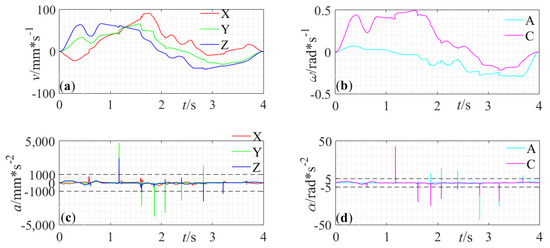
Figure 17.
Axial velocities and accelerations using parameter synchronization—(a) Translational axial velocities. (b) Rotary axial velocities. (c) Translational axial accelerations. (d) Rotary axial accelerations.
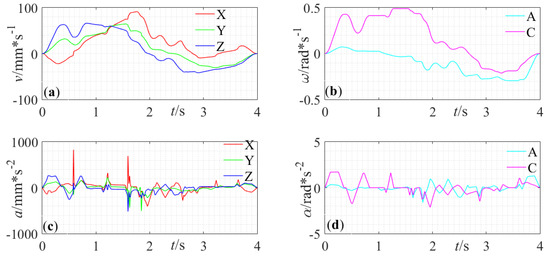
Figure 18.
Proposed axial velocities and accelerations—(a) Translational axial velocities. (b) Rotary axial velocities. (c) Translational axial accelerations. (d) Rotary axial accelerations.

Table 2.
Maximum axial velocities and accelerationsusing different methods.
The S-shape test piece made of Aluminum Alloy 1060 is machined on the experimental five-axis table-tilting machine tool with a cutter of diameter 10 mm. The machining process consists of three steps: rough machining, semi-finishing and finishing. The CNC system reads the trajectories using the proposed curve-fitting and feedrate scheduling method and then the axial commands are generated and sent to the controller. The machining results are shown in Figure 19.

Figure 19.
Machining results of S-shaped workpiece.
The machining accuracy of the S-shape workpiece is affected by many factors, such as theoretical error, geometric error of the machine tool, and quality of toolpath [36]. Also, the measurement of freeform workpiece is very complicated. In this experiment, quality of toolpath (fitting error) is mainly concerned. According to drive commands of the machine tool, the real tool-tip position and tool orientation are reversely computed using forward kinematic transformation and the real fitting error in the WCS is calculated. The real maximum and average fitting errors with the traditional parameter synchronization method and the proposed method are demonstrated in Table 3. Due to large variance of axial kinematics, the maximum and average fitting errors with the traditional parameter synchronization show greater values, especially for the tool orientation (40.0% greater for the maximum fitting error).

Table 3.
Fitting error of the experiments.
The real axial velocities and accelerations shown in Figure 20 are obtained by differentiating the real axial positions with the sampling period of 1 ms. The real axial velocities and accelerations are both under control and the large fluctuations are further reduced in the real machining process (the acceleration for X-axis is reduced by 44.3%). Experimental results show that the proposed method can generate trajectories with allowable fitting error and smooth motion.
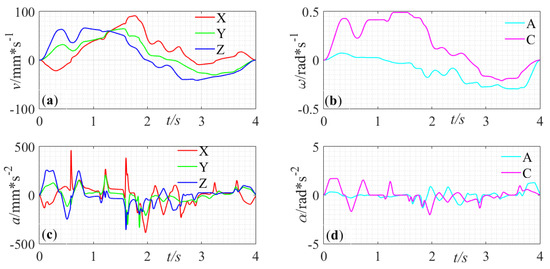
Figure 20.
Real axial kinematics—(a) Translational axial velocities. (b) Rotary axial velocities. (c) Translational axial accelerations. (d) Rotary axial accelerations.
5. Conclusions
This paper proposes a double B-spline curve-fitting and synchronization-integrated feedrate scheduling method for five-axis linear-segment toolpath. The main technical characteristics are as follows—(1) the tool-tip position and tool orientation are fitted by two cubic B-spline curves respectively so that the discontinuities caused by transition corners of five-axis linear-segment toolpath are handled and the fitting error is strictly respected; (2) the axial kinematic constraints are mapped and satisfied in the feedrate scheduling process of the tool-tip position; (3) the synchronization and smooth rotary motion is obtained using feedrate deformation for tool orientation.
Simulations and experiments are carried out to validate the feasibility and effectiveness of the proposed method. For a toolpath of 12 CL data points from the S-shape test piece, the proposed curve-fitting method constrains the fitting error under fitting tolerance. The proposed machining time is reduced significantly by 44.2% in comparison with the original linear-segment toolpath. To verify the smooth motion of the proposed feedrate scheduling method, we compare the proposed method with the method does not consider axial kinematic constraints and the method using parameter synchronization. The results show that the proposed rotary motion is smooth and the axial motions are under kinematic limits. The experiments are conducted on the S-shape test piece. The real tool-tip position and tool orientation are reversely computed using the real axial positions to confirm that the proposed method can generate a smooth toolpath with allowable fitting error. The real axial kinematics are further smoothed in the real machining process.
Despite the progress made in this study, only fitting error and smoothness are considered for the fitted curve. However, the machining accuracy is affected by other factors such as thermal error, geometric errors of machine tool, dynamic error and so forth, and workpiece measurement to evaluate the surface quality directly is not conducted. Therefore, further research should be done in our future study.
Author Contributions
Conceptualization, X.G.; Formal analysis, S.Z., L.Q., X.L., Z.W. and Y.W.; Investigation, S.Z., L.Q., X.L., Z.W. and Y.W.; Methodology, X.G.; Project administration, S.Z. and L.Q.; Software, X.G.; Writing—original draft, X.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China grant number 51675478 and 51875516, and the Natural Science Foundation of Zhejiang Province grant number LY18E050001.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Cutter Location Data

Table A1.
Experimental cutter location data.
Table A1.
Experimental cutter location data.
| No. | (mm) | (mm) | (mm) | |||
|---|---|---|---|---|---|---|
| 1 | 113.560775 | 7.735266 | −2.209314 | −0.107258 | 0.624902 | 0.773300 |
| 2 | 117.864949 | −10.950074 | −0.974065 | −0.003002 | 0.653008 | 0.757345 |
| 3 | 110.502860 | −34.808781 | 1.779567 | 0.135034 | 0.648777 | 0.748902 |
| 4 | 104.086026 | −55.840098 | 2.682644 | 0.263922 | 0.596758 | 0.757776 |
| 5 | 95.225652 | −63.959571 | 4.073524 | 0.317154 | 0.551822 | 0.771301 |
| 6 | 88.820589 | −65.972318 | 6.021818 | 0.329520 | 0.516103 | 0.790603 |
| 7 | 80.162816 | −65.096397 | 7.031464 | 0.326785 | 0.478040 | 0.815285 |
| 8 | 72.478246 | −61.109537 | 6.863103 | 0.313696 | 0.446069 | 0.838223 |
| 9 | 65.985754 | −54.666365 | 6.143037 | 0.288698 | 0.416448 | 0.862105 |
| 10 | 54.251993 | −39.568096 | 4.931174 | 0.217010 | 0.357492 | 0.908354 |
| 11 | 38.038952 | −23.111532 | 3.536073 | 0.129479 | 0.261821 | 0.956391 |
| 12 | 31.679054 | −18.711329 | 3.017623 | 0.105499 | 0.220895 | 0.969575 |
References
- Jywe, W.-Y.; Hsieh, T.-H.; Chen, P.-Y.; Wang, M.-S. An Online Simultaneous Measurement of the Dual-Axis Straightness Error for Machine Tools. Appl. Sci. 2018, 8, 2130. [Google Scholar] [CrossRef]
- Wei, X.; Su, Z.; Yang, X.; Lv, Z.; Yang, Z.; Zhang, H.; Li, X.; Fang, F. A Novel Method for the Measurement of Geometric Errors in the Linear Motion of CNC Machine Tools. Appl. Sci. 2019, 9, 3357. [Google Scholar] [CrossRef]
- Zhang, Y.; Ye, P.; Zhang, H.; Zhao, M. A Local and Analytical Curvature-Smooth Method with Jerk-Continuous Feedrate Scheduling along Linear Toolpath. Int. J. Precis. Eng. Manuf. 2018, 19, 1529–1538. [Google Scholar] [CrossRef]
- Liang, F.; Zhao, J.; Ji, S.; Fan, C.; Zhang, B. A novel knot selection method for the error-bounded B-spline curve fitting of sampling points in the measuring process. Meas. Sci. Technol. 2017, 28, 065015. [Google Scholar] [CrossRef]
- Sun, S.; Yu, D.; Wang, C.; Xie, C. A smooth tool path generation and real-time interpolation algorithm based on B-spline curves. Adv. Mech. Eng. 2018, 10, 1687814017750281. [Google Scholar] [CrossRef]
- Zhao, H.; Zhu, L.; Ding, H. A real-time look-ahead interpolation methodology with curvature-continuous B-spline transition scheme for CNC machining of short line segments. Int. J. Mach. Tools Manuf. 2013, 65, 88–98. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, M.; Ye, P.; Zhang, H. A G4 continuous B-spline transition algorithm for CNC machining with jerk-smooth feedrate scheduling along linear segments. Comput. Aided Des. 2019, 115, 231–243. [Google Scholar] [CrossRef]
- Fan, W.; Lee, C.-H.; Chen, J.-H. A realtime curvature-smooth interpolation scheme and motion planning for CNC machining of short line segments. Int. J. Mach. Tools Manuf. 2015, 96, 27–46. [Google Scholar] [CrossRef]
- Fan, W.; Lee, C.; Chen, J.; Xiao, Y. Real-time Bezier interpolation satisfying chord error constraint for CNC tool path. Sci. China Technol. Sci. 2016, 59, 203–213. [Google Scholar] [CrossRef]
- Fan, W.; Ji, J.; Wu, P.; Wu, D.; Chen, H. Modeling and simulation of trajectory smoothing and feedrate scheduling for vibration-damping CNC machining. Simul. Model. Pract. Theory 2020, 99, 102028. [Google Scholar] [CrossRef]
- Walton, D.J.; Meek, D.S. G2 blends of linear segments with cubics and Pythagorean-hodograph quintics. Int. J. Comput. Math. 2009, 86, 1498–1511. [Google Scholar] [CrossRef]
- Shi, J.; Bi, Q.; Wang, Y.; Liu, G. Development of Real-time Look-ahead Methodology Based on Quintic PH Curve with G(2) Continuity for High-speed Machining. Intell. Mater. Mechatronics 2014, 464, 258. [Google Scholar] [CrossRef]
- Bi, Q.; Huang, J.; Lu, Y.; Zhu, L.; Ding, H. A general, fast and robust B-spline fitting scheme for micro-line tool path under chord error constraint. Sci. China Technol. Sci. 2019, 62, 321–332. [Google Scholar] [CrossRef]
- He, S.; Ou, D.; Yann, C.; Lee, C.-H. A chord error conforming tool path B-spline fitting method for NC machining based on energy minimization and LSPIA. J. Comput. Des. Eng. 2015, 2, 218–232. [Google Scholar] [CrossRef]
- Lin, F.; Shen, L.-Y.; Yuan, C.-M.; Mi, Z. Certified space curve fitting and trajectory planning for CNC machining with cubic B-splines. Comput. Aided Des. 2019, 106, 13–29. [Google Scholar] [CrossRef]
- Zhong, G.; Liu, P.; Mei, X.; Wang, Y.; Xu, F.; Yang, S. Design Optimization Approach of a Large-Scale Moving Framework for a Large 5-Axis Machining Center. Appl. Sci. 2018, 8, 1598. [Google Scholar] [CrossRef]
- Li, C.; Liu, X.; Li, R.; Wu, S.; Song, H. Geometric Error Identification and Analysis of Rotary Axes on Five-Axis Machine Tool Based on Precision Balls. Appl. Sci. 2020, 10, 100. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, L.; Zhang, K.; Mao, J. Double NURBS trajectory generation and synchronous interpolation for five-axis machining based on dual quaternion algorithm. Int. J. Adv. Manuf. Technol. 2016, 83, 2015–2025. [Google Scholar] [CrossRef]
- Tulsyan, S.; Altintas, Y. Local toolpath smoothing for five-axis machine tools. Int. J. Mach. Tools Manuf. 2015, 96, 15–26. [Google Scholar] [CrossRef]
- Yang, J.; Yuen, A. An analytical local corner smoothing algorithm for five-axis CNC machining. Int. J. Mach. Tools Manuf. 2017, 123, 22–35. [Google Scholar] [CrossRef]
- Jin, Y.; Bi, Q.; Wang, Y. Dual-Bezier path smoothing and interpolation for five-axis linear tool path in workpiece coordinate system. Adv. Mech. Eng. 2015, 7. [Google Scholar] [CrossRef]
- Yuen, A.; Zhang, K.; Altintas, Y. Smooth trajectory generation for five-axis machine tools. Int. J. Mach. Tools Manuf. 2013, 71, 11–19. [Google Scholar] [CrossRef]
- Li, D.; Zhang, W.; Zhou, W.; Shang, T.; Fleischer, J. Dual NURBS Path Smoothing for 5-Axis Linear Path of Flank Milling. Int. J. Precis. Eng. Manuf. 2018, 19, 1811–1820. [Google Scholar] [CrossRef]
- Wang, Y.; Ma, X.; Chen, L.; Han, Z. Realization methodology of a 5-axis spline interpolator in an open CNC system. Chin. J. Aeronaut. 2007, 20, 362–369. [Google Scholar] [CrossRef][Green Version]
- Du, X.; Huang, J.; Zhun, L.-M. A complete S-shape feed rate scheduling approach for NURBS interpolator. J. Comput. Des. Eng. 2015, 2, 206–217. [Google Scholar] [CrossRef]
- Lee, A.-C.; Lin, M.-T.; Pan, Y.-R.; Lin, W.-Y. The feedrate scheduling of NURBS interpolator for CNC machine tools. Comput. Aided Des. 2011, 43, 612–628. [Google Scholar] [CrossRef]
- Zhao, D.; Guo, H. A Trajectory Planning Method for Polishing Optical Elements Based on a Non-Uniform Rational B-Spline Curve. Appl. Sci. 2018, 8, 1355. [Google Scholar] [CrossRef]
- Beudaert, X.; Lavernhe, S.; Tournier, C. Feedrate interpolation with axis jerk constraints on 5-axis NURBS and G1 tool path. Int. J. Mach. Tools Manuf. 2012, 57, 73–82. [Google Scholar] [CrossRef]
- Fan, W.; Gao, X.-S.; Lee, C.-H.; Zhang, K.; Zhang, Q. Time-optimal interpolation for five-axis CNC machining along parametric tool path based on linear programming. Int. J. Adv. Manuf. Technol. 2013, 69, 1373–1388. [Google Scholar] [CrossRef]
- Liu, H.; Liu, Q.; Sun, P.; Liu, Q.; Yuan, S. The optimal feedrate planning on five-axis parametric tool path with geometric and kinematic constraints for CNC machine tools. Int. J. Prod. Res. 2017, 55, 3715–3731. [Google Scholar] [CrossRef]
- Erkorkmaz, K.; Chen, Q.-G.; Zhao, M.-Y.; Beudaert, X.; Gao, X.-S. Linear programming and windowing based feedrate optimization for spline toolpaths. Cirp Ann. Manuf. Technol. 2017, 66, 393–396. [Google Scholar] [CrossRef]
- Huang, J.; Lu, Y.; Zhu, L.-M. Real-time feedrate scheduling for five-axis machining by simultaneously planning linear and angular trajectories. Int. J. Mach. Tools Manuf. 2018, 135, 78–96. [Google Scholar] [CrossRef]
- Piegl, L.; Tiller, W. The NURBS Book, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 1997; p. 646. [Google Scholar]
- Fleisig, R.V.; Spence, A.D. A constant feed and reduced angular acceleration interpolation algorithm for multi-axis machining. Comput. Aided Des. 2001, 33, 1–15. [Google Scholar] [CrossRef]
- Guan, L.; Mo, J.; Fu, M.; Wang, L. Theoretical error compensation when measuring an S-shaped test piece. Int. J. Adv. Manuf. Technol. 2017, 93, 2975–2984. [Google Scholar] [CrossRef]
- Wang, Q.; Wu, C.; Fan, J.; Xie, G.; Wang, L. A novel causation analysis method of machining defects for five-axis machine tools based on error spatial morphology of S-shaped test piece. Int. J. Adv. Manuf. Technol. 2019, 103, 3529–3556. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).