Characterization and Modelling of Various Sized Mountain Bike Tires and the Effects of Tire Tread Knobs and Inflation Pressure
Abstract
:1. Introduction
2. Materials and Methods
2.1. Measurement
2.1.1. Tire Inflated Radius
2.1.2. Tire Profile
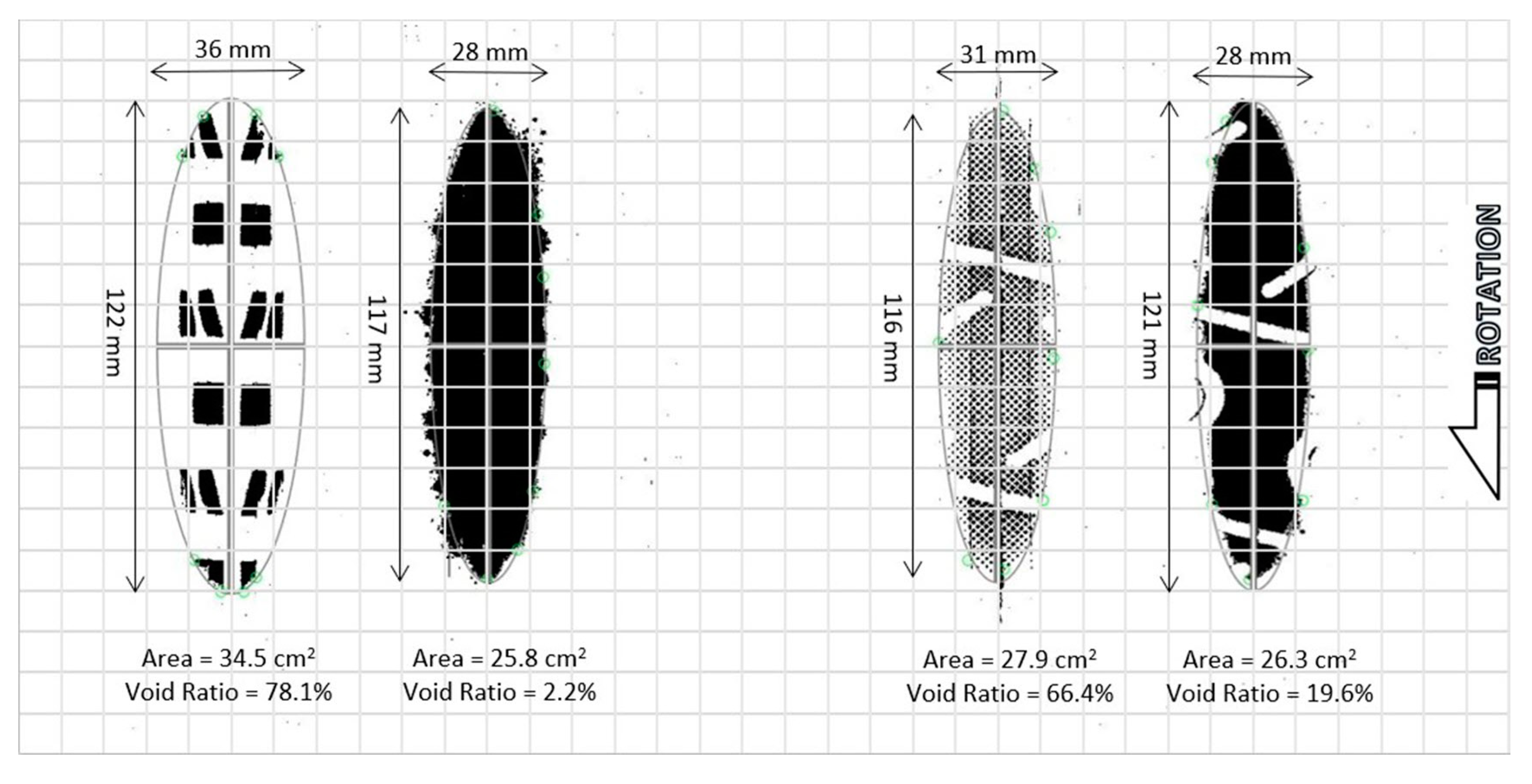
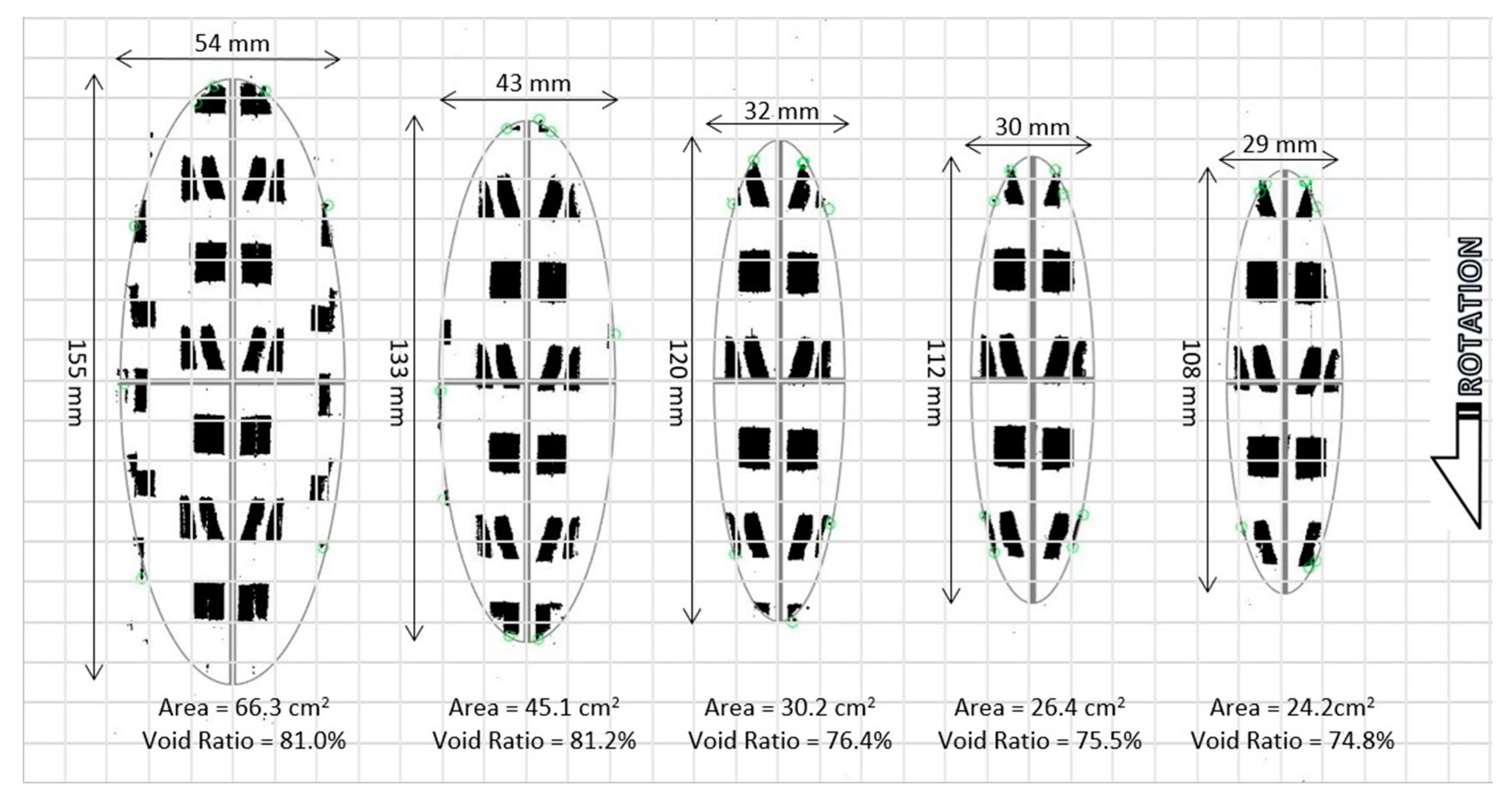
2.1.3. Footprints
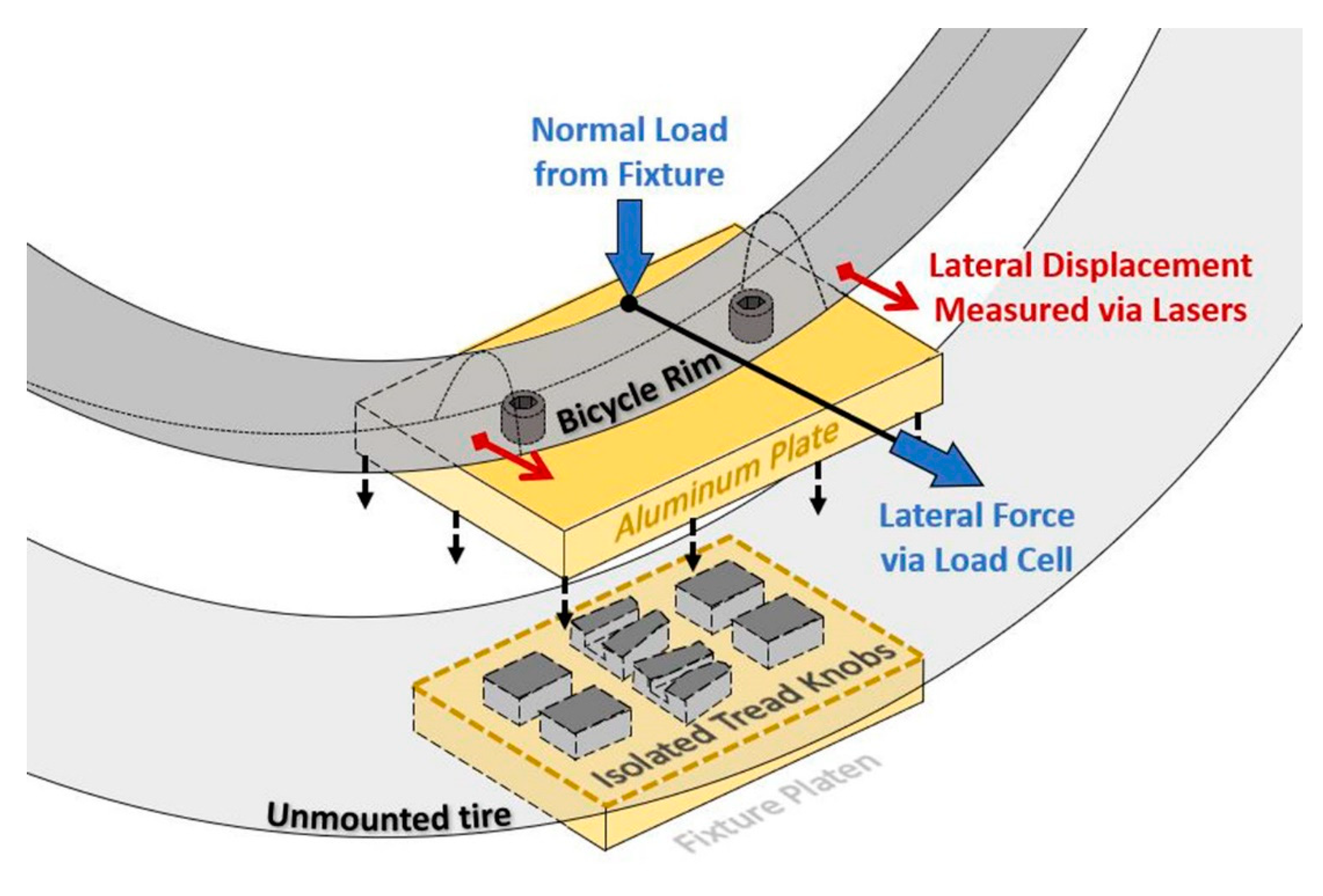
2.1.4. Force and Moment
2.1.5. Static Lateral and Radial Stiffness
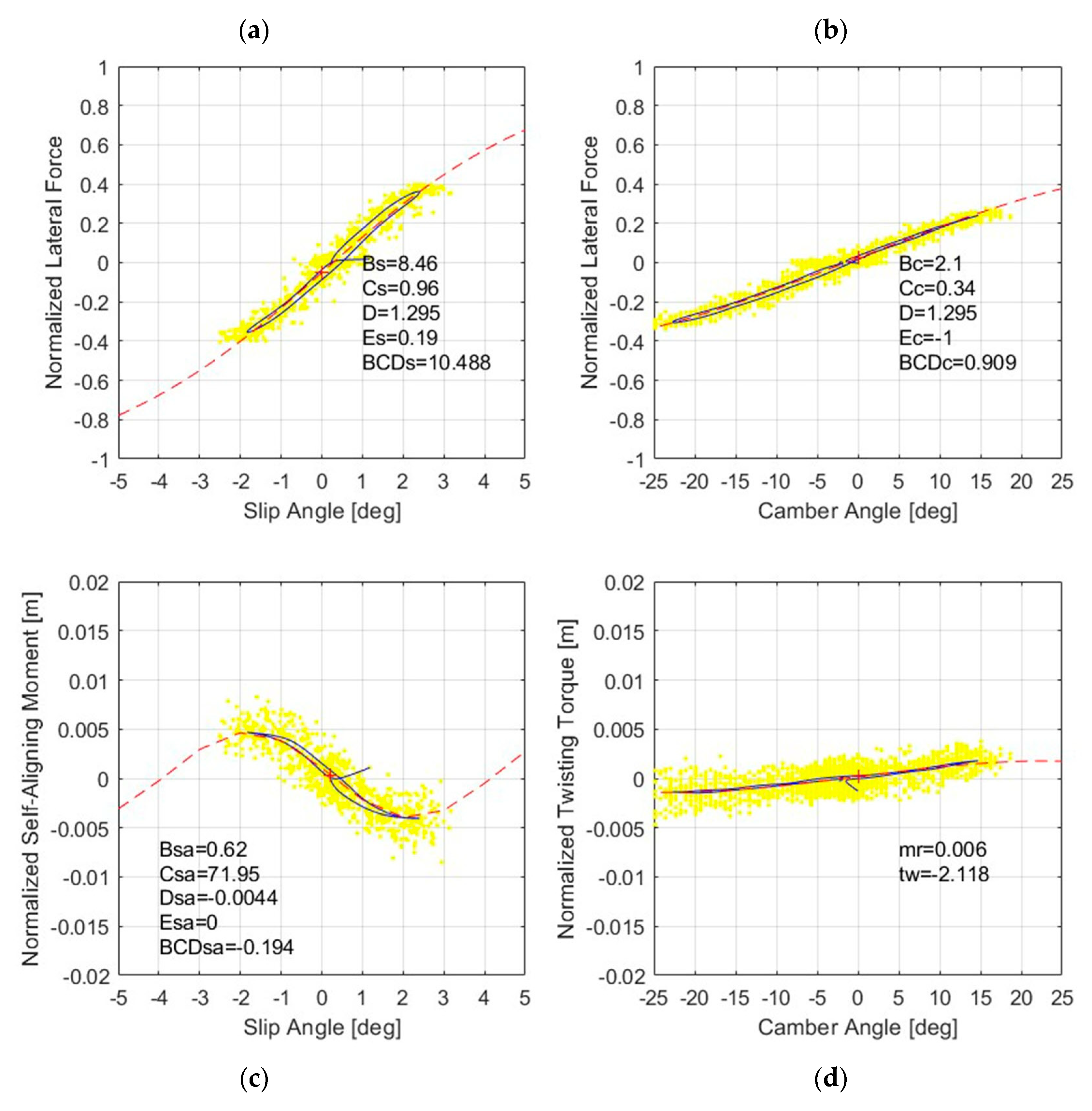
2.2. Fitting the Data
- : output variable. In this case, either lateral force, , or self-aligning moment, ;
- : input variable; here, either slip or camber angle in radians;and
- : stiffness factor, which determined the slope at the origin;
- : shape factor, which controlled the limits of the range of the sine function;
- : peak value (when C was constrained as specified);
- : curvature factor for the peak, controlling its horizontal position;
- : horizontal shift;
- : vertical shift.
- : twisting torque due to camber, which was then normalized by
- : the tire normal load in Newtons;and
- : camber angle in radians;
- : linear twisting torque coefficient;
- : non-linear twisting torque coefficient.
3. Results and Discussion
3.1. Various Sizes of Mountain Bike Tires
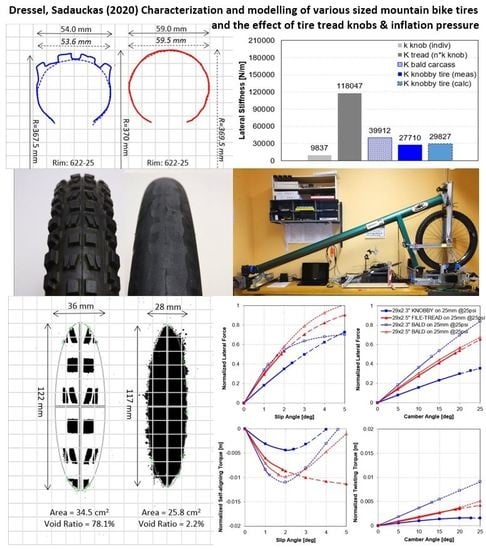
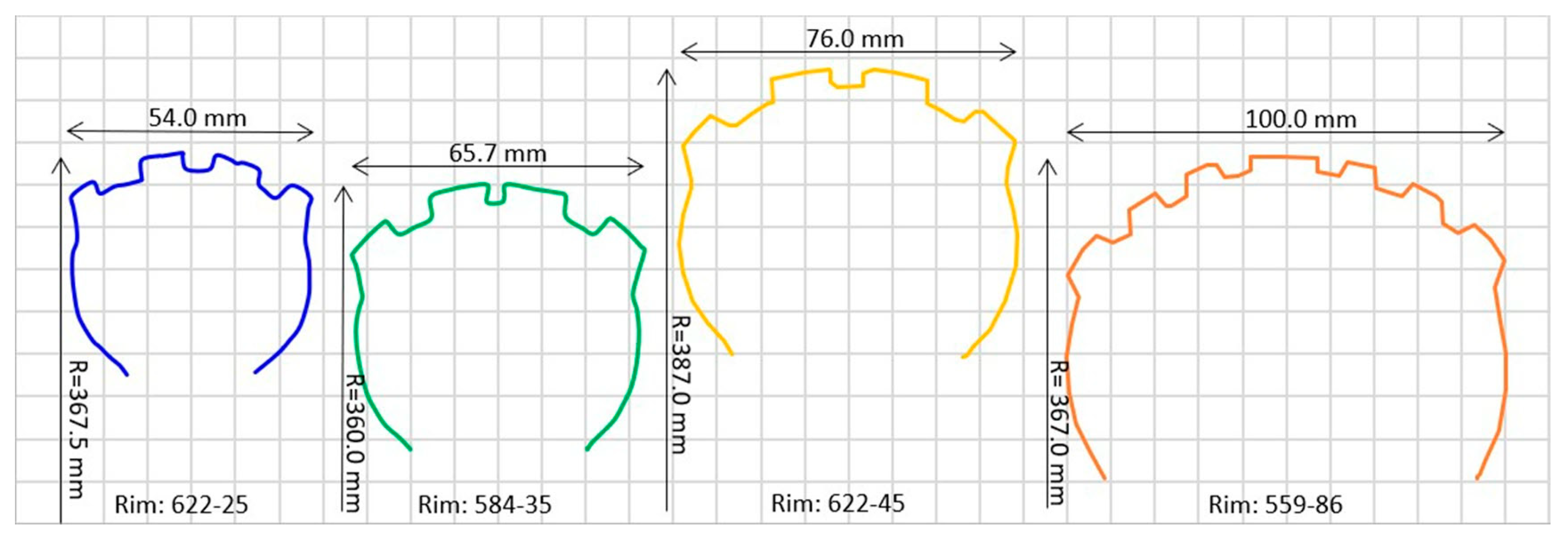
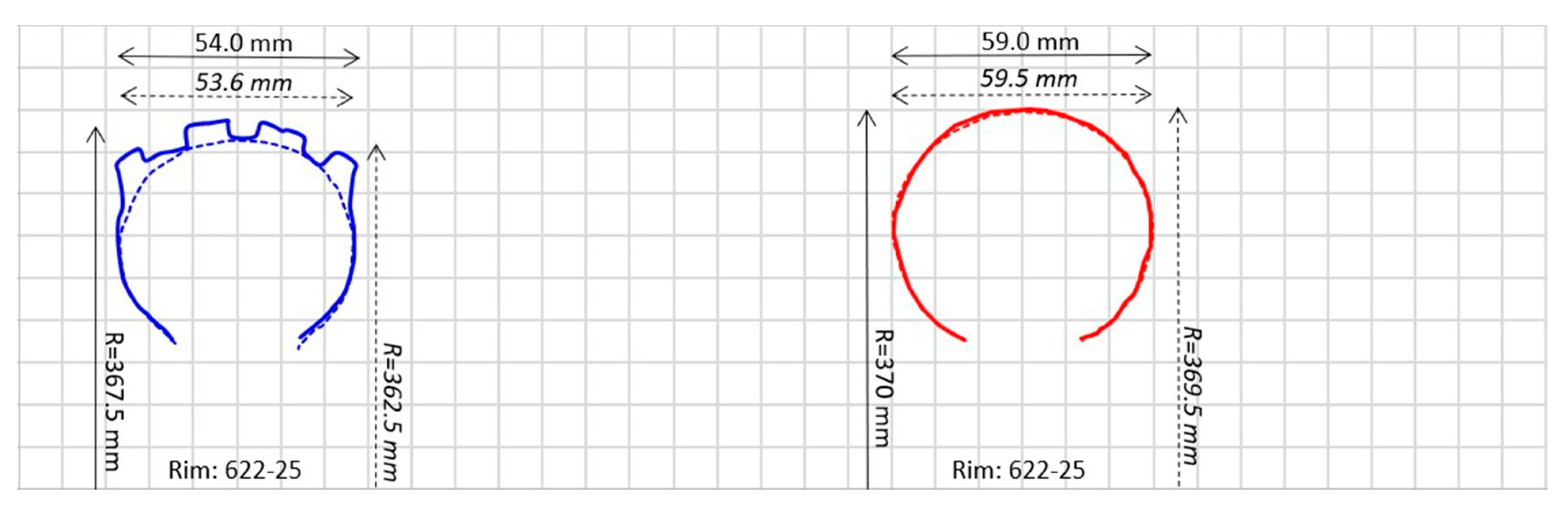
3.1.1. Cross-Sectional Profiles
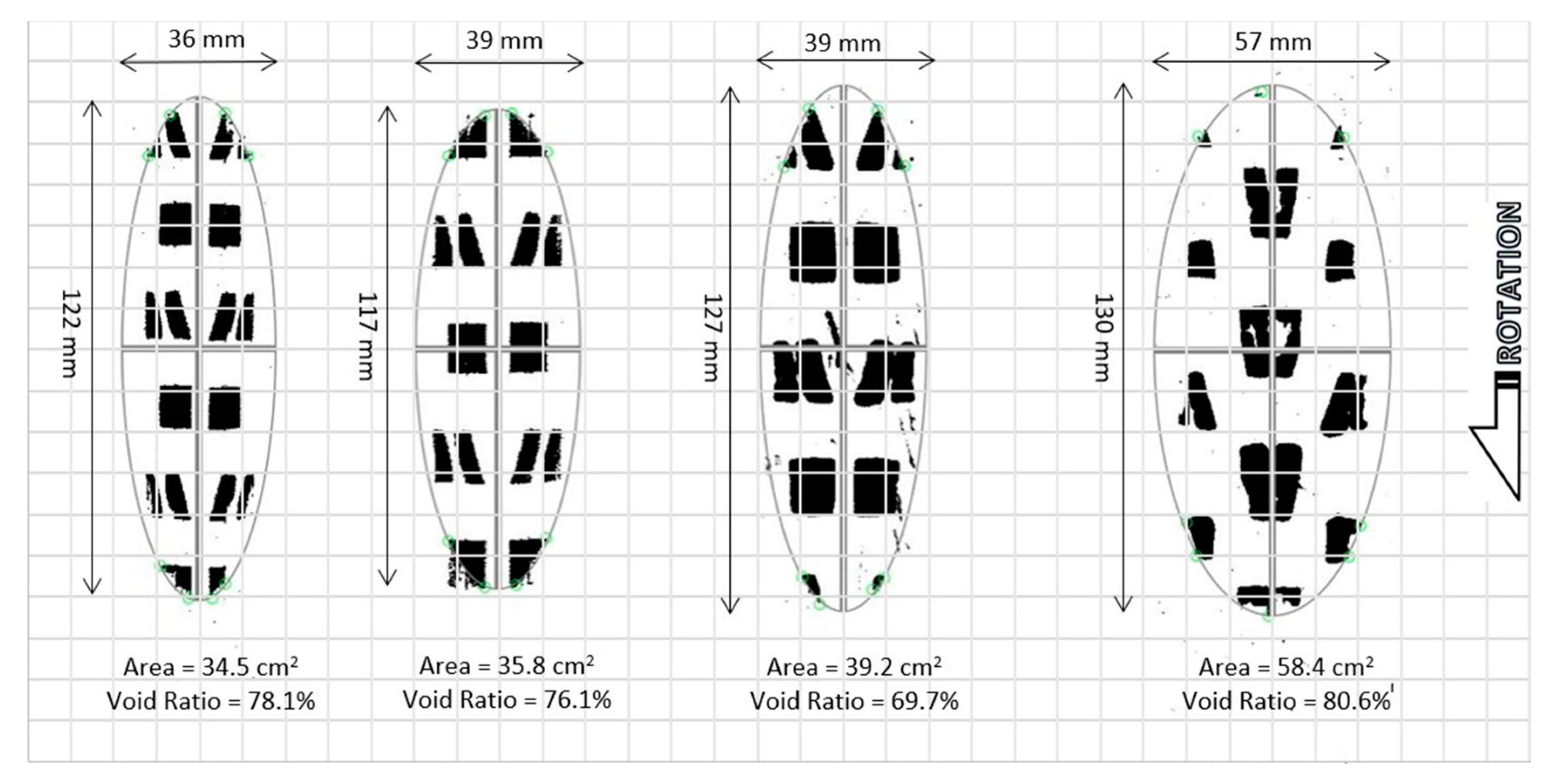
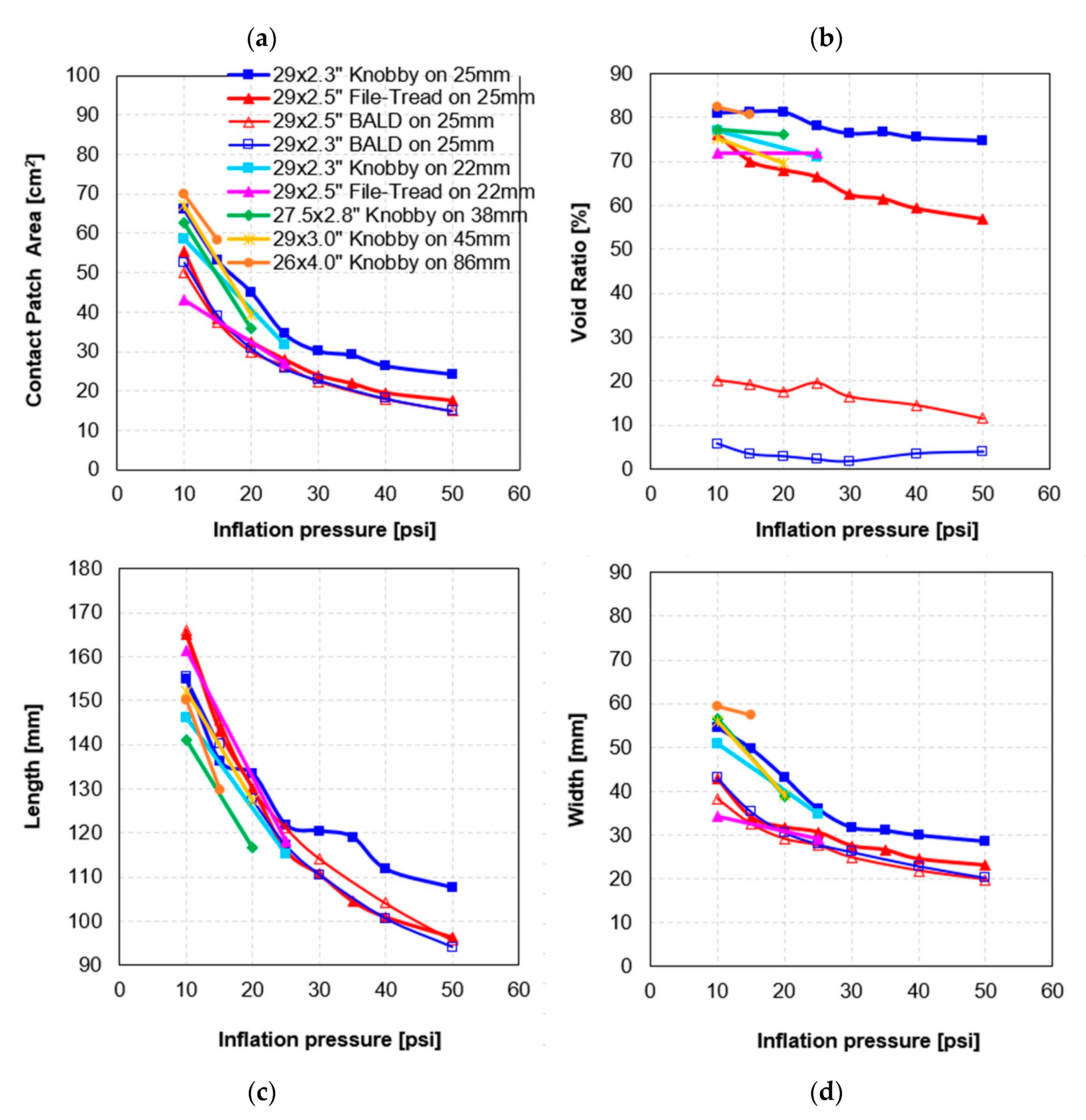
3.1.2. Footprints
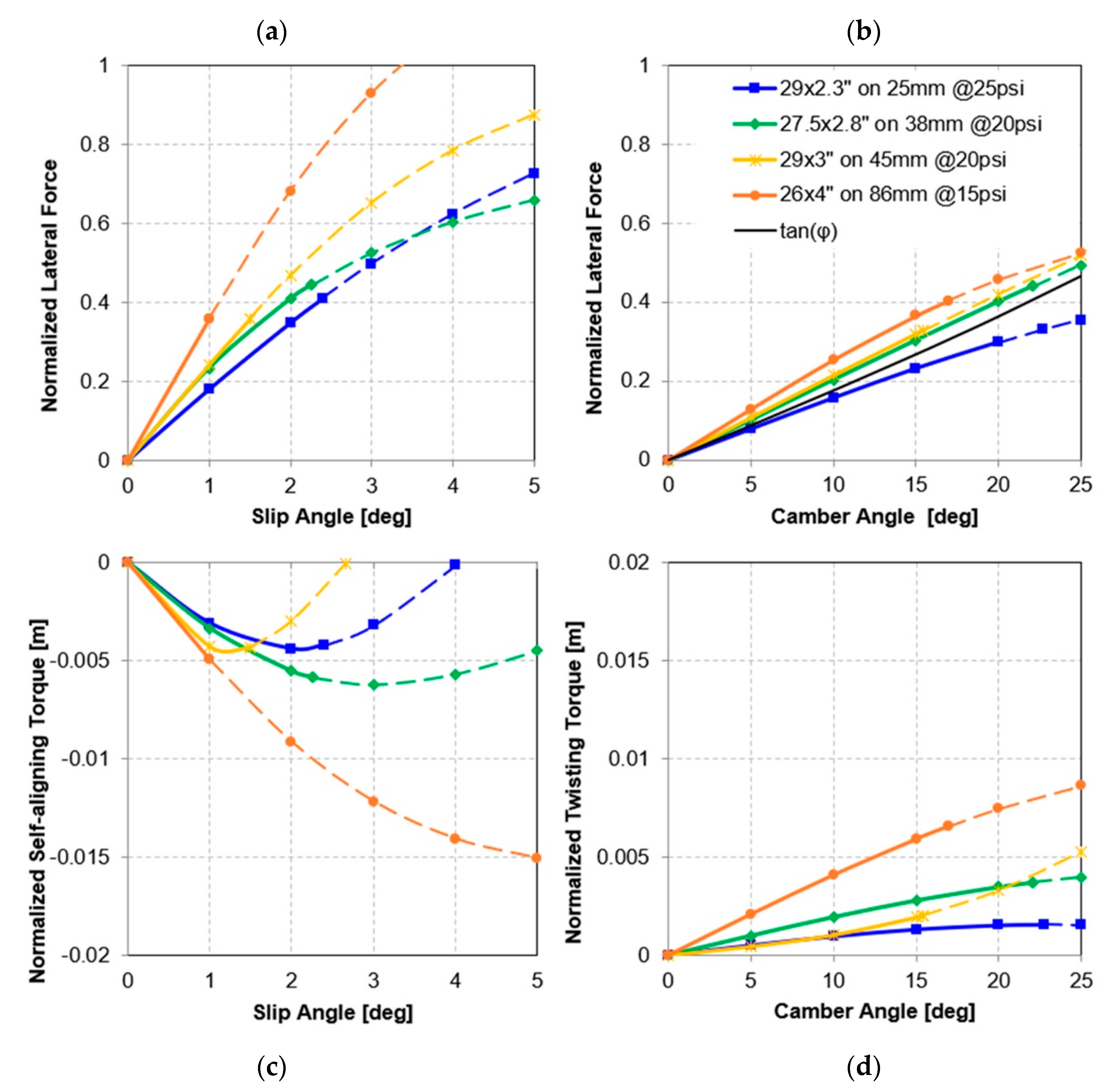
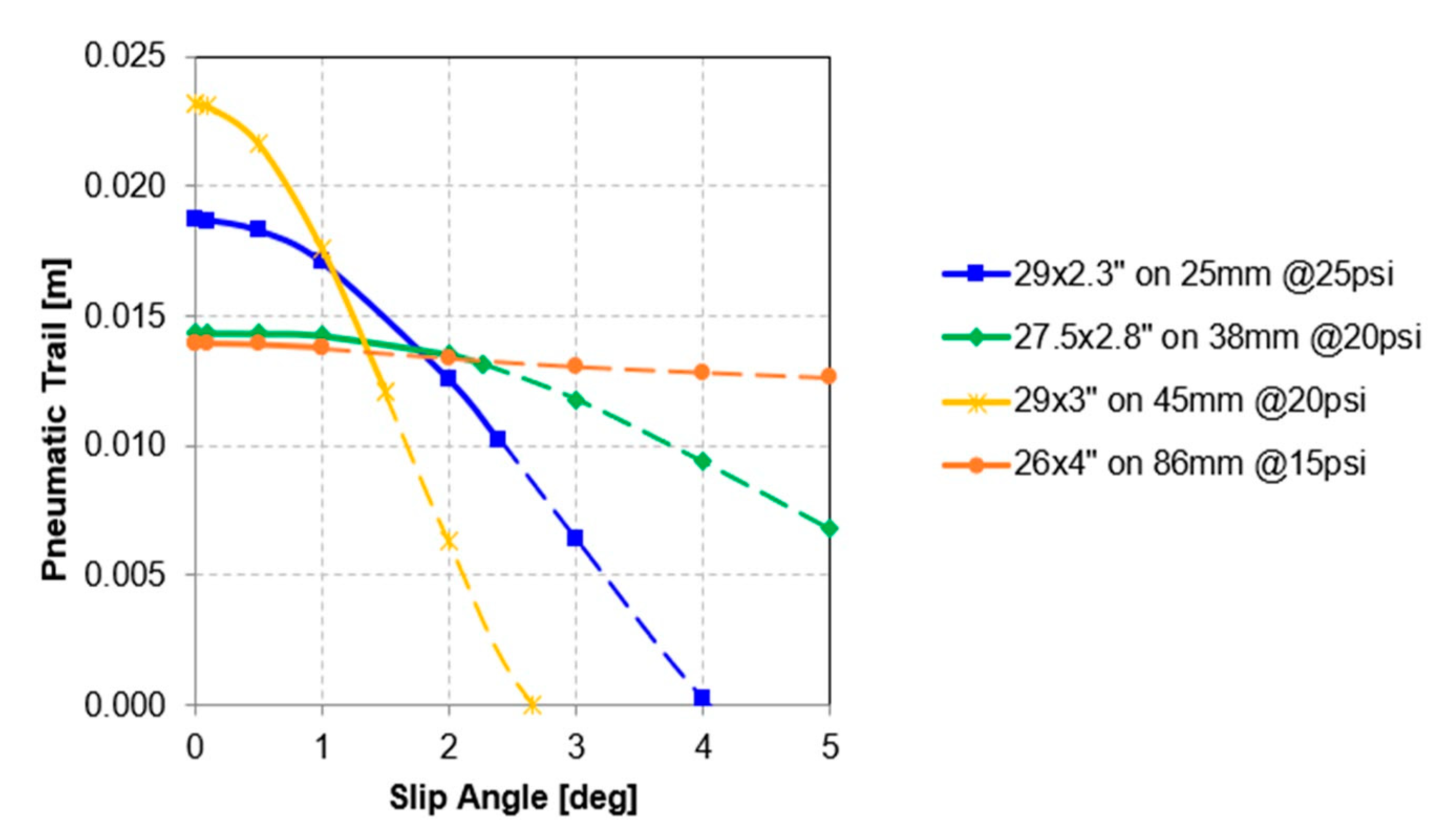
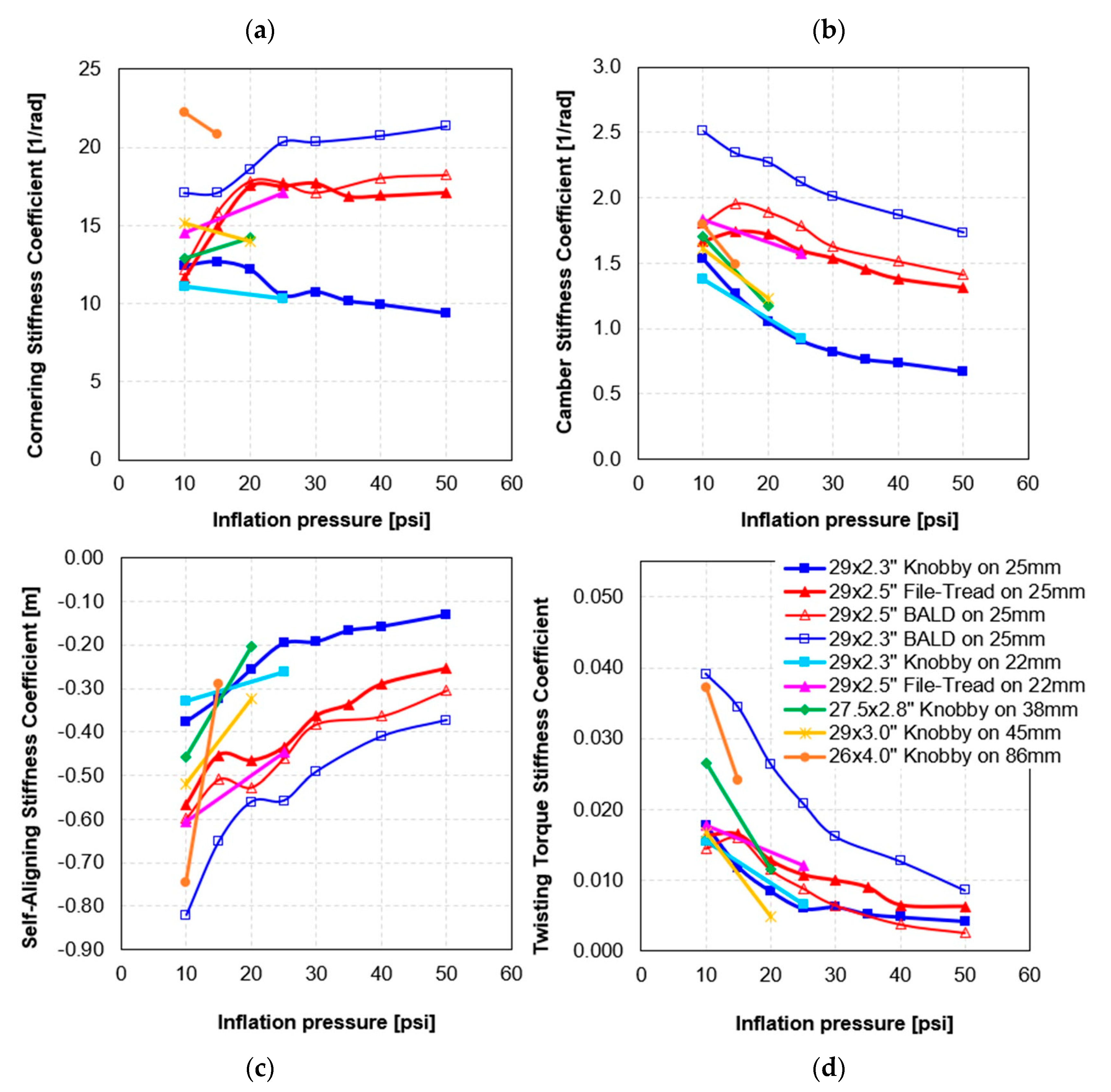
3.1.3. Forces and Moments
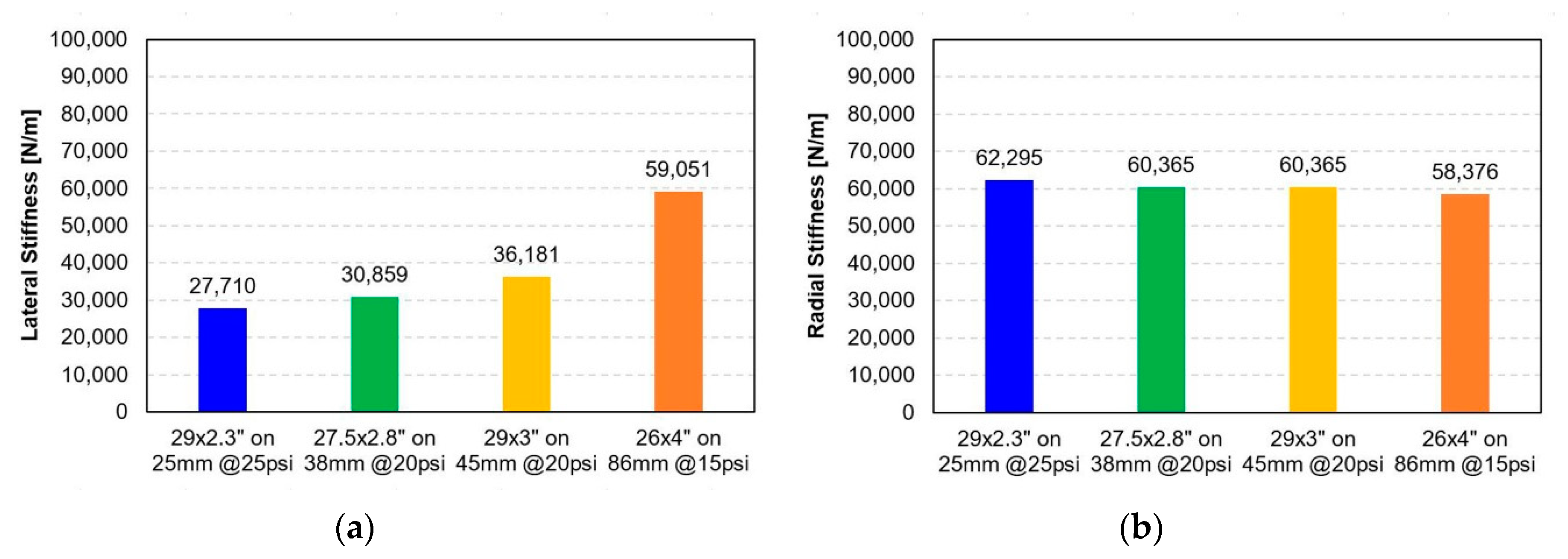
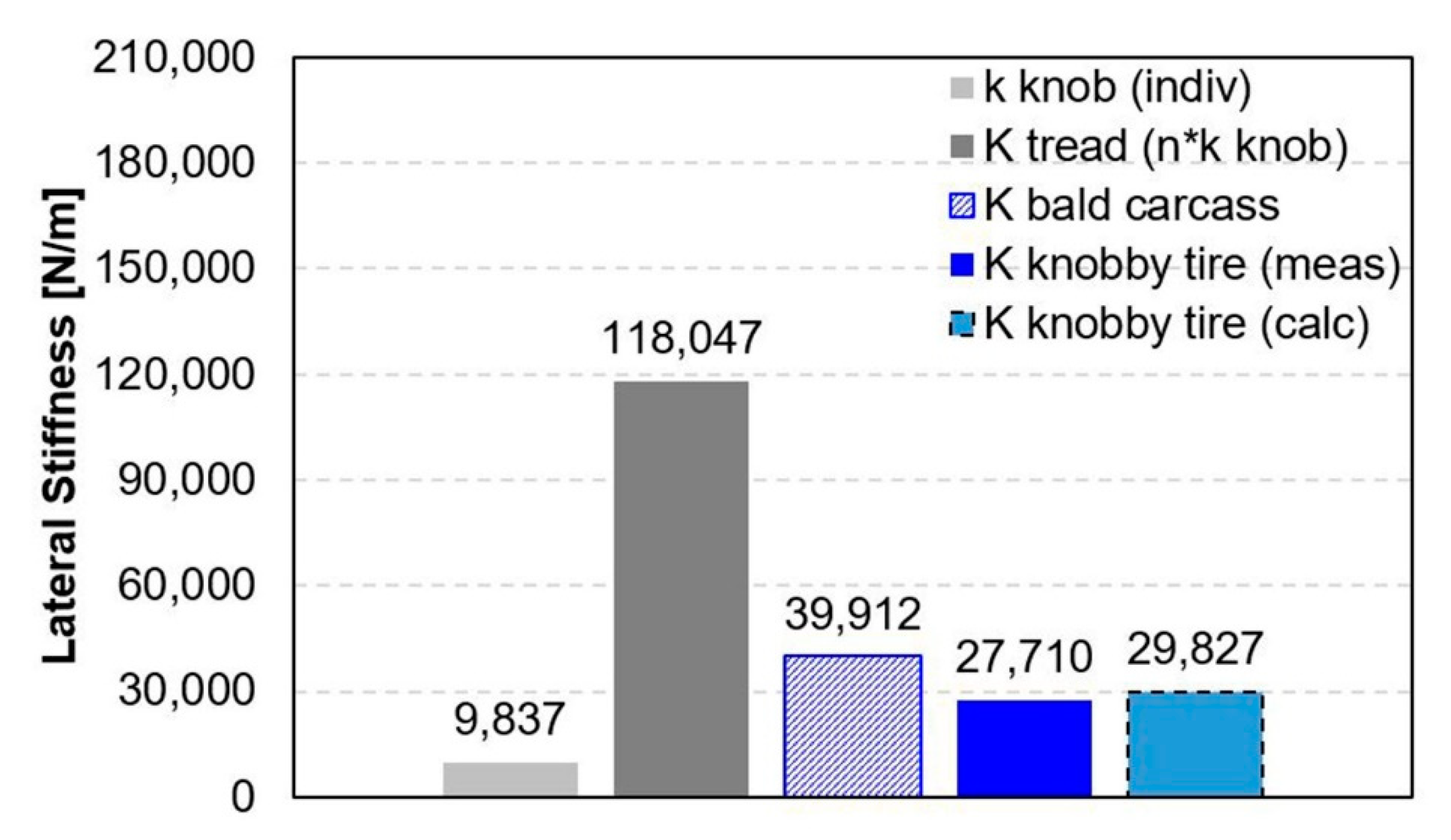
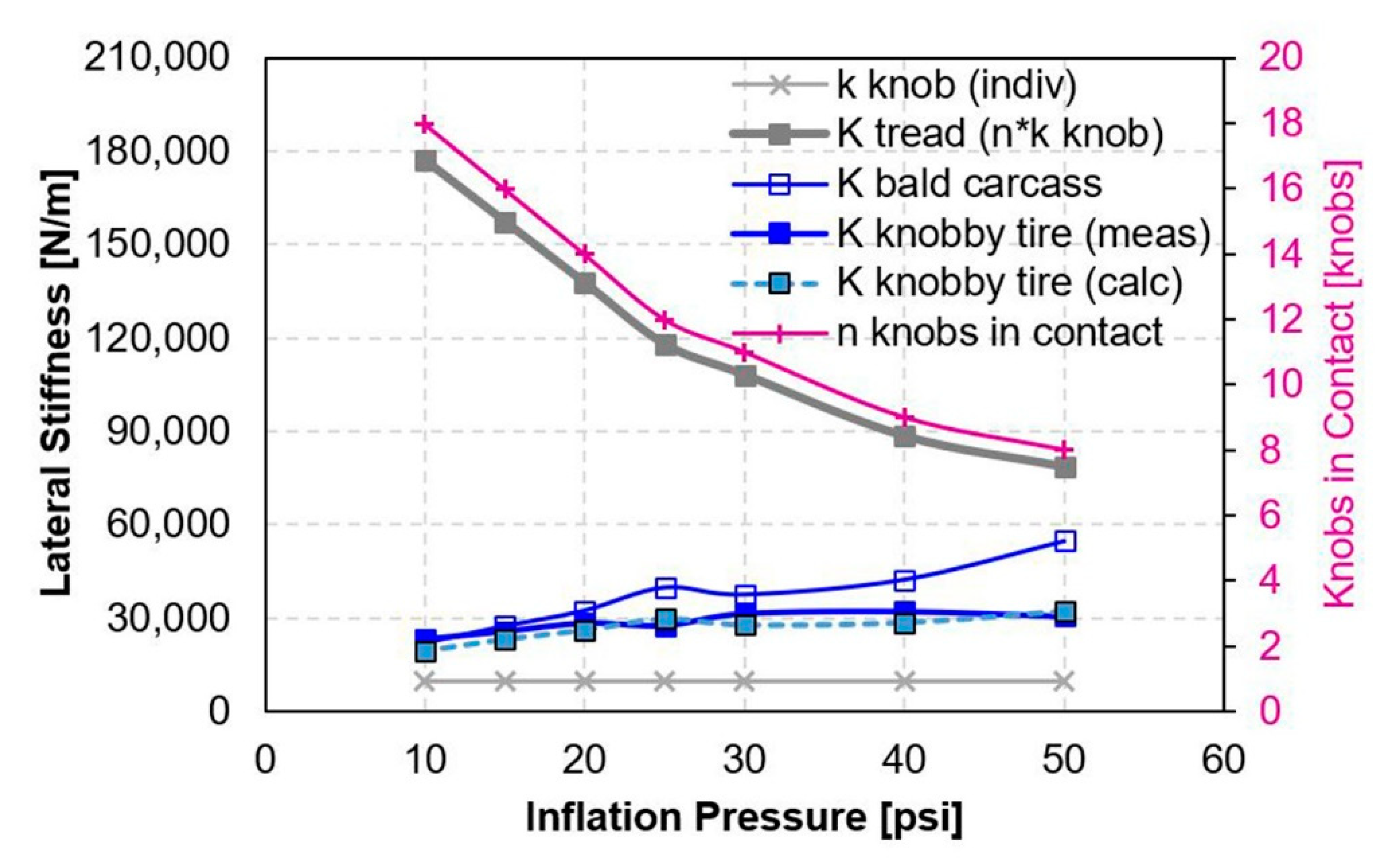
3.1.4. Static Lateral and Radial Stiffness
3.2. Effect of Tread Knobs
3.2.1. Cross-Sectional Profiles
3.2.2. Footprints
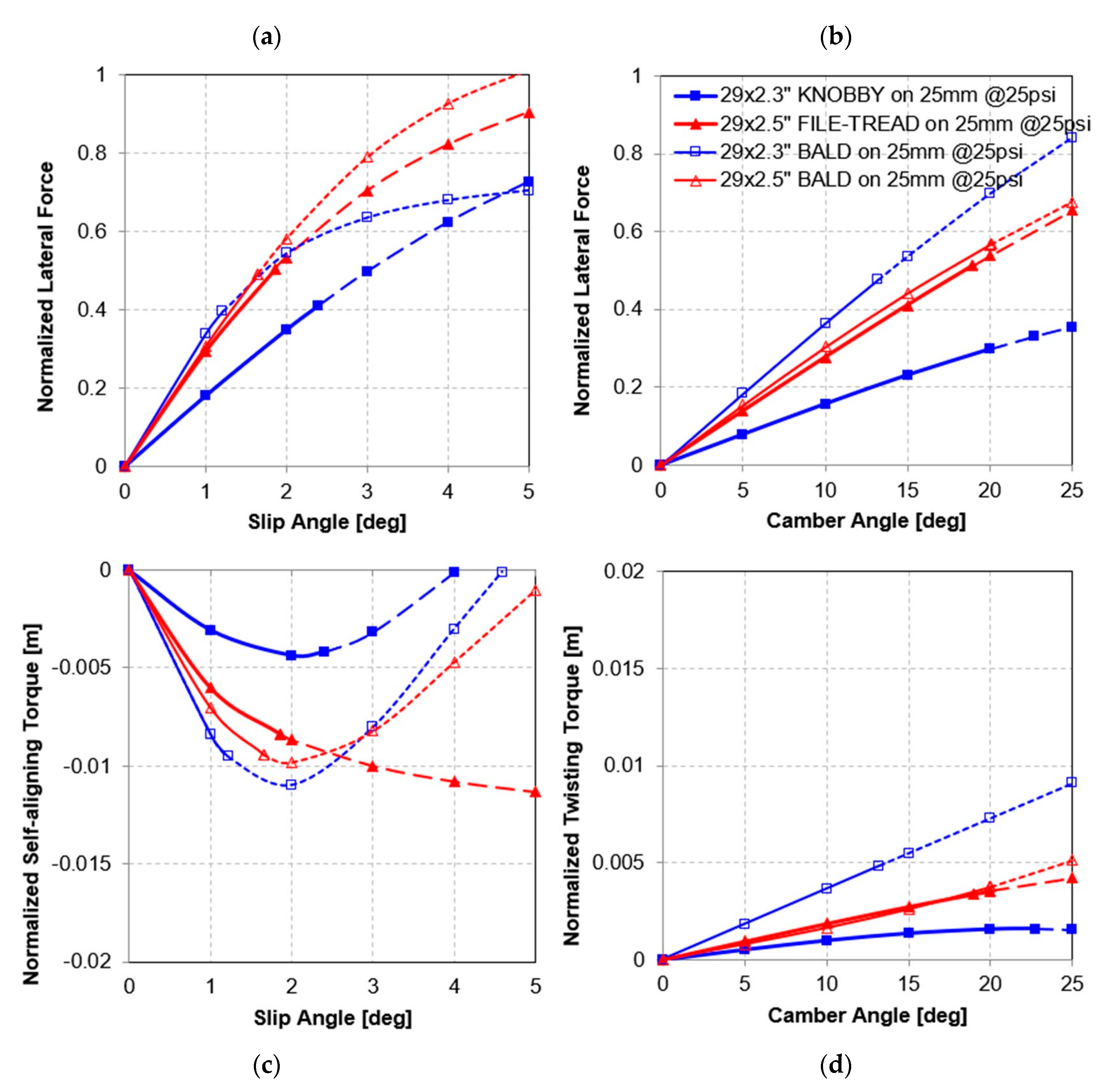
3.2.3. Forces and Moments
3.2.4. Static Lateral Stiffness
3.3. Effect of Inflation Pressures and Rim Width
3.3.1. Footprints
3.3.2. Forces and Moments
3.3.3. Static Lateral Stiffness
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Statista: Number of Participants in Mountain/Non-Paved Surface Bicycling in the United States from 2011 to 2018 (in Millions). Available online: https://www.statista.com/statistics/763737/mountain-non-paved-surface-bicycling-participants-us/ (accessed on 3 April 2019).
- Statista: Bicycle Sales in the United States by Category of Bike in 2017. Available online: https://www.statista.com/statistics/236150/us-retail-sales-of-bicycles-and-supplies/J.Y. (accessed on 3 April 2019).
- Dressel, A. Measuring and Modeling the Mechanical Properties of Bicycle Tires. Ph.D. Thesis, The University of Wisconsin-Milwaukee, Milwaukee, WI, USA, 2013. [Google Scholar]
- Pacejka, H.B. Tyre and Vehicle Dynamics, 2nd ed.; Butterworth and Heinemann: Oxford, UK, 2006. [Google Scholar]
- FastBike 6.3.1 User Manual; Dynamotion: Padova, Italy, 2006; p. 36.
- Doria, A.; Tognazzo, M.; Cusimano, G.; Bulsink, V.; Cooke, A.; Koopman, B. Identification of the mechanical properties of bicycle tyres for modelling of bicycle dynamics. Veh. Syst. Dyn. 2013, 51, 405–420. [Google Scholar] [CrossRef]
- Cossalter, V. Motorcycle Dynamics, 2nd ed.; Lulu Press: Morrisville, NC, USA, 2006. [Google Scholar]
- Gent, A.; Walter, J. The Pneumatic Tire; NHTSA: Washington, DC, USA, 2006. [Google Scholar]
- Cossalter, V.; Doria, A. The relation between contact path geometry and the mechanical properties of motorcycle tires. Veh. Syst. Dyn. 2005, 43, 156–167. [Google Scholar] [CrossRef]
- Wallaschek, J.; Wies, B. Tyre tread-block friction: Modelling, simulation and experimental validation. Veh. Syst. Dyn. 2013, 51, 1017–1026. [Google Scholar] [CrossRef]
- Jansen, S.; Schmeitz, A.; Akkermans, L. Study on Some Safety-Related Aspects of Tyre Use; European Commission: Brussels, Belgium, 2014. [Google Scholar]
- Klug, S.; Moia, A.; Verhagen, A.; Georges, D.; Savaresi, S. Control-Oriented modeling and validation of bicycle curve dynamics with focus on lateral tire parameters. In Proceedings of the 2017 IEEE Conference on Control Technology and Applications (CCTA), Mauna Lani, HI, USA, 27–30 August 2017; pp. 86–93. [Google Scholar]



| Tire Size (in) | ETRTO (mm) |
|---|---|
| 29 × 2.3” | 58–622 |
| 29 × 2.5” | 63–622 |
| 29 × 3.0” | 76–622 |
| 27.5 × 2.8” | 71–584 |
| 26 × 4.0” | 102–559 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dressel, A.; Sadauckas, J. Characterization and Modelling of Various Sized Mountain Bike Tires and the Effects of Tire Tread Knobs and Inflation Pressure. Appl. Sci. 2020, 10, 3156. https://doi.org/10.3390/app10093156
Dressel A, Sadauckas J. Characterization and Modelling of Various Sized Mountain Bike Tires and the Effects of Tire Tread Knobs and Inflation Pressure. Applied Sciences. 2020; 10(9):3156. https://doi.org/10.3390/app10093156
Chicago/Turabian StyleDressel, Andrew, and James Sadauckas. 2020. "Characterization and Modelling of Various Sized Mountain Bike Tires and the Effects of Tire Tread Knobs and Inflation Pressure" Applied Sciences 10, no. 9: 3156. https://doi.org/10.3390/app10093156
APA StyleDressel, A., & Sadauckas, J. (2020). Characterization and Modelling of Various Sized Mountain Bike Tires and the Effects of Tire Tread Knobs and Inflation Pressure. Applied Sciences, 10(9), 3156. https://doi.org/10.3390/app10093156