ProLSFEO-LDL: Prototype Selection and Label- Specific Feature Evolutionary Optimization for Label Distribution Learning
Abstract
1. Introduction
2. Preliminaries
2.1. Foundations of Label Distribution Learning
2.2. Prototype Selection and Label-Specific Feature Learning
2.3. Evolutionary Optimization
3. ProLSFEO-LDL: Protoype Selection and Label-Specific Feature Evolutionary Optimization for Label Distribution Learning
| Algorithm 1: ProLSFEO-LDL: Prototype selection and Label-Specific Feature Evolutionary Optimization for Label Distribution Learning |
 |
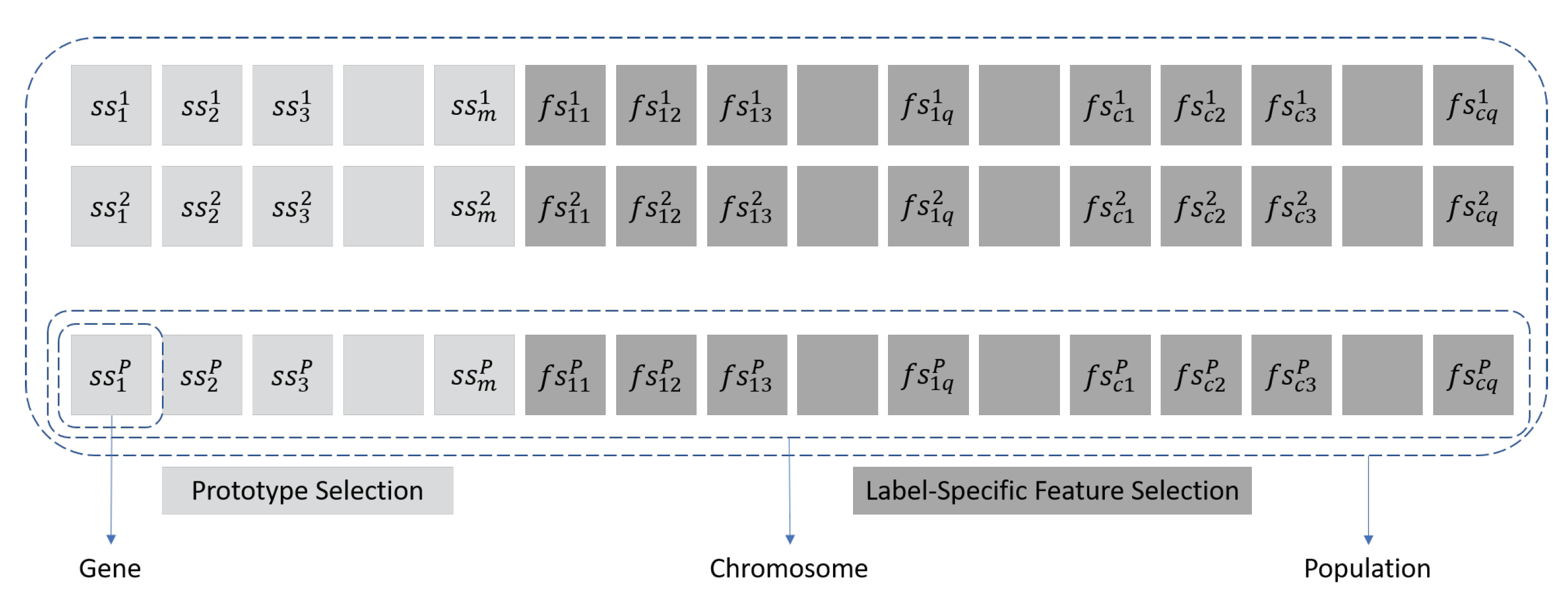
3.1. Representation of Individuals
3.2. Crossover
3.3. Fitness Function
- Create a subset of instances: the selected prototypes are coded in the first m genes of the chromosome. We create a subset T by keeping only the elements of the original training set S which have an associated gene value = 1.
- Prediction phase: we use the subset T as the training set for AA-kNN. The prediction is then computed over a set merged from the test predictions of a 10-fold cross validation set (10-fcv) created from the original training set S.
- Evaluation phase: in order to measure the fitness of the chromosome, we calculate the distance between the predicted label distribution and the real label distribution D using the Kullback–Leibler divergence formula , where and are the description degree of the particular jth label. In our case the fitness of the chromosome directly matchs with the KL divergence.
3.4. Reinitialization
4. Experimental Framework
4.1. Datasets
4.2. Evaluation Measure Selection
- Chebyshev Distance: is a metric defined on a vector space where the distance between two vectors is the greatest of their differences along any coordinate dimension.
- Clark Distance: the Clark distance also called coefficient of divergence is the squared root of half of the divergence distance.
- Canberra Metric: is a numerical measure of the distance between pairs of points in a vector space. It is a weighted version of Manhattan distance. The Canberra distance is a metric function often used for data scattered around an origin.
- Kullback–Leibler Divergence: which is closely related to relative entropy, information divergence, and information for discrimination, is a non-symmetric measure of the difference between two probability distributions and . Specifically, the Kullback–Leibler divergence of from is a measure of the information lost when is used to approximate .
- Cosine coefficient: is a metric used to measure how similar two non-zero vectors are irrespective of their size. It measures the cosine of the angle between two vectors projected in a multidimensional space. The smaller the angle, higher the cosine similarity.
- Intersection similarity: has its largest value, 1, when all the terms of the first probability distribution are identical to the corresponding terms of the second probability distribution. Otherwise, the similarity is less than 1. In the extreme case, when both distributions are very different, then the similarity will be close to 0.
4.3. Experimental Setting
5. Results and Analysis
- The results of the different measures shown in Table 4 highlights the best ranking of ProLSFEO-LDL in the large majority of the datasets and measures.
- The Wilcoxon Signed Ranks test corroborates the significance of the differences between our approach and AA-kNN. As we can see in Table 5, all the hypotheses of equivalence are rejected with small p-values.
- With regard to the Bayesian Sign test, Figure 2 graphically represent the statistical significance in terms of precision between ProLSFEO-LDL and AA-kNN. The following heat-maps clearly indicate the significant superiority of ProLSFEO-LDL, as the computed distributions are always located in the right region.
6. Conclusions
- Complement the experimental analysis by dealing with larger datasets (Big Data). To this end, we will complement the current proposal with some of the big data reduction techniques presented in [71].
- The experimental settings use the AA-KNN learner to measure the quality of the solution applied over the pre-processed dataset. Other more powerful LDL learners could be considered for this task but they must previously be adapted to support the label-specific feature selection. With this we will be able to carry out more adequate comparisons with state-of-the-art LDL methods like LDLFs proposed in [17] or StructRF [20].
- Another interesting study that we will undertake is how the presence of noise at the label side can affect the performance. In real scenarios the data gathering is often an automatic procedure that can lead to incorrect sample labelling. It would be interesting to inject some artificial noise to the training labels in order to check the robustness of the implemented approach.
Author Contributions
Funding
Conflicts of Interest
References
- Barutcuoglu, Z.; Schapire, R.E.; Troyanskaya, O.G. Hierarchical multi-label prediction of gene function. Bioinformatics 2006, 22, 830–836. [Google Scholar] [CrossRef] [PubMed]
- Boutell, M.R.; Luo, J.; Shen, X.; Brown, C.M. Learning multi-label scene classification. Pattern Recognit. 2004, 37, 1757–1771. [Google Scholar] [CrossRef]
- Gibaja, E.; Ventura, S. A tutorial on multilabel learning. ACM Comput. Surv. (CSUR) 2015, 47, 1–38. [Google Scholar] [CrossRef]
- Herrera, F.; Charte, F.; Rivera, A.J.; Del Jesus, M.J. Multilabel Classification; Springer: Berlin/Heidelberg, Germany, 2016; pp. 17–31. [Google Scholar]
- Triguero, I.; Vens, C. Labelling strategies for hierarchical multi-label classification techniques. Pattern Recognit. 2016, 56, 170–183. [Google Scholar] [CrossRef]
- Moyano, J.M.; Gibaja, E.L.; Cios, K.J.; Ventura, S. Review of ensembles of multi-label classifiers: Models, experimental study and prospects. Inf. Fusion 2018, 44, 33–45. [Google Scholar] [CrossRef]
- Eisen, M.B.; Spellman, P.T.; Brown, P.O.; Botstein, D. Cluster analysis and display of genome-wide expression patterns. Proc. Natl. Acad. Sci. USA 1998, 95, 14863–14868. [Google Scholar] [CrossRef]
- Geng, X.; Yin, C.; Zhou, Z.H. Facial age estimation by learning from label distributions. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 2401–2412. [Google Scholar] [CrossRef]
- Geng, X. Label distribution learning. IEEE Trans. Knowl. Data Eng. 2016, 28, 1734–1748. [Google Scholar] [CrossRef]
- Geng, X.; Hou, P. Pre-release prediction of crowd opinion on movies by label distribution learning. In Proceedings of the Twenty-Fourth International Joint Conference on Artificial Intelligence, Buenos Aires, Argentina, 25–31 July 2015; pp. 3511–3517. [Google Scholar]
- Zhang, Z.; Wang, M.; Geng, X. Crowd counting in public video surveillance by label distribution learning. Neurocomputing 2015, 166, 151–163. [Google Scholar] [CrossRef]
- Ren, Y.; Geng, X. Sense Beauty by Label Distribution Learning. In Proceedings of the International Joint Conferences on Artificial Intelligence, Melbourne, Australia, 19–25 August 2017; pp. 2648–2654. [Google Scholar]
- Yang, J.; She, D.; Sun, M. Joint Image Emotion Classification and Distribution Learning via Deep Convolutional Neural Network. In Proceedings of the International Joint Conferences on Artificial Intelligence, Melbourne, Australia, 19–25 August 2017; pp. 3266–3272. [Google Scholar]
- Xue, D.; Hong, Z.; Guo, S.; Gao, L.; Wu, L.; Zheng, J.; Zhao, N. Personality recognition on social media with label distribution learning. IEEE Access 2017, 5, 13478–13488. [Google Scholar] [CrossRef]
- Xu, L.; Chen, J.; Gan, Y. Head pose estimation using improved label distribution learning with fewer annotations. Multimed. Tools Appl. 2019, 78, 19141–19162. [Google Scholar] [CrossRef]
- Zheng, X.; Jia, X.; Li, W. Label distribution learning by exploiting sample correlations locally. In Proceedings of the 32nd AAAI Conference on Artificial Intelligence, AAAI 2018, New Orleans, LO, USA, 2–7 February 2018; pp. 4556–4563. [Google Scholar]
- Shen, W.; Zhao, K.; Guo, Y.; Yuille, A.L. Label distribution learning forests. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, US, 4–9 December 2017; pp. 834–843. [Google Scholar]
- Gao, B.B.; Xing, C.; Xie, C.W.; Wu, J.; Geng, X. Deep label distribution learning with label ambiguity. IEEE Trans. Image Process. 2017, 26, 2825–2838. [Google Scholar] [CrossRef]
- Xing, C.; Geng, X.; Xue, H. Logistic boosting regression for label distribution learning. In Proceedings of the IEEE conference on computer vision and pattern recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 4489–4497. [Google Scholar]
- Chen, M.; Wang, X.; Feng, B.; Liu, W. Structured random forest for label distribution learning. Neurocomputing 2018, 320, 171–182. [Google Scholar] [CrossRef]
- Arrieta, A.B.; Díaz-Rodríguez, N.; Del Ser, J.; Bennetot, A.; Tabik, S.; Barbado, A.; García, S.; Gil-López, S.; Molina, D.; Benjamins, R.; et al. Explainable Artificial Intelligence (XAI): Concepts, taxonomies, opportunities and challenges toward responsible AI. Inf. Fusion 2020, 58, 82–115. [Google Scholar] [CrossRef]
- García, S.; Luengo, J.; Herrera, F. Data Preprocessing in Data Mining; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Liu, H.; Motoda, H. On issues of instance selection. Data Min. Knowl. Discov. 2002, 6, 115–130. [Google Scholar] [CrossRef]
- Garcia, S.; Derrac, J.; Cano, J.; Herrera, F. Prototype selection for nearest neighbor classification: Taxonomy and empirical study. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 417–435. [Google Scholar] [CrossRef]
- Tang, J.; Alelyani, S.; Liu, H. Feature selection for classification: A review. In Data Classification: Algorithms and Applications; CRC Press: Boca Raton, FL, USA, 2014; pp. 37–64. [Google Scholar]
- Kanj, S.; Abdallah, F.; Denoeux, T.; Tout, K. Editing training data for multi-label classification with the k-nearest neighbor rule. Pattern Anal. Appl. 2016, 19, 145–161. [Google Scholar] [CrossRef]
- Arnaiz-González, Á.; Díez-Pastor, J.F.; Rodríguez, J.J.; García-Osorio, C. Local sets for multi-label instance selection. Appl. Soft Comput. 2018, 68, 651–666. [Google Scholar] [CrossRef]
- Charte, F.; Rivera, A.J.; del Jesus, M.J.; Herrera, F. REMEDIAL-HwR: Tackling multilabel imbalance through label decoupling and data resampling hybridization. Neurocomputing 2019, 326, 110–122. [Google Scholar] [CrossRef]
- Zhang, M.L.; Wu, L. Lift: Multi-label learning with label-specific features. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 37, 107–120. [Google Scholar] [CrossRef]
- Huang, J.; Li, G.; Huang, Q.; Wu, X. Learning label-specific features and class-dependent labels for multi-label classification. IEEE Trans. Knowl. Data Eng. 2016, 28, 3309–3323. [Google Scholar] [CrossRef]
- Ren, T.; Jia, X.; Li, W.; Chen, L.; Li, Z. Label distribution learning with label-specific features. In Proceedings of the 28th International Joint Conference on Artificial Intelligence, Macao, China, 10–16 August 2019; pp. 3318–3324. [Google Scholar]
- Zhou, Z.H.; Yu, Y.; Qian, C. Evolutionary Learning: Advances in Theories and Algorithms; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Derrac, J.; García, S.; Molina, D.; Herrera, F. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evol. Comput. 2011, 1, 3–18. [Google Scholar] [CrossRef]
- Benavoli, A.; Corani, G.; Demšar, J.; Zaffalon, M. Time for a change: A tutorial for comparing multiple classifiers through Bayesian analysis. J. Mach. Learn. Res. 2017, 18, 2653–2688. [Google Scholar]
- Carrasco, J.; García, S.; Rueda, M.; Das, S.; Herrera, F. Recent trends in the use of statistical tests for comparing swarm and evolutionary computing algorithms: Practical guidelines and a critical review. Swarm Evol. Comput. 2020, 54, 100665. [Google Scholar] [CrossRef]
- Fernández-Delgado, M.; Cernadas, E.; Barro, S.; Amorim, D. Do we need hundreds of classifiers to solve real world classification problems? J. Mach. Learn. Res. 2014, 15, 3133–3181. [Google Scholar]
- Aha, D.W.; Kibler, D.; Albert, M.K. Instance-based learning algorithms. Mach. Learn. 1991, 6, 37–66. [Google Scholar] [CrossRef]
- Zhai, Y.; Dai, J.; Shi, H. Label Distribution Learning Based on Ensemble Neural Networks. In Proceedings of the International Conference on Neural Information Processing, Siem Reap, Cambodia, 13–16 December 2018; pp. 593–602. [Google Scholar]
- Kontschieder, P.; Fiterau, M.; Criminisi, A.; Rota Bulo, S. Deep neural decision forests. In Proceedings of the IEEE international conference on computer vision, Santiago, Chile, 7–13 December 2015; pp. 1467–1475. [Google Scholar]
- Wang, K.; Geng, X. Binary Coding based Label Distribution Learning. In Proceedings of the International Joint Conferences on Artificial Intelligence, Stockholm, Sweden, 13–19 July 2018; pp. 2783–2789. [Google Scholar]
- Wang, K.; Geng, X. Discrete binary coding based label distribution learning. In Proceedings of the 28th International Joint Conference on Artificial Intelligence, Macao, China, 10–16 August 2019; pp. 3733–3739. [Google Scholar]
- Wang, J.; Geng, X. Classification with label distribution learning. In Proceedings of the 28th International Joint Conference on Artificial Intelligence, Macao, China, 10–16 August 2019; pp. 3712–3718. [Google Scholar]
- Wang, Y.; Dai, J. Label Distribution Feature Selection Based on Mutual Information in Fuzzy Rough Set Theory. In Proceedings of the 2019 International Joint Conference on Neural Networks (IJCNN), Budapest, Hungary, 14–19 July 2019; pp. 1–2. [Google Scholar]
- Millán-Giraldo, M.; García, V.; Sánchez, J. Instance Selection Methods and Resampling Techniques for Dissimilarity Representation with Imbalanced Data Sets. In Pattern Recognition-Applications and Methods; Springer: Berlin/Heidelberg, Germany, 2013; pp. 149–160. [Google Scholar]
- Ramírez-Gallego, S.; Krawczyk, B.; García, S.; Woźniak, M.; Herrera, F. A survey on data preprocessing for data stream mining: Current status and future directions. Neurocomputing 2017, 239, 39–57. [Google Scholar] [CrossRef]
- Song, Y.; Liang, J.; Lu, J.; Zhao, X. An efficient instance selection algorithm for k nearest neighbor regression. Neurocomputing 2017, 251, 26–34. [Google Scholar] [CrossRef]
- Cano, J.R.; García, S.; Herrera, F. Subgroup discover in large size data sets preprocessed using stratified instance selection for increasing the presence of minority classes. Pattern Recognit. Lett. 2008, 29, 2156–2164. [Google Scholar] [CrossRef]
- García, V.; Sánchez, J.S.; Ochoa-Ortiz, A.; López-Najera, A. Instance Selection for the Nearest Neighbor Classifier: Connecting the Performance to the Underlying Data Structure. In Proceedings of the Iberian Conference on Pattern Recognition and Image Analysis, Madrid, Spain, 1–4 July 2019; pp. 249–256. [Google Scholar]
- Cano, J.R.; Aljohani, N.R.; Abbasi, R.A.; Alowidbi, J.S.; Garcia, S. Prototype selection to improve monotonic nearest neighbor. Eng. Appl. Artif. Intell. 2017, 60, 128–135. [Google Scholar] [CrossRef]
- Cruz, R.M.; Sabourin, R.; Cavalcanti, G.D. Analyzing different prototype selection techniques for dynamic classifier and ensemble selection. In Proceedings of the 2017 International Joint Conference on Neural Networks (IJCNN), Anchorage, AK, USA, 14–19 May 2017; pp. 3959–3966. [Google Scholar]
- Zhang, J.; Li, C.; Cao, D.; Lin, Y.; Su, S.; Dai, L.; Li, S. Multi-label learning with label-specific features by resolving label correlations. Knowl. Based Syst. 2018, 159, 148–157. [Google Scholar] [CrossRef]
- Khan, S.S.; Quadri, S.; Peer, M. Genetic Algorithm for Biomarker Search Problem and Class Prediction. Int. J. Intell. Syst. Appl. 2016, 8, 47. [Google Scholar] [CrossRef]
- Ali, A.F.; Tawhid, M.A. A hybrid particle swarm optimization and genetic algorithm with population partitioning for large scale optimization problems. Ain Shams Eng. J. 2017, 8, 191–206. [Google Scholar] [CrossRef]
- Eshelman, L.J. The CHC adaptive search algorithm: How to have safe search when engaging in nontraditional genetic recombination. In Foundations of Genetic Algorithms; Elsevier: Amsterdam, The Netherlands, 1991; Volume 1, pp. 265–283. [Google Scholar]
- García, S.; Cano, J.R.; Herrera, F. A memetic algorithm for evolutionary prototype selection: A scaling up approach. Pattern Recognit. 2008, 41, 2693–2709. [Google Scholar] [CrossRef]
- Garcia, S.; Cano, J.R.; Bernado-Mansilla, E.; Herrera, F. Diagnose effective evolutionary prototype selection using an overlapping measure. Int. J. Pattern Recognit. Artif. Intell. 2009, 23, 1527–1548. [Google Scholar] [CrossRef]
- García, S.; Herrera, F. Evolutionary undersampling for classification with imbalanced datasets: Proposals and taxonomy. Evol. Comput. 2009, 17, 275–306. [Google Scholar] [CrossRef]
- Vluymans, S.; Triguero, I.; Cornelis, C.; Saeys, Y. EPRENNID: An evolutionary prototype reduction based ensemble for nearest neighbor classification of imbalanced data. Neurocomputing 2016, 216, 596–610. [Google Scholar] [CrossRef]
- Kordos, M.; Arnaiz-González, Á.; García-Osorio, C. Evolutionary prototype selection for multi-output regression. Neurocomputing 2019, 358, 309–320. [Google Scholar] [CrossRef]
- Yin, J.; Tao, T.; Xu, J. A multi-label feature selection algorithm based on multi-objective optimization. In Proceedings of the 2015 International Joint Conference on Neural Networks (IJCNN), Killarney, Ireland, 12–16 July 2015; pp. 1–7. [Google Scholar]
- Lee, J.; Kim, D.W. Memetic feature selection algorithm for multi-label classification. Inf. Sci. 2015, 293, 80–96. [Google Scholar] [CrossRef]
- Zhang, Y.; Gong, D.W.; Rong, M. Multi-objective differential evolution algorithm for multi-label feature selection in classification. In Proceedings of the International Conference in Swarm Intelligence, Beijing, China, 25–28 June 2015; pp. 339–345. [Google Scholar]
- Khan, M.; Ekbal, A.; Mencía, E.; Fürnkranz, J. Multi-objective Optimisation-Based Feature Selection for Multi-label Classification. In Proceedings of the International Conference on Applications of Natural Language to Information Systems, Paris, France, 13–15 June 2017; pp. 38–41. [Google Scholar] [CrossRef]
- Lyons, M.; Akamatsu, S.; Kamachi, M.; Gyoba, J. Coding facial expressions with gabor wavelets. In Proceedings of the Third IEEE international conference on automatic face and gesture recognition, Nara, Japan, 14–16 April 1998; pp. 200–205. [Google Scholar]
- Yin, L.; Wei, X.; Sun, Y.; Wang, J.; Rosato, M.J. A 3D facial expression database for facial behavior research. In Proceedings of the 7th international conference on automatic face and gesture recognition (FGR06), Los Alamitos, CA, USA, 10–12 April 2006; pp. 211–216. [Google Scholar]
- Ahonen, T.; Hadid, A.; Pietikainen, M. Face description with local binary patterns: Application to face recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 2037–2041. [Google Scholar] [CrossRef]
- Geng, X.; Luo, L. Multilabel ranking with inconsistent rankers. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 3742–3747. [Google Scholar]
- Cha, S.H. Comprehensive survey on distance/similarity measures between probability density functions. Int. J. Math. Model. Methods Appl. Sci. 2007, 1, 300–307. [Google Scholar]
- Triguero, I.; González, S.; Moyano, J.M.; García, S.; Alcalá-Fdez, J.; Luengo, J.; Fernández, A.; del Jesús, M.J.; Sánchez, L.; Herrera, F. KEEL 3.0: An Open Source Software for Multi-Stage Analysis in Data Mining. Int. J. Comput. Intell. Syst. 2017, 10, 1238–1249. [Google Scholar] [CrossRef]
- Carrasco, J.; García, S.; del Mar Rueda, M.; Herrera, F. rnpbst: An R package covering non-parametric and bayesian statistical tests. In Proceedings of the International Conference on Hybrid Artificial Intelligence Systems, La Rioja, Spain, 21–23 June 2017; pp. 281–292. [Google Scholar]
- Luengo, J.; García-Gil, D.; Ramírez-Gallego, S.; García, S.; Herrera, F. Big Data Preprocessing: Enabling Smart Data; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]

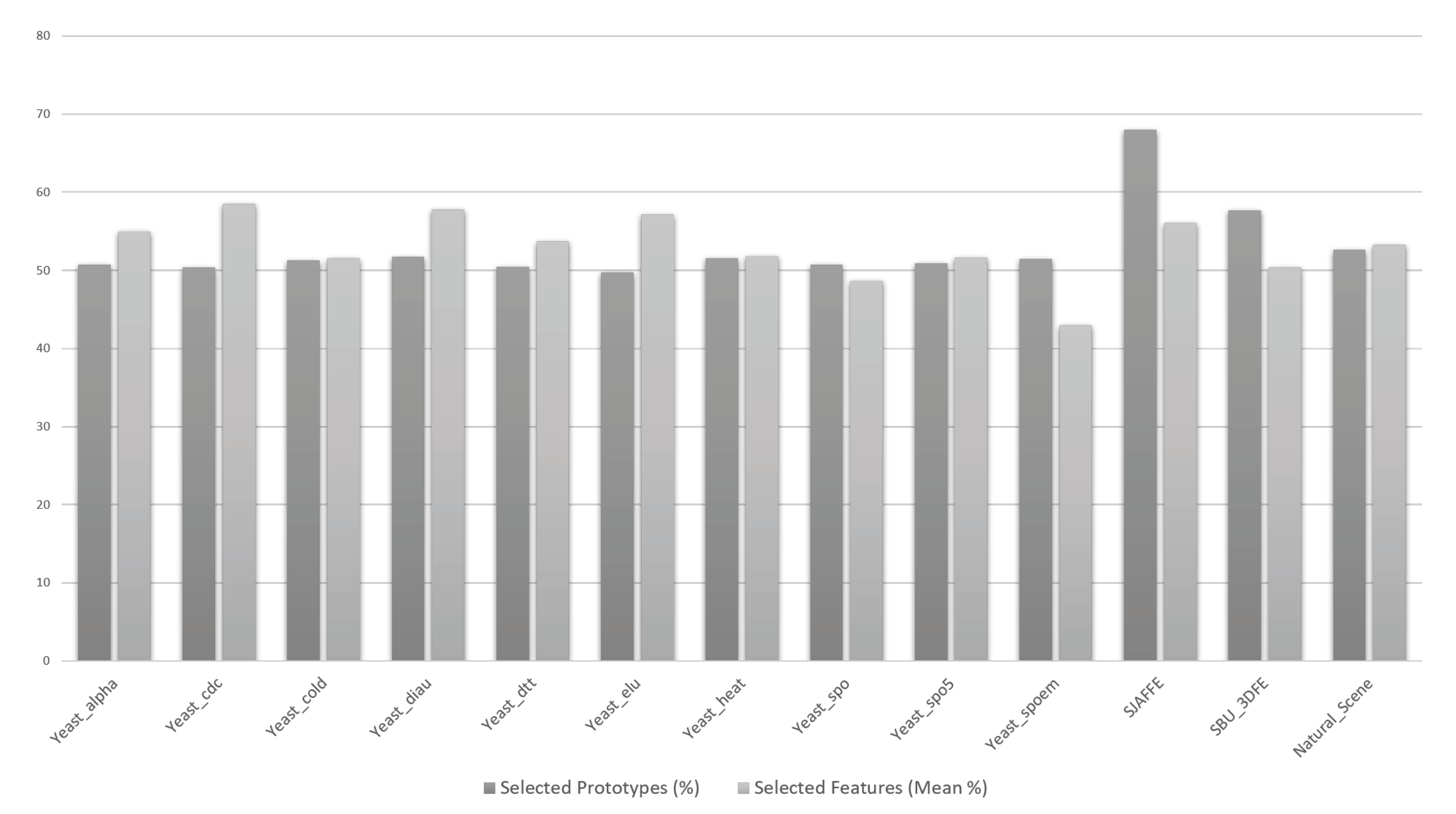
| No. | Datasets | Examples (m) | Features (q) | Labels (c) |
|---|---|---|---|---|
| 1 | Yeast_alpha | 2465 | 24 | 18 |
| 2 | Yeast_cdc | 2465 | 24 | 15 |
| 3 | Yeast_cold | 2465 | 24 | 4 |
| 4 | Yeast_diau | 2465 | 24 | 7 |
| 5 | Yeast_dtt | 2465 | 24 | 4 |
| 6 | Yeast_elu | 2465 | 24 | 14 |
| 7 | Yeast_heat | 2465 | 24 | 6 |
| 8 | Yeast_spo | 2465 | 24 | 6 |
| 9 | Yeast_spo5 | 2465 | 24 | 3 |
| 10 | Yeast_spoem | 2465 | 24 | 2 |
| 11 | SJAFFE | 213 | 243 | 6 |
| 12 | SBU_3DFE | 2500 | 243 | 6 |
| 13 | Natural_Scene | 2000 | 294 | 9 |
| Name | Formula |
|---|---|
| Chebyshev(Cheby)↓ | |
| Clark↓ | |
| Canberra(Can)↓ | |
| Kullback–Leibler(KL)↓ | |
| Cosine(Cos)↑ | |
| Intersection(Inter)↑ |
| Algorithm | Parameter | Description | Value |
|---|---|---|---|
| ProLSFEO-LDL | N | Population size | 100 |
| G | Number of generations | 500 | |
| t | Threshold | 10 | |
| k | Number of selected neighbors | 4 | |
| in AA-kNN used for fitness function | |||
| AA-kNN | k | Number of selected neighbors | 4 |
| Cheby ↓ | Clark ↓ | Can ↓ | ||||
|---|---|---|---|---|---|---|
| Dataset | AA-kNN | ProLSFEO-LDL | AA-kNN | ProLSFEO-LDL | AA-kNN | ProLSFEO-LDL |
| Yeast_alpha | 0.0148 ± 0.0007 | 0.0145 ± 0.0007 | 0.2321 ± 0.0112 | 0.2280 ± 0.0111 | 0.7577 ± 0.0372 | 0.7451 ± 0.0376 |
| Yeast_cdc | 0.0177 ± 0.0010 | 0.0174 ± 0.0009 | 0.2375 ± 0.0134 | 0.2316 ± 0.0129 | 0.7179 ± 0.0395 | 0.6972 ± 0.0395 |
| Yeast_cold | 0.0554 ± 0.0021 | 0.0545 ± 0.0015 | 0.1509 ± 0.0070 | 0.1485 ± 0.0050 | 0.2611 ± 0.0129 | 0.2563 ± 0.0090 |
| Yeast_diau | 0.0393 ± 0.0009 | 0.0397 ± 0.0013 | 0.2122 ± 0.0042 | 0.2125 ± 0.0055 | 0.4560 ± 0.0109 | 0.4528 ± 0.0126 |
| Yeast_dtt | 0.0393 ± 0.0016 | 0.0381 ± 0.0013 | 0.1068 ± 0.0045 | 0.1035 ± 0.0036 | 0.1836 ± 0.0075 | 0.1778 ± 0.0050 |
| Yeast_elu | 0.0177 ± 0.0005 | 0.0174 ± 0.0004 | 0.2182 ± 0.0048 | 0.2137 ± 0.0048 | 0.6444 ± 0.0155 | 0.6285 ± 0.0137 |
| Yeast_heat | 0.0451 ± 0.0012 | 0.0445 ± 0.0007 | 0.1955 ± 0.0044 | 0.1928 ± 0.0035 | 0.3924 ± 0.0096 | 0.3867 ± 0.0078 |
| Yeast_spo | 0.0643 ± 0.0024 | 0.0637 ± 0.0030 | 0.2715 ± 0.0112 | 0.2690 ± 0.0124 | 0.5594 ± 0.0232 | 0.5499 ± 0.0248 |
| Yeast_spo5 | 0.0962 ± 0.0043 | 0.0951 ± 0.0052 | 0.1933 ± 0.0099 | 0.1914 ± 0.0110 | 0.2972 ± 0.0145 | 0.2938 ± 0.0169 |
| Yeast_spoem | 0.0924 ± 0.0036 | 0.0887 ± 0.0036 | 0.1374 ± 0.0053 | 0.1320 ± 0.0055 | 0.1913 ± 0.0074 | 0.1837 ± 0.0076 |
| SJAFFE | 0.1155 ± 0.0180 | 0.1088 ± 0.0090 | 0.4137 ± 0.0489 | 0.4070 ± 0.0285 | 0.8527 ± 0.0962 | 0.8359 ± 0.0624 |
| SBU_3DFE | 0.1350 ± 0.0048 | 0.1272 ± 0.0056 | 0.4255 ± 0.0134 | 0.4068 ± 0.0146 | 0.8746 ± 0.0290 | 0.8332 ± 0.0313 |
| Natural_Scene | 0.3168 ± 0.0081 | 0.3046 ± 0.0118 | 1.8253 ± 0.0343 | 1.9161 ± 0.0347 | 4.2609 ± 0.0866 | 4.5848 ± 0.1206 |
| Average | 0.0807 ± 0.0038 | 0.0780 ± 0.0035 | 0.3554 ± 0.0133 | 0.3579 ± 0.0118 | 0.8038 ± 0.0300 | 0.8174 ± 0.0299 |
| KL↓ | Cos↑ | Inter↑ | ||||
| Dataset | AA-kNN | ProLSFEO-LDL | AA-kNN | ProLSFEO-LDL | AA-kNN | ProLSFEO-LDL |
| Yeast_alpha | 0.0066 ± 0.0006 | 0.0064 ± 0.0006 | 0.9935 ± 0.0006 | 0.9937 ± 0.0006 | 0.9581 ± 0.0020 | 0.9588 ± 0.0021 |
| Yeast_cdc | 0.0083 ± 0.0009 | 0.0080 ± 0.0009 | 0.9920 ± 0.0008 | 0.9924 ± 0.0008 | 0.9527 ± 0.0025 | 0.9541 ± 0.0026 |
| Yeast_cold | 0.0142 ± 0.0014 | 0.0137 ± 0.0012 | 0.9866 ± 0.0012 | 0.9871 ± 0.0010 | 0.9356 ± 0.0031 | 0.9368 ± 0.0022 |
| Yeast_diau | 0.0150 ± 0.0008 | 0.0146 ± 0.0009 | 0.9862 ± 0.0008 | 0.9866 ± 0.0009 | 0.9367 ± 0.0017 | 0.9372 ± 0.0018 |
| Yeast_dtt | 0.0073 ± 0.0007 | 0.0069 ± 0.0006 | 0.9931 ± 0.0005 | 0.9934 ± 0.0004 | 0.9547 ± 0.0017 | 0.9561 ± 0.0011 |
| Yeast_elu | 0.0074 ± 0.0003 | 0.0071 ± 0.0003 | 0.9928 ± 0.0003 | 0.9932 ± 0.0003 | 0.9545 ± 0.0011 | 0.9556 ± 0.0003 |
| Yeast_heat | 0.0146 ± 0.0007 | 0.0142 ± 0.0005 | 0.9861 ± 0.0007 | 0.9865 ± 0.0005 | 0.9356 ± 0.0017 | 0.9365 ± 0.0013 |
| Yeast_spo | 0.0302 ± 0.0024 | 0.0287 ± 0.0026 | 0.9716 ± 0.0020 | 0.9730 ± 0.0023 | 0.9076 ± 0.0036 | 0.9093 ± 0.0040 |
| Yeast_spo5 | 0.0333 ± 0.0033 | 0.0315 ± 0.0030 | 0.9705 ± 0.0025 | 0.9720 ± 0.0024 | 0.9038 ± 0.0043 | 0.9049 ± 0.0052 |
| Yeast_spoem | 0.0285 ± 0.0023 | 0.0256 ± 0.0021 | 0.9754 ± 0.0019 | 0.9777 ± 0.0019 | 0.9076 ± 0.0036 | 0.9113 ± 0.0036 |
| SJAFFE | 0.0730 ± 0.0162 | 0.0672 ± 0.0091 | 0.9308 ± 0.0163 | 0.9366 ± 0.0085 | 0.8529 ± 0.0176 | 0.8572 ± 0.0106 |
| SBU_3DFE | 0.0907 ± 0.0048 | 0.0816 ± 0.0061 | 0.9118 ± 0.0047 | 0.9197 ± 0.0058 | 0.8394 ± 0.0053 | 0.8474 ± 0.0060 |
| Natural_Scene | 1.1924 ± 0.0765 | 0.9908 ± 0.0654 | 0.7043 ± 0.0137 | 0.7295 ± 0.0126 | 0.5634 ± 0.0098 | 0.5705 ± 0.0125 |
| Average | 0.1170 ± 0.0085 | 0.0997 ± 0.0072 | 0.9534 ± 0.0035 | 0.9570 ± 0.0029 | 0.8925 ± 0.0045 | 0.8951 ± 0.0041 |
| Measure | p-Value | ||
|---|---|---|---|
| Cheby | 87 | 4 | 0.0017 |
| Clark | 77 | 14 | 0.0266 |
| Can | 78 | 13 | 0.0215 |
| KL | 91 | 0 | 0.0002 |
| Cos | 91 | 0 | 0.0002 |
| Inter | 91 | 0 | 0.0002 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
González, M.; Cano, J.-R.; García, S. ProLSFEO-LDL: Prototype Selection and Label- Specific Feature Evolutionary Optimization for Label Distribution Learning. Appl. Sci. 2020, 10, 3089. https://doi.org/10.3390/app10093089
González M, Cano J-R, García S. ProLSFEO-LDL: Prototype Selection and Label- Specific Feature Evolutionary Optimization for Label Distribution Learning. Applied Sciences. 2020; 10(9):3089. https://doi.org/10.3390/app10093089
Chicago/Turabian StyleGonzález, Manuel, José-Ramón Cano, and Salvador García. 2020. "ProLSFEO-LDL: Prototype Selection and Label- Specific Feature Evolutionary Optimization for Label Distribution Learning" Applied Sciences 10, no. 9: 3089. https://doi.org/10.3390/app10093089
APA StyleGonzález, M., Cano, J.-R., & García, S. (2020). ProLSFEO-LDL: Prototype Selection and Label- Specific Feature Evolutionary Optimization for Label Distribution Learning. Applied Sciences, 10(9), 3089. https://doi.org/10.3390/app10093089






